Abstract
Within STEM (Science, Technology, Engineering, and Mathematics) education, integrating real-world problem scenarios is paramount. Within interdisciplinary education, modeling is an approach to fostering student learning and skill development in a student-centered learning environment. This study focuses on an integrated physics and mathematics course in STEM education based on modeling for first-year engineering students. The main objectives of this study are to analyze students’ models, assess the effectiveness of the pedagogical approach, and evaluate the benefits of integrative education. This study uses a Model-Application Activity as a closure for the quadratic model and extends the models built to a two-dimensional motion situation. The core activity involves a real-world experiment where students attempt to roll a ball down a ramp into a cup. While most groups successfully constructed theoretical models, only a few hit the target, highlighting the complexities of applying theoretical knowledge to real-world scenarios. The study also emphasizes the seamless integration of physics and mathematics, enriching the learning experience and making the models more robust and versatile. Despite the promising results, the study identifies a gap between theoretical understanding and practical application, suggesting the need for more hands-on activities in the curriculum. In conclusion, this study underlines the value of integrating physics and mathematics through modeling and a student-centered approach, setting the stage for future research to enhance the effectiveness of STEM education.
1. Introduction
As evidenced by prior research, model development sequences comprise a series of interconnected activities designed to cultivate a framework of generalizable and reusable relationships [1,2]. According to Gifford and Finkelstein [3] and Lo et al. [4], it is crucial for educators to tailor their instructional approaches in mathematical modeling to align with their students’ individual needs and capabilities. This involves incorporating a variety of objectives and learning tasks that offer varying levels of learning experiences. Within engineering mathematics, understanding the role of modeling in facilitating student learning and skill development is paramount [5,6,7]. In the following theoretical framework, we will address the significance and scope of student-centered learning, STEM (Science, Technology, Engineering, and Mathematics) education, and mathematical modeling through real-world problem scenarios.
2. Framework
2.1. Active Learning and STEM Education
In Latin American countries, the shift towards a more active classroom teaching paradigm has been a slower process compared to First World countries. Nevertheless, the efforts have yielded positive results, and nowadays, more institutions are joining this paradigm shift [8]. It is well-documented that active learning is a highly positive teaching alternative for students’ learning and skill development in STEM areas [9,10]. The use of strategies that promote this approach is based on peer interaction, collaborative learning, collective and individual reflection, constructive discussion, feedback, and critical thinking [11,12,13]. These strategies serve as frameworks to enhance students learning in traditionally challenging disciplines, such as physics and mathematics [14,15,16,17,18,19].
On the other hand, Quezada-Espinoza et al. [20] compared student samples from two countries, Chile and Mexico, and demonstrated in their research that in university settings that promote student-centered education, students’ perceptions of the relevance of physics to their engineering studies, and even their future as professionals, significantly improve. Beliefs and perceptions of the relevance of physics and mathematics are related to learning and can be enhanced through classroom activities [21,22,23,24]. This literature review leads us to reflect on placing the student at the center of their learning, both inside and outside the classroom, by encouraging activities that enable them to engage meaningfully.
As we have seen, several research studies focus on addressing conceptual challenges within specific disciplines. Traditionally, in STEM fields, courses are taught separately, which has led to the compartmentalization of concepts and issues, making it difficult for students (and even educators) to perceive the interconnections among these disciplines. Martín-Páez et al. [25] mention that STEM education is a cross-disciplinary field that not only integrates four disciplines but also communicates results from the teaching, as well as the cognitive, procedural, and attitudinal benefits for students. It engages students at various levels, enhancing problem-solving, analytical, and communication skills through experiential learning. Likewise, according to Zhao et al. [26], collaborative learning in STEM education enhances communication and elevates student satisfaction in teaching and learning activities. This approach promotes group discussions, facilitating the exchange of ideas among students. Furthermore, students recognize that technology-based STEM education involves complex experiments often best accomplished through collaboration to achieve success.
We acknowledge that as generations change, the methodologies employed within academic institutions should adapt accordingly. It is imperative to explore new horizons, and this endeavor is facilitated by the instructional approach we employ in our dynamic classrooms, exemplified here by using mathematical models applied to real-world scenarios. As articulated by Martynenko et al. [27], our students encompass a diverse array of learning preferences and inclinations, and it is our responsibility as educators to discern the most effective means to prepare them for the demands of the professional world.
2.2. Modeling Activities and Real-World Scenarios
Zhai’s work underscores that proficiency in scientific modeling necessitates reasoning, abstract thinking, and the ability to construct models that elucidate or forecast real-world phenomena [28]. The study revealed that high-achieving students often find representing information more challenging than grasping and applying scientific principles. This observation accentuates the need for targeted educational strategies to bolster students’ scientific competencies [28]. Complementing this, Zwickl and colleagues identified a strong correlation between students’ limited pre-existing conceptual understanding and their difficulties in model construction within physics laboratory settings [29]. In this context, Lo et al. [4] also recommended that modeling activities be carried out precisely with students with prior physics and mathematics knowledge. Incorporating data-driven modeling across diverse academic disciplines can amplify mathematical problem solving and investigative capabilities, particularly when applying engineering design principles [5,30,31,32].
For effective modeling, the scenarios must be rooted in real-world contexts. This assertion is not only accurate but also of critical importance. Real-world challenges are optimal for stimulating student motivation and creativity [4,5,6,9,33,34,35,36]. Several research studies exemplify the application of analysis to model real-life situations. For instance, Langman [37] presents a study that employs tissue engineering and regenerative medicine concepts to model real-world scenarios. Riyanto et al. [6] use a nutrition context to perform modeling activities. For their part, Peretz et al. [38] use the chocolate production process as a real scenario for modeling.
Similarly, Zhai [28] explores the dynamics of sinking stones within the framework of Newton’s laws, offering another example of research that models everyday phenomena. English [31] investigates the flow times of simulated lavas of different viscosities, providing valuable insights for students’ reasoning. Borish and colleagues [39] extend this line of inquiry by examining various physical phenomena to model real-world situations. Researchers have noted that the specific attributes of projects can substantially influence students’ approach to model construction, affecting both the necessity for and the success of such efforts [39]. Therefore, educators have the opportunity to strategically guide students toward projects with particular characteristics, customizing them to encourage desired learning outcomes.
Furthermore, students can engage in modeling activities without costly equipment, democratizing access to hands-on learning experiences [40]. Research indicates that students often encounter more significant difficulties when applying their knowledge to problem-solving tasks, a phenomenon highlighted in previous studies [28,41]. Students tend to default to mathematical concepts they are already comfortable with rather than utilizing newly acquired knowledge. This behavioral pattern highlights a significant challenge in seamlessly incorporating authentic engineering-focused curricula into existing mathematics courses, as elaborated upon in prior research [37].
In the context of the integrated Physics and Mathematics course (Fis-Mat, for its acronym in Spanish), which served as the foundational framework for the developmental sequences examined in this study, the course structure actively promotes the formulation of mathematical and physical models [41]. This pedagogical approach is especially apt, given that applying mathematical concepts naturally complements the study of kinematics, the core subject matter of the physics component. As articulated by Wang et al. [42], integrating STEM education offers students an invaluable opportunity to engage in learning within authentic, real-world scenarios instead of accumulating fragmented knowledge that requires later synthesis. Echoing this sentiment, Ryu et al. [43] and Bostic et al. [44] advocate for classroom experimentation centered on real-world challenges. Students can delve into interdisciplinary research initiatives addressing pressing global issues such as food security, bioenergy, and climate change. Industry-based case studies can further enrich their understanding. This holistic educational strategy facilitates a deeper comprehension of the intricate interrelationships among STEM disciplines, which the mere acronym ‘STEM’ fails to convey adequately [4].
One pedagogical approach facilitating such group-based learning experiences is model-eliciting activities (MEAs) [1,2,7,24,34,41]. In this framework, clients present engineering challenges that require tailored solutions for specific scenarios, such as optimizing production or developing mathematical models. When these challenges focus on model elicitation, students are guided away from unproductive tangents often encountered in open-ended problems. This focus simultaneously fosters the generation of diverse yet viable solutions within predefined constraints [44,45,46,47,48,49,50,51]. Dominguez et al. [52] argue that successfully applying classroom-learned mathematical techniques to solve these real-world problems is a compelling demonstration of the practical utility of classroom mathematics, extending its relevance beyond academic settings into real-world problem-solving contexts.
Within the context of the established research framework, this study aims to achieve three objectives:
Objective 1: To analyze students’ models when solving an activity that requires the integration and extension of previous concepts and models constructed.
Objective 2: To assess the effectiveness of the pedagogical approach of integrating physics and mathematics through modeling instruction in translating theoretical knowledge into practical application.
Objective 3: To evaluate the benefits of integrating physics and mathematics in educational settings.
The ensuing section will thoroughly explore the educational experiences aligned with these objectives. This will be succeeded by an exhaustive presentation of the research methodology employed, followed by the unveiling of the study’s findings. The manuscript will culminate in a comprehensive discussion and conclusion, providing in-depth insights into the research implications.
3. Methodology
The present study was implemented in an integrated first-year engineering course, Fis-Mat, to close the gap between calculus and physics [24,41]. It involved redesigning the course content, combining teaching strategies, reshaping the classroom setting, and using technology. The course is in the first semester for engineering students in a large private university in the northern part of Mexico. Students from different engineering majors take this course, such as mechanical, mechatronics, and industrial engineering. The course combined the first-semester calculus class with the introductory physics course and its associated laboratory [41]. Before the redesign, the students used to take the calculus and physics courses separately. The separated courses focused on solving calculus or physics end-of-the-chapter problems. After the redesign and integration, it emphasized using mathematical principles to examine physical phenomena and underscored the practical application of mathematical concepts in physics. The main objectives of the integrated course were to improve students’ abilities to make connections between physics and mathematics, increase students’ motivation to advance in their engineering studies, and develop diverse competencies, such as critical thinking and the ability to work collaboratively [24]. The following section explains the modeling experience students have during the semester.
3.1. The Modeling Experience
The modeling development sequence (Figure 1) starts with a Model-Eliciting Activity (MEA) [50] that serves dual purposes: gauges students’ pre-existing knowledge and it acts as a catalyst for formalizing the quadratic model and the concept of motion with constant acceleration [53]. During the exploration phase, a series of activities enable students to delve into various aspects of quadratic functions, including their graphical representations, equations, derivative functions, and qualitative and quantitative analyses. These activities also extend to applications in physical contexts, addressing problem-solving scenarios in one-dimensional (1D) and two-dimensional (2D) spaces. The 2D exercises incorporate elements of vector analysis and foundational trigonometry. Throughout this phase, using multiple representations empowers students to construct more robust models. This model development sequence spans two weeks and culminates in a Model-Application Activity (MAA), which challenges students to synthesize, connect, and extend their knowledge in real-world problems. By the time the Model-Application Activity took place (4th week of the semester), the students had worked with the first two iterations (cycles); see Table 1.

Figure 1.
Model development sequence embedded in modeling instruction (adapted from [24]).

Table 1.
Description of the nine modeling cycles (iterations) during the Fis-Mat 1st semester.
Simultaneously, the students are encouraged to construct mathematical and physical models, fostering an integrative approach. This methodology promotes a seamless interaction between the mathematical and physical models, ensuring that both are equally prioritized over the other.
This study’s foundation for constructing and applying physical models is rooted in Modeling Instruction [54]. Within this pedagogical framework, physical scenarios are primarily introduced as investigative exercises [55]. These exercises allow students to explore, deduce, test, refine, and report findings. When necessary, the instructor introduces new representational tools to aid the investigation. Students then apply these new representations with their existing knowledge base during the model construction phase. Throughout the problem-solving process, students engage in ongoing dialogues within small groups. Periodic whole-class discussions are interspersed to ensure that all the groups are progressing cohesively. By the session’s conclusion, each group presents its model and articulates its underlying rationale to the class. The newly introduced representations are assimilated at this juncture, culminating in an incrementally developed and more robust model. The specific instructional approach employed in the classroom [24] is visually depicted in Figure 1.
For the authors, representations are the media used to depict a situation, express the relationship between variables, communicate an idea, and synthesize specific situation characteristics. It is understood that “different media emphasize (and deemphasize) different aspects of the systems they were intended to describe” [56] (p. 12). During the process of constructing a model, the more representations used, the more robust the model is, and this involves the use of different representations in a coherent and articulated way.
Nine complete iterations of this process are followed during the semester, each adding more complexity to the built model. Each cycle focuses on one of the topics typically covered in a physics course. Table 1 shows the nine different cycles.
By the fourth week of the semester, when this investigation takes place, the students have access to various representational tools. These include (a) drawings for visualizing the phenomena under study, (b) motion graphs that capture position, velocity, and acceleration, (c) tables that enumerate the coordinate values of functional relationships, and (d) motion maps that offer qualitative velocity vectors to indicate both the magnitude and direction of motion. The students have also gained proficiency in vector addition and the derivation of kinematic equations from graphs. They have constructed models for one-dimensional motion with constant velocity and acceleration, recognizing the former as a specialized instance of the latter. Leveraging this understanding, they are prompted to extend their reasoning to two-dimensional models with constant acceleration, analyzing each component independently. In the mathematical realm, students are equipped to analyze and graph both linear and quadratic functions, solve corresponding equations, compute derivatives and antiderivatives of polynomial functions, and apply fundamental trigonometric relationships in the context of right triangles.
The students apply their constructed models to real-world scenarios in the Model-Application Activity (MAA) featured in this study. They engage in intellectual activities throughout this process, including conjecture, discussion, strategic planning, computation, and empirical testing. The MAA serves as a platform for students to validate the efficacy of their models, thereby reinforcing the connection between the abstract modeling processes and their tangible applications in real-world contexts.
3.2. Data Collection
The study focuses on the second cycle (see Table 1) of the Fis-Mat course. There were 54 engineering students from different fields, e.g., mechanical engineering, chemical engineering, bioengineering, etc. The students were divided into 18 collaborative groups of three to tackle the activity. For the group formation, we used the following criteria: (1) three groups of three students per table, (2) at least three women per table, (3) different engineering programs per group as much as possible, and (4) high school GPA (mixing high-score students with middle- and low-), as much as possible. The first cycle centers on constant acceleration in one dimension, while the second delves into constant acceleration in two dimensions. Both scenarios align with a mathematical quadratic model and can be simplified to a linear model under specific constraints.
In the first scenario, the students learn to represent position, velocity, and acceleration within a week through graphical means. The focal point of this activity is the application of their graph-based understanding to formulate equations for one-dimensional motion under conditions of constant acceleration, corresponding to a quadratic model.
The study’s objective focuses on analyzing students’ models within a Model-Application Activity (MAA) that involves using the quadratic model to understand motion under constant acceleration. Specifically, the activity asks students to determine the optimal positions for a ball on a ramp and a cup on the floor, such that the ball will roll down the ramp and land inside the cup (as illustrated in Figure 2). The teacher built the ramp and measured h1 (height of the table), h2 height of the cup, and two sides of the triangle formed by the ramp (students calculated the angle). All the groups worked with the same information; they needed to determine the ball’s initial position on the ramp (d) and the position of the cup for the ball to fall inside (D). This activity occurred during the fourth week of the semester, during which students had already developed linear and quadratic models and could apply them to one-dimensional and two-dimensional motion scenarios. They achieved this using various representational tools in a productive and conceptually coherent manner. Notably, while this stage had theoretically deduced the two-dimensional motion model, it had yet to be empirically validated; this activity served as the inaugural test of its real-world applicability.
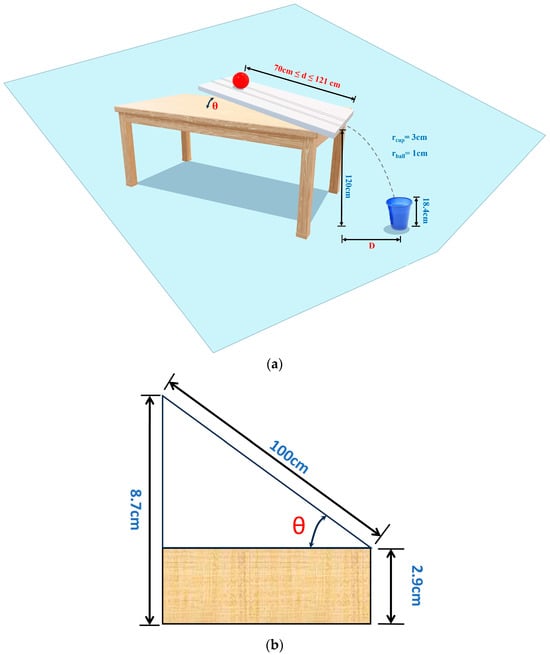
Figure 2.
Drawing of the situation indicating the measurements in blue and the unknowns in red. (a) realistic representation and (b) a triangle used to calculate the ramp’s angle.
Given that the problem is grounded in a real-world context, it commences with measuring essential parameters. The instructor measures variables as requested by the students, including the cup’s height, the table’s height, and the dimensions of the ramp, to compute the angle (marked in blue in Figure 2). The two unknowns (marked in red in Figure 2), d and D, are interrelated: the position of the cup on the floor (D) is contingent upon the ball’s initial position on the ramp (d). To prevent trivial solutions (d = 0), a minimum value for d is established (70 cm ≤ d ≤ 121 cm). A classroom sketch depicting the scenario, complete with the actual measured values, is presented in Figure 2.
Since the classroom setting has big round tables that seat nine students, we have three groups per table. Therefore, the students can see and interact with students from other groups. Also, the students are in a free-movement classroom; there are interactions among groups, although those interactions are not promoted [41]. The Model-Application Activity (MAA) is designed to be completed within a single session. After 40 min of collaborative work, each team submits a sheet detailing their calculated values for d and D. Once all the submissions are collected, the empirical testing phase commences. The students congregate around the ramp setup, and each team takes turns implementing their specific values. They place the ball—a steel marble—at the predetermined position on the ramp and position the cup at the calculated location on the floor where they anticipate the ball will land (as illustrated in Figure 3). The testing phase becomes particularly emotive as the ball approaches the cup, either narrowly missing, striking the edge, or cleanly entering the target. To ensure that all the students have an optimal vantage point for this crucial phase, the ramp setup is projected onto four screens distributed throughout the classroom.

Figure 3.
During the Model-Application Activity (MAA), students worked in groups and gathered around the ramp to test their values (d and D).
3.3. Data Analysis
The students’ work was preserved on whiteboards for subsequent analysis. The analysis followed a qualitative approach with search criteria that emerged organically. Our primary focus was to understand how the model was developed. To approach the analysis of the whiteboards, we initiated the process by systematically generating, observing, and thoroughly scrutinizing the comprehensive solution model. Following this initial examination, we analyzed each student group’s whiteboards to identify and categorize the prevailing qualitative errors. Subsequently, we conducted a meticulous, image-by-image examination of the teams’ work to unearth elements that resonated with the established qualitative error categories.
Throughout the semester, it became customary for the teams to capture photographs of their whiteboards and upload them to a private digital repository. This digital space served as a resource for both reviewing and researching purposes. Notably, we “randomized” the group numbers to ensure no direct connection, thus preserving the students’ anonymity and identity, a crucial facet of our qualitative research methodology.
The identified errors in the analysis are as follows:
- -
- Angle: This involves disregarding the directional aspect of velocity, particularly overlooking that the ball’s initial velocity begins at a particular angle when it descends in the air.
- -
- Acceleration: This involves computing the ball’s acceleration along the ramp (1D).
- -
- Quadratic model: The initial stage involves a consistent one-dimensional (1D) acceleration, which is described by a quadratic model.
- -
- Final/initial velocity: Identifying that the final velocity at the end of the ramp is the initial velocity for the free ball motion.
- -
- Quadratic+linear model: The second stage comprises constant acceleration within a two-dimensional (2D) framework, employing a linear model along the horizontal axis and a quadratic model along the vertical axis.
- -
- Hit: Whether the ball enters the cup or not.
4. Results
This section presents the analysis results conducted on the groups of students’ responses displayed on the whiteboards. It is worth noting that the students sometimes return days later, either after identifying their errors or harboring uncertainties about potential mistakes. A standard error among students is the inconsistent use of units for distance measurements, such as mixing centimeters and meters. This often results in seemingly plausible answers that only reveal their inaccuracies when the physical test is conducted. Another frequent oversight is neglecting to account for the directional component of velocity, mainly ignoring that the ball’s initial velocity starts at a specific angle when it falls in the air.
To successfully navigate the problem, students must scrutinize two distinct phases of motion: (1) the ball’s descent along the ramp, and (2) its subsequent trajectory through the air. The first phase involves constant acceleration in a one-dimensional (1D) context, which is modeled quadratically (as indicated in the fourth column of Table 1). The preliminary calculations require determining the precise angle of the ramp (utilizing the triangle depicted in Figure 2) and ascertaining the ball’s rate of acceleration while on the ramp (outlined in the second and third columns of Table 1). The second phase involves constant acceleration in a two-dimensional (2D) context, represented by a linear model on the horizontal axis and a quadratic model on the vertical axis (as shown in the sixth column of Table 1). The terminal velocity attained in the first phase serves as the initial velocity for the second phase (referenced in the fifth column of Table 1). Table 2 comprehensively summarizes the students’ models as captured on their whiteboards.

Table 2.
Results for the 2D cup model. Interpretation and values were taken from students’ whiteboards.
Five of the eighteen participating teams had their ball land in the cup. A closer examination of the specific errors reveals that most students could construct appropriate models for each scenario. The teams that failed to arrive at the correct solution primarily did so due to either a flawed interpretation of the problem or a failure to consistently apply units in their equations, such as inadvertently combining centimeters with meters. The term ‘No’ in Table 2, in the Final/Initial Velocity column, means the anticipated quadratic model was not successfully formulated. One team erred in applying the quadratic formula, neglecting to include the initial negative sign, thereby affecting the calculation of the ball’s point of impact with the ground. The detailed work of two representative groups is illustrated in Figure 4.

Figure 4.
Two whiteboards of students’ groups showing their work in solving the Model-Application Activity.
The two whiteboards depicted serve as comprehensive examples of the group’s work, clearly delineating the two sections being solved. Of the 16 whiteboards submitted by the students, 11 are well-organized and easily legible, while the remaining five need to be more organized and are difficult to interpret.
Observations of student discussions during the activity reveal that once students grasp the ball’s behavior, they have little difficulty recalling or applying the appropriate equations. Teams that struggle are generally those that prematurely attempt to solve the problem without first meticulously constructing the model, necessitating several rounds of revision and backtracking.
5. Discussion
5.1. Interpretation of Results
Our study’s results indicate that the students successfully applied theoretical models to real-world scenarios, such as the ball-on-ramp experiment. Five teams used the models and completed the task by having their ball land inside the cup (Objective 1). This success suggests that the pedagogical approach of integrating physics and mathematics through modeling instruction is effective in helping students translate theoretical knowledge into practical application (Objective 2). However, three other groups applied complete and correct models but failed to have the ball land inside the cup. These mistakes were related to the mix of units and an algebraic error in their equation. This highlights the importance of meticulous attention to detail in real-world applications, which often involve multiple variables and units. Additionally, six other groups were partially successful in applying their models, indicating that while the theoretical understanding is present, the practical application is not straightforward. This complexity could be due to various factors, such as the models’ limitations or the students’ understanding of how to apply them.
Another noteworthy observation is the role of collaboration in the study. The students worked in groups to construct and apply their models, likely contributing to the overall success rate. Figure 3 shows the students collaborating in the process. As in Hunter et al. [57], students engage in the solution process during the collaborative activity. However, the varying degrees of success among different groups also raise questions about how collaborative dynamics and individual contributions impact the effectiveness of the models. It would be interesting to explore whether the groups’ size or composition significantly impacts the outcomes. Furthermore, the study could delve into the psychological aspects of group work, such as the role of leadership, communication styles, and conflict resolution in the effectiveness of collaborative learning.
5.2. Importance of Modeling Instruction
Our findings underscore the importance of modeling instruction in physics and mathematics education. The pedagogical approach allowed students to explore, deduce, test, refine, and report findings, thereby fostering a deeper understanding of the subject matter. Evidence shows that students participate in their own learning (Figure 3) by discussing, collaborating, and experiencing a real-world scenario to solve, similar to the reflective discourse that the activities foster [58,59]. There is also evidence that students use a high-level thinking process (Figure 4) above what is usually used in a traditional classroom. This method of instruction encourages active learning and critical thinking, which are essential skills for students in these disciplines.
Modeling instruction inherently promotes collaborative learning. Our study observed that the students engaged in ongoing small-group dialogues and participated in periodic whole-class discussions. This collaborative environment helped students construct more robust models and facilitated peer-to-peer learning, which is invaluable in educational settings.
The study also highlighted the interdisciplinary benefits of modeling instruction. By integrating physics and mathematics, the students could construct models that were both theoretically sound and practically applicable. This interdisciplinary approach enriches the learning experience and prepares students for real-world challenges that often require a multifaceted understanding of problems.
While the study revealed some challenges in applying theoretical models to real-world scenarios, it also demonstrated that modeling instruction is a valuable tool for addressing this complexity. As suggested by Yildirim et al. [60], modeling activities can improve conceptual understanding and be a means for assessing the problem-solving process. However, these benefits will only be successful if the activities are correctly implemented. The iterative process of exploring, deducing, testing, and refining allows students to adapt and improve their models in response to real-world variables, thereby bridging the gap between theory and practice. This suggests that modeling instruction could be further optimized to address these challenges, perhaps by incorporating more real-world examples or providing additional guidance on navigating the complexities of real-world applications.
5.3. Integration of Physics and Mathematics
The study also demonstrated the seamless integration of physics and mathematics through modeling (objective 3). This interdisciplinary approach enriched the learning experience by allowing students to see the interconnectedness of these two fields. Instead of treating physics and mathematics as isolated subjects, the integration helped students understand how mathematical concepts can be applied to solve physical problems and vice versa. This has significant implications for curriculum design, suggesting that more integrated courses could provide a more holistic educational experience. The students faced a real scenario with equipment in a classroom, with space to work together and experiment with equipment. To solve the task, they had the physics model to understand which physical laws to apply, but also, in each part of the ball’s motion, a mathematical model to represent the experiment and to calculate the actual variables for the experiment. However, the challenges faced in real-world applications suggest that while interdisciplinary learning is beneficial, it may not prepare students for all the complexities they may encounter in practical scenarios.
Following Sands [61], who emphasizes the importance of understanding how mathematical operations connect to and describe physics concepts, and the need for students to be able to connect physical and mathematical models to effectively use mathematics in solving physics problems, the interdisciplinary nature of this study made the constructed models more robust and applicable to various scenarios. For instance, the students could apply mathematical concepts like derivatives and integrals in understanding physical phenomena like forces and motion (Figure 4). This versatility is crucial for preparing students for real-world challenges that often require a multifaceted approach. It also suggests that interdisciplinary approaches could benefit other scientific disciplines, not just physics and mathematics.
The integration of physics and mathematics also facilitated a deeper conceptual understanding. For example, mathematical representations let students grasp the vector nature of forces and momentum. This solidified their understanding of individual concepts and provided a toolkit of integrated knowledge more readily applicable in practical scenarios. This raises the question of how such integrated learning experiences could be scaled to more extensive educational settings and what resources would be necessary to facilitate this kind of deep, interdisciplinary learning.
6. Conclusions
The Model-Application Activity consisted of predicting where to locate a ball rolling down a ramp so it falls into a cup on the floor (position to be defined); solving this activity fulfills two purposes. The first one applies and integrates the knowledge built until that point in the semester concerning the physical and mathematical models. The second is to empower the students by bridging the gap between models built from ideal situations and those used in solving problems from real-life situations. The attitude of the students at the end of the session, finding whether (or not) their calculations and model work, makes this activity engaging and challenging. The satisfaction of the teams whose ball enters the cup makes them realize that constructing a model to represent real-life situations is doable. It paves the ground for building more complex models (or their refinement). The teams whose model made the ball hit the edge of the cup came to realize the importance of significant figures in their calculations. The teams that missed the target realized the importance of working with congruence units and coherence among representations.
The students also realized that sometimes, a drawing or combining different representations can help them better understand specific situations. Trying to use particular formulas without understanding (as often occurs when solving problems from the end of a textbook chapter) does not help when presented with more complex situations that can be approached with more than one strategy. This allows students to use different representations and calculations to reach the same answer, corroborating its correctness. In our experience, a student can rarely make the same mistake by solving a problem graphically and using equations. Moreover, moving from one representation to the other and back allows students to verify their reasoning and assumptions. That resonates with the statement by Lesh and Doerr [56] (p. 12): “Solution processes for model-development activities (or other types of problem-solving experiences) often involve shifting back and forth among a variety of relevant representations”.
The findings have significant implications for pedagogy in science and engineering education. The study underscores the importance of modeling as a vital skill for enhancing students’ research and problem-solving abilities. However, the challenges students face in real-world applications suggest that more hands-on activities and practical experiments should be incorporated into the curriculum.
The study successfully demonstrated the seamless integration of physics and mathematics, enriching the learning experience and making the models more robust. This interdisciplinary approach is particularly beneficial for engineering students, who often need to apply a multifaceted understanding of problems in their future careers.
The collaborative nature of the activities enhanced the learning experience. The students could engage in meaningful dialogues within small groups, which likely contributed to the successful construction of models. However, the varying degrees of success among different groups also raise questions about how collaborative dynamics impact the effectiveness of the models.
One limitation of our study is the relatively small sample size of first-year engineering students. Future research could involve a more diverse set of participants to generalize the findings. Further studies could also focus on identifying the areas where students struggle and developing targeted instructional methods to address these challenges.
In conclusion, our study underlines the value of integrating physics and mathematics through modeling and a student-centered approach in STEM education. While the study provides valuable insights into the effectiveness of this pedagogical strategy, it also highlights areas for improvement. It sets the stage for future research to enhance the effectiveness of STEM education.
Author Contributions
Conceptualization, A.D., J.D.l.G. and G.Z.; methodology, A.D. and J.D.l.G.; formal analysis, A.D. and J.D.l.G.; investigation, A.D. and J.D.l.G.; writing—original draft, A.D. and J.D.l.G.; writing—review and editing, M.Q.-E. and G.Z.; supervision, G.Z.; project administration, A.D.; funding acquisition, A.D. and G.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Ethics Committee of Instituto Tecnologico y de Estudios Superiores de Monterrey (protocol code EHE-2023-09 on 18 December 2023).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.
Acknowledgments
The authors acknowledge the technical and financial support of Writing Lab, Institute for the Future of Education, Tecnologico de Monterrey, Mexico, in the production of this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Doerr, H.M.; English, L.D. A modeling perspective on students’ mathematical reasoning about data. J. Res. Math. Educ. 2003, 34, 110–136. [Google Scholar] [CrossRef]
- Lesh, R.A.; Cramer, K.; Doerr, H.M.; Post, T.; Zawojewski, J. Model development sequences. In Beyond Constructivism: Models and Modeling Perspectives on Mathematics Problem Solving, Learning and Teaching; Lesh, R.A., Doerr, H.M., Eds.; Erlbaum: Mahwah, NJ, USA, 2003; pp. 35–58. [Google Scholar]
- Gifford, J.D.; Finkelstein, N.D. A framework for curriculum design to support mathematical sense making. In 2020 Physics Education Research Conference Proceedings; Wolf, S.F., Bennett, M.B., Frank, B.W., Eds.; American Association of Physics Teachers: College Park, MD, USA, 2020; pp. 173–178. [Google Scholar] [CrossRef]
- Lo, C.K.; Huang, X.; Cheung, K.L. Toward a Design Framework for Mathematical Modeling Activities: An Analysis of Official Exemplars in Hong Kong Mathematics Education. Sustainability 2022, 14, 9757. [Google Scholar] [CrossRef]
- Lyon, J.A.; Magana, A.J. A review of mathematical modeling in engineering education. Int. J. Eng. Educ. 2020, 36, 101–116. [Google Scholar]
- Riyanto, B.; Zulkardi; Putri, R.I.I.; Darmawijoyo. Mathematical Learning through Modeling Task in Senior High School: Using Nutrition Context. J. Phys. Conf. Ser. 2018, 1097, 012102. [Google Scholar] [CrossRef]
- Chimmalee, B.; Anupan, A. Effect of Model-Eliciting Activities Using Cloud Technology on the Mathematical Problem-Solving Ability of Undergraduate Students. Int. J. Instr. 2022, 15, 981–996. [Google Scholar] [CrossRef]
- Dominguez, A.; Truyol, M.E.; Zavala, G. Professional development program to promote active learning in an engineering classroom. Int. J. Eng. Educ. 2019, 35, 424–433. [Google Scholar]
- Kovarik, M.L.; Robinson, J.K.; Wenzel, T.J. Why Use Active Learning? In Active Learning in the Analytical Chemistry Curriculum; ACS Symposium Series; American Chemical Society: Washington, DC, USA, 2022; Volume 1409, pp. 1–12. [Google Scholar] [CrossRef]
- Leandro, A.C.S.; Maia, E.C.; Alves, I.C.; Santos, L.P.C.; de Andrade, T.C.F.; de Moura, C.F.S.; Viana, D.M.; Shzu, M.A.M.; Lisniowski, S.A.; de Paula, A.S. Online adaptation strategies for active learning methodologies in STEM education. Int. Symp. Proj. Approaches Eng. Educ. 2021, 11, 316–323. [Google Scholar] [CrossRef]
- Caratozzolo, P.; Lara-Prieto, V.; Hosseini, S.; Membrillo-Hernández, J. The use of video essays and podcasts to enhance creativity and critical thinking in engineering. Int. J. Interact. Des. Manuf. 2022, 16, 1231–1251. [Google Scholar] [CrossRef]
- Lapitan, L.D.; Chan, A.L.A.; Sabarillo, N.S.; Sumalinog, D.A.G.; Diaz, J.M.S. Design, implementation, and evaluation of an online flipped classroom with collaborative learning model in an undergraduate chemical engineering course. Educ. Chem. Eng. 2023, 43, 58–72. [Google Scholar] [CrossRef]
- Foote, K.T.; Neumeyer, X.; Henderson, C.; Darcy, M.H.; Beichner, R.J. Diffusion of research-based instructional strategies: The case of SCALE-UP. Int. J. STEM Educ. 2014, 1, 10. [Google Scholar] [CrossRef]
- Docktor, J.L.; Mestre, J.P. Synthesis of discipline-based education research in physics. Phys. Rev. Spec. Top. Phys. Educ. Res. 2014, 10, 020119. [Google Scholar] [CrossRef]
- English, L.D. Integrating engineering within early STEM and STEAM education. In Embedding STEAM in Early Childhood Education and Care; Cohrssen, C., Garvis, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar] [CrossRef]
- Luque, A.; Mullinix, J.; Anderson, M.; Williams, K.S.; Bowers, J. Aligning Calculus with Life Sciences Disciplines: The Argument for Integrating Statistical Reasoning. PRIMUS 2022, 32, 199–217. [Google Scholar] [CrossRef]
- Robertson, A.D.; Goodhew, L.M.; Bauman, L.C.; Hansen, B.; Alesandrini, A.T. Identifying student conceptual resources for understanding physics: A practical guide for researchers. Phys. Rev. Phys. Educ. Res. 2023, 19, 020138. [Google Scholar] [CrossRef]
- Campos, E.; Tecpan, S.; Zavala, G. Argumentation in the teaching of electrical circuits by applying active learning. Rev. Bras. Ensino Fis. 2021, 43, e20200463. [Google Scholar] [CrossRef]
- Campos, E.; Zuza, K.; Guisasola, J.; Zavala, G. Recognition and conversion of electric field representations: The case of electric field lines. Phys. Rev. Phys. Educ. Res. 2023, 19, 020117. [Google Scholar] [CrossRef]
- Quezada-Espinoza, M.; Dominguez, A.; Zavala, G. Academic and Professional Relevance of Physics: Comparing Perceptions of Engineering Students from Mexico and Chile. Int. J. Eng. Educ. 2021, 37, 1174–1185. [Google Scholar]
- Flegg, J.; Mallet, D.; Lupton, M. Students’ perceptions of the relevance of mathematics in engineering. Int. J. Math. Educ. Sci. Technol. 2012, 43, 717–732. [Google Scholar] [CrossRef]
- Lee, M.; Larkin, C.J.K.; Hoekstra, S. Impacts of Problem-Based Instruction on Students’ Beliefs about Physics and Learning Physics. Educ. Sci. 2023, 13, 321. [Google Scholar] [CrossRef]
- Zavala, G.; Dominguez, A. Engineering students’ perception of relevance of physics and mathematics. In Proceedings of the 2016 ASEE Annual Conference and Exposition, New Orleans, LA, USA, 26–29 June 2016. [Google Scholar] [CrossRef]
- Dominguez, A.; Hernandez-Armenta, I.; de la Garza Becerra, J.E. Towards a full integration of physics and math concepts: The path full of traps. In Proceedings of the 2018 ASEE Annual Conference & Exposition, Salt Lake City, UT, USA, 23 June–27 December 2018. [Google Scholar] [CrossRef]
- Martín-Páez, T.; Aguilera, D.; Perales-Palacios, F.J.; Vílchez-González, J.M. What are we talking about when we talk about STEM education? A review of literature. Sci. Educ. 2019, 103, 799–822. [Google Scholar] [CrossRef]
- Zhao, J.; Wijaya, T.T.; Mailizar, M.; Habibi, A. Factors Influencing Student Satisfaction toward STEM Education: Exploratory Study Using Structural Equation Modeling. Appl. Sci. 2022, 12, 9717. [Google Scholar] [CrossRef]
- Martynenko, O.O.; Pashanova, O.V.; Korzhuev, A.V.; Prokopyev, A.I.; Sokolova, N.L.; Sokolova, E.G. Exploring attitudes towards STEM education: A global analysis of university, middle school, and elementary school perspectives. Eurasia J. Math. Sci. Technol. Educ. 2023, 19, em2234. [Google Scholar] [CrossRef] [PubMed]
- Zhai, X. Assessing high-school students’ modeling performance on Newtonian mechanics. J. Res. Sci. Teach. 2022, 59, 1313–1353. [Google Scholar] [CrossRef]
- Zwickl, B.M.; Hu, D.; Finkelstein, N.; Lewandowski, H.J. Model-based reasoning in the physics laboratory: Framework and initial results. Phys. Rev. Spec. Top. Phys. Educ. Res. 2015, 11, 020113. [Google Scholar] [CrossRef]
- Bowers, J.; Anderson, M.; Beckhard, K. A Mathematics Educator Walks into a Physics Class: Identifying Math Skills in Students’ Physics Problem-Solving Practices. J. STEM Educ. Res. 2023, 0123456789. [Google Scholar] [CrossRef]
- English, L.D. Fifth-grade Students’ Quantitative Modeling in a STEM Investigation. J. STEM Educ. Res. 2022, 5, 134–162. [Google Scholar] [CrossRef]
- Sirnoorkar, A.; Bergeron, P.D.O.; Laverty, J.T. Sensemaking and scientific modeling: Intertwined processes analyzed in the context of physics problem-solving. Phys. Rev. Phys. Educ. Res. 2023, 19, 10118. [Google Scholar] [CrossRef]
- McNeill, G.; Sondag, M.; Powell, S.; Asplin, P.; Turkay, C.; Moller, F.; Archambault, D. From Asymptomatics to Zombies: Visualization-Based Education of Disease Modeling for Children. In Proceedings of the 2023 CHI Conference on Human Factors in Computing Systems, Hamburg, Germany, 23–28 April 2023. [Google Scholar] [CrossRef]
- Shahbari, J.A.; Tabach, M. Making sense of the average concept through engagement in model-eliciting activities. Int. J. Math. Educ. Sci. Technol. 2021, 52, 1143–1160. [Google Scholar] [CrossRef]
- Lozada, E.; Guerrero-Ortiz, C.; Coronel, A.; Medina, R. Proposal of a Mathematical Modelling Activity to Facilitate Students’ Learning of Ordinary Differential Equation Concepts. Sustainability 2023, 15, 12483. [Google Scholar] [CrossRef]
- Baker, C.K.; Galanti, T.M.; Kraft, T.; Hjalmarson, M.; Nelson, J.K. Researchers as Coaches: Developing Mathematics Teaching Capacity Using MEAs for STEM Integration. Investig. Math. Learn. 2022, 14, 28–48. [Google Scholar] [CrossRef]
- Langman, C.; Zawojewski, J.; McNicholas, P.; Cinar, A.; Brey, E.; Bilgic, M.; Mehdizadeh, H. Disciplinary learning from an authentic engineering context. J. Pre-Coll. Eng. Educ. Res. 2018, 9, 77–94. [Google Scholar] [CrossRef]
- Peretz, R.; Dori, D.; Dori, Y.J. Developing and assessing pre- and in-service science and engineering teachers’ systems thinking and modeling skills through an asynchronous online course. Front. Educ. 2023, 8, 1154893. [Google Scholar] [CrossRef]
- Borish, V.; Hoehn, J.R.; Lewandowski, H.J. Student engagement with modeling in multiweek student-designed lab projects. Phys. Rev. Phys. Educ. Res. 2022, 18, 20135. [Google Scholar] [CrossRef]
- Peretz, R.; Tal, M.; Akiri, E.; Dori, D.; Dori, Y.J. Fostering engineering and science students’ and teachers’ systems thinking and conceptual modeling skills. Instr. Sci. 2023, 51, 509–543. [Google Scholar] [CrossRef] [PubMed]
- Dominguez, A.; Zavala, G.; Alanis, J.A. Integrated physics and math course for engineering students: A first experience. In Proceedings of the 2013 ASEE Annual Conference & Exposition, Atlanta, GA, USA, 23–26 June 2023; pp. 23.766.1–23.766.9. [Google Scholar] [CrossRef]
- Wang, H.; Moore, T.J.; Roehrig, G.H.; Park, M.S. STEM Integration: Teacher Perceptions and Practice STEM Integration: Teacher Perceptions and Practice. J. Pre-Coll. Eng. Educ. Res. 2011, 1, 2. [Google Scholar] [CrossRef]
- Ryu, M.; Mentzer, N.; Knobloch, N. Preservice teachers’ experiences of STEM integration: Challenges and implications for integrated STEM teacher preparation. Int. J. Technol. Des. Educ. 2019, 29, 493–512. [Google Scholar] [CrossRef]
- Bostic, J.D.; Clark, Q.M.; Vo, T.; Esters, L.T.; Knoblach, N.A. A design process for developing agricultural life science-focused model eliciting activities. Sch. Sci. Math. 2021, 121, 13–24. [Google Scholar] [CrossRef]
- Moore, T.J.; Doerr, H.M.; Glancy, A.W.; Ntow, F.D. Preserving pelicans with models that make sense. Math. Teach. Middle Sch. 2015, 20, 358–364. [Google Scholar] [CrossRef]
- McLean, J.A.; Brady, C.; Jung, H.; Dominguez, A.; Glancy, A.W. Seeing the Forest for the Trees: Investigating Students’ Data Moves in a Citizen Science Based Model-Eliciting Activity. In Advancing and Consolidating Mathematical Modelling; Greefrath, G., Carreira, S., Stillman, G.A., Eds.; International Perspectives on the Teaching and Learning of Mathematical Modelling; Springer: Cham, Switzerland, 2023. [Google Scholar]
- Lyon, J.A.; Magana, A.J.; Streveler, R.A. Characterizing Computational Thinking in the Context of Model-Planning Activities. Modelling 2022, 3, 344–358. [Google Scholar] [CrossRef]
- Stohlmann, M. Model Eliciting Activities: Fostering 21st Century Learners. J. Math. Educ. Teach. Coll. 2013, 4, 60–65. [Google Scholar] [CrossRef]
- Liu, Z.L.; Xia, J. Enhancing computational thinking in undergraduate engineering courses using model-eliciting activities. Comput. Appl. Eng. Educ. 2020, 29, 102–113. [Google Scholar] [CrossRef]
- Dominguez, A. Single Solution, Multiple Perspectives. In Modeling Students’ Mathematical Modeling Competencies; Lesh, R., Galbraith, P., Haines, C., Hurford, A., Eds.; Springer: Boston, MA, USA, 2010. [Google Scholar] [CrossRef]
- Chamberlin, S.A.; Parks, K. A comparison of student affect after engaging in a mathematical modeling activity. Int. J. Educ. Math. Sci. Technol. 2020, 8, 177–189. [Google Scholar] [CrossRef]
- Dominguez, A.; De la Garza, J.; Zavala, G. Models and Modelling in an Integrated Physics and Mathematics Course. In Mathematical Modelling in Education Research and Practice: Cultural, Social and Cognitive Influences, International Perspectives on the Teaching and Learning of Mathematical Modelling; Stillman, G.A., Blum, W., Salett Biembengut, M., Eds.; Springer: New York, NY, USA, 2015; pp. 513–522. [Google Scholar] [CrossRef]
- Ärlebäck, J.; Doerr, H.M.; O’Neil, A.M. A modeling perspective on interpreting rate of change in context. Math. Think. Learn. 2013, 15, 314–336. [Google Scholar] [CrossRef]
- Halloun, I.A.; Hestenes, D. Modeling instruction in mechanics. Am. J. Phys. 1987, 53, 1043–1055. [Google Scholar] [CrossRef]
- Brewe, E. Modeling theory applied: Modeling instruction in introductory physics. Am. J. Phys. 2008, 76, 1155–1160. [Google Scholar] [CrossRef]
- Lesh, R.A.; Doerr, H.M. Foundations of a Models and Modeling Perspective on Mathematics Teaching, Learning, and Problem Solving. In Beyond Constructivism: Models and Modeling Perspectives on Mathematics Problem Solving, Learning and Teaching; Lesh, R.A., Doerr, H.M., Eds.; Erlbaum: Mahwah, NJ, USA, 2003; pp. 3–33. [Google Scholar]
- Hunter, K.H.; Rodriguez, J.G.; Becker, N.M. Making sense of sensemaking: Using the sensemaking epistemic game to investigate student discourse during a collaborative gas law activity. Chem. Educ. Res. Pract. 2021, 22, 328–346. [Google Scholar] [CrossRef]
- Brady, C.; Jung, H.; McLean, J.A.; Dominguez, A.; Glancy, A.W. Student Presentations of Mathematical Modelling Solutions as a Setting for Fostering Reflective Discourse. In International Perspectives on the Teaching and Learning of Mathematical Modelling; Kaiser, G., Stillman, G., Eds.; Springer: Cham, Swizerland, 2023; pp. 61–76. [Google Scholar] [CrossRef]
- Dominguez, A.; de la Garza Becerra, J.E. Closing the gap between physics and calculus: Use of models in an integrated course. In Proceedings of the 2015 ASEE Annual Conference & Exposition, Seattle, WA, USA, 14–17 June 2015; pp. 26.353.1–26.353.14. [Google Scholar] [CrossRef][Green Version]
- Yildirim, T.P.; Shuman, L.; Shuman, L.; Besterfield-Sacre, M. Model-Eliciting Activities: Assessing engineering student problem-solving and skill integration processes. Int. J. Eng. Educ. 2010, 26, 831–845. [Google Scholar]
- Sands, D. Modeling as sensemaking: Towards a theory of modelling in physics education. Eur. J. Phys. 2021, 42, 064001. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).