Teaching Mathematics in a Context of Lockdown: A Study Focused on Teachers’ Praxeologies

Abstract

This study aims to explore how teachers from four countries—France, Israel, Italy, and Germany—manage their teaching–learning activity in the context of lockdown due to the COVID-19 pandemic. About 700 teachers from the four countries participated in this study. They were given an online questionnaire that involved 22 open-ended items, in which they were requested to complete the items that were structured taking into account the relationships between teacher, students, mathematics and resources. The qualitative analysis of teachers’ answers was carried out, referring to both the meta-didactical transposition model and Bishop’s framework on values to investigate teachers’ teaching–learning activities and the reasons underlying their choices. The empirical analysis suggests four tasks corresponding to the main challenges that teachers had to face during the time of lockdown: (a) managing distance learning to support students’ learning through specific methodologies; (b) managing distance learning to develop assessment; (c) managing distance learning to support those students that face difficulties and/or are living a difficult situation/developing inclusive teaching; and (d) managing distance learning to exploit its potentialities for fostering typical mathematical processes. The values that motivated the teachers to change their teaching–learning activities are discussed, conclusions of how the time of lockdown affects the mathematics teaching is drawn, and finally, recommendations and insights from this study are shared.

1. Introduction

February 2020: In most parts of the world, the mathematics classroom is a place where students and teachers meet, explore mathematical concepts, share ideas and learn together. Teachers interact with students, they keep track of and support the students’ learning, and many teachers use multiple—digital and non-digital—resources for the teaching and learning of mathematics.

March 2020: In many parts of the world, teachers and students are isolated. Schools are closed and—if at all—the only connection to other students or to the teacher is by phone or virtual meetings. Teachers reflect on their teaching and feel the challenge of securing educational justice by what they do.

Education is a total fact [1]. This means that education is directly linked to the whole organization of a society. The school is one of the institutions that make up society. It is based on human values that require the advancement of society, passing on to future generations the knowledge accumulated over centuries with the will to develop it for the good and security of all citizens. When an event happens that upsets the entire organization of society, the school has to adapt and show that it can do it.

“It would be a mistake to talk about school as a small independent world. It has no end and no law of its own. Made by the country, for the country, at all times school is accountable to the country. Especially in the time we are living in!” (“Ce serait une erreur de parler de l’école comme d’un petit monde indépendant. Elle n’a ni fin ni sa loi en elle-même. Faite par le pays, pour le pays, en tout temps elle lui doit des comptes. Combien plus dans celui que nous traversons!”) [2] (p. 233, translated by the authors).

This sentence, written by Buisson in 1915 after the terrible ordeal of World War I, can still be applied to this unprecedented period we are going through. The current health crisis is an unprecedented, unforeseen event, which has surprised and profoundly changed the way society functions. The question therefore arises: How did the school react? In particular, distance learning (DL) has spread to all countries without prior preparation. Although many studies have been carried out in recent decades on distance learning [3,4], including MOOC [5], these have always been experiments involving volunteer teachers and students. This event has brought about a radical change of scale. It is precisely this change that we wished to understand by looking at the key players in this transformation, the teachers, and in our case, the mathematics teachers. We therefore wished to ask them on the spot about how they were—and still are—managing this situation.

We also wanted to observe and analyze the mathematics teachers’ behavior in our four countries (France, Italy, Israel and Germany) and we propose a study of the teaching methods and conditions of teaching. We, too, were in a lockdown situation and we had to adapt our research methodologies and research questions to this particular situation. As mathematics educators, we attach great importance to the knowledge at stake. We based our study on a questionnaire that has been sent to teachers, using professional and research organization channels. Even if the number of answers is sufficient to give statistically relevant results, the data collection could not be scientifically verified to the point where we could reasonably report statistics, and we preferred to analyze the data collected in a qualitative manner. The main question that this paper addresses is:

How do teachers manage mathematics teaching–learning during lockdown and how do they justify their actions and choices?

In the first part of the paper, we explain in detail the theoretical framework and the methodology, both for the elaboration of the questionnaire we sent to teachers, and for the way we analyzed the data. The second part of the paper proposes the main results we have drawn from the analysis of the data.

2. Theoretical Framework

To identify the challenges and the opportunities teachers met during time of lockdown, we used three theoretical ideas: (a) The idea of the didactical tetrahedron [6] that guided our design of the questionnaire and supported us in framing teachers’ answers; (b) meta-didactical transposition [7], by which we identified the meta-didactical praxeologies; and (c) Bishop’s framework [8] on values in mathematics education, by which we interpret the factors that motivate teachers’ behavior and choices.

2.1. Didactical Tetrahedron Model

The didactical tetrahedron is a model that describes the relation between students, teachers, resources and mathematics. It has been extensively used, especially in the context of mathematics teaching and learning, to capture and describe the complexity of educational phenomena. In recent years, special attention has been paid to the role of resources used in the mathematics classroom (e.g., [6,9,10]), some of which have special focuses, e.g., on digital tools [11] or professional development [12]. Whereas the term resources in the didactical tetrahedron is used in a general way, the context of this paper focuses on digital resources.

The use of didactical tetrahedron allows a structured way to address different kinds of phenomena and their intertwined relation. On the one hand, the model was used in a constructive way to structure the questionnaire used in this study. In other words, certain questions address specific vertices, edges or faces of the didactical tetrahedron (Figure 1). On the other hand, it was also used, as a starting point, to identify the main focus of teachers’ answers from an analytical perspective.

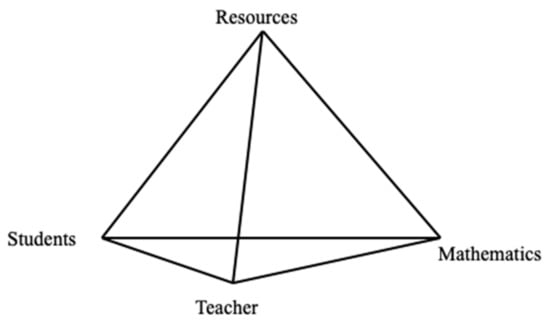
Figure 1. Didactical tetrahedron model.

2.2. Meta-Didactical Transposition

Although the didactical tetrahedron allows us to address the components that are involved in teaching–learning processes during the lockdown, and the interaction among them, it was limited in describing the activities conducted by teachers during the teaching processes and in reflecting on the reasons that guided their choices. To do so, we used the Meta-Didactical Transposition (MDT) model [7].

The MDT is based on the Anthropological Theory of didactics [13,14], which postulates that any activity related to the production, diffusion, or acquisition of knowledge should be interpreted as an ordinary human activity, and thus proposes a general model of human activities built on the key notion of praxeology. Relying on the etymology of the word praxeology, Chevallard [14] defines it as interrelated components of praxis and logos. Praxis is the practical part and logos refers to human thinking and reasoning. Praxis is composed of “types of tasks” and a set of “techniques” to carry out some of the tasks of the given type. The logos is made of two levels of description and justification of the praxis. The first level is called a “technology”, in the sense of the “discourse” (logos) of the technique, i.e., the term technology is used in the sense of justification and validation of the chosen technique. The second level is called the “theory”, and its role is to provide a basis and support for the technological discourse. In our paper, we will refer to the logos level with the term justifying discourses, as introduced by Arzarello et al. [7].

Meta-didactical praxeologies (in the following, MDP) are developed when a reflection on a didactical praxeology is carried out. This reflection is focused on the thoughts that guide teachers’ actions and is aimed at describing the techniques and at justifying the choice of these techniques in a given context. The MDT was initially used in the context of professional development programs. Later on, it was adapted for the case of collaborative research, which we use here in the broad sense of research involving different communities and institutions [15,16,17,18,19,20].

Teaching mathematics in a time of lockdown, a hitherto unseen context, required mathematics teachers to adapt their usual didactical praxeologies (DP) to fit the new situation. The teachers’ answers to the open-ended items of the questionnaire used in this study could be conceived as an initiation of a potential dialogue between teachers and researchers. Due to the questionnaire, in fact, teachers are invited to present the adaptation of their DP, developing justifications about the choices they made. This interpretation poses teachers’ answers at a meta-level, since it is the beginning of sharing their reflections with the researchers. The fact that the teachers do not limit themselves to only describing what they do (they, in fact, share ideas, reflections, doubts, etc.) represents evidence of teachers’ need to pose their discourse at a meta-level. Hence, we found that the MDT framework was effective for our investigation.

2.3. Values in Mathematics Education

While the MDT framework allows us to identify, within teachers’ reflections, the praxeologies they used to manage the teaching process in time of lockdown, it does not help us to interpret the teachers’ motivation for changing their praxeologies. To understand the teachers’ motivations for adapting previous praxis to the new situation, we adopted Bishop’s framework on values [8].

We refer to the idea of values because we think that the choices that teachers made with respect to the lockdown were influenced by the set of values (often unaware) they had developed, even if they were not explicitly declared. In particular, we will focus on values related to mathematics and its teaching; we are aware that it is also possible to adopt a more general perspective, reflecting on human values in general, but we are adopting an educational—not philosophical—perspective on values.

Bishop [8,21] stresses that values can be highlighted when people have the possibility to choose between alternatives: “values are revealed at choice points” [21] (p. 6). This time of lockdown could be seen as a moment in which teachers had to confront a choice of what to do in relation to the main task that is in front of them: facing DL. To identify the values that guide teachers’ practices, we will refer to the six pairs of values that Bishop introduced within the three categories of ideological, individual and social values [8]:

“Mathematics, as a cultural phenomenon, only makes sense if those values are also made explicit. I have described them as complementary pairs, where rationalism and objectivism are the twin ideologies of Mathematics, those of control and progress are the attitudinal values which drive Mathematical development and, sociologically, the values of openness and mystery are those related to potential ownership of, or distance from Mathematical knowledge and the relationship between the people who generate that knowledge and others.” [22] (p. 82—quoted by Bishop et al. in [23], p. 8).

In Bishop et al. [23], teachers’ values are investigated both in the realm of mathematics and science education. In particular, the value of empiricism is substituted for that of objectivism.

Hence, the research questions to be investigated within this study are:

• Which sub-tasks for teachers and corresponding MDP (including techniques and justifying discourses) can be identified in the context of distance learning in mathematics during the pandemic?
• How are the MDP related to the didactical tetrahedron?
• What values lead the logos part of these MDP?

3. Methodology

The study aims at getting insights into the praxis of mathematics teaching and learning in the context of the COVID-19 pandemic. This situation is characterized by the need to find new ways of acting within society, and this holds especially true for education. Hence, there is no scientific empirical evidence about how teachers and students deal with this kind of situation. Therefore, empirical evidence is needed, but the process of gathering data is also affected by the pandemic. On the one hand, detailed knowledge is needed in order to find out more about the educational praxis. On the other hand, it can be expected that these praxes are very different and depend on many (e.g., social, political, and institutional) factors. Hence, there is also a need for a wider view that captures these differences.

3.1. The Questionnaire

To answer our research questions, we structured a questionnaire that included 20 open-ended items and two closed items. We grouped the questionnaire items into five sections. The first section was devoted to general information about the teachers, while the other four sections referred to the tetrahedron vertices, edges and faces.

Although the focus of the items in each section is different, all items were focused on the teaching–learning of mathematics in the context of lockdown.

The questions of the first group focused on the interactions that teachers (and students) have with resources (hence, T-S-R face): in the emergency of the situation, what tools are teachers turning to? What guides their choices, between institutional recommendations and teachers’/students’ familiarity?

The questions in the second group were aimed at investigating the way in which teachers use specific resources to manage fundamental tasks related to the teaching of mathematics at distance (organization of the lessons, assessment, support to students who face difficulties), their level of confidence with these tools and also the feelings that the situation gives them (mainly faces T-S-R and T-R-M).

Through the third group of questions, we particularly focused on how teachers were managing the interactions between their students and the knowledge at stake (face T-S-M) and on how they evaluate the effects of these interactions in terms of students’ participation and learning (face S-R-M).

Finally, the fourth group of questions focused on the mathematical knowledge that teachers taught during this period (face T-R-M), with a particular focus on teachers’ feelings about the potentialities and disincentives of the situation.

3.2. Participants and Context

In total, 684 teachers from four countries volunteered to answer an online questionnaire authored especially with the aim of this study in mind. Table 1 summarizes the distribution of the teachers’ numbers in each country and the grade level in which they are teaching.

Table 1. Distribution of the teachers in each country and the grade level.

	France	Germany	Israel	Italy	Total
Primary	10 (age 6 to 10)	4 (age 6–10)	50 (age 5–11)	40 (age 6–11)
Middle school			47 (age 12–15)
Lower secondary	76 (age 11 to 14)	98 (age 11–18)	60 (age 16–18)	35 (age 12–14)
Upper secondary University level	79 (age 15 to 18) 24 (age > 18)		13 (age > 18)	157 (age 15–19)
no answer	0	0	3	0
Total number of answers	177 1	102	173	232	684

¹ This number is not the sum of the numbers in the same column, due to multiple affiliations (some teachers work at different levels).

3.3. Data Collection

To collect the data, we prepared a Google form for the items of the questionnaire. The questionnaire was distributed widely and randomly using teachers’ professional lists, personal contacts or announcements in professional journals. Teachers who agreed to participate in this study submitted the filled-out questionnaire. Participation in this study was anonymous, and personal information about the participants was not collected. In this way, we created a database of the teachers’ responses, which served as the data for this study.

3.4. Data Analysis

The data analysis was carried out in two rounds. Although we had a large amount of data, our aim was to carry out a qualitative analysis to understand how the teachers manage their teaching in time of lockdown. In the first round, we read through the teachers’ answers of the questionnaire and identified challenges within the main task of managing the teaching processes in the lockdown. Each of these challenges corresponds to a sub-task (see Section 4). Independently each researcher identified challenges that teachers made explicit within their answers, including the choices they made to face these challenges, the techniques they used and underlying justifications. Once each researcher had identified the subtasks for his/her country, a common decision was made in order to identify sub tasks relevant to all countries.

In the second round of the analysis, specific questions within the questionnaire were associated with each of the identified sub-task. This enabled us to develop a coding of each item within teachers’ questionnaire. We then focused on teachers’ answers to the questions associated with each sub-task with the aim of developing an in-depth analysis of teachers’ answers to identify different MDP corresponding to each sub-task. There were cases where the teacher’s answer did not clearly represent a certain MDP. In the cases in which the teacher’s answer to a specific question did not support us in identifying a specific MDP, the answers were cross-checked with other answers by that teacher in order to get a clear result. If there was no clear result, the item was marked as “not sure”. Within the course of the data analysis of the teachers’ answers significant examples including techniques and justifications were identified. Additionally, the distribution of the sub-tasks and the corresponding MDP over the questionnaire was determined.

4. Results and Discussion

The result of the first round of our analysis was the identification of four sub-tasks, within the main task of managing DL in time of lockdown:

• Sub-task 1: managing DL to support students’ learning through specific methodologies
• Sub-task 2: managing DL to develop assessment
• Sub-task 3: managing DL to support those students that face difficulties and/or are living a difficult situation/developing inclusive teaching
• Sub-task 4: managing DL to exploit its potentialities for fostering typical mathematical processes

For each of these sub-tasks we identified two MDP, thanks to the second round of analysis, allowing us to classify the answers and to give an overview of the techniques and of the justifications of these techniques linked to the fundamental values on which teachers rely. The following table (Table 2) summarizes, for each sub-task, how the task can be framed referring to the didactical tetrahedron (column 2) and the MDP connected to the task itself (column 3). The characterization of the MDP, together with an analytical presentation of the results of the second round of our analysis will be proposed in the next paragraphs.

Table 2. The four sub-tasks, their reference to the didactical-tetrahedron and the corresponding meta-didactical praxeologies.

Sub-Task	Reference to the Didactical Tetrahedron	MD-Praxeologies
Sub-task 1: Managing DL to support students’ learning through specific methodologies	This sub-task refers to the face T-S-R of the tetrahedron. Moreover, the focus is on the influence of the face T-S-R on the face S-R-M (see Figure 1).	(1a) Meta-didactical praxeology related to a transmissive approach to teaching (1b) Meta-didactical praxeology related to an approach to teaching focused on the teachers’ interaction with students
Sub-task 2: Managing DL to develop assessment	This sub-task refers both to the faces T-S-M and S-R-M (see Figure 1).	(2a) Meta-didactical praxeology related to a formative conception of assessment (2b) Meta-didactical praxeology related to a summative conception of assessment
Sub-task 3: Managing DL to support those students that face difficulties and/or are living a difficult situation/developing inclusive teaching	This sub-task refers to the faces T-S-R and T-S-M (see Figure 1).	(3a) Meta-didactical praxeology connected to a “traditional” perspective on supporting students with difficulties (3b) Meta-didactical praxeology connected to a vision of supporting students with difficulties through individualized teaching–learning
Sub-task 4: Managing DL to exploit its potentialities for fostering typical mathematical processes	This sub-task refers to both faces T-R-M and S-R-M (see Figure 1).	(4a) Meta-didactical praxeology focused on teaching for conceptual/relational understanding (4b) Meta-didactical praxeology focused on teaching for instrumental/procedural understanding

4.1. Sub-Task 1: Managing DL to Support Students’ Learning through Specific Methodologies

The task of managing DL to support students’ learning was accomplished using techniques based on the teachers’ convictions, which we analyzed through the answers given to the questionnaire. The management at stake is the result of interactions between teachers and students in their relationship to available and usable resources. In addition, the results of this management concern the students’ relationship with knowledge by using resources. In this section, we distinguish two MDP, one related to a transmissive approach to learning and another focusing more on the interactions with students. The widespread ideas related to these MDP are summarized in the Table 3 and Table 4, supported with excerpts from teachers’ answers.

Table 3. Meta-didactical praxeology related to a transmissive approach to teaching.

Widespread Ideas in Teachers’ Reflections	Excerpts from Teachers’ Answers
The particular conditions do not allow teaching in any way other than face to face	“I also miss collaborative learning. I propose a problem and the students work together discussing, or I guide the problem on the blackboard and they propose solutions and come to write on the blackboard. They attempt; they reason. One stands up and then another, and together they find the solution many times. With distance learning it is not possible or, at least, I can’t do it... and it’s a shame.” (Italy, upper secondary) “Communication is reduced; teaching in this manner becomes—at times—more teacher-centered (“frontal”) and more instructive” (Germany, Gymnasium)
Techniques linked to a precise organization of the work	“I manage it by sending them several documents: a work program; the corrections of the exercises; the course of the day, and the exercises to be done for the next session, all in PDF format. I send them the work on Mondays, Wednesdays, and Fridays by email. I shoot videos explaining the corrections, the lessons, and the methods that I put on an unlisted Youtube channel created for the occasion.” (France, upper secondary) “I check the tasks they send (enter the grades in the system) and send them messages asking if they understood the material. (Israel, lower secondary)”
Justifications linked to a willingness of maintaining continuity of learning	“As in normal lessons: mental arithmetic projected on the screen, activities, exercises. The course is read instead of written.” (France, lower and upper secondary) “That’s what corresponded the most to my way of working, and I don’t see how I can continue to hook my students without oral and visual explanations (hence the videos).” (France, upper secondary) “I follow the progress in the curriculum from day to day, and if they fail to solve what is sent to them, this means that there is a problem before. And also through the output, I get from the system after they solve the exercise” (Israel, middle school)
Willingness to keep requirements to a minimum	“The introduction of new themes is more than difficult. Realizing inquiry-based learning is very difficult because the students often cannot transfer their discoveries into written language well enough. A direct exchange between all students in the classroom plenary is not possible, either.” (Germany, Gymnasium) “We’re not in a learning process. We’re in a do-it-yourself process. We have to keep them awake so that they don’t lose what was built before. I’ve seen some new notions, but many of them don’t acquire them.” (France, upper secondary)
Difficulties in maintaining the continuity due to the conditions	“So, I am trying to navigate on sight, and I do not rule out looking for other ways, above all because in the present situation I cannot support students in difficulty well” (Italy, upper secondary) “But it is necessary to have VERY humble objectives and to be very careful that my working conditions do not impact my private family life.” (France, upper secondary) “(...) Someone who is not getting in touch with me, drops through the cracks” (fällt durchs Netz) (Germany, Gymnasium)

Table 4. Meta-didactical praxeology related to an approach to teaching focused on the teachers’ interaction with students.

Widespread Ideas in Teachers’ Reflections	Excerpts from Teachers’ Answers
Willingness to maintain contact with students	“(...) I manage to maintain the social and pedagogical link with all my students...” (France, upper secondary) “Daily connection between the students and me. That’s what I loved in distance learning. That is talking and also recording through Whatsapp messages. They express their opinions, questions, and feelings.” (Israel, primary) “Many directly asked questions. Students communicate with each other intensively.” (Germany, Gymnasium) “I also organized remote group work on the topic of problem-solving. Pupils discuss and try to solve problems.” (Italy, Primary)
A new kind of relationships with students	“It’s strange: the students who communicate the most are not always the ones who participated the most in class. I am discovering the interest of some students who are usually more withdrawn.” (France, lower secondary)
Adopting this MDP requires a demanding work	“My teaching is essentially based on an interaction between students, at a distance, it is almost impossible.” (France, lower secondary) “I answer questions also during the nighttime and at the weekend, I have trouble relaxing” (Germany, Gymnasium)
An opportunity to make mathematics differently	“The main challenge was to ensure that the lessons were not flat and a-personal: I love doing math in a practical way with glue and scissors, having to go through a screen has put me in crisis. Especially because math lessons are not transmission, but we build knowledge together: recording a video lesson takes away from me the interlocutors who build knowledge with me. I solved by making schematic and maximum 10 min video-lessons that anticipate the concepts so that during the video lessons you can immediately move on to the part of interacting with the kids” (Italy, lower secondary) “Using Geogebra for geometry or functions, distance learning creates a sort of continuous mathematical laboratory and therefore can be an advantage“ (Italy, upper secondary) “I gave the recipe for the bread I make at home and a mixed activity between calculations of volumes (container, dough rising), percentages (with the increase in dough volume: double height in a truncated cone is not worth double the volume) and other questions.” (France, upper secondary)

4.1.1. Meta-Didactical Praxeology Related to a Transmissive Approach to Teaching

As expressed by the teachers, adopting this praxeology stems either from a conviction of a way of teaching based on learning hypotheses of a rather transmissive nature, or from the impossibility of setting up classroom situations in which students would be more active players in their learning.

In the four countries, this praxeology was the most represented, with around 70% of the interpretable answers with non-significant differences between countries.

The techniques that teachers put forward are often linked to a precise organization of the courses, relying on tools, either institutional (when institutional injunctions are strong), or shared and familiar to the students. Teachers justify this strict organization by the desire to maintain continuity between the classroom activities they used to give and the new online activities.

Teachers describe a struggle between the willingness to carry on as before in the classroom and the disappointment of not achieving exactly what they want, in particular in the case of those students that they cannot reach because of the working conditions. Even if they actually see the limitations of these techniques, particularly to introduce new contents, they mostly want to take advantage of DL to consolidate previously acquired knowledge.

The values of control and rationalism, which can be associated with the general idea that the main role of school is to essentially transmit knowledge, support the logos part of the praxeology. In this uncertain time, the willingness to assure security to students leaning on precise and established rules, using shared and confident tools leads teachers to focus on maintaining acquired knowledge and competencies:

“I prefer the usual tools (numerical, manual, …)” and “The work sent back is often more careful and rigorous than that usually rendered.” (France, upper secondary).

4.1.2. Meta-Didactical Praxeology Related to an Approach to Teaching Focused on the Teachers’ Interaction with Students

In this MDP, the techniques that were mainly put forward were similar to those in the previous praxeology, but the justifications focused more on the need to maintain contact with students and encourage their work, by arranging meetings with the teacher or mutual aid. Teachers highlight the new kind of relationships that they have established with their students. However, this personal investment is demanding for teachers because of the difficulties linked to the working conditions (unstable network, poor reliability of institutional platforms, family constraints) and also to the impossibility to reach all students and particularly those who have difficulties.

The main justifying discourses that teachers develop are centered on students’ capacity to learn through social interactions. For this reason, we associate this MDP with values of empiricism, openness and progress, which means focusing on an experimental view of mathematics as a field to develop creativity and criticism.

4.2. Sub-Task 2: Managing DL to Develop Assessment

A task that is of great importance for teachers is to assess students. There is a distinction between the functions of assessment that can be described as assessment of learning and assessment for learning, often classified as summative assessment and formative assessment [24,25]. Through the analysis of teachers’ reflections on the changes and adaptations of their ways of assessing students due to the emergency situation, we have highlighted that both forms of assessment still exist, and we identified two corresponding main MDPs associated with a formative and a summative conception of assessment (in the following FA and SA, respectively). The widespread ideas related to these MDP are summarized in the Table 5 and Table 6, supported with excerpts from teachers’ answers.

Table 5. Meta-didactical praxeology related to a formative conception of assessment.

Widespread Ideas in Teachers’ Reflections	Excerpts from Teachers’ Answers
Assessment as monitoring students’ work at distance to highlight their understanding and give support and feedback to students	“Through examining the exercises, they submit to me, I identify the difficulties. In addition, I initiate support talks where students raise their difficulties.” (Israel, lower secondary) “Week plans are handed in and checked at random, the students get solutions for self-control” (Germany, Gymnasium) “I have created some formative assessments [...] to check their understanding.” (France, lower secondary) “I do not give any marks based on the result, but the results are for me to understand how many are able to ‘keep up’ and to each individual student to self-evaluate their preparation.” (Italy, upper secondary)
Assessment as sharing the learning objectives with students and highlighting their real understanding	“I can verify with the children what they have really acquired, above all by asking them to explain the reasoning made to answer any questions or solve problems” (Italy, primary) “In a learning diary they document which tasks they did and when and if they had problems—and if yes, if and how they solved them.” (Germany, no school named by teacher) “I give them exercises and let them open the camera or voice and express their opinion.” (Israel, lower secondary)
Assessment as activating students as resources for one another	“I create work groups in my virtual classroom to make differentiation but also to make the pupils work together in small clusters, to make them collaborate, to mutualize skills, the strongest help the weakest...” (France, upper secondary) “The creation of small groups allowed an exchange and a direct confrontation both with the teacher and with the classmates. I can follow the path of almost everyone.” (Italy, primary)
Assessment as developing classroom discussions to highlight students’ understanding and give in-the-moment feedback.	“During the videoconference meetings, the strategies adopted are discussed and commented on. In conducting the discussion, I use an animated presentation where the students’ work and my comments are summarized.” (Italy, lower secondary) “Checking their solution and telling them where they went wrong. Let them share the white board in zoom. Letting them ask questions. I also ask other students to explain.” (Israel, lower secondary)
Assessment as fostering students in becoming responsible for their own learning: learning as an aware choice for students	“The other idea I have tried to convey to students is that DL must now really be their choice. It’s easy to hide behind a screen and copy, send all the right things, pretending they know everything. Learning becomes a conscious choice.” (Italy, upper secondary). “Younger students are much less independent than I thought. This is a big problem in these times. They must learn earlier to take responsibility for their own learning.” (Germany, Gymnasium)

Table 6. Meta-didactical praxeology related to a summative conception of assessment.

Widespread Ideas in Teachers’ Reflections	Excerpts from Teachers’ Answers
Challenges for teachers who want to perform a summative assessment at a distance.	(a) difficulty in integrating the marks given before the lockdown and the distance-assessment: “Correctly integrate the assessments given in the presence in the previous period (and therefore authentic) with the assessment of their homework in this remote period, where the assessments are always very fragmented and, in any case, conditioned by their possible access to materials and help even during the videos—lessons.” (Italy, upper secondary) (b) impossibility of maintaining fairness: The main challenge of giving marks is “the lack of written tests without tools or help of parents, learning-justice for socially weak learners” (Germany, Gymnasium) “To choose between the worst and the worst. There’s no good solution. To favor what has already been assessed is to shoot those who could have progressed; to continue to assess is to shoot those who have bad conditions to work at the moment.” (France, university level) (c) difficulties in identifying new effective foci for assessment: “(The main challenge is to) understand what I have to evaluate: the commitment? The punctuality with which they upload the required task? The correctness of the home-made tests (which will then be carried out independently or with parents’ help?)? The presence and participation in the video lessons?” (Italy, primary) (d) impossibility of grasping students’ reactions through their gazes, gestures, and attitudes. “What is missing is the possibility of expressing oneself through gestures or of being able to see well the looks of the pupils, who often say a lot about their understanding” (Italy, upper secondary)
Focus on the difficulty of identifying reliable tests to minimize the phenomenon of cheating and to overcome technical problems	“A reliable test: it is not possible to evaluate only through the test. (…) what if a student does not deliver within the expected time due to network connection, computer problems, or other reasons? For the oral tests, there are still problems, sometimes the student is visibly helped by a third person…” (Italy, upper secondary) “The written tests online completely lack credibility…there are infinite ways to do cheating (copy from classmates, receive suggestions, or get results thanks to apps/sites or other tools). It is also difficult to carry out oral tests if the student does not have a blackboard on which to do exercises.” (Italy, upper secondary) “(The challenge is) that the students got a home test and cheated.” (Israel, lower secondary) “Ideally (I would assess) with diagnostic tests, but it is hard because you cannot know who is copying the work of someone else. It would be easier in German class because you could identify the writing style” (Germany, lower secondary) “Sometimes I feel that this student deserves a higher score, or sometimes I feel that some students have copied the solution from their friends... ” (Israel, middle school) “(The challenge is) to be sure it’s not someone else’s job. So I don’t grade, I impose the multiple-choice questionnaire, seriously, but it is not graded.” (France, upper secondary) “I don’t see my students! I don’t even know if they’re there once they’re logged in. Out of a class of 35 students, between 18 and 23 log in. Between 2 and 4 are logged out along the way. On the remaining 16, when I do a poll (...), 11 answers. I must deduce that 5 are doing something else. And there are still 4 good answers!” (France, upper secondary).
Teachers’ powerlessness in front of students that are not honest	“Those who had good academic performance are working well and fully acquiring all the new topics. Those in difficulty manage to hide like never before, they are there, but they are not there when they are consulted, they have problems with the connection (!), Many do nothing, during the tests they are not honest.” (Italy, upper secondary) “I can only be supportive if a student asks me for help. If he doesn’t do it for his reasons, I can’t know about his difficulties” (Italy, upper secondary) “But for those who don’t want to turn on their microphone in class and who don’t hand in any work: nothing!” (France, lower secondary) “How do I follow the learning progress? Not at all. I appeal to my students very much at their personal responsibility concerning ZP10-/Abitur-results.” (Germany, Gymnasium)

4.2.1. Meta-Didactical Praxeology Related to a Formative Conception of Assessment

Most of the teachers, in all countries, showed that the quarantine time forced them into adopting a FA perspective, focusing on an assessment aimed at helping students in their learning:

“The dramatic conditions of the historical period we are experiencing are such that even imagining to evaluate numerically as before student learning is incorrect, prone to systematic errors and inadequate with respect to the motivations and skills of students. I think it is more appropriate to observe and enhance”.

(Italy, upper secondary)

Teachers employed different techniques to develop FA processes. Some of these techniques were adopted also by teachers who showed a SA perspective: asking students to send their homework, reading and correcting the written files shared by students, proposing tests without marks (for example, multiple-choice questionnaires), stimulating students in explaining their difficulties in order to support them and give new explanations.

In their justifying discourses about these techniques, teachers mainly stress on the need for monitoring students’ work at distance to highlight their understanding and give support and feedback to students about where they are in their learning [26].

Other techniques are justified by teachers referring, implicitly, to specific FA strategies [25]: (1) asking students to take notes of their daily work, explain their reasoning and construct argumentations, with the aim of sharing the learning objectives with students and highlighting their real understanding; (2) making students work in small groups, which is linked to the aim of activating students as resources for each other; (3) developing classroom discussions to highlight students’ understanding and give in-the-moment feedback, to make students focus on mistakes as resources to reflect on their learning and become aware of their difficulties; (4) fostering students in becoming responsible for their own learning, which is expressed through the idea that DL makes learning an aware choice for students.

For the teachers who adopted an FA perspective, assessment was conceived of as a way to keep contact with students and to support them in developing ongoing reflections on their learning processes, creating a context in which the comparison of ideas and the reflections at a metacognitive level become a shared habit of the agents involved in the FA process. For this reason, this praxeology could be associated with the values of empiricism and openness.

4.2.2. Meta-Didactical Praxeology Related to a Summative Conception of Assessment

Even when teachers declared that they did not (or must not) give marks and that the traditional way of assessing is not possible in DL, in many cases their discourses highlight a SA perspective. This is evident, for example, in the case of those teachers who declare that, in front of the impossibility of controlling the personal work of students, they prefer not to assess rather than to radically change their assessment habits. In their complaints about the impossibility of assessing at distance, teachers refer to ideas such as: (a) the difficulty in integrating the marks given before the lockdown (perceived as authentic marks) and the distance-assessment; (b) the impossibility of maintaining fairness; (c) the difficulty associated with the need for identifying new effective foci for assessment (commitment, punctuality, participation, correction of mistakes…); and (d) the impossibility of grasping students’ reactions through their gazes, gestures and attitudes.

The main techniques adopted by the teachers whose answers refer to this MDP are oral tests or written tests in the form of multiple-choice or open-ended questionnaires. Most of the teachers’ justifying discourses refer to the lack of reliability of tests when they are developed at distance and to the main problems that could prevent teachers from effectively using these techniques, such as students’ lack of tools needed to effectively assess them or, on the opposite side, students’ use of digital resources that could support students too much in solving tasks in written tests.

Another frequent element in teachers’ reflections about assessment is a focus on the fundamental role played by students. While teachers who display a FA perspective stress on the importance of making students take responsibility of their own learning, the teachers who show a SA perspective mainly complain about their powerlessness in front of students that are not honest.

Since the justifications proposed by teachers who adopted a SA perspective, even when they refer to the final aim of fostering ideas such as fairness and equity, mainly lean on the willingness to maintain established rules that should characterize mathematics teaching and learning, the logos of this praxeology can be mainly linked to the value of control.

4.3. Sub-Task 3: Managing DL to Support Those Students that Face Difficulties and/or Are Living in a Difficult Situation/Developing Inclusive Teaching

Supporting students who face difficulties in the learning process is a central task for teachers: enabling students to overcome their difficulties is particularly important to effectively involve them in the teaching–learning process and to motivate them.

We identified two main MDP associated with this task: the first one connected to a “traditional perspective”; the second one associated to an individualized approach to teaching–learning processes. The widespread ideas related to these MDP are summarized in the Table 7 and Table 8, supported with excerpts from teachers’ answers.

Table 7. Meta-didactical praxeology related to traditional perspective on supporting students with difficulties.

Widespread Ideas in Teachers’ Reflections	Excerpts from Teachers’ Answers
Devoting time to answer students’ questions and to re-explain topics	“Students who are struggling, who have questions, connect [to the platform] and stay for as long as it takes.” (France, lower secondary) “Session dedicated to specific questions at the end of the virtual classroom.” (France, lower secondary). “I provide them with detailed explanations through the online lesson or video” (Israel, lower secondary) “very little direct feedback, difficulties can be hardly collectively addressed, solutions have to be repeated often” (Germany, Gymnasium)
Providing materials that help students to follow the lessons at their personal rate	“I adapt the activities on Calcul@TICE (https://calculatice.ac-lille.fr/) and I choose the adapted pages of the Capmaths (ed. Hatier) textbook” (France, primary) “The videos and the shared whiteboards of the lessons allow those who are most in difficulty to look at the same contents several times.” (Italy, upper secondary) “I assign exercises to the group of students according to their level, and I send them different kind of videos clips to help them follow the lesson” (Israel, middle school)
Providing corrections of some exercises that students solved and organizing the lessons on students’ doubts	“We are in contact via email (I try to answer within a few hours), I upload the corrections of the most difficult exercises, and I have created a question section on a classroom that I consult before the video lessons in order to organize them according to their doubts” (Italy, upper secondary) The corrections on their works, I re-explain and above all, I send to all the self-correction files with the execution of the exercises and the explanations of the steps.” (Italy, upper secondary)

Table 8. Meta-didactical praxeology connected to a vision of supporting students with difficulties through individualized teaching–learning.

Widespread Ideas in Teachers’ Reflections	Excerpts from Teachers’ Answers
Using several tools to support students individually	“I am mostly available via messenger, that the students also use. (...)” (Germany, upper secondary) “Individual exchange by email, via the (institutional platform) discussion thread, by telephone.” (France, lower secondary) “I chose to use what in its modalities allowed me to reconcile the need to continue with a coherent educational proposal without neglecting the greatest possible inclusion. I have chosen, at least in part, to sacrifice the effectiveness and potential of some tools in order not to cut out those who already have difficulty accessing those we use” (Italy, upper secondary) “MS Teams also offers the possibility of exchanging posts with the whole class or personalized chats. In this way, you can easily communicate with a particular student to find out how the exercises are going, etc. Often, I follow a personalized conversation to the publication of a solution; other times, I ask the student to send me his/her solutions, which I then comment” (Italy, upper secondary) “One-to-one communication in the chat, screenshots” (Germany, Gymnasium) “WhatsApp, recordings and private help, YouTube videos with more explanations targeted to individuals” (Israel, middle school) “I am more patient and try to help them by several means like telephone calls, or one-to-one WhatsApp messages” (Israel, primary)
Focus on FA strategies such as developing peer assessment and activating students as responsible for their learning	“I am fortunate to have a vast majority of motivated students who also help each other through social networks such as Discord” (France, upper secondary) I encourage students to work together since they know their difficulties and know how to manage them. I also assist them if they need my help. (Israel, lower secondary) “I create workgroups in my virtual classroom to make differentiation but also to make the pupils work together in islands, to make them collaborate, to mutualize skills, the strongest help the weakest...” (France, upper secondary) “Each lesson starts with the students, they are asked to express some difficulties they have encountered in working at home, often they must be stimulated repeatedly for someone to expose themselves” (Italy, upper secondary)

4.3.1. Meta-Didactical Praxeology Connected to a Traditional Perspective on Supporting Students with Difficulties

The majority of the teachers in the four countries (about 70%) adopt this perspective to support their students during the time of lockdown.

The techniques mainly used in this praxeology lean on a direct interaction with students and they are related to the use of available tools: referring to the school textbooks, correcting exercises, taking time to explain and re-explain contents to students, and sharing videos or other resources that address students’ difficulties.

The main theme in teachers’ justifying discourses that makes us associate these discourses to a “traditional perspective” on supporting students is that teachers stress the idea that the most effective form of support consists in providing further explanations to the students. Although some teachers declare that they try to involve students directly in the teaching–learning process, devoting time to moments in which students are asked to formulate their own questions before each lesson and adapting the exercises proposed to students to their level in mathematics, the main focus of their discourses is on the fact that supporting means providing general (not individualized) other materials, such as corrections of exercises, that students are asked to use to be able to follow the lessons at their personal rate.

Since the focus is, therefore, on procedures and rules that must be learnt and repeated until they become adopted and incorporated as a basic knowledge available to students, we associate this MDP to the values of control and rationalism.

4.3.2. Meta-Didactical Praxeology Connected to a Vision of Supporting Students with Difficulties through Individualized Teaching–Learning

The main idea related to this MDP is that giving support to students means individualizing the didactical paths in order to enable all the students to reach common objectives.

This MDP is related to an approach to teaching focused on the teachers’ interaction with students (MDP 1a), since teachers show to have adopted a bi-directional and direct communication with their students, characterized by an interactive approach.

Some teachers declare that, in the quarantine time, supporting students who face difficulties is an easier task to manage than in normal times: “Paradoxically, having the time and energy, I think it is almost easier to help students in difficulty in this situation than in a traditional environment” (Italy, upper secondary school).

The techniques mainly used to develop this approach are: using a variety of digital tools such as phone, mail, forum to interact individually with students, making students work in small groups, giving individual explanations through audio or video-recordings, adding specific comments to the students’ answers.

In their justifying discourses, teachers emphasize that individualized support is required to address students’ individual differences. Moreover, they refer to an FA perspective on teaching, identifying in peer-assessment an effective way of supporting students, since students themselves are aware of the difficulties their classmates might face and can give meaningful feedback to them. Another frequent element in teachers’ discourses is a stress on the importance of involving students as being responsible for their own learning: students’ willingness of participating in the teaching–learning process is a necessary condition for effectively supporting them.

We relate this MDP to the value of openness, since the teachers aim to develop students’ understanding of mathematical constructions allowing them to develop their own explanations built on discussions and personal constructs, either through teacher–student interaction or student–student interaction.

4.4. Sub-Task 4: Managing DL and Exploiting Its Potentialities for Fostering Typical Mathematical Processes

It is of considerable interest to study the way the teaching of certain mathematical topics and concepts has changed during DL. Due to the emergency situation, teachers had to adapt their teaching, reflecting on the kind of mathematics that has a certain (or no) potential for learning in this special period. This especially includes the potentialities and limitations for fostering typical mathematical processes. Skemp’s [27] theoretical concepts of relational versus instrumental understanding as well as conceptual versus procedural knowledge [28] describe two aspects that are both essential for mathematical understanding. In the case of DL, in quarantine time, there is, for many teachers, an internal fight between what seems good and what seems possible or what is possible with their own technological knowledge and the context in which they work and in which their students work.

The following reflection highlights that some teachers felt forced to adopt a procedural approach to teaching, not in tune with their idea of teaching:

“Difficulty in learning mathematical concepts that I simplified so that they could be accessible to everyone, but probably not a correct choice. I have minimized the conceptual difficulty and I am implementing a procedural type of mathematics, more reassuring, but less effective” (Italy, primary).

Looking at the data some teachers seemed to be challenged by the new situation in a positive way and especially addressed conceptual thinking and inquiry-based learning settings during distance learning. Others seemed to reduce the conceptual challenges or stayed with teaching rather procedural notions of mathematical concepts.

Hence, we distinguish two MDP, one that focuses on teaching for conceptual/relational understanding and another that focuses on teaching for instrumental/procedural understanding.

The widespread ideas related to these MDP are summarized in the Table 9 and Table 10, supported with excerpts from teachers’ answers.

Table 9. Meta-didactical praxeology focused on teaching for conceptual/relational understanding.

Widespread Ideas in Teachers’ Reflections	Excerpts from Teachers’ Answers
A focus on making students experience a “living” mathematics	“We need to let pupils manipulate, to hear the reasoning of other pupils, to visualize methods, to learn from others” (France, primary) “Multiplication and division, because there are many games that help the student understand the meaning of multiplication and division. (Israel, primary). “I try to propose - living mathematics. Count with pieces of pasta, group dozens with chickpeas, invent your - problems and questions whenever possible. Unfortunately, even this at a distance is often complex due to parents’ mediation.” (Italy, primary)
Key-role of interaction with multiple-representations	“Like in the regular class, it is important for me to use different representation modes and flexibly change between them.” (Germany, Gymnasium) “To a large extent, I use multiple-representations, as much as I can, like in regular teaching.” (Israel, middle school) “Learning mathematics in low secondary school necessarily involves multiple representations. All the media mentioned above are tools for this from a technical point of view. And the different types of tasks are a tool for theoretical input.” (France, lower secondary)
Contraposition between an approach focused on relational understanding and an approach focused on instrumental understanding	“In my view, the greatest potential is mathematics made up of concrete workshops, where you get involved, ask yourself why and observe what is about to happen... an exercise has less mathematical potential, since it is boring for the students and useless. At the same time, the use of “ready meals” such as those that run on the internet, I think are harmful to the class group because they were not prepared for that class. I like to think that my lessons are a tailoring suit, they are tailor-made on my children and their times could not go for others” (Italy, primary)
Key-role played by inquiry-based learning, developed in interaction with others	“I propose discovery activities of a concept carried out in small groups, pooling, debate, argumentation, part of the lesson projected and explained, commented, demonstrations to be researched and presented by a student orally.” (France, upper secondary) “I find a good reaction when I propose them to solve problems, better if unusual, those that somehow deviate from the standard exercise… I focus on those that may represent a new challenge for them.” (Italy, upper secondary) “An example of an activity I created for Grade 8: Create a table of values and the graph of the functions y = 1x2, y = 2x2, y = 3x2; y = −1x2, y = −2x2 and formulate a sentence based on your observation. (Germany, upper classes of Gymnasium)

Table 10. Meta-didactical praxeology focused on teaching for instrumental/procedural understanding.

Widespread Ideas in Teachers’ Reflections	Excerpts from Teachers’ Answers
Focus on procedural aspects of mathematical concepts	“It is easier for me to teach technical topics such as investigating the Quotient function.” (Israel, lower secondary) “The typical tasks I give is to read lessons and to solve training exercises.” (France, upper secondary) “I think that everything that has to do with algebra has potential in DL, because with well-structured videos that can be viewed and reviewed if not well understood, you can follow fixed and precise rules, without improvising anything.” (Italy, upper secondary) “I focus on preparation based on the annals of competitive entrance exams at baccalaureate level” (France, upper secondary) “The showing of calculation-procedures, geometric constructions and ways to approach tasks is possible to watch with learning videos again and again. (...)” (Germany, Gymnasium)
Procedural/instrumental teaching–learning as the only possible choice in DL	“Repeating tasks are all possible, new themes are generally more difficult” (Germany, Gymnasium) “DL is just good for solving exercises. (Israel, lower secondary) “The mathematics that has more potential in DL is the one linked to calculation mechanisms that can be easily reproduced, or with procedures that are linked to algorithms that can be divided into sub-passages (to proceed more slowly, considering that students have to carry out most of the topics independently).” (Italy, upper secondary) “I believe that the part most properly linked to the consolidation of techniques or skills of a procedural nature can find a natural place in this remote mode. Distance learning can, however, in my opinion be decidedly ineffective in learning situations more marked by exploration and discovery. In these cases, I believe that the physical presence of peers and of the teacher who activates himself directly is essential” (Italy, lower secondary)

4.4.1. Meta-Didactical Praxeology Focused on Teaching for Conceptual/Relational Understanding

This MDP, adopted by a minority of teachers in our survey (about 30%) with no significant differences between the countries, is related to a view on mathematics that puts conceptual understanding to the fore and it is often based on the idea that mathematics is a science of patterns and structures (c. f. [29,30,31]). The techniques related to this view especially include to propose mathematical situations where students can experience their mathematical knowledge, problem solving, real mathematics, or “living” mathematics. The description of such techniques shows the need for curiosity and creativity.

There is also a wish to pose problems that foster critical thinking and an understanding of the current situation:

“I asked my students to model the evolution of the number of deaths by the Covid19, it was necessary to use a spreadsheet and a dynamic geometry software (GeoGebra)” (France, upper secondary).

“Modelling of the Covid 19-infection numbers in different countries with the current data of johns Hopkins related to different models (exponential, (...) logistic) (...).” (Germany, upper classes of Gymnasium).

The teachers justify these techniques by referring to a strong conviction that good mathematics teaching requires the students to grasp conceptual/relational understanding. Hence, even at distance, doing mathematics is to be confronted to conceptually challenging mathematical situations. Mathematical epistemology suggests that mathematical objects can live when manipulated, experienced and deduced by reasoning grounded on the structures. Teachers’ justifications focus on the importance of guiding students to ask themselves “why” and develop conjectures starting from their direct exploration of problems. Some teachers, in particular, stress that inquiry-based learning activities, to be developed by students in groups to foster comparison and reflection, play an important role during DL. A widespread idea in teachers’ discourses, which is strictly related to a focus on inquiry-based teaching–learning, refers to the key role that multiple-representations play in fostering students’ construction of mathematical objects as the basement for conceptual understanding. Teachers stress that DL is an opportunity to exploit the potentialities of digital representations, stressing the possibility of exploring mathematical situations taking into account different facets of the same object.

Since teachers’ focus is on mathematical situations that foster students’ interest, exploration and creativity (associated with an experimental view of mathematics), we relate this MDP to the values of empiricism, openness and progress.

4.4.2. Meta-Didactical Praxeology Focused on Teaching for Instrumental/Procedural Understanding

This MDP is related to a view on mathematics that puts a rather procedural and instrumental understanding of mathematics to the fore. Typical related techniques include proposing exercises to apply results, focusing on calculation, using online learning-videos mainly focused on procedural aspects of mathematical concepts instead of conceptual understanding. The teachers’ focus is, therefore, on activities aimed at training students to an operational and mechanical mathematics.

Many teachers from all countries justify these techniques, stressing that technical topics are predominantly used for teaching during DL. This focus on a procedural/instrumental approach to mathematics teaching–learning is not necessarily related to a vision of teaching for procedural understanding. Instead, teachers seem to stress that DL can only be carried out by teaching rather procedural topics, since, when students work on technical skills, it is easier to follow their work and to correct them.

Since the choice of focusing on procedural teaching–learning highlights a vision of mathematics as a language that needs to be mastered in order to explore its world, this MDP is associated with values of rationalism and control.

5. Conclusions and Outlook

The debate triggered at the beginning of the COVID-19 emergency has led researchers to exchange results with the aim of sharing reflections about the main consequences that this emergency could have for mathematics education [32,33,34]. Among the challenges that this situation has brought, a central role is played by the contrast between the potentialities provided by digital resources in fostering the creation of effective interactive environments for teachers and students and the risk that the actual situation could amplify the social gap that exists in the world [33]. Different studies developed in recent months have highlighted that, although the influence of the pandemic has shocked teachers at all levels, the emergency has also inspired them to find solutions to problems they had not encountered before [35]. The research documented in this paper is in tune with these results. The main question that we addressed is: How do mathematics teachers from different countries manage their teaching in the context of lockdown and which values underlie their MDP? As an answer, this paper describes different sub-tasks and corresponding MDP including techniques and justifying discourses based on teachers answers to a qualitative questionnaire. These sub-tasks, as well as the MDP, were identified in all four countries. Although the scope of this study is of a qualitative nature, the distribution of the different MDP suggests many similarities among the four countries, e.g., in respect to the dominance of the transmissive approach to teaching during time of lockdown. The data also shows that the lockdown prompts many teachers to change their praxeologies, e.g., in respect to assessment habits in mathematics during distance learning.

Teachers are teaching following their conception of teaching, their learning hypothesis, and their personal epistemology within a particular context, which includes the general education system of their country, but also the school in which they teach and the classes they teach in and which are constituted of particular students. The function of the education system is to overcome feelings constructed in the family sphere by taking a universal point of view. Therefore, in a democratic society, values that have to be transmitted are those allowing young people to develop their own judgment. In addition, the teachers relied on the democratic value system to develop their praxeologies, even in such peculiar and disturbing teaching conditions. Following the deduction line, MDP could be characterized by the tasks aiming at transmitting values and norms facilitating the awareness of universal values and the possibility to criticize them. In the context of lockdown, the main values that underlie the teaching of mathematics remain but the techniques (or most of the techniques) commonly used are no more at disposal. We refer in this paper only to the mathematical values, adopting Bishop’s framework, but the issue of the maintaining a universality of school during the lockdown remains lively and merits further study. However, the six value clusters that Bishop originally identified constituted a filter allowing to go through and interpret the questionnaire answers, in terms of MDP developed by the teachers.

In addition to the sub-tasks described in the section above, many teachers wrote deep and detailed reflections that could not be described in this paper in detail. One of the most dominant results is the reflection by the teachers on the role of norms. Many teachers address the challenge to secure fairness and equity especially for students with low achievements, some of them suffer that they cannot secure educational justice, i.e., by only dealing with students’ written documents. In that context, many teachers also address the lack of interaction with the students (“DL is the death of interaction”, upper secondary, Italian teacher), as well as having eye-contact and using gestures during these interactions. Therefore, many teachers write, the role of the parents becomes crucial for corresponding with the students, while others (especially secondary school teachers) stress that DL increases the responsibility of the students for their individual learning. Finally, many teachers stress that the insight from the time of lockdown is that school has the opportunity to change: “Of course, school MUST take this opportunity to radically change its ancient teaching method. it is not about bringing small changes or somehow inserting some technological tool; it is about building a new type of school that responds to today’s time.” (lower secondary, Italian teacher).

Of course, to some extent, such reflections represent singular opinions and they are not representative, which is one of the limitations of this study. Although almost 700 teachers participated in this study, the aim was to get deep insights into the meta-didactical praxeologies—the techniques used, as well as the justifying discourses and the underlying values. The distribution of these MDP among the countries suggests certain tendencies, but this study is limited with respect to quantitative findings due to its qualitative nature. A second limitation can be seen also in respect to the choice of the involved countries, which—by all differences—are comparable e.g., in respect to their educational systems or socio-economic factors. This study did not give respect to challenges for example in less developed countries. However, it is of great interest to note that in these difficult times individualized relationships with pupils have particularly developed; it is in the analysis of meta-didactical praxeologies that we can highlight the willingness of teachers to make the classroom as inclusive as possible. This would certainly be a question that would need to be explored in depth, in particular to see whether changes in attitudes really occur and if they will continue under normal teaching conditions to develop for a more inclusive education [36,37,38].

This study generated sub-tasks and corresponding MDP, which will enable us to formulate clear hypotheses, which can be used for rigorous quantitative research. As an agenda beyond the identification of the sub-tasks and the MDP, we first set out to investigate the distributions of the identified MDP quantitatively. Additionally, countries of different backgrounds have to be considered in future research. To better investigate the MDP, students should also be involved in the process of interpreting the teachers’ activities. Finally, the process of development of new praxeologies on the level of the individual teacher has to be considered.

As an overall conclusion, we see that the pandemic has affected mathematics teaching intensely. The teachers’ reflective contributions to this study enabled us to identify MDP common to all the four involved countries. As a next important step, we will (and recommend to) share these results with teachers (not only those involved in the survey) to reflect with them about the MDP, the techniques, the justifying discourses as well as the underlying values we identified and to have a feedback about our interpretation of teachers’ answers. For us, one of the potentials of this study is to deepen the dialogue between teachers and researchers in order to be aware of and to reflect on the choices we can take in the case of future pandemics.