Data Envelopment Analysis-Based Approach to Improving of the Budget Allocation System for Decarbonization Targets

Abstract

Energy innovation plays an important role in the transition to a zero-carbon economy. Governments in IEA member countries are investing in the R&D, demonstration, and deployment of new energy technologies as part of their energy and climate policies. However, government subsidies for energy innovation are not always efficient in achieving climate policy goals. This paper proposes a two-stage Data Envelopment Analysis model with shared inputs to determine the optimal allocation of public funds for the energy innovation process. The innovation process is divided into two stages: the R&D stage and the commercialization stage. The inputs to the model (budget expenditures for energy innovations) are distributed between the first and second stages. As intermediate products, we use the number of patents in clean energy and hydrocarbon energy. The outputs of the model are the changes in carbon intensity and energy efficiency. This model can be used to assess the effectiveness of government spending on energy innovation. The results show that some IEA member countries should allocate a large part of the fossil fuel technology budget (more than 70%) to the research and development phase. The proposed model can support decision making at the international level to increase the effectiveness of public policies in achieving decarbonization and energy efficiency goals.

1. Introduction

In recent years, the decarbonization of the global economy has become a top priority for sustainable development. According to the International Energy Agency (IEA), achieving net-zero CO₂ emissions by 2050 requires a significant increase in investment and a shift in capital allocation to transform the global energy system. The Net Zero Energy (NZE) plan aims to increase annual energy investment from the current global average of just over USD 2 trillion to nearly USD 5 trillion by 2030 and USD 4.5 trillion by 2050. The total annual capital investment in energy in the NZE is projected to increase from approximately 2.5% of global GDP in recent years to around 4.5% in 2030 before decreasing to 2.5% by 2050 (Bouckaert et al. 2021; Kober et al. 2020).

In moving towards a carbon-free economy, innovations play a significant role. Accelerating clean energy innovation is crucial, and governments should prioritize R&D, demonstration, and deployment in their energy and climate policies. According to statistical data, IEA member countries have consistently allocated significant funds (from federal budgets and from state-owned companies) to energy research and innovation over the past 12 years (see Figure 1). Although there was a slight dip in 2015–2016, the funding for energy innovation has since increased significantly.

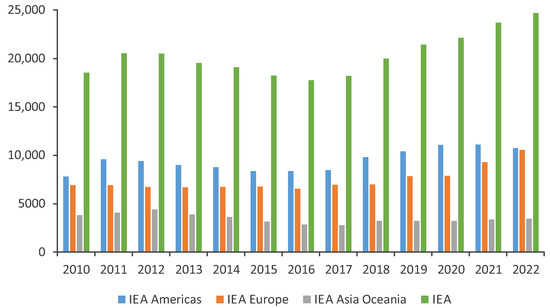
Figure 1. RD&D budgets of IEA member countries (in millions USD 2022 prices and PPP). Source: based on data from https://www.iea.org/data-and-statistics/data-product/energy-technology-rd-and-d-budget-database-2 (accessed on 25 April 2024).

The IEA reports that if the world maintains it current levels of funding and efficiency in developing and implementing energy innovations, it will still result in about 22 billion tons of CO₂ emissions worldwide in 2050. This will lead to a temperature rise of about 2.1 °C in 2100. A major innovation effort will be needed in this decade to bring these new technologies to market in time. According to the IEA, about USD 90 billion in public funding needs to be mobilized globally as soon as possible to complete a portfolio of demonstration projects by 2030, while the current budget for this period is only about USD 25 billion. Since an explosion in funding is unlikely in the current difficult economic and geopolitical environment, the focus should shift to improving the efficiency of government subsidies for the development of innovative energy technologies. In the future, achieving net-zero will require not only the rapid deployment of available energy technologies but also the deployment of technologies that are not yet on the market. By 2050, almost half of the abatement will come from technologies that are currently at the demonstration or prototype stage (Bouckaert et al. 2021). Deficit public R&D spending should therefore be reprioritized and optimized.

The above information suggests that optimizing the allocation of financial resources to innovation in the energy sector is a highly relevant problem. In order to solve this problem, it is necessary to know which country is more efficient at allocating funds and why. The assessment of the comparative effectiveness of different countries in achieving decarbonization goals through government incentives for energy innovation helps to identify the most effective policies. This kind of knowledge helps to proactively develop and implement the innovations most conducive to achieving decarbonization goals. Data Envelopment Analysis (DEA) can be proposed as an effective solution for this task. DEA is a well-developed methodology for assessing the comparative efficiency of homogeneous economic systems or agents often used to calculate the efficiency of innovation processes.

Conventional DEA is a popular nonparametric technique for measuring the performance of homogeneous decision-making units (DMUs) that use multiple inputs to produce multiple outputs. A DMU is efficient (score equals 1) if no other DMU can produce more outputs with fewer or equal inputs. In addition to identifying efficient and inefficient units (scores less than 1), the DEA approach also allows each inefficient unit to calculate target values of inputs (or outputs) at which this unit can become efficient. This kind of information is very useful for optimizing resource allocation.

In recent years, a more sophisticated approach has been gaining popularity in the literature, which allows us to split the DMUs under the study into several stages and investigate the integrated efficiency of the DMU, thus taking into account the contribution of each stage to the overall (system) efficiency. This approach is called Network DEA (NDEA), and it is considered to be more informative than traditional DEA models. DEA applications need to recognize the distinction in the shared inputs between two-stage processes to avoid underestimating efficiency. For this reason, NDEA has been actively used in recent years to evaluate and select the most efficient innovation systems, which, as a rule, are always decomposed into two parts: one representing the research and development process and the other the process of commercialization of innovations. The application of NDEA allows us to better identify the source of inefficiencies in the innovation system and to propose options for optimizing the allocation of resources at each stage.

However, when modeling complex innovation processes using DEA, a number of issues that often arise in practice are still poorly understood. In particular, the question of optimal resource allocation between the two stages of the innovation process is one of them. Actual statistics collected at the country and enterprise level often do not distinguish between the proportion of resources spent on R&D and the commercialization of innovations. These types of NDEA problems are of particular interest, because their solution can help decision makers to optimize resource allocation not only at each stage of the innovation process separately but also between stages.

The contribution of this study is twofold: first, this paper proposes an NDEA model with shared inputs for assessing the efficiency of government spending on energy innovation in IEA member countries; second, this study provides some insights into the issue of resource allocation between R&D and deployment of innovations.

The remainder of this study is structured as follows: Section 2 reviews previous research papers that have used for Network DEA with shared inputs; Section 3 describes the NDEA methodology and applies it to the problem of choosing the optimal resource allocation strategy; Section 4 describes the data; Section 5 presents the results of calculations; and Section 6 provides their discussion; the paper concludes with Section 7, thus summarizing the key findings, policy implications, limitations of the study, and future research directions.

2. Literature Review: NDEA Models with Shared Inputs

The idea of the DEA approach originated in the seminal papers of Farrell (1957) and Farrell and Fieldhouse (1962), who conducted the first empirical study on efficiency measurement. At the end of the 1970s, the approach was generalized and reformulated in the form we use today by Charnes et al. (1978). Since that time, DEA has gained immense popularity as a method that allows the researcher to assess the comparative efficiency of homogeneous economic agents just by knowing information about their inputs (volumes of resources consumed) and outputs (volumes of products produced). To date, the DEA methodology has been greatly developed (Emrouznejad and Yang 2018), thus extending its capabilities to an increasing number of problems in which the modeled economic agents (decision-making units, or DMUs) have a complex structure: two- and three-stage structures, network structures with feedback, loops, shared inputs, undesired outputs, etc. (Kao 2014; Ratner and Lychev 2019). In the last few years, models of systems that have a network structure have undergone a great deal of development and have been referred to as Network DEA (Ratner et al. 2023).

One of the major differences between DEA and NDEA is the depth of analysis. DEA is primarily used to evaluate the efficiency of individual DMUs by comparing their inputs and outputs, while NDEA focuses on evaluating the efficiency of entire networks or systems composed of interconnected subprocesses. This means that NDEA can provide a more accurate measure of the efficiency of a complex system, thus taking into account the interdependencies and interactions between different subdivisions (Kao 2023).

Additionally, NDEA can handle more complex and dynamic systems compared to traditional DEA models. By modeling the interdependencies between decision-making units, NDEA can account for the consideration of the flow of inputs and outputs among units within a network. This makes NDEA a more suitable method for evaluating the efficiency of systems with multiple interconnected components. This approach enables the identification of potential avenues for optimization and improvement in network settings.

One of the features of NDEA models is the presence of so-called shared inputs, where the same type of resource is consumed in more than one stage of the modeled production process (a DMU). In numerous DEA applications, inputs are utilized by multiple processes. While the total amount of input is known, insufficient information exists regarding the quantity consumed by each process. The DEA literature classifies this situation as shared inputs. It is important to distinguish shared inputs from another scenario where inputs enter the production processes of multiple outputs simultaneously, but the input for one output does not affect the use of the same input for another output. This case is referred to in the literature as joint inputs (Cherchye et al. 2014).

The extensive literature on NDEA shared inputs is primarily due to their frequent occurrence in real-world applications. Consequently, studies often examine shared input NDEA applications in the context of banks and bank branches (Amirteimoori et al. 2016; Cook et al. 2000; Haas 2003; Omrani et al. 2023; Toloo et al. 2017; Zha and Liang 2010). For example, Zha and Liang (2010) considered employees, assets, and equity as shared inputs in bank operations. Toloo et al. (2017) considered fixed assets, the number of employees, and IT investment as shared inputs in generating deposits. In the second stage, banks use the deposits generated in the first stage as a source of funding to invest in securities and issue loans. The outputs in this stage were determined by the returns and risks associated with these activities. Each input was allocated to both the deposit and loan stages.

Tsai and Mar Molinero (2002) considered a multiactivity model for National Health Service (NHS) trusts in the UK and used as the input the total operating expenditure, which reflects the cost of providing patient care and services. This expenditure was shared between all five categories of specialties: medical, surgical, maternity, psychiatric, and ‘other’. The ‘other’ category includes general practice, radiotherapy, pathology specialties and radiology, anesthetics, and accident and emergency. These inputs were used to assess the operational performance of the trusts. The model explored the allocation of resources between trusts and the internal allocation of resources within inefficient trusts.

Yu and coauthors studied the efficiency of road transportation companies, and the shared inputs for highway bus service and urban bus service included the number of managers, employees, and mechanics used by both modes (Yu 2008; Yu and Fan 2006). Amirteimoori and Yang (2014) developed the model for a two-stage parallel series production process, which consists of two production lines arranged in series: a structure production line and a doors and windows production line. The shared inputs in the two-stage production process are woods, aluminums, and glasses. Li et al. (2022) modeled airlines as parallel subsystems, which are separate departments or components involved in air passenger and freight transport. These subsystems had their own inputs, outputs, and resources, but they also shared certain inputs and outputs, such as operating costs.

Lei et al. (2015) measured the performance of participating nations in the Olympic Games. Shared inputs in the model referred to the inputs that are used by both the Winter Olympic Games and the Summer Olympic Games, which are considered parallel processes. The shared inputs in the model are the GDP per capita and the population of the participating nation, which are the most important factors that affect the economic and demographic power of the participating nation. Villa and Lozano (2024) proposed an approach, which considers the inputs consumed by different subprocesses within a football team, such as salaries and sporting results, and examined how these inputs are transformed into market value. Li et al. (2018) investigated the fire protection system in the US. The first stage of the fire protection system evaluation involves the fire hazard defense subsystem, while the second stage addresses the fire incident fighting activities. The shared inputs in the model are the gross state product (GSP) and the population.

Nematizadeh et al. (2020) applied a three-stage DEA model to the problem of water usage. The shared inputs mentioned in their study include water and capital. The first and second stages consume input vectors and shared inputs, and they produce desirable and undesirable outputs. The third stage utilizes inputs from the previous stages, as well as additional inputs, and it produces desirable and undesirable outputs. Each stage has its own set of inputs and outputs, and they are interconnected in a parallel series structure. Water is used as an input in the industrial, agricultural, household, and environmental categories. Capital is also considered as a shared input in these categories.

A common feature of the above models is the treatment of the proportion of shared inputs utilized by various processes as decision variables to be estimated by the efficiency assessment model. The exact amount of each input consumed by each subprocess is unknown, but the shared-input NDEA model allows for the evaluation of the efficiency of these processes and the allocation of shared inputs between parallel or sequential processes. The models with shared intermediate products were considered in (Tavares et al. 2021; Zegordi and Omid 2018).

Most commonly, DEA network models with shared inputs are used to model innovation processes and academic activities (Despotis et al. 2015; Lu 2012), for example, technology innovations in high-technology companies (e.g., (Ma 2015; Wang et al. 2020)), regions (Broekel et al. 2018), or research in universities (e.g., (Chen et al. 2023; Ding et al. 2023; Lee and Worthington 2016)). This is because the innovation process is naturally divided into two stages: the research and the commercialization of innovations. Many types of resources, including human, financial, and equipment, are used at both stages. The same approach is applicable to the study of the performance of universities that combine educational and research activities. In the context of measuring university efficiency, shared inputs can include resources such as full-time teachers and graduate students who contribute to both the teaching and research stages of universities. These inputs cannot be divided between the stages and need to be incorporated into the efficiency analysis (Chen et al. 2023). Toloo et al. (2017) changed the sequence of the research and education process in a two-stage model and considered research income as an outcome from the first stage, which can be used as a source of funds to improve students’ education in the second stage. As shared inputs, they considered general expenditure, equipment expenditure, and research income. These inputs were used in both the first stage (researching) and the second stage (teaching) of the university’s processes.

Even when resources can be shared between stages, statistics often fail to distinguish the proportion of resources used exclusively in the first stage from those used exclusively in the second stage. For example, Zhang et al. (2019) considered a two-stage model to represent the innovation process in high-tech enterprises. The initial stage, which focused on research and development, involved inputs such as research equipment expenses and the number of researchers. The second input was allocated between the first and second stages according to exogenously given factors. The outputs of the first stage, serving as inputs for the second stage, included patent applications and patents in force. The second stage, centered on commercialization, encompassed expenses for technical upgrades, the procurement of national and international technologies, technology adaptation costs, and new product development expenditures. The system outputs included the revenue generated from the sales of newly introduced products and the number of contracts within the domestic market. A similar network model was employed by Wei et al. (2017) for innovation-oriented city assessment and by Zhang and Cui (2020) to examine regional innovation efficiency.

These studies collectively demonstrate the versatility and applicability of DEA with shared inputs in various industries and contexts. However, although the literature on DEA network models with shared inputs is quite representative, the issue of the optimal allocation of inputs between competing processes (or stages) is poorly understood. Most studies have assumed that all DMUs share their inputs in a certain proportion. We have not encountered studies in which each unit could independently determine the proportion of input sharing between stages or parallel processes. The focus of this study is, therefore, on whether DMUs can optimize the allocation of their resources in such a way as to maximize the overall system efficiency. Applied to the question of improving the efficiency of energy innovation, this research question can be formulated as follows: can each country optimize public funding for innovation in a way that comes as close as possible to achieving its decarbonization targets?

3. Materials and Methods

Consider a two-stage DEA model with shared inputs. Suppose that each DMU_j ($j=1,\cdots ,n$) consumes vector of resources $X_j={\left(x_{1j},\cdots ,x_{mj}\right)}^{\mathsf{T}}$ to produce output vector $Y_j={\left(y_{1j},\cdots ,y_{rj}\right)}^{\mathsf{T}}$. In a two-stage model with shared inputs, some part of the resources $X_j^1$ is used at the first stage, and the remaining part $X_j^2$ is consumed at the second stage, i.e., $X_j=X_j^1+X_j^2$. Let $\alpha ={\left({\alpha }_1,\cdots ,{\alpha }_m\right)}^{\mathsf{T}}$ be the vector of coefficients that represent shares of inputs that are used at the first stage. All coefficients of $\alpha$ satisfy ${\alpha }_i\in \left[0,1\right]$, where $i=1,\cdots ,m$. Given the vector $\alpha$, the input vector of jth DMU at the first stage $X_j^1={\left(x_{1j}^1,\cdots ,x_{mj}^1\right)}^{\mathsf{T}}$ is calculated as $X_j^1={\left({\alpha }_1{x}_{1j},\cdots ,{\alpha }_m{x}_{mj}\right)}^{\mathsf{T}}$ and as $X_j^2={\left(x_{1j}^2,\cdots ,x_{mj}^2\right)}^{\mathsf{T}}={\left((1-{\alpha }_1)x_{1j},\cdots ,(1-{\alpha }_m)x_{mj}\right)}^{\mathsf{T}}$ at the second stage. Outputs of the first stage $Z_j^1={\left(z_{1j}^1,\cdots ,z_{dj}^1\right)}^{\mathsf{T}}$ are called intermediate products; they are considered as inputs $Z_j^2={\left(z_{1j}^2,\cdots ,z_{dj}^2\right)}^{\mathsf{T}}$ at the second stage of the production process. The typical structure of two-stage DEA models with shared inputs is depicted in Figure 2 below. Note that according to the classification of network models proposed by Kao (2014), this model has the simplest series network structure.

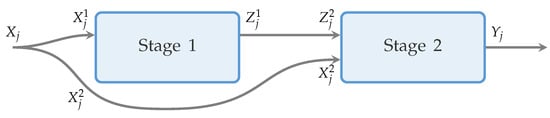
Figure 2. Two-stage process with shared inputs for DMU_j.

The production possibility set T of a two-stage model with shared inputs is determined as a set of such vectors $(X^1,Z^1,X^2,Z^2,Y)$, where the outputs Y can be produced from the inputs $X^1$ and $X^2$ using intermediate products such that $Z^1\ge Z^2$.

Since some outputs in the data are negative, we should use a special type of DEA model that allows us to evaluate the efficiency scores in the presence of negative data. In this paper, we used the Range Directional Measure (RDM) model to evaluate efficiency scores. This model represents the variable returns to scale, and other returns to scale assumptions cannot be incorporated into this model. In our previous study (Lychev et al. 2023), we compared several two-stage DEA models with negative system outputs and with different returns-to-scale assumptions. Among the considered models, the RDM model displaying the variable returns to scale demonstrated the highest measure of model consistency, which was evaluated by comparing the efficiency scores of the two-stage model and the conventional whole-unit model, where the DMU was treated as a black box.

In the RDM model, two ideal points are introduced for the first and second stages, respectively:

$$\begin{array}{cc}\hfill I_1& ={\left({\overline{x}}_1^1,\cdots ,{\overline{x}}_m^1,{\overline{z}}_1^1,\cdots ,{\overline{z}}_d^1\right)}^{\mathsf{T}},\hfill \\ \hfill I_2& ={\left({\overline{x}}_1^2,\cdots ,{\overline{x}}_m^2,{\overline{z}}_1^2,\cdots ,{\overline{z}}_d^2,{\overline{y}}_1,\cdots ,{\overline{y}}_r\right)}^{\mathsf{T}},\hfill \end{array}$$

where ${\overline{x}}_i^1={min}_j{x}_{ij}^1$, ${\overline{x}}_i^2={min}_j{x}_{ij}^2$, $i=1,\cdots ,m$, ${\overline{z}}_q^1={max}_j{z}_{qj}^1$, ${\overline{z}}_q^2={min}_j{z}_{qj}^2$, $q=1,\cdots ,d$, ${\overline{y}}_k={max}_j{y}_{kj}$, and $k=1,\cdots ,r$. Next, the directional vectors from DMU_p to ideal points $I_1$ and $I_2$ in the first and second stages, respectively,

$$\begin{array}{cc}\hfill \left(R_p^{X1},R_p^{Z1}\right)& =\left(R_{1p}^{X1},\cdots ,R_{mp}^{X1},R_{1p}^{Z1},\cdots ,R_{dp}^{Z1}\right),\hfill \\ \hfill \left(R_p^{X2},R_p^{Z2},R_p^Y\right)& =\left(R_{1p}^{X2},\cdots ,R_{mp}^{X2},R_{1p}^{Z2},\cdots ,R_{dp}^{Z2},R_{1p}^Y,\cdots ,R_{rp}^Y\right),\hfill \end{array}$$

are determined as follows:

$$\begin{array}{cccc}\hfill R_{ip}^{X1}& =x_{ip}^1-{\overline{x}}_i^1,\hfill & \hfill i& =1,\cdots ,m\hfill \\ \hfill R_{qp}^{Z1}& ={\overline{z}}_q^1-z_{qp}^1,\hfill & \hfill q& =1,\cdots ,d\hfill \\ \hfill R_{ip}^{X2}& =x_{ip}^2-{\overline{x}}_i^2,\hfill & \hfill i& =1,\cdots ,m\hfill \\ \hfill R_{qp}^{Z2}& =z_{qp}^2-{\overline{z}}_q^2,\hfill & \hfill q& =1,\cdots ,d\hfill \\ \hfill R_{kp}^Y& ={\overline{y}}_k-y_{kp},\hfill & \hfill k& =1,\cdots ,r.\hfill \end{array}$$

The two-stage RDM model with shared inputs is written as follows (Ratner and Lychev 2023):

$$\begin{array}{cc}\hfill max& {\theta }_1{w}_1+{\theta }_2{w}_2\hfill \\ \hfill \text{s.t.}& \sum _{j=1}^n{x}_{ij}^1{\lambda }_j\le x_{ip}^1-{\theta }_1{R}_{ip}^{X1},i=1,\cdots ,m\hfill \\ \hfill & \sum _{j=1}^n{z}_{qj}^1{\lambda }_j\ge z_{qp}^1+{\theta }_1{R}_{qp}^{Z1},q=1,\dots ,d,\hfill \\ \hfill & \sum _{j=1}^n{\lambda }_j=1,{\lambda }_j\ge 0,j=1,\cdots ,n\hfill \\ \hfill & \sum _{j=1}^n{x}_{ij}^2{\mu }_j\le x_{ip}^2-{\theta }_2{R}_{ip}^{X2},i=1,\dots ,m\hfill \\ \hfill & \sum _{j=1}^n{z}_{qj}^2{\mu }_j\le z_{qp}^2-{\theta }_2{R}_{qp}^{Z2},q=1,\dots ,d,\hfill \\ \hfill & \sum _{j=1}^n{y}_{kj}{\mu }_j\ge y_{kp}+{\theta }_2{R}_{kp}^Y,k=1,\cdots ,r\hfill \\ \hfill & \sum _{j=1}^n{\mu }_j=1,{\mu }_j\ge 0,j=1,\cdots ,n,\hfill \\ \hfill & \sum _{j=1}^n{z}_{qj}^1{\lambda }_j\ge \sum _{j=1}^n{z}_{qj}^2{\mu }_j,q=1,\cdots ,d,\hfill \end{array}$$

(1)

where weights $w_1$ and $w_2$ represent the importance of each stage in the whole process and satisfy $w_1+w_2=1$. In model (1), the first three constraints refer to the first stage of the network model; the next four constraints determine the technology of the second stage; and the last constraint reflects the linkage between the technologies of the stages.

The model possesses useful properties (translation invariance and unit invariance) that enable the efficiency measurement of using negative system outputs. The efficiency score of the first stage is calculated as ${\rho }_1=1-{\theta }_1^{*}$, where ${\theta }_1^{*}$ is optimal in model (1). In the second stage, the efficiency score is obtained in a similar way as ${\rho }_2=1-{\theta }_2^{*}$. The overall efficiency is defined as the weighted sum of the efficiency scores in each of the stages and can be measured as $\rho =w_1{\rho }_1+w_2{\rho }_2=1-(w_1{\theta }_1^{*}+w_2{\theta }_2^{*})$.

To evaluate efficiency scores, model (1) requires information for each DMU on how input resources are distributed between two stages. In many practical applications, such information is not available. Therefore, there are two approaches to overcoming this situation.

The first approach uses expert knowledge and experience to make estimations of $\alpha$ values. We apply such an approach for the evaluation of the efficiency of countries’ government spending on energy innovations in (Ratner and Lychev 2023).

The other approach is to find the impact of how the shared inputs are distributed in a two-stage process so that efficiency is maximized. Chen et al. (2006) developed a nonlinear programming model to investigate the influence of shared inputs on two-stage model efficiencies. To overcome the nonlinearity issues, Toloo et al. (2017) proposed a linear DEA model for dealing with shared inputs. However, a model with only one intermediate product was considered. If there are multiple intermediate measures, the transformation of the fractional program into a linear program should be carried out.

The models described above are not designed to work with negative data. At least, the authors did not consider such a possibility in their research. Moreover, the existing methods were developed for radial measurements with constant returns-to-scale (CRS) technology assumption and cannot be applied directly to the RDM model.

The problem involves selecting proportions (weight coefficients $\alpha$) to distribute inputs between two stages in a way that maximizes the overall efficiency measure for the evaluated DMU. The proportion remains fixed for the rest of the DMU.

The RDM model is distinctive in that as the input shares between the two stages change, the position of the ideal points $I_1$ and $I_2$ relative to which efficiency is measured changes. This results in the following nonlinear model:

$$\begin{array}{cc}\hfill max& {\theta }_1{w}_1+{\theta }_2{w}_2\hfill \\ \hfill \text{s.t.}& \sum _{j=1}^n{\alpha }_{0i}{x}_{ij}{\lambda }_j\le {\alpha }_i{x}_{ip}-{\theta }_1{R}_{ip}^{X1},i=1,\cdots ,m,\hfill \\ \hfill & \sum _{j=1}^n{z}_{qj}^1{\lambda }_j\ge z_{qp}^1+{\theta }_1{R}_{qp}^{Z1},q=1,\cdots ,d,\hfill \\ \hfill & \sum _{j=1}^n{\lambda }_j=1,{\lambda }_j\ge 0,j=1,\dots ,n,\hfill \\ \hfill & \sum _{j=1}^n(1-{\alpha }_{0i})x_{ij}{\mu }_j\le (1-{\alpha }_i)x_{ip}-{\theta }_2{R}_{ip}^{X2},i=1,\cdots ,m,\hfill \\ \hfill & \sum _{j=1}^n{z}_{qj}^2{\mu }_j\le z_{qp}^2-{\theta }_2{R}_{qp}^{Z2},q=1,\cdots ,d,\hfill \\ \hfill & \sum _{j=1}^n{y}_{kj}{\mu }_j\ge y_{kp}+{\theta }_2{R}_{kp}^Y,k=1,\cdots ,r,\hfill \\ \hfill & \sum _{j=1}^n{\mu }_j=1,{\mu }_j\ge 0,j=1,\dots ,n,\hfill \\ \hfill & \sum _{j=1}^n{z}_{qj}^1{\lambda }_j\ge \sum _{j=1}^n{z}_{qj}^2{\mu }_j,q=1,\cdots ,d,\hfill \\ \hfill & L\le {\alpha }_i\le U,i=1,\cdots ,m,\hfill \end{array}$$

(2)

where vector ${\alpha }_0$ is fixed for all DMUs; parameters L and U satisfy $0<L\le U<1$. Note that directional vectors $\left(R_p^{X1},R_p^{Z1}\right)$ and $\left(R_p^{X2},R_p^{Z2},R_p^Y\right)$ depend on vector $\alpha$ in model (2), because the position of ideal points $I_1$ and $I_2$ also depends on $\alpha$ weights.

This paper proposes an optimization method based on simulated annealing to solve this model. The algorithm is given below.

In the initial stages of Algorithm 1, the temperature parameter $t_k$ is set at a high value, thus allowing for the acceptance of $\alpha$ variation that may lead to significant improvement in the efficiency score. This enables a thorough exploration of the weights space. As $t_k$ gradually decreases, only transitions that improve the efficiency score or have minimal negative impact are accepted. Eventually, as $t_k$ approaches zero, any deterioration in the efficiency score is rejected, thus resulting in the simulated annealing algorithm resembling a Monte Carlo algorithm.

Algorithm 1 Solving the model (2).

Input: $(X_p,Z_p,Y_p)$—evaluated DMU, ${\alpha }_0$—vector of input shares for other DMUs, except for the one being evaluated; $t_0$—initial temperature; $t_{\min }$—temperature threshold (stopping criterion); $\beta$—cooling rate. Output: $\alpha$—vector of input shares; $\rho$—efficiency score.   1: Set $\alpha \leftarrow {\alpha }_0$, $\rho \leftarrow 0$, $k\leftarrow 0$.                         ▹ Initialization   2: do   3:     Generate vector $\overline{\alpha }$ from the neighborhood of the current solution $\alpha$         such that $L\le \overline{\alpha }\le U$.   4:     Given the vector $\widehat{\alpha }$, calculate $X_p^1$, $X_p^2$, $R_p^{X1}$, $R_p^{X2}$, solve model (1), and find         efficiency score $\widehat{\rho }$.   5:     if $\widehat{\rho }>\rho$ then   6:         Set $\alpha \leftarrow \widehat{\alpha }$, $\rho \leftarrow \widehat{\rho }$.                      ▹$\widehat{\alpha }$ becomes the current solution   7:     else   8:          $\widehat{\alpha }$ becomes the current solution $\alpha$ and $\widehat{\rho }$ becomes the current efficiency score $\rho$           with probability $exp((\widehat{\rho }-\rho )/t_k)$.   9:     end if 10:    Set $k\leftarrow k+1$. 11:    Compute $t_k\leftarrow t_{k-1}/\beta$. 12: while $t_k>t_{\min }$ and $\rho <1$ 13: return $\alpha$, $\rho$.

The iterative process of Algorithm 1 solves model (1) multiple times with varying proportions of shares between the two stages to determine the optimal allocation of inputs. This iterative process allows us to fine-tune the allocation of resources within the DMU to maximize efficiency.

4. Data Description and Variable Selection

The data on the amount of public funding for research and development and energy demonstration projects (RD&D) for various energy technologies were obtained from the IEA Energy Technology RD&D Budgets database. The whole process of developing and implementing innovations in the energy sector has been modeled as a two-stage process and was divided into the R&D stage and the commercialization stage. Since demonstration projects, as a rule, belong to the stage of commercialization of innovations, budget expenditures should be distributed between the first and second stages in some unknown proportion.

As an intermediate output of the first stage, which at the same time is an output for the second stage, the number of patents in the energy field is considered, which is divided by the number of patents in the clean energy field and in the hydrocarbon energy field. The data on patents were taken from the IEA Energy Technology Patents Data Explorer (https://www.iea.org/data-and-statistics/data-tools/energy-technology-patents-data-explorer, accessed on 25 April 2024).

The outputs of the second stage were the changes in the carbon intensity (CO₂ metric tons per unit of GDP) and the energy efficiency (constant 2017 PPP $ per kg of oil equivalent) of each country over time. To smooth out the impact of small fluctuations in business activity, we used a three-year smoothing and took into account the difference between the averages for 2010–2012 and the averages for 2016–2018. The data for calculations were obtained from the World Bank database.

The final sample included 23 countries: Australia, Austria, Belgium, Brazil, Canada, Czech Republic, Denmark, Finland, France, Germany, Hungary, Ireland, Italy, Japan, South Korea, the Netherlands, Norway, Poland, Spain, Sweden, Switzerland, UK, and the USA.

To remove the influence of the size of a country and its economy, we converted all variables into relative values: percentage of GDP (for budgets) or number per 1000 inhabitants (for patents).

We have also taken into account the fact that the process of developing and implementing innovations is spread out over time. For this purpose, we have introduced the assumption that the time lag between investing in R&D and obtaining a scientific result (patent) is three years, and the time lag between obtaining a patent and its practical implementation is also three years.

The conceptualization of the model is presented in Figure 3.

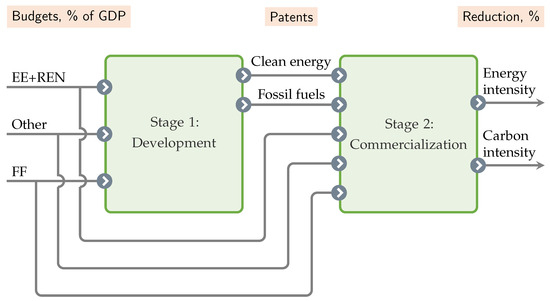
Figure 3. NDEA model for innovation processes in energy field.

According to the statistics for 2010–2018, not all countries in the sample have increased their energy efficiency and reduced their carbon intensity. From a technical point of view, this means that for some DMUs, the system outputs are negative. In DEA, such problems require the use of special solution methods, which were discussed in detail in a previous paper by the authors (Lychev et al. 2023).

5. Computational Results

As a starting point and for reference purposes, we present the computations that were performed earlier (Ratner and Lychev 2023) for the case when each of the inputs is shared between two stages equally for all DMUs. The results are provided in Table 1.

Table 1. Efficiency scores in two-stage RDM model with shared inputs (${\alpha }_{\mathrm{FF}}={\alpha }_{\mathrm{EE}+\mathrm{REN}}={\alpha }_{\mathrm{Other}}=0.5$). Source: taken from Ratner and Lychev (2023).

Country	Efficiency Scores
	Stage 1	Stage 2	Overall
Australia	100%	100%	100%
Austria	97.24%	99.61%	98.42%
Belgium	99.34%	100%	99.67%
Brazil	100%	100%	100%
Canada	79.93%	96.12%	88.02%
Czech Republic	100%	100%	100%
Denmark	94.10%	94.17%	94.14%
Finland	100%	84.76%	92.38%
France	75.12%	96.11%	85.62%
Germany	100%	98.95%	99.48%
Hungary	100%	100%	100%
Ireland	100%	100%	100%
Italy	91.95%	100%	95.97%
Japan	100%	97.10%	98.55%
South Korea	100%	96.93%	98.46%
Netherlands	97.36%	100%	98.68%
Norway	100%	96.07%	98.03%
Poland	87.91%	100%	93.96%
Spain	50.91%	100%	75.46%
Sweden	100%	100%	100%
Switzerland	86.22%	100%	93.11%
UK	100%	100%	100%
USA	100%	97.80%	98.90%

In order to ascertain the optimal allocation of public funding for the energy innovation process, we have applied Algorithm 1 with different feasible ranges of $\alpha$ weights variation, which have been set by the parameters L and U. Algorithm 1 was implemented in C#. For solving model (1), we have used ILOG CPLEX software, version 12.6.2.

Table 2 shows the calculation results when the coefficients ${\alpha }_i$ were varied from 0.3 to 0.7. The calculation was performed as follows. A production possibility set was built on the assumption that all DMUs share inputs equally between two stages, but for the evaluated DMU, the weights of ${\alpha }_i$ may vary. Furthermore, each input can be shared according to its own specific ratio. The value ${\alpha }_i$ shows that the share of the input i allocated to the first stage. Accordingly, the value $(1-{\alpha }_i)$ is allocated to the second stage.

Table 2. Efficiency scores and optimal $\alpha$ weights in a two-stage RDM model with shared inputs ($L=0.3$, $U=0.7$). Source: own calculations.

Country	$\mathit{\alpha }$ Weights			Efficiency Scores
	FF	EE + REN	Other	Stage 1	Stage 2	Overall
Australia	0.5	0.5	0.5	100%	100%	100%
Austria	0.5002	0.3482	0.5814	100%	100%	100%
Belgium	0.6920	0.4157	0.5260	100%	100%	100%
Brazil	0.5	0.5	0.5	100%	100%	100%
Canada	0.4142	0.3433	0.6995	100%	96.13%	98.06%
Czech Republic	0.5	0.5	0.5	100%	100%	100%
Denmark	0.6832	0.3013	0.5956	97.54%	100%	98.77%
Finland	0.3100	0.6948	0.6991	100%	91.57%	95.79%
France	0.3459	0.3001	0.6681	96.62%	93.86%	95.24%
Germany	0.4511	0.5677	0.5694	100%	100%	100%
Hungary	0.5	0.5	0.5	100%	100%	100%
Ireland	0.5	0.5	0.5	100%	100%	100%
Italy	0.6152	0.4461	0.4139	100%	100%	100%
Japan	0.6368	0.6999	0.6901	100%	100%	100%
South Korea	0.4109	0.6969	0.6901	100%	100%	100%
Netherlands	0.5503	0.5421	0.3586	100%	100%	100%
Norway	0.3593	0.6995	0.6831	100%	98.73%	99.37%
Poland	0.4900	0.3427	0.6578	100%	100%	100%
Spain	0.3005	0.4619	0.5307	61.28%	100%	80.64%
Sweden	0.5	0.5	0.5	100%	100%	100%
Switzerland	0.4528	0.3284	0.4984	100%	100%	100%
UK	0.5	0.5	0.5	100%	100%	100%
USA	0.6818	0.6972	0.4803	100%	100%	100%

Table 3 and Table 4 show that as restrictions on weight coefficients were gradually relaxed, the number of efficient DMUs increased.

Table 3. Efficiency scores and optimal $\alpha$ weights in two-stage RDM model with shared inputs ($L=0.2$, $U=0.8$). Source: own calculations.

Country	$\mathit{\alpha }$ Weights			Efficiency Scores
	FF	EE + REN	Other	Stage 1	Stage 2	Overall
Australia	0.5	0.5	0.5	100%	100%	100%
Austria	0.3481	0.3548	0.6668	100%	100%	100%
Belgium	0.4761	0.4501	0.5860	100%	100%	100%
Brazil	0.5	0.5	0.5	100%	100%	100%
Canada	0.6489	0.3428	0.7994	100%	96.91%	98.46%
Czech Republic	0.5	0.5	0.5	100%	100%	100%
Denmark	0.7187	0.7243	0.2034	100%	100%	100%
Finland	0.7969	0.2086	0.7988	100%	97.50%	98.75%
France	0.2842	0.2782	0.7996	100%	94.24%	97.12%
Germany	0.3745	0.5827	0.5366	100%	100%	100%
Hungary	0.5	0.5	0.5	100%	100%	100%
Ireland	0.5	0.5	0.5	100%	100%	100%
Italy	0.5900	0.4071	0.4373	100%	100%	100%
Japan	0.5949	0.6996	0.3799	100%	100%	100%
South Korea	0.4847	0.7218	0.6905	100%	100%	100%
Netherlands	0.7496	0.6278	0.2737	100%	100%	100%
Norway	0.4963	0.7445	0.5965	100%	100%	100%
Poland	0.4799	0.5805	0.2016	100%	100%	100%
Spain	0.2000	0.6938	0.7085	68.30%	100%	84.15%
Sweden	0.5	0.5	0.5	100%	100%	100%
Switzerland	0.3994	0.3431	0.5339	100%	100%	100%
UK	0.5	0.5	0.5	100%	100%	100%
USA	0.4169	0.7423	0.2222	100%	100%	100%

Table 4. Efficiency scores and optimal $\alpha$ weights in two-stage RDM model with shared inputs ($L=0.1$, $U=0.9$). Source: own calculations.

Country	$\mathit{\alpha }$ Weights			Efficiency Scores
	FF	EE + REN	Other	Stage 1	Stage 2	Overall
Australia	0.5	0.5	0.5	100%	100%	100%
Austria	0.4554	0.2312	0.5899	100%	100%	100%
Belgium	0.5568	0.4127	0.4604	100%	100%	100%
Brazil	0.5	0.5	0.5	100%	100%	100%
Canada	0.1395	0.7718	0.1270	100%	100%	100%
Czech Republic	0.5	0.5	0.5	100%	100%	100%
Denmark	0.8335	0.2316	0.8289	100%	100%	100%
Finland	0.8961	0.1146	0.8391	100%	100%	100%
France	0.4777	0.2724	0.9000	100%	97.80%	98.90%
Germany	0.8104	0.5341	0.6968	100%	100%	100%
Hungary	0.5	0.5	0.5	100%	100%	100%
Ireland	0.5	0.5	0.5	100%	100%	100%
Italy	0.7350	0.3685	0.5613	100%	100%	100%
Japan	0.8039	0.6871	0.5948	100%	100%	100%
South Korea	0.8956	0.7694	0.6487	100%	100%	100%
Netherlands	0.7734	0.5654	0.3166	100%	100%	100%
Norway	0.7740	0.8505	0.3100	100%	100%	100%
Poland	0.3954	0.3100	0.5787	100%	100%	100%
Spain	0.1006	0.1750	0.8304	77.02%	100%	88.51%
Sweden	0.5	0.5	0.5	100%	100%	100%
Switzerland	0.4836	0.3758	0.3164	100%	100%	100%
UK	0.5	0.5	0.5	100%	100%	100%
USA	0.8787	0.5608	0.3951	100%	100%	100%

The last experiment was carried out without any restrictions on the weight coefficients, i.e., the parameter L was chosen close to zero, and the parameter U was chosen close to one. As a consequence, all the units demonstrated a 100% efficiency score. This result demonstrates that when allocating inputs arbitrarily, there will always be proportions that make the unit efficient. Additionally, limiting the range of inputs will result in fewer efficient DMUs as the restrictions become stricter.

Further adjustments to the model can be made by changing the way the initial production possibility set is built. In our experiments, it was built so that all the DMUs shared inputs equally between the two stages. This proportion can be adjusted based on expert opinion. The range of $\alpha$ weight coefficient restrictions can be modified depending on the specifics of the problem. These restrictions may vary for different inputs or have the flexibility to be adjusted individually for each DMU.

6. Discussion

Although our results show that if we remove all restrictions on the share in which budgetary funds are allocated between the R&D and commercialization stages, wherein all countries in the sample can achieve optimal efficiency, from a practical point of view, this situation is hardly possible. Each country should maintain at least a minimum level of research activity to be able to absorb new technologies. Therefore, let us consider in more detail the results of calculations obtained under the assumption that the share in which budgetary funds can be spread between the first and second stages of the innovation process ranges from 10% to 90% (Table 4).

According to our results, in order to maximize efficiency, countries such as Denmark, Finland, Germany, Italy, Japan, Korea, the Netherlands, Norway, and the United States should allocate a large share of fossil fuel technology budget funding (more than 70%) to the research and development phases. In contrast, Canada and Spain should allocate more than 75% of their fossil fuel technology funding to the commercialization and deployment phase. The other countries in the sample can allocate their hydrocarbon technology budgets in a relatively balanced way.

In the field of renewable energy and energy efficiency technologies, Canada, Korea, Japan, and Norway should allocate 70% of their budget funding to research and development to maximize efficiency, while Austria, Denmark, Finland, France, Italy, Poland, Spain, and Switzerland, on the contrary, should allocate their budgets to the implementation stage.

For all other energy technologies, Denmark, Finland, France, Germany, Korea, and Spain (more than 70%) should prioritize R&D when allocating public funding. Conversely, Canada, the Netherlands, Norway, and the USA should give preference to commercialization-stage funding in order to increase their efficiency.

The most balanced financing of innovation activities can be found in Australia, Brazil, the Czech Republic, Hungary, Ireland, Sweden, and the United Kingdom. Moreover, an equal balance between the stages of research and development and commercialization can be observed for all groups of technologies.

7. Conclusions

The main objective of this study was to develop a mathematical model to determine the optimal allocation of public funds to the energy innovation process in order to achieve decarbonization and energy efficiency goals as soon as possible. The proposed approach is based on a two-stage DEA model with shared inputs between the first and second stages.

The main advantage of the proposed approach is its high degree of potential automation. This makes it possible to include new countries in the analysis and to update the results by importing new data. This does not require any changes in the model construction, but only the execution of a new computational procedure. Therefore, this model can become the basis of a decision support system for assessing and monitoring the effectiveness of public funding for the decarbonization of national economies. It can be used at the level of the International Energy Agency or the UN Climate Program to improve the quality of recommendations for improving the effectiveness of public policies.

The limitations of our proposed approach are the assumptions of a three-year lag between investing in R&D and obtaining a scientific result reflected in a patent, as well as a three-year lag between obtaining a patent and its implementation in technology and practice. These limitations can be overcome by building a dynamic model, which is the direction of the authors’ further research.