Remaining Useful Life Prediction of Electronic Power Components Based on a Hybrid Model Combining Bidirectional Long Short-Term Memory Networks and Gaussian Process Regression

Abstract

The performance degradation of electronic power components during long-term operation can compromise system reliability and safety. Therefore, accurately predicting their remaining useful life (RUL) is critical for the reliability of safety-critical systems that utilize these components. This paper proposes a hybrid model integrating bidirectional long short-term memory networks (BiLSTM) and Gaussian process regression (GPR) for RUL prediction of electronic power components. The BiLSTM module provides high-precision point predictions, while the GPR module leverages the sequence features and trend information extracted by BiLSTM to deliver reliable interval predictions and high-confidence probabilistic outputs. The model’s predictive accuracy was validated using NASA’s publicly available lithium-ion battery dataset. Experimental results demonstrate that, compared to existing models, the proposed model achieves at least a 9.6% improvement in point prediction performance and a 63% improvement in interval prediction performance, fully validating the reliability and accuracy of the BiLSTM-GPR approach. The model was further applied to predict the RUL of DC-DC power modules. The predicted Continuous Ranked Probability Score (CRPS) reached a maximum of 0.050405, while the Probability Integral Transform (PIT) results exhibited a uniform distribution within the (0,1) range, further demonstrating the model’s high reliability and predictive confidence.

1. Introduction

Electronic power components are critical elements in the field of power electronics [1], widely applied in safety-critical scenarios requiring efficient electrical energy control, such as automotive electronics [2], industrial control [3], rail transportation [4], and aerospace [5]. However, prolonged operation leads to device degradation, causing a gradual decline in performance that ultimately compromises system reliability and safety. Moreover, the degradation of electronic power components is not an isolated event but a progressive process with distinct temporal dependency and cumulative effects. Early-stage stress and damage accumulation continuously influence subsequent performance changes, exhibiting statistical regularities throughout the device’s lifecycle [6]. Research into the reliability of electronic power components has become critical for enhancing the long-term stable operation of power electronic systems [7]. Therefore, accurately predicting the State of Health (SOH) and Remaining Useful Life (RUL) of these devices is essential for the application of electronic power components [8].

Currently, RUL prediction methods for electronic power components can be broadly categorized into two types: model-based approaches [9] and data-driven approaches [10]. Model-based methods require constructing equivalent circuit models and electrochemical models based on the underlying mechanisms, subsequently deriving performance evolution patterns closely linked to intrinsic degradation mechanisms [11]. This approach offers high prediction accuracy and strong interpretability but involves complex modeling and time-consuming solutions [12]. Particularly for electronic power components with intricate internal structures and significant multiphysics coupling, establishing physical models proves excessively challenging and costly, limiting their widespread application in practical engineering [13]. Data-driven approaches utilize statistical correlation methods [14] to extract degradation information and health evolution patterns from historical data [15], becoming mainstream in Prognostics and Health Management (PHM) [16]. Existing data-driven methods fall into two categories: statistical analysis [17] and machine learning [18]. Statistical analysis methods typically rely on assumptions about degradation monotonicity and stationarity. For instance, Bakdi et al. [19] introduced principal component analysis (PCA) for fault detection in complex systems. Wang [20] and colleagues employed kernel principal component analysis (KPCA) to extract multi-domain features reflecting bearing degradation states for predicting the remaining life of rolling bearings. However, such methods struggle to characterize the nonlinear and non-stationary features of devices under complex operating conditions and are sensitive to noise. Concurrently, to overcome the limitations of statistical methods, researchers have increasingly turned to more flexible machine learning approaches. Song et al. [21] employed support vector machines (SVM) for rolling bearing fault diagnosis. Similarly, Mrabet et al. [22] utilized random forests (RF) to detect fault locations and durations in power systems. While these traditional machine learning approaches partially address overly stringent model assumptions, they struggle to effectively capture long-term dependencies in device degradation. Recurrent Neural Networks (RNNs) were introduced to address this limitation. Guo et al. [23] employed RNNs to construct health indices for equipment condition assessment. While this approach resolves temporal dependencies, it exhibits instability in predicting long-term degradation trends. Long Short-Term Memory (LSTM) networks effectively mitigate the vanishing gradient problem in RNNs by introducing gating mechanisms. They efficiently transmit and express information across extended time sequences without discarding valuable historical data. Zhang et al. [24] employed LSTMs to achieve independent battery remaining life estimation without offline training data. Han et al. [25] processed time series data from an aviation engine degradation simulation dataset using LSTMs, effectively preventing loss of critical elements in the data. Gorrachategui et al. [26] utilized a hybrid model combining convolutional neural networks (CNNs) and LSTMs for precise lithium-ion battery RUL prediction. Building upon this, the bidirectional LSTM (BiLSTM) variant enhances context awareness in time series through its bidirectional structure, ensuring model generalization under limited samples [27]. While BiLSTM improves contextual understanding of device degradation processes and demonstrates excellent point prediction accuracy, its deterministic modeling inherently struggles to provide confidence intervals for predictions. Compared to mainstream RUL prediction methods—such as ref. [28], which enhances long-term prediction stability through global dependency modeling using transformer models; Ref. [29], which develops a Physical Information Neural Network (PINN) framework to embed device thermo-electrical coupling equations into loss functions for improved extrapolation capability; and ref. [30], which combines Variational Autoencoders (VAE) with LSTM for probabilistic generation of degradation trajectories—BiLSTM achieves temporal feature extraction without requiring strong physical assumptions. Its lower model complexity makes it more suitable for handling high-noise, stringent safety-constrained RUL prediction tasks in real-world engineering. Particularly for electronic power components demanding high safety and reliability, point-based prediction results no longer meet requirements. Therefore, this paper proposes a fusion strategy that utilizes BiLSTM to capture nonlinear temporal features as input for Gaussian Process Regression (GPR). As a nonparametric Bayesian method [31], GPR captures complex relationships between data by specifying kernel functions and provides uncertainty estimates, enabling highly accurate predictions.

Although GPR has spawned numerous variants in recent years—such as the sparse Gaussian process in ref. [32], which reduces computational complexity by introducing induced points; the deep Gaussian process, which enhances nonlinear modeling capabilities through stacked latent variable layers; and the multi-task GPR in ref. [33], designed for cross-operating-condition knowledge transfer—these variants typically come at the cost of sacrificing model interpretability or introducing additional hyperparameters. Considering that degradation data for electronic power components often features limited sample sizes, high signal-to-noise ratio fluctuations, and stringent requirements for quantifying prediction uncertainty accuracy, this paper selects standard GPR as the core probabilistic modeling approach. Its nonparametric Bayesian nature provides an analytical posterior distribution under small-sample conditions without imposing strong functional assumptions on degradation paths, aligning better with the need for reliable confidence intervals in safety-critical scenarios.

Therefore, this paper proposes a hybrid model based on Bi-directional Long Short-Term Memory (BiLSTM) and Gaussian Process Regression (GPR) for predicting the RUL of electronic power components. Its main contributions are summarized as follows:

(1)

A Hybrid Intelligent Prediction Framework with Uncertainty Quantification Capability. To address the challenge that existing data-driven methods for RUL prediction of electronic power components often struggle to effectively model temporal dependencies while simultaneously quantifying prediction uncertainties, this paper proposes a novel deeply integrated BiLSTM-GPR architecture. Rather than a simple sequential connection, this framework implements feature-adaptive alignment and probabilistic mapping mechanisms to achieve synergistic optimization between the deep temporal features extracted by BiLSTM and the kernel functions of GPR. Consequently, the unified model can perform both high-accuracy point predictions and generate reliable confidence intervals.

(2)

A Multi-Dimensional and Interpretable Probabilistic Prediction Evaluation System. Moving beyond the common limitation in existing research that predominantly focuses on single-point prediction accuracy, this study establishes a comprehensive evaluation standard suitable for safety-critical scenarios from three dimensions: point prediction accuracy, interval prediction reliability, and overall probabilistic prediction quality. This evaluation system not only quantifies predictive performance but also provides directly actionable confidence information to support risk warning and maintenance decision-making in practical engineering applications.

(3)

Cross-Domain Validation from Simulated Data to Real-World Engineering Scenarios. To thoroughly validate the generalization capability and engineering practicality of the proposed model, performance comparison tests were conducted not only on the publicly available NASA lithium-ion battery dataset but also on a degradation dataset collected from actual DC-DC power modules. These modules operate under complex working conditions with significant noise degradation. The reliable prediction results achieved on such real-world data robustly demonstrate the model’s ability to address practical engineering challenges and its strong potential for transfer and application.

2. Methods

To address reliability issues of electronic power components, this paper proposes BiLSTM-GPR for RUL prediction of electronic power components. The specific method is outlined as follows:

2.1. BiLSTM-Based Life Prediction

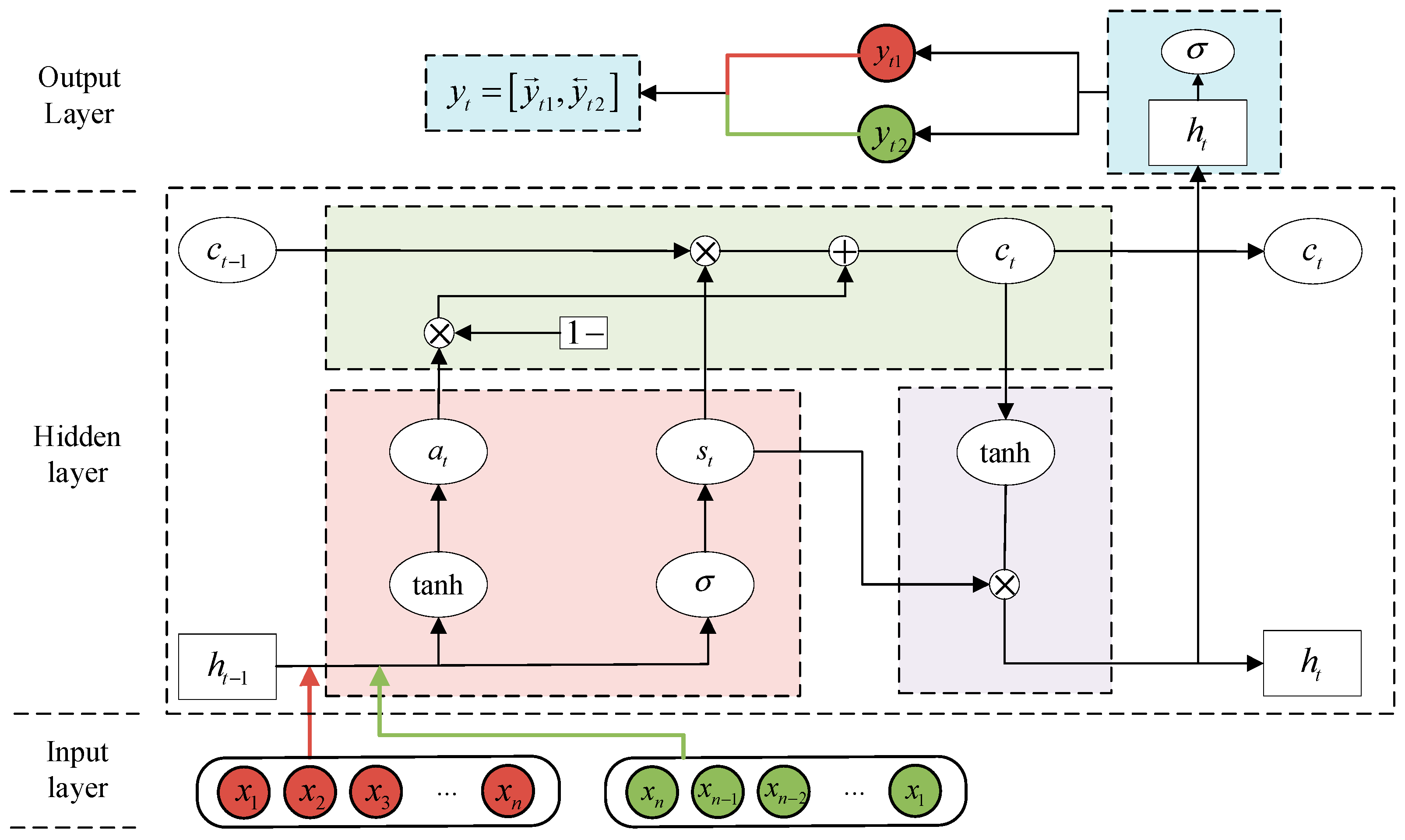
To effectively capture the bidirectional temporal dependencies inherent in degradation data, a BiLSTM is employed as the feature extractor, with its workflow illustrated in Figure 1. Unlike a single LSTM, a BiLSTM consists of two independent LSTM units processing data in forward and backward time directions [34]. Each unit processes information from different temporal directions of the input sequence, concatenating the corresponding hidden states at each time step to achieve joint modeling of historical and future information.

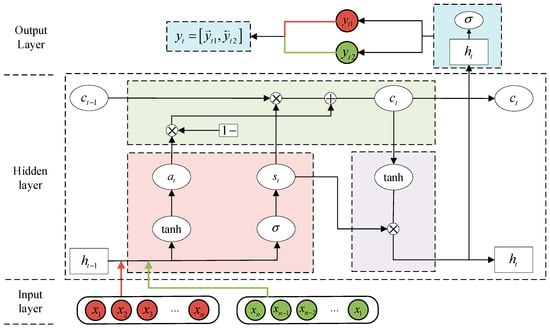
Figure 1. BiLSTM Flowchart.

In Figure 1, $x_t$, $s_t$, and $a_t$ represent the input to the input layer, output layer, and current state information of the BiLSTM, respectively. They can be expressed as:

$$s_t=\sigma (w_h·h_{t-1}+w_x·x_t+b)$$

(1)

$$a_t=\tanh (w_h·h_{t-1}+w_x·x_t+b)$$

(2)

$c_{t-1}$ and $c_t$ denote the states of the previous and current time steps, respectively, expressed as:

$$c_t=s_t\times c_{t-1}+(1-s_t)\times a_t$$

(3)

$h_{t-1}$ and $h_t$ represent the input and output of the hidden layer in the previous and current time steps, respectively, specifically expressed as:

$$h_t=s_t\times \tanh (c_t)$$

(4)

$y_t$ denotes the predicted value for the current time step, expressed as:

$$y_t=\sigma (w_y{h}_t+b_y)$$

(5)

$\sigma$ and $\tanh$ represent the activation functions for the Sigmoid and tanh functions, respectively, calculated as follows:

$$\sigma ={\displaystyle \frac{1}{1+e^{-x}}}$$

(6)

$$\tanh (x)={\displaystyle \frac{e^x-e^{-x}}{e^x+e^{-x}}}$$

(7)

To further enhance model robustness, the adaptive optimizer Adam was employed during training, combined with a learning rate decay strategy to accelerate convergence and prevent getting stuck in local minima.

The BiLSTM design balances temporal modeling capability and feature extraction efficiency [35], enabling it to automatically learn discriminative low-dimensional representations from raw degraded data, providing high-quality inputs for subsequent probabilistic prediction tasks. In this paper, the BiLSTM network comprises two stacked bidirectional LSTM units with hidden layer sizes of 32 and 16, respectively. The network’s output layer generates the final feature representation through an 8-dimensional fully connected layer. During training, the Adam optimizer is employed with an initial learning rate of 0.001, combined with the ReduceLROnPlateau learning rate scheduling strategy to accelerate convergence and avoid local optima. To prevent overfitting, Dropout regularization is introduced between the two LSTM layers with a dropout rate of 0.2. Model training employs 3-fold cross-validation with a batch size of 32 and a maximum of 100 training epochs.

2.2. GPR-Based Uncertainty Modeling

To quantify prediction uncertainty for electronic power components, GPR is introduced as the final prediction module based on BiLSTM. GPR is a Bayesian statistical machine learning algorithm that directly models the function space by defining prior distributions, offering advantages such as strong generalization capability and ease of implementation. GPR is defined as a set of random variables, where each point conforms to a joint Gaussian distribution. These variables are determined by the mean function and covariance function. The covariance function serves as a measure of correlation between the training and testing datasets, constituting a critical factor influencing the predictive performance of GPR models [36]. In this model, the mean function of GPR employs a learnable ConstantMean, while the covariance function utilizes an RBF Kernel with ScaleKernel, i.e., the kernel function:

$$k(x,x^{\prime })={{\sigma }_f}^2\exp (-{\displaystyle \frac{{‖x-x^{\prime }‖}^2}{2l^2}})$$

(8)

This kernel function exhibits infinite differentiability, enabling effective modeling of the smooth, continuous, and monotonic/quasi-monotonic performance degradation trends commonly observed during the deterioration process of electronic power components. Compared to periodic kernels or linear kernels, the RBF kernel does not presuppose specific patterns (such as periodicity or linearity), granting it stronger universal approximation capabilities. Compared to composite kernels, the single RBF kernel in this task can adaptively capture variations in degradation rates by automatically learning the length scale l and signal variance ${\sigma }_f$, while avoiding overfitting. More importantly, the Gaussian process induced by the RBF kernel exhibits maximum entropy properties, yielding the most conservative uncertainty estimates for unknown regions under given second-order statistics. This is particularly critical in power electronics systems demanding high safety standards. All hyperparameters were learned end-to-end via Exact Marginal Log-Likelihood. The optimization process employed the Adam algorithm with an initial learning rate of 0.1, undergoing 100 training iterations. Since actual data typically contains noise, we assume a regression model with noise as follows:

$$Y=y+\epsilon$$

(9)

where $Y$ denotes the observed value and $y$ denotes the prediction target, and further assuming noise $\epsilon \sim N(0,{{\sigma }_n}^2)$, the prior distribution of $Y$ can be obtained and expressed as:

$$Y\sim N(0,k(X,X)+{{\sigma }_n}^2{I}_n)$$

(10)

The joint prior distribution of $Y$ and $y$ is expressed as:

$$\left[{\displaystyle \frac{Y}{y}}\right]\sim N(0,[\begin{array}{cc}k(X,X)+{{\sigma }_n}^2{I}_n& k(X,x_{\ast })\\ k(x_{\ast },X)& k(x_{\ast },x_{\ast })\end{array}])=N(0,\begin{array}{cc}k& {k_{\ast }}^{\mathrm{T}}\\ k_{\ast }& {k_{\ast }}_{\ast }\end{array})$$

(11)

$k(X,X)$ denotes the symmetric positive definite covariance matrix of order n, and $k(X,x_{\ast })=k{(x_{\ast },X)}^{\mathrm{T}}$ represents the covariance matrix between the test point $x_{\ast }$ and the input $X$. From this, the posterior distribution of the predicted value $y$ can be calculated as:

$$y | X\sim N(\overline{y},{{\sigma }_y}^2)$$

(12)

Among these, $\overline{y}$ is the estimated value of $y$, and ${{\sigma }_y}^2$ is the covariance matrix of the test set, represented as:

$$\overline{y}=k(x_{\ast },X){\left[k(X,X)+{{\sigma }_n}^2{I}_n\right]}^{-1}y=k_{\ast }{k}^{-1}y$$

(13)

$$\begin{array}{cc}{{\sigma }_y}^2& =k(x_{\ast },x_{\ast })-k(x_{\ast },X)\times {\left[k(X,X)+{{\sigma }_n}^2{I}_n\right]}^{-1}k(X,x_{\ast })\\ & =k_{\ast \ast }-k_{\ast }{k}^{-1}{k_{\ast }}^{{\rm T}}\hfill \end{array}$$

(14)

Among these, $\overline{y}$ represents the point prediction results of GPR. To further evaluate the reliability of the predictions, a 95% confidence interval was constructed as $\left[\overline{y}-1.96{\sigma }_y,\overline{y}+1.96{\sigma }_y\right]$

2.3. RUL Prediction Based on BiLSTM-GPR

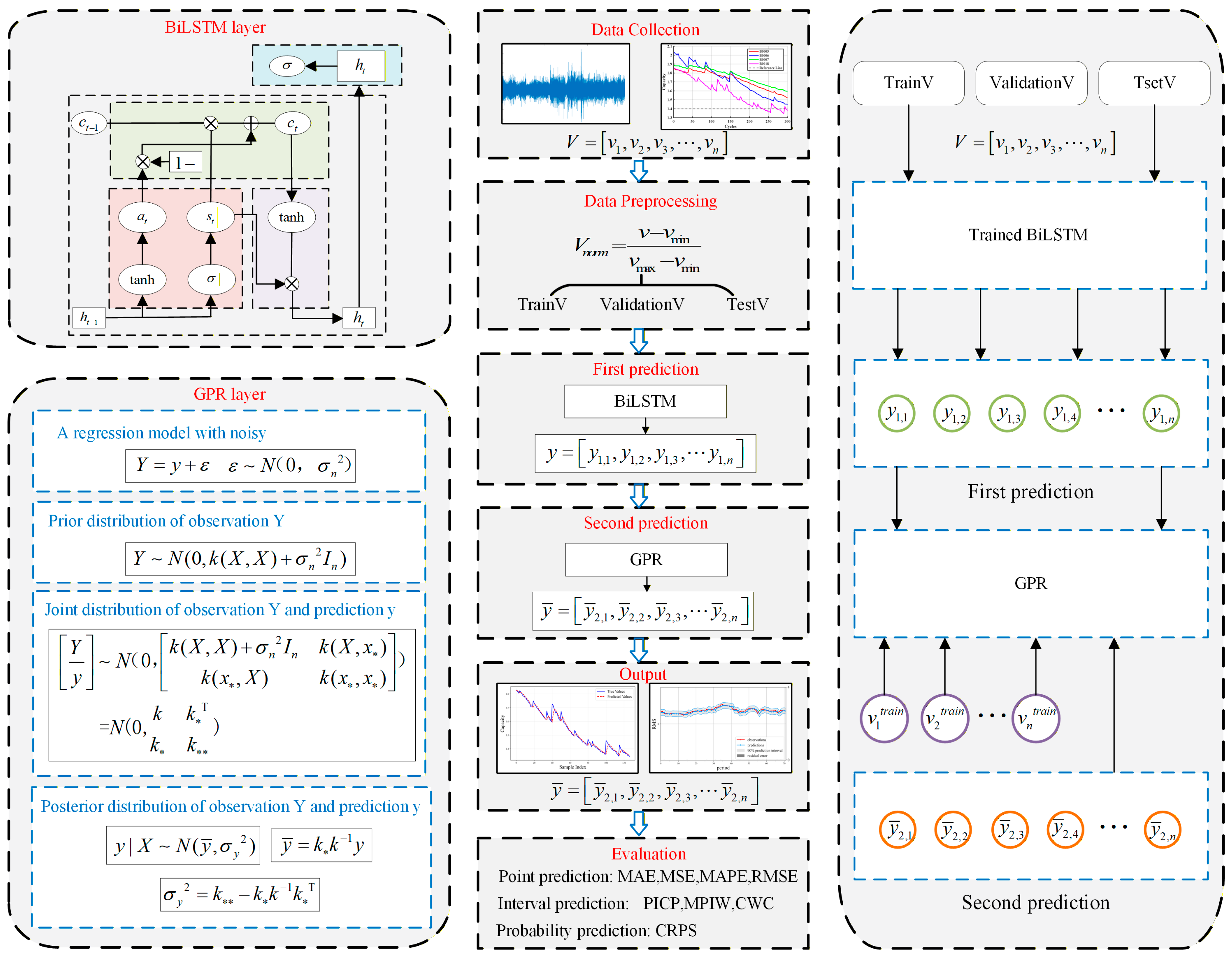
Given the high point prediction accuracy of BiLSTM and the reliable probabilistic predictions from GPR, combining these two models yields highly precise point forecasts, highly reliable interval predictions, and high-confidence probabilistic forecasts. The prediction process comprises two stages: Stage 1 involves fully training BiLSTM by feeding the training and test datasets into it for an initial prediction. The second stage feeds the initial prediction values and observed values into GPR for final predictions, including point estimates, interval estimates, and probability estimates. The key advantage lies in preserving the high-precision point estimates from BiLSTM while incorporating GPR to obtain reliable interval estimates and probability estimates. The overall prediction workflow of this hybrid model is illustrated in Figure 2.

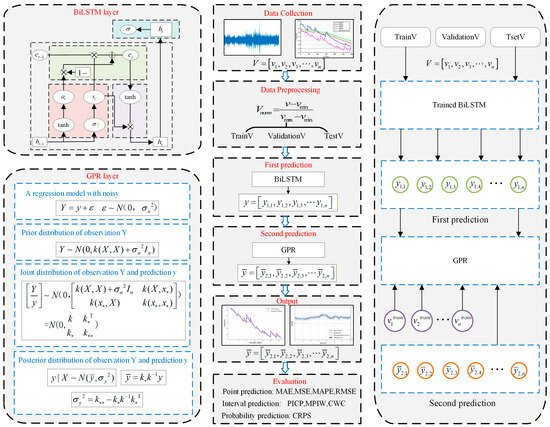
Figure 2. Overall Model Prediction Flowchart.

Figure 2 systematically presents the overall architecture and workflow of the BiLSTM-GPR model. The framework is divided into three sections: the left side summarizes the theoretical principles of BiLSTM and GPR, the middle section depicts the complete prediction process, and the right side visually illustrates the model’s operational mechanism on the dataset. The core mechanism of this framework lies in the feature-adaptive alignment and probabilistic mapping mechanism of BiLSTM and GPR. For a given input $x_t$ sequence of length T, BiLSTM encodes it into a fixed-dimensional feature vector:

$$z=f_{BiLSTM}(X;{\Theta }_{BiLSTM}),\hspace{1em}z\in R^m$$

(15)

Among these, ${\Theta }_{BiLSTM}$ represents the network parameters of BiLSTM, and $m=8$. The GPR receives the feature vector $z$ as input and models the latent function $g:R^m\to R$ from the feature space to the remaining lifetime $y$. It is assumed that this function follows a Gaussian process prior:

$$g(z)\sim N(0,k(z,z^{\prime };\theta ))$$

(16)

where $\theta$ is its hyperparameter, and the observation $y$ can be computed as:

$$y=g(z)+\epsilon$$

(17)

This enables RUL prediction. The “feature-adaptive alignment” mechanism is achieved through the specific form of the kernel function. This paper employs an RBF kernel as the kernel function, as shown in Equation (8). Its essence lies in the independent learning of each length scale $l$ during model training. This process involves the model automatically weighting, filtering, and aligning different feature dimensions—the “feature-adaptive alignment.” For a new test vector $z$, the predicted RUL distribution—the “probability mapping” output—constitutes the posterior distribution of the GPR, as expressed in Equation (12). Its mean provides the final predicted RUL value, while the variance precisely quantifies the model’s uncertainty regarding the mapping relationship $g$ from features to RUL for a given test vector. This ensures the interpretability of said uncertainty.

3. Model Evaluation

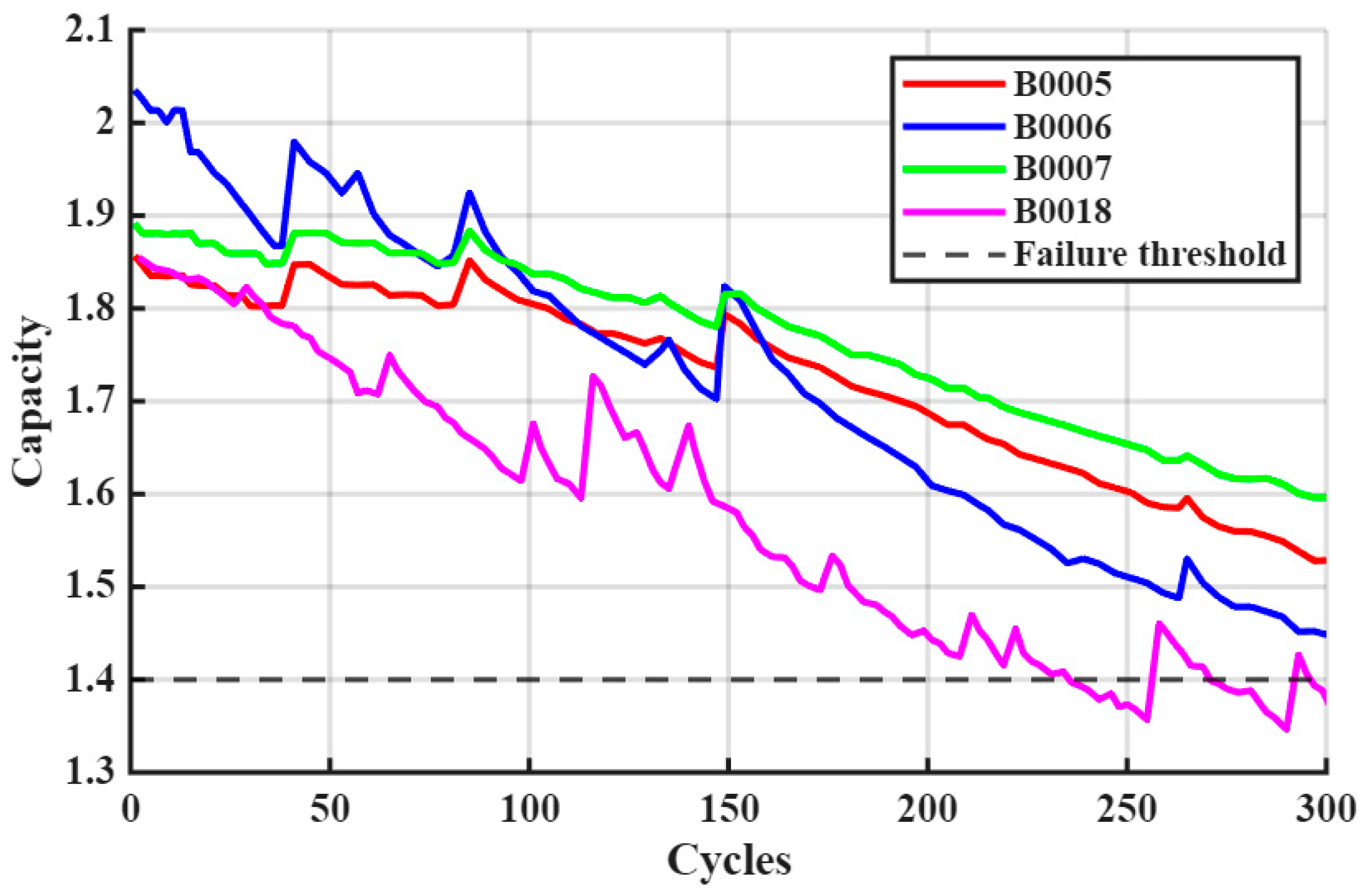
To validate the accuracy of BiLSTM-GPR predictions, this study employs lithium-ion battery datasets from NASA’s Center of Excellence for Prediction data repository [37], selecting datasets B5, B6, B7, and B18 for experimentation. Battery cycling comprises three processes: charging, discharging, and impedance testing [38]. Initial capacities vary across datasets: B5, B6, B7, and B18 have initial capacities of 1.86 Ah, 2.04 Ah, 1.89 Ah, and 1.86 Ah, respectively, with rated capacities uniformly set at 2 Ah. Capacity changes during battery discharge cycles are illustrated in Figure 3.

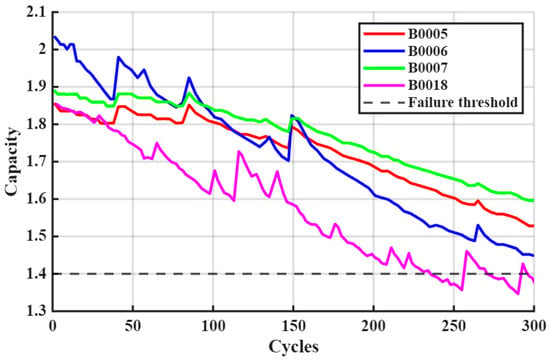
Figure 3. Battery Discharge Cycle Capacity Variation.

The experiment employed three-fold cross-validation to ensure accuracy [39]. Datasets B5, B6, B7, and B18 served as the test set, training set, and validation set, respectively. All models were evaluated on B18, eliminating performance fluctuations caused by different test sets while enabling direct comparison of models trained on different folds. Fixing B18 as the test set better simulates the model’s predictive capability for new batteries and ensures the test set remains completely independent from the training process, thereby avoiding data leakage risks, as detailed in Table 1.

Table 1. Three-fold cross-validation setup.

	Training Set	Validation Set	Test Set
Fold1	B5, B6	B7	B18
Fold2	B5, B7	B6	B18
Fold3	B6, B7	B5	B18

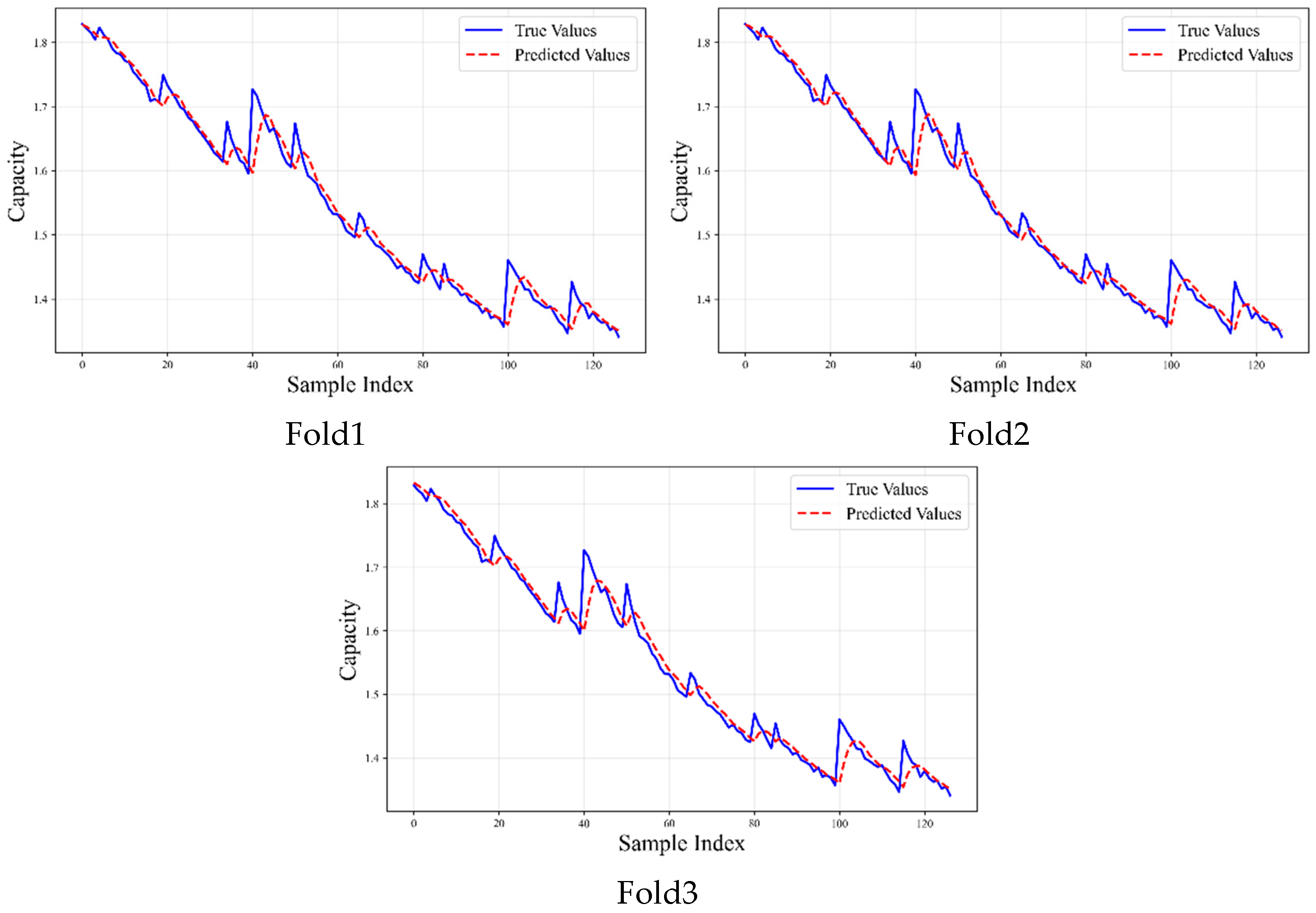
This paper selects the charging curves of V and I as input features, taking 10 samples from each curve and averaging them. Data normalization is performed using maximum–minimum scaling. A sliding window method is employed to construct input–output sequence pairs, with a window length of 5. A window length that is too short may hinder the model’s ability to capture battery degradation trends, while an excessively long window introduces noise and increases the risk of overfitting. The sliding step size is set to 1, and regularization is applied to mitigate overfitting. The comparison results between the model’s predicted capacity and actual capacity are shown in Figure 4.

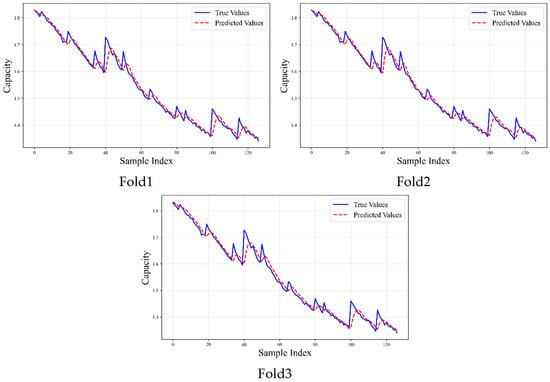
Figure 4. Comparison of Model-Predicted Capacity and Actual Capacity.

Figure 4 indicates that the model’s predictions show good agreement with actual values. To comprehensively evaluate the model’s performance in lithium-ion battery RUL prediction, an assessment framework was constructed across multiple dimensions. This framework encompasses two core aspects: point prediction accuracy and interval prediction reliability, systematically quantifying the model’s performance in terms of accuracy, stability, and uncertainty.

3.1. Point Prediction Performance Evaluation

Point prediction metrics provide the most direct measure of deviation between model predictions and actual values. These include Mean Absolute Error (MAE), Mean Squared Error (MSE), Root Mean Squared Error (RMSE), Mean Absolute Percentage Error (MAPE), and Coefficient of Determination ($R^2$), reflecting the model’s accuracy and stability in point predictions [40]. The calculation formulas are as follows:

$$MAE={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N\left|y_i-{\widehat{y}}_i\right|}$$

(18)

$$MSE={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N{(y_i-{\widehat{y}}_i)}^2}$$

(19)

$$RMSE=\sqrt{{\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N{\left(y_i-{\widehat{y}}_i\right)}^2}}$$

(20)

$$MAPE={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N\left|\frac{y_i-{\widehat{y}}_i}{y_i}\right|}$$

(21)

$$R^2=1-{\displaystyle \frac{{\displaystyle \sum _i{\left({\widehat{y}}_i-y_i\right)}^2}}{{\displaystyle \sum _i{\left({\overline{y}}_i-y_i\right)}^2}}}$$

(22)

where $y_i$ and ${\widehat{y}}_i$ represent the actual and predicted values, respectively, and N denotes the number of periods.

These metrics collectively reveal the distribution characteristics of the model’s prediction errors. MAE is suitable for measuring overall error, MSE aids in identifying extreme prediction failures, MAPE provides a relative error perspective, and $R^2$ assesses the model’s fitting performance [41]. The results are shown in Table 2.

Table 2. Model Point Forecast Results.

	MAE	MSE	MAPE	RMSE	${\mathit{R}}^2$
Fold1	0.014445	0.000571	0.009320	0.023893	97.34%
Fold2	0.013431	0.000548	0.008647	0.023423	97.45%
Fold3	0.015099	0.000571	0.009704	0.023898	97.34%

Analysis of Table 2 reveals that the BiLSTM-GPR hybrid model demonstrates outstanding point prediction performance across folds 1 to 3, with consistently low error values. The $R^2$ values exceed 90% and approach 1, indicating excellent alignment between predicted and actual values.

3.2. Reliability Assessment of Interval Predictions

Although point prediction results are intuitive and clear, they fail to reflect prediction uncertainty. This is particularly true during battery aging, where degradation processes are influenced by complex factors such as temperature, manufacturing variations, and charge/discharge rates, exhibiting inherent randomness [42]. Therefore, interval prediction metrics are introduced to provide confidence intervals, thereby comprehensively characterizing the reliable range of prediction results [43]. The model’s interval prediction performance is evaluated using the Prediction Interval Coverage Probability (PICP) and the Mean Prediction Interval Width (MPIW), calculated as follows:

$$PICP={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N{c}_i}$$

(23)

$$MPIW={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N({{\widehat{y}}_i}^U-{{\widehat{y}}_i}^L)}$$

(24)

where ${{\widehat{y}}_i}^U$ and ${{\widehat{y}}_i}^L$ represent the upper and lower bounds of the predicted value, respectively. When the actual value $y_i\in [{{\widehat{y}}_i}^U,{{\widehat{y}}_i}^L]$, $c_i=1$, conversely, $c_i=0$.

PICP measures the probability that the true value falls within the predicted interval, while MPIW reflects the average width of the prediction interval. Under the premise of ensuring PICP, a smaller MPIW indicates more precise uncertainty estimation by the model. To comprehensively balance PICP and MPIW, the Coverage Width Criterion (CWC) is introduced, calculated as follows:

$$CWC={\displaystyle \frac{MPIW}{PICP}}$$

(25)

Ideally, PICP should approach the 95% confidence level, while MPIW should be minimized to achieve the smallest CWC value. A lower CWC indicates superior interval prediction performance—achieving the narrowest prediction interval while maintaining high coverage. For lithium-ion battery degradation data, the model’s interval prediction results are shown in Table 3.

Table 3. Model Interval Prediction Results.

	PICP	MPIW	CWC
Fold1	93.7007%	0.054322	0.057974
Fold2	92.1259%	0.044849	0.048682
Fold3	96.8503%	0.090291	0.093227

Analysis of the interval prediction results shows that the PICP values for the three folds are 93.7007%, 92.1259%, and 96.8503%, respectively. All are close to the ideal 95% and deviate from the target by no more than 3%. This indicates that the model’s prediction intervals have good coverage capability. Values that are too high suggest the model is overly conservative, while values that are too low indicate the model is overly confident. The MPIW values are 0.054322, 0.044849, and 0.090291, respectively, all falling within the 0.04–0.1 range. This indicates that the model can provide precise uncertainty estimates while maintaining high confidence levels. Concurrently, the CWC comprehensively measures coverage capability and interval width, with results remaining at extremely low levels below 10%. Overall, the model demonstrates excellent interval prediction performance, fully validating its optimal state in the “accuracy–reliability” trade-off.

3.3. Continuous-Rated Probability Score

Additionally, the Continuous Ranked Probability Score (CRPS) was introduced to comprehensively evaluate the quality of the entire prediction distribution, balancing accuracy and calibration. This metric measures the deviation between the predicted cumulative distribution function (PDF) and the observed empirical distribution function (CDF), i.e., the $F({\widehat{y}}_i)$, calculated as follows:

$$CRPS={\displaystyle \int {(F({\widehat{y}}_i)-1_{\left\{{\widehat{y}}_i\ge y_i\right\}})}^{2}dx}$$

(26)

CRPS results are presented in Table 4.

Table 4. Model CRPS Results.

	Fold1	Fold2	Fold3
CRPS	0.011383	0.010718	0.013129

Lower CRPS values indicate not only reduced bias in the prediction distribution—meaning the center point of the predicted distribution is closer to the true value—but also good calibration uncertainty. Analysis of the model’s predicted CRPS results reveals an average CRPS of 0.011743 across the three test sets. This outcome demonstrates that the model not only delivers highly accurate point predictions but also exhibits a prediction distribution that closely aligns with the true distribution, indicating excellent calibration and distribution fitting capabilities.

3.4. Ablation Study

To validate the effectiveness of the BiLSTM-GPR model in prediction tasks, systematic ablation experiments were conducted to compare the performance of different modules in battery capacity degradation prediction. The comparison results are illustrated in Figure 5.

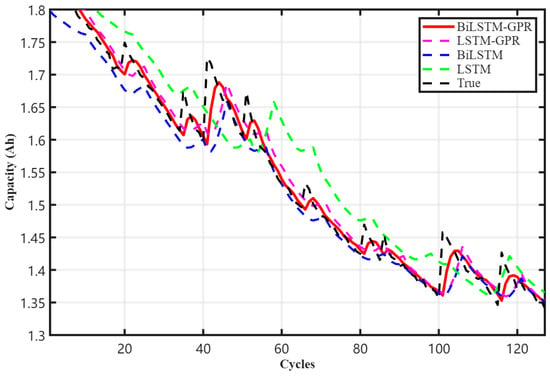
Figure 5. Comparison of ablation experiment results.

The capacity-vs-cycle trend curves in Figure 5 reveal that the BiLSTM-GPR model achieves the best fit between predicted and actual values, demonstrating superior long-term trend capture and noise resistance. Its point and interval prediction results are further detailed in Table 5.

Table 5. The Results of Ablation Study.

Algorithms	MAE	MSE	MAPE	RMSE	${\mathit{R}}^2$	CWC
LSTM	0.022063	0.001201	0.013812	0.034659	94.4112%	\
BiLSTM	0.016626	0.000666	0.010684	0.025801	96.8926%	\
LSTM-GPR	0.017689	0.000711	0.011418	0.026617	96.6810%	0.125298
BiLSTM-GPR	0.014325	0.000563	0.009223	0.023738	97.3884%	0.066627

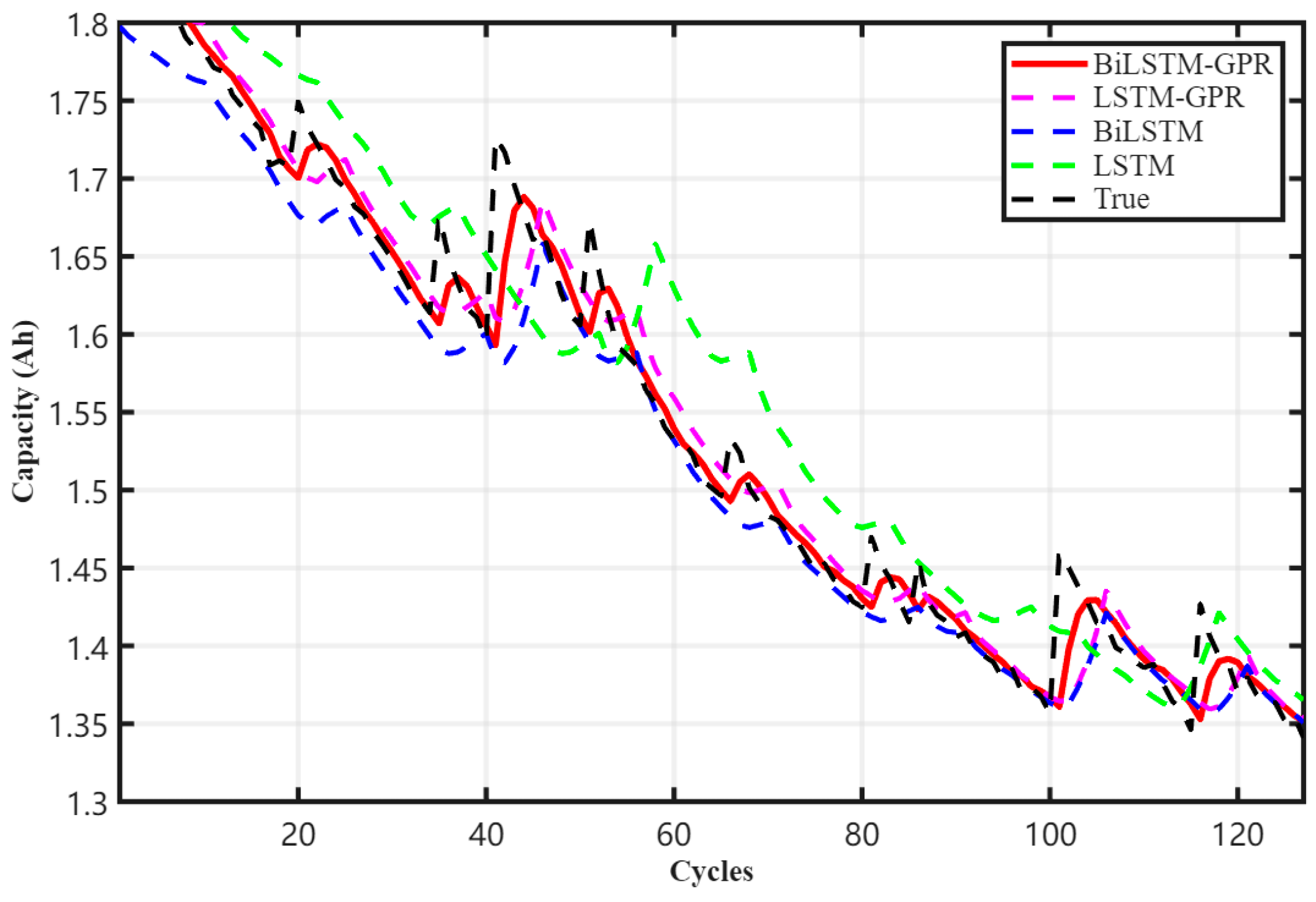
As shown in Table 5, the model demonstrates optimal performance across all evaluation metrics. Notably, its CWC for interval prediction is the lowest at 0.066627, indicating not only precise point predictions but also reliable uncertainty estimates. In contrast, while standalone LSTM and BiLSTM models demonstrate relatively strong fitting capabilities, they cannot provide uncertainty estimates for predictions. Although the LSTM-GPR model incorporates GPR, it fails to fully leverage bidirectional information and lacks the ability to fuse historical and future contextual data, resulting in limited generalization performance on complex nonlinear degradation trajectories.

Overall, BiLSTM more accurately captures the evolution of battery capacity degradation compared to LSTM. When further combined with GPR, the model not only retains its original point prediction capability but also enhances the estimation of prediction confidence, thereby achieving more precise and stable capacity prediction.

3.5. Comparative Experiments

Furthermore, the model was compared with current mainstream prediction models to validate the effectiveness and superiority of the BiLSTM-GPR model in RUL prediction. The comparison images are shown in Figure 6.

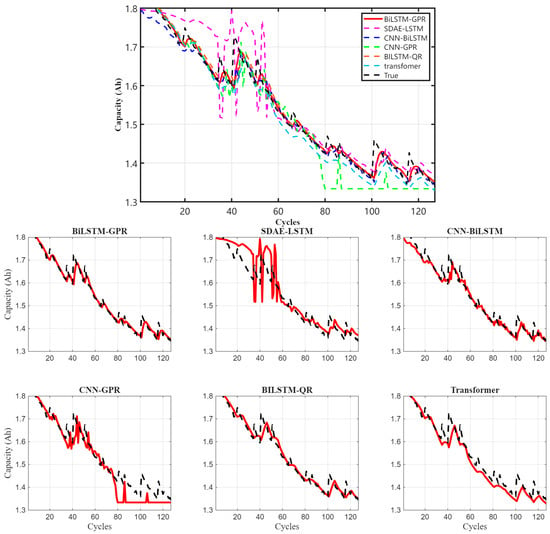
Figure 6. Comparison of the Model with Mainstream Models.

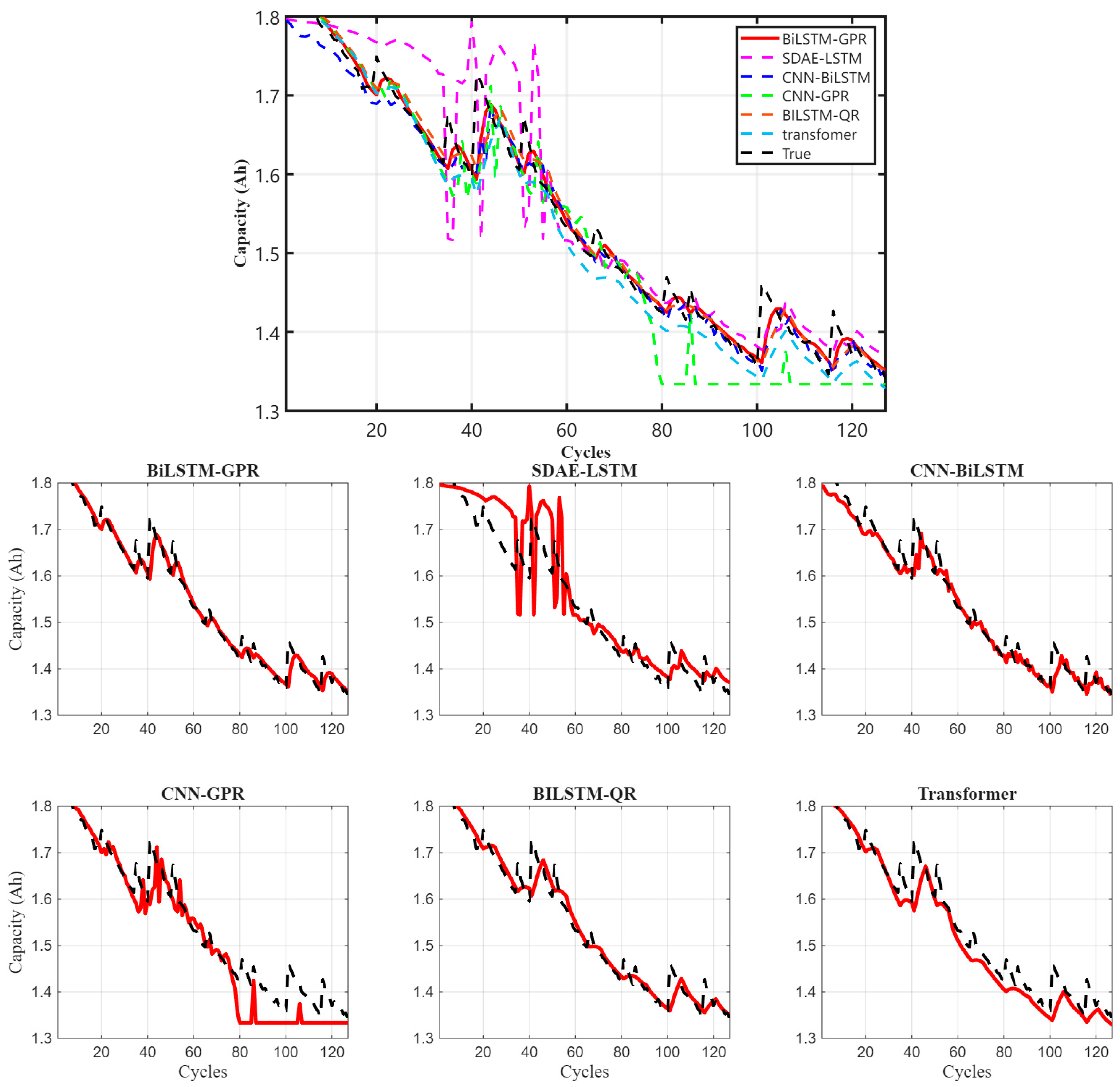
Figure 6 demonstrates that the BiLSTM-GPR model exhibits higher accuracy in overall trend fitting, particularly excelling at capturing capacity variation characteristics during the battery capacity regeneration phase. The black line represents the actual value, while the red lines represent the predictions from various models. In contrast, the SDAE-LSTM or CNN-GPR models exhibit significant fluctuations in the early stages, with noticeable prediction errors. While the Transformer model possesses strong global modeling capabilities, it still shows some deviations in local details, such as capacity regeneration. To further quantify the prediction performance of each model, multiple evaluation metrics on the lithium-ion battery degradation dataset are presented in Table 6.

Table 6. Model Comparison Prediction Results.

Algorithms	MAE	MSE	MAPE	RMSE	${\mathit{R}}^2$	CWC
Transformer	0.024338	0.001261	0.015955	0.035506	94.1211%	/
CNN-BiLSTM	0.018739	0.000627	0.012179	0.025043	96.3230%	/
SDAE-LSTM	0.026459	0.001086	0.016935	0.032955	82.6262%	/
BiLSTM-QR	0.017548	0.000675	0.012196	0.026007	96.8521%	0.044081
CNN-GPR	0.037657	0.002541	0.025304	0.050412	88.1639%	0.182523
BiLSTM-GPR	0.014325	0.000563	0.009223	0.023738	97.3884%	0.066627

Table 6 shows that the BiLSTM-GPR model achieves the best performance in point forecasting. Although its interval forecasting metrics are inferior to those of the BiLSTM-QR model, the latter’s PICP is only 72%, indicating insufficient coverage capability. The SDAE-LSTM model is relatively complex. The cascaded structure of SDAE and LSTM results in an excessive number of model parameters, making it prone to overfitting on limited battery data. Furthermore, the reconstruction loss and capacity prediction loss in SDAE exhibit conflicting optimization objectives, leading to weak generalization capabilities and a lack of uncertainty quantification. Overall, the BiLSTM-GPR model demonstrates the best performance across all metrics.

4. RUL Prediction for DC-DC Power Modules

DC-DC power modules are power electronic devices that convert DC voltage to different levels of DC voltage, serving as indispensable key components in modern electronic systems. During long-term operation, DC-DC power modules experience performance degradation due to factors such as thermal stress, humidity stress, electrical stress, and vibration. Their degradation mechanisms encompass the most typical failure modes in electronic power components. Therefore, this paper conducts multi-stress accelerated degradation testing on DC-DC power modules. This approach not only aids in predicting their RUL but also provides a reference basis for reliability modeling, failure prediction, and condition-based maintenance (CBM) of other electronic power components. It holds significant importance for enhancing system robustness, extending service life, and enabling intelligent operation and maintenance.

Given the extended operational lifespan characteristic of DC-DC power modules, multi-stress accelerated degradation testing was conducted to comprehensively investigate their entire degradation process. The experimental setup is illustrated in Figure 7.

Figure 7. Experimental Environment for DC-DC Power Modules.

A total of 1200 h of reliability testing was conducted on six DC-DC power modules, comprising 912 h of high-temperature/high-humidity testing and 288 h of combined environmental testing. The high-temperature and high-humidity test conditions were set at 80 °C and 80% relative humidity. The combined environmental test conditions comprised temperature cycling, vibration stress, and electrical stress. The low-temperature condition was −20 °C, and the high-temperature condition was 80 °C, with each temperature maintained for 1 h. The electrical stress condition involved applying a 24 V DC voltage to the test specimens. By deploying voltage sensing points and Hall-effect current sensors to capture internal voltage and current data from each DC-DC power module at a sampling frequency of 5 kHz, approximately 16 million data points were obtained. Following stratified sampling principles, multiple data extracts were formed to constitute experimental test groups, with each group containing roughly 160,000 voltage and current values. These are designated as Dataset1 through Dataset6. As DC-DC power modules operate long-term, degradation increases voltage fluctuations. Therefore, when predicting the RUL of DC-DC power modules, the RMS value of voltage was selected as the model output. RMS effectively reflects output voltage fluctuations, thereby characterizing health status. The calculation method is as follows:

$$RMS=\sqrt{{\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N{(v_i)}^2}}$$

(27)

For the degradation data obtained from this reliability experiment, BiLSTM-GPR was employed to predict the RUL for the six degradation datasets. The prediction results are shown in Figure 8.

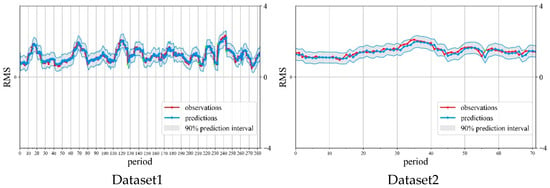
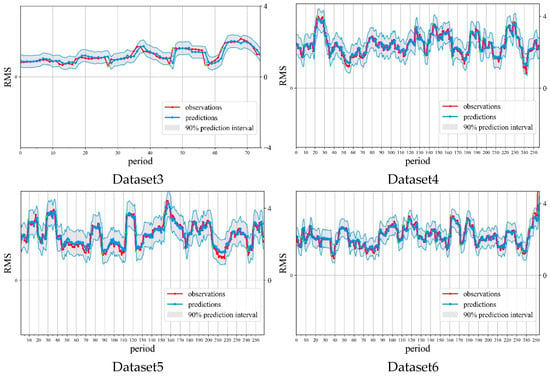
Figure 8. Comparison of predicted and actual values for DC-DC power modules.

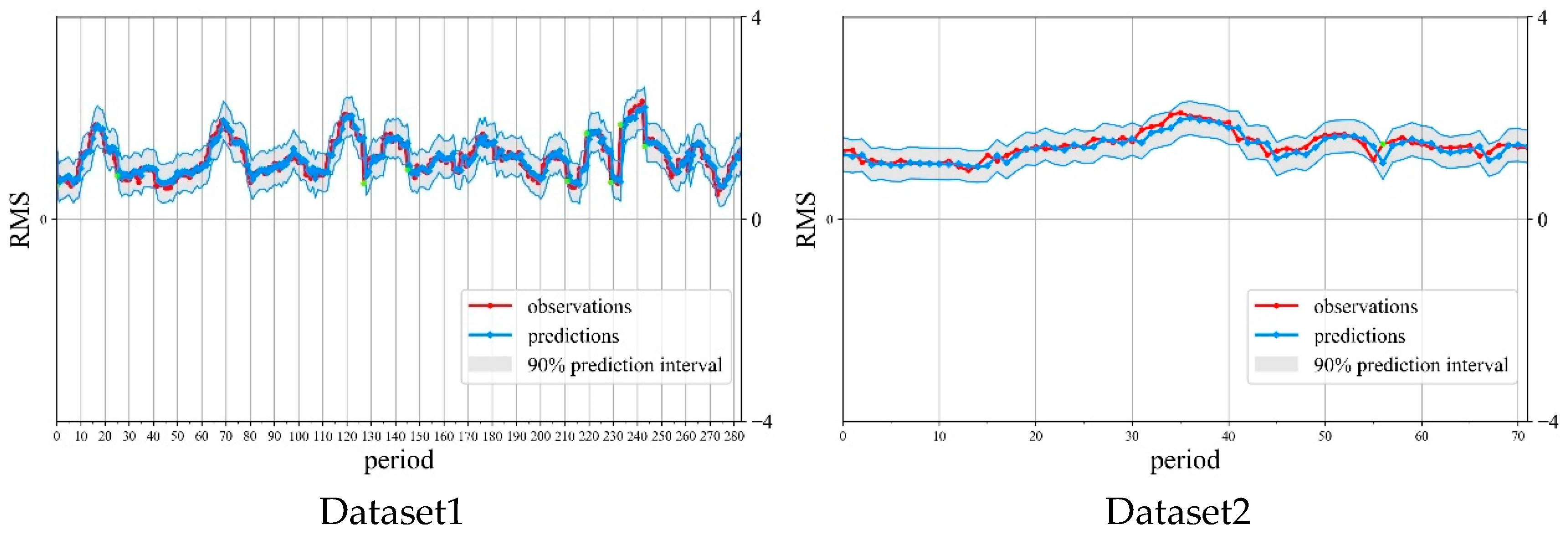
Figure 8 demonstrates that the model’s predicted values generally align well with actual values, with most falling within the 90% confidence interval. This indicates strong predictive capability. Preliminary analysis suggests the BiLSTM-GPR model exhibits excellent generalization ability and stability for this prediction task. To further evaluate prediction accuracy, point prediction results are summarized in Table 7.

Table 7. Model Point Prediction Results.

Datasets	MAE	MSE	MAPE	RMSE
Dataset1	0.001378	0.000004	0.101609	0.002129
Dataset2	0.001155	0.000002	0.063965	0.001498
Dataset3	0.001505	0.000006	0.115061	0.002469
Dataset4	0.002401	0.000001	0.086368	0.003403
Dataset5	0.002344	0.000001	0.090042	0.003596
Dataset6	0.002403	0.000001	0.092083	0.003642

As shown in Table 7, the point prediction results of the model remain at a low level across Datasets 1–6, further validating the high-precision point prediction capability of BiLSTM-GPR on different datasets. Among them, Dataset 2 exhibits the optimal point prediction performance, while Dataset 3 shows relatively higher error, potentially attributed to greater fluctuations in input features or noise interference. To further assess prediction uncertainty, the model’s interval predictions at the 95% confidence level and continuous graded probability scores were calculated, as shown in Table 8.

Table 8. Model Interval Prediction Results and Continuous Graded Probability Scores.

Datasets	PICP	MPIW	CWC	CRPS
Dataset1	96.8309%	0.686669	0.709142	0.021504
Dataset2	91.7647%	0.490222	0.534217	0.035512
Dataset3	93.3333%	0.618807	0.663007	0.050405
Dataset4	94.9416%	0.536206	0.564774	0.036890
Dataset5	94.5946%	0.585884	0.619363	0.035334
Dataset6	92.9412%	0.516371	0.555589	0.035512

Table 8 shows that the PICP values of all models are around 95%, indicating high coverage capability of the prediction intervals. Meanwhile, the MPIW values are small, all below 1, suggesting narrow prediction interval widths. However, relying solely on PICP and MPIW cannot comprehensively evaluate the quality of interval predictions. Therefore, CWC is used to synthesize these metrics. The CWC results for Datasets 1–6 are all below 1, with Dataset 2 showing the optimal performance. This aligns with the point prediction results, indicating superior overall model performance on this dataset.

Furthermore, the CRPS metric evaluates the overall performance of the probability density function predicted by the BiLSTM-GPR model. It comprehensively assesses both point prediction and interval prediction metrics while encompassing the overall performance of the probability density function. Results show that CRPS values across all datasets remain at relatively low levels, indicating the model exhibits good consistency and stability in probability prediction.

After evaluating the BiLSTM-GPR predictions through point forecasting, interval forecasting, and probability forecasting, we further tested the reliability of its predictions to ensure the validity of the results. Prediction reliability refers to the statistical consistency between predicted and actual values. The Probability Integral Transform (PIT) was selected to assess prediction reliability, with the PIT formula defined as follows:

$$PIT=F({\widehat{y}}_i)={\displaystyle {\int }_{-\infty }^{{\widehat{y}}_i}p(x)dx}$$

(28)

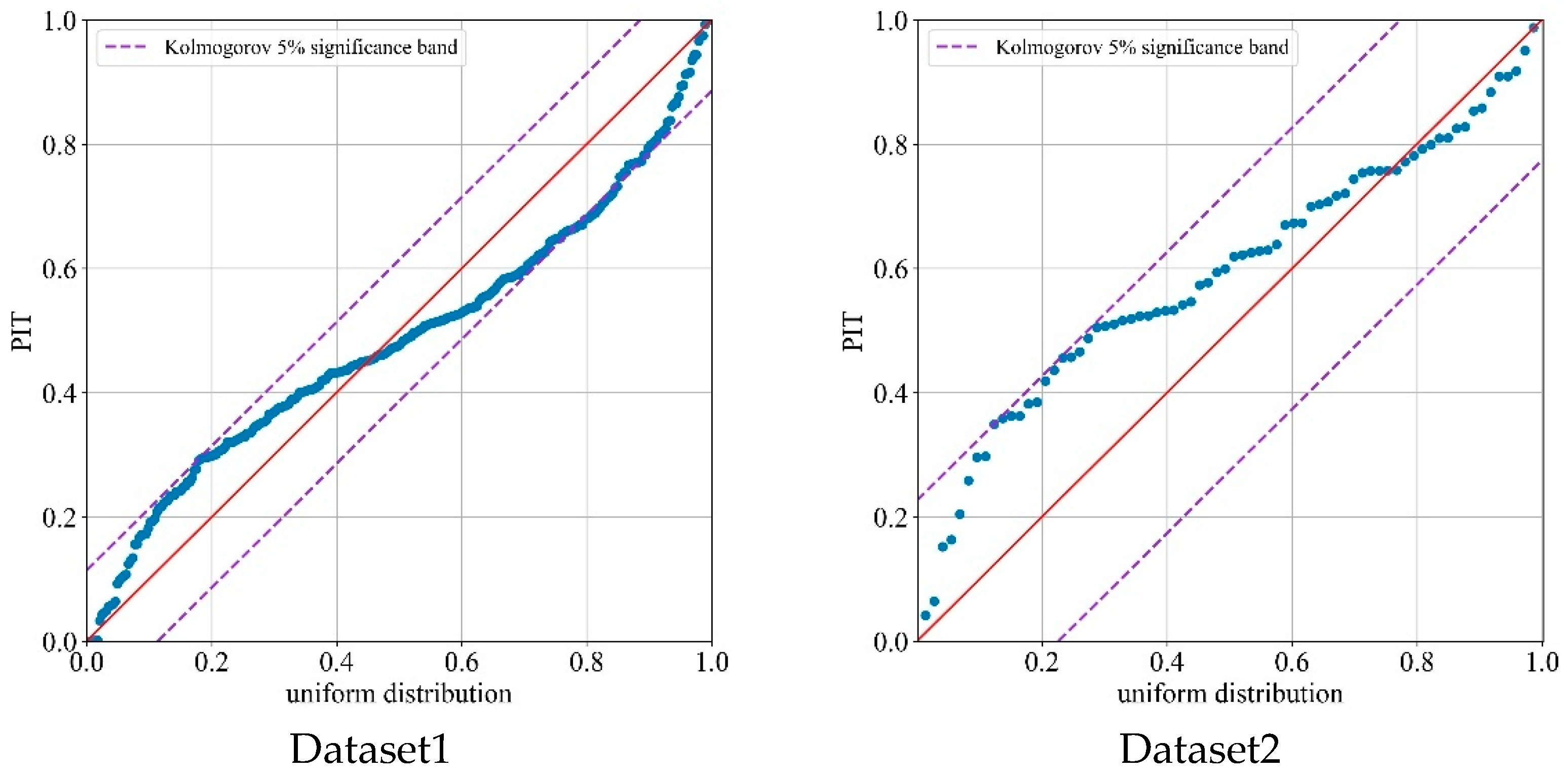
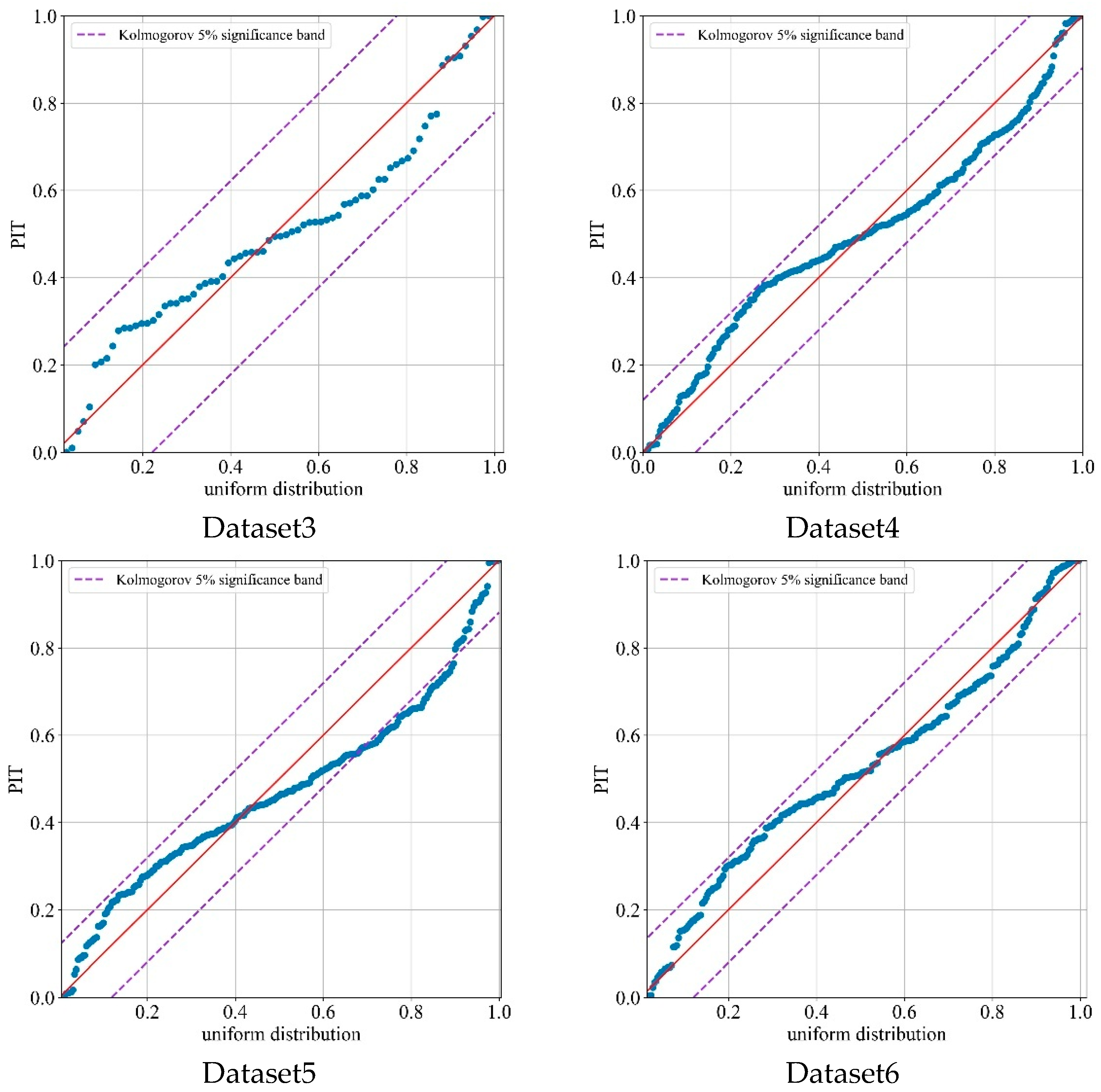
If the PIT value follows a uniform distribution within $\left(0\sim 1\right)$, the prediction result is considered reliable. The PIT results for BiLSTM-GPR are shown in Figure 9.

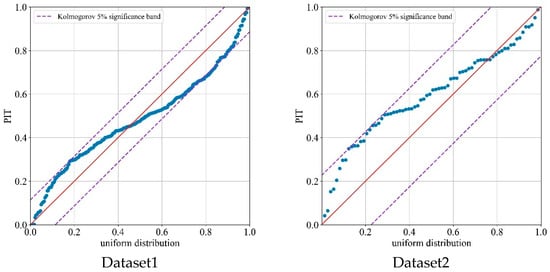
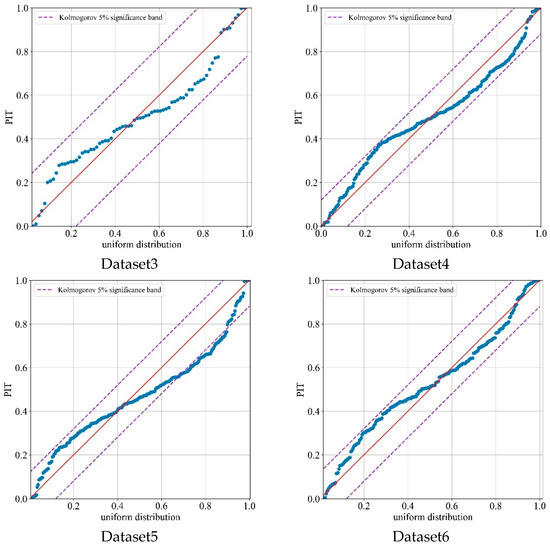
Figure 9. PIT results of BiLSTM-GPR on DC-DC power modules.

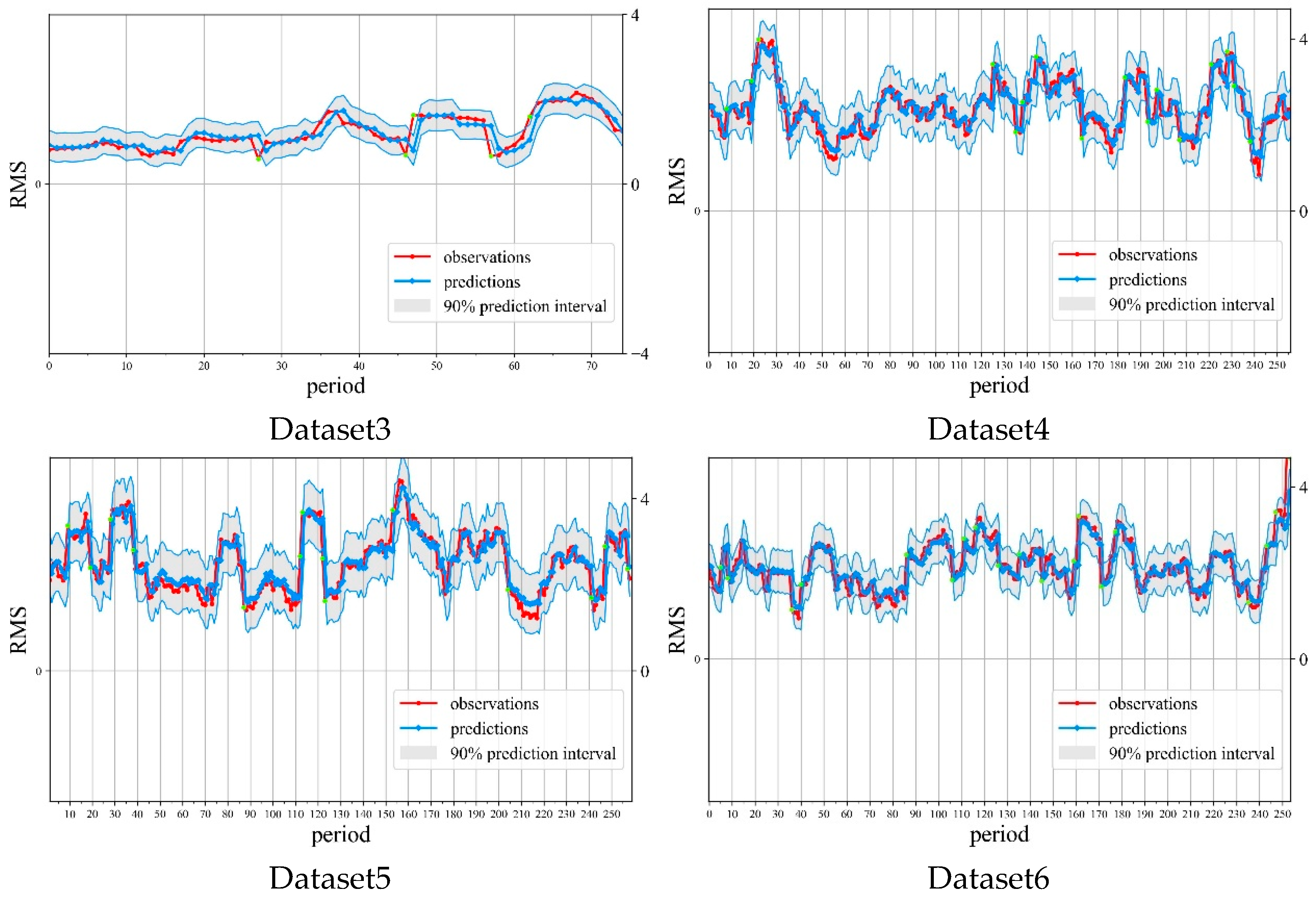
As shown in Figure 9, the PIT results for Datasets 1–6 are clustered near the diagonal, uniformly covering the range [0, 1]. The vast majority of PIT points fall within the Kolmogorov 5% confidence interval, further demonstrating the reliability of the BiLSTM-GPR prediction results.

5. Conclusions

Obtaining reliable RUL predictions is critical for the application of electronic power components. To simultaneously achieve high-precision point prediction metrics and highly reliable interval prediction results, this paper proposes the BiLSTM-GPR model for RUL prediction of electronic power components. First, BiLSTM delivers high-precision point predictions, followed by secondary GPR predictions to achieve highly reliable interval forecasts. The model’s accuracy was validated using NASA’s public lithium-ion dataset across point predictions, interval predictions, and probability predictions. Comparisons with mainstream prediction models revealed that BiLSTM-GPR demonstrated optimal performance in both point prediction levels and interval prediction results, fully validating its predictive accuracy. Further application of this model to RUL prediction for DC-DC power modules yielded results that closely matched actual values. Probability predictions demonstrated well-calibrated performance, and the predicted intervals exhibited accurate coverage capability. This practical application reaffirmed the model’s reliability and utility, offering novel insights and technical approaches for health management of electronic power components in the electronics field. However, current models rely on offline-collected complete degradation sequences for training. When confronted with online incremental data or sudden operational condition switching scenarios, the model update mechanism requires further optimization. Future research may explore embedding physical prior knowledge as soft constraints within the network architecture to construct hybrid intelligent models with enhanced mechanism consistency.