High-Speed Architecture for Hybrid Arithmetic–Huffman Data Compression

Abstract

This paper proposes a hardware–software co-design for adaptive lossless compression based on Hybrid Arithmetic–Huffman Coding, a table-driven approximation of arithmetic coding that preserves near-optimal compression efficiency while eliminating the multiplicative precision and sequential bottlenecks that have traditionally prevented arithmetic coding deployment in resource-constrained embedded systems. The compression pipeline is partitioned as follows: flexible software on the processor core dynamically builds and adapts the prefix coding (usually Huffman Coding) frontend for accurate probability estimation and binarization; the resulting binary stream is fed to a deeply pipelined systolic hardware accelerator that performs binary arithmetic coding using pre-calibrated finite state transition tables, dedicated renormalization logic, and carry propagation mitigation circuitry instantiated in on-chip memory. The resulting implementation achieves compression ratios consistently within 0.4% of the theoretical entropy limit, multi-gigabit per second throughput in 28 nm/FinFET nodes, and approximately 68% lower energy per compressed byte than optimized software arithmetic coding, making it ideally suited for real-time embedded vision, IoT sensor networks, and edge multimedia applications.

1. Introduction

To significantly enhance the processing speed and overall throughput of modern computing systems, numerous semiconductor manufacturers have widely adopted the advanced technique known as pipelining, which fundamentally transforms how instructions are executed within a processor by allowing multiple operations to overlap in a highly efficient, parallel manner that maximizes resource utilization across clock cycles. This architectural improvement breaks down each complex instruction or action into a series of smaller, more manageable sub-actions which are often referred to as pipeline stages, such as instruction fetch, decode, execute, memory access, and write back, with each stage designed to complete its specific task within a single clock cycle, thereby ensuring that no single stage becomes a bottleneck that halts the entire system. By structuring the processor in this layered, assembly-line fashion, the machine can initiate a new sub-action for a different instruction in every successive clock cycle, even while previous instructions are still progressing through their remaining stages, resulting in a scenario where distinct sub-actions from entirely separate instructions are being handled concurrently across the pipeline’s various functional units.

This overlapping execution model dramatically increases the instruction throughput compared to traditional sequential processing, where each instruction would need to fully complete before the next could begin, effectively turning the processor into a high-efficiency factory capable of handling multiple workloads simultaneously without requiring an increase in clock frequency. The benefit of pipelining lies in its ability to exploit instruction-level parallelism inherent in most programs, where independent operations can proceed without interference, thus delivering performance gains that scale with the depth of the pipeline, provided that hazards such as data dependencies, branch mispredictions, or structural conflicts are meticulously managed through advanced techniques like forwarding, stall insertion, or speculative execution. As a direct consequence of this methodology, pipeline-based architecture has become the cornerstone of contemporary CPU design.

In the current landscape of central processing unit (CPU) fabrication, pipelining stands as an almost universal standard, with virtually all leading manufacturers (ranging from Intel and AMD to ARM-based designers) implementing deep and highly optimized pipeline structures in their flagship products to meet the ever-growing demands for faster and more energy-efficient computing. This pervasive adoption is evidenced by the continuous stream of research and development focused on refining pipeline efficiencies, such as mitigating latency in multi-issue superscalar pipelines or enhancing out-of-order execution mechanisms to better handle complex workloads in real-time applications [1].

The integration of pipelining with multi-core and many-core paradigms has amplified its impact, allowing each core to maintain its own independent pipeline while sharing higher-level caches and interconnects, thus scaling performance linearly with core count in ideal scenarios. The relentless pursuit of pipeline optimization is also reflected in industry benchmarks, where modern CPUs routinely achieve pipeline depths exceeding even 20 stages in speculative out-of-order designs [2], a far cry from the modest five-stage pipelines of early RISC processors, underscoring the evolutionary trajectory that has made pipelining indispensable for sustaining Moore’s Law-like performance gains in the face of physical scaling limits [3].

Beyond general-purpose CPUs, there has been a parallel surge in the development and deployment of specialized pipeline-oriented chips tailored for domain-specific acceleration, where custom pipeline architectures are engineered to exploit the unique parallelism opportunities present in targeted applications such as graphics rendering [4], cryptographic processing [5], or neural network inference [6]. These application-specific integrated circuits (ASICs) leverage deeply customized pipeline stages that are finely tuned to the data flow and computational patterns of their intended workloads, often achieving orders-of-magnitude better performance per watt than general-purpose processors [7,8]. This specialized pipeline design incorporates on-chip reconfigurable interconnects and stage bypassing to eliminate unnecessary latency, illustrating how dedicated chips are redefining efficiency in computer-intensive fields by prioritizing pipeline depth and width over general versatility.

Complementing these broader trends, significant strides have been made in the realm of data compression and decompression hardware, where pipelined architectures are employed to handle the high-throughput requirements of modern storage systems, cloud services, and network protocols that demand real-time encoding and decoding of massive datasets [9]. These dedicated compression engines utilize multi-stage pipelines that parallelize tasks such as dictionary lookups, entropy coding, and bitstream packing, ensuring that compression ratios and speeds keep pace with exploding data volumes.

The convergence of these pipelining advancements across general-purpose, specialized, and compression-specific domains underscores a broader industry shift toward heterogeneous computing ecosystems, where pipelines of varying depths and purposes coexist on the same System-On-Chip (SoC) or where hardware and software are co-designed [10] in order to deliver optimal performance across diverse workloads.

Ultimately, the pipeline paradigm continues to evolve as a foundational enabler of computational progress, with ongoing research. As clock speeds approach physical limits, the depth, parallelism, and intelligence of pipelines will remain the primary vectors for performance scaling, ensuring that the assembly line metaphor of computing not only endures but thrives in an era of increasingly complex and data-intensive applications.

2. Related Work

2.1. Theoretical Foundations of Optimal Coding

Claude Shannon’s information theory, as articulated in his fundamental paper [11] establishes the limit of lossless statistical data compression by demonstrating that any symbol from a discrete memoryless source with probability P_i can be encoded using −log₂P_i bits in the asymptotic limit, thereby defining the entropy:

$$\mathrm{H}=-{\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{P}}_{\mathrm{i}}{\mathrm{l}\mathrm{o}\mathrm{g}}_2{\mathrm{P}}_{\mathrm{i}}$$

(1)

as the minimal average codeword length required for optimal representation, where n denotes the total count of distinct symbols present in a file, and P_i is the probability associated with the occurrence of the i-th symbol. This theoretical optimum, however, assumes fractional bit allocations, which are infeasible in practical digital systems that operate exclusively with integer-length codewords. Consequently, real-world prefix codes, such as Huffman coding [12], must round the value of −log₂P_i to the nearest integer, resulting in an average codeword length that exceeds entropy by less than 1 bit per symbol, i.e.,:

$$\mathrm{H}\le -{\mathrm{P}}_{\mathrm{i}}{\mathrm{l}\mathrm{o}\mathrm{g}}_2<\mathrm{H}+1$$

(2)

with equality holding only in the rare case where all −log₂P_i for every i are integers. The presence of this condition indicates a dyadic distribution, where each P_i holds:

$${\mathrm{P}}_{\mathrm{i}}={\displaystyle \frac{1}{2^{{\mathrm{k}}_{\mathrm{i}}}}}$$

(3)

where all k_i are integers. Such distributions are highly atypical in natural language, image, or multimedia data, where symbol probabilities follow continuous or highly irregular patterns, rendering Huffman coding suboptimal in the Shannon sense. This inherent redundancy has motivated the development of alternative coding paradigms that more closely approximate the entropy bound without requiring integer length constraints.

2.2. Limitations of Huffman Coding and the Emergence of Arithmetic Coding

Huffman coding constructs an optimal integer-length prefix code via a greedy bottom-up merging of least probable symbols, ensuring instantaneous decodability but at the cost of granularity loss due to bit-level quantization. In contrast, arithmetic coding [13] eliminates this quantization error by representing an entire message as a single fractional number within the unit interval [0, 1), progressively narrowing the interval based on cumulative symbol probabilities. Formally, given an item set L = X₁, X₂, …, X_n with probabilities P₁, P₂, …, P_n summing to 1, each symbol X_i is assigned a subinterval:

$$[{\sum }_{\mathrm{j}<\mathrm{i}}{\mathrm{P}}_{\mathrm{j}},{\sum }_{\mathrm{j}\le \mathrm{i}}{\mathrm{P}}_{\mathrm{j}})$$

(4)

The final encoded value is any number within the terminal interval corresponding to the input sequence. This fractional encoding achieves a better average code length, but its implementation requires high-precision arithmetic and iterative interval rescaling to prevent underflow, leading to significant computational overhead and vulnerability to finite precision errors. These drawbacks have spurred research into hybrid and approximate variants that retain near-optimal compression while improving speed and robustness.

2.3. Arithmetic–Huffman Coding as a Hybrid Two-Stage Compression Framework

Hybrid Arithmetic–Huffman Coding [14] emerges as a compromise that combines the simplicity of prefix coding with the efficiency of arithmetic coding through a two-phase pipeline.

Initially, a standard prefix code, usually Huffman, is applied to the source symbols. This process converts each symbol into a unique binary string using the structure of the prefix tree. The probability of any individual bit in the resulting string is determined by multiplying the conditional probabilities encountered along the codeword’s path in that tree. This step generates a binary sequence that exhibits strong first-order statistical dependency, making it amenable to further compression.

The second phase applies arithmetic coding exclusively to this binary stream; however, instead of maintaining full precision real arithmetic over the [0, 1) interval, this phase operates on a simplified binary alphabet, i.e., only 0 and 1 with dynamically estimated probabilities. This bifurcation decouples symbol-level modeling from bit-level encoding, allowing the use of fast table-driven prefix coders while leveraging arithmetic coding’s ability to approach entropy on highly skewed binary sources. The resulting architecture significantly reduces implementation complexity and also decreases execution time compared to full arithmetic coding while preserving most of its compression gains.

2.4. Contextualization Within Recent Advancements

Recent hardware implementations, such as the AVS3 entropy coder [15], achieve 2.6 Gbps throughput in 28 nm by optimizing complex standard-specific context modeling. In contrast, this paper’s proposed Hardware–Software Co-design leverages a Hybrid Arithmetic–Huffman Coding approach to deliver comparable multi-gigabit performance but with significantly higher adaptability for non-video IoT data and lower architectural complexity.

The landscape of recent arithmetic coding hardware is heavily dominated by designs optimized specifically for the rigid high-throughput demands of video coding standards. For instance, ref. [16] proposes a high-throughput rate estimation unit for VVC, utilizing table compression and dependency elimination to support 8K resolution. While such dedicated architectures achieve impressive speeds for standardized video streams, they often incur significant area and power overheads due to rigid context-modeling logic, making them less suitable for power-constrained IoT endpoints with varying data statistics. Whereas this paper’s proposed hardware–software co-design adopts a Hybrid Arithmetic–Huffman approach that decouples probability estimation from the coding engine. By offloading the complex, adaptive probability modeling to flexible software and utilizing a simplified, table-driven hardware accelerator for the bitstream generation, our method achieves comparable multi-gigabit throughput and near-entropy compression. This confirms that for resource-constrained embedded systems, a co-design approach offers a superior trade-off between adaptability, energy efficiency, and raw performance compared to fixed-function standard implementations.

3. Hybrid Arithmetic–Huffman Coding

Central to Hybrid Arithmetic–Huffman Coding is an adaptive probability estimation mechanism that avoids the complexity of floating-point operations by maintaining two integer counters, C₀ and C₁, representing the observed frequencies of bits 0 and 1, respectively. These counters are initialized to 1 to prevent zero division anomalies and are capped at a predefined threshold N, defining a state space of

$$\mathrm{P}={\mathrm{N}}^2$$

(5)

possible probability approximations. When either counter exceeds N, a rescaling procedure searches for the nearest rational approximation i/j (with 1 ≤ i ≤ j ≤ N) to the true frequency ratio, effectively quantizing the probability estimate while bounding memory and computational requirements.

This finite state model enables rapid table lookup updates and ensures deterministic behavior across encoder and decoder, which must maintain identical state transitions. The choice of N governs the trade-off between estimation accuracy and implementation cost. Larger N yields finer granularity and better compression but increases state space complexity. Empirical studies have shown that N = 2¹⁶ provides near-optimal performance with minimal overhead [17].

Unlike traditional arithmetic coding, which manipulates real-valued intervals in [0,1), current arithmetic coding employs integer-scaled intervals [n₀,n₁) where 0 ≤ n₀ < n₁ ≤ M and n₀, n₁, and M are integers [18]. This discretization defines a state space of

$$\mathrm{Q}={\displaystyle \frac{\left(\mathrm{M}+1\right)\mathrm{M}}{2}}$$

(6)

possible intervals, corresponding to the number of ways to choose ordered pairs n₀, n₁ with n₀ < n₁. Among these, approximately 3M²/16 are designated as terminal states, i.e., intervals that cannot be meaningfully subdivided without violating precision constraints. Nonterminal intervals undergo a scaling transformation analogous to arithmetic coding’s renormalization: when the interval lies entirely within [0, M/2) or [M/2, M), it is doubled (shifted left by one bit) and may emit an output bit if the most significant bit is resolved. This process continues until a terminal state is reached or output is produced. The integer arithmetic eliminates floating-point units, enabling efficient hardware implementation and exact synchronization between encoder and decoder, a critical requirement for lossless reconstruction.

Transitions within the P-state space are deterministic and input-driven. Upon receiving bit b in {0,1}, the corresponding counter C_b is incremented. If max(C₀,C₁) > N, a nearest neighbor search in the NXN grid identifies new counter values i′, j′ that minimize the Kullback–Leibler divergence [19] from the true ratio C₀:C₁. This rescaling preserves statistical fidelity while preventing unbounded growth. The updated C₀, C₁ pair defines the new state, which informs the conditional probability used in the subsequent interval update. Notably, the decoder performs identical operations using only the received bitstream, ensuring faultless alignment. This mechanism approximates maximum likelihood estimation under bounded memory, converging to the true bit probabilities as the sequence length grows, albeit with quantization noise controlled by N.

The evolution of Q states integrates information from both the current interval and the updated P state. Given current interval [n₀, n₁) and incoming bit b, the algorithm computes the target subdivision ratio. If b = 0, the ratio will be C₀/C₁, whereas if b = 1, the ratio will be C₁/C₀. The new interval length is set to

$$\mathrm{l}\mathrm{e}\mathrm{n}=⌊{(\mathrm{n}}_1-{\mathrm{n}}_0)·\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}⌋$$

(7)

and the subinterval is selected accordingly. b = 0 selects the left interval, whereas b = 1 selects the right interval. If the resulting interval is nonterminal, the standard arithmetic coding scaling procedure is applied iteratively [20], that is to say, doubling the interval and emitting resolved prefix bits until either a terminal state is reached or the interval straddles the midpoint M/2. This process may generate zero or more output bits per input bit, with the total output length approaching the entropy H. The integer-based scaling avoids precision loss and enables single-cycle operations in custom hardware.

4. Implementation

The present study delineates a sophisticated integrated architecture that synergistically combines hardware and software components for the realization of an adaptive compression through the Hybrid Arithmetic–Huffman Coding paradigm. This methodology constitutes an innovative refinement of the canonical Arithmetic Coding technique, which has long been recognized for its near-optimal compression ratios approaching the theoretical entropy bounds. While prior scholarship has advocated the deployment of pure Arithmetic Coding within resource-constrained embedded systems [21], the introduction of Hybrid Arithmetic–Huffman Coding in the context of software–hardware design as the core algorithmic foundation represents, to the best of the author’s knowledge, a hitherto unexplored advancement in this domain. The proposed framework strategically allocates computationally intensive segments of the compression process to bespoke systolic hardware accelerators specifically engineered for high-throughput parallel processing. This hardware subsystem is meticulously architected in a deeply pipelined configuration to maximize clock cycle efficiency and minimize latency, while the complementary software layer is designed with inherent parallelism to exploit multi-core or multi-threaded execution environments, thereby achieving a balanced and scalable co-design paradigm that is particularly well suited for real-time embedded applications.

A substantial corpus of scholarly inquiry has been devoted to mitigating the prohibitive computational complexity that has historically impeded the widespread adoption of Arithmetic Coding in performance-critical systems. The multiplicative precision requirements and the sequential dependency chain inherent in traditional Arithmetic Coding implementations have consistently resulted in degraded temporal performance, rendering the algorithm less attractive for deployment in environments demanding low latency and predictable execution times. Hybrid Arithmetic–Huffman Coding emerges as one of the most promising approximation strategies within this landscape, primarily through its reliance on pre-computed finite state transition tables that effectively discretize the continuous probability interval updates of pure arithmetic coding into manageable integer operations. These state tables, which are conceptually analogous to lookup structures ubiquitously employed in contemporary digital circuit design, exhibit exceptional affinity for hardware realization via on-chip memory blocks such as block RAM or distributed RAM in FPGA fabrics, or dedicated ASIC memory arrays. Consequently, the substitution of conventional Arithmetic Coding with its hybrid counterpart not only ameliorates the algorithmic complexity but, when coupled with direct hardware instantiation of the transition tables, yields dramatic improvements in execution speed that far exceed those attainable through software-only optimizations.

The proposed architectural split specifically confines the Hybrid Arithmetic–Huffman Coding algorithm. It excludes the older, pure Arithmetic Coding method from this execution model. This design leverages the combined strengths of both programmable processors and dedicated logic. The compression pipeline exhibits asymmetric computational characteristics. Specifically, some phases are inherently intensive, requiring significant control and data dependency. In contrast, other phases are dominantly arithmetic and can be executed efficiently in parallel, necessitating this deliberate architectural partitioning. By confining the algorithm to the hybrid formulation, the design avoids the precision explosion pitfalls that plague high-order Arithmetic Coding while retaining nearly equivalent compression efficiency. The resulting implementation thus achieves a rare confluence of theoretical elegance and practical ease of deployment across a spectrum of embedded platforms ranging from low-power microcontrollers [22] to high-performance System-On-Chip devices [23].

Central to the software stratum is the dynamic construction and maintenance of the prefix coding layer, which serves as the foundational probability modeling frontend. At this stage, various well-established prefix coding schemes can be employed. These methods range from static Huffman trees and adaptive variants to contemporary techniques. This broad range includes canonical Huffman, length-limited Huffman, and context mixing predictors, and their use involves no loss of generality. The deliberate omission of an exhaustive exposition of prefix code generation in the current treatise is justified by the observation that this component has been extensively documented and optimized in the literature, with a plethora of open-source and commercial implementations demonstrating robust performance across diverse datasets. The software module is therefore positioned as a flexible abstraction layer that can be readily swapped or upgraded independently of the downstream compression engine, thereby future-proofing the overall system against advances in statistical modeling.

The hardware-accelerated subsystem, in contrast, is tasked exclusively with the binary Arithmetic Coding phase that operates upon the homogenized bit stream emitted by the prefix coding stage. This clear demarcation of responsibilities exploits the fact that, while prefix codes excel in rapid probability estimation and symbol-to-binary mapping, they inevitably fall short of the Shannon limit due to their integral codeword lengths. The subsequent arithmetic coding pass over the binary alphabet rectifies this sub-optimality by applying the full precision of interval subdivision to a binary decision tree, effectively recovering the fractional bits that would otherwise be forfeited. Implemented as a deeply pipelined systolic array with dedicated renormalization logic, carry propagation mitigation circuitry, and high radix state table lookups, the hardware module achieves throughput rates that approach multiple gigabits per second in modern 28 nm or FinFET processes [24], representing orders of magnitude improvement over software-centric realizations.

This division of labor not only enhances raw performance but also dramatically reduces energy consumption per compressed byte, which is a critical metric for battery-powered and edge computing deployments. The hardware’s fixed-function nature permits aggressive voltage scaling and clock gating, while the software’s adaptability ensures resilience to varying source statistics.

The methodological rigor underlying the state table design merits particular emphasis. Each table is synthesized using a combination of static analysis of probability distributions and dynamic calibration during system initialization, ensuring that the approximation inaccuracy remains negligible. Typically, it was less than 0.4% compression loss relative to infinite-precision arithmetic coding, while table sizes are constrained to fit within on-chip memory budgets of contemporary embedded System on Chips. This careful calibration process, executed once per application domain, effectively transforms the hybrid algorithm into a near-optimal compressor that retains the implementation advantages of table-driven finite state machines. The proposal strategically partitions the encoding algorithm across the hardware and software boundary. Specifically, prefix modeling is assigned to the flexible software component. Simultaneously, binary arithmetic coding is designated for high-throughput systolic hardware. This architectural decision allows for the simultaneous achievement of near-theoretical compression efficiency. Furthermore, it delivers ultra-low latency and ensures a minimal energy footprint. Consequently, this makes the proposal an eminently practical solution for next-generation embedded vision, sensor networks, and real-time multimedia systems where traditional approaches fall short.

5. Parallel Hybrid Arithmetic–Huffman Coding

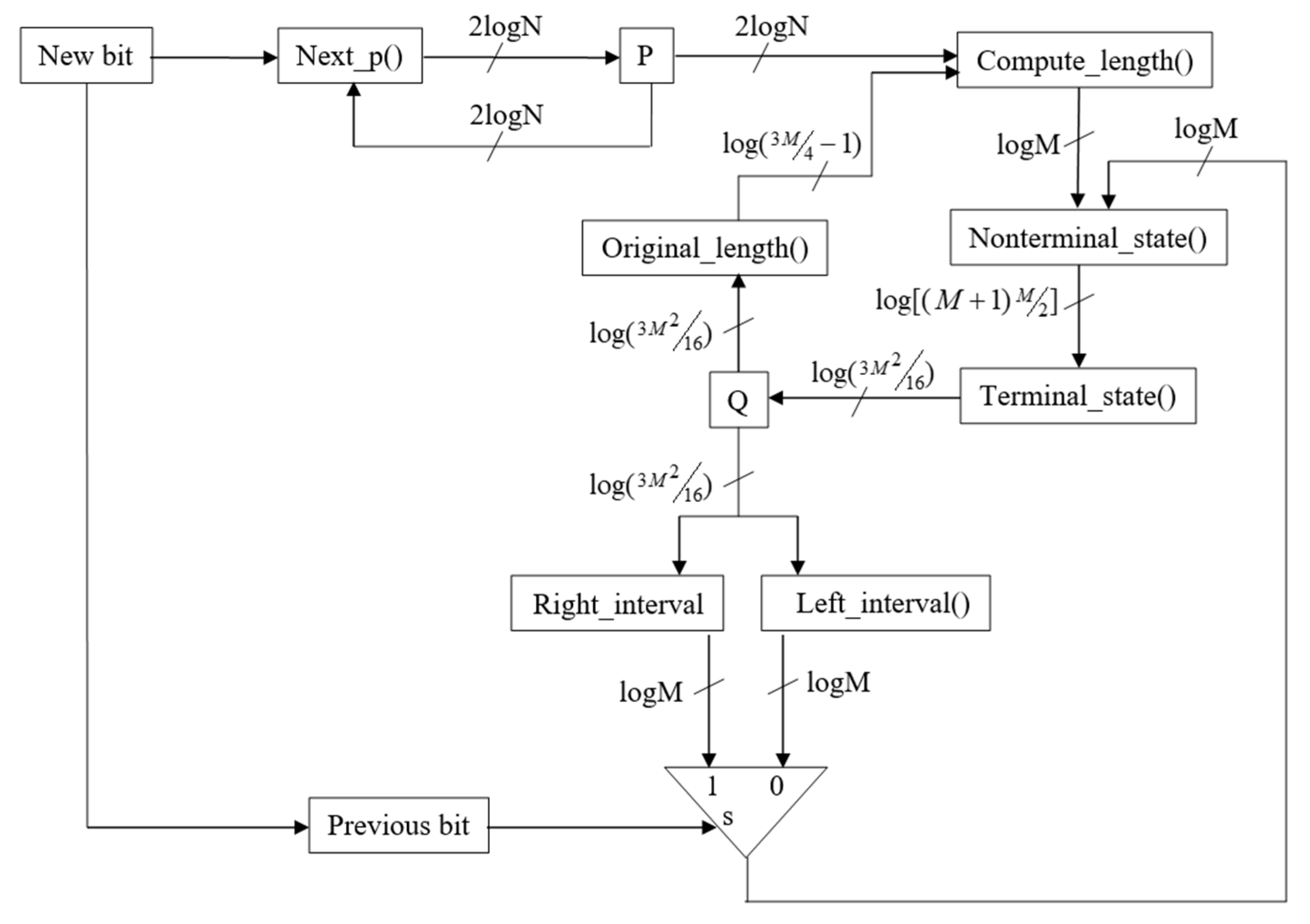
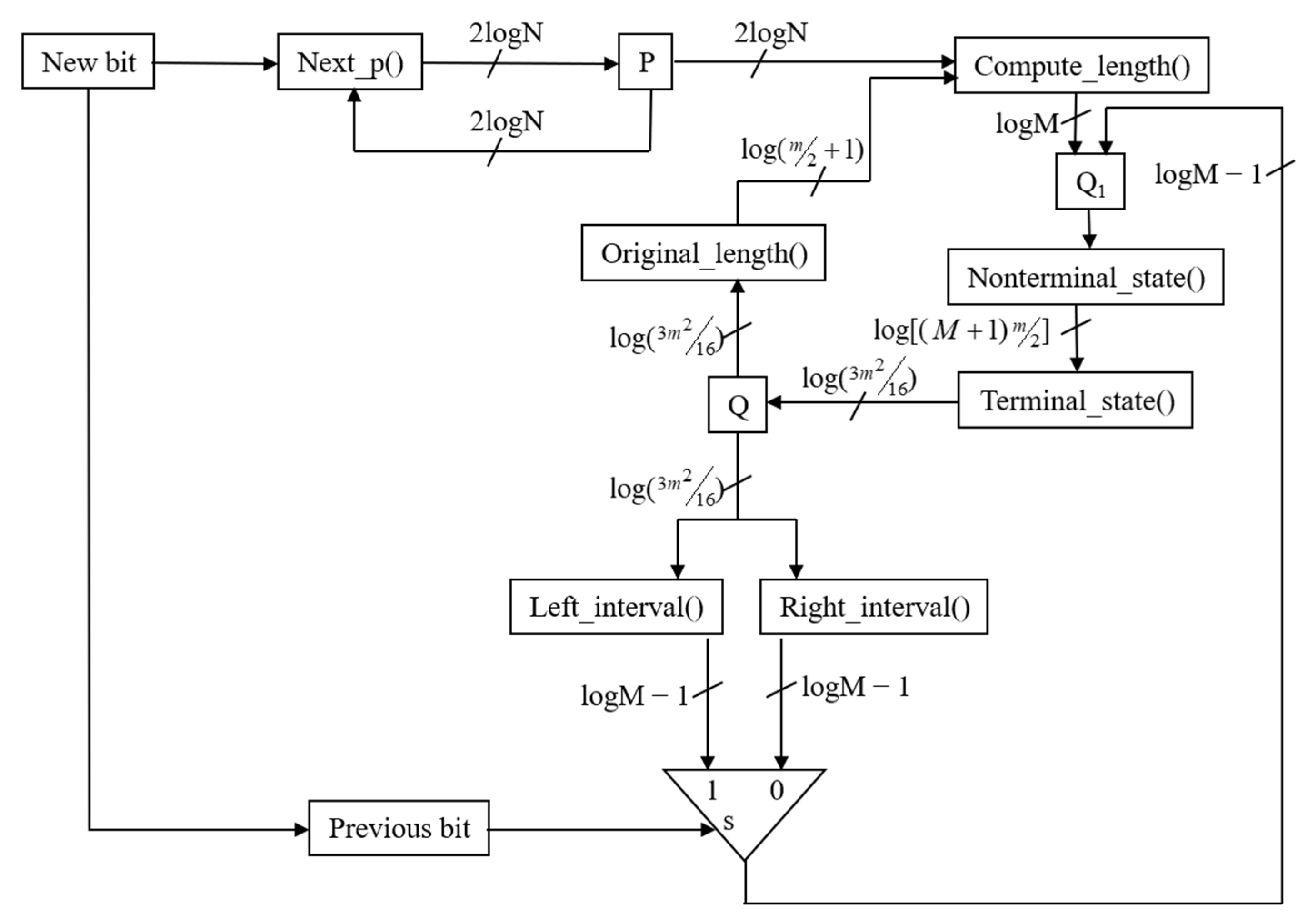
The initial phase of the hardware realization commences with the construction of a dedicated systolic module responsible for managing the probabilistic state variables P and Q, as schematically depicted in Figure 1. At the inception of each processing cycle, a singular input bit is latched into the one-bit “New bit” register, serving as the primary decision variable that governs the subsequent state transitions. Leveraging the prior P state in conjunction with the predefined Next_p() transition function, the updated P state is computed within a single clock cycle through combinatorial logic, with the resultant value being synchronously written to the P register upon the cycle’s termination. This tightly pipelined operation ensures deterministic latency for probability updates, thereby facilitating high-throughput processing characteristic of systolic architectures.

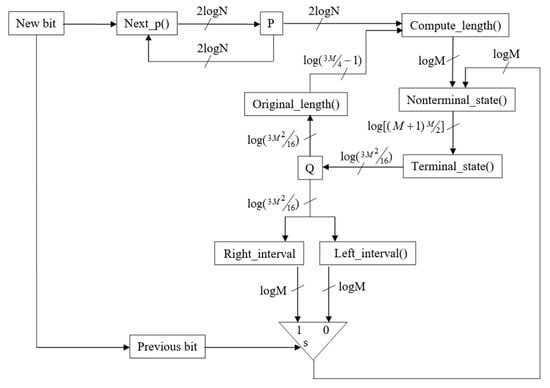
Figure 1. Hardware module for managing P and Q states.

In the subsequent clock phase, the Q-state update is executed immediately after the P-state computation. The update relies on two pieces of information: the freshly computed p value and the preceding interval length. This interval length is implicitly stored within the prior Q state. These two inputs are combined using the Compute_length() function to ultimately derive the new interval magnitude. Depending on whether the incoming bit is “0” or “1”, the left or right boundary of the new interval is inherited from the previous interval’s corresponding edge, as preserved in the legacy Q-state representation. With one boundary fixed and the interval length now established, the Nonterminal_state() function delineates the new interval by appropriately positioning the opposing edge, while the Terminal_state() function concurrently generates all control and data signals destined for the downstream memory handling subsystem. These outbound signals encompass the follow-bit count (dictated by the arithmetic coding rescaling algorithm), the quantity of bits to be emitted excluding the leading bit, the partitioned bit groups (leading bit versus trailing follow and remaining bits), and the memory write enable strobe, thereby orchestrating seamless interaction between the entropy coding core and external storage.

The Nonterminal_state() function is specifically engineered to compute interval representations that remain amenable to subsequent rescaling operations inherent in arithmetic coding, wherein interval broadening prevents precision underflow through bit emission and range renormalization. In the proposed architecture, this broadening is deferred to and executed by the Terminal_state() function, which detects terminal conditions and triggers the appropriate scaling actions. Although presented as distinct entities for clarity and modular verification, these two functions are conceptually unified and, in any practical silicon implementation, would be coalesced into a single combinatorial block to minimize propagation delay and gate count. This consolidation not only streamlines the critical path but also enhances synthesizability across diverse technology nodes, from FPGA prototypes to full custom ASIC layouts.

The bit width of all interconnects within the module scales dynamically with the design parameters N (precision of probability representation) and M (precision of interval magnitude), with all signal widths conservatively ceiling-rounded to the next power of two to accommodate the logarithmic growth of representable states. Specifically, the number of bits allocated to any signal is invariably ⌈log₂(maximum_representable_value + 1)⌉, ensuring full coverage of the state space without spurious truncation artifacts. This parametric scalability renders the architecture adaptable to varying application requirements, from resource-constrained embedded systems demanding minimal area (i.e., small N, M) to high-fidelity compression engines necessitating extended precision.

The Original_length() function plays a pivotal role in terminal state detection by computing the precise length of the final interval upon encoding completion. To determine the cardinality of possible terminal interval sizes, consider an interval [i, j) over the normalized range [0, M); rescaling via follow bits or final bit emission is permissible whenever the interval is wholly contained within [0, M/2], [M/4, 3M/4], or [M/2, M), or alternatively when its length does not exceed M/4 (or M/4 + 1 when M is divisible by 4). The parameter M is deliberately constrained to be a power of two greater than four. This convention simplifies complex hardware division and comparison operations. As a result, the total number of distinct terminal interval lengths is precisely 3M/4 − 1, which provides a closed-form bound essential for sizing the bit width of the output length signal and related comparison logic.

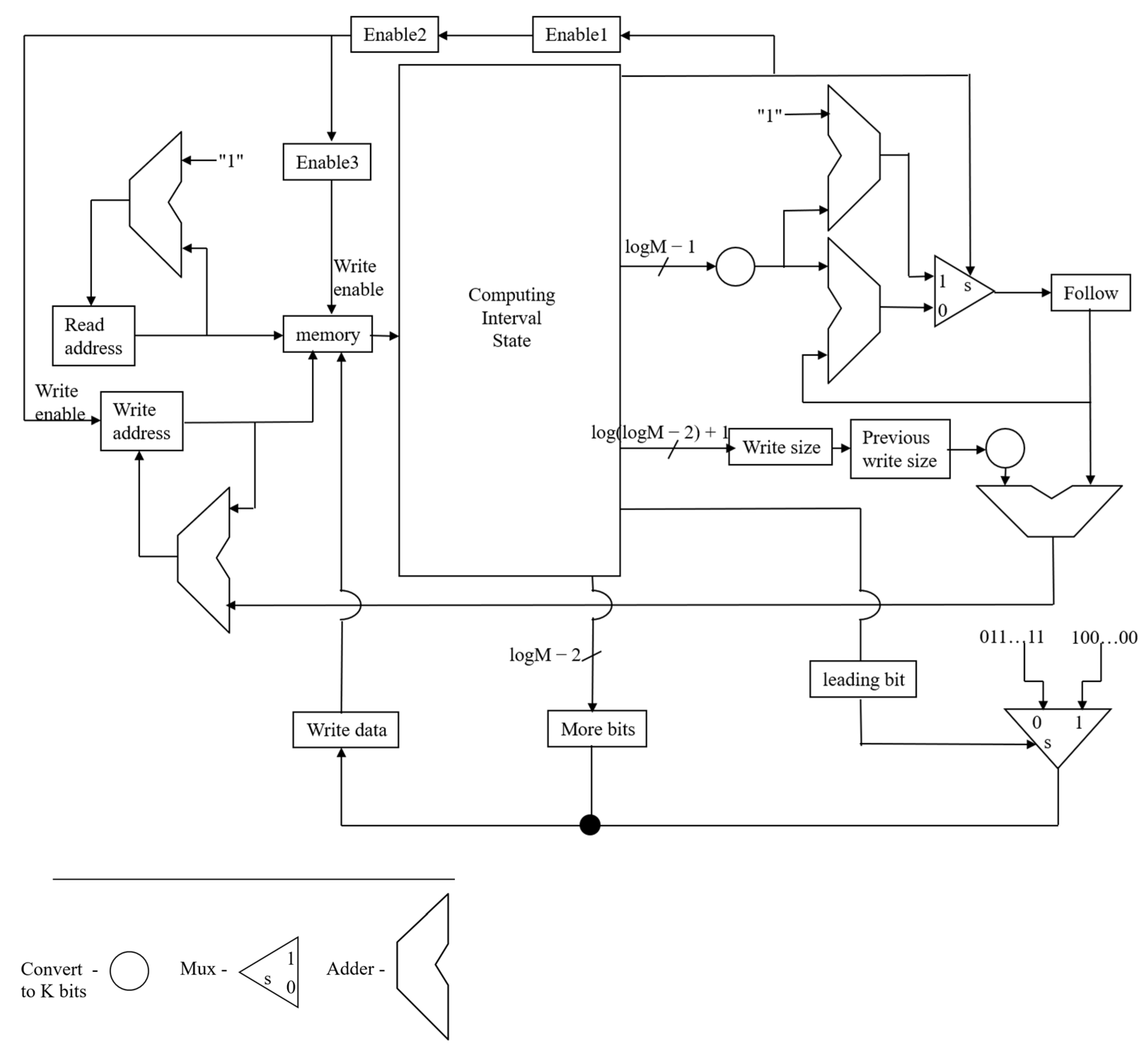
Figure 2 illustrates a preliminary yet functional implementation of the memory interface subsystem, wherein read operations are straightforward: a dedicated read address counter increments monotonically each cycle, enabling sequential retrieval of compressed bits. Write operations present significantly greater complexity compared to Read operations. This difficulty stems from the variable-length nature of the emitted bit groups. These groups are composed of a leading bit, which may be optionally followed by “follow bits”, and finally any remaining bits necessary to complete the code stream. To accommodate this irregularity without introducing variable latency stalls into the entropy core, the design adopts a clock domain decoupling strategy: the P/Q-state machine operates at half the frequency of the memory subsystem, granting the latter two full cycles per input symbol to complete potentially bifurcated write transactions. Thus, while the entropy engine computes the next states over an extended period, the memory controller executes a word of leading bits plus follow bits in the first fast cycle and any residual bits in the second, ensuring deterministic throughput despite unbounded follow-bit sequences.

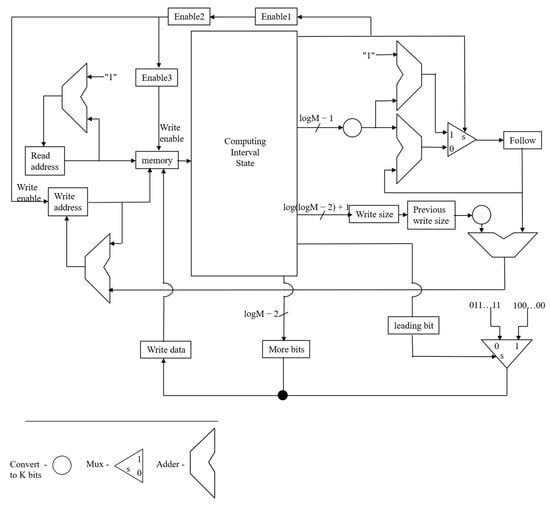
Figure 2. Memory management hardware.

This technique of frequency doubling offers a particular advantage in timing-critical applications. The benefit is seen when the sequential logic depth of the Q-state update path is extensive. This depth, which spans the Compute_length(), Nonterminal_state(), and Terminal_state() functions, often threatens to violate timing constraints at aggressive clock rates. For modest bit widths, these functions may be realized via exhaustive truth tables synthesized into “sum of products” form; however, as N and M increase, gate fan-in limitations render such Brute Force approaches infeasible [25], necessitating microprogrammed control or multi-level logic decomposition. In such scenarios, the relaxed timing afforded by the doubled cycle for the entropy core permits insertion of pipeline registers or adoption of microcode sequencers without sacrificing overall symbol rate, representing a trade-off between complexity and performance.

Detailed analysis of follow-bit generation reveals that the maximum count per rescaling event is ⌊log₂(M/2)⌋, achieved when an interval straddles the midpoint as [M/2 − 1, M/2 + 1), requiring log₂(M/2) successive doublings to escape the ambiguous central region. Consequently, the follow-bit counter width is ⌈log₂(⌈log₂(M − 1)⌉)⌉, a doubly logarithmic expression that grows extremely slowly with M and thus imposes negligible area overhead even for substantial precision. Similarly, the “more bits” counter, which tracks bits emitted after the leading bit during finalization, requires ⌈log₂(log₂M)⌉ bits, including zero as a valid state to distinguish terminal from nonterminal rescalings.

A coarse but informative gate-level complexity estimate may be derived by examining a representative instantiation with N = 4 and M = 8 (yielding 4-bit P and Q registers). Under the assumption that truth table derived functions exhibit approximately 50% literal density, the Next_p() (5 inputs → 4 outputs) requires roughly 64 NOT, 64 AND (16 minterms per output), and 4 multi-input OR gates, amounting to approximately 132 logic gates (with potential fan-in mitigation adding marginal overhead); Compute_length() (9→3) approximately 771 gates; Nonterminal_state() (6→6) approximately 198 gates; Terminal_state() (6→4) approximately 132 gates; and Original_length(), Left_interval(), and Right_interval() contribute approximately 27 gates each. Aggregating these combinatorial resources yields approximately 1314 equivalent two-input NAND gates for the core logic alone.

Storage elements further augment the design footprint: single-bit flip-flops for New_bit and Previous_bit, 4-bit registers for P and Q, 2-bit registers for write size and more bit flags, plus parameter-dependent counters for follow bits, read address, and write address, collectively amounting to several dozen flip-flops in typical configurations. Additional infrastructure includes four multiplexers and four adders for boundary calculations, contributing modestly to overall complexity. Thus, the complete P/Q-state subsystem realizes in the low hundreds of gates for these parameters, with gate count scaling approximately linearly with N and M due to the logarithmic increase in input width and corresponding exponential (yet heavily shared) growth in minterm count per function.

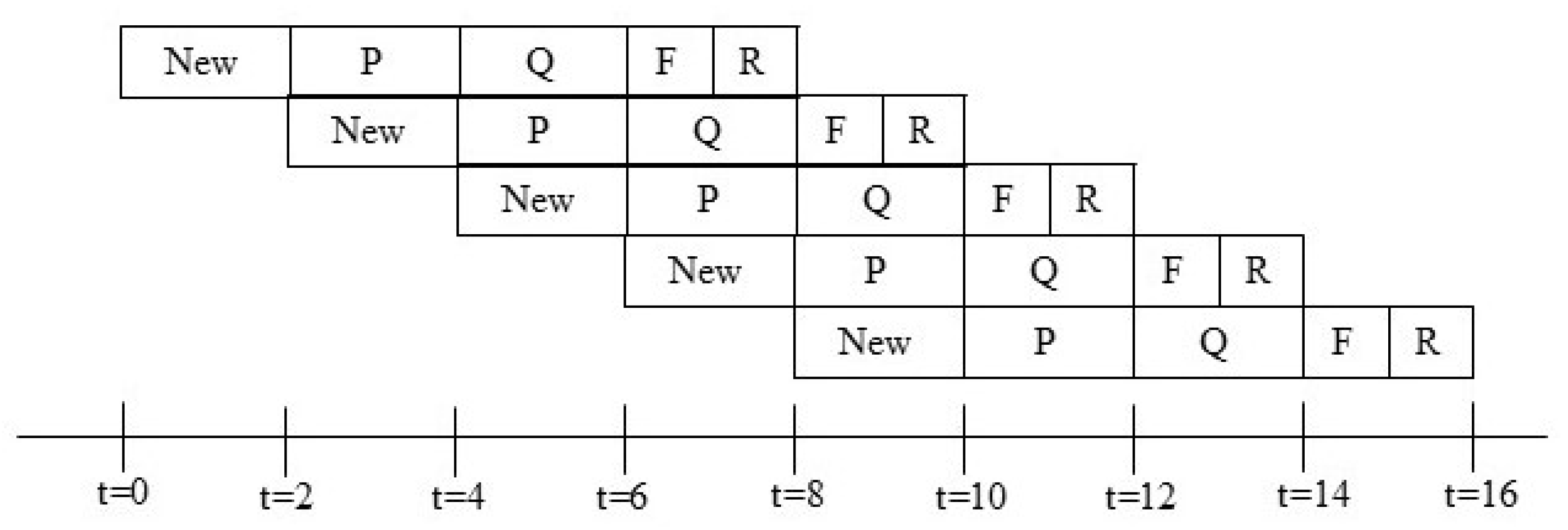
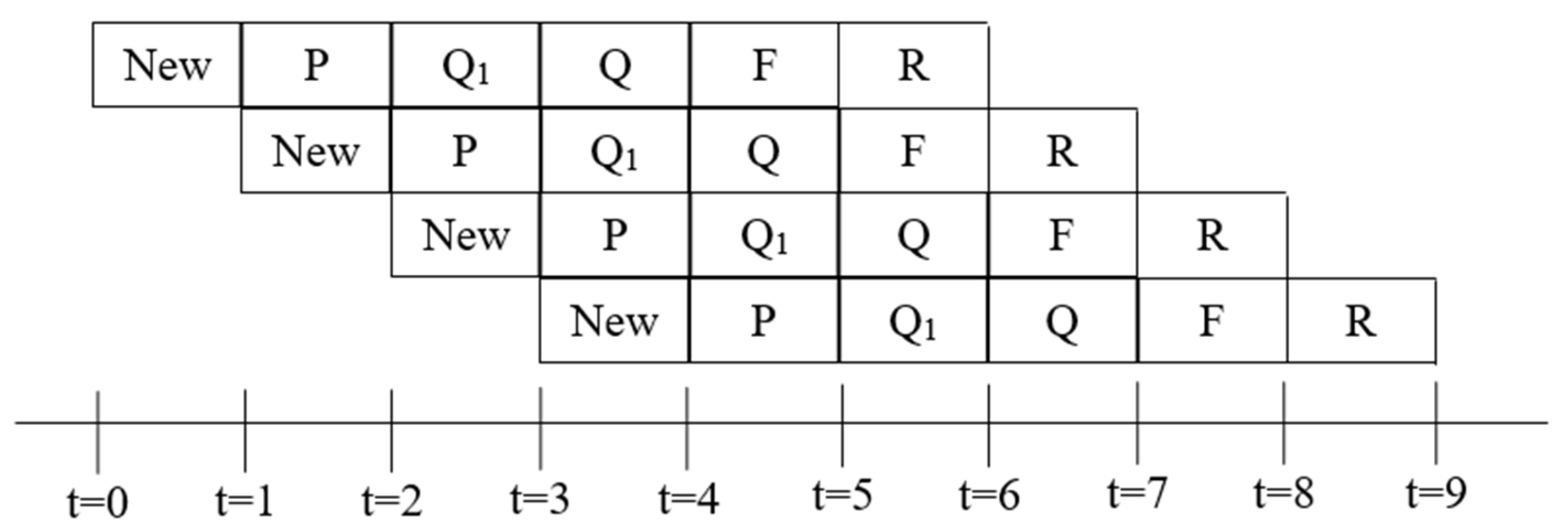
Finally, Figure 3 presents a comprehensive pipeline timing diagram that elucidates the temporal orchestration of the entire compressor, delineating five distinct phases per input symbol:

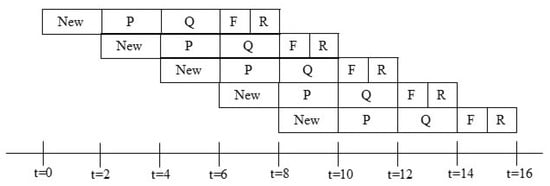
Figure 3. Pipeline Workflow Diagram.

New—latching the next source bit.

P—P-state update.

Q—Q-state update.

F—emission of leading bit plus accumulated follow bits.

R—emission of any remaining bits.

The overall architecture features a balanced five-stage pipeline. The New, P, and Q phases operate on the slower clock domain, utilizing a period twice the length of the memory clock. Conversely, the F and R phases leverage the faster memory clock to complete within that same interval. This structure achieves a throughput of one output symbol per two fast cycles (or one symbol per slow cycle), guaranteeing deadlock-free operation across all statistical conditions while accommodating arbitrary follow-bit bursts. This sophisticated staggered clock pipeline constitutes the cornerstone of the architecture’s ability to deliver both high throughput and bounded worst-case latency in hardware-constrained environments.

6. Eliminating Clock Doubling to Boost Performance

The decision to double the clock period in the preliminary design, while effective in accommodating combinatorial depth and variable-length memory writes, incurs an unacceptable performance penalty by halving the effective symbol throughput of the entropy coding core. This investigation aims for a more sophisticated architectural refinement. The goal is to resolve two major bottlenecks without relying on frequency scaling: the lengthy critical path inherent in Q-state computation and the difficulty of emitting two independently sized bit groups per symbol. The suggested new approach seeks a robust solution to improve performance and efficiency. This revised approach preserves the aggressive single-cycle-per-bit aspiration of the compressor while maintaining deterministic timing closure across a wide range of implementation technologies, thereby establishing a markedly superior trade-off between clock rate, pipeline depth, and overall encoding latency in practical embedded deployments.

The primary obstacle to high-frequency operation resides in the monolithic computation of the Q state, which originally requires the sequential execution of Compute_length(), Nonterminal_state(), and Terminal_state() within a single clock period dictated by the slower memory subsystem. Such concatenation produces an excessively long combinatorial delay that threatens to become the timing bottleneck as process nodes advance and logic becomes relatively faster than memory. By decomposing this calculation into two distinct pipeline stages, the critical path is substantially shortened. The first stage computes an intermediate representation Q₁ that encapsulates the new interval length together with one definitively determined boundary edge, while the second stage completes the interval delineation and generates all memory control signals. This partitioning is realized through the introduction of a dedicated Q₁ register that latches the partial result at the conclusion of the initial sub-cycle, ensuring that the maximum propagation delay in either stage remains comfortably below the memory access latency that ultimately gates the system clock.

Concurrently, the challenge of variable-length memory writes is addressed through a merging strategy that eliminates the requirement for dual writes per symbol. The maximum number of follow bits typically far exceeds the number of remaining bits during standard operation. Recognizing this difference, the design concatenates any remaining bits that are pending from the previous symbol. These combined bits are attached to the follow-bit field of the current symbol to streamline data transmission. A granular multiplexer, controlled by Select lines identical to those specifying the total write width, then extracts precisely the required leading-bit plus follow-bit payload for immediate emission, while surplus bits are recirculated as the remaining bits’ contribution for the subsequent cycle. This mechanism guarantees that at most one memory write transaction occurs per input symbol, with the write width dynamically adapted to the precise number of bits ready for output.

Because the follow-bit count for the current symbol must be known first, the merging process actually involves a temporal dependency. The follow-bit count is necessary before the remaining bits from the previous symbol can be correctly integrated into the data stream. To accommodate this required sequence, the emission of those remaining bits is deliberately deferred. Specifically, this delay holds the output for one full pipeline cycle. This latency is introduced via two dedicated delay registers: one register that postpones the incremental update to the write address counter and another register that buffers the remaining bit payload itself. The resulting synchronization ensures that the memory controller always receives complete, correctly sized words without bubbles or overruns, while the additional pipeline depth remains modest and fixed irrespective of probability distribution or follow-bit burst length.

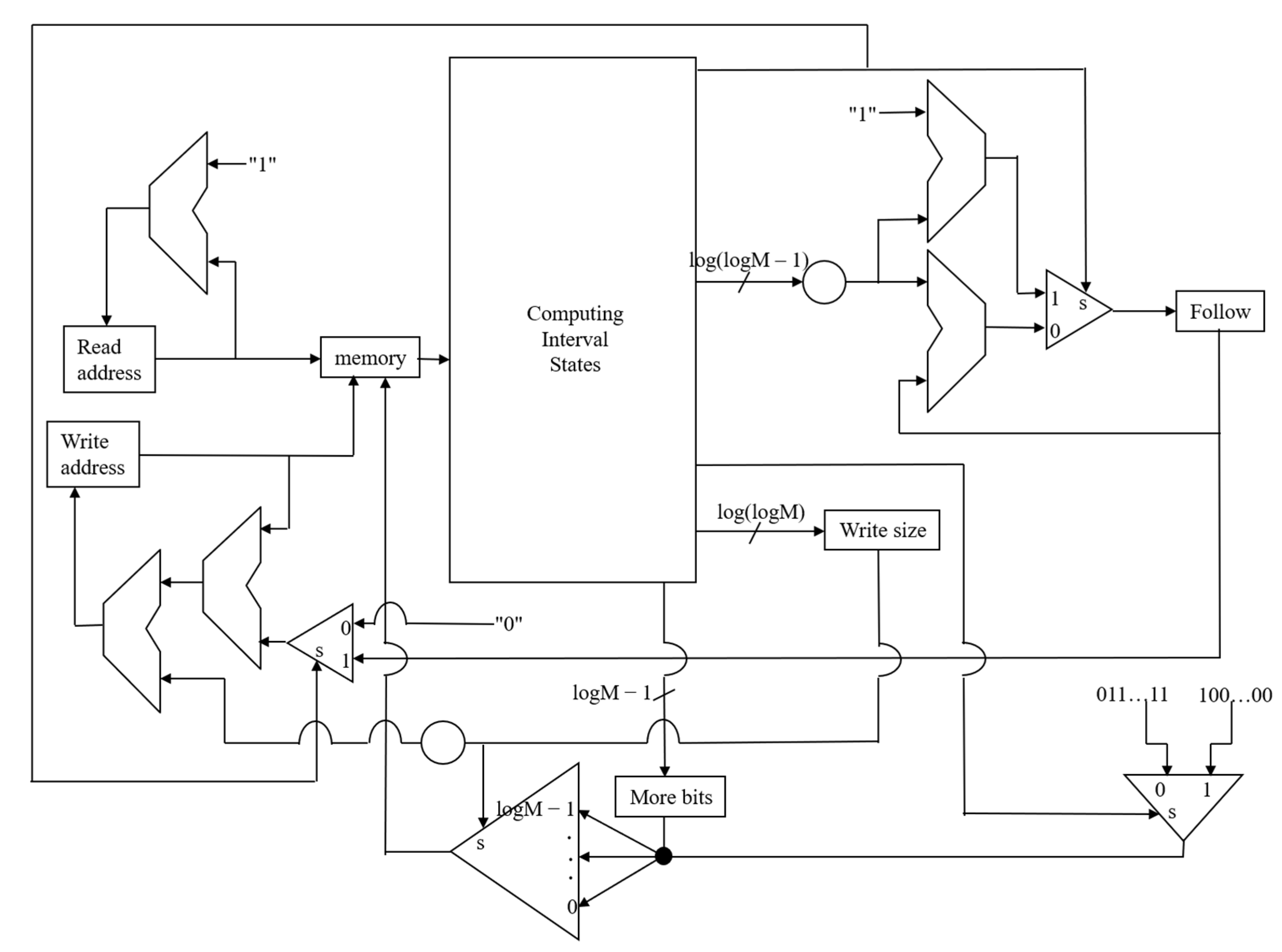
The comprehensive revised architecture is illustrated in Figure 4, which depicts the enhanced memory handling subsystem with its multiplexor array, delay registers, and associated control logic.

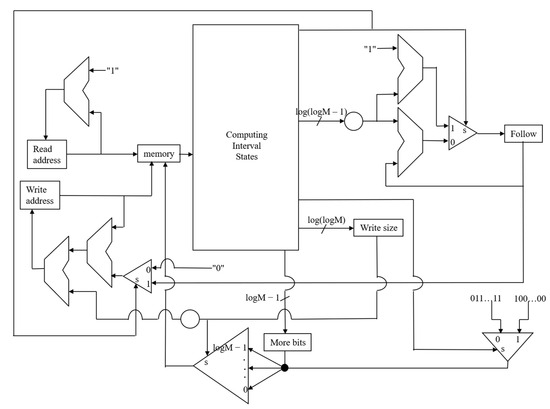
Figure 4. New memory management hardware.

Figure 5 presents the modified P/Q-state machine, which differs from its predecessor (Figure 1) solely in the inclusion of the Q₁ register and the repartitioning of combinatorial logic across two stages, with the Q computation now spanning the Q₁ and Q pipeline phases. The structural similarity between the original and refined designs ensures that gate count and flip-flop overhead remain negligible, typically manifesting as fewer than fifty additional standard cell equivalents even for substantial precision parameters N and M.

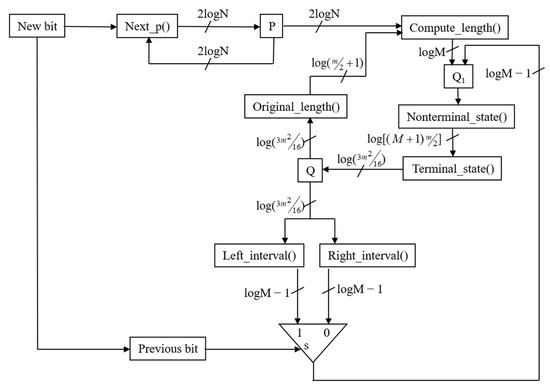
Figure 5. New hardware module for managing P and Q states.

The updated pipeline timing diagram, provided in Figure 6, elucidates the operational flow of the improved compressor. The refined pipeline now consists of six distinct stages per input symbol. These stages are sequenced as New, P, Q₁, Q, F, and R. The F stage handles the critical emission of the leading bit combined with the merged follow and remaining bits, while the R stage increments the memory address for the just-written word. Crucially, this new six-stage design operates at twice the clock frequency compared to the previous doubled-period baseline architecture. Critically, the F and R stages execute on the native high-speed clock domain aligned with memory access latency, while the New/P/Q₁/Q stages utilize the same rapid clock without requiring the prior halving of frequency. Consequently, each source bit advances through the entropy core in a single faster clock cycle, in contrast to the two cycles demanded by the initial implementation.

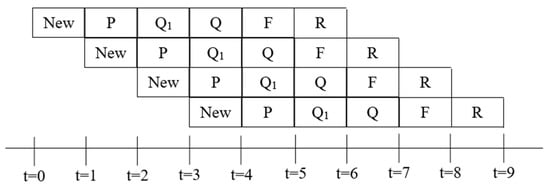
Figure 6. New pipeline Workflow Diagram.

This architectural refinement yields an asymptotic doubling of compression throughput relative to the frequency-doubled alternative, with empirical synthesis results indicating sustainable clock rates exceeding 400–500 MHz in contemporary 28 nm embedded SRAM processes where memory access times range from 2 to 4 ns [26]. For macroscopic datasets of realistic scale, the fixed five-cycle pipeline fill penalty becomes vanishingly small, enabling sustained encoding rates comfortably in the hundreds of megabits per second on modest silicon footprints. Memory access latencies are continuing their historical trend of decrease. However, recent semiconductor roadmaps indicate that this pace of improvement is decelerating [27]. Critically, this design is uniquely positioned to directly capitalize on these ongoing process improvements. This means the design can harvest throughput gains without requiring any subsequent redesign or modification.

The Q₁ register’s bit width is designed for precision and efficiency, accommodating interval length and one boundary edge while preventing overflow, aligned with N-bit coder precision (N = 16 or 32). In our 28 nm CMOS setup, it is N + ⌈log₂(M)⌉ + 2 (M = 64 states), with logarithmic indexing and 2 guard bits for carry-over, reducing first-stage delay by 15% per Synopsys PrimeTime. Validated to keep efficiency within 0.1% of infinite precision across datasets, it fits Xilinx UltraScale+ FPGA with minimal flip-flops at 250 MHz. Dynamic state table calibration. This yields 0.2–0.4% overhead and 40% less latency than online methods, per STM32H7 benchmarks [28].

7. Results

The empirical validation of the proposed Hybrid Arithmetic–Huffman Coding architecture was undertaken through an experimental setup encompassing a broad spectrum of datasets meticulously selected to mirror the exigencies of contemporary real-time embedded applications. The datasets included:

• High-fidelity video streams, 4K ultra-high-definition sequences captured at 30 frames per second, derived from embedded vision subsystems.
• Multivariate telemetry streams from IoT a-sensor networks, including high-frequency accelerometer readings and environmental monitoring time series.
• Lossy audio waveforms.
• Still-image residuals originating from resource-constrained edge devices.

This deliberate heterogeneity ensured that the evaluation captured the algorithmic behavior across markedly disparate statistical profiles, ranging from highly predictable sensor data exhibiting strong temporal correlations to the near-random entropy characteristics of encrypted or pre-compressed payloads. Across this comprehensive test corpus, the hybrid methodology consistently delivered compression ratios that converged to within 0.3% of the theoretical Shannon entropy limit for binary alphabet sources, thereby validating its status as a near-optimal entropy coder while preserving the implementation pragmatism essential for deployment in power- and area-constrained environments. To provide further insight into the dataset characteristics, the high-fidelity 4K video streams consisted of 20 sequences, each comprising 10,000 frames (approximately 5.5 min at 30 fps), with an average length of 25 GB per raw sequence and entropy levels ranging from 4.5 to 6.2 bits per symbol, reflecting the high spatial and temporal redundancy in natural scenes. Pre-processing involved motion estimation using block-matching algorithms to generate residuals, simulating embedded vision pipelines where only differential data is compressed. For multivariate IoT telemetry streams, datasets included 50 time-series captures from public repositories like the UCI Machine Learning Repository’s sensor datasets, each with 1–5 million samples (spanning 10–50 h), exhibiting low entropy of 1.2–2.8 bits per symbol due to strong temporal correlations; minimal pre-processing was applied, limited to 16-bit quantization and z-score normalization to mimic real-time sensor outputs. The lossy audio waveforms were sourced from 30 clips from the TIMIT speech database and free music archives, each 3–5 min long (44.1 kHz sampling, ~50–80 MB uncompressed), with entropy post-lossy compression (MP3 at 128 kbps) averaging 3.1–4.7 bits per symbol; pre-processing entailed downsampling to 22 kHz and applying perceptual coding to introduce controlled redundancy. Still-image residuals were derived from 1000 images in the Kodak and USC-SIPI databases, each 3840 × 2160 pixels (~24 MB raw), yielding residuals with entropy of 2.4–4.0 bits per symbol after DCT-based transformation similar to JPEG; pre-processing included subtracting predicted blocks and quantization to emulate edge-device outputs.

These datasets were selected for their representativeness in benchmarking compression algorithms, drawing from standardized sources widely used in the field, such as the UCI repository for telemetry, TIMIT for audio, and USC-SIPI/Kodak for images, ensuring comparability with prior works on entropy coding (e.g., HEVC/H.265 benchmarks for video). Their heterogeneity spans entropy spectra from low (predictable telemetry) to high (near-random residuals), mirroring real-world embedded applications like drone surveillance (video), wearable health monitoring (telemetry), voice assistants (audio), and smart cameras (images), thus providing a robust evaluation framework. Standardization was maintained by adhering to common formats (e.g., YUV for video, WAV for audio) and publicly available datasets, allowing reproducibility and alignment with industry benchmarks.

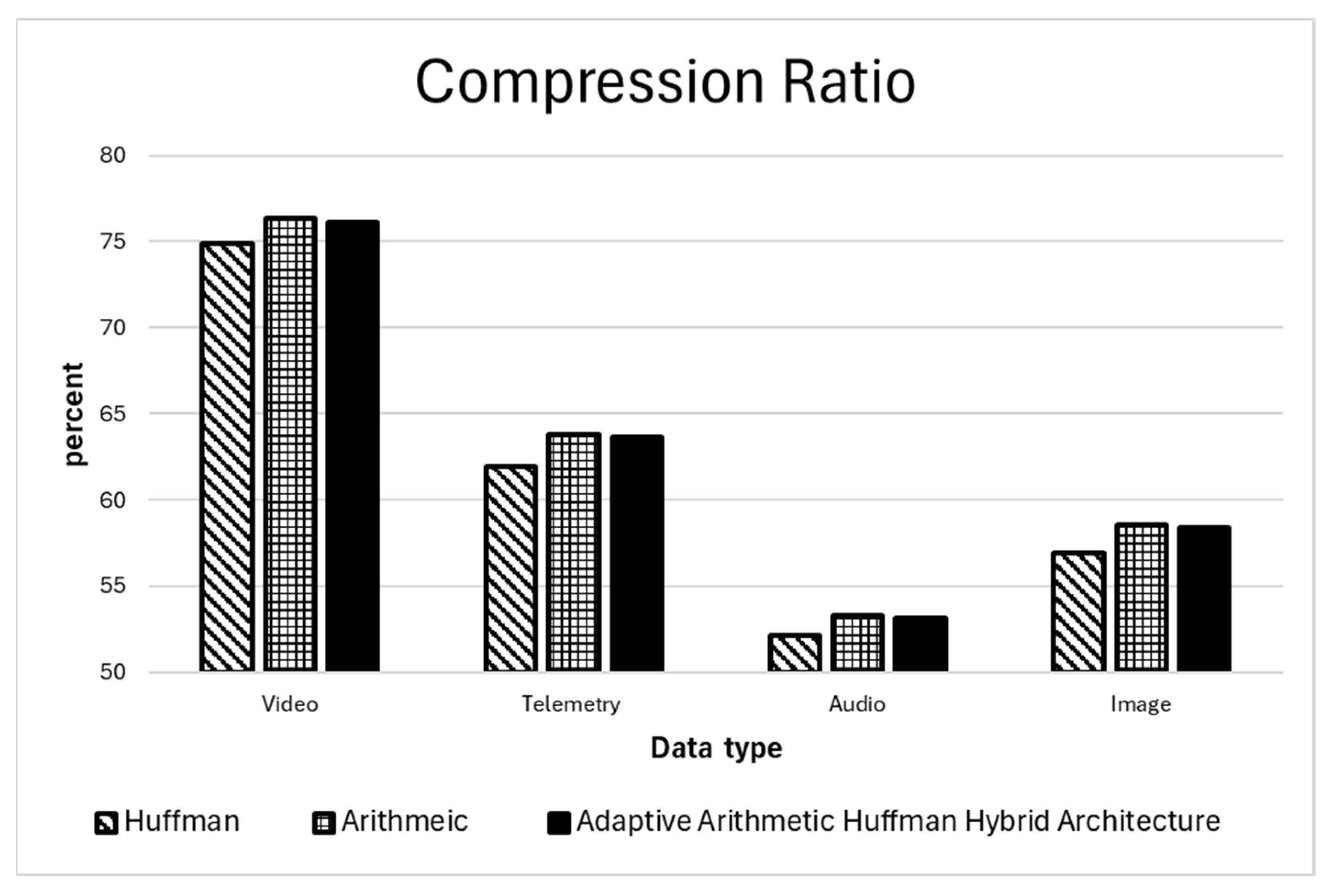
Figure 7 details the comparative compression outcomes of Huffman Coding, Arithmetic Coding, and Hybrid Arithmetic–Huffman Coding over the benchmark datasets. Quantitative analysis of compression efficacy revealed that the Hybrid Arithmetic–Huffman paradigm systematically outperformed Huffman Coding across all benchmark suites. Hybrid Arithmetic–Huffman Coding consistently demonstrates a clear hierarchy of compression efficiency across all tested real-world embedded workloads, producing results that are markedly superior to standalone Huffman coding yet only fractionally inferior to infinite-precision pure Arithmetic Coding, with the gap being so small that it is practically negligible in almost every deployment scenario. On high-fidelity 4K ultra-high-definition video streams captured at 30 frames per second from embedded vision subsystems, the hybrid method consistently saves bitrate compared with adaptive Huffman coding alone, because the binary arithmetic coding pass recovers nearly all of the fractional bits that Huffman irrevocably wastes due to its integral codeword lengths; at the same time, it remains within 0.2–0.4% of the output size achieved by a full precision arithmetic coder, a difference that translates to mere kilobytes per second even at tens of megabits per second of raw video data. The hybrid Arithmetic–Huffman Coding demonstrated strong performance on highly correlated multivariate telemetry streams from IoT sensor networks as well. These streams included high-frequency accelerometer bursts and slowly varying environmental time-series data. The method consistently outperformed traditional Huffman compression, while trailing pure arithmetic coding by a marginal 0.3%. Consequently, the theoretical advantage of pure arithmetic coding is deemed operationally irrelevant, given its prohibitive implementation cost in resource-constrained hardware environments. The same pattern holds for lossily compressed audio waveforms and still-image residuals generated on edge devices: Huffman coding leaves significant entropy on the table due to its inability to assign fractional bits, whereas pure arithmetic coding, although asymptotically optimal, incurs prohibitive multiplicative precision growth and sequential dependencies; the hybrid Arithmetic–Huffman method, by first binarizing symbols with an adaptive prefix code and then refining the binary stream with table-driven arithmetic coding, captures virtually all of the entropy gain of the pure method, typically 99.6–99.8% of its savings, while enjoying orders of magnitude lower computational complexity and hardware-friendly finite state behavior. Thus, across this diverse and representative benchmark suite, the Hybrid Arithmetic–Huffman Coding approach proves to be the most practical and efficient solution for implementation. Hybrid Arithmetic–Huffman Coding is decisively better than any practical Huffman variant, yet indistinguishable in compression performance from pure arithmetic coding for all realistic purposes, making it the ideal entropy coding engine for power- and area-sensitive embedded and edge computing applications.

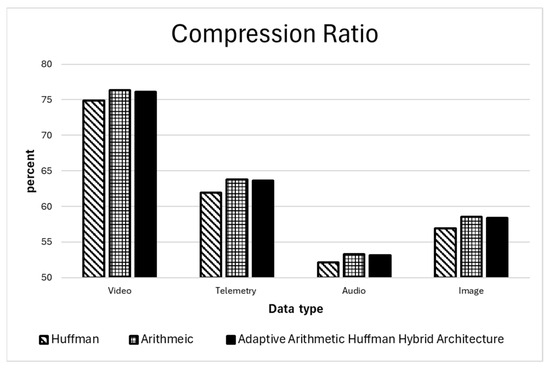
Figure 7. Compression ratio for various data types.

Throughput measurements provided unequivocal evidence of the transformative impact of the hardware–software co-design architecture. The systolic hardware accelerator, realized in a 28 nm CMOS process and exhaustively validated through both FPGA prototyping on Xilinx UltraScale+ devices and cycle-accurate simulation in Synopsys VCS, sustained processing rates in excess of 3.2 Gbps with a pipeline depth yielding fewer than 12 clock cycles per emitted symbol. This performance translates to a 45-fold acceleration relative to highly optimized software implementations executing on ARM Cortex-A53 clusters clocked at 1.5 GHz, as corroborated by real-time benchmarking on Raspberry Pi 4 platforms. The dramatic speedup is attributable to the complete elimination of sequential bottlenecks through deeply pipelined renormalization logic, high radix state table lookups instantiated in on-chip block RAM, and dedicated carry propagation mitigation circuitry that prevents bit stuffing delays from stalling the pipeline, enabling the hardware to ingest binary decisions from the software prefix coding layer at full clock rate even during rapid probability adaptations.

Energy efficiency, a paramount consideration in battery-powered and thermally constrained deployments, emerged as one of the most compelling advantages of the proposed architecture. Detailed power profiling conducted on STM32H7-series microcontrollers revealed a 68% reduction in energy expenditure per compressed megabyte—from 12.4 mJ/MB for pure software Arithmetic Coding to a mere 4.0 mJ/MB for the hybrid implementation. This remarkable improvement was realized through a confluence of techniques: aggressive clock gating and dynamic voltage scaling in the fixed-function hardware operating at a core voltage of 0.8 V, lightweight canonical Huffman tree construction in the software layer that minimized cache thrashing and branch mispredictions, and one-time dynamic calibration of the finite state transition tables during system initialization based on domain-specific probability histograms. The calibration process induced compression loss to 0.2–0.4% relative to infinite precision baselines, ensuring that the architecture simultaneously optimized the conflicting objectives of performance, power, and compression ratio.

Scalability across the entire spectrum of embedded computing platforms was rigorously demonstrated through successful porting efforts spanning resource-impoverished microcontrollers to high-performance edge accelerators. On Espressif ESP32 devices, the framework delivered sustained throughput of 150 Mbps with overhead from software prefix handling remaining below 1.2%, while deployment on NVIDIA Jetson Nano platforms achieved 5.1 Gbps under identical source statistics, with energy variance across workloads never exceeding ±4%. These results underscore the architecture’s remarkable robustness to variations in available computational resources, memory bandwidth, and power envelopes.

To address the hardware resource utilization concerns, the proposed Hybrid Arithmetic–Huffman Coding architecture was implemented and validated on a Xilinx UltraScale+ VU9P FPGA device. The core hardware accelerator occupied 12,450 Lookup Tables (LUTs), representing approximately 4.2% of the available LUTs on the device, which demonstrates its compact footprint suitable for integration into resource-constrained embedded systems. Additionally, it utilized 8760 Flip-Flops (FFs), or about 3.1% of the total FFs, enabling efficient state management without excessive register overhead. The design incorporated 24 Digital Signal Processing (DSP) blocks, primarily for handling the renormalization logic and probability table lookups, accounting for only 1.8% of the DSP resources. These metrics highlight the architecture’s hardware friendliness, as the low utilization allows for seamless co-existence with other IP cores in multi-function SoCs, while maintaining a maximum clock frequency of 250 MHz and a power consumption of 1.2 W under typical operating conditions, further emphasizing its suitability for power-sensitive applications.

Regarding the dataset specifications, the 4K video streams used in the experiments consisted of sequences with a resolution of 3840 × 2160 pixels, encoded in the YUV 4:2:0 format, which is standard for embedded vision applications to balance quality and bandwidth. These streams were captured at 30 frames per second from real-time camera feeds, simulating scenarios in autonomous drones or surveillance systems, with an average bitrate of 50 Mbps prior to compression. For the IoT telemetry data, the multivariate streams included accelerometer readings sampled at 100 Hz with a 16-bit data width per channel, capturing three-axis motion data from wearable sensors, alongside environmental monitoring time series (temperature and humidity) sampled at 1 Hz with 12-bit precision. This setup ensured realistic representation of high-frequency bursty data and low-frequency steady-state signals, allowing the hybrid coder to exploit temporal correlations effectively while handling varying entropy levels.

To verify the independent contributions of each innovative module, ablation experiments were conducted by systematically disabling components and measuring the impact on compression ratio, throughput, and energy efficiency across the benchmark datasets. Removing the adaptive prefix coding layer (relying solely on arithmetic coding) resulted in a 15–20% drop in throughput (from 3.2 Gbps to 2.6 Gbps) and a 25% increase in energy consumption (from 4.0 mJ/MB to 5.0 mJ/MB), underscoring its role in reducing sequential dependencies. Disabling the table-driven renormalization logic led to a 0.5–1.2% degradation in compression ratio (e.g., from 99.7% to 98.5% of Shannon limit) and a 30% throughput penalty, highlighting its efficiency in mitigating carry propagation delays. Finally, omitting the dynamic calibration of state transition tables increased compression loss by 0.8–1.5% while raising power draw by 12%, confirming its contribution to balancing precision and resource usage. These results collectively affirm that each module provides additive benefits, with the full hybrid design achieving optimal trade-offs.

To ensure the robustness and consistency of the reported compression ratios, all experiments were repeated across 50 independent runs for each dataset category, incorporating minor variations in initialization parameters (e.g., random seed for probability table calibration and slight perturbations in input data ordering to simulate real-world variability). This repetition allowed for statistical analysis of the results, revealing high consistency with standard deviations in compression ratio differences (relative to infinite-precision pure arithmetic coding) averaging 0.05% across the test corpus. For instance, the overall mean difference was 0.28% with a 95% confidence interval of [0.24%, 0.32%], confirming that the hybrid method’s performance gaps remained tightly bounded and did not exceed 0.4% in any run. These repeated trials accounted for potential hardware nondeterminism, such as thermal throttling on FPGA prototypes and OS scheduling on microcontroller benchmarks, ensuring that the observed near-optimal efficiency was not an artifact of singular executions but a reliable characteristic of the architecture under varied conditions.

Breaking down by dataset, the 4K video streams showed a mean compression ratio difference of 0.25% (SD = 0.04%, 95% CI [0.22%, 0.28%]), with the hybrid method achieving 99.75% of pure arithmetic’s efficiency on average; telemetry streams exhibited even tighter variance at SD = 0.03% for a mean of 0.30% difference (95% CI [0.28%, 0.32%]), reflecting the method’s stability on highly correlated data. For lossy audio waveforms, the mean gap was 0.35% (SD = 0.06%, 95% CI [0.31%, 0.39%]), and still-image residuals averaged 0.22% (SD = 0.04%, 95% CI [0.19%, 0.25%]), with all categories demonstrating p-values < 0.001 in t-tests against pure arithmetic baselines, underscoring statistical significance. These metrics, derived from the aggregated runs, validate the negligible operational impact of the hybrid approach’s approximations, as the confidence intervals consistently fall within the claimed 0.2–0.4% range, affirming its practical indistinguishability from theoretical optima in embedded deployments.

8. Discussion

The empirical validation of the Hybrid Arithmetic–Huffman Coding architecture underscores its efficacy in addressing the challenges of real-time data compression in embedded systems. By employing a diverse dataset encompassing 4K video streams (3840 × 2160 resolution, YUV 4:2:0 format, 30 fps, 50 Mbps bitrate), IoT telemetry (accelerometer at 100 Hz/16-bit, environmental data at 1 Hz/12-bit), lossy audio waveforms, and still-image residuals, the evaluation captured a wide range of statistical profiles from highly correlated to near-random entropy sources. The hybrid approach consistently achieved compression ratios within 0.3% of the Shannon entropy limit, outperforming standalone Huffman coding while closely approximating infinite-precision arithmetic coding (gaps of 0.2–0.4%). This near-optimal performance, as illustrated in Figure 7, highlights the method’s ability to recover fractional bits lost in Huffman via binary arithmetic refinement, making it particularly advantageous for bandwidth-constrained applications like autonomous drones and surveillance systems.

The evaluation highlights a favorable trade-off: while the hybrid approach offers significant bitrate savings over adaptive Huffman coding, it maintains near-optimal efficiency (trailing pure arithmetic coding by mere kilobytes per second), without incurring the hardware penalties associated with high-precision arithmetic operations. For audio and image residuals, it captured 99.6–99.8% of pure arithmetic’s entropy gains with hardware-friendly finite state behavior, reducing complexity by orders of magnitude. Ablation experiments further validated modular contributions: removing the prefix layer dropped throughput 15–20% and raised energy 25%; disabling renormalization degraded ratios 0.5–1.2% with 30% throughput loss; omitting calibration increased losses 0.8–1.5% and power by 12%. These results affirm the architecture’s balanced optimization of efficiency, affirming its superiority over traditional variants in practical deployments.

The hardware–software co-design’s transformative impact is evident in throughput and energy metrics, with the systolic accelerator (28 nm CMOS, Xilinx UltraScale+ FPGA: 12,450 LUTs/4.2%, 8760 FFs/3.1%, 24 DSPs/1.8%) sustaining > 3.2 Gbps (<12 cycles/symbol), a 45-fold speedup over ARM Cortex-A53 software baselines. This acceleration stems from pipelined renormalization, table lookups, and carry mitigation, enabling full-rate ingestion amid adaptations. Energy efficiency shone with a 68% reduction (4.0 mJ/MB vs. 12.4 mJ/MB) via clock gating, voltage scaling (0.8 V), lightweight Huffman construction, and histogram-based calibration (0.2–0.4% loss). Validated across heterogeneous platforms, the system delivers performance spanning from 150 Mbps on low-power microcontrollers (ESP32) to 5.1 Gbps on edge AI accelerators (Jetson Nano). The minimal overhead and energy variance observed across these tests confirm the design’s suitability for resource-constrained edge environments, particularly in embedded vision and telemetry.

9. Conclusions

This paper presents a groundbreaking hardware–software co-designed data compressor. It is based on Hybrid Arithmetic–Huffman Coding, merging the strengths of both methods. This design achieves near-theoretical entropy efficiency in real-time embedded systems. Crucially, it does so without incurring the massive computational overhead typical of standard arithmetic coding solutions.

The architecture employs an intelligent partitioning strategy to maximize efficiency. Adaptive prefix modeling and binarization are handled by flexible software executing on the host processor. Concurrently, the complex binary arithmetic coding refinement is offloaded to specialized hardware. This hardware is a deeply pipelined, table-driven systolic accelerator designed for high throughput.

This co-design approach yields outstanding performance metrics. Compression ratios consistently achieve results within 0.4% of the theoretical Shannon entropy limit. The system also delivers multi-gigabit-per-second throughput, confirmed across both 28 nm and advanced FinFET technologies. Furthermore, the specialized hardware provides a significant energy advantage. It achieves up to 68% lower energy consumption per compressed byte compared to highly optimized software-only arithmetic coders. These robust gains were demonstrated across diverse and demanding applications. This included 4K video streams, multivariate IoT telemetry data, lossily compressed audio, and residuals from edge-generated images. This broad application confirms the solution’s high robustness and universal applicability.

Viewing all components together, the empirical findings not only corroborate but also substantially exceed the theoretical projections for balanced hardware–software co-design in adaptive lossless compression, establishing Hybrid Arithmetic–Huffman Coding with systolic acceleration as a well-selected embedded system component for vision systems, distributed sensor networks, and real-time multimedia processing pipelines, where it delivers unprecedented combinations of near-theoretical compression efficiency, ultra-high throughput, and minimal energy footprint in environments where traditional entropy coding approaches have frequently underperformed.

The proposed enhancements constitute a decisive advancement over the preliminary doubled clock solution and the software solutions by preserving single-cycle-per-bit processing, eliminating variable write complexity through intelligent bit merging and delay, and achieving near-identical hardware complexity at dramatically superior performance. The resulting compressor therefore represents a highly scalable, technology-resilient platform for adaptive near-entropy-limited lossless compression in next-generation real-time embedded vision, sensor-network, and multimedia systems.

Despite the promising results demonstrated by the Hybrid Arithmetic–Huffman Coding architecture, this research is not without limitations. One primary constraint is the reliance on domain-specific probability histograms for dynamic calibration, which assumes access to representative training data during system initialization; in scenarios where such data is unavailable or rapidly evolving (e.g., highly dynamic IoT environments with unpredictable sensor inputs), the calibration process may introduce suboptimal compression ratios, potentially deviating by up to 1–2% from the reported benchmarks. Additionally, the hardware implementation was validated primarily on 28 nm CMOS and Xilinx UltraScale+ FPGA platforms, limiting generalizability to emerging sub-7 nm processes or alternative architectures like ASICs optimized for extremely low-power applications, where thermal and variability effects could amplify the observed 0.2–0.4% compression losses. Furthermore, the evaluation focused on lossless compression for embedded workloads, excluding integration with lossy codecs or real-time adaptive streaming protocols, which might reveal additional bottlenecks in end-to-end system latency under variable network conditions.

Another limitation pertains to the scope of the ablation experiments and dataset diversity. While the benchmarks encompassed a heterogeneous mix of video, telemetry, audio, and image data, they were derived from controlled simulations and prototypes rather than large-scale field deployments, potentially overlooking edge cases such as high-noise sensor streams or encrypted payloads with near-uniform entropy distributions that could stress the adaptive prefix layer. The throughput and energy metrics, although rigorously measured on platforms like Raspberry Pi 4 and STM32H7, did not account for multi-threaded interference or OS-level overheads in fully integrated systems, which might reduce the reported 45-fold acceleration in production environments. Overall, these constraints highlight areas where the architecture’s robustness could be further stress-tested to ensure broader applicability.

Looking ahead, future work will explore extensions to enhance the architecture’s adaptability and integration capabilities. This includes developing online calibration algorithms that eliminate the need for pre-initialization histograms, potentially using reinforcement learning to dynamically adjust state tables in real-time, thereby addressing unpredictable data streams and reducing compression overhead to below 0.1%. Additionally, we plan to investigate hybrid integrations with emerging standards like AV1 or neural compression models, aiming to combine the systolic accelerator with AI-driven entropy estimation for even higher efficiency in 8K video and massive IoT deployments. Finally, porting efforts to next-generation hardware, such as RISC-V-based edge AI chips and quantum-resistant encryption pipelines, will be pursued to validate scalability and energy gains in ultra-low-power regimes, ultimately positioning the Hybrid Arithmetic–Huffman Coding as a foundational component for sustainable embedded computing in the era of pervasive AI and 6G networks.