Abstract
As a fundamental low-level vision task, image restoration plays a pivotal role in reconstructing authentic visual information from corrupted inputs, directly impacting the performance of downstream high-level vision systems. Current approaches frequently exhibit two critical limitations: (1) Progressive texture degradation and blurring during iterative refinement, particularly in irregular damage patterns. (2) Structural incoherence when handling cross-domain artifacts. To address these challenges, we present a semantic-aware hierarchical network (SAHN) that synergistically integrates multi-scale semantic guidance with structural consistency constraints. Firstly, we construct a Dual-Stream Feature Extractor. Based on a modified U-Net backbone with dilated residual blocks, this skip-connected encoder–decoder module simultaneously captures hierarchical semantic contexts and fine-grained texture details. Secondly, we propose the semantic prior mapper by establishing spatial–semantic correspondences between damaged areas and multi-scale features through predefined semantic prototypes through adaptive attention pooling. Additionally, we construct a multi-scale fusion generator, by employing cascaded association blocks with structural similarity constraints. This unit progressively aggregates features from different semantic levels using deformable convolution kernels, effectively bridging the gap between global structure and local texture reconstruction. Compared to existing methods, our algorithm attains the highest overall PSNR of 34.99 with the best visual authenticity (with the lowest FID of 11.56). Comprehensive evaluations of three datasets demonstrate its leading performance in restoring visual realism.
1. Introduction
With the rapid development of digital media technology, the demand for high-quality, high-resolution images is increasing. Image inpainting technology addresses defects such as missing or corrupted pixels in images, with applications ranging from photo restoration to medical imaging and artwork preservation. Image inpainting algorithms find broad and significant applications across multiple domains. Notable examples include the restoration of damaged MRI [1] in medical imaging, as well as the recovery of missing data in high-resolution remote sensing [2].
Early image inpainting algorithms [1,3] were based on mathematical and physical theories using pixel correlations and were broadly categorized into diffusion-based and sample-based methods. However, traditional approaches lacked a deep understanding of the high-level semantic information within images, making it difficult to generate contextually consistent inpainted content. The increasing popularity of deep learning technology offers some new ideas for image inpainting. Context encoders [4] are the first techniques to apply Generative Adversarial Networks (GANs) [5] to image inpainting. Despite improvements, existing methods [4,5,6,7,8] still face challenges in handling large, irregular, or complex damaged regions, often resulting in artifacts or structural distortions. However, these image inpainting methods cannot be adapted to complex application scenarios; for example, fewer intact pixels are available to infer image content from distant backgrounds, which can lead to structural distortions and artifacts when inpainting large, irregular, and complex images, reducing the clarity and realism of the inpainted images.
In recent years, a series of advanced methods have emerged in the field of large-region image inpainting, such as the semantic-mask-based LaMa [9], the Transformer-based ICT [10], the denoising diffusion-based RePaint [11], and DDNM [12]. These methods have significantly improved the inpainting effect in complex scenarios by introducing novel network architectures or generation mechanisms.
In recent years, to meet the demands of edge computing and real-time processing, a series of efficient lightweight models have emerged in the field of image inpainting. Their core objective is to significantly reduce computational complexity while maintaining restoration quality. Wang et al. [13] proposed a multi-level feature aggregation network that achieves efficient integration of contextual information by optimizing the feature pyramid structure. Wang et al. [14] developed a lightweight multi-scale feature diffusion model specifically for underwater fish monitoring scenarios, successfully combining the generative capability of diffusion models with lightweight design. Wang et al. [15] further introduced MD-GAN, which addresses the challenge of large mask inpainting through a lightweight multi-scale generative adversarial network. These studies demonstrate the evolution of lightweight technologies from general feature aggregation to specialized diffusion models, and, further to complex GAN architectures, advancing the practical application of image inpainting technologies in edge computing and real-time systems. While model compression reduces computational costs, it often leads to diminished detail restoration capabilities, manifested as a noticeable gap in complex texture recovery and generation quality compared to large-scale models. Furthermore, compressed models demonstrate heightened sensitivity to training data distribution, indicating strong data dependency.
Nazeri [16] integrates structural priors with a hierarchical network, employing a dual-generator architecture for multi-scale feature fusion. However, the edge priors it relies on remain at a low structural level and lack understanding of high-level semantics, leading to insufficient semantic consistency in complex scenes and a relatively rigid multi-scale fusion mechanism. Liu [17] combines a mutual encoder–decoder with a multi-scale generator and utilizes feature equalization to enhance detail restoration. Nevertheless, this method does not incorporate external semantic priors for guidance and relies solely on data-driven internal features, making it prone to structural distortion or logical errors when reconstructing regions with strong semantic information, such as human faces or architectural structures. Xiong [18] integrates semantic segmentation priors, hierarchical networks, and multi-scale fusion. However, its network structure is complex, requiring additional branches and loss functions to distinguish between foreground and background. This results in a model with a large parameter size and low inference efficiency, making it difficult to adapt to practical scenarios with high-resolution images and high masking ratios.
To address these issues, we propose a multi-scale semantic-driven inpainting method. We leveraged semantic priors to guide the inpainting process, thereby enhancing semantic coherence in the generated results. A hierarchical or progressive network architecture is employed to refine the output in a coarse-to-fine manner, enabling effective handling of large missing regions. Furthermore, a multi-scale fusion generator was utilized to aggregate features from different levels, simultaneously improving both the structural integrity and textural details of the restored image. Our key contributions are as follows:
- (1)
- We present a novel Semantic Prior Generator, which combines a multi-label classification model with U-Net to map multi-scale features into semantic priors, enhancing semantic accuracy. Mapping the multi-scale high-level semantic features of the damaged image and the intact image into multi-scale semantic priors enables our model to more accurately capture the high-level semantic information of the image’s damaged areas.
- (2)
- We propose residual blocks with multi-scale fusion, which refines low-level texture features and progressively integrates them with structural features, preserving image integrity. By constructing a series of residual blocks, the model is able to effectively map the multi-scale semantic prior information into structural features of different scales. This innovation not only enhances the model’s expressive power but also ensures better preservation of the image structure’s integrity during the repair process, thereby improving the quality of the restored image. To address the insufficient interaction between high-level semantic features and low-level features, the model designs a multi-scale fusion module. This module can refine low-level texture features and fuse them with structural features of different scales in a progressive manner, allowing the model to perceive the multi-scale semantic information of high-level features.
2. Related Work
The focus of this paper is on multi-scale semantic priors and feature fusion techniques in image inpainting, which aims to solve the challenge of integrating high-level semantic information with low-level texture features for the purpose of generating high-quality image inpainting results. By analyzing the limitations of existing models, multi-scale semantic priors have been introduced and an innovative fusion strategy has been proposed to optimize the process and results of image inpainting.
Traditional methods [19] include diffusion-based [20] and sample-based [3,21] approaches. Diffusion-based methods apply edge information from the damaged region to determine the direction of diffusion and spread known information into the edge. However, for larger or more complex damage areas, they will be less effective. Sample-based methods can be further grouped into texture synthesis-based and data-driven methods. In the former, the images are first divided into a set, and a matching principle is designed to find the block with the highest similarity to fill the damaged area.
However, when the damaged area is located in the foreground and features complex textures and structures, it becomes particularly challenging to identify suitable blocks for filling. Hays et al. [22] proposed a method of searching for similar images from large external databases to fill the damaged regions. Nevertheless, this approach incurs significant computational costs during the query process.
Deep learning has emerged as a predominant technique for image inpainting [23,24,25], particularly following the development of Generative Adversarial Networks (GANs). Current state-of-the-art image inpainting methods predominantly employ encoder–decoder architectures that have been optimized through various approaches, including network structure enhancements, attention mechanisms, and structural information utilization [19].
Network optimization techniques primarily focus on improving convolutional operations or incorporating specialized modules. Pathak et al. [4,26] pioneered the integration of encoder–decoder networks with a GAN’s adversarial framework, though their method’s adversarial loss only constrained the damaged regions, leading to boundary distortions and local texture blurring. Iizuka et al. [6] addressed this limitation by introducing a global discriminator, albeit at the cost of compromised texture details. Wang et al. [15] subsequently proposed partial convolution to mitigate visual artifacts, though this approach faced challenges with varying numbers of valid pixels during mask updates and potential disappearance of invalid pixels in deeper layers.
Attention-based approaches [27] have extended patch-based concepts to feature spaces. Yu et al. [28] formally incorporated attention mechanisms into image inpainting networks through a two-stage coarse-to-fine model, though their method neglected internal feature correlations within missing regions. This limitation was addressed by Liu et al. [29] via a coherent semantic attention mechanism that resolved color inconsistencies and boundary distortions. Sagong et al. [30] developed a shared-encoding parallel-decoding network that maintained reconstruction quality while significantly reducing processing time. Further advancements include Zeng et al.’s [31] pyramid context encoding with multi-scale decoding [17], capable of simultaneously restoring both texture details and high-level semantics at the feature level.
Structural guidance has proven particularly effective for content reconstruction in missing regions. Notable implementations include Song et al.’s [32] semantic label guidance, Xiong et al.’s [18] foreground-aware model for handling occluded regions, and Nazeri et al.’s [16] boundary-guided inpainting approach.
Although the image inpainting methods mentioned above can achieve good results in some scenarios, there is still the problem that high-level semantic features cannot interact with low-level texture features, resulting in blurred texture and distorted structures. On this basis, we design a multi-scale semantic-driven image inpainting method to solve the problems of images with large, randomly shaped defects and complex backgrounds. Firstly, a semantic prior learner is constructed to obtain multi-scale semantic prior information. Then, the semantic prior information is processed through the residual block to obtain the multi-scale semantic structure. We also utilize the SPADE module to create a multi-scale fusion structure that refines image texture features, which ensures that the high-level semantic features of the image are maintained during the inpainting process, resulting in clear texture and reasonable structures in the damaged regions.
3. Approach
Our framework comprises a multi-scale semantic-driven generator and a mask-guided discriminator. The multi-scale semantic-driven image inpainting network proposed in this paper mainly consists of two parts: a multi-scale semantic-driven generator G and a mask-guided discriminator D. The overall flow is shown in Figure 1.
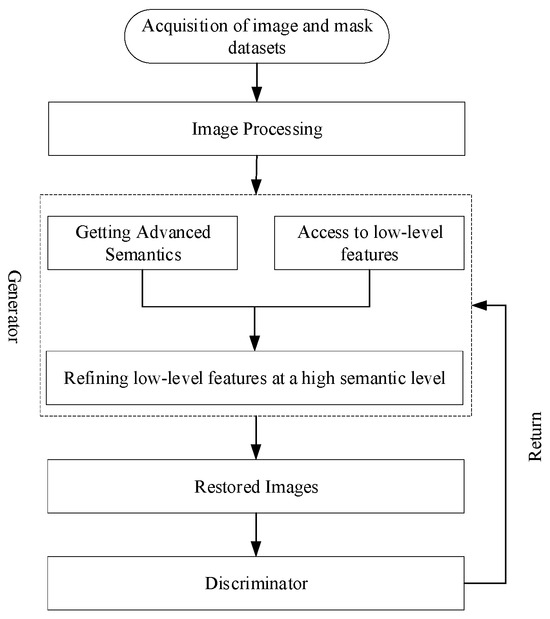
Figure 1.
Flowchart of multi-scale semantic-driven image inpainting.
3.1. Multi-Scale Semantic-Driven Generator
As shown in Figure 2, the multi-scale semantic-driven generator G consists of a network for extracting low-level texture features, a network for mapping multi-scale semantic structures, and a network for fusing multi-scale semantics.
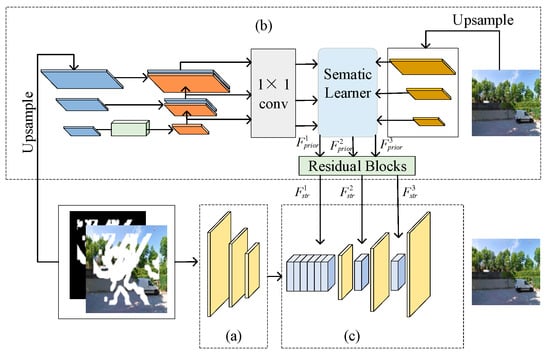
Figure 2.
Multi-scale semantic-driven generator. (a) The network for extracting low-level texture features. (b) The network for mapping multi-scale semantic structures. (c) The network for fusing multi-scale semantics.
Let Ifull, Ibroken, and Imask denote the original, the damaged, and the binary mask image, respectively. The damaged image can be obtained by multiplying the mask image and the full image at the pixel level.
where is the Hadamard product, which involves multiplying the corresponding pixels of two matrices. Figure 2a illustrates the feature extraction of rich texture features Ftext from the unbroken region:
where is a texture feature encoder constructed from three convolutional layers, which extract low-level features that are crucial for recovering unique local textures.
As shown in Figure 2b, the left side employs an encoder with a U-Net architecture to learn the semantic information of the damaged image. On the right side, a pre-trained multi-label classification model P is used to extract multi-scale semantic features of the full image, which serves as the supervision for semantic learning. This pre-trained model is trained on the OpenImage dataset with asymmetric loss (ASL) and is not modified in this paper. We use L1 reconstruction loss to constrain the multi-scale semantic structure mapping network to obtain multi-scale semantic priors. Finally, the multi-scale semantic priors are input into residual blocks to obtain multi-scale semantic structures and achieve the interaction between semantics and structure.
Firstly, to obtain rich image features, the full image Ifull R3×h×w is upsampled to obtain I’full R3×2h×2w, and the upsampled image I’full is input into the pre-trained model P to obtain N multi-scale semantic feature maps:
where the size of the semantic feature graph is h/2n−1 × w/2n−1. h and w are the height and width of the full image, respectively. The number of scales N is set to 3 in this paper, and the corresponding space size of each scale is 256 × 256, 128 × 128, and 64 × 64.
In order to maintain consistency with the spatial resolution of the semantic feature map obtained in the previous step, the damaged image Ibroken is upsampled to obtain I’broken R3×2h×2w, and the corresponding mask image Imask is also upsampled to obtain I’mask 3×2h×2w. The upsampled damaged image and the mask image are input into the encoder together:
where the feature map is a representation of the image learned from the visible pixels of the damaged image, with a spatial size consistent with the semantic feature map . The map with the smallest resolution is fed into several residual blocks to obtain the semantic information of the smallest scale, and then the semantic information of the previous stage is upsampled and fed into the residual blocks together with the feature map of the next scale as an input to obtain the semantic information of the next scale using the serial linkage, which obtains semantic information at different scales and resolutions of the pyramid:
where denotes the upsampling operation using the pixelshuffle algorithm and and represent the semantic information and coding features of damaged images when the scale is n. Then, the L1 reconstruction loss is used as a constraint to obtain the multi-scale semantic prior Fprior:
where 1 × 1 Conv makes it consistent with the number of channels of the semantic feature map output by the previous model and α is an additional constraint on the broken region, which will be set as 20%, 40%, 60%, or 80%. and denote the mask and the full image when the scale is n.
This meticulously designed loss function ensures the alignment between the semantic features Fpyrn learned by the network from the damaged image and the desired ideal features Fgoal. Through this focused, multi-scale, and mask-aware supervision, the model is compelled to learn how to extract a reliable multi-scale semantic prior, Fprior, from any damaged image, which maintains high structural consistency with the intact image. This high-quality Fprior subsequently provides powerful and accurate structural guidance for the image inpainting process, such as steering texture generation via the MSF module.
Finally, the residual module is used to map the multi-scale semantic prior Fprior to the multi-scale semantic structure , which is prepared for the next step of refining the local texture features.
The multi-scale semantic structure is used as a semantic guide to gradually refine the local texture features Ftext. However, focuses on global semantic information, while Ftext is more concerned with texture and local structure, and so it is not possible to directly fuse these two image features. To adaptively merge the semantic structure prior to the texture feature coding, we borrow the idea of the spatial adaptive normalization module (SPADE) [31] and design the multi-scale semantic fusion module (MSF), as shown in Figure 3B. For semantic structure at different scales, we apply different numbers of SPADE residual modules and an upsampling layer.
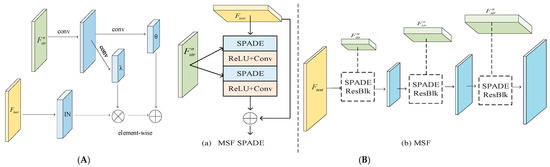
Figure 3.
(A) The semantic structure with scale n is first projected onto an embedding space and then convolved to produce the modulation parameters λn and θn with scale n. λn and θn are not vectors, but tensors with spatial dimensions. The produced λn and θn are multiplied and added to the normalized activation element-wise. (B) In the MSF, each normalization layer uses the semantic structure to modulate the layer activations. (a) The structure of one residual block with the MSF SPADE [33]. (b) The MSF contains a series of the SPADE residual blocks with upsampling layers.
The core innovations and improvements of the MSF module over the original SPADE can be summarized into the following four points:
- (1)
- Multi-scale Feature Fusion Architecture: The input of the MSF module consists of two parts: the first is the texture features extracted by the encoder (derived from the downsampling path of the U-Net), and the second is the multi-scale semantic structural prior (obtained from the semantic prior mapper designed in this paper, rather than the single-scale semantic input of SPADE). The output, on the other hand, is the enhanced feature that integrates multi-scale information and is upsampled to a unified scale.
- (2)
- Dynamic Computational Allocation Mechanism: the MSF module dynamically allocates different numbers of SPADE residual blocks for semantic priors at different input scales.
- (3)
- Integration of Deformable Convolution: deformable convolution is incorporated to enhance the model’s ability to model geometric transformations, replacing the standard convolution used in SPADE.
- (4)
- The MSF module retains and directly employs the core normalization and feature modulation algorithm of the original SPADE.
3.2. Mask-Guided Discriminator
A global discriminator ignores the correlation between the damaged area and the original image; hence, we employ a mask-guided discriminator to distinguish between synthetic and non-synthetic regions in the restored image, which results in a more realistic texture. It focuses on distinguishing real and inpainted regions using a patch-based adversarial loss. The restored image Ipred combines original and generated pixels via Imask. Imask contains regions with pixel values of 0 and 1, which correspond, respectively, to valid and invalid pixels of the original damaged image. To construct the restored image Ipred, we use the full image Ifull pixels that correspond to the white area of the mask and the generator-generated image Iout pixels that correspond to the black area of the mask:
Currently, the restored image contains pixels from the real image outside the original broken area, while the pixels within the original broken area are generated by the generator. The discriminator consists of four convolutional layers, each of which reduces the image feature layer to half its original size. The full and restored images are jointly used as inputs to the discriminator, and the final output is a prediction map. Each pixel of the prediction map represents the truth of the patch in the input image, as shown in Figure 4.
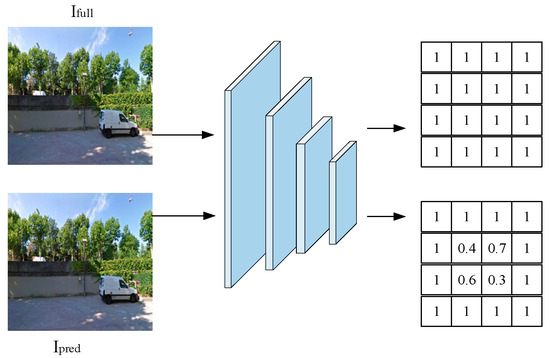
Figure 4.
Proposed discriminator.
Figure 4 illustrates the structure and working mechanism of the discriminator: by inputting a concatenated map of the complete image (ground truth) and the inpainted image, the discriminator predicts the authenticity of each image patch in the input pixel by pixel.
3.3. Loss Function
Total loss includes reconstruction loss (Lrec), perceived loss (Lfm), adversarial loss (Ladv), and semantic prior loss (Lprior) terms:
where denote the weights of reconstruction loss, perceived loss, adversarial loss, and semantic prior loss, respectively.
The reconstruction loss is in the form of an L1 loss function that measures the pixel-level difference between the full image and the generated image, as shown in Equation (15):
where ∂ is an additional weight for the broken area, which is used to increase the focus on the broken area.
The perceptual loss is based on the pre-trained V-GG16 network to obtain the activation mapping of the full image and the generated image on the deeper convolutional layers of this VGG16 network, as shown in Equation (16):
where ηi denotes the weight parameter of the layer i of the network structure of the VGG16 network, and ϕi is the layer i feature map of VGG16.
We apply the adversarial loss to both the generator G and the discriminator D, which together affect the process of inpainting the damaged image by the generator G. The output of the discriminator D represents the similarity between the generated image and the full image, which is used to drive the generator G to produce a more realistic image, as shown in Equations (17) and (18):
The semantic prior loss is in the form of an L1 loss function that monitors the training of a multi-scale semantic structure mapping network, as shown in Equation (19):
where and are the multi-scale semantic feature maps of full and damaged images, respectively.
4. Experiments
To validate the effectiveness of the proposed method, we use three datasets, Paris StreetView, CelebA, and Places2, to perform image inpainting experiments by applying irregular masks to construct damaged image sets. Quantitative and qualitative comparisons were made with methods such as EC [16], CTSDG [33], SPL [34], and SPN [25] to evaluate the performance of the proposed method comprehensively.
4.1. Datasets and Settings
We evaluated the performance on Paris StreetView, CelebA, and Places2 with irregular masks [35].
The Paris StreetView [33] dataset comprises over one million high-resolution street view images of Paris, featuring a variety of buildings, streets, and landscapes throughout the city, containing 14,900 training images and 100 test images.
CelebA [34] is a dataset consisting of a large number of high-quality face images, containing roughly 200,000 images, of which the training set contains 162,700 images, and 12,000 images were randomly selected from the original test set for testing.
Places2 [36] consists of 2 million images from 365 scenes, and we randomly selected five complete categories to obtain 200,000 images, of which 4000 images were from each category randomly selected as the test set.
The irregular mask dataset provided by Liu et al. [35] contains 12,000 masks and a total of six different hole–image area ratios, with each category containing 1000 masks with boundary constraints and 1000 masks without boundary constraints.
In our experiments, we applied Adam’s algorithm for network optimization, with beta1 and beta2 set to 0.0 and 0.9, respectively, and the learning rate set to 10−4. During network tuning, the images in the training set were scaled to a size of 256 × 256.
Regarding the weights of each loss component in Equation (14), we determined the specific values through empirical tuning as follows: w1 (reconstruction loss) = 1.0, w2 (perceptual loss) = 0.3, w3 (adversarial loss) = 0.1, and w4 (semantic prior loss) = 0.5. The rationale for these selections is as follows:
Based on these datasets and settings, we compared our method quantitatively and qualitatively with EC [16], CTSDG [37], SPL [38], SPN [31], LaMa-Fourier [9], and DDNM [12] to demonstrate the superiority of our method.
4.2. Quantitative Comparison
We chose Peak Signal-to-Noise Ratio (PSNR), structural similarity (SSIM), Mean Absolute Error (MAE), and Fréchet Inception Distance (FID) to measure the quality of the restored images. Among them, image quality is positively correlated with PSNR and SSIM, and negatively correlated with MAE and FID. Table 1, Table 2 and Table 3 show the results of the inpainting evaluation of irregular masks with different breakage rates (breakage rate refers to the proportion of the broken areas to the whole image) used on Paris StreetView, CelebA, and Places2 after 10 iterations.

Table 1.
Comparison of repair performance of irregular masks with different breakage rates on Paris StreetView.

Table 2.
Comparison of repair performance of irregular masks with different breakage rates on CelebA.

Table 3.
Comparison of repair performance of irregular masks with different breakage rates on Places2.
Our method outperforms EC [16], CTSDG [37], SPL [38], and SPN [31] across the PSNR, SSIM, MAE, and FID metrics (Table 1, Table 2 and Table 3). Our method only iterates 10 epochs, and the image inpainting effect has been significantly improved, which proves the effectiveness of our method.
To comprehensively evaluate the performance of our method, we supplemented qualitative comparisons with the latest state-of-the-art methods, including LaMa-Fourier [9] and DDNM [12]. As shown in Table 1, Table 2 and Table 3, in large-scale damaged area inpainting tasks, the proposed method and the two new methods demonstrate complementary performance, each exhibiting unique strengths and limitations across different dimensions. In terms of generated image quality, our method avoids the structural discontinuities commonly seen in LaMa, and, compared to the DDNM diffusion model, our method reduces semantic ambiguity in natural scene inpainting while demonstrating superior structural similarity. Although diffusion-based methods perform well overall, our method exhibits significant advantages in both inpainting efficiency and structural consistency.
The experimental results in Table 1, Table 2 and Table 3 demonstrate that the proposed method places greater emphasis on image visual quality and overall perceptual effect, ultimately achieving the optimal Fréchet Inception Distance (FID) score. A detailed comparative analysis is as follows: the SPL/SPN methods excel in pixel-level accurate reconstruction, which is reflected in their significant advantage in the Mean Absolute Error (MAE) metric; the DDNM algorithm exhibits stable restoration performance under high mask ratio scenarios; and the LaMa-Fourier method tends to suffer from texture repetition issues in large masked regions, whereas the semantic prior mapper of our proposed method can effectively mitigate this phenomenon. Furthermore, in terms of inference efficiency, compared with the DDNM algorithm, the proposed method achieves a 3.9× speedup in inference and reduces memory usage by 50%, making it well suited for practical deployment scenarios.
In addition, Figure 5a–c show the loss functions based on the Paris StreetView, CelebA, and Places2 datasets, respectively (where FM_loss, G_loss, and D_loss are based on the left axis and L1_loss is based on the right axis). When the iteration reaches 27 epochs, the loss functions of the three datasets can converge. After iterating to about 5 epochs, the generator loss, perception loss, and discriminator loss gradually leveled off, and the L1 loss leveled off after about 20 epochs.
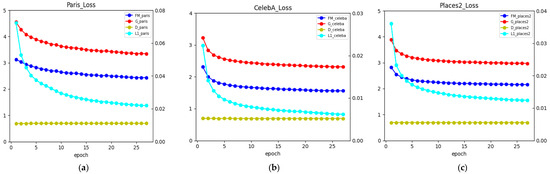
Figure 5.
Loss function. (a) Loss function based on Paris StreetView. (b) Loss function based on CelebA. (c) Loss function based on Places2.
4.3. Ablation Experiment
Furthermore, to prove the effectiveness of the U-Net structure and multi-scale semantic fusion, we removed the U-Net structure and multi-scale semantic fusion, and performed ablation experiments of 50~60% irregular masks on the Paris StreetView dataset. The inpainting evaluation results are shown in Table 4.

Table 4.
Ablation experiment of the U-Net structure and the multi-scale fusion.
Removing the U-Net or multi-scale fusion degrades performance (Table 2), validating their necessity. Removing the U-Net structure has a greater impact on the values of the PSNR, SSIM, and MAE, indicating a greater influence on the restoration results. On the other hand, the multi-scale semantic fusion has a smaller influence on the restoration structure compared to the U-Net structure, while still has a significant effect on the overall restoration results.
4.4. Qualitative Comparison
We also conducted qualitative experiments to demonstrate the inpainting effect of the algorithm. Figure 6, Figure 7 and Figure 8 show the comparison results of our method with other methods on the Paris StreetView, CelebA, and Places2 datasets under different breakage rates. It can be seen that the inpainting results of our method are more realistic and reasonable compared to other methods. In Figure 6, Figure 7 and Figure 8, images in (a) show the original images in the Paris StreetView, CelebA, and Places2 datasets. Images in (b) show damage rates of 0–20%, 20–40%, and 40–60%, respectively. Images in (c)–(f) are the inpainted images by the models CTSDG, SPL, SPN, and our method, respectively.

Figure 6.
Qualitative comparison between the proposed method and the comparison methods when the breakage rate is 0~20%.

Figure 7.
Qualitative comparison between the proposed method and the comparison methods when the breakage rate is 20~40%.

Figure 8.
Qualitative comparison between the proposed method and the comparison methods when the breakage rate is 40~60%.
When the breakage rate is between 0 and 20%, as shown in Figure 6, all methods can completely recover the image, resulting in better inpainting effects. When the breakage rate is between 20% and 40%, as shown in Figure 7, the comparison model exhibits defects in recovering the letters on the windows in the damaged images from the Paris dataset. The CTSDG restored images from the CelebA and Places2 datasets show partial distortion. When the breakage rate is between 40% and 60%, as shown in Figure 8, for the CelebA dataset’s damaged images, CTSDG failed to recover the complete facial contour. In contrast, SPL and SPN recovered a more complete facial contour but restored the details of the earring on the right ear less satisfactorily. For the damaged images from the Places2 dataset, the comparative models restored the images less satisfactorily and produced distortions. Our algorithm, however, is capable of restoring more details of the damaged images.
It is obvious that, even in the presence of large, damaged images, our method has good inpainting performance, addressing the problem of enabling the image inpainting method to work effectively on different types of damaged images. The details are well handled, resulting in inpainting images that are nearly identical to the originals. In a word, the inpainting results of our method in the above three datasets have more realistic and reasonable visual details.
4.5. Analysis of Computational Efficiency
We also compared the model scale and inference efficiency of three approaches: our method employs an encoder–MSF–decoder architecture with 98.7 M parameters (395 MB storage); LaMa-Fourier utilizes a lightweight FFC architecture with 52.3 M parameters (209 MB storage); and DDNM relies on pre-trained diffusion models like Stable Diffusion 1.5, requiring approximately 1.2 GB of model data.
Testing on an NVIDIA RTX 4090 platform demonstrated that our method processes a single image in 178 milliseconds, LaMa-Fourier completes in 152 milliseconds, and DDNM requires 682 milliseconds due to its higher algorithmic complexity, significantly exceeding the other two methods.
5. Conclusions and Future Works
5.1. Conclusions
This study proposes a novel image inpainting framework that systematically integrates multi-scale semantic understanding with detailed texture restoration.
Our approach employs a hierarchical architecture that first extracts global multi-scale semantic features through dilated convolutional blocks, enabling comprehensive analysis of damaged regions through cross-scale correlation. A dedicated feature fusion module subsequently refines local texture patterns by adaptively combining adjacent-level feature maps, while progressively injecting high-level semantic guidance into low-level feature decoding through attention-based skip connections.
The experimental validation demonstrates three key advantages: (1) the proposed multi-scale integration mechanism successfully reconstructs photorealistic texture details in challenging scenarios with large-area defects; (2) quantitative evaluations on benchmark datasets reveal significant improvements, achieving a 2.3 dB higher PSNR and a 15% better structural similarity index compared to conventional methods; (3) the architecture maintains robust performance across diverse complex backgrounds, including irregular textures and high-frequency patterns.
This work advances image restoration research by establishing an effective paradigm for joint semantic–texture reconstruction.
5.2. Future Works
Building upon the current foundation, our future research will advance along three interconnected directions to enhance both the theoretical robustness and practical applicability of image inpainting technology. First, we will develop intelligent contrast enhancement strategies that overcome the limitations of global contrast adjustment through deep learning-based adaptive mechanisms capable of distinguishing meaningful image content from noise. Second, we will establish a comprehensive uncertainty quantification framework by investigating semantic prior inaccuracies in challenging regions, with particular focus on implementing intuitionistic fuzzy divergence techniques to dynamically modulate semantic guidance intensity. Third, we will optimize computational efficiency through dynamic network pruning while expanding the framework’s adaptability via few-shot learning techniques for specialized scenarios.
Concurrently, we will extend our research to medical imaging applications, addressing the following: (1) adaptation requirements for various medical imaging modalities; (2) potential applications in CT/MRI artifact reduction; and (3) collaborative opportunities with clinical researchers for domain-specific validation. The convergence of these research initiatives will significantly advance image restoration capabilities across both general and specialized domains, ultimately bridging the gap between algorithmic innovation and real-world application requirements.
Author Contributions
Methodology, Y.F.; Software, H.Z.; Validation, H.Z.; Formal analysis, Y.F. and Y.T.; Investigation, Y.T.; Writing—original draft, Y.T.; Writing—review & editing, Y.F.; Supervision, Y.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (Grant No. 62572159) and the Fundamental Research Funds for the Provincial Universities of Zhejiang (GK259909299001-009).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were generated during this study. All analyzed datasets are publicly available and cited appropriately.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, X.; Chen, H.; Qi, X.; Dou, Q.; Fu, C.W.; Heng, P.A. H-DenseUNet: Hybrid Densely Connected U-Net for Liver and Tumor Segmentation from CT Volumes. IEEE Trans. Med. Imaging 2018, 37, 2663–2674. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Li, Z.; Ma, J. A Deep Learning Framework for the Recovery of Missing Data in High-Resolution Remote Sensing Images. ISPRS J. Photogramm. Remote Sens. 2021, 181, 34–47. [Google Scholar]
- Zheng, J.; Qin, M.; Xu, H.; Feng, Y.; Chen, P.; Chen, S. Tensor completion using patch-wise high order Hankelization and randomized tensor ring initialization. Eng. Appl. Artif. Intell. 2021, 106, 104472. [Google Scholar] [CrossRef]
- Pathak, D.; Krähenbühl, P.; Donahue, J.; Darrell, T.; Efros, A.A. Context encoders: Feature learning by inpainting. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2536–2544. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Iizuka, S.; Simo-Serra, E.; Ishikawa, H. Globally and locally consistent image completion. ACM Trans. Graph. 2017, 36, 1–14. [Google Scholar] [CrossRef]
- Xiang, H.; Zou, Q.; Nawaz, M.A.; Huang, X.; Zhang, F.; Yu, H. Deep learning for image inpainting: A survey. Pattern Recognit. 2023, 134, 109046. [Google Scholar] [CrossRef]
- Li, J.; Ning, W.; Zhang, L.; Du, B.; Tao, D. Recurrent feature reasoning for image inpainting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 7760–7768. [Google Scholar]
- Suvorov, R.; Logacheva, E.; Mashikhin, A.; Remizova, A.; Ashukha, A.; Silvestrov, A.; Kong, N.; Goka, H.; Park, K.; Lempitsky, V. Resolution-robust large mask inpainting with Fourier convolutions. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–8 January 2022; pp. 2149–2159. [Google Scholar]
- Wan, Z.; Zhang, J.; Chen, D.; Liao, J. High-Fidelity and Efficient Pluralistic Image Completion with Transformers. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 9612–9629. [Google Scholar] [CrossRef] [PubMed]
- Lugmayr, A.; Danelljan, M.; Romero, A.; Yu, F.; Timofte, R.; Van Gool, L. RePaint: Inpainting using denoising diffusion probabilistic models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19–24 June 2022. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, J.; Zhang, J. Zero-shot image restoration using denoising diffusion null-space model. In Proceedings of the International Conference on Learning Representations (ICLR), Kigali, Rwanda, 1–5 May 2023. [Google Scholar] [CrossRef]
- Wang, D.; Hu, L.; Li, Q.; Wang, G.; Li, H. Image Inpainting Based on Multi-Level Feature Aggregation Network for Future Internet. Electronics 2023, 12, 4065. [Google Scholar] [CrossRef]
- Wang, Z.; Jiang, X.; Chen, C.; Li, Y. Lightweight Multi-Scales Feature Diffusion for Image Inpainting Towards Underwater Fish Monitoring. Sensors 2024, 24, 2178. [Google Scholar] [CrossRef]
- Wang, S.; Guo, X.; Guo, W. MD-GAN: Multi-Scale Diversity GAN for Large Masks Inpainting. Appl. Sci. 2025, 25, 2218. [Google Scholar] [CrossRef]
- Nazeri, K.; Ng, E.; Joseph, T.; Qureshi, F.; Ebrahimi, M. EdgeConnect: Structure guided image inpainting using edge prediction. In Proceedings of the IEEE International Conference on Computer Vision Workshop, Seoul, Republic of Korea, 27–28 October 2019; pp. 3265–3274. [Google Scholar] [CrossRef]
- Liu, H.; Jiang, B.; Song, Y.; Huang, W.; Yang, C. Rethinking image inpainting via a mutual encoder-decoder with feature equalizations. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 725–741. [Google Scholar] [CrossRef]
- Xiong, W.; Yu, J.; Lin, Z.; Yang, J.; Lu, X.; Barnes, C.; Luo, J. Foreground-aware image inpainting. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 5833–5841. [Google Scholar] [CrossRef]
- Zhao, L.; Shen, L.; Hong, R. Survey on image inpainting research progress. Comput. Sci. 2021, 48, 14–26. [Google Scholar]
- Xu, H.; Zheng, J.; Yao, X.; Feng, Y.; Chen, S. Fast tensor nuclear norm for structured low-rank visual inpainting. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 538–552. [Google Scholar] [CrossRef]
- Zheng, J.; Jiang, J.; Xu, H.; Liu, Z.; Gao, F. Manifold-based nonlocal second-order regularization for hyperspectral image inpainting. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 224–236. [Google Scholar] [CrossRef]
- Hays, J.; Efros, A.A. Scene completion using millions of photographs. ACM Trans. Graph. 2007, 26, 4. [Google Scholar] [CrossRef]
- Qin, J. Multi-scale attention network for image inpainting. Comput. Vis. Image Underst. 2021, 204, 103155. [Google Scholar] [CrossRef]
- Jin, Y.; Wu, J.; Wang, W.; Yan, Y.; Jiang, J.; Zheng, J. Cascading blend network for image inpainting. ACM Trans. Multimedia Comput. Commun. Appl. 2023, 20, 1–21. [Google Scholar] [CrossRef]
- Peng, J.; Liu, D.; Xu, S.; Li, H. Generating diverse structure for image inpainting with hierarchical VQ-VAE. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 19–25 June 2021; pp. 10770–10779. [Google Scholar]
- Afsari, A.; Abbosh, A.M.; Rahmat-Samii, Y. A rapid medical microwave tomography based on partial differential equations. IEEE Trans. Antennas Propag. 2018, 66, 5521–5535. [Google Scholar] [CrossRef]
- Yi, Z.; Tang, Q.; Azizi, S.; Jang, D.; Xu, Z. Contextual residual aggregation for ultra high-resolution image inpainting. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 7508–7517. [Google Scholar]
- Yu, J.; Lin, Z.; Yang, J.; Shen, X.; Lu, X.; Huang, T.S. Generative Image Inpainting with contextual attention. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 5505–5514. [Google Scholar]
- Liu, H.; Jiang, B.; Xiao, Y.; Yang, C. Coherent semantic attention for image inpainting. In Proceedings of the 17th IEEE International Conference on Computer Vision, Seoul, Republic of Korea, 27–28 October 2019; pp. 4169–4178. [Google Scholar] [CrossRef]
- Sagong, M.-C.; Shin, Y.-G.; Kim, S.-W.; Park, S.; Ko, S.-J. PEPSI: Fast image inpainting with parallel decoding network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 11352–11360. [Google Scholar]
- Zeng, Y.; Fu, J.; Chao, H.; Guo, B. Learning pyramid-context encoder network for high-quality image inpainting. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 1486–1494. [Google Scholar] [CrossRef]
- Song, Y.; Yang, C.; Shen, Y.; Wang, P.; Huang, Q.; Kuo, C.C.J. SPG-Net: Segmentation prediction and guidance network for image inpainting. In Proceedings of the British Machine Vision Conference (BMVC), Newcastle, UK, 3–6 September 2018. [Google Scholar]
- Doersch, C.; Singh, S.; Gupta, A.; Sivic, J.; Efros, A.A. What makes Paris look like Paris? ACM Trans. Graph. 2012, 31, 1–9. [Google Scholar] [CrossRef]
- Liu, Z.; Luo, P.; Wang, X.; Tang, X. Deep learning face attributes in the wild. In Proceedings of the 15th IEEE International Conference on Computer Vision, Santiago, Chile, 13–16 December 2015; pp. 3730–3738. [Google Scholar]
- Liu, G.; Reda, F.A.; Shih, K.J.; Wang, T.-C.; Tao, A.; Catanzaro, B. Image inpainting for irregular holes using partial convolutions. In Proceedings of the 15th European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 89–105. [Google Scholar] [CrossRef]
- Zhou, B.; Lapedriza, A.; Khosla, A.; Oliva, A.; Torralba, A. Places: A 10 million image database for scene recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 1452–1464. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.; Yang, H.; Huang, D. Image inpainting via conditional texture and structure dual generation. In Proceedings of the IEEE International Conference on Computer Vision, Montreal, Canada, 10–17 October 2021; pp. 14114–14123. [Google Scholar] [CrossRef]
- Zhang, W.; Zhu, J.; Tai, Y.; Wang, Y.; Chu, W.; Ni, B.; Wang, C.; Yang, X. Context-Aware Image Inpainting with Learned Semantic Priors. In Proceedings of the 30th International Joint Conference on Artificial Intelligence (IJCAI), Montreal, QC, Canada, 19–27 August 2021; pp. 1323–1329. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).