Abstract
Understanding the density of possible prices in one-minute intervals provides traders, investors, and financial institutions with the data necessary for making informed decisions, managing risk, optimizing trading strategies, and enhancing the overall efficiency of the cryptocurrency market. While high accuracy is critical for researchers and investors, market nonlinearity and hidden dependencies pose challenges. In this study, the filtered historical simulation is used to generate pathways for the next hour on the one-minute step for Bitcoin and Ethereum quotes. The innovations in the simulation are standardized historical returns resampled with the method of block bootstrapping, which helps to capture any hidden dependencies in the residuals of a conditional parameterization in the mean and variance. Ordinary bootstrapping requires the feed innovations to be free of any dependencies. To deal with complex data structures and dependencies found in ultra-high-frequency data, this study employs block bootstrap to resample contiguous segments, thereby preserving the sequential dependencies and sectoral clustering within the market. These techniques enhance decision-making and risk measures in investment strategies despite the complexities inherent in financial data. This offers a new dimension in measuring the market risk of cryptocurrency prices and can help market participants price these assets, as well as improve the timing of their entry and exit trades.
Keywords:
filtered historical simulation; risk management; high-frequency cryptocurrency markets; block bootstrapping; forecasting; tail risks JEL Classification:
C15; C53; G17; G32
1. Introduction
Knowing the density of possible cryptocurrency prices over one-minute intervals can be highly valuable for several reasons, particularly in the context of trading, risk management, and market analysis. It can be valuable in building predictive models for future price movements. A probability density function (PDF) provides insight into how likely it is that prices will fall within certain ranges, which is crucial for short-term forecasting. High volatility means that prices fluctuate widely within a short period, making trading strategy design more critical. Traders can optimize their entry and exit points by understanding the distribution of prices. If a price is near the lower end of its expected range, it might be a good buying opportunity, while prices near the upper end could be a signal to sell. High-frequency trading firms, which execute a large number of trades in very short periods, rely heavily on understanding the very short-term distribution of prices. The density of one-minute intervals is crucial for these firms to detect profitable trading opportunities and minimize execution risks. Many trading algorithms, especially those relying on statistical models (e.g., mean-reversion strategies or momentum-based strategies), need an understanding of the distribution of price changes over time to optimize their decision-making processes. By understanding the density of possible price movements, traders can assess the likelihood of extreme events (e.g., significant price drops) and plan their risk exposure accordingly. Furthermore, analyzing the density of price changes over short intervals provides insights into the microstructure of the cryptocurrency market. For instance, it can reveal the impact of liquidity, the presence of large traders, or the effects of news and external events. A detailed understanding of price density allows for the detection of anomalies or unusual patterns in the market. If prices deviate significantly from the expected density, it might indicate manipulation, market inefficiency, or impending significant market events. The shape of the price distribution can also reflect market sentiment. For example, a skewed distribution might indicate that the market is more bullish or bearish during a particular period. Understanding this can help traders position themselves correctly relative to prevailing sentiment. Traders can optimize their entry and exit points by understanding the distribution of prices.
Like conventional financial assets, digital currencies’ time series are generally characterized by heteroscedasticity, serial correlation, leptokurtosis, and fat tails (Shahzad et al. 2019). This combination of factors makes cryptocurrencies a fascinating field of exploration, attracting both investors seeking innovative opportunities and academics and professionals focused on analyzing their distributional characteristics and market behavior. Unlike traditional assets, cryptocurrencies display distinct behaviors that are impacted by several factors, including technological advancements, regulatory modifications, and market sentiment (Chowdhury et al. 2023). Also, traders and researchers interested in risk management and price prediction are frequently drawn to the extreme volatility of cryptocurrency markets (Liu et al. 2023). Furthermore, investors and engineers are interested in the underlying blockchain technology because it presents novel approaches and fresh financial paradigms (Kristjanpoller et al. 2024). Finally, according to Nekhili et al. (2023), cryptocurrencies offer chances for diversification and, possibly, large returns. While these stylized facts impose the correct modeling of both the return and volatility, financial risk management focuses on the tail of the distribution. For instance, the regulatory frameworks for banking and insurance sectors require tail-based risk measures. The standard metrics models, such as the value-at-risk (VaR) and the expected shortfall (ES) models, rely on an ad hoc distributional assumption, often normal distribution, and leave any serial correlation present in the financial data untreated (Nekhili and Sultan 2022).
Simulation methods are essential tools in financial modeling, enabling traders, investors, and risk managers to create realistic scenarios for asset prices. By using different methods, such as Monte Carlo simulations, stochastic volatility models, or mean-reverting processes, practitioners can model a wide range of market conditions and behaviors, leading to better-informed decisions and more robust risk management strategies. Each simulation method used in market risk management has its strengths and weaknesses, depending on the characteristics of the asset being modeled, the market conditions, and the specific risk management objectives. Monte Carlo simulation can be applied to a wide range of asset types, models, and complex derivatives. It provides a detailed and accurate view of risk by generating a large number of potential future scenarios and can incorporate various stochastic processes, jump-diffusion models, and volatility structures. However, the simulation requires significant computational power, especially for large trading books or highly complex instruments, and can take a long time to run, making real-time trading or risk management challenging. This is because it relies on modeling all the pairwise dependencies of the assets. The number of pairwise dependencies increases at a quadratic rate with the number of assets in the trading book. In addition, the Monte Carlo simulation requires the correct specification of the joint distribution that describes the changes in all the assets.
Filtered historical simulation (FHS), introduced by Barone-Adesi et al. (1998, 1999), was motivated by the relaxing of distributional assumptions and the need to address some of the computational challenges faced by Monte Carlo simulation, particularly in the context of market risk management. FHS is a multistep price density prediction technique to primarily estimate the potential losses that a portfolio or financial institution may face due to adverse market movements. It enhances the traditional historical simulation method by filtering the data to account for time-varying volatility. Rather than generating synthetic data through complex simulations, filtered historical simulation reuses the daily volatility-adjusted historical residual returns, thereby avoiding the need to simulate from scratch. In the multi-asset portfolio context, filtered historical simulation is much less computationally intensive than Monte Carlo simulation, as the latter requires maintaining and simulating the correlations between multiple assets, which adds considerable computational overhead, especially when the covariance matrix becomes large. In the filtered historical simulation, correlations are implicitly embedded in the historical data. The historical returns already reflect the co-movements between assets, so filtered historical simulation does not require explicitly recalculating correlations, which saves computational effort and possibly considerably reduces the model risk. Overall, the filtered historical simulation naturally incorporates historical tail events and volatility patterns, making it more efficient at capturing realistic market behavior with fewer computations.
Filtered historical simulation offers a powerful, adaptable, and data-driven approach for forecasting the density of ultra-high-frequency cryptocurrency prices, especially in markets characterized by non-stationarity, high volatility, and complex distributional properties. Its ability to incorporate recent data and volatility patterns makes it an excellent choice for the nuanced forecasting needs of cryptocurrency markets.
Several studies have tested the filtered historical simulation method in various market contexts, focusing on its ability to predict value-at-risk (VaR) and handle volatility clustering. Barone-Adesi et al. (2002) conducted one of the pioneering studies on backtesting the filtered historical simulation. They tested the method on derivative portfolios and found that the filtered historical simulation provided more accurate risk estimates than traditional historical simulation. Their study highlighted filtered historical simulation’s robustness in dealing with portfolios containing options and other nonlinear instruments. The main finding was that filtered historical simulation is better equipped to adapt to changing market conditions, particularly in capturing volatility dynamics that standard models fail to account for. Kuester et al. (2006) compared various VaR forecasting models, including filtered historical simulation. Their study found that filtered historical simulation outperformed simpler models like traditional historical simulation and GARCH-based models in forecasting risk under volatile market conditions. The main advantage of filtered historical simulation, as highlighted by the study, was its ability to incorporate time-varying volatility directly from historical data, leading to more reliable risk predictions. Christoffersen’s (2009) work on value-at-risk (VaR) models included an evaluation of filtered historical simulation. The study demonstrated that filtered historical simulation, by incorporating models like GARCH to filter historical data, was better at capturing the conditional nature of market risks. It showed improved performance in backtesting exercises, particularly in scenarios with high volatility or market stress. The findings suggested that filtered historical simulation outperformed standard historical simulation in both the accuracy and reliability of VaR estimates. These studies demonstrate that filtered historical simulation is a robust method for market risk management, particularly in environments with significant volatility and nonlinear price behaviors.
Although these non-parametric filtering techniques prove valuable for assessing non-normal risks and tail events, their limitations and potential biases need further exploration to ensure effectiveness in real-world scenarios. For example, when the original sample is biased or not representative of the population, ordinary bootstrapping will not correct for that bias and will leave the same underlying issues in the generated resamples. Filtered historical simulation, while powerful, can be subject to several biases that could affect its accuracy in estimating risk. These biases primarily stem from the method’s reliance on historical data, model assumptions, and the filtering process. Filtered historical simulation relies on conditional volatility models to mimic current market conditions. In turn, the conditional volatility models look backward and will not predict shocks in market prices, which will undermine their ability to predict future risks accurately. This limitation will be of limited concern in high-frequency trading, as many shocks will require several minutes or hours to manifest fully. Shortly after the jumps in realized volatility, the GARCH model will “digest” the shocks and adjust its volatility forecast. Yet, filtered historical simulation, like any model-based approach, is susceptible to model risk—the risk that the chosen model does not accurately represent the underlying dynamics of the market. For example, if the GARCH model used in filtered historical simulation does not appropriately capture the real volatility dynamics, the risk estimates will be biased. The biases in the filtered historical simulation are primarily related to its reliance on historical data, assumptions about volatility, and the models used for filtering. These biases can lead to the underestimation of tail risks, misestimation of volatility dynamics, and overfitting of past data, potentially resulting in inaccurate risk assessments. Proper calibration, model selection, and the use of robust backtesting methods are crucial to mitigate these biases (Christoffersen 2009).
Against these drawbacks, this study deals with hidden dependencies and non-linearities by applying the filtered historical simulation and the block bootstrap method as an alternative to the ordinary bootstrap method. Block bootstrap breaks up the dependency while carrying out the bootstrap simulation. It offers several improvements in the accuracy of the standard bootstrap, as it can better simulate the nonlinear dependency properties of the data. In the block bootstrap, we implicitly assume that even though there might be no further dependency on the residual returns, it cannot produce worse estimates than the standard bootstrap (Cogneau and Zakamouline 2013).
Instead of resampling individual data points (as in the standard bootstrap), the block bootstrap resamples entire blocks of sequential observations. Block bootstrap is used in time series or spatial data to account for dependencies within the data by resampling blocks of consecutive observations rather than individual observations. This involves selecting blocks with replacements to construct a new bootstrap sample. In the filtered historical simulation, instead of individual standardized residual returns, a large number of random blocks of sequential standardized returns is resampled.
To put this in an empirical setting, a risk analysis is carried out on the cryptocurrency market using high-frequency data for Bitcoin and Ethereum. Several researchers have relied on the bootstrap method, which was introduced by Hall (1985) and Kunsch (1989), to capture the dependence structure in the return series while estimating the parameter of interest of the return distribution. Shahzad et al. (2019) treated inherent serial dependence using a random block bootstrapping technique for a predictability analysis of the safe heaven role of Bitcoin, gold, and commodities. Grobys and Junttila (2021) employ block bootstrap to cryptocurrency time series to overcome issues regarding non-normality, proneness to outliers, extreme events evidence, and regime switching in the first moment of the time series.
The present study identifies several gaps in the current understanding and application of market risk in high-frequency cryptocurrency markets. Firstly, while the filtered historical simulation approach proves valuable for assessing market risk and tail events, its limitations and potential biases need further exploration to ensure its effectiveness in real-world scenarios. The study reveals discrepancies in confidence bands generated by block bootstrap methods compared to ordinary bootstrap methods, suggesting a need for a deeper understanding of the factors influencing these differences and their implications for risk management strategies. Furthermore, by emphasizing the need for rigorous out-of-sample back testing, especially during turbulent market conditions, this study promotes more robust and reliable risk analysis practices in high-frequency cryptocurrency markets. Overall, the findings offer valuable insights that can inform decision-making processes and enhance trading and risk management strategies in the rapidly evolving landscape of cryptocurrency markets.
The rest of this study is structured as follows. Section 2 describes the methods, Section 3 addresses the empirical results of the high-frequency (one-minute) returns of Bitcoin and Ethereum, and Section 4 presents the discussion and conclusions, as well as the limitations, of this study and recommendations for future research.
2. Methods
2.1. Filtered Historical Simulation Approach
Barone-Adesi et al. (1998, 1999), introduced the filtered historical simulation to forecast the density distribution of future asset prices. This is a resampling method of filtered historical residual returns adjusted with current market conditions. At each step in the forecasting horizon, the set of the random, historical standardized residuals is multiplied by the simulated volatility to reflect the predicted market conditions. The generated density of price and volatility predictions provided market risk estimates of investor portfolios. The general ARMA()-GARCH() model specification is as follows:
In Equation (1) the AR term, δ, accounts for the correlation between an observation and several lagged observations, and the term θ captures the influence of past forecast errors on the current observation. The error term, εt, could follow any conditional distribution, denoted by D. Although, in line with the stylized facts observed in the cryptocurrency market (see for example, Zhang et al. 2021), distributions other than the normal will be used. The variance Equation (2) is specified as a GARCH (). The use of such a general model is appealing for modeling asset returns with the efficient estimation of parameters, leading to reliable inferences about the underlying processes. Ultimately the right specification in the models in Equations (1) and (2) will lead to the removal of dependencies in the return series, leaving residuals to be random. For each of the two cryptocurrency return series, several specifications of the ARMA and volatility, including asymmetric GARCH, IGARCH, TARCH, and GJR-GARCH, will be estimated. The criteria that will be used to select the right specification will be mainly the residual diagnostics and volatility forecasting performance, as measured by the proportion of variance in the realized volatility that is explained by the forecasted volatility, i.e., the adjusted R-squared from the regression of the squared residuals against the conditional variance.1
Nevertheless, removing all dependencies can be challenging, but it is of paramount importance in the simulation to ensure that the generated values accurately reflect the real-world relationships between variables. In addition, when the best possible parameterization of conditional mean and variance fails to capture all hidden dependencies in the series, the block bootstrap can be considered an alternative to the standard bootstrap.
2.2. Block Bootstrapping Method
As pointed out by Cogneau and Zakamouline (2013), the bootstrap methods implicitly assume that the data are generated by a stationary process. This means that the statistical properties of the residuals obtained from Equations (1) and (2) do not change over time. They argue that when bootstrapping non-stationary data, the resampled data (bootstrap samples) may not be representative of the true distribution of the underlying process. This is because the bootstrap procedure tends to replicate the distribution of the data at the time of resampling, which might not hold over time in a non-stationary environment.
Block bootstrap, on the other hand, resamples contiguous blocks of data, preserving the local dependencies within those blocks. By treating each block as a unit, the method captures any hidden dependencies present within each block. There are different types of block bootstrap methods, using either overlapping or non-overlapping blocks and constant or dynamic block length. The block bootstrap method generally requires the specification of the block length. The block length determines how much of the dependence structure is preserved during resampling. If the block length is too short, the dependence structure might not be adequately captured. If it is too long, the blocks might overlap too much, reducing the variability of the resampled data.
The most popular methods of choosing the block size are Hall et al. (1995) and Politis and White (2004). This study will follow the method of Hall et al. (1995) in choosing an optimal block length, which relies on a cross-validation process using a type of subsampling to estimate the mean squared error (MSE) incurred by the bootstrap at various block lengths. The optimal block length will be determined using the bootstrap mean squared error (BMSE) criterion. The BMSE requires dividing the data into blocks of different lengths from 2 to 50 consecutive observations. The key steps involve resampling the data, estimating the parameter of interest for each resampled dataset, calculating the squared errors, and then averaging them over all resamples. This process is repeated for different block lengths, and the results are plotted to analyze the behavior of the estimator with changing block lengths. Consider the time series , , with observations , and assume an integer ranging between 1 and , the non-overlapping block bootstrapping method considers a constant block length and divides the series in disjoint blocks, where the i-th block is given by for , with is the number of blocks within the bootstrap sample. In the moving block bootstrap method, a certain number of blocks, , is chosen randomly from the set , with the same number of observations. Let us denote the randomly resampled block from the blocks using , and then we obtain a bootstrap version of , as follows:
3. Results
3.1. Preliminary Analysis and Block Bootstrapping
The dataset consists of intraday, one-minute intervals for two cryptocurrencies, Bitcoin versus the U.S. dollar (Bloomberg ticker: BTCUSD) and Ethereum versus the U.S. dollar (Bloomberg ticker: ETHUSD). Both cryptocurrencies are known for their large market capitalizations compared to other cryptocurrencies and are the most commonly traded in monetary transactions (Theiri et al. 2023). In addition, as opposed to conventional currencies, cryptocurrency markets are 24-h trading markets that are open seven days a week and characterized by high liquidity comparable to that of foreign exchange markets (Nekhili et al. 2023). The dataset covers the period between 7 September and 14 October 2022, for a total of 39,192 observations. Table 1 reports the summary statistics of the 1-min log-return series, including the mean, standard deviation, minimum, maximum, skewness, and kurtosis for each cryptocurrency. Ethereum has the highest standard deviation, and the two cryptocurrencies display excess kurtosis.

Table 1.
Descriptive statistics of 1-min log-returns of Bitcoin and Ethereum.
Cryptocurrency returns are known for their complexity and non-standard behavior, Baur et al. (2018). They can exhibit extreme volatility, abrupt changes in market sentiment, and sudden price spikes, which are not always well-captured by traditional financial models. Various orders in the ARMA() in the mean and conditional variance equations were estimated with the quasi-maximum likelihood (QML) method.2 Three different probability distributions for the conditional error, , in the likelihood function were used, the normal distribution, the Student-t distribution, and the generalized extreme value (GEV) distribution. The degrees of freedom in the last two were estimated jointly with the parameters in Equation (2). The coefficient estimates and their standard errors are reported in Table 2 and Table 3, respectively, for Bitcoin and Ethereum returns.

Table 2.
Estimation of the conditional mean and variance model for the Bitcoin returns.

Table 3.
Estimation of the conditional mean and variance model for the Ethereum returns.
Table 2 reports the estimation results for Bitcoin returns. The one-minute price changes are filtered using conditional mean and variance equations from the ARMA(0,0)-GARCH(1,2) model, with the Student-t distribution identified as the most appropriate for the error term, εt, in the log-likelihood function. The parameter d represents the degrees of freedom of the Student-t distribution. A value of 4.32 reveals fat tails in the conditional distribution of ε. The small number of degrees of freedom reveals fat tails in the Bitcoin return data, which is much heavier than what a normal distribution would predict. The return series follows a random walk, but its volatility is heteroskedastic with GARCH effects, considering the aggregate value of the first and second order of the ARCH terms.
Likewise, the parameters in Equation (1), with various orders in the ARMA and the conditional variance of the Ethereum return series, were estimated with each of the three probability distributions of the error term in the likelihood function. The most appropriate model for the conditional variance was found to be ARMA(0,0)-GJR-GARCH(1,2). Equation (2) considers an additional term, γ, that captures the leverage effect of bad and good news and is written as follows:
where can take a value of 1 for ; otherwise, it takes a value of 0. The coefficient estimates with the corresponding standard errors are shown in Table 3. The minute interval of the rate of return for Ethereum also follows a random walk, but its variance, in addition to the heteroskedastic long memory, has parts that represent asymmetric properties. The asymmetric effects are captured by the γ coefficient, which is statistically significant and has a negative sign, revealing that negative shocks (bad news) increase volatility more than positive shocks (good news) of the same magnitude. The degrees of freedom in the t-distribution of the returns are reported to be quite low, suggesting a high probability of extreme returns far from the central tendency. This supports the presence of fat tails in the distribution.
This research proceeds further with testing for dependency in the standardized and squared standardized residuals. The different tests are carried out on the GARCH residual and standardized residual returns to investigate the hypothesis of i.i.d. Five tests are chosen, as in Brockwell and Davis (2016), and the results are reported in Table 4 for the statistics and their significance.

Table 4.
Diagnostic tests on standardized residuals and squared standardized residual returns.
The tests for various statistics, such as the Ljung-Box, turning points, difference sign, and rank tests, have low p-values in many cases, indicating the presence of unexplained patterns or dependencies in the standardized residuals and squared standardized residuals. This indicates that there are still correlations and patterns in the data that the model did not account for, even though returns were filtered using every feasible ARMA-GARCH specification before conducting the tests on the residual returns.
The analysis follows by performing the block bootstrapping method. Table 5 presents the results for the optimal block length and the corresponding minimum squared error (MSE) values, which are calculated using the block bootstrap method from Hall et al. (1995).

Table 5.
Determining the optimal block length.
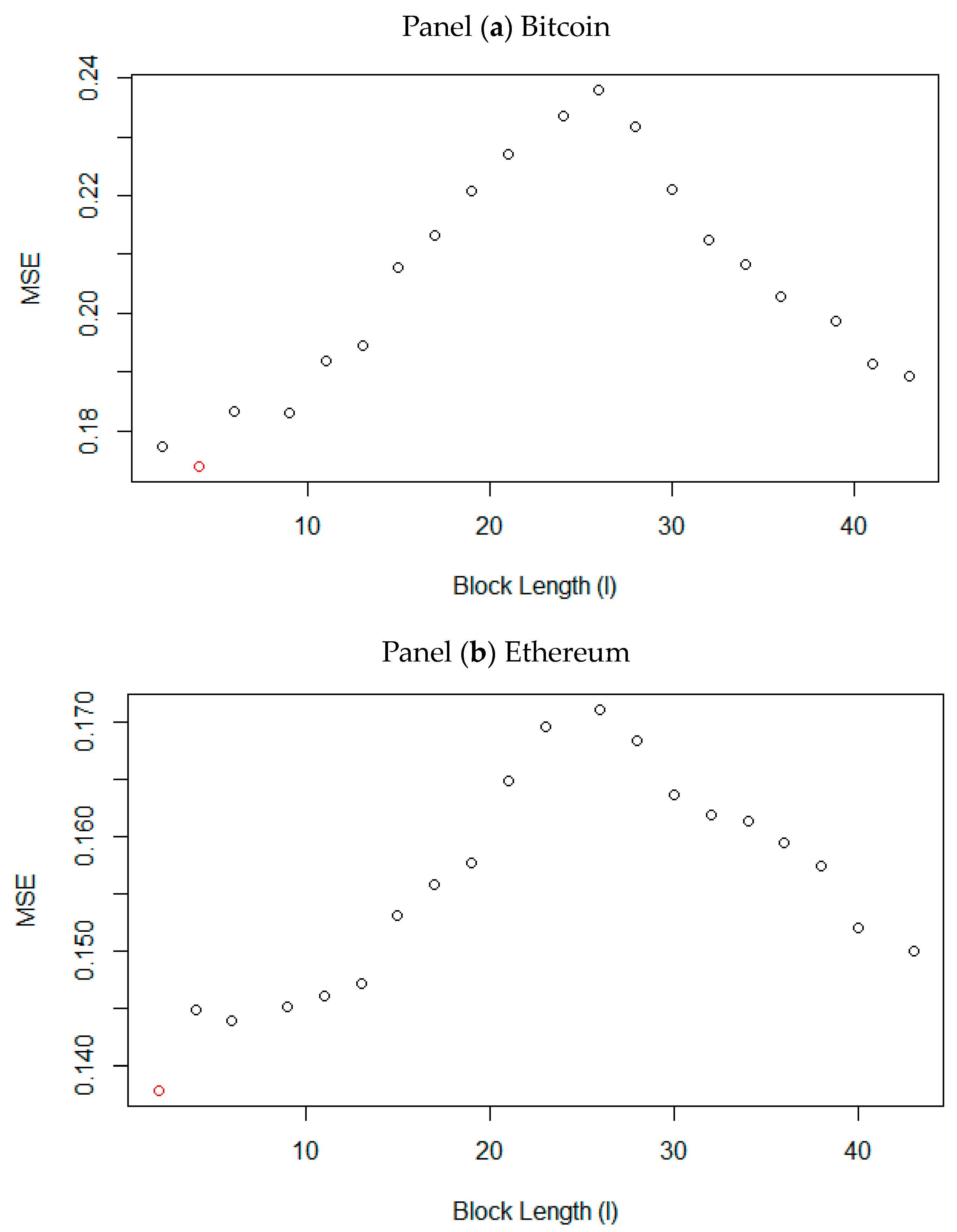
To better visualize the choice of the optimal block length, Figure 1 plots the criterion of optimality for the selection of the block length, namely, the minimum squared error in the function of the block length.
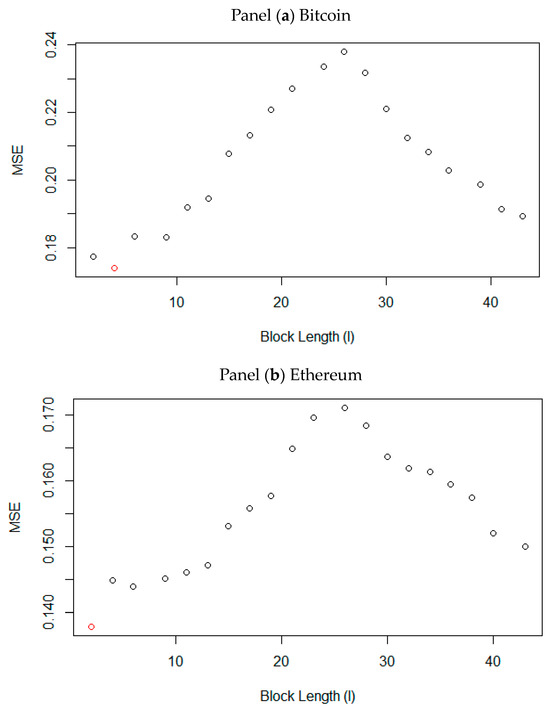
Figure 1.
Bootstrap mean squared error at different block lengths panel. The red dot corresponds to the optimal block length that minimizes the MSE. Panel (a) shows that the optimal block length for Bitcoin is five (5), and that of Ethereum is two (2) (Panel b).
3.2. Simulation and Price Forecast
Following Barone-Adesi et al. (1999), multistep forecasts for the price and variance equations were generated by plugging in innovations randomly selected from the historical set of standardized residuals. The simulation methodology stands as follows: Firstly, with a block of five and two, respectively, consecutive standardized residual returns, which are denoted by min, are drawn to form a set of innovations εt in the simulation of the pathways for Bitcoin and Ethereum.
These estimated residuals are divided by the corresponding volatility estimates, which are denoted by , to form the set of innovations, which are denoted by . Secondly, to generate one step ahead, , of the simulated value for the innovation, a random standardized residual return from the dataset is drawn and then scaled with the volatility of the period . We denote this by , with , where the coefficients () are estimated using Equation (2). Finally, a simulation of the asset return at time , which is denoted by , is obtained as follows: , where the coefficients () are estimated using Equation (2). With these simulated returns, we can derive the corresponding simulated asset price.
For other simulation pathways, , the volatility is unknown and must be simulated from the randomly selected re-scaled residuals as and the simulated returns as .
With the optimal block length identified earlier, the sequence of standardized residuals is then used in multistep forecasting. A total of 1,000,000 pathways for 60 one-minute intervals were generated for each of the two cryptocurrencies.
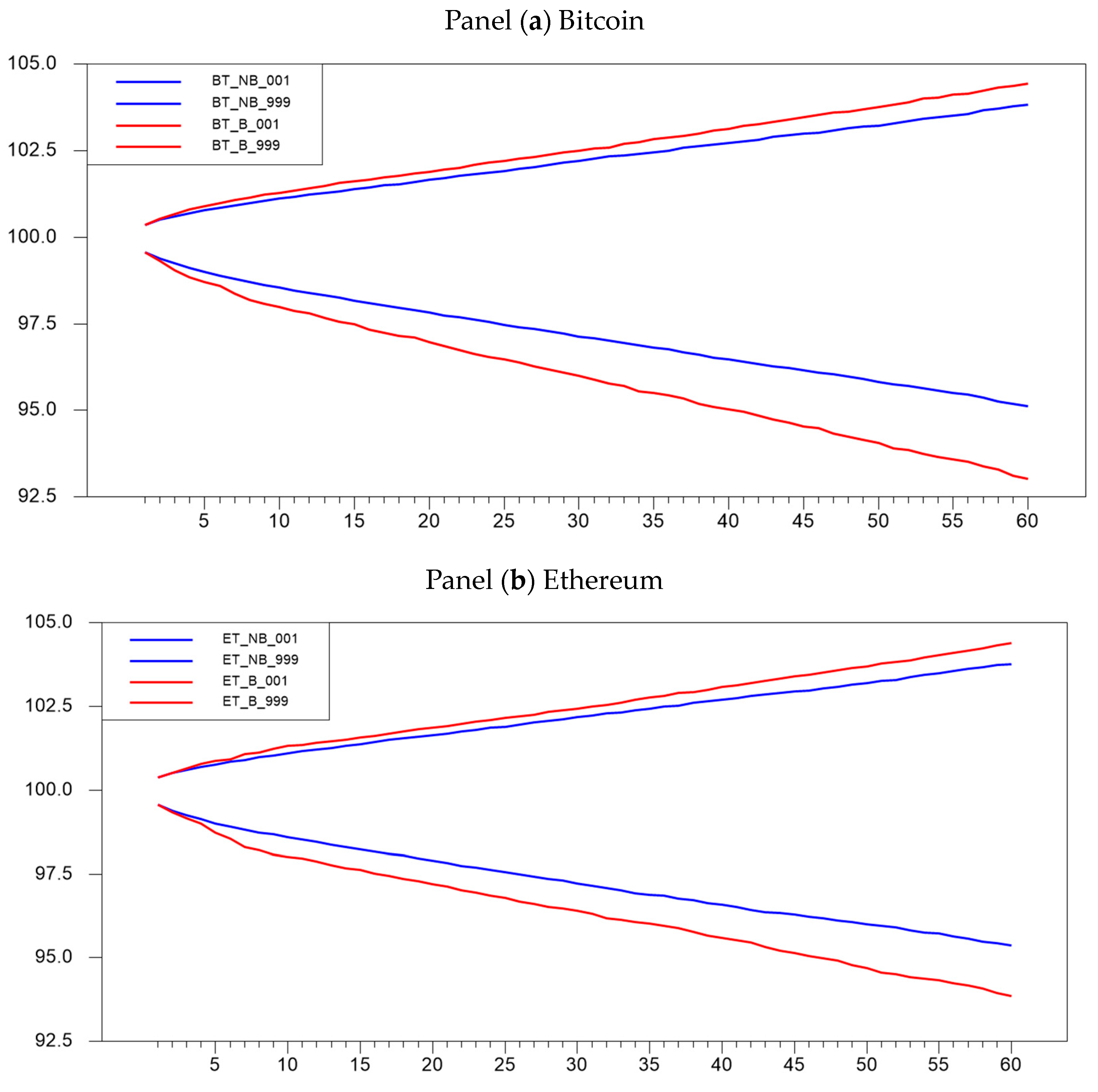
The confidence bands at 0.1% and 99.9% are reported in Figure 2 panel (a) for the Bitcoin series and panel (b) for the Ethereum series.
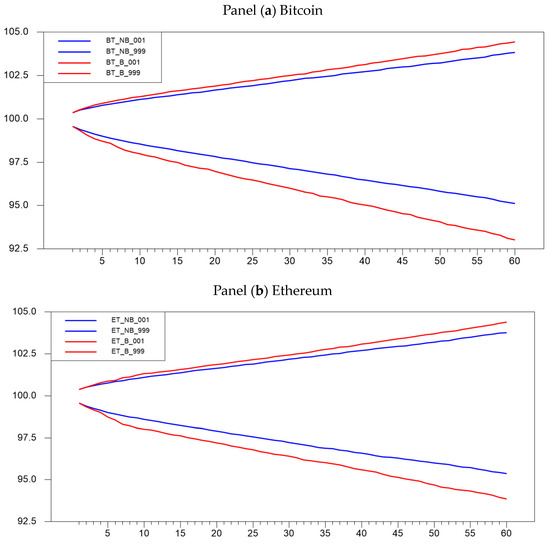
Figure 2.
Forecast confidence bands: block vs. regular bootstrap. For both panels (a,b), the forecasted bands are at 99.9% and 0.1% confidence levels.
In the graphs above, the red lines denote the confidence bands, also known as prediction intervals, for block bootstrap, while the blue lines depict the confidence bands for ordinary bootstrap. These prediction intervals provide insights into potential price movements over 60 one-minute time intervals. To facilitate comparisons of forecast intervals, the initial prices for each cryptocurrency are standardized to USD 100. The results show that in both series, the predictions by the block bootstrap follow wider price movement intervals when compared to the ordinary bootstrap.
Table 6 and Table 7 display the projected prediction confidence intervals for additional percentiles, utilizing both the block bootstrap, which is denoted with the letter “B”, and the ordinary bootstrap, which is denoted with “NB”.

Table 6.
Bitcoin projected confidence intervals for selected percentiles for 10-, …, 60-min horizons.

Table 7.
Ethereum projected confidence intervals for selected percentiles for 10-, …, 60-min horizons.
Table 6 and Table 7 offer insights into the confidence intervals for selected percentiles of Bitcoin and Ethereum returns across various time horizons, spanning from 10 to 60 min, employing two distinct methods, as follows: block (BT_B) and ordinary bootstrap (BT_NB). It delineates percentiles from 0.1% to 99.9%, including the 1% and 99% thresholds, signifying different positions within the Bitcoin return distribution, from extremely low to exceptionally high returns. The table facilitates a comparison between the two bootstrap methods in estimating confidence intervals across different percentiles and time horizons, enabling the observation of any discernible trends, such as the widening or narrowing of intervals as the time horizon increases.
In summary, the filtered historical simulation based on block bootstrap consistently provides slightly wider prediction intervals than the ordinary bootstrap method. The variation in intervals between the two methods is more pronounced at extreme percentiles (0.1%, 99.9%) compared to the closer range percentiles (1%, 99%). Understanding these confidence intervals is crucial for assessing the uncertainty and potential variability in the forecasted prices, helping in risk management and decision-making processes.
4. Discussion and Conclusions
Knowing the density of possible cryptocurrency prices over short intervals, such as one-minute intervals, is crucial for a wide range of applications, including price prediction, risk management, market behavior analysis, and strategy optimization. Cryptocurrencies are highly volatile and often subject to extreme price movements, making a deep understanding of price density especially important for traders and analysts operating in this space. Traders can optimize their entry and exit points by understanding the distribution of prices. If a price is near the lower end of its expected range, it might be a good buying opportunity, while prices near the upper end could be a signal to sell. By knowing the density of prices, traders can estimate the likelihood of tail events (large price swings) and employ strategies like stop-loss orders or options to hedge against these risks.
The filtered historical simulation can be a valuable tool in risk analysis, particularly for assessing non-normal risks and tail events in financial markets. It allows for a more realistic and data-driven approach to risk assessment. This study introduced a variant of the filtered historical simulation to deal with the hidden dependencies in ultra-high-frequency Bitcoin and Ethereum returns. As the ARMA-GARCH parameterizations failed to remove all complex dependencies in the two cryptocurrencies, the innovations were drawn as a sequential block of constant length, but different for each cryptocurrency, to produce price and volatility pathways for the Bitcoin and Ethereum prices. Many simulated price pathways were generated to produce the density at each of the sixty-one-minute forward price nods for each of the two cryptocurrencies and each of the two variants of the filtered historical simulation. The simulated confidence bands for the price pathways in the block bootstrap variant are found to be wider across the entire sixty-minute horizon. This divergence between the two filtered historical simulation variants is particularly apparent at the extreme percentiles (0.1%, 99.9%) compared to the less extreme percentiles (1%, 99%). Profound backtesting is necessary to assess the accuracy of each filtered historical simulation variant in estimating the risk of ultra-high-frequency price series.
Furthermore, this analysis highlights trends in confidence intervals across different percentiles and time horizons, shedding light on how intervals may widen or narrow as the time horizon increases. Overall, these findings enhance our understanding of uncertainty assessment in high-frequency cryptocurrency markets and provide valuable insights for both researchers and practitioners in the field, thereby enhancing the effectiveness of risk management and decision-making processes.
These findings may serve as a tool for portfolio risk management, allowing for the prediction of cryptocurrency tail risk. More accurate forecasts of cryptocurrency volatility can serve as a gauge of short-term risk, helping to assess the appeal of these assets relative to less risky alternatives. In addition, high-frequency traders and prospective investors may be interested in a more precise model for predicting cryptocurrency return and volatility. Block bootstrapping can help to assess the probability of tail events.
The results of this study align closely with findings from previous studies conducted recently. Similar research has emphasized the importance of adopting innovative risk analysis techniques to address the complexities of high-frequency cryptocurrency markets. For instance, studies by Zhang et al. (2021) and Ahelegbey et al. (2021) have highlighted the significance of volatility modeling and tail risk assessment in understanding the dynamics of cryptocurrency markets. Furthermore, research by Bouri et al. (2019) has underscored the need to consider behavioral aspects and market efficiency when analyzing risk in cryptocurrency trading. The proposed filtered historical simulation approach builds upon these findings by offering a comprehensive and data-driven framework for risk analysis, contributing to the ongoing discourse on effective risk management strategies in high-frequency cryptocurrency markets.
As much as this research sheds light on the intraday price patterns of cryptocurrencies, a number of limitations need to be accepted, and recommendations for further studies must be made. While this study illustrates the effectiveness of the block bootstrap method for constructing confidence bands and tail risk estimation, more comprehensive out-of-sample backtesting is still needed in terms of the robustness and predictive accuracy of such methods over different market conditions and eventual extraordinary turbulence or volatility in the markets.
Further research should be directed to very intense backtesting across several market conditions to test the reliability of the forecasts generated by combining block bootstrapping and filtered historical simulation.
Author Contributions
Conceptualization, K.G. and R.N.; methodology, K.G.; software, K.G. and R.N.; validation, K.G., R.N. and C.C.-V.; formal analysis, R.N.; writing—original draft preparation, R.N. and K.G.; writing—review and editing, K.G., R.N. and C.C.-V.; visualization, R.N.; supervision, K.G.; project administration, K.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data will be made available on request.
Acknowledgments
We would like to thank Les Vosper for his helpful comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
Notes
| 1 | This study aims to introduce a variant of the filtered historical simulation that suits the ultra-high-frequency data. Therefore, in the next session, the results will only report the coefficient estimates of the most appropriate ARMA-GARCH model of all the different parameterizations that were estimated. |
| 2 | We have checked the autocorrelation and partial autocorrelation functions to identify the AR and MA orders. The inclusion of these terms comes from a preliminary analysis conducted as a guide to following the right model. All possible combinations were taken into consideration, and the selection of the adequate model is based on the Akaike information criterion (AIC). All estimation results are available. |
References
- Ahelegbey, Daniel Felix, Paolo Giudici, and Fetemeh Mojtahedi. 2021. Tail risk measurement in cypto-asset markets. International Review of Financial Analysis 73: 101604. [Google Scholar] [CrossRef]
- Barone-Adesi, Giovanni, Frederick Bourgoin, and Kostas Giannopoulos. 1998. Don’t Look Back. Risk 11: 100–4. [Google Scholar]
- Barone-Adesi, Giovanni, Kostas Giannopoulos, and Les Vosper. 1999. VaR Without Correlations for Non-Linear Portfolios. Journal of Futures Markets 19: 583–602. [Google Scholar] [CrossRef]
- Barone-Adesi, Giovanni, Kostas Giannopoulos, and Les Vosper. 2002. Backtesting Derivative Portfolios with Filtered Historical Simulation (FHS). European Financial Management 8: 31–58. [Google Scholar] [CrossRef]
- Baur, Dirk G., KiHoon Hong, and Adrian D. Lee. 2018. Bitcoin: Medium of exchange or speculative assets? Journal of International Financial Markets, Institutions and Money 54: 177–89. [Google Scholar] [CrossRef]
- Bouri, Elie, Rangan Gupta, and David Roubaud. 2019. Herding behaviour in cryptocurrencies. Finance Research Letters 29: 216–21. [Google Scholar] [CrossRef]
- Brockwell, Peter J., and Richard A. Davis. 2016. Introduction to Time Series and Forecasting, 3rd ed. Berlin: Springer. [Google Scholar]
- Chowdhury, Mohammad Ashraful Ferdous, Mohammad Abdullah, Masud Alam, Mohammad Zeynul Abedin, and Baofeng Shi. 2023. NFTs, DeFi, and other assets efficiency and volatility dynamics: An asymmetric multifractality analysis. International Review of Financial Analysis 87: 102642. [Google Scholar] [CrossRef]
- Christoffersen, Peter. 2009. Value-at-Risk Models. In Handbook of Financial Time Series. Berlin: Springer, pp. 753–66. [Google Scholar] [CrossRef]
- Cogneau, Philippe, and Valeri Zakamouline. 2013. Block bootstrap methods and the choice of stocks for the long run. Quantitative Finance 13: 1443–57. [Google Scholar] [CrossRef]
- Grobys, Klaus, and Juha Junttila. 2021. Speculation and lottery-like demand in cryptocurrency markets. Journal of International Financial Markets, Institutions and Money 71: 101289. [Google Scholar] [CrossRef]
- Hall, Peter. 1985. Resampling a Coverage Process. Stochastic Processes and Their Applications 20: 231–46. [Google Scholar] [CrossRef]
- Hall, Peter, Joel L. Horowitz, and Bing-Yi Jing. 1995. On blocking rules for the bootstrap with dependent data. Biometrika 82: 561–74. [Google Scholar] [CrossRef]
- Kristjanpoller, Werner, Ramzi Nekhili, and Elie Bouri. 2024. Blockchain ETFs and the cryptocurrency and Nasdaq markets: Multifractal and asymmetric cross-correlations. Physica A: Statistical Mechanics and its Applications 637: 129589. [Google Scholar] [CrossRef]
- Kuester, Keith, Stefan Mittnik, and Marc S. Paolella. 2006. Value-at-Risk Prediction: A Comparison of Alternative Strategies. Journal of Financial Econometrics 4: 53–89. [Google Scholar] [CrossRef]
- Kunsch, Hans R. 1989. The Jackknife and the Bootstrap for General Stationary Observations. Annals of Statistics 17: 1217–41. [Google Scholar] [CrossRef]
- Liu, Yujun, Zhongfei Li, Ramzi Nekhili, and Jahangir Sultan. 2023. Forecasting Cryptocurrency Returns with Machine Learning. Research in International Business and Finance 64: 101905. [Google Scholar] [CrossRef]
- Nekhili, Ramzi, and Jahangir Sultan. 2022. Hedging Bitcoin with Conventional Assets. Borsa Istanbul Review 22: 641–65. [Google Scholar] [CrossRef]
- Nekhili, Ramzi, Jahangir Sultan, and Elie Bouri. 2023. Liquidity spillovers between cryptocurrency and foreign exchange markets. North American Journal of Economics and Finance 68: 101969. [Google Scholar] [CrossRef]
- Politis, Dimitris, and Halbert White. 2004. Automatic Block-Length Selection for the Dependent Bootstrap. Econometric Reviews 23: 53–70. [Google Scholar] [CrossRef]
- Shahzad, Syed Jawad Hussain, Elie Bouri, David Roubaud, Ladislav Kristoufek, and Brian Lucey. 2019. Is Bitcoin a better safe-haven investment than gold and commodities? International Review of Financial Analysis 63: 322–30. [Google Scholar] [CrossRef]
- Theiri, Saliha, Ramzi Nekhili, and Jahangir Sultan. 2023. Cryptocurrency Liquidity During the Russia-Ukraine War: The Case of Bitcoin and Ethereum. Journal of Risk Finance 24: 59–71. [Google Scholar] [CrossRef]
- Zhang, Yue-Jun, Elie Bouri, Rangan Gupta, and Shu-Jiao Ma. 2021. Risk spillover between Bitcoin and conventional financial markets: An expectile-based approach. The North American Journal of Economics and Finance 55: 101296. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).