Abstract
The growing adoption of unmanned aerial vehicles (UAVs) for urban parcel delivery highlights the need for efficient distribution center placement. Particularly in dense urban environments, obstacle avoidance usually increases real path distances beyond straight-line measurements. Considering these distance differences, this study first employs the Informed-RRT* algorithm with spatial indexing to calculate real UAV flight paths between locations. We use the real path distances instead of straight-line distances to determine service coverage areas in the distribution center layout model. In this model, we aim to minimize the total economic cost and maximize customer satisfaction, considering the service range, the balance between delivery capability and demand, and the constraints of the distribution mode. An immune-algorithm-enhanced genetic algorithm, the immune genetic algorithm, is used to solve the model, acquiring the distribution center layout. We conduct a simulation experiment in Shenzhen’s low-altitude airspace and compare the layout results between the real path distance criterion and the straight-line path distance criterion. The results show that using the real path distances instead of the straight-line distances leads to changes in distribution center layout, demonstrating the necessity of this framework.
1. Introduction
In recent years, e-commerce transactions have been growing at an explosive rate, with the global e-commerce market more than doubling between 2016 and 2020, and the total transaction volume is expected to exceed USD 8 trillion by 2027 [1]. Research shows that consumers’ intention to shop at offline stores after the COVID-19 outbreak dropped from 54% to 40% [2]. The continued growth of e-commerce transactions is an inevitable trend. It is necessary to build a logistics and transportation system in line with the growth trend of e-transactions. The key problem is to rationally dispatch logistics and transportation resources to meet the growing volume of express demand. Using unmanned aerial vehicle (UAV) distribution instead of traditional methods can reduce economic costs. This approach also decreases environmental pollutant emissions from highway freight transportation [3]. Urban areas face dense population distribution, saturated ground transportation resources, and a widespread e-commerce industry. Therefore, these areas are suited to the method of UAV delivery. Amazon, Google, UPS, and other companies have begun experiments on UAV logistics and distribution in cities. They have explored UAV delivery routes and put them into use in some areas [4,5]. For example, Amazon.com launched its Amazon Prime Next Day Delivery service to put UAVs into logistics and distribution use [6]. UPS successfully conducted UAV delivery test flights in Florida. It also announced a partnership with German UAV maker Wingcopter to develop next-generation parcel delivery UAVs for a variety of use cases in the U.S. and internationally [7].
Low-altitude airspace has great application potential. Using logistics UAVs instead of trucks for distribution can help alleviate ground traffic congestion. This approach also solves the ‘last kilometer’ problem in logistics and distribution. However, when it comes to the UAV distribution center layout issue, a common simplification in current research is to use straight-line distance as the criterion to determine whether a recipient address falls within the service coverage of a distribution center. This simplification ignores obstacle avoidance and leads to inaccurate assessments of risk and economic cost. Specifically, this simplification reveals the following shortcomings: First, there is a lack of a path planning algorithm capable of efficiently finding a globally optimal path suitable for urban environments. Secondly, there is no location model that uses actual path distance—rather than straight-line distance—to determine a distribution center’s service range. Lastly, there is a lack of an optimization algorithm with a high probability of finding the optimal solution to the location model.
Therefore, to design a scientific distribution center layout for the urban UAV logistic system, this study carries out the following research to overcome the above problems:
1. A spatial index structure is incorporated into the Informed-RRT* algorithm to enable efficient global path planning in urban environments. This allows for the calculation of real path distances that account for obstacles.
2. An immune-enhanced genetic algorithm is employed, balancing local optimization with diversity preservation to improve the accuracy of urban logistics coverage assessments with real path flight distances.
3. A simulation experiment is conducted based on a real-world environment. The experiment compares the impacts of using real path versus straight-line distances on service coverage range, validating the superiority of the proposed path planning and immune genetic algorithm.
2. Related Work
Given the complexities involved in optimizing UAV paths in real-world environments, selecting an effective path planning algorithm becomes crucial. Among the various path planning algorithms, under conditions where the global environment is known, topology-based path planning algorithms are a widely used method for finding the global shortest path. The problem of finding the shortest path between two points in a plane with obstacles is a classical issue in geometry and has been extensively studied. Hershberger and Suri pioneered the shortest path map algorithm, which utilizes the core concept of the incremental Dijkstra algorithm to achieve shortest path searches with a time and space complexity of O(nlogn), making it the most well-recognized theoretical optimal algorithm for solving the Euclidean shortest path problem, where n represents the total number of vertices of the obstacles in the plane [8]. Building on the shortest path map algorithm, researchers have proposed dividing the wavefront propagation operations into O(logn) phases. In each phase, persistent binary trees that are irrelevant to the subsequent stages of the algorithm are discarded, reducing the space complexity of the algorithm to O(n) [9]. Subsequently, by employing a global problem decomposition based on an extended corridor structure in triangulated rectilinear domains, the time complexity of the algorithm has been further reduced to O(n + hlogh), demonstrating excellent performance in scenarios with a small number of obstacles but complex structures [10]. In summary, this method of searching for the shortest path in a two-dimensional plane based on deterministic decisions has been continuously optimized and has achieved new theoretical optimal values in terms of time and space complexities. Concurrently, another category of path planning algorithms based on random search, represented by the Rapidly Exploring Random Tree (RRT) algorithm, has also been gradually developed and improved. The RRT class algorithm utilizes random sampling to explore feasible regions in the configuration space, gradually covering the space through a tree-like structure to reduce time consumption, making it more suitable for large-scale scenarios. It uses a random sampling method and a dynamic tree expansion mechanism to achieve near-globally optimal solutions [11]. Its improved RRT* algorithm introduces an asymptotic optimization strategy, which reduces the path cost through node reconnection [12]. The further improved Informed-RRT* algorithm constructs an elliptic region based on the current optimal path length and the starting and ending positions, and constrains the sampling space to the region. This boosts the convergence efficiency of the algorithm and has a high probability of obtaining the globally optimal solution [13]. Once the true path is determined using the Informed-RRT* algorithm, it can be integrated into the subsequent location model to enhance the accuracy and efficiency of site selection.
In logistics UAV distribution center location research, economic factors include transportation costs, warehousing costs, and construction costs. These costs are often linearly related to the transportation path length and depend on the delivery capability and number of distribution centers and facility points. Operational efficiency is usually measured by customer satisfaction. A common mathematical approach is to model satisfaction vs. time using a segmented fitting function. Currently, a popular mathematical method is to construct a segmented fit function of satisfaction and time and adjust the specific mathematical expression according to the experimental scenario [14].
Traditional ground-based facility site selection considers capacity–demand matching, flow limits, and load limits, while logistics UAV distribution center site selection must also account for UAV energy consumption [15], airspace restrictions [16], and weather conditions (wind, temperature, precipitation) [17]. In some research, more factors are considered, including noise [18], electromagnetic fields [19], navigation equipment [20], and public acceptance [21]. These additional factors make UAV distribution center site selection more complex than ground facilities. Developing efficient modeling and optimization methods remains an active research area.
The UAV distribution center location problem is a classical optimization problem in operations research. It involves selecting the optimal set of facilities from multiple candidate locations and assigning them to meet the demands of various points. To address this challenge, a number of facility location models have been developed, including the p-median problem, which minimizes the total transportation distance [22]; the Maximum Covering Location Problem (MCLP), which aims to maximize the coverage of demand points with a limited number of facilities [23]; the Location-Routing Problem (LRP), which seeks to achieve the optimal integration of facility location and route allocation [24]; and the Capacitated Facility Location Problem (CFLP), which incorporates capacity or service constraints into the facility selection process [25], among others. Effectively solving these models typically requires the application of optimization algorithms, which serve as essential tools for achieving high-quality solutions.
Once the location problem has been formulated as a mathematical model, it is necessary to generate an initial feasible solution and then iteratively improve it until the objective is optimized. Commonly applied algorithms include, but are not limited to, genetic algorithms and immunization algorithms. Genetic algorithms solve complex problems by simulating biological evolution’s chromosome operations [26]. Immunization algorithms prevent local optima by mimicking antibody–antigen matching [27]. Both enable flexible global searching. These optimization methods, together with facility location models, form a robust framework for constructing and solving UAV distribution center location models in urban scenarios.
From the current literature, most of the existing studies focus on analyzing the impact of specific factors of the model on the model as a whole [28] or exploring efficient model-solving algorithms [14,29,30]. As research progresses, the optimization objectives and constraints of the UAV distribution center problem are gradually being solved, and the system is gradually becoming mature. Delivery operations, as one of four key factors affecting UAV energy consumption [31], remain a major research focus. Dukkanci’s UAV facility location review [32] highlights two key future research needs: First, precise energy consumption estimation for UAVs. Second, optimal combinations of UAVs with varying ranges, payloads, battery capacities, energy functions, and costs. In line with this, recent UAV coverage research emphasizes energy constraints. Studies examine energy consumption patterns during transport [32,33]. New delivery methods, including the continuous approximation (CA) model [34] and the two-tiered delivery model with a time window, are raised. Analysis of the composition of the fleet during the delivery process is also carried out [35,36,37]. Despite these advancements, there are still unresolved challenges, particularly when considering the practical constraints associated with UAV operations. When considering the limitations imposed by the UAV range, it becomes apparent that current research on UAV distribution centers still faces several shortcomings.
While classic location models have a well-established and comprehensive framework capable of conducting theoretical target optimization studies for various site selection issues, most of them rely on Euclidean distance. This approach can lead to significant deviations from actual transportation routes in complex terrains, urban road networks, and unmanned aerial vehicle (UAV) scenarios, potentially resulting in overestimated coverage areas (service capacity) and unrealistic facility layouts [38]. In real-world operational environments, decision-making must take into account multiple interrelated factors—not just the economic costs of constructing a single facility or transportation distance. Among these, facility capacity constraints are particularly significant in logistics systems. Therefore, developing a reasonable drone delivery center location model is a critical prerequisite for the development of low-altitude logistics.
Building on this, a key challenge in current UAV-related site selection research is how service range coverage is determined. Most studies determine service range coverage using straight-line distances between points, ignoring real flight conditions. This evaluation method either assumes that UAVs operate in zones free from building interference [38] or it uses simplified models that entirely ignore the impact of buildings [39]. Both approaches disregard real-world obstacle avoidance requirements. A few studies limit flight to high altitudes and only consider a small number of buildings higher than this altitude as obstacles. For example, Wang’s study [40] analyzed obstacle impacts on airport coverage. He set flight altitudes between 110 and 120m, treating taller buildings as obstacles. The research developed a three-stage multi-objective delivery model and a two-layer genetic algorithm for solution optimization. The study first determined the overall structure, and then adjusted for coverage. This approach caused shifting relationships between primary and secondary points during adjustments, increasing process complexity [41]. Hong studied the obstacle effects on charging pile coverage in Phoenix. Under real-world conditions, this research optimized site locations to maximize service coverage within UAV and charging facility range limits. Such research confirms the importance of modeling real-world building obstructions and significantly improves UAV facility layout planning accuracy.
In the context of UAV distribution center location in urban environments, directly using straight-line distance to determine the service range overlooks the actual need for detours around buildings and obstacles. This can easily lead to erroneous estimates of actual transportation time and cost, and may also adversely affect the assessment of service coverage and the results of location–allocation decisions. In terms of model solving, traditional optimization algorithms are prone to becoming trapped in local optima, which compromises solution quality. Moreover, efficient algorithms for planning globally optimal paths are still lacking and require further research and development. These issues together highlight the importance of employing improved algorithms to obtain true path distances and adopting more effective optimization methods, which are essential for enhancing the accuracy of UAV delivery distribution center decisions.
3. Experimental Methods
This study employs an Informed-RRT* algorithm with a spatial index structure to carry out path planning tasks and calculate real path lengths. These lengths form the basis for determining whether a recipient address lies within the service range of a distribution center. The location model of the distribution center optimizes economic cost and customer satisfaction while incorporating service range and delivery demand balance constraints. Finally, an immune genetic algorithm is used to solve the model and establish the optimal logistics distribution layout.
3.1. Informed-RRT* Algorithm with Spatial Index Structure
Algorithms such as RRT achieve the efficient exploration of high-dimensional spaces through random sampling and tree expansion. Their core advantage is feasible path generation without pre-modeling obstacles. However, the original RRT algorithm ensures only probabilistic completeness and often produces redundant path length [11]. To address these limitations, the RRT* algorithm was developed, which introduced an asymptotic optimality mechanism in the path expansion process. By iteratively reconnecting neighboring nodes and optimizing parent node selection, RRT can progressively reduce overall path cost [12]. Despite these improvements, RRT* still relies on global random sampling, which entails significant computational overhead for frequent neighbor searches and collision checks. Moreover, the probability of identifying globally optimal solutions remains relatively low in complex environments. To further enhance search efficiency and optimality, the Informed-RRT* algorithm was developed, which introduced a dynamically constrained search space [13]. The dynamic search space adjustment mechanism consisted of elliptical sampling region constraints and a dynamic search radius attenuation strategy.
Specifically, Informed-RRT* restricts sampling to an elliptical region whose major axis is defined by the line between the initial point (qstart) and goal point (qgoal), and whose size is determined by the current best path length (cbest). By confining sampling to the ellipse, the algorithm focuses the search within zones with a greater likelihood of improvement. As the number of iterations increases and cbest converges towards the theoretical shortest path, the ellipse shrinks accordingly, further localizing the search. This iterative refinement of the sampling space is illustrated in Figure 1.
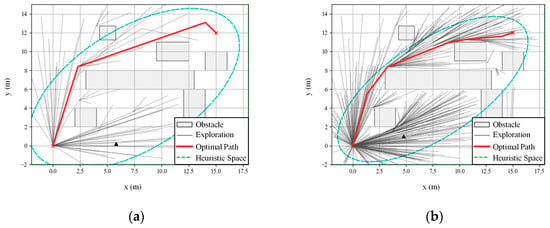
Figure 1.
(a) Schematic of Informed-RRT* sampling elliptic constraint in early stage. (b) Schematic of Informed-RRT* sampling elliptical constraint in late stage.
In addition, Informed-RRT* employs a dynamic search radius attenuation strategy, as described by Equation (1), in which the search radius is exponentially reduced as the tree expands. This approach maintains global exploration in early iterations and suppresses redundant sampling oscillations in later stages, thereby improving both sampling efficiency and convergence speed.
where rcurrent is the current search radius, n is the number of nodes in the current tree, and r is the radius of the next stage of the search.
Although Informed-RRT* demonstrates a higher probability of identifying globally optimal solutions, it still exhibits notable deficiencies. In particular, the algorithm relies on brute-force methods for neighbor node searches and collision detection, leading to a surge in computational time in urban environments with dense obstacles.
To overcome these challenges, this paper adopts Informed-RRT* as the foundational framework and enhances it through multi-level spatial index optimization. Specifically, we introduce KDTree (K-Dimensional Tree)-based neighbor search and STRTree (Sort-Tile-Recursive Tree)-based collision detection within the Informed-RRT* framework. This dual-index structure significantly improves both node retrieval and collision detection efficiency, thereby addressing the major efficiency bottlenecks of traditional brute-force methods in RRT-class algorithms.
The KDTree is essentially a spatial partitioning structure. During each construction process, all nodes are partitioned based on the dimension with the maximum variance (the axis along which the nodes are most widely dispersed). After sorting nodes by the selected dimension, the median node is chosen as the root of the current subtree, and the remaining nodes are divided into two subtrees. This recursive partitioning procedure continues for each subtree, each time along the axis of maximum variance, and at the median, until the number of nodes within a subspace falls below a predefined threshold [42]. Figure 2 illustrates a simplified KDTree partitioning process.
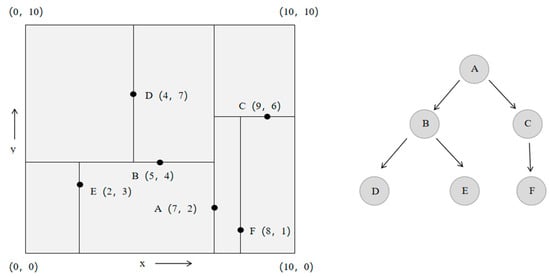
Figure 2.
Schematic diagram of KDTree construction.
During nearest neighbor querying, at each split node, the coordinate of the query point along the current splitting axis is compared with the node’s split value. If the query point coordinate is less, the search proceeds recursively to the left subtree; otherwise, it enters the right subtree. Once a candidate’s nearest node is found, the algorithm records the distance dmin to the query point and defines a circular search region (with dmin as the radius) centered at this node. The algorithm then checks whether the subspace intersects with the search circle to determine whether to perform backtracking. If an intersection exists, the algorithm explores the corresponding subtree to potentially find a closer node; if not, it prunes the search space to avoid redundant computations. After a new node is inserted, only the relevant path nodes need updating, which maintains an efficient lightweight index without global reconstruction. Compared to traditional brute-force nearest neighbor search which computes distances to all nodes, KDTree’s recursive partitioning confines searches to relevant branches. It also mitigates query errors via backtracking, thereby improving search efficiency.
STRTree is an efficient spatial index structure for collision detection. During preprocessing, each obstacle is assigned a minimum bounding rectangle (MBR). These MBRs are then grouped, sorted, partitioned by spatial proximity, and hierarchically aggregated from the bottom up. In STRTree, leaf nodes store actual obstacles and are located at the base of the tree. Non-leaf nodes store only collections of child node MBRs and pointers, not actual obstacle information, and are located exclusively in upper tree levels [43]. STRTree minimizes overlap among non-leaf nodes at higher levels. Figure 3 visualizes this storage hierarchy, where R8, R9, and R10 are leaf nodes; the remaining nodes are non-leaf aggregates.
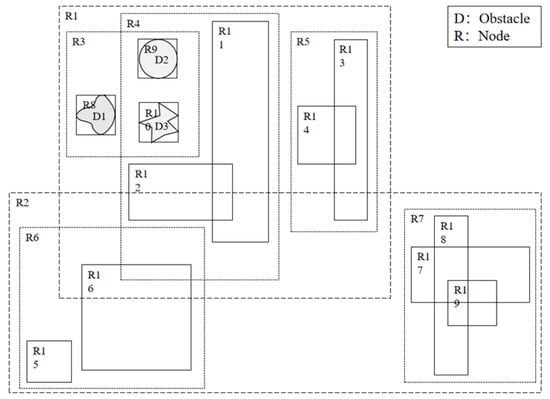
Figure 3.
Schematic of STRTree construction.
For collision detection, when presented with a candidate path segment, STRTree first rapidly filters all MBRs intersecting the segment’s MBR, thus eliminating most irrelevant obstacles before detailed geometric collision checking. After integrating STRTree into the Informed-RRT* framework, collision detection is restricted only to spatially relevant obstacles. The algorithm recursively traverses only those branches whose MBRs intersect with the path segment, advancing to child nodes only as needed, and halts when actual obstacles are reached or no intersection remains. This focused traversal significantly expedites the path planning process.
3.2. UAV Distribution Center Location Model Construction Considering Real Paths
This section aims to solve the urban logistics “last kilometer” problem, using logistics UAVs for center-to-end-point deliveries to alleviate congested ground traffic.
We aim to determine distribution centers and assign service relationships from a set of potential locations without predefining the number of centers. Our model simultaneously optimizes two objectives, minimizing economic costs and maximizing customer satisfaction, while considering the service capacity limits of each center. In addition, to align with the development trends of China’s drone logistics industry, we first establish secure and reliable flight routes before determining the final site selection. Therefore, we use the Capacitated Facility Location Problem model [25] as the basis and extend its cost functions and constraints to fit this application.
Distribution centers are chosen from existing logistics nodes. To achieve a robust spatial layout, the model incorporates both basic parameters (such as logistics point node coordinates, demand, and construction costs) and additional ones (such as center delivery capacity and service range). Furthermore, the modeling framework is tailored for the high-density and high-frequency characteristics of urban UAV logistics. These considerations collectively define our UAV distribution center location model.
To simplify the model, this paper has the following premise for its existence:
(1) Logistics UAVs perform “point-to-point” distribution. Our premise is that UAVs carry out only one single task at a time, and return immediately after completion of the distribution.
(2) We construct a distribution center–logistics point secondary site layout. A terminal logistics point can only be served by a distribution center, and there is no interconnection between end logistics points and distribution centers.
(3) The UAV is flying at a constant speed; the constant speed is 10 km/h in our model.
(4) We neglect the influence of environmental and unexpected factors such as temperature and humidity changes, human operational errors, and UAV collisions on the UAV flight process.
(5) The default UAV can take off and land vertically at all the logistics points selected.
(6) The UAVs used are of the same type, with the same range, payload, and power. Here we set 10 km as the range of flight in our model.
(7) The time for loading the goods, climbing, descending, and unloading the goods is not counted.
(8) In our model, all parameter settings are taken from the available existing UAV data sources, including SF (SF Express, a Chinese express delivery enterprise) and DJI (DJI-Innovations, a Chinese unmanned aerial vehicle manufacturer).
To facilitate the mathematical expression of the model, the parameters of the constructed model are replaced by symbols in the expression, and Table 1 explains the symbols in the model.

Table 1.
Explanation of variable symbols.
Both economic cost and customer satisfaction are key factors in UAV logistics delivery. They determine whether this industry can develop in the long term. Hence, this section selects the total transportation cost and customer satisfaction as the dual objectives for optimization, and the objectives are introduced as follows:
(1) Total transportation costs
Transportation economic costs contain logistics transportation costs, distribution center establishment costs, and warehousing costs.
where Cdel denotes the transportation cost of using UAVs for distribution, Csto denotes the warehousing cost of the distribution center, and Cde denotes the construction cost of the distribution center.
(2) Customer satisfaction
In this paper, a customer time satisfaction function is adopted to measure customer satisfaction. The segmented customer satisfaction function proposed in the literature [9] is used to describe the level of customer satisfaction with the response time of UAV delivery.
where S is the customer satisfaction, tij is the time from the distribution center i to its service logistics point j using UAVs for distribution, k is the time sensitivity coefficient, and tL and tB are the node times needed, respectively, to separate the customer satisfaction into a three-segmented function. When tij < tL, the customer satisfaction is considered to be 1; when tL < tij < tB, the customer satisfaction is calculated by
; and when tij > tB, customer satisfaction is considered to be 0.
Considering the constraints of distribution methods, delivery capability–demand balance, and the service range of distribution centers, we place the following constraints on the model:
(1) Distribution center quantity constraints
The number of logistics points selected as distribution centers is not greater than the total number of logistics points, i.e.,
(2) Delivery capability and demand balance constraints
Demand is met at each logistics point/delivery capability is greater than or equal to demand, i.e.,
(3) Distribution method constraints
Each logistics point can only be served by one distribution center, i.e.,
In the distribution center–logistics point secondary site layout, there is no transportation route between the logistics point and the logistics point not selected as a distribution center, i.e.,
(4) Distribution center service scope constraints
It is noteworthy that, in the actual operation of drone logistics, the straight-line distance often fails to accurately represent the flight path. Due to the presence of dense obstacles in urban environments, UAVs must frequently detour around obstacles. In this study, the Informed-RRT* algorithm with a spatial index structure is introduced for path planning, enabling the determination of the actual point-to-point flight distance (dij), which is subsequently utilized in a service coverage constraint assessment.
When the distance of a logistics point exceeds the service radius of a facility point, the facility point cannot provide service to that demand point, i.e.,
where dij is the real path length obtained from the planning of the Informed-RRT* algorithm with spatial index structure, rather than straight-line length, and R is taken as half of the maximum range of the UAV.
This approach allows the model to quantify the actual impact of obstacle avoidance detours on both logistics costs and service times, thereby significantly improving its practical applicability. Compared to traditional location models that rely solely on point-to-point straight-line distances, the proposed model incorporates the true flight paths, providing precise modeling of complex routes in high-density urban environments. As a result, the scientific rigor and practical relevance of facility location decisions are greatly enhanced.
(5) Distribution center service capacity constraints
A logistics point will be selected as a distribution center only when the number of demand points served by the logistics point is not less than β, i.e.,
There is a service ceiling for distribution centers, and a distribution center can serve up to a fixed number of logistics points, i.e.,
3.3. Immune Genetic Algorithm
As two typical types of bio-inspired heuristic algorithms, genetic algorithm (GA) and immune algorithm (IA) exhibit complementary characteristics in solution space optimization.
GA can effectively handle complex, multi-modal, and high-dimensional search spaces. It simulates the biological evolution mechanisms—selection, crossover, and mutation—for global search and diversity preservation, thereby reducing the risk of convergence to local optima [26]. However, GA often suffers from slow convergence and is prone to premature convergence due to the decline of population diversity.
IA emulates the antigen–antibody recognition process of the immune system. It uses a memory bank to retain historically high-quality solutions and applies antibody concentration control to inhibit population aggregation. These strategies enhance the solution space exploration efficiency, particularly for local search tasks [27]. However, the high computational complexity of IA restricts its scalability in large-scale applications.
To address these limitations, this study proposes an immune genetic algorithm (IA-GA) that integrates the core mechanisms of GA and IA to achieve complementary effects. The algorithm retains GA’s evolutionary operators (crossover and mutation) to maintain global search capabilities, and introduces IA’s clonal selection and hypermutation mechanisms to accelerate local convergence.
Operationally, both GA and IA select high-fitness individuals to progress to the next generation. To further increase the probability of high-fitness individuals advancing, IA-GA employs a diversity dynamic regulation strategy, which consists of a memory bank elite retention mechanism and an antibody concentration feedback control mechanism. These strategies enable IA-GA to balance the entry of high-quality solutions into genetic operations and enable the maintenance of population diversity.
The memory bank elite retention strategy is based on an immune memory bank which stores historical Pareto-optimal solutions. This prevents random operations from losing good genes, enhancing convergence stability. The antibody concentration feedback control calculates the antibody similarity based on Equation (11), where
is the local density value of the antibody
;
is the distance radius that defines the neighborhood range and determines which antibodies are considered “close” to
; N is the total number of the antibody population; and
is the indicator function to determine whether antibody
is within the neighborhood of
.
Equation (11) dynamically adjusts the selection pressure to inhibit the aggregation of the population and maintain the diversity. In addition, IA-GA adopts a periodic memory reset strategy. This strategy updates the strategy after every specified number of iterations, balances the conflict between historical experience inheritance and new region exploration, and avoids the trap of local attraction domains.
Through these mechanisms, IA-GA guides the population to rapidly converge toward high-quality solution regions while suppressing excessive aggregation within the population. This enhances exploration capability and achieves a dynamic balance between exploration and exploitation, providing an efficient solution for the optimization model.
In addition, while retaining the aforementioned core mechanisms, the algorithm operations have been specifically modified to address the constraint that the same point cannot be selected more than once as a distribution center in the facility location problem. The proposed IA-GA employs both swap mutation and insertion mutation operations, with mutation probability adaptively decreasing as the number of iterations increases. In swap mutation, two genes are randomly selected and their distribution center assignments are exchanged. In insertion mutation, the insertion of a new gene is accompanied by an automatic adjustment of the order of subsequent genes. Both operations inherently prevent the duplication of distribution center selections at the mutation stage. Furthermore, to balance the retention of globally optimal solutions with the risk of population dominance by highly similar individuals, an elite retention strategy incorporating a similarity threshold is implemented in the memory bank. When the similarity between a candidate individual and any existing individual in the memory bank exceeds the threshold, the candidate is excluded. This ensures that the memory bank maintains elite individuals from diverse regions of the solution space.
4. Experimental Results
4.1. Data and Simulation Environment Setup
Shenzhen is one of China’s first low-altitude flight pilot cities, featuring dense urban structures and developing low-altitude airspace logistics industry chains. The city combines demand for express delivery on a mega-city scale with enterprise test UAV routes (Meituan, Shunfeng, etc.). Thus, to fit in with the background of the study of logistics UAVs in urban areas, this study selects a typical urban area of Shenzhen as the experimental scenario. The scenario includes a certain number of sites with express delivery and receipt needs and functions and has the conditions needed for the construction of UAV distribution centers. The area features densely packed buildings of varying heights. This configuration represents typical urban logistics environments and thus can effectively simulate building–UAV collision risks during delivery. The distribution of buildings is shown in Figure 4, and the information on logistics points is shown in Table 2, in which the information in the demand column comes from the results of the questionnaire survey. We set the demand for UAV delivery at each logistics point in proportion to the research data on the demand volume of each express delivery point.
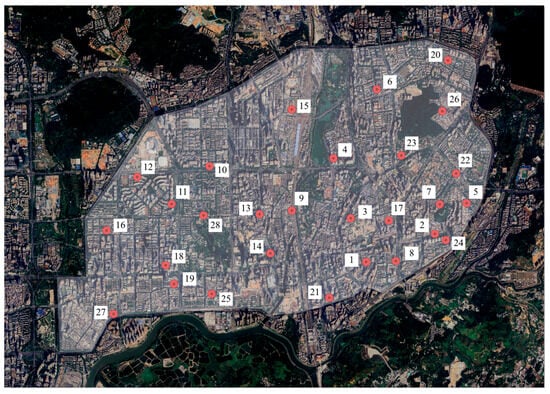
Figure 4.
Satellite map of the experimental scene.

Table 2.
Logistics point information.
In this study, buildings in the simulation are considered as static risks. To simplify the model, dynamic obstacles and meteorological factors are ignored. It should be noted that, in practical applications, factors such as environmental impacts, regulatory restrictions, and drone collisions are unavoidable. However, to isolate the effect of using real path distance instead of straight-line distance on UAV distribution center site selection, these factors were simplified in our model. Therefore, the applicability of our model in real-world scenarios remains limited, and careful consideration is needed when applying it.
This experiment is carried out on the Windows 10 system, with the following processor information: Intel(R)Core(TM)i7-10700 CPU @ 2.90GHz 2.90 GHz. The simulation experiment is performed through Python version 3.9.13, and the software development environment is Anaconda 3.
4.2. Analysis of UAV Path Planning Results Based on Informed-RRT* Algorithm with Spatial Index Structure
This paper selects Informed-RRT* as the basic framework for algorithm improvement. To justify this choice, we compare three algorithms’ performances in the same scene (RRT, RRT*, and Informed-RRT*).
The test uses randomly placed rectangular obstacles to simulate distributions of urban buildings and carries out path planning evaluation. Figure 5a–c show the path planning results of the RRT algorithm, the RRT* algorithm, and Informed-RRT* algorithm in turn, and the specific path iteration information is shown in Table 3.

Figure 5.
(a) Planning results of RRT algorithm. (b) Planning results of RRT* algorithm. (c) Planning results of Informed-RRT* algorithm.

Table 3.
Comparison of path information between RRT-class algorithms.
From the experimental results, the Informed-RRT* algorithm has the highest probability of obtaining the globally optimal solution. This benefits from its asymptotic optimization mechanism. Although its computation time exceeds the RRT and RRT* algorithms, this consumption of time cost is acceptable. In actual large-scale scenarios, logistics scheduling scenarios often require optimal solutions, which justify longer computation times. Optimal paths reduce transportation cost and safety risk in the process of practical application, thus fitting real-world applications.
Traditional RRT and RRT* algorithm variants perform blind searches. The Informed-RRT* algorithm limits the sampling space theoretically and enables near-optimal solutions efficiently. Thus, it fits the real-world scenario where the goal of path planning is to acquire a globally optimal solution within an acceptable time. Furthermore, its effectiveness relies on probabilistic completeness theory rather than a specific scenario scale, thus possessing asymptotic optimality in all scale scenarios. Therefore, in this section, the Informed-RRT* algorithm is selected as the basis for algorithm improvement. The enhanced Informed-RRT* algorithm maintains solution quality. The spatial index structure is introduced to address the long iterations problem, enhancing search efficiency. The experimental comparisons of the improved algorithms in real scenarios are as follows:
From the literature [44], small UAVs operating at 50 m above the urban ground for 15 s produce a noise sound level of 66.2 dBA on the ground. A study [45] shows that long-term exposure to 65 dBA traffic noise reduces cognitive function, especially in attention and memory, and this effect is especially significant for patients with mental illness. To reduce noise impacts on residents, we set a 50 m minimum flight height, and only obstacles with heights greater than 50 m were considered in path planning.
To verify the effectiveness of the improved algorithm, this study selects a typical urban scene in Shenzhen to compare the performance of the Informed-RRT* and the Informed-RRT* with spatial index structure (we simply call it enhanced Informed-RRT* in the figure caption). Figure 6 shows a comparison of the two algorithms in the same scene between the same pair of logistics points with the path planning effect. Figure 6a–d show the path planning result at 60 s, 120 s, 180 s, and 240 s in turn, and a specific iteration information comparison is shown in Table 4.
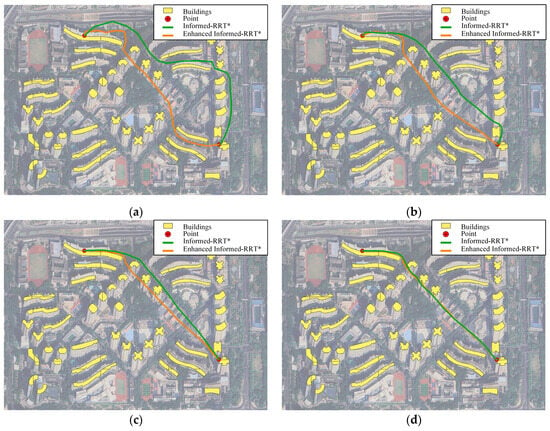
Figure 6.
(a) Comparison of algorithm planning at 60 s. (b) Comparison of algorithm planning at 120 s. (c) Comparison of algorithm planning at 180 s. (d) Comparison of algorithm planning at 240 s.

Table 4.
Comparison of path information.
The Informed-RRT* algorithm, incorporating ellipse-based sampling region restriction and dynamic search radius adjustment strategies, generates paths that approach theoretical optimality. The Informed-RRT* algorithm with the spatial index structure algorithm preserves these core mechanisms. Hence, path generation logic remains unchanged and path lengths show minimal variation. By introducing the KDTree-driven neighbor node retrieval and STRTree-assisted collision detection process, the enhanced algorithm eliminates the redundant exploration of invalid regions. This modification reduces the computational complexity of nearest neighbor search from O(N) to O(logN+K), significantly decreasing per-iteration time consumption and improving node retrieval efficiency. Consequently, the Informed-RRT* algorithm with the spatial index structure, which maintains path quality and reduces planning time, is suitable for UAV path planning in complex environments.
To validate the algorithm’s universality, this section employs straight-line distance distribution as the basis for determining the number of randomly selected samples. We statistically analyze the distribution of station pairs across different straight-line distance intervals in the current scenario, categorizing these intervals as summarized in Table 5. We randomly draw samples from each interval and compare path planning results between the Informed-RRT* algorithm and its enhancement. Specific sample numbers in each interval are guided by the distance distribution results. The detailed configuration and comparative metrics are systematically presented in Table 6. We use ➀ instead of Informed-RRT* and ➁ instead of Informed-RRT* containing spatial index structures, providing a quantitative evaluation of both algorithms’ performances.

Table 5.
Distribution of linear distance values.

Table 6.
Comparison of multi-route path planning information.
To assess the numerical differences between the two algorithms under the same scenario across various metrics, we first perform a normal distribution test based on Formula (12) [46].
where ai is the standard normal distribution calculation weight coefficient, xi is the sample value, n is the sample size, and
is the sample mean.
The p-values for path length and planning time are 0.00016 and 0.02502, respectively, both less than 0.05, indicating that the data does not meet the assumption of normality. Given that the total experimental sample size is 10, the analysis objective is to examine metric changes within the same group of samples, and the data does not follow a normal distribution, we select the Wilcoxon signed-rank test for paired sample analysis and use the bootstrap method to estimate the median confidence interval [47,48].
According to the calculation results, the path length metric test T-value is 0, the p-value is 0.00195, the median metric difference is 7.08, and the 95% confidence interval is [1.59, 20.32]; the planning time metric test T-value is 0, the p-value is 0.00195, the median metric difference is 42.34, and the 95% confidence interval is [27.23, 58.26]. Since the confidence intervals for both metrics are entirely greater than 0, in a statistically significant sense, we conclude that the Informed-RRT* algorithm with spatial indexing structures is superior to or at least not inferior to the pre-improved version in terms of path length and planning time.
Given that the present algorithmic improvement focuses on optimizing planning time, a detailed analysis of planning time data is conducted. Across ten experimental groups, the mean planning time of the Informed-RRT* algorithm is 602.33 s, with a standard deviation of 411.77 s and a variance of 169,551.98 s2, while the Informed-RRT* algorithm incorporating spatial index structure achieves a mean planning time of 528.56 s, a standard deviation of 359.05 s, and a variance of 128,916.31 s2. All three metrics—mean, standard deviation, and variance—are lower with the improved algorithm. Overall, this indicates a clear enhancement in planning efficiency and reduced fluctuation in planning time, demonstrating improved stability.
From the specific numerical analysis of the experimental results, according to the comparison data in Table 6, we can see that the Informed-RRT* algorithm with spatial index structure significantly improves the planning time. It reduces the planning time by 13.56% on average and keeps the path quality at the same time. In this section, we use multiple sets of experiments to exclude the random interference of the results of a single experiment. Results show that the introduction of spatial indexing structure does not destroy the asymptotic optimality of the Informed-RRT* algorithm. It decreases the computational complexity of a single iteration and thus improves the efficiency of the retrieval of neighboring nodes and collision detection.
In addition, to separately analyze the effects of KDTree and STRTree on Informed-RRT*, we designed an ablation study comparing the planning time of the original Informed-RRT* algorithm, the Informed-RRT* algorithm with KDTree, the Informed-RRT* algorithm with STRTree, and the Informed-RRT* algorithm incorporating both KDTree and STRTree under identical experimental scenarios. Here, we used the ten experimental scenarios from Table 6 for comparison. The detailed results are shown in Table 7, where I, II, III, and Ⅳ correspond to the original Informed-RRT* algorithm, the Informed-RRT* algorithm with KDTree, the Informed-RRT* algorithm with STRTree, and the Informed-RRT* algorithm incorporating both KDTree and STRTree, respectively.

Table 7.
Ablation study results for planning time.
Following the same analytical procedure as above, we first conduct a normal distribution test based on Equation (12). According to the statistical analysis results, the p-values for the planning times of all four algorithms are less than 0.05, indicating that none of them follow a normal distribution. Therefore, we proceed with the Wilcoxon signed-rank test and calculate the 95% confidence intervals. As multiple pairwise comparisons are involved, the results are summarized in Table 8.

Table 8.
Results of pairwise comparisons between algorithms.
The results show that, compared to Algorithm I, Algorithms II, III, and IV all exhibit a significant reduction in planning time. Further pairwise comparisons among II, III, and IV reveal that III improves upon II, indicating that the introduction of STRTree achieves better performance improvements in our experimental setting. Furthermore, IV outperforms all individual variants, suggesting that the combined use of KDTree and STRTree yields a synergistic effect. Overall, the incorporation of both KDTree and STRTree improves the planning time of the Informed-RRT* algorithm, and their combined use leads to better outcomes than utilizing either individually.
In the strategic phase of urban low-altitude logistics UAV path planning in this study, the path planning goal is to obtain the globally optimal path without collision. Experimental data show that compared to the traditional Informed-RRT* algorithm, the Informed-RRT* algorithm with spatial index has a higher possibility of obtaining the globally optimal solution. The introduction of the spatial index structure gives the algorithm higher efficiency and accuracy, making it more suitable for complex environments. This enhanced algorithm provides reliable technical support for the site selection and path co-optimization of the distribution center of the UAV.
4.3. Immune Genetic Algorithm Solution Model Performance Validation
To evaluate the effectiveness of IA-GA, we use the model from Section 3.2 to test the algorithm. All the parameters are recorded in Table 9. We test three algorithms, GA, the genetic algorithm with the introduction of the memory bank (M-GA), and IA-GA, and compare their performance in UAV distribution center selection. The convergence curves of the three algorithms in the same experimental scenario with the distribution of fitness values are shown in Figure 7.
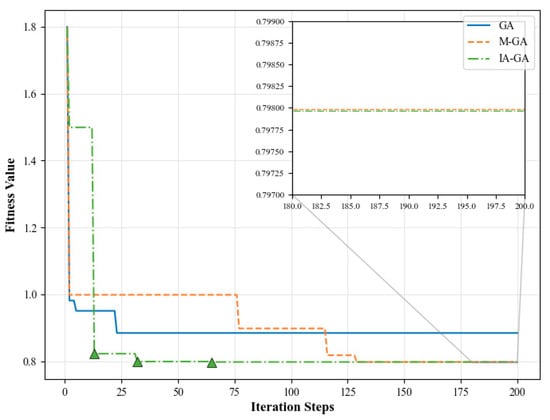
Figure 7.
Comparison of GA, M-GA, and IA-GA iteration results.

Table 9.
Experimental parameter settings.
Table 9.
Experimental parameter settings.
| Parameter | Value |
|---|---|
| Unit transportation cost c1 (CNY/km) | 8 |
| Unit storage cost c2 (CNY/piece) | 6 |
| Distribution center construction cost c3 (CNY) | 80,000 |
| Time sensitivity coefficient k | 1 |
| Customer absolute satisfaction time threshold tL (min) | 5 |
| Customer absolute dissatisfaction time threshold tB (min) | 15 |
| UAV flight speed (km/h) | 10 |
| Distribution center service radius R (km) | 10 |
| Minimum number of distribution center service logistics points β | 3 |
| Maximum number of distribution center service logistics points C | 8 |
From the numerical analysis of solution quality and convergence efficiency, although GA still maintains a faster convergence speed than M-GA and IA-GA, its solution quality is significantly lower than that of M-GA and IA-GA. Meanwhile, IA-GA shortens the convergence time by 49.23% compared to M-GA, and is able to maintain the stability of the optimal solution. From the analysis of the iteration results, the final fitness value of 0.7980 for M-GA and IA-GA is improved by 9.80% compared to the optimal fitness value of 0.8847 for GA. This indicates that the introduction of the memory bank significantly enhances the algorithm’s global optimization ability. The adaptation value of IA-GA reaches 99.84% of the globally optimal solution in the 32nd iteration, and the 66th iteration reaches the globally optimal solution. The adaptation value of M-GA reaches 99.88% of the globally optimal solution in the 130th generation, and the 139th iteration reaches the globally optimal solution. This result proves that the antibody concentration feedback control strategy significantly improves the efficiency of the algorithm search.
The above results show that IA-GA effectively solves the multi-constraint, non-linear combinatorial optimization problem in the UAV distribution center selection model by integrating the memory bank mechanism and the immune optimization strategy and provides algorithmic support with a great probability of obtaining the globally optimal solution together with relatively high efficiency for the UAV distribution center layout.
Due to the direct impact of objective function weights on experimental outcomes, we conducted controlled experiments to analyze how parameter variations specifically affect the objective function values. The experiments emphasized the impact of economic costs in site selection and layout, while also considering customer satisfaction factors. Therefore, we restricted the weight of the total transportation cost objective to the range [0.5, 1) and selected five groups of tests within this interval for comparative analysis. Figure 8 illustrates the trend of the objective function values as the objective weight changed.
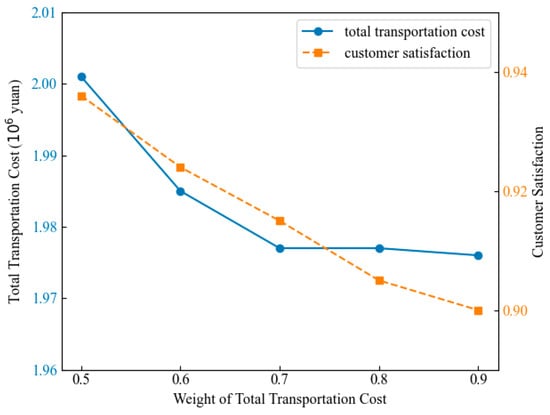
Figure 8.
Change curve of objective function values with weights.
Furthermore, since the model involved multi-objective optimization, we selected the NSGA-II algorithm—an improved genetic algorithm (GA) widely used for such tasks—for comparison. As a classical multi-objective optimization algorithm, NSGA-II can automatically search for the optimal Pareto set without requiring weight settings [49]. We used both NSGA-II and IA-GA to solve the same model, each running 30 times to find the optimal solutions. The comparison is shown in Table 10.

Table 10.
Comparison of IA-GA (with different objective weights) and NSGA-II.
Table 10.
Comparison of IA-GA (with different objective weights) and NSGA-II.
| Algorithm | Weight of Total Transportation Cost | Total Transportation Cost (×106 yuan) | Customer Satisfaction |
|---|---|---|---|
| IA-GA | 0.5 | 2.001 | 0.935 |
| 0.6 | 1.985 | 0.925 | |
| 0.7 | 1.977 | 0.915 | |
| 0.8 | 1.977 | 0.905 | |
| 0.9 | 1.976 | 0.895 | |
| NSGA-II | - | 2.010 | 0.952 |
To comprehensively evaluate the experimental performance under multiple objectives, we adopted the Range Normalization and the Weighted Sum Model (WSM) to assess the experimental data across different algorithms and different objective weights of the same algorithm. This method is a well-established approach for systematic and comprehensive multi-criteria evaluation [50]. For indicators with different dimensions, normalization is first performed to map the values to the interval [0,1]. Here, since customer satisfaction is intrinsically bounded within [0,1], it requires no normalization. Total transportation cost is a cost-type indicator, so normalization is conducted according to Equation (13).
where
is the normalized value;
is the maximum value for the indicator and
is the minimum value for the indicator, respectively; and
is the original indicator value.
Subsequently, the weighted average is used to obtain the comprehensive score for the multi-indicator system. In this study, we adopt an equal weights scheme, calculated as follows:
where
is the weighted mean, and
is the quantity of the indicator.
According to the above procedure, among all sets of comprehensive indicator scores, the IA-GA achieves the optimal overall cost when the weight of total transportation costs is set to 0.7. Therefore, we ultimately selected the immune genetic algorithm to solve the model and set the weight of total transportation cost to 0.7.
4.4. Distribution Center Layout
We use the location model in Section 3.2 and set parameters according to common UAV data from SF and DJI.The geographic location and demand information of each logistics point are shown in Table 2.
According to the above experimental parameters, this section uses straight-line distance and real path distance as distribution center determination criteria for solving the location model, respectively, and visualizes the results. The layout of the UAV distribution center under the two determination criteria is shown in Figure 9a,b. The results of economic cost and customer satisfaction are compared in Table 11.
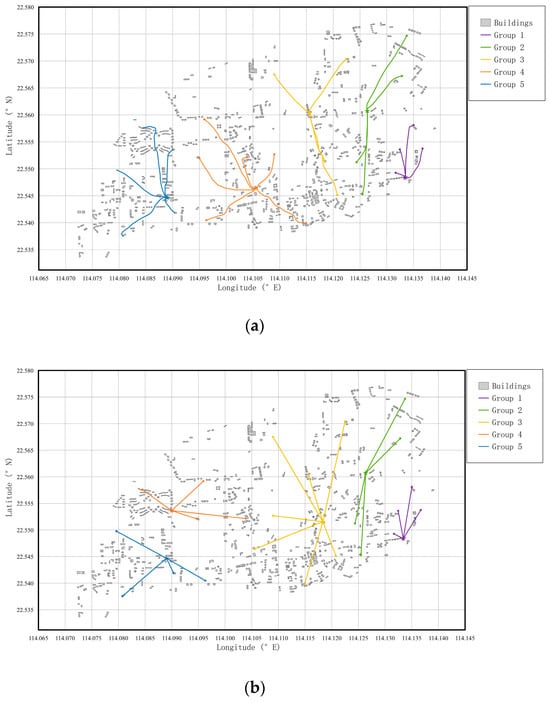
Figure 9.
(a) Schematic of UAV distribution center layout based on real path distance criterion. (b) Schematic of UAV distribution center layout based on straight-line distance criterion.

Table 11.
Comparison of objective functions.
Experimental results show significant discrepancies in UAV distribution center placement layouts when using different coverage criteria. This finding reveals the limitation of the traditional straight-line distance model, highlighting that the direct use of the straight-line distance assumption for the distribution path reduces the accuracy of the model. Using straight-line distance simplification affects the feasibility of the theoretical research and further affects the practical application. It is particularly critical in aerospace logistics systems which require precise spatial coordination between unmanned aerial vehicles and ground infrastructure.
Analyzing the target values, the economic cost of the real path model increases by 4.58% and customer satisfaction decreases by 0.18% compared to the linear model. The core difference in the change in target values comes from the structural increase in transportation costs. Comparative analysis of true path distances versus straight-line distances for inter-station route planning reveals that 95.24% of station pairs require bypass flights to avoid obstacles. The real path distance for these site pairs exceeds their straight-line distance by an average of 4.28%, with maximum deviations reaching 18.37%. The growth of the distribution path length directly leads to the linear increase in energy consumption and the extension of the distribution time; therefore, there exists a decrease in target value. Although the objective function shows a weakening of the optimization effect, the nature of this result reveals the limitations of the traditional straight-line distance model. It highlights the irreplaceability of real path planning in the complex urban airspace. This methodology improves the degree of conformity between the model establishment of the site selection layout of the UAV distribution center, avoiding the decision-making trap of “theoretically optimal but practically infeasible” at the strategic stage.
5. Conclusions and Future Work
This study addresses the optimization of urban UAV distribution center layout and introduces a novel decision-making framework based on real path distance. Compared to the traditional straight-line coverage criterion, utilizing real path distances more accurately captures the constraints that urban obstacles impose on UAV operations. The main contributions are summarized as follows:
(1) UAV Distribution Center Location Model Based on Real Path Distance
We propose a model that uses real path distances as the coverage criterion, quantitatively capturing the impact of urban obstacles on UAV obstacle avoidance behaviors. Moreover, the effectiveness of the proposed model is validated through experiments. In future research, further refinement of the model construction is required, incorporating factors such as demand volatility and unexpected disruptions (e.g., regional congestion and node failures) to enhance the model’s practical applicability.
(2) Dual-Algorithm-Driven Optimization Framework
We adopt a dual-algorithm-driven optimization framework that integrates the Informed-RRT* algorithm with spatial index structure and the immune genetic algorithm (IA-GA). The former improves path planning speed while maintaining a high probability of obtaining the global optimum; the latter overcomes the premature convergence problem of traditional genetic algorithms and enhances global search capability. This system enables effective research on location layout optimization under guaranteed safe paths. In future research, in order to further improve the efficiency of path search, methods such as breadth-first search can be used to generate better initial paths. Then we can proceed with the subsequent iterative optimization. This method can alleviate the increase in search time caused by lengthy initial solutions and has good research prospects.
(3) Model Validation and Transferability
We validated the effectiveness and transferability of the model through simulation experiments in Shenzhen, accurately quantifying changes in transportation and time costs under real path constraints, thus providing a reliable data foundation for the UAV distribution center layout. This experiment was conducted within a specific urban block. However, by adjusting relevant parameters, this model can be applied to different urban scenarios and strategies. By integrating multiple urban blocks, the network scale can be gradually expanded, thereby addressing the demand for UAV distribution center location selection in urban environments.
Compared to traditional models, our system can quantify the impact of obstacle avoidance maneuvers during actual flights on site selection results. However, since the research objective is to obtain a feasible site selection layout at the strategic level, and to quantify the impact of obstacle avoidance detours on site selection decisions, we made several simplifying assumptions, disregarding real-time factors such as weather conditions, real-time flight path adjustments, and potential conflicts. The path planning algorithms and the model itself addressed in this study are applicable at the strategic level. Future work should incorporate considerations of real-time operational factors to enhance the practical viability of these algorithms and models in real-world applications. More precisely, future work could include the following: a. Refining considerations for real-time air traffic conditions, potential human errors, UAV collisions, and temporary flight path adjustments during actual operations; b. incorporating regulatory constraints (such as no-fly zones); and c. accounting for weather factors (particularly wind conditions) and their impact on flight operations, allowing for further refinement of flight paths and site layouts to enhance the model’s alignment with real-world scenarios and to thus increase its practical feasibility.
Author Contributions
Conceptualization, L.D., N.Z., L.W., and Y.T.; methodology, L.D., N.Z., and S.H.; software, L.D., L.W., and S.H.; formal analysis, L.D.; investigation, L.D., L.W., and S.H.; writing—review and editing, L.D., N.Z., Y.T., and S.H.; visualization, L.D.; supervision, Y.T. and N.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was sponsored by the National Natural Science Foundation of China (Grant 72471115), the 2023 Excellent Postdoctoral Fellow of Jiangsu Province (grant 339414), and the NUAA Research Start-up Fund (grant 90YAT23004).
Data Availability Statement
The dataset is available on request from the authors.
Acknowledgments
We gratefully acknowledge the valuable comments and suggestions provided by the editors and reviewers.
Conflicts of Interest
This research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Statista Research Department. Global Retail E-Commerce Sales Worldwide from 2014 to 2027; Statista Research Department: Hamburg, Germany, 2024. [Google Scholar]
- UPS Smart E-Commerce Report 2021. Available online: https://rethink.industries/wpcontent/uploads/2021/04/UPS_SmartEcommerce_Report_2021.pdf (accessed on 29 March 2022).
- Peppel, M.; Ringbeck, J.; Spinler, S. How will last-mile delivery be shaped in 2040? A Delphi-based scenario study. Technol. Forecast. Soc. Change 2022, 177, 121493. [Google Scholar] [CrossRef]
- Saraceni, A.; Oleko, R.; Guan, L.; Bagaria, A.; Quintens, L. Autonomization and digitalization: Index of last mile 4.0 inclusive transition. In Proceedings of the IFIP International Conference on Advances in Production Management Systems, Nantes, France, 5–9 September 2021. [Google Scholar]
- Schmidt, S.; Saraceni, A. Consumer acceptance of drone-based technology for last mile delivery. Res. Transp. Econ. 2024, 103, 101404. [Google Scholar] [CrossRef]
- How Amazon Is building Its Drone Delivery System. Available online: https://www.aboutamazon.com/news/transportation/how-amazon-is-building-its-drone-delivery-system (accessed on 16 August 2022).
- UPS Tests Drone Package Delivery. Available online: https://insideunmannedsystems.com/ups-tests-drone-package-delivery/ (accessed on 23 February 2017).
- Hershberger, J.; Suri, S. An optimal algorithm for Euclidean shortest paths in the plane. SIAM J. Comput. 1999, 28, 2215–2256. [Google Scholar] [CrossRef]
- Wang, H. Shortest paths among obstacles in the plane revisited. In Proceedings of the 2021 ACM-SIAM Symposium on Discrete Algorithms, Philadelphia, PA, USA, 10–13 January 2021. [Google Scholar]
- Wang, H. A new algorithm for Euclidean shortest paths in the plane. J. ACM 2023, 70, 1–62. [Google Scholar] [CrossRef]
- LaValle, S. Rapidly-Exploring Random Trees: A New Tool for Path Planning; The Annual Research Report 9811; Department of Computer Science, Iowa State University: Ames, IA, USA, 1998. [Google Scholar]
- Karaman, S.; Frazzoli, E. Sampling-based algorithms for optimal motion planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Gammell, J.D.; Srinivasa, S.S.; Barfoot, T.D. Informed RRT*: Optimal sampling-based path planning focused via direct sampling of an admissible ellipsoidal heuristic. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014. [Google Scholar]
- Zhang, H.; Feng, D.; Zhang, X.; Liu, H.; Zhong, G.; Zhang, L. Research on the layout planning of urban logistics UAV landing sites. Transp. Syst. Eng. Inf. 2022, 22, 207–214. [Google Scholar]
- Elsayed, M.; Mohamed, M. The impact of airspace regulations on unmanned aerial vehicles in last-mile operation. Transp. Res. Part D 2020, 87, 7–10. [Google Scholar] [CrossRef]
- Beigi, P.; Rajabi, M.S.; Aghakhani, S. An overview of drone energy consumption factors and models. arXiv 2022, arXiv:2206.10775. [Google Scholar] [CrossRef]
- Gao, M.; Hugenholtz, C.H.; Fox, T.A.; Kucharczyk, M.; Barchyn, T.E.; Nesbit, P.R. Weather constraints on global drone flyability. Sci. Rep. 2021, 11, 12092. [Google Scholar] [CrossRef] [PubMed]
- Tan, Q.; Hou, J.; Li, Y.; Qu, R.; Zhou, P.; Hong, K.L.; Zhang, X. Exploring noise reduction strategies: Optimizing drone station placement for last-mile delivery. Transp. Res. Part D 2024, 133, 104306. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, Y.; Zhang, Y.; Qian, B. Strong Electromagnetic Interference and Protection in UAVs. Electronics 2024, 13, 393. [Google Scholar] [CrossRef]
- Mohsan, S.A.H.; Othman, N.Q.H.; Li, Y.; Mohammed, H.; Khan, A.M.A. Unmanned aerial vehicles (UAVs): Practical aspects, applications, open challenges, security issues, and future trends. Intell. Serv. Robot. 2023, 16, 109–137. [Google Scholar] [CrossRef]
- Sabino, H.; Almeida, R.V.S.; Moraes, L.B.; Silva, W.P.; Guerra, R.G.; Malcher, C.; Passos, D.; Passos, F.G.O. A systematic literature review on the main factors for public acceptance of drones. Technol. Soc. 2022, 71, 6–9. [Google Scholar] [CrossRef]
- Hakimi, S.L. Optimum locations of switching centers and the absolute centers and medians of a graph. Oper. Res. 1964, 12, 450–459. [Google Scholar] [CrossRef]
- Megiddo, N.; Zemel, E.; Hakimi, S.L. The maximum coverage location problem. SIAM J. Algebraic Discrete Methods 1983, 4, 253–261. [Google Scholar] [CrossRef]
- Nagy, G.; Salhi, S. Location-routing: Issues, models and methods. Eur. J. Oper. Res. 2007, 177, 649–672. [Google Scholar] [CrossRef]
- Klose, A.; Drexl, A. Facility location models for distribution system design. Eur. J. Oper. Res. 2005, 162, 4–29. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Castro, L.D.; Timmis, J. Artificial Immune Systems and Their Applications, 3rd ed.; Springer Science & Business Media: London, UK, 2012; pp. 57–62. [Google Scholar]
- Shavarani, S.M.; Mosallaeipour, S.; Golabi, M.; Izbirak, G. A congested capacitated multi-level fuzzy facility location problem: An efficient drone delivery system. Comput. Oper. Res. 2019, 108, 57–68. [Google Scholar] [CrossRef]
- Li, X. Research on Layout Planning and Safety Analysis of Logistics Drone Delivery Network. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, June 2020. [Google Scholar]
- Feng, D.K. Research on the Planning Method of Logistics UAV Landing Site Layout in Urban Areas. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, May 2022. [Google Scholar]
- Zhang, J.; Campbell, J.F.; Ii, D.C.S.; Hupman, A.C. Energy consumption models for delivery drones: A comparison and assessment. Transp. Res. Part D 2021, 90, 2–10. [Google Scholar] [CrossRef]
- Dukkanci, O.; Campbell, J.F.; Kara, B.Y. Facility location decisions for drone delivery with riding: A literature review. Comput. Oper. Res. 2024, 167, 26. [Google Scholar] [CrossRef]
- Chauhan, D.; Unnikrishnan, A.; Figliozzi, M. Maximum coverage capacitated facility location problem with range constrained drones. Transp. Res. Part C 2019, 99, 3–15. [Google Scholar] [CrossRef]
- Chowdhury, S.; Emelogu, A.; Marufuzzaman, M.; Nurre, S.G.; Bian, L. drones for disaster response and relief operations: A continuous approximation model. Int. J. Prod. Econ. 2017, 171–176. [Google Scholar] [CrossRef]
- Bakach, I.; Campbell, A.M.; Ehmke, J.F. A two-tier urban delivery network with robot-based deliveries. Networks 2021, 78, 461–483. [Google Scholar] [CrossRef]
- Gentili, M.; Mirchandani, P.B.; Agnetis, A.; Ghelichi, Z. Locating platforms and scheduling a fleet of drones for emergency delivery of perishable items. Comput. Ind. Eng. 2022, 168, 3–12. [Google Scholar] [CrossRef]
- Bruni, M.E.; Khodaparasti, S.; Perboli, G. Energy efficient UAV-based last-mile delivery: A tactical-operational model with shared depots and non-linear energy consumption. IEEE Access 2023, 11, 18562–18570. [Google Scholar] [CrossRef]
- Campbell, J.F.; O’Kelly, M.E. Twenty-five years of hub location research. Transp. Sci. 2012, 46, 153–169. [Google Scholar] [CrossRef]
- Ye, M.; Zhao, J.; Guan, Q.; Zhang, X. Research on eVTOL Air Route Network Planning Based on Improved A* Algorithm. Sustainability 2024, 16, 561. [Google Scholar] [CrossRef]
- Wang, J. Site-Path Study of UAV Urban Delivery Based on Two-Layer Planning. Master’s Thesis, Civil Aviation University of China, Tianjin, China, 2023. [Google Scholar]
- Hong, I.; Kuby, M.; Murray, A.T. A range-restricted recharging station coverage model for drone delivery service planning. Transp. Res. Part C 2018, 90, 200–210. [Google Scholar] [CrossRef]
- Bentley, J.L. Multidimensional binary search trees used for associative searching. Commun. ACM 1975, 18, 509–517. [Google Scholar] [CrossRef]
- Leutenegger, S.T.; Lopez, M.A.; Edgington, J. STR: A simple and efficient algorithm for R-tree packing. In Proceedings of the 13th International Conference on Data Engineering, Birmingham, UK, 7–11 April 1997. [Google Scholar]
- Torija, A.J.; Li, Z.; Self, R.H. Effects of a hovering unmanned aerial vehicle on urban soundscapes perception. Transp. Res. Part D 2020, 78, 3–12. [Google Scholar] [CrossRef]
- Hahad, O.; Kuntic, M.; Al-Kindi, S.; Kuntic, I.; Gilan, D.; Petrowski, K.; Daiber, A.; Münzel, T. Noise and mental health: Evidence, mechanisms, and consequences. J. Expo. Sci. Environ. Epidemiol. 2025, 35, 19–20. [Google Scholar] [CrossRef]
- Shaphiro, S.; Wilk, M. An analysis of variance test for normality. Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual comparisons by ranking methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
- Efron, B. Bootstrap methods: Another look at the jackknife. Ann. Stat. 1979, 7, 1–26. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Keeney, R.L.; Raiffa, H. Decisions with Multiple Objectives: Preferences and Value Trade-Offs; Cambridge University Press: London, UK, 1993; pp. 50–52. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).