Distributed Impulsive Multi-Spacecraft Approach Trajectory Optimization Based on Cooperative Game Negotiation

Abstract

A cooperative game negotiation strategy considering multiple constraints is proposed for distributed impulsive multi-spacecraft approach missions in the presence of defending spacecraft. It is a dual-stage decision-making method that includes offline trajectory planning and online distributed negotiation. In the trajectory planning stage, a relative orbital dynamics model is first established based on the Clohessy–Wiltshire (CW) equations, and the state transition equations for impulsive maneuvers are derived. Subsequently, a multi-objective optimization model is formulated based on the NSGA-II algorithm, utilizing a constraint dominance principle (CDP) to address various constraints and generate Pareto front solutions for each spacecraft. In the distributed negotiation stage, the negotiation strategy among spacecraft is modeled as a cooperative game. A potential function is constructed to further analyze the existence and global convergence of Nash equilibrium. Additionally, a simulated annealing negotiation strategy is developed to iteratively select the optimal comprehensive approach strategy from the Pareto fronts. Simulation results demonstrate that the proposed method effectively optimizes approach trajectories for multi-spacecraft under complex constraints. By leveraging inter-satellite iterative negotiation, the method converges to a Nash equilibrium. Additionally, the simulated annealing negotiation strategy enhances global search performance, avoiding entrapment in local optima. Finally, the effectiveness and robustness of the dual-stage decision-making method were further demonstrated through Monte Carlo simulations.

1. Introduction

With the rapid development of space technology, space competition has become increasingly intense, and threats to space security are on the rise. In response to the complex and changing space situation, countries around the world are competing to enhance spacecraft performance, achieving significant breakthroughs in computational capability, maneuverability, and intelligence levels. Against this backdrop, orbital games [1] have received widespread attention, with typical application scenarios including orbital pursuit–evasion [2], orbital defense [3], and orbital pursuit–defense [4]. However, a single satellite is limited by computational resources, maneuvering energy, and payload capacity, which leads to evident limitations in executing tasks in orbit. Therefore, the collaborative deployment and application of multi-aircraft motion systems have become a current research hotspot in the field of aerospace, and it is essential to develop high-performance distributed cooperative control technologies. Distributed spacecraft cooperative control methods are fundamental to tasks such as in-orbit servicing, space target surveillance, and orbital games. Given the complexity of future orbital tasks, as well as the high operational costs and limited resources of spacecraft, the trajectory planning must consider spacecraft safety while optimizing objectives like fuel consumption and time efficiency. Therefore, the flight trajectories of multi-spacecraft need to be optimized to achieve the best cooperative approach strategy.

Currently, spacecraft trajectory planning methods have been widely studied. Traditional planning methods can generally be categorized into two main types: indirect methods and direct methods. Indirect methods adopt an analytical optimization approach based on optimal control theory. They reformulate the optimal control problem as a boundary value problem (BVP) and derive the first-order necessary conditions (FONCs) for optimal trajectories using variational principles. However, as spacecraft missions grow increasingly complex, trajectory planning problems also scale in size and difficulty, with more constraints being introduced. Such complexities significantly increase the challenges of deriving and numerically solving FONCs, leading to higher computational costs. Moreover, indirect methods are highly sensitive to initial values, which limits their practical application in real-world engineering scenarios [5]. Direct methods discretize the state and control variables, transforming the continuous-time optimal control problem into a finite-dimensional nonlinear programming (NLP) problem, that can be solved using numerical optimization techniques. Compared to indirect methods, although direct methods sacrifice some accuracy, they have gained widespread attention due to their numerical robustness, efficiency, and ability to handle complex constraints. Gradient-based techniques [6] leverage numerical optimization algorithms like sequential quadratic programming (SQP) to solve trajectory planning problems, while convexification approaches [7] transform non-convex optimization problems into convex ones to improve computational efficiency. Some researchers have attempted to combine direct methods and indirect methods to leverage their complementary advantages in addressing the complex problems of spacecraft trajectory planning [8]. However, direct methods tend to converge to local optima due to their gradient-based nature, and the computational cost increases with the addition of constraints.

Heuristic methods provide innovative approaches to trajectory optimization, with representative techniques including Genetic Algorithms (GA) [9], Particle Swarm Optimization (PSO) [10], and Ant Colony Optimization (ACO) [11] demonstrating success in solving complex optimization problems. Such methods are particularly effective for solving complex nonlinear, multi-modal, non-convex, or discontinuous optimization problems, which are common in engineering scenarios. Their strong global search capabilities can effectively address the issue of sensitivity to initial conditions and demonstrate outstanding performance in engineering applications [11]. In the early stages of spacecraft trajectory planning, the focus was typically on optimizing a single objective, such as fuel consumption or flight time. In recent years, researchers have increasingly turned their interest toward multi-objective trajectory optimization problems. Solving such problems can be viewed as a process of determining the Pareto front. Advanced multi-objective optimization algorithms, such as MOPSO [12] and NSGAII [13,14,15], have already been successfully applied to single-spacecraft trajectory optimization. Such methods explore the solution space through iterative optimization. To improve the computational efficiency of trajectory planning for spacecraft, the Clohessy–Wiltshire (CW) equations are typically adopted as the foundational model [13,15,16]. This model is derived from the precise nonlinear equations of motion in the Local Vertical Local Horizontal (LVLH) coordinate system, linearized to obtain relative dynamics equations. The simplifications made during the derivation result in insufficient accuracy for modeling elliptical orbits, limiting its applicability to circular orbits and short-range approach scenarios. However, the linearization characteristics of the CW equations enables the explicit derivation of the relationship between impulsive maneuvers and terminal states, allowing the rapid evaluation of solution quality in each iteration without numerical integration. This not only enhances computational efficiency but also facilitates future engineering implementation for on-orbit applications. Therefore, this study focuses on approach decision-making methods for near-circular orbits based on the CW equations. Future work could extend the proposed trajectory planning method to the elliptical orbits by reducing the complexity of the computational solution of nonlinear dynamic equations and improving computational efficiency [17]. Additionally, intelligent methods such as imitation learning [18] and reinforcement learning [19] can be combined to achieve approach control for long-distance, high-eccentricity orbits.

When faced with more complex space missions, single-spacecraft systems encounter significant limitations due to constraints such as computational resources, maneuvering energy, and payload capacity. In contrast, multi-spacecraft systems, with the advantages of high fault tolerance, flexibility, and efficiency, have gradually become a research focus in the aerospace field. They are widely applied in tasks such as formation flying, orbital maintenance, and deep space exploration [20]. Centralized control requires a central node to gather global information and make unified decisions. However, due to the constraints of spacecraft sensing, communication, and computing capabilities, achieving efficient and reliable on-orbit decision-making is challenging. In comparison, distributed control distributes computational tasks among multiple nodes, with each node only processing information from itself and nearby nodes. This significantly reduces computational complexity, improves efficiency, and is better suited for the demands of high-dynamic, cooperative operations. In [21], the computational efficiency of spacecraft formation reconfiguration path planning using a distributed method is approximately seven times higher than that of a centralized method. This highlights that distributed control methods are a key technological trend for addressing complex tasks in future high-dynamic space environments. In recent years, numerous spacecraft swarm control methods have emerged. However, most are based on continuous maneuvering models and primarily target tasks such as formation maintenance and orbital adjustments. Common methods include leader–follower control [22], artificial potential fields [23], and swarm control [24]. However, these methods often fail to meet the demands of long-distance maneuvering and rapid approach to targets under an impulsive maneuvering mode. To achieve coordinated target approach for multi-spacecraft, there is an urgent need to develop a cooperative path-planning method suitable for the impulsive maneuvering mode.

Distributed negotiation strategies are often used to achieve task balancing in the multi-spacecraft system. In [25], a networked game model based on a game-theoretic negotiation mechanism is proposed. Through cooperation with neighbors, individual actions are updated iteratively to reach a Nash equilibrium. Similarly, in [26], the self-organizing task allocation problem in multi-spacecraft systems was modeled as a potential game, and a distributed task allocation algorithm based on game learning was proposed. Inspired by this, the study attempted to use a distributed negotiation method to determine the cooperative approach strategy. However, due to information asymmetry among spacecraft in distributed conditions, decentralized computational methods struggle to plan approach paths from a global perspective, which means global optimality cannot be guaranteed. To address this, this paper studies cooperative approach strategies in multi-spacecraft systems under distributed conditions. Facing challenges such as complex constraints, opponent interception, information asymmetry, and the tendency to fall into local optima, a cooperative game negotiation strategy combining offline trajectory planning and online distributed negotiation is proposed. The main contributions are as follows:

• A multi-objective optimization model considering multiple constraints is established, and a constraint-handling mechanism based on the constraint dominance principle (CDP) is introduced. By combining the NSGAII method, the NSGAII-CDP algorithm is designed to efficiently generate the Pareto front, thereby obtaining a set of approach paths that meet the constraint.
• The negotiation strategy among multi-spacecraft is modeled as a cooperative game, with defined players, strategy space, and local reward functions. Based on this, the existence and convergence of the Nash equilibrium under distributed conditions are theoretically analyzed and verified by constructing an exact potential function.
• A distributed negotiation strategy based on simulated annealing is proposed, effectively overcoming the problem of negotiation strategies tending to fall into local optima and improving global optimization performance.

The remaining sections of this paper are organized as follows. Section 2 describes the multi-spacecraft coordinated approach problem and the relative dynamics model. Section 3 presents the multi-objective optimization algorithm, including the optimization variables, objective functions, constraints, mathematical model and the design of NSGAII-CPD. In Section 4, the distributed negotiation strategy based on simulated annealing is presented, and the existence and convergence of the Nash equilibrium are discussed. Section 5 demonstrates the effectiveness and superiority of the proposed method through numerical simulations. Finally, Section 6 draws the conclusions of this paper.

2. Multi-Spacecraft Coordinated Approach

2.1. Problem Description

In the scenario of a multi-spacecraft approach, pursuers are required to evade the defenders while approaching the target to accomplish a coordinated approach task. Due to constraints such as fuel consumption and mission requirements, it is assumed that the target cannot autonomously evade potential threats.

To accomplish the cooperative approach task for the pursuers, a cooperative game negotiation strategy is proposed, which is a dual-stage decision-making method that includes offline trajectory planning and online distributed negotiation. Figure 1 illustrates the cooperative game negotiation strategy.

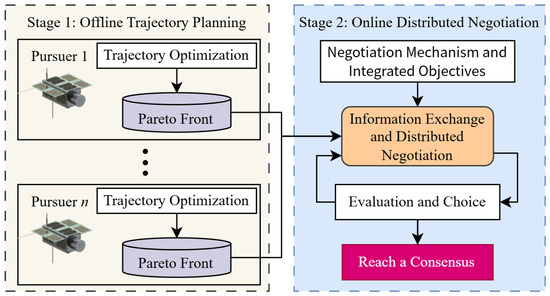
Figure 1. Illustration of cooperative game negotiation strategy.

Stage 1: Use a multi-objective optimization algorithm to solve the pursuers’ approach trajectory planning under complex and multi-constrained conditions. Multiple objectives, such as flight time, fuel consumption, and terminal distance, are comprehensively considered to generate a Pareto front that represents a set of feasible approach paths.

Stage 2: A distributed negotiation strategy is proposed by establishing a decentralized communication and decision-making mechanism among the pursuers. By taking the total mission cost into account, the globally optimal collaborative approach strategy is determined through information exchange and distributed negotiation.

2.2. Relative Dynamics Model

To describe the motion of the pursuers $\mathrm{P}$ and the defenders $\mathrm{D}$ relative to the target $\mathrm{T}$, an LVLH coordinate system is established at the center of the target, as shown in Figure 2. The origin o is located at the center of mass of the target. The x-axis extends from the Earth’s center to the target’s barycenter, the y-axis is perpendicular to the x-axis within the orbital plane, oriented positively towards the direction of flight, and the z-axis aligns with the normal of the target’s orbital plane. Additionally, the Earth-Centered Inertial (ECI) coordinate system is defined with its origin O at the Earth’s mass center.

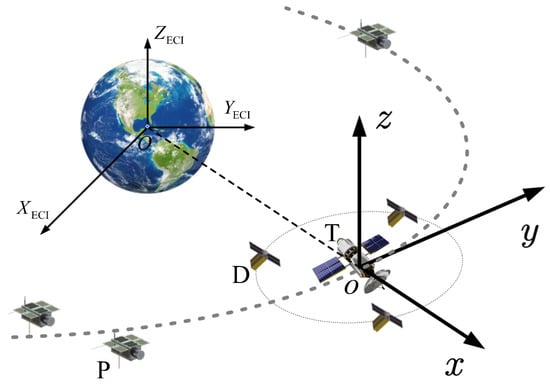
Figure 2. Orbital coordinate system.

Under the assumption of a near-circular orbit and neglecting perturbations, relative motion can be expressed using the CW equations:

$$\left\{\begin{array}{c}\ddot{x}-2\omega \dot{y}-3{\omega }^{2}x=u_x\hfill \\ \ddot{y}+2\omega \dot{x}=u_y\hfill \\ \ddot{z}+{\omega }^{2}z=u_z\hfill \end{array}\right.$$

(1)

where $\omega$ refers to the orbital angular velocity of the target, $\mathit{r}={[x,y,z]}^{\mathrm{T}}$ stands for the relative position components, and $\mathit{u}={[u_x,u_y,u_z]}^{\mathrm{T}}$ represents the three-axis thrust acceleration.

Assuming the spacecraft performs no orbit maneuvers ($\mathit{u}={[0,0,0]}^{\mathrm{T}}$), the relative state $\mathit{x}={[x,y,z,\dot{x},\dot{y},\dot{z}]}^{\mathrm{T}}$ can be determined using the state transition matrix as follows:

$$\mathit{x}\left(t\right)=\Phi \left(t,t_0\right){\mathit{x}}_0$$

(2)

Here, ${\mathit{x}}_0={[x_0,y_0,z_0,{\dot{x}}_0,{\dot{y}}_0,{\dot{z}}_0]}^{\mathrm{T}}$ is the initial relative state, and $\Phi \left(t,t_0\right)$ is the state transition matrix:

$$\Phi \left(t,t_0\right)=\left[\begin{array}{cc}{\Phi }_{rr}& {\Phi }_{rv}\\ {\Phi }_{vr}& {\Phi }_{vv}\end{array}\right].$$

(3)

And the specific expressions of the sub-matrices are expressed as follows:

$${\Phi }_{rr}=\left[\begin{array}{ccc}4-3cos\left(\omega t\right)& 0& 0\\ 6\left(sin\left(\omega t\right)-\omega t\right)& 1& 0\\ 0& 0& cos\left(\omega t\right)\end{array}\right]$$

(4)

$${\Phi }_{rv}=\left[\begin{array}{ccc}{\displaystyle \frac{sin\left(\omega t\right)}{\omega }}& {\displaystyle \frac{2\left(1-cos\left(\omega t\right)\right)}{\omega }}& 0\\ {\displaystyle \frac{2\left(cos\left(\omega t\right)-1\right)}{\omega }}& {\displaystyle \frac{4sin\left(\omega t\right)-3\omega t}{\omega }}& 0\\ 0& 0& {\displaystyle \frac{sin\left(\omega t\right)}{\omega }}\end{array}\right]$$

(5)

$${\Phi }_{vr}=\left[\begin{array}{ccc}3\omega sin\left(\omega t\right)& 0& 0\\ 6\omega \left(cos\left(\omega t\right)-1\right)& 0& 0\\ 0& 0& -\omega sin\left(\omega t\right)\end{array}\right]$$

(6)

$${\Phi }_{vv}=\left[\begin{array}{ccc}cos\left(\omega t\right)& 2sin\left(\omega t\right)& 0\\ -2sin\left(\omega t\right)& 4cos\left(\omega t\right)-3& 0\\ 0& 0& cos\left(\omega t\right)\end{array}\right].$$

(7)

When the spacecraft performs n orbital maneuvers at times $t_1,t_2,\dots ,t_n$, with control vectors ${\mathit{u}}_1,{\mathit{u}}_2,\dots ,{\mathit{u}}_n$, the propagation equation of the relative state $\mathit{x}$ is given as

$$\mathit{x}\left(t\right)=\Phi (t,t_0){\mathit{x}}_0+\sum _{k=1}^n\Phi (t,t_k)\left[\begin{array}{c}{\mathbf{0}}_{3\times 1}\hfill \\ {\mathit{u}}_k\hfill \end{array}\right],k=1,\dots ,n.$$

(8)

The final relative state after a series of orbital maneuvers can be determined from (8).

3. Multi-Objective Optimization

This section takes the ith pursuer ${\mathrm{P}}_i$ as an example to illustrate the design and application of the multi-objective optimization algorithm. The optimization variables consist of the time intervals ${\{\Delta t_k\}}_{k=1}^n$ between consecutive impulses and the velocity increments ${\left\{{\mathit{u}}_k\right\}}_{k=1}^n$ associated with each impulse.

To facilitate the constraint on the maximum velocity increment for each impulse, the kth velocity increment vector is transformed into spherical coordinates ${\mathit{v}}_k=[\Delta v_k,{\theta }_k,{\phi }_k]$, where $\Delta v_k$ denotes the magnitude of the velocity increment, ${\theta }_k\in [-\pi /2,\pi /2]$ is the angle between the velocity vector and the x-y plane, and ${\phi }_k\in [-\pi ,\pi ]$ is the angle between the projection of the velocity vector onto the x-y plane and the x-axis. Therefore, ${\mathit{u}}_k$ is defined as

$${\mathit{u}}_k=[\Delta v_k\cos {\theta }_k\cos {\phi }_k,\Delta v_k\cos {\theta }_k\sin {\phi }_k,\Delta v_k\sin {\theta }_k].$$

(9)

Define ${\mathit{u}}_k^{\mathrm{ECI}}$ as the velocity increment corresponding to the transformation of ${\mathit{u}}_k$ into the Earth-Centered Inertial (ECI) coordinate system. The optimization variables can be represented as a set of parameters ${\mathit{F}}_k=[\Delta t_k,\Delta v_k,{\theta }_k,{\phi }_k],k=1,\dots ,n$, and the total number of optimization variables is $4n$.

3.1. Objective Functions

Considering the timeliness of space game tasks, it is required that pursuers complete the approach task within a relatively short period. Furthermore, the total fuel consumption during the mission and the successful completion of the approach task are also crucial. Therefore, three optimization objectives are defined as follows:

• The total flight time:

  $$\begin{array}{c}\hfill J_1=\sum _{k=1}^n\Delta t_k.\end{array}$$

  (10)
• The total fuel consumption:

  $$\begin{array}{c}\hfill J_2=\sum _{k=1}^n\Delta v_k.\end{array}$$

  (11)
• The terminal distance:

  $$\begin{array}{c}\hfill J_3=d_{{\mathrm{P}}_i-\mathrm{T}}\left(t_f\right)\end{array}$$

  (12)

  where $d_{{\mathrm{P}}_i-\mathrm{T}}$ denotes the distance between pursuer ${\mathrm{P}}_i$ and target $\mathrm{T}$. The parameter $t_f$ specifies the terminal moment of the mission.

3.2. Constraints

Firstly, the relative dynamics constraint between the pursuer and the target must be satisfied and is expressed as follows:

$${\mathit{x}}_k-\Phi (t_k,t_{k-1}){\mathit{x}}_{k-1}-\left[\begin{array}{c}{\mathbf{0}}_{3\times 1}\hfill \\ {\mathit{u}}_k\hfill \end{array}\right]={\mathbf{0}}_{6\times 1},k=1,\dots ,n.$$

(13)

The initial relative state conditions should satisfy the following constraints:

$$\mathit{x}\left(t_0\right)={\mathit{x}}_0.$$

(14)

The maneuvering time should satisfy the following constraints:

$$\left\{\begin{array}{c}{t}_k={\displaystyle \sum _{i=1}^k}\Delta t_i\hfill \\ \Delta t_{min}\le \Delta t_k\le \Delta t_{max}\hfill \\ t_n=t_f\le t_{max}\hfill \end{array}\right.,k=1,\dots ,n$$

(15)

where $t_k$ represents the maneuvering moment of the kth impulse. $\Delta t_{\min }$ defines the minimum time interval either between two impulses or between the moment of the first impulse and the initial time. This ensures that the pursuer has sufficient time for iterative optimization or attitude adjustments before executing a maneuvering decision. $\Delta t_{\max }$ represents the maximum time interval, while $t_{\max }$ denotes the maximum total mission time.

Due to the limitation of the thruster capacity, the velocity increment of a single-impulse maneuver operation and the total velocity increment should satisfy the following constraints:

$$\left\{\begin{array}{c}\Delta v_k\le \Delta v_{max}\hfill \\ {\displaystyle \sum _{k=1}^n}\Delta v_k\le u_{\mathrm{total}}\hfill \end{array}\right.,k=1,\dots ,n$$

(16)

where $\Delta v_{max}$ represents the maximum velocity increment of a single-impulse maneuver operation, and $u_{\mathrm{total}}$ stands for the maximum total velocity increment available from the thruster.

In addition, to ensure that the pursuer avoids interception, the following passive safety constraints must be satisfied:

$$d_{{\mathrm{P}}_i-{\mathrm{D}}_j}>r_{\mathrm{safe}},j=1,\dots ,M$$

(17)

where $d_{{\mathrm{P}}_i-{\mathrm{D}}_j}$ denotes the distance between pursuer ${\mathrm{P}}_i$ and defender ${\mathrm{D}}_j$, and $r_{\mathrm{safe}}$ represents the safe distance. Furthermore, M is the number of defenders.

Finally, to achieve the final approach operation, corresponding terminal constraints are established, which mainly include constraints on the terminal distance and terminal relative velocity.

The terminal distance constraint requires that, at the final moment, the distance between the pursuer and the target must be less than the specified distance $r_{\mathrm{final}}$ to accomplish the approach operation:

$$d_{{\mathrm{P}}_i-\mathrm{T}}\left(t_f\right)<r_{\mathrm{final}}.$$

(18)

The terminal relative velocity constraint requires that, at the final moment, the relative velocity between the pursuer and the target must be less than the relative velocity $\Delta v_{\mathrm{final}}$:

$$\Delta v_{{\mathrm{P}}_i-\mathrm{T}}\left(t_f\right)<\Delta v_{\mathrm{final}}$$

(19)

where $\Delta v_{{\mathrm{P}}_i-\mathrm{T}}$ denotes the relative velocity between pursuer ${\mathrm{P}}_i$ and target $\mathrm{T}$.

3.3. Mathematical Model

The mathematical model of the multi-objective optimization problem (MOOP) studied in this study can be expressed as follows:

$$\begin{array}{c}minJ\left(\mathit{F}\right)=min[J_1,J_2,J_3]\hfill \\ s.t.\hfill \\ \left\{\begin{array}{c}{\mathit{x}}_k-\Phi (t_k,t_{k-1}){\mathit{x}}_{k-1}-\left[\begin{array}{c}{\mathbf{0}}_{3\times 1}\hfill \\ {\mathit{u}}_k\hfill \end{array}\right]={\mathbf{0}}_{6\times 1}\hfill \\ \mathit{x}\left(t_0\right)={\mathit{x}}_0\hfill \\ t_k={\displaystyle \sum _{i=1}^k}\Delta t_i\hfill \\ \Delta t_{min}\le \Delta t_k\le \Delta t_{max}\hfill \\ t_n=t_f\le t_{max},k=1\dots n\hfill \\ \Delta v_k\le \Delta v_{max}\hfill \\ {\displaystyle \sum _{k=1}^n}\Delta v_k\le u_{total}\hfill \\ d_{{\mathrm{P}}_i-{\mathrm{D}}_j}>r_{\mathrm{safe}},j=1,\dots ,M\hfill \\ d_{{\mathrm{P}}_i-\mathrm{T}}\left(t_f\right)<r_{\mathrm{final}}\hfill \\ \Delta v_{{\mathrm{P}}_i-\mathrm{T}}\left(t_f\right)<\Delta v_{\mathrm{final}}\hfill \end{array}\right.\hfill \end{array}$$

(20)

where

$$\left\{\begin{array}{c}{J}_1={\displaystyle \sum _{k=1}^n}\Delta t_k\hfill \\ J_2={\displaystyle \sum _{k=1}^n}\Delta v_k\hfill \\ J_3=d_{{\mathrm{P}}_i-T}\left(t_f\right).\hfill \end{array}\right.$$

(21)

The MOOP described by (20) and (21) can be formulated as a problem of finding the Pareto optimal solutions. Multi-objective optimization algorithms can be used to obtain the Pareto optimal front.

3.4. NSGAII-CDP

NSGAII is an improved multi-objective evolutionary algorithm (MOEA) based on NSGA [27]. Based on NSGAII, Simulated Binary Crossover (SBX) and Polynomial Mutation are applied to continuous variables, eliminating the need for additional encoding or decoding steps and improving the efficiency and adaptability of the algorithm. Specifically, given two parent individuals $f^1$ and $f^2$, two offspring individuals $c^1$ and $c^2$ are generated using the SBX operator:

$$\begin{array}{c}{c}^1=0.5\times [(1+\beta )f^1+(1-\beta )f^2]\hfill \\ c^2=0.5\times [(1-\beta )f^1+(1+\beta )f^1]\hfill \end{array}$$

(22)

$$\beta =\left\{\begin{array}{cc}{(Rand\times 2)}^{1/(1+{\eta }_c)}\hfill & Rand\le 0.5\\ {(1/(2-Rand\times 2\left)\right)}^{1/(1+{\eta }_c)}\hfill & Rand>0.5\end{array}\right.$$

(23)

where $Rand$ is a random variable uniformly distributed between 0 and 1, denoted as $Rand\sim \mathcal{U}(0,1)$. $\beta$ is dynamically and randomly determined by the distribution factor ${\eta }_c$ according to (23).

Individual f undergoes polynomial mutation and transforms into

$$f^{\prime }=f+\delta (f_u-f_l)$$

(24)

$$\delta =\left\{\begin{array}{cc}{(2\times Rand)}^{1/(1+{\eta }_p)}-1\hfill & Rand\le 0.5\\ 1-{\left(2\right(1-Rand\left)\right)}^{1/(1+{\eta }_p)}\hfill & Rand>0.5\end{array}\right.$$

(25)

where $f_u$ and $f_l$ denote the variable’s upper and lower bounds. $\delta$ is dynamically and randomly determined by the distribution factor ${\eta }_p$ according to (25).

Furthermore, for constraint handling, common techniques include the CDP, adaptive penalty methods, and adaptive trade-off models. Among these, CDP performs the best [28]. Therefore, this paper adopts CDP to handle multiple constraints, including the following three basic rules [29]:

• Any feasible solution is preferred to any infeasible solution.
• Among two feasible solutions, the one with a better objective function value is preferred.
• Among two infeasible solutions, the one with a smaller constraint violation is preferred.

For this purpose, an error operator e is introduced to calculate the overall degree of constraint violation independently of the objective function. e is defined as follows:

$$\left\{\begin{array}{c}{e}_1=max((J_1-t_{\max })/3600,0)\hfill \\ e_2=max(J_2-u_{\mathrm{total}},0)\hfill \\ e_3=max((J_3-r_{\mathrm{final}})/1000,0)\hfill \\ e_4=max(\Delta v_{{\mathrm{P}}_i-\mathrm{T}}\left(t_f\right)-\Delta v_{\mathrm{final}},0)\hfill \end{array}\right.$$

(26)

$$e=e_1+e_2+e_3+e_4.$$

(27)

During population sorting, solutions are first divided into feasible and infeasible based on whether e equals zero. Feasible solutions are sorted using the non-dominated sorting method, while infeasible solutions are ordered in ascending degree of constraint violation and positioned after the feasible ones. The flowchart of NSGAII-CDP is shown in Figure 3.

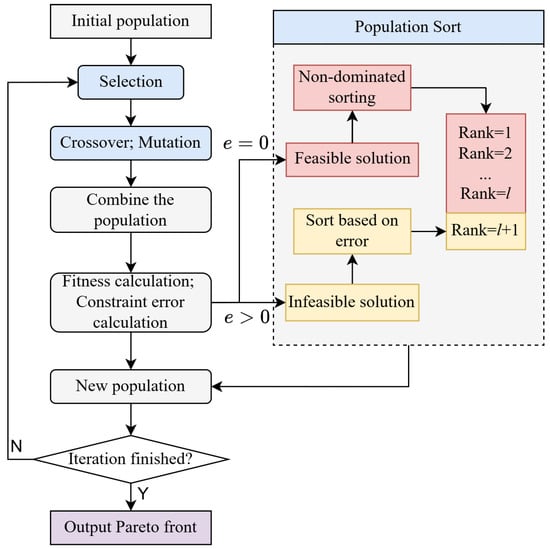
Figure 3. Flowchart of NSGAII-CDP.

4. Distributed Negotiation

A distributed cooperative game negotiation method is employed among the pursuers to jointly negotiate based on the existing Pareto front and determine an optimal comprehensive approach strategy that balances objectives such as flight time intervals, total flight time, and total fuel consumption.

4.1. Communication Topology

The communication topology is modeled using graph theory, with an undirected graph $\mathbb{G}=\{\mathbb{V},\mathbb{E}\}$ describing the communication topology of the multi-spacecraft system. $\mathbb{V}=\{1,2,\dots ,N\}$ represents the set of nodes, and $\mathbb{E}\subseteq \left\{\right\{i,j\left\}\right|i,j\in \mathbb{V},i\ne j\}$ represents the set of edges in the connections. Node $i\in \mathbb{V}$ corresponds to pursuer ${\mathrm{P}}_i$, and edge $\{i,j\}\in \mathbb{E}$ indicates that ${\mathrm{P}}_i$ can exchange information with ${\mathrm{P}}_j$.

Due to communication resource constraints, each spacecraft can only communicate with a limited number of other spacecraft. An adjacency matrix $\mathit{A}=\left\{a_{ij}\right\}\in {\{0,1\}}^{N\times N}$ is defined to describe inter-satellite communication, specifically expressed as

$$\left\{\begin{array}{c}{a}_{ij}=1\{i,j\}\in \mathbb{E}\hfill \\ a_{ij}=0\{i,j\}\notin \mathbb{E}.\hfill \end{array}\right.$$

(28)

Since the communication network is undirected, the adjacency matrix $\mathit{A}$ is symmetric, meaning $a_{ij}=a_{ji}$ for all $i,j\in \mathbb{V}$. Assume that the communication topology contains at least one spanning tree, ensuring the connectivity of the communication network.

4.2. Distributed Cooperative Game Model

To achieve efficient strategy negotiation, this section models the cooperative game problem as $G=\{\mathbb{N},\mathbb{S},\mathbb{U}\}$, where $\mathbb{N}=\{{\mathrm{P}}_1,{\mathrm{P}}_2,\dots ,{\mathrm{P}}_N\}$ represents the set of players (i.e., the pursuers), and each player acts as an independent decision-maker. $\mathbb{S}=S_1\times S_2\times \dots \times S_N$ represents the strategy space, where $s_i$ is the Pareto front for ${\mathrm{P}}_i$. $\mathit{s}={\left(s_i\right)}_{i\in [1,N]}\in \mathbb{S}$ represents the combination of strategies of all players, where $S_i$ is the feasible strategy set for ${\mathrm{P}}_i$, derived from its Pareto front obtained through multi-objective optimization. $\mathbb{U}={\left(U_i\right)}_{i\in [1,N]}$ denotes the payoff functions for all players, while $U_i=U_i(s_i,s_{-i})$ represents the individual payoff of a player. Here, $s_{-i}$ represents the strategies of the other players. During the cooperative game process, ${\mathrm{P}}_i$ continuously adjusts its strategy and exchanges information with other players to maximize its own payoff $U_i$.

Pursuers aim to achieve a balance that prioritizes ensuring the most consistent arrival time possible while simultaneously minimizing the total flight time and reducing their respective fuel consumption as much as possible. Therefore, the utility function $U_i$ is defined as

$$U_i(s_i,s_{-i})=-\alpha ·\sum _{j\ne i}^{N}a·a_{ij}|T_i-T_j|-\beta ·b·T_i-\gamma ·c·F_i$$

(29)

where $T_i$ and $F_i$ represent the total flight time and total fuel consumption of ${\mathrm{P}}_i$, respectively, while $T_j$ denotes the total flight time of ${\mathrm{P}}_j$. Dimensionless parameters $a,b$, and c are introduced to standardize these indicators. Coefficients $\alpha ,\beta$, and $\gamma$ serve as weighting factors. The overall optimization objective is obtained through a weighted linear summation, allowing for different weighting schemes to be set according to varying requirements.

4.3. Nash Equilibrium Existence and Convergence

Each pursuer optimizes its strategy based on its payoff function to achieve an optimal planning outcome. The system reaches Nash equilibrium [30] when no individual pursuer can unilaterally adjust its strategy to gain a greater benefit. Importantly, at the end of each cooperative game round, pursuers must exchange their strategies to maintain consistency in collective understanding.

4.3.1. Existence of Nash Equilibrium

Theorem 1. 

Every game with a finite number of players and action profiles has at least one Nash equilibrium [31].

In the negotiation and decision-making process of pursuers, the number of pursuers is finite, and the size of the Pareto front obtained from multi-objective optimization is also finite. Referring to Theorem 1, it can be concluded that a Nash equilibrium exists in the distributed negotiation process.

4.3.2. Convergence of Nash Equilibrium

To further illustrate the global convergence of Nash equilibrium, construct a potential function

$$P(s_i,s_{-i})=-\alpha a·\sum _{i=1}^N\sum _{j\ne i}^N{\displaystyle \frac{a_{ij}}{2}}|T_i-T_j|-\beta b·\sum _{i=1}^N{T}_i-\gamma c·\sum _{i=1}^N{F}_i.$$

(30)

Analysis indicates that the following condition holds for all pursuers:

$$P(s_i^{g+1},s_{-i})-P(s_i^g,s_{-i})=U_i(s_i^{g+1},s_{-i})-U_i(s_i^g,s_{-i})$$

(31)

where $s_i^g$ and $s_i^{g+1}$ represent the strategy choices of ${\mathrm{P}}_i$ in the gth and $(g+1)$th iteration, respectively. Therefore, G is a potential game with an exact potential function [32].

This study is based on the best response selection strategy, which can be described as

$$s_i^{*}=\underset{s_i\in S_i}{argmax}{U}_i(s_i,s_{-i}).$$

(32)

Each pursuer selects the most advantageous strategy based on the current partial information. In other words, each round of decision-making must ensure the maximization of current benefits $U_i(s_i,s_{-i})$, such that the payoff of each individual after each round of the game is guaranteed to be non-decreasing. According to (31), the following can be derived:

$$\Delta P=P(s_i^{g+1},s_{-i})-P(s_i^g,s_{-i})\ge 0.$$

(33)

Since the strategy space is finite, Equation (30) is monotonically increasing and bounded. During the strategy adjustment process, when no single player can unilaterally change their strategy to achieve a higher payoff, the system is deemed to have reached a stable state, corresponding to a Nash equilibrium. Consequently, with a sufficient number of iterations, it is guaranteed that the decision-making process will converge to a locally optimal solution, and potentially even achieve a globally optimal solution.

4.4. Simulated Annealing Distributed Negotiation

However, due to factors such as incomplete information decision-making and the mutual influence of strategies, it is challenging to converge the global optimal solution. Therefore, a distributed cooperative game negotiation strategy with a simulated annealing mechanism is designed to escape from local optima and search for better solutions. The process of simulated annealing cooperative game negotiation is shown in Figure 4.

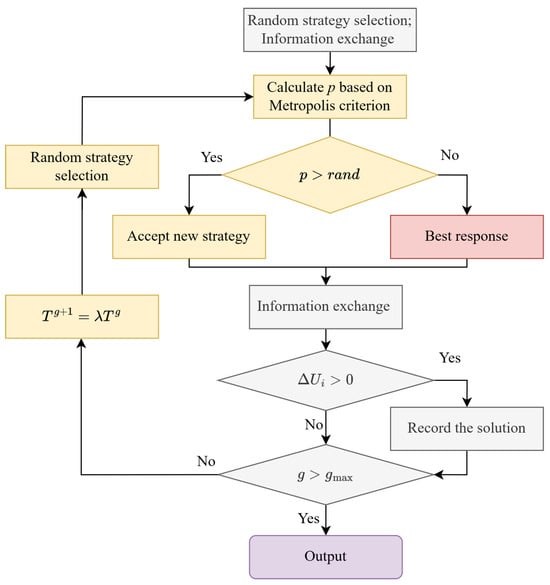
Figure 4. The process of simulated annealing cooperative game negotiation.

In each round of the cooperative game, pursuer ${\mathrm{P}}_i$ randomly selects a strategy and calculates its payoff. Then, the strategy is accepted with probability p. If not accepted, ${\mathrm{P}}_i$ optimizes its strategy according to (32). The acceptance probability p is determined by the Metropolis criterion:

$$p=\left\{\begin{array}{c}1,U_i(s_i^{g+1},s_{-i})>U_i(s_i^g,s_{-i})\hfill \\ e^{\Delta U_i/T},U_i(s_i^{g+1},s_{-i})\le U_i(s_i^g,s_{-i})\hfill \end{array}\right.$$

(34)

where T represents the annealing temperature, and $\Delta U_i=U_i(s_i^{g+1},s_{-i})-U_i(s_i^g,s_{-i})$ denotes the payoff difference. From (34), it can be concluded that

• When $\Delta U_i>0$, the strategy is accepted fully.
• When $\Delta U_i\le 0$, the strategy is adjusted according to the probability in (34).
• The value of p is influenced by the temperature T and the payoff difference $\Delta U_i$. The higher the temperature T, the larger the p. Conversely, the worse the payoff of the new strategy, the smaller the p. Therefore, when the temperature is very high, there is still a high probability of accepting the new strategy, even if its payoff is significantly lower.

To ensure proper convergence of the algorithm, the temperature T is annealed using an exponential decay approach, defined as

$$T^{g+1}=\lambda T^g,\lambda \in (0,1)$$

(35)

where $T^g$ and $T^{g+1}$ represent the annealing temperature in the gth and $(g+1)$th iteration, respectively. $\lambda$ is the annealing parameter that represents the decay rate. Algorithm 1 illustrates the iterative process for pursuer ${\mathrm{P}}_i$ to find a cooperative approach strategy.

Algorithm 1: Simulated Annealing Distributed Negotiation Process

1 Obtains the Pareto front $S_i$ through NSGAII-CDP    2 Initialize $\lambda ={\lambda }_0\in (0,1)$ and $T^1=T_0$    3 Randomly select an initial strategy $s^1\in S_i$    4 for $g=1$ to $g_{\max }$ do    5       if $p=min\{1,e^{\Delta U_i/T^g}\}<\mathrm{random}(0,1)$    6             $s_i^{g+1}=s^g$    7       else    8             $s_i^{g+1}=\underset{s_i\in S_i}{argmax}{U}_i(s_i^g,s_{-i}^g)$    9       end if  10       $T^{g+1}=\lambda T^g$  11       Randomly select a new strategy $s^{g+1}\in S_i$  12 end for  13 Output

5. Simulation Verification

5.1. Problem Configuration

To demonstrate the effectiveness of the proposed method, this section adopts the collaborative detection of high-orbit targets as the application scenario, where four pursuers are required to accomplish a coordinated approach detection mission under multiple constraints, while the target is guarded by four defenders. The pursuers must satisfy the following constraints:

• Approach within $1\mathrm{km}$ of the target for detection;
• Achieve terminal relative velocity less than $1\mathrm{m}/\mathrm{s}$;
• Synchronize the arrival times of all pursuers as closely as possible;
• Successfully evade interception by the defenders.

Space perturbation effects such as J2 perturbation, three-body gravitational forces, and solar radiation pressure may lead to decreased control efficiency and increased deviation. To validate the reliability of the decision-making method proposed in this study, a high-fidelity dynamics simulation environment was established. At the initial stage of the simulation, the pursuers execute the mission by following the approach trajectory generated through the cooperative game negotiation strategy. At $t=900\mathrm{s}$, the target perceives the threat, and the defenders immediately initiate an interception maneuver based on Lambert guidance, aiming to intercept the pursuers within 8 hours. Faced with the interception threat, the pursuers renegotiate and replan a cooperative approach trajectory. It should be noted that, for simplicity of analysis, this section assumes the defenders execute only one interception maneuver. If the defenders adjust their interception strategies multiple times, the pursuers must renegotiate their approach strategies to enhance mission robustness in complex environments. The orbital elements of all spacecraft at the initial time are shown in Table 1. The maneuver performed by the defenders at the beginning is shown in Table 2. The communication topology of the pursuers is shown in Figure 5, and the adjacency matrix is defined as

$$\mathit{A}=\left[\begin{array}{cccc}0& 1& 1& 0\\ 1& 0& 1& 1\\ 1& 1& 0& 0\\ 0& 1& 0& 0\end{array}\right].$$

(36)

Table 1. Orbital elements at the initial time.

	Semi-Major Axis (km)	Eccentricity	Inclination (°)	Longitude of the Ascending Node (°)	Argument of Periapsis (°)	True Anomaly (°)
$\mathrm{T}$	42,164.169000	$0.000000$	$0.131020$	$90.900407$	$0.000000$	$8.700026$
${\mathrm{P}}_1$	42,150.758669	$0.000000$	$0.101020$	$90.900407$	$0.000000$	$8.637026$
${\mathrm{P}}_2$	42,146.758669	$0.000000$	$0.151020$	$90.900407$	$0.000000$	$8.640026$
${\mathrm{P}}_3$	42,176.058669	$0.000000$	$0.091020$	$90.900407$	$0.000000$	$8.765026$
${\mathrm{P}}_4$	42,173.058669	$0.000000$	$0.141020$	$90.900407$	$0.000000$	$8.761026$
${\mathrm{D}}_1$	42,164.216433	$0.000474$	$0.131020$	$90.900407$	$98.591316$	$270.054355$
${\mathrm{D}}_2$	42,164.159522	$0.000474$	$0.131020$	$90.900407$	$188.700026$	$180.000000$
${\mathrm{D}}_3$	42,164.216433	$0.000474$	$0.131020$	$90.900407$	$278.808735$	$89.945645$
${\mathrm{D}}_4$	42,164.159504	$0.000474$	$0.131020$	$90.900407$	$8.700026$	$0.000000$

Table 2. The maneuver performed by the defenders.

Defender	${\mathit{u}}^{\mathbf{ECI}}(m/s)$
${\mathrm{D}}_1$	$[0.3487,0.7764,-1.5901]$
${\mathrm{D}}_2$	$[0.4703,-0.4025,1.0588]$
${\mathrm{D}}_3$	$[-0.4860,-0.2627,-2.1200]$
${\mathrm{D}}_4$	$[-0.2965,-1.1094,0.5309]$

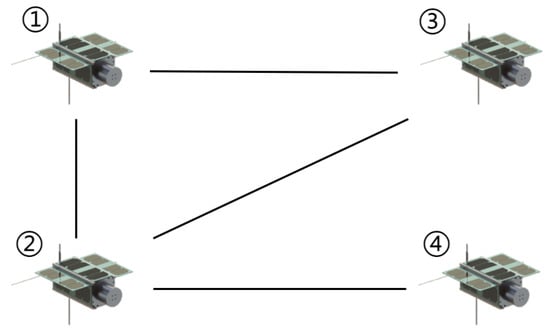
Figure 5. The communication topology of the pursuers.

During the multi-objective optimization stage, the NSGAII-CDP algorithm is used to find the feasible solution set. The main simulation parameters are shown in Table 3. In the distributed negotiation stage, the simulated annealing game negotiation method is employed to achieve distributed decision-making. The main simulation parameters are shown in Table 4.

Table 3. Simulation parameters for the multi-objective optimization stage.

Parameter	Value
Population size	2000
Maximum number of generations $g_{\max }$	500
Probability of crossover	$0.6$
Distribution factor ${\eta }_c$	20
Probability of mutation	$0.3$
Distribution factor ${\eta }_p$	40
Number of impulses n	6
Minimum time interval $\Delta t_{min}\left(\mathrm{s}\right)$	300
Maximum time interval $\Delta t_{max}\left(\mathrm{s}\right)$	7200
Maximum total mission time $t_{max}\left(\mathrm{s}\right)$	36,000
Maximum velocity increment of a single impulse maneuver $\Delta v_{max}(\mathrm{m}/\mathrm{s})$	1
Maximum total velocity increment $u_{\mathrm{total}}(\mathrm{m}/\mathrm{s})$	5
Safe distance $r_{\mathrm{safe}}\left(\mathrm{km}\right)$	5
Terminal distance $r_{\mathrm{final}}\left(\mathrm{km}\right)$	1
Terminal relative velocity $\Delta v_{\mathrm{final}}(\mathrm{m}/\mathrm{s})$	1

Table 4. Simulation parameters for the distributed negotiation stage.

Parameter	Value
Dimensionless parameters $a,b,c$	1/900, 1/36,000, 1/5
Weighting factors $\alpha ,\beta ,\gamma$	$0.4,0.3,0.3$
Initial temperature $T_0$	1
Annealing parameter $\lambda$	$0.999$
Maximum iterations K	100

5.2. Simulation Results and Analysis

First, the NSGAII-CDP algorithm is applied to solve the MOOP, and the relationship between different optimization objectives in the (21) is obtained, namely, the Pareto front. Figure 6 illustrates the Pareto front derived from trajectory optimization for each pursuer.

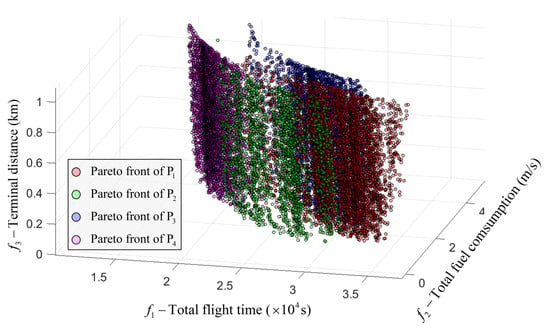
Figure 6. Pareto front of pursuers.

Subsequently, a distributed cooperative game negotiation strategy based on simulated annealing (Algorithm $\mathrm{I}$) is employed to iteratively optimize the cooperative strategy in order to achieve a comprehensive optimal solution. To demonstrate the superiority of Algorithm $\mathrm{I}$, comparisons were made with a random negotiation strategy (Algorithm $\mathrm{I}\mathrm{I}$) and a traditional negotiation strategy (Algorithm $\mathrm{I}\mathrm{I}\mathrm{I}$), respectively. As shown in Figure 7, the changes in the potential function of Equation (30) during the iterative process are presented. The analysis shows that Algorithm $\mathrm{I}\mathrm{I}\mathrm{I}$ converges to a local minimum but becomes trapped, failing to discover superior solutions. Although Algorithm $\mathrm{I}\mathrm{I}$ can effectively escape local optima, its optimization efficiency and performance are both inferior to those of the proposed Algorithm $\mathrm{I}$. The corresponding Pareto optimal solution set for the pursuers is presented in Table 5.

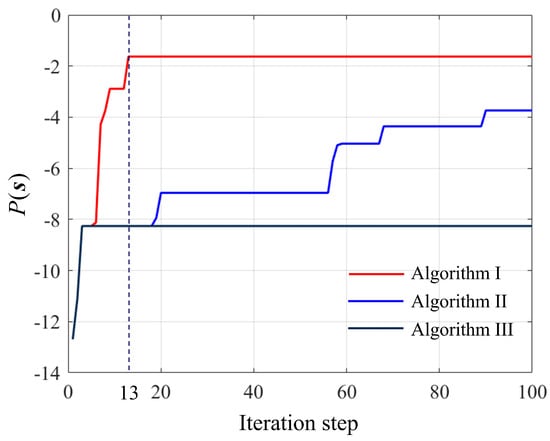
Figure 7. Changes in the potential function during the iterative process.

Table 5. Pareto optimal solution obtained through negotiation.

	${\mathit{J}}_1\left(\mathbf{s}\right)$	${\mathit{J}}_2(\mathbf{m}/\mathbf{s})$	${\mathit{J}}_3\left(\mathbf{km}\right)$
Strategy of ${\mathrm{P}}_1$	33,274.39	$1.42$	$0.113$
Strategy of ${\mathrm{P}}_2$	33,289.03	$0.66$	$0.883$
Strategy of ${\mathrm{P}}_3$	33,346.13	$2.44$	$0.768$
Strategy of ${\mathrm{P}}_4$	33,310.12	$1.05$	$0.428$

Furthermore, Table 6 presents the orbital maneuver strategies corresponding to the Pareto optimal solutions shown in Table 5, including the time intervals ${\{\Delta t_k\}}_{k=1}^n$ between consecutive impulses and the velocity increments ${\left\{{\mathit{u}}_k^{\mathrm{ECI}}\right\}}_{k=1}^n$ in the ECI coordinate system. Figure 8 illustrates the relative motion trajectories of multi-spacecraft. It shows the interception trajectories after the defenders execute the maneuver scheme described in Table 2, as well as the avoidance and approach trajectories resulting from the orbital maneuver scheme in Table 6 executed by the pursuers. Figure 9 shows the changes in the relative state during the approach process of the pursuers. Specifically, Figure 9a,b represent the variations in three-axis relative position and velocity, respectively. In addition, Figure 10a,b illustrate the changes in distance and velocity of the pursuers relative to the target.

Table 6. Orbital maneuver strategies corresponding to the Pareto optimal solutions in Table 5.

	Strategy of ${\mathbf{P}}_1$	Strategy of ${\mathbf{P}}_2$	Strategy of ${\mathbf{P}}_3$	Strategy of ${\mathbf{P}}_4$
$\Delta t_1\left(\mathrm{s}\right)$	$3415.26$	$4299.87$	$6925.39$	$2089.80$
${\mathit{u}}_1^{\mathrm{ECI}}(\mathrm{m}/\mathrm{s})$	$[-0.32;0.40;0.49]$	$[0.15;0.38;-0.52]$	$[0.32;-0.19;0.38]$	$[0.48;-0.21;-0.25]$
$\Delta t_2\left(\mathrm{s}\right)$	$3834.51$	$5637.22$	$4352.07$	$6781.67$
${\mathit{u}}_2^{\mathrm{ECI}}(\mathrm{m}/\mathrm{s})$	$[-0.00;0.00;0.38]$	$[0.00;0.00;0.00]$	$[-0.02;-0.31;0.65]$	$[0.12;-0.18;-0.12]$
$\Delta t_3\left(\mathrm{s}\right)$	$6591.94$	$5717.67$	$5857.91$	$6642.05$
${\mathit{u}}_3^{\mathrm{ECI}}(\mathrm{m}/\mathrm{s})$	$[0.00;0.00;0.00]$	$[0.00;0.00;0.00]$	$[0.00;0.00;0.03]$	$[0.00;0.00;0.00]$
$\Delta t_4\left(\mathrm{s}\right)$	$5063.92$	$6983.27$	$6216.72$	$7031.07$
${\mathit{u}}_4^{\mathrm{ECI}}(\mathrm{m}/\mathrm{s})$	$[0.00;0.00;0.00]$	$[0.00;0.00;0.00]$	$[0.10;-0.01;-0.10]$	$[0.00;0.00;0.12]$
$\Delta t_5\left(\mathrm{s}\right)$	$7154.10$	$3591.62$	$3880.09$	$5420.71$
${\mathit{u}}_5^{\mathrm{ECI}}(\mathrm{m}/\mathrm{s})$	$[0.00;0.00;0.00]$	$[0.00;0.00;0.00]$	$[0.00;0.00;0.00]$	$[0.08;-0.01;-0.04]$
$\Delta t_6\left(\mathrm{s}\right)$	$7187.67$	$7058.92$	$6113.95$	$5344.82$
${\mathit{u}}_6^{\mathrm{ECI}}(\mathrm{m}/\mathrm{s})$	$[-0.19;0.00;-0.28]$	$[0.00;0.00;0.00]$	$[0.57;0.03;-0.82]$	$[0.00;0.00;0.00]$

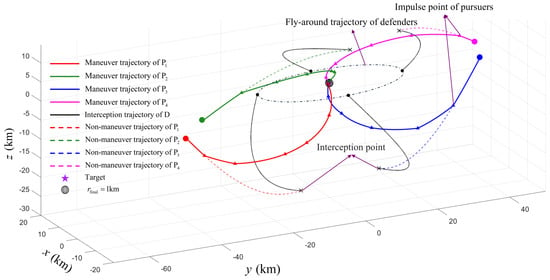
Figure 8. Orbital maneuver trajectories corresponding to the Pareto optimal solutions in Table 5.

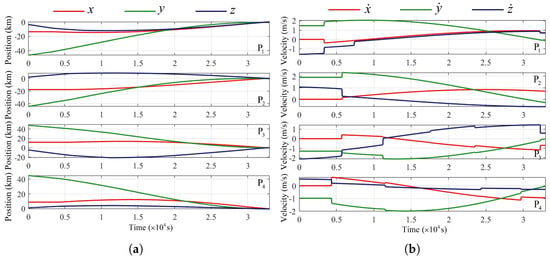
Figure 9. Relative state variations. (a) Relative position variations. (b) Relative velocity variations.

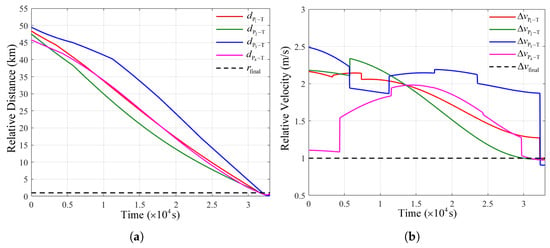
Figure 10. Relative distance and velocity variations. (a) Distance variations of the pursuers relative to the target. (b) Velocity variations of the pursuers relative to the target.

An integrated analysis of Table 5 and Table 6, along with Figure 8, Figure 9 and Figure 10, reveals the following: (1) Without executing any maneuvers, the pursuers would be intercepted by the defenders. (2) By performing the specific maneuver sequence, the pursuers successfully avoided the defenders and successfully approached the target. (3) At the terminal time, the pursuers satisfied the mission’s terminal constraints, with the terminal distance and relative velocity being within the limits ($r_{\mathrm{final}}<1\mathrm{km},\Delta v_{\mathrm{final}}<1\mathrm{m}/\mathrm{s}$). (4) The maneuver time intervals and velocity increments adhered to the predefined constraints. Moreover, the total flight time and total fuel consumption did not exceed the mission requirements. (5) For all pursuers, the total flight times were nearly identical.

To further validate the effectiveness of the proposed method, Monte Carlo simulation experiments with a sufficient sample size were conducted based on the existing Pareto front with two different weighting schemes. These experiments aimed to evaluate the performance of the simulated annealing distributed negotiation strategy. Specifically, a total of 1000 Monte Carlo simulations were performed for each weighting scheme. In each simulation, the initial strategy was randomly selected, and distributed optimization was then carried out using Algorithm $\mathrm{I}$, Algorithm $\mathrm{I}\mathrm{I}$, and Algorithm $\mathrm{I}\mathrm{I}\mathrm{I}$. To comprehensively evaluate the performance of the strategies, several key metrics were recorded for each simulation, including the potential function values after convergence $P_f$, the maximum approach time difference $e_{\max }$, the average flight time $\overline{t}$, and the average fuel consumption $\overline{u}$. Figure 11 illustrates the distribution of key metrics under two weight schemes. Table 7 provides a statistical analysis of the metrics, including their mean, standard deviation, and maximum and minimum values.

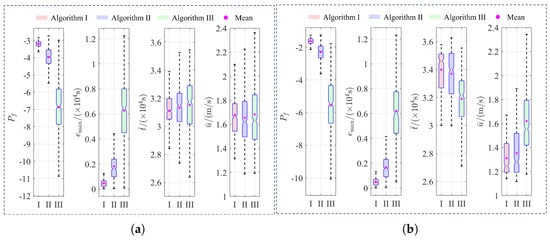
Figure 11. Results of 1000 Monte Carlo simulations. (a) Case 1: $\alpha =0.1,\beta =0.1,\gamma =0.8$. (b) Case 2: $\alpha =0.1,\beta =0.8,\gamma =0.1$.

Table 7. Analysis of the results of 1000 Monte Carlo simulations.

		Case1			Case2
		I	II	III	I	II	III
$P_f$	mean	−1.6287	−2.2890	−5.5530	−3.2003	−3.9703	−6.8707
	std	0.1807	0.4798	1.7125	0.1637	0.5491	1.5955
	min	−2.3299	−3.7734	−10.6150	−3.8143	−5.5203	−11.5970
	max	−1.2661	−1.2559	−1.7837	−2.8485	−2.7321	−2.9873
$e_{\max }$ $(\times {10}^4\mathrm{s})$	mean	0.0501	0.1671	0.6204	0.0466	0.1806	0.6270
	std	0.0317	0.0955	0.2549	0.0305	0.1100	0.2549
	min	0.0014	0.0046	0.0503	0.0018	0.0032	0.0083
	max	0.1442	0.5576	0.6022	0.1838	0.5851	1.2241
$\overline{t}$ $(\times {10}^4\mathrm{s})$	mean	3.3990	3.3697	2.1905	3.1119	3.1330	3.1533
	std	0.1300	0.1606	0.1773	0.1095	0.1780	0.1904
	min	3.0007	2.9982	2.7103	2.6880	2.6116	2.5693
	max	3.5772	3.6266	3.5530	3.3904	3.5574	3.5447
$\overline{u}$ $(\mathrm{m}/\mathrm{s})$	mean	1.3111	1.3532	1.6204	1.6783	1.6554	1.6822
	std	0.1397	0.1782	0.2713	0.1700	0.2627	0.2877
	min	1.1404	1.1173	1.1780	1.3132	1.1874	1.1924
	max	1.8319	1.8895	2.3539	2.3397	2.6468	2.7114

Based on the data from Figure 11 and Table 7, the distribution of potential function values and statistical results indicate that the simulated annealing distributed negotiation strategy demonstrates significantly better optimization performance compared to the traditional strategy. In Case 1, Algorithm $\mathrm{I}$ achieved $28.85\%$ and $70.67\%$ improvements in the mean value of $P_f$ compared to Algorithm $\mathrm{I}\mathrm{I}$ and Algorithm $\mathrm{I}\mathrm{I}\mathrm{I}$, respectively. In Case 2, the mean value of $P_f$ of Algorithm I increased by $19.40\%$ and $53.42\%$, respectively. These results demonstrate that the simulated annealing negotiation strategy proposed in this study delivers superior optimization efficiency. Moreover, the standard deviation and range of extreme values for the simulated annealing strategy indicate a more concentrated distribution of $P_f\left(\mathit{s}\right)$, stronger optimization depth, and greater stability and robustness. Additionally, the simulated annealing strategy exhibits a clear advantage in controlling the maximum approach time difference $e_{\max }$, with a lower mean value and reduced variability, effectively enhancing the coordination capability of multi-spacecraft. Further analysis of $\overline{t}$ and $\overline{u}$ data reveals that longer total flight times result in lower total fuel consumption, and vice versa. In practical applications, the choice of specific weighting schemes should be balanced based on mission requirements.

Overall, the dual-stage decision-making method based on cooperative game negotiation proposed in this study effectively enhances distributed optimization capabilities and achieves coordinated and safe approach among pursuers.

6. Conclusions

This study proposes a dual-stage decision-making method based on cooperative game negotiation for cooperative approach tasks of multi-spacecraft. For the multi-objective optimization stage, a multi-objective optimization model considering various constraints was constructed, and the multi-objective optimization algorithm NSGAII-CDP is applied to solve the model, obtaining the Pareto front. In the distributed negotiation stage, the negotiation strategy among multi-spacecraft is modeled as a cooperative game, and the existence and global convergence of Nash equilibrium solutions are analyzed. Furthermore, a simulated annealing distributed negotiation strategy was designed for the iterative selection of the optimal comprehensive approach strategy from the Pareto front. The feasibility of the proposed method was validated through simulation results, and its superiority and stability were further demonstrated via extensive Monte Carlo simulations. This method provides a reliable and effective solution for distributed multi-spacecraft trajectory optimization under multiple constraints. Future research will focus on overcoming the challenges of cooperative approach problems involving multi-spacecraft under nonlinear dynamic constraints, particularly the real-time control challenges in complex maneuvering scenarios of the defenders.