Abstract
The module division scheme of commercial aircraft and other complex system products has a significant impact on the functionality, performance, and cost of the aircraft. To obtain scientifically rational modular division solutions for commercial aircraft, this study establishes an Analytic Hierarchy Process–Gray Fuzzy Comprehensive Evaluation (AHP-GFCE) model by integrating hierarchical analysis method and gray fuzzy evaluation theory. This model develops a comprehensive evaluation methodology for aircraft modular division schemes. The proposed method was applied to evaluate the structural modular division scheme of the nose structure section of a certain type of aircraft. Results demonstrate that the AHP-GFCE model successfully identified the optimal nose structure modular division scheme. Compared with traditional installation processes, this optimal solution achieves a 40% improvement in overall assembly efficiency and a 25% reduction in total production cycle duration while better aligning with the engineering and manufacturing requirements of nose structure fabrication, thus revealing the superiority of the AHP-GFCE model in modular division evaluation. This research provides novel insights for modular division schemes of complex system products like commercial aircraft, and the methodology can be extended to modular maintenance domains of sophisticated products such as aero-engines. Although there remains room for model refinement, the findings carry significant theoretical and practical implications for modular division of complex system products.
1. Introduction
With the aviation industry transitioning toward intelligent and low-carbon development, aircraft modular design has emerged as a critical technical pathway for optimizing whole-lifecycle performance. The Boeing 787 adopts a super-modular design philosophy, achieving a 50% composite material utilization rate, with its fuselage composed of three prefabricated modules (forward, mid, and aft sections), significantly reducing the final assembly cycle to 3 days [1]. The Airbus A350XWB(Harbin Hafei-Airbus Composite Manufacturing Centre, Harbin, China) employs double-curvature panel integral forming technology, enabling rapid cabin section integration through 36 primary functional modules, attaining a fuselage modularization rate of 45% [2]. Current research indicates that next-generation aircraft modular design will integrate Model-Based Systems Engineering (MBSE) with digital twin technology, targeting a breakthrough in full-aircraft modularization rates exceeding 75% [3].
Current research on modular division for complex products like commercial aircraft remains predominantly conceptual, with few mature modeling frameworks. Wei et al. developed a multi-criteria modular division mathematical model, employing multi-objective evolutionary algorithms for solution derivation and fuzzy set evaluation methods to identify optimal solutions, thereby generating modular division schemes that support complex product platform design [4]. Chen Yanhui et al. proposed a max-min division approach, where initial grouping follows a maximum division principle, followed by cluster analysis within the resulting subsets using minimum division units, ultimately determining product modularization schemes based on inter-module aggregation metrics [5]. These traditional modular division methods, predominantly based on static functional decomposition principles, struggle to address challenges such as multi-disciplinary coupling (e.g., structural–thermodynamic–electromagnetic compatibility), dynamic mission requirements (e.g., reconfigurable aircraft), and data heterogeneity (e.g., multi-source sensors and simulation data). Although topology optimization [6] and digital twin technology [7] have significantly enhanced modular design efficiency, their limitations in fuzzy requirement quantification and unstructured conflict resolution continue to constrain the global optimality of complex systems.
Consequently, hybrid decision-making frameworks integrating the Analytic Hierarchy Process (AHP) and Gray Fuzzy Comprehensive Extension (GFCE) theory have emerged as a novel research direction to address these bottlenecks. While AHP enables multi-criteria prioritization through hierarchical weight allocation, its static weighting mechanism struggles to adapt to dynamic design requirements [8]. In contrast, GFCE effectively addresses uncertainties and data scarcity in modular division by synthesizing gray relational analysis with fuzzy membership functions [9]. Their synergistic integration preserves AHP’s strengths in structured decision-making while enhancing model robustness against complex constraints via GFCE’s dynamic feedback mechanisms. Furthermore, Pareto-optimal solution sets are autonomously generated through gray fuzzy clustering algorithms [10].
The AHP-GFCE model established in this paper, by integrating AHP and GFCE theory, can effectively handle multi-factor, multi-criteria decision-making problems in complex systems and guide the scientific conduct of modularization work for commercial aircraft. The model has the following advantages:
- It has significant advantages in terms of scientific nature and adaptability, integrating the strengths of the AHP and GFCE theory. It can simultaneously handle indicator weights, uncertainties, and fuzziness. It also has advantages such as mitigating subjective bias in expert scoring and handling high computational complexity; the establishment of a dynamic weight-updating mechanism enhances the scientific rigor and accuracy of the evaluation process.
- It can effectively deal with multi-factor, multi-criteria decision-making problems in complex systems, ensuring that complex system products with multiple objectives and requirements obtain the optimal solution.
2. The Analytic Hierarchy Process–Gray Fuzzy Comprehensive Evaluation Model
The AHP-GFCE model mainly consists of two parts: the Analytic Hierarchy Process and the Gray Fuzzy Comprehensive Evaluation System [11,12]. The AHP is used to determine the weights of each evaluation criterion. By constructing a judgment matrix and quantifying the relative importance of each criterion through expert scoring, the weights are calculated. Gray system theory is primarily used to deal with the uncertainty of data and the incompleteness of information. Through gray relational analysis, the degree of correlation between each scheme and the ideal scheme is calculated. The GFCE is carried out on the basis of the AHP. The two complement each other and together enhance the scientific nature, reliability, and effectiveness of the evaluation. The overall evaluation approach is shown in Figure 1.
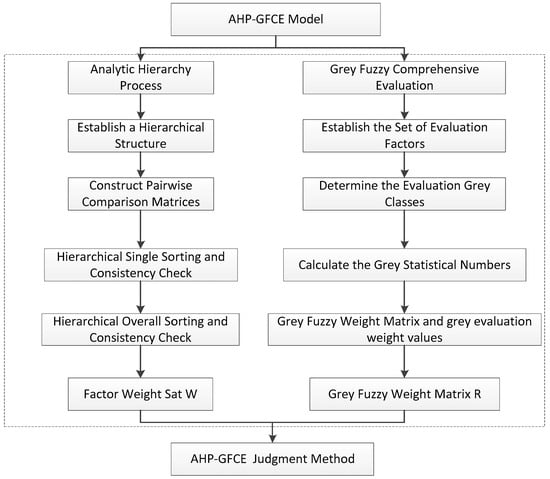
Figure 1.
Analytic Hierarchy Process—Gray Fuzzy Comprehensive Evaluation model.
Before determining the weights of the evaluation indicators for the modularization scheme of commercial aircraft, it is necessary to establish a corresponding evaluation indicator system. Through research on commercial aircraft materials [13], the modularization of commercial aircraft mainly focuses on five key indicators: product quality reliability, product accessory selection, product functionality, manufacturing and maintenance, and overall product structure composition. These five key indicators can further be divided into eighteen sub-indicators. The evaluation indicator system for the modularization scheme of commercial aircraft is established based on this, as shown in Figure 2.
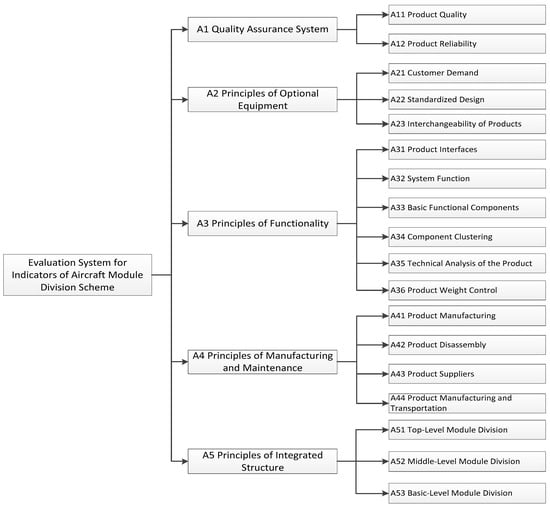
Figure 2.
Evaluation index system for aircraft module division scheme.
2.1. Hierarchical Single Sorting and Consistency Check
Based on the fundamental calculation principles of the AHP, the consistency index of each level’s judgment matrix is calculated. To verify the consistency of the judgment matrix, the consistency ratio (CR) is introduced. The larger the CR, the worse the consistency of the matrix. The Consistency Index (CI) is defined as , where λmax is the maximum eigenvalue of the judgment matrix, and n is the order of the matrix. The random consistency index (RI) is a value that depends on the order of the matrix. The CR is calculated as , If CR < 0.1, the consistency of the judgment matrix is considered satisfactory. If the judgment matrix has significant deviations and the evaluation results are unreasonable, the judgment matrix should be adjusted accordingly. The specific calculation results are presented in Table 1.

Table 1.
Computation of index entry judgment matrix, weight, and CR.
Similarly, The CR value of Indicator A1 is calculated as 0. The CR value of Indicator A2 is calculated as 0.03. The CR value of Indicator A3 is calculated as 0.04. The CR value of Indicator A4 is calculated as 0.02. The CR value of Indicator A5 is calculated as 0.02. Therefore, the judgment matrices meet the requirement for consistency.
2.2. Determining Indicator Weights
Hierarchical total sorting refers to the calculation of the relative importance of each factor in a certain level with respect to all factors in the upper level. Since hierarchical total sorting is conducted from the highest level to the lowest level, it also represents the calculation of the relative importance of each factor in a certain level with respect to the highest level. The hierarchical total sorting can then be obtained based on the results of hierarchical single sorting. The results are shown in Table 2.

Table 2.
Calculation table for the weights of module division evaluation indicators.
2.3. Determining Evaluation Grades
Evaluation grades are used to classify and compare the comprehensive performance of the evaluated objects by dividing them into several levels. Typically, these levels are divided into four categories: “Good”, “Fairly Good”, “Average”, and “Poor”. The scores for each level are determined using the expert scoring method, with a 10-point scale. The scores for each grade are as follows: C = {10, 7, 5, 2}.
2.4. Determination of the Evaluation Gray Degree
The determination of evaluation gray classes is based on the evaluation grades and relies on qualitative analysis. Let the evaluation value of the k-th member of the evaluation group denoted by for the j-th indicator (j = 1,2,…,n) be denoted as . The matrix composed of h is called the sample matrix of the indicator set U. The whitening weight functions selected in this paper are as follows:
- The gray number of grade “Good” is expressed as . Its whitening weight function is as follows:
- The gray number of grade “Fairly Good” is expressed as . Its whitening weight function is as follows:
- The gray number of grade “Average” is expressed as . Its whitening weight function is as follows:
- The gray number of grade “Poor” is expressed as . Its whitening weight function is as follows:
2.5. Determining the Gray Statistical Numbers
After establishing the evaluation gray classes for the four grades, the gray statistical method can be used to calculate the weight of the j-th evaluation criterion. Additionally, the gray statistics and total gray statistics of the evaluation matrix can be obtained by using . The specific calculations are as follows:
2.6. Calculating the Gray Fuzzy Weight Matrix and Gray Evaluation Weight Values
Taking into account the evaluation opinions of r experts on the i-th factor, the grey evaluation weight for the j-th evaluation criterion is obtained as follows:
The single-factor gray fuzzy weight matrix composed of is shown as follows:
2.7. Calculate the Gray Fuzzy Evaluation Matrix
The gray fuzzy evaluation matrix is obtained by compounding the fuzzy weighted matrix and the fuzzy comprehensive evaluation matrix.
Among , is obtained after normalization.
2.8. Calculate the Final Evaluation Result
Calculate the final comprehensive evaluation results via the following equation:
3. Case Study on the Evaluation of Modularization Schemes for the Nose Structure Section of Commercial Aircraft
The AHP-GFCE model is applicable to the assessment of module division schemes for different types of commercial aircraft, including regional jets, narrow-body aircraft, and wide-body aircraft. To validate the scientific validity of this evaluation model, this paper selects the nose structure section for module division scheme evaluation. The design and manufacturing of the nose structure have a profound impact on the overall performance of the aircraft. A rational nose structure section design can not only enhance the aircraft’s aerodynamic performance and structural strength but also facilitate equipment installation and maintenance. Additionally, it meets ergonomic requirements and reduces production and operational costs [14,15]. This paper evaluates the modularization schemes for the nose structure section to seek the optimal division plan. The nose structure section includes the First frame, cockpit components, Hatch Assembly, and so on. The specific components are mainly shown in Table 3.

Table 3.
The specific components included in the nose structure.
Based on the design and manufacturing experience of aircraft noses and integrating considerations of structural functionality, manufacturing processes, and comprehensive optimization, three nose structure section schemes for a certain type of aircraft have been developed, as shown in Figure 3, Figure 4 and Figure 5.

Figure 3.
Module division Scheme A.

Figure 4.
Module division Scheme B.
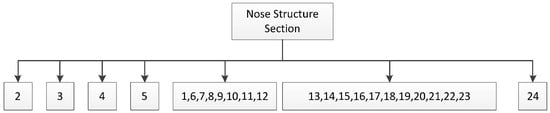
Figure 5.
Module division Scheme C.
Six experts with approximately 20 years of experience in commercial aircraft design were invited to evaluate module division Schemes A, B, and C. The expert panel consisted of two aircraft overall design experts, one aircraft structural design expert, one aircraft systems design expert, one aircraft configuration division expert, and one aircraft manufacturing expert. The evaluation sample matrices for each scheme were obtained through expert scoring, where six experts were invited to rate each scheme using a 10-point scoring system. All members of the evaluation panel were stipulated to have equal weighting.
The evaluation sample size matrix of Schemes A, B, and C is shown in Table 4. According to the evaluation process, the comprehensive evaluation results of Schemes A, B, and C are 6.98, 8.15, and 7.95.

Table 4.
The evaluation sample size matrix of Schemes A, B, and C.
Based on the final evaluation results obtained for the three schemes, the ranking of the schemes can be determined as follows: 8.15 > 7.56 > 6.98. This means that Scheme B is the optimal scheme, followed by Scheme C, with Scheme A being relatively less favorable. Therefore, it is evident that Scheme B is the best option. Therefore, the module division scheme for the nose structure section of a certain type of aircraft can be obtained as shown in Figure 6.
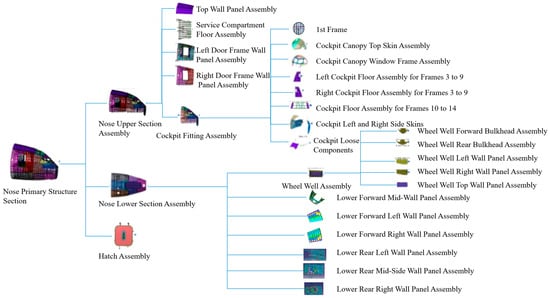
Figure 6.
The module division scheme for the nose structure section of a certain type of aircraft.
Modular integrated manufacturing refers to the primary manufacturer focusing on final assembly and integration while controlling manufacturing specifications and product interfaces. Following a modular production approach, the installation of internal system components/equipment and component-level system functional testing are completed during the subunit assembly phase. During the final assembly stage, the primary responsibilities include the installation of remaining system components/equipment and full-aircraft functional testing.
Taking the nose structure section scheme of a certain aircraft type as an example: traditionally, all 24 submodules of the nose structure were installed during the nose subunit assembly phase. The traditional installation process faced issues such as excessive process overlaps, high rework rates, and inefficient resource allocation. Through the implementation of the optimized module division scheme for the nose structure outlined in the aforementioned paper, a modular pre-assembly strategy was adopted. Through the implementation of the optimized module division scheme for the nose structure outlined in the aforementioned paper, a modular pre-assembly strategy was adopted, as shown in Figure 7. The 24 submodules were decomposed into independent modules, such as Hatch Assembly, Nose Upper Section Assembly, and Nose Lower Section Assembly. Leveraging standardized interface designs, independent pre-assembly and parallel operations were achieved. Compared to the traditional process, the overall assembly efficiency of a certain type of aircraft’s nose structure improved by 40%, the total cycle time was reduced by 25%, and the approach better aligned with the engineering and manufacturing requirements of nose structures.
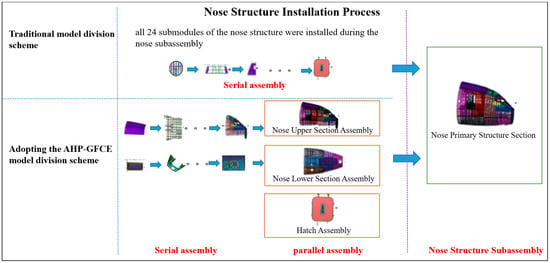
Figure 7.
Nose structure installation process.
4. Discussion
This study aims to explore the scientific validity of module division schemes for commercial aircraft. By employing the AHP-GFCE model to conduct a comprehensive evaluation of commercial aircraft module division schemes, this assessment method is applicable to the full lifecycle development of regional, narrow-body, and wide-body aircraft, as well as processes such as commercial aircraft design, manufacturing, and supplier management. The research findings demonstrate the scientific rigor and efficiency of the AHP-GFCE model in commercial aircraft module division, showcasing its significant advantages in comprehensive decision-making over traditional Product Breakdown Structure (PBS) decomposition methods, as illustrated in Table 5.

Table 5.
Comparative advantage analysis of the AHP-GFCE model versus traditional DBS/PBS frameworks.
The theoretical contribution of this study lies in proposing the AHP-GFCE model, which provides a new perspective for evaluating modular division schemes of commercial aircraft. In practical terms, our findings hold potential value for the modular division of commercial aircraft, such as offering scientific division schemes for various aircraft sections. These discoveries establish a scientific basis for module division in complex system products, particularly commercial aircraft, while the research outcomes can be extended to modular maintenance fields involving complex products like aero-engines.
Although this study has achieved certain results, there remains room for improvement. First, experts may still exhibit subjective bias in scheme scoring despite our fuzzification approach. Future research could consider expanding the sample size and employing more advanced evaluation models to overcome these limitations. Second, subsequent work could utilize SysML language to construct dynamic requirement models, enabling seamless integration of the AHP-GFCE evaluation model with MBSE tools (e.g., CATIA Magic) and automatic mapping of requirement changes to modular interface parameters.
In conclusion, this study established an AHP-GFCE model to assess modular division schemes for commercial aircraft, revealing a scientific methodology for modular division of complex system products and providing novel insights into the evaluation of such schemes. Despite its limitations, the findings hold significant implications for both theoretical understanding and practical applications of modular division in complex system products.
5. Conclusions
This study aims to explore evaluation methods for commercial aircraft modular division schemes to support modular design, decomposing complex systems into functionally independent modules for efficient design, manufacturing, assembly, and maintenance, thereby enhancing aircraft cost-effectiveness. By innovatively establishing the AHP-GFCE model and applying it to a case study of structural modular division in the nose structure section of a certain type of aircraft, the optimal nose structure modular division scheme was derived. This scheme demonstrated a 40% improvement in overall assembly efficiency and a 25% reduction in total cycle time compared to traditional installation processes, better aligning with the engineering and manufacturing requirements of nose structures. These results highlight the advanced capabilities of the AHP-GFCE model in modular division evaluation. The research outcomes not only validate the scientific rigor of the AHP-GFCE model in assessing modular division schemes but also provide new theoretical perspectives and practical guidance for modular division of complex system products. The methodology can be extended to modular maintenance fields for complex products such as aero-engines. While this study has limitations, its theoretical contributions and practical significance remain noteworthy. Future research could further explore seamless integration of the AHP-GFCE model with MBSE tools (e.g., CATIA Magic) to enable automatic mapping of requirement changes to modular interface parameters and enhance traceability of modular attribute data, thereby expanding the applicability of the findings.
Author Contributions
Methodology and data curation, H.X.; project administration, L.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Data Availability Statement
The data in this study have been presented in the article, and the unpublished data can be obtained from the corresponding author.
Acknowledgments
The authors would like to express their sincere gratitude to the modularization special project team at the Shanghai Aircraft Design and Research Institute.
Conflicts of Interest
The authors declare that they have no competing interests. They have no financial or personal relationships with other people or organizations that could inappropriately influence their work. The research was conducted independently, and the results are presented without bias.
References
- Schmuck, R. Global supply chain quality integration strategies and the case of the Boeing 787 Dreamliner development. Procedia Manuf. 2021, 54, 88–94. [Google Scholar] [CrossRef]
- Chen, H.; Airbus Group. Dual-Curvature Panel Integration in A350XWB: A Breakthrough in Modular Assembly. Compos. Struct. 2021, 278, 114532. [Google Scholar]
- Zheng, X.; Hu, X.; Lu, J.; Arista, R.; Lentes, J.; Kiritsis, D. An aircraft assembly process formalism and verification method based on semantic modeling and MBSE. Adv. Eng. Inform. 2024, 60, 102412. [Google Scholar] [CrossRef]
- Wei, W.; Liu, A.; Lu, S.C.Y.; Wuest, T. A multi-principle module identification method for product platform design. J. Zhejiang Univ. Sci. A Appl. Phys. Eng. 2015, 16, 1–10. [Google Scholar] [CrossRef]
- Chen, Y.H.; Zhou, D.J.; Yuan, H.Y.; Feng, Z.J. A Min-Max Partition Modularization Method for Complex Products. Comput. Integr. Manuf. Syst. 2012, 18, 9–14. [Google Scholar]
- Zhang, Y.; Liu, H.; Wang, Q. Integrated modular architecture for next-generation aircraft design. Aerosp. Sci. Technol. 2024, 156, 112–125. [Google Scholar]
- García, J.; O’Connor, R. Digital twin-enabled modular design optimization in aircraft manufacturing. J. Manuf. Syst. 2023, 68, 234–247. [Google Scholar]
- Feng, L.; Wang, Q.; Xu, T. Dynamic weight adaptation in AHP for reconfigurable modular systems. Syst. Eng. Electron. 2025, 47, 1123–1137. [Google Scholar]
- Al-Falasi, A.; Weston, R. Grey-fuzzy extension theory for handling uncertainty in complex system modularization. Fuzzy Sets Syst. 2024, 492, 108765. [Google Scholar]
- Russo, D.; Beauchemin, P. Pareto frontier generation in multi-objective modular design via grey-fuzzy clustering. Comput. Ind. Eng. 2025, 195, 109234. [Google Scholar]
- Wei, C.-C.; Chien, C.-F.; Wang, M.-J.J. An AHP-based approach to ERP system selection. Int. J. Prod. Econ. 2005, 96, 47–62. [Google Scholar] [CrossRef]
- Feng, Z.; Hou, H.Y.; Lan, H.F. Understanding university students’ perceptions of classroom environment: A synergistic approach integrating grounded theory and AHP. J. Build. Eng. 2025, 42, 105–118. [Google Scholar]
- Overmeyer, L.; Bentlage, A. Small-Scaled Modular Design for Aircraft Wings. In New Production Technologies in Aerospace Industry; Springer: Cham, Switzerland, 2013; pp. 55–62. [Google Scholar]
- George, M. Composites Lift off In Primary Aerostructures. Reinf. Plast. 2004, 48, 22–27. [Google Scholar]
- Wang, J.; Baker, A.; Chang, P. Hybrid approaches for aircraft primary structure repairs. Compos. Struct. 2019, 207, 190–203. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).