Experimental and Simulation Studies on Bird Strike Impact of Carbon Fiber Composite Laminates with Different Ply Directions

Abstract

Composite materials are widely used in aircraft due to their high specific strength and stiffness, superior impact resistance, and excellent fatigue performance. Bird strikes can inflict severe damage to critical aircraft components such as the fuselage, engines, and wings, thereby compromising flight safety. Aircraft certification regulations require that all components demonstrate a specified level of bird strike resistance before aircraft installation. Given these requirements, this study focused on the use of carbon fiber composite laminates in aircraft components. By varying impact velocity, impact angle, and ply orientation, the study investigated the resulting patterns of bird-strike impact behavior in composite materials. The derived patterns provide a theoretical reference for further research into the impact mechanics of composite materials subjected to bird strikes.

1. Introduction

Bird strikes during takeoff and landing are more common with private airplanes. Before using an aircraft, all components must meet aircraft certification requirements for resistance to bird impact to assure aviation safety [1,2]. Composite materials offer high specific strength, high specific stiffness, good fatigue resistance, high-temperature resistance, strong designability, and impact resistance [3,4,5]. It is widely utilized across numerous sectors, including automotive, medical, sports, and aerospace [6,7]. Through an in-depth investigation into the failure mechanisms of composite structures during bird strikes, significant theoretical and engineering applications helped reduce both the incidence and severity of bird strikes.

Experimental testing is often costly and time-consuming. Consequently, numerical simulation is widely used to analyze bird strikes and accelerate structural optimization [8,9]. Researchers conducted extensive parametric studies to investigate the effects of bird strikes. Meguid et al. [10] examined bird strikes across different avian geometries, with the cylindrical configuration being the most common. Puneeth et al. [11] demonstrated that high-mass birds result in a sharp increase in stress and strain. Wu et al. [12] conducted simulation studies at varying impact heights. They found that the increased height of the bird strike reduces the impact force due to the greater blade twist angle. Some researchers investigated how composite mechanical characteristics affect the ecosystem, including factors such as heat, humidity, UV light, salt spray, wind, and sand. Several academics have refined the layering technique. The π/4 stacking approach is applied to aeronautical structures. Quad laminates with high strength and stiffness in specific positions and directions are produced by varying the quantity and placement of 0°, 90°, and ±45° stacking. This article examined the effects of various laminated composites on the birds’ impact.

The progressive failure approach for composite materials gained popularity in the 1980s. Numerous published studies contributed to the maturation of progressive failure analysis. Given the impact of layup thickness on material strength, Catalanotti et al. [13] proposed a set of failure criteria that considers the longitudinal and transverse failure mechanisms. Their test results and the projected results agreed well. Numerous failure criteria have been established for fiber-reinforced polymers. Tsai and Wu [14] avoided specifying a particular failure mechanism when they initially applied a secondary failure criterion to stress space. Hashin [15,16] developed the fiber and matrix-failure criterion based on the Mohr-Coulomb failure hypothesis. Chang-Chang [17] suggested stress-based transverse and longitudinal tension standards for substrates and fibers.

Numerous researchers conducted finite-element numerical studies of the damage mechanism and mechanical response of composite laminates to low-speed bird impacts. Zhao and Cho [18], Riccio et al. [19] and Li et al. [20] used the Hashin standard. Meo et al. [21] used the Chang-Chang standard. Donadon et al. [22], Faggiani and Falzon [23], Shi et al. [24], and Feng and Aymerich [25] used the Puck standard. These failure standards are generally applicable under quasi-static loads, although their application to dynamic loads still requires clarification [26]. This article primarily uses experimental data to validate the finite element simulation results before conducting an exploratory simulation experiment. Carbon fiber composite fiber tension, compression, and matrix tension failure standards are based on the three-dimensional (3D) Hashin standard. In contrast, the matrix compression failure standard is based on the puck [27] standard.

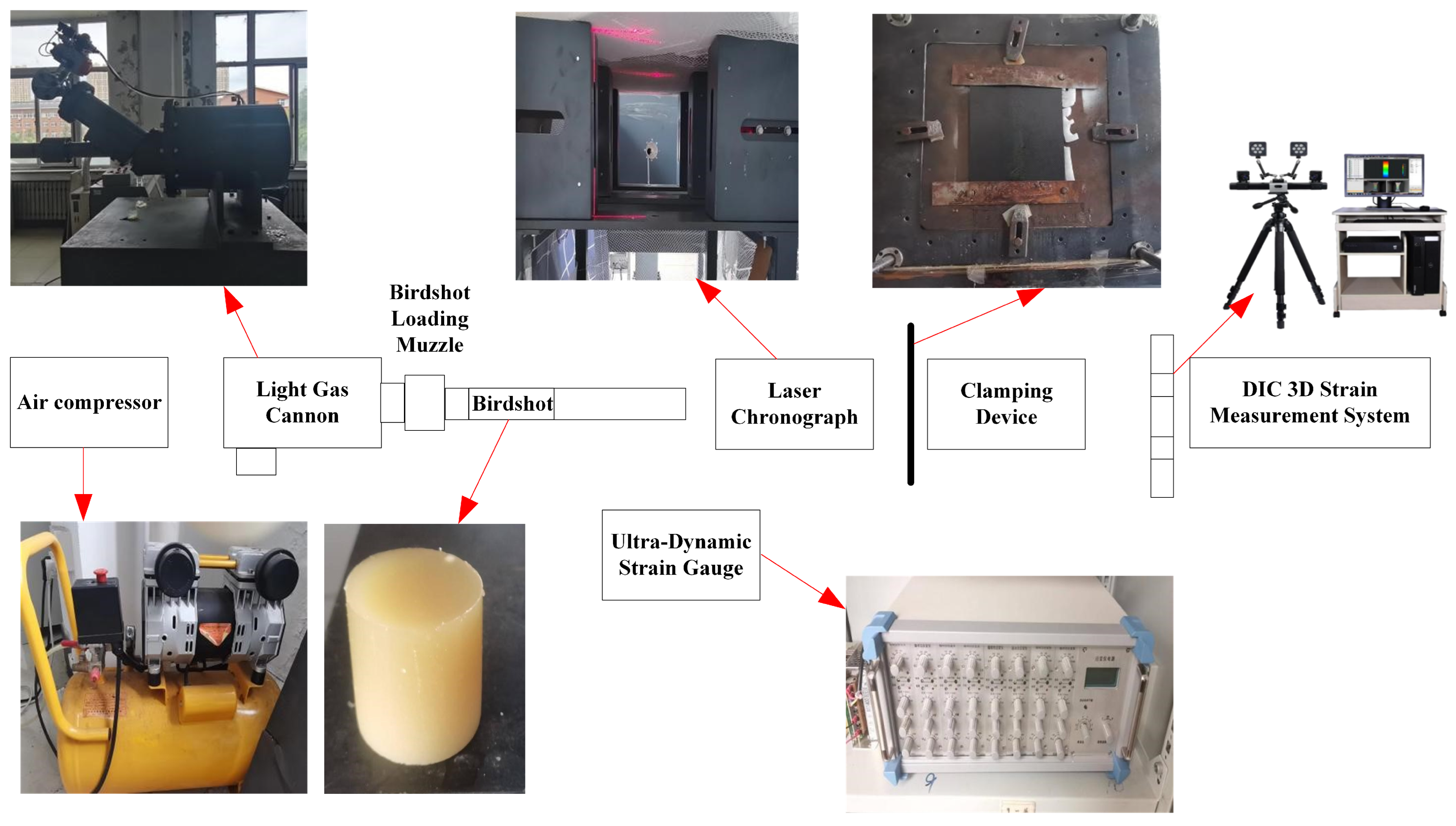
2. Experimentation

2.1. Experimental Scheme

This study used J3K-CT300 carbon fiber/epoxy composite material. Eight layers of ±45° twill braid material were employed to create a 300 × 300 mm plate up to 2.5 mm thickness. Carbon fiber laminates were tested by exposing them to bird-strike impacts at three distinct speeds—34, 36, and 38 m/s. The three experimental groups varied, but they verified each other because of the minimal difference in speed intervals. The primary goal of using a strain gauge was to obtain laminate strain data accurately for the simulation model.

2.2. Experimental Method

The experiment utilizes a light-air cannon to simulate a bird impact and regulates the air pressure in the light-air gun to control the speed of the bird bomb. A homemade gelatin bird bomb, with a mass of 115 g, a diameter of 50 mm, a height of 50 mm, and a density of 1126 kg/m³, was used to replicate the features of a bird impact. Figure 1 shows the platform for bird impact. The super-dynamic strain gauge is primarily used to collect strain during the impact.

2.3. Strain Gauge

The dynamic deformation of carbon fiber laminate during impact is referred to as strain. First, the impact position is identified as the plate’s center position after modifying the clamping position through pre-experiment. For carbon fiber laminates, five measurement locations were established. Strain gauges were attached 20 mm apart. Figure 2 shows the S3 as the impact center, and S1, S2, S4, and S5 as the impact edges.

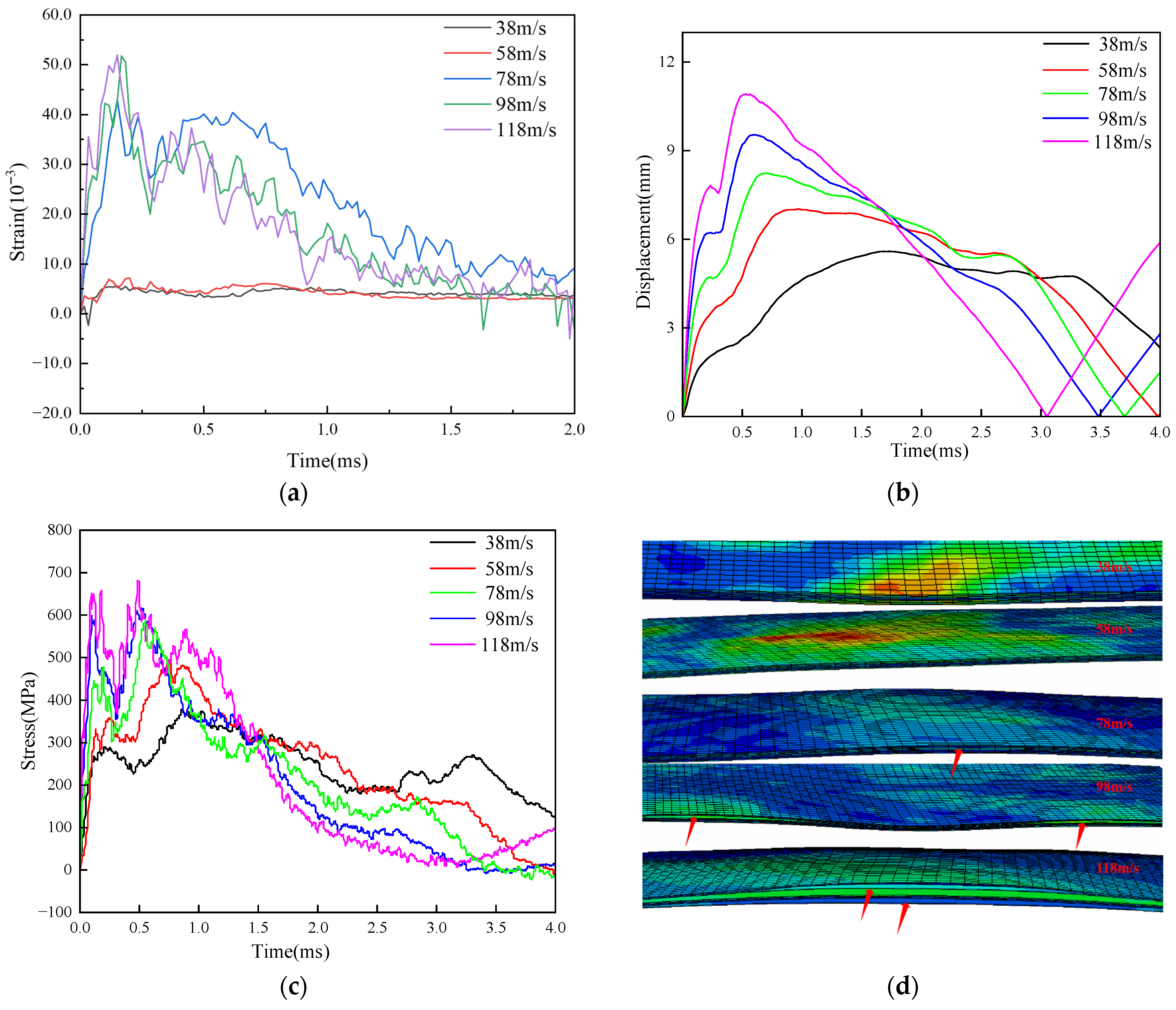
2.4. Experimental Results

This section examines the strain fluctuation curves of the T300 carbon fiber/epoxy composite under low-speed impact at various impact speeds (Figure 3). The strain curves of the carbon fiber/epoxy composite for the three low-speed impact states show that the composite experiences compressive strain, followed by tensile strain. At 34 m/s, the highest compressive strain is 0.26% (Figure 3a). The maximum compressive strain of 36 m/s is 0.37% (Figure 3b). At 38 m/s, the compressive strain is 0.47% (Figure 3c). The strain at 36 m/s was 0.11% higher than that at 34 m/s, while the strain at 38 m/s was 0.10% higher than that at 36 m/s. Impact primarily shows elastic deformation at low speeds. Because the speed intervals of the three groups are small, the strain data exhibit high repeatability, indicating the true reliability of the three groups. As a result, the variation in strain curves is the same across all three groups.

3. Simulation Methods

3.1. Bird Collision Impact Simulation Modeling

3.1.1. Bird Bullet Modeling

Figure 4a shows the simulation bird projectile model in ABAQUS (vrsion 6.13). The diameter of the bird’s body is 50 mm, and its height is 50 mm. This study utilized a gelatin bird projectile with a density of 1126 kg/m³. The properties of the simulated bird body match those of the bird projectile used in the experiment. The bird projectile is meshed, transforming the bird’s body into particles (SPH), as shown in Figure 4b. This study used a 5 mm bird projectile grid size because it is not an analysis object. The study used 960 grids for the bird projectile, with 1243 nodes. The bird projectile is assigned a velocity through predefined fields, as shown in Figure 5, and then assembled with the composite laminate.

3.1.2. Bird’s Body Constitutive State Equation

The SPH unit, combined with the state equation to create the bird’s body, can describe the bird’s fluid in high-speed motion. Since the SPH has no specific mesh restriction, it can address mesh distortion and discontinuity. The Mie-Gruneisen state equation of the bird’s body is expressed as follows:

$$P={\displaystyle \frac{{\rho }_0{c}_0^2\eta }{{\left(1-s\eta \right)}^2}}\left(1-{\displaystyle \frac{{\Gamma }_0\eta }{2}}\right)+{\Gamma }_0{\rho }_{0}e$$

(1)

where the material’s sound propagation speed c₀ is 1480 m/s, the starting density is ρ₀. Material constant ${\Gamma }_0$ is 0, and slope coefficient s is 0.

3.1.3. Composite Laminate Modeling

A solid model of a carbon fiber composite laminate was developed, measuring 300 × 300 mm, with the material divided into eight layers. The material orientation is assigned in the properties. A finite-thickness cohesive model between layers was developed to simulate the interlayer composite material properties. The composite laminate was meshed with a 3 mm grid size, as shown in Figure 6a. The laminate consists of 47,432 C3D8R elements and 41,503 COH3D8 elements, totaling 97,344 nodes. The boundary of the composite material was constrained by applying boundary conditions. Figure 7 shows that the four sides of the composite laminate are fully constrained. A rigid frame is added to the back of the composite laminate to constrain the composite laminate, as shown in Figure 6b. Finally, it is assembled with the bird’s body.

3.2. Composite Material Constitutive Model

Composite failure due to bird impacts can be done in two ways. One is fiber fracture-induced damage, also known as intralayer failure. The other is the occurrence of stratification or interlayer collapse between neighboring layers. The progressive damage model uses the failure initiation criterion, the damage evolution model, and the continuous damage model to simulate the impact damage [26].

In-Layer Stress–Strain Relationship

Equation (2) illustrates the initial stress–strain relationship. A continuous damage model describes the progressive failure behavior of composite materials [22] due to cumulative damage and deterioration properties of composite laminates under impact load.

$${\sigma }_{\mathit{ij}}{=C}_{\mathit{ijkl}}{\epsilon }_{\mathit{kl}}$$

(2)

where 1, 2, and 3 at the lower corner mark are the three fiber directions, and σ_ij, C_ijkl, and ε_kl (i, j, k, l = 1, 2, 3) for engineering stress, stiffness matrix, and engineering strain, respectively. When the composite satisfies the requirements for damage initiation, the symmetric damage stiffness matrix can be expressed in terms of five independent engineering constants, as used in Equations (3) and (4). There are three independent engineering constants (E_ij, ν_ij, G_ij). The symmetric damage stiffness matrix can be established when the composite satisfies the requirements for damage initiation given in Equations (3) and (4) [28].

In Equation (4), the damage variables for the fiber and matrix are denoted by d_f and dm, respectively. These variables were derived from the corresponding damage variables d_I. The fiber and matrix damage during stretching are represented by ft and mt, respectively, and during compression are given by fc and mc, respectively. In this case, the shear stiffness loss due to matrix damage under tensile and compressive loads is controlled by the stiffness correction coefficients of the fiber and matrix under tensile and compressive loads [29] (S_mt and S_mc). The existing literature [29,30,31,32] used the S_mt and S_mc values of 0.9 and 0.5, respectively.

$$C^d={\displaystyle \frac{1}{\Delta }}\left[\begin{array}{llllll}{d}_f{E}_{11}(1-d_m{\nu }_{23}{\nu }_{32})& { d}_f{d}_m{E}_{11}({\nu }_{21}+{\nu }_{23}{\nu }_{31})& { d}_f{E}_{11}({\nu }_{31}+d_m{\nu }_{21}{\nu }_{32})& & & \\ & {\hspace{1em} d}_m{E}_{11}(1-d_f{\nu }_{13}{\nu }_{31})& \hspace{1em} d_m{E}_{22}({\nu }_{32}+d_f{\nu }_{12}{\nu }_{31})& & & \\ & & \hspace{1em} \hspace{1em} E_{33}(1-d_f{d}_m{\nu }_{12}{\nu }_{21})& & & \\ & \hspace{1em} \mathit{symmetric}& & K_1& & \\ & & & & K_2& \\ & & & & & K_3\end{array}\right]$$

(3)

$$\begin{array}{l}{K}_1=\Delta d_f{d}_m{G}_{12}\\ K_2=\Delta d_f{d}_m{G}_{23}\\ K_3=\Delta d_f{d}_m{G}_{13}\\ d_f=(1-d_{\mathrm{ft}})(1-d_{\mathrm{fc}})\\ d_m=(1-S_{\mathrm{mt}}{d}_{\mathrm{mt}})(1-S_{\mathrm{mc}}{d}_{\mathrm{mc}})\\ \Delta =1-d_f{d}_m{\nu }_{12}{\nu }_{21}-d_m{\nu }_{23}{\nu }_{32}-d_f{\nu }_{13}{\nu }_{31}-2d_f{d}_m{\nu }_{21}{\nu }_{32}{\nu }_{31}\end{array}$$

(4)

3.3. Failure Criterion and Damage Evolution Law of Composite Materials

Stress or strain can be used to establish the failure criterion for both fiber and matrix. Hashin proposed fiber and matrix criteria based on stress. Because strain is more continuous than stress during the damage evolution of composite materials [33], Huang and Lee’s experiments suggested that strain is a better indicator of failure. The Puck standard accounts for matrix-compression-induced fracture surfaces in addition to the Hashin and Chang-Chang standards. This study used the puck standard for the matrix-compression damage equation. Donadon et al. [23] also employed this method in their study to perform an impact analysis. Liu et al. [26] evaluated the three criteria (except matrix compression) for calculating fiber stretching, fiber compression, and matrix stretching, finding that they were essentially the same.

3.3.1. Fiber’s Tension and Compression

Equations (5) and (6) express the fibers’ tensile and compressive failure criteria.

$$F_{11}^T={\left({\displaystyle \frac{E_{11}}{E_{0,1}^T}}\right)}^2-1\ge 0$$

(5)

$$F_{11}^C={\left({\displaystyle \frac{E_{11}}{E_{0,1}^C}}\right)}^2-1\ge 0$$

(6)

where Equation (7) provides the initial values of the tensile failure strain (represented by $E_{0,1}^T$) and compressive failure strain (represented by $E_{0,1}^C$).

$$E_{0,1}^T={\displaystyle \frac{X^T}{E_1}},E_{0,1}^C={\displaystyle \frac{X^C}{E_1}}$$

(7)

The evolution law of fiber tensile and compressive damage with X^T and X^C representing the fibers’ respective tensile and compressive strengths is expressed as follows:

$$d_{11}^{T\left(C\right)}={\displaystyle \frac{E_{f,1}^{T\left(C\right)}}{E_{f,1}^{T\left(C\right)}-E_{0,1}^{T\left(C\right)}}}\left(1-{\displaystyle \frac{E_{0,1}^{T\left(C\right)}}{E_{11}}}\right)$$

(8)

When the damage variable approaches 1, the critical failure strain is represented by $E_{0,1}^{T\left(C\right)}$ and $E_{f,1}^{T\left(C\right)}$.

3.3.2. Matrix Stretch

Although micro-buckling causes fiber compression, it does not result in total collapse, even though it lowers the load-carrying capacity. The residual strength, or the fiber’s compressive strength, equals the matrix’s compressive strength [34]. Consequently, it is assumed that the damage caused by fiber compression and stretching is the same. There are various matrix tensile-compression failure criteria, but the most common matrix compression failure criteria and the evolution rules are given in Equations (9) and (10).

$$F_{22}^T={\left({\displaystyle \frac{E_{22}}{E_{0,2}^T}}\right)}^2-1\ge 0,{ E}_{0,2}^T={\displaystyle \frac{Y^T}{E_2}}$$

(9)

where $E_{0,2}^T$ is the matrix’s initial tensile failure strain, and Y^T represents its tensile strength.

The matrix’s tensile damage development law is expressed as follows:

$$d_{22}^T={\displaystyle \frac{E_{f,2}^T}{E_{f,2}^T-E_{0,2}^T}}\left(1-{\displaystyle \frac{E_{0,2}^T}{E_{22}}}\right)$$

(10)

where $E_{f,2}^T$ is the matrix tension’s critical failure strain.

3.3.3. Matrix Compression

Shear failure of unidirectional composite laminates occurs under transverse compression. Puck and Schürmann’s experimental [27] investigation shows that the angle of the fracture plane (θ_f) is 53 ± 2° concerning the thickness direction. The failure criterion based on Mohr-Coulomb theory is considered more appropriate since the fracture angle combines two or three stress transitions [22,24]. To obtain more accurate data under the Puck failure standard, Liu et al. [26] selected three distinct failure criteria for matrix compression. They compared the data and verified the findings. This study used the Puck failure standard Equations (11) and (12) as the matrix compression failure criterion.

$$\left\{\begin{array}{l}F(S_{\mathit{NN},}{S}_{\mathit{NT},}{S}_{\mathit{NL}})={\left({\displaystyle \frac{S_{\mathit{TN}}}{{\hat{S}}_{23}^A{+\mu }_{\mathit{TN}}{S}_{\mathit{NN}}}}\right)}^2+{\left({\displaystyle \frac{S_{\mathit{LN}}}{{\hat{S}}_{12}{+\mu }_{\mathit{LN}}{S}_{\mathit{NN}}}}\right)}^2\ge 1\\ S_{\mathit{LTN}}={T\left(\alpha \right)S}_{123}{T\left(\alpha \right)}^T,{ \mu }_{\mathit{TN}}=\mathit{tan}\left(\phi \right)=\mathit{tan}(2{\theta }_f-90)\\ T\left(\alpha \right)=\left[\begin{array}{ccc}1& 0& 0\\ 0& \mathit{cos}\left({\theta }_f\right)& {\mathit{sin}(\theta }_f)\\ 0& {-\mathit{sin}(\theta }_f)& {\mathit{cos}(\theta }_f)\end{array}\right], {\hat{S}}_{23}^A={\displaystyle \frac{Y^C}{2}}\left[{\displaystyle \frac{1-\mathit{sin}\left(\phi \right)}{\mathit{cos}\left(\phi \right)}}\right]\\ \phi =2{\theta }_f-90,{\displaystyle \frac{{\mu }_{\mathit{TN}}}{{\hat{S}}_{23}^A}}={\displaystyle \frac{{\mu }_{\mathit{NL}}}{{\hat{S}}_{12}}}\end{array}\right\}$$

(11)

where A and L are tangential with respect to the fracture surface’s direction, and N is along the normal direction. Y^C denotes the transverse compressive strength. The Piola Kirchhoff rotational stress S_ij (i = 1, 2, 3) transfers to the fracture surface, and the transformation matrix T(α) yields the stress S_ij (i = L, T, N). ${\hat{S}}_{23}^A$ is the transverse shear strength of the fracture surface, which is determined by the transverse compressive strength Y^C and the material friction angle $\phi$.

The damage evolution law follows the application of a bilinear model to the fracture surface, which can be expressed as:

$$\begin{array}{l}{d}_{22}^C{(\gamma }_{\mathit{NT}}{,\gamma }_{\mathit{NL}})={\displaystyle \frac{{\gamma }_{\gamma }^{\mathit{max}}}{{\gamma }_{\gamma }^{\mathit{max}}{-\gamma }_{\gamma }^f}}\left(1-{\displaystyle \frac{{\gamma }^f}{{\gamma }_{\gamma }}}\right)\\ {\gamma }_{\gamma }=\sqrt{{\gamma }_{\mathit{NT}}^2{+\gamma }_{\mathit{NL}}^2}{,\gamma }_{\gamma }^{\mathit{max}}={\displaystyle \frac{2{\Gamma }_{22}^C}{S_r^{0}l}},S=\sqrt{S_{\mathit{TN}}^2{+S}_{\mathit{NL}}^2}\end{array}$$

(12)

where the initial and critical combined shear strains are denoted by ${\gamma }_{\gamma }^f$ and ${\gamma }_{\gamma }^{\mathit{max}}$, respectively, strains γ_NT and γ_NL are related to stress S_NT and S_NL, respectively, and $S_r^0$ is the shear stress at initial failure. ${\Gamma }_{22}^C$ is the matrix compressive fracture energy.

3.4. Interlayer Cracking Model

The binding zone element, based on the bilinear tractor-separation relationship, is used to model interlayer delamination at the interface between adjacent layers in the composite. Mixed-mode loading determines hierarchical initiation and the associated restoration behavior. Therefore, this study assumed the beginning and spread of stratified damage using the secondary failure and the B-K standards [35], as represented in the equations:

$${\displaystyle \frac{{〈t_n〉}^2}{N^2}}+{\displaystyle \frac{t_s^2}{S^2}}+{\displaystyle \frac{t_t^2}{T^2}}=1$$

(13)

$$G^C{=G}_n^C+(G_s^C-G_n^C){\left\{{\displaystyle \frac{G_S}{G_T}}\right\}}^{\eta }$$

(14)

where N, S, and T are normal and shear strengths, respectively, whereas t_n, t_s, and t_t are normal and shear tractive forces, respectively. The total, normal, and tangential critical fracture energies are G^C, $G_n^c$, and $G_s^c$, respectively. G_S denotes the energy consumed by the plane. The total energy consumed in three directions is known as G_T. In the B-K equation, η is the material coefficient.

3.5. Material Parameters

Using a simplified integral element (C3D8R), the impacts of various damage initiation standards, evolution techniques, and numerical modeling methods of the interface model were examined to predict the low-speed impact behavior of carbon fiber composite layers. The Puck standard and finite-thickness clustering model has the highest computation accuracy among the various modeling techniques [29]. The finite-thickness bilinear cohesive unit (COH3D8) simulated the interlayer delamination. The parameters are listed in

Table 1. Modeling parameters of carbon fiber laminates.

Name	Parameters
Properties of carbon fiber composite material layers	$E_1=130 \mathrm{GPa}, E_2=E_3=7.7 \mathrm{GPa};$ $G_{23}=3.8 \mathrm{GPa}, G_{12}=G_{13}=4.8 \mathrm{GPa};$ ${\upsilon }_{12}={\upsilon }_{13} = 0.33, {\upsilon }_{23} = 0.35;$ $X^T= 2080 \mathrm{MPa}, X^C= 1250 \mathrm{MPa};$ $Y^T= 60 \mathrm{MPa}, Y^C= 140 \mathrm{MPa}; {\hat{S}}_{12}= {\hat{S}}_{13}= {\hat{S}}_{23} = 110 \mathrm{MPa},$ ${\Gamma }_{11}^T= 133 \mathrm{N/mm}, {\Gamma }_{22}^T= 0.6 \mathrm{N/mm};$ ${\Gamma }_{11}^C= 40 \mathrm{N/mm}, {\Gamma }_{22}^C=2.1\mathrm{N/mm}$
Interlayer properties	$E_n=E_s = E_t=10 \mathrm{GPa/mm}$ $N=S=T=30 \mathrm{MPa}$ $G_n^s= 0.6 \mathrm{N/mm}; G_S^C=2.1 \mathrm{N/mm}$ η = 1.45

. One common way laminates fail is through lamination damage, which significantly reduces the laminates’ bearing capacity. In stratified damage analysis, creating interlayer bonding contact or inserting a bonding device with zero/finite thickness (0.001 mm) is frequently employed. This article’s model grid comprises 35,000 COH3D8 elements and 40,000 C3D8R elements. The cohesive contact model, which accounts for the traction separation between layers, is developed to describe the delamination damage in the composite.

4. Simulation Results

4.1. Comparison of Experiment and Simulation Results

By comparing the strain, displacement, stress, and other parameters that represent the impact resistance of carbon fiber composites, the deformation can be predicted more accurately. Figure 8 compares the strain data obtained from the simulation and the test at the S3 position. The simulation and test data for the carbon fiber composite plate follow the compressive and tensile strain. The simulation model accurately replicated the test results, with the maximum compressive strain peak value being essentially identical.

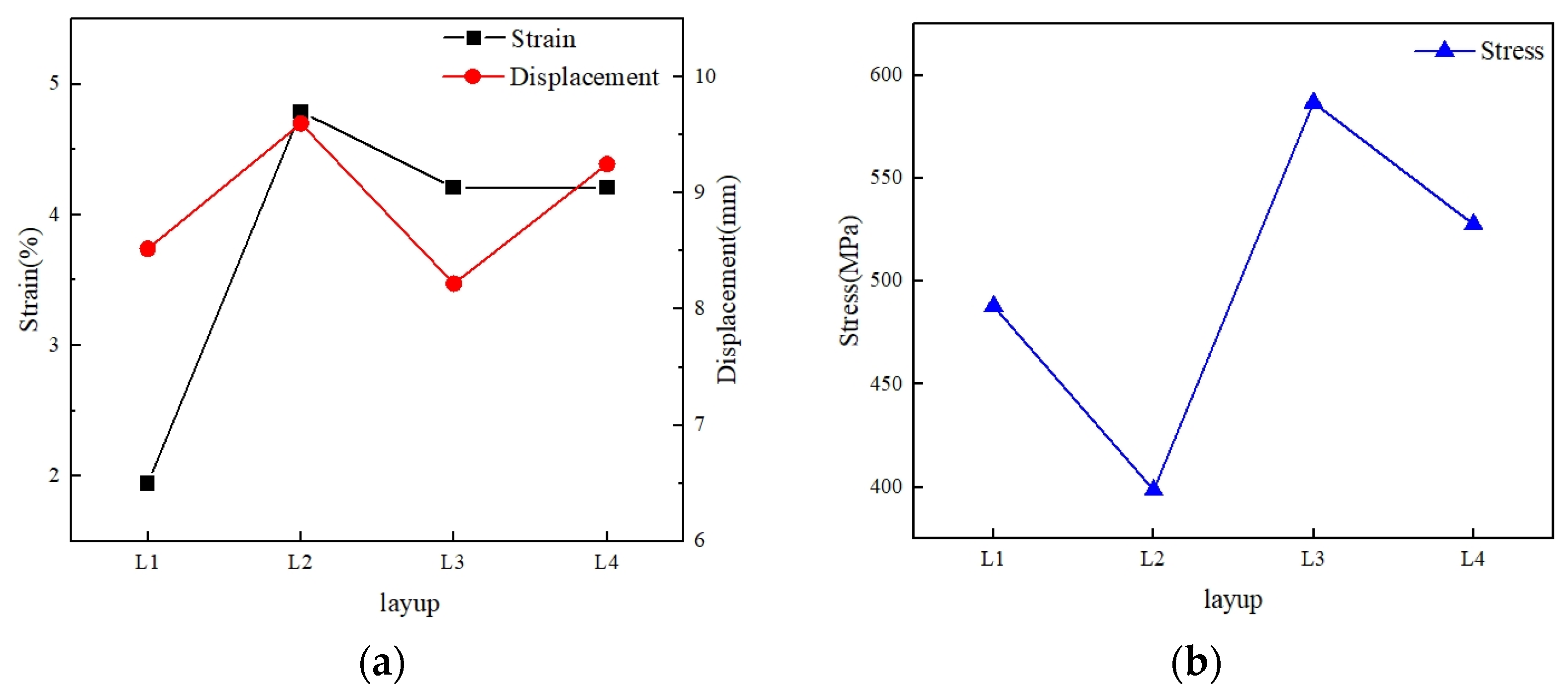
4.2. 115 g Bird Impacts on Different Carbon Fiber Layering

The mass of a 115 g bird impact is used to evaluate the effect of the carbon fiber laminate by varying the direction of layup. Since carbon fiber laminates are expensive and testing is uneconomical, this study used simulation to predict how various pavement layers are affected by birds impact.

The strain (Figure 9a), displacement (Figure 9b), and stress (Figure 9c) curves are shown at the S3 point of the L1[45/−45/45/−45]2S layup. The S3 point is the impact of the central location. Similarly, the subsequent layup spots are chosen. The impact velocities are 38 m/s, 58 m/s, 78 m/s, 98 m/s and 118 m/s. At 38 m/s and 58 m/s, the strains are 0.39% and 0.83%, respectively; the stresses are 319.64 MPa and 419.03 MPa, respectively; the displacements are 5.63 mm and 7.24 mm, respectively. At 78 m/s, the strain increases to 1.94%, the stress rises to 487.93 MPa, and the displacement increases to 8.52 mm. A slight delamination failure between the composite’s layers is observed when combined with the impact speed of 78 m/s, as shown in Figure 9d. The strain is 3.10% at 98 m/s, and the stratification is more noticeable at 98 m/s and 118 m/s. The displacement is 9.97 mm, and the stress is 523.40 MPa. The displacement increases from 9.97 mm (at 98 m/s) to 10.97 mm, the stress changes to 637.98 MPa, and the maximum strain at 118 m/s reaches 7.85%. It can be concluded that the L1 laminated carbon fiber sheet initiates delamination failure at 98 m/s when combined with the impact shape at 98 m/s, as shown in Figure 9d. In this study, all impact morphology diagrams are selected from the dynamic impact process, corresponding to the states when the delamination failure effect is most prominent at different velocities.

Figure 10 shows the changes in strain, displacement, and stress under the L2[45/0/45/0]2S scheme. The strain mutation speed of L2 paving is 58 m/s, and its strain reaches 3.90% (Figure 10a), stress 309.88 MPa (Figure 10c), and displacement is 8.30 mm (Figure 10b). Comparing with Figure 9, it is evident that the displacement is 1.06 mm greater than that of the L1 layer, and the L2 layer’s strain at 58 m/s is four times that of the L1 layer. Figure 10d’s impact form indicates no discernible delamination at 58 m/s. However, at 78 m/s, 98 m/s, and 118 m/s, delamination failure is apparent, and the corresponding stresses are 398.60 MPa, 527.01 MPa, and 619.40 MPa (Figure 10c), respectively. At 78 m/s, failure of the L2 layer initiates. The strain was distributed between 4% and 5.5% (Figure 10a).

The strain and displacement of L2 are compared with those of L1. The displacement of the L2 layer at 118 m/s is greater than that of L1, but the strain is more minor. Its stress exceeds the matrix’s tensile strength but not that of the fibers, indicating that the matrix has failed. At other speeds, the displacement and strain under the L2 layer are greater than those under the L1 layer, indicating that the L2 layer absorbs less impact energy than the L1 layer. The displacement recovery also shows that the composite under the L2 layer recovers less than the L1 layer, indicating that the L1 layer has greater stiffness.

The strain (Figure 11a), displacement (Figure 11b), and stress (Figure 11c) curves change during L3[45/0/−45/90]2S layup. At 78 m/s, the strain of this layup abruptly changes (i.e., 4.21%), the displacement increases to 8.22 mm, and the stress reaches 586.7 MPa. If the displacement value of 0.08 mm is less than that of the L1 layer, it is disregarded because the strain becomes twice that of the L1 layer at 78 m/s. However, the stress of L1 paving is lower. When compared with the impact states shown in Figure 9d and Figure 11d, it is evident that the delamination failure of the two pavement layers at 78 m/s is negligible and can be disregarded. L3 layering failure is more obvious at 98 m/s and 118 m/s. The entire plate is layered in the middle position, and the degree of delamination failure is greater than that of the L1 layering. The displacement of the L3 layering is 10.9 mm at 118 m/s, and the stress reaches 674.5 MPa, making it more susceptible to fiber fracture and other forms of failure. It demonstrates that the L1 fiber layering technique offers greater impact energy absorption, along with superior substrate and matrix stress and strain energy transfer. Furthermore, the carbon fiber layer and substrate beneath the L1 layer are better bonded, thereby hindering lamination failure.

The strain (Figure 12a), displacement (Figure 12b), and stress (Figure 12c) curves change under L4[0/90/0/90]2S layup. At 78 m/s, the layup strain reaches 4.21%, with a displacement of 9.25 mm and a stress of 527.6 MPa. Compared to the L1 layer, the strain is doubled, the displacement is greater by about 0.75 mm, and the stress is greater by approximately 41.6 MPa. The laminates exhibit noticeable delamination at 78 m/s under the impact condition, as shown in Figure 12d. The delamination failure degree of L4 is higher at 98 m/s and 118 m/s with maximum strains of 5.60% and 5.71%, maximum displacements of 10.7 mm and 12.06 mm, and maximum stresses of 723.88 MPa and 810.59 MPa, respectively. L4 varies insignificantly at 118 m/s, yet the stress and displacement are greater than those of L1, as compared to L4’s strain, displacement, and stress. L1 pavement exhibits a lower failure degree than L4 when strain, stress, and delamination at 78 m/s and 98 m/s are considered.

The examination of the four data sets indicates that failure occurs at 78 m/s except for the L1 layer, which fails at 98 m/s. The maximum stress, strain, and displacement of the four layup groups vary at 78 m/s. From the four bedding groups, L2 bedding exhibits minimal stress and the maximum strain and displacement. The stratification is relatively clear at 78 m/s for the L2, as shown in Figure 10d. Although the L4 pavement’s layered impact morphology is evident (Figure 12d), its peak strain and displacement rank second out of the four paving groups, and its stress is comparatively low. The strain and displacement of L1 and L3 bedding are less than those of the other two groups, as shown by the fluctuation trend in Figure 13a. However, stress (Figure 13b) shows the opposite pattern. Given that the 78 m/s impact state diagram (Figure 9d and Figure 11d) indicates a minimum degree of delamination failure, it can be inferred that the carbon fiber composite’s failure depends on the values of strain and displacement. The four paving groups can be ranked as L1, L3, L4, and L2. This is primarily due to the prevalence of 0° layers in the L2, which increases the overall longitudinal stiffness. During impact, the reduced bending deformation results in higher peak contact forces, causing the impact to dissipate more energy through delamination rather than being absorbed by overall deformation. Besides 0° layers, L4 contains 90° layers, which increases the overall transverse stiffness. During the impact phase, shear stress is more significant than normal stress in initiating delamination. Therefore, the performance of L2 was inferior to that of L4.

4.3. Influence of Various Impact Angles on Bird Impact

The purpose of this simulation is to examine how various paving layers react dynamically due to the bird impacts. This study examines which layering sequence performs better against bird impacts when various layering sequences are affected by the same angle. The study determined the best layup for a bird’s impact at multiple angles.

This section examines the dynamic response of carbon fiber composite laminates to a 115 g gelatin birdshot impact at 78 m/s. Figure 14 illustrates the varied angles at which carbon fiber composite laminates and birdshot laminates are created. Since the laminates’ normal vector is 0°, four angles are set at 0°, 22.5°, 45°, and 67.5°.

At various impact angles of 0°, 22.5°, 45°, and 67.5°, the morphology of L1[45/−45/45/−45]2S, L2[45/0/45/0]2S, L3[45/0/−45/90]2S and L4[0/90/0/90]2S pavement impacting the carbon fiber laminates, as shown in Figure 15. After simulating the layers struck at several speeds, it was found that nearly all layers were unable to stratify at 78 m/s when hit by a 115 g bird. Figure 15a shows the impact morphology at all angles, indicating no obvious delamination failure or fiber fracture at all angles. This also implies that L1 layering failure is not significantly related to the impact angle. Delamination failure in the L2 layer occurs at 0° impact when compared with the impact morphology of Figure 15b. However, at 22.5°, 45°, and 67.5° angles, the impact delamination failure disappears, suggesting that the impact damage of carbon fiber composite impact laminates is minimized at these angles. It also demonstrates how the angle of the birdshot and composite laminates affects the extent of impact damage. Compared with the impact morphology shown in Figure 15c, it is evident that the four sets of angles under the L3 paving layer do not cause any visible delamination failure or other failure modes. As shown in Figure 15d, the layer and plate of the L4 layering have the lowest impact resistance. It is the only group that experiences delamination failure under the impact of a bird at 22.5°. No delamination failure occurred in the four groups at 22.5° (Figure 15) when compared with the three other groups.

The displacement, strain, and stress attain the maximum values at 0° when the impact occurs in the normal direction of the composite material. The maximum strain of four sets of distinct bedding layers is affected by birdshot at various angles, as shown in Figure 16a. The figure indicates that the peak value of strain is greatly impacted by changes in the impact angle, with the L1 bedding strain being the only one that is least impacted. The other three bedding layers are all susceptible to changes in the impact angle. Figure 16b shows that the displacement evenly diminishes as the impact angle increases. The maximum displacement decreases dramatically around 67.5°, whereas the reduction in displacement across the four groups of distinct pavement layers matches closely. L1 and L3 paving have superior anti-bird impact performance due to minimal displacement compared to L2 and L4. Angle affects the stress beneath the four paving layers (Figure 16c). At 45° and 67.5°, the stress of the L1 paving layer drops dramatically, but the stress of the L2 paving layer remains constant with varying angles. At 0°, 22.5°, and 45°, the stress of the L3 and L4 pavement layers is larger. At an impact angle of 67.5°, the stress decreases significantly. The results obtained indicate that L1 pavement offers the best impact resistance.

5. Conclusions

This study primarily used the simulation data of carbon fiber composites with four fiber orientations. The simulation investigated the 115 g bird’s impact at various angles against carbon fiber composite panels with different fiber orientations: L1, L2, L3, and L4. The bird’s impact on the panels was studied at 22.5°, 45°, 67.5°, and 90° relative to the normal vector of the carbon fiber composite panel.

Stress, strain, displacement, and the laminates’ impact state diagram were studied to predict the failure and determine other properties. The results showed that the L1 layer exhibits a higher delamination failure rate, indicating superior impact resistance. Among the four groups of layers, the L2 layer demonstrated the least bird-impact resistance.

The failure state of carbon fiber composites depends primarily on strain and displacement. It is only weakly related to stress, as determined by comparing the strain and displacement of the four layering groups with the delamination failure. The best performance of four sets of layers follows L1, L3, L4, and L2 under the 115 g bird’s projectile impact.

The impact angle significantly influences the force exerted during bird collisions. The strain value varies depending on the angle of impact. The strain value varies insignificantly across angles, with the maximum occurring at 0°. Displacement decreases evenly as the impact angle increases. Angular variations influence the stress distribution beneath the four layers, yet no clear patterns or characteristics emerge. As a result, it is more trustworthy to examine their anti-bird impact performance considering strain and displacement.