GPS-Based Relative Navigation for Laser Crosslink Alignment in the VISION CubeSat Mission
Abstract
1. Introduction
2. The VISION Mission
2.1. Mission Overview
2.2. Mission Requirements
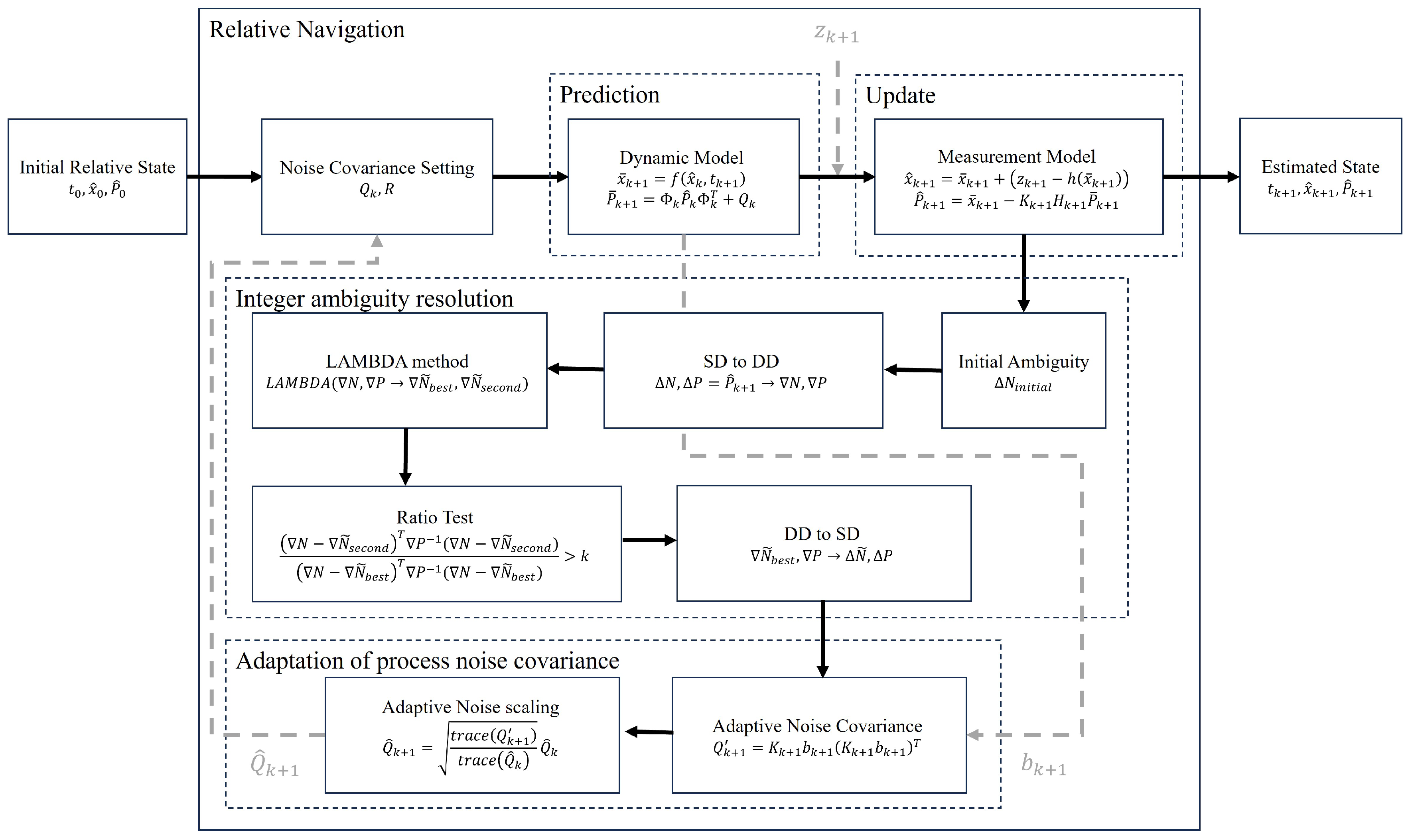
3. Development of VISION Relative Navigation System
3.1. Filter System
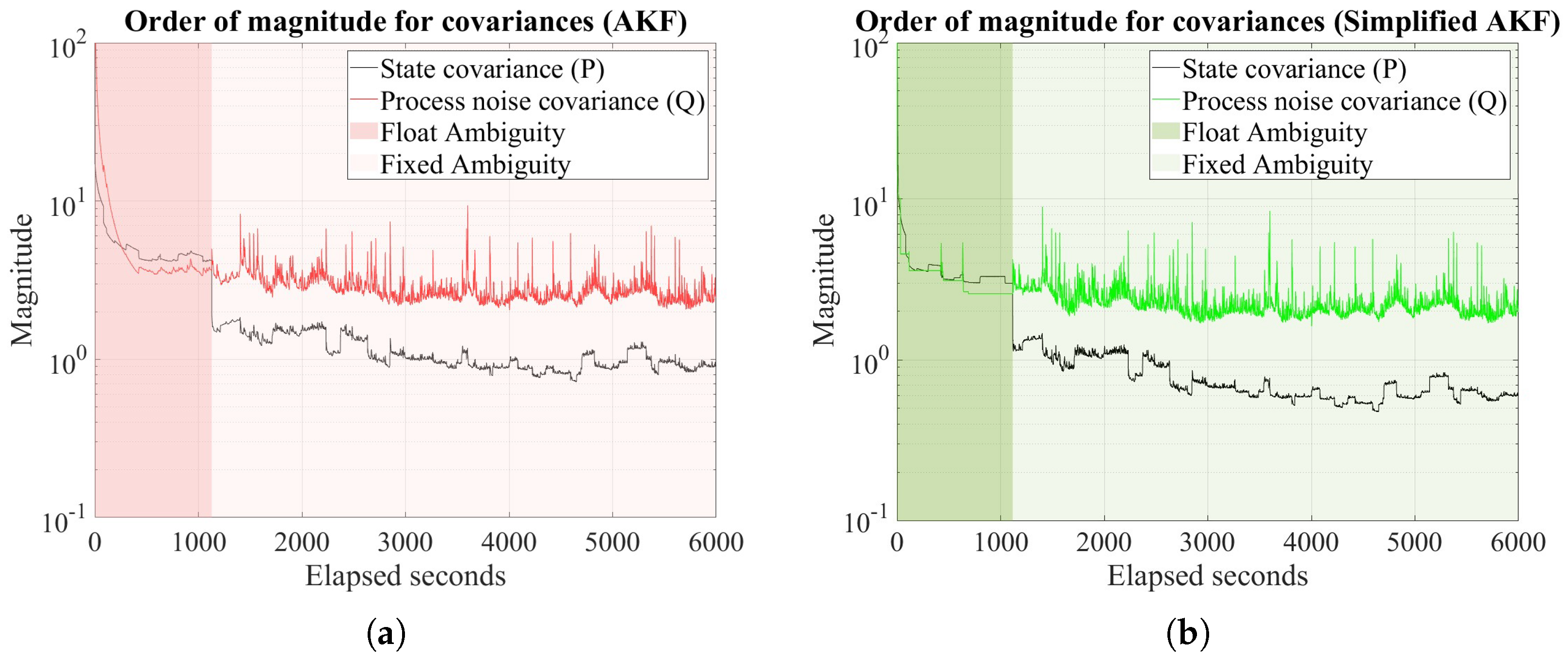
3.2. Adaptive Process Noise Covariance
3.3. Ambiguity Resolution and Cycle Slip Effect
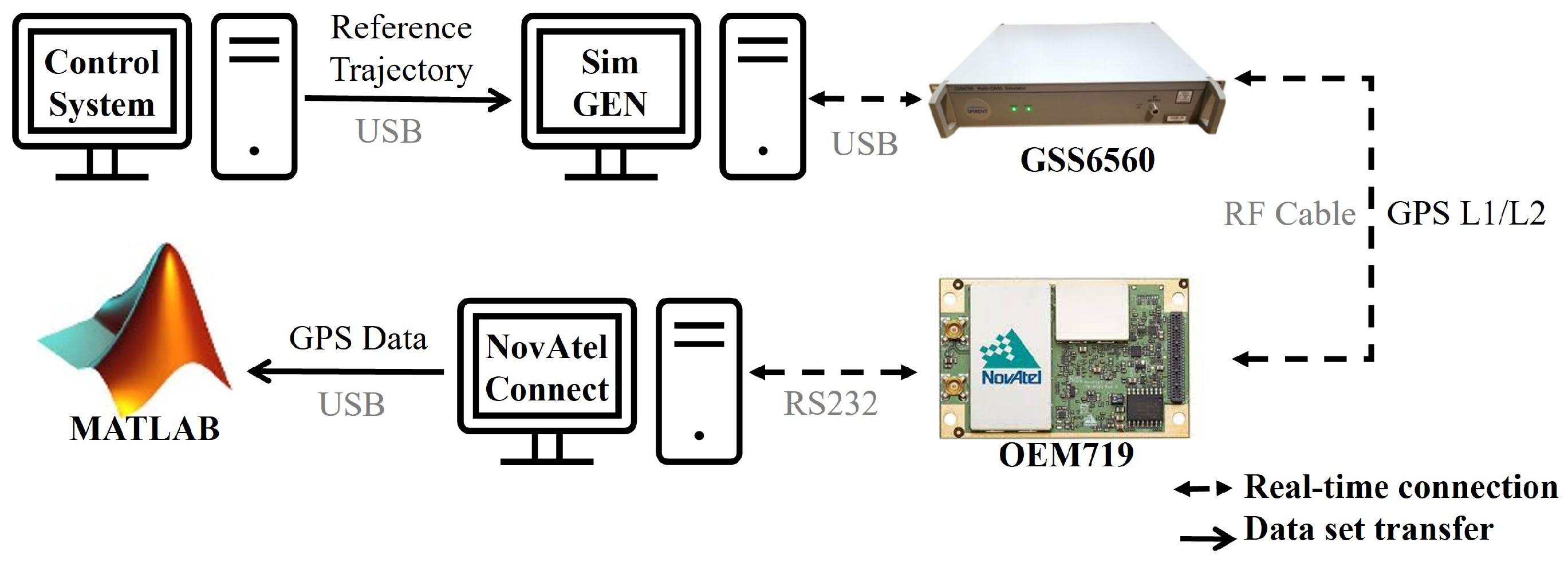
4. Numerical Assessment with Hardware Integration
4.1. Simulation Setup
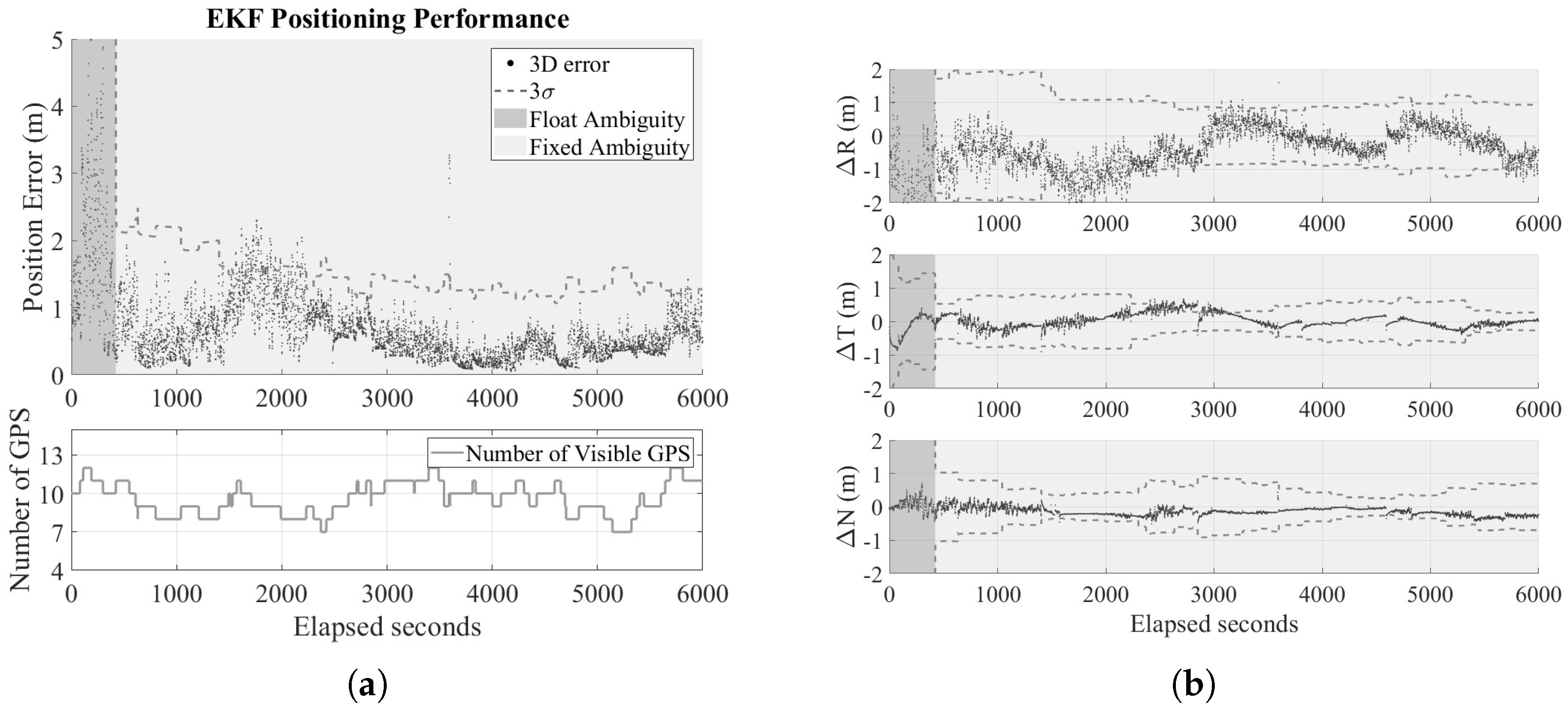
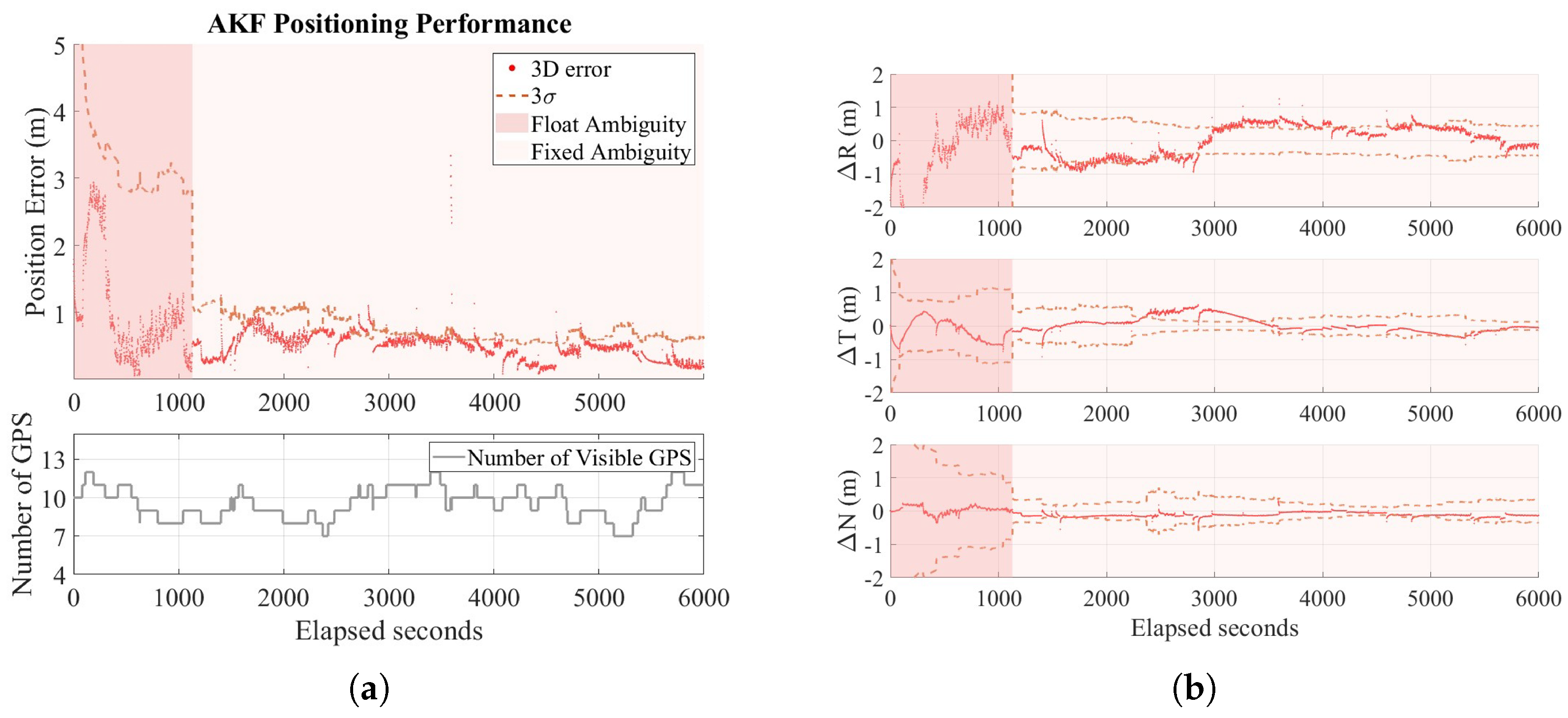
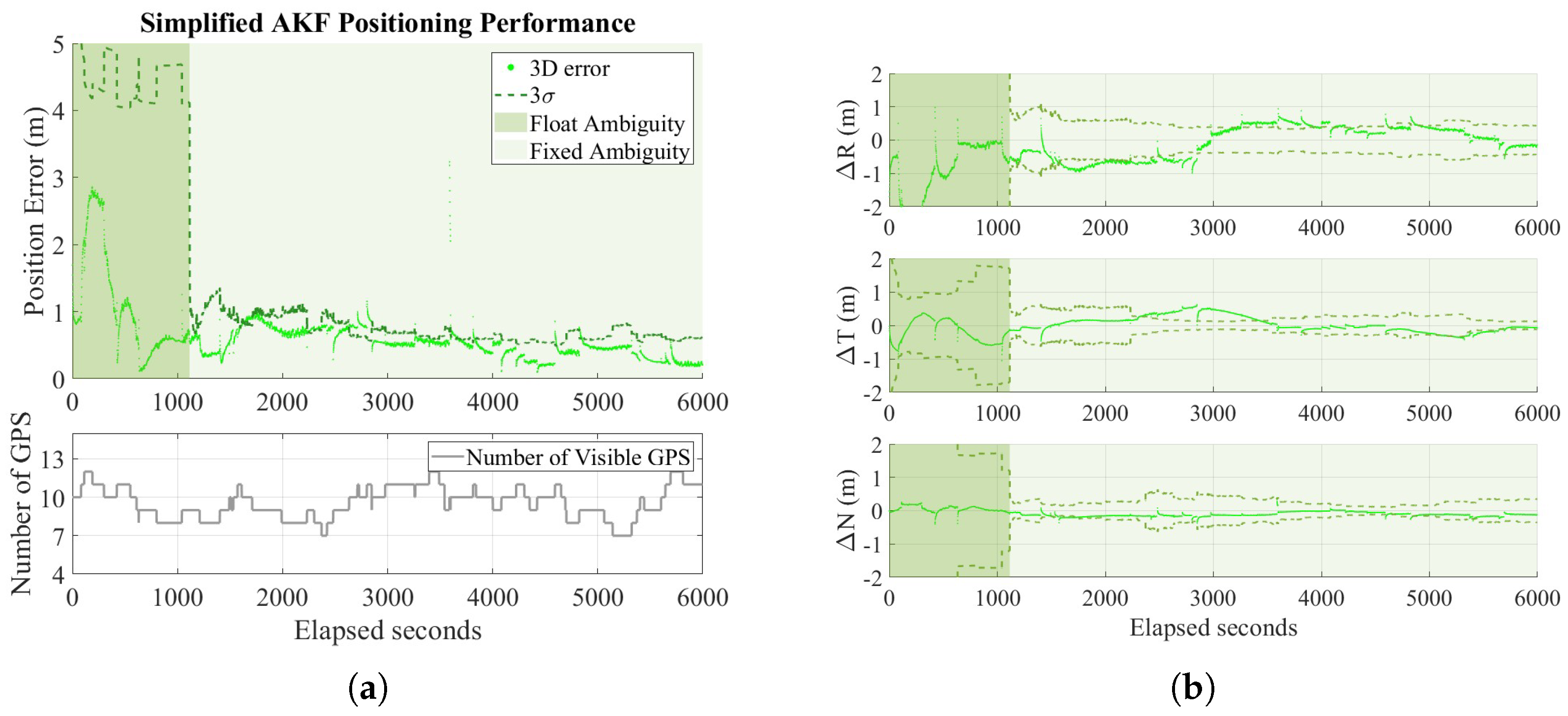
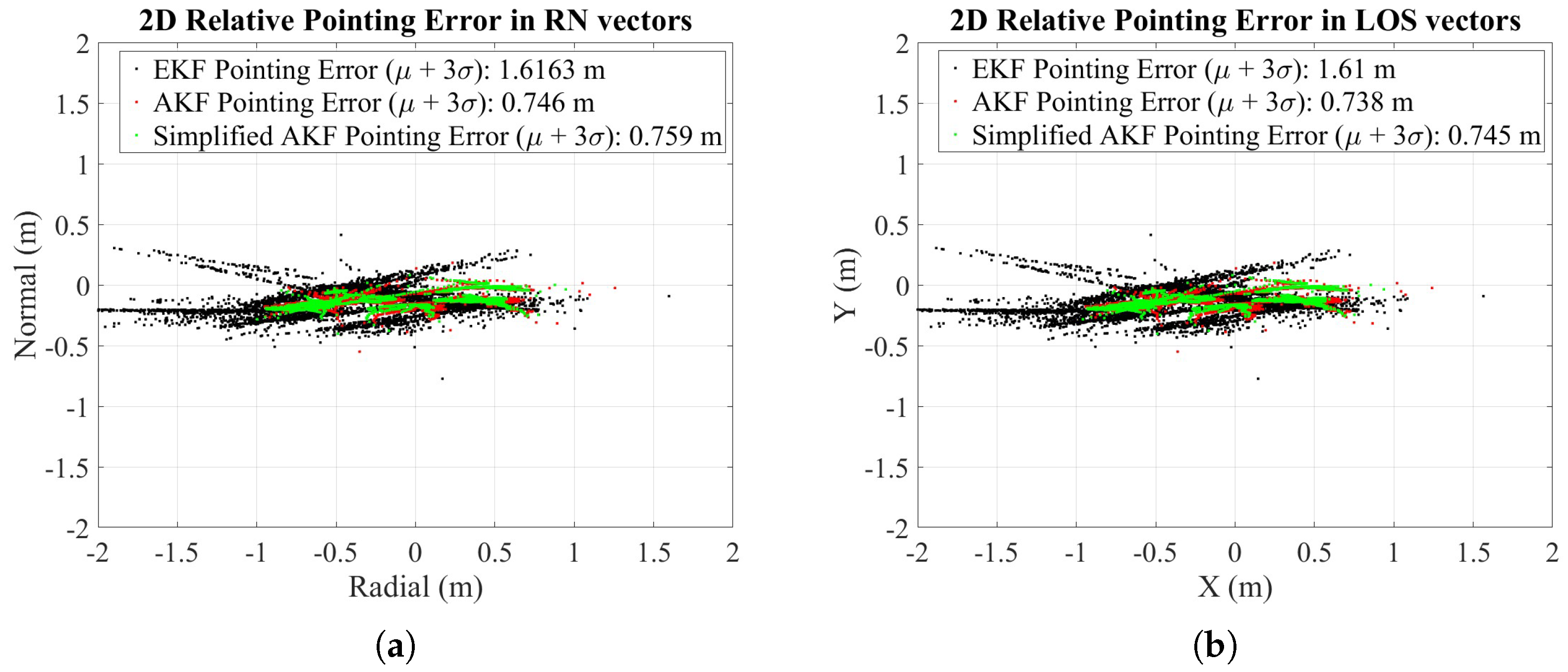
4.2. Simulation Results
5. Performance Evaluation of VISION Laser Crosslink Alignment
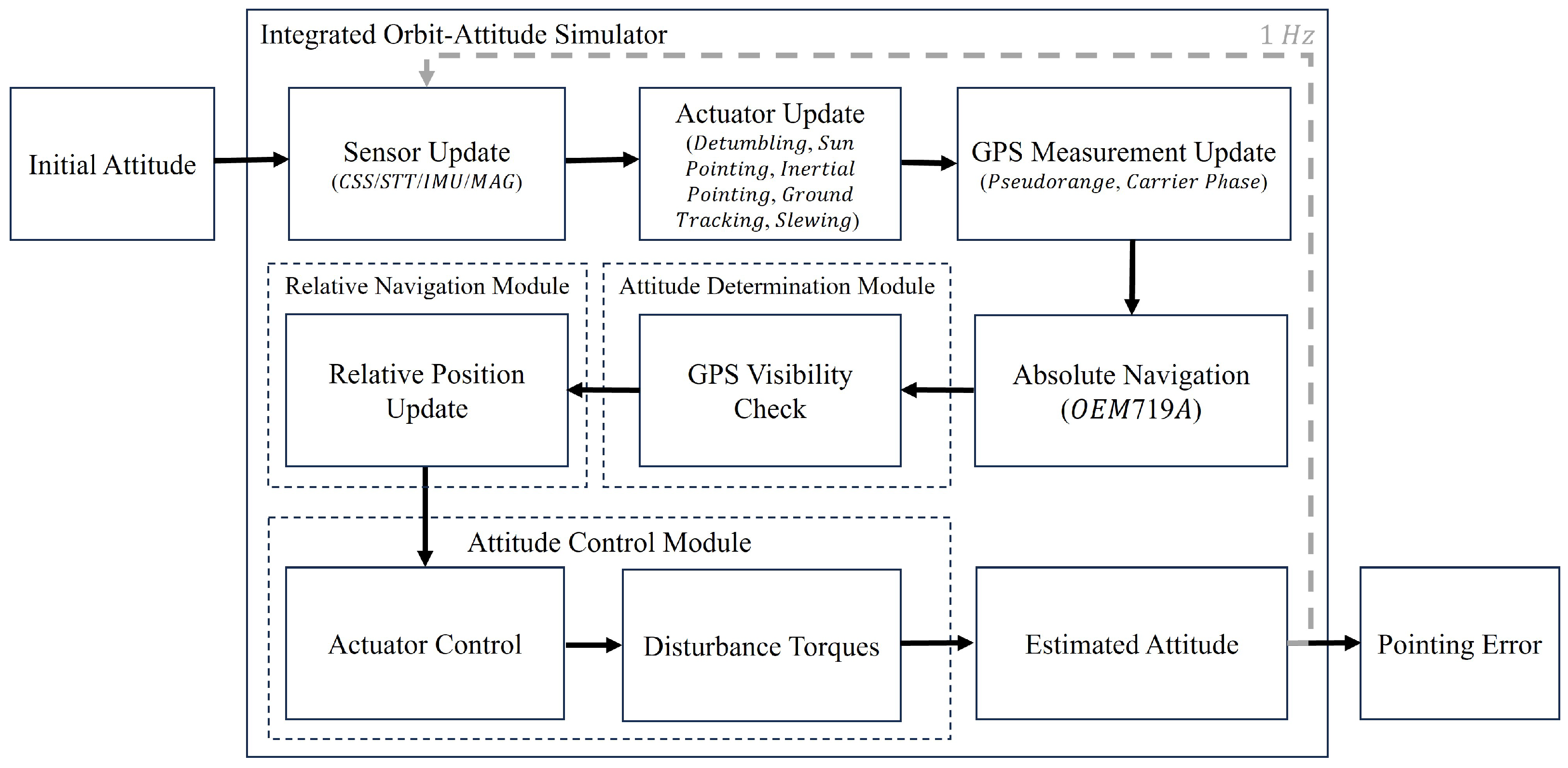
5.1. Integrated Orbit–Attitude Framework
5.2. Laser Crosslink System Tests
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- NGMN Alliance e.V. Non-Terrestrial Networks Position Paper; Project: Extreme Long-Range Communications for Deep Rural Coverage, Issue 11; NGMN Alliance e.V.: Dusseldorf, Germany, 2019. [Google Scholar]
- 3GPP. Study on New Radio (NR) to Support Non-Terrestrial Networks; Technical Report TR 38.811, V15.0.0; 3rd Generation Partnership Project (3GPP): Valbonne, France, 2020. [Google Scholar]
- Heidt, H.; Puig-Suari, J.; Moore, A.; Nakasuka, S.; Twiggs, R. CubeSat: A New Generation of Picosatellite for Education and Industry Low-Cost Space Experimentation. In Proceedings of the 14th Annual AIAA/USU Conference on Small Satellites, Logan, UT, USA, 21–24 August 2000. Paper No. SSC00-V-5; Utah State University Digital Commons. [Google Scholar]
- Toyoshima, M. Trends in Satellite Communications and the Role of Optical Free-Space Communications. J. Opt. Netw. 2005, 4, 300–311. [Google Scholar] [CrossRef]
- Saeed, N.; Elzanaty, A.; Almorad, H.; Dahrouj, H.; Al-Naffouri, T.Y.; Alouini, M.S. CubeSat Communications: Recent Advances and Future Challenges. IEEE Commun. Surv. Tutor. 2020, 22, 1839–1862. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The Gravity Recovery and Climate Experiment: Mission Overview and Early Results. Geophys. Res. Lett. 2004, 31, L09607. [Google Scholar] [CrossRef]
- Zink, M.; Krieger, G.; Fiedler, H.; Moreira, A. The TanDEM-X Mission: Overview and Status. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Barcelona, Spain, 23–27 July 2007; pp. 3944–3947. [Google Scholar]
- Serra, P.; Cierny, O.; Diez, R.; Grenfell, P.; Gunnison, G.; Kammerer, W.; Kusters, J.; Payne, C.; Murphy, J.; Sevigny, T.; et al. Optical Communications Crosslink Payload Prototype Development for the CubeSat Laser Infrared Crosslink (CLICK) Mission. In Proceedings of the 33rd Annual AIAA/USU Conference on Small Satellites, Logan, UT, USA, 3–8 August 2019. Paper No. SSC19-109; Utah State University Digital Commons. [Google Scholar]
- Orr, N.G.; Eyer, J.K.; Larouche, B.P.; Zee, R.E. Precision Formation Flight: The CanX-4 and CanX-5 Dual Nanosatellite Mission. In Proceedings of the 21st Annual AIAA/USU Conference on Small Satellites, Logan, UT, USA, 13–16 August 2007. Paper No. SSC07-VI-2; Utah State University Digital Commons. [Google Scholar]
- Kim, G.-N.; Park, S.-Y.; Kang, D.-E.; Son, J.; Lee, T.; Jeon, S.; Kim, N.; Park, Y.-K. Development of CubeSats for CANYVAL-C Mission in Formation Flying. In Proceedings of the Asia Pacific International Symposium on Aerospace Technology (2019: Gold Coast, Qld.), Gold Coast, Australia,, 4–6 December 2019; pp. 813–824, Engineers Australia. [Google Scholar]
- Scholz, A.; Giesselmann, J.; Duda, C. CubeSat Technical Aspects. In Proceedings of the 55th International Astronautical Congress of the International Astronautical Federation, the International Academy of Astronautics, and the International Institute of Space Law, Vancouver, BC, Canada, 4–8 October 2004. Paper No. IAC-04-P.5.08. [Google Scholar]
- Reddy Tummala, A.; Dutta, A. An Overview of Cube-Satellite Propulsion Technologies and Trends. Aerospace 2017, 4, 58. [Google Scholar] [CrossRef]
- Welle, R.P.; Janson, S.; Rowen, D.; Rose, T. CubeSat-Scale Laser Communications. In Proceedings of the 31st Space Symposium, Colorado Springs, CO, USA, 13–16 April 2015. [Google Scholar]
- Kaushal, H.; Kaddoum, G. Optical Communication in Space: Challenges and Mitigation Techniques. IEEE Commun. Surv. Tutor. 2016, 19, 57–96. [Google Scholar] [CrossRef]
- Carrasco-Casado, A.; Biswas, A.; Fields, R.; Grefenstette, B.; Harrison, F.; Sburlan, S.; Toyoshima, M. Optical Communication on CubeSats-Enabling the Next Era in Space Science. In Proceedings of the 2017 IEEE International Conference on Space Optical Systems and Applications (ICSOS), Tokyo, Japan, 14–16 November 2017; pp. 46–52. [Google Scholar]
- Rose, T.S.; Rowen, D.W.; LaLumondiere, S.; Werner, N.I.; Linares, R.; Faler, A.; Wicker, J.; Coffman, C.M.; Maul, G.A.; Chien, D.H.; et al. Optical Communications Downlink from a 1.5 U CubeSat: OCSD Program. In Proceedings of the International Conference on Space Optics-ICSO 2018, Chania, Greece, 9–12 October 2018; Meynart, R., Sodnik, Z., Cugny, B., Eds.; SPIE: Bellingham, WA, USA, 2019; Volume 11180, pp. 201–212. [Google Scholar]
- Sansone, F.; Francesconi, A.; Corvaja, R.; Vallone, G.; Antonello, R.; Branz, F.; Villoresi, P. LaserCube Optical Communication Terminal for Nano and Micro Satellites. Acta Astronaut. 2020, 173, 310–319. [Google Scholar] [CrossRef]
- Pimentel, P.M.; Rödiger, B.; Schmidt, C.; Fuchs, C.; Rochow, C.; Hiemstra, T.; Zager, A.; Wertz, P.; Knopp, M.; Lehmann, M.; et al. Cube Laser Communication Terminal (CubeLCT) State of the Art. Acta Astronaut. 2023, 211, 326–332. [Google Scholar] [CrossRef]
- Rödiger, B.; Menninger, C.; Fuchs, C.; Grillmayer, L.; Arnold, S.; Rochow, C.; Wertz, P.; Schmidt, C. High Data-Rate Optical Communication Payload for CubeSats. In Laser Communication and Propagation Through the Atmosphere and Oceans IX; Hammel, H.T., Shaw, J.A., Eds.; SPIE: Bellingham, WA, USA, 2020; Volume 11506, pp. 12–24. [Google Scholar]
- Schmidt, C.; Rödiger, B.; Rosano, J.; Papadopoulos, C.; Hahn, M.T.; Moll, F.; Fuchs, C. DLR’s Optical Communication Terminals for CubeSats. In Proceedings of the 2022 IEEE International Conference on Space Optical Systems and Applications (ICSOS), Cocoa Beach, FL, USA, 28–31 March 2022; pp. 175–180. [Google Scholar]
- Kammerer, W.; Grenfell, P.; Hyest, L.; Serra, P.; Tomio, H.; Belsten, N.; Lindsay, C.; Cierny, O.; Cahoy, K.; Clark, M.; et al. CLICK Mission Flight Terminal Optomechanical Integration and Testing. In Proceedings of the International Conference on Space Optics-ICSO 2022, Antibes Juan-les-Pins, France, 3–7 October 2022; Sodnik, Z., Cugny, B., Cornwell, C., Eds.; SPIE: Bellingham, WA, USA, 2023; Volume 12777, pp. 1292–1307. [Google Scholar]
- Cahoy, K.; Grenfell, P.; Crews, A.; Long, M.; Serra, P.; Nguyen, A.; Fitzgerald, R.; Haughwout, C.; Diez, R.; Aguilar, A.; et al. The CubeSat Laser Infrared Crosslink Mission (CLICK). In Proceedings of the International Conference on Space Optics-ICSO 2018, Chania, Greece, 9–12 October 2018; Sodnik, Z., Cugny, B., Cornwell, C., Eds.; SPIE: Bellingham, WA, USA, 2019; Volume 11180, pp. 358–369. [Google Scholar]
- Grenfell, P.; Aguilar, A.; Cahoy, K.; Long, M. Pointing, Acquisition, and Tracking for Small Satellite Laser Communications. In Proceedings of the 32nd Annual AIAA/USU Conference on Small Satellites, Logan, UT, USA, 4 August 2018. Paper No. SSC18-WKIX-05; Utah State University Digital Commons. [Google Scholar]
- Kim, G.-N.; Park, S.-Y.; Seong, S.; Lee, J.; Choi, S.; Kim, Y.-E.; Ryu, H.-G.; Lee, S.; Choi, J.-Y.; Han, S.-K. The VISION–Concept of Laser Crosslink Systems Using Nanosatellites in Formation Flying. Acta Astronaut. 2023, 211, 877–897. [Google Scholar] [CrossRef]
- Kim, G.-N.; Park, S.-Y.; Seong, S.; Choi, J.-Y.; Han, S.-K.; Kim, Y.-E.; Choi, S.; Lee, J.; Lee, S.; Ryu, H.-G.; et al. Design of Novel Laser Crosslink Systems Using Nanosatellites in Formation Flying: The VISION. Aerospace 2022, 9, 423. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, P.; Ryu, H.-G.; Park, S.-Y. Evaluating the On-Orbit Relative Navigation Performance of Modified Adaptive Kalman Filter with GPS Ambiguity Resolution. In Proceedings of the 2024 International Technical Meeting of The Institute of Navigation, Long Beach, CA, USA, 22–25 January 2024; pp. 658–676. [Google Scholar]
- Kim, Y.; Kim, P.; Ryu, H.-G.; Park, S.-Y. Performance Analysis of a Pointing, Acquisition, and Tracking System for the VISION Laser Crosslink Mission. In Proceedings of the 38th Annual AIAA/USU Conference on Small Satellites, Logan, UT, USA, 3 August 2024; pp. 658–676, Paper No.SSC24-S3-08; Utah State University Digital Commons. [Google Scholar]
- Minetto, A.; Falco, G.; Dovis, F. On the trade-off between computational complexity and collaborative GNSS hybridization. In Proceedings of the 2019 IEEE 90th Vehicular Technology Conference (VTC2019-Fall), Honolulu, HI, USA, 22–25 September 2019; pp. 1–5. [Google Scholar]
- Kahr, E.; Roth, N.; Montenbruck, O.; Risi, B.; Zee, R.E. GPS relative navigation for the CanX-4 and CanX-5 formation-flying nanosatellites. J. Spacecr. Rocket. 2018, 55, 1545–1558. [Google Scholar] [CrossRef]
- Lee, J. Development of Relative Navigation Algorithm for Inter-Satellite Free-Space Optical Communication Micro-Satellite Mission in Low Earth Orbit and Long Baseline Environment. Master’s Thesis, Yonsei University, Seoul, Republic of Korea, 2022. [Google Scholar]
- Teunissen, P.J.G. The least-squares ambiguity decorrelation adjustment: A method for fast GPS integer ambiguity estimation. J. Geod. 1995, 70, 65–82. [Google Scholar] [CrossRef]
- Welch, G.; Bishop, G. An Introduction to the Kalman Filter; University of North Carolina at Chapel Hill, Department of Computer Science: Chapel Hill, NC, USA, 1995. [Google Scholar]
- Parkinson, B.W. Global Positioning System: Theory and Applications II. In Progress in Astronautics and Aeronautics; Parkinson, B.W., Spilker, J.J., Eds.; AIAA: Washington, DC, USA, 1996; Volume 164, pp. 3–50. [Google Scholar]
- Kroes, R.; Montenbruck, O.; Bertiger, W.; Visser, P. Precise GRACE baseline determination using GPS. GPS Solut. 2005, 9, 21–31. [Google Scholar] [CrossRef]
- Bucy, R.S.; Joseph, P.D. Filtering for Stochastic Processes with Applications to Guidance; American Mathematical Society: Providence, RI, USA, 2005; Volume 326. [Google Scholar]
- Odijk, D. Ionosphere-Free Phase Combinations for Modernized GPS. J. Surv. Eng. 2003, 129, 165–173. [Google Scholar] [CrossRef]
- Simon, D. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Gao, Z.; Zhong, Y.; Zong, H.; Gao, G. Adaptive Random Weighted H∞ Estimation for System Noise Statistics. Int. J. Adapt. Control Signal Process. 2025, 39, 214–230. [Google Scholar] [CrossRef]
- Gao, B.; Gao, S.; Hu, G.; Zhong, Y.; Gu, C. Maximum likelihood principle and moving horizon estimation based adaptive unscented Kalman filter. Aerosp. Sci. Technol. 2018, 73, 184–196. [Google Scholar] [CrossRef]
- Gao, Z.; Zong, H.; Zhong, Y.; Gao, G. Limited memory-based random-weighted Kalman filter. Sensors 2024, 24, 3850. [Google Scholar] [CrossRef]
- Zong, H.; Gao, Z.; Wei, W.; Zhong, Y.; Gu, C. Randomly weighted CKF for multisensor integrated systems. J. Sens. 2019, 2019, 1216838. [Google Scholar] [CrossRef]
- Zhang, J.; Gao, S.; Zhong, Y.; Qi, X.; Xia, J.; Yang, J. An advanced cubature information filtering for indoor multiple wideband source tracking with a distributed noise statistics estimator. IEEE Access 2019, 7, 151851–151866. [Google Scholar] [CrossRef]
- Gao, S.; Hu, G.; Zhong, Y. Windowing and random weighting-based adaptive unscented Kalman filter. Int. J. Adapt. Control Signal Process. 2015, 29, 201–223. [Google Scholar] [CrossRef]
- Mehra, R. On the identification of variances and adaptive Kalman filtering. IEEE Trans. Autom. Control 1970, 15, 175–184. [Google Scholar] [CrossRef]
- Mohamed, A.H.; Schwarz, K.P. Adaptive Kalman filtering for INS/GPS. J. Geod. 1999, 73, 193–203. [Google Scholar] [CrossRef]
- Sage, A.P.; Husa, G.W. Adaptive filtering with unknown prior statistics. In Proceedings of the Joint Automatic Control Conference, Boulder, CO, USA, 5–7 August 1969; pp. 760–769. [Google Scholar]
- Särkkä, S.; Nummenmaa, A. Recursive noise adaptive Kalman filtering by variational Bayesian approximations. IEEE Trans. Autom. Control 2009, 54, 596–600. [Google Scholar] [CrossRef]
- Lee, E.; Son, J.; Park, S.Y. Relative navigation technique with constrained GNSS data for formation-flying CubeSat mission, CANYVAL-C. NAVIGATION J. Inst. Navig. 2021, 68, 559–575. [Google Scholar] [CrossRef]
- Almagbile, A.; Wang, J.; Ding, W. Evaluating the performances of adaptive Kalman filter methods in GPS/INS integration. J. Glob. Position. Syst. 2010, 9, 33–40. [Google Scholar] [CrossRef]
- Akhlaghi, S.; Zhou, N.; Huang, Z. Adaptive adjustment of noise covariance in Kalman filter for dynamic state estimation. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar]
- Gao, G.; Gao, B.; Gao, S.; Hu, G.; Zhong, Y. A hypothesis test-constrained robust Kalman filter for INS/GNSS integration with abnormal measurement. IEEE Trans. Veh. Technol. 2022, 72, 1662–1673. [Google Scholar] [CrossRef]
- Gao, B.; Hu, G.; Zhu, X.; Zhong, Y. A robust cubature Kalman filter with abnormal observations identification using the Mahalanobis distance criterion for vehicular INS/GNSS integration. Sensors 2019, 19, 5149. [Google Scholar] [CrossRef] [PubMed]
- Hu, G.; Gao, B.; Zhong, Y.; Ni, L.; Gu, C. Robust unscented Kalman filtering with measurement error detection for tightly coupled INS/GNSS integration in hypersonic vehicle navigation. IEEE Access 2019, 7, 151409–151421. [Google Scholar] [CrossRef]
- Gao, G.; Zhong, Y.; Gao, S.; Gao, B. Double-channel sequential probability ratio test for failure detection in multisensor integrated systems. IEEE Trans. Instrum. Meas. 2021, 70, 1–14. [Google Scholar] [CrossRef]
- Langer, M.; Bouwmeester, J. Reliability of CubeSats-Statistical Data, Developers’ Beliefs and the Way Forward. In Proceedings of the 30th Annual AIAA/USU Conference on Small Satellites, Logan, UT, USA, 6–11 August 2016. SSC16-X-2. [Google Scholar]
- Zhang, L.; Wang, S.; Selezneva, M.S.; Neusypin, K.A. A new adaptive Kalman filter for navigation systems of carrier-based aircraft. Chin. J. Aeronaut. 2022, 35, 416–425. [Google Scholar] [CrossRef]
- Ding, W.; Wang, J.; Rizos, C.; Kinlyside, D. Improving adaptive Kalman estimation in GPS/INS integration. J. Navig. 2007, 60, 517–529. [Google Scholar] [CrossRef]
- Teunissen, P.J.; Montenbruck, O. (Eds.) Springer Handbook of Global Navigation Satellite Systems; Springer International Publishing: Cham, Switzerland, 2017; Volume 10. [Google Scholar]
- Teunissen, P.J.; Amiri-Simkooei, A.R. Least-squares variance component estimation. J. Geod. 2008, 82, 65–82. [Google Scholar] [CrossRef]
- Euler, H.-J.; Schaffrin, B. On a measure for the discernibility between different ambiguity solutions in the static-kinematic GPS-mode. In Kinematic Systems in Geodesy, Surveying, and Remote Sensing: Symposium No. 107, Banff, AB, Canada, 10–13 September 1990; Schwarz, K.-P., Ed.; Springer: New York, NY, USA, 1991; pp. 285–295. [Google Scholar]
- Takasu, T.; Yasuda, A. Development of the low-cost RTK-GPS receiver with an open source program package RTKLIB. In Proceedings of the International Symposium on GPS/GNSS, Seogwipo-si, Republic of Korea, 4–6 November 2009; Volume 1, pp. 1–6. [Google Scholar]
- Misra, P.; Enge, P. Global positioning system: Signals, measurements, and performance. IEEE Aerosp. Electron. Syst. Mag. 2002, 17, 36–37. [Google Scholar] [CrossRef]
- Kuusniemi, H. User-Level Reliability and Quality Monitoring in Satellite-Based Personal Navigation. Ph.D. Thesis, Tampere University of Technology, Tampere, Finland, 2005. [Google Scholar]
- Roth, N.H.; Risi, B.; Grant, C.; Zee, R.E. Flight Results from the CanX-4 and CanX-5 Formation Flying Mission. In Proceedings of the Small Satellites, Systems & Services Symposium (4S), Valletta, Malta, 30 May 2016; Volume 30. [Google Scholar]
- Kim, Y. Attitude Controller Design and Analysis of Micro-Satellite for Free Space Optical Communication. Master’s Thesis, Yonsei University, Seoul, Republic of Korea, 2022. [Google Scholar]




| Phase | Operation |
|---|---|
| LEOP | Launch and separation |
| Detumbling | |
| Deployment of UHF antenna and solar panel | |
| DRSKP | Orbit maneuver and control |
| Station keeping | |
| Deployment of S-band antenna | |
| NOP | RF crosslink |
| Laser crosslink | |
| Pointing, Acquisition, and Tracking |
| Stage | Operation | Duration | Sensor | Error Budget |
|---|---|---|---|---|
| I. BIS | Beam detection | ≤ | Relative Navigation and Star Tracker | 400 μrad
μrad |
| II. CPS | Search | ≤ | CAM Feedback (Relative Navigation and Star Tracker) | μrad
μrad |
| Acquisition | ≤ | CAM Feedback and AOA Calibration (Relative Navigation and Star Tracker) | ||
| Detection | ≤ | CAM Feedback and FSM (Relative Navigation and Star Tracker) | ||
| III. FPS | Hand-off | ≤ | CAM Feedback and FSM and QC (Relative Navigation and Star Tracker) | μrad μrad |
| Tracking and COM | > | CAM Feedback and FSM and QC (Relative Navigation and Star Tracker) |
| Orbital Element | Value | Property | Value |
|---|---|---|---|
| Semi-major axis | km | Mass | kg |
| Eccentricity | Gravity model | JGM-3 (70 × 70) | |
| Inclination | Solar radiation pressure | 1.8 | |
| Right ascension of the ascending node | Drag coefficient | 2.2 | |
| Argument of periapsis | Solar radiation pressure area | 0.14 m2 | |
| True anomaly (Altair) | Drag area | 0.06 m2 | |
| True anomaly (Vega) | Clock model | Gauss–Markov 2nd order | |
| Mask angle | 5° | TEC model | Constant TEC |
| Parameter | Value |
|---|---|
| Initial covariance of state vector, | (position), (velocity) |
| Initial covariance of clock error and ionospheric delay, | |
| Initial process noise of state vector, | (position), (velocity) |
| Initial process noise of clock error and ionospheric delay, | |
| Fixed process noise of state, clock, and ionospheric delay, | |
| Pseudorange measurement noise, | |
| Carrier-phase measurement noise, |
| Estimated Relative Position Error | |||||
|---|---|---|---|---|---|
| Relative Distance | 50 km | 100 km | 200 km | 500 km | 1000 km |
| (3D) | 15.4 cm | 15.0 cm | 18.1 cm | 24.5 cm | 50.7 cm |
| (3D) | 24.8 cm | 24.7 cm | 35.6 cm | 59.8 cm | 63.2 cm |
| R (99.7%) | 29.3 cm | 25.0 cm | 31.0 cm | 62.8 cm | 93.9 cm |
| T (99.7%) | 27.6 cm | 27.3 cm | 35.2 cm | 37.8 cm | 58.6 cm |
| N (99.7%) | 10.1 cm | 17.3 cm | 20.7 cm | 18.8 cm | 26.0 cm |
| Property | Value |
|---|---|
| Moment of inertia (MOI) | |
| Cross-section | |
| Attitude | |
| RWs |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.; Kim, P.; Ryu, H.-G.; Eun, Y.; Park, S.-Y. GPS-Based Relative Navigation for Laser Crosslink Alignment in the VISION CubeSat Mission. Aerospace 2025, 12, 928. https://doi.org/10.3390/aerospace12100928
Kim Y, Kim P, Ryu H-G, Eun Y, Park S-Y. GPS-Based Relative Navigation for Laser Crosslink Alignment in the VISION CubeSat Mission. Aerospace. 2025; 12(10):928. https://doi.org/10.3390/aerospace12100928
Chicago/Turabian StyleKim, Yeji, Pureum Kim, Han-Gyeol Ryu, Youngho Eun, and Sang-Young Park. 2025. "GPS-Based Relative Navigation for Laser Crosslink Alignment in the VISION CubeSat Mission" Aerospace 12, no. 10: 928. https://doi.org/10.3390/aerospace12100928
APA StyleKim, Y., Kim, P., Ryu, H.-G., Eun, Y., & Park, S.-Y. (2025). GPS-Based Relative Navigation for Laser Crosslink Alignment in the VISION CubeSat Mission. Aerospace, 12(10), 928. https://doi.org/10.3390/aerospace12100928






