Abstract
Aircraft envelope expansion during the installation of new underwing stores presents significant challenges, particularly due to the aeroelastic flutter phenomenon. Accurate modeling of aeroelastic behavior often necessitates flight testing, which poses risks due to the potential catastrophic consequences of reaching the flutter point. Traditional methods, like frequency sweeps, are effective but require prolonged exposure to flutter conditions, making them less suitable for transonic flight validations. This paper introduces a robust deep learning approach to process sine dwell signals from aeroelastic flutter flight tests, characterized by short data lengths (less than 5 s) and low frequencies (less than 10 Hz). We explore the preliminary viability of different deep learning networks and compare their performances to existing methods such as the PRESTO algorithm and Laplace Wavelet Matching Pursuit estimation. Deep learning algorithms demonstrate substantial accuracy and robustness, providing reliable parameter identification for flutter analysis while significantly reducing the time spent near flutter conditions. Although the results with the networks trained show less accuracy than the PRESTO algorithm, they are more accurate than the Laplace Wavelet estimation, and the results are promising enough to justify extended investigation on this area. This approach is validated using both synthetic data and real F-18 flight test signals, which highlights its potential for real-time analysis and broader applicability in aeroelastic testing.
Keywords:
aeroelastic flutter; flight testing; deep learning; convolutional neural network; deep neural network; multi-layer perceptron; sine dwell; system identification; damping; natural frequency; PRESTO algorithm; Laplace wavelet matching pursuit; real-time analysis; aircraft envelope expansion; real data analysis 1. Introduction
The validation of aircraft airworthiness during flutter flight tests is a critical step in expanding the flight envelope of new or modified aircraft designs, as described in [,]. These tests involve different steps, one of which is the identification of aeroelastic flutter, a condition where aerodynamic forces couple with structural dynamics, resulting in self-excited oscillations. One of the final steps during flutter testing is the analysis of signals captured during flight (at different dynamic pressure flight conditions) to estimate parameters, such as natural frequencies and damping, which are essential for determining safe flight conditions at each point of the flight envelope.
Traditional methodologies, such as frequency sweeps, remain the most commonly used approach in flutter flight tests []. These methods, often analyzed using the Rational Fraction Polynomials technique [,,], have been enhanced by advanced modal estimation techniques such as Polymax and Stochastic Subspace Identification (SSI) [,]. Although effective, these techniques require a significant amount of time near flutter conditions, particularly during transonic regime testing, where aeroelastic behavior becomes highly nonlinear and less predictable [,]. This prolonged exposure significantly increases safety risks and operational complexity.
An alternative to frequency sweeps is the use of sine dwell excitations, which involve short-duration, low-frequency signals []. Although sine dwell excitations offer significant advantages in minimizing the time spent near critical flutter conditions, their use in flutter analysis has been limited, mainly due to the complexity of analyzing short-duration and low-frequency signals. For this reason, few researchers have explored this approach in depth. Notable examples include Lind [], who applied Laplace Wavelet techniques to estimate modal parameters, and Barros-Rodriguez et al. [], who utilized Singular Value Decomposition (SVD) filtering to address noise challenges. Mehra [] used the Prony method for parameter identification, while Chabalko et al. [] investigated the use of continuous wavelet transforms to analyze short-duration signals. A more recent method, the Power Spectrum Short Time Optimization (PRESTO) approach, was introduced in []. This technique begins with a rapid initialization of parameters using basic spectral analysis, providing a robust starting point. It then refines these parameters through a time-domain optimization process employing a trust-region-reflective algorithm, ensuring precise and reliable results.
Although these methods have shown promise in specific applications, they face notable limitations, such as computational inefficiency, reduced accuracy in low signal-to-noise ratio environments, and difficulties in handling short data lengths characteristic of sine dwell signals. These challenges highlight the need for innovative approaches to effectively and reliably analyze such data.
Deep learning (DL) has emerged in recent years as a transformative tool in fields such as signal processing, image recognition, and system identification []. Convolutional Neural Networks (CNNs) and Deep Neural Networks (DNNs), in particular, have shown exceptional performance in processing complex, noisy datasets. However, their application in flutter flight testing remains largely unexplored to date. Although studies like [,,] have utilized DL to classify flutter conditions or predict airspeed thresholds, the direct estimation of aeroelastic parameters from flight test data has received limited attention. This is particularly true for sine dwell signals. Challenges such as adapting DL architectures to the specific nature of flutter data and ensuring robust performance with noisy, short-duration signals remain unresolved.
This paper proposes a novel application of DL techniques, including CNNs and DNNs, to process sine dwell signals for accurate parameter identification in flutter testing. By leveraging synthetic datasets for training and comparing DL methods against established techniques such as PRESTO [] and Laplace Wavelet Matching Pursuit estimations [], we aim to demonstrate the feasibility and advantages of DL in this domain. The proposed approach addresses key limitations of existing methods, such as computational inefficiency and reduced accuracy in noisy environments, while facilitating the development of real-time in-flight analysis.
The remainder of this paper is structured as follows. Section 3 provides an overview of the materials and methods, including the generation of synthetic datasets, DL architectures, and evaluation metrics. Section 4 presents the experimental results, comparing DL methods with traditional approaches on both synthetic and real flight test data. Finally, Section 5 examines the implications of these findings and outlines future directions for research in this area.
2. Scope and Limitations
The objective of this paper is to present a novel deep learning-based method to analyze sine dwell flutter signals, subject to the following limitations:
- Preliminary viability analysis. The resources available to the authors to train networks are limited, and therefore a small-scale model has been presented. This factor affects the number of networks that were trained and the characteristics of the inputs and outputs.
- Limited number of modes. Although it is possible to generate an unlimited number of signals with any number of modes, each new mode introduces at least four new parameters, and therefore the number of different combinations increases exponentially with the power of 4. While it is not uncommon to see interactions of three different modes in real flutter flight tests, this analysis will take into consideration the simplest case of two different modes. However, note that the model is not limited by the nature of the interacting modes, meaning that the modes do not need to be perfectly orthogonal for the analysis to yield useful results.
- Real data parameters are not validated. The F-18 signals were acquired during flutter flight tests from a real source. However, data on the estimated parameters, airspeeds, or altitudes were not provided either before (preparation) or after (analysis) the tests. This imposes a strong limitation on the metrics available for real data analysis, allowing only a plot of real vs. reconstructed data to be used.
3. Materials and Methods
This section describes the methodology and resources used in this study. The aim is to evaluate the use of deep learning techniques to identify aeroelastic flutter parameters from sine dwell signals. The generation of synthetic datasets, the design of neural network architectures, and the evaluation metrics are explained. Comparisons with traditional methods such as the PRESTO algorithm and Laplace Wavelet Matching Pursuit estimation are also provided for reference.
PRESTO and Laplace Wavelet Matching Pursuit are similar processing techniques that rely on models described in standards [,], offering precise solutions. However, the application of machine learning in this field remains largely unexplored. To date, no study has specifically focused on flutter parameters identification from flight test data.
Regarding recent investigations, [] employed DNN-based methods to predict flutter airspeed during the analysis phase, prior to flight testing. Although their work focuses on pre-flight analysis, it does not address the direct identification of flutter parameters during flight.
In [,], the authors presented approaches that align more closely with the objectives of this paper by utilizing CNN models. Their methods were applied to flight test data, but validation was primarily based on wind tunnel test data. Instead of identifying system parameters, these studies classified flight conditions as flutter or no-flutter.
Similarly, [] applied a DNN to analyze flight test data. However, their study focused on modeling the global behavior of the structure rather than on identifying specific flutter parameters.
Perhaps the most comparable work is that of [], who explored techniques such as CNNs and Multi-Layer Perceptrons (MLPs), in the context of helicopter rotor blade applications. While their work is similar to this study, it does not involve the analysis of sine dwell data analysis.
The method proposed by the authors focuses on accurately identifying the flutter parameters of the aeroelastic equations of motion. The main advantages of this method include the ability of MLPs, DNNs, and CNNs to provide near-instantaneous results once trained, even on a low-end personal computer. This capability could enable effective real-time analysis. Additionally, if the training set includes a sufficiently broad range of training parameters, it might be possible to identify accurate flutter parameters for a given number of modes, not just two.
The main limitation of this method is the need for an accurate model to provide reliable data. Obtaining reliable real flight data with accurate output parameters, such as those derived from Ground Vibration Tests, is challenging. There is no public source of reliable data to match estimated mode values with the signals themselves. Instead, the signal model from [] was used to generate synthetic training sets (and will be the model employed to fit the data and identify parameters) using Equation (1):
where N is the number of vibration modes, is a constant representing the initial amplitude of mode j, is the damping factor of mode j, represents the natural angular frequency of the structure, t is the time variable in seconds, is the damped angular frequency of mode j, represents the phase angle of mode j at , and accounts for structural and aerodynamic noise, which is assumed to be random.
The parameters required to characterize the aeroelastic behavior of the j-th mode are the amplitude , the damping factor , the natural angular frequency , and the phase angle .
Even though this model may seem simplistic by assuming a linear relationship between various factors (aerodynamic and other linear and nonlinear interactions, such as gaps, hysteresis from structural damping, etc.) that are not properly modeled in Equation (1), [] ultimately calls for monitoring two main parameters for the critical flutter modes: modal frequency and damping. Assuming that the mechanism responsible for flutter can be modeled by a second-order linear Ordinary Differential Equation (ODE), all interactions are simplified to Equation (1).
It is important to note that the authors are not dismissing the significance of other nonlinear interactions with the natural modes by assuming that the second-order linear ODE will govern the flutter mechanism. These interactions will influence the approach to the flutter phenomenon, either accelerating or delaying flutter onset, which is crucial given the severe consequences of reaching a flutter point. This limitation must be considered when applying any analysis technique. Experienced engineers shall develop a sensible test plan based on all available information, noting that the methodology described in this paper will not provide information on flutter onset.
Considering all caveats and limitations, the potential of this technique is substantial, and it is worth exploring to develop accurate trained networks with the described advantages.
3.1. Input Layer
Two processes are defined for adapting the input data, depending on the network type: MLP-based (including MLPs and DNNs) and CNNs.
3.1.1. MLP-Based Networks Input Layer
The adaptation process for MLP-based networks, including data transformation steps, is illustrated in Figure 1. The initial dataset consists of a time signal extracted from one of the aircraft sensors, typically a 5 s signal sampled at 80 Hz. However, the duration may vary depending on the expected modal frequencies of the critical flutter modes.
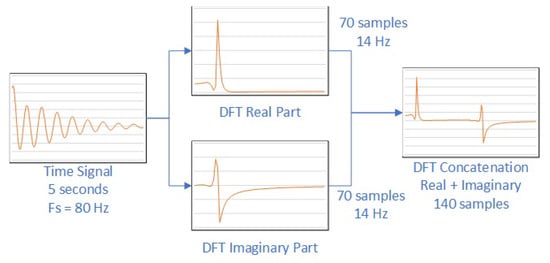
Figure 1.
Diagram of data preparation for MLP and DNN networks.
The following algorithm is followed:
- A Discrete Fourier Transform (DFT) is applied to the time-domain signal, and the real and imaginary parts are separated.
- From each subset, 70 frequency samples are extracted (corresponding to a maximum frequency of 14 Hz if 5 s signals are used).
- The positive frequency components of both the real and imaginary parts of the DFT are then concatenated.
This process results in a new signal, 140 samples long, composed of the concatenated real and imaginary parts of the DFT, which will be used as input for the MLP-based network.
3.1.2. CNNs Input Layer
For CNNs, a different approach must be followed. A 2D matrix of input data is required instead of a vector. Additionally, the authors emphasized the need to introduce as much phase information from the signals as possible. Given the characteristics of the different stages of the CNN, which reduce the number of neurons on each pooling process, a sensitive measure is to create an input layer with enough rows as to allow for the pooling process to reduce without losing information, and therefore redundancy in the form of projections was chosen.
The starting dataset is the same as for MLP-based networks. To convert it into a 2D matrix, the following preprocessing steps are performed:
- Define a list of unitary vectors on the complex plane, which will constitute the basis for a vector space , defined by a set of vectors . Each vector is calculated as:where k is the index of the vector, K is the total number of vectors (in this application, , which includes 14 unitary vectors, along with the real part and the imaginary part), and represents the frequency data points. These vectors are equally distributed around the unit circle in the complex plane. Refer to Figure 2 for visualization.
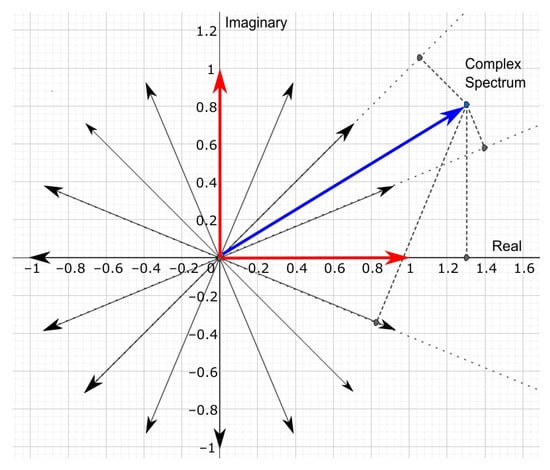 Figure 2. Construction of the input matrix for CNN processing. Once the time series dataset is transformed into a complex frequency spectrum, each point (example as a blue vector) will be represented in the base B (red vectors) and projected onto the vector space V (black vectors). Note that the unit vectors B are a subset of V.
Figure 2. Construction of the input matrix for CNN processing. Once the time series dataset is transformed into a complex frequency spectrum, each point (example as a blue vector) will be represented in the base B (red vectors) and projected onto the vector space V (black vectors). Note that the unit vectors B are a subset of V. - Trim the original time series signal to 5 s samples, or apply zero-padding until 5 s of signal are reached.
- Calculate the DFT of the time series. The result is a vector with 200 elements defined on the base B.
- Select the first 70 data points, which correspond to a maximum frequency of 14 Hz.
- Project each frequency vector onto the vector space defined in step 1 above. The projection values will be used to introduce redundancy, and the 16 projection values will constitute the rows of the input matrix. See Figure 2.
Finally, the input will be a matrix including redundant information.
3.2. Output Layer
In all cases, the output layer will consist of 4 neurons, corresponding to the natural frequencies and damping factors of the two modes analyzed (2 natural frequencies and 2 damping factors).
Note that the original parameter list to be identified also includes the amplitude and phase angle for each mode. These amplitudes and phase angles were estimated using a classical matching pursuit process [].
3.3. Networks Design
Three types of neural networks are utilized: MLPs, DNNs, and CNNs. While detailed descriptions of each network are beyond the scope of this paper, refer to [] for foundational information.
3.3.1. Multi-Layer Perceptron Design
The MLPs consist of an input layer with 140 neurons, one hidden layer with a varying number of neurons depending on the network configuration, and an output layer with 4 neurons. The hidden layer employs the sigmoid activation function, enabling nonlinear transformations to capture complex relationships within the data. A diagram of these networks is shown in Figure 3.
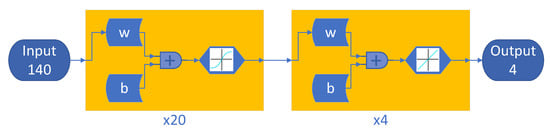
Figure 3.
Multi-Layer Perceptron sample network diagram. This example depicts an MLP with 20 neurons in the hidden layer.
In this paper, the number after each MLP designation indicates the number of neurons in the hidden layer. For example, MLP 20 indicates that the network has 20 neurons in its hidden layer.
3.3.2. Deep Neural Networks Design
DNNs are an extension of MLP networks. In this case, the network comprises more than one hidden layer, but follows exactly the same approach as MLP networks in Section 3.3.1 above. An example of the DNN design can be found in Figure 4. As in the case of the MLPs, our application also considers 140 input samples and 4 outputs, with a different number of hidden layers. Again, the activation function selected for the hidden layers is the sigmoid function.
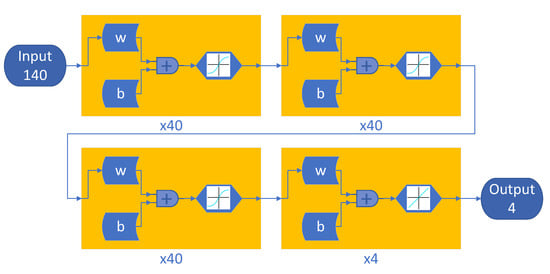
Figure 4.
DNN sample. In this case, a DNN with one input layer, three hidden layers, and one output layer is depicted. Each hidden layer has 40 neurons.
In the case of DNNs, the DNN designation indicates the number of hidden layers and the number of neurons in each hidden layer. For example, DNN 2 × 20 indicates a DNN with 2 hidden layers and 20 neurons in each hidden layer.
3.3.3. Convolutional Neural Networks Design
CNNs are similar to DNNs as they both consist of multiple hidden layers. However, the primary difference lies in how they compute the output parameters of the layers. CNNs use a convolution operation between the input matrices and the different layer parameter matrices, unlike DNNs that rely on compositions of linear transformations. The complete block diagram of a CNN with two hidden layers is depicted in Figure 5. Although there are various CNN architectures, the one used in this paper is detailed below with two hidden layers. Each layer involves different steps, and the process applied to our system is as follows:
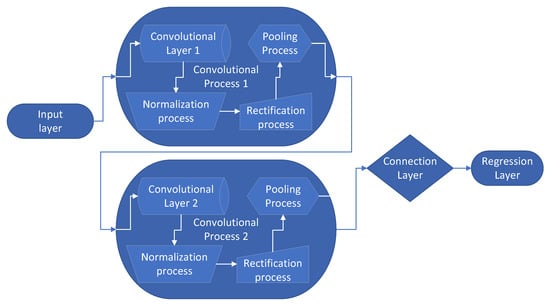
Figure 5.
Sample CNN. This example illustrates a CNN with one input layer, two convolutional layers, one connection layer, and one regression layer. Each convolutional layer employs a different number of neurons and convolutional processes.
- Input Layer. The inputs are matrices for each dataset, which are formatted to represent a regular pattern, typically an image. In our case, the input is a data matrix as described in Section 3.1.2. So, the input layer will consist of neurons.
- Convolutional process. Each convolutional process, depicted in Figure 5 as an elliptic box, includes a convolutional layer followed by several processes to improve operational performance:
- (a)
- Convolutional Layer. This layer performs the convolution operation on the input matrix using the weights matrix.
- (b)
- Normalization Process. This step normalizes the outputs to control their range and prevent saturation. A bias is added and a multiplier is applied, both of which are adjusted during training.
- (c)
- Rectification Process. This step converts negative values to zero.
- (d)
- Pooling Process. The convolutional matrices are downsampled using smaller windows.
- Connection Layer. This layer connects and reduces all outputs from the final convolutional block to the four output parameters. It functions as a classical perceptron layer, collecting outputs from the convolutional layers and generating outputs for the regression problem.
- Regression Layer. Before returning the final parameters, a regression layer is applied to optimize the outputs.
This example illustrates a CNN with two hidden convolutional blocks. However, more or fewer blocks can be used. In this paper, the trained CNNs employ 5 and 6 hidden layers for different networks.
In the case of CNNs, the designation specifies the number of convolutional blocks and the number of neurons in each convolutional layer within the convolutional blocks. For example, CNN indicates a Convolutional Neural Network with 5 convolutional processes and 100 neurons in each convolutional layer.
3.4. Training Process
The training signals were synthetically generated using Equation (1), with parameters randomly sampled from Table 1. The training process was carried out using backpropagation on a workstation provided by the Universidad de Alcalá, implemented in MATLAB. The workstation had the following characteristics:

Table 1.
Signal parameters ranges.
- CPU: The CPU used was an AMD Ryzen 9 5950X 16-Core 3.4GHz.
- Memory: The workstation had 128 GB of RAM.
- GPU: The GPU used was an NVIDIA RTX 2090 with 24 GB of memory.
With this workstation, the average training times were as follows:
- MLPs: ≈2500 s;
- DNNs: ≈9000 s;
- CNNs: ≈11,000 s.
The noise in the training dataset was modeled as white noise with a signal-to-noise ratio (SNR) of 5 dB. Random seeds were used to generate unique noise profiles for each signal. Additionally, a separate synthetic dataset, independent of the training dataset, was created to evaluate the performance during the testing process. A comprehensive summary of the training dataset distribution is presented in Table 2, while details of the DNN techniques and architectures explored are outlined in Table 3.

Table 2.
Distribution of training datasets.

Table 3.
Neural network architectures.
Several additional considerations were taken into account during the training process:
- Signal Ranges: The limited range of frequencies is due to the preliminary nature of this study. A broader range of frequencies, representative of the frequencies found in the real data available, will be employed in future papers, possibly including a different network design.
- Dampings Upscaling: The dampings were upscaled by a factor of 15 to reach a range of values in the same order of magnitude as the rest of the parameters. The upscaling was applied in the following manner. The training dataset was created with the actual damping values, but during the backpropagation process, the output damping values provided were upscaled. The formula employed is as follows:After the estimation is finished, the damping results will need to be adjusted inversely using the same scaling factor.
3.5. Analysis Methodology
To study the results, two sets of experiments were conducted: one with synthetic data and another with real data:
- Synthetic data processing: A set of 10,000 synthetic signals dataset was created with known parameters and no noise addition. Taking this dataset as a baseline, and following the same approach as with the training dataset, 5 dB SNR white noise was added. The synthetic process measured the standard deviations of errors in parameters (frequency and damping), skewness, kurtosis, and histograms of errors.
- Real data processing: A set of real data from F-18 flutter tests was employed. The datasets were analyzed using all the previously described techniques (PRESTO, Laplace Wavelet Matching Pursuit, and all the deep learning models). The data were reconstructed using Equation (1) with the estimated parameters, and the results of the original vs. reconstructed data were plotted. From there, the Mean Square Error (MSE), the Mean Absolute Error (MAE) and the Maximum Absolute Error (MaxAE), along with the regression coefficients (, slope, and y-intercept) were compared. The networks employed were trained with the synthetic datasets. It would be possible to use networks trained with real datasets. However, in absence of truth source parameters data, only an estimation on the parameters can be made. The techniques used to estimate those signals parameters were employed also to compare the performance of the networks. Consequently, training with real data would introduce a bias in the results.
4. Results
This section presents the experimental results, comparing DL methods with traditional approaches on both synthetic and real flight test data. After processing the data, the following key results were obtained:
4.1. Synthetic Data Processing
As described in Section 3.4, several processing techniques were employed. All the DNNs were compared to two reference methods: Laplace Wavelet Matching Pursuit processing [] and PRESTO processing [] as reference. Table 4 shows the results for an SNR of 5 dB, considering the case closest to the real conditions. The analysis of this table reveals several noteworthy insights.

Table 4.
Statistical summary for modes and damping with 5 dB SNR synthetic data.
PRESTO and Laplace Wavelet Matching Pursuit were included in the analysis as reference methods for comparison. PRESTO returns the highest standard deviation compared to the average across the neural networks, with values higher for frequency and higher for damping. However, it is strongly leptokurtic, noticeably above the rest of the methods also (4 points above for frequency and 30 points above for damping). Regarding the skewness coefficient, even though it is the only method that returns a negative skewness in frequency, it is still within the limits of symmetry, like the rest of the methods. However, for damping, the skewness is also the highest among the techniques. Even though most methods are skewed to the left due to the negative coefficient, PRESTO exhibits the most pronounced skewness. The conclusion is that PRESTO returns more accurate results than the neural network-based techniques, at the cost of the most extreme outliers and a significantly longer processing time (approximately 3 orders of magnitude).
On the other hand, Laplace Wavelet Matching Pursuit returns similar values to the rest of the neural network methods. Even though the standard deviation in frequency is higher than the other neural networks, in damping it is below the average. The damping values are specifically around the same as the CNNs, as several DNNs increase the overall average substantially. For kurtosis, both frequency and damping is more leptokurtic than the average, with values points above in frequency (including CNNs) and 2 points higher for damping, although still below the CNNs. Lastly, the frequency skewness is substantially low, at one order of magnitude below the average, indicating a strongly symmetric distribution compared to the rest of the methods. For damping, it is also skewed to the left, but remains around the average of the other methods. The conclusion is that it is a method similar to the other neural network techniques. However, its nominal processing time is approximately 3 orders of magnitude higher, which introduces a significant limitation. To achieve similar accuracy to the other techniques, it was necessary to fine-tune the dictionaries to the data being analyzed, keeping them as small as possible to avoid memory limitations on the computers used. If the dictionary ranges were the same as those used for PRESTO, the processing time was estimated to increase by at least 3 additional orders of magnitude (resulting in being 6 orders of magnitude higher than the neural network techniques). This fact may also account for the relatively low values for standard deviation, although this cannot be confirmed.
Figure 6 presents a comparison between the error histograms of PRESTO, Laplace Wavelet Matching Pursuit, a CNN with 100 × 6 neurons, and a DNN with 100 × 100 × 100 neurons as samples for comparison. It should be noted that the other neural network processing techniques exhibit a similar behavior. The plot reveals a very similar distribution for the CNN and Laplace methods. The CNN demonstrates notably better performance in damping and frequency, while the DNN performs slightly worse in frequency.
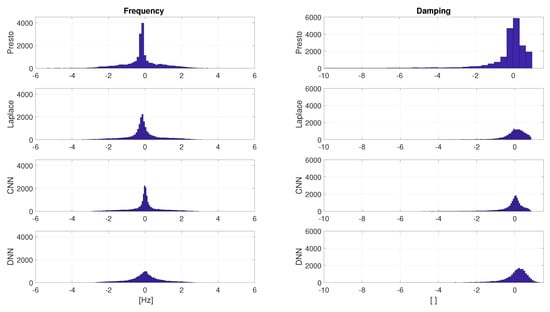
Figure 6.
Error histograms for frequency and damping for PRESTO, Laplace Wavelet Matching Pursuit, CNN 100 × 6, and DNN 100 × 100 × 100 chosen as sample methods. The other neural network methods exhibit a similar distribution to those depicted here. The damping plot for the PRESTO method was truncated at relative damping due to the tail extending to .
4.2. Real Data Processing
A set of F-18 flutter flight test data, from the Spanish Air Force CLAEX, was processed and analyzed by the aforementioned techniques. Table 5 shows the results of the analysis process.

Table 5.
Statistical summary for real data. The parameters m, n, and correspond to the regression curve parameters, where the equation is . The second half of the table presents the average statistics comparing all the DL methods (CNNs, DNNs, and MLPs) with the values from PRESTO and Laplace.
The dataset comprised 640 signals, extracted from 10 extensometers (6 torsion and 4 bending) and 8 flight envelope test points. Additionally, 8 excitation frequency runs were performed for each test point, resulting in a total of 640 signals. Note that in real-world scenarios, pure bending–torsion flutter modes rarely appear. Usually, the nodes lines are not parallel and perpendicular to the cord line, but hold particular shapes, and therefore it is common to see energy from both modes in each sensor. However, only approximately to of the 640 signals carried information related to the natural modes of the structure, since during the sine dwell runs the frequencies are changed with every excitation. Depending on the natural mode frequencies and the test run frequency, it was possible to capture energy from one, two, or three excitation runs, but rarely more.
Considering the aforementioned, even though the 640 signals were analyzed, only the 150 best signals participated in the statistics in Table 5. The original data were processed by the different techniques and the signals reconstructed from the estimated parameters. The original signal values were assigned to the x-axis, while the reconstructed signal values were assigned to the y-axis. This process generated a scatter plot of original vs. reconstructed data (Figure 7) and enabled the calculation of regression metrics. Note that the datasets analyzed by the different methods are identical. The 150 filtered signals plotted were selected as the best fits for the DL-processed signals.
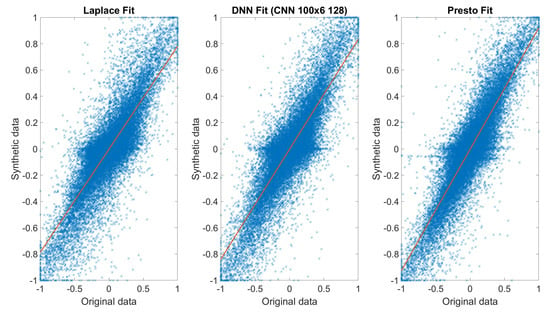
Figure 7.
Scatter plot comparing the regression curves of real data and synthetic reconstructed data. A comparison between Laplace Wavelet Matching Pursuit, PRESTO, and a CNN 100 × 6, taken as a sample method, is shown. The horizontal axis shows the normalized original time series data, while the vertical axis represents the respective reconstructed normalized signals. The red line represents the linear regression curve.
The analysis of the data allows drawing several conclusions. In general, the behavior of the DL techniques on real data is similar to the results on synthetic data, being globally slightly worse than PRESTO but similar or slightly better than Laplace. It does not constitute a validation of the synthetic results, but is still significant. Another conclusion is that all the DNN techniques exhibit a similar behavior compared to each other. The comparison between different deep learning techniques focuses on the relationship between m (slope of the regression curve), , and the different error metrics. Note that even though all the confidence intervals overlap, these differences cannot be assumed significant. However, there is a consistent trend in the averages of certain metrics being higher than others. In general, the error metrics for DNNs and MLPs are similar, with slightly higher values for CNNs. Conversely, the regression metrics exhibit the opposite trend.
Comparing the DL results with Laplace, the aforementioned conclusions can also be extrapolated. Assuming only the average values and ignoring the confidence intervals, Laplace can be positioned between CNNs and MLPs, which is very similar to DNNs. However, the results for PRESTO are sensibly higher than the rest of the techniques, out of the confidence intervals. In this case, given that the average values of the CNN techniques consistently lie in the upper bound of the rest of the techniques, the distance to PRESTO is lower, although not particularly significant. This behavior is consistent across all the error metrics and regression coefficients. The slope is closer to 1 in PRESTO, indicating that the large values of amplitude are better fitted. The error metrics for PRESTO are lower also, meaning that the lower values in amplitude do not impact a biased fit (for example, if one method tends to fit higher values but ignores lower, then those errors end up accumulating in the error metrics). There is also no significant difference between the MSE and MAE across methods, indicating that no significant outliers impacted one method above another. This is further confirmed by a similar trend in MaxAE.
5. Discussion
The results presented in this study indicate that, although the PRESTO technique currently outperforms DL methods in terms of accuracy, the latter show significant potential for analyzing sine dwell excitations during flutter tests. This represents a promising advance, in particular for transonic regime envelope expansion. The main advantage of deep learning techniques lies in their extraordinarily short processing times compared to PRESTO and Laplace Wavelet Matching Pursuit. This makes them highly suitable for real-time analysis during flight tests, where rapid decision-making is critical.
When comparing the deep learning techniques, no single method demonstrated clearly superior performance. While the increased complexity of CNNs led to slightly better results in some cases, the necessity to artificially construct a 2D input matrix with redundant data probably impacted the benefits of this architecture. Consequently, the improvements in accuracy were not proportional to the additional architectural complexity, as seen when comparing the performance of the simplest MLP configuration (20 neurons) with the most sophisticated CNN, which did not yield the expected gains in performance.
This observation suggests that further refinement of the architecture may be necessary. Potential modifications may include redesigning the input and output layers to better capture the relationships between parameters or adopting a multi-network approach. For example, individual networks could be dedicated to identifying specific parameters, and their outputs could be integrated into a higher-level network along with the input data. This hierarchical approach would resemble the iterative structure of the PRESTO technique, potentially leading to more accurate and efficient parameter identification.
6. Conclusions
This study explored the application of deep learning techniques for identifying aeroelastic flutter parameters from sine dwell excitations, presenting a potential alternative to traditional methods such as PRESTO and Laplace Wavelet Matching Pursuit. The findings highlight several advantages and challenges associated with the application of deep learning techniques.
Deep learning techniques, particularly MLPs, DNNs, and CNNs, demonstrate significant potential due to their extraordinarily short processing times, which entitles them as a promising solution for real-time analysis during flight tests, in particular during the transonic regime, where the numerical models cannot provide a reliable estimation of the aeroelastic behavior. However, in terms of accuracy, the traditional PRESTO method outperforms the evaluated deep learning models, whose performance is comparable to, or slightly better than, Laplace Wavelet Matching Pursuit. This highlights the necessity for further refinement before deep learning can fully replace established methods.
The analysis revealed no substantial differences in accuracy among the tested deep learning architectures, despite the varying levels of complexity. For example, while CNNs showed slightly better results in some cases, their higher computational demands and the need for redundant input data limited their overall effectiveness. This lack of a clear performance advantage among architectures suggests that the current designs may not be fully optimized for the specific challenges posed by flutter parameter identification.
To address these limitations, future work should focus on redesigning the input and output layers of the networks and potentially adopting a multi-network architecture. Specialized networks dedicated to identifying specific parameters, followed by a higher-level network to integrate these results, could improve accuracy and efficiency.
Author Contributions
Conceptualization: R.G.-P., S.A.-K.; Methodology: S.A.-K.; Software: S.A.-K., R.G.-P.; Validation: M.R.-Z., R.G.-P.; Formal analysis: M.R.-Z.; Investigation: S.A.-K.; Resources: M.R.-Z.; Data curation: R.G.-P.; Original draft preparation: S.A.-K.; Review and editing: R.G.-P., M.R.-Z.; Visualization: S.A.-K.; Supervision: R.G.-P., M.R.-Z.; Project administration: R.G.-P.; Funding acquisition: M.R.-Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Spanish Ministry of Science and Innovation under Project PID2021-129043OB-I00 (funded by MCIN/AEI/10.13039/501100011033/FEDER, EU), and by the Community of Madrid and University of Alcalá under project EPU-INV/2020/003.
Data Availability Statement
The data employed in this paper belong to the Spanish Air Force. The authors were authorized to use the data with restrictions for research purposes.
Acknowledgments
The authors show their appreciation to the Spanish Air Force for the authorization to employ the data used for this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| 2D | Two-Dimensional |
| CLAEX | Centro Logistico de Armamento y Experimentacion (as Spanish acronym) |
| CNN | Convolutional Neural Network |
| dB | Decibel |
| DFT | Discrete Fourier Transform |
| DL | Deep Learning |
| DNN | Deep Neural Network |
| Hz | Hertz |
| Kurt. | Kurtosis Coefficient |
| m | Slope of the Regression Curve |
| MAE | Mean Absolute Error |
| MaxAE | Maximum Absolute Error |
| MLP | Multi-Layer Perceptron |
| ms | Milliseconds |
| MSE | Mean Square Error |
| n | y-intercept of the Regression Curve |
| ODE | Ordinary Differential Equation |
| PRESTO | Power Spectrum Short Time Optimization |
| Skew. | Skewness Coefficient |
| SNR | Signal-to-Noise Ratio |
| SSI | Stochastic Subspace Identification |
| Std. | Standard Deviation |
| SVD | Singular Values Decomposition |
References
- Airworthiness Certification Criteria; Technical Report MIL-HDBK-516C; DoD: Arlington, VR, USA, 2014; Available online: http://everyspec.com/MIL-HDBK/MIL-HDBK-0500-0599/MIL-HDBK-516C_52120/ (accessed on 8 January 2025).
- EASA. CS-25. Certification Specifications and Acceptable Means of Compliance for Large Aeroplanes. Available online: https://www.easa.europa.eu/en/downloads/136622/en (accessed on 8 January 2025).
- Norton, J.W. Structures Flight Test Handbook; Technical Report AFFTC-TIH-90-001; USAF Test Pilot School: Edwards, CA, USA, 1990; Available online: https://apps.dtic.mil/sti/pdfs/ADA257262.pdf (accessed on 8 January 2025).
- Formenti, D.; Richardson, M. Paramenter Estimation from Frequency Response Measurements Using Rational Fraction Polynomials. In Proceedings of the 1st IMAC Conference, Orlando, FL, USA, 8–10 November 1982; pp. 1–15. [Google Scholar]
- Formenti, D.; Hill, M. Paramenter Estimation from Frequency Response Measurements Using Rational Fraction Polynomials (Twenty Years of Progress). In Proceedings of the 20th IMAC Conference, Los Angeles, CA, USA, 4–7 February 2002; pp. 373–382. [Google Scholar]
- Coll, F. JFlutter Real Time Flutter Analysis in Flight Test. In Proceedings of the SFTE-EC, SFTE, Nuremberg, Germany, 10–12 May 2016. [Google Scholar]
- Peeters, B.; Van des Auweraer, H. PolyMAX A Revolution in Modal Parameter Estimation. In Proceedings of the 1st international Operational Modal Analysis Conference, Copenhagen, Denmark, 26–27 April 2005; pp. 1–13. [Google Scholar]
- Peeters, B.; De Roeck, G. Reference-Based Stochastic Subspace Identification for Output-Only Modal Analysis. Mech. Syst. Signal Process. 1999, 13, 855–878. [Google Scholar] [CrossRef]
- Volkmar, R.; Soal, K.; Govers, Y.; Böswald, M. Experimental and operational modal analysis: Automated system identification for safety-critical applications. Mech. Syst. Signal Process. 2023, 183, 109658. [Google Scholar] [CrossRef]
- Govers, Y.; Mai, H.; Arnold, J.; Dillinger, J.K.; Pereira, A.K.; Breviglieri, C.; Takara, E.K.; Correa, M.S.; Mello, O.A.; Marques, R.F.; et al. Wind tunnel flutter testing on a highly flexible wing for aeroelastic validation in the transonic regime within the HMAE1 project. In Proceedings of the International Forum on Aeroelasticity and Structural Dynamics 2019, IFASD 2019, Savannah, GA, USA, 9–13 June 2019; pp. 1–25. [Google Scholar]
- Lind, R.; Brenner, M.; Freudinger, L.C. Wavelet Applications for flight flutter testing. In Proceedings of the International Forum on Aeroelasticity and Structural Dynamics, Williamsburg, VA, USA, 22–25 June 1999; pp. 393–402. Available online: https://ntrs.nasa.gov/api/citations/19990061885/downloads/19990061885.pdf (accessed on 8 January 2025).
- Barros-Rodriguez, J. Metodología de Ejecución y Explotación de los Ensayos en Vuelo de Flameo. Ph.D. Thesis, Universidad Politecnica de Madrid, Madrid, Spain, 2014. [Google Scholar]
- Mehra, R.K.; Mahmood, S.; Waissman, R. Identification of Aircraft and Rotorcraft Aeroelastic Modes Using State Space System Identification. In Proceedings of the International Conference on Control Applications, Albany, NJ, USA, 28–29 September 1995; pp. 432–437. [Google Scholar] [CrossRef]
- Chabalko, C.C.; Hajj, M.R.; Silva, W.A. Interrogative Testing for Nonlinear Identification of Aeroelastic Systems. AIAA J. 2008, 46, 2657–2658. [Google Scholar] [CrossRef]
- Abou-Kebeh, S.; Gil-Pita, R.; Rosa-Zurera, M. Multimodal Estimation of Sine Dwell Vibrational Responses from Aeroelastic Flutter Flight Tests. Aerospace 2021, 8, 325. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; Number 1-2; The MIT Press: Cambridge, NA, USA, 2016. [Google Scholar]
- Wang, Y.R.; Wang, Y.J. Flutter speed prediction by using deep learning. Adv. Mech. Eng. 2021, 13, 1–15. [Google Scholar] [CrossRef]
- Zheng, H.; Wu, Z.; Duan, S.; Zhou, J. Feature Extracted Method for Flutter Test Based on EMD and CNN. Int. J. Aerosp. Eng. 2021, 2021, 10. [Google Scholar] [CrossRef]
- Duan, S.; Zheng, H.; Liu, J. A Novel Classification Method for Flutter Signals Based on the CNN and STFT. Int. J. Aerosp. Eng. 2019, 2019, 9375437. [Google Scholar] [CrossRef]
- Military Specification: Airplane Strength and Rigidity. Vibration, Flutter and Divergence; Technical Report MIL-A-8870C; DoD: Arlington, VR, USA, 1993; Available online: http://everyspec.com/MIL-SPECS/MIL-SPECS-MIL-A/MIL-A-8870C_6746/ (accessed on 8 January 2025).
- Joint Service Specification Guide. Aircraft Structures; Technical Report JSSG-2006; DoD: Arlington, VR, USA, 1998; Available online: http://everyspec.com/USAF/USAF-General/JSSG-2006_10206/ (accessed on 8 January 2025).
- Li, K.; Kou, J.; Zhang, W. Deep neural network for unsteady aerodynamic and aeroelastic modeling across multiple Mach numbers. Nonlinear Dyn. 2019, 96, 2157–2177. [Google Scholar] [CrossRef]
- Chatterjee, T.; Essien, A.; Ganguli, R.; Friswell, M.I. The stochastic aeroelastic response analysis of helicopter rotors using deep and shallow machine learning. Neural Comput. Appl. 2021, 33, 16809–16828. [Google Scholar] [CrossRef]
- Goodwin, M. Matching pursuit with damped sinusoids. In Proceedings of the 1997 IEEE International Conference on Acoustics, Speech, and Signal Processing, Munich, Germany, 21–24 April 1997; Volume 3, pp. 2037–2040. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).