Remaining Useful Life Prediction for Aircraft Engines under High-Pressure Compressor Degradation Faults Based on FC-AMSLSTM
Abstract
1. Introduction
2. Related Work
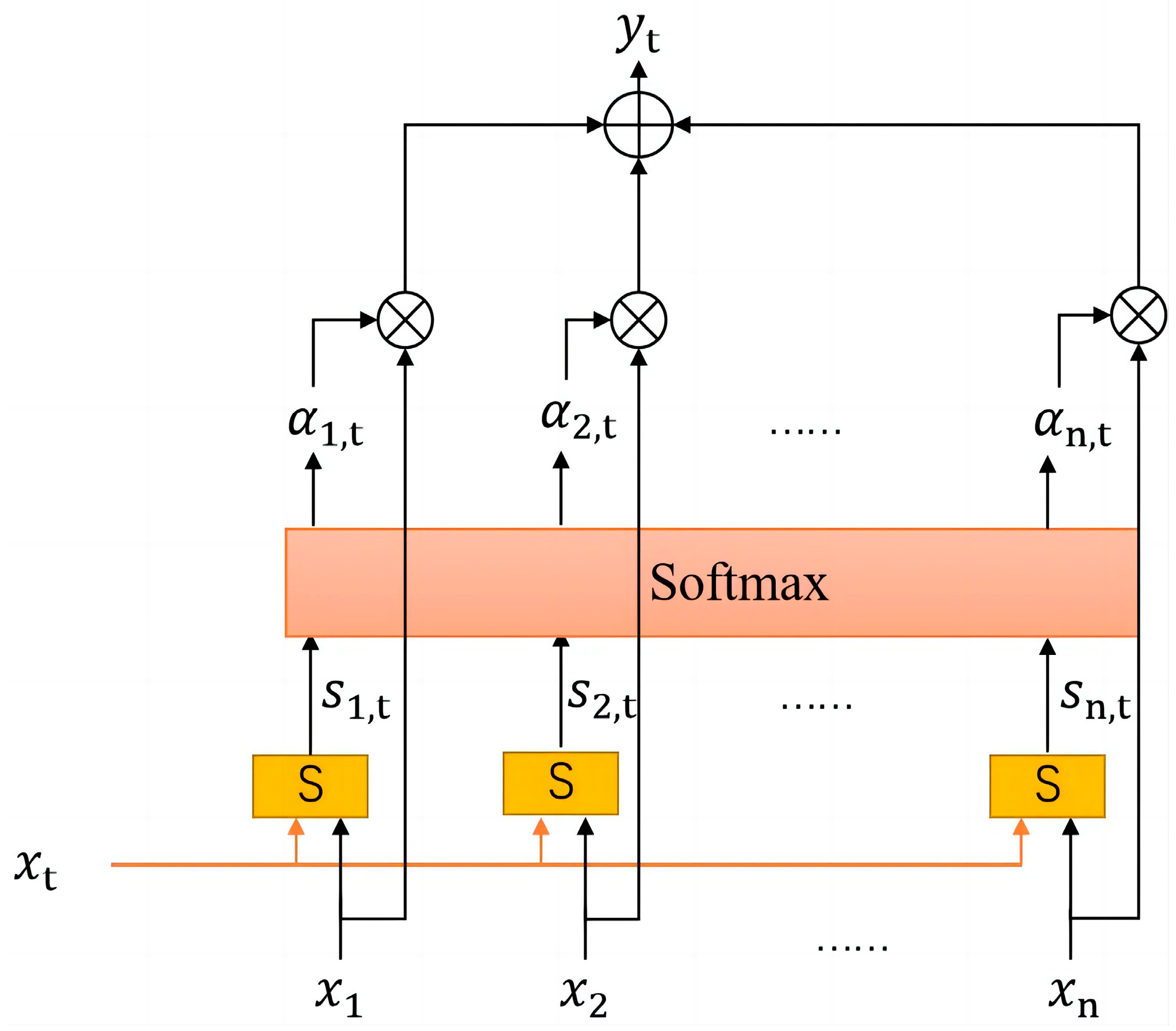
2.1. Attention Mechanism
2.2. Multi-Scale Convolutional Neural Network
2.3. LSTM
3. Method
3.1. The Experiment Dataset
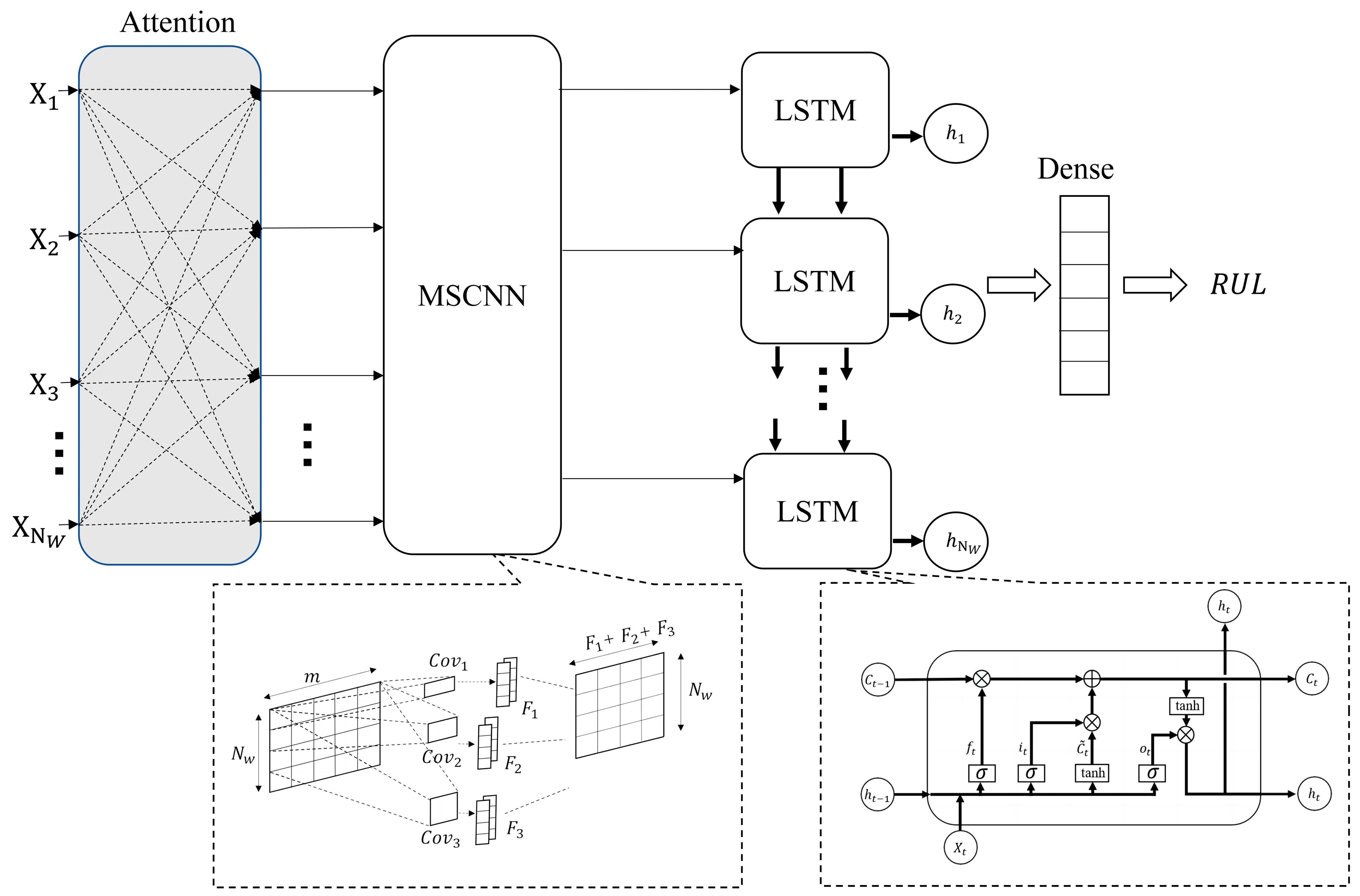
3.2. Prediction Process and Network Architecture
3.3. Fault Classification Method
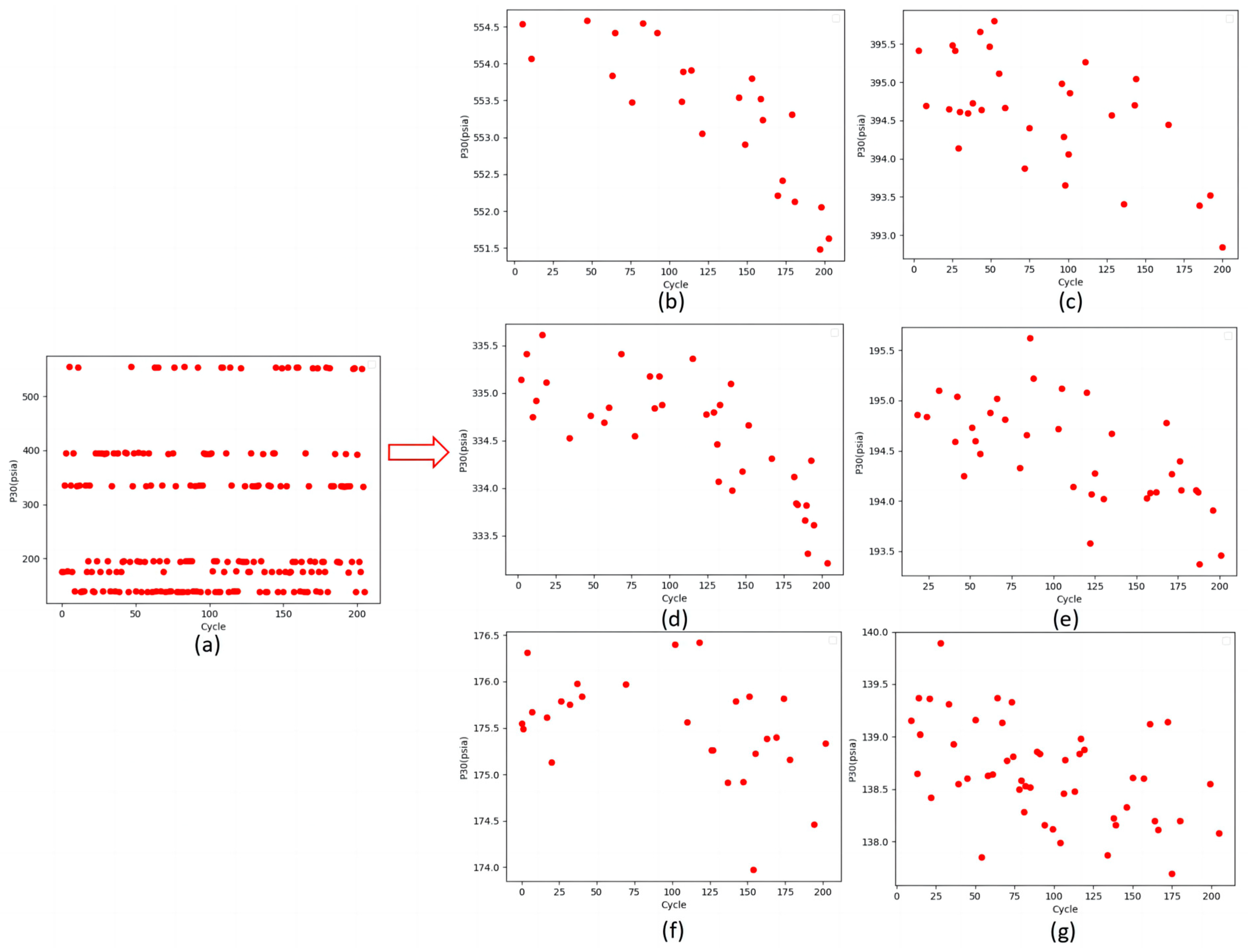
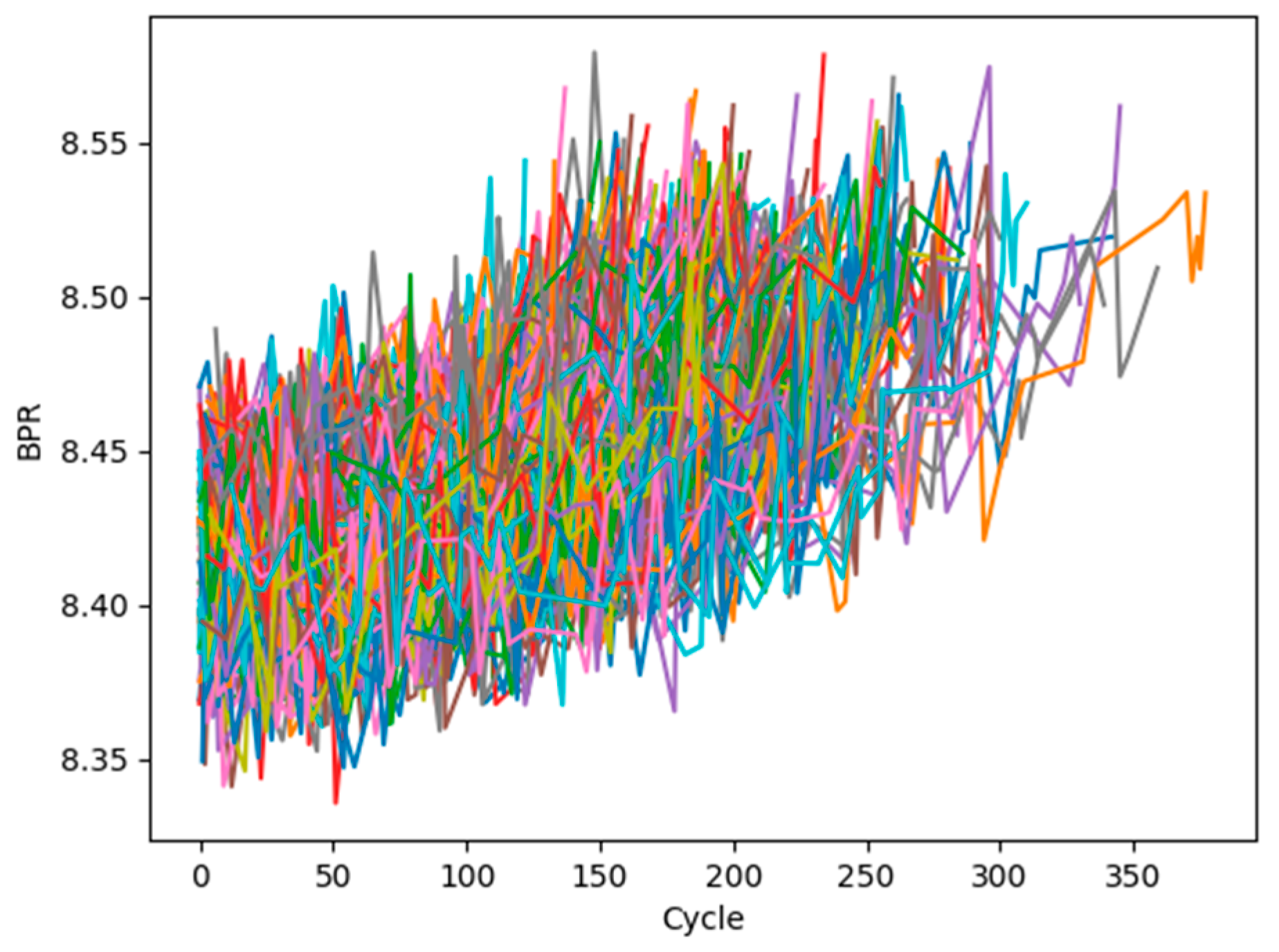
3.4. Data Preprocessing
3.5. Network Parameter Configuration
3.6. Evaluation Metrics
4. Experimental Results and Discussion
4.1. Fault Classification Results
4.2. Prediction Results and Degradation Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kamran, J.; Rafael, G.; Noureddine, Z. State of the art and taxonomy of prognostics approaches, trends of prognostics applications and open issues towards maturity at different technology readiness levels. Mech. Syst. Signal Process. 2017, 94, 214–236. [Google Scholar]
- Zhao, Z.; Liang, B.; Wang, X.; Lu, W. Remaining useful life prediction of aircraft engine based on degradation pattern learning. Reliab. Eng. Syst. Saf. 2017, 164, 74–83. [Google Scholar] [CrossRef]
- Lee, J.; Wu, F.; Zhao, W.; Ghaffari, M.; Liao, L.; Siegel, D. Prognostics and health management design for rotary machinery systems-reviews, methodology and applications. Mech. Syst. Signal Process. 2014, 42, 314–334. [Google Scholar] [CrossRef]
- Bolander, N.; Qiu, H.; Eklund, N.; Hindle, E.; Rosenfeld, T. Physics-based remaining useful life prediction for aircraft engine bearing prognosis. In Proceedings of the Annual Conference of the PHM Society, San Diego, CA, USA, 27 September–1 October 2009. [Google Scholar]
- Matthew, J.D.; Goebel, K. Model-Based Prognostics with Concurrent Damage Progression Processes. IEEE Trans. Syst. Man Cybern. 2013, 43, 535–546. [Google Scholar]
- Jaouher, B.A.; Brigitte, C.; Lotfi, S.; Simon, M.; Farhat, F. Accurate bearing remaining useful life prediction based on Weibull distribution and artificial neural network. Mech. Syst. Signal Process. 2015, 56, 150–172. [Google Scholar]
- Yu, W.; Tu, W.; Kim, I.; Mechefske, C. A nonlinear-drift-driven Wiener process model for remaining useful life estimation considering three sources of variability. Reliab. Eng. Syst. Saf. 2021, 212, 107631. [Google Scholar] [CrossRef]
- Yan, J.; Lee, J. Degradation Assessment and Fault Modes Classification Using Logistic Regression. J. Manuf. Sci. Eng. 2005, 127, 912–914. [Google Scholar] [CrossRef]
- Chen, Z.; Li, Y.; Xia, T.; Pan, E. Hidden Markov model with auto-correlated observations for remaining useful life prediction and optimal maintenance policy. Reliab. Eng. Syst. Saf. 2019, 184, 123–136. [Google Scholar] [CrossRef]
- Li, X.; Wu, S.; Li, X.; Yuan, H.; Zhao, D. Particle swarm optimization-support vector machine model for machinery fault diagnoses in high-voltage circuit breakers. Chin. J. Mech. Eng. 2020, 33, 104–113. [Google Scholar] [CrossRef]
- Babu, G.S.; Zhao, P.; Li, X.L. Deep Convolutional Neural Network Based Regression Approach for Estimation of Remaining Useful Life. In Database Systems for Advanced Applications Navathe; Navathe, S., Wu, W., Shekhar, S., Du, X., Wang, X., Xiong, H., Eds.; Springer: Cham, Switzerland, 2016; pp. 214–228. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Kong, Z.; Cui, Y.; Xia, Z.; Lv, H. Convolution and long short-term memory hybrid deep neural networks for remaining useful life prognostics. Appl. Sci. 2009, 9, 4156. [Google Scholar] [CrossRef]
- Boujamza, A.; Elhaq, S. Attention-based LSTM for Remaining Useful Life Estimation of Aircraft Engines. IFAC PapersOnLine 2022, 55, 450–455. [Google Scholar] [CrossRef]
- Liu, L.; Song, X.; Zhou, Z. Aircraft engine remaining useful life estimation via a double attention-based data-driven architecture. Reliab. Eng. Syst. Saf. 2022, 221, 108330. [Google Scholar] [CrossRef]
- Khumprom, P.; Grewell, D.; Yodo, N. Deep Neural Network Feature Selection Approaches for Data-Driven Prognostic Model of Aircraft Engines. Aerospace 2020, 7, 132. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, K.; Ji, J.C.; Yu, K.; Ren, Z.; Liu, Z. Dynamic Model-Assisted Bearing Remaining Useful Life Prediction Using the Cross-Domain Transformer Network. IEEE/ASME Trans. Mechatron. 2023, 28, 1070–1080. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, K.; Lei, Z.; Ge, J.; Xu, Y.; Li, Z.; Ren, Z.; Feng, K. Integrated intelligent fault diagnosis approach of offshore wind turbine bearing based on information stream fusion and semi-supervised learning. Expert Syst. Appl. 2023, 232, 120854. [Google Scholar] [CrossRef]
- Xiang, F.; Zhang, Y.; Zhang, S.; Wang, Z.; Qiu, L.; Choi, J.H. Bayesian gated-transformer model for risk-aware prediction of aero-engine remaining useful life. Expert Syst. Appl. 2024, 238, 121859. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, J.; Wang, j.; Jin, Y.; Wang, L.; Liu, Z. PAOLTransformer: Pruning-adaptive optimal lightweight Transformer model for aero-engine remaining useful life prediction. Reliab. Eng. Syst. Saf. 2023, 240, 109605. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, M.; Zhao, R.; Guretno, F.; Yan, R.; Li, X. Machine Remaining Useful Life Prediction via an Attention-Based Deep Learning Approach. IEEE Trans. Ind. Electron. 2021, 68, 2521–2531. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Q.; Shao, S.; Niu, T.; Yang, X. Attention-Based LSTM Network for Rotatory Machine Remaining Useful Life Prediction. IEEE Access 2020, 8, 132188–132199. [Google Scholar] [CrossRef]
- Ren, L.; Dong, J.; Wang, X.; Meng, Z.; Zhao, L.; Deen, M.J. A Data-Driven Auto-CNN-LSTM Prediction Model for Lithium-Ion Battery Remaining Useful Life. IEEE Trans. Ind. Inform. 2021, 17, 3478. [Google Scholar] [CrossRef]
- Chen, W.; Liu, C.; Chen, Q.; Wu, P. Multi-scale memory-enhanced method for predicting the remaining useful life of aircraft engines. Neural Comput. Appl. 2023, 35, 2225–2241. [Google Scholar] [CrossRef]
- Meng, M.; Mao, Z. Deep-Convolution-Based LSTM Network for Remaining Useful Life Prediction. IEEE Trans. Ind. Inform. 2021, 17, 1658–1667. [Google Scholar]
- Saxena, A.; Goebel, K.; Simon, D.; Eklund, N. Damage Propagation Modeling for Aircraft Engine Run-to-Failure Simulation. In Proceedings of the International Conference on Prognostics and Health Management (PHM), Denver, CO, USA, 6–9 October 2008; pp. 1–9. [Google Scholar]
- Saxena, A.; Goebel, K. Turbofan Engine Degradation Simulation Data Set; NASA Ames Prognostics Data Repository; NASA Ames: Moffett Field, CA, USA, 2008.
- Luo, M. Data-Driven Fault Detection Using Trending Analysis. Doctoral Dissertation, Louisiana State University and Agricultural and Mechanical College, Baton Rouge, LA, USA, 2006. [Google Scholar]
- Zheng, S.; Ristovski, K.; Farahat, A.; Gupta, C. Long Short-Term Memory Network for Remaining Useful Life estimation. In Proceedings of the 2017 IEEE International Conference on Prognostics and Health Management (ICPHM), Dallas, TX, USA, 19–21 June 2017; pp. 88–95. [Google Scholar]
- Wang, H.; Cheng, Y.; Song, K. Remaining useful life estimation of aircraft engines using a joint deep learning model based on TCNN and transformer. Comput. Intell. Neurosci. 2021, 2021, 5185938. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Li, Y.; Zhang, Y.; Jia, L. Spatio-temporal graph convolutional neural network for remaining useful life estimation of aircraft engines. Aerosp. Syst. 2021, 4, 29–36. [Google Scholar] [CrossRef]
- Zhang, Z.; Song, W.; Li, Q. Dual-aspect self-attention based on transformer for remaining useful life prediction. IEEE Trans. Instrum. Meas. 2022, 71, 1–11. [Google Scholar] [CrossRef]
- Zhang, J.; Jiang, Y.; Wu, S.; Li, X.; Luo, H.; Yin, S. Prediction of remaining useful life based on bidirectional gated recurrent unit with temporal self-attention mechanism. Reliab. Eng. Syst. Saf. 2022, 221, 108297. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y.; Xu, Y.; Liu, X.; Zheng, T.; Zheng, B. Remaining Useful Life Prediction for Aero-Engines Using a Time-Enhanced Multi-Head Self-Attention Model. Aerospace 2023, 10, 80. [Google Scholar] [CrossRef]




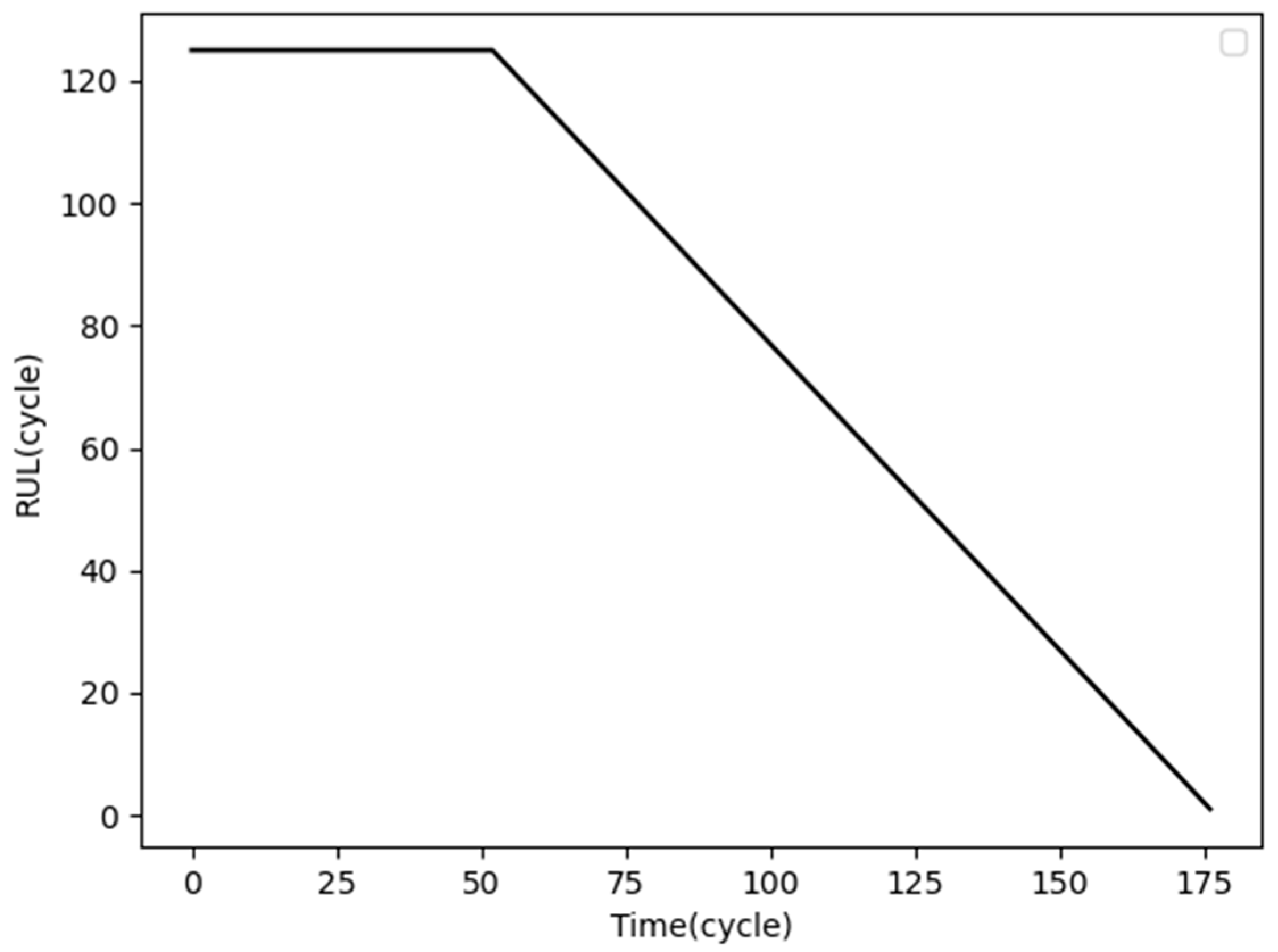
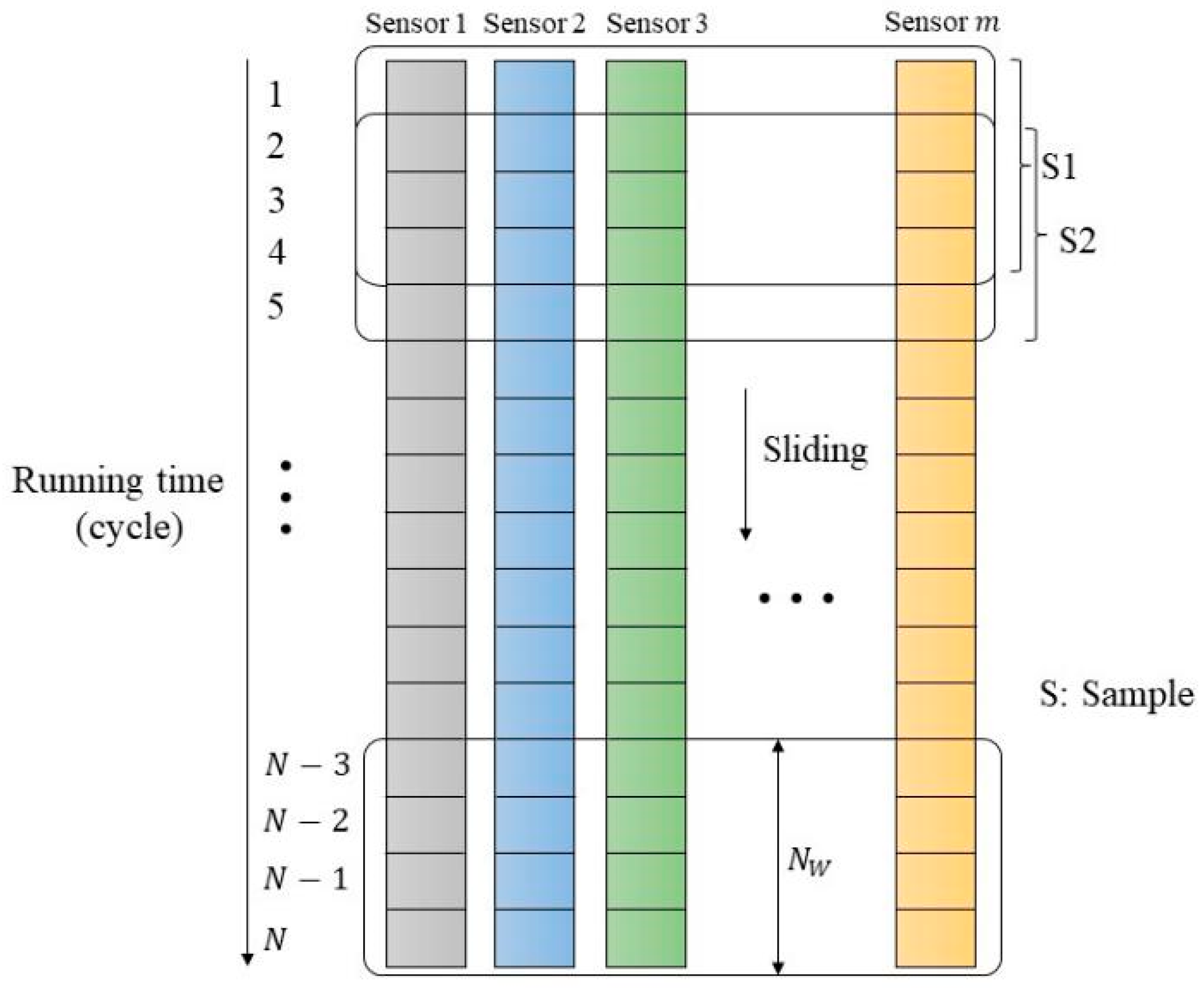
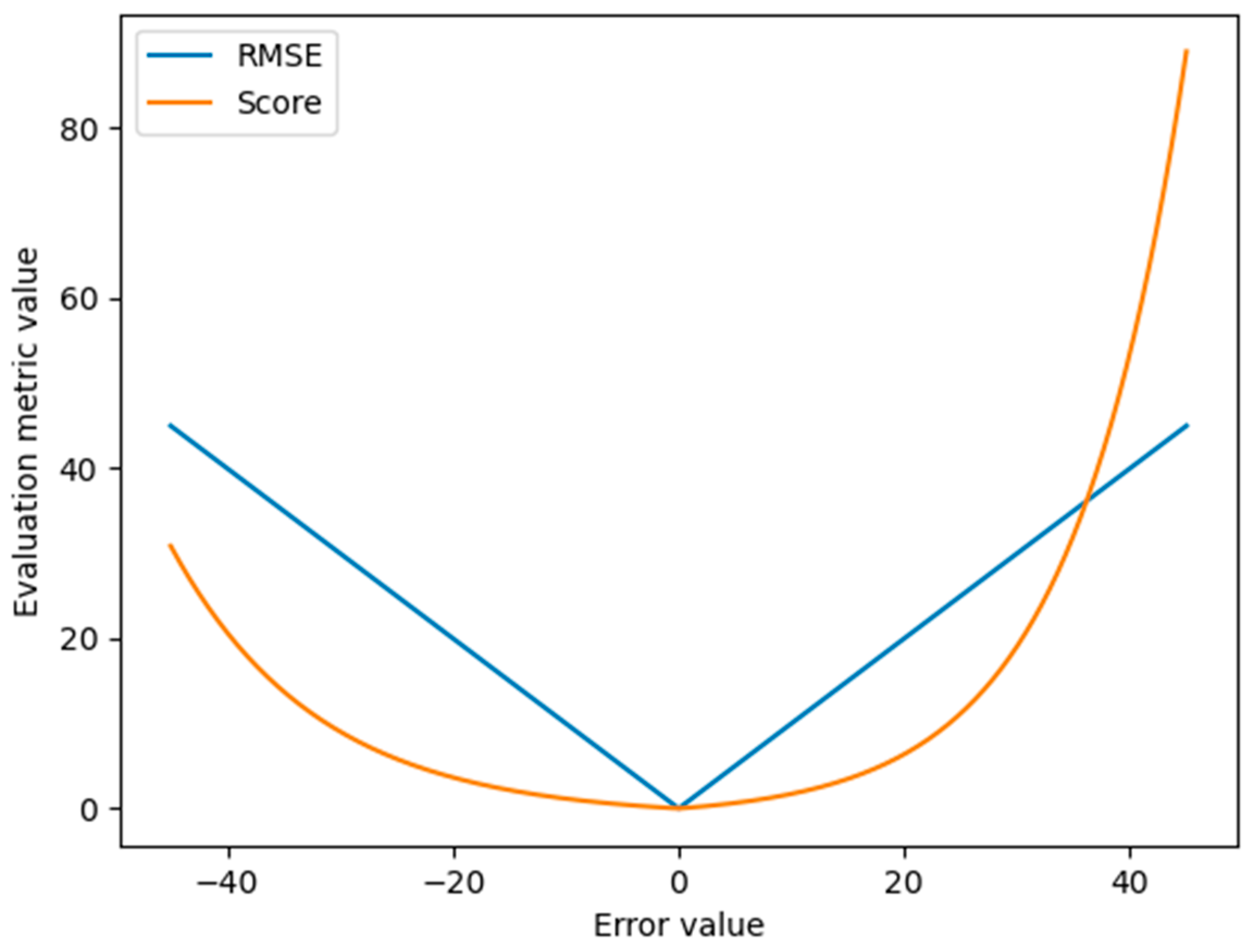
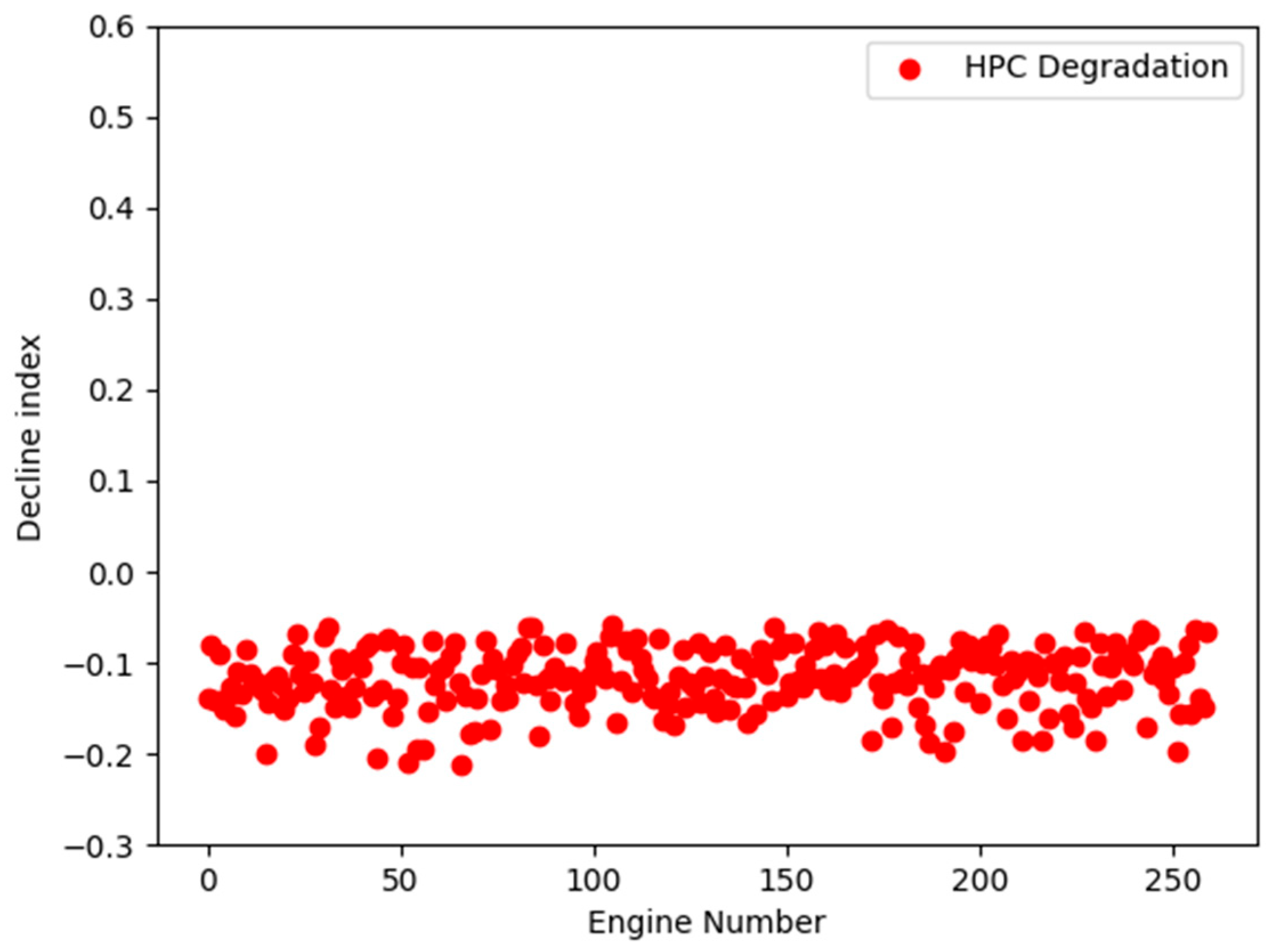
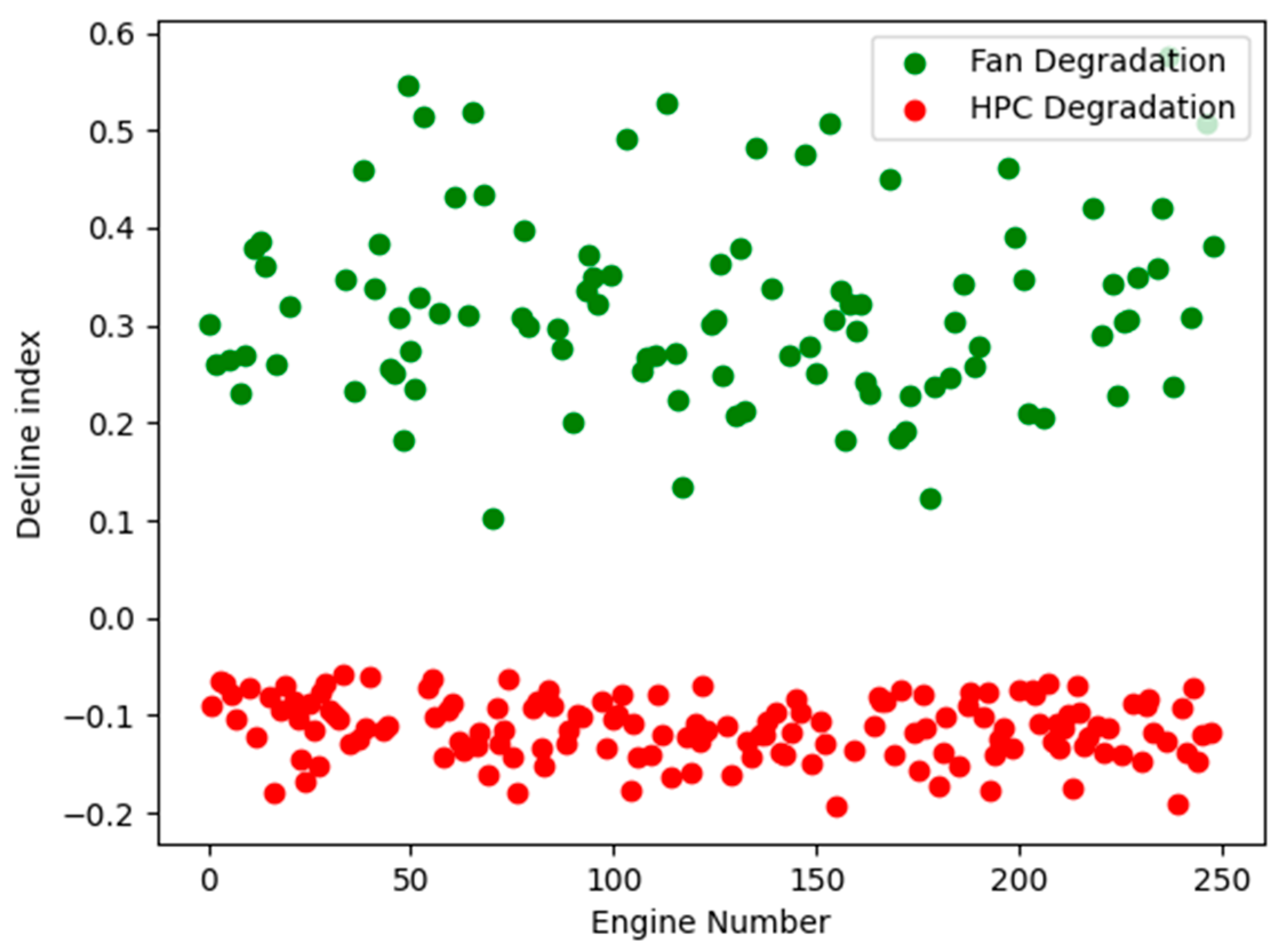
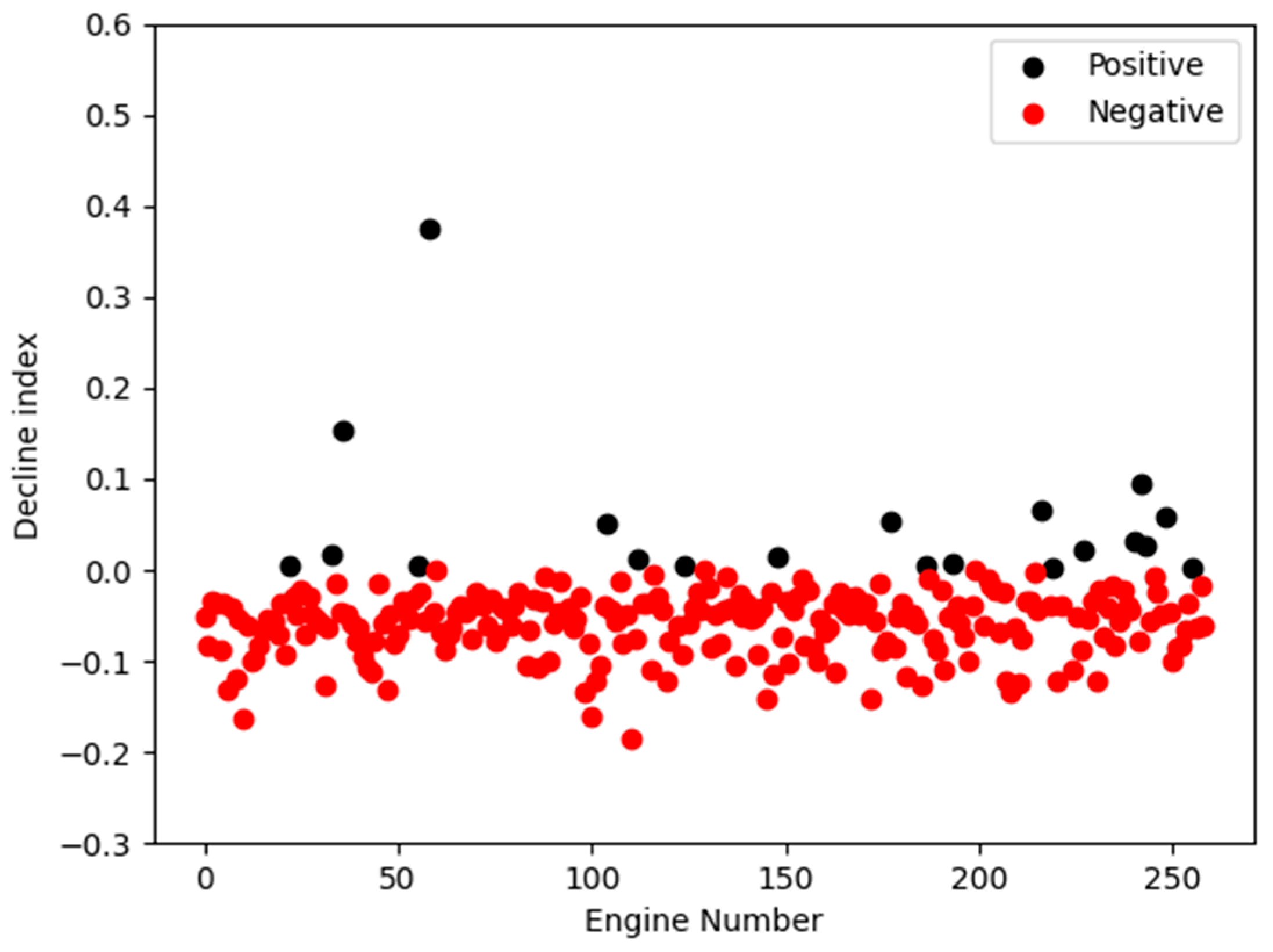
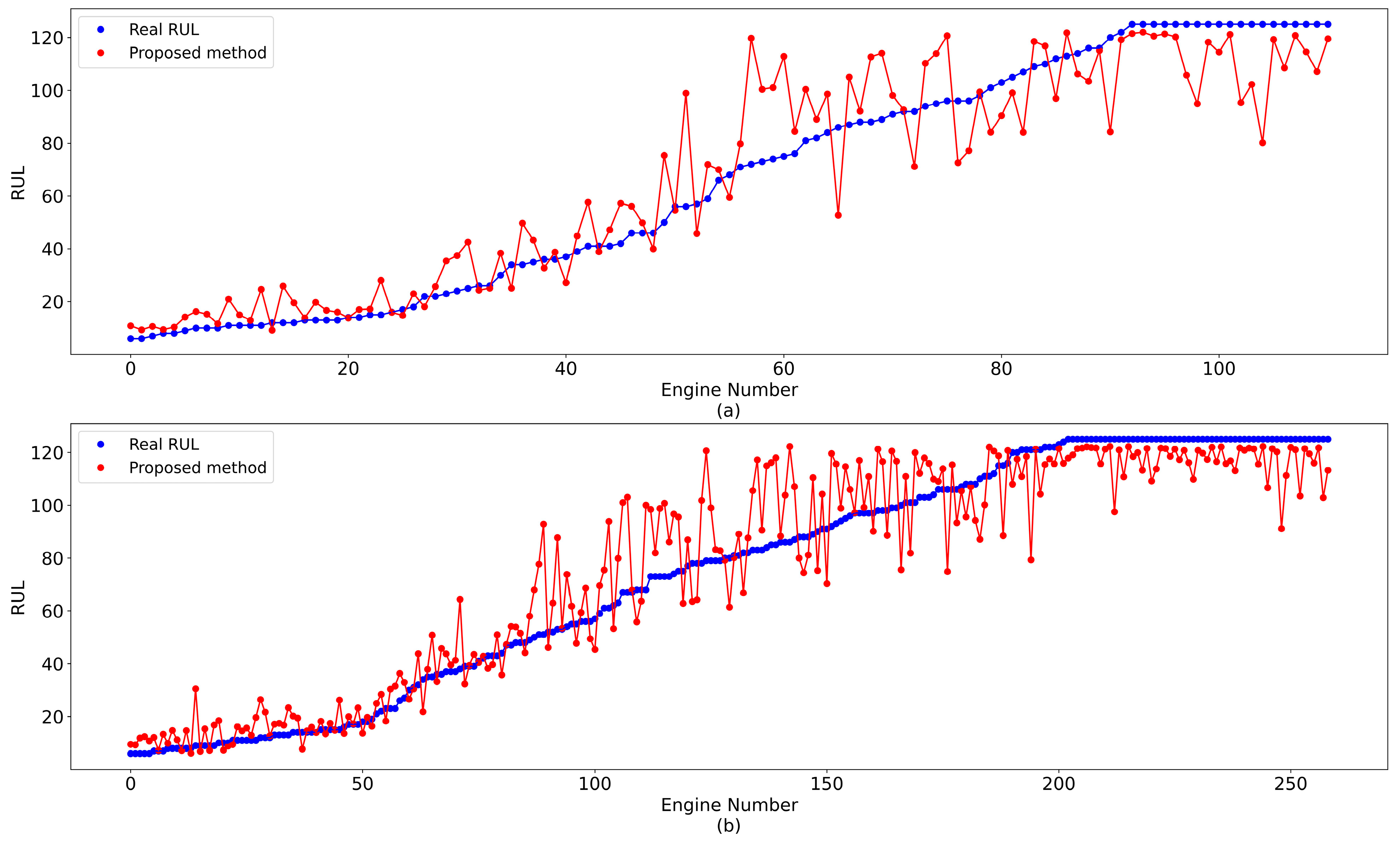

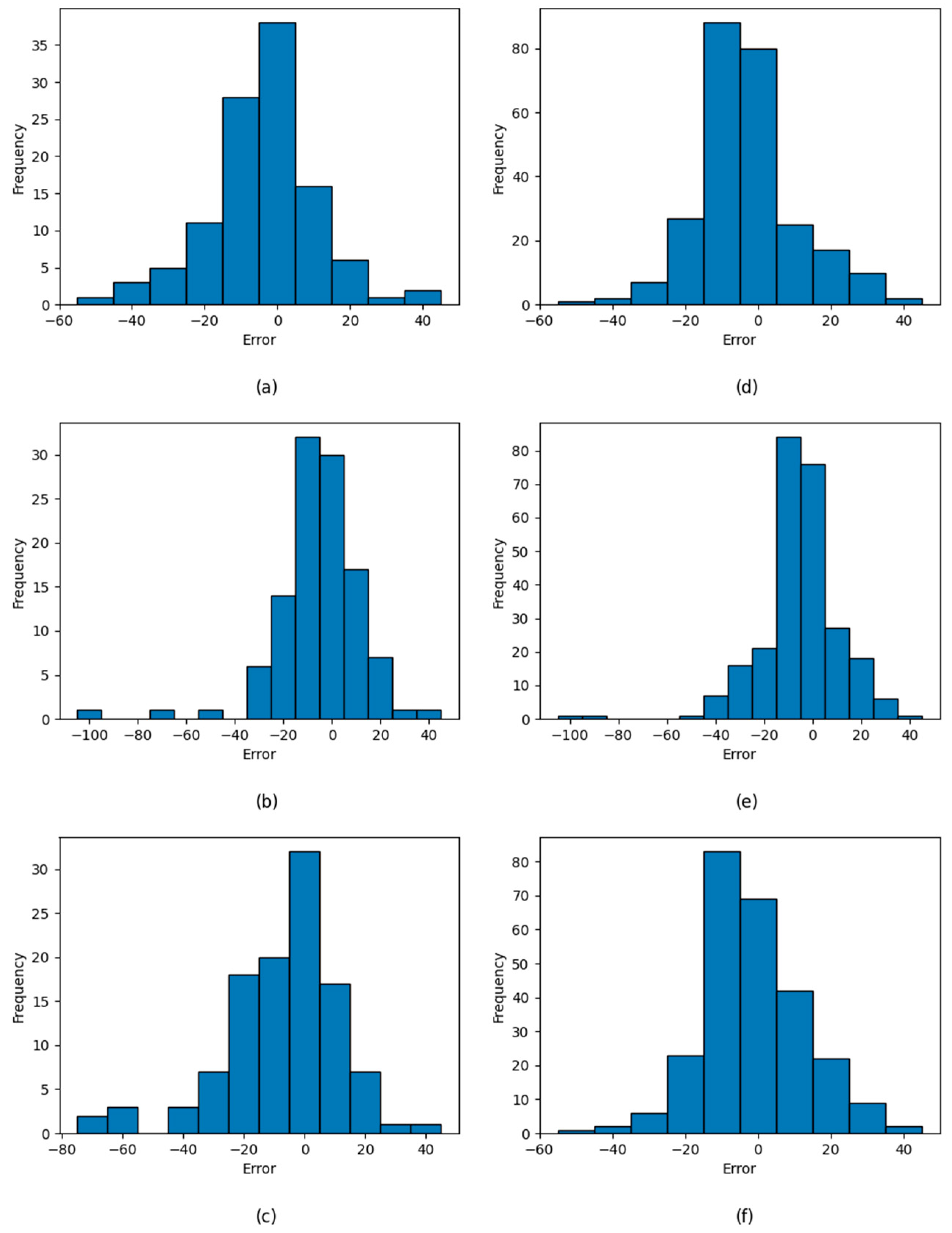
| NO | Description | Units |
|---|---|---|
| 1 | Total temperature at fan inlet | |
| 2 | Total temperature at LPC outlet | |
| 3 | Total temperature at HPC outlet | |
| 4 | Total temperature at LPT outlet | |
| 5 | Pressure at fan inlet | psia |
| 6 | Total pressure in bypass duct | psia |
| 7 | Total pressure at HPC outlet | psia |
| 8 | Physical fan speed | rpm |
| 9 | Physical core speed | rpm |
| 10 | Engine pressure ratio (P50/P2) | - |
| 11 | Static pressure at HPC outlet | psia |
| 12 | Ratio of fuel flow to Ps30 | pps/psi |
| 13 | Corrected fan speed | rpm |
| 14 | Corrected core speed | rpm |
| 15 | Bypass ratio | - |
| 16 | Burner fuel–air ratio | - |
| 17 | Bleed enthalpy | - |
| 18 | Demanded fan speed | rpm |
| 19 | Demanded corrected fan speed | rpm |
| 20 | HPT coolant bleed | lbm/s |
| 21 | LPT coolant bleed | lbm/s |
| Dataset | FD001 | FD002 | FD003 | FD004 |
|---|---|---|---|---|
| Number of training engines | 100 | 260 | 100 | 249 |
| Number of test engines | 100 | 259 | 100 | 248 |
| Max/Min cycles for training engines | 362/128 | 378/128 | 525/145 | 543/128 |
| Max/Min cycles for test engines | 303/31 | 367/21 | 475/38 | 486/19 |
| Operating conditions | 1 | 6 | 1 | 6 |
| Fault modes | 1 | 1 | 2 | 2 |
| Operating Conditions | Altitude (kft) | Mach Number | Sea-Level Temperature (°F) |
|---|---|---|---|
| Operating condition 1 | 0 | 0 | 100 |
| Operating condition 2 | 10 | 0.25 | 100 |
| Operating condition 3 | 20 | 0.7 | 100 |
| Operating condition 4 | 25 | 0.62 | 60 |
| Operating condition 5 | 35 | 0.84 | 100 |
| Operating condition 6 | 42 | 0.84 | 100 |
| Hyperparameter | Value | Hyperparameter | Value |
|---|---|---|---|
| Window size | 60 | Activation in LSTM layer | tanh |
| Number of neurons in attention model | 32 | Number of LSTM layers | 2 |
| Kernel sizes for Conv1 to Conv3 | 7/12/17 | Number of dense layers | 1 |
| Number of convolution kernels for Conv1 to Conv3 | 10/10/10 | Dropout rate | 0.1 |
| Number of convolution layer | 3 | Activation in dense layer | linear |
| Padding | Same | Batch size | 256 |
| Activation in convolution layer | Relu | Loss function | MSE |
| Number of neurons in LSTM layer | 100 | Optimization function | Adam |
| Dataset | Engine Number |
|---|---|
| FD004 training dataset | 2, 4, 5, 7, 8, 11, 13, 16, 17, 19, 20, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 36, 38, 40, 41, 44, 45, 55, 56, 57, 59, 60, 61, 63, 64, 67, 68, 70, 72, 73, 74, 75, 76, 77, 81, 82, 83, 84, 85, 86, 89, 90, 92, 93, 98, 99, 101, 102, 103, 105, 106, 107, 110, 112, 113, 115, 119, 120, 121, 122, 123, 124, 129, 130, 134, 135, 137, 138, 139, 141, 142, 143, 145, 146, 147, 150, 152, 153, 156, 160, 165, 166, 167, 168, 170, 172, 175, 176, 177, 178, 181, 182, 183, 186, 188, 189, 192, 193, 194, 195, 196, 197, 199, 201, 204, 205, 206, 208, 209, 210, 211, 212, 213, 214, 215, 216, 217, 218, 220, 222, 223, 226, 229, 231, 232, 233, 234, 237, 240, 241, 242, 244, 245, 246, 248 |
| FD004 test dataset | 2, 7, 8, 10, 14, 20, 22, 23, 26, 27, 31, 32, 35, 38, 42, 43, 47, 53, 58, 63, 67, 68, 69, 73, 77, 78, 80, 81, 82, 88, 90, 91, 92, 94, 96, 98, 101, 103, 106, 107, 113, 115, 116, 117, 120, 121, 124, 126, 131, 132, 136, 145, 147, 148, 150, 153, 154, 155, 156, 158, 159, 162, 163, 166, 167, 168, 169, 170, 172, 173, 174, 176, 177, 181, 182, 183, 184, 185, 187, 188, 196, 197, 198, 199, 200, 202, 204, 205, 208, 209, 210, 215, 216, 217, 218, 219, 224, 225, 226, 229, 230, 233, 234, 237, 238, 239, 241, 242, 244, 247, 248 |
| Training Dataset | FD002 Test Dataset | FD004 Test Dataset (HPC Degradation) | ||
|---|---|---|---|---|
| RMSE | Score | RMSE | Score | |
| FD002 training dataset + FD004 training dataset (HPC degradation) | 13.59 | 893.55 | 15.25 | 520.00 |
| FD002 training dataset + FD004 training dataset | 16.44 | 2721.62 | 17.54 | 2221.76 |
| FD002 training dataset | 14.29 | 1003.13 | - | - |
| FD004 training dataset | - | - | 19.48 | 935.42 |
| Threshold | FD004 Test Dataset (HPC Degradation) | |||
|---|---|---|---|---|
| RMSE | Score | Total Engine Number | AS | |
| −0.02 | 15.25 | 520.00 | 111 | 4.68 |
| −0.03 | 14.64 | 406.52 | 99 | 4.11 |
| −0.04 | 13.33 | 308.10 | 83 | 3.71 |
| −0.05 | 12.70 | 268.21 | 72 | 3.73 |
| −0.06 | 12.13 | 223.21 | 62 | 3.60 |
| Number | FD002 Test Dataset | FD004 Test Dataset (HPC Degradation) | ||
|---|---|---|---|---|
| RMSE | Score | RMSE | Score | |
| 16 | 15.64 | 1045.75 | 16.88 | 704.64 |
| 32 | 13.59 | 893.55 | 15.25 | 520.00 |
| 64 | 14.55 | 963.13 | 16.33 | 645.53 |
| Number | Total Parameters | FD002 Test Dataset | FD004 Test Dataset (HPC Degradation) | ||
|---|---|---|---|---|---|
| RMSE | Score | RMSE | Score | ||
| 1 | 141,900 | 15.14 | 1046.23 | 17.23 | 721.54 |
| 2 | 152,730 | 14.28 | 983.45 | 16.68 | 680.77 |
| 3 | 163,560 | 13.59 | 893.55 | 15.25 | 520.00 |
| 4 | 174,390 | 13.76 | 920.43 | 15.78 | 542.61 |
| Number | Total Parameters | FD002 Test Dataset | FD004 Test Dataset (HPC Degradation) | ||
|---|---|---|---|---|---|
| RMSE | Score | RMSE | Score | ||
| 1 | 83,160 | 15.22 | 1123.21 | 16.85 | 702.59 |
| 2 | 163,560 | 13.59 | 893.55 | 15.25 | 520.00 |
| 3 | 243,960 | 14.55 | 1022.14 | 16.22 | 611.23 |
| Method | FD002 Test Dataset | FD004 Test Dataset (HPC Degradation) | |||
|---|---|---|---|---|---|
| RMSE | Score | AS | RMSE | AS | |
| LSTM [29] (2017) | 24.49 | 4450 | 17.87 | 28.17 | 22.38 |
| Transformer + TCNN [30] (2021) | 15.35 | 1267 | 5.09 | 18.35 | 8.55 |
| Spatio-temporal GCN [31] (2021) | 17.74 | 2485.02 | 9.98 | 18.08 | 10.38 |
| DAST [32] (2022) | 15.25 | 924.96 | 3.71 | 18.36 | 6.01 |
| BiGRU-TSAM [33] (2022) | 18.94 | 2264.13 | 9.09 | 20.47 | 14.56 |
| Double attention-based architecture [15] (2022) | 17.08 | 1575 | 6.33 | 19.86 | 7.02 |
| Transformer Encoder + Attention [34] (2023) | 15.82 | 1008.08 | 3.89 | 17.35 | 7.06 |
| MSDCNN [24] (2023) | 18.70 | 1873.86 | 7.53 | 21.57 | 10.88 |
| Proposed method | 13.59 | 893.55 | 3.59 | 15.25 | 4.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Z.; Wang, Q.; Liu, Z.; He, R. Remaining Useful Life Prediction for Aircraft Engines under High-Pressure Compressor Degradation Faults Based on FC-AMSLSTM. Aerospace 2024, 11, 293. https://doi.org/10.3390/aerospace11040293
Peng Z, Wang Q, Liu Z, He R. Remaining Useful Life Prediction for Aircraft Engines under High-Pressure Compressor Degradation Faults Based on FC-AMSLSTM. Aerospace. 2024; 11(4):293. https://doi.org/10.3390/aerospace11040293
Chicago/Turabian StylePeng, Zhiqiang, Quanbao Wang, Zongrui Liu, and Renjun He. 2024. "Remaining Useful Life Prediction for Aircraft Engines under High-Pressure Compressor Degradation Faults Based on FC-AMSLSTM" Aerospace 11, no. 4: 293. https://doi.org/10.3390/aerospace11040293
APA StylePeng, Z., Wang, Q., Liu, Z., & He, R. (2024). Remaining Useful Life Prediction for Aircraft Engines under High-Pressure Compressor Degradation Faults Based on FC-AMSLSTM. Aerospace, 11(4), 293. https://doi.org/10.3390/aerospace11040293





