Abstract
The propagation mechanism of flow disturbance under acoustic excitations plays a crucial role in thermoacoustic instability, especially when considering the effect of non-premixed combustion on heat release due to reactant mixing and diffusion. This relationship leads to a complex coupling between the spatial distribution of the equivalence ratio and the propagation mechanism of flow disturbance. In the present study, the response of a methane-air non-premixed swirling flame to low-frequency acoustic excitations was investigated experimentally. By applying Proper Orthogonal Decomposition (POD) analysis to CH* chemiluminescence images, the harmonic flame response was revealed. Large Eddy Simulation (LES) was utilized to analyze the correlation between the vortex motion within the shear layers and the harmonic response under non-reacting conditions at excitation frequencies of 20 Hz, 50 Hz, and 150 Hz. The results showed that the harmonic flame response was mainly due to the harmonic velocity pulsations within the shear layers. The acoustically induced vortices within the shear layer exhibited motion patterns susceptible to harmonic interference, with spatial distribution characteristics closely related to the oscillation modes of the non-premixed combustion.
1. Introduction
Thermoacoustic instability arises from the closed-loop coupling effect between acoustic pulsations and unstable heat release in combustion chambers. The flow disturbance induced by acoustic pulsations significantly influences the fluctuation of the flame’s heat release rate [1,2], necessitating an in-depth exploration of flow disturbance generation and response mechanism.
The mechanism of flow disturbance generation falls into inherent and externally induced categories. Inherent flow disturbance is mainly influenced by stable combustion structures within the flow passage, such as the shedding of large-scale coherent vortices downstream of bluff bodies [3], Kelvin–Helmholtz instabilities with sudden expansions [4], and vortex structures with swirling flow [5]. Externally induced disturbance refers to changes in flow velocity within a combustion chamber caused directly by acoustic waves, which can alter the evolution of turbulent and vortical structures, leading to new forms of flow disturbance.
Investigating the response mechanism of flow disturbance to acoustic excitation is a critical research area in thermoacoustic instability. A previous study [6] suggested that the axial velocity perturbation at the combustion chamber’s inlet generated azimuthal vorticity waves within post-swirler passage, subsequently initiating transverse velocity perturbations and fluctuating vortex shedding at the burner outlet. Sujith [7] observed vortex fragmentation under different excitation frequencies, noting that low-frequency excitation enhanced flow mixing through entrainment and vortex breakdown effects. Karimi [8] compared the impact of different acoustic excitation amplitudes on the dynamics of premixed flames and found that high-amplitude acoustic excitations generated large-scale vortices, which had a significant non-linear effect on the flow field, thus affecting the distribution of turbulence in the recirculation zone and shear layers.
Further investigations have explored the connection between flame response and flow disturbance. Idahosa [9] established the flame transfer function, revealing that the flame response to upstream velocity perturbation depended on the normalized acoustic frequency (flame Strouhal number, Stf). Low-frequency disturbance induced notable responses, while high-frequency oscillations had minimal influence. Using the flame describing function, Pan [10] studied nonlinear heat release response, finding that flame length was sensitive to excitation frequency and amplitude, and the flame exhibited low-pass filtering characteristics. Palies [6,11] highlighted the interference between vortex shedding and flame angle oscillations, which affected local gain peaks and valleys in the vortex–flame transfer function. At high-frequency excitations, the flame–vortex interactions at the flame tip led to phase-shifted heat release oscillations, resulting in a weak global flame response.
Harmonic flame response has garnered attention as nonlinear behavior. Balachandran’s study [12] on turbulent premixed flames noted that high-amplitude excitations caused vortex roll-up in the shear layers, localized flame extinction, and high-order harmonic heat release responses. Kim [13] observed similar phenomena in stratified premixed flames, finding a correlation between coherent vortex structure and harmonic flame response. Recently, Liu [14] examined low-swirl premixed flames’ harmonic response over a wide range of perturbation amplitudes at different frequencies, attributing the response to the complex flame structure and fluctuating velocity-induced vortex interactions. Combined with flame dynamics analysis, shear layer instability due to acoustically induced vortices emerged as a significant factor in nonlinear flame response. While reacting flows informed current understanding, Santhosh [15] stressed non-reacting flow field response to acoustic excitation in uncovering periodically excited vortex motion’s essential nature. A previous study [16] showed that, in swirling combustion, the formation and detachment of vortex were primarily governed by the universal vortex dynamics principles, which exhibited fundamental similarities to non-reacting flows. Analyzing the response of flow disturbance to acoustic excitations from a non-reacting flow perspective could offer a clearer insight into the correlation between the shear layers’ vortex motion and harmonic response.
Although previous research has primarily focused on the flow disturbance response in premixed combustion, recent studies have increasingly investigated the self-excited oscillations of non-premixed flames [17,18]. Compared to premixed combustions, non-premixed combustions are more sensitive to reactant mixing and diffusion, and flow disturbance has more complex effects on the location and frequency of heat release in their combustion chamber. Li [19] and Darabkhani [20] identified fuel–air mixing’s role in non-premixed combustion flames’ vortex structure formation and oscillation frequency. Magina et al. [21,22] reviewed non-premixed jet flames’ disturbance response modes, contrasting them with premixed flames and highlighting their distinct heat release oscillation distribution. Consequently, comprehending the response mechanism to flow disturbance in non-premixed combustions requires further exploration.
This study experimentally investigated methane–air non-premixed swirling flame’s response to low-frequency acoustic excitations. Proper Orthogonal Decomposition (POD) of the forced flame was applied to identify the harmonic flame response. Large Eddy Simulation (LES) was employed to analyze the characteristics of the non-reacting flow response under 20 Hz, 50 Hz, and 150 Hz acoustic excitations, focusing on the reactant mixing and the vortex structure evolution. The results could serve as a fundamental basis for a deeper understanding of the complex interactions between flow disturbance, flames, and acoustic waves in non-premixed combustions.
2. Experimental Setup
This study focused on a non-premixed swirling burner, which is depicted in Figure 1. The combustion chamber is square with an open outlet connected to the atmosphere. The burner design consists of an annular duct surrounding a conical bluff body with a diameter of 20 mm, through which air is supplied to the combustion chamber. The central fuel duct carries dry methane (CH4) fuel, which mixes with the air in the annular duct through 12 symmetrical orifices located in the burner head. Each orifice has a diameter of 1.5 mm. The swirling flow is generated by the 12 axial swirler blades positioned at an angle of . The estimated swirl number is . The combustion chamber has dimensions of 300 mm in length and 80 mm in width. In addition, the air tube has an internal diameter of 38 mm, and the fuel tube has an external diameter of 14 mm. For ease of analysis, a three-dimensional coordinate system was established with the center of the burner inlet ring as the origin. In this coordinate system, the z-axis was aligned with the axis of the bluff body, while the x- and y-axes were in the plane of the inlet ring.
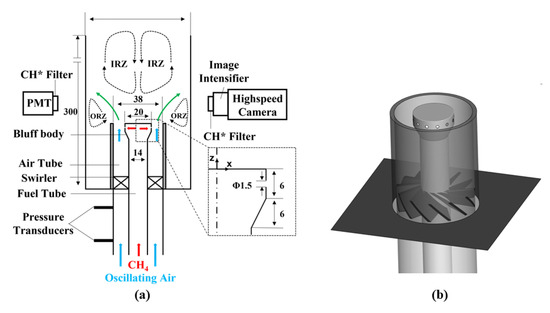
Figure 1.
(a) Schematic representation of the burner (Green arrow represents the mixed flow). (b) Three-dimensional view of the burner.
To monitor the chemiluminescent emission of CH* from the flame, a narrow-bandpass filter (Thorlabs FB430-10) was installed on a Thorlabs PMM01 photomultiplier tube (PMT) at a wavelength of 430 ± 10 nm, with the PMT signal proportional to the heat release [13]. To capture the release of CH radicals from the flame, a FASTCAM Nova S16 high-speed camera (HSC) integrated with an image intensifier (EyeiTS S-HQB-F) and a narrow-bandpass filter with a wavelength of 430 ± 10 nm was employed. The camera operated at a sampling rate of 4000 fps, with each imge being exposed for 0.2 ms.
The experimental configuration included an acoustic excitation system consisting of a wave generator, a 280 W power amplifier, and a loudspeaker strategically positioned in the lower section. The wave generator produced a sinusoidal excitation signal, which was then amplified by the 280 W power amplifier. The amplified signal was sent to the loudspeaker to produce sound waves of the desired amplitude and frequency. To measure the amplitude of the velocity fluctuations in the tube, a dual-microphone technique [23] was used, with two microphones positioned 95 mm and 245 mm upstream of the burner inlet annulus.
A Z-type schlieren imaging system was constructed, consisting of a pair of parabolic mirrors (250 mm in diameter, 2.5 m in focal length), a point light source, a knife edge, and a high-speed camera (AgileDevice, M220). The high-speed camera is manufactured by HF Agile Device Co., Ltd. (Newton, MA, USA) and the equipment is sourced in Hefei, Anhui Province, China. Schlieren images were captured at a frame rate of 2000 fps and an exposure time of 0.05 ms.
3. Numerical Approach
3.1. LES Model
The fundamental principle of Large Eddy Simulation (LES) involves directly solving for large-scale vortex structures and employing the subgrid-scale model to represent small-scale vortex structures. The flow velocity used in this study had a Mach number less than 0.3. For flows with low Mach numbers, the governing equations are approximated by the Navier–Stokes equations for incompressible fluids. In LES, these equations for mass and momentum are spatially filtered and can be written as follows:
where t is time; ui is the velocity components in the xi direction; ρ is density; p is pressure; and ν is the kinematic viscosity. Quantities with overbars are spatially filtered. In the governing equations, unknown terms appear as a result of spatial filtering. These unknown terms account for the effect of the filtered turbulence scales; hence, they are known as the residual stress tensor τij. According to the Boussinesq assumption,
Here, νsgs is the subgrid-scale viscosity and is the filtered strain-rate tensor for the resolved scale. To fully describe the governing equations, the subgrid-scale viscosity, υsgs, is modeled using the wall-adapting local eddy-viscosity (WALE) model [24]. This model eliminates the need for additional wall or damping functions, making it suitable for turbulent transition regimes. The subgrid-scale viscosity of the model is defined as follows:
where ksgs is the subgrid-scale kinetic energy, and Sijd is the velocity gradient tensor. Ck = 0.094 and CW = 0.325, which are constants.
3.2. Computational Domain
As shown in Figure 2a, the Integrated Computer Engineering and Manufacturing code for Computational Fluid Dynamics (ICEM-CFD) was employed to generate a global structured mesh with 1.76 × 106 cells in the computational domain. To ensure simulation accuracy, the mesh was refined in areas such as the swirler, nozzle, and shear layers while gradually coarsening downstream to improve computational efficiency. The minimum mesh size near the wall was set to 0.07 mm, ensuring a y+ value less than 1.0 to accurately capture flow details near the wall [25].
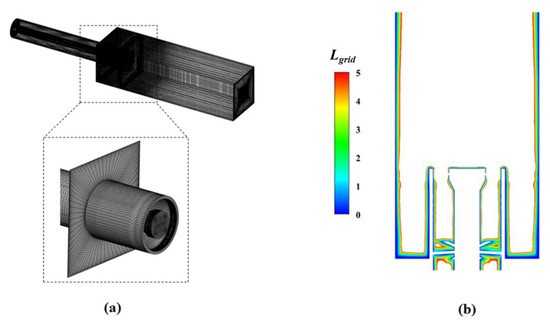
Figure 2.
(a) Computational domain mesh. (b) Contour of mesh quality according to the criterion (Equation (10)).
In LES, the mesh resolution determines the proportion of turbulent kinetic energy that is directly resolved. The suitability of the LES mesh used in this study was evaluated by analyzing the turbulent integral length scale l0, which was obtained from a precursor RANS simulation employing the realizable k-ε model [26]:
Here, k is the turbulent kinetic energy, and ε is the turbulent dissipation rate, with both being calculated by using RANS. The resolved turbulent kinetic energy for a given mesh size is then estimated from the local l0 value. Celik et al. [27] suggested that in order to resolve 80% of the turbulent kinetic energy using LES, approximately 5 or more cells over the integral length scale l0 would be required. The ratio between the turbulent integral length scale l0 and the cubic root of the cell volume Δ is characterized by the defined parameter Lgrid:
Figure 2b illustrates the contour of Lgrid, where values exceeding 5 had been clipped so that the well-resolved areas did not appear, and the not-so-well-resolved regions could be identified easily. The most critical regions for mesh refinement were represented by the inner and outer shear layers at the burner outlet. It could be observed that the mesh met the computational requirements for LES in almost all regions. Therefore, this mesh was used for further calculations.
3.3. Numerical Setup Details
The combustion chamber was subjected to inlet velocity and outlet pressure boundary conditions. The inlet air and fuel parameters were determined based on the operating conditions of a natural gas flow rate of 4 L/min and an air flow rate of 54.4 L/min (equivalence ratio of 0.7). To investigate the response of the flow field in the non-premixed burner under external acoustic excitations, velocity perturbations were applied at the air inlet according to Equation (11):
where Vin and V0 represent the inlet velocities with and without acoustic excitation, respectively. Additionally, A and f denote the amplitude and frequency of the excitation, respectively. In this study, a uniform excitation amplitude of 0.3 was employed, while the excitation frequency varied among three values: 20 Hz, 50 Hz, and 150 Hz.
To ensure accuracy, the temporal and spatial variables in the LES were treated with second-order precision. The governing equations’ pressure–velocity coupling was handled using the SIMPLEC algorithm. A dynamically adjusted time step was utilized throughout the computation, with a maximum time step of 5 × 10−5 s. This approach guaranteed that the global Courant number remained below the threshold of 0.4 at all times.
3.4. Description of Monitoring Points
Nine monitoring points were strategically placed on the y = 0 plane of the computational domain, as shown in Figure 3. These monitoring points were specifically chosen to capture the behavior of the inner shear layer (ISL), outer shear layer (OSL), and vortex ring generation regions. Monitoring point A was positioned at the center of the inlet annulus while monitoring points B1 to B3 were located near the outer shear layer. Similarly, monitoring points C1 to C3 were placed near the inner shear layer, and monitoring points D and E corresponded to the regions where the outer vortex ring (OVR) and inner vortex ring (IVR) were formed. The coordinates of each monitoring point are presented in Table 1.
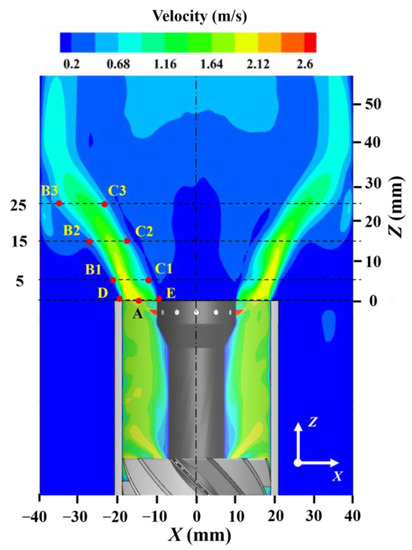
Figure 3.
Schematic of monitoring points.

Table 1.
Coordinates of monitoring points in the computational domain.
3.5. Validation
The accuracy of the numerical results was validated by comparing the vortex motion obtained from the schlieren images with the vortex motion calculated using LES. The reliability of schlieren imaging in validating LES has been established in previous studies [28].
Schlieren imaging relies on the deflection of light caused by changes in the refractive index resulting from density variations. To enhance the clarity of the schlieren images in the cold state, a 100 W heating tape was wrapped around the upstream tube of the swirler to moderately heat the jet air. Schlieren imaging was performed on the non-reacting flow field, which was exposed to acoustic excitation at a frequency of 50 Hz and an amplitude of 0.3. The resulting schlieren images, adjusted for contrast, were then compared with the velocity vector maps obtained from the LES under the same inlet excitation conditions, as shown in Figure 4. The velocity vector field was color-coded based on vorticity. By maintaining consistent excitation during the initial phase at time zero, the motion trends of the vortex within a 4 ms timeframe were observed. The black line in Figure 4 represents the height of the vector center in the LES. The observation results showed good qualitative agreement between the vortex motion trends obtained from the LES and the experimental schlieren imaging.
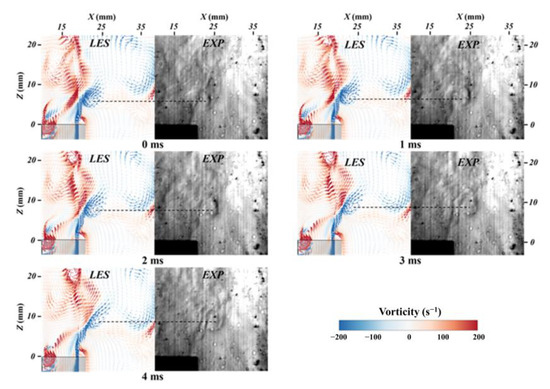
Figure 4.
Temporal evolution of vortices obtained from LES (left) and schlieren imaging (right) under 50 Hz excitation.
4. Proper Orthogonal Decomposition (POD) Method
The Proper Orthogonal Decomposition (POD) method is a widely used technique for dimensionality reduction. It is recognized as an effective approach for extracting significant features from unsteady processes [29,30]. The core principle of the POD method involves the orthogonal decomposition of a matrix A(s,t) containing both temporal and spatial information into mutually orthogonal data superposition modes:
Here, s represents the data values of the parameter, t denotes the time coordinate, M denotes the number of modes, αi is the temporal coefficient of mode i, and φ characterizes the spatial distribution features of mode i. The data sets are chronologically organized to form a matrix as follows:
where n represents the number of time series, and ai corresponds to the one-dimensional matrix of data at time i. By employing the singular value decomposition (SVD) method [31], matrix A can be decomposed as follows:
where U represents the spatial modal matrix, V denotes the temporal modal matrix, Σ stands for the diagonal matrix of eigenvalues, un signifies the nth-order spatial mode, vn represents the nth-order time series, and σi denotes the eigenvalue corresponding to each mode. These eigenvalues are indicative of the proportion of energy carried by each mode within the system. Since the eigenvalues obtained by SVD are arranged in descending order, the modes obtained using the POD method are ranked according to their energy. An analysis of the higher-energy modes reveals the main variations in the data.
5. Results and Discussion
5.1. Flame Response
This section discusses the flame response to different excitation frequencies, including changes in the height at the center of mass of the flame (Hcom), as well as the pulsation characteristics of acoustic pressure and heat release rate. To reveal the dynamics of the forced flame, additional POD analysis was performed on the flame images to explore their spatial structural characteristics and local spectral features.
Figure 5 illustrates the time-averaged distribution of CH* chemiluminescence in the flame. The center of mass of the flame is depicted as a black dashed line, calculated using the formula from reference [10]. A decreasing trend in Hcom was observed with increasing excitation frequencies, measured at 18.2 mm, 17.1 mm, and 16.0 mm, respectively. The flame Strouhal number (Stf), based on the Hcom and the mean inlet jet velocity Uj (1.105 m/s), was calculated to be 0.329, 0.774, and 2.172. The Stf represents the number of perturbations induced by acoustic excitations along the Hcom and relates the flame oscillation frequency to the upstream fluid dynamics [32,33].
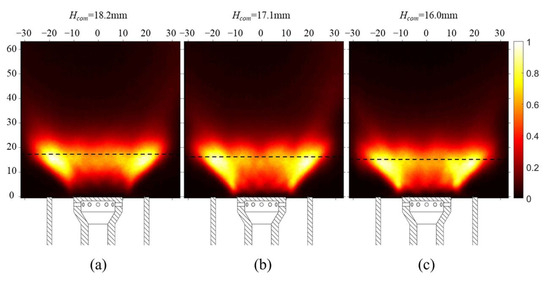
Figure 5.
The time-averaged distributions of CH* chemiluminescence under (a) 20 Hz, (b) 50 Hz, and (c) 150 Hz excitations.
Figure 6 presents the spectra of acoustic pressure, as measured by the dual microphones, and the heat release rate, as measured by the PMT. Notably, phenomena related to harmonic flame response were observed. As the excitation frequency increased, a diminishing trend was evident in the harmonic flame response. This trend was consistent with the findings reported by Liu [14] regarding premixed flames. Specifically, under 20 Hz excitation, an evident harmonic response emerged at 40 Hz. Under 50 Hz excitation, a relatively weak 100 Hz response was observed. However, under 150 Hz excitation, the harmonic response was virtually absent.
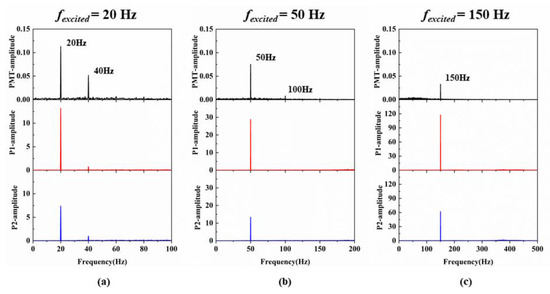
Figure 6.
Spectral plots of acoustic pressure and heat release rate under (a) 20 Hz, (b) 50 Hz, and (c) 150 Hz excitations.
To investigate the spatial structure and local spectral characteristics of the flame, Proper Orthogonal Decomposition (POD) analysis was conducted using the instantaneous CH* chemiluminescence snapshots. The POD method applies orthogonal modal decomposition to oscillatory systems, thereby reducing the complexity of oscillation phenomena and providing a lower-dimensional representation of the spatial distribution, temporal coefficients, and energy contributions of multiple modes [34]. Typically, the initial modes shown in the POD results represent the dominant oscillation patterns in systems with combustion instability. The spectral plots of the first four temporal coefficients αi and the spatial structures φi obtained from the POD analysis are presented in Figure 7.
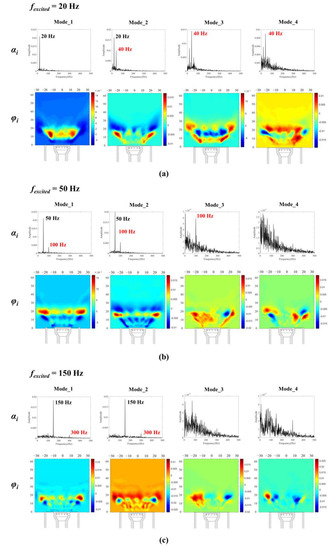
Figure 7.
First four POD modes of the CH* images of the flame under (a) 20 Hz, (b) 50 Hz, and (c) 150 Hz excitations.
Under 20 Hz excitation, the dominant mode of the flame was the 20 Hz frequency-flashing mode. However, higher modes were influenced by harmonic responses, leading to alternating axial oscillations in their spatial distribution. Conversely, under 50 Hz and 150 Hz excitations, the flame’s first two modes demonstrated alternating axial oscillations. The FFT analysis of the temporal coefficients revealed that under these conditions, the flame’s first two modes were predominantly governed by the fundamental frequency, accompanied by minor harmonic responses. The distinction between these two cases was in the number of oscillation regions within the first mode within the Hcom: two regions for the 50 Hz excitation and three regions for the 150 Hz excitation.
These POD results confirmed both the presence of harmonic flame response and its impact on flame oscillation patterns. Harmonic flame response has garnered considerable attention in research on the nonlinear response of premixed flames [12,13,14,35]. Notably, the phenomenon of harmonic response was observed in the non-premixed flame in this study as well. Previous investigations have predominantly focused on analyzing the connection between coherent vortex structures within the shear layers and harmonic response under reacting conditions. Nevertheless, given the intricate interplay between fluid flow and chemical reactions inherent to combustion, our study was dedicated to examining the response of flow disturbance to acoustic excitations in a non-reacting flow field. This could offer a clearer understanding of the intricate correlation between the shear layers’ vortex motion and harmonic response. Large Eddy Simulation (LES) was used for quantitative analysis, focusing on the dynamic characteristics of vorticity, axial velocity, and equivalence ratio, and the results are presented in the following sections. In addition, the simulation excluded the influence of the acoustic device on the experimental results.
5.2. Flow Dynamics
5.2.1. Spatial Response Characteristics
Non-premixed combustion exhibits spatially distributed heat release, which is influenced by the reactant mixing process. This section presents an analysis of the spatial response characteristics in a non-reacting flow field, shedding light on the evolution of the vortex structure and spatial distribution of the reactants under different excitations, as shown in Figure 8. Iso-surfaces set at an equivalence ratio of 1 [36] were employed to visualize the spatial distribution of the reactants at the stoichiometric ratio. The Q-criterion, described by Equation (18) [37], was utilized for identifying and quantifying vortex structures in the flow field. It relied on the nine-component velocity gradient calculation and provided a quantitative assessment of vortex morphology and intensity. An iso-surface with Q = 1.5 × 105 was used here to describe the vortex structures. Additionally, the influence of the vortex structures on the reactant mixing process was assessed by color-coding the vortex structures according to the equivalence ratio.
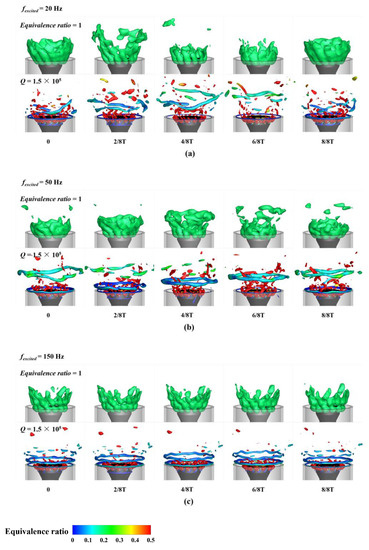
Figure 8.
Spatial response characteristics of the flow field under (a) 20 Hz, (b) 50 Hz, and (c) 150 Hz excitations.
The motion patterns of the outer vortex rings displayed a significant correlation with the spatial distribution of the reactants under different excitation frequencies. Under 150 Hz excitation, vortex rings corresponding to the excitation frequency were generated in the step region and propagated downstream. Specifically, during the 0-2/8T phase, vortex generation corresponded to the radial expansion of the first wrinkle in the equivalence ratio iso-surface. In the 2/8T-6/8T phase, vortices detached from the step region and propagated downstream, accompanied by axial expansion of the first wrinkle in the equivalence ratio iso-surface. The ensuing vortex formation in the 6/8T-8/8T phase coincided with the radial expansion of a new wrinkle in the equivalence ratio iso-surface. Under 50 Hz excitation, outer vortex rings corresponding to the excitation frequency were generated and propagated downstream, similar to the 150 Hz excitation. However, at 50 Hz, distinct spatial shifts were noticeable in both the vortex structures and the equivalence ratio iso-surface. During the 0-2/8T phase, vortex generation correlated with the axial stretching of the equivalence ratio iso-surface. In the subsequent 2/8T-6/8T phase, vortices propagated downstream and dissipated, reflecting the fragmentation, discontinuity, and retraction phenomena within the equivalence ratio iso-surface. The ensuing vortex generation during the 6/8T-8/8T phase aligned with the radial expansion of the bottom layer in the equivalence ratio iso-surface. Conversely, under 20 Hz excitation, observing the formation of vortex rings corresponding to the excitation frequency proved to be challenging. Instead, a greater number of fragmented, small vortex structures developed downstream in a disordered manner. Compared to 50 Hz, the vortex structures induced by 20 Hz excitation extended further downstream. This extension was accompanied by heightened axial stretching and fracturing of the equivalence ratio iso-surface, subsequently influencing the reactant mixing process along its trajectory.
These observations highlighted regional variations in how different excitation frequencies impacted vortex structures and the spatial distribution of the reactants. Specifically, under 150 Hz excitation, vortex structures are predominantly localized near the nozzle, with minimal downstream impact. However, as the excitation frequency decreased to 50 Hz and 20 Hz, the induced vortex structures propagated downstream, thereby impacting the reactant mixing process along its trajectory. This effect was accompanied by axial stretching and retraction of the equivalence ratio iso-surface. Notably, these observed phenomena bear similarity to the localized stretch–extinction behavior observed in non-premixed flames under low-frequency excitation [10,38,39,40]. This similarity further strengthens the connection between the dynamic attributes of non-premixed flames and the spatial distribution of reactants. Moreover, based on the evolving characteristics of the vortex iso-surface under 20 Hz excitation, we hypothesized that the vortex generation mechanism might be connected with harmonic responses. A more comprehensive investigation into vortex motion is provided in Section 5.2.3.
5.2.2. Axial Velocity Spectra in the Shear Layer
The axial velocity in the shear layers was statistically analyzed to investigate the influence of excitation frequencies on the harmonic responses, and the spectra are depicted in Figure 9. Excitation at 20 Hz resulted in a dominant response at 20 Hz, accompanied by subharmonic and multiple harmonic responses (10 Hz, 40 Hz, 60 Hz, 80 Hz, 100 Hz, and 120 Hz). Under 50 Hz excitation, responses were observed at 50 Hz, with a subharmonic response at 25 Hz and a harmonic response at 100 Hz. Similarly, under 150 Hz excitation, responses were observed at 150 Hz, with a subharmonic response at 75 Hz and a harmonic response at 300 Hz. Notably, the occurrence of multiple harmonic responses under 50 Hz and 150 Hz excitations showed a reduction in both number and amplitude compared to 20 Hz excitation.
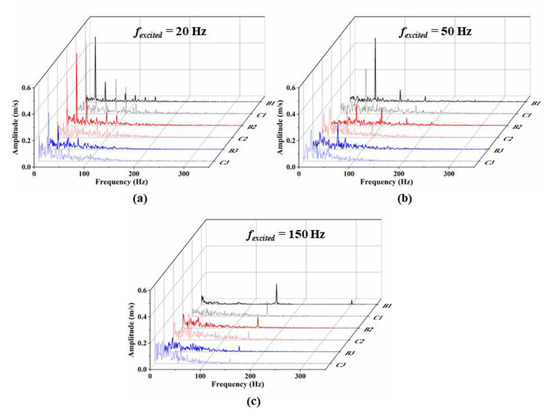
Figure 9.
Axial velocity spectra of the monitoring points in the OSL and ISL under (a) 20 Hz, (b) 50 Hz, and (c) 150 Hz excitations.
To facilitate direct comparison and assessment of the relative intensities, the normalized amplitudes of the subharmonic and harmonic responses were compiled based on the axial velocity spectra at the monitoring points. The detailed data can be found in Table 2. The normalization process involved using the amplitude of the excitation frequency at point B1 as the baseline value and dividing the amplitudes of the other response frequencies by this baseline value.

Table 2.
Normalized response amplitude of the monitoring points in the OSL and ISL.
The axial velocity in the shear layers’ monitoring points exhibited sensitivity and response characteristics to different excitation frequencies. As the axial distance increased, the response amplitudes of the excitation frequencies gradually decreased, indicating the dissipation of excitation signals within the shear layers. Higher-frequency amplitudes dissipated faster, indicating a stronger damping and dissipation effect on higher-frequency excitation signals in the flow field. Additionally, harmonic responses were observed under 20 Hz and 50 Hz excitations. Under 20 Hz excitation, strong responses up to the sixth harmonic were captured at points C1 and C2. It is noteworthy that in the current investigation of non-reacting flow fields, we identified harmonic responses within the axial velocity spectra of the monitoring points in the shear layers. This finding suggested that the experimentally observed harmonic flame response, as detailed in Section 5.1, was mainly due to harmonic velocity pulsations within the shear layers under non-reacting flows. The harmonic velocity response may be further enhanced or diminished by the thermal expansion of the flame. This finding served as an additional explanation to previous research on the source of harmonic response [14].
5.2.3. Vortex Motion Characteristics
It is widely accepted that the generation of the initial vortex is due to periodic velocity fluctuations in the upstream gas flow [41,42]. Accordingly, the temporal variations in axial velocity and acceleration at monitoring point A, located at the center of the inlet annulus, as well as the temporal evolution of the initial vorticity for the outer and inner vortices at points D and E, were plotted, as shown in Figure 10. In addition, the fluctuation of the equivalence ratio at points B3 and C3 is also shown in the figure. These data captured the dynamic changes over two excitation periods and were compared using the normalized time, denoted as t, with respect to the excitation period, T. Under the higher-frequency excitation of 150 Hz, the vorticity variations at monitoring point D exhibited consistent behavior with the axial velocity and acceleration. The vorticity peaks corresponded to the axial velocity peaks, displaying a distinct sinusoidal waveform, and the positive acceleration corresponded to the growth phase of vorticity. The downstream monitoring points showed almost no fluctuation in the equivalence ratio. These findings were consistent with previous experimental results reported by Wang [16] and provided significant support to our understanding of vortex formation mechanism. However, under 50 Hz and 20 Hz excitations, noticeable interference frequencies were observed in the axial velocity and acceleration at the inlet, as explicitly demonstrated in the spectral analysis of the acceleration at point A in Figure 10d. The presence of multiple harmonic responses under 50 Hz and 20 Hz excitations caused more complex dynamics in vorticity variations, leading to significant fluctuations in the equivalence ratio at the downstream monitoring points. Although certain periodic trends could still be observed in the overall growth and dissipation of vorticity, analyzing the finer details of vorticity variations proved challenging. Moreover, a consistent trend was observed for the variations in vorticity at monitoring points D and E, albeit with a phase delay [16]. This phase delay might be due to different patterns of motion between the outer vortex and inner vortex [43,44,45]. It is hypothesized that the phase delay at the inlet could be responsible for the harmonic responses observed in the axial velocity at the monitoring points within the shear layers.
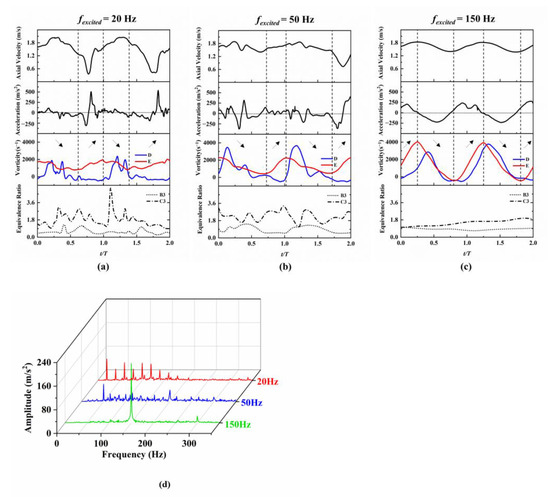
Figure 10.
Evolution of axial velocity and acceleration at point A equivalence ratio at point B3 and C3, and vorticity at points D and E under (a) 20 Hz, (b) 50 Hz, and (c) 150 Hz excitations. (d) Spectral plot of acceleration at point A.
The distribution of vorticity and equivalence ratio at the y = 0 plane during one excitation period is presented in Figure 11. In the vorticity contour, the blue dashed line represents the evolution of the external vortex structure, the red dashed line represents the flame height (Hcom) measured under the respective excitation conditions experimentally, and the black solid line shows the expected flame shape under stoichiometric fraction. Significant differences in vortex generation and axial convective velocity were observed under the influence of harmonic responses to different excitation frequencies. Under 150 Hz excitation, a single vortex was formed at the inlet that underwent complete evolution, including growth, detachment, and downstream propagation. The coexistence of multiple vortices downstream of the nozzle corresponded to folds in the local equivalence ratio distribution. The expected flame height was relatively stable during the excitation period. However, under 50 Hz excitation, a larger outer vortex and fragmented smaller vortices were discernible within the excitation period. This phenomenon could be attributed to the interference of the 100 Hz harmonic response on the flow field’s reaction to the 50 Hz excitation. The motion of the larger outer vortex aligned with the fragmentation of the equivalence ratio field, and a fracture even appeared in the expected flame shape (2/8T). Under 20 Hz excitation, the vortex structure within the period became more intricate, indicating the presence of stronger harmonic responses. Compared to 50 Hz, the axial stretching and fragmentation of the equivalence ratio field became more pronounced, leading to a more complex, expected flame shape. To analyze the vortex convective transport process, the axial convective wavelength λ [46] was defined as the axial height at which the vortex propagated downstream within one excitation period. The axial convective wavelengths of the vortex under different excitations are annotated in Figure 11. By calculating the ratio of the excitation period t to the axial convective wavelength λ, the axial convective velocity Ue of the vortex could be determined, which played a crucial role in calculating the flame delay time. The vortex axial convective velocity decreased with increasing excitation frequencies, with respective values of 0.803 m/s, 0.783 m/s, and 0.496 m/s. Further calculations for the ratio of vortex axial convective velocity to the mean inlet jet velocity Uj (1.105 m/s) revealed that under excitation frequencies of 20 Hz, the axial vortex convective velocity is slightly less than the jet velocity. This supported the assumption that the vortex convective velocity was often regarded as the jet velocity [6,47]. Future research is necessary to explore the influence of flame thermal expansion on vortex convective velocity under reacting conditions. Specific values can be found in Table 3.
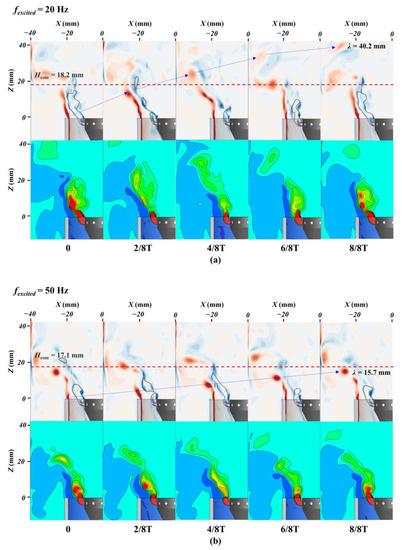
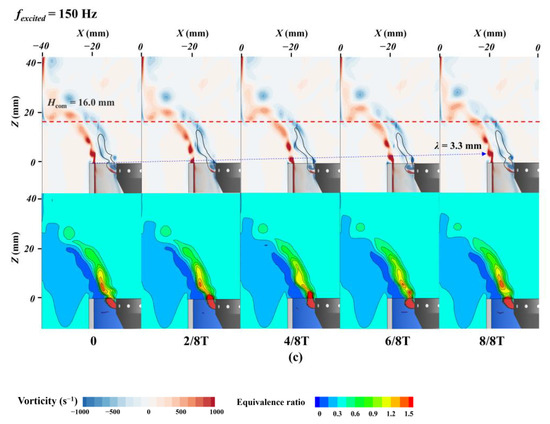
Figure 11.
Evolution of vorticity and equivalence ratio under (a) 20 Hz, (b) 50 Hz, and (c) 150 Hz excitations.

Table 3.
Parameters related to the propagation characteristics of flow disturbance.
Additionally, the spatial distribution characteristics of the vortex in non-reacting conditions, as shown in Figure 11, were closely aligned with the first-mode spatial oscillation mode obtained using the POD method, as described in Section 5.1. Within the Hcom corresponding to the 150 Hz excitation, the coexistence of three vortices was observed for the majority of the time; similarly, the coexistence of two vortices was predominant for the Hcom corresponding to the 50 Hz excitation. The number of coexisting vortices at these excitation frequencies was consistent with the number of oscillation regions revealed by the first-mode POD results. As for the 20 Hz excitation, the observation predominantly showed one vortex existing within the Hcom, which was consistent with the frequency-flashing mode of the first-mode POD results. The comparative analysis between LES and POD results revealed that the oscillation modes in non-premixed combustion were primarily influenced by the spatial distribution characteristics of vortices within the shear layers. In the non-reacting flows, the vortices within the shear layers under acoustic excitations exhibited motion patterns that are susceptible to harmonic interference, with the strength of this harmonic motion becoming more pronounced as the excitation frequency decreased. These acoustically induced vortices affected the mixing process of reactants, potentially driving the harmonic response in the flame’s heat release rate.
6. Conclusions
This study presents an experimental investigation of the response characteristics of a methane–air non-premixed swirling flame subjected to low-frequency acoustic excitations. By employing Proper Orthogonal Decomposition (POD) analysis on CH* chemiluminescence images, the harmonic flame response was revealed. To analyze the flow disturbance response to acoustic excitations, Large Eddy Simulation (LES) was utilized to analyze the dynamic variations in the non-reacting flow field under different excitation frequencies of 20 Hz, 50 Hz, and 150 Hz, specifically focusing on vorticity field, axial velocity, and equivalence ratio distribution. The results showed that the harmonic flame response was mainly due to the harmonic velocity pulsations within the shear layers under non-reacting conditions. Further examination revealed that the harmonic response affected the vortex generation and axial convective velocity within the shear layers. Specifically, under 150 Hz excitation, the vortex shedding frequency was aligned with the excitation frequency. While under 50 Hz and 20 Hz excitations, the interference in the harmonic response resulted in multiple vortex-shedding events being observed within one excitation period. The vortex axial convective velocity decreased with increasing excitation frequencies, with respective values of 0.80 m/s, 0.78 m/s, and 0.50 m/s. Additionally, the motion pattern of the spatial vortex closely matched the oscillation mode of the non-premixed flame obtained from the POD analysis.
These findings provide clearer insights into harmonic flame response and underscore the crucial role of vortex spatial distribution and its harmonic interactions in shaping the oscillation behavior of non-premixed flames. Future research should focus on investigating the impact of thermal expansion effects under reacting conditions, aiming to further explore the response mechanism of flow disturbance in non-premixed combustion.
Author Contributions
Conceptualization, T.Z., D.P. and J.B.; Methodology, C.J.; Software, J.B. and D.P.; Validation, J.B.; Formal Analysis, T.Z. and J.B.; Investigation, J.B. and D.P.; Resources, T.Z. and C.J.; Data Curation, J.B. and Z.Z.; Writing—Original Draft Preparation, J.B., C.J. and C.Z.; Writing—Review & Editing, J.B. and C.Z.; Visualization, J.B. and D.P.; Supervision, T.Z.; Project Administration, T.Z.; Funding Acquisition, T.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 51976140, and the Science and Technology Commission of Shanghai Municipality, grant number 20DZ1204902.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Schadow, K.; Gutmark, E. Combustion instability related to vortex shedding in dump combustors and their passive control. Prog. Energy Combust. Sci. 1992, 18, 117–132. [Google Scholar] [CrossRef]
- Sun, Y.; Zhao, D.; Zhu, X. Generation and Mitigation mechanism studies of nonlinear thermoacoustic instability in a modelled swirling combustor with a heat exchanger. Aerospace 2021, 8, 60. [Google Scholar] [CrossRef]
- Rogers, D.E.; Marble, F.E. A mechanism for high-frequency oscillation in ramjet combustors and afterburners. J. Jet Propuls. 1956, 26, 456–462. [Google Scholar] [CrossRef]
- Keller, J.O.; Daily, J. The effects of highly exothermic chemical reaction on a two-dimensional mixing layer. AIAA J. 1985, 23, 1937–1945. [Google Scholar] [CrossRef]
- Syred, N. A review of oscillation mechanisms and the role of the precessing vortex core (PVC) in swirl combustion systems. Prog. Energy Combust. Sci. 2006, 32, 93–161. [Google Scholar] [CrossRef]
- Palies, P.; Durox, D.; Schuller, T.; Candel, S. The combined dynamics of swirler and turbulent premixed swirling flames. Combust. Flame 2010, 157, 1698–1717. [Google Scholar] [CrossRef]
- Sujith, R. An experimental investigation of jets in a strong acoustic field. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 2003; p. 1276. [Google Scholar]
- Karimi, N.; Brear, M.J.; Jin, S.-H.; Monty, J.P. Linear and non-linear forced response of a conical, ducted, laminar premixed flame. Combust. Flame 2009, 156, 2201–2212. [Google Scholar] [CrossRef]
- Idahosa, U.; Saha, A.; Xu, C.; Basu, S. Non-premixed acoustically perturbed swirling flame dynamics. Combust. Flame 2010, 157, 1800–1814. [Google Scholar] [CrossRef]
- Pan, D.; Ji, C.; Zhu, T. Characterization of Nonlinear Responses of Non-Premixed Flames to Low-Frequency Acoustic Excitations. Appl. Sci. 2023, 13, 6237. [Google Scholar] [CrossRef]
- Palies, P.; Schuller, T.; Durox, D.; Gicquel, L.; Candel, S. Acoustically perturbed turbulent premixed swirling flames. Phys. Fluids 2011, 23, 037101. [Google Scholar] [CrossRef]
- Balachandran, R.; Ayoola, B.O.; Kaminski, C.F.; Dowling, A.P.; Mastorakos, E. Experimental investigation of the nonlinear response of turbulent premixed flames to imposed inlet velocity oscillations. Combust. Flame 2005, 143, 37–55. [Google Scholar] [CrossRef]
- Kim, K.T.; Hochgreb, S. The nonlinear heat release response of stratified lean-premixed flames to acoustic velocity oscillations. Combust. Flame 2011, 158, 2482–2499. [Google Scholar] [CrossRef]
- Liu, W.; Xue, R.; Zhang, L.; Yang, Q.; Wang, H. Nonlinear response of a premixed low-swirl flame to acoustic excitation with large amplitude. Combust. Flame 2022, 235, 111733. [Google Scholar] [CrossRef]
- Santhosh, R.; Miglani, A.; Basu, S. Transition and acoustic response of recirculation structures in an unconfined co-axial isothermal swirling flow. Phys. Fluids 2013, 25, 083603. [Google Scholar] [CrossRef]
- Wang, G.; Liu, X.; Xia, X.; Wang, S.; Qi, F. Dynamics of periodically-excited vortices in swirling flames. Proc. Combust. Inst. 2021, 38, 6183–6191. [Google Scholar] [CrossRef]
- Ahn, B.; Lee, J.; Jung, S.; Kim, K.T. Low-frequency combustion instabilities of an airblast swirl injector in a liquid-fuel combustor. Combust. Flame 2018, 196, 424–438. [Google Scholar] [CrossRef]
- Fu, X.; Yang, F.; Guo, Z. Combustion instability of pilot flame in a pilot bluff body stabilized combustor. Chin. J. Aeronaut. 2015, 28, 1606–1615. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Y. Fuel mixing effect on the flickering of jet diffusion flames. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2011, 225, 155–162. [Google Scholar] [CrossRef]
- Darabkhani, H.G.; Zhang, Y. Methane diffusion flame dynamics at elevated pressures. Combust. Sci. Technol. 2010, 182, 231–251. [Google Scholar] [CrossRef]
- Magina, N.; Shin, D.-H.; Acharya, V.; Lieuwen, T. Response of non-premixed flames to bulk flow perturbations. Proc. Combust. Inst. 2013, 34, 963–971. [Google Scholar] [CrossRef]
- Magina, N.; Acharya, V.; Lieuwen, T. Forced response of laminar non-premixed jet flames. Prog. Energy Combust. Sci. 2019, 70, 89–118. [Google Scholar] [CrossRef]
- Chung, J.; Blaser, D. Transfer function method of measuring in-duct acoustic properties. I. Theory. J. Acoust. Soc. Am. 1980, 68, 907–913. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Georgiadis, N.J.; Rizzetta, D.P.; Fureby, C. Large-Eddy Simulation: Current Capabilities, Recommended Practices, and Future Research. AIAA J. 2010, 48, 1772–1784. [Google Scholar] [CrossRef]
- De Santis, A.; Clements, A.G.; Pranzitelli, A.; Ingham, D.B.; Pourkashanian, M. Assessment of the impact of subgrid-scale stress models and mesh resolution on the LES of a partially-premixed swirling flame. Fuel 2020, 281, 118620. [Google Scholar] [CrossRef]
- Celik, I.B.; Cehreli, Z.N.; Yavuz, I. Index of resolution quality for large eddy simulations. J. Fluids Eng.-Trans. Asme 2005, 127, 949–958. [Google Scholar] [CrossRef]
- Mattsson, R.; Kupiainen, M.; Gren, P.; Wahlin, A.; Carlsson, T.E.; Fureby, C. Pulsed TV holography and schlieren studies, and large eddy simulations of a turbulent jet diffusion flame. Combust. Flame 2004, 139, 1–15. [Google Scholar] [CrossRef]
- Sui, J.; Zhao, D.; Zhang, B.; Gao, N. Experimental study of Rijke-type thermoacoustic instability by using proper orthogonal decomposition method. Exp. Therm. Fluid Sci. 2017, 81, 336–344. [Google Scholar] [CrossRef]
- Song, X.; Zhu, T.; Pan, D.; Wang, Z.; Ji, C.; Zhao, D. Numerical investigations on the beating behavior of self-excited combustion instability in a hydrogen-fueled Rijke type combustor. Aerosp. Sci. Technol. 2022, 126, 107624. [Google Scholar] [CrossRef]
- Liang, Y.; Lee, H.; Lim, S.; Lin, W.; Lee, K.; Wu, C. Proper orthogonal decomposition and its applications—Part I: Theory. J. Sound Vib. 2002, 252, 527–544. [Google Scholar] [CrossRef]
- Kim, D.; Lee, J.G.; Quay, B.D.; Santavicca, D.A.; Kim, K.; Srinivasan, S. Effect of Flame Structure on the Flame Transfer Function in a Premixed Gas Turbine Combustor. J. Eng. Gas Turbines Power 2009, 132, 021502. [Google Scholar] [CrossRef]
- Ranalli, J.A.; Ferguson, D.; Martin, C. Simple analysis of flame dynamics via flexible convected disturbance models. J. Propuls. Power 2012, 28, 1268–1276. [Google Scholar] [CrossRef]
- Chen, H.; Reuss, D.L.; Sick, V. On the use and interpretation of proper orthogonal decomposition of in-cylinder engine flows. Meas. Sci. Technol. 2012, 23, 085302. [Google Scholar] [CrossRef]
- Schimek, S.; Moeck, J.P.; Paschereit, C.O. An Experimental Investigation of the Nonlinear Response of an Atmospheric Swirl-Stabilized Premixed Flame. J. Eng. Gas Turbines Power-Trans. Asme 2011, 133, 101502. [Google Scholar] [CrossRef]
- Turns, S.R. An Introduction to Combustion: Concepts and Applications. 2000. Available online: https://old.amu.ac.in/emp/studym/100007211.pdf (accessed on 10 August 2023).
- Jeong, J.; Hussain, F. On the identification of a vortex. J. Fluid Mech. 1995, 285, 69–94. [Google Scholar] [CrossRef]
- Jiang, J.; Jing, L.; Zhu, M.; Jiang, X. A comparative study of instabilities in forced reacting plumes of nonpremixed flames. J. Energy Inst. 2016, 89, 456–467. [Google Scholar] [CrossRef]
- Kim, T.; Ahn, M.; Lim, D.; Yoon, Y. Flame describing function and combustion instability analysis of non-premixed coaxial jet flames. Exp. Therm. Fluid Sci. 2022, 136, 110642. [Google Scholar] [CrossRef]
- Sun, Y.; Zhao, D.; Ni, S.; David, T.; Zhang, Y. Entropy and flame transfer function analysis of a hydrogen-fueled diffusion flame in a longitudinal combustor. Energy 2020, 194, 116870. [Google Scholar] [CrossRef]
- Aydemir, E.; Worth, N.A.; Dawson, J.R. The formation of vortex rings in a strongly forced round jet. Exp. Fluids 2012, 52, 729–742. [Google Scholar] [CrossRef]
- Gharib, M.; Rambod, E.; Shariff, K. A universal time scale for vortex ring formation. J. Fluid Mech. 1998, 360, 121–140. [Google Scholar] [CrossRef]
- Buntine, J.D.; Pullin, D.I. Merger and cancellation of strained vortices. J. Fluid Mech. 1989, 205, 263–295. [Google Scholar] [CrossRef]
- Zhang, J.; Ratner, A. Effect of pressure variation on acoustically perturbed swirling flames. Proc. Combust. Inst. 2017, 36, 3881–3888. [Google Scholar] [CrossRef]
- Huang, Y.; Ratner, A. Experimental Investigation of Thermoacoustic Coupling for Low-Swirl Lean Premixed Flames. J. Propuls. Power 2009, 25, 365–373. [Google Scholar] [CrossRef]
- Shin, D.-H.; Lieuwen, T. Flame wrinkle destruction processes in harmonically forced, turbulent premixed flames. J. Fluid Mech. 2013, 721, 484–513. [Google Scholar] [CrossRef]
- Ranalli, J.; Ferguson, D. Measurement of Flame Frequency Response Functions Under Exhaust Gas Recirculation Conditions. J. Eng. Gas Turbines Power-Trans. Asme 2012, 134, 091502. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).