Abstract
In this paper, a novel 3D (three-dimensional) soft-landing dynamic theoretical model of a legged lander is developed in detail as well as its numerical solution process. The six degrees of freedom motion (6-DOF) of the base model of the lander with mass center offset setting is considered in the model as well as the spatial motion (3-DOF) of each landing gear. The characteristics of the buffering force, the footpad–ground contact, and the inter-structure friction are also taken into account during the motion of each landing gear. The direct constraint violation correction is used to control the constraint stabilization of the nonlinear dynamic equation. Comparative studies between the results from the proposed model and the simulated model (built in MSC Adams) under four classical load cases show the validity of the model. Additionally, the influences of different types of contact force models, friction force models, and a friction correction model used in the soft-landing dynamic model are further investigated as a step toward understanding the soft-landing dynamic performance and the feasibility of the dynamic model method of a legged lander. The results indicate that a precise lateral force model of the footpad–ground contact is necessary to obtain the soft-landing performance of one lander during soft landing.
1. Introduction
The overall goal of China’s lunar program is to achieve China’s first manned landing on the moon by 2030 and carry out lunar scientific exploration and related technological experiments [1]. Different types of exploration equipment will be landing in the lunar polar region, which has complex lunar surface morphology and discrete lunar soil-bearing capacity characteristics [2]. Many types of modular landers with different masses, volumes, configurations, and sizes will be needed in the new-generation extraterrestrial exploration, such as landers with orientation capability [3], multifunctional landers with soft landing and locomotion [4,5,6], etc. The soft-landing dynamic theoretical model is an important method to evaluate the soft-landing performance of landers and optimize the design and arrangement of structures [7,8]. In comparison with other models (MBD (Multi-Rigid/flexible-Body Dynamic model), the FEM model, and physical test), the theoretical model has several advantages: (1) a better understanding of the load–deformation mechanism among each component, such as the footpad/ground bearing load–deformation relation; (2) easier implementation of modular designs to realize the quick design of a lander; (3) integration of multiple theoretical models to meet various design and analysis requirements; (4) reduces dependence on the commercial software such as MSC Adams or Abaqus. Therefore, it is necessary to develop a theoretical model that will satisfy the requirements of the new-generation extraterrestrial exploration and enable the easy and quick design and analysis of the next-generation lander.
In the process of soft-landing theoretical dynamic modeling, two issues require special attention: the dynamic model of the lander and the interaction force model between the footpad and the landing surface. Typically, the dynamic model of the lander comprises the main body of the lander and four landing gears (one landing gear consists of one primary and two secondary struts, an energy absorber in each strut, and one footpad) and is frequently modeled using the Newton–Euler equation method. Early works on the soft-landing dynamic theoretical model were predominantly carried out by the United States during lunar landing projects such as the Apollo mission, leading to the development of diverse theoretical models [9,10,11]. Despite the development of various theoretical models for soft-landing dynamics, many of these models were simplified, such as the simplified 3D model and two-dimensional model. As a result, the accuracy of these models may be limited in predicting the behavior of the lander during the landing process. Lavender [9] simplified the lander into a two-dimensional rigid body model with a hinged leg including elastic, damping, and crushing effects, while Alderson and Wells [10] developed a theoretical model for the Surveyor lunar lander that treated the spacecraft as a rigid body with compressible leg sets. The leg sets were treated as a plane linkage with a rigid lower link hinged to the spacecraft and a compressible, energy absorber upper link to the footpad. Zupp and Doiron [11] discussed the shortcomings of NASA’s previous soft-landing dynamics model and established a 3D dynamic simulation model. Its predictor-corrector method was the backward difference formula that maintains a specified accuracy in the integration. Takao etc. [12], based on a two-dimensional simplified landing model of a lander, proposed an improved footpad/soil-resistant theory to minimize the risk of tipping during landing. China is the third country to achieve a lunar landing, and some Chinese scholars in the field of lunar research also have conducted a large number of studies on the analytical model. Wan [13] established a 3D soft-landing model with the software MATLAB/SIMULINK and did not give the detailed calculation program flow. Yue etc. [14] built a soft-landing model of the launch vehicle using the Quasi-three-dimensional landing model and researched seven extreme landing conditions. Ke etc. [15] designed an innovative six-legged mobile lander with repetitive landing capacity and built a simplified 3D dynamic model and assessment criteria. Lin etc. [16] built a two-dimensional soft-landing theoretical model of a lunar lander, using a 7-DOF soft-landing dynamic model, and discussed the impact on soft-landing dynamic characteristics by different initial horizontal velocities, pitch angles, and inclinations of the lunar slope, etc. Yin [17] developed a planar dynamic model of a three-legged lander considering the asymmetric characteristic and the leg–leg coupling to understand the landing process of the asteroid probe with the three-legged cushioning mechanism. Yang [18] established a 3D dynamics model of China’s Mars lander considering plastic deformation parts and nonlinear contact forces. The equation of the model is too complex to be widely used in other landers. In summary, the majority of ongoing research on soft-landing dynamics were predominantly reliant on two-dimensional models, which are limited in their usage and only analyze some classical load cases. Although a few 3D models have been developed, the scalability and usability of these modeling methods are slightly insufficient, making them unable to better support future research.
The interactive model between the footpad and the lunar soil is of paramount importance, as it directly impacts the successful soft landing of the lander and its corresponding research work after soft landing. The dynamic response of the lunar soil during landings, such as the penetration depth of the footpad and the soil’s vertical and horizontal load-bearing capacity, are critical parameters in determining the stable position and angle of the lander after landing. There are three kinds of contact force models that have been derived: (1) the added mass model [19]; (2) the load model based on the Bekker theory [20], which defines contact force F as a function of the indentation depth δ: F = K × δn, where K represents the stiffness parameter, and the exponent n depends on the topological properties of the contacting surfaces; (3) the simplified dynamic bearing model in the form of the function on the force versus depth and velocity [18]. Moreover, many studies of fixed-shape (non-locomoting) objects impacting and penetrating dry granular media have revealed reaction forces that can be described by
where v and z are the velocity and depth of one object. Fp(z) is a depth-dependent force. α is the inertial drag coefficient [19]. However, during the impact, several different mechanical phenomena can occur. Tension and shear failure, localized deformation, effects of adiabatic shear, and crack propagation are only some of the important phenomena that may occur individually or simultaneously. Then, there is no uniform view on the footpad–ground bearing model when the bearing model considers other items such as penetration speed (linear and nonlinear relation), the shape of the footpad, contact type, loading weight, etc.
To meet the future design requirements and the soft-landing performance analysis of the legged lander, a 3D soft-landing dynamic theoretical model of a legged lander and its numerical solution process is developed, validated, and analyzed. In Section 2, the 3D soft-landing model of a legged lander is introduced, and the equations of kinematics and dynamics for the base model, landing gear, and footpad–ground bearing model are derived. In Section 3, the simulation program for the soft-landing model of the legged lander is developed based on the proposed method using the software MATLAB and validated by MSC Adams prototype under four classical load cases. In Section 4, different types of contact models and friction models in the footpad–ground bearing model are discussed. Furthermore, the inter-structure friction of the primary strut is also discussed.
2. Soft-Landing Model
2.1. Model Definition
A soft-landing dynamic model of the lander is shown in Figure 1. The lander consists of four landing gears, the simplified base model, and other components. Each landing gear consists of a primary strut, a footpad, and two secondary struts. Each strut is composed of outer and inner tubes connected by the sliding hinge. Moreover, the connection joints located at the points ai, bi, and ci in the No. i landing gear are the universal hinge, while the joints located at the points di, ei and fi are the ball hinge.
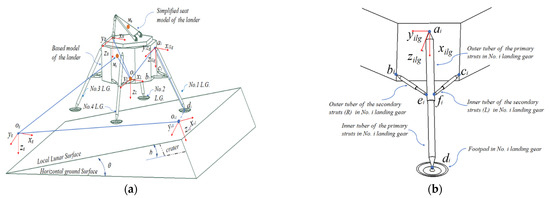
Figure 1.
A soft-landing dynamic model of a legged lander. (a) A simplified soft-landing dynamic model; (b) No. i landing gear (L.G.) sketch description. Red arrows are for coordinate system. Blue arrows are for labelling.
Moreover, there are five key coordinate systems in this model: (1) the global coordinate system and local lunar coordinate system, Og-xgygzg and Osi-xsiysizsi, are used to define the base reference coordinate system and the position and angle of the local lunar surface, respectively; (2) the lander coordination system, OL-xLyLzL, is used to define the structural distribution and motion state of the lander, where OL is the geometry center of the lander; (3) the No. I landing gear coordinate system, OL-xilgyilgzilg, is used to define the motion and load of the No. i landing gear; (4) the No. i primary strut coordinate system with origin point ai, ai-xilgyilgzilg, is used to define the position and velocity of the primary strut.
Based on the theory of spatial descriptions and transformations [21,22], the relative motion of the body or joint rotations is frequently expressed using the transition matrix in the Euler angles format. The transformation matrix consists of a translation matrix and a rotation matrix represented by Z-Y-X rotations, which are as follows.
To express the velocity and coordinates of the landing gear conveniently, the relations of the defined coordinate systems used in the soft-landing dynamic model are defined, which is shown in Figure 2. For example, the transformation matrix from the lander coordinate system to the No. i landing gear coordinate system can be obtained according to the rotation matrix and the translation matrix . The calculation equation of the rotation and translation matrix can be found in Nomenclature.
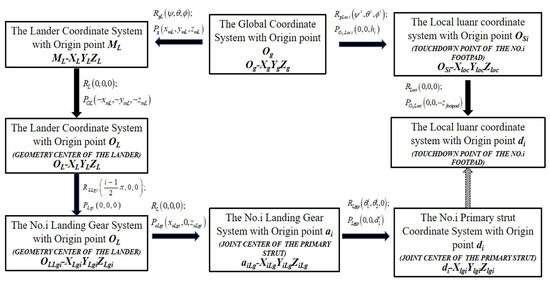
Figure 2.
The translation relations of the coordinate systems used in the soft-landing dynamic model.
To express the soft-landing dynamic model clearly, the relation of each component in the soft-landing dynamic model is shown in Figure 3. Section 2.2 aims to calculate the position and velocity of the key point of the lander, such as the mass center of the lander ML to use in Section 2.3, the touchdown point di in the No. i landing gear to use in Section 2.5, and the origin point OLgi of the No. i landing gear to use in Section 2.4. Moreover, Section 2.3 is used to calculate the landing gear’s velocity and length in the No. i landing gear coordinate system under the buffer and friction effect described in Section 2.6 and Section 2.7. Section 2.5 aims to calculate the binding force of the ground on the footpad, which is passed to the main body of the lander after being buffered by the landing gear.
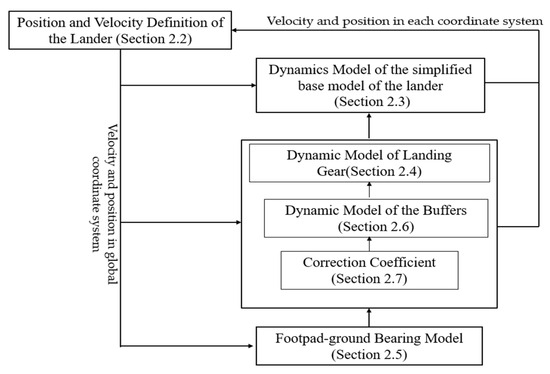
Figure 3.
The relation of each component in the soft-landing dynamic model.
2.2. Position and Velocity Definition of the Lander
According to the geometric relations defined in Figure 2, the coordinates of the points under the global coordinate system, Og-xgygzg, can be denoted as follows using the calculation equations of the translation matrix in Equation (2).
where
Similarly, each point in the No. i landing gear coordinate system can be obtained. Since and are the given design parameters of the lander to define the install position of the landing gear structure, some vectors and can be denoted using the generalized coordinate, , according to the theory of spatial descriptions and transformations.
According to the above equation and the principle of the virtual work, the velocity of the points in the global coordinate system, Og-xgygzg, can be expressed by the Jacobian matrix and the generalized velocity, , which are as follows.
Moreover, the constraint equations of the geometric relationships in the landing gear can be shown in Equation (6).
Similarly, the velocity of point, diLg in the No. i landing gear coordinate system, Olgi-xlgiylgizlgi, can be expressed by the Jacobian matrix and the generalized coordinate velocity, , which is as follows:
where
Additionally, according to the principle of virtual work, the equivalent dynamic force, FLgi, can be obtained by the Jacobian matrix.
2.3. Dynamics Model of the Simplified Base Model of the Lander
Assuming that the simplified base model of the lander is a rigid body and that its total mass and the relative position of the mass center remain constant throughout the landing process, the kinematics and dynamics of the lander can be described using a 12-state variable, 6 degrees of freedom model, as outlined by the following equations [21]. Moreover, to understand the dynamic model of the whole system easily, the free-body diagram of the lander is shown in Figure 4.
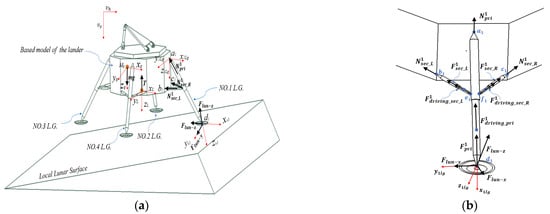
Figure 4.
The free-body diagram of the legged lander. (a) The simplified base model of the lander; (b) No. 1 landing gear (L.G.). Red arrows are for the coordinate system. Black arrows are for the force. Blue arrows are for Blue arrows is for labelling.
Typically, the forces acting on the lander include gravitational force mg, engine thrust force T, and the forces transferred from the No. i landing gear . These force and moment matrices, F and M, acting on the lander can be denoted as follows.
where
, and are the vectors expressed in the global coordinate system. The transmission force in the struts, , can be shown as follows:
The equivalent dynamic forces and can be obtained by Equation (10). , and are the crushing forces of the primary and secondary struts, which can be obtained by Equations (22)–(26). Meanwhile, the remaining driving force matrix can be denoted as:
where
2.4. Dynamic Model of Landing Gear
According to the principle of the Lagrange multiplier form of dynamic equations, the dynamic equation of each landing gear can be denoted as:
is the driving force in the generalized coordinate system. is the generalized internal force matrix, which is the velocity coupling force, and is the generalized gravity force matrix of the landing gear struts.
However, considering that the constraint relation Φ cannot be invalidated or deleted and is changed with the time variable during the soft landing, the Φqt and Φtt also equal zero, thus the constraint matrix γ is listed as follows.
Additionally, the numerical method for this dynamic model is direct integration with direct constraint violation correction [23,24], which can efficiently control the violations of constraint equations within any given accuracy at each time step. Compared to conventional methods such as the Newmark method or the generalized method, this method has a clear physical meaning, less calculation, an obvious correction effect, and a minor effect on the form of the dynamic equation of systems. The detailed algorithm of the method used in this paper is in Section 3.
2.5. Footpad–Ground Bearing Model
The footpad–ground bearing model comprises the vertical bearing model and the horizontal bearing model. While the vertical bearing model has been extensively studied in previous research, there is no uniform view of the calculation function, despite there being four calculation models available. To establish a widely accepted calculation model, the approximate contact calculation equation integrated into MSC Adams was utilized in this model. Meanwhile, since the surface soil exhibits low bearing capacity in the horizontal direction and is more easily movable, the horizontal bearing force is usually equal to the friction force acting on the footpad–ground interface caused by the vertical bearing force. Thus, the footpad–ground contact force vector under the local lunar coordinate system is expressed based on the geometry relation of the lander. The calculated force equation can be expressed as follows.
2.6. Dynamic Model of the Buffers
The previous lander was equipped with multiple types of buffers in its landing gear, including the AL-honeycomb buffer, the large plastic deformation rod buffer, and the hydro-pneumatic buffer. Each buffer can be modeled as a normalized equation form, which can be expressed as follows.
Moreover, this equation is derived based on the principles of virtual work and the geometric relations defined by the generalized coordinates of the multi-body system. It takes the following form.
Due to the slow touchdown velocity of the lander, the strain rate effect of the Al-honeycomb buffer is not considered. Then, the force of the Al-honeycomb buffer in the primary strut can be denoted as:
Similarly, the crushing force of the Al-honeycomb in the secondary strut can be denoted as:
Moreover, in the lander with the cantilever beam landing gear, the friction force between the outer and inner tubes in the primary strut must be considered. Then, the contact force can be denoted as follows:
The forces can be obtained by Equation (10). The generalized crush force of the primary strut in the No. i landing gear can be denoted as:
Further, the calculation equation of η is listed in Section 2.7.
2.7. Correction Coefficient η
Due to the force-transmitting feature of the landing gear, the lateral denominational force of the primary strut was equal to the force acted by the secondary struts. Therefore, the correction coefficient η was only used in the contact force calculation between the outer and inner tubes in the primary strut. Figure 5 illustrates the force relation among the outer, inner, and secondary struts in one landing gear. Based on the structural characteristics and the contact behavior of the primary strut, two assumptions were given: (1) the deflection and angle of each cross-section at the landing gear are consistent with the deformation coordination relationship; (2) the contact pressure p upon the outer tube is distributed in the form of a cosine function by the inner tube, p = pm × cos(θ), where pm is the maximum pressure acting on the outer tube and with the same direction as NE/F; (3) the contact angle θ between the outer and inner tubes is assumed to be π/2 since the inner diameter of the outer tube is approximately equal to the outer diameter of the inner tube. The force diagrams among the outer, inner, and secondary struts in one landing gear are shown in Figure 4.
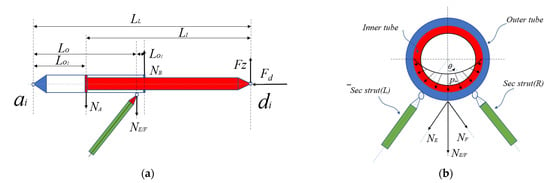
Figure 5.
Force diagrams among the outer, inner, and secondary struts in one landing gear: (a) force diagram between the outer and inner tube; (b) force diagram between the outer and inner tube in cross-section.
Then, according to the above assumptions, the calculation equation of the correction coefficient η is denoted as follows:
According to the force relations in the landing gear, the calculation equations for these correction factors are as follows. LO, L1, and LL are the lengths of the different areas in one landing gear. A detailed introduction is shown in Figure 5.
3. Simulation and Model Validation
3.1. Program Flow
A four-legged lunar lander with a total mass of 16 tons was established as a demonstrative application to validate the dynamic model used in this paper, based on our previous research [25]. The numerical simulation was performed using MATLAB R2021a on a desktop computer with a 5.3 GHz CPU and 64 GB RAM. With a time step of 0.000005 s for a total simulation setting of 1 s, so the model only required 290 s to complete. Moreover, the numerical method in this dynamic model was the direct integration with the direct constraint violation correction to control the constraint stabilization. The calculation steps in this model code can be shown as follows.
Step 1: at time t0 = 0, define the initial values of the designed variable:
The design variables of the lunar lander include the initial position and velocity matrix, mass property values of the lander, design parameters of the landing gear such as the crushing force of each strut, and the install position and length parameters of one landing gear. Additionally, the loading coefficient of the soil, the friction coefficient between the structure and ground or structure, as well as the value of the time increment and total simulation time, are also considered design variables.
Step 2: at time tn, identify whether the footpad of the No. i landing gear touched down on the relative local surface or not:
Based on the generalized position and velocity of the No. i landing gear, and the position and velocity vector (at time tn) of the lander, calculate the position and velocity matrix of point di, in the No. i local lunar surface coordinate system using the Jacobian matrix in Equation (5) and the translation matrix in Equation (2). If dlociz < 0, the transmission force of the No. i landing gear is equal to zero, then perform step 5; if touch down happens, obtain the footpad–ground bearing force vector using Equations (17) and (18). Based on the Jacobian matrix in Equations (7) and (8), calculate the equivalent dynamic force matrix in the No. i landing gear and the component force in each strut.
Step 3: at time tn, identify whether the buffer of the No. i landing gear is crushed or not:
According to the current value of the length and velocity in each strut at time tn, obtain the crushing force of the Al-honeycomb buffer of each strut using Equations (21)–(26). According to Equations (12)–(13), the transmission force in the struts and the driving force of the relative struts can be obtained. Using the driving force of the relative strut, the dynamic model of one landing gear is calculated using Equations (14)–(16). In addition, using the transmission force of the relative strut, the forces and moments acting on the lander can be obtained from the No. i landing gear using Equation (11). When the equivalent dynamic force is no less than the defined crush force of the Al-honeycomb buffer of the strut, the buffer begins to crush. The transmission force in the strut is equal to the crushing force of the relative strut. Moreover, the driving force in the relative strut is equal to the remaining force. However, if the equivalent force is less than the crushing force, the buffer does not crush. The driving force in the relative strut is equal to zero, and the transmission force in the strut in the No. i landing gear is equal to the equivalent dynamic force.
Step4: at time tn, calculate the dynamic model of the landing gear i and check the constraint stabilization:
Solve the variables in Equation (11), then the position and velocity , are obtained in turn using the direct integration method. Check the constraint stabilization of the nonlinear equation, if the result satisfies the constraint stabilization equation: , , then , go to step 5.
Otherwise, firstly, calculate to carry out the displacement constraint violation correction, then obtain , check again, and, if not satisfied, perform the above calculation process again until the equation satisfies. Secondly, using the obtained from the above displacement correction, perform the velocity constraint violation correction then obtain , check again, and, if not satisfied, perform the above calculation process again until the equation is satisfied. At last, the position and after constraint violation correction will be taken in the next dynamic model.
Step 5: identify whether all landing gears have been calculated or not:
If the transmission force of all the landing gears has been calculated, then go to step 6. Otherwise, return to step 2.
Step 6: at time tn, calculate the dynamic model of the lander:
Based on the forces and moments from all the landing gear systems, solve the acceleration variable of the lander using Equations (9) and (10) and obtain the position and velocity vector (at time tn+1) of the lander in the lander coordinate system in turn using the direct integration. Then, based on the transient matrix theory, calculate the position and velocity value of the lander in the global coordinate system.
Step 7: repeat steps 2 to 7 until the total time is over:
To clearly introduce the detailed calculation steps for the soft-landing model, the flow chart of the touch down dynamic model of the lander during a soft landing is presented in Figure 6.
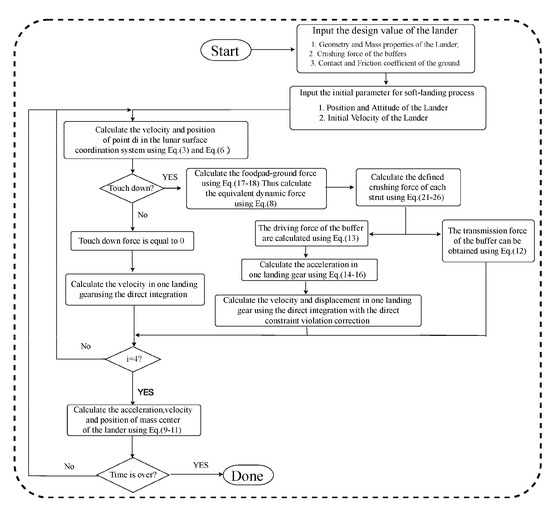
Figure 6.
Flow chart of the touch down dynamic model of the lander during soft landing.
3.2. Program Flow
Figure 7 and Table 1 present the configuration and parameters of a legged lander. Further details on the parameters and modeling of the lander can be found in [25]. To analyze the soft-landing dynamics of a legged lander, four severe load cases [25] are chosen in Table 2, including vertical loading load case (LC-1), the high-overloading load case (LC-2), the easily turnover load case (LC-3), and the maximum compression of primary strut load case (LC-4). To conduct a comparative analysis, two analytical models for the lander were generated using the methodology proposed in this paper and MSC Adams. Notably, there are three main differences between the two models, consisting of (1) the contact and friction force calculation equation differs: the STEP functions used in Adams are non-linear and non-clearly expression equations, while the functions used in the proposed method are linear functions; (2) the defined method of the crushing force: in MSC Adams, the widely used method of the SFROCE function was used, only considering the velocity’s direction and the crushing displacement of the buffer, without the maximum/minimum history displacement; (3) the numerical calculation method: the Runge–Kutta numerical method was used in MSC Adams, while the direct integration with the direct constraint violation correction was used in the proposed model.
Figure 7.
Soft-landing model of lander built in MSC Adams.

Table 1.
The parameter information of a lunar lander.

Table 2.
The load case information for soft-landing analysis.
Since the crushing length of each buffer after landing is the most direct and effective way to validate the simulated results [18], the crushing length of each strut after touch down is thereby analyzed emphatically in this work as well as the deviation data of the crushing length. Table 3 and Figure 8 show the crushing length of each strut in the four classical load cases as well as their error data under the theoretical dynamic model and multi-body model in MSC Adams. The comparative results show that the crushing length of each strut from the theoretical dynamic model was close to that from MSC Adams in general. Most of the error ratios of the results ranged between 2.0% and 7.0%. The max deviation crushing length was nearly 20.9 mm at the primary strut of LG-3 (No. 3 landing gear) in LC-4, and the relative error ratio was 17.0% based on the crushing length from MSC Adams that was 261.6 mm. The main reason for this calculation deviation is the differences between the calculation equations for contact and friction force, especially the calculation of friction force. Moreover, the other reason may be the SFROCE function used in the definition of the buffer force between the software and the theoretical model, which causes a small error during landing. The SFROCE function defined in MSC Adams does not consider the maximum history displacement of each strut. Once the reciprocating motion of a strut occurred during landing, some errors were taken in.

Table 3.
The crush length of each Al-honeycomb buffer during soft landing.
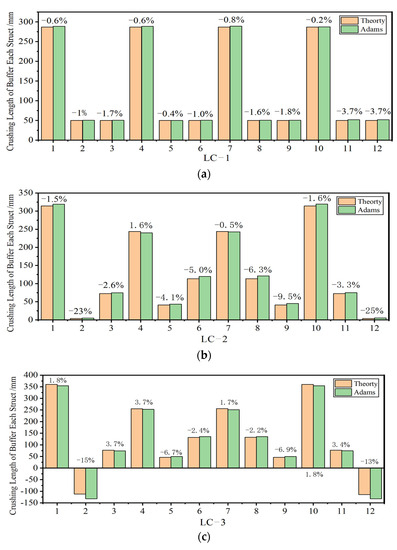
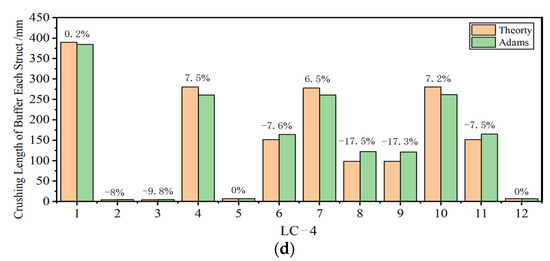
Figure 8.
The error data of the crushing length and the crushing length of each strut of the lander during soft landing under four typical cases. (a) load case−1 results; (b) load case−2 results; (c) load case−3 results; (d) load case−4 results.
Furthermore, it also can be found that the max error ratios were 23% at LC-2 based on the fact that the crushing length from MSC Adams was 5.2 mm. Its relative deviation was 1.7 mm at the secondary struts in LG-1 and LG-4. The reason may be the different numerical solution process between the software and the theoretical model, which causes a small error during landing. In the numerical method, as we all know, there is, more or less, some deviation between the results from each other method. Moreover, according to Figure 9, it is easily found that the stroke of each strut in the lander from two models have good agreement under four load cases. In conclusion, the agreement of the results proves the availability of soft-landing prediction of the theoretical dynamic model proposed in this paper.
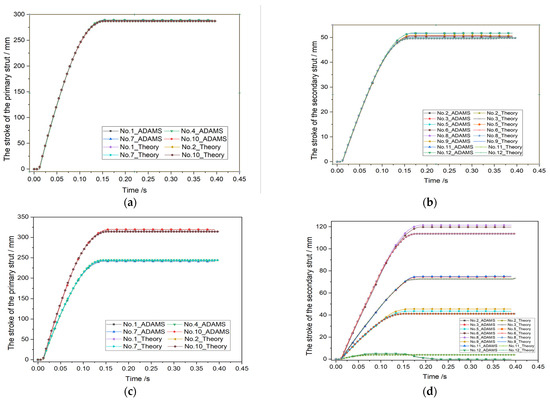
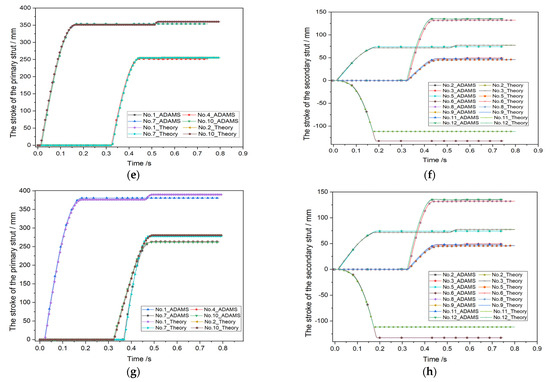
Figure 9.
The stroke of each strut of the lander during landing. (a) The primary strut of the lander in LC-1; (b) the secondary strut of the lander in LC-1; (c) the primary strut of the lander in LC-2; (d) the secondary strut of the lander in LC-2; (e) the primary strut of the lander in LC-3; (f) the secondary strut of the lander in LC-3; (g) the primary strut of the lander in LC-4; (h) the secondary strut of the lander in LC-4.
4. Discussions
4.1. Different Kinds of the Footpad–Ground Bearing Models
Although there are different types of footpad–ground bearing models, there is no uniform view of the functional form of the footpad–ground bearing model. The essence of the footpad–ground bearing model is a dissipative contact force model, which is a pivotal tool to predict the contact force and energy dissipation characteristics of the soil during soft landing. The soft-landing performance of a lander is therefore highly dependent on the accuracy and precision of the contact force model. To better understand the differences and similarities between contact force models, some frequently used impact contact force models, such as the Hertz contact model [26], Hertz contact + linear damping factor model [27], Hertz contact + step damping factor model [28,29] Hertz contact + bilinear damping factor model [19], and Hertz contact + hysteresis damping factor model [30], were discussed in this section, which are listed in Table 4. According to Table 4, it was easy to see that the difference between the five contact models was the damping option, aimed to accurately describe energy dissipation in the collision process. Detailed advantages and disadvantages for most contact models are discussed in reference [31]. Table 5 shows the parameter information of the five different contact force calculation models. To discuss the effect of the five different contact force models on the soft-landing performance, the parameters of each contact force model were chosen based on the rigid surface contact theory of MSC Adams. Moreover, the friction calculation method was the penalty function method, and the friction coefficient us = ud = 0.4.

Table 4.
Some commonly used contact force models defined in this work.

Table 5.
The parameter information of the five different contact force calculation models.
Table 6 and Figure 10 present the error data and crushing length of each strut under five different contact models for two classical load cases (LC-1 and LC-2). The simulation results, based on a comparative analysis of each buffer in the lunar lander after landing, indicated that the crushing length of each strut in the theoretical dynamic model under different contact force models was generally similar. The deviation ratios of most results under the five contact force models were less than 5%. The maximum deviation ratio of crushing length was nearly 200% at the secondary struts of L.G.-1 in LC-2 under the H–C contact force model, and the crushing value was 12.1 mm. The reason is due to the differences in the contact force calculation equations. To better understand these differences, the results of LC-1 were analyzed, primarily focusing on the deviation of the contact force time history curves of the footpad–ground bearing model, as shown in Figure 11. The results in Figure 11 indicated that the Hunt–Crossley contact model, the Hertz contact model, and the Kelvin–Voigt 1 model were the most influential models on the footpad–ground bearing force, with many oscillations in the load time history curves of these three models. This is the main reason for the deviation in the crushing length results of each strut. In contrast, the load time history curves of the Kelvin–Voigt and Kelvin–Voigt 2 models have fewer oscillations. Compared to the results of the Hertz contact model, the reason for this difference may be the effect of the velocity option in the calculation equation of the contact force model, which is usually used as a damping option to describe the energy dissipation and suppress data fluctuations during the collision process.

Table 6.
The crush length of each Al-honeycomb buffer under five contact models.
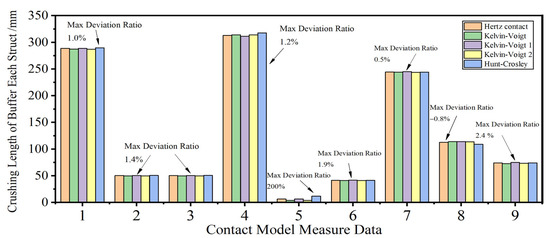
Figure 10.
The results for the lander during soft−landing under five typical contact models.
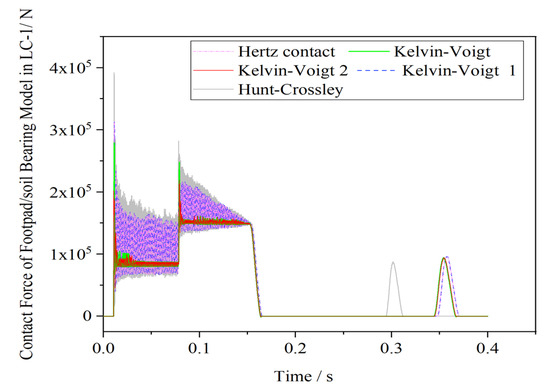
Figure 11.
Contact force of the footpad–ground bearing model in LC-1.
4.2. Friction Analysis
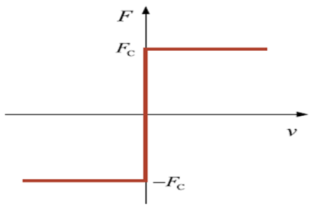
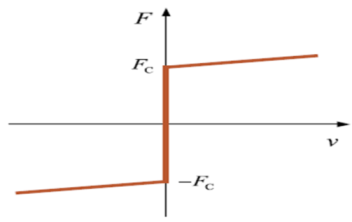
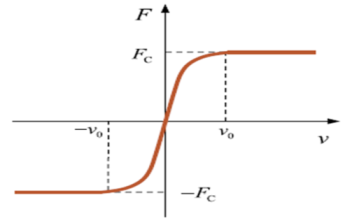
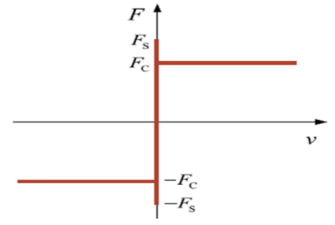
Friction is important in various fields such as engineering, physics, and materials science. Usually, the magnitude of the friction force depends on the normal force pressing the two surfaces together and the coefficient of friction between the two surfaces. The friction coefficient is a dimensionless constant that represents the friction characteristics of the two surfaces. It depends on various factors such as the nature of the two surfaces in contact, the roughness of the surfaces, the temperature, the relative speed of the surfaces, etc. To understand more clearly the lateral interaction of the footpad–ground bearing model, the default contact force model shown in Equations (17) and (18) were chosen first. Meanwhile, six commonly used friction models [32,33] were discussed in this section. The force calculation equations for the six classical friction models used in the engineering field are shown in Table 7. Table 8 provides the parameter information for the six different friction calculation models.

Table 7.
The force calculation equations of the six different friction calculation models.

Table 8.
The parameter information of the six different friction calculation models.
Table 9 and Figure 12 show the deviation ratio of the crushing length and the crushing length of each strut under six different friction models in the two classical load cases. Based on the comparative results of each strut in the lander, it is shown that the crushing length of each strut from the theoretical dynamic model under different friction force models was close to each other. The max deviation for crushing length was 54.3 mm at LC-2 under TY-1 and TY-4 models, and the relative error was 17.3% at the primary struts, while the relative value of the crushing length from the theory model was 312.4 mm. The max deviation ratio for crushing length was 18.7% at LC-2 under TY-1 and TY-4 models, and the relative deviation was 21.2 mm at the secondary struts, while the relative value of the crushing length from the theory model was 113.6 mm. Causing these calculation deviations was the velocity option defined in the friction calculation model and its coupling cumulative deviation mechanism. Since the TY-1 and TY-4 friction models do not consider the constraint of the speed option, its component force in the direction of the main strut is less than that of the other friction force models. Meanwhile, due to less influence on the friction model by the lateral velocity of the lander in LC-1, the results among each friction model were relatively closer than those in LC-2. In addition, compared with the results of the contact force model, it was found that the influence of the friction model on the results was greater than that of the contact force model. Therefore, more attention should be paid to the friction force model in the footpad–ground force model during the modeling and analysis process of the soft-landing dynamics of the lander.

Table 9.
The crush length of each Al-honeycomb buffer after soft landing.
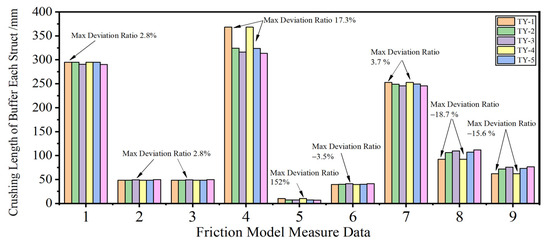
Figure 12.
The results for the lander during soft landing under different typical friction models.
4.3. Correction Coefficient η
According to the force-transmitting feature of the landing gear, the lateral denominational force of the primary strut equals the force acted by the secondary strut. The correction coefficient η is thereby only used in the contact force calculation between the outer and inner tube in the primary strut. To analyze the effect of the correction factor η, the comparison analysis of the crushing length and its deviations were discussed in this section.
Table 10 and Figure 13 show the deviation data of the crushing length and the crushing length of each strut with and without correction factor η in the two classical load cases. According to the comparative results of each buffer, the simulation results showed that the crushing length of each strut in the theory dynamic model with and without friction correction was close to each other in general. The max error in crushing length was 13.1 mm at the primary strut 1/4 in LC-2, and the relative error ratio was 4.4%. Causing this calculation deviation was mainly the added friction in the crushing force of the primary strut, which is mainly led by the lateral force. In fact, the friction force upon the primary strut is decided by two factors, namely the friction coefficient and the lateral force in the landing gear. Since the friction coefficient is only dependent on the material properties, the added friction is thereby only decided by the lateral force in the landing gear. According to Equations (23) and (24), the lateral force upon the primary strut was mainly decided by the defined crushing force and the relative velocity of the secondary strut.

Table 10.
The crush length of each Al-honeycomb buffer during soft landing for correction factor.
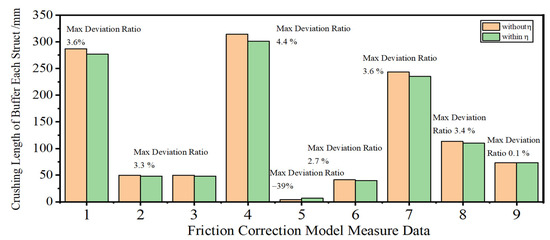
Figure 13.
The results for the lander during soft landing under the correction model.
The deviation ratios of the results in the secondary strut ranged between 0.1% and 4.4%. However, there is a large deviation ratio among the results, 39% at the primary strut in LC-2. Considering that the base value is 4.0 and some deviation may exist, the result can be accepted. In conclusion, the agreement of the results proved the friction force upon the primary strut has few effects on the soft-landing performance of the legged lander.
5. Conclusions
A novel 3D soft-landing dynamic theoretical model of a legged lander is developed in detail as well as its numerical solution process. The six degrees of freedom motion (6-DOF) of the base model of the lander with mass center offset setting is considered in the model as well as the spatial motion (3-DOF) of each landing gear. The characteristics of the buffering force, the footpad–ground contact, and the inter-structure friction are also taken into account during the motion of each landing gear. Some salient conclusions are summarized as follows:
Comparative analysis between the theory dynamic model and multi-body model in MSC Adams under four classical load cases were carried out. The results show that the crushing length of each strut from the theory dynamic model is close to that from the MSC Adams Software in general. Despite there being some max deviation error in some struts, the theoretical dynamic model established in this paper remains feasible due to the differences in the contact and friction force calculation models as well as the solving method in each numerical solution process.
Comparative analysis among the five classical contact models and the six commonly used friction models shows that the crushing lengths of most struts from the theory dynamic model are relatively close to each other. However, it is in the friction model result that the max deviation of crushing length is 53.8 mm at the primary strut in LG-3 at LC-2, and the average relative error is 17.3%. The relative value from the theoretical model is 312.4 mm. Causing the deviation error is the difference between the velocity option in the friction models. Therefore, building a precise friction model in the footpad–ground bearing model during the soft-landing process is necessary to obtain the soft-landing performance of one lander.
The friction correction between the outer and inner tubes in the primary strut is also discussed. The results show that the deviation of the model with and without the friction correction coefficient is not significantly obvious.
Author Contributions
Writing—original draft preparation, Z.W. and G.Z.; writing—review and editing, C.C. and G.Z.; visualization, J.C. and G.Z.; supervision, J.C.; project administration, J.C.; funding acquisition, C.C. and G.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the State Key Laboratory of Mechanics and Control of Mechanical Structures (Nanjing University of Aeronautics and Astronautics), China, grant number No. MCMS-E-0221Y01, in part by the Project of Key Laboratory of Impact and Safety Engineering (Ningbo University), Ministry of Education, China (No. CJ202107), and in part by the National Natural Science Foundation of China, grant number No. 52275113. The authors would like to acknowledge this support gratefully.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| = | The transformation matrix from the No. i-1 coordinate system to the No. i coordinate system. | |
| = | Unit matrix. | |
| = | Rotation matrix from the No. i-1 coordinate system to the No. i coordinate system in terms of Z-Y-X axis in the Euler angle way . ; ; ; ; | |
| = | Translation matrix relative to the No. i coordinate system. | |
| = | Translation vector relative to the No. i landing gear coordinate system. | |
| = | Translation vector relative to the No. i landing gear coordinate system. | |
| = | Translation vector relative to the No. i landing gear coordinate system. | |
| = | yaw(z) angle of the primary strut in the Euler angle form under the No. i landing gear coordinate system, aiLg-xiLgyiLgziLg. | |
| = | pitch(y) angle of the primary strut in the Euler angle form under the No. i landing gear coordinate system, aiLg-xiLgyiLgziLg. | |
| = | x-component value in the No. i primary strut coordinate system, aiLg-xiLgyiLgziLg. | |
| = | The yaw(z) angle of the primary strut in the Euler angle form under the No. i landing gear coordinate system, biLg-xiLgyiLgziLg and ciLg-xiLgyiLgziLg, respectively. | |
| = | pitch(y) angle of the primary strut in the Euler angle form under the No. i landing gear coordinate system, biLg-xiLgyiLgziLg and ciLg-xiLgyiLgziLg, respectively. | |
| = | x-component value in the No. i secondary strut coordinate system, bi-xilgyilgzilg and ci-xilgyilgzilg, respectively. | |
| = | The velocity matrix of the points ML, di, ei, fi in the global coordinate system, Og-xgygzg. | |
| = | The Jacobian matrices for different mapping relationships. | |
| FLgi | = | The equivalent dynamic force matrix in the No. i landing gear coordinate system, OLgi-xLgiyLgizLgi. |
| Fg | = | The footpad–ground force matrix. |
| FXLgi | = | The x component of the footpad–ground force in the No. i landing gear coordinate system, OLgi-xLgiyLgizLgi. |
| FYLgi | = | The y component of the footpad–ground force in the No. i landing gear coordinate system, OLgi-xLgiyLgizLgi. |
| FZLgi | = | The z component of the footpad–ground force in the No. i landing gear coordinate system, OLgi-xLgiyLgizLgi. |
| = | The equivalent dynamic forces in the primary strut of the No. i landing gear coordinate system. | |
| = | The equivalent dynamic forces in the left secondary strut of the No. i landing gear coordinate system. | |
| = | The equivalent dynamic forces in the right secondary strut of the No. i landing gear coordinate system. | |
| = | x, y, z component of the translation acceleration vector of mass center of the lander in the lander coordinate system. | |
| = | x, y, z component of the angle acceleration vector of mass center of the lander in the lander coordinate system. | |
| = | x, y, z component of the translation velocity vector of mass center of the lander in the global coordinate system. | |
| = | The Euler rates in terms of Euler angles (Z-Y-X) from the global coordinate system to the lander coordinate system. | |
| = | The x, y, z component of the force acting on the mass center of the lander in the lander coordinate system. | |
| = | The x, y, z component of the moment acting on the mass center of the lander in the lander coordinate system. | |
| = | The x, y, z scale component for the moment of momentum in the lander coordinate system. | |
| = | Mass moments of inertia of the lander about x, y, and z axes in the lander coordinate system. | |
| = | The products of the inertia of the lander in the lander coordinate system. | |
| = | The transmission force in the primary strut of the No. i landing gear coordinate system. | |
| = | The transmission force in the left secondary strut of the No. i landing gear coordinate system. | |
| = | The transmission force in the right secondary strut of the No. i landing gear coordinate system. | |
| = | The crushing force of buffer in the primary strut. | |
| = | The tensile crushing force of buffer in the secondary strut. | |
| = | The compression crushing force of buffer in the secondary strut. | |
| = | The remaining driving force in the primary strut of the No. i landing gear coordinate system. | |
| = | The remaining driving force in the left secondary strut of the No. i landing gear coordinate system. | |
| = | The remaining driving force in the left secondary strut of the No. i landing gear coordinate system. | |
| M | = | Generalized mass matrix of each landing gear system. |
| = | Generalized coordination vectors matrix, | |
| = | The generalized acceleration vectors matrix, | |
| Φq | = | The Jacobi matrix of the constraint equation (Equation (7)). |
| λ | = | Lagrange multiplier column matrix. |
| γ | = | Constraint matrix. |
| = | The remaining driving force matrix in the generalized coordinate system. | |
| Flun | = | Footpad–ground contact force. |
| n | = | Exponential coefficient of the penetration depth. |
| µ | = | Frictional coefficient of the contact force. |
| Kg, Cg | = | Penetration stiffness and damping coefficient of the footpad–ground model. |
| = | x, y, z component of the displacement of the No. i footpad in the lunar surface coordinate system. | |
| = | x, y, z component of the translation velocity of the No. i footpad in the lunar surface coordinate system. | |
| D, D1, D2 | = | Defined displacement parameters in contact model. |
| = | Contact parameter. | |
| ,, | = | Crushing acceleration, velocity, and displacement of the buffer. |
| a, b, c, d | = | Coefficients of inertia, viscosity, stiffness, and constant resistance of the buffer. |
| F1, F2 | = | Crush forces of the first and second step of the buffer in the primary strut. |
| F3 | = | Transmission force after the AL-honeycomb is crushed. |
| s0 | = | Initial length of the primary strut. |
| s1, s2 | = | Lengths of the primary strut when the first and second step foam crush are done. |
| shismin | = | Minimum length of the primary strut before the currently measured time. |
| sc1, st1 | = | Length value of the secondary strut when the compaction buffer or the tension buffer crush are done. |
| Fcom, FTen | = | Compaction and tension force of the buffer in the secondary struts. |
| Fcom1, FTen1 | = | Compaction and tension transmission force of the buffer in the secondary struts after the AL-honeycomb is crushed. |
| = | Maximum length of the secondary strut before the currently measured time. | |
| = | Minimum length of the secondary strut before the currently measured time. | |
| = | Total normal contact force acted upon the No. i primary strut by the relative secondary struts. | |
| = | y component of the contact force matrix in the No. i primary strut coordinate system. | |
| = | z component of the contact force matrix in the No. i primary strut coordinate system. | |
| = | Contact force matrix acted upon the No. i primary strut and by the secondary struts in the No. i primary strut coordinate system, di-xilgyilgzilg. | |
| η | = | Correction coefficient of the contact between the outer and inner tube in the primary strut. |
| µ1 | = | Friction factor of the contact between the outer and inner tube in the primary strut. |
| η1 | = | Correction factor accounts for the changing length of the landing gear during the soft-landing process. |
| η2 | = | Correction factor takes into consideration the effect on the contact pressure distribution. |
| NA | = | Lateral force caused by the upper contact action of the tubes. |
| NB | = | Lateral force caused by the below contact action of the tubes. |
| μk | = | Kinetic coefficient of friction. |
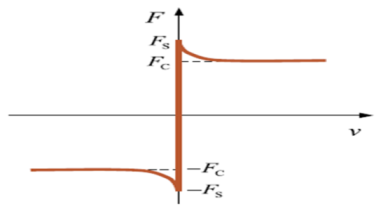
| FC | = | The magnitude of friction force. |
| FS | = | Static friction force. |
| FD | = | Dynamic friction force. |
| Fe | = | External tangential force. |
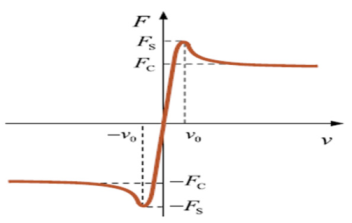
| v | = | The relative tangential velocity of the contacting surfaces. |
| vo | = | Stiction velocity. |
| p | = | Contact pressure. |
| pm | = | Maximum contact pressure. |
| = | Contact angle between the outer and inner tube in the primary strut. | |
| l | = | Arc length of the contact between the outer and inner tube in the primary strut. |
| lR | The inner radius of the outer tube in the primary strut. | |
| = | Constraint function in the No. i landing gear. | |
| = | Generalized coordinate displacement and velocity by numerical integration at time step tn+1. | |
| Correction displacement and velocity item at time step tn+1. | ||
| Subscripts | ||
| Soft landing | Any type of spacecraft landing that does not result in significant damage to or destruction of the vehicle or its payload. | |
| MC | Center of mass. | |
| C.L. | Coordinate location. | |
| No. | Number order. | |
| C.S. | Coordinate system. | |
| L.G. | Landing gear. | |
| LC | Load case. | |
| Pri. Strut | Primary strut. | |
| Sec. Strut | Secondary strut. |
References
- China Unveils Preliminary Plan on Manned Lunar Landing. Available online: http://english.www.gov.cnnews/202305/29/content_WS64748c46c6d03ffcca6ed781.html (accessed on 12 July 2023).
- Yang, J.; Wu, Q.; Yu, D.; Jiang, S.; Xu, Z.; Cui, P. Preliminary Study on Key Technologies for Construction and Operation of Robotics Lunar Scientific Base. J. Deep. Space Explor. 2020, 7, 111–117. (In Chinese) [Google Scholar]
- Lin, R.; Guo, W.; Zhao, C.; He, M. Conceptual design and analysis of legged landers with orientation capability. Chin. J. Aeronaut. 2023, 36, 171–183. [Google Scholar] [CrossRef]
- Hu, Y.; Guo, W.; Lin, R. An Investigation on the Effect of Actuation Pattern on the Power Consumption of Legged Robots for Extraterrestrial Exploration. IEEE Trans. Robot. 2023, 39, 923–940. [Google Scholar] [CrossRef]
- Zhou, J.; Ma, H.; Chen, J.; Jia, S.; Tian, S. Motion characteristics and gait planning methods analysis for the walkable lunar lander to optimize the performances of terrain adaptability. Aerosp. Sci. Technol. 2023, 132, 44–46. [Google Scholar] [CrossRef]
- John, F.C. After LM: NASA Lunar Lander Concepts beyond Apollo. Available online: https://ntrs.nasa.gov/citations/20190031985 (accessed on 22 June 2023).
- Rogers, W.F. Apollo Experience Report-Lunar Module Landing Gear Subsystem. Available online: https://ntrs.nasa.gov/citations/19720018253 (accessed on 22 June 2023).
- Liang, D.; Chai, H.; Chen, T. Overview of Lunar Lander Soft Landing Dynamic Modeling and Analysis. Spacecr. Eng. 2011, 20, 104–112. (In Chinese) [Google Scholar]
- Lavender, R.E. Equations for Two-Dimensional Analysis of Touchdown Dynamics of Spacecraft with Hinged Legs Including Elastic, Damping, and Crushing Effects. Available online: https://ntrs.nasa.gov/citations/19660014379 (accessed on 22 June 2023).
- Alderson, R.G.; Wells, D.A. Surveyor Lunar Touchdown Stability Study Final Report, July 1965–July 1966. Available online: https://ntrs.nasa.gov/citations/19670003854 (accessed on 22 June 2023).
- Zupp, G.A.; Doiron, H.H. A Mathematical Procedure for Predicting the Touchdown Dynamics of a Soft-Landing Vehicle. Available online: https://ntrs.nasa.gov/citations/19710007293 (accessed on 22 June 2023).
- Maeda, T.; Ozaki, T.; Hara, S.; Matsui, S. Touchdown Dynamics of Planetary Lander with Translation–Rotation Motion Conversion Mechanism. J. Spacecr. Rocket. 2017, 54, 973–980. [Google Scholar] [CrossRef]
- Wan, J. Research on Soft Landing Dynamic Analysis and Several Key Technologies of Lunar Lander. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2010. [Google Scholar]
- Yue, S.; Lin, Q.; Zheng, G.; Du, Z. Touchdown Dynamics of Planetary Lander with Translation–Rotation Motion Conversion Mechanism. Chin. J. Aeronaut. 2022, 35, 156–172. [Google Scholar] [CrossRef]
- Yin, K.; Sun, Q.; Gao, F.; Zhou, S. Lunar surface soft-landing analysis of a novel six-legged mobile lander with repetitive landing capacity. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 236, 1214–1233. [Google Scholar] [CrossRef]
- Lin, Q.; Ren, J. Investigation on the Horizontal Landing Velocity and Pitch Angle Impact on the Soft-Landing Dynamic Characteristics. Int. J. Aerosp. Eng. 2022, 2022, 1214–1233. [Google Scholar] [CrossRef]
- Yin, C.; Quan, Q.; Tang, D.; Deng, Z. Landing of the asteroid probe with three-legged cushioning: Planar asymmetric dynamics and safety margin. Adv. Space Res. 2023, 71, 2075–2094. [Google Scholar] [CrossRef]
- Dong, Y.; Ding, J.; Wang, C.; Wang, H.; Liu, X. Soft landing stability analysis of a Mars lander under uncertain terrain. Chin. J. Aeronaut. 2022, 35, 377–388. [Google Scholar] [CrossRef]
- Jeffrey, A.; Goldman, D.I. Robophysical study of jumping dynamics on granular media. Nat. Phys. 2016, 12, 278–283. [Google Scholar]
- Wu, S.; Wang, Y.; Hou, X.; Xue, P.; Long, L. Research on Theoretical Model of Vertical Impact of Foot Pad on Lunar Soil. Manned Spacefl. 2016, 26, 135–141. (In Chinese) [Google Scholar]
- Nelson, R.C. Flight Stability and Automatic Control, 1st ed.; McGraw-Hill College: New York, NY, USA, 1989; pp. 50–90. [Google Scholar]
- Craig, J.J. Introduction to Robotics Mechanics and Control, 3rd ed.; Pearson Education, Inc.: River Street Hoboken, NJ, USA, 2005; pp. 40–80. [Google Scholar]
- Yu, Q.; Chen, I.-M. A direct violation correction method in numerical simulation of constrained multibody systems. Comput. Mech. 2000, 26, 52–57. [Google Scholar] [CrossRef]
- Hong, J. Computational Dynamics of Multibody Systems, 1st ed.; Higher Education Press: Beijing, China, 1999; pp. 360–380. [Google Scholar]
- Chen, H. Investigation on Energy-Absorption Nanomaterials for Lunar Lander and Analysis on Soft-Landing Performance. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2017. [Google Scholar]
- Zhao, D.; Liu, Y. Improved Damping Constant of Hertz-Damp Model for Pounding between Structures. Math. Probl. Eng. 2016, 2016, 52–57. [Google Scholar] [CrossRef]
- Paulo, F.; Margarida, M.; Silva, M.T.; Martins, J.M. On the continuous contact force models for soft materials in multibody dynamics. Multibody Syst. Dyn. 2011, 25, 357–375. [Google Scholar]
- Jankowski, R. Non-linear viscoelastic modelling of earthquake-induced structural pounding. Earthq. Eng. Struct. Dyn. 2005, 34, 595–611. [Google Scholar] [CrossRef]
- Jankowski, R. Analytical expression between the impact damping ratio and the coefficient of restitution in the non-linear viscoelastic model of structural pounding. Earthq. Eng. Struct. Dyn. 2005, 35, 517–524. [Google Scholar] [CrossRef]
- Hunt, K.H.; Crossley, F.R.E. Coefficient of Restitution Interpreted as Damping in Vibroimpact. J. Appl. Mech. 1975, 42, 440–445. [Google Scholar] [CrossRef]
- Wang, G.; Ma, D.; Liu, Y.; Liu, C. Coefficient of Restitution Interpreted as Damping in Vibroimpact. Chin. J. Theor. Appl. Mech. 2022, 54, 3239–3266. [Google Scholar]
- Filipe, M.; Paulo, F.; Pimenta Claro, J.C.; Lankarani, H.M. Modeling and analysis of friction including rolling effects in multibody dynamics: A review. Nonlinear Dyn. 2016, 45, 223–244. [Google Scholar]
- Filipe, M.; Paulo, F.; Pimenta Claro, J.C.; Lankarani, H.M. A survey and comparison of several friction force models for dynamic analysis of multibody mechanical systems. Nonlinear Dyn. 2016, 86, 1407–1443. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).