Abstract
Landslides can be triggered by intense or prolonged rainfall. Rain gauge measurements are commonly used to predict landslides even if satellite rainfall estimates are available. Recent research focuses on the comparison of satellite estimates and gauge measurements. The rain gauge data from the Italian network (collected in the system database “Verifica Rischio Frana”, VRF) are compared with the National Aeronautics and Space Administration (NASA) Tropical Rainfall Measuring Mission (TRMM) products. For the purpose, we couple point gauge and satellite rainfall estimates at individual grid cells, evaluating the correlation between gauge and satellite data in different morpho-climatological conditions. We then analyze the statistical distributions of both rainfall data types and the rainfall events derived from them. Results show that satellite data underestimates ground data, with the largest differences in mountainous areas. Power-law models, are more appropriate to correlate gauge and satellite data. The gauge and satellite-based products exhibit different statistical distributions and the rainfall events derived from them differ. In conclusion, satellite rainfall cannot be directly compared with ground data, requiring local investigation to account for specific morpho-climatological settings. Results suggest that satellite data can be used for forecasting landslides, only performing a local scaling between satellite and ground data.
1. Introduction
Rainfall-induced landslides are widespread phenomena that cause casualties and extensive damages every year. In Italy, rainfall is the primary trigger of landslides, which have caused more than 6300 casualties in the period from 1950 to 2013 [1,2]. Forecasting the occurrence of the rainfall-induced landslide is challenging due to the nature of these hazards and the information required to assess the triggering phenomena. Rainfall-induced landslides predominately occur within steep topography where intense or prolonged rainfall increases pore water pressures and decreases soil cohesion in the subsurface, causing the driving forces to overcome resisting forces on a hill slope and activate a landslide [3]. Approaches to analyze rainfall-induced landslide triggering include: (i) empirical approaches focus on the determination of rainfall thresholds [4,5,6,7]; and (ii) deterministic approaches use a physically-based modelling schema that generally couples an infiltration model to an instability model to estimate slope stability/instability conditions [8,9,10]. The deterministic approach is applied mainly to investigate single instability phenomena or a small catchment whereas the empirical approach is used to analyze rainfall-induced landslide triggering at a range of local to global scales.
For both approaches, spatial and temporal information on rainfall is necessary to analyze the triggering mechanisms of the rainfall-induced landslides. At present, the two approaches primarily exploit rainfall measurements obtained from in situ rain gauge networks [11]. The empirical approach has been integrated into operational and pre-operational early-warning systems that are used to forecast the possible occurrence of rainfall-induced landslides. These early-warning systems attempt to predict rainfall-induced landslides through the comparison of measurements of rainfall duration D, cumulated rainfall E, and mean rainfall intensity I, using empirical rainfall thresholds of the intensity-duration (ID) and cumulated rainfall—duration (ED) types [6,7]. While most of these systems exploit rainfall measurements obtained from networks of rain gauges [12], there are some examples of early-warning systems that exploit rainfall estimates obtained from satellites [13,14]. Evaluation of one of these satellite-based systems indicated that regional rather than global triggering relationships should be evaluated to better account for heterogeneities in climatology and morphology among different regions [15,16].
Despite the availability of satellite rainfall estimates and their experimental use in existing early-warning systems, surprisingly limited research has been done to compare satellite rainfall estimates and rain gauge data for the explicit analysis of landslide triggering mechanisms, and for evaluating and forecasting the possible occurrence rainfall-induced landslide events. In particular, analyses based on the use of satellite estimates would allow to investigate rainfall-landslide triggering relations where the instrumental gauge network is missing, but also to improve the investigations where the network is not dense enough. Most of the literature focuses on the comparison of satellite rainfall estimates and ground measurements to evaluate the accuracy of the satellite-derived products in different areas of the globe, at different spatial and temporal scales [17]. The research focused on the validation of the TRMM products [18], available for various regions of the globe, and at different scales, and are limited to the comparison of monthly, or seasonal data [19,20,21,22,23,24]. Comparisons of sub-monthly data were performed for Bangladesh [25], the India–Sri Lanka area [26], and the Ethiopian highlands [27]. Recently, the comparison of high-resolution TRMM rain products with ground-based measures at the daily scale was performed for the United States of America [28,29], Australia [30], Asia [31,32,33,34], Africa [35], and Europe [36]. In Europe, the Mediterranean region is the most studied [36,37]. Feidas [37] has compared different satellite rainfall products available for Greece at different spatial and temporal scales, and Villarini [38] has compared satellite estimates and rain gauge data in the Rome metropolitan area, Italy. Other comparisons have evaluated the performance of TMPA (TRMM Multi-satellite Precipitation Analysis) Versions 6 and 7 for hydrological applications over various regions [39,40]. In the cited examples, the emphasis was focused more on the statistical evaluation of satellite-based precipitation data relative to in situ gauge networks. In this work, differently from the other literature papers, we focus on the evaluation of the possible use of satellite rainfall products for the forecast of rainfall-induced landslides, introducing specific analyses.
In particular, this work analyses the relationships between rainfall measurements (hereafter VRF) obtained from a dense network of rain gauges in Italy, and TMPA satellite rainfall products [18,41] for the same area. Even if NASA’s Global Precipitation Measurement (GPM [42]) mission derived rainfall products are nowadays available, we did not consider them in this study, due to their limited temporal availability (i.e., GPM data available since March 2014 do not cover the selected analysis period from 1 September 2009 to 31 August 2010) [43]. The paper is organized as follows. First, we describe the rainfall and landslide data and information used for the analysis. Next, the different satellite rainfall products are evaluated through pairwise correlations between the VRF and the TMPA estimates for the whole of Italy and for different morphological and climatological zones in Italy. Next, the distributions of the different rainfall products are compared using several statistical approaches. Finally, the paper evaluates the rainfall signatures of known landslide events in Italy and compares the observed rainfall to the overall distribution of the rainfall events from VRF and the TMPA data. We conclude by discussing the success of different parametric and non-parametric models and providing recommendations for the possible exploitation of satellite rainfall products in hydrological models and for rainfall thresholds for possible landslide occurrence.
2. Materials and Methods and Results
2.1. Climatic and Morphological Framework
This study focuses on the analysis and comparison of TMPA and VRF data in Italy, where the climate variability is large and where landslides and other instability processes are frequent. The study area extends for more than 13 degrees in latitude. The Alpine mountain chain bounds the area to the north, and the Apennines mountain chain divides the area in two parts, an eastern part bounded by the Adriatic and Ionian Seas, and a western part bounded by the Liguria and the Tyrrhenian Seas (Figure 1a).
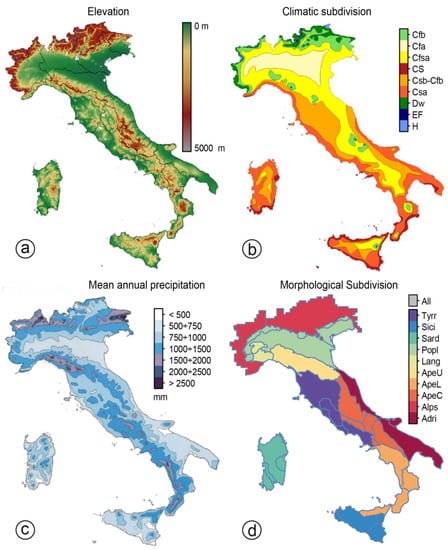
Figure 1.
(a) Digital Elevation Model (DEM) at 230 m × 230 m pixel resolution; (b) Climatic subdivision of the Italian territory (see details in Table 1) derived from [44,45]; (c) Mean annual rainfall map [46,47,48]; (d) Morphological subdivision of the Italian territory (see details in Table 2) derived by Guzzetti and Reichenbach [49].
2.1.1. Climate Variability
Based on the Köppen-Geiger climate classification system [50,51,52], the Italian peninsula has a Mediterranean subtropical, dry summer climate. The climate variability is significant among the different regions within Italy, mainly depending on the distance to the sea and the European continent, but also due to the orographic structure and the large latitude extent. The different climates characterizing the Italian territory (Figure 1b) have been identified by Pinna and Vittorini [44,45] and they are summarized in Table 1.

Table 1.
Climates among the different regions within Italy territory (Figure 1b) identified by Pinna [44] following the Köppen-Geiger climate classification system [52].
There are considerable temperature differences from north to south during the winter, with less extreme gradients during the summer. Differences in the mean annual precipitation [46] can be extreme (Figure 1c). The highest peaks (>2000 mm per year) were observed in the Carnic Alps, in the Apuane Alps, and in the Northern Apennines. Low mean annual precipitation (<500 mm per year) values were observed in the SE (Puglia) and in the SW (Sardinia, Sicily) parts of Italy. Different types of precipitation characterize the territory. Convective precipitation, generally short duration and intense rainfall, is observed generally in the summer and in the autumn period but can occur in other seasons as well [53]. Stratiform precipitation, characterized by less intense and longer duration precipitation, is caused by frontal systems that frequently occur throughout the year. In mountainous regions, orography can play a substantial role in modulating characteristic precipitation patterns in the area.
2.1.2. Morphological Subdivision
In most of the territories in Italy, climatic variability can be strongly influenced by morphology. For this reason, the study considers the distributions and correlations of VRF and satellite rainfall estimates for the dominant morphological (and climatological) conditions across the Italian territories. We used the morphological subdivision of Italy proposed by Guzzetti and Reichenbach [49]. The subdivision classifies the Italian territory into 8 major topographic provinces and 30 minor sections, starting from a coarse resolution, 230 m × 230 m DEM (Figure 1a). We heuristically aggregated the 30 minor subdivisions (sections) into ten macro-subdivisions, considering latitude and aspect to reflect different morphologic and climatologic conditions in Italy. Figure 1d shows a map of the morpho-climatological subdivisions, and Table 2 summarizes values for the morphological parameters in each subdivision.

Table 2.
Morphological parameters associated with morpho-climatological subdivisions. Values taken from Table 2 in [49].
2.2. Rainfall Data
For our analyses, we used rainfall data for one hydrological year from 1 September to 31 August.
The rainfall data included: (i) rainfall measurements captured by a national network of 1950 rain gauges in Italy; and (ii) satellite rainfall estimates over Italy obtained for several TMPA products.
2.2.1. Rain Gauge Measurements (VRF)
The VRF data were obtained from a network of 1950 rain gauges in Italy (Figure 2a) managed by the Italian Civil Protection Department and the Regional and Provincial governments of Italy, for civil protection purposes. The rainfall data covered the 10-year period between 2003 and 2012. For our experiment, we selected the period from 1 September 2009 to 31 August 2010, corresponding to a complete hydrological year. Such period was chosen to account for the maximum number of complete VRF data series. Indeed, selecting a period between 2003 and 2005, the percentage of complete data series decreases up to about the 20% with a more limited spatial and less representative coverage of the Italian peninsula. Considering larger period (i.e., including more hydrological years) will possibly slightly change the results of the analyses, but it will not modify substantially the final manuscript conclusions.
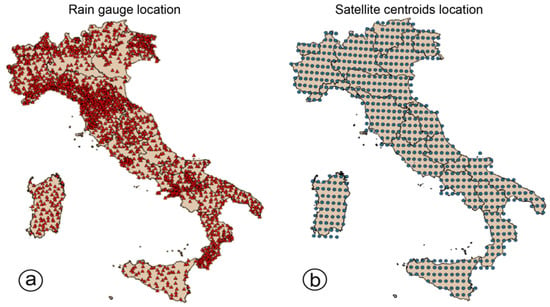
Figure 2.
(a) Location of the rain gauges along the Italian territory (available through the Experience Platform of the Italian Civil Protection Department [54]); (b) Location of TRMM cell centroids (0.25° × 0.25° resolution) covering the Italian territory.
Different types of rain gauges were present in the network, each with different temporal samplings and accuracies of the rainfall measurements. The temporal sampling varied from 1 to 60 min, with the majority of the measurements taken every 30 min (semi-hourly sampling). The accuracy of the rain gauges was between 0.2 and 1.0 mm. Gaps, errors, and measurement discontinuities were present in the time series, and a specific procedure was used to evaluate the quality of the rainfall records. The procedure evaluated the reliability of the rain gauges by comparing the Cumulated Annual Precipitation (CAP) for each the rain gauge in the examined period with a reference Mean Annual Precipitation (MAP) measured in the same general area. The reference values of MAP were derived from the historical rainfall information in the period 1961–1990 available from the archive of Global Historical Climatology Network-Monthly managed by the National Climatic Data Center or NOAA [55,56]. The set of criteria used to estimate the reliability of the rain gauges is listed in Table 3. The evaluation of rain gauge reliability indicated that 1488 rain gauges (76%) in the network worked properly in the evaluated period.

Table 3.
Criteria for the estimation of rain gauge reliability.
2.2.2. Satellite Rainfall Estimates
The satellite rainfall estimates were obtained from the Tropical Rainfall Measuring Mission (TRMM) Multi-satellite Precipitation Analysis (TMPA) [18,41]. Four TRMM products were considered for the analysis (Table 4), including: (i) Version 6 re-analysis product (TMPA-V6); (ii) Version 6 Real-Time (RT) product (TMPA-V6-RT); (iii) Version 7 re-analysis product (TMPA-V7); and (iv) Version 7 Real-Time product (TMPA-V7-RT).

Table 4.
Types and sources of the TMPA products used in this study.
TMPA rainfall data were considered because they provide a continuous rainfall product from 50° N to 50° S (i.e., covering the entire Italian peninsula study area ranging from 35° N to 48° N) at 0.25° × 0.25° latitude-longitude resolution every 3 h [18,41]. The TMPA methodology merges high-quality microwave and infrared precipitation estimates after calibration to the combined TRMM Precipitation Radar (PR)—TRMM Microwave Imager (TMI) precipitation product from the TRMM satellite, and factors in monthly precipitation gauge analyses to create the 3-hourly product. Precipitation fields are reported as precipitation rate effective at the nominal observation time. The TMPA RT products are near real-time precipitation estimates produced in four stages: (i) passive microwave (PMW) precipitation estimates are calibrated and combined; (ii) infrared (IR) precipitation estimates are created using the calibrated microwave precipitation; (iii) PMW and IR estimates are combined; and (iv) rain station gauge (SG) data are incorporated. From hereafter T will denote satellite rainfall estimates.
In 2012, an upgraded Version 7 set of TMPA reanalysis and near real-time products were released to improve upon some issues identified in the Version 6 algorithms. The TMPA data was then reprocessed back to the launch of the TRMM, with TRMM-V6-RT which was replaced by TRMM-V7-RT available from March 2000 to the present, and TRMM-V6 which was replaced by TRMM-V7 available since January 1998. In this analysis, all four products are evaluated to determine the relative differences of these products relative to the available gauge network. As a secondary focus, this inter-comparison can help to provide a bridge from previous Version 6 studies to the currently-available Version 7 data.
2.3. Analysis of Cumulated Rainfall
The four TMPA 0.25° × 0.25° regular grid cells, were linked spatially to the location of the geographical centre of each grid cell (centroid). Figure 2b shows the location of the 638 TMPA cell centroids extracted over Italy. We first performed a comparative analysis of the cumulated rainfall measured by the individual rain gauges and estimated by the four satellite products. The cumulated rainfall was analyzed in place of peak rainfall intensity because is one of the most significant parameters in analyzing the triggering of different type of hydrological/hydrogeological processes. A minimum distance criterion was used to link each TMPA cell centroid to one or more rain gauges (see Appendix A). Figure 3 shows the result of this procedure obtained for the Umbria region, in Central Italy.
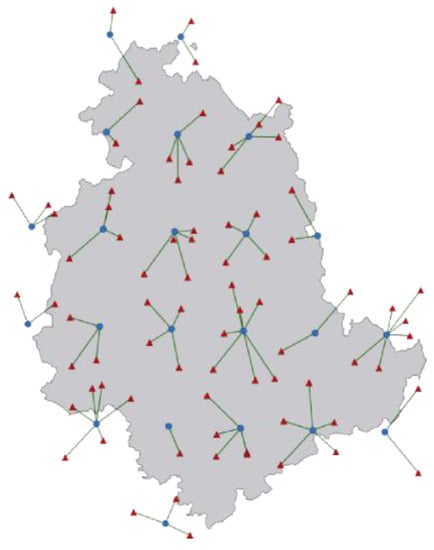
Figure 3.
Minimum distance criteria used to couple, each TMPA centroid (blue circles) with one or more VRF rain gauge stations (red triangles). The example refers to the coupling in the Umbria region (Central Italy).
We computed the cumulated amount of rainfall measured at the individual rain gauges and estimated at the individual cell centroids for different rainfall durations (3, 12, 24, 48, and 72-h periods). For the comparison, the hourly rain gauge data were cumulated in the same periods used for the aggregation of the satellite data. In such a way, it was possible to compare rainfall measures and estimates referred to the same temporal windows. A procedure excluded from the calculation VRF-TMPA pairs that could not be compared, due (i) to the presence of missing data, gaps, and errors in the rainfall records; (ii) to the incomparable temporal resolutions of the VRF and the TMPA records.
2.3.1. Correlation Analysis
To analyse the correlation between the cumulated rainfall in a period measured by the rain gauges (R) and estimated by the satellite products (T), we adopted linear (Equation (1)) and power-law (Equation (2)) regression models.
In the equations, a is the coefficient for the linear model, b is the exponent of the power-law model, and R and T are the cumulated rainfall measured by the rain gauges and estimated by the satellite products for different rainfall durations. For simplicity, here we show only the results obtained for the 72-h accumulation period, also because similar results were obtained for other accumulation periods. Once the cumulated rainfall values were obtained for each VRF-TMPA pair, we aggregated the pairs for the morpho-climatic domains illustrated in Figure 1d, and listed in Table 2. Using a peak over threshold (POT) approach [57], we filtered the rainfall series taking values above specific thresholds i.e., 0, 2, 4, 6, 8, 10, 12, 14, 16, 18 and 20 mm. For each threshold, we estimated the linear (a) and the power-law (b) fitting parameters, their determination coefficients (R2, measuring the goodness of fit), and the confidence and prediction intervals. The analysis was performed for the whole of Italy and for the individual morpho-climatic subdivisions, using the four different TMPA products. Figure 4 shows an example of the results for the TMPA-V6 product in the Alps (Table 2 and Figure 1), using a minimum threshold of cumulated rainfall of 16 mm.
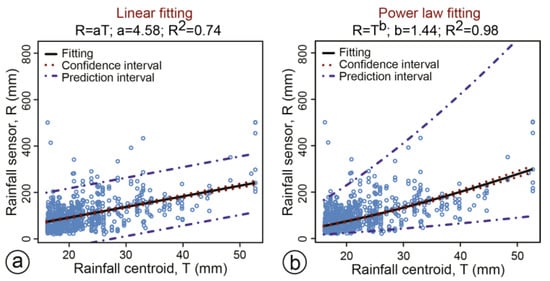
Figure 4.
Linear (a) and power-law (b) fitting between TMPA-V6 rainfall estimates T and rain gauge measures R. The two regression examples are for the 72-h cumulative rainfall in the Alpine region (Alps, see Table 2 and Figure 1) filtered using a rainfall threshold of 16 mm. Solid black lines is the best fitting, dotted red and dot-dashed blue lines are the confidence and the prediction intervals respectively.
Figure 5, Figure 6, Figure 7 and Figure 8 show the variation of the linear and the power-law determination coefficients obtained in the different morpho-climatic subdivisions, using different thresholds for the four TRMM products (TMPA-V6, TMPA-V6-RT, TMPA-V7 and TMPA-V7-RT).
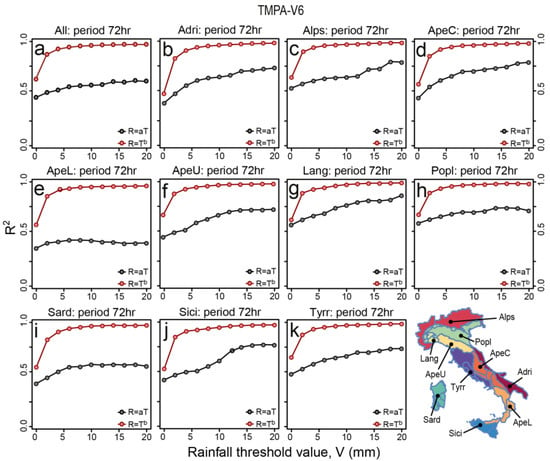
Figure 5.
Linear (grey dots) and power-law (red dots) fitting (between TMPA-V6 rainfall estimates and VRF ground data) determination coefficients for 72-h cumulative rainfall filtered using a peak over threshold approach taking values above different thresholds: 0, 2, 4, 6, 8, 10, 12, 14, 16, 18 and 20 mm. The different plots show results for different morphological subdivisions: (a) entire Italian territory; (b) Adri; (c) Alps; (d) ApeC; (e) ApeL; (f) ApeU; (g) Lang; (h) Popl; (i) Sard; (j) Sici; (k) Tyrr.
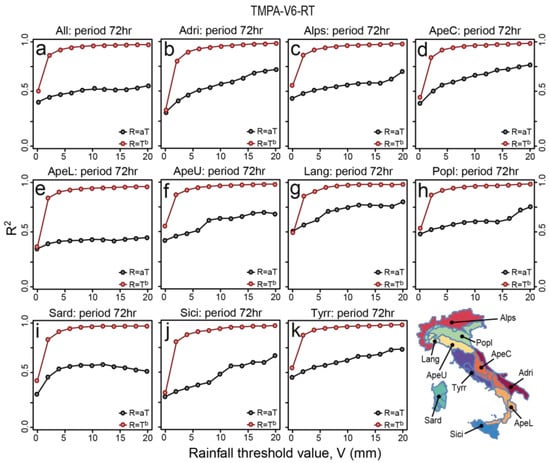
Figure 6.
Linear (grey dots) and power-law (red dots) fitting (between TMPA-V6-RT rainfall estimates and VRF ground data) determination coefficients for the 72-h cumulative rainfall filtered using a peak over threshold approach taking values above different thresholds: 0, 2, 4, 6, 8, 10, 12, 14, 16, 18 and 20 mm. The different plots show results for different Italian morphological subdivisions: (a) entire Italian territory; (b) Adri; (c) Alps; (d) ApeC; (e) ApeL; (f) ApeU; (g) Lang; (h) Popl; (i) Sard; (j) Sici; (k) Tyrr.
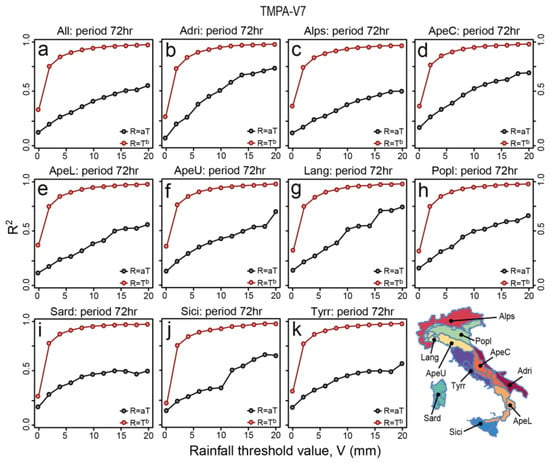
Figure 7.
Linear (grey dots) and power-law (red dots) fitting (between TMPA-V7 rainfall estimates and VRF ground data) determination coefficients for the 72-h cumulative rainfall filtered using a peak over threshold approach taking values above different thresholds: 0, 2, 4, 6, 8, 10, 12, 14, 16, 18 and 20 mm. The different plots show results for different Italian morphological subdivisions: (a) entire Italian territory; (b) Adri; (c) Alps; (d) ApeC; (e) ApeL; (f) ApeU; (g) Lang; (h) Popl; (i) Sard; (j) Sici; (k) Tyrr.
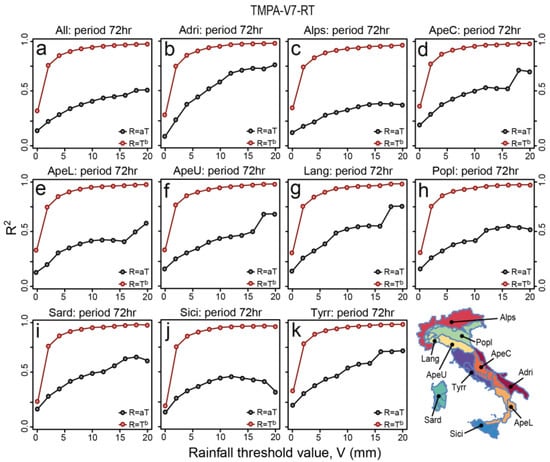
Figure 8.
Linear (grey dots) and power-law (red dots) fitting (between TMPA-V7-RT rainfall estimates and VRF ground data) determination coefficients for the 72-h cumulative rainfall filtered using a peak over threshold approach taking values above different thresholds: 0, 2, 4, 6, 8, 10, 12, 14, 16, 18 and 20 mm. The different plots show results for different Italian morphological subdivisions: (a) entire Italian territory; (b) Adri; (c) Alps; (d) ApeC; (e) ApeL; (f) ApeU; (g) Lang; (h) Popl; (i) Sard; (j) Sici; (k) Tyrr.
Figure 9 summarizes the variability of the linear (Figure 9a,e,i,m) and the power-law (Figure 9c,g,k,o) fitting parameters, and the variability of the linear (Figure 9b,f,j,n) and the power-law (Figure 9d,h,l,p) determination coefficients.
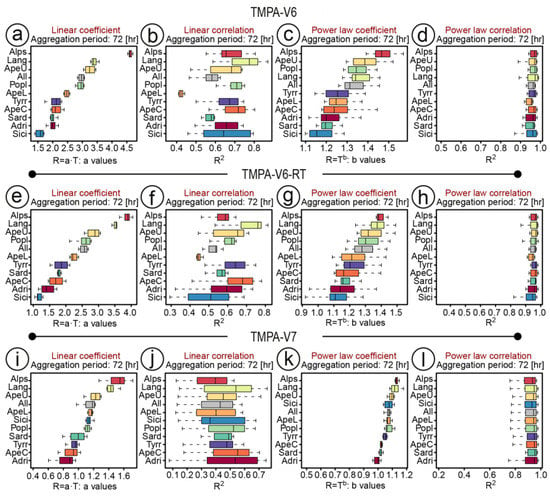
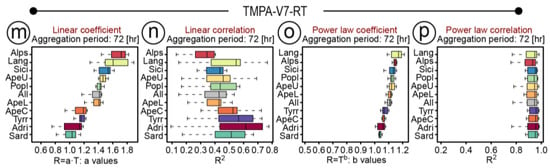
Figure 9.
Variability of the linear coefficients (a,e,i,m) and the relative determination coefficients (b,f,j,n), and the power-law coefficients (c,g,k,o) and the relative determination coefficients (d,h,l,p) for different rainfall thresholds values (see Figure 5, Figure 6, Figure 7 and Figure 8) in the entire Italian territory and in the different morphological subdivisions (see Table 2 and Figure 1).
2.3.2. Statistical Distribution Estimation
The distributions of the satellite and the rain gauge cumulated rainfall are heavy-tailed. To evaluate the distributions, we used the Histogram Density Estimation (HDE) method [58] to estimate the frequency of the logarithm of the cumulated rainfall for the rainfall measurements and the satellite estimates. Using a Kernel Density Estimation (KDE) method [59], and adopting a Gaussian kernel, we then calculated the kernel densities of the logarithm of the rainfall series, and we compared the kernel densities with the densities obtained using the histogram estimation method. Figure 10 shows the results of the comparison for the rainfall measurements and the satellite estimates (TMPA-V6, TMPA-V6-RT, TMPA-V7, TMPA-V7-RT), for Italy and for the single morpho-climatic subdivisions.
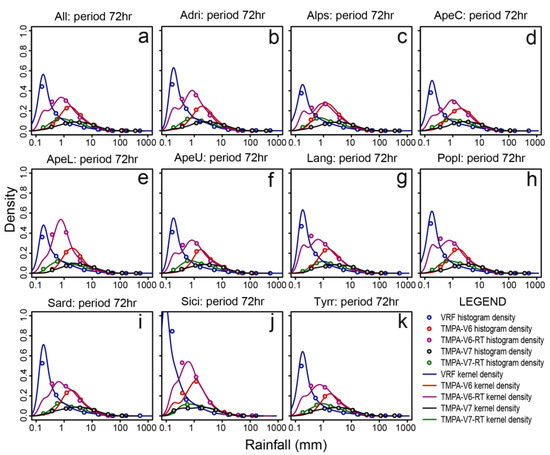
Figure 10.
Comparison of the probability density (see Table 5 for Kolmogorov-Smirnov test results) of the logarithm of 72-h cumulative rainfall estimated using HDE (points) and KDE (lines) method for VRF data and for the different satellite rainfall estimates (TMPA-V6, TMPA-V6-RT, TMPA-V7, TMPA-V7-RT) thresholds in the entire Italian territory and in the different morphological subdivisions (see Table 2 and Figure 1).
To quantify the comparison, we applied the bootstrapped [60] Kolmogorov-Smirnov test [61,62] using the “greater” hypothesis [63] to compare the VRF data and the four TMPA estimates. Given this comparison order, and using the test “greater” hypothesis, the test p-values close to 0 corresponds to values of the test statistic D+ greater than 0, indicating that the cumulated distribution function (CDF) of the VRF data lies above (or to the left) of the CDF of the TMPA estimates. This indicates that the distribution of the TMPA estimates is statistically “greater” than the distribution of the VRF data. To simplify the quantile values of VRF data are lower than those calculated for the satellite estimates series. If instead the p-values are close to 1, the test statistic D+ is close to 0 indicating that the CDF of VRF data lies below (or to the right) of the CDF of the satellite rainfall estimates, and hence that the distribution of VRF data is not statistically “greater” than the distribution for the rainfall estimates. Table 5 summarizes the results of the test for the four TMPA products for Italy and for each morpho-climatic subdivision.

Table 5.
Results of bootstrapped Kolmogorov-Smirnov test (hypothesis: greater) comparing the VRF data and the different satellite rainfall estimates (TMPA-V6, TMPA-V6-RT, TMPA-V7, TMPA-V7-RT) calculated in the entire Italian territory and in the different morphological subdivisions (see Table 2 and Figure 2). Given this comparison order and using the test greater hypothesis, p-values ≅ 0 (for D+ >> 0) indicate that the CDF of VRF data lies above (or to the left) of the CDF of the satellite estimates, and hence the satellite rainfall estimates distribution is statistically greater than that characterizing the VRF data (see Figure 10).
Using a bootstrap procedure, we estimated the error associated with the exponential model. We sampled the original rainfall series 100 times (bootstrap resampling), and estimated the exponential model parameters (rate), and the associated modelled probabilities, for each sample. We then calculated the mean (μ) and the standard deviation (σ) of the modelled probabilities, assigning μ ± σ error bars. To measure the goodness of fit for each model, we first generated the exponential distribution of the rainfall series using the estimated parameters, and we prepared quantile-quantile (QQ) plots [64] (insets in Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15) comparing the raw and the exponential modelled data. In the plots, quantile curves close to the bisecting line indicate that the raw and the modelled data are comparable, and hence that the exponential distribution is appropriate to describe the rainfall series. We then performed a bootstrapped [60] version of the “two-sided” Kolmogorov-Smirnov test [61,62,63] to quantify the distance between the empirical distribution function and the exponential distribution function (used as reference) of the rainfall measurements (VRF) and satellite estimates (TMPA-V6, TMPA-V6-RT, TMPA-V7, TMPA-V7-RT). In this specific “two-sided” test formulation, p-values ≅ 1 (for D ≅ 0) indicate that the reference distribution (i.e., the exponential distribution) is appropriate to describe the rainfall series. The estimated exponential parameters (rate), and the Kolmogorov-Smirnov test statistics (D and p-value) calculated for Italy and for the morpho-climatic subdivisions are shown in Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15, and summarized in Table 6.
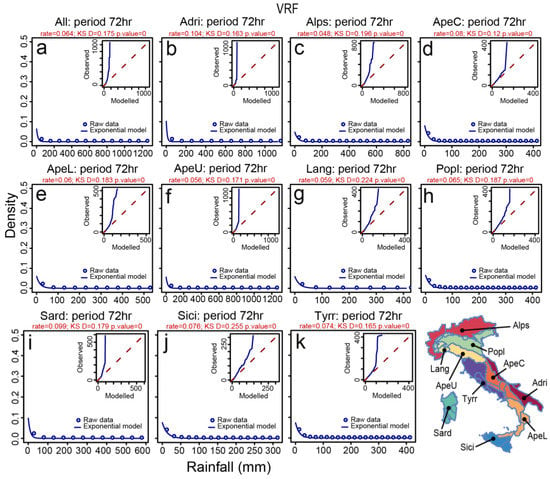
Figure 11.
Exponential distribution estimated for 72-h cumulative rainfall using the MLE method for VRF data. The different plots show results for different Italian morphological subdivisions: (a) entire Italian territory; (b) Adri; (c) Alps; (d) ApeC; (e) ApeL; (f) ApeU; (g) Lang; (h) Popl; (i) Sard; (j) Sici; (k) Tyrr. The insets show QQ-plot measuring the fitting performance of the exponential model. KS D and p-value are two-sided bootstrapped Kolmogorov-Smirnov test statistics (see Table 6).
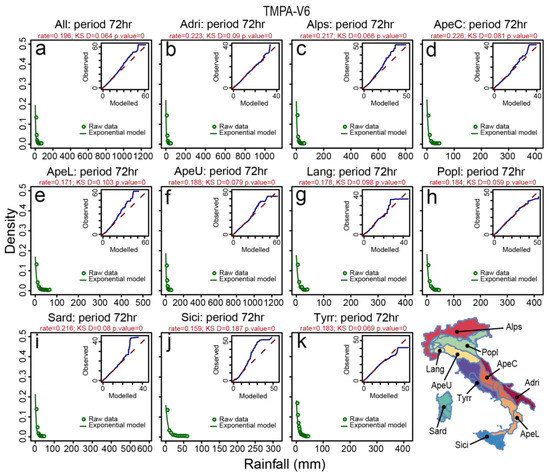
Figure 12.
Exponential distribution estimated for 72-h cumulative rainfall using the MLE method for satellite estimates (TMPA-V6). The different plots show results for different Italian morphological subdivisions: (a) entire Italian territory; (b) Adri; (c) Alps; (d) ApeC; (e) ApeL; (f) ApeU; (g) Lang; (h) Popl; (i) Sard; (j) Sici; (k) Tyrr. The insets show QQ-plot measuring the fitting performance of the exponential model. KS D and p-value are two-sided bootstrapped Kolmogorov-Smirnov test statistics (see Table 6).
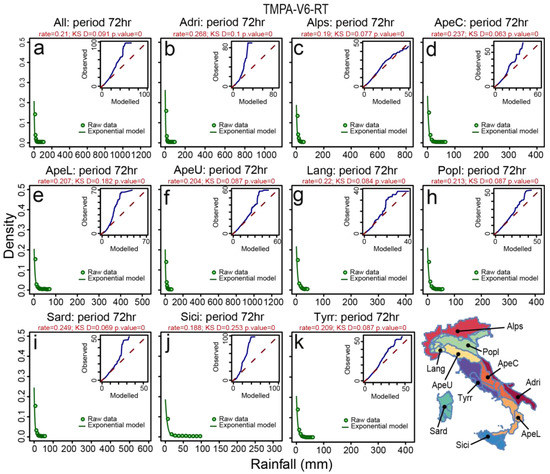
Figure 13.
Exponential distribution estimated for 72-h cumulative rainfall using the MLE method satellite estimates (TMPA-V6-RT). The different plots show results for different Italian morphological subdivisions: (a) entire Italian territory; (b) Adri; (c) Alps; (d) ApeC; (e) ApeL; (f) ApeU; (g) Lang; (h) Popl; (i) Sard; (j) Sici; (k) Tyrr. The insets show QQ-plot measuring the fitting performance of the exponential model. KS D and p-value are two-sided bootstrapped Kolmogorov-Smirnov test statistics (see Table 6).
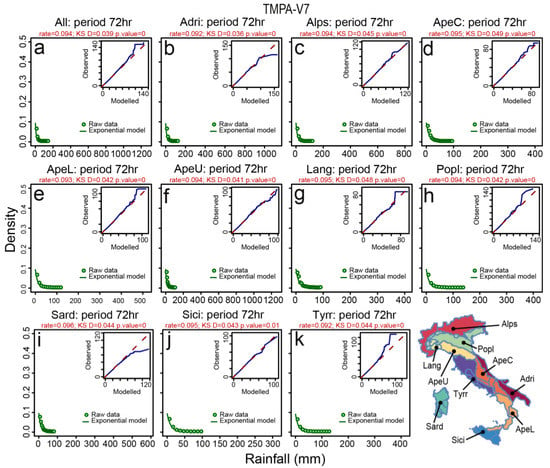
Figure 14.
Exponential distribution estimated for 72-h cumulative rainfall using the MLE method for satellite estimates (TMPA-V7). The different plots show results for different Italian morphological subdivisions: (a) entire Italian territory; (b) Adri; (c) Alps; (d) ApeC; (e) ApeL; (f) ApeU; (g) Lang; (h) Popl; (i) Sard; (j) Sici; (k) Tyrr. The insets show QQ-plot measuring the fitting performance of the exponential model. KS D and p-value are two-sided bootstrapped Kolmogorov-Smirnov test statistics (see Table 6).
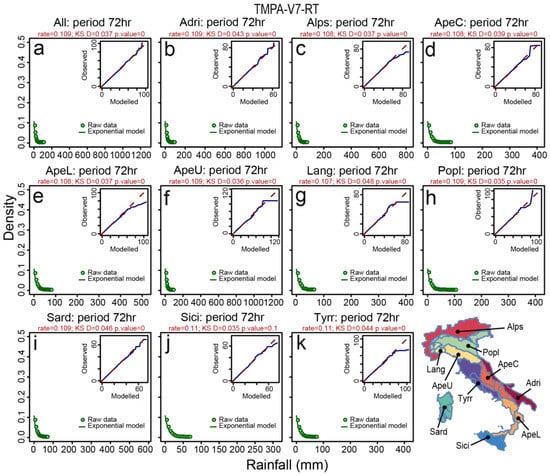
Figure 15.
Exponential distribution estimated for 72-h cumulative rainfall using the MLE method for satellite estimates (TMPA-V7-RT). The different plots show results for different Italian morphological subdivisions: (a) entire Italian territory; (b) Adri; (c) Alps; (d) ApeC; (e) ApeL; (f) ApeU; (g) Lang; (h) Popl; (i) Sard; (j) Sici; (k) Tyrr. The insets show QQ-plot measuring the fitting performance of the exponential model. KS D and p-value are two-sided bootstrapped Kolmogorov-Smirnov test statistics (see Table 6).

Table 6.
Results of bootstrapped Kolmogorov-Smirnov test (hypothesis: two-sided) to test if an exponential distribution (used as the reference distribution, see Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15) is appropriate to describe the VRF and TMPA data. Using the test two-sided hypothesis, p-values ≅ 1 (for D ≅ 0) indicate that the reference distribution is appropriate to describe the rainfall data.
2.4. Analysis of Rainfall Events
The analysis of the rainfall-induced landslide triggering condition is often performed identifying the specific rainfall event causing the instability phenomena. This is done determining the beginning, end, and cumulative rainfall of events that triggered landslides. The analysis of rainfall events derived from different data series could be meaningful to prove the ability of different rainfall product to highlight the real triggering mechanism of the instability phenomena.
To avoid the intrinsic subjectivity in the definition of the rainfall events [12,17,68] we adopted the automatic procedure proposed by Rossi et al. [69].
2.4.1. Identification of Rainfall Events
The proposed procedure is applied to the original rainfall record and singles out the characteristic rainfall events, where a rainfall event is defined as the cumulative amount of rainfall occurring during a period in hours where the rainfall values are continuous. To separate rainfall events, the procedure considers a minimum separation period (in hours) with accumulated rainfall (in mm) below a given threshold (Figure 16).
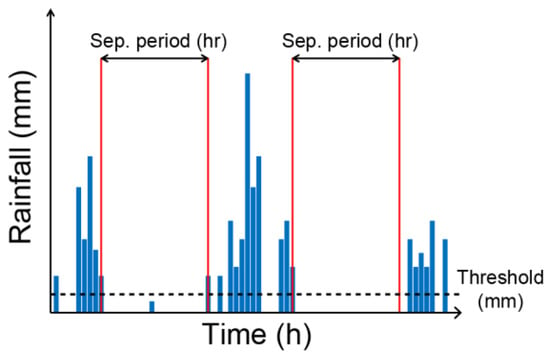
Figure 16.
Events separation criteria implemented in the automatic procedure for the detection rainfall events. The procedure main parameters are the separation period (in hours) and the rainfall threshold values (in mm).
Two rainfall events are separated by a period of a given length without rainfall, or with rainfall below a given threshold. The separation period and the threshold values are user-defined parameters in the automatic procedure, and control the duration and the cumulative rainfall of the events detected by the procedure. For this study, we used a 72-h separation period (a period similar to the period used for manual detection of the events e.g., by [17], and a minimum threshold of 0.2 mm of rainfall for the VRF data, and of 0 mm of rainfall for the satellite rainfall estimates. Preliminarily the procedure cleans the raw data series (removal of error codes and missing data), then using a moving window corresponding to the separation period, iteratively determines and identifies the start and the end times, and the duration and cumulated rainfall for each event (see Appendix A for details about the implementation).
We used the automatic procedure to detect rainfall events using the VRF data and the TMPA estimates (TMPA-V6, TMPA-V6-RT, TMPA-V7, and TMPA-V7-RT) in Italy.
2.4.2. Comparison of Rainfall Events
Rainfall events for VRF and TMPA data were calculated using the automated procedure. The cumulated total rainfall E, and the rainfall duration for the events were determined for all the events in Italy in the observation period. Results were plotted in a log-log plot (Figure 17a–e). These were compared to the rainfall events associated with 753 known rainfall-induced landslides (Figure 17f) obtained for the Italian territory through a thorough literature search, including international journals, conference proceedings, and event and technical reports describing single or multiple rainfall-induced landslides [6,7].
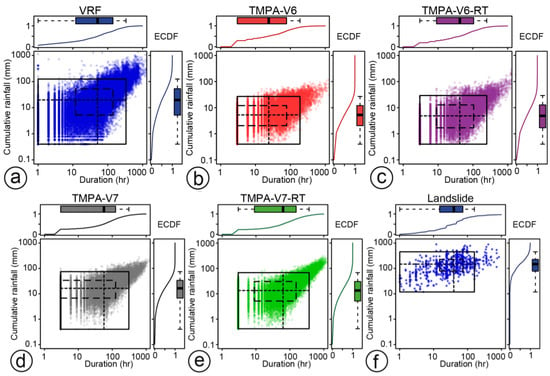
Figure 17.
Duration and cumulative rainfall of the events detected by the automatic procedure in the entire Italian territory in the period September 2009–August 2010 for the VRF data (a) and for the TMPA-V6 (b), TMPA-V6-RT (c), TMPA-V7 (d), TMPA-V7-RT (e) satellite rainfall estimates. (f) Rainfall events associated with landslides in the Italian territory. The boxplots and the ECDF plots (lines) describe the empirical distributions of the duration and cumulative rainfall of the events. Overlapped quantile grids (drawn from the marginal boxplot values) highlight the bivariate median (dotted lines), the bivariate interquartile ranges (dashed lines) and bivariate notches ranges (solid lines) of the rainfall events.
We then prepared boxplots, and Empirical Cumulative Distribution Function (ECDF) plots to describe the empirical distributions of the rainfall duration D, and the cumulated rainfall, for the rainfall events (marginal plots in Figure 17). We overlapped quantile grids, drawn from the marginal boxplot values, to each bivariate ED plot (grids in Figure 17), to highlight differences in the bivariate medians (a measure for the central tendency) and in the bivariate interquartile ranges, and notches ranges of the rainfall events (a measure for the statistical dispersion).
Finally, for each rain gauge and satellite centroid we calculated descriptive statistics of the events, including: (i) the mean of the cumulated rainfall of the events; (ii) the mean duration for the events; and (iii) the average number of events detected by the procedure for each rain gauge or TMPA grid cell centroid. Using an inverse distance weighting approach [68,69], we interpolated the values obtained for the VRF and TMPA data . The results are shown in Figure 18.
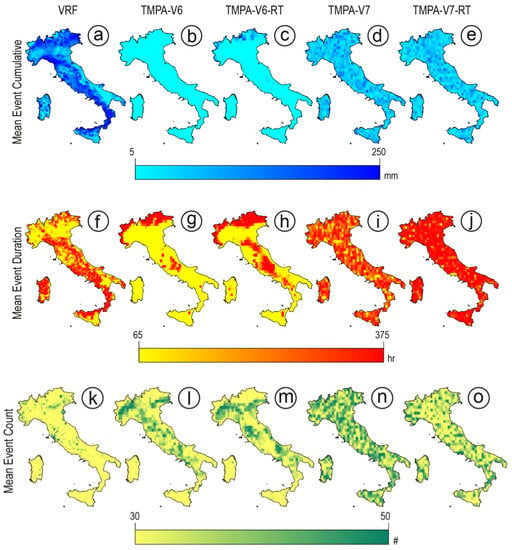
Figure 18.
Maps of mean cumulative rainfall (1st row), mean rainfall event duration (2nd row), and mean number of events (3rd row) detected by the automatic procedure in the entire Italian territory in the period September 2009–August 2010 for the VRF data (a,f,k) and for the TMPA-V6 (b,g,l), TMPA-V6-RT (c,h,m), TMPA-V7 (d,i,n), TMPA-V7-RT (e,j,o) satellite rainfall estimates.
3. Discussion
In the following, for each performed analyses, we first describe the results of the comparison of the two different type of rainfall data (i.e., VRF vs. TMPA data) and then we discuss their impact on the analysis of the triggering of rainfall induced-landslide and on their possible use in empirical prediction models at the base of most of the landslide early warning systems.
We compared four TMPA satellite rainfall products against VRF rain gauge data in Italy to determine and quantify if, and to what extent, satellite rainfall estimates may be applied in landslide triggering rainfall thresholds Italy, or as inputs to hydrological models. Previous studies have indicated that rainfall intensity and duration (ID) thresholds should be classified by climatologic or morphologic zone for more accurate representation of the regional conditions initiating slope failures [7,16]. We consider how the satellite and gauge rainfall data vary by aggregating and comparing data in different Italian morphological subdivisions derived from Guzzetti and Reichenbach [49].
We analyze the correlation between cumulative VRF and TMPA data for a 72-h duration period (Section 2.3.1) using linear and power-law fitting models. We repeat the analysis for rainfall above different thresholds for unique morphologic and climatologic conditions. Figure 5, Figure 6, Figure 7 and Figure 8 show how the R2 squared estimated for both fitting models vary for different rainfall threshold values in the entire territory and in each morphological zones. In all cases, the determination coefficients estimated for the power-law model are higher than those calculated for the linear models. Overall, the power-law regression models provided the best fitting performance compared to the linear regression models but at the expense of larger prediction intervals (i.e., the estimate of the intervals in which future observations will fall; [70,71] in particular for high rainfall values (see the example given in Figure 4a,b). The coefficients for the power-law models exhibit an increasing trend, stabilizing quickly towards high values, but in general for threshold values from 5 (TMPA-V6 and TMPA-V6-RT) to 10 mm (TMPA-V7 and TMPA-V7-RT). The linear determination coefficients are more sensitive to the threshold values along their entire range with general increasing trends except for: APEL, POPL for TMPA-V6 (Figure 5e,h), SARD for TMPA-V6-RT (Figure 6i), SARD, TYRR for TMPA-V7 (Figure 7i,k), and ALPS, APEL, POPL, SARD, SICI for TMPA-V7-RT (Figure 8c,e,h–j). An increasing trend along the threshold values range means that the more extreme the rainfall considered, the higher the correlation between VRF and TMPA data. However, for a few cases (e.g., 12 mm for SICI for TMPA-V7-RT show in Figure 8j), the higher correlation corresponds to specific threshold rainfall values. On average the lowest determination coefficient values and the largest differences between the linear and the power-law models are observed for the TMPA-V7 and TMPA-V7-RT products (Figure 7 and Figure 8). These two satellite products also show a peculiar sudden increase of the linear determination coefficients towards high threshold values for APEU, LANG, SICI with TMPA-V7 (Figure 7f,g,j), and APEC, APEL, APEU, LANG, SARD, TYRR with TMPA-V7-RT (Figure 8d–g,i,k), indicating a much better correlation for higher rainfall values.
Boxplots in Figure 9 describe the variation of parameters and of R2 estimates for different rainfall thresholds in Italy and in each Italian morphological zones. For both fitting models (linear and power-law) the regression parameters change in different morphological zones, indicating a complex correlation between TMPA and VRF data. In general, results show that satellite data underestimates the ground data (as shown by the coefficient greater than 1 in Figure 9a,e,i,m,c,g,k,o) particularly in high elevation areas such as the Alps (ALPS) and the northern Apennines (APEU), rather than in low altitude areas (SICI, ADRI, SARD). Results for some morphological subdivisions (POPL, APEC, LANG) are not consistent with this finding. This is probably due to the generalized aggregation procedure that does not directly consider some important territory characteristics such as relief orientation (aspect) and climatic differences (see Figure 1). The differences of the linear (Figure 9a,e,i,m) and power-law coefficients (Figure 9c,g,k,o) obtained for the four TRMM products also show that the range of the degree of underestimation is less pronounced for TMPA-V7-RT (Figure 9m,o), followed by TMPA-V7 (Figure 9i,k), TMPA-V6-RT (Figure 9e,g), and finally by TMPA-V6 (Figure 9a,c). Moreover, the variability of the linear determination coefficients estimated for the TMPA-V7 (Figure 9j) and TMPA-V7-RT (Figure 9n), in the different morphological subdivisions, is larger than the variability for the other two products TMPA-V6 (Figure 9c) and TMPA-V6-RT (Figure 9f) and in particular they are inversely correlated with the linear model coefficients (Figure 9i,m). For all the satellite products, the power-law regression models provided the best fitting performance (i.e., the power-law correlation values in Figure 9d,h,i,p are higher than the linear correlation ones in Figure 9b,f,j,n).
The results indicate that for the new TMPA products, the larger the underestimation of the VRF data, the larger the variability in the linear model estimation (i.e., the box plots in the linear correlation plots associated with the highest linear coefficients are larger compared to those relative to old TMPA V6 products). These finding have a direct impact on the use of TMPA products in the analysis of rainfall triggering mechanisms and in landslide prediction models. For instance, TMPA rainfall estimates cannot be used directly in landslide early warning systems unless a correct local scaling of the satellite estimates is performed due to the significant differences that may result in the empirical rainfall thresholds [6,7,12].
We further analyzed the statistical distribution of satellite and rain gauge 72-h cumulative rainfall data using non-parametric (HDE, KDE) and parametric (MLE) estimation methods (Section 2.3.2). Empirical frequency distributions (Figure 10) of the logarithm of the VRF and TMPA data (obtained using histogram density estimation methods points in Figure 10) are different, as shown by the difference in the modes (most frequent rainfall values) and by the different distribution tails. Similar differences can be observed by analyzing the probability densities of the logarithm of VRF and TMPA rainfall data calculated using the KDE method (lines in Figure 10). All the satellite products show single modal values, except for TMPA-V6-RT (for all the morphological subdivisions) and TMPA-V6 (for SICI and TYRR) that show two modal values or a significant density variation in correspondence of the mode of VRF data. The difference of rain gauge and the satellite empirical frequency distributions is also confirmed by the p-values resulting from the bootstrapped Kolmogorov-Smirnov test (alternative “greater”; Table 5), which are all equal to 0, indicating that the distributions of rainfall values of the different satellite products are statistically “greater” than the distribution of the VRF data. This indicates that the CDF of the VRF data lies above (or to the left) of the CDF of the satellite rainfall estimates, or to simplify, the quantile values of VRF data series are lower than those calculated for the satellite estimates series. Even if this seems in conflict with the results of the cumulated rainfall analysis, actually it is not. In fact, this result indicates that in the VRF, low rainfall values are more frequent than in the satellite series, but those values are not necessarily lower than the corresponding satellite ones when the coupling in the cumulated analysis is performed. In all the morphological subdivisions, both the empirical density estimation methods show that the distribution of the TMPA-V6-RT data is the closest to characterizing the VRF data, having the closest mode (Figure 10). This is also confirmed by the lower values of the D+ statistics of the bootstrapped Kolmogorov-Smirnov test (alternative greater) associated with the TMPA-V6-RT product in Table 5. In particular, for this satellite product, the closest distribution is that obtained for the lower Apennines (ApeL, Figure 10e). Observing the D+ statistics values for the other satellite products (Table 5) and also their associate empirical densities (Figure 10), the distributions going from most to least similar are TMPA-V6-RT, then TMPA-V6, TMPA-V7-RT and TMPA-V7.
Using the MLE, we then estimated exponential model parameters starting from raw cumulative rainfall data series. We use QQ-plots to compare observed and modelled data (Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15) and the bootstrapped Kolmogorov-Smirnov test (hypothesis two-sided, Table 6) to evaluate quantitatively how much the exponential distribution is appropriate to describe the different rainfall data series. The p-values of the bootstrapped Kolmogorov-Smirnov test (alternative two-sided; Table 6) indicate that the exponential distribution is statistically appropriate just to describe the TMPA-V7 and TMPA-V7-RT estimates in Sicily (Sici). However, if we look in detail the D statistics values (measuring the max difference between the observed and modelled CDFs) and the distances of quantile curves from the bisecting lines in the QQ-plots, the modelled exponential distributions obtained from the VRF data D statistics values in Table 6 and in Figure 11 are the furthest from the observed ones. The closest modelled distributions to the observed data are shown by the D values in Table 6 and range from best to worst fit for TMPA-V7, TMPA-V7-RT, TMPA-V6, and TMPA-V6-RT. In particular, for the highest values of the TMPA-V6 and the TMPA-V6-RT satellite estimates (Figure 12 and Figure 13) we observe a positive deviation from the QQ-plots bisecting lines, indicating that the exponential distribution tends to increasingly underestimate the higher tails of the rainfall satellite estimates in the different morphological zones. Summarizing this analysis indicates that VRF and TMPA data are fundamentally characterized by different distributions. The satellite rainfall estimates are best described by an exponential distribution, whereas the gauge-based data not. Results are consistent within the different Italian morphological zones.
The comparison of rainfall events identified from VRF and TMPA raw rainfall series using an automatic procedure, with rainfall events associated with landslides (Section 2.4.2) showed that they are characterized by different distributions (Figure 17). In fact, the boxplots and ECDF plots in the margins show that the marginal empirical distributions of the cumulative and duration of rainfall events calculated from the VRF (Figure 17a) and TMPA data (Figure 17b–e) have different shapes. The satellite products tend to not resolve precipitation rainfall events less than 3 h, owing to the sampling resolution of the satellite products, and the cumulative rainfall shows lower total values for the highest duration events. The quantile grids for those data series show larger differences in the central tendency and in the dispersion of the cumulative rainfall values with respect to the duration ones. Rainfall events from TMPA-V6 and TMPA-V6-RT data (Figure 17b,c) are on average shorter and less intense than the other rainfall data (VRF, TMPA-V7, TMPA-V7-RT; Figure 17a,d,e). Instead, the rainfall events derived from the other satellite products (TMPA-V7, TMPA-V7-RT; Figure 17d,e) are slightly less intense than those derived from VRF data (Figure 17a), as in agreement also with the ED maximum and minimum values in the plots. The data dispersion (quantile grid maximum extent or area) is higher for the rainfall events from VRF data, followed in order by those derived from TMPA-V7-RT, TMPA-V7, TMPA-V6-RT and TMPA-V6 satellite data.
Rainfall events associated with landslides and derived from VRF data (Landslide; Figure 17f) are comparable with the VRF data in terms of duration but they are much more intense (VRF; Figure 17a). The lowest dispersion of cumulative rainfall for landslide events indicates that the landslide events are triggered by a certain type of rainfall conditions. Although this is significant, the distributions of landslide rainfall events and of the events derived from VRF data overlap (Landslide and VRF data; Figure 17a,f). Instead, the overlapping of distributions of landslide rainfall events (Landslide; Figure 17f) and of rainfall events derived from satellite data (TMPA-V6, TMPA-V6-RT, TMPA-V7, TMPA-V7-RT; Figure 17b–e) is much more limited. It is statistically feasible to expect a similar overlapping when deriving landslide rainfall events from satellite data and it is expected that the distribution of the satellite rainfall events would shift towards lower cumulative rainfall values relative to the events derived from VRF data. On the contrary, this is not the case with satellite data having a larger shift amount depending on the satellite product analyzed. Any type of empirical or calibrated model will be conditioned by this finding. For instance, a landslide rainfall threshold derived from the TMPA satellite estimates should result in lower values than those derived using VRF data in the same area and exploiting the same landslide data [17]. This makes inappropriate using satellite estimates in empirical or calibrated models derived from VRF data.
The analysis of the maps of mean cumulative rainfall (Figure 18a–e), mean rainfall duration (Figure 18f–j), and mean number of events (Figure 18k,l–o) of the rainfall events detected by the automatic procedure shows different spatial arrangements and patterns of these variables across the Italian territory. Rainfall events derived from rain gauges are strongly influenced by the morphology (Figure 1a), with the more intense and longer events occurring mainly in elevated areas (VRF data; Figure 18a,f). Among the different satellite products, only the TMPA-V6 and TMPA-V6-RT show a dependence from the morphology, and in particular considering the mean duration (Figure 18g,h) and the mean number (Figure 18l,m) of the events. The mean cumulative of the rainfall events derived from TMPA-V7 and TMPA-V7-RT (Figure 18d,e) is generally higher than that characterizing the TMPA-V6 and TMPA-V6-RT (Figure 18b,c) but lower than that derived from VRF data (Figure 18a), and it is independent (or less conditioned) by the morphology. Interestingly, the mean number of these rainfall events (TMPA-V7 and TMPA-V7-RT; Figure 18n,o) is inversely correlated with their relative durations (Figure 18i,j), meaning that in the TMPA-V7 product rainfall events are on average shorter but more numerous than the events in the TMPA-V7-RT product.
These findings again indicate that satellite estimates cannot be applied for use within empirical rainfall thresholds derived from VRF data, or within other calibrated hydrogeological models (i.e., models derived or calibrated using VRF data, unless an appropriate local scaling/tuning (i.e., local analysis of the degree of correlation) of these data is performed. However, the similar ranges in the number and duration of rainfall events identified from rain gauge and satellite data suggest that TMPA products can be used to identify possible triggering rainfall events. Therefore, satellite data may be used to define new rainfall thresholds potentially applicable to the existing landslide early warning systems, or to derive any other type of calibrated model for the analysis of the instability phenomena. In this context, the procedure for rainfall event determination could be a fundamental tool for identifying and analyzing rainfall conditions that trigger landslides when exploiting both rain gauge and satellite rainfall data. The procedure can also be used to decrease the uncertainty related to the heuristic identification of rainfall events associated with landslides [17].
There are several reasons for why the satellite-based rainfall estimates and gauge data diverge both in the resolution of cumulative rainfall as well as in identifying individual rainfall events. First, the sampling strategy of the TMPA algorithm pulls in different instrument data within a 3-h window to essentially provide an instantaneous “snapshot” of the precipitation over every 0.25 × 0.25 degree pixel. As a result, it is likely that the TMPA products can often miss the peak rainfall occurring within a 3-h window, whereas gauges have a more local and continuous record to record such changes and more accurately characterize total accumulation. The instruments used to create the TMPA dataset also struggle with resolving shallow orographic rainfall, as do most satellite-based rainfall sensors, and as such, these tend to be biased in mountain areas. Lastly, the TRMM satellite, which anchors the TMPA products, only orbits from 35° N to 35° S. This means that all of Italy actually falls outside the range of the TRMM satellite. As a result, the TMPA merged product is based on other passive microwave sensors and infrared data that are possibly not as well calibrated for the study area, which includes both complex terrain and land/sea boundaries that complicate and frequently bias the instrument data. The GPM mission, which was launched in February 2014, provides similar instruments to those on board the TRMM satellite but will extend the original latitude orbit range (i.e., 35° N to 35° S) to 65° N to 65° S. GPM products and particularly the IMERG product [43] will potentially perform better than the TMPA once. Among the other advantages, GPM will provide a coordinated global picture of rain and snowfall information at higher spatial and temporal resolution (30-min, 0.1° × 0.1°). We believe that analyses similar to those applied in this work have to be realized to evaluate the performances and the reliability of this new product (i.e., which algorithms are still susceptible to changes) to estimate the rainfall measured close to ground.
4. Conclusions
In this work, we have compared rain gauge measurements and satellite estimates from four different TMPA products in Italy, in the period from 1 September 2009 to 31 August 2010. This area, given its morphological and climatological variability and the high frequency of hydrological disasters, was a perfect case study to compare the two rainfall data sources, and to investigate the possible use of satellite data within existing hydrogeological models. This was done considering the entire Italian territory and its different morphological and climatological zones by: (i) analyzing the pairwise correlations among VRF and different TMPA satellite data; (ii) comparing the distributions of all the rainfall datasets using different statistical approaches; and (iii) deriving and analyzing rainfall events from the different sources of rainfall information.
Results show that all satellite products tend to underestimate the rain gauge rainfall. In this sense, the new TMPA products (TMPA-V7 and TMPA-V7-RT) are more efficient in estimating the rainfall close to the ground as measured by rain gauges relative to the TMPA-V6 and TMPA-V6-RT satellite products. Underestimation is higher in elevated areas (like in the Alps and in northern Apennines) rather than in low altitude areas, but results for some morphological subdivisions are not consistent with this finding. Variability in these findings are likely a result of the generalized aggregation procedure applied in this analyses for grouping together the different morphological subdivisions originally identified by Guzzetti and Reichenbach [49], that does not directly consider important territory characteristics such as relief orientation (aspect) and climatic differences. Power-law and linear models are shown to be useful to correlate the ground and satellite data, with the first having the highest determination coefficients but at the expense of the highest prediction intervals. The degree of correlation between VRF and TMPA data is higher for the more intense rainfall values, which are basically those triggering landslides. Even if the new TMPA products (TMPA-V7 and TMPA-V7-RT) are closer to the VRF data (in particular if one considers the cumulated rainfall data analysis), they exhibit the lowest determination coefficients and the largest estimation variability. This probably will reflect in a simpler scaling/tuning process when using the TMPA-V6 and TMPA-V6-RT, in place of TMPA-V7 and TMPA-V7-RT satellite products.
The results of the statistical distribution within the different morpho-climatic zones show that the VRF and the TMPA data are characterized by different distributions, with the exponential distribution being appropriate just to describe some of the satellite rainfall estimate products (TMPA V7 and TMPA-V7-RT).
Rainfall events derived exploiting an automatic procedure using the different rainfall data types are statistically different, as well as their spatial arrangements and patterns across the Italian territory. The new TMPA products, TMPA-V7 and TMPA-V7-RT, compared to TMPA-V6 and TMPA-V6-RT, failed to capture the dependence/conditioning given by the morphology identified by the VRF data.
In conclusion, a complex relationship exists between rain gauge and the different satellite rainfall data in different morpho-climatic settings characterizing the Italian territory. The study suggests that satellite rainfall estimates from TMPA do not scale consistently with VRF ground measurements and require a detailed local investigation of the degree of correlation. These finding have a direct impact on the use of TRMM products in the analysis of rainfall triggering mechanisms and in the use of this data in landslide prediction models. Hence, satellite rainfall estimates cannot be used directly in empirical or in calibrated hydrogeological models if derived from gauge-based data, unless a correct local scaling of the satellite estimates is performed. Nevertheless, the results suggest that satellite rainfall data can be exploited to investigate the rainfall conditions that can trigger landslides, and other geo-hydrological phenomena or should be calibrated independently against landslide information to determine more appropriate triggering thresholds. In particular, satellite rainfall estimate could be helpful to define empirical rainfall threshold for landslide initiation, or in general for other hydrogeological models to predict instability phenomena over large areas. GPM IMERG products, providing higher spatial and temporal resolution as well as improved accuracy could be exploited to potentially improve on some of the inconsistencies currently observed between satellite-based rainfall estimates and gauge-based products. We believe that when stable version of the IMERG product will be available, the approaches used in this work can be appropriate and useful to evaluate its performances and reliability to estimate the rainfall measured close to the ground.
Acknowledgments
Work supported by a grant from the Italian Department for Civil Protection (DPC). Rain gauge network data were provided by the Italian Department for Civil Protection and they are not accessible to the public. These data can be provided upon specific conditions contacting Centro funzionale centrale—settore idro e settore meteo, Ufficio—Rischi Idrogeologici e Antropici, Dipartimento della Protezione Civile, Via Vitorchiano 2—00189 Roma, Italia. Precipitation data from the NASA’s Tropical Rainfall Measuring Mission (TRMM) is free and open to the public. The data can be accessed at http://pmm.nasa.gov/data-access/downloads/trmm. The software procedures used in the analyses performed in this paper were specifically designed and implemented by Mauro Rossi (see Appendix A for the details) and can be made available upon specific request contacting the developer (mauro.rossi@irpi.cnr.it).
Author Contributions
Mauro Rossi conceived, designed and performed the experiments and wrote the paper. Dalia Kirschbaum collected, exported and organized the TRMM satellite rainfall data, participated in the experiment design and contributed to the paper writing. Daniela Valigi participated in the design of the experiment, contributed to the VRF data elaboration and to the paper writing. Alessandro Cesare Mondini participated in the experiments design, contributed to the analyses and discussion and to the paper writing. Fausto Guzzetti participated in the design of the experiment and to paper writing.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Appendix A
All the analyses realized in this paper use open source software. VRF data (Section 2.2.1) and satellite rainfall estimates (Section 2.2.2) were stored and managed in specific spatial database (Section 2.2) using PostgreSQL, an open source object-relational database system [72], and its geographical spatial extension PostGIS [73]. The spatial association of individual rain gauges to the centroids of the TMPA grid cells was based on a minimum distance criterion (Section 2.3) and realized using the “v.distance” module available under GRASS GIS [74,75], a free and open source Geographic Information System (GIS). Specific procedures were realized in R (an open source software environment for statistical computing and graphics [76]) to filter, compare and analyze rainfall data series. In particular, those procedures were designed to (i) analyze the correlation of cumulative gauge and satellite rainfall data (Section 2.3.1); (ii) to estimate and analyze the statistical distribution of cumulated rainfall data series (Section 2.3.2); (iii) to identify rainfall events starting from raw rainfall data series (Section 2.4.1); and (iv) to analyze and compare the statistical and spatial rainfall events distributions (Section 2.4.2).
References
- Salvati, P.; Bianchi, C.; Rossi, M.; Guzzetti, F. Societal landslide and flood risk in Italy. Nat. Hazards Earth Syst. Sci. 2010, 10, 465–483. [Google Scholar] [CrossRef]
- Polaris. Available online: http://polaris.irpi.cnr.it/ (accessed on 14 October 2017).
- Wieczorek, G.F. Landslide triggering mechanisms. Landslides Investig. Mitig. 1996, 247, 76–90. [Google Scholar]
- Caine, N. The Rainfall Intensity: Duration Control of Shallow Landslides and Debris Flows. Geogr. Ann. Ser. Phys. Geogr. 1980, 62, 23–27. [Google Scholar] [CrossRef]
- Innes, J.L. Debris flows. Prog. Phys. Geogr. 1983, 7, 469–501. [Google Scholar] [CrossRef]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. Rainfall thresholds for the initiation of landslides in central and southern Europe. Meteorol. Atmospheric Phys. 2007, 98, 239–267. [Google Scholar] [CrossRef]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. The rainfall intensity–duration control of shallow landslides and debris flows: an update. Landslides 2008, 5, 3–17. [Google Scholar] [CrossRef]
- Wu, W.; Sidle, R.C. A Distributed Slope Stability Model for Steep Forested Basins. Water Resour. Res. 1995, 31, 2097–2110. [Google Scholar] [CrossRef]
- Montgomery, D.R.; Dietrich, W.E. A physically based model for the topographic control on shallow landsliding. Water Resour. Res. 1994, 30, 1153–1171. [Google Scholar] [CrossRef]
- Iverson, R.M. Landslide triggering by rain infiltration. Water Resour. Res. 2000, 36, 1897–1910. [Google Scholar] [CrossRef]
- Crosta, G. Regionalization of rainfall thresholds: an aid to landslide hazard evaluation. Environ. Geol. 1998, 35, 131–145. [Google Scholar] [CrossRef]
- Rossi, M.; Peruccacci, S.; Brunetti, M.; Marchesini, I.; Luciani, S.; Ardizzone, F.; Balducci, V.; Bianchi, C.; Cardinali, M.; Fiorucci, F.; et al. SANF: National warning system for rainfall-induced landslides in Italy. Landslides Eng. Slopes Prot. Soc. Improv. Underst. 2012, 2, 1895–1899. [Google Scholar]
- Hong, Y.; Adler, R.; Huffman, G. Evaluation of the potential of NASA multi-satellite precipitation analysis in global landslide hazard assessment. Geophys. Res. Lett. 2006, 33, L22402. [Google Scholar] [CrossRef]
- Liao, Z.; Hong, Y.; Kirschbaum, D.; Liu, C. Assessment of shallow landslides from Hurricane Mitch in central America using a physically based model. Environ. Earth Sci. 2012, 66, 1697–1705. [Google Scholar] [CrossRef]
- Kirschbaum, D.; Adler, R.; Hong, Y.; Lerner-Lam, A. Evaluation of a preliminary satellite-based landslide hazard algorithm using global landslide inventories. Nat. Hazards Earth Syst. Sci. 2009, 9, 673–686. [Google Scholar] [CrossRef]
- Kirschbaum, D.B.; Adler, R.; Hong, Y.; Kumar, S.; Peters-Lidard, C.; Lerner-Lam, A. Advances in landslide nowcasting: evaluation of a global and regional modeling approach. Environ. Earth Sci. 2012, 66, 1683–1696. [Google Scholar] [CrossRef]
- Rossi, M.; Luciani, S.; Valigi, D.; Kirschbaum, D.; Brunetti, M.T.; Peruccacci, S.; Guzzetti, F. Statistical approaches for the definition of landslide rainfall thresholds and their uncertainty using rain gauge and satellite data. Geomorphology 2017, 285, 16–27. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Ud din, S.; Al-Dousari, A.; Ramdan, A.; Al Ghadban, A. Site-specific precipitation estimate from TRMM data using bilinear weighted interpolation technique: An example from Kuwait. J. Arid Environ. 2008, 72, 1320–1328. [Google Scholar] [CrossRef]
- Jia, S.; Zhu, W.; Lű, A.; Yan, T. A statistical spatial downscaling algorithm of TRMM precipitation based on NDVI and DEM in the Qaidam Basin of China. Remote Sens. Environ. 2011, 115, 3069–3079. [Google Scholar] [CrossRef]
- Duncan, J.M.A.; Biggs, E.M. Assessing the accuracy and applied use of satellite-derived precipitation estimates over Nepal. Appl. Geogr. 2012, 34, 626–638. [Google Scholar] [CrossRef]
- Ji, X.; Chen, Y. Characterizing spatial patterns of precipitation based on corrected TRMM 3B43 data over the mid Tianshan Mountains of China. J. Mt. Sci. 2012, 9, 628–645. [Google Scholar] [CrossRef]
- Karaseva, M.O.; Prakash, S.; Gairola, R.M. Validation of high-resolution TRMM-3B43 precipitation product using rain gauge measurements over Kyrgyzstan. Theor. Appl. Climatol. 2012, 108, 147–157. [Google Scholar] [CrossRef]
- Semire, F.A.; Mohd-Mokhtar, R.; Ismail, W.; Mohamad, N.; Mandeep, J.S. Ground validation of space-borne satellite rainfall products in Malaysia. Adv. Space Res. 2012, 50, 1241–1249. [Google Scholar] [CrossRef]
- Islam, M.N.; Uyeda, H. Use of TRMM in determining the climatic characteristics of rainfall over Bangladesh. Remote Sens. Environ. 2007, 108, 264–276. [Google Scholar] [CrossRef]
- Brown, J.E.M. An analysis of the performance of hybrid infrared and microwave satellite precipitation algorithms over India and adjacent regions. Remote Sens. Environ. 2006, 101, 63–81. [Google Scholar] [CrossRef]
- Dinku, T.; Connor, S.J.; Ceccato, P. Comparison of CMORPH and TRMM-3B42 over Mountainous Regions of Africa and South America. In Satellite Rainfall Applications for Surface Hydrology; Springer: Dordrecht, The Netherlands, 2010; pp. 193–204. ISBN 978-90-481-2914-0. [Google Scholar]
- Villarini, G.; Krajewski, W.F. Evaluation of the research version TMPA three-hourly 0.25° × 0.25° rainfall estimates over Oklahoma. Geophys. Res. Lett. 2007, 34, L05402. [Google Scholar] [CrossRef]
- Habib, E.; Henschke, A.; Adler, R.F. Evaluation of TMPA satellite-based research and real-time rainfall estimates during six tropical-related heavy rainfall events over Louisiana, USA. Atmospheric Res. 2009, 94, 373–388. [Google Scholar] [CrossRef]
- Fleming, K.; Awange, J.; Kuhn, M.; Featherstone, W. Evaluating the TRMM 3B43 monthly precipitation product using gridded rain-gauge data over Australia. Aust. Meteorol. Oceanogr. J. 2011, 61, 171–184. [Google Scholar] [CrossRef]
- Chokngamwong, R.; Chiu, L.S. Thailand daily rainfall and comparison with TRMM products. J. Hydrometeorol. 2008, 9, 256–266. [Google Scholar] [CrossRef]
- Islam, M.N.; Das, S.; Uyeda, H. Calibration of TRMM derived rainfall over Nepal during 1998–2007. Open Atmos. Sci. J. 2010, 4, 12–23. [Google Scholar] [CrossRef]
- Almazroui, M. Calibration of TRMM rainfall climatology over Saudi Arabia during 1998–2009. Atmospheric Res. 2011, 99, 400–414. [Google Scholar] [CrossRef]
- Chen, G.; Sha, W.; Iwasaki, T.; Ueno, K. Diurnal variation of rainfall in the Yangtze River Valley during the spring-summer transition from TRMM measurements. J. Geophys. Res. Atmospheres 2012, 117, D06106. [Google Scholar] [CrossRef]
- Haile, A.T.; Habib, E.; Elsaadani, M.; Rientjes, T. Inter-comparison of satellite rainfall products for representing rainfall diurnal cycle over the Nile basin. Int. J. Appl. Earth Obs. Geoinformation 2013, 21, 230–240. [Google Scholar] [CrossRef]
- Katsanos, D.; Lagouvardos, K.; Kotroni, V.; Huffmann, G.J. Statistical evaluation of MPA-RT high-resolution precipitation estimates from satellite platforms over the central and eastern Mediterranean. Geophys. Res. Lett. 2004, 31, L06116. [Google Scholar] [CrossRef]
- Feidas, H. Validation of satellite rainfall products over Greece. Theor. Appl. Climatol. 2010, 99, 193–216. [Google Scholar] [CrossRef]
- Villarini, G. Evaluation of the Research-Version TMPA Rainfall Estimate at Its Finest Spatial and Temporal Scales over the Rome Metropolitan Area. J. Appl. Meteorol. Climatol. 2010, 49, 2591–2602. [Google Scholar] [CrossRef]
- Zulkafli, Z.; Buytaert, W.; Onof, C.; Manz, B.; Tarnavsky, E.; Lavado, W.; Guyot, J.-L. A Comparative Performance Analysis of TRMM 3B42 (TMPA) Versions 6 and 7 for Hydrological Applications over Andean–Amazon River Basins. J. Hydrometeorol. 2013, 15, 581–592. [Google Scholar] [CrossRef]
- Yong, B.; Chen, B.; Gourley, J.J.; Ren, L.; Hong, Y.; Chen, X.; Wang, W.; Chen, S.; Gong, L. Intercomparison of the Version-6 and Version-7 TMPA precipitation products over high and low latitudes basins with independent gauge networks: Is the newer version better in both real-time and post-real-time analysis for water resources and hydrologic extremes? J. Hydrol. 2014, 508, 77–87. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Nelkin, E.J. The TRMM Multi-Satellite Precipitation Analysis (TMPA). In Satellite Rainfall Applications for Surface Hydrology; Springer: Dordrecht, The Netherlands, 2010; pp. 3–22. ISBN 978-90-481-2914-0. [Google Scholar]
- Jenner, L. GPM - Global Precipitation Measurement. Available online: http://www.nasa.gov/mission_pages/GPM/main/index.html (accessed on 30 November 2017).
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Xie, P.; Yoo, S.-H. Algorithm Theoretical Basis Document (ATBD) Version 5.1, NASA Global Precipitation Measurement (GPM) Integrated Multi-Satellite Retrievals for GPM (IMERG); NASA: Greenbelt, MD, USA, 2014.
- Pinna, M. L’atmosfera e il Clima; Utet: Torino, Italy, 1978. [Google Scholar]
- Pinna, M.; Vittorini, S. Contributo alla determinazione dei regimi pluviometrici in Italia. Mem. Soc. Geogr. Ital. 1985, 34, 147–167. [Google Scholar]
- L’Abate, G.; Costantini, E. Il GIS pedoclimatico d’Italia. In Atti del convegno annuale SISS 2003 “Qualità del suolo, impatto antropico e qualità dei prodotti agricoli, l’agricoltura che produce paesaggio”; Boll. Soc. It. Sc. Suolo: Siena, Italy, 2004; pp. 439–444. [Google Scholar]
- Fratianni, S.; Acquaotta, F. The Climate of Italy. In Landscapes and Landforms of Italy; World Geomorphological Landscapes; Springer: Cham, Germany, 2017; pp. 29–38. ISBN 978-3-319-26192-8. [Google Scholar]
- SCIA. Available online: http://www.scia.isprambiente.it/documentazione.asp# (accessed on 20 November 2017).
- Guzzetti, F.; Reichenbach, P. Towards a definition of topographic divisions for Italy. Geomorphology 1994, 11, 57–74. [Google Scholar] [CrossRef]
- Köppen, W. The climates of the earth. Geogr. Rev. 1933, 23, 433–440. [Google Scholar]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World Map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Geiger, R. Köppen-Geiger, Klima der Erde; Klett-Perthes Verlag: Gotha, Germany, 1961. [Google Scholar]
- Brunetti, M.; Maugeri, M.; Nanni, T. Changes in total precipitation, rainy days and extreme events in northeastern Italy. Int. J. Climatol. 2001, 21, 861–871. [Google Scholar] [CrossRef]
- What is... | Civil Protection Department. Available online: http://www.protezionecivile.gov.it/jcms/en/che_cose.wp?request_locale=en&contentId=APP34611 (accessed on 17 October 2017).
- GHCN Monthly | National Centers for Environmental Information (NCEI). Available online: https://www.ncdc.noaa.gov/ghcnm/ (accessed on 14 October 2017).
- Peterson, T.C.; Vose, R.S. An Overview of the Global Historical Climatology Network Temperature Database. Bull. Am. Meteorol. Soc. 1997, 78, 2837–2849. [Google Scholar] [CrossRef]
- Leadbetter, M.R. On a basis for ‘Peaks over Threshold’ modeling. Stat. Probab. Lett. 1991, 12, 357–362. [Google Scholar] [CrossRef]
- Venables, W.N.; Ripley, B.D. Tree-based Methods. In Modern Applied Statistics with S-PLUS; Statistics and Computing; Springer: New York, NY, USA, 1999; pp. 303–327. ISBN 978-1-4757-3123-1. [Google Scholar]
- Parzen, E. On Estimation of a Probability Density Function and Mode. Ann. Math. Stat. 1962, 33, 1065–1076. [Google Scholar] [CrossRef]
- Sekhon, J.S. Multivariate and Propensity Score Matching Software with Automated Balance Optimization: The Matching Package for R; Social Science Research Network: Rochester, NY, USA, 2008. [Google Scholar]
- Smirnov, N.V. Estimate of deviation between empirical distribution functions in two independent samples. Bull. Mosc. Univ. 1939, 2, 3–16. [Google Scholar]
- Kolmogorov, A. Grundbegriffe der Wahrscheinlichkeitsrechnung; Julius Springer: Berlin, Germany, 1956. [Google Scholar]
- Conover, W. One-Sample “Kolmogorov” Test/Two-Sample “Smirnov” Test; John Wiley & Sons: New York, NY, USA, 1971; pp. 295–301. [Google Scholar]
- Wilk, M.B.; Gnanadesikan, R. Probability plotting methods for the analysis for the analysis of data. Biometrika 1968, 55, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Fisher, R.A. On the Mathematical Foundations of Theoretical Statistics. Philos. Trans. R. Soc. Lond. Ser. Contain. Pap. Math. Phys. Character 1922, 222, 309–368. [Google Scholar] [CrossRef]
- Fisher, R.A. The Goodness of Fit of Regression Formulae, and the Distribution of Regression Coefficients. J. R. Stat. Soc. 1922, 85, 597–612. [Google Scholar] [CrossRef]
- White, E.P.; Enquist, B.J.; Green, J.L. On Estimating the Exponent of Power-Law Frequency Distributions. Ecology 2008, 89, 905–912. [Google Scholar] [CrossRef] [PubMed]
- Melillo, M.; Brunetti, M.T.; Peruccacci, S.; Gariano, S.L.; Guzzetti, F. An algorithm for the objective reconstruction of rainfall events responsible for landslides. Landslides 2015, 12, 311–320. [Google Scholar] [CrossRef]
- Rossi, M.; Kirschbaum, D.; Luciani, S.; Mondini, A.C.; Guzzetti, F. TRMM satellite rainfall estimates for landslide early warning in Italy: preliminary results. Proc. of SPIE 2012, 8523, 85230D–1. [Google Scholar]
- Becker, R.A.; Chambers, J.M.; Wilks, A.R. The New S Language; Wadsworth & Brooks: Pacific Grove, CA, USA, 1988. [Google Scholar]
- Geisser, S. Predictive Inference; Chapman and Hall: New York, NY, USA, 1993. [Google Scholar]
- PostgreSQL: The World’s Most Advanced Open Source Database. Available online: https://www.postgresql.org/ (accessed on 14 October 2017).
- PostGIS—Spatial and Geographic Objects for PostgreSQL. Available online: http://postgis.net/ (accessed on 14 October 2017).
- Open Source GIS; Neteler, M.; Mitasova, H. (Eds.) Springer: Boston, MA, USA, 2008; ISBN 978-0-387-35767-6. [Google Scholar]
- GRASS GIS - Home. Available online: https://grass.osgeo.org/ (accessed on 14 October 2017).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2014. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).