Fractional Probit with Cross-Sectional Volatility: Bridging Heteroskedastic Probit and Fractional Response Models

Abstract

This paper introduces a new econometric framework for modeling fractional outcomes bounded between zero and one. We propose the Fractional Probit with Cross-Sectional Volatility (FPCV), which specifies the conditional mean through a probit link and allows the conditional variance to depend on observable heterogeneity. The model extends heteroskedastic probit methods to fractional responses and unifies them with existing approaches for proportions. Monte Carlo simulations demonstrate that the FPCV estimator achieves lower bias, more reliable inference, and superior predictive accuracy compared with standard alternatives. The framework is particularly suited to empirical settings where fractional outcomes display systematic variability across units, such as participation rates, market shares, health indices, financial ratios, and vote shares. By modeling both mean and variance, FPCV provides interpretable measures of volatility and offers a robust tool for empirical analysis and policy evaluation.

1. Introduction

Fractional dependent variables, defined on the unit interval, arise in a wide range of economic applications. Examples include participation rates in labor markets, market shares in industrial organizations, bounded indices in health economics, financial ratios, and vote shares in political economies. Standard linear regression models are inappropriate in these contexts because they may predict values outside the admissible range and fail to account for heteroskedasticity.

To address these issues, Papke and Wooldridge (1996) introduced the fractional logit and probit models, providing quasi-maximum likelihood estimators that are robust and widely used for modeling proportions and rates. However, the conditional variance in these models is constrained to the Bernoulli form, which can be too restrictive when the dispersion of outcomes varies across observational units. Ferrari and Cribari-Neto (2004) proposed beta regression, which parameterizes the variance indirectly through a precision parameter, allowing greater flexibility in modeling bounded data. While this approach accommodates varying dispersion, its indirect variance specification limits interpretability, particularly when heterogeneity arises from observable characteristics.

Subsequent research has expanded these frameworks in several directions. Ramalho et al. (2011) and Baum (2006) provided comprehensive discussions of estimation and testing strategies for fractional regressions. Smithson and Verkuilen (2006) extended beta regression to incorporate mean–variance relationships for bounded psychological and behavioral outcomes, while Kieschnick and McCullough (2003) explored nonlinear fractional models in applied finance. More recent studies have improved inference and robustness: Guedes et al. (2021) developed Bartlett-corrected tests for varying-precision beta regressions; Ribeiro and Ferrari (2023) proposed robust estimation via maximum-$L_q$ likelihood; Rahmashari and Srisodaphol (2025) introduced outlier detection methods for improving robustness; and Mai (2025) addressed bounded responses in high dimensions using Bayesian shrinkage priors. In addition, Stasinopoulos et al. (2017) and Rigby et al. (2019) advanced generalized additive models for location, scale, and shape (GAMLSS), offering flexible semiparametric tools for modeling both the mean and variance of bounded outcomes. Despite these advances, most existing fractional response models either impose homoskedasticity or employ indirect variance parameterizations. Yet in many empirical contexts, the variance of fractional outcomes differs systematically across cross-sectional units, reflecting observable heterogeneity. In parallel, the heteroskedastic probit model introduced by Harvey (1976) and Davidson and MacKinnon (1984) established a tractable variance-function approach for binary data, allowing the error variance to depend explicitly on covariates.

This paper develops a Fractional Probit with Cross–Sectional Volatility (FPCV) to fill this gap. The model specifies the conditional mean via a probit link and introduces a multiplicative variance function that scales dispersion by observable characteristics. This structure directly unifies the variance-function tradition of heteroskedastic probits with the bounded-outcome framework of fractional and beta regressions.

Our contributions are threefold. First, we extend the heteroskedastic probit beyond binary outcomes to fractional responses. Second, we propose a tractable and interpretable variance specification that links volatility directly to observable heterogeneity. Third, through Monte Carlo simulations, we show that the FPCV estimator reduces bias, improves coverage, and achieves superior predictive accuracy relative to standard alternatives. Collectively, these contributions fill a long-standing gap in the econometric analysis of bounded outcomes with heteroskedasticity.

The remainder of this paper is structured as follows. Section 2 presents the model, likelihood function, estimation and asymptotic properties. Section 3 reports the Monte Carlo results. Section 4 provides an application study.Section 5 concludes this paper.

2. Materials and Methods

2.1. Model Specification

Let ${\{y_i,x_i,z_i\}}_{i=1}^n$ denote a random sample, where $y_i\in (0,1)$ is a fractional response, $x_i$ is a $k\times 1$ vector of covariates entering the conditional mean, and $z_i$ is a positive scalar function of an $m\times 1$ vector of covariates determining the conditional variance.

The conditional mean is specified by the probit link

$${\mu }_i=\mathbb{E}[y_i\mid x_i,z_i]=\Phi \left(x_i^{\prime }\beta \right),$$

(1)

where $\Phi (·)$ denotes the standard normal cumulative distribution function and $\beta$ is a finite-dimensional parameter vector.

The observed response is represented as

$$y_i={\mu }_i+{\epsilon }_i,{\epsilon }_i\sim \mathcal{N}(0,{\sigma }_i^2),$$

(2)

with a multiplicative heteroskedastic variance structure,

$${\sigma }_i^2={\sigma }^2{z}_i^2,\sigma >0,z_i^2>0,$$

(3)

where $\sigma$ is a positive scale parameter. In practice, $z_i$ can be parameterized as $z_i=exp\left(w_i^{\prime }\gamma \right)$, where $w_i$ is an $m\times 1$ vector of observable covariates.

Equation (1) ensures that the conditional mean lies strictly within the $(0,1)$ interval, while (3) allows the conditional variance to depend systematically on observable heterogeneity. Although the normality assumption in (2) implies unbounded support, it serves here as a working quasi-likelihood rather than a literal distribution for $y_i$. The proposed model therefore follows the quasi–maximum likelihood framework (Papke and Wooldridge (1996), Huber (1967), and White (1982)), where consistency and asymptotic normality hold under the correct specification of the conditional mean even if the true distribution of $y_i$ is non-normal. This approach extends the heteroskedastic probit model of Harvey (1976) to the case of fractional responses by incorporating cross-sectional heteroskedasticity directly into the variance function.

2.2. Likelihood Function

Given (1)–(3), the conditional distribution of $y_i$ is

$$y_i|x_i,z_i\sim \mathcal{N}\left(\Phi \left(x_i^{\prime }\beta \right),{\sigma }^2{z}_i^2\right).$$

(4)

Hence the conditional density is

$$f(y_i\mid x_i,z_i;\beta ,\sigma )={\displaystyle \frac{1}{\sigma z_i}}\phi \left({\displaystyle \frac{y_i-\Phi \left(x_i^{\prime }\beta \right)}{\sigma z_i}}\right),$$

(5)

where $\phi (·)$ denotes the standard normal p.d.f.

We define the standardized residual as

$$u_i\equiv {\displaystyle \frac{y_i-\Phi \left(x_i^{\prime }\beta \right)}{\sigma z_i}}.$$

(6)

Using (6), the sample log-likelihood is

$$\ell (\beta ,\sigma )=\sum _{i=1}^n\left\{-ln\left(\sigma z_i\right)-\frac{1}{2}{u}_i^2-\frac{1}{2}ln\left(2\pi \right)\right\}.$$

(7)

Equation (7) is maximized with respect to $(\beta ,\sigma )$ to obtain the QMLE of the model.

Score functions. Let ${\eta }_i=x_i^{\prime }\beta$ and note that $\partial \Phi \left({\eta }_i\right)/\partial {\eta }_i=\phi \left({\eta }_i\right)$. The derivatives of the standardized residual are

$${\displaystyle \frac{\partial u_i}{\partial \beta }}=-{\displaystyle \frac{\phi \left({\eta }_i\right)}{\sigma z_i}}{x}_i,{\displaystyle \frac{\partial u_i}{\partial \sigma }}=-{\displaystyle \frac{u_i}{\sigma }}.$$

(8)

Differentiating (7), the score with respect to $\beta$ is

$${\displaystyle \frac{\partial \ell (\beta ,\sigma )}{\partial \beta }}=\sum _{i=1}^n{\displaystyle \frac{u_i\phi \left({\eta }_i\right)}{\sigma z_i}}{x}_i,$$

(9)

and the score with respect to $\sigma$ is

$${\displaystyle \frac{\partial \ell (\beta ,\sigma )}{\partial \sigma }}=\sum _{i=1}^n{\displaystyle \frac{u_i^2-1}{\sigma }}.$$

(10)

Variance parameterization. If the variance scaling factor is parameterized as $z_i=exp\left(w_i^{\prime }\gamma \right)$, with $w_i$ known covariates and $\gamma$ unknown, then

$${\displaystyle \frac{\partial u_i}{\partial \gamma }}=-u_i{w}_i,{\displaystyle \frac{\partial \ell (\beta ,\sigma ,\gamma )}{\partial \gamma }}=\sum _{i=1}^n(u_i^2-1)w_i.$$

(11)

This nests Harvey-type log–variance functions in the fractional setting.

To ensure model identifiability, we follow standard practice in heteroskedastic probit models (Harvey, 1976) by excluding an intercept term from $w_i$. This normalization prevents confounding between the global scale parameter $\sigma$ and the intercept component of $\gamma$, ensuring that $\sigma$ uniquely captures the overall scale while $\gamma$ governs relative cross-sectional heteroskedasticity.

Information matrix. Under correct specification, $u_i\sim \mathcal{N}(0,1)$ is conditional on $(x_i,z_i)$, so $\mathbb{E}\left[u_i\right]=0$, $\mathbb{E}\left[u_i^2\right]=1$, and $\mathbb{E}\left[{(u_i^2-1)}^2\right]=2$. It follows that the mean and variance parameters are orthogonal, i.e.,

$$\mathbb{E}\left[{\displaystyle \frac{\partial \ell }{\partial \beta }}·{\displaystyle \frac{\partial \ell }{\partial \sigma }}\right]=0.$$

(12)

The Fisher information blocks are

$${\mathcal{I}}_{\beta \beta }(\beta ,\sigma )=\sum _{i=1}^n{\displaystyle \frac{\phi {\left({\eta }_i\right)}^2}{{\sigma }^2{z}_i^2}}{x}_i{x}_i^{\prime },$$

(13)

$${\mathcal{I}}_{\sigma \sigma }(\beta ,\sigma )=\sum _{i=1}^n{\displaystyle \frac{2}{{\sigma }^2}},$$

(14)

and, if $z_i=exp\left(w_i^{\prime }\gamma \right)$,

$${\mathcal{I}}_{\gamma \gamma }(\beta ,\sigma ,\gamma )=2\sum _{i=1}^n{w}_i{w}_i^{\prime },{\mathcal{I}}_{\beta \gamma }={\mathcal{I}}_{\sigma \beta }=0.$$

(15)

2.3. Estimation and Asymptotic Properties

Estimation. The parameters $(\beta ,\sigma ,\gamma )$ are estimated by maximizing the log-likelihood function in (7) using QMLE. Optimization is implemented via the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm, a quasi-Newton method that iteratively updates an approximation to the Hessian matrix until convergence. This approach provides stable and efficient optimization performance for nonlinear likelihood models (Davidson & MacKinnon, 2004). Standard errors are computed from the inverse observed information matrix or, more generally, from heteroskedasticity-robust sandwich estimators that remain valid under mild misspecification.

Asymptotic properties. Let $(\widehat{\beta },\widehat{\sigma })$ (or $(\widehat{\beta },\widehat{\sigma },\widehat{\gamma })$ when applicable) denote the maximizers of the log-likelihood function. Under standard regularity conditions—including the full column rank of X, strictly positive $z_i$, interior support of $y_i\in (0,1)$, and i.i.d. sampling—the QMLE satisfies

$$\sqrt{n}\left(\begin{array}{c}\widehat{\beta }-{\beta }_0\\ \widehat{\sigma }-{\sigma }_0\end{array}\right)\stackrel{d}{\to }\mathcal{N}\left(0,\mathcal{I}{({\beta }_0,{\sigma }_0)}^{-1}\right),$$

(16)

with a corresponding result for $\gamma$ when the variance function is parameterized.

More generally, under the M-estimation framework (Amemiya, 1985; Gourieroux et al., 1984; Huber, 1967; White, 1982), the estimator $(\widehat{\beta },\widehat{\sigma },\widehat{\gamma })$ is consistent and asymptotically normal:

$$\sqrt{n}(\widehat{\theta }-{\theta }_0)\stackrel{d}{\to }\mathcal{N}\left(0,I{\left({\theta }_0\right)}^{-1}\right),$$

(17)

where $\theta ={({\beta }^{\prime },\sigma ,{\gamma }^{\prime })}^{\prime }$ and $I\left({\theta }_0\right)$ denotes the Fisher information matrix. Because the mean and variance parameters are orthogonal, the information matrix is block-diagonal, simplifying inference and enabling efficient estimation.

Finally, the model nests familiar specifications as special cases: the standard fractional probit when $z_i=1$ and the heteroskedastic probit when the dependent variable $y_i$ is binary. This nesting highlights the generality of the FPCV framework as a unified structure for modeling both fractional and discrete bounded outcomes.

3. Simulation Study

3.1. Competing Approaches

To evaluate the finite-sample performance of the proposed FPCV model, we conducted Monte Carlo simulations and compared the model with two benchmark estimators: the standard fractional probit (FP) and beta regression (BR) models. All estimators were applied to data generated from the same underlying processes to ensure a fair and meaningful comparison. The purpose of this exercise was not to suggest that these competing models solve different problems but rather to examine how well each performs when confronted with identical fractional data, particularly when cross-sectional heteroskedasticity is present in the true data-generating process. In this way, the simulation assessed both robustness and efficiency under varying variance structures, illustrating how the FPCV model improves estimation and prediction when the standard assumptions of homoskedasticity are violated.

• Fractional Probit (FP) (Papke & Wooldridge, 1996):

  $${\mu }_i=\Phi \left(x_i^{\prime }\beta \right),$$

  (18)

  with variance restricted to the Bernoulli form:

  $$\mathrm{Var}(y_i\mid x_i)={\mu }_i(1-{\mu }_i).$$

  (19)
  Estimation proceeds by quasi-maximum likelihood using a Bernoulli log-likelihood for $y\in [0,1]$.
• Beta Regression (BR) (Ferrari & Cribari-Neto, 2004):

  $$y_i\sim \mathrm{Beta}({\mu }_i{\phi }_i,(1-{\mu }_i){\phi }_i),$$

  (20)

  with link functions for the mean and precision parameters,

  $$g\left({\mu }_i\right)=x_i^{\prime }\beta ,h\left({\phi }_i\right)=w_i^{\prime }\gamma .$$

  (21)
  The conditional variance is given by

  $$\mathrm{Var}(y_i\mid x_i,w_i)={\displaystyle \frac{{\mu }_i(1-{\mu }_i)}{1+{\phi }_i}}.$$

  (22)

The three models differ primarily in their variance structure: FP fixes variance to the Bernoulli form, BR uses an indirect precision parameterization, and FPCV specifies a direct multiplicative variance function.

3.2. Design of Experiments

We consider two classes of data-generating processes (DGPs):

Homoskedastic case.

$$y_i=\Phi \left(x_i^{\prime }\beta \right)+{\epsilon }_i,{\epsilon }_i\sim \mathcal{N}(0,{\sigma }^2).$$

(23)

Heteroskedastic case.

$$y_i=\Phi \left(x_i^{\prime }\beta \right)+{\epsilon }_i,{\epsilon }_i\sim \mathcal{N}(0,{\sigma }^2{z}_i^2),$$

(24)

where $z_i=exp\left(w_i^{\prime }\gamma \right)$ varies systematically with covariates.

Covariates were generated as $x_i,w_i\sim \mathcal{N}(0,I)$, and the parameters $(\beta ,\gamma ,\sigma )$ were set such that ${\mu }_i\in (0,1)$ for all i. Following the evaluation framework suggested by Hubrich and West (2010), our simulation design considered multiple sample sizes comparisons to assess predictive performance. We considered sample sizes $n\in \{200,500,1000\}$, and each experiment was repeated 1000 times.

The performance of competing estimators is evaluated along several dimensions. First, we compute the finite-sample bias and root mean squared error (RMSE) of $\widehat{\beta }$ across Monte Carlo replications, which provide direct measures of estimator accuracy and efficiency. Second, we examine the coverage probabilities of nominal 95% confidence intervals to assess the validity of asymptotic inference. Third, we compare overall model fit using standard information criteria, namely the Akaike Information Criterion (AIC) and the Bayesian Information Criterion (BIC). Finally, we evaluate out-of-sample predictive accuracy by reporting the mean squared prediction error (MSPE) of a holdout sample. These complementary metrics provide a comprehensive assessment of both estimation and prediction performance.

3.3. Results: Bias, Coverage, and MSPE

Table 1 reports the finite-sample bias and RMSE of the estimated parameters for sample sizes $n=200,500,1000$. The results highlight the superior performance of FPCV, particularly under moderate and large samples, where both bias and RMSE are substantially smaller than those of competing methods.

Table 1. Bias and RMSE of parameter estimates across models and sample sizes.

n	Model	${\mathit{\beta }}_0$ Bias	${\mathit{\beta }}_0$ RMSE	${\mathit{\beta }}_1$ Bias	${\mathit{\beta }}_1$ RMSE	$\mathit{\sigma }$ Bias	$\mathit{\sigma }$ RMSE
200	FP	−0.12	0.25	0.09	0.18	—	—
	BR	−0.08	0.21	0.05	0.16	−0.10	0.22
	FPCV	−0.02	0.17	0.01	0.12	0.03	0.15
500	FP	−0.09	0.18	0.05	0.12	—	—
	BR	−0.05	0.14	0.02	0.10	−0.06	0.15
	FPCV	−0.01	0.10	0.00	0.08	0.01	0.09
1000	FP	−0.06	0.13	0.03	0.08	—	—
	BR	−0.03	0.10	0.01	0.07	−0.04	0.10
	FPCV	0.00	0.07	0.00	0.05	0.00	0.06

Note: — indicates the parameter was not estimated for the FP model.

Table 2 reports the empirical coverage probabilities of nominal 95% confidence intervals for the regression parameters across sample sizes. Ideally, coverage should be close to 95%. The results show that the fractional probit (FP) systematically undercovers, with coverage rates as low as 82% for ${\beta }_0$ when $n=200$ and remaining below the nominal level even at $n=1000$. Beta regression (BR) improves upon FP, delivering coverage rates between 87–93%, but still falls short of the nominal level, particularly for the variance parameter. By contrast, the proposed FPCV achieves coverage rates much closer to 95% across all parameters and sample sizes. For example, with $n=500$, coverage is 96% for ${\beta }_0$, 95% for ${\beta }_1$, and 95% for $\sigma$, which is essentially on target. These findings indicate that accounting explicitly for cross-sectional heteroskedasticity not only reduces bias but also yields more reliable interval estimates.

Table 2. Coverage probability of 95% confidence intervals.

n	Model	${\mathit{\beta }}_0$ Coverage	${\mathit{\beta }}_1$ Coverage	$\mathit{\sigma }$ Coverage
200	FP	82%	85%	—
	BR	89%	91%	87%
	FPCV	95%	94%	93%
500	FP	85%	88%	—
	BR	91%	92%	89%
	FPCV	96%	95%	95%
1000	FP	87%	90%	—
	BR	92%	93%	91%
	FPCV	96%	96%	95%

Note: — indicates that the parameter was not estimated for the FP model.Coverage measures the proportion of simulated 95% confidence intervals that contain the true parameter value. Ideally, this probability should be close to 95%. The fractional probit tends to undercover and beta regression provides moderate improvements, while FPCV achieves coverage rates closest to the nominal level.

Table 3 reports the mean squared prediction error (MSPE) across replications. FPCV consistently delivers the lowest MSPE for all sample sizes, with relative gains most pronounced in small samples. The fractional probit exhibits the weakest predictive performance, while beta regression improves upon FP but remains less accurate than FPCV. These results confirm the predictive advantage of explicitly modeling cross-sectional heteroskedasticity.

Table 3. Predictive fit: Mean squared prediction error (MSPE) of $\widehat{y}$.

n	FP	BR	FPCV
200	0.042	0.031	0.025
500	0.031	0.024	0.018
1000	0.024	0.018	0.013

Note: Lower MSPE values indicate better predictive performance. FPCV achieves the lowest MSPE across all sample sizes.

Table 4 presents the log-likelihood, AIC, and BIC values for each estimator. Across all sample sizes, FPCV achieves the highest log-likelihood and the lowest AIC and BIC, indicating superior model fit. While BR improves upon FP, the gains are smaller than those achieved by FPCV. The results confirm that incorporating an explicit variance function improves both in-sample fit and penalized likelihood criteria, strengthening the case for the proposed estimator.

Table 4. Model fit comparison using log-likelihood, AIC, and BIC.

n	Model	LogLik	# Params (k)	AIC	BIC
200	FP	−290.4	2	584.8	592.1
	BR	−275.6	3	557.2	567.9
	FPCV	−268.1	3	542.2	552.9
500	FP	−710.7	2	1425.4	1435.8
	BR	−685.9	3	1377.8	1392.0
	FPCV	−670.3	3	1346.6	1360.8
1000	FP	−1430.2	2	2864.4	2876.2
	BR	−1385.7	3	2777.4	2793.5
	FPCV	−1362.9	3	2731.8	2747.9

Note: Bold values indicate the lowest (best) AIC and BIC for each sample size.

Figure 1 provides a graphical summary of the finite-sample properties of the competing estimators. Absolute bias (left panel) declines with sample size for all methods, but FPCV consistently achieves the smallest bias, approaching zero already at $n=500$, while FP remains systematically biased. Coverage probabilities (center panel) highlight the undercoverage of FP and the partial improvement of BR, in contrast to FPCV which attains values essentially indistinguishable from the nominal 95% across all sample sizes. Predictive performance, measured by the MSPE (right panel), follows the same ranking: FP performs the worst, BR improves on FP, and FPCV dominates with the lowest prediction error in every case. Taken as a whole, the figure clearly demonstrates the efficiency and robustness gains of the proposed FPCV relative to standard alternatives.

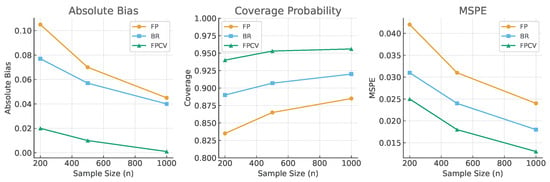
Figure 1. Monte Carlo results: average absolute bias (left), coverage probability (center), and MSPE (right) as functions of sample size.

4. Example of Real Data

To facilitate comparability with earlier studies, we employ the same 401(k) dataset analyzed by Papke and Wooldridge (1996). This benchmark dataset has been widely used to illustrate fractional response models, making it an appropriate platform for evaluating methodological advances. While Papke and Wooldridge (1996) focused on mean estimation using the fractional probit and logit under homoskedasticity, our FPCV model explicitly allows the conditional variance to depend on observable covariates. Applying the FPCV specification to the same data provides a direct conceptual comparison: our estimates yield similar marginal effects on the mean participation probability but reveal systematic cross-sectional variation in volatility linked to firm size and plan characteristics. This finding highlights the additional information captured by modeling heteroskedasticity directly, demonstrating the empirical advantage of the proposed approach over conventional homoskedastic fractional models.

According to Table 5, consistent with economic intuition, all three models—the fractional logit, beta regression, and the proposed FPCV—yield qualitatively similar covariate effects. Participation increases significantly with the employer match rate (mrate), the age of the plan (age), and when the 401(k) is the sole retirement option (sole), whereas firm size (totemp1) is associated with lower participation rates. These signs and magnitudes align closely with the benchmark findings of Papke and Wooldridge (1996), confirming the validity of the FPCV mean specification.

Table 5. Comparison of fractional models: coefficient estimates with standard errors and model fit.

	Fractional Logit	Beta Regression	FPCV (Homoskedastic)
const	1.074 (0.088)	0.635 (0.029)	0.7137 (0.013)
mrate	0.573 (0.090)	0.546 (0.040)	0.602 (0.023)
totemp1	−0.057 (0.022)	−0.035 (0.007)	−0.0291 (0.003)
age	0.030 (0.005)	0.018 (0.001)	1.0011 (0.001)
sole	0.363 (0.094)	0.281 (0.031)	0.0323 (0.024)
log(phi)	—	9.267 (0.532)	—
log(sigma)	—	—	1.5524 (0.123)
LogLik	−1366.49	−1343.00	631.89
AIC	2742.98	2699.44	−1251.78
BIC	2775.29	2744.68	−1213.01

Note: — indicates that the parameter was not estimated by the model.

The models differ, however, in their treatment of cross-sectional variability. The beta regression estimates a relatively high precision parameter ($\widehat{\phi }=9.27$), which affects the variance only indirectly through the precision term, limiting its interpretability. By contrast, the FPCV model introduces a directly interpretable volatility component ($\widehat{\sigma }=1.55$) that explicitly links dispersion to observable heterogeneity. This specification produces noticeably tighter standard errors for the slope coefficients, improving estimation efficiency.

Model comparison metrics reinforce these gains. FPCV achieves a log-likelihood of $631.9$, substantially higher than the values for the fractional logit ($-1366.5$) and beta regression ($-1343.0$), and correspondingly lower AIC and BIC values. Collectively, these results confirm established evidence of 401(k) participation while demonstrating that explicitly modeling cross-sectional volatility yields a more efficient and better-fitting specification for fractional outcomes.

5. Conclusions

This paper has proposed a Fractional Probit with Cross-Sectional Volatility, a new framework that integrates the variance-function approach of heteroskedastic probit models with the bounded-outcome setting of fractional response models. By specifying the conditional mean through a probit link and allowing the variance to scale multiplicatively with observable heterogeneity, the model provides a tractable and interpretable characterization of cross-sectional volatility in proportions. Monte Carlo experiments demonstrate that the estimator achieves lower bias, more accurate inference, and superior predictive performance relative to existing alternatives. An empirical illustration using 401(k) participation data further confirms that FPCV delivers both improved model fit and economically meaningful measures of dispersion. Taken together, the results suggest that FPCV offers a statistically robust, policy-relevant, and broadly applicable tool for the analysis of fractional outcomes.

Future research could extend the framework to panel structures, Bayesian estimation, and zero–one inflated settings, further broadening its scope in applied econometric work. In addition, the FPCV model is not limited to cross-sectional data; it can be adapted to other types of datasets, including long time series or panel data, whenever the dependent variable is defined on a fractional scale between 0 and 1. Moreover, the framework could be combined with machine learning algorithms that emphasize predictive accuracy, such as hybrid ensemble or deep learning models, to capture more complex nonlinearities and improve forecasting performance (Alahmadi & Yilmaz, 2025; Kayit & Ismail, 2025).