Abstract
The paper presents a novel methodology for the control management of a swarm of autonomous vehicles. The vehicles, or agents, may have different skills, and be employed for different missions. The methodology is based on the definition of descriptor functions that model the capabilities of the single agent and each task or mission. The swarm motion is controlled by minimizing a suitable norm of the error between agents’ descriptor functions and other descriptor functions which models the entire mission. The validity of the proposed technique is tested via numerical simulation, using different task assignment scenarios.
1. Introduction
Control of swarms of vehicles has received a lot of attention from the scientific community for the theoretical challenges and potential use. The concept of swarm has a number of advantages in many aerospace applications due to the decentralized nature and capability of performing missions not possible for large UAVs and single platforms. One of the most difficult problems in swarm motion is the design of a control management structure general enough to accommodate vehicles with different properties and with limited information exchange, which move in an adverse environment to achieve the same objective. The problem under consideration here consists of a number of agents, which may be heterogeneous in terms of size, autonomy of decision, payload capability, and task assignment. A high level controller should (loosely speaking) optimize the dynamics of the swarm (i.e., position and velocity), its shape, dimension(s), and motion with respect to the mission objectives, within a scenario characterized by the absence-presence of a mission operator. The dynamics of a single agent must be a combination of mathematical tractability and essential physical reality.
There are several methods and strategies that can be used in order to address the above problem; one of the most promising is the set of knowledge tools derived from biology (especially bird flocking, fish schooling, insect foraging techniques, predator hunting, boids, etc.) [1,2]. One of the most used behavioral features is the leader/follower structure, and in many instances [3,4], the different characteristics among agents of a swarm may be compared to some flocking behavior that includes leaders and followers. This structure can be used for establishing formation geometries optimized for performance and mission objectives. In addition, a leader/follower structure appears to be appropriate for separating agents according to their task and/or capabilities. Flocking and schooling motions can also provide insight and algorithms for implementation of the relative motion with respect to obstacles and obstacle management [5]. Finally, one of the most promising bio-inspired features is the neural structure of some species and how we can transfer such a structure into a decentralized form of communication, decision-making, and decentralized control. Control management of swarms has been addressed in the past and it is a current and very active area of research. Topological geometry, algebraic graph theory, consensus estimation, decentralized control and optimization of sensor networks are some of the methods used primarily in this context [6,7,8,9,10]. Still, one of the limitations, or open areas of research found from literature, is the absence of a structured relationship between the general swarm control problem and its connection to actual mission and tasks objectives. Path planning and task assignment problems, have been traditionally studied, in reference to standard UAVs (single, multiple), but not so much with respect to miniature vehicles and swarms [6]. Early research in autonomous cooperative multi-vehicle control addressed the problem from a global optimization point of view, which is certainly the most attractive avenue, and for which there is a large amount of literature [11,12]. However, the generality of the problem, the variety of scenarios, the number of tasks and vehicle’s constraints make global optimality unfeasible except for very simple applications. The type of vehicle (size, shape, performance), the payload (processing unit, sensors, communications suites), the number of agents (swarm, many, single) are in fact very dependent on the type of mission, so that a unified theory is probably not the best avenue.
2. Literature Review
The problem of control management of a swarm of vehicles or a distributed allocation of resources over some environment has been addressed in the past using different tools, depending on the driving application and the mathematical background. The following paragraphs give a brief summary of the current state of the art.
2.1. Behavioral Approaches
The understanding and development of tools derived from biology (especially bird flocking, fish schooling, foraging techniques, predator hunting, boids, etc.) is an attractive source of potentially useful models for dynamic behavior as well as control of multi-agents. Reynolds’ work [13] is perhaps the most widely known attempt to devise a simulation environment that describes flocking and schooling. It is based on particle motion dynamics and a set of rules to be followed by each particle (in particular, collision avoidance with neighbors and obstacles, same velocity of close by particles, and attraction to the center of the swarm). Clerc [7] and Reynolds’ [13] research are among the first that relate the motion of animal swarms with formal optimization techniques. Giulietti et al. [14] relate behaviors in migratory birds, with dynamical performance of formations. Passino [15] provides some formal definitions and relationships to describe animal and bacterial foraging, and their potential use in engineering applications such as unmanned aerial and ground vehicles search missions, and more generally, task assignment problems. Different foraging strategies are catalogued and associated with gradient and non-gradient based optimization algorithms. In another work, Passino [16] establishes a bridge between behavioral swarms and more traditional system theory properties, such as stability and global convergence to computable equilibrium points. A theoretical framework for design and analysis of distributed flocking algorithms is presented in [5], while Tanner and coworkers associate flocking behavior to fixed and dynamic topologies, in order to take advantage of the tools of graph theory for the modeling of splitting and recomposing of swarms [17,18]. One of the first applications of flocking in migratory birds is found in [3]. Social and greedy behaviors shown by geese and storks respectively are used to develop formation control algorithms, and to extend the principle of virtual leader, to the new concept of formation geometry leader. Bio mimicry techniques are presented in [19], where the problems of obstacle avoidance, and swarm consensus are solved using artificial potential based controllers. An interesting example is found in [20], where the authors present simple and yet useful modeling of moth swarming behavior during mating. Another analysis of swarm intelligence can be found in the work described in [2]. Although wider in scope, the book by Bonabeau and coworkers concentrates on the understanding, and algorithmic implementation of “social behaviors” shown by several species of insects. In particular, the concept of stigmergy is described in detail. Stigmergy is defined as that set of indirect interactions, which modifies the behavior of a colony member, due to changes caused by other members. A typical application of stigmergy is found in the coordination and regulation of mobile robots.
2.2. Consensus Protocols
The consensus protocol is a technique that formalizes what we call the “agreement” on a set of shared variables defining some properties common to the entire swarm. This asymptotic convergence is reached via local communications, which means that the algorithm is decentralized in nature. Consensus problems have a long history in computer science and statistical analysis forming the core of the so called distributed computing [21]. A consensus theoretical framework was introduced by Olfati-Saber and coworkers in [22], with a correlation to graph theory and graph topology. In this context, asymptotic convergence to a single equilibrium condition is achieved for static as well as dynamic topologies, provided some connectivity conditions on the underlying graphs are satisfied. These conditions in fact have an equivalent in Laplacian matrix theory and their spectral properties. One of the most appealing aspects of consensus is that the variable or variables that should agree to a common steady state value can be motion related (position, velocity), or representative of any other physical or system property (temperature, voltage, density, sociological behavior, etc.). This makes the methodology applicable not only to the control of motion of vehicles, but also to many “distributed systems” problems. Information and sensor networks and communications networks are typical examples found in the literature. A comprehensive treatment of consensus can be found in the text by Beard and Ren [9].
2.3. Coverage and Connectivity
Coverage control deals, in a general sense, with the optimal distribution of a large amount of resources over some environment. These resources can be robots, sensor networks, and diversified assets, all characterized by a decentralized and distributed evolution. In coverage approaches, the focus is on the use of tools such as proximity graphs (Voronoi diagrams, Delaunay tessellations, etc.) to determine the best distribution of resources for a given task (for example, swarms of vehicles in a rendezvous problem). Given a coordination task to be performed by the network as well as a proximity graph representing communication constraints, gradient flows can be used. Other approaches use the notion of neighboring agents and an interaction law between them is found in [23]. Another method is based on optimizing local objective functions to achieve the desired global task [24]. Graphs can model local interactions among agents, when individual agents are constrained by limited knowledge of others. The whole purpose of a coordinated coverage by a multi-agent system is to evolve towards the fulfillment of a global objective. This typically requires the minimization (or maximization) of a cost associated with each global configuration. Muhammad and Egerstedt [25] and Ji and Egerstedt [26] show some optimal coverage applications when the global objective is a function of the graphical abstraction of the formation, instead of the full configuration space of the system.
2.4. Abstractions and Models
The use of mathematical and physical abstractions is an appealing concept in swarm control management. One useful application of mathematical abstractions is the identification of a limited number of variables as a way of reducing the swarm shape to a “small” manageable set from the computation standpoint, as well as from the point of maintaining full capability of management. The literature presents several approaches that use this idea. In a paper by Belta and Kumar [27], the concepts of center of mass and moments of inertia are used as consensus variables for shaping the geometry of a swarm of homogeneous agents. Pimenta et al. [28] describe the problem of pattern generation in obstacle-filled environments by a swarm of mobile robots. Decentralized controllers are devised by using the Smoothed Particle Hydrodynamics (SPH) method, where the swarm is modeled as an incompressible fluid subjected to external forces. In a work by Jung and Sukhatme [29], starting from deployment and target tracking applications, the authors develop a controller that tries to minimize the difference between an optimal location (or target location) density and the density of the agents in the scenario. The density function described in [29] is the actual number of agents per unit of volume (or area). The main concept is based on the assumptions that for two comparably sized regions, more agents should be deployed in the one with the higher number of targets, and that the environment can be divided into topologically simple convex regions. The studies by Rimon and Koditschek [30] and Leonard et al. [31] are just two examples of the large amount of work that has been done using a potential field paradigm, where the motion of the agents (and also attraction and repulsion forces between single vehicles) is managed by forces generated by appropriate fields [19]. One advantage from the use of this technique is that classical stability can be easily casted into a Lyapunov framework by appropriate choice of potential functions.
The objective of this paper is to present a new technique for the high level control management of swarms of vehicles which is capable of modeling a large class of coordination problems. The environment and mission(s) under consideration are as general as possible, as well as the characteristics of the agents which may be all identical or heterogeneous. This condition is seldom found in the literature regarding high level control, and it comes into consideration usually only at the task assignment level. The number of agents is assumed to be “large”, and therefore the size of a single vehicle is considered negligible. Secondly, due to that, each agent may be limited in its capability as an individual, but could help optimize the overall behavior in terms of performance, robustness, probability of success. Thirdly, we will assume that the swarm may be subjected to losses (or planned expendabilities); therefore, the performances are better evaluated as a whole, rather than at the individual level. With the above assumptions, the main idea is to associate a function to each agent, and one or more functions to the mission (see [32] for more details on the mathematical framework). These functions (called descriptor functions) will have a different analytical description depending on the scenario, but their relationships are otherwise general and scenario independent, so that they could be applied to different vehicles and different tasks with little or no modification.
3. The Descriptor Function Framework
The Descriptor Functions method was recently introduced in [32] to address control management issues for a swarm of heterogeneous agents. The concept is general, and it is associated with the capability of an agent (UAV, vehicle, node of a sensor network, etc.) of performing some action. A brief review of the main definitions is presented herein.
Consider a system composed by N heterogeneous agents Vj, i = 1, … N and some mission composed of M tasks. At each time instant, the set of agents executing the same task forms a team. The number of teams may be up to M, and each agent may be part of one or more teams simultaneously. The domain where agents operate is Q ⊂ Rn, defining a spatial environment, as well as non-spatial related variables, and the position of agent i at time t is defined as pi(t). Without loss of generality, we make the following assumptions: Q is closed and bounded; each vehicle is capable of multitasking, but its behavior is optimized for only one task; the agents’ motions are limited to a single integrator kinematics with unity gain (no unicycle-type motion or dynamics are considered here):
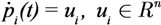
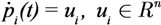
In a general multi-tasking framework (although not considered in the paper), the task that agent i-th is executing at time t is denoted by Ti(t) and the team performing the same task is defined as:
Tk(t) = {Vi: k ∈ Ti(t)}, k = 1, …, M
For each task k at location q ∈ Q, the Agent Descriptor Function (Agent DF) encodes the capability of task execution of the agent and is defined as:
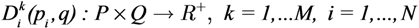
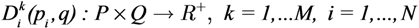
The Current Task Descriptor Function (Current TDF) is defined as the sum of the descriptor functions of the agents that are executing that task: Dk(p,q): PN ×Q → R+, i.e.,
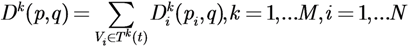 where p is the vector containing all vehicles’ positions. The Desired Task Descriptor Function (Desired TDF) specifies how the agents that are executing a specific task should be distributed. Specifically, it encodes the need of resources of a given type at each point q of the environment and is formalized as:
where p is the vector containing all vehicles’ positions. The Desired Task Descriptor Function (Desired TDF) specifies how the agents that are executing a specific task should be distributed. Specifically, it encodes the need of resources of a given type at each point q of the environment and is formalized as:
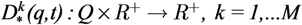
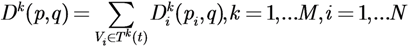
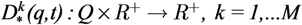
Although the above framework is set for multitasking, the present paper limits itself to a single task scenario for clarity’s sake.
Figure 1a shows an example of the Descriptor Functions framework. The bottom layer shows the trajectories of five agents moving in a 2D environment. The corresponding Agents DFs and the Current TDF are shown in the top layer, both at the beginning and at the end of the simulation.
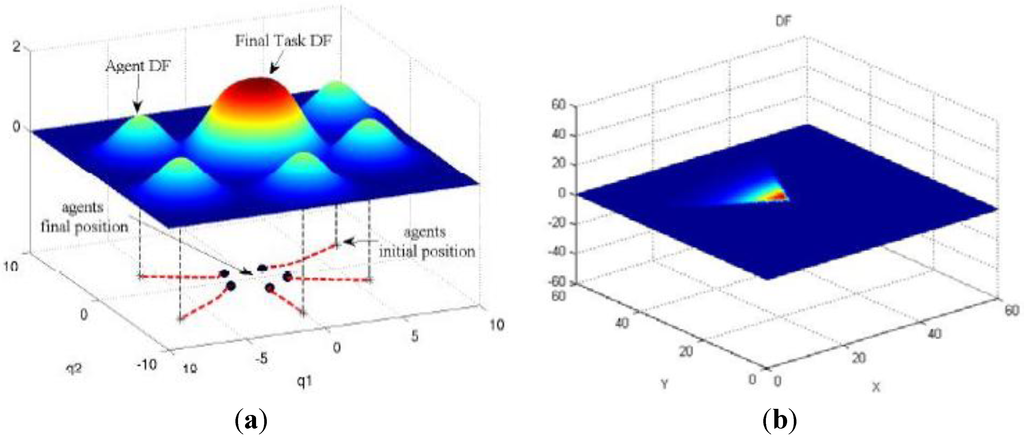
Figure 1.
Example of Descriptor Function Framework: Gaussian (a), Limited (b).
The aim of the swarm is to reduce the difference between their combined DFs and the desired one. To this end, we introduce the Task Error Function (TEF), which is defined as the difference between the Desired TDF and the Current TDF:
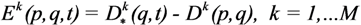
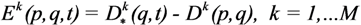
For the current mission and for each point of the environment, the TEF determines if there is a lack of resources (Ek(p,q,t) >0) or an excess of resources (Ek(p,q,t) <0), and therefore if there is a need for action by the swarm.
In this context, the objective is assumed to be completed if its TEF is equal or less than 0 at each point of the environment of interest for that task. The main advantage in using descriptor functions is the potential generality of the approach. Agent DFs could for instance describe a sensor capability, a sensor type, a rotary wing vehicle as opposed to a fixed wing one, etc. Task DFs, in a similar fashion, could describe task assignment, type of task, region coverage, etc. In work by Niccolini et al. [32], an example of DF modeled as a uniform Gaussian distribution is given, which could be appropriate for a “coverage” task (see Figure 1a). Ferrari-Braga et al. use a DF representing a limited field of view sensor in [33] (see Figure 1b). Once the above framework is set for a given scenario, the swarm control law can be synthesized based on the reduction of the task error function expression.
4. The Swarm Control Law
This section presents three control laws for the motion of the agents. The first control law was originally introduced in [31], and its effectiveness was demonstrated using an area coverage task within a synthetic environment developed in [34]. It is repeated here for clarity’s sake. Since the control law is based on a first order gradient optimization, it shows a potential weakness when the environment (location of agents and location of the areas of TEF > 0) is sparse and the DF of the agents are limited in range. In order to address this problem, a different controller is presented, based on Potential Field theory. Finally, a combined version of the two control laws is derived, exploiting each controller advantage, for achieving better performance. We remind the reader that, due to the proof of concept nature of the work, the selected controllers are not to be considered the optimal ones. In addition, due to the scope of the work, no obstacle avoidance controller is incorporated in the agents’ structures, leaving this problem for future studies.
4.1. Gradient-Based Control
Since the aim of the agents that belong to the same team is to satisfy the need of resources, a control law was designed to minimize a global measure of the TEF, which can be represented by the cost function:
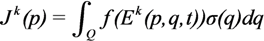 where f(.) is a limited, continuous, and continuously differentiable function of Ek for which f(
where f(.) is a limited, continuous, and continuously differentiable function of Ek for which f( 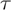 ) ≥ 0, ∀
) ≥ 0, ∀ 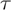 ∈ R+ and f(t) = 0, “t < 0”; σ(q) ≥ 0, ∀q ∈ Q, is an appropriate weighting function. The assumptions on f(.) are necessary in order to penalize only the lack of resources. In fact, the excess of resources does not foreclose task completion. The control problem is then formulated as an optimization and the resulting control law for each agent i derives directly from the gradient of the cost function, via steepest descent:
∈ R+ and f(t) = 0, “t < 0”; σ(q) ≥ 0, ∀q ∈ Q, is an appropriate weighting function. The assumptions on f(.) are necessary in order to penalize only the lack of resources. In fact, the excess of resources does not foreclose task completion. The control problem is then formulated as an optimization and the resulting control law for each agent i derives directly from the gradient of the cost function, via steepest descent:
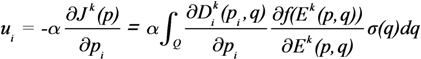
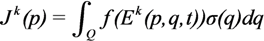
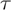 ) ≥ 0, ∀
) ≥ 0, ∀ 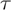 ∈ R+ and f(t) = 0, “t < 0”; σ(q) ≥ 0, ∀q ∈ Q, is an appropriate weighting function. The assumptions on f(.) are necessary in order to penalize only the lack of resources. In fact, the excess of resources does not foreclose task completion. The control problem is then formulated as an optimization and the resulting control law for each agent i derives directly from the gradient of the cost function, via steepest descent:
∈ R+ and f(t) = 0, “t < 0”; σ(q) ≥ 0, ∀q ∈ Q, is an appropriate weighting function. The assumptions on f(.) are necessary in order to penalize only the lack of resources. In fact, the excess of resources does not foreclose task completion. The control problem is then formulated as an optimization and the resulting control law for each agent i derives directly from the gradient of the cost function, via steepest descent:
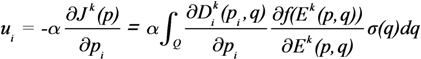
The control law described above requires the knowledge of TEF by each agent, at each point of the environment. This may be unrealistic from a practical as well as an analytical point of view, since it would require full swarm connectivity and unlimited distribution of the descriptor function of each agent (although the sigmoidal distribution makes agents far away almost irrelevant). There are several ways to decentralize the above control law. A formal approach would require a process of computing the current task descriptor function, from the estimation of the state of neighbor agents only. This could be achieved, for instance, by a consensus estimation algorithm with associated connectivity graph, or by discretization of the environment with a finite grid [35]. In this paper, we take a more heuristic approach, and we assume a spatial limitation of each descriptor function. If the Agent DFs are limited in space, the control law is decentralized, i.e., each agent can compute its control using the knowledge of the TEF within its neighborhood only. A generic form of f(Ek(p,q)) precludes an analytical solution of the global minimum for Jk. In fact, if an agent has a symmetric and limited DF, and if the TEF in its neighborhood is constant, the resulting control would be 0 yielding a local minimum. The control law in Equation (8) works well only locally and it is especially suited for high density environments, when the agents are near to each other, and their relative motion keeps the TEF non-stationary.
The control law in Equation (8) can also be written in terms of attractive forces generated in the environment by the Task Error Function. If the Agent DFs are symmetric, with a peak centered at the agent position pi and decreasing as the distance d from its position increases, the integrand of Equation (8) is a vector pointing from pi towards the point in space q, whose modulus depends on the TEF at that point weighted by the derivative of the Agent DF with respect to distance. This yields:
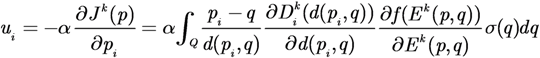 where d(pi,q) is the distance between agent i and the point q, and
where d(pi,q) is the distance between agent i and the point q, and 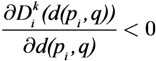
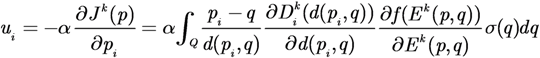
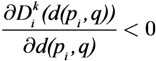
Note that if the agents’ DFs are limited in range, i.e., they are 0 and their derivative is 0 for all q beyond a given distance d(pi,q) from the agent position pi, the integrand in Equation (9) becomes zero, and the total control signal ui may become zero as well when the i-th agent is far enough from all tasks.
4.2. Potential Field-Based Control
In order to solve the convergence issues of the previous controller with DFs limited in range, a modified control law is proposed, which is based on the attractive-repulsive properties of field potentials, already known in the literature. The philosophy is similar to the framework of reactive robotics (known also as behavior-based robotics) introduced by Rodney Brooks [36]. The basic idea of behavior-based robotics is that robots should be built from the bottom up using ecologically adapted behaviors. Each behavior outputs a desired output vector, which corresponds, roughly, to the speed and orientation of a moving robot. The behaviors are described using a potential field. From the derivative of the potential field it is possible to compute the velocity vector that should be imposed to the agent. The collection of velocity vectors generated at each point of the environment is called Potential Field because it represents synthetic energy potentials that the robot will follow. The most common behaviors are the Seek-Goal and the Avoid-Obstacle. The Seek Goal is an example of attractive potential because the field causes the robot to be attracted to the goal. The Avoid-Obstacle is an example of repulsive potential because all the vectors point away from the obstacle [36,37].
The control problem can be formulated in terms of Potential Field, with the objective of moving the agents such that the Current TDF equals the Desired TDF. Recalling the definition of DF error in Equation (6), we can place an attractive potential field Y at each point of the environment, where there is a need for resources, that is at q ∈ Q, for which E(p,q) > 0.
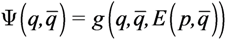
This potential field (Error Potential Field, EPF) maps the TEF at point q into velocity vectors associated to each point q ∈ Q of the environment as:
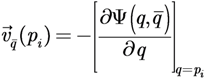
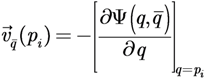
The total velocity of the agent is then computed as the integral of the EPFs generated by all the points q ∈ Q:
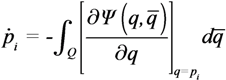
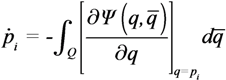
The presence of an agent reduces the current TEF at the points where the agent DF is not 0. For this reason, the EPFs generated in the environment change as the agents move. The function g(·) in Equation (10) can be seen as a measure of the importance that an agent assigns to the error at each point of the environment, and can be chosen according to the derivative of the Agent DF. In particular, it can be selected to weight the error in the whole environment even if the Agent DFs are limited.
Since we associate an attractive potential to multiple points of the environment q ∈ Q for which E(q) > 0, the use of the paraboloid shaped potential, commonly used for the Seek-Goal behavior over the entire environment, does not appear appropriate since we do not have, in general, a single goal point. If we consider target assignment as application, it is preferable for the agents to be more attracted towards the points of the environment for which the TEF is greater than 0. Since the Avoid-Obstacle Potential Field gives more importance to points that are near an agent, the direction of this potential should be changed in order to make it attractive. With this in mind, let us assume:
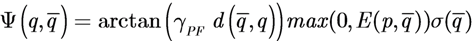
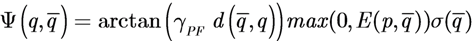
The resulting control law is then given by:
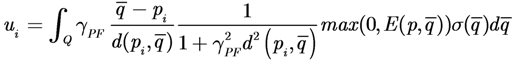
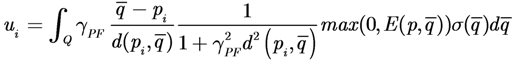
The control law tends to drive the agents towards regions of the space where the “density of the error” is larger. The choice of the potential gain gPF determines the strength of the force induced by the points of the environment. If the gain is large, areas of large TEF, which are far away from the agent may induce small velocities and this characterizes the tendency of the agents to prefer areas of positive TEF nearer to them. Moreover, this may cause slower convergence rates, i.e., smaller velocity commands for the agents, thus longer mission time. In order to have control both on the convergence rate and of the tendency to prefer areas of TEF > 0 in the agent’s neighborhood, an additional degree of freedom gD > 0 is introduced yielding:
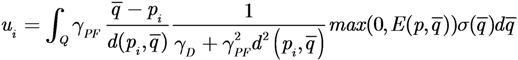
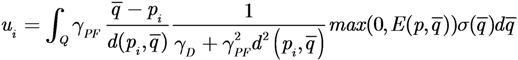
The two gains gD and gPF constitute the tradeoff between the two objectives.
The main drawback of this control law is that it does not guarantee that the agents will eventually stop and does not minimize any measure of the TEF. On the other hand, this control law does not suffer from the problems described in Section 4.1, since it weights the error in the whole environment. The equilibrium points, if any, are the ones for which the weighted TEF is balanced with respect to all the agents. However, agents may end in local minima as well. This is one of the most common issues related to the application of Potential Field. Since the Potential Field depends on the position of all the agents and changes during mission execution, it is difficult to anticipate the presence of local minima. Contrary to a static obstacle-goal configuration, local minima are dynamic and an agent can get out from them thanks to the movement of another agent, which creates asymmetry in the environment. This approach appears realistic in lieu of generally asymmetric nature of a swarm.
4.3. Combined (Switching) Control Law
In the previous paragraphs, two controllers were described, which have advantages and disadvantages when applied singularly. In particular, a gradient based controller is not suited in cases where the agent DF is limited in space and does not intersect, neither in a small amount, the descriptor function which describes the desired value. The controller derived using potential fields, on the other hand, has no guarantee of minimizing the computed error function. It is possible, however, to take advantage of positive aspects of both approaches, and to derive a combined controller. The Potential Field control law should be employed by the agents that are stuck in configurations for which there is no contribution to the reduction of the TEF such as when they are far from the areas where TEF > 0. The Gradient based control law should be used instead by the agents to locally optimize the cost function of Equation (7) when they are sufficiently near the goal.
Let us assume that each vehicle is capable of measuring its contribution to the reduction of the TEF as:
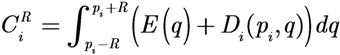
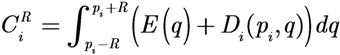
The agent evaluates the amount of TEF that it is covering in a neighborhood of radius R. The switching is performed by comparing 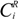 with a function of the total contribution that the agent could provide. If
with a function of the total contribution that the agent could provide. If 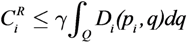 then the Potential Field control law is used, otherwise the Gradient based controller law is used. Roughly speaking, an agent switches to the Potential Field control law if in its neighborhood it is not contributing to a sufficient reduction of the TEF. We must note that, at this point, the above conjecture has no formal proof of the stability of the overall dynamic behavior. To illustrate the behavior of the agents under the three control laws, let us consider four agents that must cover a circular region centered in [0, 0] and radius 4. The results are shown in Figure 2, where in red the footprint of the desired DF is shown. The cost function was built using: f(t) = max(0, t)2, and σ was set equal to 1.
then the Potential Field control law is used, otherwise the Gradient based controller law is used. Roughly speaking, an agent switches to the Potential Field control law if in its neighborhood it is not contributing to a sufficient reduction of the TEF. We must note that, at this point, the above conjecture has no formal proof of the stability of the overall dynamic behavior. To illustrate the behavior of the agents under the three control laws, let us consider four agents that must cover a circular region centered in [0, 0] and radius 4. The results are shown in Figure 2, where in red the footprint of the desired DF is shown. The cost function was built using: f(t) = max(0, t)2, and σ was set equal to 1.
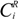 with a function of the total contribution that the agent could provide. If
with a function of the total contribution that the agent could provide. If 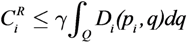 then the Potential Field control law is used, otherwise the Gradient based controller law is used. Roughly speaking, an agent switches to the Potential Field control law if in its neighborhood it is not contributing to a sufficient reduction of the TEF. We must note that, at this point, the above conjecture has no formal proof of the stability of the overall dynamic behavior. To illustrate the behavior of the agents under the three control laws, let us consider four agents that must cover a circular region centered in [0, 0] and radius 4. The results are shown in Figure 2, where in red the footprint of the desired DF is shown. The cost function was built using: f(t) = max(0, t)2, and σ was set equal to 1.
then the Potential Field control law is used, otherwise the Gradient based controller law is used. Roughly speaking, an agent switches to the Potential Field control law if in its neighborhood it is not contributing to a sufficient reduction of the TEF. We must note that, at this point, the above conjecture has no formal proof of the stability of the overall dynamic behavior. To illustrate the behavior of the agents under the three control laws, let us consider four agents that must cover a circular region centered in [0, 0] and radius 4. The results are shown in Figure 2, where in red the footprint of the desired DF is shown. The cost function was built using: f(t) = max(0, t)2, and σ was set equal to 1. 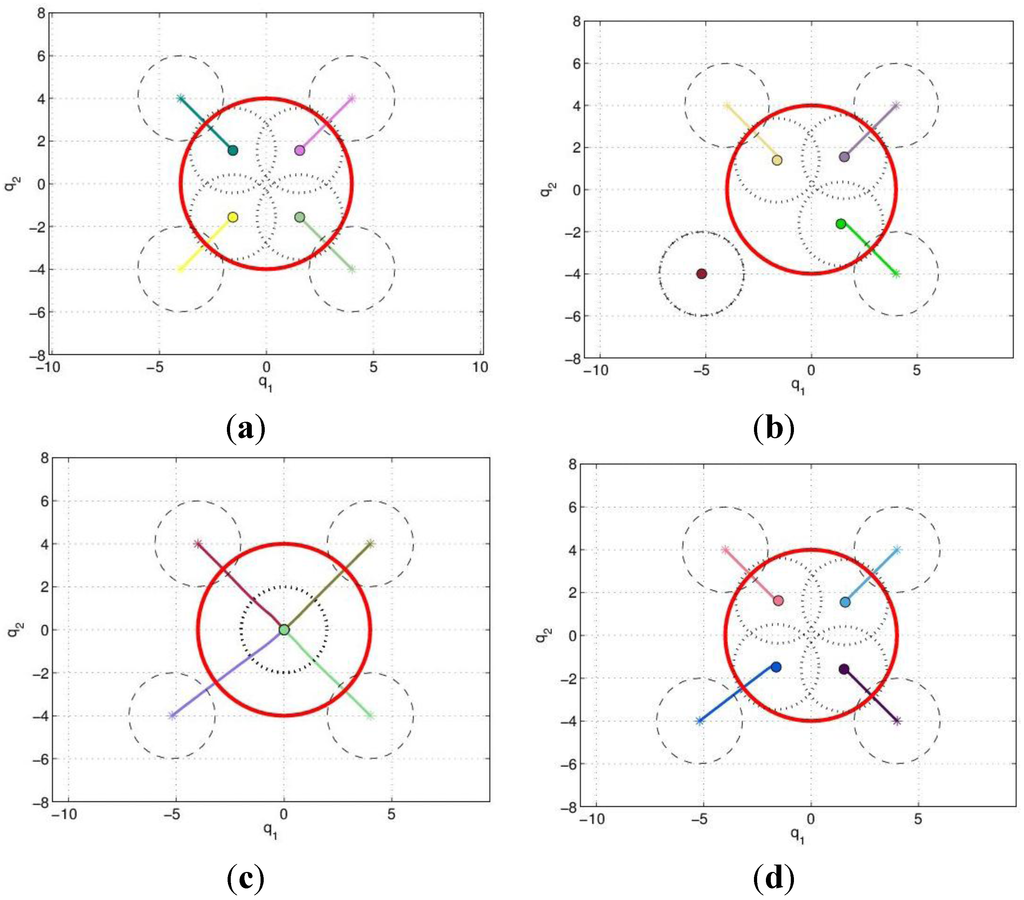
Figure 2.
(a) Gradient controller performance. (b) Gradient controller with a local minimum. (c) Potential field controller performance. (d) Complete controller performance.
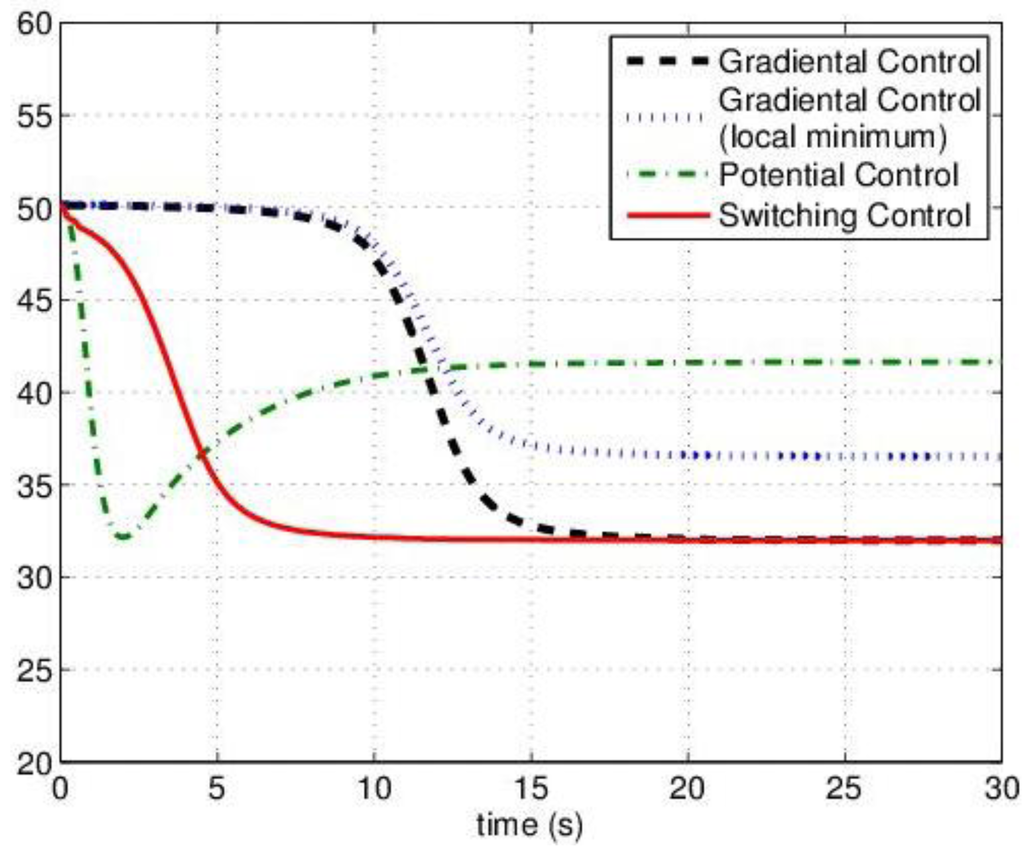
Figure 3.
Cost function comparison.
Figure 2a shows a successful implementation of a gradient based controller, unlike Figure 2b, in which case the bottom left agent is not affected by the cost minimization (no contribution to the desired DF). The potential field controller performance is shown in Figure 2c. Here, all agents move to the same point, which is the center of the area to be covered (due to the symmetry of the problem). Finally, the beneficial effect of the combined controller described by Equation (14) is evident in Figure 2d. Now the bottom left agent is directed towards the desired location by the attractive field component. Once all agents influence the error DF, the gradient based controller provides satisfactory coverage and yields a global minimum. Another interesting performance comparison is shown in Figure 3. Here, the cost function behavior clearly shows how the combined control law (switching controller) achieves the optimal solution.
5. Case Study: Target Assignment
The proposed concept of descriptor function was successfully applied to a coverage scenario using the controller in Section 4.1 [32]. Here, we present a target assignment (TA) mission, with the purpose of confirming the viability of descriptor functions, as well as a comparison of the proposed controllers.
Consider a mission where N agents must reach Nw targets. The desired D* is selected as given by Nw “small” disjoint areas, possibly far from each other and from the initial positions of the agents.
To formalize the problem, a single task is considered and the corresponding superscript k is indicated as TA. All agents have the same DF, 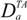 (pi,q). Given the position of the targets wi ∈ Q, the desired TDF is constructed as:
(pi,q). Given the position of the targets wi ∈ Q, the desired TDF is constructed as:
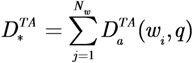
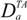 (pi,q). Given the position of the targets wi ∈ Q, the desired TDF is constructed as:
(pi,q). Given the position of the targets wi ∈ Q, the desired TDF is constructed as:
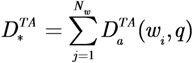
The DF of the agents and targets are spatially limited, thus:
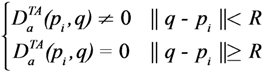
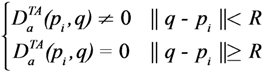
Furthermore, a target is said to be “observed” if the TEF in its neighborhood  is zero. Each agent moves using the switching control law presented in Section 4.3. In particular, it uses the gradient control law when it is far from the targets and the Potential Field controller when its DF intersects the DF of at least one target of a given amount, selected by design.
is zero. Each agent moves using the switching control law presented in Section 4.3. In particular, it uses the gradient control law when it is far from the targets and the Potential Field controller when its DF intersects the DF of at least one target of a given amount, selected by design.
 is zero. Each agent moves using the switching control law presented in Section 4.3. In particular, it uses the gradient control law when it is far from the targets and the Potential Field controller when its DF intersects the DF of at least one target of a given amount, selected by design.
is zero. Each agent moves using the switching control law presented in Section 4.3. In particular, it uses the gradient control law when it is far from the targets and the Potential Field controller when its DF intersects the DF of at least one target of a given amount, selected by design.The simulations presented in this section are performed using agents and targets modeled with descriptor functions with Gaussian shape:
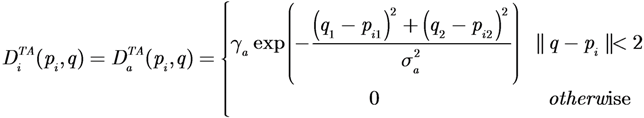 where the amplitude ga and the dispersion sa were selected as 1. The shape of the DF is very similar to the model of sensors that have a peak at the agent position and a decreasing performance with the distance.
where the amplitude ga and the dispersion sa were selected as 1. The shape of the DF is very similar to the model of sensors that have a peak at the agent position and a decreasing performance with the distance.
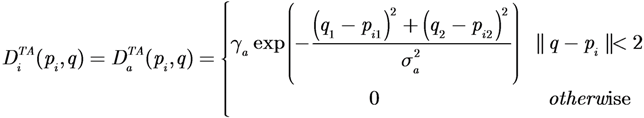
The first set of simulations uses the switching controller and a comparison with the Potential Field controller is shown in the second set of simulations. In both cases, the cost function is given by Equation (7) with: f(t) = max(0, t)2.
The above selection is extensively motivated in [32]. The gain for the switching condition was selected to be g = 0.4.
5.1. Example 1
In this first example, we consider five agents and a changing number of targets (5, 3, and 10, respectively). The agents have all the same capability (same DF) as shown by their equal footprints in the numerical simulations results below. The selected gains for the potential field based controller were selected to be:
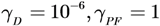
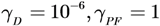
The initial positions of the agents are:
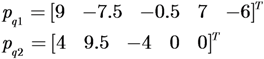
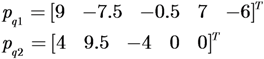
Figure 4a shows the trajectories of the agents when the number agents and of targets is the same (five in this case). Although initially more agents go to the same target, full assignment is achieved. The corresponding cost function is on the top right of the figure. The final value of the cost function is 0; that means that the DFs of the targets are completely covered by the DFs of the agents.
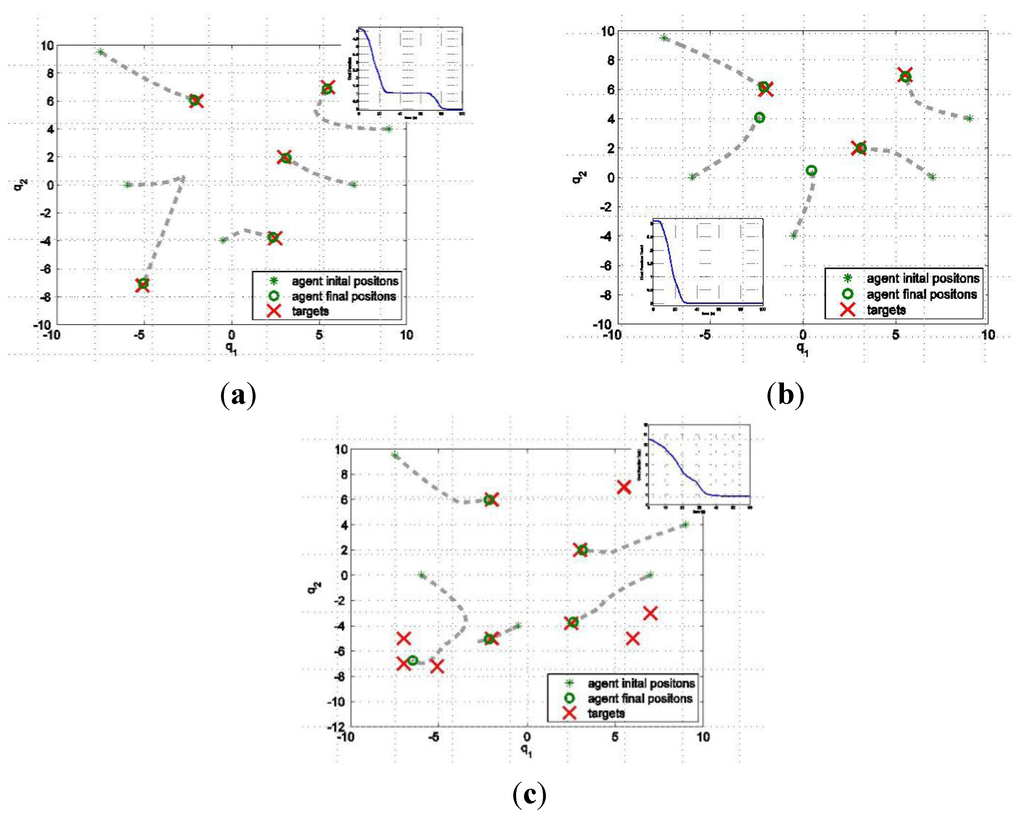
Figure 4.
(a) Five agents and five target assignments. (b) Five agents and three target assignments. (c) Five agents and 10 target assignments.
The plateau in the cost function between 12 and 24 s is due to the use of the Potential Field control by one agent (the one in the bottom left corner) while the other four agents are already covering the corresponding targets. After 24 s, the DF of this agent intersects the DF of the target, and the cost function decreases again.
Similar results are obtained if the number of the targets is less than the number of agents as shown in Figure 4b. In this simulation, the DFs of two targets are covered by two agents each. As expected, the final value of the cost function is 0. The behavior of the system in such situation depends on the initial position of the agents and on the position of the targets. Since no special target assignment rule is used, when N > Nw agents in excess may also stop without covering any target.
Figure 4c shows the trajectories of five agents, when 10 targets are present in the scenario. In this case, each agent is assigned to a target. The final value of the cost function is greater than zero since the DFs of the agents are not sufficient to cover the DFs of the targets, however all targets are covered. Again, in this example, no specific target priority was assigned, nor agents were required to cover all targets.
5.2. Example 2
This example highlights the improvement made by the switching control law over the Potential Field based controller. The latter controller weights the error over the whole environment, and it may force the agents towards unexpected or undesirable equilibrium configurations, due to asymmetries in the descriptor functions of agents and targets.
Consider a scenario composed of five agents and seven targets. All the agents and six of the targets are modeled with the descriptor function of Equation (17). The seventh target (bottom left corner) has a larger DF, indicating possibly a higher priority or a request of more resources, and given by Equation (20), with wi = [-5 -6]T
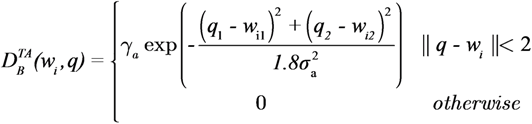
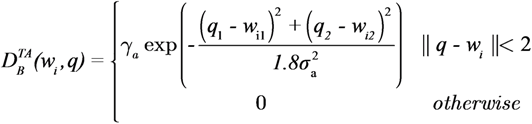
Full use of the potential field based controller produces the trajectories shown in Figure 5.
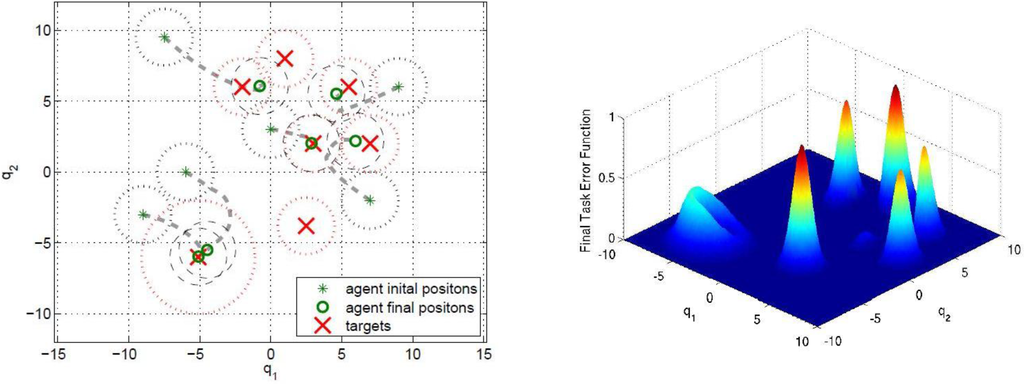
Figure 5.
Potential field controller performance (Example 2).
The agents get close but not sufficiently (for the requirements in the example) to the targets. The final shape of the task error function indicates a large remaining error not compensated by the assignment, and shown by the five multicolored peaks. The larger error peaks belong obviously to the two targets not covered by the agents.
The use of switching controller improves the overall scenario performance as shown in Figure 6. In this case in fact, four agents move to four of the six targets having the same priority (same DFs), while the two remaining agents cover the target with a large DF. The task error function now is sensibly reduced, and consists primarily of the lone two peaks associated with the two targets in excess. The global measure of performance is indicated in Figure 7. Here, the smoother decrease in overall cost is shown by the dashed line, as compared with the higher value of cost achievable with the potential field controller. Again, we remind the reader that this simple academic example did not require visiting all targets.
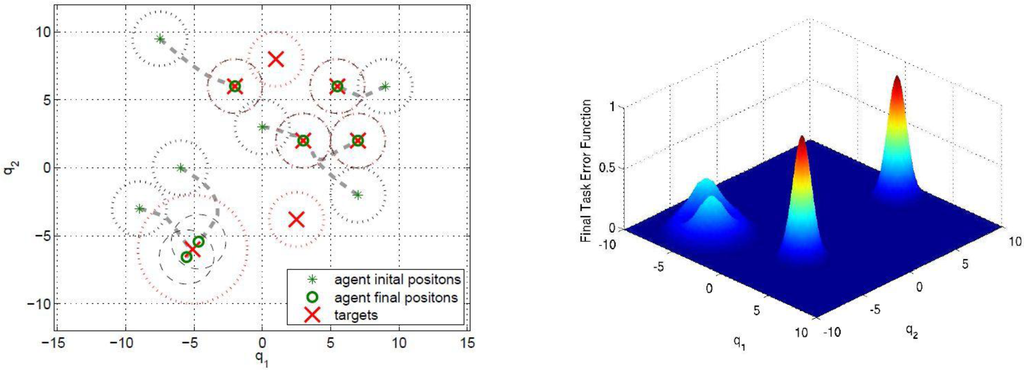
Figure 6.
Switching controller performance (Example 2).
Figure 7.
Cost function comparison (Example 2).
The real time implementation of the concepts presented in the paper, and described by the above examples, was partially performed with RC cars, and can be found in [38].
6. Conclusions
The paper presents the comparison of different controllers for the management of a swarm of vehicles using the descriptor function approach. The performance of the approach are evaluated in a simple task assignment scenario, and advantages and disadvantages of the proposed controllers evaluated. Future work will be directed towards formal decentralization and multi-tasking.
Acknowledgments
Mario Innocenti thanks the National Academies and the Air Force Research Laboratory, Munitions Directorate, Eglin AFB, Florida for their partial support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kennedy, J.; Eberhart, R.C. Swarm Intelligence; Academic Press: London, UK, 2001. [Google Scholar]
- Bonabeau, E.; Dorigo, M.; Theraulaz, G. Swarm Intelligence: From Natural to Artificial Systems; Oxford University Press: Oxford, NY, USA, 1999. [Google Scholar]
- Giulietti, F.; Pollini, L.; Innocenti, M. Autonomous formation flight. IEEE Control Syst. 2000, 20, 34–44. [Google Scholar] [CrossRef]
- Giulietti, F.; Innocenti, M.; Napolitano, M.; Pollini, L. Dynamic and control issues of formation flight. Aerosp. Sci. Technol. 2005, 9, 65–71. [Google Scholar] [CrossRef]
- Olfati-Saber, R. Flocking for multi-agent dynamic systems: Algorithms and theory. IEEE Trans. Autom. Control 2006, 51, 401–420. [Google Scholar] [CrossRef]
- Bracci, A.; Innocenti, M.; Pollini, L. Cooperative Task Assignment Using Dynamic Ranking. In Proceedings of the 17th IFAC World Congress, Seoul, Korea, 6–11 July 2008.
- Clerc, M. Particle Swarm Optimization; ISTE Ltd.: London, UK, 2005. [Google Scholar]
- Bullo, F.; Cortés, J.; Martínez, S. Distributed Control of Robotic Net-Works; Applied Mathematics Series; Princeton University Press: Princeton, NJ, 2008. [Google Scholar]
- Beard, R.L.; Ren, W. Distributed Consensus in Multi Vehicle Cooperative Control; Springer-Verlag: London, UK, 2008. [Google Scholar]
- Freeman, R.A.; Yang, P.; Lynch, K.M. Distributed Estimation and Control of Swarm Formation Statistics. In Proceedings of the American Control Conference, Minneapolis, MN, USA, June 2006. [CrossRef]
- Munkres, J. Algorithms for the assignment and transportation problems. SIAM J. 1957, 5, 32–38. [Google Scholar]
- Schouwenaars, T.; DeMoor, B.; Feron, E.; How, J. Mixed Integer Linear Programming for Multi-Vehicle Path Planning. In Proceedings of the European Control Conference 2001, Porto, Portugal, 4–7 September 2001; pp. 2603–2608.
- Reynolds, C. Flocks, herds, and schools: A distributed behavioral model. Comput. Graph. 1987, 21, 25–34. [Google Scholar] [CrossRef]
- Giulietti, F.; Pollini, L.; Innocenti, M. Formation Flight: A Behavioral Approach. In Proceedings of the AIAA Guidance, Navigation, and Control, Montreal, QC, Canada, 6–9 August 2001. [CrossRef]
- Passino, K.M. Biomimicry for Optimization, Control, and Automation; Springer-Verlag: London, UK, 2005. [Google Scholar]
- Passino, K.M. Stability analysis of swarms. IEEE Trans. Autom. Control 2003, 48, 692–697. [Google Scholar]
- Tanner, H.G.; Jadbabaie, A.; Pappas, G.J. Stable Flocking of mobile Agents, Part I: Fixed Topology. In Proceedings of the IEEE Control and Decision Conference, Maui, HI, USA, 9–12 December 2003. [CrossRef]
- Tanner, H.G.; Jadbabaie, A.; Pappas, G.J. Stable Flocking of mobile Agents, Part II: Dynamic Topology. In Proceedings of the IEEE Control and Decision Conference, Maui, HI, USA, 9–12 December 2003. [CrossRef]
- Ronchieri, E.; Innocenti, M.; Pollini, L. Decentralized Control of a Swarm of Unmanned Air Vehicles. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Hilton Head, SC, USA, 20–23 August 2007. [CrossRef]
- Hague, M.H.; Egerstedt, M.; Martin, C.F. First-Order Networked Control Models of Swarming Silkworm Moths. In Proceedings of the American Control Conference, Seattle, WA, USA, 11–13 June 2008. [CrossRef]
- De Groot, M.H. Reaching a consensus. J. Am. Stat. Soc. 1974, 69, 118–121. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Murray, R.M. Consensus problems in networks of agents with switching topology and time delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef]
- Jadbabaie, A.; Lin, J.; Morse, A.S. Coordination of groups of mobile autonomous agents using nearest neighbor rules. IEEE Trans. Autom. Control 2003, 48, 988–1001. [Google Scholar] [CrossRef]
- Cortes, J.; Bullo, F. Coordination and geometric optimization via distributed dynamical systems. SIAM J. Control Optim. 2005, 44, 1543–1574. [Google Scholar] [CrossRef]
- Muhammad, A.; Egerstedt, M. Connectivity graphs as models of local interactions. Appl. Math. Comput. 2005, 168, 243–269. [Google Scholar] [CrossRef]
- Ji, M.; Egerstedt, M. Distributed coordination control of multi-agent systems while preserving connectedness. IEEE Trans. Robot. 2007, 23, 693–703. [Google Scholar] [CrossRef]
- Belta, C.; Kumar, V. Abstractions and control for groups of robots. IEEE Trans. Robot. 2004, 20, 865–875. [Google Scholar] [CrossRef]
- Pimenta, L.C.; Nathan, M.; Mesquita, R.C. Control of Swarms Based on Hydrodynamic Models. In Proceedings of the IEEE Inter-national Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008.
- Jung, B.; Sukhatme, S.G. A Generalized Region-Based Approach for Multi-Target Tracking in Outdoor Environments. In Proceedings of the IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004; pp. 2189–2195.
- Rimon, E.; Koditschek, D. Exact robot navigation using artificial potential functions. IEEE Trans. Robot. Autom. 1992, 8, 501–518. [Google Scholar] [CrossRef]
- Leonard, N.; Lekien, F. Non-uniform coverage and cartograms. SIAM J. Control Optim. 2009, 48. [Google Scholar] [CrossRef]
- Niccolini, M.; Innocenti, M.; Pollini, L. Near Optimal Swarm Deployment Using Descriptor Functions. In Proceedings of the IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; Volume 1, pp. 4952–4957.
- Ferrari-Braga, A.; Innocenti, M.; Pollini, L. Multi-Agent Coordination with Arbitrarily Shaped Descriptor Functions. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Boston, MA, USA, 19–22 August 2013.
- Pollini, L.; Innocenti, M. A synthetic environment for dynamic systems control and distributed simulation. IEEE Control Syst. 2000, 20, 49–61. [Google Scholar] [CrossRef]
- Niccolini, M. Swarm Abstractions for Distributed Estimation and Control. Ph.D. Dissertation, Department of Electrical Systems and Automation, University of Pisa, Pisa, Italy, July 2011. [Google Scholar]
- Brooks, R.A. Cambrian Intelligence: The Early History of the New AI; MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Murphy, R.R. Introduction to AI Robotics; MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Pollini, L.; Niccolini, M.; Rosellini, M.; Innocenti, M. Human-Swarm Interface for Abstraction Based Control. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Chicago, IL, USA, 10–13 August 2009.
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).