A Novel Map-Based Dead-Reckoning Algorithm for Indoor Localization
Abstract
:1. Introduction

2. Related Work
3. Step Counting Dead-Reckoning
3.1. Sensor’s Orientation Determination and Step Detection
3.2. Step Length Estimation and Step Direction Estimation
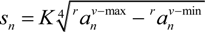
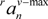 and
and 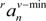 are the maximum and minimum values of its vertical components, respectively. K is a constant determined by training.
are the maximum and minimum values of its vertical components, respectively. K is a constant determined by training.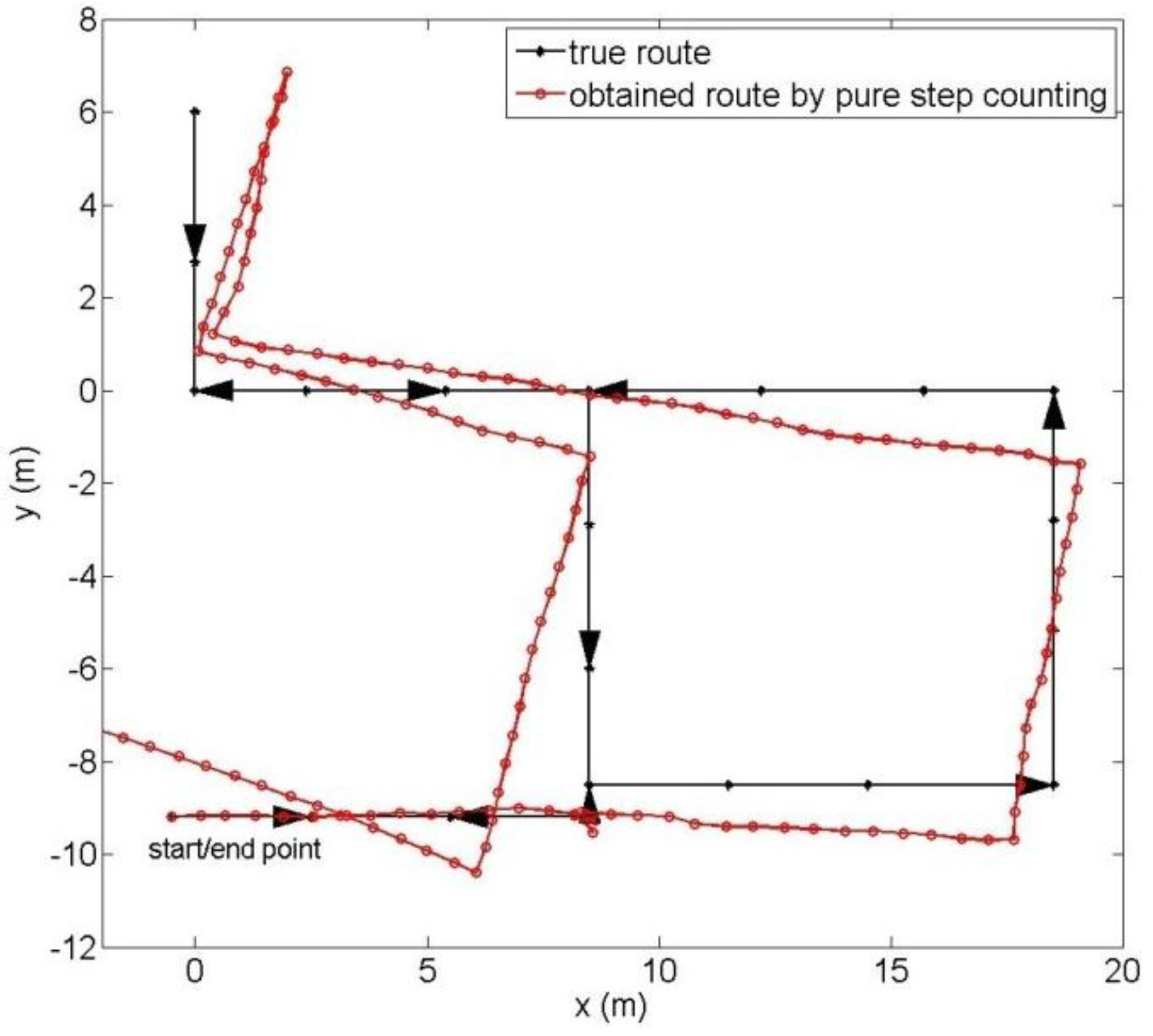
4. Particle Filter and Map Matching
4.1. Particle Filter
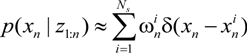
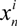 , i = 1,…, Ns} is a set of supporting particles at time n with the associated weights {
, i = 1,…, Ns} is a set of supporting particles at time n with the associated weights { 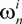 , i = 1,…, Ns}. Ns are set to 100 in our algorithm.
, i = 1,…, Ns}. Ns are set to 100 in our algorithm.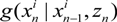 is the importance density.
is the importance density.
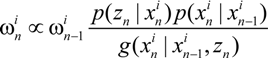
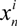 =
= 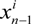 + sndn +
+ sndn + 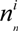
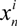 and
and 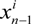 are the 2D states after n steps and n − 1 steps, respectively, and sn and dn are step-n’s length and direction, respectively.
are the 2D states after n steps and n − 1 steps, respectively, and sn and dn are step-n’s length and direction, respectively. 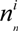 is a random variable with Gaussian distribution.
is a random variable with Gaussian distribution.
4.2. Map Matching
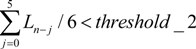 .
.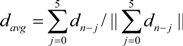 should meet ||dot(davg, dc)|| < threshold_3, where dot(.) means the dot product.
should meet ||dot(davg, dc)|| < threshold_3, where dot(.) means the dot product.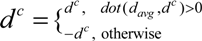
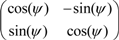 , and the rectified directions {
, and the rectified directions { 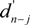 , j = 0, 1,… Nt − 1} are solved using:
, j = 0, 1,… Nt − 1} are solved using:
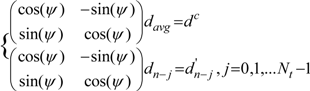
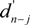 , j = Nt − 1,…, 1, 0
, j = Nt − 1,…, 1, 0
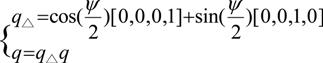

4.3. Particle Filter + Map Matching
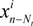 ) are regenerated with the mean xc, n−Nt.
) are regenerated with the mean xc, n−Nt.
5. Improved Particle Filter
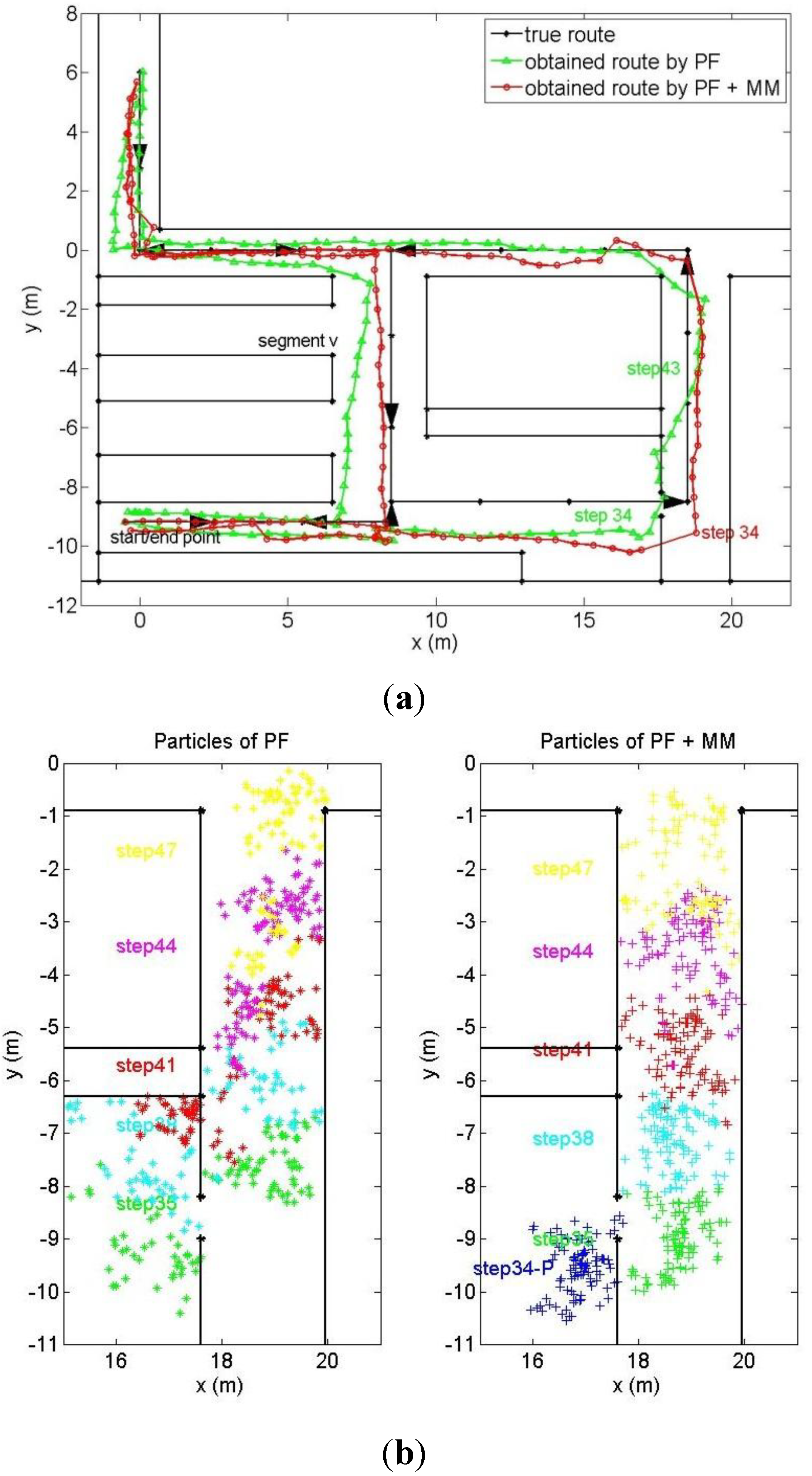
 and n
and n 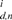 represent the noise in length and direction estimation, respectively. b
represent the noise in length and direction estimation, respectively. b 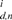 is to compensate the direction estimation drift for particle i in step n, which will be explained later.
is to compensate the direction estimation drift for particle i in step n, which will be explained later.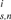 and n
and n 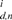 are set as Gaussian variables with small variance. Suppose, initially, the direction estimation is accurate, so that
are set as Gaussian variables with small variance. Suppose, initially, the direction estimation is accurate, so that 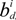 1 = 0. b
1 = 0. b 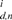 is updated as follows:
is updated as follows:
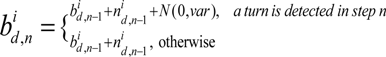
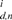 and n
and n 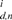 . The choice of its value is further refined by the pattern that large uncertainty occurs during turning. In this way, this model describes the pedestrian walk better than the previous one. Impossible paths, as well as erroneous directions can be eliminated in this algorithm.
. The choice of its value is further refined by the pattern that large uncertainty occurs during turning. In this way, this model describes the pedestrian walk better than the previous one. Impossible paths, as well as erroneous directions can be eliminated in this algorithm. 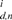 estimation in the direction estimation and retains the correct ones. Compared to the MM algorithm, the improved PF rectifies the direction estimation without specifically defining the corridors. Its CPU cost is the same as the original PF, which is less than the MM-enabled PF algorithm.
estimation in the direction estimation and retains the correct ones. Compared to the MM algorithm, the improved PF rectifies the direction estimation without specifically defining the corridors. Its CPU cost is the same as the original PF, which is less than the MM-enabled PF algorithm.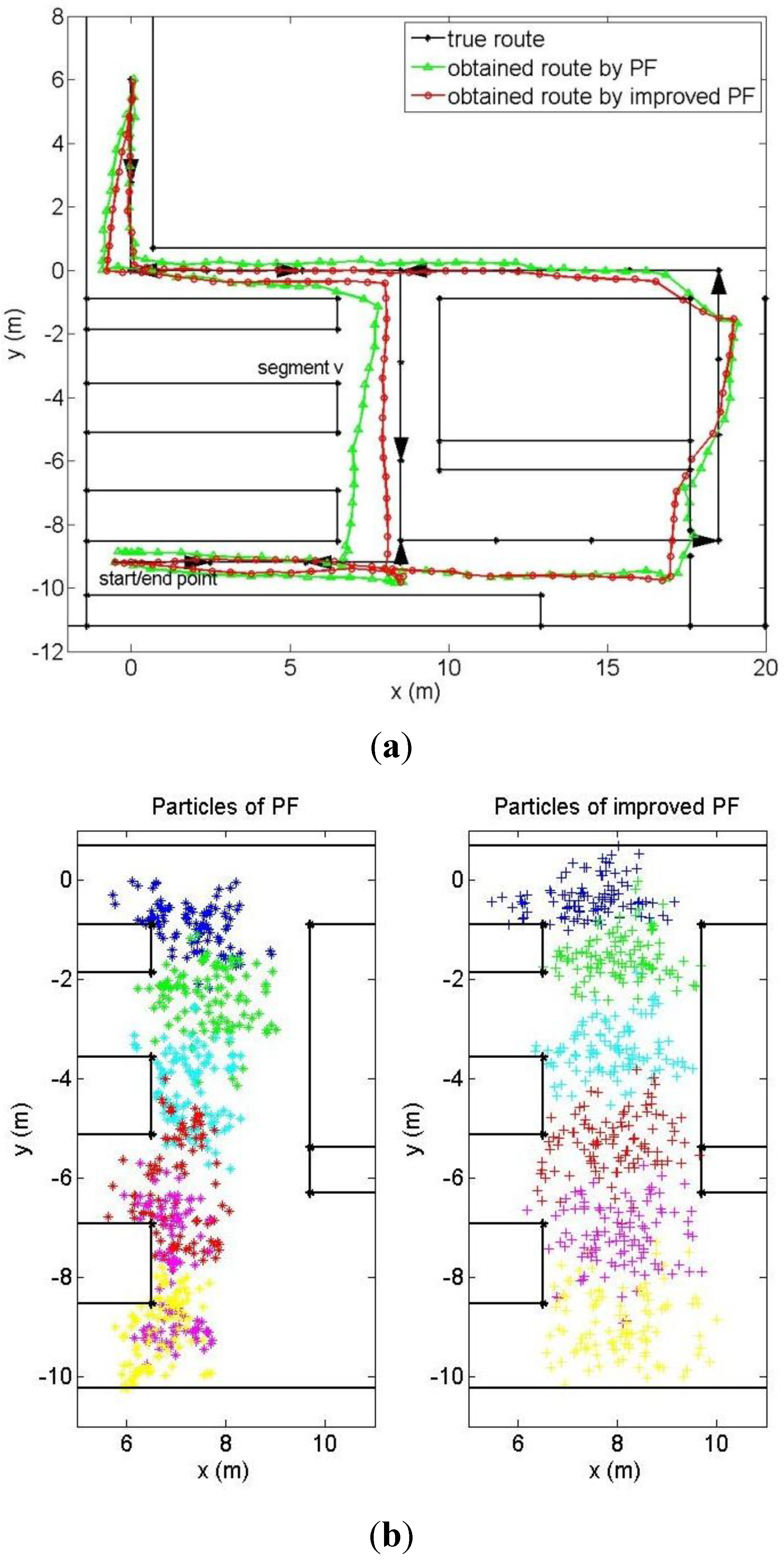
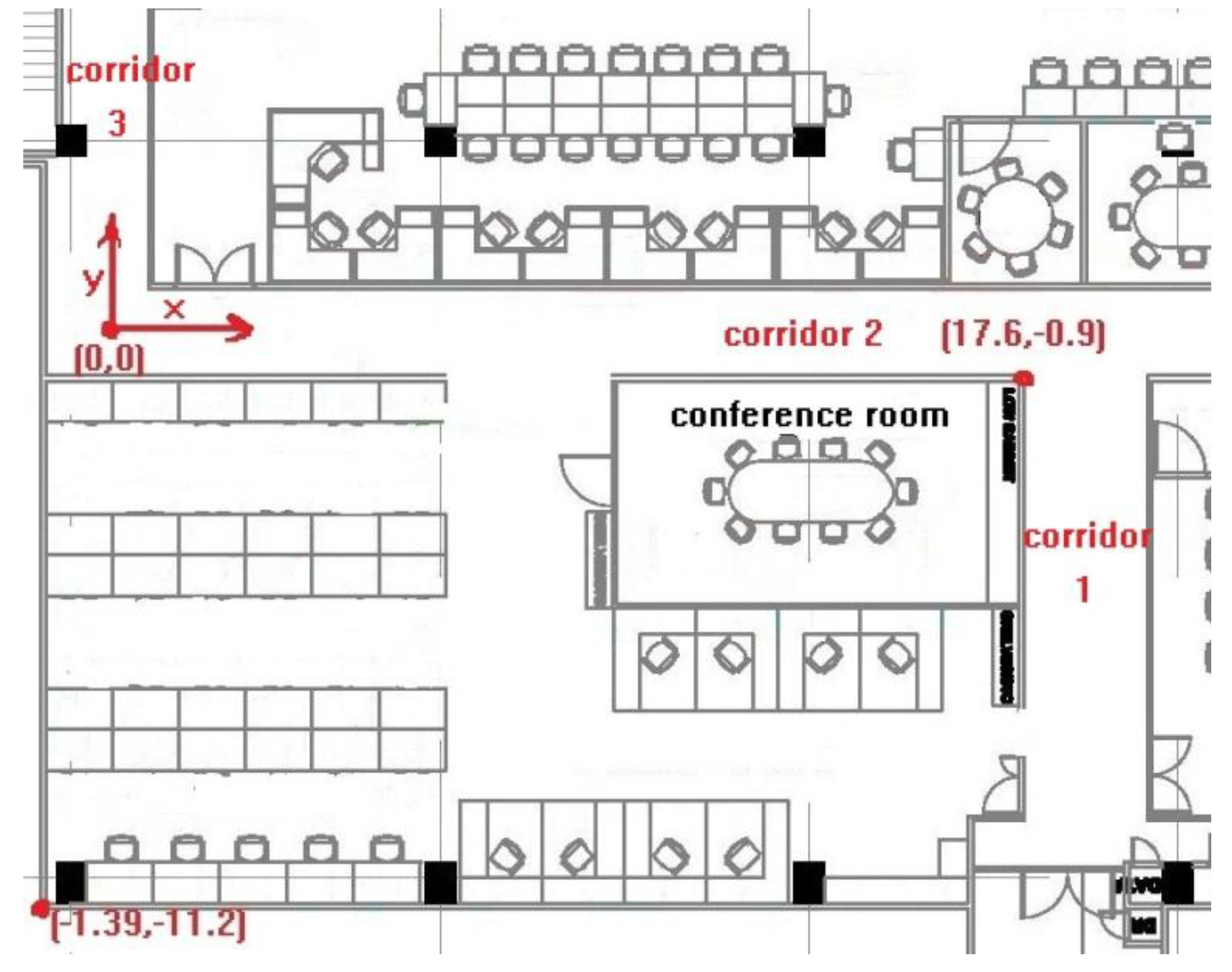
6. Evaluation
6.1. Performance on Full Map Information
| Applied Methods | Average Error (m) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Avg | |
| Step counting | 1.31 | 1.16 | 1.22 | 1.63 | 2.02 | 0.90 | 0.97 | 1.71 | 0.86 | 2.03 | 1.38 |
| PF | 1.04 | 0.82 | 0.77 | 0.86 | 0.60 | 1.46 | 0.73 | 1.09 | 0.68 | 0.72 | 0.88 |
| MM | 0.49 | 0.59 | 0.62 | 0.44 | 0.41 | 0.65 | 0.70 | 0.83 | 0.69 | 0.60 | 0.60 |
| PF + MM | 0.68 | 0.67 | 0.61 | 0.68 | 0.68 | 0.75 | 0.60 | 0.86 | 0.88 | 0.77 | 0.72 |
| Improved PF | 0.62 | 0.41 | 0.56 | 0.47 | 0.58 | 0.56 | 0.39 | 0.75 | 0.51 | 0.68 | 0.55 |
| Applied Methods | Average Error (m) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Avg | |
| Step counting | 1.71 | 1.10 | 0.95 | 1.47 | 1.15 | 1.11 | 1.36 | 1.32 | 1.25 | 1.56 | 1.30 |
| PF | 0.94 | 0.84 | 0.93 | 0.94 | 1.57 | 0.81 | 0.91 | 1.01 | 1.00 | 1.06 | 1.00 |
| MM | 0.75 | 0.58 | 0.86 | 1.09 | 1.52 | 0.65 | 0.61 | 0.73 | 1.01 | 0.85 | 0.87 |
| PF + MM | 0.48 | 0.72 | 0.78 | 1.14 | 1.27 | 0.50 | 0.58 | 0.72 | 0.86 | 0.75 | 0.78 |
| Improved PF | 0.97 | 0.68 | 0.74 | 1.15 | 1.37 | 0.75 | 0.84 | 0.73 | 0.97 | 1.12 | 0.93 |
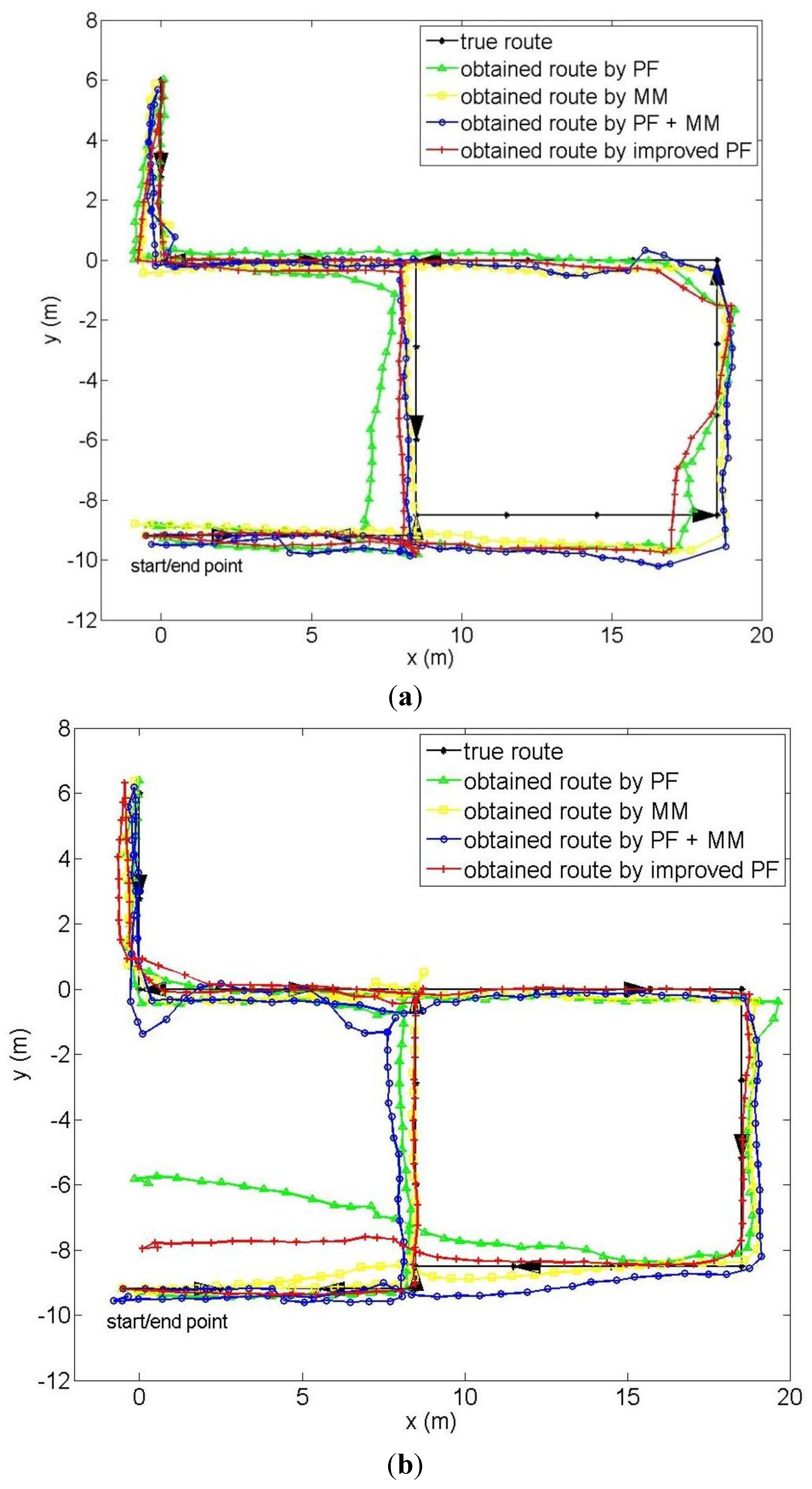
6.2. Performance on Incomplete Map Information

| Applied Methods | Average Error (m) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Step counting | 1.31 | 1.16 | 1.22 | 1.63 | 2.02 | 0.90 | 0.97 | 1.71 | 0.86 | 2.03 |
| PF | 1.78 | 1.28 | 1.54 | 1.46 | 1.09 | 1.22 | 1.00 | 1.30 | 1.68 | 1.21 |
| MM | 0.96 | 1.22 | 1.07 | 1.90 | 2.17 | 1.08 | 0.92 | 1.64 | 0.90 | 1.80 |
| PF + MM | 1.65 | 1.22 | 1.42 | 1.20 | 0.86 | 1.38 | 1.38 | 1.24 | 1.28 | 1.24 |
| Improved PF | 1.25 | 1.02 | 1.27 | 1.07 | 0.99 | 1.07 | 1.12 | 0.99 | 1.00 | 1.14 |
| Applied Methods | Average Error (m) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Step counting | 1.71 | 1.10 | 0.95 | 1.47 | 1.15 | 1.11 | 1.36 | 1.32 | 1.25 | 1.56 |
| PF | 1.90 | 1.06 | 1.54 | 1.41 | 1.56 | 1.70 | 1.24 | 1.78 | 1.61 | 1.75 |
| MM | 1.03 | 1.65 | 1.05 | 1.47 | 1.36 | 0.86 | 2.01 | 0.75 | 0.99 | 0.99 |
| PF + MM | 2.00 | 0.81 | 1.62 | 1.47 | 1.63 | 1.74 | 0.83 | 1.61 | 1.83 | 1.79 |
| Improved PF | 1.62 | 0.77 | 1.21 | 1.07 | 1.28 | 1.52 | 0.86 | 1.06 | 1.27 | 1.37 |
| Applied Methods | Average Error (m) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Step counting | 1.31 | 1.16 | 1.22 | 1.63 | 2.02 | 0.90 | 0.97 | 1.71 | 0.86 | 2.03 |
| PF | 1.75 | 1.48 | 1.64 | 2.08 | 1.74 | 1.19 | 1.43 | 1.93 | 1.55 | 1.90 |
| MM | 2.32 | 0.92 | 1.80 | 0.55 | 1.09 | 0.84 | 0.97 | 1.10 | 1.91 | 0.95 |
| PF + MM | 1.80 | 1.01 | 1.36 | 0.89 | 0.87 | 1.05 | 1.17 | 1.13 | 1.62 | 1.05 |
| Improved PF | 1.57 | 0.70 | 0.92 | 1.09 | 1.64 | 1.07 | 1.24 | 1.52 | 1.15 | 1.38 |
| Applied Methods | Average Error (m) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Step counting | 1.71 | 1.10 | 0.95 | 1.47 | 1.15 | 1.11 | 1.36 | 1.32 | 1.25 | 1.56 |
| PF | 1.38 | 1.29 | 0.88 | 1.45 | 1.48 | 1.21 | 1.03 | 1.37 | 1.21 | 1.26 |
| MM | 1.41 | 0.77 | 1.03 | 1.29 | 1.31 | 0.97 | 1.01 | 1.43 | 1.14 | 1.84 |
| PF + MM | 1.41 | 0.65 | 1.04 | 0.99 | 1.54 | 1.44 | 0.87 | 1.35 | 1.10 | 1.67 |
| Improved PF | 1.58 | 1.26 | 0.91 | 1.49 | 1.43 | 1.19 | 1.21 | 0.89 | 1.14 | 1.31 |
| Average Over | Error for Applied Methods (m) | ||||
|---|---|---|---|---|---|
| Step Counting | PF | MM | PF + MM | Improved PF | |
| Map 1 | 1.34 | 1.46 | 1.29 | 1.41 | 1.15 |
| Map 2 | 1.34 | 1.46 | 1.23 | 1.20 | 1.23 |
| Overall | 1.34 | 1.46 | 1.26 | 1.31 | 1.19 |
7. Conclusion
Acknowledgments
Conflicts of Interest
References
- Otsason, V.; Varshavsky, A.; LaMarca, A.; Lara, E.D. Accurate GSM Indoor Localization. In Proceedings of the International Conference on Ubiquitous Computing, Tokyo, Japan, 11–14 September 2005; pp. 141–158.
- Manodham, T.; Loyola, L.; Miki, T. A novel wireless positioning system for seamless internet connectivity based on the WLAN infrastructure. Wirel. Pers. Commun. 2008, 44, 295–309. [Google Scholar] [CrossRef]
- Lin, H.H.; Tsai, C.C.; Hsu, J.C. Ultrasonic localization and pose tracking of an autonomous mobile robot via fuzzy adaptive extended information filtering. IEEE Trans. Instrum. Meas. 2008, 57, 2024–2034. [Google Scholar] [CrossRef]
- Wendlandt, K.; Berbig, M.; Robertson, P. Indoor Localization with Probability Density Functions Based on BLUETOOTH. In Proceedings of the IEEE International Symposium on Personal Indoor and Mobile Radio Communications, Berlin, Germany, 11–14 September 2005; pp. 2040–2044.
- Jin, Y.; Toh, H.; Soh, W.S.; Wong, W.C. A Robust Dead-Reckoning Pedestrian Tracking System with Low Cost Sensors. In Proceedings of the IEEE International Conference on Pervasive Computing and Communications, Seattle, WA, USA, 21–25 March 2011; pp. 222–230.
- Kourogi, M.; Kurata, T. Personal Positioning Based on Walking Locomotion Analysis with Self-Contained Sensors and a Wearable Camera. In Proceedings of the 2nd IEEE and ACM International Symposium on Mixed and Augmented Reality, Tokyo, Japan, 7–10 October 2003; pp. 103–112.
- Ladetto, Q. On Foot Navigation: Continuous Step Calibration Using both Complementary Recursive Prediction and Adaptive Kalman Filtering. In Proceedings of the ION GPS 2000, Salt Lake, UT, USA, 19–22 September 2000; pp. 1735–1740.
- Kim, J.W.; Jang, H.J.; Hwang, D.H.; Park, C. A Step, Stride and Heading Determination for the Pedestrian Navigation System. In Proceedings of the International Symposium on GNSS/GPS, Sydney, Australia, 6–8 December 2004.
- Krach, B.; Roberston, P. Cascaded Estimation Architecture for Integration of Foot-Mounted Inertial Sensors. In Proceedings of the 2008 IEEE/ION Position Location and Navigation Symposium, Monterey, CA, USA, 5–8 May 2008; pp. 112–119.
- Klepal, M.; Beauregard, S. A Backtracking Particle Filter for Fusing Building Plans with PDR Displacement Estimates. In Proceedings of the 5th Workshop on Positioning Navigation and Communication, Hannover, Germany, 27 March 2008; pp. 207–212.
- Afzal, M.H.; Renaudin, V.; Lachapelle, G. Use of earth’s magnetic field for mtigating gyroscope errors regardless of magnetic perturbation. Sensors 2011, 11, 11390–11414. [Google Scholar] [CrossRef]
- Afzal, M.H.; Renaudin, V.; Lachapelle, G. Assessment of Indoor Magnetic Field Anomalies Using Multiple Magnetometers. In Proceedings of the ION GNSS 2010, Session F1. Portland, OR, USA, 21–24 September 2010.
- ADIS16400/16405 Data Sheet. Available online: http://www.analog.com/static/imported-files/data_sheets/ADIS16400_16405.pdf (accessed on 10 December 2013).
- Ichikawa, F.; Chipchase, J.; Grignani, R. Where’s the Phone? A Study of Mobile Phone Location in Public Spaces. In Proceedings of the 2nd International Conference Mobile Technology Applications and Systems, Guangzhou, China, 15–17 November 2005; p. 142.
- Lee, S.W.; Mase, K. Activity and location recognition using wearable sensor. IEEE Pervasive Comput. 2002, 1, 24–32. [Google Scholar] [CrossRef]
- Roetenberg, D.; Slycke, P.J.; Veltink, P.H. Ambulatory position and orientation tracking fusing magnetic and inertial sensing. IEEE Trans. Biomed. Eng. 2007, 54, 883–890. [Google Scholar] [CrossRef]
- Alvarez, D.; Gonzalez, R.C.; Lopez, A.; Alvarez, J.C. Comparison of step length estimators from wearable accelerometer devices. Int. Conf. IEEE Eng. Med. Biol. Soc. 2006, 1, 5964–5967. [Google Scholar]
- Blanke, U.; Schiele, B. Sensing Location in the Pocket. In Proceedings of Ubiquitous Computing 2008, Seoul, Korea, 21–24 September 2008.
- Steinhoff, U.; Schiele, B. Dead Reckoning from the Pocket—An Experimental Study. In Proceedings of the 8th Annual IEEE International Conference in Pervasive Computing and Communications, Mannheim, Germany, 29 March–2 April 2010; pp. 162–170.
- Kunze, K.; Lukowicz, P.; Partridge, K.; Begole, B. Which Way Am I Facing: Inferring Horizontal Device Orientation from an Accelerometer Signal. In Proceedings of the International Symposium on Wearable Computers, Linz, Austria, 4–7 September 2009; pp. 149–150.
- Jang, H.J.; Kim, J.W.; Hwang, D.H. Robust step detection method for pedestrian navigation systems. Electron. Lett. 2007, 43. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Q.; Lu, S.; Lu, H. A New Method of Double Electric Compass for Localization in Automobile Navigation. In Proceedings of the 2006 IEEE International Conference on Mechatronics and Automation, Luoyang, China, 25–28 June 2006; pp. 514–519.
- Roetenberg, D.; Luinge, H.J.; Baten, C.T.M.; Veltink, P.H. Compensation of magnetic disturbances improves inertial and magnetic sensing of human body segment orientation. IEEE Trans. Neural Syst. Rehabil. Eng. 2005, 13, 395–405. [Google Scholar] [CrossRef]
- Roetenberg, D.; Baten, C.T.M.; Veltink, P.H. Estimating body segment orientation by applying inertial and magnetic sensing near ferromagnetic materials. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 469–471. [Google Scholar] [CrossRef]
- Kemppi, P.; Rautiainen, T.; Ranki, V.; Belloni, F.; Pajunen, J. Hybrid Positioning System Combining Angle-Based Localization, Pedestrian Dead Reckoning and Map Filtering. In Proceedings of the 2010 International Conference on Indoor Positioning and Indoor Navigation, Zurich, Switzerland, 15–17 September 2010; pp. 1–7.
- Davidson, P.; Collin, J.; Takala, J. Application of Particle Filters for Indoor Positioning Using Floor Plans. In Proceedings of the Ubiquitous Positioning Indoor Navigation and Location Based Service, Kirkkonummi, Finland, 14–15 October 2010; pp. 1–4.
- Vildjiounaite, E.; Malm, E.J.; Kaartinen, J.; Alahuhta, P. Location Estimation Indoors by Means of Small Computing Power Devices, Accelerometers, Magnetic Sensors, and Map Knowledge. In Pervasive Computing; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2414, pp. 211–224. [Google Scholar]
- Spassov, I.; Bierlaire, M.; Merminod, B. Map Matching for Pedestrians via Bayesian Inference. In Proceedings of the European Navigation Conference—Global Navigation Satellite Systems, Manchester, UK, 7–10 May 2006.
- Quddusa, M.A.; Ochiengb, W.Y.; Nolandb, R.B. Current map-matching algorithms for transport applications: State-of-the art and future research directions. Transp. Res. Part C Emerg. Technol. 2007, 15, 312–328. [Google Scholar] [CrossRef]
- Bao, H.; Wong, W.C. An Indoor Dead-Reckoning Algorithm with Map Matching. In Proceedings of the IEEE International Wireless Communications and Mobile Computing Conference, Cagliari, Italy, 1–5 July 2013; pp. 1534–1539.
- Yun, X.; Bachmann, E.R.; McGhee, R.B. A simplified quaternion-based algorithm for orientation estimation from earth gravity and magnetic field measurements. IEEE Trans. Instrum. Meas. 2008, 57, 638–650. [Google Scholar] [CrossRef]
- Choukroun, D.; Itzhack, I.Y.B.; Oshman, Y. Novel quaternion Kalman filter. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 174–190. [Google Scholar] [CrossRef]
- Bao, H.; Wong, W.C. Improved PCA Based Step Direction Estimation for Dead-Reckoning. In Proceedings of the 2nd International Workshop on Smart Sensor, Beijing, China, 10–12 October 2013.
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Bao, H.; Wong, W.-C. A Novel Map-Based Dead-Reckoning Algorithm for Indoor Localization. J. Sens. Actuator Netw. 2014, 3, 44-63. https://doi.org/10.3390/jsan3010044
Bao H, Wong W-C. A Novel Map-Based Dead-Reckoning Algorithm for Indoor Localization. Journal of Sensor and Actuator Networks. 2014; 3(1):44-63. https://doi.org/10.3390/jsan3010044
Chicago/Turabian StyleBao, Haitao, and Wai-Choong Wong. 2014. "A Novel Map-Based Dead-Reckoning Algorithm for Indoor Localization" Journal of Sensor and Actuator Networks 3, no. 1: 44-63. https://doi.org/10.3390/jsan3010044
APA StyleBao, H., & Wong, W.-C. (2014). A Novel Map-Based Dead-Reckoning Algorithm for Indoor Localization. Journal of Sensor and Actuator Networks, 3(1), 44-63. https://doi.org/10.3390/jsan3010044




