Abstract
Field sampling is an important way of collecting soil information for the modeling and evaluation steps during digital soil mapping (DSM). However, some predesigned samples may not be accessible in the field due to natural or anthropogenic reasons. Simply abandoning the inaccessible samples or casually selecting substitutes from other locations may affect the quality of the corresponding DSM. To address this issue, we propose a new method of dynamically recommending substitute locations for inaccessible samples, which was implemented in a prototype system on a smart phone platform. The proposed method takes into concern the original sampling strategy and recommends substitute sample locations based on a measure of suitability index. The suitability index is calculated to incorporate a substitutive degree as well as the sampling cost involved. The substitutive degree depicts to what extent a substitute location may replace the original sample in the context of soil mapping, while the sampling cost characterizes the travel expense to the substitute location following the overall fieldwork route arrangements. The proposed method currently supports four commonly used sampling strategies, i.e., simple random sampling, stratified random sampling, grid sampling, and purposive sampling based on environmental similarity. Two substitute sampling scenarios, instant sampling and subsequent sampling, are considered by the proposed method, to adapt to surveyors’ actual field sampling route arrangements when estimating the accessibility and sampling cost of potential substitute locations. Monte Carlo simulation experiments in a study area (about 5800 km2) located in Anhui province of China were conducted to use the proposed method to recommend substitute locations for two modeling sample sets designed based on purposive sampling strategy and stratified random sampling strategy respectively (59 points for each set) from other 224 previously obtained samples. Experimental results evaluated based on 57 independent evaluation samples showed that the proposed method was able to recommend substitute locations without affecting the performance of DSM, when less than 10% samples were replaced by substitute samples. A subsequent sampling scenario was revealed to incur lower sampling cost than an instant sampling scenario.
1. Introduction
Detailed spatial soil information is a key input for applications and practices including watershed process simulation, soil pollution control, and precision agriculture. Currently, such information is mainly obtained through digital soil mapping (DSM), which uses soil sample data and environmental covariates data with predictive soil mapping models to infer soil distribution [1]. Field sampling is normally conducted at a set of predesigned locations based on a specific sampling strategy, such as simple or stratified random sampling, grid sampling, and purposive sampling based on environmental similarity [2,3,4,5]. Besides the factors considered by the sampling strategy (such as number, density, and representativeness of soil sample locations) [6,7,8], the completeness of collecting the predesigned locations in the field work directly affects the accuracy of DSM results.
It is often the case that during field sampling some predesigned samples are found to be inaccessible or uncollectible due to natural or anthropogenic reasons (such as inaccessible locations and land use change at the sample location). If these samples are simply discarded, the quality of the collected sample set may affect the performance of DSM. It is also very inefficient and costly to start another round of sampling design and field campaign. Even if it might be possible for another round, the same situation may still occur. Therefore, it is desirable to collect substitute samples at adequate locations in a timely manner.
Some studies proposed methods to address this issue during the indoor sample-design stage before a field campaign. Sample accessibility was considered as a factor to reduce the possibility of designing soil samples at inaccessible locations [9,10]. However, this method cannot eliminate such possibility completely due to the variability and complexity of the field in reality. Even if substitute locations can be prepared for all samples during the indoor sample-design stage [11,12], some substitute locations could also be inaccessible during the field campaign.
Dynamic recommendation of substitute locations for inaccessible soil samples during the field campaign guarantees the collection of necessary soil samples while in the field. Recently, Wei [13] proposed a method of recommending substitute sample locations specifically for purposive sampling based on environmental similarity [4,5,8,14] in the field. With his method, substitute sample locations are recommended to be those with the highest similarity to the uncollectible samples from the perspective of environmental conditions, as well as those with high accessibility from the field surveyor’s current location. This method mainly fits DSM applications with the purposive sampling strategy based on environmental similarity, such as the Soil Land Inference Model (SoLIM) [15]. Moreover, the method considers the accessibility and access cost of substitute locations only from the field surveyor’s current location, that is, the location of the inaccessible sample. Note that in real field campaigns that often last several days long, it may be more economical and feasible for the field surveyors to collect substitute samples close to other predesigned sample locations that may be planned to be collected later. Considering only the accessibility and cost from the current location of the field surveyor may not result in the best substitute locations.
To address the above issues, this paper proposes a method of dynamically recommending substitute locations for inaccessible soil samples during field sampling campaign. Substitute sample locations are recommended based on a suitability index measure considering both the substitutive degree and sampling cost. The proposed method supports different sampling strategies and can estimate the accessibility of substitute locations under different sampling scenarios (i.e., surveyors’ field sampling route arrangements). The detailed methodology is presented in Section 2. Section 3 summarizes the architecture of the prototype system implemented with the proposed method, and Section 4 details a validation experiment. The experiment results are presented and discussed in Section 5, and Section 6 draws the conclusion.
2. Design of the Proposed Method
When a predesigned sample location is deemed to be inaccessible in the field, locations nearby may be used to collect substitute samples, but each location bears a different degree to which it can represent the original sample based on the original sampling strategy. A central idea of our proposed method is to select substitute sample locations according to a suitability index considering both the substitutive degree and sampling cost. The substitutive degree is calculated as a substitutive score, while sampling cost is quantified to an accessibility score. Recommended substitute sample locations should incur low sampling cost or have high accessibility (such as short distance and ease for walking) following the field surveyors’ sampling plan. The sampling plan may collect substitute samples immediately after a sample is deemed inaccessible or postpone collection until a later time so that a substitute sample is collected adjacent to other remaining sample locations.
Based on the above idea, the proposed method consists of three main steps as follows.
2.1. Step 1: Selecting Potential Substitute Locations with High Substitutive Scores
The current method supports four commonly used sampling strategies for which substitute locations can be dynamically recommended in the field when a predesigned sample is inaccessible. They are simple random sampling, stratified random sampling, grid sampling, and purposive sampling based on environmental similarity (purposive sampling for short). The substitutive score is a value between 0 and 1, with 0 being the lowest degree and 1 being the highest substitutive degree. For different sampling strategies, the score is calculated as follows.
- Simple random sampling. If a sample location designed with simple random sampling was inaccessible, its substitute location should also be randomly selected. Thus, the proposed method randomly generates some potential substitute locations (different from those samples in the original sampling plan) in the study area, and assigns each with a substitutive score of 1 as they are equally substitutive. A buffer to other samples in the original sampling plan may be used to prevent the potential substitute locations from being unreasonably close to existing samples. Such a buffer restriction is also available for the rest four situations in this step.
- Stratified random sampling. For an inaccessible sample designed with stratified random sampling, its potential substitute locations should be randomly selected using the same stratifying factor (i.e., with the same class value of the stratified factor) as the inaccessible sample. These potential substitute locations are assigned with a substitutive score of 1.
- Grid sampling. For an inaccessible sample from grid sampling, its potential substitute locations are selected near the inaccessible sample, so that the layout of collected samples can still roughly fit the regular grid adopted in the original design of the grid sampling. It should be as close as possible to the inaccessible sample. The substitutive score of each potential substitute location is calculated as 1 minus the distance between the potential substitute location and the inaccessible sample divided by the grid size.
- Purposive sampling. Purposive sampling is to design samples based on samples’ representativeness of the geographic environment. Sample representativeness is often quantified based on the similarity of environmental conditions between the sample and other locations in the area [4,5,16]. Therefore, for an inaccessible sample from purposive sampling, the substitutive score of a potential substitute location is determined by its environmental similarity to the inaccessible sample. In our method, the environmental similarity is calculated as in Zhu et al. [17], which consists of three steps. The first step is to choose environmental covariates that closely relate to the spatial variation of soils in the study area. Then, the similarity of each individual environmental covariate between two locations (i.e., the inaccessible sample and one of its potential substitute locations) is calculated. If the covariate is nominal or ordinal, the similarity based on this covariate is either 1 or 0. If the covariate is interval or ratio, the similarity is calculated with a Gaussian-shaped curve [17,18]:where is the environmental similarity between two locations, and are the v-th environmental covariate values at location i and j respectively, and is the standard deviation of v-th environmental covariate in the study area. The width of the Gaussian-shaped curve is controlled by to ensure that the curve is reasonably spread over the value range of v-th environmental covariate. The Gaussian-shaped curve assigns high similarity to locations with close covariate values. Finally, the environmental similarity between two locations is assigned to be the minimum among all similarities based on individual environmental covariates, which is based on the limiting factor principle [17,19].
- Unknown or other possible sampling strategies. For other sampling strategies, the approach used to calculate the substitutive score for purposive sampling can be adopted as in Wei [13].
2.2. Step 2: Calculating the Accessibility Score for each Candidate Substitute Location
The accessibility score is calculated to reflect the sampling cost related to the difficulty to reach the target sample location. It is usually related to the terrain (such as slope), the type of land use (such as grassland, sparse woodland, bushland, and lake), and the distance to roads. It was quantitatively measured by indicators such as distance and cost [20]. The proposed method uses the least accumulative cost distance [21] to measure the sampling cost. Its calculation needs two layers, i.e., a source layer and a cost layer. The source layer marks the source locations where the least accumulated cost distance starts to accumulate, while the cost layer records the impedance or cost of moving through each cell.
For an inaccessible sample during the actual field campaign, the proposed method currently supports two scenarios for collecting substitute samples.
- The instant sampling scenario. This is when the surveyor plans to collect the substitute sample right away. A lower cost means a shorter distance from the surveyor’s current location to a substitutive location. Under this scenario, the proposed method uses the surveyor’s current location as the source position in the source layer to calculate accumulative costs. If the surveyor’s position is not available, the location of the inaccessible sample will be treated as the source location. Under this scenario, it is assumed that the surveyor would immediately request the substitute location to be identified when a predesigned sample was found to be inaccessible.
- The subsequent sampling scenario. This is when the surveyor plans to collect the substitute sample at a later time during collecting other remaining predesigned samples and not right away. Under this scenario, the big picture of the sampling progress will be considered. The proposed method uses the locations of all uncollected samples as potential sources in the source layer.
With the cost layer and the source layer for the user-assigned scenario, the proposed method calculates the minimum accumulative cost distance for every potential substitute location and normalizes it to be the accessibility score:
where Disti is the minimum accumulative cost distance for the i-th potential substitute location and Distmax is designed to be a constant for a particular study area with a specific cost layer:
where Height and Width are respectively the height and width of the study area, and is the average cost value over the study area. For a regular area, such Distmax is approximately the cost distance over half of the study area. A location with a cost distance over this value will not be considered as a potential substitute location due to its high sampling cost. The higher Ai, the easier it is to reach this potential substitute location.
2.3. Step 3: Recommending the Final Substitute Sample Location
Only those potential substitute locations with both scores higher than set thresholds are considered to be recommended to the surveyor. With the proposed method, the default threshold for accessibility score is 0.5. Locations scoring lower than 0.5 are considered comparatively inconvenient to collect samples considering time and financial budget. The default threshold of the substitutive score for purposive sampling is set to be 0.9 to guarantee that the substitute location bears significant high environmental similarity to the predesigned sample. For other sampling strategies, the threshold of the substitutive score is set to be 0.5 in operation. The reason is that with simple random sampling and stratified random sampling, the score is either 1 or 0, and a threshold of 0.5 is able to separate the suitable substitute locations from others. For grid sampling, setting the threshold to 0.5 means that substitute locations with distances more than half the grid size from the original sample locations are not deemed suitable to be substitute locations.
For each potential substitute location of an inaccessible sample, its substitutive score and accessibility score are integrated to form a quantitative suitability index to indicate its overall suitability. This is done by calculating the weighted average of the two individual scores. Currently, the proposed method uses equal weights for the two scores, assuming substitutability and accessibility are of equal importance in field survey, which may be adjusted for specific sampling applications if this assumption does not hold. Finally, the potential substitute locations of an inaccessible sample are sorted according to their suitability index values. The location(s) with the highest suitability will be recommended to surveyors as the substitute location(s) of an inaccessible sample.
3. The Prototype System
The proposed method was implemented in a prototype system on a mobile phone platform. The system consists of two components (Figure 1): The mobile terminal for user interface, and the server including a function module and a database module. The two components are connected using WebService for network communication. Through the mobile terminal, users can set all parameters in the proposed method, including marking the inaccessible sample and the collected samples, setting the scenarios for collecting the substitute samples, and modifying the thresholds and weights based on the actual situation. This architecture utilizes the portability of the mobile device and the powerful computing capability of the server to facilitate field surveyors’ flexible operation during the field campaign with guaranteed computation efficiency.
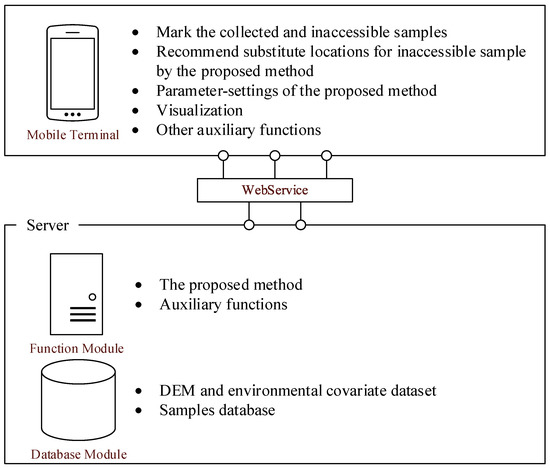
Figure 1.
The architecture of the prototype system.
4. Case Study
4.1. Study Area
The study area (Figure 2) is about 5800 km2, located in Xuancheng County in Anhui province, China. It lies in a transition zone between the mountainous southern Anhui and the middle and lower reaches of the Yangtze river. The northwestern part of the study area is plain, while the eastern and southern parts are low hills. The elevation in the area ranges from 5–825 m.
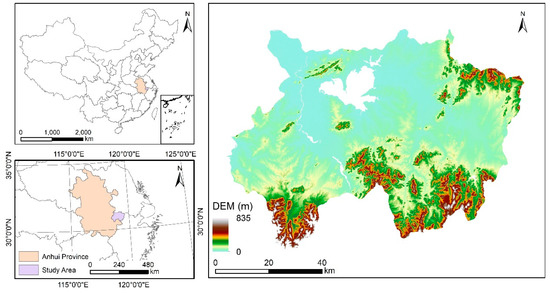
Figure 2.
Map of the study area.
4.2. Data Preparation
4.2.1. Environmental Covariate Data
In order to calculate the substitutive scores of potential substitute locations for the purposive sampling strategy, the environmental covariates need to be chosen based on knowledge of the soil-environment relationship in the study area. Based on understanding of the local soil-environment relationships and previous work in this study area [22], three types of environmental factors (parent material, topography, and climate) were considered and a total of eight environmental covariates (i.e., parent material, elevation, slope, planform curvature, profile curvature, topographic wetness index, annual average temperature, and annual average precipitation) were selected in this case study.
The parent material data for this area was rasterized from the 1:500,000 geological map of China. The digital elevation model (DEM) data for calculating topographic covariates was SRTM DEM with a resolution of 90 m (http://srtm.csi.cgiar.org/). Among the topographic variates used in this case study, the slope, planform curvature, and profile curvature were computed using the terrain analysis software 3DMapper (http://www.terrainanalytics.com), and the topographic wetness index was calculated with the algorithm proposed by Qin et al. [23]. The climate data (i.e., annual average temperature, and annual average precipitation) were obtained from the China Eco-Environment Database of the Chinese Academy of Agriculture Sciences. The spatial resolution adopted in this case study is 90 m.
4.2.2. Soil Sample Data
From previous field campaigns in the study area, we obtained a total of 399 soil samples (Figure 3). Among them, there are two complete sets of modeling samples for DSM used in previous studies, i.e., a set of 59 samples designed based on purposive sampling strategy with environmental similarity calculated from the above-mentioned environmental covariates (“purposive sample set,” for short) [22], and another set of 59 samples designed using stratified random sampling strategy stratified with the parent material variable (“stratified random sample set,” for short) [8]. Aside from these two sample sets, there are 57 samples designed using grid sampling strategy (“grid sample set,” for short) used as independent evaluation samples for evaluating DSM methods [24]. The other 224 samples (“mixed sample set,” for short) were collected during multiple field campaigns and originally used for testing other field sampling design and DSM methods [8,25]. The values (in the unit of %) of soil organic material (SOM) in the depth of 20—40 cm were recorded for all these soil samples and used as the target soil property in this experiment.
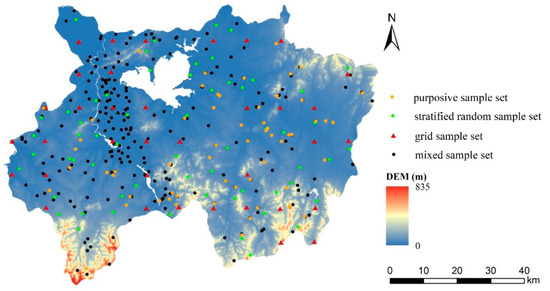
Figure 3.
Soil samples used in the case study.
4.2.3. Sampling Cost Layer
In this case study, we mainly considered the walking difficulty for preparing the sampling cost layer. Thus, the cost layer for calculating accessibility scores of potential substitute locations was prepared to integrate slope gradient and land use type. Different slope gradient range and land use type incur different cost values, as listed in Table 1 and Table 2. Specifically, the smaller the slope is, the easier it is for the surveyor to walk through, and land use types like grasslands and roads are easier to walk through than bushlands and lakes [20,26]. For a given cell, the sampling cost value was computed as the average of the cost incurred by slope gradient and that by land use. The slope data is the same as that used for the environmental covariates, and the land use type data was derived from the 1:100,000 land use map obtained from the Resource and Environmental Science Data Cloud Platform of Chinese Academy of Sciences.

Table 1.
The sampling cost value assigned corresponding to slope.

Table 2.
The sampling cost value assigned corresponding to land use types.
4.3. Experimental Design
Currently, the stratified random sampling and purposive sampling are the most commonly used sampling strategies in DSM [2,4,5,27]. Thus, our evaluation focuses on these two strategies to illustrate and evaluate the proposed method for recommending substitute sample locations.
In this case study, we made full advantage of those soil samples previously obtained in the study area instead of carrying out new field sampling. This was implemented by setting the locations with existing soil samples to be the only accessible area. When recommending substitute locations for the purposive sample set, for example, only locations of samples in the mixed sample set and stratified random sample set are considered as potential substitute locations. Substitute locations were then scored and ranked with the proposed method using default parameter settings. We should note that in such an experiment, the substitute locations recommended by the proposed method may not bare the highest suitability index value across the whole study area.
Results of the above experiment were evaluated in two aspects. The first examined the rationality and efficiency of the two sampling scenarios, i.e., instant sampling and subsequent sampling. The second was to evaluate the quality of the substitute locations recommended by the proposed method.
4.3.1. Evaluating Sampling Scenarios
In order to examine the rationality and efficiency of the two sampling scenarios supported by the proposed method, we simulated field campaigns during which some samples in the purposive sample set and stratified random sample set had been collected and the others had not yet. Then, a sample was randomly selected from those assumed-to-be-uncollected samples and was assumed to be inaccessible. Samples were then recommended at substitute locations under the instant and subsequent sampling scenarios, respectively. The resulting substitute locations under the two sampling scenarios, as well as their substitutive scores and accessibility scores, were compared and discussed.
4.3.2. Evaluating the Quality of Substitute Locations
In order to evaluate the quality of the substitute locations recommended by the proposed method, the purposive sample set and the stratified sample set were handled differently. For the purposive sample set, we analyzed the consistency between the soil-environmental relationship for DSM built with the original modeling sample set and that built with the sample set with some substitute samples. If the sample set with inaccessible samples were used as modeling sample set for DSM, the less difference between the substitute samples and the corresponding original samples in terms of soil property values, the more consistent the soil-environmental relationships. Therefore, the differences in the soil property (i.e., SOM in this case study) between the original samples and substitute samples were analyzed against the substitutive score level. In order to evaluate whether higher substitutive degree suggests higher consistency, all the potential substitutes are included in the comparison regardless of the substitutive score threshold.
Furthermore, two Monte Carlo simulation experiments were conducted to apply the proposed method to collecting modeling sample sets for DSM with both purposive sampling and stratified random sampling. The Monte Carlo simulation is based on the concept of multiple realizations [28] and simulates a set of input realizations for a model. Each of the simulated input realizations is a possible input for the model. The statistics of the model outputs corresponding to input realizations can be used as quantitative indicators of the performance of the model. For a DSM model using an input sample set, the effects of the input sample set with substitute samples can be evaluated through such Monte Carlo simulation experiments.
Taking the purposive sample set as an example, the proposed method under the instant sampling scenario was first applied to recommending substitute locations for each sample in the purposive sample set. Then, a few samples (varying from 1 to 10 in this experiment) in the original sample set were randomly selected to be assumed as inaccessible and replaced with substitute samples. Each time, a new sample set realization was created. Such sample set realizations were used as inputs to the individual predictive soil mapping model (iPSM) [17], a DSM model suitable for the samples from purposive sampling. The iPSM assumes that each soil sample can individually represent the locations with similar environmental conditions, thus can be used to predict the soil properties (i.e., the SOM in this case study) of these locations based on the environmental similarity:
where n’ is the number of soil samples with acceptable similarity values (i.e., higher than a threshold) to an unvisited location, is the environmental similarity between the unvisited location i and the soil sample location j, while and are the soil property values on i and j, respectively. The DSM output realizations (i.e., the resulting soil property maps) were then evaluated with evaluation indices such as Root Mean Squared Error (RMSE) with the independent samples from the grid sample set. This process was repeated for 100 times for each number of inaccessible samples (1–10). The quantitative indices from all realizations form a distribution, which can be compared with that from the original purposive sample set from a statistical perspective. The difference will reflect the effects that substitute locations cast on the accuracy of the DSM model. The iPSM can also calculate mapping uncertainty on each predicted cell [17]:
where are the similarities between the predicted location i and samples (1,2,…,n) used for predictive mapping with Equation (4). The mapping uncertainty quantifies the reliability of predictive mapping results and also provides a measure of the representativeness of the sample sets to the study area. Therefore, the uncertainty map realizations from sample set with substitutes will also be discussed.
In a similar way, the above Monte Carlo experiment was conducted on the stratified random sample set. The difference is that the DSM model was changed to multiple linear regression (MLR), which is commonly used in DSM [29,30]. RMSE was calculated as before to evaluate the DSM performance. As there is no prediction uncertainty map generated with MLR, we used the R-square of MLR to denote the fitness between samples and the MLR model. Moreover, the realizations of sample layout were evaluated whether the use of substitute locations can maintain the randomness of the stratified random sample set. For each realization of sample layout, the coefficient of variation (CV) was calculated by generating Voronoi tessellation polygons in the study area from the sample set [31]:
where is the standard deviation of the polygons’ areas and is the average area of the polygons. When samples are randomly distributed, the areas of Voronoi tessellation tend to be similar and the CV value is close to 0. When samples are with cluster distribution, the CV value is close to 1. Thus CV can be used to quantitatively denote the randomness of the sample layout [31].
5. Results and Discussion
5.1. The Two Sampling Scenarios in the Proposed Method
As outlined in Section 4.3.1, substitute sample locations were recommended for the purposive sample and stratified random sample sets (Figure 4, Table 3). In Figure 4, the triangle points are predesigned samples. The gray-colored points are those assumed to have been collected and green are not yet. Areas with different colors indicate different stratifications (parent material) in stratified random sampling. The selected inaccessible stratified random sample and its substitutes are colored in red and those with purposive sampling are in yellow. The star-shaped points are substitute locations recommended under the instant sampling scenario which appear closer to the original sample. The cross-shape points are recommended under the subsequent sampling scenario and thus show up near the not yet collected samples.
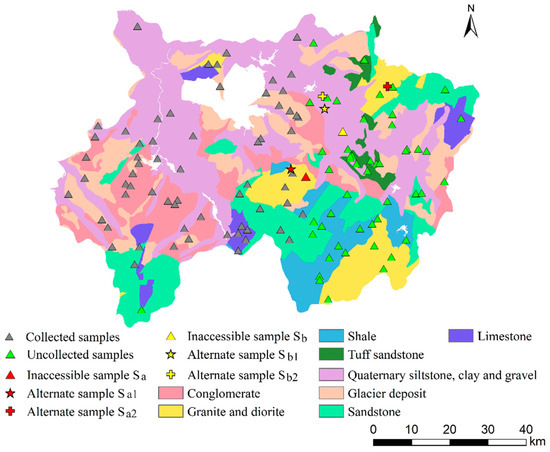
Figure 4.
Substitute locations recommended by the proposed method under two sampling scenarios. (The subscript letters a and b represent the stratified random sampling and purposive sampling, respectively; the subscript numbers 1 and 2 represent the instant sampling and subsequent sampling scenarios, respectively.).

Table 3.
The substitutive scores and accessibility scores of substitute locations under two sampling scenarios.
Table 3 indicates that the substitutive scores obtained in the two scenarios do not exhibit much difference, but the accessibility scores are higher in the subsequent sampling scenario, implying higher accessibility and, thus, lower sampling cost. A subsequent sampling strategy introduces more flexibility in a field campaign by recommending substitute locations with lower sampling cost when postponing the collection of substitute samples to when remaining samples are to be collected. The proposed method allows surveyors to interact with the substitute sampling design and choose the desirable sampling scenario to effectively reduce the sampling cost.
5.2. The Substitute Samples for Purposive Sampling
For the purposive sample set, only 38 of the original samples obtained satisfactory substitute locations due to the restricted default setting of substitutive score threshold and the limited number of potential substitute locations. The substitutive scores of the obtained substitute locations are distributed in the range of (0.90, 0.99) with an average value of 0.94. In the following sections, the substitute soil samples are evaluated in the aspects of sample deviation, mapping accuracy, and prediction uncertainty, respectively.
5.2.1. Sample Deviation
For each sample in the purposive sample set, we computed its substitutive score at every possible location and compared the SOM content deviations between the original samples and the substitute samples. There are, in total, 1978 entries with substitutive scores higher than 0. To reveal the patterns the deviations versus substitutive scores in such a large number of data points, a frequency distribution plot is shown in Figure 5. With the frequency plot, the horizontal axis is the ranges of SOM content deviations between substitutive samples and corresponding original samples, and the vertical axis is the frequency (or ratio) of the substitute samples within each of the SOM content deviation ranges as well as with a substitutive score range among all substitute locations with the substitutive score range. It appears that the substitute locations with lower substitutive scores generally have lower frequency on deviation groups with SOM content deviation lower than 6%. Meanwhile, on deviation groups with SOM content deviation higher than 9%, the substitute locations with lower substitutive scores tend to show a higher frequency than those with higher scores. This pattern indicates that substitute locations with higher substitutive scores are more likely to have lower SOM content deviation with the original samples. Less deviation on soil attributes indicates that the DSM model built with substitute samples is more similar to that built with original samples. Therefore, substitute locations with higher substitutive scores help approach the performance of the original DSM model with the original sample set. The existence of large SOM content deviations for some substitute samples with high substitutive scores might be attributed to that some of soil variation cannot be fully characterized by the dataset of environmental covariates used in this case study.
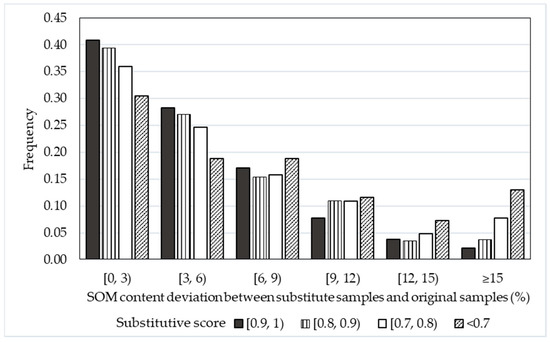
Figure 5.
The frequency of SOM content deviations in different ranges for substitute samples with varied substitutive scores.
5.2.2. Mapping Accuracy
Some examples of the resulting SOM content maps from the input realizations are shown in Figure 6. Figure 6 shows that the mapping results hold very similar spatial distribution when different numbers of original samples were substituted. Generally, the northwest area has lower SOM content and southeast shows higher SOM content. The highest SOM is seen in a small area at the southwest corner of the study area. The locations of these distinct parts are consistent across the different mapping results, though the precise predicted values of SOM content vary with input realizations. This illustrates that substitute locations recommended for different modeling samples by the proposed method can be used to build soil-environment relationships similar to that built with the original modeling sample set.

Figure 6.
Mapping results examples of SOM content with different substitute soil samples.
The RMSE distributions of the DSM realizations are shown in a boxplot in Figure 7. Figure 7 shows the change of RMSEs when the number of inaccessible predesigned samples replaced by recommended substitutes increases from 1 to 10. It is observed that the range of RMSE values, as well as the deviation from the original results, both increase when more substitutes are used. When the number of inaccessible samples is less than six (about 10% of the size of original sample set), the medians of RMSE remain close to the RMSE from the original sample set and most deviations of RMSE from that of original sample set are less than 0.2. As the number of inaccessible samples grows larger, the medians are parting from that of the original sample set and more outliers appear. This suggests that the substitute samples work well when there are not many inaccessible samples.
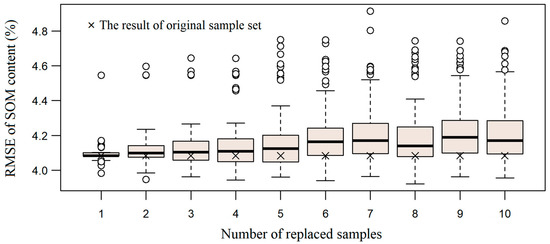
Figure 7.
RMSE of the SOM content (20-40 cm) mapping result using substitute soil samples for different numbers of inaccessible samples.
5.2.3. Prediction Uncertainty
The prediction uncertainties of the independent evaluation samples were calculated with iPSM and the sums of the uncertainty values of all 57 independent samples were plotted in the boxplots in Figure 8. Similar to RMSE, when the number of replaced samples increases, the uncertainty generally increases too. With less than six samples substituted, the medians of the uncertainty values are close to the mapping uncertainty of the original sample set. When the number of replaced samples increased to as many as 10, the deviation of the sum of uncertainties from that of original sample set is smaller than 0.4. Considering all 57 independent evaluation samples, the average uncertainty deviation for each sample is less than 0.007, which is rather trivial. When more substitute samples participate in predictive mapping, the overall representativeness of the sample set to the soil-environment relationship in the study area might decrease. This might be because the original purposive samples were designed to be the most representative [4,5,8]. The other possible reason is that, in this experiment, the proposed method only considered those locations with previously obtained samples for substitute location recommended, which might not be optimal. The decline in overall representativeness of sample set brings about the increase of prediction uncertainty in results of iPSM with such modeling sample set. The prediction uncertainty reflects the reliability of predicted SOM value, and explains the change of RMSE in Figure 6 as well: When mapping uncertainties increase, the mapping results are less accurate, thus higher RMSE. In this case study, the influences of substitute samples are in overall trivial when the number of inaccessible samples changes from one to 10, but are more insignificant when less than six substitute samples are used.
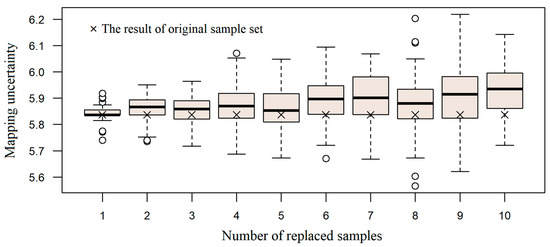
Figure 8.
Boxplot of summed mapping uncertainty values of independent evaluation soil samples for different numbers of inaccessible samples.
Previous research concerning DSM based on environmental similarity suggested that the predictive mapping results are comparatively reliable for areas with mapping uncertainties lower than 0.5 [5,8]. Thus, we calculated the percentage of predicted area with different uncertainty thresholds (i.e., 0.4, 0.3, and 0.2) for the DSM realizations. The results from input realizations with different number of inaccessible samples were compared with that from the original purposive sample set, that is, when the number of inaccessible samples being zero (Table 4). Low uncertainty indicates a prediction with confidence. Thus, the larger the area with low uncertainty, the more representative the sample set is of the study area. Table 4 shows that for the same threshold, as the number of replaced samples increases, the average percentage of predicted area declines. When the number is less than six, the declination is slighter, with declination for each increment lower than 0.1%. When the number continues to increase, the declination becomes more obvious, but all remain lower than 0.3%. This indicates that the use of substitute soil samples may slightly reduce the mapping area with low uncertainty, but the declination is trivial compared to the total mapping area, especially when replaced samples are less than six. In other words, the representativeness of the sample set to the study area is mildly impacted when substitute samples are used. This is because the predesigned samples were the optimal choices, while substitutes are suboptimal. It is also important to note that in this experiment, only those locations with previously obtained samples were considered as potential substitute locations by the proposed method due to the consideration of evaluation. This means some locations without samples existing, which should be recommended as the foremost substitute locations for those assumed-to-be-uncollected samples by the proposed method in real application, might be unnecessarily ignored in this experiment. In summary, we recognize that the least impact is achieved when the number of inaccessible samples is less than six in this case study.

Table 4.
Area percentages on the predictive mapping results under different uncertainty thresholds.
The results of the above experiments are all consistent. The analysis of sample deviations with regard to different substitutive score suggests that higher substitutive score means similar soil property. For the purpose of DSM, analyses of RMSE, prediction uncertainties, and mapping area with low uncertainty consistently indicate that when the number of inaccessible samples is less than six (or to say 10% of the size of the original sample set in this experiment), the mapping performances with substitute samples match that with the original purpose sample set.
5.3. Substitute Samples for Stratified Random Sampling
For the stratified random sample set containing 59 samples, a substitute soil sample was recommended for each original sample using the proposed method. As with the purposive sampling experiment, a few samples (varying from one to 10) in the original sample set were randomly selected to be assumed as inaccessible and replaced with substitute samples. With each number of inaccessible samples, 100 Monte Carlo realizations were used for DSM.
5.3.1. Sample Layout
Figure 8 shows the distribution of CVs of the resulting sample sets at different numbers of replaced samples. According to Duyckaerts and Godefroy [32], random distributions have CV between 33% and 64%, with a higher than 64% CV meaning the distribution closer to being clustered, while a CV lower than 33% suggesting regular distribution. Figure 9 shows that when the input realizations with the number of replaced samples changes from 1oneto 10, the CV varies between 46% and 51%, and centers around 48%. All decrease in the random distribution range. This indicates that for stratified random sampling, the use of substitute soil samples recommended with the proposed method does not change the distribution pattern and randomness of the original sample set.
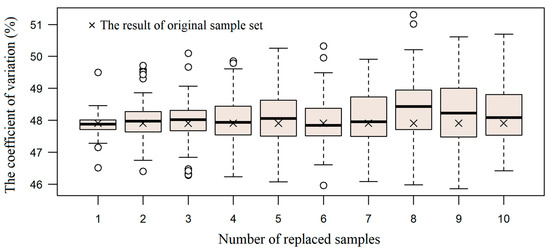
Figure 9.
The distribution of samples with substitute soil samples recommended by the proposed method introduced to the original sample set.
5.3.2. The Effect on Soil Mapping
DSM was conducted with MLR for each realization. The distribution of R-squares of the DSM results at different numbers of replaced samples are also shown in boxplots (Figure 10). Figure 10 shows that the R-square values fall in the range (0.27, 0.35), with the R-square from the original sample set being 0.30. For most cases, the R-square values lie evenly above and below that of the original set, indicating a random change in the model performance. From Figure 9, we can also see that when substitute samples are less than six, the decrease of R-square is less than 0.03 and the lower quartiles are above 0.30, meaning three-quarters of the results are over 0.30. The influence of substitute samples on the DSM model is comparatively small under this situation.
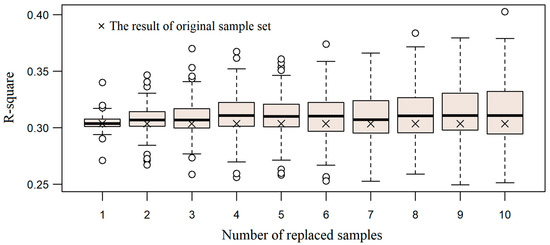
Figure 10.
Distribution of R-square values for SOM content (20–40 cm) mapping using substitute soil samples recommended by the proposed method.
The RMSE results of SOM content prediction is shown in Figure 11. The median values of RMSE for all numbers of substitute samples are fairly close to that of the original sample set. With less than six substitute samples, the RMSE values lie mostly in the range (4.6%, 5.4%), with the RMSE of original sample set being about 5.0%. The range of RMSE does appear larger when the number of substitute samples is greater than five. However, in most cases, the deviations are smaller than 0.6, and the RMSE results distribute evenly around that of the original sample set. This is in agreement previous findings on that substitute samples’ influences on DSM model performance relatively small when only a small number of samples are replaced.
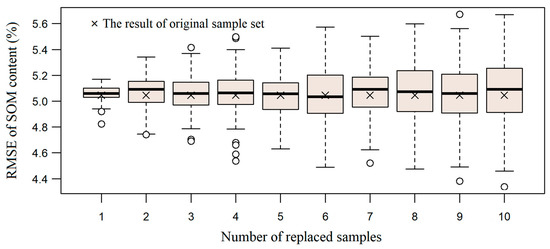
Figure 11.
RMSE values of the SOM content (20–40 cm) mapping result involving substitute soil samples recommended by the proposed method.
To summarize, findings from this experiment are that the use of substitute soil samples recommended by the proposed method for stratified random sampling shows very small influence on DSM mapping results in terms of sample distribution (CV), samples’ fitness with linear models (R-square) and mapping accuracy (RMSE). When the number of replaced samples are less than six (or to say 10% of the size of the original sample set in this experiment), the influence is trivial.
5.4. Further Discussion
In the proposed method, every sample location is assumed to be the center of the corresponding cell, which is in agreement with the restriction in existing soil sampling strategies and DSM methods. The spatial variation inside one single cell is ignored. When a predesigned sample location is inaccessible, the proposed method assumes that the area of the corresponding cell cannot be considered for substitute location recommendation in the field.
Another issue in the application of the proposed method, as well as other existing DSM-related methods based on soil-environment relationships, is the selection of environmental covariates and the preparation of environmental covariates dataset, which should be different among study areas and is often depended on the domain knowledge [1,16]. When the environmental covariates dataset adopted cannot well characterize the spatial variation of soil in the study area, the performance of the proposed method for recommending substitute locations based on environmental similarity will be impacted. In this case study, the environmental covariates adopted by the proposed method were selected based on the understanding of the local soil-environment relationships and previous work in the study area [22], which are the same as those adopted for designing original purposive sample set and stratified random sample set.
The proposed method is flexible to set the resist layer for calculating the accessibility scores of candidate substitute locations, according to user’s concern. More factors such as distance to roads can be included for preparing the resist layer. In the case study, the proposed method mainly considered the walking difficulty during the calculation of the accessibility score. According to previous researches [9,10,11,20,26], slope and land use type are among the factors that mainly contribute to walking difficulty. Thus, the resist layer was assigned with cost values according to slope and land use type. Note that the use of land use may cause a preference for urban land in substitute locations recommendation, which could bias the mapping results of soil properties. However, in the case study, the proposed method only considered those locations with previously obtained samples for substitute location recommended. The land use types of the soil sample locations considered in this experiment mainly consist of cropland (63%) and forest (28%). Most substitute locations recommended by the proposed method in the case study are located in cropland and forest as corresponding original samples are. Thus, there is a possible preference toward the above-mentioned due to the consideration of land use type for determining accessibility, which has little impact on the evaluation results in the case study.
6. Conclusions
This paper presents a new method to dynamically recommend substitute samples during field campaigns when predesigned samples are deemed inaccessible. It considers both the existing sampling strategy and the actual field work plan to compute and recommend substitute locations. A set of preliminary evaluation experiments with a prototype system in the Xuancheng study area shows that the proposed method has much flexibility and efficiency in actual field work. It is noted that the subsequent sampling scenario designed with this method can effectively reduce sampling cost at substitute locations. In the case of purposive sampling, the substitutive score computed by the proposed method is a sound measure of potential substitute locations’ substitutive degree of the inaccessible samples. Experiments were conducted to test the substitute samples’ influence on mapping accuracy, the reliability of soil property prediction, and sample set’s representativeness to the study area. Results show that when there are a small number of inaccessible samples (less than six samples in this experiment, or less than 10% of the original sample size), the recommended substitute locations by the proposed method demonstrate little impact on DSM model performances. In the case of stratified random sampling, the introduction of substitute samples recommended by the proposed method caused little change on the random distribution of the sample set. The fitness of MLR models and mapping accuracies are slightly influenced in a random manner. In agreement with the purposive sample, the influence from substitute samples is considerably less when there are fewer inaccessible samples involved (less than six samples in this experiment, or less than 10% of the original sample size).
As indicated previously, the evaluation experiments were conducted using a pool of existing field samples. Recommended samples were selected from such existing samples instead of from all possible locations with higher substitutive scores. The evaluation results are thus rather conservative. Taking purposive sample as an example, if potential locations bearing the highest similarity with the inaccessible samples were sampled and used, the impact of such substitute samples on DSM performance could be even less significant. In future studies, the proposed method can be better evaluated if actual field sampling can be conducted. The proposed method could also be extended to other natural resource mapping fields requiring sample collection.
Author Contributions
Conceptualization, Fang-He Zhao and Cheng-Zhi Qin; methodology, Fang-He Zhao and Cheng-Zhi Qin; software, Fang-He Zhao and Teng-Fei Wei; validation, Fang-He Zhao, Feng Qi and Jun-Zhi Liu; formal analysis, Fang-He Zhao , Teng-Fei Wei and Tian-Wu Ma; resources, Cheng-Zhi Qin and A-Xing Zhu; writing—original draft preparation, Fang-He Zhao; writing—review and editing, Cheng-Zhi Qin, Feng Qi, and A-Xing Zhu; supervision, Cheng-Zhi Qin; funding acquisition, Cheng-Zhi Qin and A-Xing Zhu.
Funding
This study was funded by the National Natural Science Foundation of China (No. 41431177, 41871300). We also thank the support from the Innovation Project of LREIS (No. O88RA20CYA), PAPD, and Outstanding Innovation Team in Colleges and Universities in Jiangsu Province.
Acknowledgments
Support to A-Xing Zhu through the Vilas Associate Award, the Hammel Faculty Fellow Award, and the Manasse Chair Professorship from the University of Wisconsin-Madison are greatly appreciated.
Conflicts of Interest
The authors declare no conflict of interest.
References
- McBratney, A.B.; Mendonça Santos, M.L.; Minasny, B. On digital soil mapping. Geoderma 2003, 117, 3–52. [Google Scholar] [CrossRef]
- Brus, D.J. Improving design-based estimation of spatial means by soil map stratification. A case study of phosphate saturation. Geoderma 1994, 62, 233–246. [Google Scholar] [CrossRef]
- Brus, D.J.; Gruijter, J.J.D. Random sampling or geostatistical modelling? Choosing between design-based and model-based sampling strategies for soil (with discussion). Geoderma 1997, 80, 1–44. [Google Scholar] [CrossRef]
- Zhu, A.X.; Yang, L.; Li, B.L.; Qin, C.Z.; English, E.; Burt, J.E.; Zhou, C.H. Purposive sampling for digital soil mapping for areas with limited data. In Digital Soil Mapping with Limited Data; Hartemink, A.E., McBratney, A.B., Mendonca Santos, M.L., Eds.; Springer: New York, NY, USA, 2008; pp. 233–245. [Google Scholar]
- Yang, L.; Zhu, A.X.; Qi, F.; Qin, C.Z.; Li, B.L.; Pei, T. An integrative hierarchical stepwise sampling strategy and its application in digital soil mapping. Int. J. Geogr. Inf. Sci. 2013, 27, 1–23. [Google Scholar] [CrossRef]
- Long, J.; Liu, Y.; Xing, S.; Qiu, L.; Huang, Q.; Zhou, B.; Shen, J.; Zhang, L. Effects of sampling density on interpolation accuracy for farmland soil organic matter concentration in a large region of complex topography. Ecol. Indic. 2018, 93, 562–571. [Google Scholar] [CrossRef]
- Zeraatpisheh, M.; Ayoubi, S.; Jafari, A.; Finke, P. Comparing the efficiency of digital and conventional soil mapping to predict soil types in a semi-arid region in Iran. Geomorphology 2017, 285, 186–204. [Google Scholar] [CrossRef]
- Zhang, S.J.; Zhu, A.X.; Liu, J.; Yang, L.; Qin, C.Z.; An, Y.M. An heuristic uncertainty directed field sampling design for digital soil mapping. Geoderma 2016, 267, 123–136. [Google Scholar] [CrossRef]
- Roudier, P.; Hewitt, A.E.; Beaudette, D.E. A conditioned Latin hypercube sampling algorithm incorporating operational constraints. In Digital Soil Assessments and Beyond; Minasny, B., Malone, B.P., McBratney, A.B., Eds.; CRC Press: Boca Raton, FL, USA, 2012; pp. 227–231. [Google Scholar]
- Mulder, V.L.; De Bruin, S.; Schaepman, M.E. Representing major soil variability at regional scale by constrained Latin Hypercube Sampling of remote sensing data. Int. J. Appl. Earth Obs. 2013, 21, 301–310. [Google Scholar] [CrossRef]
- Clifford, D.; Payne, J.E.; Pringle, M.J.; Searle, R.; Butler, N. Pragmatic soil survey design using flexible Latin hypercube sampling. Comput. Geosci. 2014, 67, 62–68. [Google Scholar] [CrossRef]
- Kidd, D.; Malone, B.; Mcbratney, A.; Minasny, B.; Webb, M. Operational sampling challenges to digital soil mapping in Tasmania, Australia. Geoderma Regional 2015, 4, 1–10. [Google Scholar] [CrossRef]
- Wei, T.F. The Research of Calculating Alternative Samples of Soil Samples in Mobile Environment. Master’s Thesis, Nanjing Normal University, Nanjing, China, 2017. (In Chinese with English Abstract). [Google Scholar]
- Zhu, A.X.; Yang, L.; Li, B.L.; Qin, C.Z.; Pei, T.; Liu, B.Y. Construction of membership functions for predictive soil mapping under fuzzy logic. Geoderma 2010, 155, 164–174. [Google Scholar] [CrossRef]
- Zhu, A.X.; Band, L.; Vertessy, R.; Dutton, B. Derivation of soil properties using a soil land inference model (SoLIM). Soil Sci. Soc. Am. J. 1997, 61, 523–533. [Google Scholar] [CrossRef]
- Zhu, A.X.; Lu, G.N.; Liu, J.; Qin, C.Z.; Zhou, C.H. Spatial prediction based on Third Law of Geography. Ann. GIS 2018, 24, 225–240. [Google Scholar] [CrossRef]
- Zhu, A.X.; Liu, J.; Du, F.; Zhang, S.J.; Qin, C.Z.; Burt, J.; Behrens, T.; Scholten, T. Predictive soil mapping with limited sample data. Eur. J. Soil Sci. 2015, 66, 535–547. [Google Scholar] [CrossRef]
- Stevens, S.S. On the theory of scales of measurement. Science 1946, 103, 677–680. [Google Scholar] [CrossRef] [PubMed]
- Zhu, A.X.; Band, L. A knowledge-based approach to data integration for soil mapping. Can. J. Remote Sens. 1994, 20, 408–418. [Google Scholar] [CrossRef]
- Chen, Z.Q.; Chen, Z.B.; Chen, H.B.; Chen, L.H. Spatial relationship between soil fertility quality and human activities accessibility in the red eroded area of southern China: A case study in Zhuxi Watershed, Changting County, Fujian Province. Sci. Soil Water Conserv. 2012, 10, 103–107, (In Chinese with English Abstract). [Google Scholar]
- Cost Distance—Help | ArcGIS Desktop. Available online: http://pro.arcgis.com/en/pro-app/tool-reference/spatial-analyst/cost-distance.htm (accessed on 17 July 2018).
- Yang, L.; Zhu, A.X.; Zhao, Y.G.; Li, D.C.; Zhang, G.L.; Zhang, S.J.; Band, L.E. Regional Soil Mapping Using Multi-Grade Representative Sampling and a Fuzzy Membership-Based Mapping Approach. Pedosphere 2017, 27, 344–357. [Google Scholar] [CrossRef]
- Qin, C.Z.; Zhu, A.X.; Pei, T.; Li, B.L.; Scholten, T.; Behrens, T.; Zhou, C.H. An approach to computing topographic wetness index based on maximum downslope gradient. Precis. Agric. 2011, 12, 32–43. [Google Scholar] [CrossRef]
- Zhang, S.J.; Zhu, A.X.; Liu, W.L.; Liu, J.; Yang, L. Mapping detailed soil property using small scale soil type maps and sparse typical samples. Chin. Geogr. Sci. 2013, 23, 680–691. [Google Scholar] [CrossRef]
- Zeng, C.Y.; Yang, L.; Zhu, A.X.; Rossiter, D.G.; Liu, J.; Liu, J.Z.; Qin, C.Z.; Wang, D.S. Mapping soil organic matter concentration at different scales using a mixed geographically weighted regression method. Geoderma 2016, 281, 69–82. [Google Scholar] [CrossRef]
- Yu, K.Z.; Duan, T.W.; Li, D.H.; Peng, J.F. Landscape accessibility as a measurement of urban green system. City Plan. Rev. 1999, 8, 8–11, (In Chinese with English Abstract). [Google Scholar]
- Brus, D.J.; Noij, I.G.A.M. Designing sampling schemes for effect monitoring nutrient leaching from agricultural soils. Eur. J. Soil Sci. 2008, 59, 292–303. [Google Scholar] [CrossRef]
- Hammersley, J.M.; Handscomb, D.C. Monte Carlo Methods; Chapman and Hall: London, UK, 1979. [Google Scholar]
- Lesch, S.M.; Strauss, D.J.; Rhoades, J.D. Spatial prediction of soil salinity using electromagnetic induction techniques: II. An efficient spatial sampling algorithm suitable for multiple linear-regression model identification and estimation. Water Resour. Res. 1995, 31, 387–398. [Google Scholar] [CrossRef]
- Razakamanarivo, R.H.; Grinand, C. Mapping organic carbon stocks in eucalyptus plantations of the central highlands of Madagascar: A multiple regression approach. Geoderma 2011, 162, 335–346. [Google Scholar] [CrossRef]
- Aurenhammer, F. Voronoi Diagrams—A survey of a fundamental geometric data structure. ACM Comput. Surv. 1991, 23, 345–405. [Google Scholar] [CrossRef]
- Duyckaerts, C.; Godefroy, G. Voronoi tessellation to study the numerical density and the spatial distribution of neurones. J. Chem. Neuroanat. 2000, 20, 83–92. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).