Abstract
In this study, we introduce the R package shp2graph, which provides tools to convert a spatial network into an ‘igraph’ graph of the igraph R package. This conversion greatly empowers a spatial network study, as the vast array of graph analytical tools provided in igraph are then readily available to the network analysis, together with the inherent advantages of being within the R statistical computing environment and its vast array of statistical functions. Through three urban road network case studies, the calculation of road network distances with shp2graph and with igraph is demonstrated through four key stages: (i) confirming the connectivity of a spatial network; (ii) integrating points/locations with a network; (iii) converting a network into a graph; and (iv) calculating network distances (and travel times). Throughout, the required R commands are given to provide a useful tutorial on the use of shp2graph.
1. Introduction
The characterization of a spatial network such as a transportation network, a river or stream network or a social network with geo-tags/locations is important to many areas of spatial science such as those found in geography, ecology, agriculture and sociology [1]. Tools exist to achieve such a characterization, often contributing to a certain element, such as savings in computational overheads. This study bridges a particular gap in this tool set where a vector-format spatial network is converted to a graph model and in doing so, benefits from a rich resource of existing and useful graph-based analytical tools, all within the R statistical computing environment. This conversion tool is provided in the R package shp2graph [2], where this study details its construction, properties and uses.
Generally, a spatial network is managed in a geospatial polyline vector format, where spatial entities are recorded as ‘spaghetti’ collections of 2D/3D geospatial coordinates [3]. This format benefits from the detailed geometrical properties of the spatial network in providing an accurate representation of the physical network. However, and following the observations made by Goodchild ([4], p. 401) “Data modelling is defined as the process discretizing spatial variation but may be confused with issues of data structure and driven by available software rather than by a concern for accurate representation.” In this respect, this study’s aim of converting a spatial network model to a graph model provides more assurance and added value to any subsequent spatial analysis to the given network and associated data, together with a reduced computational burden. To conceptualize a spatial network model as a graph data model entails viewing the network as a set of nodes, occupying particular positions, that are joined in pairs by physical or ephemeral constructs [5]. In this manner, the graph data model represents the physical network with logical graph topologies, that is, a set of nodes joined together in pairs as edges. This structure enables computation along a network to benefit directly from graph theory [6] and the associated computational savings therein [7].
This research initially stemmed from a need to find shortest paths or calculate network distances for a set of locations and an associated spatial network, all within the R statistical computing environment [8], so that a local spatial regression model for hedonic house price could be directly calibrated using different distance metrics [9]. Here the R package gdistance provides routines to calculate least-cost distances and routes on geographic grids [10] but it is not applicable when a spatial network is in a vector format, for example, a SpatialLines or SpatialLinesDataFrame object in R [11]. For this, the only solution is to work outside of R with tools provided in ArcGIS [12], GRASS GIS [13], pgRouting [14] and OSMnx [15,16], say; or using packages such as NetworkX [17] and OSMnx [15] within Python, a GIS protocol [18], OSM tools in spatialite [19] and Axwoman [20], say. This is of course problematic given the statistical functions and associated tools reside in R (e.g., for a local regression application, see [21,22]). Fortunately, the C library igraph provides such a collection of network analysis tools and has an interface in R, that is, the igraph package [23] but where the computations have to be carried out with a special class of graphs in R, namely ‘igraph.’ Thus, to bridge this gap within the R environment, the package shp2graph was developed for converting a spatial network of vector format into an ‘igraph’ object, which is now presented in its entirety. Through this conversion, travel time distances, shortest paths and network distances can be calculated efficiently via a range of classic algorithms, including Dijkstra’s algorithm [24], Bellman–Ford’s algorithm [25,26] and Johnson’s algorithm [27].
This article is constructed in the following four sections. First, the basics of converting a spatial network to an ‘igraph’ graph are introduced. Secondly, the step by step procedure for calculating network distances with shp2graph and igraph is given. Thirdly, the same procedure is summarized and useful extensions are proposed. Finally, a summary is given together with suggestions for future spatial network tools.
2. Converting a Spatial Network into an ‘igraph’ Graph
2.1. The Graph Data Model
The graph data model plays a vital role in analyzing network structures. According to Beauquier, Berstel and Chrétienne in Mathis ([28], p xvi): “Graphs constitute the most widely used theoretical tool for the modelling and research of the properties of structured sets. They are employed each time we want to represent and study a set of connections (whether directed or not) between the elements of a finite set of objects.” From graph theory, a graph is generally constituted of two finite collections of vertices and edges (links between vertices), where its formulaic expression can be denoted as:
G = (V, E), where V = is the set of vertices and E = is the set of edges.
Note the edges can be defined by a weighting function to qualify or quantify the relationships between vertices. Specifically, an edge is directed when it is attributed with an orientation. Conversely, it is an undirected edge if no orientation is clarified. A graph is called a directed graph if it contains directed edges; otherwise, it is known as an undirected graph.
The graph data model provides a simplifying tool to define and represent a network structure with three types of relations:
- (i)
- vertex-vertex relations, where the adjacency relationship is defined between two vertices if they are connected by an undirected or directed edge;
- (ii)
- vertex-edge relations, where the member-owner relationship is defined if it is a starting or ending vertex of an edge;
- (iii)
- edge-edge relations, where the contiguity relationship between two edges is defined if they share one or more vertex.
A graph can be constructed with all these relations properly externalized. For a vector-format spatial network, it can be simply represented by a graph constituted by a set of vertices occupying particular positions in space and edges from physical connections [4]. In this sense, we can convert a spatial network into an ‘igraph’ graph in three steps:
- Step 1.
- Extract objects from the spatial network as vertices and include an identifier (ID) and 2-D coordinate (x, y) for each vertex;
- Step 2.
- Construct all the edges according to the vertex-vertex adjacency relationships and deliver them as an adjacency matrix or 2-D array;
- Step 3.
- Use existing functions in igraph to create an ‘igraph’ graph.
These three steps can be conducted using the shp2graph functions readshpnw and nel2igraph where we provide examples in the following section.
2.2. Data Conversion
A vector-format spatial network is usually read as a SpatialLines or SpatialLinesDataFrame object in R, where each individual polyline is expressed as a set of coordinates connected sequentially [11]. In shp2graph, the default input for graph conversion is assumed to be a SpatialLines or SpatialLinesDataFrame object. The most straightforward conversion is to take all the endpoints or junctions as vertices, that is, obtaining the first and last locations of each polyline as the starting and ending vertices, respectively, of an edge in the converted graph. Observe that the endpoints from equivalent coordinates are regarded as a single vertex (i.e., a junction in the network); where the numerical precision of the coordinates may affect this conversion (i.e., a lower-level floating point definition may cause false junctions to be recognized). As an example, the following R code (snippet 1, with shp2graph loaded) converts a sampled part of the ‘Ontario road network’ (ORN) [29], as shown in Figure 1a into an ‘igraph’ graph, as shown in Figure 1b. Observe that the coordinates of the vertices have been incorporated autonomously as vertex attributes “x” and “y.”
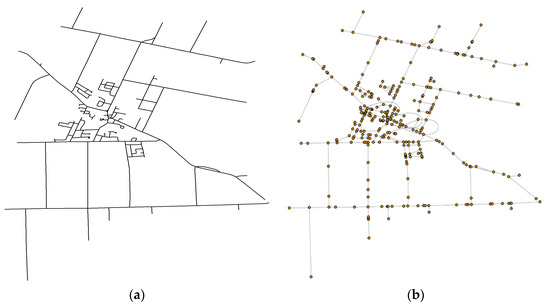
Figure 1.
Network to graph conversion by taking all the endpoints or junctions as vertices (Ontario road data). (a) The ORN spatial network, (b) The resultant ‘igraph’ graph.
Code snippet 1: data(ORN) plot(ORN.nt) title(“The ORN spatial network”) rtNEL1 <-readshpnw(ORN.nt) igr1 <-nel2igraph(rtNEL1[[2]], rtNEL1[[3]]) plot(igr1, vertex.label = NA, vertex.size = 2, vertex.size2 = 2, mark.col = “green”, main = “The converted igraph graph”) summary(igr1) IGRAPH U--- 298 343 -- + attr: x (v/n), y (v/n)
This first conversion strategy constructs a graph by removing geometric detail in the spatial network and in doing so, we get an efficient expression in return. If we want to keep the geometric properties in the converted graph, then the function readshpnw can be used where all the coordinates are taken as vertices if the parameter Detailed is specified as TRUE. For example, with the following R code (snippet 2), a second ‘igraph’ graph is produced with all geometric detail retained (Figure 2). It looks the same as the spatial network and is comprised of 597 vertices and 642 edges. This contrasts with the first graph conversion (Figure 1b), which has a much smaller number of vertices and edges, that is, 298 and 343, respectively. Observe that the parameter ea.prop is used here to denote whether the attributes of each polyline should be kept for the edges.
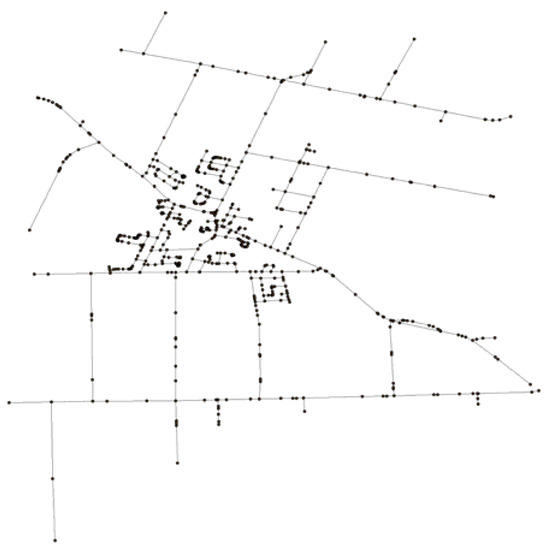
Figure 2.
The converted ‘igraph’ graph with all geometric properties retained (Ontario road data).
Code snippet 2: rtNEL2 <-readshpnw(ORN.nt, Detailed = TRUE, ea.prop = rep(0, 37)) igr2 <-nel2igraph(rtNEL2[[2]], rtNEL2[[3]]) plot(igr2, vertex.label = NA, vertex.size = 1, vertex.size2 = 1, main = “The converted igraph graph with all the geometric properties”) summary(igr2) IGRAPH U--- 597 642 -- + attr: x (v/n), y (v/n)
Thus, we have provided two strategies for converting a spatial network into an ‘igraph’ object and the desired network-based analysis can follow accordingly, where it is enhanced by having the many useful functions and algorithms in igraph now readily available. For example, we can calculate network distances or shortest paths with shp2graph and igraph in R and this process is detailed below. Furthermore, shp2graph can easily be extended to different conversion strategies. For example, taking complex objects as vertices (see master_node definition in [30]), or taking polylines themselves as vertices for conversion to a connectivity graph [31]. Note that this conversion would assume planarity in the produced ‘igraph’ object (see similar conversions defined in [32]), which is largely dependent on the data structure of the original spatial network (like 2-D coordinates), or models with them. However, overpasses (viaducts) and underpasses (tunnels) in an urban road network bring typical nonplanarity [33], which can only be properly treated here by ensuring topological correctness at overpasses or underpasses, that is, no intersections.
3. Calculating Network Distances with Shp2graph and Igraph
The development of shp2graph was motivated by the need to provide solutions to the calculation of network distances and shortest paths within the R statistical computing environment. The shp2graph R package provides routines to convert a vector-format spatial network into an ‘igraph’ graph, allowing functions such as distances, distance_table, shortest_paths and all_shortest_paths in the igraph R package to be utilized. In practice, however, the conversions are rarely straightforward, where extra pre-processing operations are often required—such as checking the topology, optimizing the network structure and so forth.
As a case study to demonstrate the calculation of network distance (and travel time) matrices, we use the same London house price data (as provided by the Nationwide Building Society of the United Kingdom) and the same London road network (as produced by the UK Ordnance Survey (OS) in 2001), as that used in the local regression study of Lu et al. [9]. These example data sets are both available the latest release of shp2graph. Thus, if the following R code is run (snippet 3), then the map of Figure 3 results, where both data sets are combined.
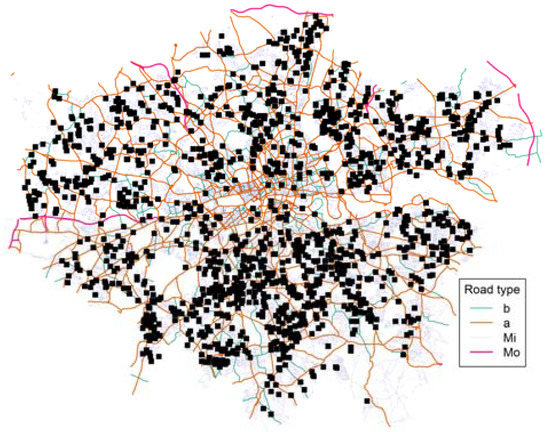
Figure 3.
Case study data sets: London house price and road network data.
Code snippet 3: require(RColorBrewer) data(LNNT) data(LNHP) road.type <- unique(LN.nt$nt_RoadTyp) idx <- match(LN.nt$nt_RoadTyp, road.type) ltypes <- c(1, 1, 3, 1) lwidths <- c(1, 1.5, 0.2, 2) shades <- brewer.pal(4, “Dark2”) plot(LN.nt, col = shades[idx], lty = ltypes[idx], lwd = lwidths[idx], cex = 0.3) points(coordinates(LN.prop), pch = 15) legend(551000, 172000, legend = road.type, lty = ltypes, lwd = lwidths, col = shades, title = “Road type”)
3.1. Confirming Connectivity in a Spatial Network
Completeness and topology correctness are fundamental for ensuring connectivity in a spatial network [34]. Whether or not a spatial network is self-connected, where no disconnected portions or islands exist in the network, that is, at least one path could be found between any pair of vertices. Connectivity is essential for calculating network distances or shortest paths successfully. To confirm the connectivity of a given spatial network the shp2graph function, nt.connect, searches through all the self-connected parts in the input network and returns a series of self-connected parts with the most vertices. In this sense, it always possible to get at least one self-connected network from this output. We can demonstrate this function as follows with this R code (snippet 4) together with the mapped output in Figure 4:
Code snippet 4: LN.nt.con <- nt.connect(LN.nt) plot(LN.nt.con)
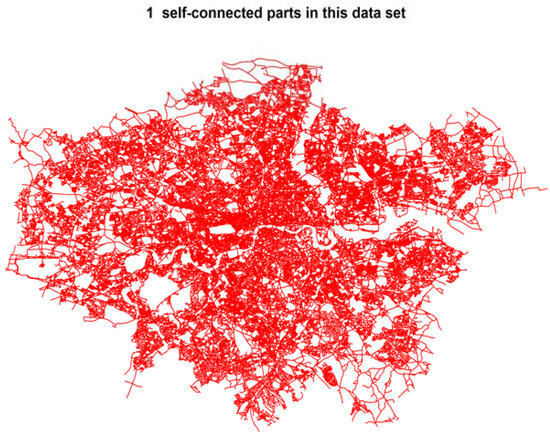
Figure 4.
Connectivity of the London road network data via the function nt.connect.
Figure 4 clearly indicates that the London road network is highly self-connected, where only one self-connected part was found (the plot title always returns this). This level of connectivity is sufficient for subsequent operations and analyses and is expected for a carefully prepared network data set. In practice, however, many spatial network data sets have poor connectivity conditions, requiring much pre-processing. In this respect, it is useful to provide another example—this time using part of the Estevan road network downloaded from OpenStreetMap [35]. Thus, the following R commands (snippet 5) returns this network’s connectivity conditions (mapped in Figure 5):
Code snippet 5: data(ERN_OSM) ERN.con <- nt.connect(ERN_OSM.nt) plot(ERN.con)
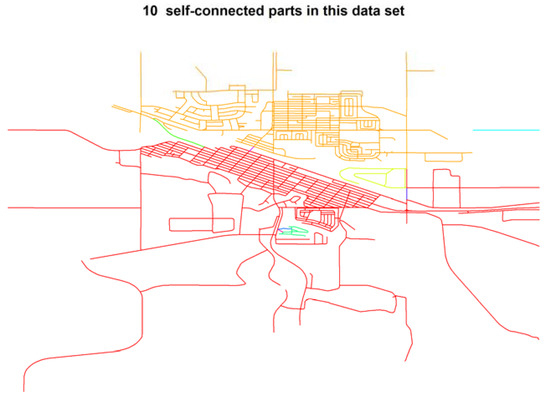
Figure 5.
Connectivity of the Estevan road network via the function nt.connect.
As shown in Figure 5, the Estevan road network is comprised of ten unconnected parts marked in ten different colors. Such poor connectivity is likely due to various topology errors, where the three most common types are: dangling arc, overshoot and undershoot [36]. These are illustrated in Figure 6a–c and are defined as follows:
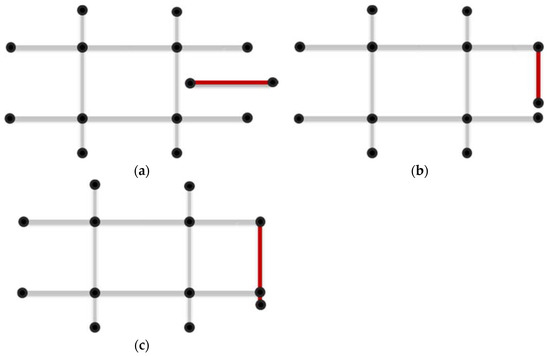
Figure 6.
Three common types of topology errors. (a) Dangling arc, (b) Undershoot, (c) Overshoot.
- ▗
- Dangling arc (Figure 6a): an arc featured by having the same polygon on both its sides and at least one vertex that does not connect to any other arc, which is especially harmful for the connectivity of the converted graph when both nodes are not connected to any other arc;
- ▗
- Overshoot (Figure 6b): an arc passes another arc which should intersect and stop there;
- ▗
- Undershoot (Figure 6c): an arc does not extend long enough to another arc which it should intersect.
Such topology errors lead to critical connectivity problems for the converted igraph graph and as a consequence, cause failures in calculating shortest paths or network distances. Using the function nt.connect allows the user to find the main self-connected part, where all remaining unconnected parts can be dropped and thus provides an immediate solution for finding a self-connected network. However, this dropping of network parts is not always acceptable, especially when the dropped (unconnected) parts are clearly important to understanding the spatial process. This is the case for the Estevan road network example, where the main self-connected part (as shown in Figure 7), a SpatialLinesDataFrame object ERN.con returned by nt.connect, does not adequately cover the study area (see the red part in Figure 6). In this instance, we have to move outside of R, where there are a number of GIS tools available to correct topology errors, for example, topology error fixes in ArcGIS [37], polyline tools in ET Geo-tools [37] and a toolset for cleaning topology in GRASS [13]. In this instance, we processed the Estevan road data with the GRASS tools and got a new network with all topology errors fixed. The topology corrected data has been incorporated into shp2graph, as demonstrated by the following R commands (snippet 6) and mapped in Figure 8:
Code snippet 6: data(ERN_OSM_correct) ERN_cor.con <- nt.connect(ERN_OSM_cor.nt)
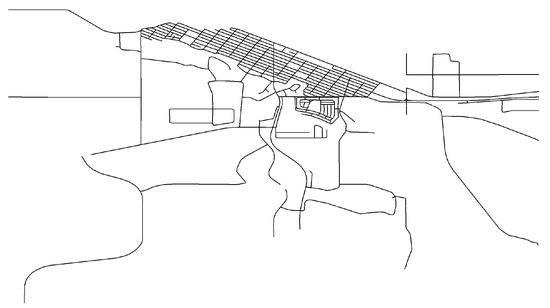
Figure 7.
The main self-connected part of the Estevan road network returned by the function nt.connect.
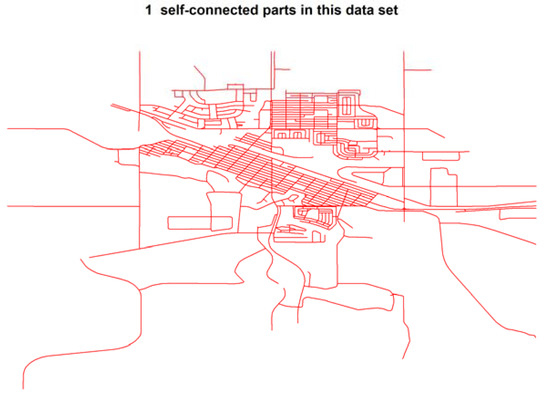
Figure 8.
Connectivity of the Estevan road network with topology errors fixed via the function nt.connect.
In summary, it is important to confirm the connectivity of a given spatial network, which can be achieved via the function nt.connect, supported by external GIS tools. Clearly, the incorporation of such GIS tools within R would be a useful advance, further avoiding troublesome data imports and exports that shp2graph goes some way in addressing. Note however, that these tools can themselves create new topology errors. For example, when a bridge crosses over a road (or multiple bridges/roads, as in the U.S. Interstate System), resulting in incorrect splits and the creation of false junctions.
3.2. Integrating Points with a Spatial Network
As illustrated in the usage of the functions distance_table, shortest_paths and all_shortest_paths from igraph, network distances or shortest paths can only be calculated between pairwise vertices of the graph. This entails that all associated points/locations (i.e., where we have sample observations) should be inherent nodes of the spatial network, that in turn, are recognized as vertices in the converted graph. This collocated situation however, rarely occurs in practice, where the points/locations and the spatial network are usually isolated from each other (e.g., the London houses appear off the road network, as shown in Figure 3). To address this issue, four strategies (solutions) are incorporated in shp2graph, all within the function points2network that allows the integration of the points/locations with the spatial network by representing each point with: (1) its nearest vertex; or (2) its nearest geometric point; or (3) adding a pseudo edge to connect each point with its nearest vertex; or (4) adding a pseudo edge to connect each point with its nearest geometric point. These four strategies are illustrated in Figure 9.
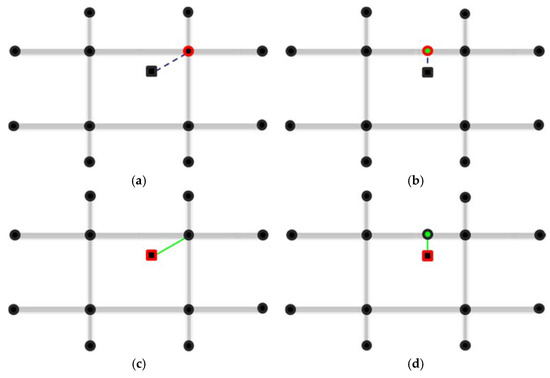
Figure 9.
Four strategies to integrate points/locations within the spatial network. (a) Strategy 1: represent each point with its nearest vertex; (b) Strategy 2: represent each point with its nearest geometric point; (c) Strategy 3: add a pseudo edge (colored green) between each point and its nearest vertex; (d) Strategy 4: Add a pseudo edge (colored green) between each point and its nearest geometric point.
As illustrated in Figure 9a, the most straightforward way (strategy 1) is to associate each point with its nearest vertex within the network, where this strategy rule is expressed as follows:
where are the coordinates for the point/location and is a vertex of the graph g to be converted with the coordinates. The nearest vertex is used to represent , as marked with a red circle in Figure 9a. Strategy 1 is simple and computationally efficient but can be inaccurate when the network is sparse, or when only the endpoints of each polyline are recognized as vertices.
To get more accurate results than that found in strategy 1, strategy 2 finds the nearest geometric position on the network for each point and takes that position as a vertex (maybe newly added or not) for representation. Thus, strategy 2 searches for the minimum distance between the point and all the line segments and then fixes the nearest position as a representative vertex. This strategy rule is expressed as follows:
where and are the coordinates of two endpoints of any line segment in the network; is the nearest position on the closest line segment and taken as the (new) vertex to represent the point ; are the coordinates of the foot point from to the straight line where the segment is located and are found as follows:
Strategies 1 and 2 take typical vertices from the original spatial network to provide a virtual representation of the given points/locations. However, they can be deficient in that a certain loss of information is likely, particularly when the network is sparse, or there are comparatively large gaps between the network and points. In this respect, two further strategies 3 and 4 are available in the function points2network that add pseudo edges between the given points and typical vertices are selected accordingly, as shown in Figure 9c,d. This way, the points/locations themselves can be recognized as vertices. Note however, that the pseudo edges created by strategies 3 and 4 do not have homologous attributes as the original ones in the network, which may result in difficulties in a subsequent analysis.
As demonstration, the following R commands (snippet 7) can be run for the Ontario road data, resulting in the network maps presented in Figure 10a–d, where the function ptsinnt.view visualizes the output from points2network. A list of vertices and the corresponding vertex-vertex adjacency matrix are returned by points2network, in preparation for subsequent conversion and associated computations (this list can be particularly important for assessing the consequences of point integration strategies 3 and 4). From Figure 10, observe that only the endpoints of the polylines are viewed as vertices, which is a default option of the function points2network. All the geometric points of each polyline are viewed as vertices if the parameter ‘Detailed’ in points2network is set as TRUE, where accuracy can improve when point integration strategies 1 or 3 are adopted. This setting should not be used for strategies 2 or 4 as outcomes are meaningless.
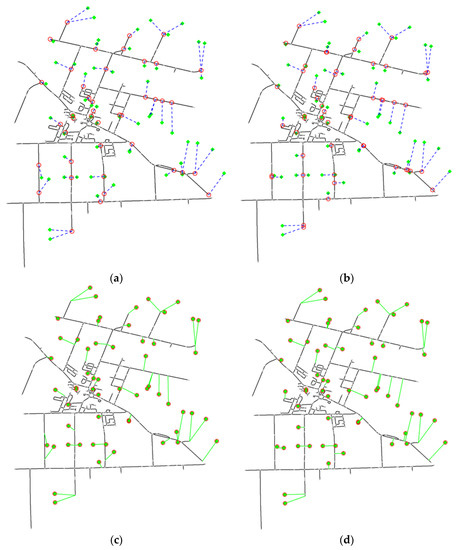
Figure 10.
Examples of integrating points/locations with a spatial network (Ontario road data), where green dots represent points given, a blue dash in (a,b) indicate the closest relationship between a point and its nearest vertex/position on the network, green lines in (c,d) mean the edges newly added and red circles mark the representative vertices. (a) Solution with strategy 1; (b) Solution with strategy 2; (c) Solution with strategy 3; (d) Solution with strategy 4.
Code snippet 7: data(ORN) pts <- spsample(ORN.nt, 100, type = “random”) ptsxy <- coordinates(pts)[, 1:2] ptsxy <- cbind(ptsxy[, 1] + 0.008, ptsxy[, 2] + 0.008) res.nv <- points2network(ntdata = ORN.nt, pointsxy = ptsxy, ELComputed = TRUE, approach = 1) ptsinnt.view(ntdata = ORN.nt, nodelist = res.nv[[1]], pointsxy = ptsxy, CoorespondIDs = res.nv[[3]]) res.np <- points2network(ntdata = ORN.nt, pointsxy = ptsxy, approach = 2, ea.prop = rep(0, 2)) ptsinnt.view(ntdata = ORN.nt, nodelist = res.np[[1]], pointsxy = ptsxy, ELComputed = TRUE, CoorespondIDs = res.np[[3]]) res.vnv <- points2network(ntdata = ORN.nt, pointsxy = ptsxy, ELComputed = TRUE, approach = 3, ea.prop = rep(0, 2)) ptsinnt.view(ntdata = ORN.nt, nodelist = res.vnv[[1]], pointsxy = ptsxy, CoorespondIDs = res.vnv[[3]], VElist = res.vnn[[7]]) res.vnp <- points2network(ntdata = ORN.nt, pointsxy = ptsxy, ELComputed = TRUE, approach = 4, ea.prop = rep(0, 2)) ptsinnt.view(ntdata = ORN.nt, nodelist = res.vnp[[1]], pointsxy = ptsxy, CoorespondIDs = res.vnp[[3]], VElist = res.vnp[[7]])
As further demonstration of points/locations integration, the integration of the London properties onto the London road network is presented in Figure 11a,b using strategies 1 and 2. Here the code snippet is not given but is directly analogous to that given in snippet 7. The whole process will take around 67 min (Computer configuration: Intel® Core™ i5-4570 Processor, 8 G RAM, Windows 7 64 bit) due to a relatively large number of points and a relatively complex network. Results suggest that both strategies achieve integration with acceptable levels of accuracy but where strategy 2 seems more accurate but is computationally costly (it uses 43 of the full 67 min). Computational efficiency could be improved by establishing a spatial index of the network, like using a boundary box to roughly track each road segment. This is a subject of on-going work.
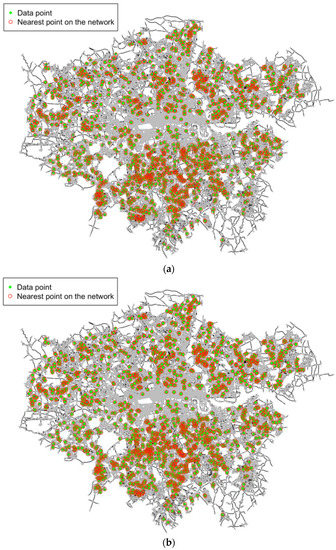
Figure 11.
Integration of the London property locations onto the London road network using strategies 1 and 2. (a) Solution with strategy 1; (b) Solution with strategy 2.
3.3. Converting a Spatial Network into an Igraph Graph
Once the procedures outlined in Section 3.1 and Section 3.2 have been completed, the spatial network is ready to convert to an igraph graph via the shp2graph function nel2igraph. To calculate network distances with converted graphs, the length of each polyline (e.g., road length) is assigned to the corresponding edge in the converted graph. The vertex lists and vertex-vertex (i.e., edge) adjacency matrices returned by points2network (from Section 3.2) are used for the conversion using the following R commands (snippet 8), for the London case study and for respective point integration strategies 1 and 2, from before:
Code snippet 8: # Strategy 1 Edge.len1 <- LN.pt2nt1[[8]] LN.ig1 <-nel2igraph(LN.pt2nt1[[1]], LN.pt2nt1[[2]], weight = Edge.len1) summary(LN.ig1) IGRAPH U-W- 75236 97800 -- + attr: x (v/n), y (v/n), weight (e/n) # Strategy 2 Edge.len2 <- LN.pt2nt2[[8]] LN.ig2 <-nel2igraph(LN.pt2nt2[[1]], LN.pt2nt2[[2]], weight = Edge.len2) summary(LN.ig2) IGRAPH U-W- 76762 99326 -- + attr: x (v/n), y (v/n), weight (e/n)
For point integration strategy 2, the vertices and edges are increased by 1526 over that using point integration strategy 1. Observe that the polyline segment (i.e., road) length is calculated by setting the parameter ELComputed of the function points2network as TRUE, which is then assigned as the default weight for each edge in the converted graph. The resultant graphs are now ready for the calculation of the network distances. Also, observe that road speed information (miles per hour) is provided for the London case study and as such, the anticipated travel cost for each road segment can be calculated. Graphs can be converted for calculating travel time distances if the edges are weighted with their travel cost. In this sense, the above R commands (snippet 8) can be edited as follows (snippet 9):
Code snippet 9: # Strategy 1 names(LN.pt2nt1[[6]]) Speed1 <- LN.pt2nt1[[6]][, 4] * 0.44704 LN.ig3 <- nel2igraph(LN.pt2nt1[[1]], LN.pt2nt1[[2]], weight = Edge.len1/Speed1) summary(LN.ig3) IGRAPH U-W- 75236 97800 -- + attr: x (v/n), y (v/n), weight (e/n) # Strategy 2 Speed2 <- LN.pt2nt2[[6]][, 4] * 0.44704 LN.ig4 <- nel2igraph(LN.pt2nt2[[1]], LN.pt2nt2[[2]], weight = Edge.len2/Speed2) summary(LN.ig4) IGRAPH U-W- 76762 99326 -- + attr: x (v/n), y (v/n), weight (e/n)
3.4. Calculating Network Distances and Travel Times
The following R commands (snippet 10) calculate the network distances between each pair of London property locations with LN.ig1 and LN.ig2, reflecting the two different point integration strategies used. The resultant matrices are different but highly correlated, as depicted in the scatterplot of Figure 12. Observe that the corresponding vertices of the input locations are marked with their orders returned by the function points2network, which provides an assessment of accuracy.
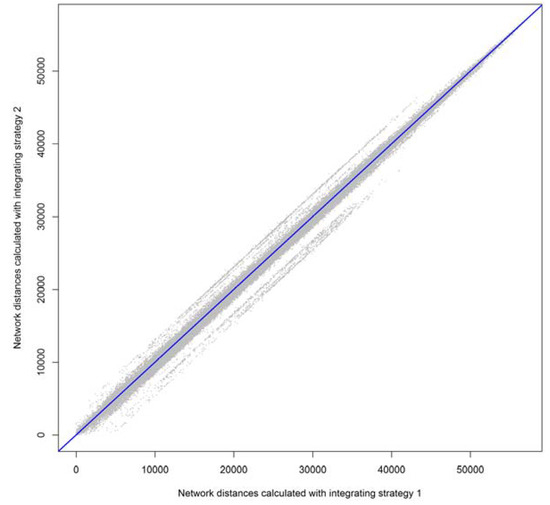
Figure 12.
Network distances calculated with two different integrating strategies (London case study).
Code snippet 10: # Strategy 1 LN.pt.VIDs1 <- as.numeric(LN.pt2nt1[[3]]) V.idx1 <- as.numeric(levels(as.factor(LN.pt.VIDs1))) ND.mat1 <- shortest.paths(LN.ig1, v = LN.pt.VIDs1, to = V.idx1) ND.mat1 <- ND.mat1[, match(LN.pt.VIDs1, V.idx1)] # Strategy 2 LN.pt.VIDs2 <- as.numeric(LN.pt2nt2[[3]]) V.idx2 <- as.numeric(levels(as.factor(LN.pt.VIDs2))) ND.mat2 <- shortest.paths(LN.ig2, v = LN.pt.VIDs2, to = V.idx2) ND.mat2 <- ND.mat2[, match(LN.pt.VIDs2, V.idx2)] # Scatterplot plot(ND.mat1, ND.mat2, pch = 16, cex = 0.2, col = “grey”, xlab = “Network distances calculated with integrating strategy 1”, ylab = “Network distances calculated with integrating strategy 2”) abline(a = 0, b = 1, col = “blue”, lwd = 2)
In addition, the corresponding travel time distances for the London case study can be calculated with the converted graphs, LN.ig3 and LN.ig4, using the following R commands (snippet 11):
Code snippet 11: # Strategy 1 TT.mat1 <- shortest.paths(LN.ig3, v = LN.pt.VIDs1, to = V.idx1) TT.mat1 <- ND.mat1[, match(LN.pt.VIDs1, V.idx1)] # Strategy 2 TT.mat2 <- shortest.paths(LN.ig2, v = LN.pt.VIDs2, to = V.idx2) TT.mat2 <- TT.mat2[, match(LN.pt.VIDs2, V.idx2)]
As a useful summary of this work, a flow chart for calculating network distances with shp2graph and igraph is given in Figure 13.
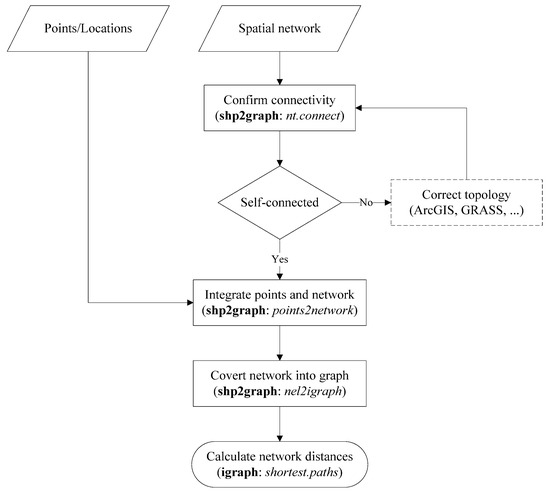
Figure 13.
Flow chart of calculating network distances with shp2graph and igraph.
3.5. Example Extensions
Shortest paths can also be found via the following set of R commends (snippet 12) for the Ontario road data where the function shortest.paths is replaced with get.shortest.paths. Here, an interactive experiment was conducted to find the shortest path between any pair of locations randomly inputted and the result is given in Figure 14.
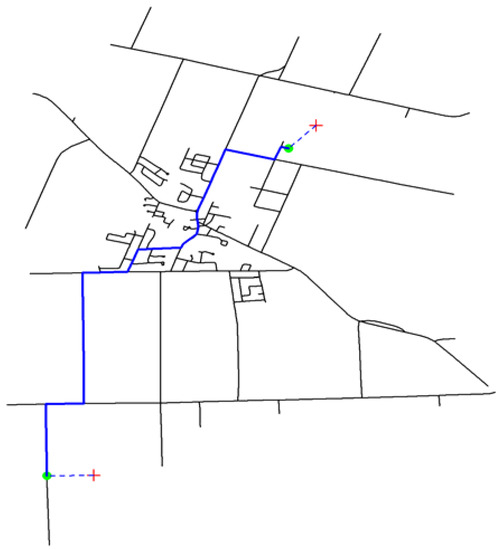
Figure 14.
An interactive example for finding the shortest path with shp2graph and igraph (Ontario road data).
Code snippet 12: plot(ORN.nt) coords <- locator(2) coords <- cbind(coords$x, coords$y) points(coords, pch = 3, col = “red”) pt2nt1 <- points2network(ntdata = ORN.nt, pointsxy = coords, Detailed = T, ELComputed = T, approach = 2, ea.prop = rep(0, 2)) V.idx3 <- as.numeric(pt2nt1[[3]]) V.coords <- cbind(pt2nt1[[4]][V.idx3], pt2nt1[[5]][V.idx3]) points(V.coords, pch = 16, col = “green”) lines(rbind(coords[1,], V.coords[1,]), lty = 2, col = “blue”) lines(rbind(coords[2,], V.coords[2,]), lty = 2, col = “blue”) igr3 <- nel2igraph(pt2nt1[[1]], pt2nt1[[2]], weight = pt2nt1[[8]]) path <- get.shortest.paths(igr3, from = V.idx3[1], to = V.idx3[2])$vpath[[1]] for(i in 1:(length(path)-1)) lines(cbind(pt2nt1[[4]][path[i,i+1]], pt2nt1[[5]][path[i,i+1]]), lwd =2, col = “blue”)
Furthermore, the igraph package provides a vast collection of graph handling and analysis tools—i.e., not just tools to calculate network distances and shortest paths, as demonstrated here. The following R code (snippet 13) showcases some extensions for shp2graph via igraph, such as calculating vertex and edge ‘betweeness’ and network diameter (as shown in Figure 15), or measuring network connectivity [38].
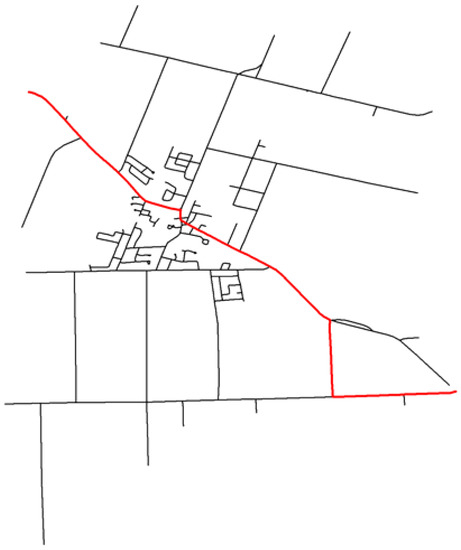
Figure 15.
Finding the network diameter with shp2graph and igraph (Ontario road data).
Code snippet 13: V.bn <- betweenness(igr2) E.bn <- edge_betweenness(igr2) G.dm <- diameter(igr2, directed = F) V.gdm <- get_diameter(igr2, directed = F) plot(ORN.nt) for(i in 1:(length(V.gdm)-1)) lines(cbind(rtNEL2[[6]][V.gdm [i,i+1]], rtNEL2[[7]][V.gdm[i,i+1]]), lwd = 2, col = “red”)
4. Summary
In this study, the R package shp2graph is demonstrated. It provides a set of tools to convert a spatial network into an ‘igraph’ graph of the igraph R package and in doing so, allows the rich set of graph handling and analysis tools in igraph to be available for a spatial network analysis, all within the R statistical computing environment. In particular, a route map for calculating road network distances for three urban case studies is presented, where functions from both shp2graph and igraph are described and applied. The calculation of travel time distances by weighting edges of the converted graph with travel costs is also presented. The shp2graph package continues to evolve, where tools such as those for topology correction and spatial indexing for improved computation times are in current development.
Author Contributions
B.L. conceived and designed the study; M.C. helped develop shp2graph, performing experiments and analyses; M.X. validated all the experiments and codes; H.S. made suggestions and provided project administration for funding this study; B.L. wrote the manuscript assisted by P.H.
Funding
Natural Science Foundation of China grant number [NSFC: U1533102] and an open Research Fund Program of Shenzhen Key Laboratory of Spatial Smart Sensing and Services (Shenzhen University).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Barthélemy, M. Spatial networks. Phys. Rep. 2011, 499, 1–101. [Google Scholar] [CrossRef]
- Lu, B.; Charlton, M. Convert a Spatial Network to a Graph in R. In Proceedings of the R User Conference, Coventry, UK, 16–18 August 2011. [Google Scholar]
- George, B.; Shekhar, S. Road maps, digital. In Encyclopedia of GIS; Shashi, S., Hui, X., Eds.; Springer: New York, NY, USA, 2008. [Google Scholar]
- Goodchild, M.F. Geographical data modeling. Comput. Geosci. 1992, 18, 401–408. [Google Scholar] [CrossRef]
- Gastner, M.T.; Newman, M.E.J. The spatial structure of networks. Eur. Phys. J. B Condens. Matter Complex Syst. 2006, 49, 247–252. [Google Scholar] [CrossRef]
- Fowler, P.A. The königsberg bridges—250 years later. Am. Math. Mon. 1988, 95, 42–43. [Google Scholar]
- Appert, M.; Chapelon, L. The space-time variability of road base accessibility: Application to london. In Graphs and Networks; Mathis, P., Ed.; ISTE: London, UK, 2007; pp. 3–28. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
- Lu, B.; Charlton, M.; Harris, P.; Fotheringham, A.S. Geographically weighted regression with a non-euclidean distance metric: A case study using hedonic house price data. Int. J. Geogr. Inf. Sci. 2014, 28, 660–681. [Google Scholar] [CrossRef]
- Van Etten, J. R package gdistance: Distances and routes on geographical grids. J. Stat. Softw. 2017, 1. [Google Scholar] [CrossRef]
- Pebesma, E.J.; Bivand, R.S. Classes and methods for spatial data in R. R News 2005, 5, 9–13. [Google Scholar]
- ESRI Corp. Arcgis Desktop: Release 10; Environmental Systems Research Institute: Redlands, CA, USA, 2011. [Google Scholar]
- GRASS Development Team. Geographic Resources Analysis Support System (Grass GIS) Software; Open Source Geospatial Foundation: Chicago, IL, USA, 2018. [Google Scholar]
- pgRouting Community. Pgrouting 2.3. Available online: https://pgrouting.org/index.html (accessed on 5 May 2018).
- Boeing, G. Osmnx: New methods for acquiring, constructing, analyzing, and visualizing complex street networks. Comput. Environ. Urban Syst. 2017, 65, 126–139. [Google Scholar] [CrossRef]
- Boeing, G. A multi-scale analysis of 27,000 urban street networks. Environ. Plan. B Urban Anal. City Sci. 2018, in press. [Google Scholar]
- Hagberg, A.; Swart, P.; S Chult, D. Exploring Network Structure, Dynamics, and Function Using NetworkX. In Proceedings of the 7th Python in Science Conference, Pasadena, CA, USA, 19–24 August 2008. [Google Scholar]
- Karduni, A.; Kermanshah, A.; Derrible, S. A protocol to convert spatial polyline data to network formats and applications to world urban road networks. Sci. Data 2016, 3, 160046. [Google Scholar] [CrossRef] [PubMed]
- Furieri, A. Spatialite-Tools, 2017-03-03 ed.; SpatiaLite: Genova, Italy, 2018. [Google Scholar]
- Jiang, B. Axwoman 6.3: An Arcgis Extension for Urban Morphological Analysis; University of Gävle: Gävle, Sweden, 2015. [Google Scholar]
- Gollini, I.; Lu, B.; Charlton, M.; Brunsdon, C.; Harris, P. Gwmodel: An R package for exploring spatial heterogeneity using geographically weighted models. J. Stat. Softw. 2015, 63, 1–50. [Google Scholar] [CrossRef]
- Lu, B.; Harris, P.; Charlton, M.; Brunsdon, C. The gwmodel r package: Further topics for exploring spatial heterogeneity using geographically weighted models. Geo-Spat. Inf. Sci. 2014, 17, 85–101. [Google Scholar] [CrossRef]
- Csardi, G.; Nepusz, T. The igraph software package for complex network research. InterJournal Complex Syst. 2006, 1695, 1–9. [Google Scholar]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Bellman, R. On a routing problem. Q. Appl. Math. 1958, 16, 87–90. [Google Scholar] [CrossRef]
- Ford, L.R. Network Flow Theory; RAND Corporation: Santa Monica, CA, USA, 1956. [Google Scholar]
- Johnson, D.B. Efficient algorithms for shortest paths in sparse networks. J. ACM 1977, 24, 1–13. [Google Scholar] [CrossRef]
- Mathis, P. (Ed.) Strengths and deficiencies of graphs for network description and modeling. In Graphs and Networks; ISTE: London, UK, 2007; p. xvi. [Google Scholar]
- Peterborough, O. Ontario Road Network; Ontario Ministry of Natural Resources: Peterborough, ON, Canada, 2006. [Google Scholar]
- Mainguenaud, M. Modelling the network component of geographical information systems. Int. J. Geogr. Inf. Syst. 1995, 9, 575–593. [Google Scholar] [CrossRef]
- Jiang, B.; Claramunt, C. A structural approach to the model generalization of an urban street network. Geoinformatica 2004, 8, 157–171. [Google Scholar] [CrossRef]
- Viana, M.P.; Strano, E.; Bordin, P.; Barthelemy, M. The simplicity of planar networks. Sci. Rep. 2013, 3, 3495. [Google Scholar] [CrossRef] [PubMed]
- Boeing, G. Planarity and street network representation in urban form analysis. arXiv, 2018; arXiv:1806.01805. [Google Scholar] [CrossRef]
- Abdulganiev, I.; Agafonov, A. Automatic Checking of Road Network Models. In Proceedings of the CEUR Workshop Proceedings, Moscow, Russia, 25–26 November 2016; pp. 249–255. [Google Scholar]
- OpenStreetMap. Estevan Road Network; OpenStreetMap Community: London, UK, 2014. [Google Scholar]
- Wade, T.; Sommer, S. A to Z GIS: An Illustrated Dictionary of Geographic Information Systems; ESRI Press: Redlands, CA, USA, 2006. [Google Scholar]
- Tchoukanski, I. Et Geotools; 11.5; ET SpatialTechniques: Faerie Glen, South Africa, 2018. [Google Scholar]
- Knight, P.L.; Marshall, W.E. The metrics of street network connectivity: Their inconsistencies. J. Urban. Int. Res. Placemarking Urban Sustain. 2015, 8, 241–259. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).