Representing the Spatiotemporal State Evolution of Geographic Entities as a Multi-Level Graph
Abstract
1. Introduction
2. Related Work and Problem Analysis
2.1. Related Work
2.2. Problem Analysis
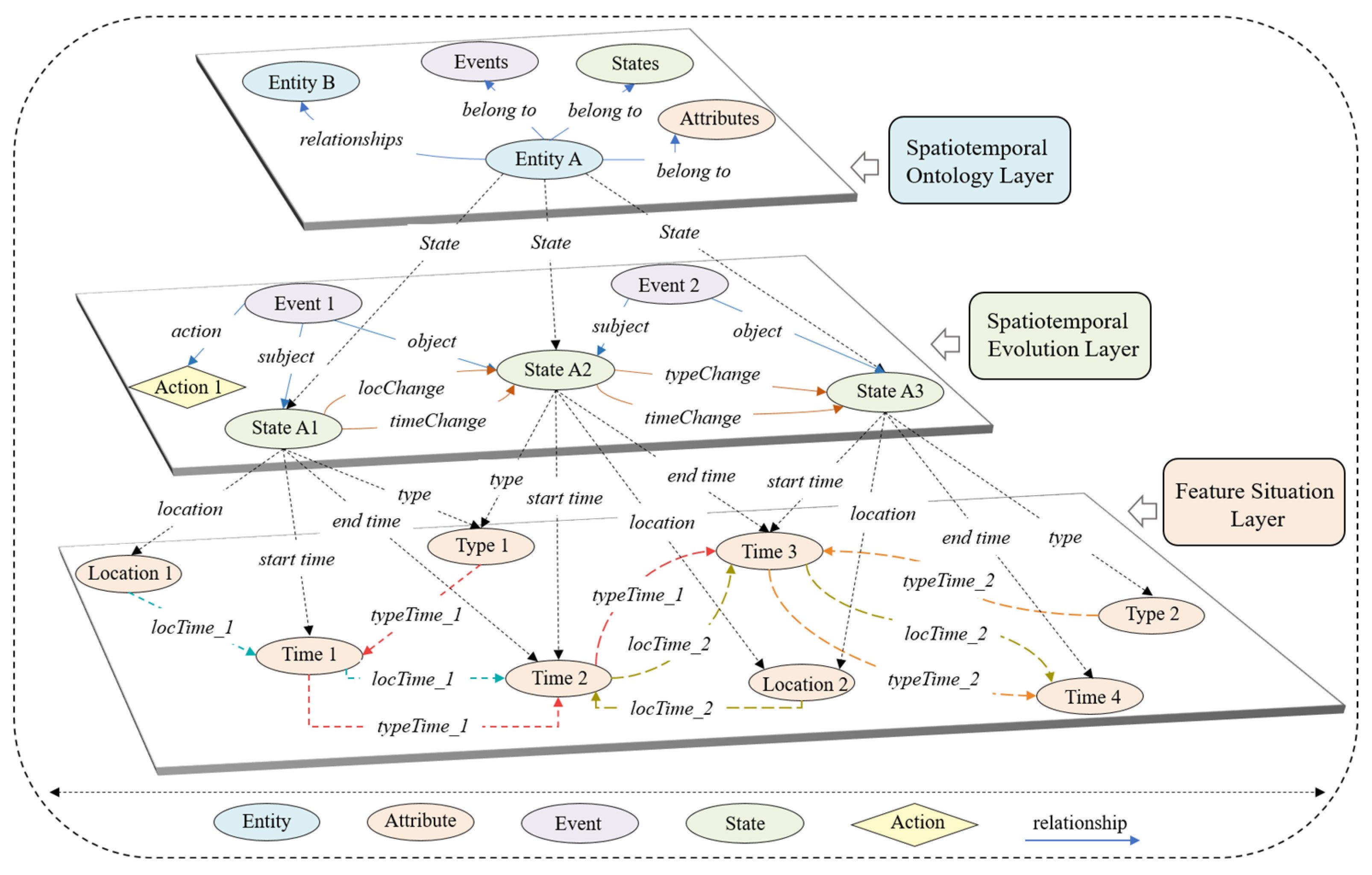
3. Spatiotemporal Evolution Hierarchical Representation Graph (STEHRG)
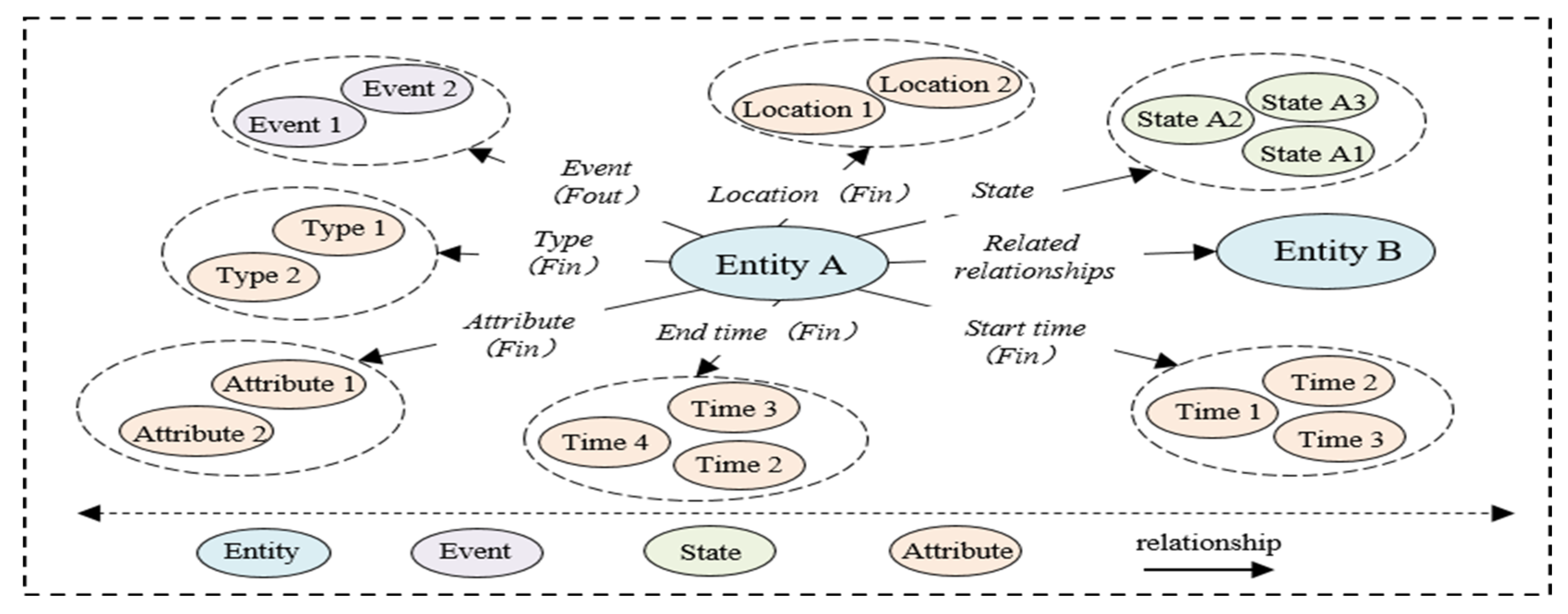
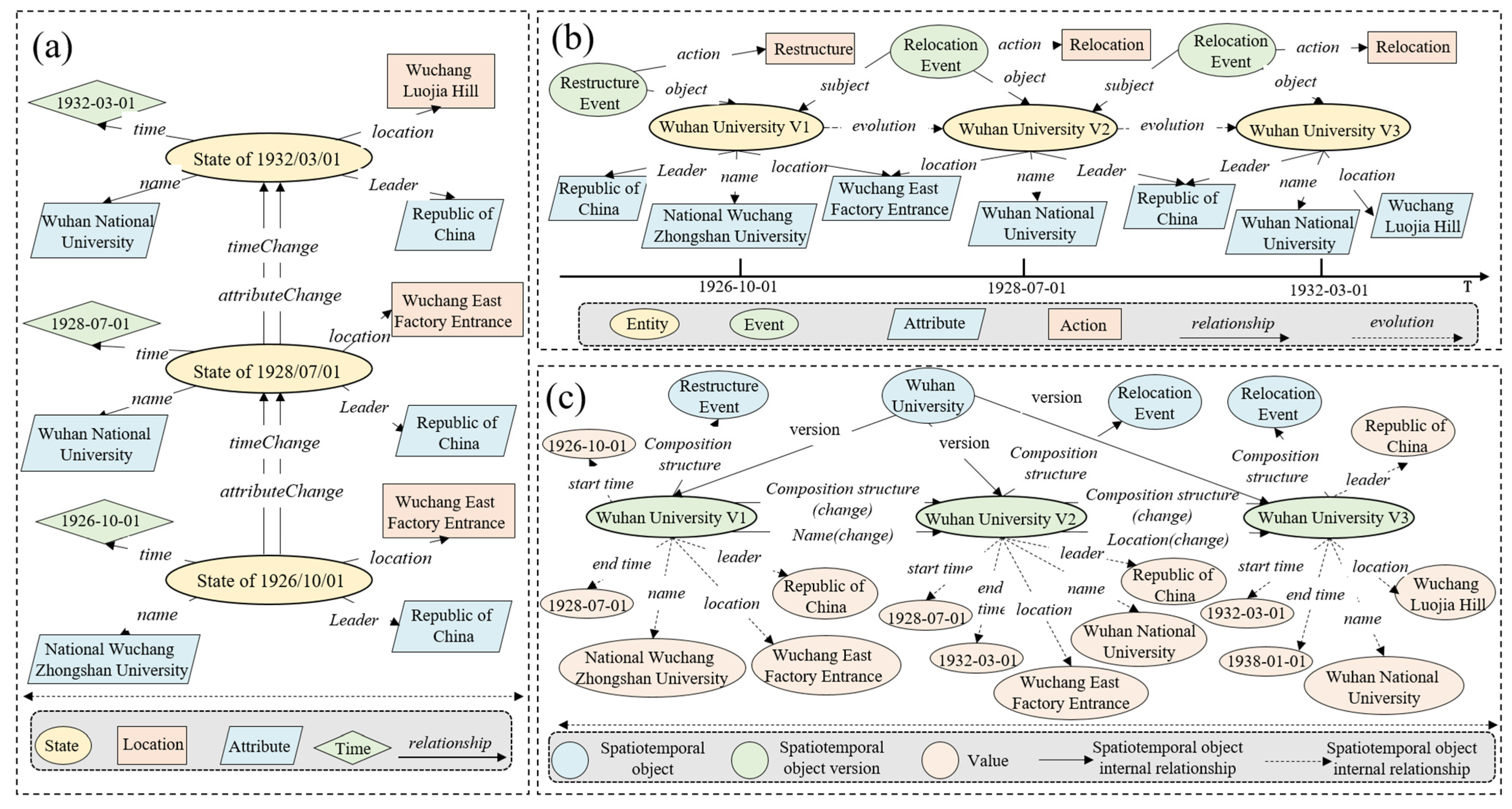
3.1. The Spatiotemporal Ontology Layer
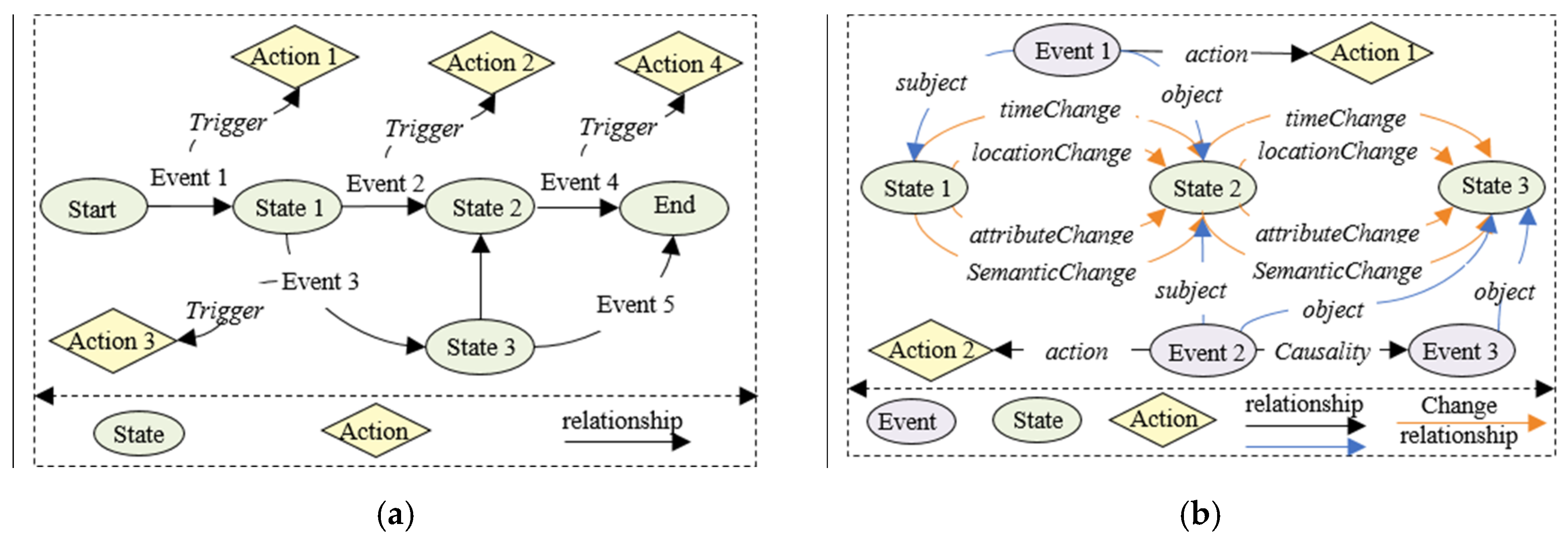
3.2. The Spatiotemporal Evolution Layer
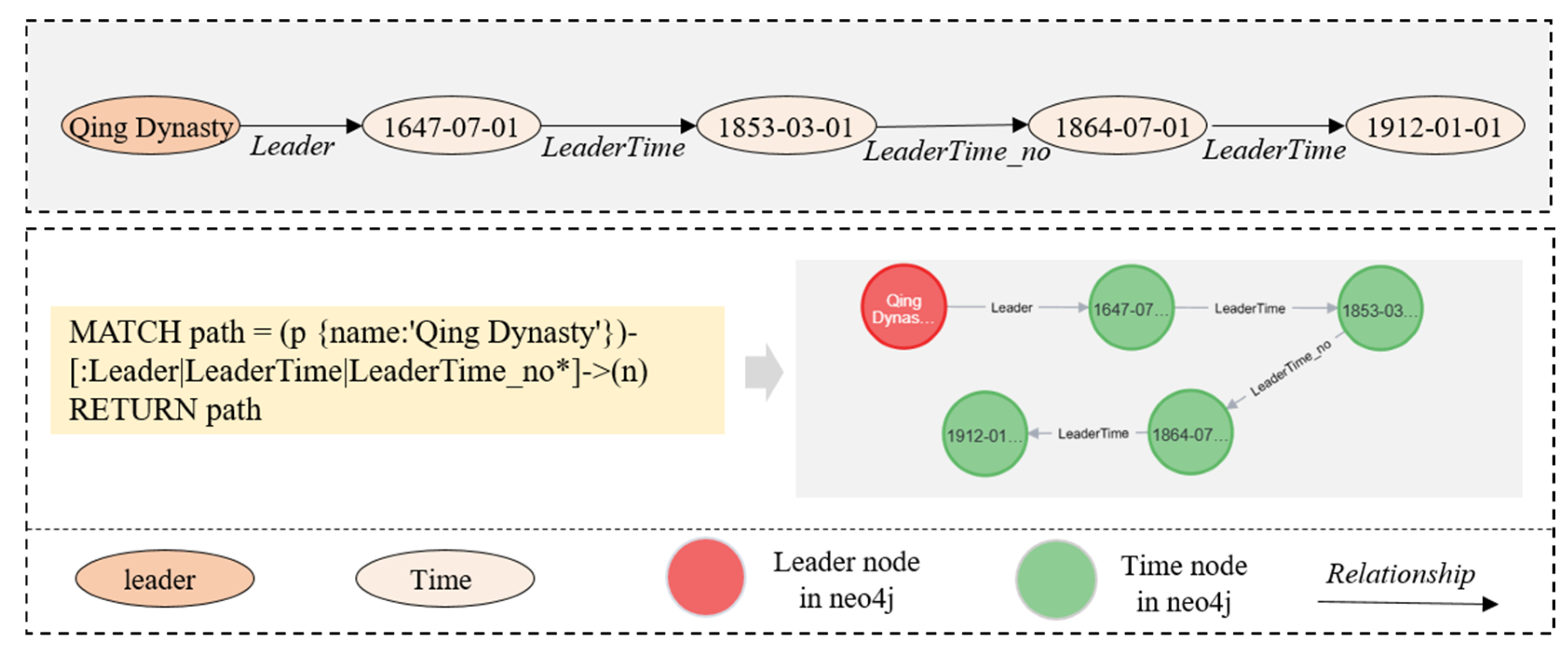
3.2.1. Explanation of the State Transition Process’s Characteristics
3.2.2. Structured Expression of Spatiotemporal State Transition
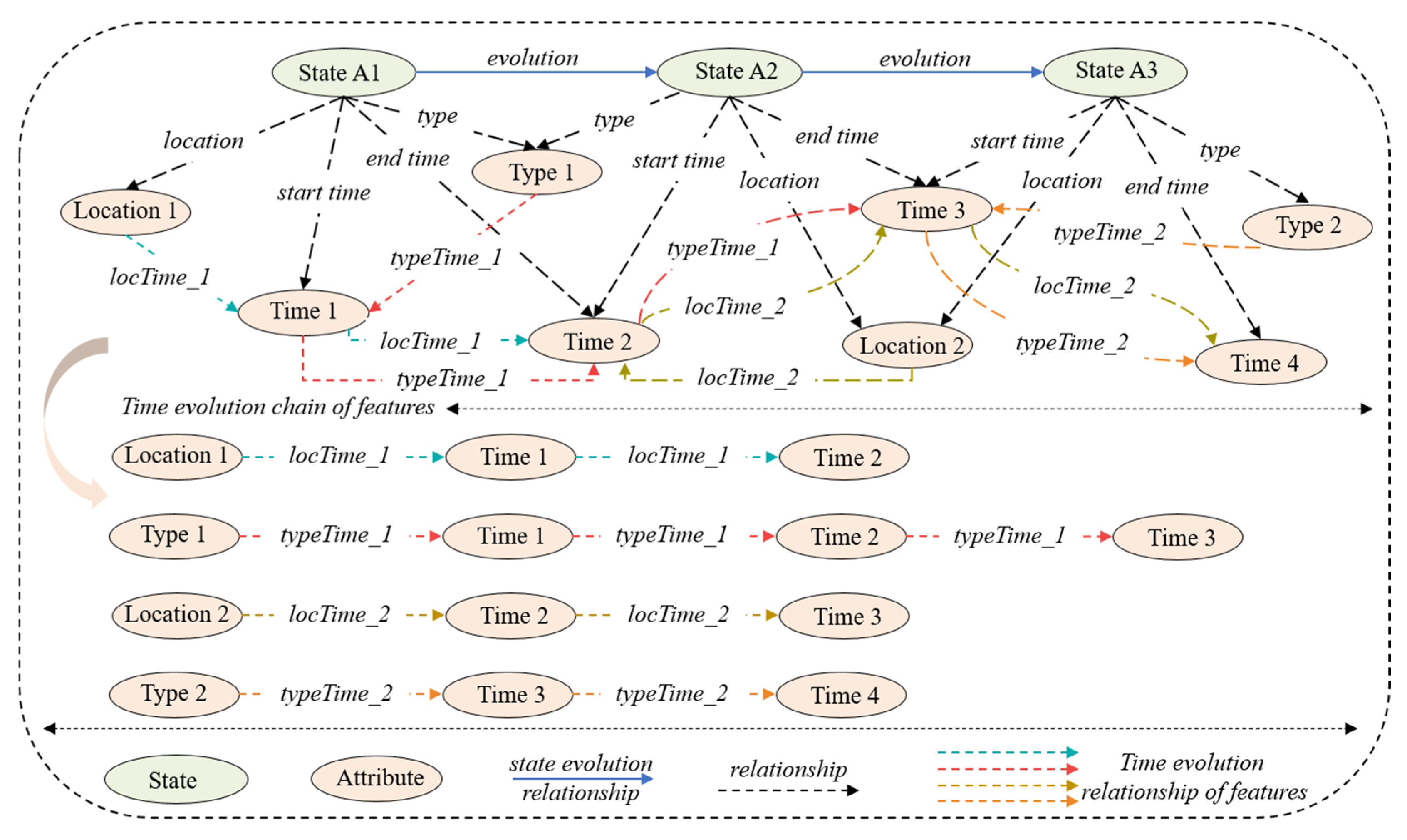
3.3. Feature Situation Layer with Time Dependency
4. Experiment A: The Evolutionary Process of Wuhan University (WHU)
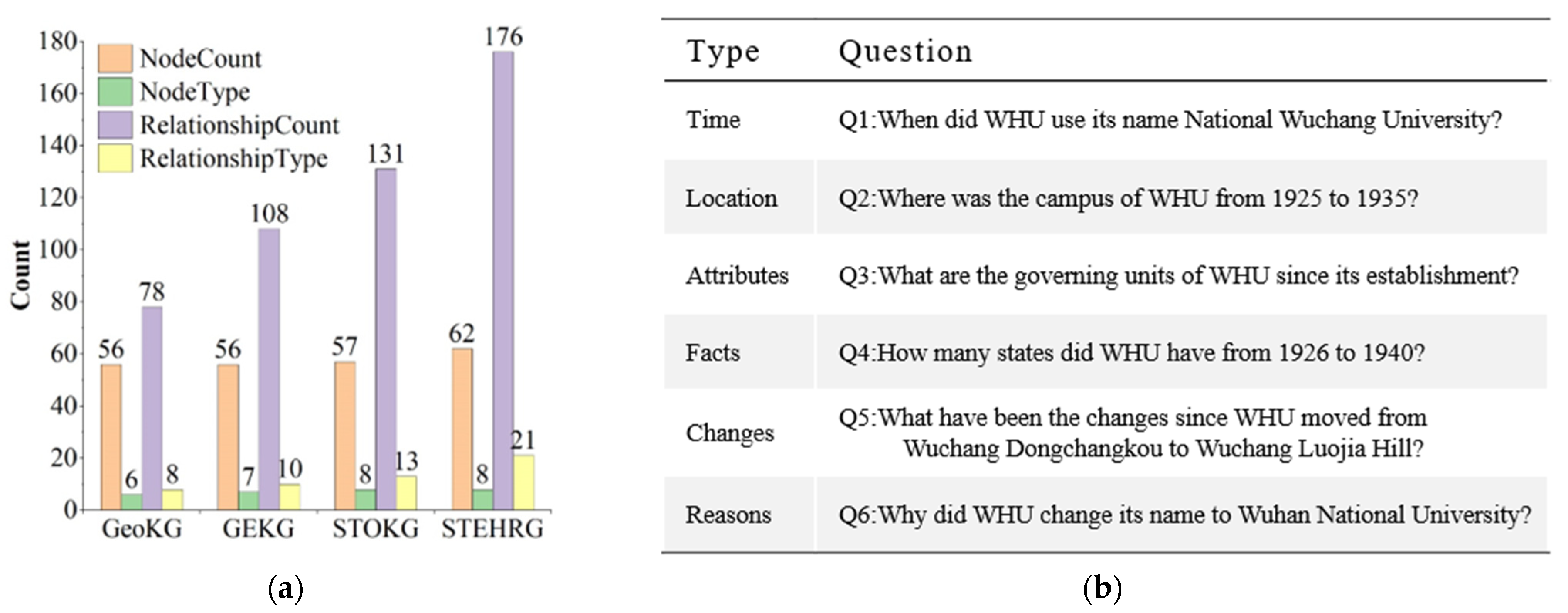
4.1. WHU Data Description
4.2. Comparisons of Four Model Structures
4.3. Comparison of Spatiotemporal Processes’ Expressive Capacities in WHU Case
5. Experiment B: The Evolutionary Process of the Nanjing Presidential Palace Attraction (NJPPA)
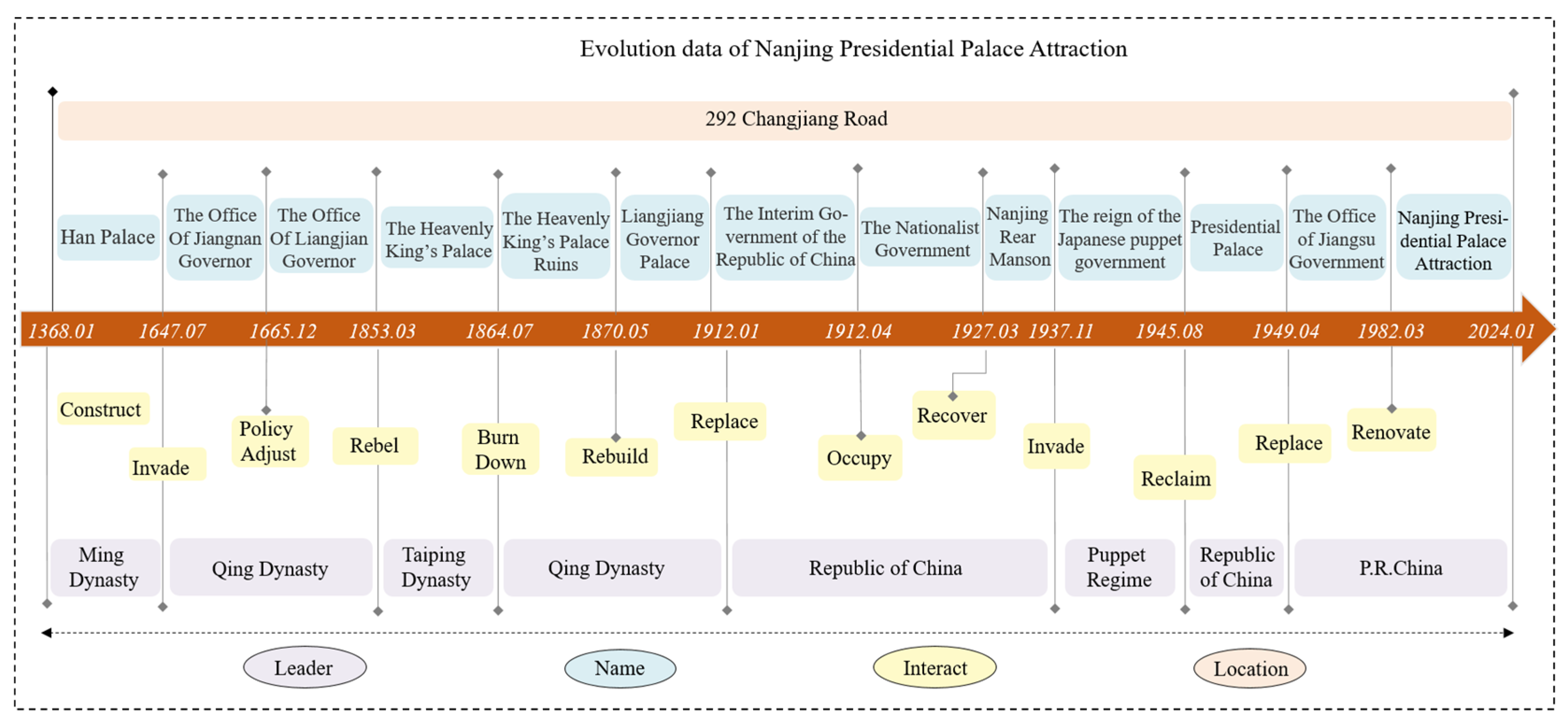
5.1. NJPPA Data Description
5.2. Comparison of Four Model Structures in NJPPA Case
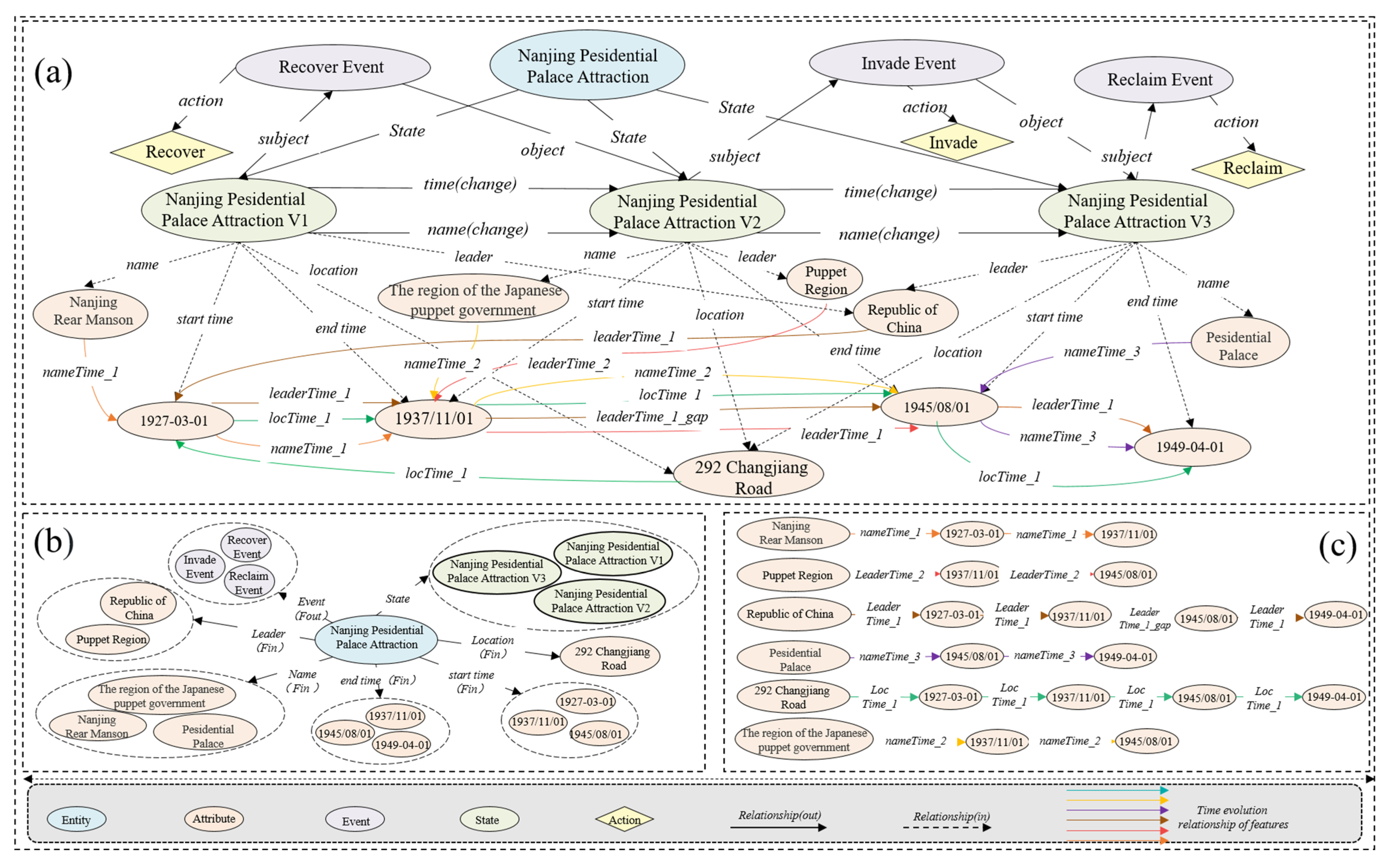
5.3. Comparison of Spatiotemporal Processes’ Expressive Capacities in NJPPA Case
6. Experiment C: The Evolutionary Process of Spatiotemporal Vessel Behaviors
6.1. Data Description
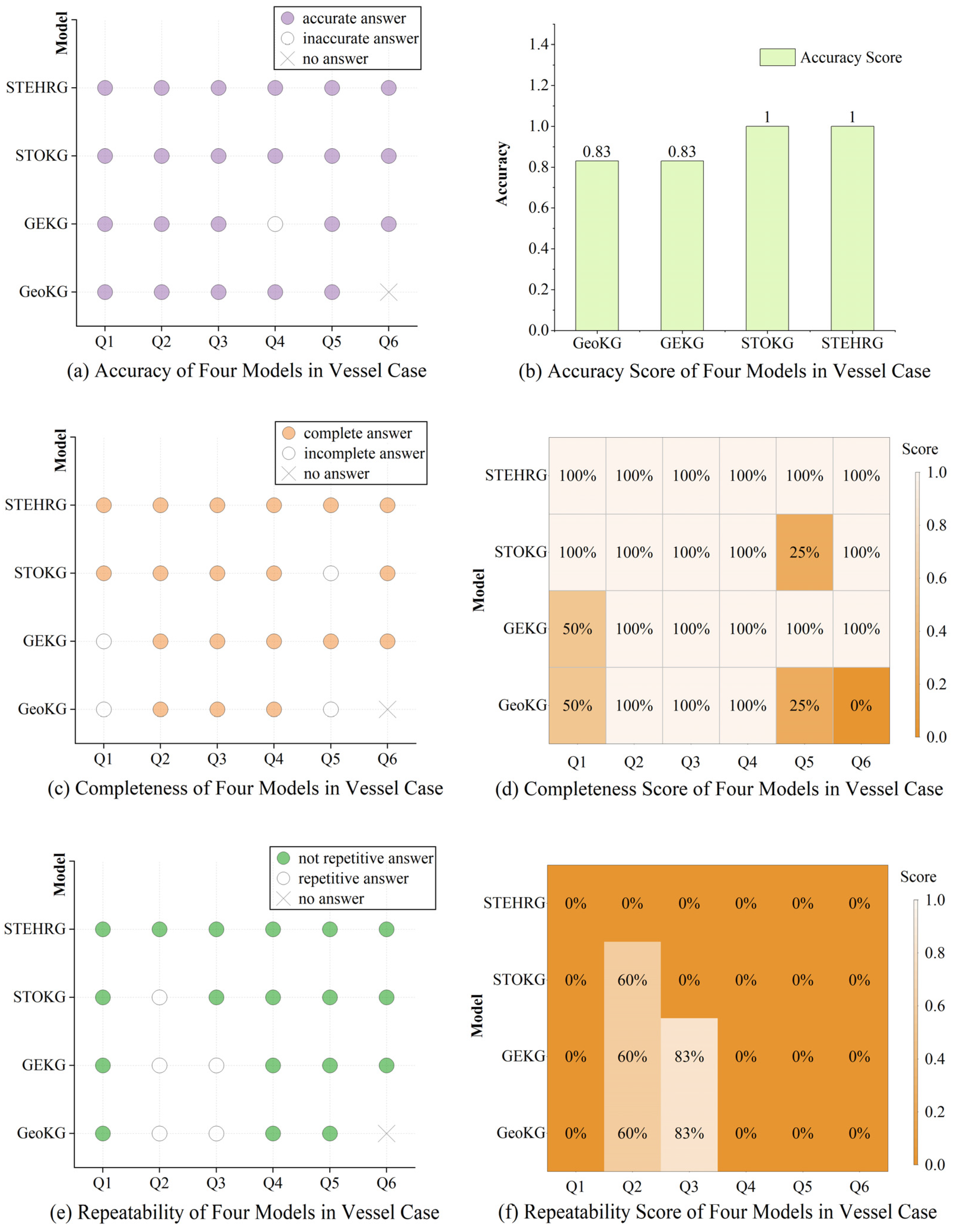
6.2. Comparison of Spatiotemporal Processes’ Expressive Capacities in Vessel Case
7. Result Analysis
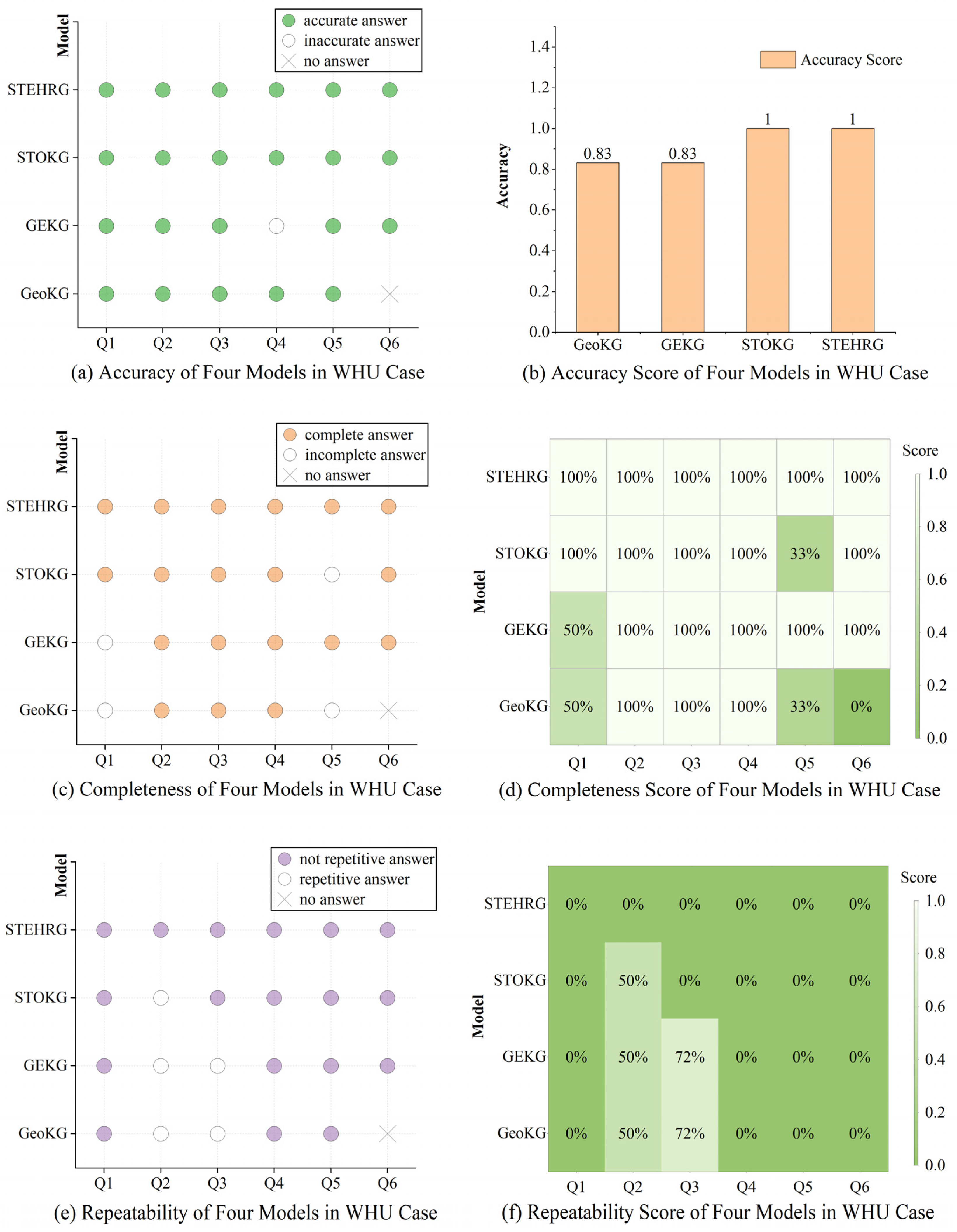
7.1. Accuracy
7.2. Completeness
7.3. Repetitiveness
7.4. Limitations of the STEHRG
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ayall, T.A.; Liu, H.; Zhou, C.; Seid, A.M.; Gereme, F.B.; Abishu, H.N.; Yacob, Y.H. Graph Computing Systems and Partitioning Techniques: A Survey. IEEE Access 2022, 10, 118523–118550. [Google Scholar] [CrossRef]
- Yao, X.; Li, G.; Xia, J.; Ben, J.; Cao, Q.; Zhao, L.; Ma, Y.; Zhang, L.; Zhu, D. Enabling the Big Earth Observation Data via Cloud Computing and DGGS: Opportunities and Challenges. Remote Sens. 2019, 12, 62. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Chen, B.Y.; Yuan, H.; Li, Q.; Shaw, S.-L.; Lam, W.H.K.; Chen, X. Spatiotemporal data model for network time geographic analysis in the era of big data. Int. J. Geogr. Inf. Sci. 2015, 30, 1041–1071. [Google Scholar] [CrossRef]
- Zhu, L.; Yu, F.R.; Wang, Y.; Ning, B.; Tang, T. Big Data Analytics in Intelligent Transportation Systems: A Survey. IEEE Trans. Intell. Transp. Syst. 2019, 20, 383–398. [Google Scholar] [CrossRef]
- Lin, H.; Chen, M.; Lu, G.; Zhu, Q.; Gong, J.; You, X.; Wen, Y.; Xu, B.; Hu, M. Virtual Geographic Environments (VGEs): A New Generation of Geographic Analysis Tool. Earth-Sci. Rev. 2013, 126, 74–84. [Google Scholar] [CrossRef]
- Hao, X.; Ji, Z.; Li, X.; Yin, L.; Liu, L.; Sun, M.; Liu, Q.; Yang, R. Construction and Application of a Knowledge Graph. Remote Sens. 2021, 13, 2511. [Google Scholar] [CrossRef]
- Kaplan, G.; Avdan, U. Monthly Analysis of Wetlands Dynamics Using Remote Sensing Data. ISPRS Int. J. Geo-Inf. 2018, 7, 411. [Google Scholar] [CrossRef]
- Lü, G.; Batty, M.; Strobl, J.; Lin, H.; Zhu, A.X.; Chen, M. Reflections and speculations on the progress in Geographic Information Systems (GIS): A geographic perspective. Int. J. Geogr. Inf. Sci. 2018, 33, 346–367. [Google Scholar] [CrossRef]
- Lin, H.; You, L.; Hu, C.; Chen, M. Prospect of Geo-Knowledge Engineering in the Era of Spatio-Temporal Big Data. Geomat. Inf. Sci. Wuhan Univ. 2018, 43, 2205–2211. [Google Scholar] [CrossRef]
- Del Mondo, G.; Rodríguez, M.A.; Claramunt, C.; Bravo, L.; Thibaud, R. Modeling consistency of spatio-temporal graphs. Data Knowl. Eng. 2013, 84, 59–80. [Google Scholar] [CrossRef]
- He, Y.; Sheng, Y.; Hofer, B.; Huang, Y.; Qin, J. Processes and events in the centre: A dynamic data model for representing spatial change. Int. J. Digit. Earth 2022, 15, 276–295. [Google Scholar] [CrossRef]
- Del Mondo, G.; Peng, P.; Gensel, J.; Claramunt, C.; Lu, F. Leveraging Spatio-Temporal Graphs and Knowledge Graphs: Perspectives in the Field of Maritime Transportation. ISPRS Int. J. Geo-Inf. 2021, 10, 541. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, X.; Ye, P.; Du, M.; Lu, Y.; Xue, H. Geographic Knowledge Graph (GeoKG): A Formalized Geographic Knowledge Representation. ISPRS Int. J. Geo-Inf. 2019, 8, 184. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, Y.; Zhang, C.; Ye, P. Geoscience Knowledge Graph (GeoKG): Development, construction and challenges. Trans. GIS 2022, 26, 2480–2494. [Google Scholar] [CrossRef]
- Zheng, K.; Xie, M.H.; Zhang, J.B.; Xie, J.; Xia, S.H. A knowledge representation model based on the geographic spatiotemporal process. Int. J. Geogr. Inf. Sci. 2021, 36, 674–691. [Google Scholar] [CrossRef]
- Zhao, X.; Cao, Y.; Wang, J.; Fan, X.; Chen, M. A hierarchical spatio-temporal object knowledge graph model for dynamic scene representation. Trans. GIS 2023, 27, 1992–2016. [Google Scholar] [CrossRef]
- Park, N.; Liu, F.; Mehta, P.; Cristofor, D.; Faloutsos, C.; Dong, Y. EvoKG: Jointly Modeling Event Time and Network Structure for Reasoning over Temporal Knowledge Graphs. In Proceedings of the Fifteenth ACM International Conference on Web Search and Data Mining, Temple, Arizona, 15 February 2022. [Google Scholar] [CrossRef]
- Tanon, T.P.; Weikum, G.; Suchanek, F. YAGO 4: A Reason-able Knowledge Base. In Proceedings of the Semantic Web: 17th International Conference, ESWC 2020, Heraklion, Greece, 31 May–4 June 2020; pp. 583–596. [Google Scholar]
- Vrandečić, D.; Krötzsch, M. Wikidata: A free collaborative knowledgebase. Commun. ACM 2014, 57, 78–85. [Google Scholar] [CrossRef]
- Lehmann, J.; Isele, R.; Jakob, M.; Jentzsch, A.; Kontokostas, D.; Mendes, P.N.; Hellmann, S.; Morsey, M.; van Kleef, P.; Auer, S.; et al. DBpedia—A large-scale, multilingual knowledge base extracted from Wikipedia. Semant. Web 2015, 6, 167–195. [Google Scholar] [CrossRef]
- Tasnim, M.; Collarana, D.; Graux, D.; Orlandi, F.; Vidal, M.E. Summarizing Entity Temporal Evolution in Knowledge Graphs. In Proceedings of the 5th Workshop on Managing the Evolution and Preservation of the Data Web, San Francisco, CA, 13 May 2019. [Google Scholar]
- He, Y.; Huang, Y.; Sheng, Y.; Su, X.; Zhou, S.; Lei, S.; Wang, X.; Xia, Y.; Chen, Y.; Shen, Z.; et al. SceneKG: A Geo-Scene Based Spatiotemporal Knowledge Representation Framework Considering Geo-Processes. Trans. GIS 2024, 29, e13270. [Google Scholar] [CrossRef]
- Mao, W.; Shen, J.; Su, Q.; Liu, S.; Pirasteh, S.; Ishii, K. A Method for Constructing an Urban Waterlogging Emergency Knowledge Graph Based on Spatiotemporal Processes. ISPRS Int. J. Geo-Inf. 2024, 13, 349. [Google Scholar] [CrossRef]
- Zhu, Y.; Sun, K.; Wang, S.; Zhou, C.; Lu, F.; Lv, H.; Qiu, Q.; Wang, X.; Qi, Y. An adaptive representation model for geoscience knowledge graphs considering complex spatiotemporal features and relationships. Sci. China Earth Sci. 2023, 66, 2563–2578. [Google Scholar] [CrossRef]
- Guan, S.; Cheng, X.; Bai, L.; Zhang, F.; Li, Z.; Zeng, Y.; Jin, X.; Guo, J. What is Event Knowledge Graph: A Survey. IEEE Trans. Knowl. Data Eng. 2022, 35, 7569–7589. [Google Scholar] [CrossRef]
- Li, X.; Yang, J.; Guan, X.; Wu, H. An Event-driven Spatiotemporal Data Model (E-ST) Supporting Dynamic Expression and Simulation of Geographic Processes. Trans. GIS 2014, 18, 76–96. [Google Scholar] [CrossRef]
- Liu, W.; Li, X.; Rahn, D.A. Storm event representation and analysis based on a directed spatiotemporal graph model. Int. J. Geogr. Inf. Sci. 2015, 30, 948–969. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, J.; Cao, Y.; Li, S.; Chen, M. A Study on a Spatiotemporal Entity-Based Event Data Model. ISPRS Int. J. Geo-Inf. 2024, 13, 360. [Google Scholar] [CrossRef]
- Han, B.; Qu, T.; Tong, X.; Wang, H.; Liu, H.; Huo, Y.; Cheng, C. AugGKG: A grid-augmented geographic knowledge graph representation and spatio-temporal query model. Int. J. Digit. Earth 2023, 16, 4934–4957. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, J.; Cao, Y.; Yang, F.; Yang, Z.; Fan, X. Spatio-temporal knowledge embedding method considering the lifecycle of geographical entities. Int. J. Appl. Earth Obs. Geoinf. 2024, 131, 103967. [Google Scholar] [CrossRef]
- Yan, B. Geographic Knowledge Graph Summarization; IOS Press: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Qiu, Q.; Li, H.; Hu, X.; Tian, M.; Ma, K.; Zhu, Y.; Sun, K.; Li, W.; Wang, S.; Xie, Z. A Knowledge-Guided Spatio-Temporal Correlation Measure Considering Rules and Dependency Syntax for Knowledge Graph Adaptive Representation. Trans. GIS 2024, 29, e13288. [Google Scholar] [CrossRef]
- Huang, Y.; Yuan, M.; Sheng, Y.; Min, X.; Cao, Y. Using Geographic Ontologies and Geo-Characterization to Represent Geographic Scenarios. ISPRS Int. J. Geo-Inf. 2019, 8, 566. [Google Scholar] [CrossRef]
- Parker, D.C.; Manson, S.M.; Janssen, M.A.; Hoffmann, M.J.; Deadman, P. Multi-Agent Systems for the Simulation of Land-Use and Land-Cover Change: A Review. Ann. Assoc. Am. Geogr. 2008, 93, 314–337. [Google Scholar] [CrossRef]
- Hu, D.; Du, X.; Li, L.; Sun, Y.; Zhang, J.; Bai, F. Robust stability mechanism of an artificial ecosystem based on biological mutations and synergies driven by ecological information. Ecol. Model. 2016, 319, 208–217. [Google Scholar] [CrossRef]
- You, J.; Huai, Y.; Nie, X.; Chen, Y. Real-time 3D visualization of forest fire spread based on tree morphology and finite state machine. Comput. Graph. 2022, 103, 109–120. [Google Scholar] [CrossRef]






| Question | Results | |||
|---|---|---|---|---|
| GeoKG | GEKG | STOKG | STEHRG | |
| Q1: When did WHU use its name National Wuchang University? | • 1925/01 <National Wuchang University, State_of_1925/01 > | • 1925-01-01 <WHU V5, 1925-01-01, National Wuchang University > | • 1925-01-01, 1926-10-01 <WHU V5, End_time, 1926-10-01 > <WHU V5, Start_time, 1925-01-01 > | • 1925-01-01, 1926-10-01 <WHU V5, End_time, 1926-10-01> <WHU V5, Start_time, 1925-01-01> |
| Q2: Where was the campus of WHU from 1925 to 1935? | • Wuchang Dongchangkou <WHU, 1925-01-01, Wuchang Dongchangkou> • Wuchang Dongchangkou <WHU, 1926-10-01, Wuchang Dongchangkou> • Wuchang Dongchangkou <WHU, 1928-07-01, Wuchang Dongchangkou> • Wuchang Luojia Hill <WHU, 1932-03-01, Wuchang Luojia Hill> | • Wuchang Dongchangkou <WHU V5, 1925-01-01, Location, Wuchang Dongchangkou> • Wuchang Dongchangkou <WHU V6, 1926-10-01, Location, Wuchang Dongchangkou> • Wuchang Dongchangkou <WHU V7, 1928-07-01, Location, Wuchang Dongchangkou> • Wuchang Luojia Hill <WHU V8, 1932-03-01, Location, Wuchang Luojia Hill> | • Wuchang Dongchangkou <WHU V5, 1925-01-01, Location, Wuchang Dongchangkou> • Wuchang Dongchangkou <WHU V6, 1926-10-01, Location, Wuchang Dongchangkou> • Wuchang Dongchangkou <WHU V7, 1928-07-01, Location, Wuchang Dongchangkou> • Wuchang Luojia Hill <WHU V8, 1932-03-01, Location, Wuchang Luojia Hill> | • Wuchang Dongchangkou <Location, Wuchang Dongchangkou> • Wuchang Luojia Hill <Location, Wuchang Luojia Hill> |
| Q3: What are the governing units of WHU since its establishment? | • <WHU, State_of_1893/01, Qing government> • <WHU, State_of_1902/10, Qing government> • <WHU, State_of_1913/07, Republic of China> • <WHU, State_of_1923/09, Republic of China > • <WHU, State_of_1925/01, Republic of China > • <WHU, State_of_1926/10, Republic of China > • <WHU, State_of_1928/07, Republic of China > • <WHU, State_of_1932/03, Republic of China > • <WHU, State_of_1938/01, Republic of China > • <WHU, State_of_1946/01, Republic of China > • <WHU, State_of_1949/08, China > | • <WHU V1, Qing government> • <WHU V2, Qing government> • <WHU V3, Republic of China> • <WHU V4, Republic of China> • <WHU V5, Republic of China> • <WHU V6, Republic of China> • <WHU V7, Republic of China> • <WHU V8, Republic of China> • <WHU V9, Republic of China> • <WHU V10, Republic of China> • <WHU V11, China> | • Qing government <WHU, Leader, Qing government> • Republic of China <WHU, Leader, Republic of China > • China <WHU, Leader, China> | • Qing government <WHU, Leader, Qing government> • Republic of China <WHU, Leader, Republic of China > • China <WHU, Leader, China> |
| Q4: How many states did WHU have from 1926 to 1940? | • State_of_1926/10 <State_of_1926/10, State, WHU > • State_of_1928/07 <State_of_1928/07, State, WHU > • State_of_1932/03 <State_of_1932/03, State, WHU > • State_of_1938/01 <State_of_1938/01, State, WHU > | • Wuhan University V6 <WHU V6,1926-10-01> • Wuhan University V7 <WHU V7,1928-07-01> • Wuhan University V8 <WHU V8,1932-03-01> • Wuhan University V9 <WHU V9,1938-01-01> | • Wuhan University V6 <WHU, version, WHU V6> • Wuhan University V7 <WHU, version, WHU V7> • Wuhan University V8 <WHU, version, WHU V8> • Wuhan University V9 <WHU, version, WHU V9> | • Wuhan University V6 <WHU, State, WHU V6> • Wuhan University V7 <WHU, State, WHU V7> • Wuhan University V8 <WHU, State, WHU V8> • Wuhan University V9 <WHU, State, WHU V9> |
| Q5: What have been the changes since WHU moved from Wuchang Dongchangkou to Wuchang Luojia Hill? | • Location_Change <State_of_1928/07, Location_Change, State_of_1932/03> • Time_Change <State_of_1928/07, Time_Change, State_of_1932/03> | • 1928-07-01, Time_Change, 1932-03-01 • Wuchang Dongchangkou, Location_Change, Wuchang Luojia Hill <WHU V7, Time, 1928-07-01, Leader, Republic of China, Name, Wuhan National University, Location, Wuchang Dongchangkou> <WHU V8, Time, 1932-03-01, Leader, Republic of China, Name, Wuhan National University, Location, Wuchang Luojia Hill> | • Location_Change <WHU V7, Location_Change, WHU V8> • Time_Change <WHU V7, Time_Change, WHU V8> | • Wuchang Dongchangkou, Location_Change, Wuchang Luojia Hill <WHU V7, Location_Change {Vo: “ Wuchang Dongchangkou”, Vt: “Wuchang Luojia Hill”, Vname: “Location”}, WHU V8 > • 1928-07-01, Time_Change, 1932-03-01 <WHU V7, Time_Change {Vo: “1928-07-01”, Vt: “1932-03-01”, Vname: “Time”}, WHU V8 > |
| Q6: Why did WHU change its name to Wuhan National University? | • / | • Restructure Event,1928-07-01 <Restructure Event, Action, Restructure, Time, 1928-07-01> | • Restructure Event, 1928-07-01 <Restructure Event, Action, Restructure, Time, 1928-07-01> | • Restructure Event, 1928-07-01 <Restructure Event, Action, Restructure, Time, 1928-07-01, Name, National Wuchang Zhongshan University, Wuhan National University > |
| Question | Results | |||
|---|---|---|---|---|
| GeoKG | GEKG | STOKG | STEHRG | |
| Q1: When did the NJPPA use its name the Nationalist Government? | • 1927/04 <The Nationalist Government, State_of_1927/04> | • 1927-04-01 <NJPPA V9, 1927-04-01, The Nationalist Government> | • 1927-04-01, 1937-12-01 <NJPPA V9, End_time, 1937-12-01> <NJPPA V9, Start_time, 1927-04-01> | • 1927-04-01, 1937-12-01 <NJPPA V9, End_time, 1937-12-01> <NJPPA V9, Start_time, 1927-04-01> |
| Q2: Where was the address of the NJPPA from 1912 to 1927 during the Republic of China period? | • 292 Changjiang Road <1 January 1912, 292 Changjiang Road> • 292 Changjiang Road <1 April 1912, 292 Changjiang Road > • 292 Changjiang Road < 1 April 1927, 292 Changjiang Road > | • 292 Changjiang Road <NJPPA V7, 292 Changjiang Road> • 292 Changjiang Road <NJPPA V8, 292 Changjiang Road > • 292 Changjiang Road < NJPPA V9, 292 Changjiang Road > | • 292 Changjiang Road <NJPPA V7, 292 Changjiang Road> • 292 Changjiang Road <NJPPA V8, 292 Changjiang Road > • 292 Changjiang Road <NJPPA V9, 292 Changjiang Road > | • 292 Changjiang Road <Location, 292 Changjiang Road> |
| Q3: What are the governing units of NJPPA since its establishment? | • <State_of_1368/01, Ming Dynasty> • <State_of_1647/01, Qing Dynasty> • <State_of_1665/07, Qing Dynasty> • <State_of_1853/03, Taiping Dynasty> • <State_of_1864/01, Qing Dynasty> • <State_of_1870/01, Qing Dynasty> • <State_of_1912/01, Republic of China> • <State_of_1912/04, Republic of China> • <State_of_1927/04, Republic of China> • <State_of_1937/12, Puppet Regime> • <State_of_1946/05, Republic of China> • <State_of_1949/04, P.R.China> • <State_of_1982/01, P.R.China> | • <NJPPA V1, Ming Dynasty> • <NJPPA V2, Qing Dynasty > • <NJPPA V3, Qing Dynasty > • <NJPPA V4, Taiping Dynasty > • <NJPPA V5, Qing Dynasty > • <NJPPA V6, Qing Dynasty > • <NJPPA V7, Republic of China > • <NJPPA V8, Republic of China > • <NJPPA V9, Republic of China > • <NJPPA V10, Puppet Regime > • <NJPPA V11, Republic of China > • <NJPPA V12, P.R.China > • <NJPPA V13, P.R.China > | • Ming Dynasty <NJPPA, Leader, Ming Dynasty> • Qing Dynasty <NJPPA, Leader, Qing Dynasty> • Taiping Dynasty <NJPPA, Leader, Taiping Dynasty> • Republic of China <NJPPA, Leader, Republic of China> • Puppet Regime <NJPPA, Leader, Puppet Regime> • P.R.China <NJPPA, Leader, P.R.China> | • Ming Dynasty <NJPPA, Leader, Ming Dynasty> • Qing Dynasty <NJPPA, Leader, Qing Dynasty> • Taiping Dynasty <NJPPA, Leader, Taiping Dynasty> • Republic of China <NJPPA, Leader, Republic of China> • Puppet Regime <NJPPA, Leader, Puppet Regime> • P.R.China <NJPPA, Leader, P.R.China> |
| Q4: How many states did NJPPA have from 1926 to 1946 | • State_of_1927/04 <State_of_1927/04, State, NJPPA> • State_of_1937/12 <State_of_1937/12, State, NJPPA > • State_of_1946/05 <State_of_1946/05, State, NJPPA> | • NJPPA V9 <NJPPA V9, 1927-04-01> • NJPPA V10 <NJPPA V10, 1937-12-01> • NJPPA V11 <NJPPA V11, 1946-05-01> | • NJPPA V9 <NJPPA, version, NJPPA V9> • NJPPA V10 <NJPPA, version, NJPPA V10> • NJPPA V11 <NJPPA, version, NJPPA V11> | • NJPPA V9 <NJPPA, State, NJPPA V9> • NJPPA V10 <NJPPA, State, NJPPA V10> • NJPPA V11 <NJPPA, State, NJPPA V11> |
| Q5: What changes have occurred in the renaming of NJPPA from the Office of Liangjiang Governor to the Interim Government of the Repub-lic of China? | • Attribute_Change <State_of_1870/01, Attribute_Change, State_of_1912/01> • Time_Change <State_of_1870/01, Time_Change, State_of_1912/01> | • 1870-05-01, Time_Change, 1912-01-01 • Qing Dynasty, Attribute_Change, Republic of China <NJPPA V6, Time, 1870-05-01, Leader, Qing Dynasty, Location, 292 Changjiang Road, Name, The Office of Liangjiang Governor> <NJPPA V7, Time, 1912-01-01, Leader, Republic of China, Location, 292 Changjiang Road, Name, The Interim Government of the Republic of China> | • Attribute_Change <NJPPA V6, Attribute_Change, NJPPA V7 > • Time_Change <NJPPA V6, Time_Change, NJPPA V7 > | • The Office of Liangjiang Governor, Name_Change, The Interim Government of the Republic of China <NJPPA V6, Name_Change {Vo: “The Office of Liangjiang Governor”, Vname: “Name”, Vt: “The Interim Government of the Republic of China”} NJPPA V7 > • 1870-05-01, Time_Change, 1912-01-01 <NJPPA V6, Time_Change {Vo: “1870-05-01”,Vname: “Time”, Vt: “1912-01-01”}, NJPPA V7> • Qing Dynasty, Leader_Change, Republic of China <NJPPA V6, Leader_Change {Vo: “Qing Dynasty”, Vt: “Republic of China”, Vname: “Leader”}, NJPPA V7> |
| Q6: Why did NJPPA change its name to The Nationalist Government? | • / | • Recover Event, 1927-04-01 <Recover Event, Action, Recover, 1927-04-01> | • Recover Event, 1927-04-01 <Recover Event, Action, Recover, Time, 1927-04-01> | • Recover Event, 1927-04-01 <Recover Event, Action, Recover, Time, 1927-04-01, Name, The Nationalist Government, Nanjing Rear Manson> |
| Data | Data1 | Data2 | … | Data2256 |
|---|---|---|---|---|
| Name | 462810245 | 477002300 | … | 477024900 |
| Class | ship | ship | … | ship |
| Time | 4 June 2019 01:16:00 | 4 June 2019 00:50:00 | … | 4 June 2019 00:12:00 |
| Length | 17 | 172.2 | … | 143.19 |
| Width | 4 | 27.5 | … | 22.82 |
| Heading | 347.5 | 17.2 | … | 70.7 |
| Sea area | South China Sea | Eastern China Sea | … | Philippine Sea |
| Longitude | 111.109924 | 121.656105 | … | 137.889830 |
| Latitude | 20.207317 | 31.339144 | … | 34.204080 |
| Question | Results | |||
|---|---|---|---|---|
| GeoKG | GEKG | STOKG | STEHRG | |
| Q1: When did entity “477089200” have a heading of 228.5? | • 20:00 <477089200, State_of_20:00, Heading:228.5> | • 20:00 <477089200, State_of_20:00-21:00, Heading:228.5> | • 20:00,22:00 <4477089200, 477089200_V10, Heading:228.5, starttime: 20:00:00, endtime: 22:00:00> | • 20:00,22:00 <4477089200, 477089200_V10, Heading:228.5, starttime: 20:00:00, endtime: 22:00:00> |
| Q2: Which sea areas did entity “477752300” transit through between 8 AM and 4 PM? | • Eastern China Sea <477752300, State_of_8:00, Eastern China Sea> • Eastern China Sea <477752300, State_of_10:00, Eastern China Sea> • Eastern China Sea <477752300, State_of_12:00, Eastern China Sea> • Yellow Sea <477752300, State_of_14:00, Yellow Sea> • Yellow Sea <477752300, State_of_16:00, Yellow Sea> | • Eastern China Sea <477752300_V4, 8:00, Eastern China Sea> • Eastern China Sea <477752300_V5, 10:00, Eastern China Sea> • Eastern China Sea <477752300_V6, 12:00, Eastern China Sea> • Yellow Sea <477752300_V7, 14:00, Yellow Sea> • Yellow Sea <477752300_V8, 16:00,Yellow Sea> | • Eastern China Sea <477752300, 477752300_V4, Eastern China Sea> • Eastern China Sea <477752300, 477752300_V5, Eastern China Sea> • Eastern China Sea <477752300, 477752300_V6, Eastern China Sea> • Yellow Sea <477752300, 477752300_V7, Yellow Sea> • Yellow Sea <477752300, 477752300_V8, Yellow Sea> | • Yellow Sea <seaarea, Yellow Sea> • Eastern China Sea <seaarea, Eastern China Sea> |
| Q3: Which sea areas did entity “477752300” pass through during the entire voyage? | • <477752300, State_of_0:00, Eastern China Sea> • <477752300, State_of_2:00, Eastern China Sea> • <477752300, State_of_4:00, Eastern China Sea> • <477752300, State_of_6:00, Eastern China Sea> • <477752300, State_of_8:00, Eastern China Sea> • <477752300, State_of_10:00, Eastern China Sea> • <477752300, State_of_12:00, Eastern China Sea> • <477752300, State_of_14:00, Yellow Sea> • <477752300, State_of_16:00, Yellow Sea> • <477752300, State_of_18:00, Yellow Sea> • <477752300, State_of_20:00, Yellow Sea> • <477752300, State_of_22:00, Yellow Sea> | • <477752300, 477752300_V0, 0:00, Eastern China Sea> • <477752300, 477752300_V1, 2:00, Eastern China Sea> • <477752300, 477752300_V2, 4:00, Eastern China Sea> • <477752300, 477752300_V3, 6:00, Eastern China Sea> • <477752300, 477752300_V4, 8:00, Eastern China Sea> • <477752300, 477752300_V5,10:00, Eastern ChinaSea> • <477752300, 477752300_V6,12:00, Eastern China Sea> • <477752300, 477752300_V7, 14:00, Yellow Sea> • <477752300, 477752300_V8, 16:00, Yellow Sea> • <477752300, 477752300_V9, 18:00, Yellow Sea> • <477752300, 477752300_V10, 20:00, Yellow Sea> • <477752300, 477752300_V11, 22:00, Yellow Sea> | • Yellow Sea <477752300, Yellow Sea> • Eastern China Sea <477752300, Eastern China Sea> | • Yellow Sea <477752300, Yellow Sea> • Eastern China Sea <477752300, Eastern China Sea> |
| Q4: How many states did entity “477089200” have between 8 AM and 12 AM? | • State_of_12:00 <477089200, state, State_of_12:00> • State_of_10:00 <477089200, state, State_of_10:00> • State_of_8:00 <477089200, state, State_of_8:00> | • 477089200_V4 <477089200_V4> • 477089200_V5 <477089200_V5> • 477089200_V6 <477089200_V6> | • 477089200_V4 <477089200, state, 477089200_V4> • 477089200_V5 <477089200, state, 477089200_V5> • 477089200_V6 <477089200, state, 477089200_V6> | • 477089200_V4 <477089200, state, 477089200_V4> • 477089200_V5 <477089200, state, 477089200_V5> • 477089200_V6 <477089200, state, 477089200_V6> |
| Q5: What changes occurred to entity “477752300” between 12 PM and 2 PM? | • Time_Change <477752300, State_of_12:00, Time_Change, State_of_14:00> • Location_Change <477752300, State_of_12:00, Location_Change, State_of_ 14:00> • Attribute_Change <477752300, State_of_12:00, Attribute_Change, State_of_ 14:00> | • 12:00,Time_Change, 14:00 • Eastern China Sea, Attribute _Change, Yellow Sea • 357.5, Attribute_Change, 355.5 • (122.40972;32.99262),Location_Change, (122.39326;33.30427) <time:12:00:00, hending:357.5, seaarea:Eastern China Sea, size:(length:261.1 m; width:32.25 m), location:(122.40972;32.99262)> <time:14:00:00, hending:355.5, seaarea:Yellow Sea, size:(length:261.1 m; width:32.25 m), location: (122.39326;33.30427)> | • 12:00,Time_Change, 14:00 • Eastern China Sea, Attribute _Change, Yellow Sea • 357.5, Attribute_Change, 355.5 • (122.40972;32.99262),Location_Change, (122.39326;33.30427) <time:12:00:00, hending:357.5, seaarea:Eastern China Sea, size:(length:261.1 m; width:32.25 m), location:(122.40972;32.99262)> <time:14:00:00, hending:355.5, seaarea:Yellow Sea, size:(length:261.1 m; width:32.25 m), location: (122.39326;33.30427)> | • 12:00,Time_Change,14:00 <477752300_V6, Time_Change {‘Vo’: ‘14:00:00’, ‘Vt’: ‘16:00:00’, ‘Vname’: ‘Time’}, 477752300_V7> • Eastern China Sea, Location_Change, Yellow Sea <477752300_V6, Attribute_Change {‘Vo’: ‘Eastern China Sea’, ‘Vname’: ‘Seaarea’, ‘Vt’: ‘Yellow Sea’}, 477752300_V7> • (122.40972;32.99262), Location_Change, (22.39326;33.30427). <477752300_V6, Location_Change {‘Vo’: ‘(122.40972;32.99262)’, ‘Vt’: ‘(122.39326;33.30427)’, ‘Vname’: ‘Location’}, 477752300_V7> • 357.5, Attribute_Change, 355.5 < 477752300_V6, Attribute_Change {‘Vo’: ‘357.5’, ‘Vname’: ‘Heading’, ‘Vt’: ‘355.5’}, 477752300_V7> |
| Q6: Why did the heading of entity “477967300” change between 5 PM and 6 PM? | - | • Earthquake Event, 17:46 <Earthquake, Earthquake Event, 17:46> | • Earthquake Event, 17:46 <Earthquake, Earthquake Event, 17:46> | • Earthquake Event, 17:46 <Earthquake Event, Action, Earthquake, 17:46, Heading, 11.2, 19.1 > |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, F.; Zhang, P.; Zhang, Q.; Zhang, Y.; Wang, A. Representing the Spatiotemporal State Evolution of Geographic Entities as a Multi-Level Graph. ISPRS Int. J. Geo-Inf. 2025, 14, 252. https://doi.org/10.3390/ijgi14070252
Yuan F, Zhang P, Zhang Q, Zhang Y, Wang A. Representing the Spatiotemporal State Evolution of Geographic Entities as a Multi-Level Graph. ISPRS International Journal of Geo-Information. 2025; 14(7):252. https://doi.org/10.3390/ijgi14070252
Chicago/Turabian StyleYuan, Feng, Penglin Zhang, Qi Zhang, Yu Zhang, and Anni Wang. 2025. "Representing the Spatiotemporal State Evolution of Geographic Entities as a Multi-Level Graph" ISPRS International Journal of Geo-Information 14, no. 7: 252. https://doi.org/10.3390/ijgi14070252
APA StyleYuan, F., Zhang, P., Zhang, Q., Zhang, Y., & Wang, A. (2025). Representing the Spatiotemporal State Evolution of Geographic Entities as a Multi-Level Graph. ISPRS International Journal of Geo-Information, 14(7), 252. https://doi.org/10.3390/ijgi14070252






