Urban Grid Population Inflow Prediction via POI-Enhanced Conditional Diffusion with Dual-Dimensional Attention

Abstract

Accurate prediction of urban grid-scale population inflow is crucial for smart city management and emergency response. However, existing methods struggle to model spatial heterogeneity and quantify prediction uncertainty, limiting their accuracy and decision-support capabilities. This paper proposes PDCDM (POI-enhanced Dual-Dimensional Conditional Diffusion Model), which integrates urban functional semantic awareness with conditional diffusion modeling. The model captures urban functional attributes through multi-scale Point of Interest (POI) feature representations and incorporates them into the diffusion generation process. A dual-dimensional Transformer architecture is employed to decouple the modeling of temporal dependencies and inter-grid interactions, enabling adaptive fusion of grid-level features with dynamic temporal patterns. Building upon this dual-dimensional modeling framework, the conditional diffusion mechanism generates probabilistic predictions with explicit uncertainty quantification. Real-world urban dataset validation demonstrates that PDCDM significantly outperforms existing state-of-the-art methods in prediction accuracy and uncertainty quantification. Comprehensive ablation studies validate the effectiveness of each component and confirm the model’s practicality in complex urban scenarios.

1. Introduction

Urban grid-scale population inflow prediction plays a pivotal role in smart city management and emergency decision-making. Based on historical flow data, population inflow prediction models estimate future inflow across urban grids, which is critical for optimizing urban planning, improving traffic control, enhancing emergency response, and allocating public service resources efficiently [1,2]. With accelerating urbanization and increasing demands for fine-grained urban management, population inflow prediction has emerged as a key research priority in urban computing and smart city domains [3]. However, urban population mobility exhibits significant spatiotemporal heterogeneity, as the underlying temporal data are governed by both periodic temporal regularities and urban spatial functional structures, thereby posing substantial challenges for accurate prediction.

Existing urban population prediction methods are primarily grounded in two paradigms: traditional time series analysis and deep learning techniques [4,5]. Traditional statistical models, including Autoregressive Integrated Moving Average (ARIMA) [6], Vector Autoregression (VAR) [7], and Kalman Filter [8], offer theoretical advantages and interpretability in capturing linear temporal trends but struggle to handle complex nonlinear relationships and high-dimensional spatial features. The emergence of deep learning methods has enabled new breakthroughs in complex forecasting tasks. Recurrent Neural Networks (RNNs) [9] and their variants, such as Long Short-Term Memory (LSTM) [10] and Gated Recurrent Unit (GRU) [11], have demonstrated strong capabilities in modeling sequential dependencies. Furthermore, graph-based approaches, including Graph Neural Networks (GNNs) [12], Graph Attention Networks (GATs) [13], and Spatiotemporal Graph Convolutional Networks (STGCNs) [14], have achieved significant progress in modeling spatial correlations. However, these methods predominantly rely on deterministic modeling frameworks that provide only deterministic point estimates without quantifying predictive uncertainty [15,16]. This limitation is particularly critical in practical urban management applications: decision-makers require not only predicted values but also assessments of prediction reliability and potential risks to formulate robust management strategies.

Despite the substantial progress achieved in spatiotemporal modeling, most existing studies continue to employ deterministic architectures that produce point estimates and neglect explicit uncertainty quantification. In contrast, some recent studies have begun to incorporate probabilistic reasoning into graph-based spatiotemporal frameworks. For example, Wang et al. [17] proposed the Prob-GNN framework for quantifying spatiotemporal uncertainty in urban travel flow prediction, marking one of the first attempts to embed probabilistic graph neural networks into traffic forecasting. Similarly, Gao et al. [18] developed an uncertainty-aware probabilistic graph learning model that explicitly captures prediction variance across multiple forecast steps for traffic risk assessment. While these approaches have demonstrated the potential of PGNNs to model spatiotemporal uncertainties, they still rely on indirect approximations for uncertainty estimation and suffer from limited calibration fidelity, leaving notable gaps in robust and scalable probabilistic prediction.

Uncertainty quantification is critical for urban prediction tasks. Existing uncertainty modeling approaches, such as Bayesian Neural Networks [19,20] and Deep Gaussian Processes [21], attempt to incorporate uncertainty estimation into neural network frameworks but often suffer from high computational complexity, convergence difficulties, or overly restrictive assumptions. In practical applications, uncertainty information provides direct value for decision-making. For instance, Figure 1 illustrates the predicted passenger flow at subway stations. As shown in the black-boxed region, deterministic methods fail to indicate prediction reliability. In contrast, the probabilistic approach reveals substantially higher uncertainty (depicted by the green shaded area), suggesting potential passenger flow surges in this region. Therefore, developing methods that simultaneously deliver accurate predictions and reliable uncertainty estimates is of paramount importance.

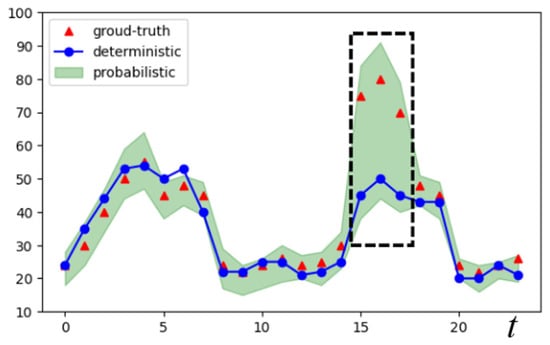
Figure 1. Motivation of probabilistic prediction.

In recent years, the advent of generative artificial intelligence has engendered novel paradigms for addressing complex prediction problems. Recent studies have investigated Variational Autoencoders (VAEs) [22] and Generative Adversarial Networks (GANs) [23] as effective tools for probabilistic representation and sample-based uncertainty modeling. Huang et al. [24] proposed a VAE-based generative model of urban human mobility that combines a latent variable architecture with a sequence-to-sequence structure, enabling realistic reconstruction and simulation of mobility trajectories under data sparsity. Mo, Fu, and Di [25] developed a PhysGAN-TSE and explicitly quantified uncertainty by integrating stochastic traffic flow models into the adversarial training process. These studies demonstrate the effectiveness of generative models in representing probabilistic distributions of urban dynamics. However, their adversarial or variational inference mechanisms often lead to unstable training, insufficient probabilistic calibration, and limited scalability in large-scale forecasting tasks.

Building on the progress of generative modeling, diffusion models have recently emerged as a powerful and theoretically grounded alternative. As a distinctive class of generative methods, diffusion models exhibit stronger training stability and sample quality compared with VAEs and GANs. Representative variants include Denoising Diffusion Probabilistic Models (DDPMs) [26,27], Score-based Generative Models [28,29], and SDE-based Diffusion Models [30]. These approaches achieve probabilistic forecasting by iteratively perturbing and reconstructing data through controlled noise processes. Recent studies have further demonstrated the effectiveness of diffusion mechanisms for time-series forecasting. Biloš et al. [31] introduced a function-space diffusion framework that models temporal dynamics as continuous stochastic processes. Their method defines perturbation and denoising operations directly on continuous functions, allowing the model to handle irregularly sampled sequences and produce calibrated probabilistic forecasts through stochastic process diffusion. Yuan et al. [32] extended the use of diffusion mechanisms to spatio-temporal point processes by proposing a unified probabilistic framework capable of learning complex joint spatial-temporal distributions. They incorporated a spatio-temporal co-attention module to capture interdependent features between event time and location, yielding significant performance improvements across tasks such as epidemic spread, urban mobility, and crime prediction. Although these studies reveal the strong capability of diffusion mechanisms for modeling stochastic temporal dependencies, there remains no research applying diffusion models to urban grid-scale population inflow prediction or integrating functional semantic information such as POI attributes as conditional guidance.

Urban functional heterogeneity is a key factor influencing population mobility patterns, as well as a core challenge for diffusion models in urban prediction. Studies in spatial econometrics and geographic information science [33,34] demonstrate that different functional zones, due to variations in service types, facility density, and spatial accessibility, exhibit distinctly different population agglomeration dynamics and temporal variations. POIs, as direct proxies for urban functions [35], encode rich spatial semantics: commercial areas exhibit significant commuting attractiveness on weekdays, and educational facility vicinities display typical tidal flow patterns, while residential zones form complementary population flow dynamics with employment centers. These spatial functional attributes not only shape the magnitude and temporal distribution of population inflow but also determine the degree and spatial variability of prediction uncertainty.

Given the limitations of existing methods and the practical demands of urban forecasting tasks, this study faces three core challenges: (1) How to quantify uncertainty while providing accurate predictions to meet risk assessment needs in urban management decision-making; (2) How to effectively integrate information about urban spatial heterogeneity, particularly the semantic constraints imposed by POI functional characteristics on population flows; (3) How to design a probabilistic modeling framework suited to the characteristics of urban grid data, handling high-dimensional time-series data in real-world scenarios while maintaining computational efficiency.

Building upon the above analysis, this study proposes PDCDM, a novel urban grid inflow prediction model. PDCDM innovatively integrates urban functional semantic information into the conditional diffusion generation process by extracting static POI features from each grid as conditional guidance. The model employs a dual-dimensional Transformer architecture to separately capture temporal dependencies and inter-grid feature correlations, achieving progressive feature fusion through residual connections. The main contributions of this study can be summarized as follows:

• Introduction of conditional diffusion models to urban grid-scale population inflow prediction, simultaneously achieving accurate point estimates and reliable uncertainty quantification through a probabilistic generative framework, thereby offering a novel modeling paradigm for risk-sensitive urban management decisions.
• Design of a POI-enhanced conditional encoding framework that systematically incorporates urban functional semantics into the diffusion process, enabling the model to capture zone-specific population agglomeration patterns and enhance spatial prediction adaptability.
• Design of a decoupled dual-dimensional attention mechanism that separately models temporal dependencies and inter-grid correlations, thereby enhancing model representation of complex spatiotemporal patterns.
• Comprehensive validation on real-world urban datasets demonstrating that the proposed model outperforms baseline approaches in both prediction accuracy and uncertainty quantification, with systematic ablation studies confirming the effectiveness of each component and the model’s practical utility in complex urban scenarios.

2. Materials and Methods

The core methodology leverages historical population inflow time series as model input, with static grid-level POI features as the primary conditioning signal, enabling predictions that capture actual urban functional zone characteristics. Figure 2 provides an overview of the complete PDCDM workflow, consisting of two major phases: the Training Phase and the Sampling Phase. In the training phase, the historical grid inflow sequences and POI-based conditional information (including the conditional mask, time embeddings, and feature embeddings) are jointly encoded and passed through the conditional denoising network to learn the diffusion process. The model is optimized to recover the true inflow distribution from noisy representations, and the best-performing checkpoint is retained as the trained model. During the sampling phase, Gaussian noise is iteratively denoised using the trained model, guided by the same conditional information to progressively reconstruct the future population inflow over each prediction step. The internal model architecture and implementation details are described later in Section 2.4.

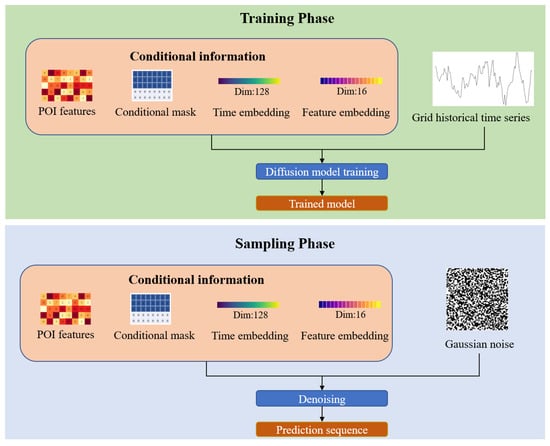
Figure 2. The overall workflow.

2.1. Problem Formulation

The objective of urban grid population flow prediction is to infer the joint future state of population flow across all grid cells given historical observations. Let $X$ denote the historical population flow data over $T$ time steps, defined as follows:

$$X=\left[X_1,X_2,\dots ,X_T\right],$$

(1)

where $X$ represents the historical observation sequence and $T$ is the number of time steps. The population inflow across all grid cells at time step $t$ is denoted as:

$$X_t=\left[x_t^{\left(1\right)},x_t^{\left(2\right)},\dots ,x_t^{\left(N\right)}\right],$$

(2)

where $X_t\in {\mathbb{R}}^N$ represents the population inflow across all grid cells at time step $t$, $N$ is the number of grid cells, and $x_t^{\left(i\right)}$ denotes the inflow to grid $k$. The goal is to predict population inflow over the next $H$ time steps based on historical observations. The prediction $\widehat{Y}$ captures the future inflow across all grids, given by:

$$\widehat{Y}=\left[{\widehat{X}}_{T+1},{\widehat{X}}_{T+2},\dots ,{\widehat{X}}_{T+H}\right],$$

(3)

where $\widehat{Y}$ represents the predicted population inflow sequence, $H$ denotes the number of prediction time steps, and ${\widehat{X}}_{T+h}$ denotes the prediction at the $h$-th future time step.

Each prediction ${\widehat{X}}_{T+h}$ comprises the population inflow across $N$ grid cells, defined as:

$${\widehat{X}}_{T+h}=\left[{\widehat{x}}_{T+h}^{\left(1\right)},{\widehat{x}}_{T+h}^{\left(1\right)},\dots ,{\widehat{x}}_{T+h}^{\left(N\right)}\right],$$

(4)

where ${\widehat{x}}_{T+h}^{\left(i\right)}$ denotes the predicted population inflow for grid cell $i$ at time step $T+h$.

Given historical observations, the goal is to predict population inflow across all grid cells over a future time window. Considering spatial dependencies between grids and POI-based functional characteristics, we define the target prediction set as:

$$\mathcal{Y}==Y^{T_{obs}+1},Y^{T_{obs}+2},\dots ,Y^{T_{obs}+T_{pred}},$$

(5)

where $\mathcal{Y}$ represents the target prediction set, $T_{obs}$ denotes the length of the observation window, $T_{pred}$ denotes the length of the prediction window, and $Y^{T_{obs}+j}$ represents the ground-truth population inflow at the $j$-th prediction time step. During training, we employ supervised learning, while during testing, ground-truth labels are not required. The model input comprises two main components: historical flow dynamics and static grid-level POI features.

Historical flow dynamics comprise the historical population inflow observations across all grid cells during the observation window, defined as:

$$X_{hist}={x_t^{\left(i\right)}}_{t=1,i=1}^{T_{obs},N},$$

(6)

where $X_{hist}$ represents the historical flow dynamics matrix. Each observation can be represented as a three-tuple:

$$x_t^{\left(i\right)}=\left(v_t^{\left(i\right)},p_t,m_t^{\left(i\right)}\right),$$

(7)

where $v_t^{\left(i\right)}$ denotes the observed population inflow for grid cell $i$ at time step $t$, $p_t\in \{\mathrm{0,1},\dots ,T_{obs}-1\}$ is the temporal position index, and $m_t^{\left(i\right)}\in \left\{\mathrm{0,1}\right\}$ is the observation mask, where $m_t^{\left(i\right)}=1$ indicates a valid observation and $m_t^{\left(i\right)}=0$ indicates a missing value.

Static grid-scale POI features are constructed from urban POI data, represented as:

$$P\in {\mathbb{R}}^{N\times D},$$

(8)

where $P$ denotes the complete POI feature matrix and $D$ is the feature dimension. The $i$-th row, $P_i\in {\mathbb{R}}^D$, represents the static POI feature vector for grid cell $i$, encoding the grid’s spatial location and functional attributes derived from POI distributions. These static characteristics remain unchanged throughout the entire prediction process and are used to capture the population attraction differences of different functional areas.

The model output is the future $T_{\mathit{pred}}$ time step long population inflow prediction sequence. Based on the probabilistic prediction paradigm of the model, the model can generate multiple prediction sample sets to quantify uncertainty. Through $S$ random sampling, we can obtain:

$${\mathcal{F}}^{\left(s\right)}=\left\{{\widehat{X}}_{T_{obs}+j}^{\left(s\right)}∣j=\mathrm{1,2},\dots ,T_{\mathit{pred}}\right\},s=\mathrm{1,2},\dots ,S,$$

(9)

where ${\mathcal{F}}^{\left(s\right)}$ represents the prediction sequence obtained by the $s$-th sampling, and ${\widehat{X}}_{T_{obs}+j}^{\left(s\right)}$ represents the sample prediction value at time $T_{obs}+j$ of the $s$-th sample.

2.2. Data Preparation

In order to evaluate the proposed framework for the multivariate spatiotemporal prediction of urban grid population inflow, we have used a Beijing dataset from Amap (Gaode Map), a Chinese navigation and mapping service operated by Alibaba Group, alongside the relevant POI data. The model input comprises two main components: time-series population inflow across grid cells and grid-level contextual features. Prior research [36] has shown that geographical factors such as land use, topography, and urban planning significantly influence population distribution patterns. Accordingly, we incorporate static POI features as spatial attributes for grid cells to enhance inflow prediction.

The population inflow data consist of grid-level records for Beijing, collected via the Amap API and spanning a period of 10 months from September 2023 to June 2024. Observations are recorded at 15 min intervals, yielding 96 time steps per day. To focus on areas with high activity, the top 10% of grid cells are selected based on their average inflow intensity.

In order to capture spatial heterogeneity and functional characteristics, we extracted 64-dimensional POI features from Beijing POI data. These features encompass a variety of urban elements, such as transport hubs, leisure and recreation facilities, and commercial districts. Taking into account the spatial spillover effects of urban functions, whereby POI distributions in neighboring grids influence population flows in target grids, we use Kernel Density Estimation (KDE) to aggregate neighborhood POI features spatially. Specifically, for each grid cell $g$ and category $c$, we identify the $k=32$ nearest POI points and compute the spatial density using a Gaussian kernel:

$$KD{E}_g^c={\displaystyle \frac{1}{2\mathsf{\pi }{h}^2}}{\sum }_{i=1,d_{gi}\ge r}^k\exp \left(-{\displaystyle \frac{d_{gi}^2}{2h^2}}\right),$$

(10)

where $d_{gi}$ denotes the distance from the center of grid cell $g$ to the $i$-th POI, $h$ is the kernel bandwidth parameter, and $r=0.35$ is the exclusion radius. We only consider POI points at distances greater than $r$ to avoid double-counting POI density within the grid itself, ensuring that the KDE features better capture spatial dependencies and neighborhood characteristics. These neighborhood features reflect the functional intensity of surrounding areas, enabling the model to better encode local geographic context.

Finally, the static features for each grid cell comprise two components: (1) POI category counts within the grid cell and spatial coordinates (reflecting intrinsic functional attributes), and (2) KDE-based neighborhood density features (capturing surrounding spatial context) [37]. All POI features undergo log1p transformation and Z-score standardization to stabilize numerical ranges and accelerate model convergence. Additionally, to encode geographic location, we apply 2D sine-cosine positional encoding to the latitude and longitude coordinates of grid centers, generating 32-dimensional spatial embeddings. To ensure spatial alignment between time-series observations and static features, we align the datasets by taking the intersection of grid IDs, ensuring that each grid cell has complete temporal records and corresponding static features.

Since the model uses a time-series forecasting framework, the data is converted into fixed-length sequences using a sliding window approach. Each sequence comprises 576 time steps, consisting of a 480-step historical window (five days of observations) and a 96-step prediction window (one-day forecast horizon). This configuration is suitable for urban planning scenarios where decision-makers require short-term forecasts based on recent observations. Figure 3 illustrates the sliding window partitioning scheme.

Figure 3. Time series segmentation structure.

To stabilize model training and accelerate convergence, we applied Z-score normalization to the temporal inflow data at the grid level:

$$x_{t,g}^{norm}={\displaystyle \frac{x_{t,g}-{\mu }_g}{{\sigma }_g}},$$

(11)

where $x_{t,g}$ denotes the observed inflow for grid cell $g$ at time step $t$, and ${\mu }_g$ and ${\sigma }_g$ are the mean and standard deviation for grid cell $g$ across the entire observation period, respectively.

To enable conditional generation in the diffusion model, we construct two binary masks for each sequence. The observation mask ($M_{obs}$) indicates data availability. Since our dataset is complete, $M_{obs}$ is set to 1 at all time steps. The ground-truth mask ($M_{gt}$) distinguishes between historical and future time steps: $M_{gt}$ is set to 1 during the observation window (training region) and 0 during the prediction window (target region). This masking strategy enables the model to learn conditional mappings from observed historical data to unobserved future values.

To ensure robust generalization across temporal patterns, we use a stratified monthly sampling strategy to partition the dataset. Specifically, we split the 10-month dataset into training (70%), validation (15%), and test (15%) sets, drawing samples proportionally from each month. For each month $m$, we calculate the total number of days $D_m$, generate candidate samples based on time step indices, and allocate them proportionally to the three subsets. This stratified approach ensures that each month is proportionally represented in all subsets, mitigating temporal bias from seasonal variations or specific time periods. Unlike spatial partitioning strategies, our approach is temporal-only: all grid cells are shared across training, validation, and test sets, but with non-overlapping time windows to prevent data leakage. Figure 4 illustrates the dataset partitioning scheme across months. Table 1 defines the structure and dimensions of the input data, while Table 2 summarizes the statistical information and partitioning configuration of the final dataset. The final dataset comprises 23,434 time series samples, covering 5853 high-traffic grids and a 10-month observation period.

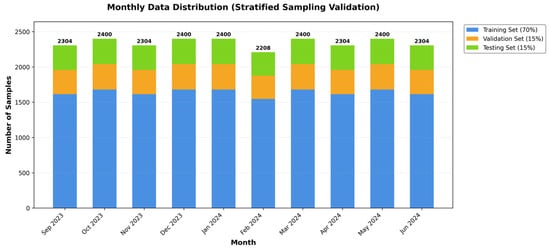
Figure 4. Distribution of monthly data.

Table 1. Input Data Structure and Dimensions.

Data Type	Dimension	Description
Temporal Inflow Data	29,184 × 5853	Z-score normalized inflow values
Observation Mask	576 × 5853	Binary mask: 1 for observed, 0 for missing
Ground Truth Mask	576 × 5853	Binary mask: 1 for history, 0 for forecast
Static POI Features	5853 × 64	Count and KDE-based neighborhood features (log1p + Z-score)
Time Position Index	576	Sequential time step indices [0, 575]
Grid Identifier	5853	Unique grid cell identifiers [0, 5852]

Table 2. Dataset Statistics and Split Configuration.

Subset	Samples	Ratio	Sampling Strategy
Training Set	16,398	70%	Stratified monthly sampling
Validation Set	3511	15%	Stratified monthly sampling
Testing Set	3525	15%	Stratified monthly sampling
Total	23,434	100%
Study Period: September 2023–June 2024|Temporal Resolution: 15 min|Batch Size: 8

2.3. Conditional Diffusion Model

This study employs diffusion probabilistic models as our generative framework for predicting grid-scale population inflow. Specifically, we leverage a conditional variant of the Denoising Diffusion Probabilistic Model (DDPM) to forecast population inflow across grid cells. Below, we present the formulation of the original DDPM and describe how we adapt it for conditional grid-scale population inflow forecasting by incorporating POI spatial features as conditional inputs.

2.3.1. Denoising Diffusion Probabilistic Models

The goal is to learn a model distribution $p_{\theta }\left(x_0\right)$ that approximates the data distribution $q\left(x_0\right)$. Let $x_t$($t=1,\dots ,T$) denote the latent variables at different diffusion time steps, where $x_0$ represents the original data and all $x_t$ reside in the same latent space $\mathsf{\chi }$. Diffusion probabilistic models are latent variable models that are composed of two processes: the forward process and the reverse process. The forward process is defined by the following Markov chain:

$$q\left(x_{1:T}|x_0\right)≔{\prod }_{t=1}^{T}q\left(x_t|x_{t-1}\right) \mathrm{where} q\left(x_t|x_{t-1}\right)≔\mathcal{N}\left(x_t;\sqrt{1-{\mathsf{\beta }}_t}{x}_{t-1},{\mathsf{\beta }}_t\mathbf{I}\right),$$

(12)

and ${\beta }_t$ is a small positive constant that represents a noise level. Sampling of $x_t$ has the closed-form written as $q\left(x_t|x_0\right)=\mathcal{N}\left(x_t;\sqrt{{\overline{\mathsf{\alpha }}}_t}{x}_0,\left(1-{\overline{\mathsf{\alpha }}}_t\right)\mathbf{I}\right)$ where ${\overline{\mathsf{\alpha }}}_t={\prod }_{s=1}^t{\mathsf{\alpha }}_s$. Then, $x_t$ can be expressed as $x_t=\sqrt{{\overline{\mathsf{\alpha }}}_t}{x}_0+\sqrt{1-{\overline{\mathsf{\alpha }}}_t}\mathsf{ϵ}$ where $\mathsf{ϵ} \sim \mathcal{ }\mathcal{N}\left(0, \mathbf{I}\right)$. On the other hand, the reverse process denoises $x_t$ to recover $x_0$, and is defined by the following Markov chain:

$$p_{\theta }\left(x_{0:T}\right)≔p\left(x_T\right){\prod }_{t=1}^T{p}_{\theta }\left(x_{t-1}|x_t\right),x_T\sim N\left(0,\mathbf{I}\right),$$

(13)

$$p_{\theta }\left(x_{t-1}|x_t\right)≔N\left(x_{t-1};{\mu }_{\theta }\left(x_t,t\right),{\mathsf{\sigma }}_{\theta }\left(x_t,t\right)\mathbf{I}\right),$$

(14)

Ho et al. [38] proposed DDPM with the following parameterization:

$${\mu }_{\theta }\left(x_t,t\right)={\displaystyle \frac{1}{\sqrt{{\alpha }_t}}}\left(x_t-{\displaystyle \frac{{\beta }_t}{\sqrt{\left(1-{\overline{\alpha }}_t\right)}}}{ϵ}_{\theta }\left(x_t,t\right)\right),$$

(15)

$${\sigma }_{\theta }\left(x_t,t\right)={\tilde{\beta }}_t^{1/2} where {\tilde{\beta }}_t=\left\{\begin{array}{c}{\displaystyle \frac{1-{\mathsf{\alpha }}_{t-1}}{1-{\mathsf{\alpha }}_t}}{\mathsf{\beta }}_t t>1\\ {\mathsf{\beta }}_1 t=1\end{array}\right.,$$

(16)

where ${ϵ}_{\theta }$ is a trainable denoising function. We denote ${\mu }_{\theta }\left(x_t,t\right)$ and ${\mathsf{\sigma }}_{\theta }\left(x_t,t\right)$ as ${\mu }^{\mathrm{D}\mathrm{D}\mathrm{P}\mathrm{M}}\left(x_t,t\right)$ and ${\sigma }^{\mathrm{D}\mathrm{D}\mathrm{P}\mathrm{M}}\left(x_t,t\right)$. The denoising function ${ϵ}_{\theta }$ also corresponds to a rescaled score model for score-based generative models [39]. Under this parameterization, the reverse process is trained by minimizing the following loss function:

$$\underset{\mathsf{\theta }}{\min }\mathcal{L}\left(\mathsf{\theta }\right)≔\underset{\mathsf{\theta }}{\min }{\mathbb{E}}_{x_0\sim q\left(x_0\right),\mathsf{ϵ}\sim \mathcal{N}\left(0,I\right),t}\left[||{\mathsf{ϵ}-{\mathsf{ϵ}}_{\mathsf{\theta }}\left(\sqrt{{\overline{\mathsf{\alpha }}}_t}{x}_0+\sqrt{1-{\overline{\mathsf{\alpha }}}_t}\mathsf{ϵ},t\right)||}^2\right],$$

(17)

The denoising function ${ϵ}_{\theta }$ is designed to estimate the noise vector $ϵ$ that has been added to the corrupted input $x_t$. This training objective can also be interpreted as a weighted form of denoising score matching, which is widely used for training score-based generative models.

2.3.2. Conditional Multivariate Time Series Forecasting Based on PDCDM

We consider more general multi-grid time series prediction tasks. Consider the following scenario: given a historical sequence $x^{hist}\in {\mathbb{R}}^{K\times L_{hist}}$, and prediction target $x^{pred}\in {\mathbb{R}}^{K\times L_{pred}}$, we generate prediction target $x^{pred}$ by conditioning on historical observation $x^{hist}$. Here, both $x^{hist}$ and $x^{pred}$ correspond to the same spatial domain across all $K$ grids. Therefore, the goal of probabilistic prediction is to use the model distribution $p_{\mathsf{\theta }}\left(x^{pred}|x^{hist},\mathit{S}\right)$ to estimate the true conditional distribution $q\left(x^{pred}|x^{hist},S\right)$, where $S\in {\mathbb{R}}^{K\times 64}$ is the grid static POI features.

Unlike general conditional generation tasks, the temporal split between historical observations and prediction targets in forecasting tasks is fixed. Specifically, $x^{hist}$ corresponds to historical time steps $t\in \{\mathrm{1,2},\dots ,L_{hist}\}$, and similarly $x^{pred}$ corresponds to future time steps $t\in \{L_{hist+1},L_{hist+2},\dots ,L\}$. This fixed temporal division reflects the causal nature of forecasting, where only past information can be used to predict the future. We define an observation mask $M^{hist}\in \{\mathrm{0,1}{\}}^{K\times L}$ to indicate the positions of historical observations (with value 1 for historical steps and 0 for prediction steps). Correspondingly, we define a prediction mask $M^{pred}\in \{\mathrm{0,1}{\}}^{K\times L}$, such that $M^{hist}+M^{pred}=\mathbf{1}$.

To leverage the diffusion model $p_{\mathsf{\theta }}\left(x^{pred}|x^{hist},S\right)$, we note that in the unconditional case, the reverse process defines the data model distribution $p_{\theta }\left(x_{0:T}\right)$ over the entire sequence. Therefore, it is natural to extend the reverse process to the conditional setting.

$$p_{\theta }\left(x_{0:T}^{pred}|x^{hist},S\right)≔p\left(x_T^{pred}\right){\prod }_{t=1}^T{p}_{\theta }\left(x_{t-1}^{pred}|x_t^{pred},x^{hist},S\right),x_T^{pred}\sim N\left(0,\mathbf{I}\right),$$

(18)

However, existing diffusion models are generally designed for data generation and do not take conditional observations $x^{hist}$ and spatial features $S$ as inputs. In order to use the diffusion model for prediction, we define the conditional denoising function ${ϵ}_{\theta }:\left({\mathbb{R}}^{K\times L}\times \mathbb{R}|x^{hist},S,M^{hist}\right)\to {\mathbb{R}}^{K\times L}$ that takes as input the noisy sequence, time step $t$, historical observations $x^{hist}$, POI features $S$, and observation mask $M^{hist}$ as conditions. Specifically, during the forward diffusion process, we only add Gaussian noise to the prediction targets $x^{pred}$ while keeping the historical observations $x^{hist}$ intact. In the reverse denoising process, we concatenate the noisy prediction targets with the original historical observations before feeding them into the network, using the following parameterization:

$${\mu }_{\theta }\left(x_t^{pred},t|x^{hist},S,M^{hist}\right)={\mu }^{DDPM}\left(x_t^{pred},t,{ϵ}_{\theta }\left(x_t^{pred},t|x^{hist},S,M^{hist}\right)\right),$$

(19)

$${\sigma }_{\theta }\left(x_t^{pred},t|x^{hist},S,M^{hist}\right)={\sigma }^{DDPM}\left(x_t^{pred},t\right),$$

(20)

where ${\mu }^{DDPM}$ and ${\sigma }^{DDPM}$ are defined in Section 2.3.1. This design ensures that historical observations remain unchanged throughout the denoising process, thus avoiding information loss while fully leveraging both the historical information and the POI features of each grid to guide the generation of prediction targets.

2.3.3. Model Training

Our training objective is to recover the original prediction targets from their noisy versions. Since the forward diffusion process is defined as a Markov chain with fixed Gaussian transitions, only the reverse denoising process needs to be learned. It has been shown that to optimize the denoising model, the learned reverse transitions should closely approximate the true posterior distribution. Furthermore, it has been established that learning to predict the original clean data is mathematically equivalent to predicting the noise that was added to it. In practice, the noise prediction formulation has been found to yield superior performance. Therefore, we adopt the noise prediction objective, and the loss function is formulated as follows:

$$\underset{\mathsf{\theta }}{\min }\mathcal{L}\left(\mathsf{\theta }\right)≔\underset{\mathsf{\theta }}{\min }{\mathbb{E}}_{x_0\sim q\left(x_0\right),\mathsf{ϵ}\sim \mathcal{N}\left(0,\mathbf{I}\right),t}\left[||\mathsf{ϵ}-{\mathsf{ϵ}}_{\mathsf{\theta }}\left(x_t^{\mathit{pred}},t∣x^{\mathit{hist} },S,M^{\mathit{hist}}\right){||}^2\odot M^{\mathit{pred} }\right],$$

(21)

The training process is shown in Figure 5.

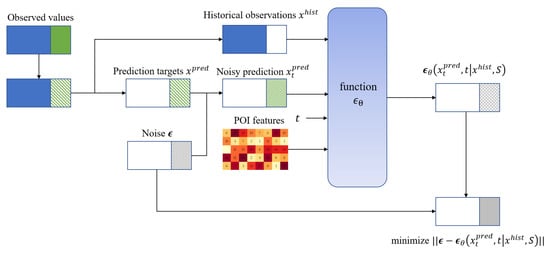
Figure 5. Self-supervised training procedure of PDCDM. Complete sequence is split into historical observations (blue, $L_{hist}$ steps) and prediction targets (green hatched, $L_{pred}$ steps). Historical observations $x^{\mathit{hist} }$ and POI features $S$ serve as conditional inputs. Prediction targets are corrupted with Gaussian noise $\mathsf{ϵ}$ and fed into the denoising network ${\mathsf{ϵ}}_{\mathsf{\theta }}$ along with diffusion step $t$. The network predicts noise and is trained by minimizing the difference from true noise.

2.4. PDCDM Model Architecture

To achieve this conditional denoising objective, we design a denoising network ${\mathsf{ϵ}}_{\mathsf{\theta }}$ that integrates temporal grid features with POI semantic information. As illustrated in Figure 6, the network employs a DiffWave-based residual block architecture [40] and incorporates a dual-dimension Transformer attention mechanism to capture long-range dependencies across both temporal and grid dimensions. Via gated activation units and cross-layer skip connections, the network adaptively fuses static POI features with dynamic grid-level temporal patterns, thereby enabling multi-scale feature aggregation.

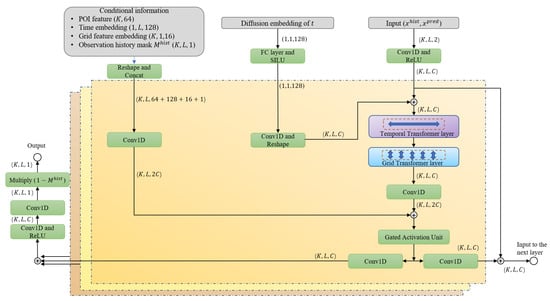
Figure 6. PDCDM Network Architecture.

2.4.1. Input Processing and Encoding

We define the denoising function as ${\mathsf{ϵ}}_{\mathsf{\theta }}\left(x_t^{\mathit{pred}},t∣x^{\mathit{hist} },S,M^{\mathit{hist}}\right)$, which takes as input the noisy prediction target, diffusion step, historical observations, POI features, and observation mask. During training, the prediction target $x^{pred}$ is progressively corrupted to $x_t^{pred}$ through the forward diffusion process, while the historical observations $x^{hist}$ remain unchanged. During sampling, the prediction region is initialized as pure Gaussian noise $x_T^{pred}\sim N\left(0,\mathbf{I}\right)$. We construct dual-channel inputs through masking operations:

$$x_{hist}=M^{hist}\odot x_0,{ x}_{noisy}=M^{pred}\odot x_t^{pred},$$

(22)

where $\odot$ denotes element-wise multiplication. $x_{hist}$ and ${ x}_{noisy}$ are concatenated along the feature dimension to form the model input $x_{input}$, which is then passed through a 1D convolutional layer followed by ReLU activation for initial feature fusion:

$$h_0=\mathrm{R}\mathrm{e}\mathrm{L}\mathrm{U}\left(\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{v}1\mathrm{D}\left(x_{input}\right)\right){\in \mathbb{R}}^{K\times L\times C},$$

(23)

where $C$ is the number of hidden channels. This design enables adaptive learning of feature representations by fusing conditioning information from historical observations with noisy prediction targets. Subsequent blocks progressively refine these representations.

2.4.2. Diffusion Timestep Embedding

To inform the network of the current diffusion step and enable adaptive denoising, we encode the timestep $t\in \{\mathrm{1,2},\dots ,T\}$ into a continuous high-dimensional vector. Following the sinusoidal positional encoding with exponentially scaled frequencies, we employ 64 sine and cosine functions:

$$e_{diff}\left(t\right)=\left[\sin \left(t\cdot f_0\right),\dots ,\sin \left(t\cdot f_{63}\right),\cos \left(t\cdot f_0\right),\dots ,\cos \left(t\cdot f_{63}\right)\right],$$

(24)

where $f_i={10}^{4i/63}\left(i\in \{\mathrm{0,1},\dots ,63\}\right)$, generating a 128-dimensional vector $e_{diff}\left(t\right)$. This embedding is then projected to the hidden dimension $C$ via a fully connected layer with SiLU activation. The resulting timestep embedding is broadcast and added to each grid location across the feature and temporal dimensions, thereby providing step-conditional information to the network.

2.4.3. Conditional Information Encoding

To incorporate the spatial semantic information of static POIs within the grid into temporal prediction, we feed the POI feature $S$ as conditional information into the network. In addition to the POI feature, we also utilize temporal embeddings, feature embeddings, and conditional masks collectively as the conditional information input into the network, guiding the training process.

The temporal embedding ${\mathrm{e}}_{time}$ captures the positional information and periodic patterns of the time series. For each time index $s_l\in \{\mathrm{1,2},\dots ,L\}$, we apply 128-dimensional sinusoidal encoding:

$$s_{embedding}\left(s_l\right)=\left(\sin \left(s_l/{\mathsf{\tau }}^{0/64}\right),\dots ,\sin \left(s_l/{\mathsf{\tau }}^{63/64}\right),\cos \left(s_l/{\mathsf{\tau }}^{0/64}\right),\dots ,\cos \left(s_l/{\mathsf{\tau }}^{63/64}\right)\right),$$

(25)

where $\tau =\mathrm{10,000}$. The grid feature embedding ${\mathrm{f}}_{emb}$ employs 16-dimensional learnable embeddings for each of the $K$ grid locations to distinguish different grids. The observation mask $M^{\mathit{hist}}$ indicates which positions are conditional inputs. All conditional information (temporal embeddings, grid embeddings, observation masks, POI features) is concatenated along the channel dimension:

$$\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\_\mathrm{i}\mathrm{n}\mathrm{f}\mathrm{o}=\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{t}\left({[\mathrm{e}}_{time},{\mathrm{f}}_{emb},M^{hist},S_{expand}]\right)\in {\mathbb{R}}^{K\times \mathrm{L}\times 209},$$

(26)

where the total dimension is 209. The concatenated conditional features are then projected to the network hidden dimension $2C$ via a 1 × 1 convolutional layer, enabling effective fusion of multi-source information. This direct concatenation design avoids the overfitting risk associated with pre-fused additional parameters, allowing the network to adaptively learn task-specific contribution weights for different conditional features.

2.4.4. Dual-Dimension Transformer Attention Mechanism

To capture the temporal-spatial dependencies, the fused features undergo a two-dimensional Transformer attention mechanism. As shown in Figure 7, this mechanism consists of a sequential arrangement of a temporal Transformer layer and a grid Transformer layer.

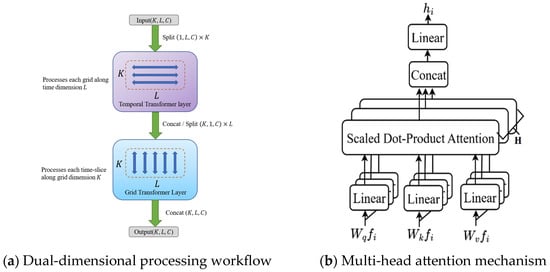
Figure 7. Dual-dimensional Transformer Attention Mechanism. (a) Dual-dimensional processing flow: $K$ represents the number of spatial grids and $L$ is the length of temporal sequence. First, independently model temporal dependencies for each grid along the time dimension $L$, then model interactions between grids along the grid dimension $K$; (b) Multi-head attention structure: Features are projected via $W_q,W_k,W_v$ to compute attention and aggregate information.

The Temporal Transformer layer models sequence dependencies across the temporal dimension. For input features, it first unrolls $K$ grid points into $K$ independent time series, then applies a self-attention mechanism along the temporal dimension to compute the correlation weights between each time step. Temporal attention enables the model to adaptively focus on critical time steps within the prediction target based on the context of historical observations, capturing periodic patterns (such as daily peaks and weekly rhythms) and long-range temporal dependencies.

The Grid Transformer layer models multi-grid interactions across the grid dimension. It divides the time-processed features into $L$ independent multi-grid snapshots across time steps. A global self-attention mechanism is then applied along the grid dimension to compute correlation weights between sampled grid cells. Unlike methods based on predefined adjacency graphs, global attention enables the model to learn dependencies between arbitrary grid pairs in a data-driven manner, without requiring manual spatial adjacency specifications. Through adaptive learning of attention weights, the Grid Transformer layer dynamically adjusts interaction strengths between different grid pairs for each time step.

The sequential design of dual-dimensional attention ensures comprehensive interaction between temporal and spatial features. Temporal attention first models time-dependent relationships within each grid, followed by grid attention modeling interactions across all grids. This “time-first, grid-second” processing sequence enables the network to first understand the temporal evolution patterns within each grid before capturing synergistic effects between grids, thereby more effectively modeling complex dependency structures among multi-grid data.

3. Experimental Settings

3.1. Dataset

To evaluate the effectiveness of the proposed PDCDM, we conduct comprehensive experiments on a real-world dataset of grid-level population inflows in Beijing, spanning 10 months from September 2023 to June 2024. Table 3 summarizes the dataset statistics.

Table 3. The information of datasets.

Item	Description
Data Source	Grid-scale population inflow data for Beijing City from Amap
Time Range	September 2023–June 2024 (10 months)
Time Granularity	15 min
Grid Quantity	5853
Grid Size	500 m × 500 m
Total Time Steps	29,184

We adopt the same stratified monthly sampling strategy described in Section 2.2 for dataset partitioning.

3.2. Evaluation Metrics

We choose the Continuous Ranked Probability Score (CPRS) as the metric to evaluate the performance of probabilistic prediction, which is commonly used to measure the compatibility of an estimated probability distribution $F$ with an observation $x$:

$$\mathrm{CRPS}\left(F,x\right)={\int }_{\mathbb{R}}{\left(F\left(z\right)-\mathbb{I}\{x\le z\}\right)}^2\hspace{0.17em}dz,$$

(27)

where $\mathbb{I}\{x\le z\}$ is an indicator function which equals one if $x\le z$, and zero otherwise. Smaller CRPS means better performance.

In addition, we leverage Mean Absolute Error (MAE) and Root Mean Squared Error (RMSE) to evaluate the performance of deterministic prediction. Let $Y$ be the label, and $\widehat{Y}$ denote the predictive result.

$$\mathrm{MAE}\left(Y,\widehat{Y}\right)={\displaystyle \frac{1}{\left|Y\right|}}{\sum }_{i=1}^{\left|Y\right|}\left|Y_i-{\widehat{Y}}_i\right|,$$

(28)

$$\mathrm{RMSE}\left(Y,\widehat{Y}\right)=\sqrt{{\displaystyle \frac{1}{\left|Y\right|}}\sum _{i=1}^{\left|Y\right|}{\left(Y_i-{\widehat{Y}}_i\right)}^2},$$

(29)

where a smaller metric means better performance.

3.3. Implementation Details

In our experiments, we set the batch size to 8 and used the Adam optimizer for parameter updates. The initial learning rate was set to 0.001 and the weight decay coefficient to 1e-6, in order to prevent overfitting. A multi-step learning rate decay strategy was implemented, reducing the learning rate to 10% of its original value at 75% and 90% of the training process, in order to achieve finer-grained parameter tuning. The model was trained using an early stopping mechanism that evaluated model performance on the validation set every 10 epochs and terminated training prematurely if the validation loss failed to improve for several consecutive evaluations. To address the computational challenges posed by high-dimensional data, we randomly sampled 100 grids per batch (selected from a total of 5853 grids) during training. This approach significantly reduced computational costs while preserving the model’s generalization capabilities. During validation, we used a 5% grid sampling rate (approximately 293 grids) to efficiently evaluate model performance. This method avoids memory overflow while yielding stable performance estimates. Additionally, we employ a quadratic noise schedule for the forward diffusion process: ${\mathsf{\beta }}_n={\left({\displaystyle \frac{N-n}{N-1}}\sqrt{{\mathsf{\beta }}_1}+{\displaystyle \frac{n-1}{N-1}}\sqrt{{\mathsf{\beta }}_N}\right)}^2$, where $N$ denotes the total diffusion steps, and ${\mathsf{\beta }}_1$ and ${\mathsf{\beta }}_N$ represent the minimum and maximum noise levels, respectively. The raw inflow data is normalized using z-score standardization to ensure comparability across different grids and timesteps.

3.4. Baseline Models

Both state-of-the-art probabilistic and deterministic models are included for the performance comparison.

Probabilistic baselines. The following methods are implemented as baselines for forecasting:

• SSSD [41], which is a diffusion model that combines structured state space models (S4) for probabilistic time series forecasting.
• DiffusionTS [42], which is a Transformer-based diffusion model tailored for probabilistic time series forecasting.
• CSDI [43], which is a diffusion-based non-autoregressive model first proposed for multivariate time series imputation.

Deterministic baselines. We choose some popular and state-of-the-art methods for comparison:

• PatchTST [44], which is a patch-based Transformer model that segments time series into patches for capturing multi-scale temporal dependencies.
• iTransformer [45], which is an inverted Transformer architecture that treats each variate as a token to effectively model inter-variate dependencies in multivariate time series.
• TimeMixer [46], which is a multi-scale mixing model that decomposes time series into macro and micro temporal patterns for multi-resolution feature fusion and forecasting.
• TimesNet [47], which is a 2D convolution-based model that reshapes 1D time series into 2D tensors to capture intra-period and inter-period variations.
• FEDformer [48], which is a frequency-domain Transformer that applies attention mechanisms via Fourier transforms to capture periodic patterns.

4. Results

4.1. Performance Comparison

Probabilistic modeling approaches for urban grid-level population inflow forecasting remain underexplored. Therefore, we benchmark PDCDM against state-of-the-art probabilistic and deterministic methods from the time series forecasting domain, including probabilistic approaches (SSSD, DiffusionTS, CSDI) and deterministic approaches (PatchTST, iTransformer, TimeMixer, TimesNet, FEDformer). We employ the Continuous Ranked Probability Score (CRPS) as the primary metric for probabilistic forecasting performance, alongside MAE and RMSE to assess point prediction accuracy across all models.

As shown in Table 4, PDCDM achieves the best performance across all evaluation metrics. Compared to the strongest baseline, PDCDM reduces MAE by 11.7%, RMSE by 14.9%, and CRPS by 8.6%. Among probabilistic baselines, DiffusionTS demonstrates strong competitive performance. As a diffusion model specifically designed for time series forecasting, DiffusionTS effectively captures temporal dependencies through its Transformer architecture, highlighting the strengths of diffusion models for sequential modeling. However, it does not account for urban spatial heterogeneity, which limits its performance on grid-level forecasting tasks. SSSD exhibits limited performance in our forecasting task, as its structured state space model struggles with high-dimensional spatial data. While CSDI demonstrates strong capability in spatial prediction, its imputation-oriented design fails to fully leverage the autoregressive nature of forecasting, thereby limiting its predictive accuracy. Beyond point forecasting accuracy, PDCDM achieves the lowest CRPS among all baselines, demonstrating improved probabilistic calibration and reduced prediction uncertainty. This confirms that PDCDM delivers not only accurate but also well-calibrated probabilistic forecasts.

Table 4. Experimental results on test set of different mainstream methods. The best result is in bold, the second-best result is underlined and “-” indicates that the model does not support probability prediction.

Method	MAE	RMSE	CRPS
PatchTST	0.279	0.886	-
iTransformer	0.325	0.912	-
TimeMixer	0.286	0.877	-
TimesNet	0.279	0.890	-
FEDformer	0.345	0.595	-
CSDI	0.258	0.523	0.256
SSSD	0.534	1.121	0.282
DiffusionTS	0.275	0.626	0.255
PDCDM (ours)	0.228	0.445	0.233
Error reduction	−11.7%	−14.9%	−8.6%

Inference Time. Generally, diffusion-based prediction methods are significantly slower than others due to the iterative denoising required during inference sampling, yet they deliver superior probabilistic prediction performance. To address this, we primarily compare the inference speeds of diffusion-based prediction methods, including SSSD, DiffusionTS, CSDI, and the proposed model PDCDM. Table 5 reports the average inference time cost for these four diffusion models when generating different numbers of samples on a single grid. We observe that SSSD is extremely time-consuming due to its recurrent state space architecture. Our model achieves approximately 30-fold acceleration compared to SSSD, owing to its non-autoregressive parallelized architecture. Despite employing a decoupled Transformer structure, DiffusionTS still incurs high inference time, requiring 103.783 s to generate 30 samples. PDCDM achieves efficient inference through parallelization in the temporal dimension and optimized network design, generating 30 samples in just 13.894 s. This places it on par with CSDI (10.662 s), which also employs a non-autoregressive architecture.

Table 5. Time cost (by seconds) of diffusion-based models (SSSD, DiffusionTS, CSDI, PDCDM).

Num_Sample/s	5	10	15	20	25	30
SSSD	64.975	130.762	197.005	262.126	324.520	388.994
CSDI	1.806	3.519	5.421	7.099	8.878	10.662
DiffusionTS	17.194	34.772	50.122	67.350	85.227	103.783
PDCDM (ours)	2.211	4.631	6.901	9.251	11.996	13.894

Visualization. To illustrate PDCDM’s forecasting performance, we visualize the probabilistic prediction distributions for representative grids in Figure 8. The model quantifies uncertainty by generating 15 prediction samples, from which we derive the median prediction (green solid line) and two confidence intervals: the 50% CI (dark green shaded area, spanning the 25th–75th percentiles) and the 90% CI (light green shaded area, spanning the 5th–95th percentiles). As shown in Figure 8, during the historical period (timesteps 0–480, marked with red crosses), observed values cluster tightly around the median prediction and fall almost entirely within the confidence intervals, demonstrating the model’s ability to accurately capture historical patterns. More critically, during the forecasting horizon (timesteps 480–576, marked with blue circles), ground truth values across all grids predominantly lie within the 90% confidence interval, validating the model’s probabilistic reliability. Across different grids, PDCDM maintains consistent prediction quality while successfully capturing spatial heterogeneity.

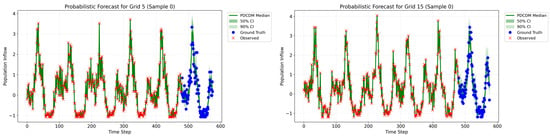
Figure 8. Probabilistic forecasting visualization.

Notably, the confidence interval width adapts to prediction difficulty: during stable periods, narrower intervals reflect higher predictive certainty, while during volatile periods (e.g., the peak region in Grid 5 at timesteps 500–570), the model produces wider uncertainty bounds, demonstrating its capability to capture prediction uncertainty. Furthermore, the visualizations clearly reveal PDCDM’s ability to learn periodic patterns in population inflow data. Regular oscillations observed during the historical period are effectively extrapolated to the forecasting horizon. For instance, in Grid 15’s forecasting period, the model accurately captures the fluctuation pattern between timesteps 520–550, with the median prediction closely aligning with ground truth. This demonstrates the model’s capacity to learn and extrapolate long-range temporal dependencies in extended forecasting scenarios. These adaptive uncertainty quantification capabilities and precise spatiotemporal pattern recognition enable PDCDM to provide reliable decision support for practical applications such as urban planning. These visualizations further confirm PDCDM’s capability to model predictive uncertainty adaptively: narrower intervals during stable phases represent higher confidence, while wider intervals during volatile periods reflect greater uncertainty awareness.

4.2. Ablation Study

To systematically evaluate the contribution of each component to the overall performance, we conduct ablation studies by removing individual modules from PDCDM. Table 6 summarizes the results across different configurations.

Table 6. Ablation study of different modules in the model.

Model Modules	MAE	CRPS
PDCDM	0.228	0.233
w/o Temporal Transformer	0.421	0.462
w/o Grid Transformer	0.331	0.362
w/o POI Feature	0.269	0.261

PDCDM comprises three core components: the POI feature fusion module, the temporal Transformer layer, and the spatial Transformer layer. We conduct systematic ablation studies by removing each component individually to assess its contribution to probabilistic forecasting performance, evaluated using MAE and CRPS.

The complete PDCDM achieves the best performance across all metrics. Removing the temporal Transformer layer yields the most severe performance degradation, with MAE and CRPS increasing to 0.421 and 0.464, corresponding to error increases of 84.6% and 98.2%, respectively. The temporal Transformer leverages self-attention to construct temporal representations for each grid, adaptively capturing periodic patterns and long-range dependencies. Without it, the model loses its capacity to model temporal dynamics, confirming that temporal dependency modeling is critical for accurate forecasting.

Removing the spatial Transformer layer causes MAE and CRPS to rise to 0.331 and 0.362, increasing errors by 45.2% and 55.4% relative to PDCDM. The spatial Transformer learns inter-grid dependencies through global self-attention. Its removal reduces the model to processing grids independently, preventing it from capturing cross-regional flow propagation and spatial coordination effects.

Removing the POI feature fusion module increases MAE and CRPS to 0.269 and 0.261, representing error increases of 18.0% and 12.0% relative to PDCDM. POI features encode urban functional attributes to provide static semantic context. Without them, the model cannot capture function-driven flow dynamics, reducing its generalization capability across heterogeneous functional zones and limiting prediction interpretability.

5. Conclusions

This paper presents PDCDM, a probabilistic forecasting framework for urban grid population inflow. PDCDM pioneers the application of conditional diffusion models to grid-scale population forecasting, overcoming the limitations of traditional deterministic approaches. Beyond delivering accurate point forecasts, it quantifies prediction uncertainty to support risk-aware urban management decisions. In particular, the model exhibits a strong capacity to represent and adaptively reduce predictive uncertainty through its probabilistic diffusion mechanism, as confirmed by its consistently lowest CRPS and well-calibrated confidence intervals across experiments.

The model incorporates a POI-enhanced conditional encoding framework that systematically integrates urban functional semantics into the diffusion process. By constructing multi-scale static POI feature representations, PDCDM effectively captures population aggregation patterns across diverse functional zones, enhancing prediction accuracy in spatially heterogeneous urban areas. Furthermore, we employ a dual-dimensional attention mechanism to decouple temporal and grid feature modeling, with separate pathways processing temporal dependencies and inter-grid spatial correlations through Transformer-based attention, while residual connections enable progressive feature fusion. Experiments on real-world urban datasets demonstrate that PDCDM outperforms numerous existing forecasting methods.

Although the current experimental validation is conducted using grid-level inflow data from Beijing due to dataset availability, the proposed PDCDM framework is theoretically generalizable to other cities or countries. The model depends only on grid-scale population inflow time series and corresponding POI features, which are widely obtainable in urban environments. Therefore, for regions lacking sufficient historical data, PDCDM can be extended through transfer learning, cross-city pretraining, or regional similarity analysis to leverage prior knowledge from data-rich areas. These strategies enhance the model’s adaptability and potential applicability across diverse urban contexts.

However, several limitations should be acknowledged. First, due to GPU memory constraints, a 5% grid sampling strategy was adopted for validation and testing, which may introduce minor sampling bias in performance assessment. Second, the model relies on static POI data that does not capture temporal variations, and excludes external factors such as weather conditions and specific temporal constraints (e.g., holidays, events). The model’s performance is also inherently dependent on the accuracy and representativeness of the POI data; if the POI information deviates from actual urban functional distributions, prediction deviations may emerge. Incorporating these factors could further improve prediction accuracy. Future work will address these limitations through full-scale evaluation on complete grid sets and by expanding the conditional framework to integrate dynamic environmental and temporal factors, thereby enhancing the model’s robustness and applicability to real-world urban management scenarios.