Characterising Active Mobility in Urban Areas Through Street Network Indices

Abstract

In the context of sustainable development, the concept of active mobility plays a key role in modern urban areas. To evaluate active mobility in these areas, we formulate a framework for characterising active mobility by calculating street network indices using global, free, and open data. This framework comprises the download and processing of pedestrian, cycling, driving, and public transport street networks from OpenStreetMap, the selection of street network indices from the academic literature, and their implementation and calculation. A total of 50 indicators are reported for each urban area distributed in eight index types, including thematic variables, proximity to Points of Interest (POIs), proximity to public transport, intersection density, street density, street length, link–node ratio, circuity, slope, and orientation entropy. To test the framework, we calculate street network indices for pedestrian and cycling networks for the urban areas of 176 cities from around the world. The resulting dataset is published as open data. An analysis of the calculated indices indicates that cities in higher-income economies generally exhibit better conditions for active mobility, especially in Europe, attributed to better map completeness, and to more compact and connected urban areas where it is easier to access amenities and public transport.

1. Introduction

More than half of the world’s population lives in urban areas, where numerous means of transportation coexist on a daily basis. Although people remain the beating heart of the city, they must share the urban arteries with bicycles, scooters, cars, trucks, buses, trams, and trains. Active mobility, which refers to any human-powered means of transportation, plays a key role in shaping urban areas and the movements of their inhabitants.

In the framework of sustainable development, the concept of active mobility contributes to the achievement of modern, smart, and sustainable cities and communities [1]. Other than walking, active mobility considers any human-powered vehicles, such as bicycles, which are also key actors in modern urban mobility. Active mobility provides sustainable and effective alternatives to motorised mobility (i.e., cars) and has been proven to be of utmost importance for improving people’s health and well-being in urban areas [2,3], enhancing air quality [4,5], reducing traffic congestion, and ameliorating equality in communities [6,7].

The evaluation of active mobility in urban areas is fundamental for their continuous improvement. In the age of smart cities and urban digital twins, having evaluation and analysis methodologies for mobility, and, in particular, for active mobility is helpful in making great strides towards the achievement of sustainability. Sustainable development is not only fundamental for metropolises and developed countries but should also guide cities and countries in emerging economies towards better, smarter, and greener settlements. This is particularly relevant for the global south, which is often neglected in active mobility studies [8]. The use of free, open, and global data is necessary for fostering collaboration, reaching urban areas anywhere in the world, and providing efficient methodologies that can be seamlessly applied. The combination of globally available data and detailed methodologies aims to provide, both for large and small cities, a baseline for their own analyses and evaluations.

In regard to data availability, a key dataset for the analysis of active mobility is the network in which said mobility occurs: the street network. Street networks are the way in which the streets of an urban area are arranged and how they are connected. They represent the roads where cars and other motorised vehicles circulate, but also the infrastructure that pedestrians and cyclists use, as well as the networks of public transport. The study and analysis of the street networks of multiple means of transportation provide a holistic view of cities and urban areas and help characterise all kinds of urban mobility, including active mobility [9].

Street networks provide spatial information on where movement occurs, conveying certain characteristics of the physical places where it takes place, as well as other functional and topological properties. From an academic perspective, multiple studies show that from the shape and arrangement of street networks, in conjunction with other data, it is possible to characterise mobility in urban areas, allowing for comparisons, showing areas of improvement, and measuring topological and functional aspects such as connectivity, compactness, utility, or proximity [10,11]. This is usually accomplished by calculating indices and indicators that extract certain characteristics of the network in a quantitative way. However, plenty of these studies consider only the road network (the network where motorised vehicles circulate) without giving proper importance to pedestrian-specific and cycling-specific infrastructure. This may lead to inaccuracies in these computations, especially when focusing on active mobility, as the road network and the cycling or pedestrian networks do not completely overlap.

This study focuses on proposing a framework for characterising active mobility in urban areas using global, free, and open data through the calculation of street network indices, primarily for pedestrian and cycling networks. In particular, we are interested in using pedestrian, cycling, driving, and public transport networks for extracting multiple characteristics of urban areas at the city scale, with a particular focus on active mobility, and following a general approach that is applicable to any urban area in the world.

This research pursues three main objectives: First, to propose a general framework for the extraction of accurate and realistic pedestrian, cycling, driving, and public transport street networks of urban areas as a robust data foundation for urban analysis; second, to use the extracted networks to calculate and analyse a curated set of street network indices (i.e., proximity to POIs, proximity to public transport, circuity, street length, link–node ratio, slope, intersections, and orientation entropy), derived from the academic literature, for characterising city-scale urban active mobility; and third, to test and validate the framework by calculating street network indices for the urban areas of 176 capital cities from around the world, publishing these results as open data.

The resulting dataset is composed of 50 indicators calculated for each capital city, including thematic socioeconomic information (e.g., population, climate, income level, etc.), and indicators related to the aforementioned indices. A comprehensive data analysis and interpretation is also provided to extract valuable insights about city-scale urban active mobility, using thematic information to group cities by similar characteristics. To the best of our knowledge, this study is the most comprehensive and wide-ranging study of urban active mobility characterisation using global open data.

This paper presents a theoretical framework in Section 2 that provides a contextualisation on how street network indices are utilised for characterising mobility in urban areas, and how their networks are digitally modelled. Section 3, the Materials and Methods Section, presents a comprehensive overview of the methodology and data used. Then, a detailed description and justification of the selected indices for the characterisation of active mobility are presented in Section 4, the Street Network Indices Section. The case study for testing the methodology is described in Section 5, along with the produced dataset and multiple analyses for extracting trends from the data. Finally, the discussion in Section 6 further contextualises and explores the results of the analyses, examining its limitations, and reflecting on future directions.

2. Theoretical Framework

This section is devoted to contextualising two key concepts relevant to this study. First, it examines the use of street network indices for the analysis and characterisation of urban areas, with particular interest in related studies. Second, it describes how graph-based models are used to digitally represent street networks while mentioning alternative modelling frameworks.

2.1. Street Network Indices for Urban Analysis

The use of indices, indicators, or metrics to characterise various properties of urban mobility has been extensively studied. Research in this domain ranges from quantitative studies analysing the topology and geometrical properties of street networks [12,13] to qualitative ones addressing more subjective dimensions such as perceived environment, safety, or attractiveness [8,14].

As a fundamental part of the urban space, the analysis of street networks has been a tool for understanding urban areas at many levels of detail, starting from the ultra-local neighbourhood scale [15] to the city scale [8,14,16] and finally to broader national, regional, and global scales [16,17,18]. This has been done by quantifying various aspects of the street network from geometrical, structural, topological, and spatial points of view, but also subjective factors like security and comfort.

From the perspective of active mobility, studies often focus on measuring walkability and cyclability from multiple points of view. Some literature reviews have been produced to identify such methodologies and the indices that are often used for measuring urban active mobility [8,10,19,20,21], showcasing how different indices characterise fundamental quantitative and qualitative aspects of street networks, such as density, diversity, design, accessibility, distance to public transport, efficiency, and connectivity, among many others. However, articles do not always take into account mode-specific networks (i.e., the road, pedestrian, and cycling networks separately) for the analysis of active mobility, in particular for measuring walkability and cyclability. This may lead to inaccurate analyses, as road networks do not have a complete overlap with pedestrian and cycling-specific networks, highlighting the importance of using mode-specific networks for measuring mode-specific mobility [22].

As a complement to street network information, various ancillary data are commonly used by researchers. Land use and land cover (LU/LC) data are used for understanding the access to different areas and services within the urban space [23,24]. Information about Points of Interest (POIs) and walking attractors is used for understanding people’s movements and well-being in urban areas, by using measurements such as the proximity to public transport and to different types of amenities [12,25,26]. Finally, thematic information, such as socioeconomic or climate data, has been used to further contextualise indices and metrics by enabling groupings and summaries, especially when considering analyses of many urban areas at once [13,27].

The usage of open data is also common practice when analysing street networks. Examples include the work of Gu et al. [28], who used open data to analyse walkability and cyclability in four cities in China. The authors analysed infrastructural properties related to safety, comfort, and convenience using open data from OpenStreetMap. Another example is the work of Boeing [13], where open data, also from OpenStreetMap, were used to extract road networks of more than 8000 urban areas to calculate a set of graph-based indices.

On the side of commercial indices, WalkScore^® and BikeScore^® usually arise as state-of-the-art indices for studying active transportation and walkability [29]. These indices use a patented methodology based on information such as proximity to amenities, road network metrics, elevation, and population density, among others, to analyse and measure how walkable and cyclable certain locations are [30,31].

The geographic extension in which urban active mobility has been studied is mostly shifted towards the global north, in particular China, the US, and Europe. Articles seldom report or pay little attention to the study of active mobility in the global south [8,32]. This trend highlights the need to perform analyses that can be implemented with ease in developing cities as baselines for fully fledged studies.

2.2. Modelling of Street Networks

To perform computations and analyses of a real-life structure such as the street network, it must first be digitally modelled. The predominant type of model for the street network is the graph [33], which most effectively captures the topological and spatial properties of street networks. Alternatively, another application-specific street network model is the raster, which is mostly used for calculating spatial correlations with other raster-based data or for its usage within convolutional neural networks [34,35]. The raster representation, however, fails to capture topological relationships.

In contrast, the graph data structure is ideal for capturing and representing complex spatial structures, enabling use cases such as routing and permitting different kinds of analyses, such as topological and flow analyses. Graphs are also used for visualisation and cartography, assuming the graph contains georeferenced information (e.g., points or lines) among their properties, also allowing for its usage inside GIS software.

A graph $G=\{N,E\}$ is a data structure composed of a set of nodes N and a set of edges E. Edges connect the nodes of the graph to create a network structure. Graphs are useful for representing both the topology of a network (i.e., the shape and arrangement of its elements) and its geometry (i.e., the physical space that the network represents).

An important property of a graph is its directedness. A graph can be directed, meaning that each edge connects a node u with node v in only one direction; or undirected, meaning that a single edge represents the connection from node u to node v and vice versa. Different algorithms and properties apply for directed and undirected graphs.

Other properties of graphs that often appear in real-life street networks are (i) parallel edges, meaning that one or more edges may exist between each pair of nodes $(u,v)$. This type of graph is called a multigraph. There are also (ii) self-loops, where an edge connects a node u with itself.

Regarding the way in which graphs represent real, physical street networks, two main graph representations are widely used: primal and dual graphs. Primal graphs [36] are the intuitive graph representation for street networks, where edges represent street segments and nodes represent junctions or intersections. This representation maintains the shape and structure of street networks, as well as their geometrical properties. Depending on the network being represented, primal graphs can be directed or undirected. As examples, a network where direction is important, such as the road network where streets can be one-way or two-way, is often represented using a directed graph, while a network where direction is not relevant, as is the case with pedestrian networks where pedestrians can freely move in both directions, can be represented by an undirected graph. On the opposite side, dual graphs [37] invert the network topology and model the intersections of the street network as edges and the street segments as nodes. This representation is known as a dual approach and is the foundation of the discipline of space syntax, where space is represented using axial lines. Dual graphs allow for relationships to be identified between spaces and are mostly used in architecture and social studies [38].

In the context of street network analysis, the selection and representation of a proper graph model are important design decisions [39]. For our study, a primal multigraph model was used to digitally represent each street network. In the case of road, cycling, and public transport networks, we consider its directed graph representation, while for the pedestrian networks, we use its undirected representation.

3. Materials and Methods

This section presents the data that were utilised for this study, discussing and justifying the selection of the datasets, and describes the proposed methodology for downloading and processing the street networks used for the calculation of the indices, highlighting the role of global open data.

3.1. Data

This study is built upon the use of global open data for characterising active mobility. Global open data enable the proposal of a general framework for characterising urban areas worldwide. To achieve this, three fundamental pieces of information were identified, forming the data foundation of this study.

First, to delimit urban areas worldwide, the Global Human Settlement-Urban Centre Database 2024 release (GHS-UCDB R2024A) [40] was selected. This dataset also contains city-scale socioeconomic information like income level and climate classification. Second, OpenStreetMap (OSM) was selected to provide information about the different street networks that compose the urban area (i.e., pedestrian, cycling, and road). OSM also provides information about POIs and public transport, which were utilised for calculating proximity indices. Finally, as we identified that the slope is a variable that greatly impacts cycling, the global Digital Elevation Model NASADEM dataset was selected as the source of open elevation data.

The next subsections further describe each of the datasets used in this study.

3.1.1. Global Human Settlement-Urban Centre Database

The Global Human Settlement-Urban Centre Database R2024A (GHS-UCDB) [40] is a global open dataset distributed by the European Commission Joint Research Centre (JRC) that provides worldwide multi-scale thematic information about urban areas. For this study, the GHS-UCDB was used to provide the delimitation of the urban areas for each analysed city, as well as valuable thematic information, such as population, income level, and climate classification. The GHS-UCDB has proven to be a useful dataset for delimiting urban areas globally, allowing for comparative analyses to be made across locations and time [41], and it is also used as a delimiter for street network analyses [13].

The GHS-UCDB delimits urban areas using cut-outs of population and built-up surface on a 1 km × 1 km regular grid covering the entire globe. A single GHS-UCDB delimited area may contain the urban areas of one or more cities or municipalities, similarly to how metropolitan areas are assembled. This dataset allowed us to consider urban areas rather than official administrative boundaries that may contain rural areas, ensuring worldwide uniformity and continuity.

3.1.2. OpenStreetMap

OpenStreetMap (OSM) [42] is a free crowdsourced map of the entire world. OSM data are widely used by the academic and open-source software community for their reasonable accuracy and worldwide coverage [43]. For this study, OSM was used for deriving the pedestrian, cycling, and driving street networks of urban areas, as well as public transport infrastructure and routes. In addition, OSM provided information about POIs, which were used for proximity analysis.

Street networks in OSM are stored in a database where each element is represented as a point, line, polygon, or relation. Each feature includes geometric data and associated tags (key–value pairs) that describe its attributes. In the context of street networks, some tags are fundamental for categorisation and filtering, including “highway” (street type), “access” (circulation permissions), and “footway”, “sidewalk”, and “cycleway” (pedestrian and cycling infrastructure).

3.1.3. NASADEM

As a source of elevation data, we used the NASADEM dataset [44]. This dataset provides global, free, and open elevation data with 30 m resolution for most of the world in raster format. The extent of the dataset ranges from 60° N to −56° S in latitude, and from −180° W to 180° E in longitude.

Although its resolution is not quite high, this dataset was selected as the source of elevation data as it provides almost-worldwide coverage and comes with an open license, aligning with our objective of providing a general methodology replicable to any urban area in the world using open data. The usage of the NASADEM dataset allowed us to enrich the extracted street networks with elevation information, which is then used to calculate the slopes of the street network’s segments. It is worth mentioning that other studies have already explored the concept of adding elevation to enrich the street network and calculate active mobility-related indices [13,19,45].

3.2. Methodology

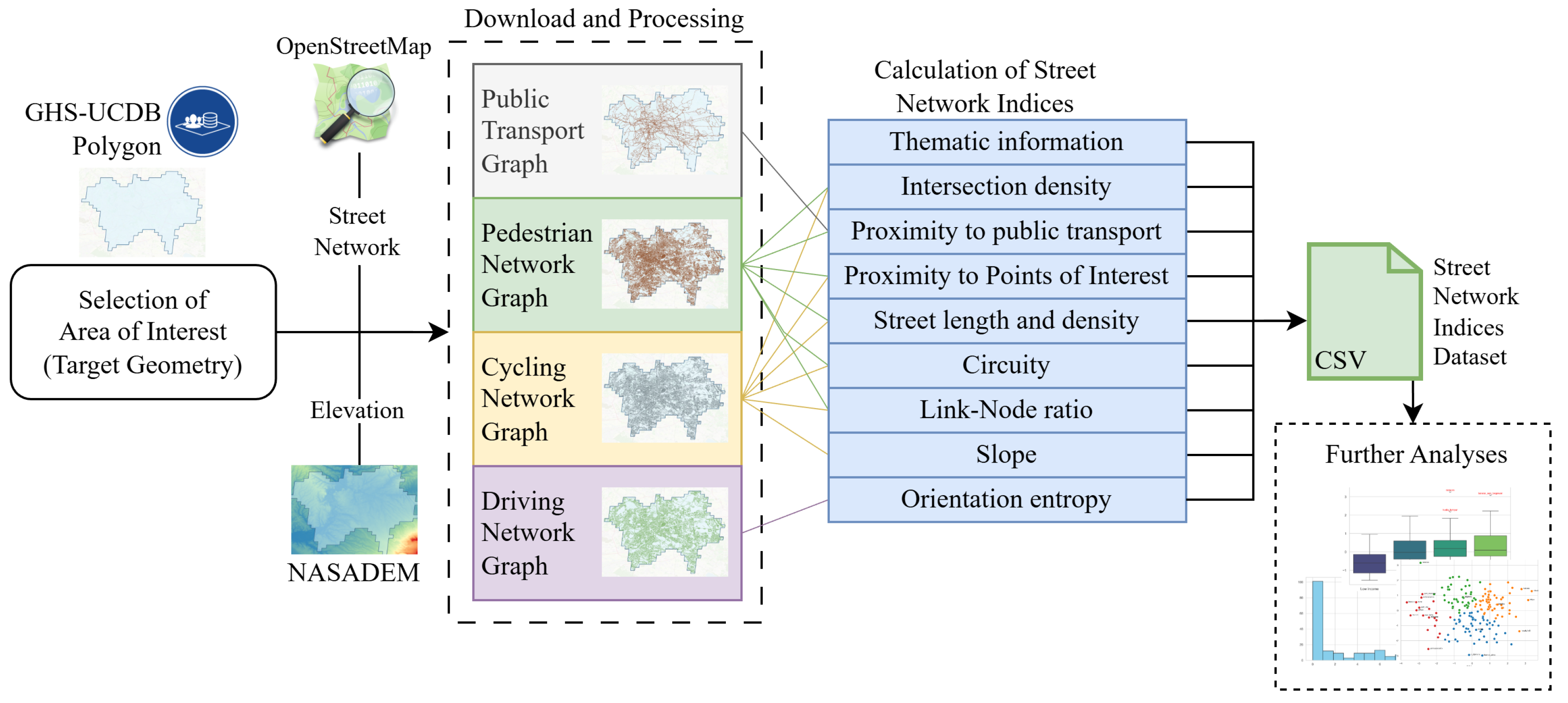
Having in mind the data availability, this section describes our methodological approach and data workflow. Figure 1 illustrates the generalised workflow for the characterisation of active mobility in urban areas, at the city scale, using open data and street network indices.

In our workflow, the initial step is to extract the area of interest (AOI) of the urban area to perform an analysis based on the GHS-UCDB dataset. Using the geometry of the AOI, the urban street networks of pedestrian, cycling, driving, and public transport are downloaded from OSM using the OSMnx Python library (version 2.0.5) [46], employing custom filters. The filtered networks are then further processed to generate refined analysis-ready graphs. The download procedure, filters, and processing are described in Section 3.3, with particular focus on the pedestrian and public transport network processing. During the download and processing steps, the street network graphs are complemented with elevation information using the NASADEM dataset.

The next step of the workflow is devoted to the calculation of street network indices for characterising urban mobility. The indices are then calculated using one or more of the extracted street network graphs, comprising indicators related to street intersections, proximity to public transport, proximity to POIs, street length, circuity, link–node ratio, slope, and orientation. In addition, thematic information of AOI is extracted and stored, including income level, climate classification, population, and geographical area. The thematic information is used to provide further context to the calculated indices, enabling analyses such as grouping and clustering according to city-scale characteristics. A complete description of the thematic information and the street network indices can be found in Section 4.

3.3. Download and Processing of Street Networks

For an accurate calculation of street network indices, having a strong data foundation, in particular with respect to the street networks, is fundamental. As this study is focused on the characterisation of active mobility, the pedestrian and cycling street networks are fundamental, but so is the road network, which is used for the calculation of orientation entropy described in Section 4.9, and the public transport network, used for the calculation of the index of proximity to public transport described in Section 4.3. All the downloaded graphs are stored in GraphML format for their further analysis, and as ShapeFile for their visualization in GIS software. GraphML, a popular data format based on XML and supported by Python’s NetworkX library, was used as the graph data format as it supports complex graph structures, as well as edge and node properties. The methodology for downloading and processing the street network graphs is based on previous work [47] and will be briefly described in the following sections.

3.4. Pedestrian Network

As pedestrians enjoy high freedom of movement, it is complex to decide when a street segment should be filtered or not from the street network. This is even more challenging in smaller urban centres and in cities from developing countries, as laws are usually less restrictive (or not enforced) with respect to pedestrian circulation, and there is lower mapping quality with respect to cities in high-income economies.

To assemble the pedestrian street network, filtered OSM data are downloaded and processed to address inconsistencies. The filter retrieves pedestrian infrastructure (i.e., sidewalks, paths, tracks, steps, and footways) and driving streets, assuming they are all walkable unless stated otherwise, consistent with the OSM pedestrian guidelines [48]. Said filter removes road segments that are inaccessible, segments where pedestrians are not allowed, and streets that specify a separately mapped sidewalk. In addition, shared cycling infrastructure is also retrieved, where pedestrians are allowed alongside bicycles. Indoor segments are removed, as they are out of scope for this study.

The processing of the pedestrian network is focused on correcting inconsistencies that filters alone can not cover. A particular case is the elimination of duplicated road segments where the sidewalk of the street is separately mapped, but the separation is not specified in its OSM tags. This problem arises from the fact that, in OSM, for a single street, it is possible to map the main road and the pedestrian sidewalk separately. That means one segment is used to represent the space where vehicles can circulate, and another where pedestrians can walk. In these cases, the road segment should specify that a separate segment is available as the sidewalk. This division is beneficial for data consumers, as, in this way, the pedestrian infrastructure is more accurate, by specifying crossings and sidewalks. However, streets that follow this pattern do not always specify the separation, generating more complexity on the resulting graph, inaccurate maps, and redundant information for data consumers. To overcome this, an algorithm was designed to detect those cases based on geometrical properties, i.e., incident angle and proximity. The algorithm uses an eroded buffer to locate nearby pedestrian infrastructure for each of the road network segments and eliminate said roads if pedestrian infrastructure is available. A more detailed description is available in [47].

The resulting graph of the pedestrian network is undirected, as, realistically, pedestrians can move in any direction when on a street or sidewalk.

3.5. Cycling Network

Given the increased freedom of movement that cycling offers with respect to private mobility, the analysis and extraction of cycling networks are challenging. In urban areas, bicycles share spaces with traffic and pedestrians but also possess separate infrastructure, such as cycleways. Ergo, the cycling network, is mostly composed of a subset of the road network where bikes are allowed, all cycling-enabled infrastructure (i.e., cycleways), and shared pedestrian infrastructure where bikes are allowed. Cycling street networks are represented as directed graphs, as they share portions of the road network in which the flow direction is fundamental.

The filters for the cycling network are devoted to retrieve all segments of the road network unless it is not explicitly stated that cycling is not allowed. Streets that do not possess information related to cycling through their OSM tags are assumed to allow bicycles, except for certain types, such as motorways, where it is implied that bicycles are not permitted. In addition to driving roads, the filter retrieves shared segments of pedestrian infrastructure where bicycles are allowed.

After filtering, cycling networks do not require extensive processing, as filters are enough to refine the network to a desirable extent. Consequently, processing for the cycling network is centred on ensuring that the graph is directed, on removing interstitial nodes, and on removing isolated edges and nodes which might be present after applying filters.

3.6. Driving Network

As OSM is primarily designed around driving networks, extracting this kind of network is not particularly challenging. Note that the driving street network is represented as a directed graph, given that the direction in which traffic flows is fundamental.

The filters for the this network are targeted on the street access level, i.e., whether vehicles are allowed or not allowed to transit through specific street segments. For this purpose, we use the same filters used by the OSMnx Python library [46] for the driving network. This filter removes segments based on the access level (e.g., private, forbidden, etc.), which is determined by the OSM tag “access”. It also removes segments that do not belong to the principal driving network, such as certain service streets, parking alleys, pedestrian infrastructure (e.g., sidewalks, paths), and cycling infrastructure (e.g., cycleways). The processing of the driving network is focused on eliminating redundant nodes and edges by eliminating interstitial nodes, as well as isolated nodes and edges.

3.7. Public Transport Network

The extraction of public transport networks is different to all other means of transportation, as public transport in OSM is represented by stations as points, and connections (routes) between them as edges. Stations and routes are linked by OSM relationships, which are collections of points, lines, and/or polygons that are associated with each other.

The public transport network is composed of relationships that include multiple stops or stations, and their corresponding connections, called routes. In its graph form, the public transport network is composed of nodes that represent each station and/or stop of one or more transport types (e.g., bus, metro, train, etc.) and edges that represent connections between them. The streets or rails where public transport vehicles physically circulate are not included. It is worth mentioning that, depending on the map completeness of the urban area, the public transport network may not contain any edges (routes) and only include stops and stations. In such cases, the graph is only composed of its nodes.

To assemble the public transport network, two download procedures are carried out. First, stops and stations are downloaded from OSM and designated as the nodes of the graph. Second, the routes of the network are downloaded as relationships and the edges are constructed. Filters for downloading the public transport nodes are applied using the OSM keys “public_transport”, “amenity”, and “highway”. For the edges, the filter is based on relationships within the area of interest that contain the key “route” and that represent one or more transport modes, i.e., train, subway, monorail, tram, bus, trolleybus, or ferry. This is consistent with the official OSM public transport wiki page [49].

After downloading the filtered nodes and edges, the processing of the public transport network consists of assembling the graph. The public transport graph is directed and is composed of stops and/or stations as the nodes and the direct route segments that connect said nodes as the edges. Each node contains information about the different modes of transportation that are available at each stop, while the edges contain route geometries and other data related to the route, such as the operator, mode, and initial and end stations.

4. Street Network Indices

For this study, we curated a set of indices, derived from the academic literature, for the characterisation of active mobility in urban areas at the city scale. As the concept of active mobility refers to walking and cycling, the selected indices are tailored for representing pedestrian and cycling mobility. In addition, city-scale socioeconomic thematic information is also extracted.

A total of eight types of indices were identified from the academic literature, namely proximity to POIs, proximity to public transport, circuity, street length, link–node ratio, slope, intersections, and orientation entropy. Each type of index has one or more indicators associated, which are the actual values that are calculated, such as the average street length (derived from the street length) or the intersection density (derived from the intersections). These indices characterise urban areas by topological properties, as street length or circuity, and also by functional aspects, such as the proximity to services or public transport.

For certain indices, statistical information is calculated at the city scale as indicators, particularly the mean, median, standard deviation, range, and interquartile range (IQR). A total of 50 indicators are reported for each urban area, which include the name of the main city representing the urban area, 6 thematic variables, and 43 city-wise indicators. The full list of the indices and their indicators can be found in

Table 1. Complete list of street network indices calculated per urban area, indicating the network(s) in which they were calculated, the index type, the concrete indicators derived from the index, and their units.

Network	Index Type	Indicators	Value Type/Unit
Driving	Orientation entropy	Orientation entropy	Nats
Pedestrian, Cycling	Proximity to POIs	Urban area-wise mean, median, range, std. deviation, and IQR	Number of distinct POI types in a network range of 15 min
Pedestrian	Proximity to public transport	Urban area-wise mean, median, range, std. deviation, and IQR	Number of public transport stations in a network range of 400 m
Pedestrian, Cycling	Circuity	Circuity	Unitless
Pedestrian, Cycling	Street length	Urban area-wise mean, median, range, std. deviation, and IQR	Metres
		Street density	Street segments/km2
		Total length	Metres
Pedestrian, Cycling	Link–Node ratio	Link–Node ratio	Unitless
Cycling	Slope	Urban area-wise mean, median, range, std. deviation, and IQR	Percentage
Pedestrian, Cycling	Intersections	Intersection density	Intersections/km2
		Intersection count	Number of intersections

, specifying the network or networks for which the index was calculated, the index type, the indicators associated with the index (e.g., mean, median, density, etc.), and their units or value types (e.g., metres, percentage, unitless, etc.).

In the following subsections, each index type is described in detail, including references and justification from the academic literature and other studies. A thorough description of their computational implementation is also included, along with value ranges associated with the index, if available.

4.1. Thematic Information

Thematic information is compiled for each urban area to complement and contextualise the indices. The information comprises the name of the main city representing the urban area, together with six thematic variables that are extracted from the GHS-UCDB. These variables correspond to the total urban area in squared kilometres (km²), the population count, the geographical area to which the city belongs (

Table 2. Geographical areas of the world and corresponding 2-letter codes used for simplification. This classification of geographical areas is based on the one provided by the GHS-UCDB dataset.

Geographical Area	Code
Sub-Saharan Africa	SA
Oceania	OC
Australia and New Zealand
Northern America	AM
Latin America and the Caribbean
Northern Africa and Western Asia	NW
Europe	EU
Eastern and South-Eastern Asia	EA
Central and Southern Asia	CA

), its built-up area in squared kilometres (km²), its income group according to the World Bank income group classification [50], and the cities’ Köppen–Geiger climate classification [51]. Thematic information is useful for further understanding and contextualising the design choices of urban areas, enabling comparisons, groupings, and clusterings in further analyses.

As a remark, to account for imbalances between geographical regions, the region of “Australia and New Zealand” was merged with “Oceania”, and the region of “Northern America” was merged with “Latin America and the Caribbean”.

4.2. Proximity to POIs

The proximity to POIs is an index widely used for measuring urban mobility and accessibility [10,11,19,45]. This index is often implemented as the amount and/or typology of services and amenities that can be reached from determined points of the network in a specified time or distance (e.g., 10 min or 1 km). In this context, POIs refer to a set of services and amenities that people have access to, such as restaurants, parks, cultural spaces, healthcare facilities, schools, etc. The list of POIs that we consider for this index are reported in

Table A1. Category and OSM value of the POIs considered for the index of proximity to POIs.

POI Category	OSM Values
Sustenance	“bar”, “biergarten”, “cafe”, “fast_food”, “food_court”, “pub”, “restaurant”, “bakery”, “butcher”, “chocolate”, “ice_cream”, “pastry”, “seafood”, “tea”, “supermarket”, “convenience”
Education	“college”, “driving_school”, “kindergarten”, “language_school”, “library”, “research_institute”, “school”, “music_school”, “university”
Transportation	“fuel”, “charging_station”, “motorcycle_parking”, “bicycle_parking”, “parking”, “taxi”
Financial	“atm”, “bank”, “bureau_de_change”, “money_transfer”
Healthcare	“clinic”, “dentist”, “doctors”, “hospital”, “nursing_home”, “pharmacy”, “social_facility”, “veterinary”
Entertainment, Arts and Culture	“arts_centre”, “casino”, “cinema”, “community_centre”, “conference_centre”, “fountain”, “nightclub”, “theatre”, “place_of_worship”, “kiosk”
Public Services	“courthouse”, “fire_station”, “police”, “post_office”, “townhall”
Green Spaces	“dog_park”, “garden”, “park”, “playground”

, in Appendix A, along with their categories. The POIs list and categories were derived from the official OSM amenity, leisure, and shop wiki pages [52,53,54].

This index is based on the fact that having access to a variety of amenities and services at a reasonable distance is beneficial for active mobility, as it encourages walking and cycling instead of driving or taking public transport. Following the framework of 15 min cities [55], 15 min was taken as the reference for the aforementioned time in which POIs must be reached. To calculate the elapsed time at each edge, a fixed speed was set for the pedestrian network at 5 km/h, and at 15 km/h for the cycling network. The time is then calculated as the length of each segment divided by the related speed.

The proximity to POIs was calculated separately for the pedestrian network and the cycling network, to individually characterise pedestrian and cycling mobility. The process for calculating this index is as follows:

• First, the POIs belonging to the categories of Table A1 are downloaded from the OSM database. Each POI is then assigned to an edge of the street network, based on distance.
• After assigning each POI to its closest edge, the index is calculated for each node of the graph as the amount of different POI categories that are reachable within 15 min. To do so, a Breadth-First Search (BFS) algorithm that counts the POI categories and stops when surpassing 15 min in network time was implemented.
• The mean, median, range, standard deviation, and interquartile range are calculated for the entirety of the pedestrian and cycling graphs using the node-wise POI count as city-scale indicators.

4.3. Proximity to Public Transport

The proximity to public transport is an index widely used as an indicator of sustainable mobility. It measures how well covered an urban area is with respect to public transport and is particularly used in walkability and pedestrian accessibility assessments [17,55,56].

This index is implemented as the count of public transport stops or stations (e.g., bus stops, metro stations, tram stops, etc.) that are reachable, for each of the nodes of the pedestrian graph, at a network radius of 400 m. The selection of the distance of 400 m is based on the concept of pedestrian catchment or pedestrian shed, which states that a distance of 0.25 miles, or around 400 m, is an easily walkable distance for most people [57]. As the proximity to public transport is mostly important for pedestrians, this index is only calculated for the pedestrian network. The public transport network is used as the public transport information for the calculation of this index. The calculation process is as follows:

• First, each node of the public transport graph is linked and accumulated to its closest edge of the pedestrian graph. By the end, each edge of the pedestrian network contains the number of closest public transport stations.
• Then, for each node of the pedestrian graph, the number of stations reachable in a 400 m network radius is calculated using a Breadth-First Search (BFS) algorithm that accumulates the number of visited stations, stopping when the network distance of 400 m is surpassed.
• When all the nodes of the pedestrian graph are processed, the mean, median, range, standard deviation, and interquartile range are calculated as city-scale indicators.

4.4. Circuity

Circuity, also called the detour index, measures the sinuosity of the street network as the ratio of network distance (the real-world length of a street segment) with respect to its straight-line length, also known as “as-the-crow-flies”. Circuity, as a street network index, has mostly been studied as an indicator of the efficiency and performance of street networks [22,58,59,60].

To calculate circuity, each edge of the graph is visited and its network length is calculated based on its geometry, while its straight-line length is calculated using the geodetic distance between the edge’s nodes. The network and straight-line lengths are accumulated for the entire graph and, finally, the global circuity value is calculated as the ratio of the total network distance divided by the total straight-line distance.

Values of circuity closer to one represent more efficient street networks, as they tend to have more ordered and straight street patterns. Higher values represent more sinuous streets with curves and turns that undermine efficiency. Circuity is calculated for the pedestrian and cycling network independently, to account for their differences.

4.5. Street Length

Street length, also referred to as block length, has been used as a street network index for characterising accessibility, network connectivity, and mobility [10,13,17,58], particularly in walkability studies. It is also a key part of composite indices such as WalkScore^® [30].

From the street lengths, seven indicators are reported, corresponding to (i)–(v) the urban area-wise street length mean, median, standard deviation, range, and interquartile range; (vi) the total street length; and (vii) the street density, calculated as the total street length divided by the urban area in squared kilometres. Street length indicators are calculated for both the pedestrian and cycling networks.

Although there is no consensus on what the ideal street length is, shorter street lengths generally indicate a more connected and accessible network, while longer street segments are representative of car-centric urban areas. Other elements, when combined with street length, such as accessibility to services, may have stronger relationships with increased walkability [61].

4.6. Link–Node Ratio

The link–node ratio (LNR) is a street network index primarily used to measure the connectivity of a street network from a network density perspective, as it determines how densely connected a network is. The LRN has been particularly used in studies related to walkability and urban form [17,62,63]. For an undirected graph, the LNR is defined as the number of edges (links) of the graph divided by the number of nodes.

For the LNR index, higher values reflect better connectivity, with 2.5 being the theoretical “maximum” as it represents the LNR of a grid, which has ideal connectivity. Normal LNR values vary between 1.1 and 1.8, with 1.4 being a desired value for urban areas.

4.7. Slope

The slope, also called grade, gradient, incline, or rise, is the measurement of the degree of elevation that a street segment has with respect to a horizontal plane. It is a critical indicator of active mobility, specially as a measurement of cycling comfort, accessibility, and practical usability. The slope has been extensively used as a measurement of cycling comfort [45,64], given that hillier urban areas are less bike-friendly compared with flat ones, as a key characteristic of the urban street network [13] in commercial cycling indices such as BikeScore^® [31] and in the public sector for defining municipal regulations [10,45]. As this index is more critical for cycling than for pedestrian networks, it was only calculated for the former.

To calculate it, the elevation of each node of the graph is extracted from the NASADEM [44] dataset. Then, the decimal slope, also called “rise over run”, is calculated for each of the edges of the dataset. Using the slope absolute value, to account for only the elevation gain in each segment, the mean, median, range, standard deviation, and interquartile range are calculated for the entire cycling graph.

The slope also characterises cycling comfort levels. Furth et al. [45] propose a six-level scale of cycling comfort levels based on slope. This scale considers a slope from 0% to 3% as high comfort; the next levels (from 3% to 5%, from 5% to 6.5%, from 6.5% to 8%, and from 8% to 9%) progressively decrease in comfort; and finally more than 9% slope is considered a high exertion zone.

4.8. Intersections

Intersections have been identified as a fundamental component of the street network, key for understanding their shape and function [10]. Due to this, the intersection density and intersection count have been used as measurements of connectivity, compactness, and street network design [13,56,62].

Intersections in street networks are defined as junctions, represented as nodes in a primal graph, that have at least two different exits. Dead-ends (also called cul-de-sacs) are also considered intersections. These considerations mean that not all the nodes of the network are considered intersections.

Two indicators are considered for this type of index: (i) the total number of intersections of the urban area; (ii) the intersection density, calculated as the total number of intersections divided by the area of the urban area in squared kilometres. Both the intersection count and intersection density were calculated for the pedestrian and the cycling street networks. Despite the fact that higher values of intersection density are commonly considered better for active mobility, when this value is too high, it may have opposite effects. However, there is no consensus on the value where the number of intersections affect mobility, nor the value ranges for intersection count or densities.

4.9. Orientation Entropy

The index of orientation entropy is an index proposed in the academic literature as a measurement of the structural “order” of street networks [65,66]. This index calculates the Shannon index of the street segment bearings (i.e., the angles of street segments) for the entire graph as a measurement of order. This index is based only on the geometry and design of urban street networks.

Lower values of orientation entropy represent more ordered street networks, as it approaches a perfect grid. Thus, theoretical values range from 1.386, representing a perfect grid, to 3.584, representing the maximum entropy or a perfectly uniform distribution of street bearings [65].

This index was calculated using only the driving street network, as it better represents the urban area layout, shape, and design, providing a more general overview of the order of the streets of an urban area.

5. Results

This section describes the case study that was used to test the methodology, the resulting dataset of the index calculations, and their subsequent data analysis.

5.1. Case Study and Selected Cities

To test our methodology, we calculated the previously described indicators for the urban areas of 176 capital cities. These cities give plenty of variability in terms of size, location, population density, income, and climate, offering global coverage.

Despite the total of sovereign states being more than 176, after an initial evaluation of the data availability, some cities were excluded from the analysis. For some countries, the capital city was replaced with another representative city of the country, based on its data availability. The countries of Andorra, Antigua and Barbuda, Bhutan, Cabo Verde, Dominica, Federated States of Micronesia, Grenada, Kiribati, Liechtenstein, Marshall Islands, Monaco, Palau, Saint Kitts and Nevis, Saint Lucia, Saint Vincent and the Grenadines, San Marino, Seychelles, and Tuvalu were excluded due to a lack of GHS-UCDB polygon on their respective capital cities or any important city in the country. The countries of Kosovo, Palestine, Taiwan, and Vatican City were excluded as they are not current members of the United Nations (as of July 2025). The country of Nauru was also excluded as it does not have an official capital city, and the country of Cyprus was excluded as its capital city is currently disputed.

Finally, the following countries had cities different than their capitals selected for the study, as the GHS-UCDB polygon was non-existent for their capital cities or only covered it partially: (i) Australia: Canberra changed to Sydney; (ii) Belize: Belmopán changed to Belize City; (iii) Eswatini: Mbabane changed to Manzini; (iv) Gambia: Banjul changed to Serrekunda; and (v) Guinea: Conakry changed to Coyah.

The full list of cities is reported in

Table A2. List of city names and countries in ISO-3 code.

Country	City	Country	City	Country	City
AFG	Kabul	GEO	Tbilisi	NOR	Oslo
ALB	Tirana	DEU	Berlin	OMN	Muscat
DZA	Algiers	GHA	Accra	PAK	Islamabad
AGO	Luanda	GRC	Athens	PAN	Panama City
ARG	Buenos Aires	GTM	Guatemala City	PNG	Port Moresby
ARM	Yerevan	GIN	Coyah	PRY	Asuncion
AUS	Sydney	GNB	Bissau	PER	Lima
AUT	Vienna	GUY	Georgetown	PHL	Manila
AZE	Baku	HTI	Port-au-Prince	POL	Warsaw
BHS	Nassau	HND	Tegucigalpa	PRT	Lisbon
BHR	Manama	HUN	Budapest	QAT	Doha
BGD	Dhaka	ISL	Reykjavik	ROU	Bucharest
BRB	Bridgetown	IND	New Delhi	RUS	Moscow
BLR	Minsk	IDN	Jakarta	RWA	Kigali
BEL	Brussels	IRN	Tehran	WSM	Apia
BLZ	Belize City	IRQ	Baghdad	STP	São Tomé
BEN	Porto-Novo	IRL	Dublin	SAU	Riyadh
BOL	Sucre	ISR	Jerusalem	GBR	Edinburgh
BIH	Sarajevo	ITA	Rome	SEN	Dakar
BWA	Gaborone	JAM	Kingston	SRB	Belgrade
BRA	Brasilia	JPN	Tokyo	SLE	Freetown
BRN	Bandar Seri Begawan	JOR	Amman	SGP	Singapore
BGR	Sofia	KAZ	Astana	SVK	Bratislava
BFA	Ouagadougou	KEN	Nairobi	SVN	Ljubljana
BDI	Gitega	KWT	Kuwait City	SLB	Honiara
KHM	Phnom Penh	KGZ	Bishkek	SOM	Mogadishu
CMR	Yaoundé	LAO	Vientiane	ZAF	Pretoria
CAN	Ottawa	LVA	Riga	KOR	Seoul
CAF	Bangui	LBN	Beirut	SSD	Juba
TCD	N’Djamena	LSO	Maseru	ESP	Madrid
CHL	Santiago	LBR	Monrovia	LKA	Colombo
CHN	Beijing	LBY	Tripoli	SDN	Khartoum
COL	Bogota	LTU	Vilnius	SUR	Paramaribo
COM	Moroni	LUX	Luxembourg	SWE	Stockholm
COD	Kinshasa	MDG	Antananarivo	CHE	Bern
COG	Brazzaville	MWI	Lilongwe	SYR	Damascus
CRI	San José	MYS	Kuala Lumpur	TJK	Dushanbe
CIV	Yamoussoukro	MDV	Malé	TZA	Dodoma
HRV	Zagreb	MLI	Bamako	THA	Bangkok
CUB	Havana	MLT	Valletta	TGO	Lomé
CZE	Prague	MRT	Nouakchott	TON	Nuku’alofa
DNK	Copenhagen	MUS	Port Louis	TTO	Port of Spain
DJI	Djibouti	MEX	Mexico City	TUN	Tunis
DOM	Santo Domingo	MDA	Chișinău	TUR	Ankara
TLS	Dili	MNG	Ulaanbaatar	TKM	Ashgabat
ECU	Quito	MNE	Podgorica	UGA	Kampala
EGY	Cairo	MAR	Rabat	UKR	Kyiv
SLV	San Salvador	MOZ	Maputo	ARE	Abu Dhabi
GBR	London	MMR	Pyinmana	USA	Washington
GNQ	Malabo	NAM	Windhoek	URY	Montevideo
ERI	Asmara	NPL	Kathmandu	UZB	Tashkent
EST	Tallinn	NLD	Amsterdam	VUT	Port Vila
SWZ	Manzini	NZL	Wellington	VEN	Caracas
ETH	Addis Ababa	NIC	Managua	VNM	Hanoi
FJI	Suva	NER	Niamey	GBR	Cardiff
FIN	Helsinki	NGA	Abuja	YEM	Sana’a
FRA	Paris	PRK	P’yŏngyang	ZMB	Lusaka
GAB	Libreville	MKD	Skopje	ZWE	Harare
GMB	Serrekunda	GBR	Belfast

, in Appendix A, providing the name of the city and its respective country in ISO-3 code. A map, displaying the geographical distribution of the selected cities, is portrayed in Figure 2.

5.2. Dataset of Calculated Street Network Indices and Data Analysis

Based on the 176 capital cities and the 50 indicators listed in Table 1, we present the results of the calculation of the street network indices as an open dataset in CSV (comma-separated values) format, along with additional metadata that provides further information and descriptions of the columns and values of the dataset [67]. The indices were calculated using street networks downloaded and processed from 25 June 2025 to 30 June 2025. In addition, the code that was used to extract street networks and calculate the indices has been made available as open-source code through a repository. The link to the repository can be found in the article’s data availability statement.

To further showcase the usage of the resulting dataset, a comprehensive data analysis was performed to derive insights and relationships regarding active mobility. In particular, the analyses were focused on grouping and pattern finding from contextual information like the geographical area, population, climate class, and income group.

5.2.1. Data Exploration

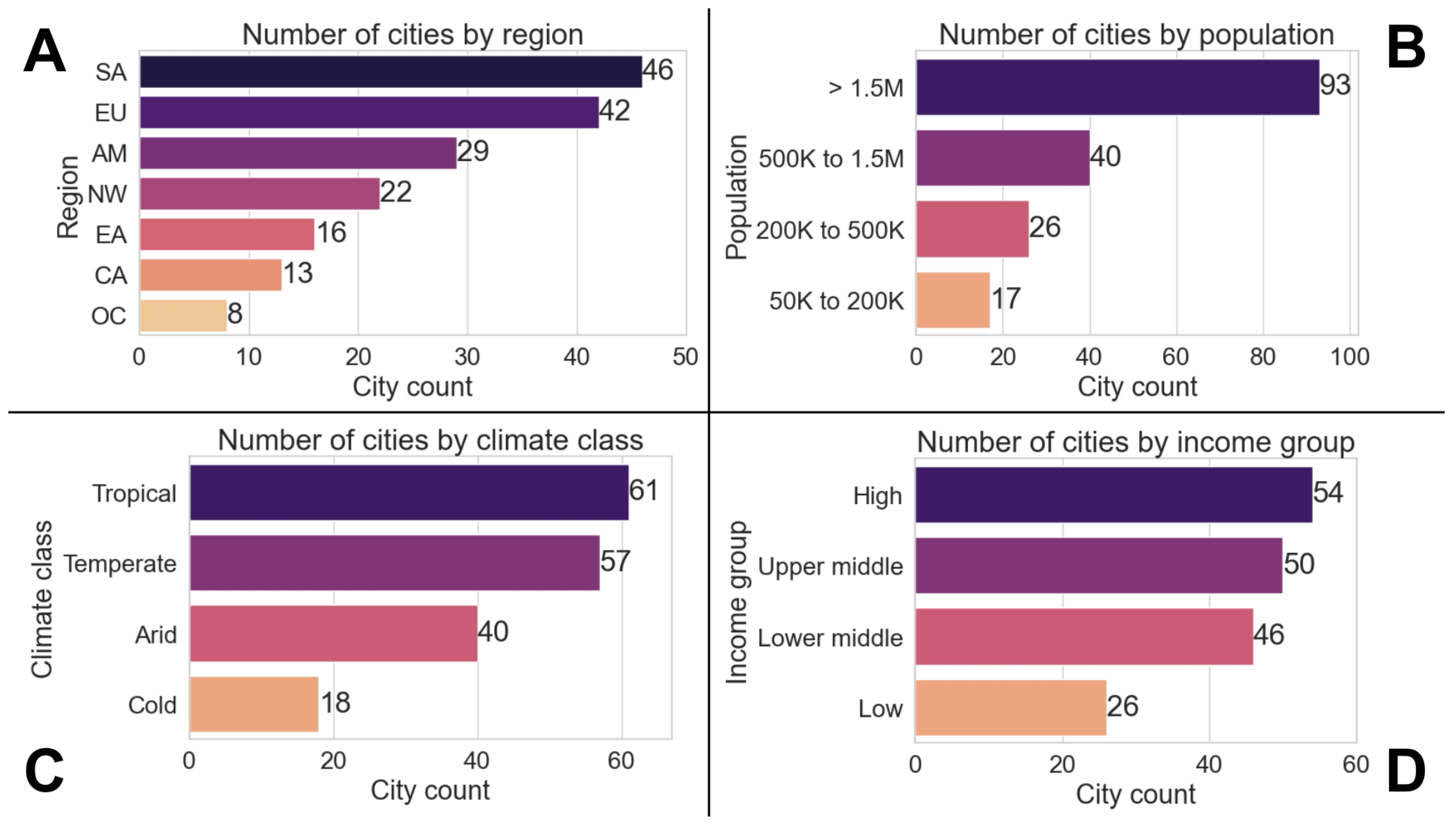
Initial data exploration was carried out to understand the distribution of the obtained indices with respect to four of the thematic variables, namely the geographical area, population, income group, and climate class. Although the population variable is continuous, each population value was reclassified to one of four population categories, i.e., (i) from 50 K to 200 K inhabitants; (ii) from 200 K to 500 K inhabitants; (iii) from 500 K to 1.5 M inhabitants; and (iv) more than 1.5 M inhabitants. Climate classes were grouped in four categories, namely tropical, arid, temperate, and cold, which correspond to the A, B, C, and D classes of the Köppen–Geiger classification, respectively. The city count for each of the variables was calculated and is reported in Figure 3.

From the data exploration, it is possible to observe that the geographic areas (panel A) with a highest number of cities are Europe and Sub-Saharan Africa, while Oceania has the lowest city count as it has less countries. From a population perspective (panel B), more than half of the analysed urban areas have more than 1.5 million inhabitants, showing that most are highly populated urban centres, as it would be expected from capital cities. As for climate (panel C), tropical and temperate climates present a larger number of cities with respect to the cold (also referred to as continental in the Köppen–Geiger classification) and arid climates. Finally, the income groups (panel D) are reasonably balanced in the high, upper-middle, and lower-middle groups, while only 15% of capital cities belong to the low-income group.

5.2.2. Global Analysis by Thematic Variables

Each city was grouped with respect to the previously explored thematic variables. To identify global trends, we generated the box plots of each of their individual indicators, assessing their dispersion, median values, and outliers.

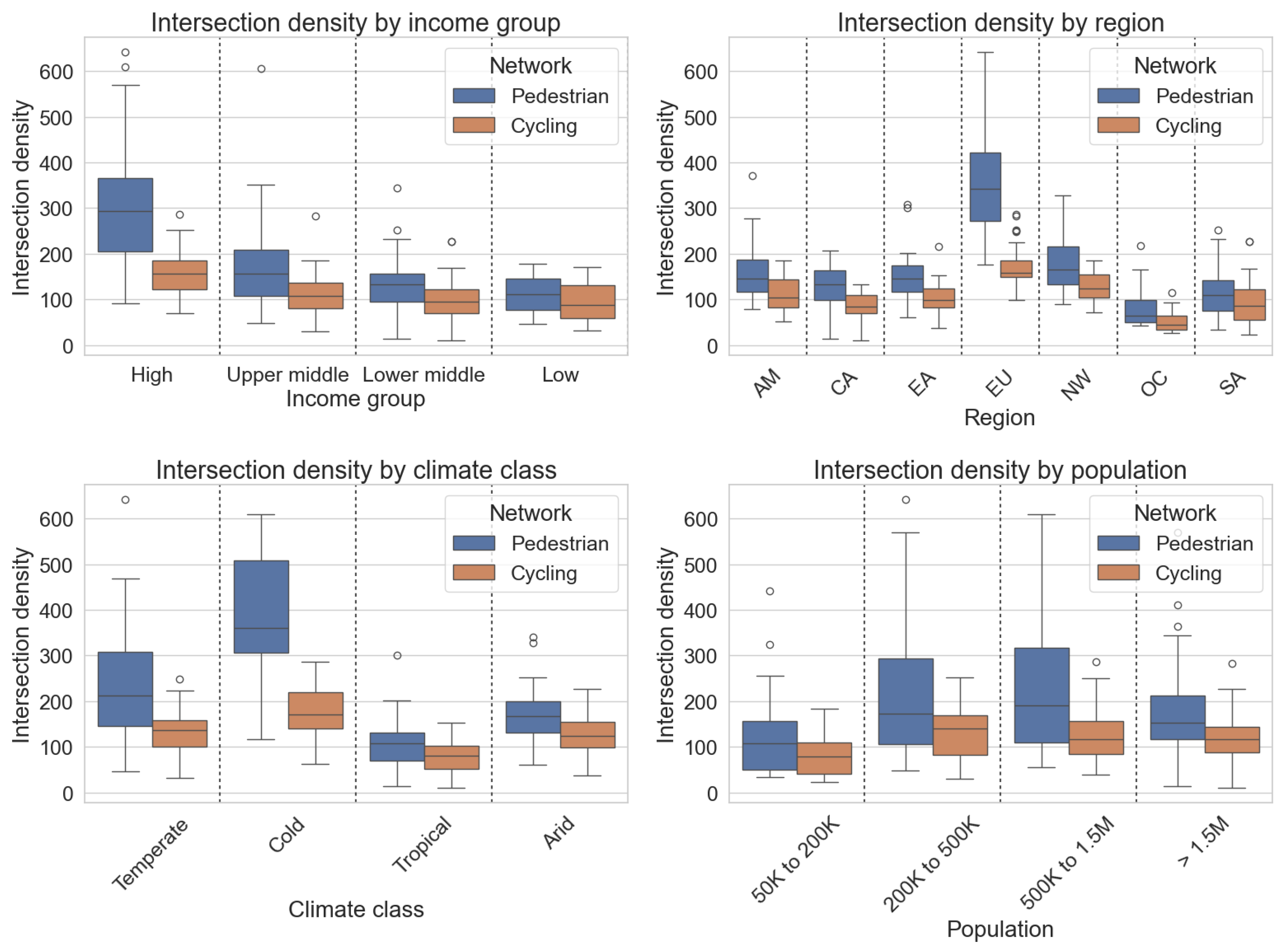
To illustrate part of the analysis, Figure 4 shows side-by-side the box plots of the intersection densities for pedestrian and cycling street networks, grouped by income group, geographical area, climate group, and population. Intersection density has been found to be an indicator of function, connectivity, and compactness of urban areas, as stated in Section 4.8. According to the literature, higher values of intersection density are highly related to more walkable urban areas [68]. With respect to cycling, the term connectivity is used to indicate a positive relationship between intersection density and cyclability [69].

From the box plots, it is possible to identify certain active mobility characteristics based on intersection density and thematic attributes. For instance, cities in high-income economies present street networks that are better suited for active mobility based on their intersection density values. This corresponds to the presence of more and better pedestrian and cycling infrastructure in cities with higher income economies, alongside an increased mapping quality by local communities which elevates the number of street segments present, therefore increasing the number of intersections. Cities in cold and temperate climates were found to present better conditions for pedestrians, but average for cyclists, while European cities have, by far, the best conditions for overall active mobility.

Another interesting relationship is that, as both the pedestrian and cycling networks possess an overall similar shape and share some network elements, similar trends emerge for each of the analysed thematic variables. In fact, for both pedestrian and cycling networks, cities with higher incomes present an overall higher intersection density, indicating increased connectivity, compactness, and improved active mobility. Other patterns shared for both networks include European cities having overall higher connectivity, while this is lowest for Oceania, and that middle sized cities, with respect to population (i.e., between 200,000 and 1.5 million inhabitants), present overall higher intersection densities than metropolises that surpass 1.5 million inhabitants.

Despite similar trends for both pedestrian and cycling networks, when closely looking at the results, differences in the magnitude and the dispersion of values vary from one mean of transportation to the other, highlighting the need to perform mode-specific analysis. With respect to magnitudes, the values of pedestrian intersection density are generally higher than their cycling counterparts, at almost almost double in some cases. Such differences in range and interquartile range can be seen for all thematic variables.

5.2.3. Proximity Trends

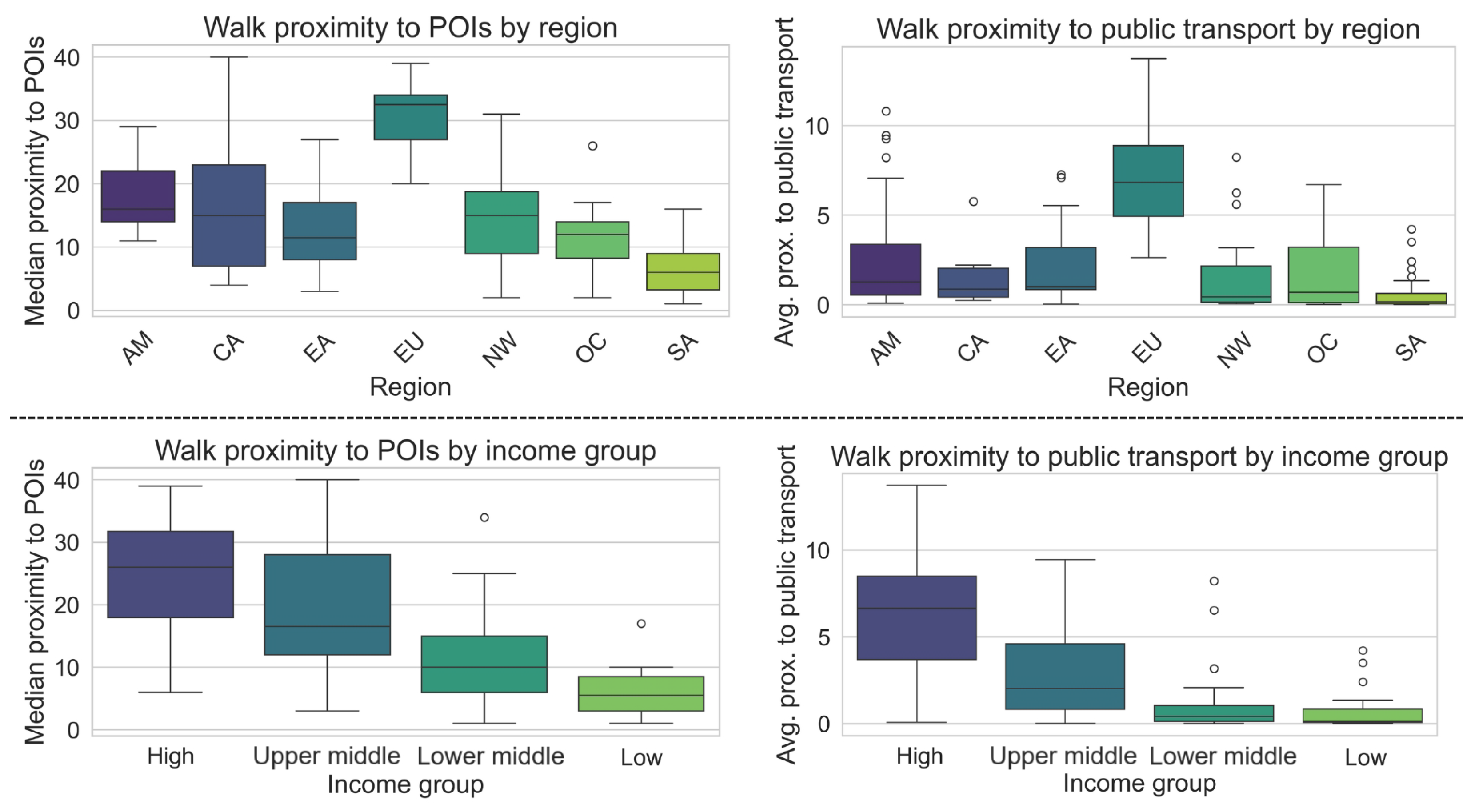
A second analysis considers functional aspects of the network using the indicators of median proximity to POIs and average proximity to public transport. Both were analysed for the pedestrian network and grouped by geographical area and income group, as shown in the box plots of Figure 5. From the figure, it is evident that higher income is related to both an increased proximity to POIs and public transport infrastructure. With respect to geographical area, European cities have higher values of proximity (both to POIs and public transport) with respect to other areas, while Sub-Saharan Africa possesses the lowest values. European capitals are generally smaller in area, more compact, and have more POIs mapped, which are ideal characteristics for active mobility. On the contrary, Sub-Saharan African cities mostly belong to low- and lower-middle-income economies, have less detailed maps in OSM, and have less developed public transport systems, which translates to lower values of proximity to both POIs and public transport, with an average value close to zero, and to worst conditions for active mobility.

5.2.4. Cluster Analysis

Finally, we performed clustering over a subset of pedestrian indicators. Clustering is a non-supervised technique for finding similarities within the elements of a dataset. An initial procedure of scaling was carried out to account for the differences in magnitudes between the different indicators of the dataset, the outliers, and the skewness. Then, a dimensionality reduction technique was applied. Principal Component Analysis (PCA) was used, reducing the dataset to two dimensions (PC1 and PC2) and allowing for the visualisation of the clusters on a 2D Cartesian plane. The indices used for the calculation of the PCA are reported in

Table 3. Main indicators considered for the Principal Component Analysis (PCA) of pedestrian networks and their resulting weights.

Indicator	PC1 Weight	PC2 Weight
Median street length	−0.3913	0.1073
Street density	0.5038	0.1512
Intersection density	0.5928	−0.0520
Median proximity to POIs	0.3432	−0.1299
Average proximity to public transport	0.3432	−0.0652
Circuity	−0.0535	−0.6865
Link–node ratio	0.0395	0.6858

, along with the weights of each index for each component. PCA also allows for a multi-criteria comparison of active mobility for cities, representing a composite walkability index.

Positive weights in the PCA indicate a direct relationship between the indicator and the dimension, while negative values indicate an inverse relationship. The PC1 dimension represents denser street network configurations, making the street and intersection densities the two indices with higher weights, with 0.50 and 0.53, respectively. It also takes into account POIs and public transport proximities, with weights of 0.34 for both, and the median street length with a weight of −0.39. The negative weight means that shorter street lengths yield higher PC1 values. The PC2 dimension represents lower values for urban centres with high circuity and low link–node ratio, with weights of −0.68 and 0.68, respectively.

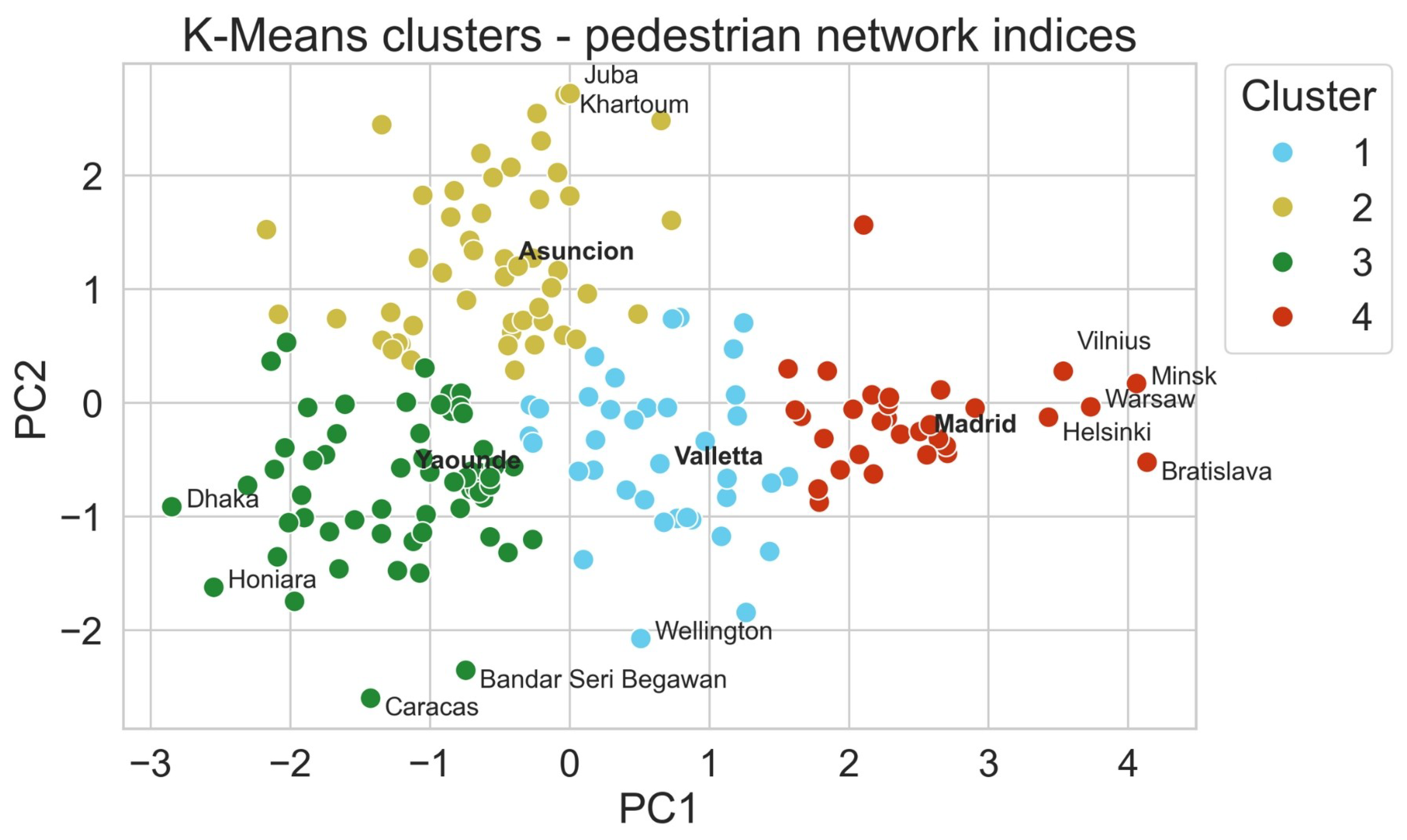
In general, higher PC1 and PC2 values indicate more walkable networks. For PC1, high intersection and street densities are indicators of connectivity, compactness, and good design, higher proximities to POIs and public transport are more desirable to pedestrians, and shorter street segments are regarded as more walkable. Consequently, higher PC2 values are achieved by lower values of circuity, which is an indicator of street network efficiency, and higher link–node ratios, which indicate increased connectivity and compactness. Both components capture 80% of the dataset variance. For each city, the value of PC1 and PC2 was calculated, and a K-Means clustering with four clusters was performed. The number of clusters was selected using an elbow test. The results of the clustering for the pedestrian networks are shown in Figure 6.

Cluster 1 (blue) contains cities with average walkability. Both components are around the average values, with few cities, such as Wellington (New Zealand), presenting lower efficiency due to high circuity. This cluster is very diverse, containing cities from all around the world (except Sub-Saharan Africa), and of lower-middle, upper-middle, and high income levels.

Cluster 2 (yellow) contains cities that present lower values of circuity and higher link–node ratios but are, overall, less compact, less connected, and less functional due to lower proximity values. This cluster contains mostly low- and lower-middle-income cities (38 out of 50 cities), which, counter-intuitively, have better efficiency than higher-income ones, as their street networks present more straight segments and exhibit more grid-like structures. This cluster is mostly composed of cities from Africa, Western Asia, and the Americas; it does not contain cities from Europe nor Oceania. A notable similarity that was found in this cluster are the cities of Juba and Khartoum, capitals of Sudan and South Sudan, respectively, which present very similar characteristics.

Cluster 3 (green) contains the less walkable cities, as it represents urban areas with higher-than-average circuity and lower link–node ratios, while also presenting lower-than-average values of connectivity and proximities. This cluster is mostly composed of cities of Sub-Saharan Africa and the Americas, with 75% of the cities belonging to lower-middle and upper-middle economies. It is worth mentioning that most of the cities in the Americas that belong to this cluster are located in Central America and the Caribbean. This cluster has the largest amount of cities but, notably, it does not contain any European cities.

Cluster 4 (red) contains cities that are regarded as more walkable due to high values of connectivity, compactness, and proximities to POIs and public transport. However, the circuity and link–node ratio values are mostly average. This cluster is almost entirely composed of European cities within high-income economies. The only non-European cities in this cluster are Tokyo and Ottawa. This cluster highlights how European cities are generally more compact, have access to more and various amenities within walking distances, and possess more organised public transport systems. However, the tendency to have average and lower-than-average values in the PC2 dimension shows how European cities have normally followed natural expansion, with more sinuous and organic street layouts, which translate to higher circuity values.

6. Discussion

Based on the analysis of the calculated street network indices, it is evident that high- and upper-middle-income economies present better conditions for active mobility, particularly in the regions of Europe, the Americas, and Northern Africa and Western Asia. The categorisation by income group and geographical region provided clearer patterns over the data with respect to other variables, such as climate. These results highlight the relationship between economic prosperity, map completeness, and improved active mobility conditions, evidenced from indices like proximity to POIs and public transport.

Principal Component Analysis (PCA) and clustering proved to be an effective way for comparing active mobility conditions for cities and extracting different trends, similarities, and particular characteristics that determine walkability. For example, Caracas (Venezuela) scored very poorly with respect to other cities in terms of efficiency (circuity) and connectivity, ranking last in circuity due to its hilly topography, featuring many small and sinuous streets, which greatly affect its active mobility conditions. In contrast, the city of Bratislava (Slovakia) ranked very highly in terms of connectivity and compactness, exhibiting improved conditions for active mobility. After visual inspection, this value is attributed to its high level of map completeness with respect to pedestrian infrastructure and its compactness, evidenced by its low average street length of only 43 m.

From clustering analysis, another interesting finding was that cities within low-income economies from Africa, Western Asia, and the Americas presented lower values of circuity, which is associated with more efficient street networks, and higher link–node ratios than their high-income counterparts, which was counter-intuitive. After visually inspecting some of the resulting street networks, the maps showed that many cities from this cluster have particularly gridded and straight street networks. Figure 7 shows four cities from the yellow cluster of Figure 6: Asunción (Paraguay); Male (Maldives); Khartoum (Sudan); and Juba (South Sudan). The experimental results from a study by Nathan et al. [70] support this finding, concluding that the order of street networks and usage of grid-like structures have been associated with post-colonial and autocratic regimes, mostly present in Africa.

6.1. Comparison with Similar Global Studies

Similar studies have utilised open data for comparing street network indices between multiple cities. Whether for global [13,65,71], region [16], or country-wise [22,27] analyses, the usage of open data has been proved to be a decisive tool. These studies mostly cover cities located in the global north, highlighting the fact that the global south is often under-represented in global analyses of urban mobility [8]. Also, these analyses are based only on the road network. To the best of our knowledge, there are no global analyses for pedestrian and cycling mobility that use mode-specific networks.

When comparing our results with a popular similar global study [13], which covers 10,351 urban areas around the world, we found divergent results. As it uses the road network for its calculations, shared indices between both studies (e.g., intersection count, street length, and circuity) drastically changed, mostly because pedestrian and cycling networks have more elements and complexity than regular driving networks due to additional infrastructure like sidewalks, footpaths, or cycleways. In fact, values of street length between both studies vary an average of 30 m for pedestrian networks, while for cycling, this is 24 m. In contrast, calculations for indices using the road network (i.e., orientation entropy) yielded similar results.

Although this study is not the one that covers the most urban areas in the literature, our focus on active mobility using mode-specific analysis with pedestrian and cycling networks differentiates it from other global analyses. The implementation of additional processing steps to refine pedestrian and cycling networks, the addition of proximity indices, and the usage of an updated version of the GHS-UCDB provides a global, unique, and in-depth perspective of urban active mobility.

6.2. About Mode-Specific Analysis

Considering the comparison with similar studies, and observing the differences in the results of pedestrian-specific and cycling-specific networks of our own study, we underline the importance of using separate networks for different means of transportation, as the values of corresponding indicators differ from one network to another. This is mostly visible from the results shown in Figure 4, where, despite the fact that similar trends can be observed for pedestrian and cycling indicators, differences in magnitude and dispersion indicate that there are substantial differences, making the analysis of mode-specific indices necessary.

This difference is more noticeable when comparing by income group. Again from Figure 4, it is evident that the values of pedestrian and cycling intersection densities are more similar as income decreases, while for high-income economies, the gap is more clear. Values related to indicators of street length, link–node ratio, street density, and proximity to POIs also exhibited this behaviour.

6.3. Limitations of the Usage of Open Data

The usage of open data is a double-edged sword. From one side, it enables analyses with global coverage embracing under-represented geographical areas, but it poses a limitation. Due to differences in the mapping quality and completeness of OpenStreetMap (OSM), density-based and proximity indices may be biased towards higher-income economies where voluntary mapping communities are stronger, therefore producing more complete maps.

Other researchers report that the quality and completeness of urban European and US cities are high [72], while the map quality of developing areas like Africa, the Middle East, and South Asia is lower or has not been assessed [73,74]. In our study, such biases may have affected the production of global consistent results, particularly for the index of proximity to public transport, where very low values were seen from cities in lower-income economies due to the lack of public transport infrastructure and coverage, both in the real world and/or mapped in OSM.

6.4. Future Directions

The general applicability of this methodology allows it to be utilised in more local contexts, e.g., cities of a single country or neighbourhoods of a single city. Other researchers have already explored this concept, providing comparisons of cities within a more homogeneous area of study [27,28]. Also for local contexts, multi-temporal analysis of urban street network indices may be used as a tool for evaluating the impact of policies, especially those that involve modifications of the urban layout. Assessments can be made by running simulations, or analysing the changes in mobility indices’ values before and after policy implementations.

High-resolution and authoritative data may also be used to improve the accuracy of the indicators, but at the expense of narrowing the global extent. The usage of, for example, standardised datasets for the definition of public transport like the GTFS (General Transit Feed Specification), high-resolution Digital Elevation Models (DEMs), or street networks with more detailed information about pedestrian and cycling infrastructure could improve accuracy. Other ancillary data like land use and land cover, perceived safety or security, landscape elements, or environmental factors could be incorporated to analyse the street network from different perspectives [10].

7. Conclusions

This study presents a comprehensive methodology for characterising active mobility in urban areas by leveraging street network indices from the academic literature and global open data. To test the proposed methodology, we calculated street network indices for multiple cities from around the world, publishing the resulting dataset as open data.

Our methodology proposes the usage of mode-specific street networks extracted from OpenStreetMap (OSM) and augmented by elevation data from the NASADEM dataset to calculate mode-specific street network indices related to proximity to POIs, proximity to public transport, circuity, street length, link–node ratio, slope, intersections, and orientation entropy. This approach addresses a prevalent gap in previous studies that often overlook the distinct characteristics of mode-specific street networks, specially for pedestrians and cyclists. We presented a comprehensive description of the methodology, describing the steps for downloading and preprocessing each street network type, as well as providing an overview of the indices that were selected from the academic literature and details about their implementation.

To showcase the capabilities of the methodology, we calculated street network indices for the urban areas of 176 cities from around the world. The urban area delimitations were defined using the Global Human Settlement-Urban Centre Database (GHS-UCDB) dataset, which also provides thematic, socioeconomic information for each urban area, including climate classification, income level, and population. The results of this study are twofold: (i) a dataset containing the calculated indicators, which was published as open data [67] alongside additional metadata and descriptions for their usage; (ii) a comprehensive data analysis over the resulting dataset for extracting global insights and characteristics of active mobility through index-specific analysis and clustering.

From the results, it can be observed that cities with higher-income economies often present better conditions for active mobility, in particular in Europe, and, to a lesser extent, in the Americas and West Asia. Characteristics of these cities include more compact and connected streets, with more accessible public transport infrastructure and amenities. Also, we highlight the importance of using mode-specific street networks for analysing diverse aspects of urban mobility. Further research should focus on utilising more localised, higher-quality data for a more accurate assessment of cities and urban areas, especially with respect to public transport infrastructure. In addition to more detailed data, the implementation of multi-temporal analysis could help analyse and assess the impact of infrastructure changes or the inclusion of public policies that affect active mobility, as an assessment tool for smart cities and urban digital twins.