Abstract
Route choice is a complex issue in simulating individual behaviors and reproducing collective phenomena during evacuations. A growing concern has been given to the individual cognitive mechanism to investigate how routing decisions are made in specific situations. However, the essential role of multiple spatio-temporal scales has not been completely considered in the current cognitive frameworks, which leads to the inaccuracy of cognition representation in evacuation decisions. This study proposes a novel spatio-temporal cognitive framework integrated with multiple spatio-temporal scales for individual route choice. First, a complete spatio-temporal cognitive mechanism is constructed to depict the individual evacuation cognition process. Second, a spatio-temporal route choice strategy that emerges from agent-based simulation and extends into the spatio-temporal potential field is designed to represent the overall time-varying cost along routes in individual subjective estimation. Finally, a spatio-temporal A* algorithm is developed for individual optimal route planning in complex outdoor evacuation scenarios. The experimental results show that the proposed framework outperformed the conventional potential field model in evacuation performance, in both objective crowd evacuation evaluation metrics and individual subjectively estimated evacuation cost in cognition, and may provide more insights on crowd evacuation management and guidance.
1. Introduction
Understanding the complex and variable patterns of behaviors exhibited by individuals during evacuations is fundamental to crowd evacuation management and guidance and is of great significance for disaster prevention and mitigation [1]. A critical individual behavioral reaction is route choice, which dramatically impacts the movement and evolution of the crowd flow. The rapid advance of behavioral and cognitive science in recent years promotes the increasing attention on the underlying cognitive mechanism of route choice to investigate how individuals perceive information, organize knowledge, and take actions in specific situations [2]. How to construct a complete and realistic cognitive framework for route choice, however, is still challenging due to the complexity and uncertainty of human behavior.
Space and time play an essential role in the individual cognitive framework for route choice. The spatio-temporal features and relationship of objects in the environment not only structure cognitive representations but also provide useful information for knowledge processing [2]. For the spatio-temporal cognitive process of route choice, existing cognitive frameworks generally evaluate the instant situations, such as the distance to exits and the crowdedness of the location, to update individual evacuation decisions at each time before reaching the destination [3,4,5]. However, few concerns are given to the completeness of multiple scales in space and time, which significantly influences the reality of the individual cognitive mechanism. The research to date has also illustrated that high-level cognition, such as inference and reasoning, emerges from the integration of multiple spatio-temporal scales, especially for complex scenarios and urgent conditions [6,7]. For example, individuals prefer to combine the present situations, short-term decisions in the near past, and the estimated evolution pattern of crowd dynamics in the long-term future to make final route decisions. The multiple spatio-temporal scales are an indispensable part of the individual cognitive mechanism of route choice and eventually contribute to proactively controlling the collective phenomenon of crowd activities.
To promote a more reliable individual evacuation simulation and further support crowd management and guidance, a novel spatio-temporal cognitive framework for individual route choice is presented. The main contributions are summarized as follows:
- (1)
- A multiple spatio-temporal scale cognitive framework for individual route choice is proposed. This framework constructs a complete spatio-temporal cognitive mechanism to depict the individual evacuation cognition process.
- (2)
- A spatio-temporal route choice strategy that emerges from agent-based simulation and extends into the spatio-temporal potential field is designed to represent the subjectively estimated overall time-varying cost along the alternative routes. In addition, a spatio-temporal A* algorithm is developed to describe the individual optimal spatio-temporal route planning in complex outdoor evacuation scenarios.
- (3)
- Finally, the performance of the proposed framework and the conventional potential field model was evaluated. The experimental results demonstrate that this framework has significant advantages in both objective crowd evacuation evaluation metrics and individual subjectively estimated evacuation cost in cognition.
The remainder of the article is organized as follows. Section 2 briefly reviews the related works of the cognitive frameworks for individual route choice and their spatio-temporal features. Section 3 describes the proposed spatio-temporal cognitive framework. The experimental results of a case study and the related analyses are discussed in Section 4. The conclusion is provided in the final section.
2. Related Works
2.1. Cognitive Framework for Individual Route Choice
The aim of the cognitive framework for individual route choice is to investigate issues of personality and individual differences (who), environmental and social impacts (what), spatio-temporal features and relationships (when and where), and corresponding actions (how) [8,9]. Numerous frameworks have been proposed to investigate the individual cognitive process in route choice, and these frameworks can be classified into three types according to different perspectives in the following sections.
2.1.1. Conceptual Framework
Individual route choice behavior is viewed as the result of hierarchical cognition processing, which is broken down into “strategic”, “tactical”, and “operational” levels [10]. The strategic level describes which exit is selected and models sequencing activities. The tactical level focus on which route to use and the timing of when to initiate the personal evacuation. The operational level concerns the decisions on avoiding collisions with crowds and obstacles along the way. The conceptual framework depicts the primary contents of the cognitive processes for individual route choice. However, it is hard to distinguish what contributes to different cognition performances and final route choice decisions, and thus it fails to be applied in actual evacuation scenarios.
2.1.2. Statistical Analysis Framework
To fill this gap, some researchers try to integrate various impact factors in the cognitive frameworks to investigate the quantitative influence of these factors on final route decisions. In these statistical analysis frameworks, firstly, individual route choice data are collected from field observations, controlled experiments, virtual reality experiments, and questionnaire surveys [11,12]. These data generally involve personal factors, such as age, gender, education level, and familiarity with the environment, and environmental factors, such as distance to exits, congestion near exits, and the capacity of different routes [13]. Secondly, statistical analysis methods, such as discrete choice models [14,15], are applied to identify the significance of these impact factors and construct a regression model to support the prediction of individual evacuation preference. Existing studies found that strangers with incomplete spatial knowledge may face more cognitive loads while navigating and cognitively mapping new surroundings and may prefer to take a longer but more reliable route to their destination than the shortest one [16,17]. These statistical analysis frameworks do not concern how each impact factor works in the individual subjective cognitive processes and thus neglect the internal mental representation of cognition in the human mind, although they can indirectly reveal the relationships between individual cognition and personal and environmental features in the real world.
2.1.3. Mental Framework
Mental frameworks are designed from cognitive neuroscience and psychobehavioral science concerning the internal representation of the external environment in the human mind. In these mental frameworks, individuals are generally treated as agents who continuously perceive external environmental stimuli, form cognition knowledge, and perform physical actions [18,19]. The cognitive map is one of the most typical works of these cognitive mental frameworks. It depicts the mental representation of spatial events and objects, such as essential points, routes, and areas, and their association and influence in the real world [20]. For example, paths refer to corridors, edges are limiting or enclosing features, districts are large spaces, nodes are the intersections of major paths or places, and landmarks are distinctive features that people use as reference points for their location [21]. Furthermore, to extend spatial cognition with temporal knowledge, the temporal cognitive map is proposed based on temporal ontology [22]. The duration time of spatial objects’ features and their association is defined by temporal assertions that reflect temporal constraints on the concepts of the cognitive map [23]. For example, the closing hours of an entrance temporally characterize the accessibility of two regions, and spatial topology in the human mind also varies in specific time intervals. Despite considering the spatio-temporal nature of the real world, the existing mental frameworks are applied to represent spatial cognition with static or periodic temporal constraints rather than time-varying constraints, which fails to represent the complex spatio-temporal characteristics and relationships completely. It is necessary to design an individual spatio-temporal cognitive framework that incorporates multiple spatio-temporal scales to construct a complete individual cognitive mechanism in the human mind.
2.2. Cognitive Mechanism of Individual Route Choice
The cognitive mechanism, as a crucial role in the individual cognitive framework, reveals how the human brain realizes the mental activities of perception, learning, memory, thinking, emotion, consciousness, and responses from different spatio-temporal scales [24].
2.2.1. Architecture
The architecture of the cognitive mechanism is generally divided into three main phases, including “perception”, “knowledge”, and “decision making” [25,26,27]. First, information perception, as the origin of all cognition, deals with how individuals can perceive information selectively and purposely from the environment. Second, information integration considers how individuals subjectively integrate environmental information into mental representations and generate related knowledge. Third, decision making describes how individuals trade off the different attributes associated with alternatives and make actions. The spatio-temporal characteristics of the cognitive mechanism have always been an important subject in behavioral and cognitive neuroscience, considering the fact that all cognition takes place in spatial regions and functions on time. Numerous studies have proved that different cognition activities may occur on different spatio-temporal scales, and the combination of multiple spatio-temporal scales shapes the complete cognitive mechanism [28]. Thus, it is of great significance to investigate multiple spatio-temporal scales’ characteristics to further extend the existing cognitive mechanism of individual route choice.
2.2.2. Multiple Spatio-Temporal Scales’ Characteristics
The completeness of the multiple spatio-temporal scales is a crucial issue in individual cognitive mechanism and determines the performance of cognition representation. Several spatio-temporal scales, such as “local” and “global” spatial scales and “instant” and “short term” temporal scales, have been considered in the existing research. These studies believe that individuals prefer observing the local interactions with adjacent crowds, obstacles, and the environment to avoid collisions and their global distribution to obtain feasible routes [29]. Furthermore, the individual spatio-temporal cognitive processes are generally treated as a sequence of independent fragments of the “instant” scale, which assumes present situations greatly impact the route choice, and it has also been confirmed that the effect of the “short term” is that individual current decisions are related to the episodic memory in the near past [28]. Individuals are likely to insist on their previous evacuation decisions in the near past if there are no drastic changes in the external environment [30,31]. Despite many efforts in this research, it fails to represent high-level cognition processing, such as imagining, inference, and reasoning, which is grounded in and emerges from more complex spatio-temporal scales. In this study, a complete multiple spatio-temporal scale cognitive mechanism is constructed by introducing the “selective” scale in space and the “long term” scale in time. The “selective” scale refers to the individual specific attention to the vital spatial objects and possible connections between them, such as the downstream crowd to targeted exits and the forward direction situations due to limited physical capabilities, while the “long term” scale refers to the long period, concerning the individual prospective thinking for the evolution of situations along routes over time.
2.3. Route Choice Strategy
Route choice strategy is another essential component in individual evacuation cognition and reflects the selection criteria for available spatio-temporal evacuation resources.
2.3.1. Spatio-Temporal Metrics
Extensive efforts have been made to design spatio-temporal metrics to evaluate the utility or cost of alternative routes in normal evacuation scenarios. Typical spatial metrics include distance to exits, congestion degree near exits, frontal space capacity, and route’s directness. For some specific scenarios, there is also the coverage of light at night and the accessibility for mobility-impaired people [32,33]. In the time dimension, besides the travel time and waiting time, some dynamic factors, such as the evacuation speed near exits and the length of the waiting queue [34], are also wildly applied to indicate the potential cost in time.
In addition, increasing attention has been paid to how to represent the comprehensive utility of alternative routes with the combination of various spatio-temporal aspects, considering the complexity of the multi-metric system. The potential field was proposed to define the minimal spatial cost of traveling from the lattice to the destination in the scenario with discrete representation. It can incorporate distance, congestion, and route capacity [35,36]. Space–time use efficiency is a novel concept that measures the utility of space and time resources based on historical or estimated crowd trajectories. It has been proven to identify evacuation bottlenecks and reduce the faster-is-slower effect in the collective phenomenon [37,38]. Despite the much progress in spatio-temporal comprehensive metrics, they generally concern partial scales of space and time. They thus cannot fully reflect the spatio-temporal characteristics of individual cognition. In this study, a comprehensive spatio-temporal metric is developed to represent the individual subjective evaluation of alternative routes.
2.3.2. Principles of Route Choice
The primary principle of individual route choice is to maximize the utility of the route choice subjectively, given the available information. The fundamental aspects of the principles have proved that individuals perceive and integrate spatial-temporal information and attributes selectively and purposely, which leads to the positive or negative feedback loops across individuals, and this cognition process is not fixed but varies with the context [21]. However, the research to date fails to provide a practical tool to construct a spatio-temporal route choice strategy, especially a lack of cognition representation for crowd dynamics and subjective route planning. Agent-based models are widely used to simulate the crowd evacuation process in the physical world [39,40] and can also be applied in the individual cognition domain. The agent-based crowd evacuation simulation can reproduce the individual subjectively estimated spatio-temporal positions and trajectories of the crowd and further support the individual optimal spatio-temporal route planning. Thus, a novel spatio-temporal route choice strategy combined with the agent-based model and spatio-temporal route planning algorithm is designed to realize the complete cognition representation of the route choice.
In summary, to bridge the gap in existing cognitive frameworks for individual route choice, a novel spatio-temporal cognitive framework is proposed to construct a complete individual cognitive mechanism in complex outdoor evacuation scenarios and further illustrate the spatio-temporal features of self-organizing phenomena in collective movements.
3. Methodology
The schematic structure of the proposed spatio-temporal cognitive framework for individual route choice is presented in Figure 1. The two core cognition modules for crowd dynamics estimation and individual route planning in the spatio-temporal cognition mechanism are described, respectively.
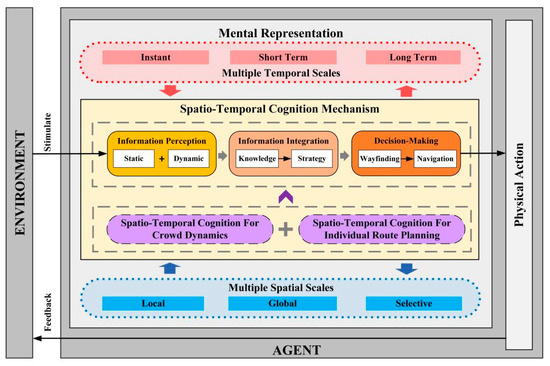
Figure 1.
Overview of the spatio-temporal cognitive framework for individual route choice.
3.1. Architecture of Spatio-Temporal Cognitive Framework
The proposed framework can be represented from three different perspectives. First, it is constructed to comprehensively describe the iterative interaction between the agent and the environment. The external environmental stimulation structures the mental representation of the real world in the human mind, and, in turn, the agent takes physical actions to adapt himself and further update the environment. Second, the proposed framework is designed based on multiple spatio-temporal scales, in which the multiple temporal scales consist of “instant”, “short term”, and “long term” scales, while multiple spatial scales include “local”, “global”, and “selective” scales. The integration of multiple spatial and temporal scales reveals different aspects of mental representations, reproduces the different levels of spatio-temporal features of cognition processing, and, finally, jointly contributes to the complete individual cognitive mechanism. Third, as the core component of the cognitive framework, the spatio-temporal cognitive mechanism consists of information perception, information integration, and decision making. It reveals how the internal representation of cognition determines the final route choice decision. In the information perception stage, the information of static objects, such as obstacles and facilities, and dynamic objects, such as events and crowds, are collected. Then, during the information integration, individuals generally utilize and process information to form spatio-temporal knowledge and generate corresponding exit and route choice strategies. Lastly, when it comes to decision making, individuals seek to find the optimal route to the targeted exits with various evacuation behaviors, such as wayfinding and navigation. Furthermore, two critical cognition modules are designed based on the aforementioned three perspectives to extend the proposed framework into real-life outdoor evacuation scenarios and to provide a realistic evacuation simulation. They are described in the following sections separately.
3.2. Spatio-Temporal Cognition for Crowd Dynamics
This section describes how individuals perceive and integrate the information of external crowd distribution to identify the downstream crowd and estimate their spatio-temporal trajectories.
3.2.1. Potential Field-Based Downstream Crowd Identification
An individual generally prefers to observe and predict the movement of the downstream crowd to support the personal route choice. In the evacuation scenario with the discrete representation, the downstream crowd of a lattice occupied by an individual can be defined as the smallest group that independently determines the individual’s subjectively estimated crowd dynamics on his way to the targeted exit when route planning. This study introduces the potential field to represent the subjectively estimated cost to the targeted exit and further identify the corresponding downstream crowd. As shown in Algorithm 1, the potential field of a lattice is denoted by , which refers to the cost to the exit from the lattice. Lattices are iteratively computed starting from the lattices occupied by the exit, while considering the distance, the crowdedness, and the route capacity. Accordingly, three intensity parameters , , and are used to reflect the individual preference of exit and route choice [36]. In detail, the crowdedness intensity parameter scales the effect of local crowdedness on the potential and indicates that the increase rate of the potential of a lattice occupied by an individual is not less than that of an unoccupied lattice. The neighboring intensity parameter scales the increase rate of the potential of a neighboring lattice in the diagonal direction and indicates that the increase rate of the potential of a neighboring lattice in a diagonal direction is not less than that of a neighboring lattice in the vertical or horizontal directions. The capacity intensity parameter scales the effect of the frontal route capacity on the potential and indicates that the increase rate of the potential of a lattice occupied by a pedestrian is not less than that of an unoccupied lattice. In this way, the potential field map representing the individual subjectively estimated cost for the specific evacuation situations can be obtained, and the flowchart of Algorithm 1 introduced from [36] is displayed in Figure A1.
| Algorithm 1: Potential field map calculation | |
| Input: Lattice set , exit set , crowdedness intensity parameter , neighboring intensity parameter , and capacity intensity parameter | |
| Output: Potential field map set //The set of individuals’ potential field maps to exits | |
| 1 | For each exit in the exit set |
| 2 | Set ;// denotes the the number of lattices occupied by exit |
| 3 | For each lattice in the lattice set |
| 4 | If is occupied by an obstacle |
| 5 | Set in potential field map , and is marked as “determined”;// denotes the potential field of lattice to exit |
| 6 | Else if is occupied by exit |
| 7 | Set in , and is marked as “determined”; |
| 8 | For with a neighboring lattice occupied by exit in the horizontal or vertical directions |
| 9 | Set in . is marked as “determined”, and is added to ;// denotes the lattice set that needs to be checked |
| 10 | Set ;// denotes the number of lattices not occupied by individuals in ; |
| 11 | Set ; |
| 12 | While exist “undetermined” lattice in |
| 13 | For each lattice in |
| 14 | If |
| 15 | Check its neighboring lattices in the horizontal or vertical directions and remove from : |
| 16 | If the potential field of lattice has not been determined |
| 17 | If is occupied by an individual and is in the horizontal or vertical directions |
| 18 | Set ; |
| 19 | Else if is not occupied by an individual and is in the horizontal or vertical directions |
| 20 | Set , ; |
| 21 | Else if is not occupied by an individual and is in a diagonal direction |
| 22 | Set ; |
| 23 | Compute the potential field by the following equation: |
| 24 | , update , is marked as “determined”, and added to |
| 25 | Set ; |
| 26 | Set ; |
| 27 | is added into ; |
| 28 | Return . |
On the basis of the potential field map calculated by Algorithm 1, the downstream crowd is calculated iteratively to determine the group that can independently impact the observed individual’s route planning in Algorithm 2. First, for a specific exit, the people whose potential field is less than the observed individual’s are identified and added to the downstream crowd. Second, the downstream crowd is extended iteratively until all the people who may impact the movement of each member of the downstream crowd are also added to this group. In a sense, an individual’s downstream crowd is the minimum group that may impact his subjective estimation of the crowd dynamics. Furthermore, to apply the preference of the different individuals, the potential field intensity parameter is introduced to adjust its threshold value, and a larger extends the group of the downstream crowd. In this way, the individual route planning can only depend on the subjectively estimated spatio-temporal movement of the downstream crowd. The flowchart of Algorithm 2 is shown in Figure A2.
| Algorithm 2: Individual’s downstream crowd identification based on potential field map | |
| Input: Lattice set L occupied by the crowd, exit set E, potential filed map set , and potential field intensity parameter | |
| Output: Downstream crowd set //The set of individuals’ downstream crowd to exits | |
| 1 | For each exit in the exit set E |
| 2 | For each lattice occupied by the crowd |
| 3 | For each lattice occupied by the crowd |
| 4 | If |
| 5 | is added into , and marked as “unchecked”;// denotes the downstream crowd of lattice to exit |
| 6 | If exist “unchecked” lattice in |
| 7 | For each “unchecked” lattice in |
| 8 | Compute subjectively estimated optimal exit of lattice by the following equation: |
| 9 | = ; |
| 10 | For each lattice in the crowd |
| 11 | If the , and |
| 12 | is added into , marked as “unchecked”, and is marked as “checked”; |
| 13 | is added into ; |
| 14 | Return . |
3.2.2. Estimation of Downstream Crowd Spatio-Temporal Trajectories
The spatio-temporal trajectories of the downstream crowd are vital for individual spatio-temporal optimal route planning. In this study, the subjective estimation of the downstream crowd’s movement is implemented by the agent-based model with the potential field. As shown in Algorithm 3, individuals in the downstream crowd constantly update their current potential field map and choose the targeted position from their available neighboring lattices according to the probability before reaching the exit. As a result, individuals can obtain a reasonable estimation of the spatio-temporal trajectories of their downstream crowd to support the personal optimal spatio-temporal route planning. Figure A3 illustrates the flowchart of Algorithm 3.
| Algorithm 3: Agent-based spatio-temporal trajectory estimation for downstream crowd | |
| Input: Lattice set occupied by the crowd, exit set E, and downstream crowd set | |
| Output: Spatio-temporal trajectories of downstream crowd set //The set of spatio-temporal trajectories of individual’s downstream crowd to exits | |
| 1 | For each exit in the exit set E |
| 2 | For each lattice occupied by the crowd |
| 3 | Select its downstream crowd from downstream crowd set ; |
| 4 | Set , record positions of downstream crowd = , and is added into ;// denotes the spatio-temporal trajectories of individual’s downstream crowd at lattice to exit |
| 5 | While exist lattice “occupied” by individuals in |
| 6 | For each “occupied” lattice in |
| 7 | If is occupied by exit |
| 8 | Update state of lattice as “unoccupied” in ; |
| 9 | Else |
| 10 | Compute the minimum potential field of its each neighboring lattice in the horizontal or vertical directions by the following equation, and is not occupied by an individual or obstacles; |
| 11 | = ; |
| 12 | Compute the probability of each lattice being selected as the targeted position in terms of the following equation: |
| 13 | ; |
| 14 | Select its neighboring lattice according to the probability . Update state of lattice as “unoccupied” and as “occupied” in ; |
| 15 | is added into ; |
| 16 | Run Algorithm 1 to calculate the potential field map set based on ;//To obtain the potential field map set for the next time step |
| 17 | ; |
| 18 | is added into ; |
| 19 | Return |
3.3. Spatio-Temporal Cognition for Individual Route Planning
This section describes how individuals construct the internal representation for alternative spatio-temporal routes based on the subjectively estimated spatio-temporal trajectories of the downstream crowd in Section 3.2.
3.3.1. Spatio-Temporal A* Algorithm for Global Route Planning
Route planning is the most representative evacuation behavior and indicates how individuals make use of evacuation resources. To construct individual decision-making cognitive processes during wayfinding, the spatio-temporal potential field that extends the conventional potential field from the spatial position into the spatio-temporal trajectory is proposed to evaluate the overall subjectively estimated cost along alternative routes. It is defined by Equation (1), where denotes the potential field to exit from lattice at time , and T refers to the time interval from departure time to estimated evacuation time .
In addition, a spatio-temporal A* algorithm is developed based on the spatio-temporal potential field to pursue the optimal spatio-temporal route in the discretized evacuation scenarios. Individuals are assumed to pursue minimizing the spatio-temporal potential field to realize their global route planning. As illustrated in Figure 2, in terms of agent 1, represented by a red dot, agent 3, represented by a blue dot, is in his downstream crowd because of the smaller potential field at departure time . Agent 1 would like to make his optimal route planning, represented by red cubes, with the spatio-temporal potential field maps and avoid the estimated spatio-temporal positions occupied by agent 3, represented by blue cubes. On the contrary, agent 2 does not participate in this wayfinding process.
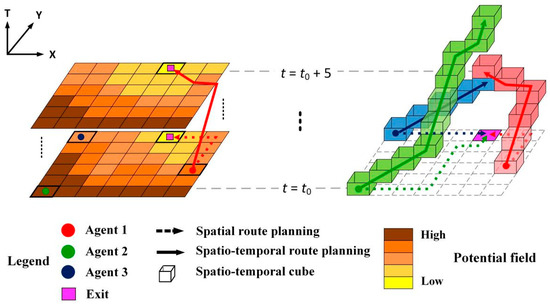
Figure 2.
Individual spatio-temporal route planning based on spatio-temporal potential field map.
A balanced strategy is designed to divide the search space, in terms of the complexity and time consumption of the spatio-temporal search, especially for large, complex evacuation scenarios. This strategy integrates the spatio-temporal A* algorithm in the spatio-temporal space and the conventional A* algorithm in the spatial space by identifying the type of search space. If the observed individual’s spatio-temporal position in the route planning is within the minimum bounding cube of the subjectively estimated spatio-temporal trajectories of the downstream crowd, the spatio-temporal A* algorithm is applied to search for the optimal route. Otherwise, the conventional A* algorithm with the potential field is used in the spatial space. In this way, the individual optimal spatio-temporal routes from the current position to each available exit can be obtained efficiently.
3.3.2. Preferred Spatio-Temporal Neighbors for Local Navigation
The optimal route planning algorithm generally can generate only one route with the least cost for the given start position and end position. However, if the targeted position along the optimal route at the next moment is occupied by other individuals before his movement, existing optimal route planning fails to provide flexible local movement. In addition, from the viewpoint of the cognition process, individuals prefer to integrate local navigation and global route planning before their movement. To fill this gap, an alternative optimal route set based on the preferred spatio-temporal neighbors is supplemented. First, the valid spatio-temporal neighbors at the next moment are identified if they are not occupied by obstacles and selected as the preferred start positions for global route planning. Second, the spatio-temporal A* algorithm is applied to generate alternative optimal routes from each preferred start position to each targeted exit and corresponding spatio-temporal potential field. Third, the probability of being selected for each alternative route can be calculated by Equation (2). Lastly, individuals are updated randomly and realize their movement.
where denotes the probability of an alternative route from the valid spatio-temporal neighbor at the next moment to the targeted exit.
As illustrated in Figure 3, there are four alternative optimal routes to the targeted exit starting from the preferred start positions numbered 1′, 2′, 4′, and 5′, and the spatio-temporal cube numbered 3′ is invalid for the global spatio-temporal route planning due to the occupation by obstacles. If it is assumed that the potential field of spatio-temporal cubes at the same time is equal; it can be observed that the alternative route starting from spatio-temporal cube 1′ represented by a blue vector has the least spatio-temporal potential field and the maximum probability of being selected as the final route decision.
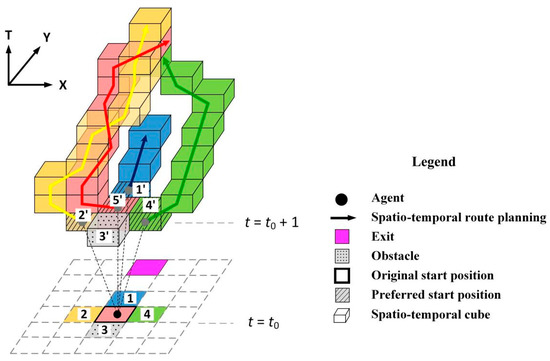
Figure 3.
Alternative optimal spatio-temporal route set based on the preferred spatio-temporal neighbors.
3.3.3. Adaptive Choice for Spatio-Temporal Optimal Route
The inertia of human cognition and the “short term” effect in decision making has been well recognized in evacuation behaviors, and individuals are likely to be impacted by their previous exit and route choice. To balance the influence of the previous decisions in the past and current options, a tolerance parameter of route choice is designed to formulate the complex adaptive exit and route choices. As displayed in Equation (3), if an alternative route satisfies the desired decrease compared with the currently optimal route to the exit previously chosen, the individual is assumed to consider this route and add it to the alternative route set.
where denotes the tolerance parameter of route choice, denotes the spatio-temporal potential field of a current alternative route from lattice to an exit at time , and denotes the spatio-temporal potential field of the currently optimal alternative route to the exit , which is chosen at time . Thus, if there is no significant decrease in the estimated evacuation cost, the individual prefers to insist on their previous exit and plan routes.
In summary, the proposed cognitive framework for individual route choice presents a complete spatio-temporal cognitive mechanism based on multiple spatio-temporal scales. This framework can provide realistic individual evacuation decision simulation and further reproduce the collective movement and evolution pattern in real-life evacuation situations.
4. Case Study
This section introduces the data of crowd distributions in the study area and discusses the crowd evacuation simulation results derived from the proposed spatio-temporal cognition framework.
4.1. Experimental Data
Our study area is the core exhibition area of Emperor Qinshihuang’s Mausoleum Site Museum, an outdoor scenario located in Xi’an, China. It is one of China’s most visited tourist attractions and draws up to 40,000 people daily. The great number of visitors and the complex environment with buildings of various sizes and routes with different capacities present a significant challenge to analyzing the crowd dynamics and its evolution patterns to support evacuation guidance and management after large-scale collective activities. As displayed in Figure 4, the evacuation scenario has dimensions in the range of 400 m × 610 m, with six temporary exits, represented by orange rectangles. The historical crowd heatmap and visitor number data in a collective activity were collected, and the crowd distribution at evacuation time was simulated. There are 2233 individuals represented by green points. The evacuation scenario is divided into regular lattices with a resolution of 1 m, considering the general occupation of an individual. In addition, individuals are assumed to be rational and have access to relatively complete external information, such as the distribution of static obstacles and dynamic crowds, from observation and guidance when making evacuation decisions.
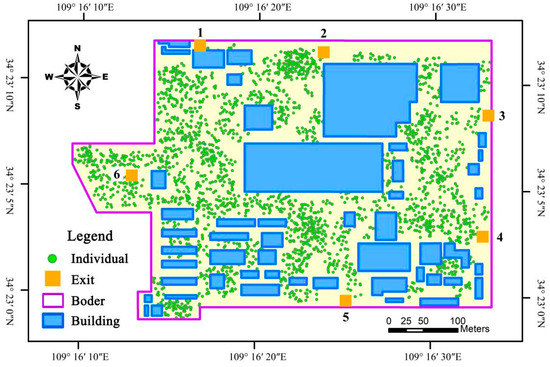
Figure 4.
The study area is the core exhibition area of Emperor Qinshihuang’s Mausoleum Site Museum in Xi’an, China.
In this study, the individual route choice is implemented with C++ on Microsoft Visual Studio 2019. All the experiments are conducted using the environment with Intel(R) Core(TM) i9-9900k CPU @3.60 GHz and 64 G memory. In addition, OpenMP is applied to implement the parallel execution for running acceleration. The parameters of Algorithm 1 and Algorithm 2 of the proposed framework are shown in Table 1.

Table 1.
Parameters of the spatio-temporal cognitive framework.
4.2. Experimental Results
One of the most remarkable characteristics of crowd movement is how people behave in forming collective phenomena. The existing research proved that the crowd evacuation process generally exhibits significant spatio-temporal movement patterns, including stochastic motion, collection, spillback, and dissipation [35,41]. The collective phenomena have also been further observed, such as herding, leader–follower, the faster-is-slower effect, and the stop-and-go wave [42]. The snapshots of the crowd evacuation process in this study are presented in Figure 5. The four representative crowd evacuation stages with different evacuation situations and individual route planning are compared. First, at the beginning of the evacuation process in Figure 5a(1), more individual-level free-flow movement can be observed, and fewer spatio-temporal collisions exist. Second, as shown in Figure 5b(1), spatio-temporal competition becomes increasingly significant over time, and a growing number of individuals gather and move along the queues to the targeted exits, producing various self-organizing crowd phenomena, such as the herding near the exits. Third, as displayed in Figure 5c(1), the individuals who stand at the end of the queues in the previous state have to move out of the queues and forward to the available positions close to the exits, and the corresponding queues gradually disappear. As a result, individuals from the mixed flow gather around the exit, and an irregular succession of arch-like crowds emerges. In this stage, when a large number of individuals seek to pass through the exits, spillback occurs because of the bottleneck of the evacuation efficiency. Lastly, the crowd remains arch-like and unchanged for some time in Figure 5d(1), and the congestion on the edge of the crowd eases, and the radius of the arch decreases as time elapses before the complete dissipation.
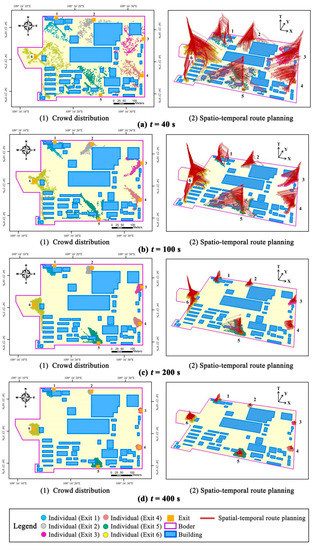
Figure 5.
Crowd evacuation simulation snapshots (a–d).
In addition, the individuals’ spatio-temporal route planning, presented by broken red lines in Figure 5a(2)–d(2), not only reveals the long-term effect of route choice on individual cognition but also suggests the subjectively estimated spatio-temporal evolution pattern of collective movement in the human mind. The slope of the route segments in the given time intervals reflects the individual average evacuation speed. The smaller slope indicates the higher speed, the larger slope presents the slower movement, and the vertical line indicates the waiting. Furthermore, the regular waiting–moving patterns derived from the spatio-temporal routes in individual cognition are discernible. More details can be investigated in Figure 6. Regarding the crowd near exit 2 at the time , individuals tend to wait at the current positions for the spaces occupied by the downstream crowd. The waiting pattern indicated by vertical line segments can be categorized into compelled waiting because of the local congestion, such as the individuals inside the crowd, and voluntary waiting for the least potential cost, such as the individuals on the edge of the crowd. Individuals try to constantly optimize their movement patterns for the subjectively optimal spatio-temporal route.
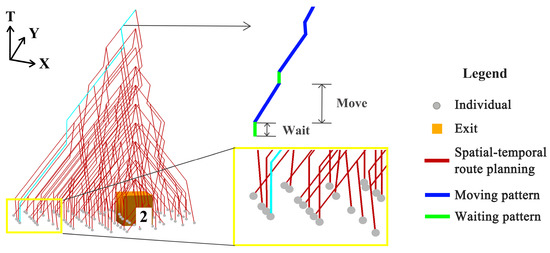
Figure 6.
The waiting–moving patterns of individual spatio-temporal route planning to exit 2 (t = 400 s).
The proposed cognitive framework based on multiple spatio-temporal scales can reproduce the complex spatio-temporal cognition process for individual route choice and is used to predict the spatio-temporal propagation and evolution pattern of crowd movement for realistic crowd guidance and control.
Regarding the above-mentioned evacuation scenario, the maximum individual evacuation time is 10.08 min, the average individual evacuation time is 3.81 min, and the average evacuation distance is 145.01 m. Moreover, for evaluating individual subjectively estimated cost in cognition, the average individual actual potential field at some point, represented by , is defined in Equation (4).
where denotes the actual potential field to the targeted exit at time , and denotes the count of the individuals in the crowd. As illustrated in Figure 7, during the crowd evacuation process, the average individual cognitive potential field decreases when individuals approach and leave the targeted exits. It is because the distance is one of the most significant factors impacting evacuation costs. When the crowd comes into the spillback stage at , spatio-temporal competition and collision increase, which leads to the relatively obvious oscillations of the cost curve. Furthermore, the trend of the cost curve also delineates that the dynamic evacuation situations generally get better from the viewpoint of the individual subjective cognition.
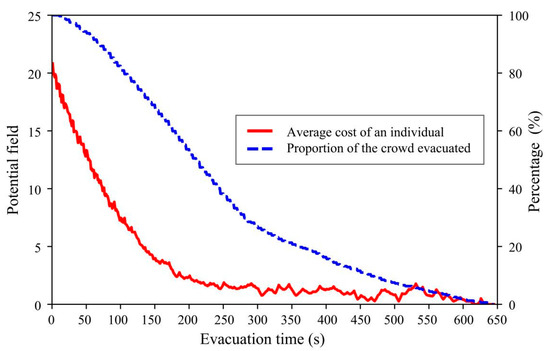
Figure 7.
Individual actual potential field to targeted exit and proportion of the crowd evacuated during evacuation process.
4.3. Experiment Analysis
This section describes the results of the extended analyses concerning the performance of the proposed cognitive framework that implements the spatio-temporal route choice strategy and the conventional one that typically implements the potential field model. All the results are the average of the 30 independent experiments in the same configurations.
4.3.1. Route Choice Strategy
As the most representative contribution of this study, the spatio-temporal route choice strategy in the proposed cognitive framework integrates more cognitive characteristics than the conventional potential field model. To compare the actual performance of route choice strategies of these two models, the conventional potential field model is extended with the adaptive route choice mechanism in Section 3.3.3. The evaluation metrics are defined by Equations (5)–(9) and can be classified into two categories. One is the objective metrics, including the average individual evacuation time , the maximum individual evacuation time , the average individual evacuation distance , and the cumulative count of individuals not evacuated . The other is the subjective performance in the human mind concerning the average individual actual evacuation cost in cognition .
where denotes the individual evacuation time, denotes the individual evacuation distance, denotes the count of individuals not evacuated at time , and denotes the individual actual potential field to the targeted exit at time .
As illustrated in Table 2, the proposed spatio-temporal cognitive framework outperforms the potential field model in all evaluation metrics. The average individual evacuation time and the maximum individual evacuation time decrease by over 10%, and the average distance decreases up to 42%. The reason is that the conventional potential field model essentially depends on the instant spatial state of evacuation situations and ignores the long-term sensibility for evacuation dynamics. In contrast, the spatio-temporal route choice strategy of the proposed framework considers the complete spatio-temporal cognitive mechanism and provides more intelligence for individual evacuation planning. In addition, the improvement of the cumulative count of individuals not evacuated and the average of the individual actual potential field also indicates that the spatio-temporal cognition in route choice can reflect the individual subjective initiative and further contribute to the optimization of the crowd evacuation performance.

Table 2.
The performance of route choice strategies of two route choice models.
Further analyses are accomplished to investigate the performance during the evacuation process. Figure 8 displays the evolutionary process of the cumulative count of the crowd not evacuated and the proportion of the crowd not evacuated with the two route choice models. The cumulative count of the crowd not evacuated can indicate the exposure degree of the crowd in specific situations, and the more people evacuated early, the smaller the value. It can be observed that the crowd with the spatio-temporal cognitive framework realizes the faster evacuation, and the gap in the curves between the two models widens along with the evacuation process. Therefore, the spatio-temporal route choice strategy of the proposed framework can encourage individuals to be aware of the crowd dynamics, utilize the spatio-temporal evacuation resources and, in turn, update the evacuation situations. Regarding the subjective viewpoint, Figure 9 illustrates the trend of the individual subjectively estimated cost and the cumulative cost of the crowd with the two models. It is obvious that, at the early stage of the evacuation process ( s), the potential field model performs better due to the least instant cost in the free flow. As the spatio-temporal competition increases over time, the advantages of the spatio-temporal cognitive framework gradually emerge. The curve of cumulative cost of the crowd with the proposed framework comes into convergence at s, while the curve with the potential field model converges at s. In addition, the average individual actual cost with the two models shows a significant difference from s. These results indicate that spatio-temporal cognition in route choice can guarantee individuals’ more high-level capabilities to integrate spatio-temporal information and aggressively schedule route planning in the long term.
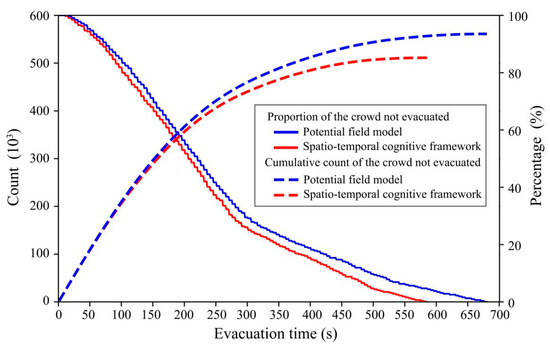
Figure 8.
The cumulative count of the crowd not evacuated and the proportion of the crowd not evacuated with two route choice models.
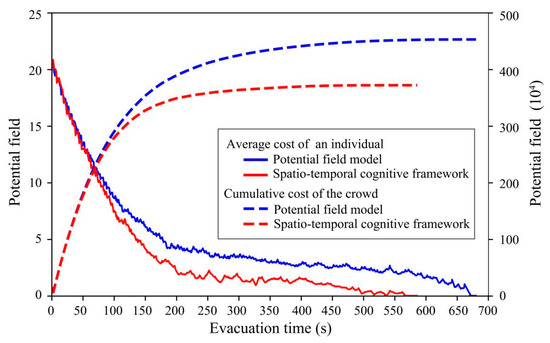
Figure 9.
Individual subjectively estimated cost and cumulative cost of the crowd with two route choice models.
Besides the metrics of evacuation performance, computation efficiency is also an important aspect of concern in practical applications. The average running time of the proposed spatio-temporal cognitive framework is 13.17 min, while the time consumption of the conventional potential field model is 1.02 min. The complete multiple spatio-temporal scales in cognition provide a realistic evacuation performance at the cost of higher complexity and computation.
4.3.2. Distribution of the Crowd
Individuals have different responses to different evacuation situations and are eventually likely to make different route choices. The proposed spatio-temporal cognitive framework is applied to two experimental evacuation scenarios with different crowd distributions shown in Figure 10. These two scenarios have the same configurations in terms of size, exits, and crowd number as the evacuation scenario in Figure 4, but the crowd distribution in Figure 10a is more concentrated in several areas, while that in Figure 10b is more uniform.
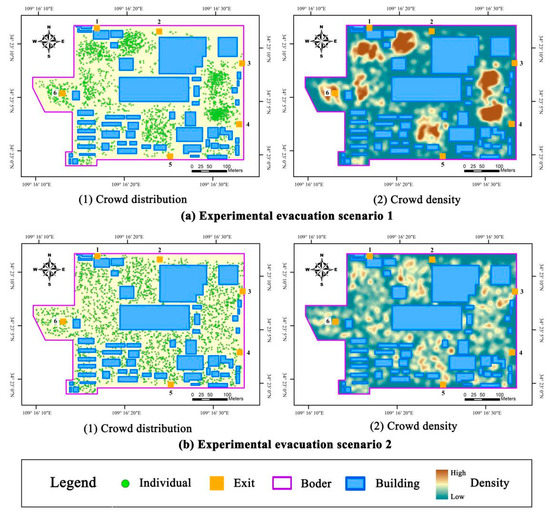
Figure 10.
Experimental evacuation scenarios with different crowd distributions.
The performance of the crowd evacuation in different crowd distributions is displayed in Table 3 and Figure 11 and Figure 12. It is evident that the crowd evolution in both cases follows a similar pattern with the evacuation process. Individual actual and subjectively estimated evacuation costs decrease along with time, and general evacuation situations gradually get better with the corresponding drop in the count of individuals left. Furthermore, the spatio-temporal cognitive framework outperforms the potential field model in all evaluation metrics, including objective and subjective aspects. It proves that considering multiple spatio-temporal aspects in route choice strategy is beneficial for improving evacuation performance in various situations. In a word, the proposed spatio-temporal cognitive framework has outstanding adaptability and robustness to produce realistic evacuation planning in the real world.

Table 3.
The performance of crowd evacuation simulation with different crowd distributions.
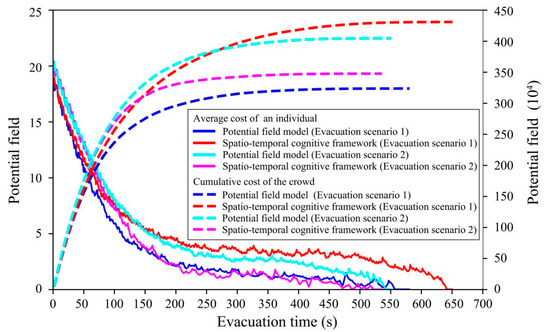
Figure 11.
The cumulative count of the crowd not evacuated and the proportion of the crowd not evacuated in different evacuation scenarios.
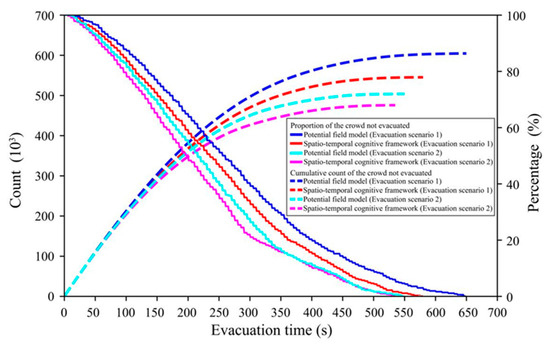
Figure 12.
Individual subjectively estimated cost and cumulative cost of the crowd in different evacuation scenarios.
5. Conclusions and Future Work
This paper proposes an innovative spatio-temporal cognitive framework for individual route choice. This framework constructs a complete spatio-temporal cognitive mechanism integrated with multiple spatio-temporal scales to depict the individual evacuation cognition process. Furthermore, a spatio-temporal route choice strategy that emerges from agent-based simulation and extends into the spatio-temporal potential field is designed to represent the overall time-varying cost along the route in individual subjective estimation. Finally, a spatio-temporal A* algorithm is developed for individual optimal route planning in complex outdoor evacuation scenarios. The case study demonstrates that the proposed framework can represent the spatio-temporal evacuation cognition in the human mind and further reproduce the spatio-temporal evolution pattern of collective movements. Extended experiments for different route choice strategies and crowd distribution also prove that the proposed framework possesses a robust, outstanding evacuation performance in both objective crowd evaluation metrics and individual subjectively estimated evacuation cost in cognition.
This study provides managers with a practical and reliable tool to design effective evacuation control and guidance planning for real-life collective activities, especially for large-scale, complex outdoor scenarios in normal situations. In addition, this proposed framework can also be extended to various scenarios when introducing specific environmental and individual characteristics, such as the light coverage in the dark.
The limitations of this study are as follows: (1) The parameters of the proposed framework come from previous simulated experiments and lack valid calibration in real evacuation scenarios; (2) The complexity of cognition representation introduces high computational burdens and may impact its practicability in real life; (3) Individuals are assumed to be relatively rational and make evacuation decisions independently, which only applies to the normal evacuation situations. Given the above problems, issues worthy of investigation in future research are aimed at the following aspects: (1) Adopting actual evacuation behavior data, such as trajectories extracted from surveillance video, to calibrate the parameters; (2) Introducing advanced parallel techniques and optimization strategies, such as CUDA and improved heuristic functions, to improve the time efficiency; (3) Introducing individual personality and social influences and extending the normal evacuation scenarios into emergencies.
Author Contributions
Conceptualization, Zhiqiang Du and Martin Werner; methodology, Fei Gao, Zhiqiang Du and Martin Werner; software, Chenyu Fang and Lin Zhou; validation, Chenyu Fang; formal analysis, Fei Gao; writing—original draft preparation, Fei Gao; writing—review and editing, Zhiqiang Du; visualization, Lin Zhou; supervision, Zhiqiang Du; funding acquisition, Zhiqiang Du. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 41971347; China Scholarship Council, grant number 202006270081.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank Ning Zhang’s advice.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
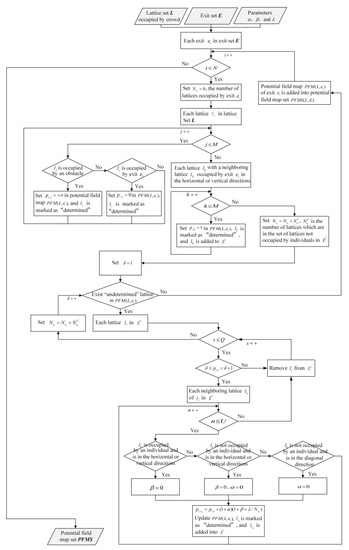
Figure A1.
Flowchart of potential field map calculation.
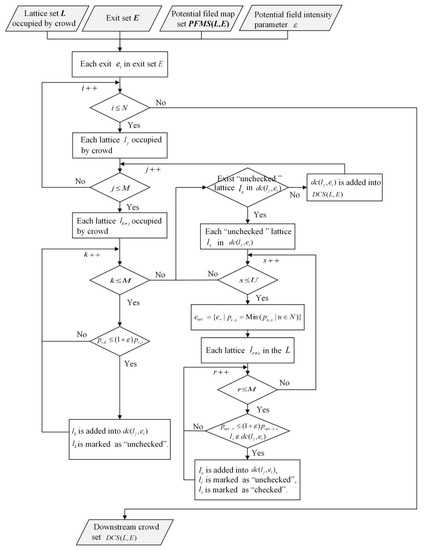
Figure A2.
Flowchart of individual’s downstream crowd identification based on potential field map.
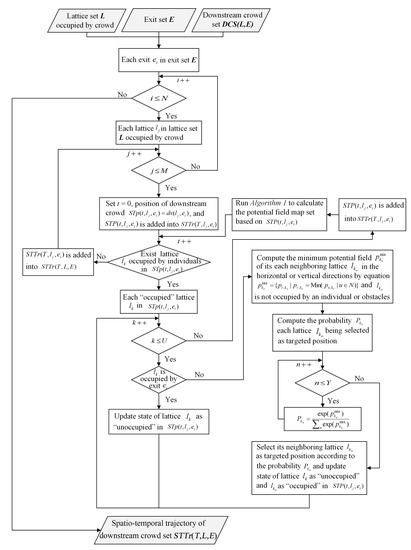
Figure A3.
Flowchart of agent-based spatio-temporal trajectory estimation for downstream crowd.
References
- Haghani, M. Optimising Crowd Evacuations: Mathematical, Architectural and Behavioural Approaches. Saf. Sci. 2020, 128, 104745. [Google Scholar] [CrossRef]
- SpringerLink. Spatial and Temporal Structures in Cognitive Processes. Available online: https://link.springer.com/chapter/10.1007/BFb0052106 (accessed on 26 August 2022).
- Ma, L.; Chen, B.; Guo, R.-Y.; Wu, P.-Y.; Zhu, Z.; Qiu, X. A Robust Potential-Based Route Choice Model for Simulating Pedestrian Evacuation. J. Stat. Mech. Theory Exp. 2019, 2019, 093405. [Google Scholar] [CrossRef]
- Vizzari, G.; Crociani, L.; Bandini, S. An Agent-Based Model for Plausible Wayfinding in Pedestrian Simulation. Eng. Appl. Artif. Intell. 2020, 87, 103241. [Google Scholar] [CrossRef]
- Shang, H.; Sun, S.; Huang, H.; Wu, W. An Extended Dynamic Model for Pedestrian Traffic Considering Individual Preference. Simul. Model. Pract. Theory 2021, 106, 102204. [Google Scholar] [CrossRef]
- Gorchetchnikov, A.; Grossberg, S. Space, Time and Learning in the Hippocampus: How Fine Spatial and Temporal Scales Are Expanded into Population Codes for Behavioral Control. Neural Netw. 2007, 20, 182–193. [Google Scholar] [CrossRef]
- Signorelli, C.M.; Dündar-Coecke, S.; Wang, V.; Coecke, B. Cognitive Structures of Space-Time. Front. Psychol. 2020, 11, 527114. [Google Scholar] [CrossRef]
- Jarecki, J.B.; Tan, J.H.; Jenny, M.A. A Framework for Building Cognitive Process Models. Psychon. Bull. Rev. 2020, 27, 1218–1229. [Google Scholar] [CrossRef]
- Gath-Morad, M.; Aguilar Melgar, L.E.; Conroy-Dalton, R.; Hölscher, C. Beyond the Shortest-Path: Towards Cognitive Occupancy Modeling in BIM. Autom. Constr. 2022, 135, 104131. [Google Scholar] [CrossRef]
- Wang, K.; Shi, X.; Goh, A.P.X.; Qian, S. A Machine Learning Based Study on Pedestrian Movement Dynamics under Emergency Evacuation. Fire Saf. J. 2019, 106, 163–176. [Google Scholar] [CrossRef]
- Li, H.; Zhang, J.; Xia, L.; Song, W.; Bode, N.W.F. Comparing the Route-Choice Behavior of Pedestrians around Obstacles in a Virtual Experiment and a Field Study. Transp. Res. Part C-Emerg. Technol. 2019, 107, 120–136. [Google Scholar] [CrossRef]
- Guo, Y.; Zhu, J.; Wang, Y.; Chai, J.; Li, W.; Fu, L.; Xu, B.; Gong, Y. A Virtual Reality Simulation Method for Crowd Evacuation in a Multiexit Indoor Fire Environment. ISPRS Int. J. Geo-Inf. 2020, 9, 750. [Google Scholar] [CrossRef]
- Zhou, J.; Guo, Y.; Dong, S.; Zhang, M.; Mao, T. Simulation of Pedestrian Evacuation Route Choice Using Social Force Model in Large-Scale Public Space: Comparison of Five Evacuation Strategies. PLoS ONE 2019, 14, e0221872. [Google Scholar] [CrossRef]
- Tan, L.; Wu, L.; Lin, H. An Individual Cognitive Evacuation Behaviour Model for Agent-Based Simulation: A Case Study of a Large Outdoor Event. Int. J. Geogr. Inf. Sci. 2015, 29, 1552–1568. [Google Scholar] [CrossRef]
- Rendón Rozo, K.; Arellana, J.; Santander-Mercado, A.; Jubiz-Diaz, M. Modelling Building Emergency Evacuation Plans Considering the Dynamic Behaviour of Pedestrians Using Agent-Based Simulation. Saf. Sci. 2019, 113, 276–284. [Google Scholar] [CrossRef]
- Chen, C.-H.; Chang, W.-C.; Chang, W.-T. Gender Differences in Relation to Wayfinding Strategies, Navigational Support Design, and Wayfinding Task Difficulty. J. Environ. Psychol. 2009, 29, 220–226. [Google Scholar] [CrossRef]
- Lin, J.; Cao, L.; Li, N. How the Completeness of Spatial Knowledge Influences the Evacuation Behavior of Passengers in Metro Stations: A VR-Based Experimental Study. Autom. Constr. 2020, 113, 103136. [Google Scholar] [CrossRef]
- Berceanu, C.; Banu, I.; Husebo, B.S.; Patrascu, M. Predictive Agent-Based Crowd Model Design Using Decentralized Control Systems. IEEE Syst. J. 2022, 1–12. [Google Scholar] [CrossRef]
- Xu, S.; Gu, Y.; Li, X.; Chen, C.; Hu, Y.; Sang, Y.; Jiang, W. Indoor Emergency Path Planning Based on the Q-Learning Optimization Algorithm. ISPRS Int. J. Geo-Inf. 2022, 11, 66. [Google Scholar] [CrossRef]
- Andresen, E.; Chraibi, M.; Seyfried, A. A Representation of Partial Spatial Knowledge: A Cognitive Map Approach for Evacuation Simulations. Transp. A Transp. Sci. 2018, 14, 433–467. [Google Scholar] [CrossRef]
- Tong, Y.; Bode, N.W.F. The Principles of Pedestrian Route Choice. J. R. Soc. Interface 2022, 19, 20220061. [Google Scholar] [CrossRef]
- Robert, A.; Genest, D.; Loiseau, S. Temporal Cognitive Maps. In Proceedings of the 12th International Conference on Agents and Artificial Intelligence, Valletta, Malta, 22–24 February 2020; SCITEPRESS—Science and Technology Publications: Setúbal, Portugal, 2020; pp. 58–68. [Google Scholar]
- Robert, A.; Genest, D.; Loiseau, S. Cognitive Map Query Language for Temporal Domains. In Agents and Artificial Intelligence, Proceedings of the 12th International Conference, ICAART 2020, Valletta, Malta, 22–24 February 2020; Rocha, A.P., Steels, L., van den Herik, J., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 215–235. [Google Scholar]
- Shi, Z. Chapter 1—Introduction. In Intelligence Science; Shi, Z., Ed.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 1–31. ISBN 978-0-323-85380-4. [Google Scholar]
- Chu, M.L.; Law, K. Computational Framework Incorporating Human Behaviors for Egress Simulations. J. Comput. Civ. Eng. 2013, 27, 699–707. [Google Scholar] [CrossRef][Green Version]
- Wijermans, N.; Jorna, R.; Jager, W.; van Vliet, T.; Adang, O. CROSS: Modelling Crowd Behaviour with Social-Cognitive Agents. J. Artif. Soc. Soc. Simul. 2013, 16, 1. [Google Scholar] [CrossRef]
- Chraibi, M.; Haensel, D. Cognitive Map Routing. In Cellular Automata, Proceedings of the 12th International Conference on Cellular Automata for Research and Industry, ACRI 2016, Fez, Morocco, 5–8 September 2016; El Yacoubi, S., Wąs, J., Bandini, S., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 210–218. [Google Scholar]
- Langley, P.; Laird, J.E.; Rogers, S. Cognitive Architectures: Research Issues and Challenges. Cogn. Syst. Res. 2009, 10, 141–160. [Google Scholar] [CrossRef]
- Kleinmeier, B.; Köster, G.; Drury, J. Agent-Based Simulation of Collective Cooperation: From Experiment to Model. J. R. Soc. Interface 2020, 17, 20200396. [Google Scholar] [CrossRef] [PubMed]
- Liao, W.; Wagoum, A.U.K.; Bode, N.W.F. Route Choice in Pedestrians: Determinants for Initial Choices and Revising Decisions. J. R. Soc. Interface 2017, 14, 20160684. [Google Scholar] [CrossRef]
- Haghani, M.; Sarvi, M. Simulating Dynamics of Adaptive Exit-Choice Changing in Crowd Evacuations: Model Implementation and Behavioural Interpretations. Transp. Res. Part C-Emerg. Technol. 2019, 103, 56–82. [Google Scholar] [CrossRef]
- Fang, Z.; Li, L.; Li, B.; Zhu, J.; Li, Q.; Xiong, S. An Artificial Bee Colony-Based Multi-Objective Route Planning Algorithm for Use in Pedestrian Navigation at Night. Int. J. Geogr. Inf. Sci. 2017, 31, 2020–2044. [Google Scholar] [CrossRef]
- Gharebaghi, A.; Mostafavi, M.-A.; Edwards, G.; Fougeyrollas, P. User-Specific Route Planning for People with Motor Disabilities: A Fuzzy Approach. ISPRS Int. J. Geo-Inf. 2021, 10, 65. [Google Scholar] [CrossRef]
- Haghani, M.; Sarvi, M. Crowd Behaviour and Motion: Empirical Methods. Transp. Res. Part B Methodol. 2018, 107, 253–294. [Google Scholar] [CrossRef]
- Guo, R.-Y.; Huang, H.-J.; Wong, S.C. Collection, Spillback, and Dissipation in Pedestrian Evacuation: A Network-Based Method. Transp. Res. Part B Methodol. 2011, 45, 490–506. [Google Scholar] [CrossRef]
- Guo, R.-Y.; Huang, H.-J.; Wong, S.C. A Potential Field Approach to the Modeling of Route Choice in Pedestrian Evacuation. J. Stat. Mech. 2013, 2013, P02010. [Google Scholar] [CrossRef]
- Fang, Z.; Li, Q.; Li, Q.; Han, L.D.; Wang, D. A Proposed Pedestrian Waiting-Time Model for Improving Space–Time Use Efficiency in Stadium Evacuation Scenarios. Build. Environ. 2011, 46, 1774–1784. [Google Scholar] [CrossRef]
- Fang, Z.; Li, Q.; Li, Q.; Han, L.D.; Shaw, S.-L. A Space–Time Efficiency Model for Optimizing Intra-Intersection Vehicle–Pedestrian Evacuation Movements. Transp. Res. Part C Emerg. Technol. 2013, 31, 112–130. [Google Scholar] [CrossRef]
- Gao, F.; Du, Z.; Werner, M.; Zhao, Y. An Improved Optimization Model for Crowd Evacuation Considering Individual Exit Choice Preference. Trans. GIS 2022, 26, 2850–2873. [Google Scholar] [CrossRef]
- Kim, H.; Han, S. Crowd Evacuation Simulation Using Active Route Choice Model Based on Human Characteristics. Simul. Model. Pract. Theory 2018, 87, 369–378. [Google Scholar] [CrossRef]
- Huang, L.; Gong, J.; Li, W. A Perception Model for Optimizing and Evaluating Evacuation Guidance Systems. ISPRS Int. J. Geo-Inf. 2021, 10, 54. [Google Scholar] [CrossRef]
- Duives, D.C.; Daamen, W.; Hoogendoorn, S.P. State-of-the-Art Crowd Motion Simulation Models. Transp. Res. Part C Emerg. Technol. 2013, 37, 193–209. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).