Abstract
With the development of urbanization and the expansion of floating populations, rental housing has become an increasingly common living choice for many people, and housing rental prices have attracted great attention from individuals, enterprises and the government. The housing rental prices are principally estimated based on structural, locational and neighborhood variables, among which the relationships are complicated and can hardly be captured entirely by simple one-dimensional models; in addition, the influence of the geographic objects on the price may vary with the increase in their quantities. However, existing pricing models usually take those structural, locational and neighborhood variables as one-dimensional inputs into neural networks, and often neglect the aggregated effects of geographical objects, which may lead to fluctuating rental price estimations. Therefore, this paper proposes a rental housing price model based on the convolutional neural network (CNN) and the synthetic spatial density of points of interest (POIs). The CNN can efficiently extract the complex characteristics among the relevant variables of housing, and the two-dimensional locational and neighborhood variables, based on the synthetic spatial density, effectively reflect the aggregated effects of the urban facilities on rental housing prices, thereby improving the accuracy of the model. Taking Wuhan, China, as the study area, the proposed method achieves satisfactory and accurate rental price estimations (coefficient of determination (R2) = 0.9097, root mean square error (RMSE) = 3.5126) in comparison with other commonly used pricing models.
1. Introduction
House renting is a considerable issue for many people in modern cities, specifically for young and relatively low-income people. Due to various limitations, numerous people have to choose renting a housing as their lifestyle before possessing property [1,2,3]. Taking China as an example, in recent years, the sizes of the floating populations in cities have expanded rapidly, and most floating populations choose rental housing for their living arrangements [4]. Under these circumstances, the government has established the housing policy of renting and buying together to encourage the development of the rental housing market [5]. With such a trend, housing rentals would become an important part of people’s daily expenses, and the prices of rental housing would become a more decisive factor in real estate investments. Rental prices are also considered a critical issue by the government in real estate, municipal planning and social security policies [6,7]. However, research on the housing rental price is usually a supplement to the housing selling price in many studies, and the precision of rental price models is lower than that of selling price models [8,9]. Fluctuating estimations may affect people’s bargaining and emotions associated with rental housing [10], and might misguide the government’s regulation and policy making with respect to public housing planning and management [11]. Therefore, both government and individuals have the requirements to make more accurate estimations on rental housing prices based on a more reliable pricing model [12].
From the perspective of the fundamental hedonic price model (HPM) of housing and rental housing prices, the influencing factors of housing prices can be divided into the following three types: structural variables, locational variables and neighborhood variables. Among them, locational variables and neighborhood variables are based on the calculation of the relationships between houses and nearby urban facilities or points of interest (POIs), such as central business districts (CBDs), schools, hospitals and parks. These diverse locational and neighborhood characteristics contain very complex relationships, and the urban facilities relevant to housing contain a massive quantity of spatial density characteristics. First, complicated relationships exist among the structural, locational and neighborhood variables of housing, and these relationships cannot be easily characterized in a simple way [13,14]. If these variables are treated as a one-dimensional vector to be modeled, as in ordinary least squares (OLS), geographically weighted regression (GWR), or some one-dimensional deep learning models [15,16], the accuracy of price forecasting would be limited. Notably, the ability of one-dimensional learning models to extract the complex relationships among massive variables is relatively limited [17,18,19]. Compared with the linear inputs of one-dimensional models, the inputs of two-dimensional neural networks are rasterized and denser; thus, the architecture and features in a two-dimensional model are more focused and concentrated, making it easier to characterize the nonlinear and complex synergistic relationships among the multiple inputs [18,19]. Therefore, a deep learning model with more than one dimension is necessary for housing price analysis. In some housing price models, two-dimensional neural networks are only applied in the part of the supplementary image features but are not used for structural, locational and neighborhood variables [12,20,21,22,23]. Due to this limitation, these “half 1-dimensional and half 2-dimensional” models also have room for improvement. Since including image features to estimate housing prices may degrade the model performance [24], and since multi-source data usually may not cover all of the samples, it is possible and appropriate to use nonimage geographic data to build an accurate housing price model, by better extracting the structural, locational and neighborhood characteristics of the housing units.
Second, apparent phenomena of spatial aggregation exist in the urban facilities and geographic objects, and the influence of the geographic objects on the pricing may vary with the increase in their quantities in a complicated way. On the one hand, the influence between the geographic objects and the housing gradually decays with their distance; on the other hand, the actual influence of a single geographic object may gradually diminish as the number of objects of the same type increases, which is implied by some concepts and thoughts in the economic geography [25,26]. However, these diminishing effects caused by the aggregation of geographical elements are rarely reflected entirely in current housing/rental price models. If locational and neighborhood variables are expressed from the perspective of the “nearest distance”, such as the distance to the nearest school, bus stop, or park, as in some studies [27,28,29], the influence from other clustered geographic objects of the same type cannot be taken into consideration. With the growing of the population, industry, commerce, and urban facilities, this is a factor that cannot be ignored, and the resulting loss of information may lead to a decrease in the accuracy of housing price or rental price models. It may be more accurate to create the locational and neighborhood variables based on the numbers of various types of POIs within a certain range [12,20,30]. Nevertheless, in this way, the fact that the influence between geographic objects decays with their distance (that is, the First Law of Geography) is not considered. The geographic field model (GFM) can also be utilized for generating the quantitative characteristics of the housing locational and neighborhood variables [14,31], which takes into account the First Law of Geography. However, GFM does not consider the fact that the actual influence of a single geographic object gradually diminishes as the number of objects of the same type increases. For example, regarding a house with only 1 supermarket nearby, this supermarket has a certain influence on this house; when there are 50 supermarkets nearby, each supermarket also has some influence on the house, but the influence of each supermarket is apparently less than in the case in which only one supermarket is present. In summary, the locational and neighborhood variables established by these current methods may be inaccurate, which might consequently reduce the performance of the resulting housing price model. The spatial density of geographic objects needs to be processed more accurately and comprehensively to generate more reliable locational and neighborhood variables.
Hence, this paper tries to explore the pricing model of urban rental housing, and taking Wuhan, China, as an example, we propose a two-dimensional rental housing price model based on a convolutional neural network (CNN) and the spatial density characteristics of POIs. On the one hand, the CNN can efficiently extract the complex characteristics among the structural, locational and neighborhood variables of housing; on the other hand, the spatial density-based locational and neighborhood variables used in this research can better reflect the spatial density characteristics of the urban facilities on rental housing prices, including the diminishing effect caused by the aggregation of the same type of geographical elements, thereby improving the accuracy of the model. The rental housing and POIs collected from the Internet provide substantial materials for the training of this method. This research may provide individuals and enterprises with suitable decision-making information for their transactions in the rental housing market; it may also provide government sectors with a valuable decision-support reference for selecting suitable locations and prices of urban public rental houses, and for deciding reasonable housing subsidy levels.
The rest of the paper is organized as follows: Section 2 reviews the relevant works on housing selling and rental price models, including the locational and neighborhood variables in the price models. Section 3 introduces the materials and methods adopted in this research. Section 4 discusses and compares the results of different methods and experiments and analyzes the proposed model. Section 5 presents the conclusions and future work ideas.
2. Literature Review
2.1. Housing Price and Rental Price Models
Methods of modeling the housing prices include the HPM [32], the GWR [33], deep learning methods, and their variants. The HPM is a fundamental pricing model for housing prices, which was first proposed in the field of economics [32]. The premise of HPM is that a person would pay for a housing not only for the living space, but also for other influencing factors, such as location advantages and the neighborhood environment. The factors in the HPM model can be divided into the structural variables (the attributes of the building), locational variables (the location characteristic of the house in the city, such as the distance to the CBD) and neighborhood variables (the characteristics related to the neighborhood, such as the distance to a nearby park, or hospital). The general form of HPM is multivariate linear regression (MLR) or OLS. HPM has been widely adopted in real estate and rental housing studies [9,27,34], due to the simplicity and effective explanation for housing prices. However, the general HPM is based on the assumption that the pattern does not change with the locations, which does not reflect the regional differences and local relationships of the variables and may result in deviations in modeling accuracy [8,33,35]. The GWR model introduced by Fotheringham [33] has focused on this concern of spatial heterogeneity [14]. Compared with the global HPM regression, GWR allows the parameters to vary with positions, and has suitable explanatory power and fitting accuracy. Therefore, it has received considerable attention and has effectively applied in the field of economy and real estate [14,35,36]. However, GWR also assumed that the relationships between independent and explanatory variables are linear, which has a clear limitation in housing price modeling, because the patterns in the housing and rental price are nonlinear and complicated [13,37]. Up-to-date studies also pointed out the disadvantages of GWR in complex spatial prediction tasks [8,38] and criticized for its reliability and restrictions [39].
In recent years, deep learning has become one of the most useful techniques for the nonlinear and complex problems, and many studies on housing price predictions have adopted the deep learning method. In many studies, including machine learning and deep learning, the structural, locational and neighborhood variables are usually treated as a one-dimensional vector to be input into the models [15,16]. In these methods, the accuracy of price forecasting may be relatively limited. As is known, the extraction capacity for the complex relationships among massive variables in the one-dimensional learning models is relatively restricted compared to other complex networks [17,18,19]. A two-dimensional neural network can be denser, and it has the strength of extracting and characterizing the complex interactive relationships among the multiple input values [18,19]. Thus, two-dimensional neural networks, such as CNNs and LSTM networks, are valuable for improving the performance of housing price modeling. Although Bency [20] used CNN as a supplement when extracting the characteristics of remote sensing images near the housing units, the one-dimensional model was still used for the structural, locational, and neighborhood variables. Due to the limited extraction for these variables, the accuracy of this method has room for improvement. Similarly, the text, indoor pictures or street view images were utilized by some studies as additional features for housing price modeling. Zhou [40] used CNN and LSTM when analyzing the description text of houses, Zhao [23] used CNN when extracting the visual characteristics of the indoor pictures, Fu [21] and Bin [22] used CNN to extract the characteristics of street view images around the houses. In these studies, although two-dimensional networks were applied for the additional features (texts, street view images, etc.), they were still not applied to the structural, locational, and neighborhood variables, which are the vital factors of the housing prices. Hence, there is still room for improvement in these “half 1-dimensional and half 2-dimensional” models. Yao [17] directly mapped the spatial distributions of several kinds of geographic objects, such as commercial institutions or educational facilities, into a two-dimensional grid, and utilized it for housing price deep learning in a CNN model together with remote sensing images. Since the remote sensing image and the distribution grids of different kinds of geo-objects are heterogeneous, the characteristics of them may not be effectively extracted if they are input as parallel channels in CNN; additionally, it might also be challenging to model both the structural variables and these features, and the information density of the distribution grid of each kind of geo-objects is not high, which may not benefit for the training of the model. As a result, the accuracy of this model was not very high. Yu [30] two-dimensionalized the locational and neighborhood variables and used the CNN and LSTM to forecast housing prices. Two-dimensional networks were applied in this method for the locational and neighborhood variables, but unfortunately, they did not consider the detailed structural variables; whether it is necessary to use the pooling layers in CNN for the housing prices regression problem still needs to be questioned and explored. Furthermore, Bin [24] suggests that including image features to estimate the housing price may degrade the performance, and usually multi-source data may not cover all of the samples. Therefore, it is possible and appropriate to use the nonimage geographic data to build an accurate housing price model, by better extracting the structural, locational and neighborhood characteristics of the housing.
In many studies, the discussion on the rental housing price is usually a supplement to the selling housing price, and the precision of rental price models is lower than that of selling price models. Liebelt [9] used the HPM to analyze housing sale and rental prices in Leipzig, Germany, particularly in terms of green space. In Won’s research [41], a spatial lag model and spatial error model were adopted to explore rental prices in Seoul. The obtained results of the above studies were not very accurate. In addition, Cajias [8] pointed out the complexity of the rental housing prices and the imitation of the GWR model in complex rental housing price forecasts. The low accuracy of estimations may affect people’s bargaining and emotions associated with rental housing [10], and might misguide the government’s regulation and policy-making with respect to public housing planning and management [11]. Therefore, at present, both the government and individuals have the requirements to make more accurate estimations based on a more reliable rental housing pricing model. Based on the nonimage POI data, this paper tries to propose a two-dimensional CNN and conduct deep learning on the structural, locational and neighborhood characteristics of housing, in order to establish a more accurate rental housing price model, and it tries to verify whether it is necessary to use pooling layers in the CNN for the housing price regression problem.
2.2. The Locational and Neighborhood Variables of Houses
The locational variables and neighborhood variables of the housing are based on the calculation of the relationships between the house and nearby urban facilities (or POIs). In many relevant studies, these variables are generated from the perspective of the “nearest distance”, such as the “distance to the nearest bus stop”, “distance to the CBD”, and “distance to the nearest hospital” [27,28], etc. As described in the introduction, if housing price or rental price models are based only on the “nearest” distances to facilities, the effects derived from the gathering of other geographical objects are not taken into account, which may lead to a decrease in model accuracy. Moreover, the influence of the geographic objects on the housing price may vary with the increase in their quantities in a complicated way. Therefore, the quantitative or density characteristics of geographical objects need to be considered when generating locational and neighborhood variables.
Geographical Field Model (GFM) is a model proposed by the geographer Harvey that borrows the concept of “field” in physics [31]. The core idea is that all geographical objects are under the influence of a “geographic field”. The geographic field changes regularly, and the influences of geographic objects on other things are decay functions from their original locations. Jiao [31] and Liang [14] used the GFM to establish housing locational and neighborhood variables, which could more reasonably evaluate the degrees of influence between geographic objects [42,43]. However, in the real world, with the increase in the number of geographic objects, the actual influence of each single object can be gradually diminished. For example, the influence of each supermarket is apparently larger when there is only one supermarket nearby than in the case that there are 50 supermarkets nearby. The GFM does not consider the diminishing effect of one single element caused by the increase in elements of the same type. Besides this, Bency [20], Yu [30] and Wang [12] counted the numbers of various POIs within a certain distance from the examined house and may use this distance as a hyperparameter in some cases. The method of counting the numbers of POIs does not consider the First Law of Geography, that the influence between geographic objects decays with the distance, so the results of them may also contain deviations. In addition, kernel density estimation (KDE) can directly infer the probability density function from an observed sample without estimating unknown parameters; thus, it presents good statistical properties and obtains asymptotically unbiased density estimates. KDE has been adopted by many applications and studies in GIS [44,45,46], but it does not consider the gradually diminishing influence of a single element with an increase in the number of geographic objects, like GFM.
In summary, some problems exist in the research on urban rental housing price models. First, existing methods for generating locational and neighborhood variables are not comprehensive enough for the density characteristics of geographic objects, since they either do not consider the law that the influence between objects gradually decay with their distance, or do not consider the fact that the actual influence of a single object gradually diminishes with the increase in the number of objects of the same type, which may consequently decrease the accuracy of the resulting pricing models. Second, complex and nonlinear relationships exist among the structural, locational and neighborhood housing price variables. The existing OLS, GWR and deep learning models usually incorporate the variables in the forms of one-dimensional vectors, without considerable extraction capacity for the complex relationships among the variables, which may also lead to a relatively insufficient modeling performance. Therefore, it is clear that to improve the precision of the rental housing price model, the proposed method should effectively characterize both the complex relationships and the spatial densities of the structural, locational and neighborhood variables. This is the main target of this study.
3. Materials and Methodology
3.1. Overall Framework
The following three main steps are required to complete the entire process in this paper (Figure 1): data collection, geographic data processing, and modeling and fitting. First, we use a web-crawler tool to obtain the rental housing data from the real estate website and collect POIs from Baidu Map for the study area (Wuhan, China). The study area and the data materials are introduced in Section 3.2 and Section 3.3. Second, the data obtained from the real estate website generally constitute the structural variables of the housing (included in Section 3.4), and the POIs from Baidu Map require geographic data processing to be transformed into locational and neighborhood variables. In this paper, we generate the locational and neighborhood variables based on the synthetic spatial densities of geographic objects. Some techniques and algorithms, such as the M function, KDE, GFM, and others, are utilized for processing the spatial density of POI data, which is demonstrated in Section 3.5. Third, the rental housing prices can be modeled based on the structural, locational and neighborhood variables, as follows: on the one hand, the variables can be modeled as baselines in fundamental housing price models such as HPM and GWR (introduced in Section 3.4); on the other hand, the housing price variables can be transformed into two dimensions and modeled by the proposed CNN model, and this approach is presented and discussed in detail in Section 3.6.
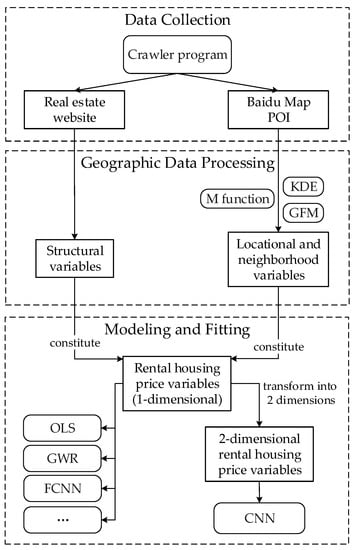
Figure 1.
The overall research flowchart of this paper.
3.2. Study Area
The study area is Wuhan (29°58′–31°22′ N, 113°41′–115°05′ E), China, which is the capital city of Hubei Province, and the largest city in central China. Wuhan is the most important industrial base as well as the scientific and educational center in central China. It is also a nationwide transportation hub in China. The city has 13 districts and a total area of 8569.15 km2 (Figure 2). The population of Wuhan was 12.45 million and the GDP was RMB 1562 billion in 2020 [47]. Among the major cities of China, Wuhan has had a high proportion of floating populations in recent years [4]. Since renting is the main way of living for floating populations, rental housing has a very large and active market in Wuhan.
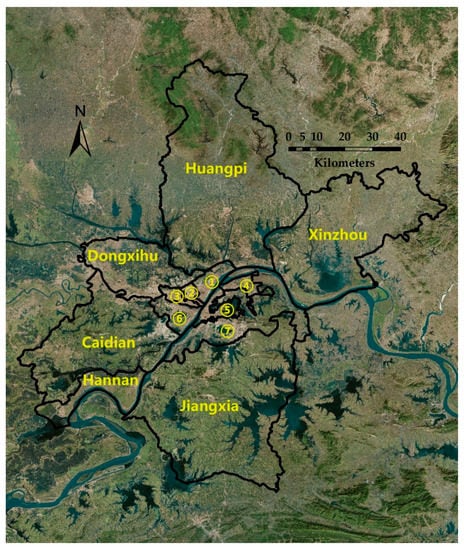
Figure 2.
The range of the study area: Wuhan, China (The municipal districts are: ① Jiang’an, ② Jianghan, ③ Qiaokou, ④ Qingshan, ⑤ Wuchang, ⑥ Hanyang and ⑦ Hongshan).
3.3. Data Collection
3.3.1. POIs
Compared with traditional geographic data, the POIs can reflect locational characteristics and human activities with a more detailed perspective and in a much finer granularity [48]. In this research, POI data collected from the Baidu Map are adopted for creating locational and neighborhood variables of the rental housing. Baidu Map is one of the largest electronic-map and LBS providers in China. A list of POIs can be acquired in the Baidu Map website by calling its open APIs or Internet services. We developed a crawler program and collected more than 550,000 POI data points of Wuhan in February 2020. The obtained POIs belong to 134 secondary types of 17 primary types, as listed in Table 1. Only POIs with user comments were adopted as the effective data in this research.

Table 1.
The POI data and categories (from Baidu Map).
3.3.2. Rental Housing
The rental housing data in the study were captured from Lianjia [49], which is a popular website for real estate and rental housing in China. There are abundant transaction data of rental houses in its client-side, and the data from this website have been proven to be effective for housing price analysis in recent studies [50,51]. All of the rental housing samples are acquired and parsed from the Lianjia app; the samples are traded between March and July 2020, and the influence of time could be ignored (the correlation coefficient with the rental price is <0.01). The structural variables of the rental housing could be easily obtained from this website. Among them, we screened out the whole rental housing belonging to the civil and fine decoration types (accounting for 69% of all collected items) and excluded extreme values; finally, a total of 91,906 rental samples were obtained.
3.4. HPM and GWR
The HPM is a fundamental price model and was first proposed in the field of economics [32]. The essence of HPM is that a customer would pay for housing (or rental housing) not only for the structure or living space, but also for other related factors, such as the location advantages, urban facilities and neighborhood environment. From an economic perspective, HPM can reveal the marginal implicit prices of the factors (variables) of a house, and is generally interpreted by means of MLR analysis, which is:
where βj represents the change in the price y when the jth variable xj changes (namely, the marginal price), and m is the number of variables. The structural variables of housing are displayed in Table 2; the locational variables and neighborhood variables are discussed in the next section. HPM is a basis and fundamental framework for other housing price models. The MLR based HPM is usually implemented with OLS and is labeled as the “OLS” model in this paper.

Table 2.
The structural variables of the rental housing in this study.
The general OLS model keeps the same pattern in the whole area, which may lead to deviations in the results when the relationships among the variables change with the locations. The GWR model introduced by Fotheringham [33] focuses on this concern and is actually a geographical extension of the global OLS. The attribute coefficients can be interpreted as the changes in the dependent variable (price) induced by independent variables as semilogarithmic functions [35]. GWR is a spatial regression technique that takes spatial heterogeneity into consideration and allows local parameters to be estimated as the coordinate varies. The model is expressed as follows:
where (ui, vi) denotes the spatial coordinate of the sample (housing) i, βk(ui, vi) denotes the regression coefficient of the kth influencing variable of the sample i, β0(ui, vi) denotes the spatial intercept, and denotes the error term. βk(ui, vi) varies with the coordinate (ui, vi), and can be estimated as follows:
where the weight matrix W is an n × n matrix whose off-diagonal elements are all zero. For the sample i, the jth diagonal element Wij is the geographical weight of sample i and sample j, which denotes the geographical influence of the sample j on sample i. The most commonly adopted function for calculating Wij is the Gaussian function: , where dij represents the distance between samples i and j, and b represents the bandwidth (nonnegative) indicating the degree of decaying effect related to the distance. Choosing an appropriate bandwidth (b) is an essential work for GWR and is usually based on the minimum Akaike information criterion (AICc) [52]. In this study, we use the AICc and the Gaussian function to determine the bandwidth and geographical weights of the GWR model. Since the factor of spatial heterogeneity is considered, the modeling accuracy of GWR is usually much better than that of the global OLS when the patterns and relationships of the data vary with geographic locations.
The OLS and GWR model are the fundamental housing price models. In this study, these two methods are used as baselines for comparison.
3.5. Spatial Density and the Locational and Neighborhood Variables
3.5.1. Modelling the Spatial Density of Geographic Objects
As mentioned in the introduction, if housing price or rental price models are based only on the “nearest” distances to facilities, the effects induced by the gathering of other geographical elements are not taken into consideration, which may lead to a decrease in model accuracy. Therefore, the quantitative characteristics of geographical elements need to be considered. KDE and the GFM are commonly used for calculating quantitative effects in geographic information science, and they can evaluate the influences among geographic elements more reasonably. However, in the real world, with the increase in the number of geographic objects, the actual influence of each single object can be gradually diminished. For example, a single supermarket is more important to a person when only one supermarket is located in the area than when there are fifty supermarkets nearby. The diminishing effect of a single object with the increase in objects of the same type can be detected by Shapley value analysis [53], which is an interpretation approach for explaining the local contributions of independent variables by calculating their marginal contributions across all possible variable–value combinations [54]. For a variable “the number of supermarkets within 2 km of the housing unit” (hereinafter referred to as “the supermarket variable”), if we build a Shapley additive explainer [55] based on an XGBoost regressor [56] for the housing rental price and the supermarket variable, we find (in Figure 3) that as the number of supermarkets increases from 0 to approximately 20, the influence of the supermarket variable on the rental price increases with the number of supermarkets; however, when the number of supermarkets exceeds 20, the influence of the supermarket variable no longer grows, suggesting that the contribution of each supermarket to the housing rental price diminishes when the number is greater than 20. KDE and the GFM do not consider the gradually diminishing influence of each single geographic object with the increasing number of the same type objects, which means that the location models based on these techniques may have certain deficiencies.
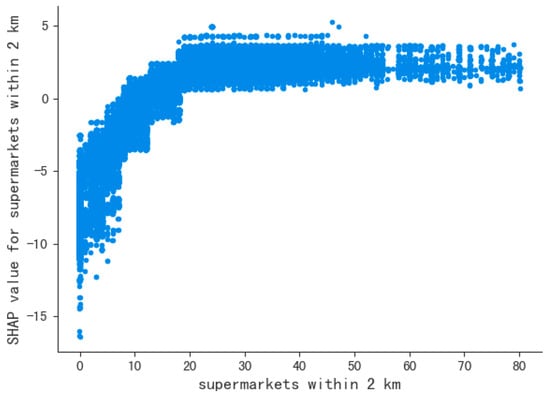
Figure 3.
The local influence of “the number of supermarkets within 2 km” on the rental housing price (based on Shapley value analysis).
The M function [26] is a measurement method for agglomeration in the fields of economic geography and spatial economics that calculates the degree of density within a range of radius r. The M function is intended to measure the aggregation degree of a certain industry relative to all industries within a certain range. Through the M function, since the process involves calculating the relative density degree of some category compared to all categories, and the relative density degree of one region compared to the whole area, the diminishing effect of a single element with the increase in the number of objects of the same type is actually smoothed. Thus, the effect of the spatial density of geographic objects may be better evaluated and explored. The related methods based on the M function have been used in many studies and have achieved effective results [57,58]. The form of the M function can be formulated as follows:
where eiSr represents the production value of the industry S in the area with the ith enterprise as the center and radius r as the range (excluding the value of the ith enterprise itself), eir represents the production value of all types of industries in the area with the ith enterprise as the center and r as the range (excluding the value of the ith enterprise itself), NS represents the number of enterprises belonging to the industry S, ES|i represents the total production value of industry S in the whole research area excluding the ith enterprise, and E|i represents the total production value of all types of industries in the whole area excluding the ith enterprise. The M function smooths the diminishing effect of the single element with the increase in the number of objects of the same type. Since this principle is homologous, if the M function is used to calculate the data of geographic elements such as POIs, housing, populations, it also measures the degrees of density of geographic elements within a certain range. Therefore, it is theoretically feasible to utilize the form of M function for the spatial density of POIs in this research. However, it is noteworthy that the calculations in the M function are based on simple quantitative accumulation, and do not consider the law that the influence between geographic objects gradually decays with their distance, which is included in the KDE and the GFM. Therefore, this indicator may need some improvements for calculating the influence of multiple geo-objects.
3.5.2. Locational and Neighborhood Variables Based on Synthetic Spatial Density
Generally speaking, KDE and the GFM take the law that the influence between geographic objects gradually decays with their distance into account, but they do not consider that the actual influence of a single geographic object gradually diminishes with the increase in the number of objects of the same type; on the contrary, the M Function considers the diminishing effect of a single object with the increase in the number of the same type of objects, but neglects the law that the influence between geo-objects decays with their distance. If these two aspects are united, thus incorporating the form of KDE (inspired by [59,60]) or GFM into the M function when calculating the quantities of geo-objects, both of the aspects can be taken into consideration. The radius r in the M function corresponds to the bandwidth of the KDE model or the influence distance of the GFM.
Therefore, we can utilize a form of the M function that incorporates the KDE or GFM method to measure the degrees of spatial density for the facilities (or POIs) in a given region around a housing unit. In our problem, eiSr can be expressed by the kernel density estimation (or the GFM effect score) of the S-type POIs in the area within a range of r (excluding the ith POI itself), eir represents the kernel density estimation (or the GFM effect score) of all types of POIs within a range of r (excluding the ith POI itself); NS represents the number of the S-type POIs; ES|i represents the total kernel density estimation (or the total GFM effect score) of the S-type POIs (excluding the ith POI) in the whole area; and E|i represents the total kernel density estimation (or the total GFM effect score) of all types of POIs (excluding the ith POI) in the whole area. From this perspective, the model can include both the law that the influence decays with the distances of geographic objects and the fact that the actual influence of a single geographic object gradually diminishes with the increase in the number of objects of the same type. The locational and neighborhood variables based on this approach may provide a more comprehensive generalization of the aggregated geographic information and may enable a more accurate analysis of related issues.
In this research, all types of the Baidu POIs (Table 1) can be processed into locational and neighborhood variables with respect to the rental housing price in the form of an M function combined with KDE or GFM. These locational and neighborhood variables are labeled “synthetic spatial density-based locational and neighborhood variables” in this paper. To distinguish whether KDE or GFM is combined, they can be subdivided as the “synthetic spatial density-based (KDE)” or “synthetic spatial density-based (GFM)” variables, respectively. For comparison, we can also establish the locational and neighborhood variables based on the “nearest distances” from the housing to the relevant POIs, and these variables are labeled as the “distance-based locational and neighborhood variables”; the locational and neighborhood variables can also be generated based solely on the KDE calculation or on the GFM model for the relevant POIs, and they are established and labeled as the “KDE-based locational and neighborhood variables” and the “GFM-based locational and neighborhood variables”, respectively. In our experiments, rental housing price models with “synthetic spatial density-based”, “distance-based”, “KDE-based” and “GFM-based” locational and neighborhood variables are applied and compared to determine which type is best for improving the model. The total POI numbers around the rental houses within the bandwidth of KDE or within the influence distance of GFM are also included in each kind of locational and neighborhood variables, respectively.
The calculation related to KDE is adopted as: , where h represents a certain house, j is the type of the POI, and pj,k represents the kth POI in the j-type POIs; for the j-type POIs, λj(h) is their density estimated value at the house h, Distance(h, pj,k) is the distance between the house h and the POI pj,k, and Nj is the number of the j-type POIs; K(·) is the kernel function of KDE, and the Epanechnikov kernel is adopted as the kernel function in this research; b is the bandwidth of the KDE, which means only points within b are effective for calculating the KDE value. The bandwidth of each variable is determined by the condition that the correlation coefficient of this KDE-generated variable with the housing rental price is maximized.
For the calculation relevant with GFM, to take the scales of the influences of externalities into consideration, the intensity function should be constrained by limiting the maximum influence distance [14,31]. The linear intensity function with a range constraint is expressed as:
where φ(x) is the field intensity (or effect score) at location x, and F is the original effect score at a distance of 0 from the object o, which should be calculated according to the object’s attributes and reflect the quality of the object. d(x) is the distance from x to object o, R is the maximum influence distance of object o, and r(x) is the relative distance measure given by dividing d(x) by R. The influence distance R of each variable is determined by the condition that the correlation coefficient of the effect scores of this variable with the price is maximized, which is similar with the process for KDE. Additionally, for each type of POIs, the number of comments of each POI are classified into 5 types with the K-means algorithm [61], and the result GroupID are listed as 0 (max) to 4 (min). Then, the original effect score F of each POI can be determined as F = 1 − GroupID/5.0. Apparently, the GFM effect score of a certain type of POIs related to a house is the sum effect scores of all POIs of this type.
In addition, variables are excluded if their correlation coefficients with the rental housing price are less than 0.01 (such as the gas station, the zoo, etc.).
3.6. The 2-Dimensional Housing Price Variables and the CNN Model
3.6.1. The CNN Deep-Learning Model for the Rental Housing Price
The housing price is a nonlinear and complex model, and with the advent of the big data era, deep learning provides an appropriate way to deal with it. Deep learning can address the nonlinear and complex relationships [17,18,19] in the input values, and the multicollinearity is not a problem, which is crucial for the modeling of housing prices. Therefore, all the 100+ kinds of geographic objects in the Baidu POIs can be processed into locational and neighborhood variables for the rental housing price, and input into the deep learning model together with the structural variables. Since the number of variables is large, in this study we fold these one-dimensional housing price variables and transform them into two-dimensional forms. In deep learning, two-dimensional inputs have more intensive information than the one-dimensional form and are more convenient for extracting characteristics and optimizing parameters. The values of the structural variables, locational variables and neighborhood variables of the housing prices can be filled into the cells in a 14 × 14 two-dimensional grid, which is discussed in Section 3.6.2. The input form of the two-dimensional housing price variables is similar to that of remote sensing images. Therefore, models similar to those utilized for image classification and feature extraction can be adopted for modeling rental housing price variables after making adaptive changes.
The structure of the CNN designed in our study is shown in Figure 4. Since previous studies have also noted that it is essential to reduce the complexity of the CNN to avoid overfitting [62], and a complex model may easily cause the overfitting phenomenon for the housing price data [17], the CNN structure is tuned as demonstrated in the figure. The proposed network includes an input layer, 2 or 3 convolutional layers, 2 fully connected layers and an output layer. Since the pooling layers are usually used for classification problems rather than regression problems, we would experiment on whether it is fine to remove pooling layers. For the convolutional layers, we would experiment which performs better if 2 or 3 layers are included, and we would also experiment which is better if the size of 3 or 5 is applied for the convolution kernel. The depths of the convolutional layers are set as 8, 16 for the 2 layers, or 8, 16, 32 for the 3 layers based on our pre-experiments. For the two fully connected layers, the sizes of them are 128 and 64, respectively. The activation function used in the convolutional layers and the fully connected layers is the rectified linear unit (ReLU) [63]. We also apply a dropout operation in the first fully connected layer that randomly disables the weights of some neurons and prevents model overfitting [19]. Since in recent studies the attention mechanism has been demonstrated effective for the deep learning of housing prices [12,22,24,64], we are inspired to wrap the first fully connected layer in our network with the attention block [22], which turns the raw features into attended features. There are many characteristics extracted by the convolutional layers before they come into the fully connected layers, and the attention mechanism helps the network to distinguish the important features that contributes to the output layer (the price), which are suitable for the gradient descent. The attention block should be used before the channels are fused [22], and can be formulated as: , . where x is the input vector (raw features), y is the output vector (attended features), h is the vector of neurons in the fully connected layer, and w is the weight. is the Softmax vector [65], distinguishing the importance of the features previously characterized by the convolutional layers. After the attention block, the deviation of the features would be significantly amplified; that is, y would have remarkably larger differences than x, which means the major features for the rental housing prices are stressed. The input layer is the 2-dimensionlized structural, locational and neighborhood variables of the housing, which is processed in the following way demonstrated in the next section. (The parameters of the models in this paper can be viewed in the Supplementary file.)
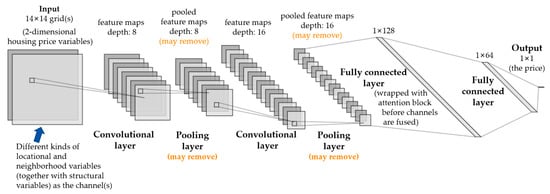
Figure 4.
The structure of the CNN model for the rental housing price.
3.6.2. Transforming Rental Housing Price Variables into Two Dimensions
Before CNN deep learning, we need to map the housing rental price variables (including the structural, locational and neighborhood variables) into a 2-dimensional space to generate the input data for the neural networks in the form of “an image”. Furthermore, it would be better if the variables with greater correlations are located at neighboring positions in this “image”, which is effective for the networks to extract characteristics from the 2-dimensional rental housing price variables. It takes 2 steps to transform the price variables into two dimensions, as shown in Figure 5. The first step is dimensionality reduction. A method should be used to transform each housing price variable into a (raw) 2-dimensional position. The second step is dividing and rasterizing the positions; specifically, the raw 2-dimensional positions are converted to a quadrate raster that can then be input into the CNN model.
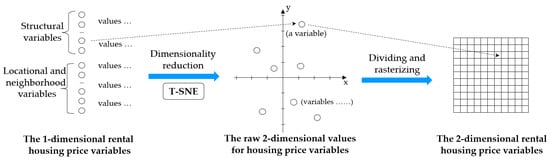
Figure 5.
The procedure of transforming the rental housing price variables into two dimensions.
For dimensionality reduction, assuming that there are N rental houses in our experiment, then for each rental housing price variable there would be N data, which means that each variable can be regarded as an N-dimensional vector. To map these N-dimensional vectors to a 2-dimensional space, a dimensionality reduction method for the high-dimensional vectors can be adopted. Currently, the commonly used dimensionality reduction methods include the principal component analysis (PCA) [66], and the t-distributed stochastic neighbor embedding (t-SNE) [67], etc. PCA uses a linear transformation to convert a set of high-dimensional variables into linearly independent low-dimensional vectors, with maximizing the variance of the projected data, and retaining the characteristics of the original data points as much as possible [66]. The t-SNE method is a nonlinear dimensionality reduction algorithm which is based on the probability distribution of random walks on the neighborhood graph to find the internal structure of the data, and can map the massive high-dimensional data into two or more dimensions [67]. In comparison, PCA cannot explain the complex polynomial relationship between features, while the data reduced by t-SNE algorithm can better maintain the characteristics of the original data; that is, when the points with similar distances in high-dimensional data space are mapped to low-dimensional space, the distances are still similar and can be expressed in relatively neighboring positions [68,69].Therefore, in the research we use the t-SNE to transform the rental housing price variables into 2 dimensions.
The t-SNE algorithm can be briefly described as follows: the high-dimensional points (the housing rental price variables) X = x1, x2, …, xn are aimed to be mapped into a low-dimensional space Y = y1, y2, …, yn (2-dimensional in this study). At first, t-SNE calculates the similarity of high-dimensional values xi and xj, which is represented by pj|i. The similarity pj|i is the conditional probability that xi picks xj as a neighbor in the case that neighbors are picked in proportion to a Gaussian density centered at xi:
where σi represents the variance of Gaussian function, which is centered at the high-dimensional location xi. The similarity is defined in a symmetrized form, that is, pi,j = (pj|i + pi|j)/2n, where n is the number of data points. For the target low-dimensional Y, the definition is extended and the similarity of them is modeled as:
Then, a heavy-tailed distribution algorithm is applied in the low-dimensional space to overcome the crowding issue of data points [67]. After subsequent operations, the dimensionality reduction in t-SNE can be completed and the data are mapped into the low-dimensional space Y.
The dividing and rasterizing process can be generalized as follows: First, suppose the data of each rental housing price variable have been reduced into 2 dimensions via t-SNE, and their 2D “coordinates” (X, Y) are obtained. For these “coordinates”, their median coordinate (Xme, Yme) can be calculated, which can represent the central point of the “image” of the 2-dimensional variables. Second, according to the central point, the 4 directions around it (the upper left, lower left, upper right and lower right) compose 4 quadrants. For the “coordinates” of every variable, it is easy to know which direction to the central point is, so as to know which quadrant they should be in. Third, the points (variables) in each quadrant can be sorted by their “x-coordinates” and equally separated by the quantiles of the “x-coordinates”; then, what row should be in the “image” can be determined for each variable. Last, the points (variables) in each row can be sorted by their “y-coordinates”, and what column should be in can be determined.
From the above steps, each rental housing price variable can be mapped to a “pixel” of a raster. The values of the pixels can be filled with the values of the housing price variables, and the pixels without filling of any variables (usually on the edge of the raster) can be filled with the default zero values. In this way, in the two-dimensional space, variables with greater correlations would be set in neighboring positions, which enhance ability of the networks to extract characteristics from the raster form of rental housing price variables.
Five kinds of locational and neighborhood variables have been previously generated for house prices, as follows: distance-based variables, KDE-based variables, GFM-based variables, synthetic spatial density-based (KDE) variables and synthetic spatial density-based (GFM) variables. They are separately filled into the grid and input into the 2-dimensional CNN model. In addition, they can practically be juxtaposed and become the parallel channels in the CNN, similar to the different bands of the images. Therefore, we separately combine the two-dimensional channels composed of these kinds of housing price variables and input them into the CNN for training. During the training process, the initial size of the input data is 14 × 14 × N (where N depends on whether combinations of different rental housing price variables are used; if we input only one kind of variables, N = 1; N = 2 or 3 if we combine different kinds of variables). At the same time, our model is compared with one-dimensional models and some recent models mentioned in other studies [17,24,30].
4. Results and Discussion
4.1. Experimental Groups and Model Accuracy Assessment
In this paper there are four kinds of rental housing price framework models as follows: OLS, GWR, a 1-dimensional fully connected neural network (FCNN) and a 2-dimensional deep learning model (CNN); there are also five kinds of locational and neighborhood variables as follows: distance-based variables, KDE-based variables, GFM-based variables, synthetic spatial density-based (KDE) variables and synthetic spatial density-based (GFM) variables. The above four framework models are generated and experimented with the five kinds of variables, respectively, and the corresponding modeling results of them are evaluated. Based on the results, the most accurate type of framework model is discussed, and which kind of locational and neighborhood variables is better for price modeling can be compared. Furthermore, different combinations of 2-dimensional locational and neighborhood variables are input into the CNN model and to find what the best model for housing rental price is. For every sample in the experimented models, the values of each variable are normalized to 0.0~1.0 to prevent model divergence. The whole dataset was randomly shuffled and split into training set (70%) and testing set (30%) for four independent times, and the final indicators are averaged to make the result more representative. The models are trained on a computer configured with the Intel i7-9700K CPU and a single NVIDIA Titan GPU.
In this research, the adjusted coefficient of determination (adj R2), the root mean squared error (RMSE) and its percentage (%RMSE) are adopted as the indicators for the accuracy evaluation of the models, which are commonly used indicators in existing studies [20,40]:
where yi,o and yi,s are the observed and predicted value of the ith housing, n represents the number of samples in the dataset, m represents the number of variables, and represents the mean observed value.
4.2. Results of 1-Dimensional and 2-Dimensional Models
To find a good architecture for the rental housing price model, experiments and comparisons are conducted on different types of neural networks. The first model is the 1-dimensional model, which is a five-layer FCNN: the input layer is a vector of one-dimensional rental housing price variables, including the structural, locational and neighborhood variables; the four hidden layers have 200, 120, 100 and 20 neurons, respectively; the output layer has one dimension, which is the value of the housing rental price. The next model is the two-dimensional CNN mentioned in Section 3.6.1. The depths of the convolutional layers are set as 8 and 16 if there are two layers, or 8, 16, and 32 if there are three layers based on our pre-experiments, and the sizes of the convolution kernel are set to three or five. A total of 2 × 2 × 2 = 8 sets of experiments are conducted for the CNN model. The backpropagation algorithm for the experiments in this study is the gradient descent algorithm [70]. The general loss function of the deep learning models is as follows: , where Y represents the predicted value, and Y* represents the true value. The learning parameters of the fully connected layers are set as follows: the L2 regularization is used with a regularization weight of 0.00005; the batch size for each training step is 32; the initial learning rate is 0.5; the decay rate of the learning rate is 0.99996; and the moving average decay is 0.99996. After the training process is completed, the models are run on the test set to estimate the fitting accuracy and predictive power for unknown samples. The locational and neighborhood variables adopted in this section are kept the same, which are the synthetic spatial density-based (GFM) locational and neighborhood variables obtained by combining the M function and the GFM approach. We preferentially combine the M function with GFM rather than with KDE because GFM usually performs better than KDE for the model in our research, which is demonstrated in Section 4.3. The results of other kinds of variables are also discussed in Section 4.3.
By conducting the training process, as shown in Figure 6, the 1-dimensional model (FCNN) becomes stable after approximately 300,000 training steps, and the 2-dimensional (CNN) model (for an average group) achieves stability after approximately 150,000 training steps. In addition, the HPM (OLS) and GWR model are used as the baseline groups, and recent deep learning models of Yao [17], Yu [30] and Bin [24] are also used to compare the results of the proposed models. (We do not consider the image part of these models since there are no image data in this study.) The models reach the fitting accuracies shown in Table 3 on the test sets.
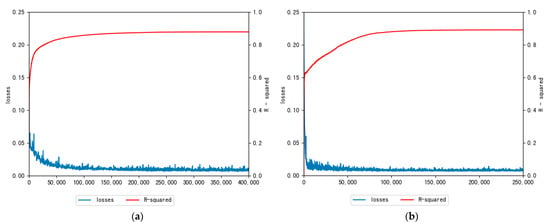
Figure 6.
Parameters observed during the training processes of the: (a) FCNN model, and (b) CNN model (for an average group).

Table 3.
Results of 1-dimensional and 2-dimensional models.
It can be seen that the fitting and prediction accuracies of the 2-dimensional models are apparently better than that of the 1-dimensional model. Therefore, transforming the rental housing price variables into two dimensions can effectively improve the fitting and predictive capabilities of the deep learning model. Since associations are regarded as linear relations in OLS and GWR, it is difficult for them to achieve increased accuracy in terms of prediction on the test set. The structure of the FCNN is 1-dimensional and relatively simple, which to some extent has difficulty extracting the complex relationships among the massive variables. Figure 7 briefly depicts the basic framework of an FCNN model and a CNN model. The input variables in an FCNN are vectorized and linear, while in a CNN model, the input variables are rasterized and dense. Therefore, the architecture and features of a CNN model are more focused and concentrated, making it easier for the network to capture and characterize the complex and interactive relationships among the multiple rental housing price variables. In the 1-dimensional FCNN, however, the features of the linearly arranged input variables are relatively scattered, and many neurons are needed to link them. When there are many input variables, the FCNN may have many redundant parameters which can decrease the performance, and more overfitting problems may occur; thus, the 1-dimensional model may have limited capacity to capture the complicated characteristics of massive variables. As a result, the 2-dimensional CNN can improve the performance of rental housing price modeling.
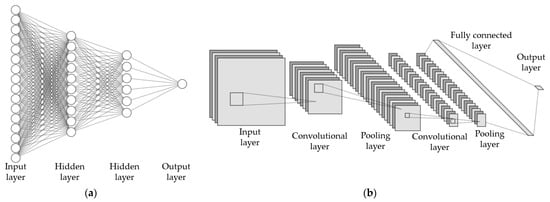
Figure 7.
The basic framework of the neurons in the neural network of (a) an example of FCNN model and (b) an example of CNN model.
For the 2-dimensional CNN models, when the size of the convolution kernel is three, and there are two convolutional layers without pooling layers (i.e., the CNN (3, 2, N)), the accuracy is optimal. For each configuration of these CNN models, when the pooling layers are removed from the framework, all of the results would be better than that with the pooling layers. Therefore, the pooling layers of CNN are not suitable or necessary for the rental housing price regression. Yu’s CNN model [30] includes the pooling layers and does not apply the useful dropout technique, thus the accuracy is lower compared with the CNNs proposed in this paper. Yao’s method [17] considers fewer variables, and there may be heterogeneous characteristics in the distribution grids of different kinds of geo-objects. Therefore, characteristics may not be extracted very effectively if features are input as parallel channels in a CNN. It is also challenging to model both the structural variables and the features extracted by Yao’s model since they are not trained simultaneously, and as a result, the performance of that model is relatively limited. Although the boosted regression trees adopted by Bin [24] can effectively improve the performance of housing price estimations, the one-dimensional neural network is utilized to extract the characteristics of the structural, locational and neighborhood variables which are different from ours, so the accuracy can still be improved in part of the nonimage data. No large discrepancy is observed between the CNN models without pooling layers in Table 3. Therefore, the following analysis of the 2-dimensional models would use the CNN (3, 2, N) network by default.
4.3. Results Based on Different Kinds of Locational and Neighborhood Variables
This section compares the effects of the different kinds of locational and neighborhood variables: distance-based, GFM-based, KDE-based, and synthetic spatial density-based (for GFM and KDE) locational variables, in the rental housing price models. These kinds of locational and neighborhood variables are applied in the framework models of OLS, GWR, FCNN, and CNN (3, 2, N), and the results are shown in Table 4:

Table 4.
Results of different kinds of locational and neighborhood variables.
From this table, it is clear that the accuracies of synthetic spatial density-based locational and neighborhood variables are higher than others in all framework models. The distance-based locational and neighborhood variables include only the distance characteristics of the geographic objects relevant to the houses, without the consideration of the quantitative characteristics; this incurs the loss of much geographic information, and the models based on these variables cannot achieve very satisfactory accuracy. For the KDE-based and GFM-based variables, although quantitative characteristics are included, they do not consider the fact that the actual influence of a single geographic object gradually diminishes with the increase in the number of objects of the same type. However, in the synthetic spatial density-based variables (for GFM and KDE), the form of the M function represents the spatial aggregation characteristics of the relevant geographic objects and urban facilities, including the diminishing effect of the single element with the increase in the number of objects of the same type; and the statistical method of the embedded GFM/KDE can reflect the First Law of Geography. Therefore, compared to the distance-based, GFM-based and KDE-based variables, the synthetic spatial density-based locational and neighborhood variables consider the information of geographic objects in a more comprehensive way, and better reflect the locational characteristics of a housing unit, which helps improve the fitting accuracy of the resulting price model.
In addition, in all experiments, the accuracies of the GFM experimental groups are higher than that of the KDE groups for the same framework model. Since GFM specifically focuses on the concept of “influence”, which can be more detailed in evaluating the impacts among the geographical objects than KDE, GFM may be more reasonable for estimating the effects of the geo-objects on housing, thus resulting in higher rental pricing models. Practically, GFM is more inclined to be applied to the studies related to housing prices [14,31], and this research also supports the GFM. In the following experiments, we are also more inclined to preferentially utilize the methods embedded with GFM.
4.4. Results of Different Combinations of 2-Dimensional Rental Housing Price Variables
The different kinds of 2-dimensional rental housing price variables, including the distance-based, GFM-based, KDE-based, and synthetic spatial density-based variables, can practically be juxtaposed and become the parallel channels in the CNN, similar to the different bands of images. Therefore, we separately combine the two-dimensional “image bands” composed of these kinds of rental housing price variables, and we input them into the CNN for training. The results of the different combinations of 2-dimensional variables are shown in Table 5. Since theoretically too many different combinations can be obtained, and the GFM usually performs better than KDE in this research (which is presented in the previous section), some combinations with the KDE are omitted.

Table 5.
Results of combinations of 2-dimensional rental housing price variables.
Among the different combinations, “distance-based + synthetic spatial density-based (GFM)” yields the best accuracy when inputted as two channels for the CNN model. According to the characteristic of relevant models and data, the reasons can be analyzed as follows:
Firstly, the distance-based locational and neighborhood variables reflect the distance characteristics of the nearest geo-object of a certain type to the housing, while the GFM-based and synthetic spatial density-based variables mainly consider the spatial density of geo-objects. Therefore, the information contained in the distance-based variables is significantly different from that contained in the other two kinds of variables. As shown in Table 6, the average correlation coefficient between the synthetic spatial density-based (GFM) and GFM-based variables is relatively high, while the (absolute values of) average correlation coefficients between the distance-based variables and the other two kinds are relatively low. Therefore, when the distance-based variables and the other two kinds of variables (one kind of them or both) are combined in the model, the information in the network is enriched, which helps improve the performance. Secondly, as seen from the results in the previous section, the accuracy values with the synthetic spatial density-based locational and neighborhood variables are clearly higher than those of the distance-based and KDE-based variables. Therefore, among the experimental groups, all of the combinations including the synthetic spatial density-based variables exhibit advantages. Finally, when all three kinds of variables are used as parallel channels in the model, the network adds more complexity but no considerable increase in information. Since the channel of “GFM-based” and the channel of “synthetic spatial density-based (GFM)” are relatively similar, the redundance is not beneficial for the model and instead causes a decrease in accuracy.

Table 6.
Average correlation indices of different kinds of locational and neighborhood variables.
In summary, the combination of the “distance-based + synthetic spatial density-based (GFM)” locational and neighborhood variables as two channels in the proposed CNN model is best for rental housing price modeling in this paper. This research is more focusing on the nonimage geographic data and the structural, locational and neighborhood variables of the housing units. The proposed neural network is very compatible for extending the data of images. We are very eager for the future of the proposed method and plan to extend it with the utilization of street view pictures or indoor pictures, as soon as the relevant data can be sufficiently available in the study area. In addition, the construction costs of houses may have a meaningful influence on rental housing prices since newly constructed houses influence the real estate industry [71,72]. The exploration of the effects of construction costs on rental housing prices and the improvements to the pricing model should be considered in future work.
5. Conclusions
With Wuhan as the study area, this study uses the HPM, the GWR model, a one-dimensional FCNN model, and a two-dimensional CNN model to estimate rental housing prices, and the accuracies of these models are compared. The results show that the two-dimensional CNN with synthetic spatial density-based locational and neighborhood variables achieves the highest price fitting and forecasting accuracies. When the size of the convolution kernel is 3 and there are 2 convolutional layers and no pooling layers, the performance of the proposed CNN is optimal. Our research indicates that the two-dimensional CNN can efficiently model the rental housing price with the structural, locational and neighborhood variables, which includes nonlinear and complex relationships, and pooling layers are not necessary for the rental housing price regression problem; the synthetic spatial density-based locational and neighborhood variables used in this research can better reflect the impacts of facilities and geo-objects on the rental housing price, thereby improving the accuracy of the final model; the combination of the “distance-based + synthetic spatial density based (GFM)” locational and neighborhood variables as two input channels of the CNN model yields the best accuracy (R2 = 0.9097, RMSE = 3.5126), since this combination contains relatively massive information and not too much redundance. The proposed model may provide individuals and enterprises with suitable decision-making information for their rental housing transactions; it may also provide the government with a valuable decision-support reference about the locations and prices of public rental housing.
Some of the discussion provided in this paper may aid in understanding rental housing price models. First, compared with one-dimensional deep learning models [15,16], the architecture and features of the proposed CNN are denser and concentrated; thus, the CNN can better characterize the complexity of the relationships and interactions among structural, locational and neighborhood variables and can perform better than the one-dimensional FCNN in our experiment. Second, when generating the locational and neighborhood variables, combining the M function [26] and GFM [14,31] (the synthetic spatial density-based variables (GFM)) can better reflect the locational characteristics of a housing unit. The form of the M function represents the spatial aggregation characteristics of the geographic objects and urban facilities, and it considers the diminishing effect of a single geo-object with the increase in the number of objects of the same type. Additionally, the embedded GFM considers the law that the influence between objects decays with their distance. Therefore, compared to the distance-based, GFM-based and KDE-based variables, the synthetic spatial density-based locational and neighborhood variables enhance the accuracy of the rental housing price model. Finally, when compared with other published models, the proposed model generally performs better. In Yao’s model [17], the distribution grids of different kinds of geo-objects (and the remote sensing images) may be heterogeneous, and characteristics may not be extracted very effectively if they are inputted as parallel channels in a CNN; besides this, how to combine the convolutional layers with structural variables in this model also needs to be further explored. Yu [30] did not remove the pooling layers from the CNN, which are experimented to be unnecessary in rental housing price regression, thus resulting in relatively limited model performance. Moreover, in half 1-dimensional and half 2-dimensional models (such as Bin’s [24]), the one-dimensional neural network is utilized to extract the characteristics of the structural, locational and neighborhood variables, so the accuracy of these models may still have room for improvement in part of the nonimage data. Certainly, the state-of-the-art aspects of these methods can provide guidance for further studies in the future.
Some improvements can be made for this study in the future. This study mainly focuses on the nonimage geographic data and the structural, locational and neighborhood variables of the rental housing prices. Other characteristics such as natural topographic features, vegetation characteristics and construction costs, are not directly reflected in the distribution of the POIs. The impacts of those relevant factors on rental housing prices still need to be explored. Since our model is very compatible for extending the images, remote sensing images, street view images and indoor pictures can be practically applied to our method in the future. In addition, more cities and more forms of attention mechanisms can be further experimented for the neural networks of the housing rental/selling price model.
Supplementary Materials
The supplementary document is available online at https://www.mdpi.com/article/10.3390/ijgi11010053/s1.
Author Contributions
Conceptualization, Hang Shen and Lin Li; methodology, Hang Shen; software, Feng Li and Hang Shen; validation, Haihong Zhu; writing—original draft preparation, Hang Shen and Haihong Zhu; writing—review & editing, Haihong Zhu and Feng Li; project administration, Lin Li. All authors have read and agreed to the published version of the manuscript.
Funding
This study is supported by the National Natural Science Foundation of China (41871298).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the experiments of this study are mainly from map.baidu.com and wh.lianjia.com (accessed on 2 November 2021).
Acknowledgments
The authors thank the editors and reviewers for providing insightful suggestions and comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Andrew, M.; Haurin, D.; Munasib, A. Explaining the route to owner-occupation: A transatlantic comparison. J. Hous. Econ. 2006, 15, 189–216. [Google Scholar] [CrossRef]
- Seko, M.; Sumita, K. Japanese Housing Tenure Choice and Welfare Implications after the Revision of the Tenant Protection Law. J. Real Estate Finance Econ. 2007, 35, 357–383. [Google Scholar] [CrossRef]
- Dong, H. The impact of income inequality on rental affordability: An empirical study in large American metropolitan areas. Urban Stud. 2017, 55, 2106–2122. [Google Scholar] [CrossRef]
- National Health Commission, PRC. Report on the Development of Floating Population in China; China Population Press: Beijing, China, 2018. [Google Scholar]
- Ministry of Housing and Urban-Rural Development, PRC. Notice of the Ministry of Housing and Urban-Rural Development of the People’s Republic of China, No. 7. 2021. Available online: http://www.mohurd.gov.cn/gongkai/fdzdgknr/gongkaiwgk/202107/20210708_762874.html (accessed on 20 August 2021).
- Saiz, A. Immigration and Housing Rents in American Cities. J. Urban Econ. 2003, 61, 345–371. [Google Scholar] [CrossRef] [Green Version]
- Su, S.; Zhang, J.; He, S.; Zhang, H.; Hu, L.; Kang, M. Unraveling the impact of TOD on housing rental prices and implications on spatial planning: A comparative analysis of five Chinese megacities. Habitat Int. 2020, 107, 102309. [Google Scholar] [CrossRef]
- Cajias, M.; Ertl, S. Spatial effects and non-linearity in hedonic modeling: Will large data sets change our assumptions? J. Prop. Invest. Financ. 2018, 36, 32–49. [Google Scholar] [CrossRef]
- Liebelt, V.; Bartke, S.; Schwarz, N. Hedonic pricing analysis of the influence of urban green spaces onto residential prices: The case of Leipzig, Germany. Eur. Plan. Stud. 2018, 26, 133–157. [Google Scholar] [CrossRef]
- Ullah, F.; Sepasgozar, S.M.E. Key Factors Influencing Purchase or Rent Decisions in Smart Real Estate Investments: A System Dynamics Approach Using Online Forum Thread Data. Sustainability 2020, 12, 4382. [Google Scholar] [CrossRef]
- Yu, T.; Song, Y. Solving the Problem of ‘Cold Weather’ of Public Rental Houses–Based on the Analysis of Government’s Purchase of Public Service. China Econ. Trade Guide 2018, 32, 74–76. [Google Scholar]
- Wang, P.-Y.; Chen, C.-T.; Su, J.-W.; Wang, T.-Y.; Huang, S.-H. Deep Learning Model for House Price Prediction Using Heterogeneous Data Analysis Along with Joint Self-Attention Mechanism. IEEE Access 2021, 9, 55244–55259. [Google Scholar] [CrossRef]
- Shimizu, C.; Karato, K.; Nishimura, K. Nonlinearity of housing price structure: Assessment of three approaches to nonlinearity in the previously owned condominium market of Tokyo. Int. J. Hous. Mark. Anal. 2014, 7, 459–488. [Google Scholar] [CrossRef]
- Liang, X.; Liu, Y.; Qiu, T.; Jing, Y.; Fang, F. The effects of locational factors on the housing prices of residential communities: The case of Ningbo, China. Habitat Int. 2018, 81, 1–11. [Google Scholar] [CrossRef]
- Jiang, Z.; Shen, G. Prediction of House Price Based on The Back Propagation Neural Network in The Keras Deep Learning Framework. In Proceedings of the 2019 6th International Conference on Systems and Informatics (ICSAI), Shanghai, China, 2–4 November 2019; pp. 1408–1412. [Google Scholar]
- Phan, T.D. Housing price prediction using machine learning algorithms: The case of Melbourne city, Australia. In Proceedings of the 2018 International Conference on Machine Learning and Data Engineering (iCMLDE), Sydney, Australia, 3–7 December 2018; pp. 35–42. [Google Scholar]
- Yao, Y.; Zhang, J.; Hong, Y.; Liang, H.; He, J. Mapping fine-scale urban housing prices by fusing remotely sensed imagery and social media data. Trans. GIS 2018, 22, 561–581. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R.R. Improving Neural Networks by Preventing Co-Adaptation of Feature Detectors. arXiv 2012, arXiv:1207.0580. [Google Scholar]
- Bency, A.J.; Rallapalli, S.; Ganti, R.K.; Srivatsa, M.; Manjunath, B.S. Beyond Spatial Auto-Regressive Models: Predicting Housing Prices with Satellite Imagery. In Proceedings of the 2017 IEEE Winter Conference on Applications of Computer Vision (WACV), Santa Rosa, CA, USA, 24–31 March 2017; pp. 320–329. [Google Scholar]
- Fu, X.; Jia, T.; Zhang, X.; Li, S.; Zhang, Y. Do street-level scene perceptions affect housing prices in Chinese megacities? An analysis using open access datasets and deep learning. PLoS ONE 2019, 14, e0217505. [Google Scholar] [CrossRef]
- Bin, J.; Gardiner, B.; Liu, Z.; Li, E. Attention-based multi-modal fusion for improved real estate appraisal: A case study in Los Angeles. Multimedia Tools Appl. 2019, 78, 31163–31184. [Google Scholar] [CrossRef]
- Zhao, Y.; Chetty, G.; Tran, D. Deep Learning with XGBoost for Real Estate Appraisal. In Proceedings of the 2019 IEEE Symposium Series on Computational Intelligence (SSCI), Xiamen, China, 6–9 December 2019; pp. 1396–1401. [Google Scholar]
- Bin, J.; Gardiner, B.; Li, E.; Liu, Z. Multi-source urban data fusion for property value assessment: A case study in Philadelphia. Neurocomputing 2020, 404, 70–83. [Google Scholar] [CrossRef]
- Billings, S.B.; Johnson, E.B. The location quotient as an estimator of industrial concentration. Reg. Sci. Urban Econ. 2012, 42, 642–647. [Google Scholar] [CrossRef]
- Marcon, E.; Puech, F. Measures of the geographic concentration of industries: Improving distance-based methods. J. Econ. Geogr. 2009, 10, 745–762. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Wang, M.; Li, W.; Peng, J.; Huang, L. Impact of Urban Green Space on Residential Housing Prices: Case Study in Shenzhen. J. Urban Plan. Dev. 2015, 141, 05014023. [Google Scholar] [CrossRef]
- Geng, B.; Bao, H.; Liang, Y. A study of the effect of a high-speed rail station on spatial variations in housing price based on the hedonic model. Habitat Int. 2015, 49, 333–339. [Google Scholar] [CrossRef]
- Zhang, Y.; Fu, X.; Lv, C.; Li, S. The Premium of Public Perceived Greenery: A Framework Using Multiscale GWR and Deep Learning. Int. J. Environ. Res. Public Health 2021, 18, 6809. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Jiao, C.; Xin, Y.; Wang, Y.; Wang, K. Prediction on Housing Price Based on Deep Learning. Int. J. Comput. Inf. Eng. 2018, 12, 90–99. [Google Scholar]
- Jiao, L.; Liu, Y. Geographic Field Model based hedonic valuation of urban open spaces in Wuhan, China. Landsc. Urban Plan. 2010, 98, 47–55. [Google Scholar] [CrossRef]
- Rosen, S. Hedonic Prices and Implicit Markets: Product Differentiation in Pure Competition. J. Politi. Econ. 1974, 82, 34–55. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; E Charlton, M.; Brunsdon, C. Geographically Weighted Regression: A Natural Evolution of the Expansion Method for Spatial Data Analysis. Environ. Plan. A: Econ. Space 1998, 30, 1905–1927. [Google Scholar] [CrossRef]
- Malpezzi, S. Hedonic Pricing Models: A Selective and Applied Review. Hous. Econ. Public Policy 2003, 67–89. [Google Scholar] [CrossRef]
- Wu, C.; Ye, X.; Ren, F.; Wan, Y.; Ning, P.; Du, Q. Spatial and Social Media Data Analytics of Housing Prices in Shenzhen, China. PLoS ONE 2016, 11, e0164553. [Google Scholar] [CrossRef]
- Huang, B.; Wu, B.; Barry, M. Geographically and temporally weighted regression for modeling spatio-temporal variation in house prices. Int. J. Geogr. Inf. Sci. 2010, 24, 383–401. [Google Scholar] [CrossRef]
- Ioannides, Y.M.; Rosenthal, S.S. Estimating the Consumption and Investment Demands for Housing and Their Effect on Housing Tenure Status. Rev. Econ. Stat. 1994, 76, 127–141. [Google Scholar] [CrossRef]
- Comber, A.; Chi, K.; Huy, M.Q.; Nguyen, Q.; Lu, B.; Phe, H.H.; Harris, P. Distance metric choice can both reduce and induce collinearity in geographically weighted regression. Environ. Plan. B Urban Anal. City Sci. 2018, 47, 489–507. [Google Scholar] [CrossRef] [Green Version]
- Hagenauer, J.; Helbich, M. A geographically weighted artificial neural network. Int. J. Geogr. Inf. Sci. 2021, 1–21. [Google Scholar] [CrossRef]
- Zhou, X.; Tong, W.; Li, D. Modeling Housing Rent in the Atlanta Metropolitan Area Using Textual Information and Deep Learning. ISPRS Int. J. Geo-Information 2019, 8, 349. [Google Scholar] [CrossRef] [Green Version]
- Won, J.; Lee, J.-S. Investigating How the Rents of Small Urban Houses are Determined: Using Spatial Hedonic Modeling for Urban Residential Housing in Seoul. Sustainability 2017, 10, 31. [Google Scholar] [CrossRef] [Green Version]
- Zhou, P.; Liu, Y.; Chen, Y.; Zeng, C.; Wang, Z. Prediction of the spatial distribution of high-rise residential buildings by the use of a geographic field based autologistic regression model. J. Hous. Built Environ. 2015, 30, 487–508. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.; Chen, S. Temporal Characteristics of Waterfronts in Wuhan City and People’s Behavioral Preferences Based on Social Media Data. Sustainability 2019, 11, 6308. [Google Scholar] [CrossRef] [Green Version]
- Xie, Z.; Yan, J. Kernel Density Estimation of traffic accidents in a network space. Comput. Environ. Urban Syst. 2008, 32, 396–406. [Google Scholar] [CrossRef] [Green Version]
- Anderson, T.K. Kernel density estimation and K-means clustering to profile road accident hotspots. Accid. Anal. Prev. 2009, 41, 359–364. [Google Scholar] [CrossRef]
- Do, T.M.T.; Dousse, O.; Miettinen, M.; Gatica-Perez, D. A probabilistic kernel method for human mobility prediction with smartphones. Pervasive Mob. Comput. 2015, 20, 13–28. [Google Scholar] [CrossRef] [Green Version]
- Wuhan Bureau of Statistics, PRC. Wuhan Statistical Yearbook 2021. Available online: http://tjj.wuhan.gov.cn/tjfw/tjnj/202112/t20211220_1877108.shtml (accessed on 2 November 2021).
- Yue, Y.; Zhuang, Y.; Yeh, A.G.-O.; Xie, J.-Y.; Ma, C.-L.; Li, Q.-Q. Measurements of POI-based mixed use and their relationships with neighbourhood vibrancy. Int. J. Geogr. Inf. Sci. 2016, 31, 658–675. [Google Scholar] [CrossRef] [Green Version]
- Lianjia. Lianjia Flagship Website. Available online: https://wh.lianjia.com/ (accessed on 2 November 2021).
- Li, H.; Wei, Y.D.; Wu, Y.; Tian, G. Analyzing housing prices in Shanghai with open data: Amenity, accessibility and urban structure. Cities 2019, 91, 165–179. [Google Scholar] [CrossRef]
- Wu, H.; Jiao, H.; Yu, Y.; Li, Z.; Peng, Z.; Liu, L.; Zeng, Z. Influence Factors and Regression Model of Urban Housing Prices Based on Internet Open Access Data. Sustainability 2018, 10, 1676. [Google Scholar] [CrossRef] [Green Version]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Roth, A.E. The Shapley Value: Essays in Honor of Lloyd S. Shapley; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Rico-Juan, J.R.; de La Paz, P.T. Machine learning with explainability or spatial hedonics tools? An analysis of the asking prices in the housing market in Alicante, Spain. Expert Syst. Appl. 2021, 171, 114590. [Google Scholar] [CrossRef]
- Lundberg, S. SHAP (SHapley Additive exPlanations). Available online: https://github.com/slundberg/shap (accessed on 2 November 2021).
- Chen, T.; Guestrin, C. Xgboost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Méndez-Ortega, C.; Arauzo-Carod, J.-M. Locating Software, Video Game, and Editing Electronics Firms: Using Microgeographic Data to Study Barcelona. J. Urban Technol. 2019, 26, 81–109. [Google Scholar] [CrossRef]
- Coll-Martínez, E.; Moreno-Monroy, A.-I.; Arauzo-Carod, J.-M. Agglomeration of creative industries: An intra-metropolitan analysis for Barcelona. Pap. Reg. Sci. 2019, 98, 409–431. [Google Scholar] [CrossRef]
- Lang, G.; Marcon, E.; Puech, F. Distance-based measures of spatial concentration: Introducing a relative density function. Ann. Reg. Sci. 2019, 64, 243–265. [Google Scholar] [CrossRef] [Green Version]
- Duranton, G.; Overman, H.G. Testing for Localization Using Micro-Geographic Data. Rev. Econ. Stud. 2005, 72, 1077–1106. [Google Scholar] [CrossRef] [Green Version]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 21 June–18 July 1965; Volume 1, pp. 281–297. [Google Scholar]
- Zhong, Y.; Fei, F.; Zhang, L. Large patch convolutional neural networks for the scene classification of high spatial resolution imagery. J. Appl. Remote Sens. 2016, 10, 25006. [Google Scholar] [CrossRef]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on International Conference on Machine Learning (ICML’10), Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Ashish, V.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. In Proceedings of the Advances in neural information processing systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Xu, K.; Ba, J.; Kiros, R.; Cho, K.; Courville, A.; Salakhudinov, R.; Zemel, R.; Bengio, Y. Show, Attend and Tell: Neural Image Caption Generation with Visual Attention. In Proceedings of the 32nd International Conference on International Conference on Machine Learning (ICML’15), Lille, France, 6–11 July 2015. [Google Scholar]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Van der Maaten, L.; Hinton, G. Visualizing Data Using T-Sne. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Li, W.; Cerise, J.E.; Yang, Y.; Han, H. Application of t-SNE to human genetic data. J. Bioinform. Comput. Biol. 2017, 15, 1750017. [Google Scholar] [CrossRef] [PubMed]
- Miao, A.; Zhuang, J.; Tang, Y.; He, Y.; Chu, X.; Luo, S. Hyperspectral Image-Based Variety Classification of Waxy Maize Seeds by the t-SNE Model and Procrustes Analysis. Sensors 2018, 18, 4391. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
- Zhang, S.; Migliaccio, G.; Zandbergen, P.A.; Guindani, M. Empirical Assessment of Geographically Based Surface Interpolation Methods for Adjusting Construction Cost Estimates by Project Location. J. Constr. Eng. Manag. 2014, 140, 04014015. [Google Scholar] [CrossRef]
- Zhang, S.; Bogus, S.M.; Lippitt, C.D.; Migliaccio, G.C. Estimating Location-Adjustment Factors for Conceptual Cost Estimating Based on Nighttime Light Satellite Imagery. J. Constr. Eng. Manag. 2017, 143, 04016087. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).