Abstract
Robots operating in human environments require a diverse set of skills, including slow and fast walking, turning, side-stepping, and more. However, developing robot controllers capable of exhibiting such a broad range of behaviors is a challenging problem that necessitates meticulous investigation for each task. To address this challenge, we introduce a trajectory optimization method that resolves the kinematic infeasibility of reference animal motions. This method, combined with a model-based controller, results in a unified data-driven model-based control framework capable of imitating various animal gaits without the need for expensive simulation training or real-world fine-tuning. Our framework is capable of imitating a variety of motor skills such as trotting, pacing, turning, and side-stepping with ease. It shows superior tracking capabilities in both simulations and the real world compared to other imitation controllers, including a model-based one and a learning-based motion imitation technique.
1. Introduction
Animals are capable of performing diverse and agile locomotion behaviors in nature, but transferring such behaviors to robots remains a challenge. Robots operating in human environments should be equipped with diverse skills such as trotting and pacing when walking slowly or speeding up, as well as the ability to turn around corners and side-step around obstacles. However, building a universal controller that is robust enough to perform such a wide range of skills is still an unsolved problem.
Motion imitation [1,2] holds the promise of learning diverse natural movements by imitating reference motions captured from real humans or animals. Traditional model-based control algorithms [3,4,5] in locomotion literature have demonstrated impressive agility and robustness, but they often require extensive effort in developing the proper mathematical models and control strategies tailored to the given task. On the other hand, many works in physically simulated agent control [1,6,7,8,9] have demonstrated that motion imitation offers a framework to learn a wide range of skills, including walking, running, jumping, and dancing; it can also easily be combined with existing motion planners such as data-driven kinematic controllers [10]. This approach does not assume any prior knowledge about input motions, and its repertoire is only limited by the given motion dataset and the learning capacity of the policy network, making it ideal for teaching robots a wide range of motions. However, learning-based motion imitation is often computationally expensive and its performance could deteriorate during real-world deployment due to sim-to-real gaps unless expensive adaptation processes are performed [2].
Our key insight is that we can combine the motion imitation paradigm with model-based control to take advantage of both approaches. In the context of model-based control, this data-driven imitation approach provides a unified framework for achieving various motor skills without the burden of task-specific modeling and tuning. From the motion imitation perspective, model-based control can play a role of tracking controllers which do not require training cost per motion, unlike learning-based methods. In addition, our controller inherits all the strengths of model-based control, such as better sim-to-real transferability.
We develop a trajectory optimization algorithm that allows for adapting animal motions that are kinematically infeasible on target robots, while still maintaining the overall style of the motion. Our approach involves fitting a rhythmic dynamic movement primitive (DMP) [11] to the input motion and optimizing a subset of its parameters using CMA-ES [12] to improve imitation performance. We combine this trajectory optimization method with a model-based control algorithm to imitate a given reference motion. Our method includes two main components: a stance controller using a low-dimensional centroidal model for the CoM from Di et al. [5], along with an online adaptation that commands desired joint positions to improve motion imitation, and a swing controller using inverse kinematics to follow swing leg trajectories augmented by a feedback term, similar to a Raibert footstep [13]. An overview of the approach is presented in Figure 1.
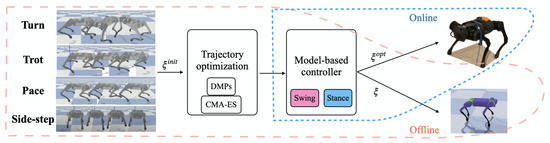
Figure 1.
An overview of our approach. We start with retargeted animal motions and use them as reference motions in a model-based controller. In simulation, we run trajectory optimization to update the reference motion and send the optimized trajectory to hardware. The optimization pipeline is used on four animal motions—turn, trot, pace, and side-step. The same hardware controller tracks these motions, resulting in diverse, agile gaits on hardware with no real-world fine-tuning.
The main contribution of this work is a trajectory optimization algorithm that addresses the kinematic infeasibility of reference motions. This algorithm can be integrated with a model-based controller, resulting in an unified control framework that is capable of imitating various animal motions. We demonstrate that our approach can seamlessly perform various motor skills, including trotting, pacing, turning, and sidestepping, using a single controller in simulation and on hardware of an A1 robot [14]. Our controller shows much better tracking capabilities compared to other state-of-the-art model-based imitation control schemes [15] and a model-free imitation learning algorithm [2].
2. Related Work
2.1. Motion Imitation
Designing controllers that generate natural-looking motions is challenging on robots and animated characters. Imitating reference motions (usually recorded by motion capture equipment), using learning based approaches has shown a lot of promise in simulation for bipeds [1,6,7,8,16,17,18,19], and quadrupeds [1,16,20]. In some cases where it is hard or impossible to get those real reference motions, manually created motions could also be used [1,16]. However, learned imitation policies are often vulnerable to the sim-to-real gap even after a long learning process [19], which can be mitigated by domain randomization [21] or online adaptation [2]. However, fine-tuning per motion in the real world is quite expensive. Instead, we present a unified controller capable of producing varied gaits, without fine-tuning on hardware.
2.2. Model-Based Legged Locomotion Control
Model-based approaches use a dynamics model to optimize actions with respect to a given cost/reward function. Several reduced-order dynamic models have been developed for legged robot control due to its complex dynamics. For bipedal robots, the inverted pendulum model and its variants have been widely used [22,23,24,25]. For quadrupedal robots, simplifying the robot into a single rigid body that is driven by the sum of external forces from stance legs is one of the reliable approaches to control [4,5,26]. However, these low-dimensional models depending on hand-designed reference motions generate gaits of which the styles are robotic and not lifelike. There have been other previous works that combined model-based controllers with reinforcement learning(RL) [27,28] to generate desired CoM acceleration, or adopted learned dynamics models [29] for planning. In this work, we adapt the model-based controller from [5] and use animal motion trajectories as the reference motion to generate diverse, agile, natural motions on an A1 quadrupedal robot. Instead of using reinforcement learning like [27], we use trajectory optimization to improve the performance of the model-based controller in simulation and transfer the optimized reference trajectory to the real robot.
Closely related to our work, recently, Kang et al. [15] presented a model-based controller that uses animal motions to create reference CoM trajectories for quadrupedal robots. However, their swing motion is not inspired by animals; they rather use a Raibert [13] stepping policy with hand-designed foot trajectories. Moreover, all the results are shown in simulations, which include trotting-like walking behaviors only. In contrast, we present four dynamic gaits – trot, pace, turn and side-step—on an A1 robot in the real world, using the swing trajectories recorded from animals, resulting in more natural looking motions. To achieve this challenging result, we present online adaptation techniques, as well as trajectory optimization to improve reference motion.
2.3. Dynamic Movement Primitives (DMPs)
Dynamic Movement Primitives (DMPs) are powerful and well-studied tools for motion imitation. In manipulation problems, DMPs have been widely explored for imitation learning [30,31,32,33], hierarchical learning [34,35], motion optimization [36,37] and reinforcement learning [38]. In legged robots, pattern generators, a subset of rhythmic DMPs, have long been used for modeling trajectories for locomotion [39,40,41]. However, central pattern generators [42] and other limit cycle approaches are not easily applicable to imitation learning scenarios. On the other hand, rhythmic DMPs can be learned from demonstrations and applied to locomotion [43]. We learn the parameters of rhythmic DMPs from animal motion, followed by optimizing a subset of the parameters to improve imitation performance.
3. Model-Based Control for Motion Imitation
We present a motion imitation framework based on a model-based low-level controller that can generalize to different target motions. We assume that the reference motions are generated using kinematic motion retargeting with hand-designed keypoints that maps animal motions to the robot. Our framework consists of two steps. (1) Trajectory optimization using a simulated robot equipped with a model-based controller. (2) Transfer of the optimized trajectory to a real-world robot using a model-based low-level controller. The trajectory optimization is performed offline in simulation, and the optimized trajectory is zero-shot transferred to the robot, without fine-tuning. Figure 1 gives an overview of this.
3.1. Motion Retargeting
We use the retargeting technique described by Peng et al. [2] to map animal motions to an A1 robot. We select key-point pairs between animal and robot, followed by inverse kinematics and manual scaling.
3.2. Model-Based Controller
Our model-based controller consists of three components: (1) A stance controller that commands desired joint angles and torques on the stance legs, (2) a swing controller that commands desired joint angles on the swing legs, and (3) a gait planner switching the legs between swing and stance. The stance and swing controllers take retargeted trajectories as a reference and produce outputs based on the current and desired robot states. The gait planner takes into account the current and desired contact states to determine either swing or stance control per leg. Additionally, we develop an online adaptation scheme to enhance stability by modulating the reference motion according to the current state of the robot. Figure 2 gives an overview of our model-based controller.
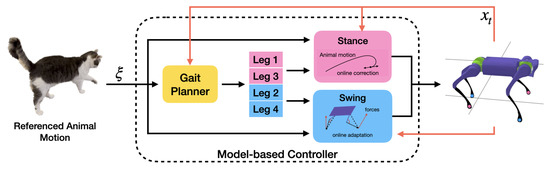
Figure 2.
An overview of our model-based controller which uses animal motions as desired trajectory input. The controller is composed of three components: a stance controller, a swing controller, and a gait planner.The stance controller plans contact force to command desired joint angles and torques on the stance legs. The swing controller commands desired joint angles on the swing legs to track the desired motion trajectory. Both the stance and swing controllers have an online adjustment module to stabilize the robot. The gait planner is responsible for switching the legs between swing and stance.
3.2.1. Gait Planner
The gait planner switches the control between swing and stance for each leg, based on the desired contact state, and the current contact state of the robot. The desired contact state is measured from the animal motion demonstration, whereas the current contact state is measured by foot sensors on the simulated/real A1 robot. If the measured vertical ground reaction force for leg i, where is the contact threshold, the leg is considered to be in stance.
Figure 3 shows the finite state machine (i.e., logic) used by our gait planner to determine the appropriate control mode for each leg. When the desired contact state deviates from the measured contact state, the gait planner initiates a transition from swing control to stance control or vice versa. For example, if the desired contact for leg i switches to swing from stance, the measured contact state would remain as stance for a short time. The gait planner detects this mismatched contact states and initiates swing on leg i. In situations such as early contact and early take-off, the current contact state can also deviate from the desired contact state. If the measured force on a swing leg is above the contact threshold while the desired state is swing, we detect early contact and start stance control on the leg. Similarly, if a stance leg leaves contact () when the desired state is in contact, we detect early take-off and switch the leg to swing control. Additionally, we add a minimum time of 100 ms between consecutive state switches to avoid the instability caused by noisy foot force measurements. This results in a robust gait planner, which generalizes across different quadrupedal gaits such as trotting, pacing and turning.
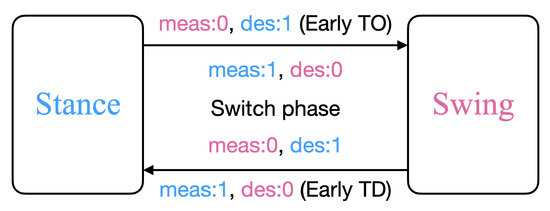
Figure 3.
Finite state machine used by the gait planner to switch leg control from swing (0) to stance (1) and vice versa. When the measured contact state deviates from the desired contact state, depending on the previous state of the leg, the gait planner initiates a switch from stance to swing, or vice versa. This also takes into account early touchdown (TD) and take off (TO). We additionally add a minimum time limit of 100 ms between consecutive switches to avoid instability due to measurement noise.
3.2.2. Stance Controller
The stance controller uses a linearized centroidal dynamics model to reason about robot CoM motion, similar to [5]: where is the inverse inertia matrix of the robot (calculated from the robot’s model), is the measured contact force on the stance legs, and is the gravity vector. We use to denote the six-dimensional CoM acceleration, consisting of both position and orientation terms in the world frame.
First, we calculate a desired CoM acceleration as , where are the desired CoM position and velocity from the reference motion that the robot is following, respectively, are the measured CoM position and velocity, and , are feedback gains, which are tuned in advance and kept fixed for all reference motions. Next, we formulate a Quadratic Program (QP) to solve for the desired instantaneous contact forces that can achieve subject to friction constraints, and the current contact state of the robot:
where are weight matrices, kept fixed for all motions. is the contact force on leg in global coordinates. is an assumed friction coefficient, and the last two constraints ensure that the robot does not violate an approximation of friction cone when in contact with the ground. is zero for legs in swing, and higher than a contact threshold for legs in stance. The QP returns desired contact forces that are converted to desired leg torques for stance legs using the leg Jacobian: , where is the rotation matrix that transforms from body to world.
Online adaptation: The above model-based controller is borrowed from [5]. During our experiments, we observed that this controller does not robustly track a wide range of target motions, especially when the target motion is dynamic or violates linearized centroidal model assumptions, which could happen frequently for motions obtained from real animals. In such cases, the controller parameters need to be tuned per reference motion to avoid instabilities. This requires expert intervention and is not scalable to large varieties of motions. Instead, we augment the stance controller with online adaptation to improve the overall robustness of the model-based controller, allowing the same parameters to generalize to different motions.
A common failure case for the robot is caused by poor CoM tracking. For example, if the CoM height is lower than desired, the swing legs might hit the ground early, causing instability. However, ‘tolerance’ to CoM tracking error is highly motion dependent, making feedback gains on CoM acceleration hard to design. To improve CoM height tracking across all motions, without requiring motion-specific tuning, we add low-gain joint position feedback to the stance legs. Specifically, at each time step t, we first estimate the foot position of stance leg i at the next time step , given the desired CoM velocity:
Here, is the stance foot location of the i-th leg at time t in the robot frame, is the desired CoM velocity in the robot frame, is the estimated foot location at the next time, and is the control frequency. In the robot frame, the stance foot moves with the inverse of the local CoM velocity; hence, the velocity of the stance foot is . Euler integration results in Equation (2). Next, we use inverse kinematics to find the corresponding joint angles per stance leg, and use low-gain position feedback on these desired positions.
Intuitively, Equation (2) estimates the future joint angles that the robot would end up in, if it followed the desired CoM velocity at the current time step. An alternative approach to determining desired joint angles for stance legs could be to use the joint angles from the reference motion directly. However, these might not be feasible on the robot at execution time. For example, if the foot configuration at the start of stance is different from the reference due to early touchdown, leg angles throughout the stance phase will be different from the reference motion. Accurately following the joint angles from the reference would require a leg to break contact and re-positioning of the foot. Instead, by using Equation (2) we can follow the CoM trajectory in stance without requiring very close correspondence between the reference and actual leg joint angles in stance. This online adaptation improves the robustness of the model-based controller and allows it to follow different animal motions using the same parameters.
3.2.3. Swing Controller
Swing foot trajectory is an important part determining the motion ‘style’ and has been shown to be distinct for different animal gaits [44]. Hence, following the swing foot motion as closely as possible is crucial for realistic motion imitation of different animal gaits.
Online adaptation: The reference motion trajectory basically does not change when the robot operates. However, feedback during swing foot placement can be important for disturbance rejection and increasing stability of legged robots [45]. Therefore, we also add online adaptation to the swing foot position to increase robot stability, especially against real-world disturbances such as early touchdown, while mimicking the original style of the animal motion as closely as possible.
The target foot position of swing leg i consists of the reference motion and feedback on the desired CoM velocity in the robot frame:
Here, K is a constant gain term and here, we take K = 0.2. The feedback term resembles a Raibert [13] stepping policy and adds a disturbance rejection mechanism to the purely feed-forward animal reference motion. For example, if the CoM velocity is higher that in the demonstration due to a disturbance, the swing trajectory compensates by stepping outwards and stabilizing the robot, while maintaining the overall style of the animal motion through . Finally, we use inverse kinematics per leg to convert the desired foot position from robot frame to joint angles and follow this joint trajectory using position control.
3.3. Trajectory Optimization with DMPs
Reference trajectories from animal motions might not be dynamically feasible for the robot, or might violate some assumptions of our model-based controller. For example, our controller assumes that the stance foot does not slip, but some animal motions might include feet sliding on the ground, making them infeasible for our model. Additionally, naively mimicking animal motion might not result in high-performing motion, due to the dynamical mismatch between robots and animals. Changing (i.e., optimizing) input reference motions as a way to resolve this inconsistency would provide better robot performance. The question arises: what is an ideal way to represent input motions and how can we modify them efficiently while maintaining the style of the original demonstration?
We choose a dynamic movement primitive (DMP) parametrization to represent swing trajectories. DMPs are trajectory generators that combine linear fixed-point attractors with function approximators whose parameters can be learned from demonstrations. We refer to Ijspeert et al. [11] for an overview of DMPs; a demonstration , which comes from the retargeted animal motion in our case, is represented by learning parameters : . Weights are weights of the non-linear function approximator and encode the overall style of the motion, while g represents the start point of the DMP and a is its amplitude. Specifically, we use rhythmic DMPs which encode cyclic motions whose time period, amplitude, and start point can be modulated by changing the parameters of the DMP. We learn separate for each dimension of the reference trajectory , using 100 basis functions per DMP. Reference motions include the CoM position in six dimensions, CoM linear and angular velocity, and swing foot trajectory in three dimensions for four legs (a total of 24 DMPs). DMPs are initialized to mimic the animal motion and then sent as a reference motion to a model-based controller in simulation.
Once DMPs are learned, their parameters are optimized to improve robot performance. More specifically, we maximize the cumulative reward of the resultant trajectory in simulation (reward described in Section 4.1). Note that we optimize only while keeping fixed to maintain the original style of the animal motion during trajectory optimization. Section 4.2 shows an example of a swing foot trajectory modified by the optimization. We use a gradient-free optimization method CMA-ES [12] to optimize the of the DMPs that represent the z-motion of swing trajectories of all 4 legs. This leads to an 8-dimensional optimization where the swing retraction (g), and amplitude (a) is optimized to maximize episodic reward: , where T is the total length of an episode, and is the step reward, detailed in Section 4.1. We optimize the DMP parameters over 200 iterations of CMA-ES taking about 50 min in simulation.
Because our offline whole-body trajectory optimization procedure takes the full dynamics of the robot, including contacts, into account to improve the reference motion, the optimized trajectory can successfully be transferred to hardware without any fine-tuning. Including domain randomization techniques can further improve the robustness of the optimized trajectory, but we leave this for future work.
4. Experiment
We evaluate our method by imitating four animal motions: trot, pace, turn, and side-step. The motion data, found publicly in the work of Zhang et al. [46], is pre-processed using the retargeting procedure (Section 3.1) to map the animal motion to an A1 robot. The target motions can be seen in Figure 1 and the Supplemental Video. Our experiments are conducted in a PyBullet simulation [47] and on hardware, with an A1 quadruped from Unitree Robotics [14] (Figure 1). A1 is a four-legged robot with three servos on each leg. It has four force sensors placed on each foot that can measure ground reaction forces, along with joint position, velocity, and torque sensors. The robot’s position is estimated using onboard IMU and kinematic filtering adapted from open-source code [2].
Our experiments show that our method can mimic the desired animal motions in simulations, and the optimized trajectory can be zero-shot transferred to hardware. We also present comparisons to RL-based approaches from the literature, which learn one policy per motion, and compare the performances in both simulation and on hardware. Additionally, we compare against variants of model-based control [15] without trajectory optimization. These experiments help us to understand how the different components in our method contribute to the robustness that we achieved.
4.1. Reward Function
We use the same reward function as Peng et al. [2] when training baseline RL policies and measuring overall performance. The per-step reward is
Individual components are:
- Joint pose reward ,
- Joint velocity reward ,
- End-effector reward ,
- CoM position reward ,
- CoM velocity reward .
Here, and stand for the desired and current joint positions, and are the desired and current joint velocities, represents the current foot position, and denote the CoM linear position and velocity, and are the CoM angular position and velocity. The higher the reward, the closer the robot motion is to the demonstration. A general intuition for tuning the weights is that for slow motion and less dynamical motion, increase the ratio of joint tracking for better joint level tracking, while for agile motions we can increase the ratio of root tracking to prevent the optimization process stacking in local optimal with relatively high joint level tracking but a short survival time.
4.2. Comparison Experiments
Here, we describe the different approaches compared in our paper. The baselines are chosen to highlight the robustness of a unified model-based controller, and the efficacy of our approach (MBC-DMP) at mimicking animal motions. Note that all model-based controller baselines also use the online adaptations described in Section 3.2, which was essential to get robust performance across the four motions considered in our experiments.
- DeepMimic (RL): We compare our approach against DeepMimic [1], a learning-based approach that learns an RL policy per reference motion. We use the reward function described in Section 4.1 and train each policy for 100 million simulation steps using Proximal Policy Optimization [48]. We use the open-source implementation to train policies for trot, pace, turn, and side-step motions. For each target motion, we train two RL policies with different random seeds and report average performance in Figure 4. We apply policies learned in simulation to hardware with no fine-tuning to make the comparison fair to our approach.
- Model-based Controller with Raibert Swing (Raibert): Next, we compare our method against a model-based method from Kang et al. [15] which uses animal reference for CoM motion, but uses linear swing trajectories of fixed time length that reach a footstep calculated using the Raibert heuristic: . Compared to Equation (3), we note that this method does not take the animal motion into account, while our approach augments the animal motion with a stabilizing feedback mechanism. Because each gait has unique swing foot motion style, using pre-defined swing trajectories could cause difficulties when reproducing natural and diverse motion styles.
- Model-based Controller (MBC): In this baseline, we send the animal motion trajectories to our model-based controller without any trajectory optimization. This experiment highlights the importance of whole-body trajectory optimization in simulation.
- Model-based Controller with DMP Optimization (MBC-DMP, ours): Our approach, which uses offline trajectory optimization to adapt the reference motion sent to the model-based controller.
- Long horizon Model-predictive control (LH): Whole-body control of quadrupedal robots can be improved by using a receding-horizon model predictive control approach that plans over multiple time steps, instead of instantaneous forces, as in Equation (1). We utilize the approach from Di et al. [5] to solve a higher-order QP to plan actions over a horizon of 10 steps, instead of a single step. During stance, this long-horizon convex MPC controller uses the linearized centroidal model to predict future states, and plans a sequence of contact forces that lead to a desired CoM trajectory. For swing control, we use the same setup as ours. This experiment aims to test if online MPC can replace offline trajectory optimization.
- Long horizon MPC with DMP Optimization (LH-DMP): Lastly, we augment the long horizon model-predictive control (LH) with our DMP-based trajectory optimization (LH-DMP). We expect that this method outperforms our method because it reasons over a longer horizon of the reference motion. However, both long-horizon predictive control methods, LH and LH-DMP, cannot easily be deployed to hardware due to their expensive computational costs. Therefore, we only conduct simulation experiments for analysis.
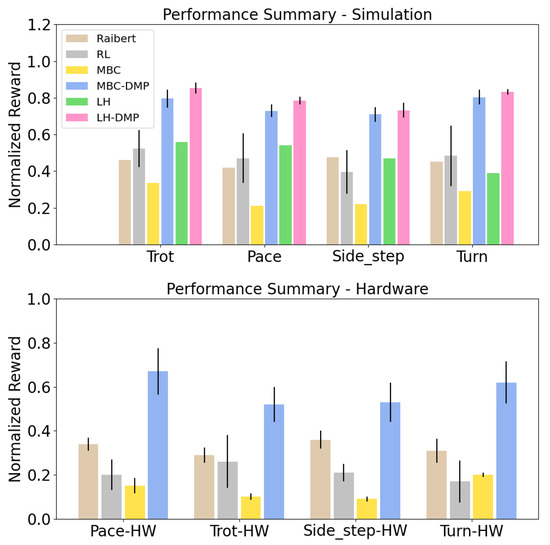
Figure 4.
Comparison against other baselines. Our method (MBC-DMP) outperforms other learning-based (RL) or model-based (Raibert, RL, MBC, LH) in simulation and on hardware, except for LH-DMP. Note that the methods with long-horizon predictions, LH and LH-DMP, cannot easily be deployed to hardware due to their computational costs.
Figure 4 shows comparison experiments between the different baseline approaches and our approach (MBC-DMP). In simulation, we observe that DeepMimic (RL) is able to replicate all target motions well. However, when transferred to hardware, we see a significant drop in performance, owing to the sim-to-real gap (e.g., in sim vs. on hardware for turn). We observe that RL policies tend to be very conservative and do not lift the robot legs sufficiently during swing. This causes early contact with hardware, which degrades the performance of the real robot. Peng et al. [2] show that online adaptation can improve the performance of RL on hardware. In contrast, our method can be generalized to hardware with no real-world adaptation.
Model-based control with no trajectory optimization (MBC) achieves good performance in pace and trot, but poor performance in side-step and turn in simulation (e.g., using MBC vs. using our approach for turn). In side-step and turn, the robot falls over due to low swing leg retraction and early contact, increasing the disturbance on the system. When applied to the real robot, the pace and trot motions also deteriorate in performance. As an example, Figure 5 shows the tracking of the left back leg during a pace motion in simulation. The x-tracking of the foot deviates from the reference during swing, made worse on hardware due to tracking errors. Although online adaptation of the model-based controller manages to maintain robot stability, the overall imitation reward is very low. On the other hand, our approach learns to optimize the swing leg retraction in simulation, also improving performance on hardware.
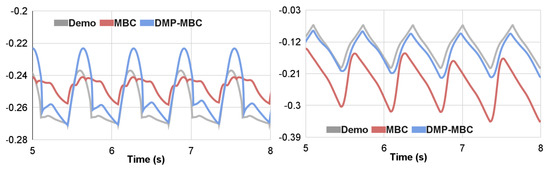
Figure 5.
(Left) Tracking in z-axis. DMP optimization increased the amplitude of the trajectory. Tracking error was decreased by 24%. (Right) Tracking in x-axis. With optimization, the constant drift was reduced. Tracking error was decreased by 92%.
The model-based baseline Raibert achieves a lower performance than our approach on all gaits, with a turning motion seeing the largest drop in simulation ( vs. ). Turning is a challenging motion, with robot legs stretching outwards, more in the rear legs and less so in the front legs. If the swing leg trajectories are designed to be symmetric across all legs, as in [15], not only is the swing motion not natural, but also the CoM turning motion does not follow the reference. This experiment highlights the importance of following both reference (animal) swing and stance motions to generate natural motions. Due to the robustness of Raibert swing trajectories combined with our model-based controller, Raibert does not experience a significant performance drop between sim and real, but the overall performance is still lower than our approach.
Our approach (MBC-DMP) outperforms all RL- and model-based baselines that plan instantaneous actions in simulation and on hardware. The DMP optimization improves motion tracking in simulation, and also generalizes to hardware with little performance deterioration in most gaits (Figure 4). Figure 5 compares the optimized vertical foot motion with the original trajectory of the back left leg in a pace gait, where the optimization increases the leg clearance for swing trajectory, improving tracking and stability. Figure 6 shows that the optimized DMP reference trajectory achieves good hardware performance for challenging motions such as turning ( in sim vs. on hardware). In the side-step motion, we observe deterioration in performance on hardware due to slipping. Side-step requires a wide robot stance, which affects the leg configuration at the edge of the friction cone, making it easy for the robot to slip. Since we do not carry out any system identification on the actual friction of the floor, the model-based controller is unable to compensate for the slippery floor. We believe that this behavior can be improved by real-world fine-tuning, which can be very efficient as once the friction coefficient is identified, it can be used for all motions.

Figure 6.
Snapshots of our approach in action on the A1 robot—Turn, Trot, Pace and Side-stepping motions. A model-based controller with online adaptation achieves all the motions, with no fine-tuning.
The hypothesis that offline trajectory optimization is not needed if planning over a long horizon is disproved in our experiments. Despite using a longer horizon, and online adaptation, long-horizon MPC (LH) performs worse than our approach on all simulated tasks ( using LH vs. using our approach for a turn). On the other hand, when the reference trajectory sent to long-horizon MPC is optimized using our DMP parametrization (LH-DMP), we see that there is a rise in performance. This further reinforces that even with long horizon planning, offline trajectory optimization is crucial for robust mimicking of varied animal motions. As compared to long-horizon MPC (LH-DMP), we observe that the loss in performance is minor when using instantaneous optimization ( using LH-DMP versus using MBC-DMP on turn.) This motivated our decision to perform hardware experiments using an instantaneous QP and leave real-world evaluation of costly LH-DMP for future work.
4.3. Motion Stitching
We create new motions by stitching different motion trajectories to verify that our method can be used for imitating very long motions. The stitched motions are created by directly concatenating individual reference motions , for example by concatenating pacing and trotting trajectories. However, these stitched trajectories cannot be directly tracked by the model-based controller since the transition between the motions is not smooth. Therefore, we first fit each elementary motion ξi independently with DMPs. Then, we optimize all DMPs together with respect to the reward function mentioned in Section 4.1. To warm start the optimization, we initialize the DMPs with the parameters for individual optimized motion. Our method successfully imitates four stitched motions: (1) Pace + Trot, (2) Trot + Turn + Trot, (3) Side Step + Trot + Turn, and (4) Trot + Side Step + Reverse trot. Real-world results can be seen in the Supplementary Video.
5. Conclusions
In this work, we propose a unified framework for transferring agile animal motions to real-world robots. Our framework uses trajectory optimization and a model-based controller with online adaptation. Experiments show that our framework can imitate reference motions robustly. We validate our framework by applying our framework to four motions in simulation and hardware. We compare our approach with learning-based and model-based baselines. In our study, we evaluate our approach against learning-based and model-based baselines. Our findings demonstrate that our method achieves superior performance compared to the baseline methods in both simulation and on the real-world A1 robot. Specifically, in simulation, the averaged reward for the learning-based baseline, model-based baseline, and our method were 0.467, 0.451, and 0.800, respectively. Similarly, for the real-world A1 robot, the averaged rewards for the learning-based baseline, model-based baseline, and our method were 0.210, 0.325, and 0.585, respectively. Although our method delivers impressive results, it lacks sim2real adaptation, which could potentially hinder its effectiveness when deploying motions on an actual robot. This limitation is evident in the shaky motion observed in the ‘side-step’ task. In the future, our plan is to incorporate sim2real techniques into our approach to improve its performance in real-world scenarios. Furthermore, we are enthusiastic about exploring the combination of our method with other learning-based approaches to acquire more dynamic motions, including backflips and jumping motions.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/robotics12030090/s1, Video S1: FastMimic: Model-Based Motion Imitation for Agile, Diverse and Generalizable Quadrupedal Locomotion
Author Contributions
The authors contributed to the paper in the following ways: conceptualization, T.L., A.R. and J.C.; software, T.L.; methodology, T.L. and A.R.; formal analysis, T.L. and J.W.; project administration, S.H. and A.R.; writing–original draft preparation, T.L.; writing–review and editing, J.W., S.H. and A.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by Meta Inc.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Peng, X.B.; Abbeel, P.; Levine, S.; van de Panne, M. Deepmimic: Example-guided deep reinforcement learning of physics-based character skills. ACM Trans. Graph. (TOG) 2018, 37, 143. [Google Scholar] [CrossRef]
- Peng, X.B.; Coumans, E.; Zhang, T.; Lee, T.W.; Tan, J.; Levine, S. Learning agile robotic locomotion skills by imitating animals. arXiv 2020, arXiv:2004.00784. [Google Scholar]
- Park, H.W.; Wensing, P.M.; Kim, S. High-speed bounding with the MIT Cheetah 2: Control design and experiments. Int. J. Robot. Res. 2017, 36, 167–192. [Google Scholar] [CrossRef]
- Bledt, G.; Powell, M.J.; Katz, B.; Di Carlo, J.; Wensing, P.M.; Kim, S. MIT Cheetah 3: Design and control of a robust, dynamic quadruped robot. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 2245–2252. [Google Scholar]
- Di Carlo, J.; Wensing, P.M.; Katz, B.; Bledt, G.; Kim, S. Dynamic locomotion in the mit cheetah 3 through convex model-predictive control. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1–9. [Google Scholar]
- Park, S.; Ryu, H.; Lee, S.; Lee, S.; Lee, J. Learning Predict-and-simulate Policies from Unorganized Human Motion Data. ACM Trans. Graph. (TOG) 2019, 38, 205. [Google Scholar] [CrossRef]
- Bergamin, K.; Clavet, S.; Holden, D.; Forbes, J.R. DReCon: Data-driven Responsive Control of Physics-based Characters. ACM Trans. Graph. (TOG) 2019, 38, 206. [Google Scholar] [CrossRef]
- Won, J.; Gopinath, D.; Hodgins, J. A scalable approach to control diverse behaviors for physically simulated characters. ACM Trans. Graph. (TOG) 2020, 39, 33. [Google Scholar] [CrossRef]
- Fussell, L.; Bergamin, K.; Holden, D. SuperTrack: Motion tracking for physically simulated characters using supervised learning. ACM Trans. Graph. (TOG) 2021, 40, 197. [Google Scholar] [CrossRef]
- Holden, D.; Komura, T.; Saito, J. Phase-functioned neural networks for character control. ACM Trans. Graph. (TOG) 2017, 36, 42. [Google Scholar] [CrossRef]
- Ijspeert, A.J.; Nakanishi, J.; Hoffmann, H.; Pastor, P.; Schaal, S. Dynamical movement primitives: Learning attractor models for motor behaviors. Neural Comput. 2013, 25, 328–373. [Google Scholar] [CrossRef]
- Hansen, N. The CMA evolution strategy: A comparing review. Towards a New Evolutionary Computation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; pp. 75–102. [Google Scholar]
- Raibert, M.H. Legged Robots That Balance; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Unitree Robotics. Available online: http://www.unitree.cc/ (accessed on 3 March 2023).
- Kang, D.; Zimmermann, S.; Coros, S. Animal Gaits on Quadrupedal Robots Using Motion Matching and Model Based Control. In Proceedings of the IROS, Prague, Czech Republic, 27 September–1 October 2021. [Google Scholar]
- Won, J.; Lee, J. Learning Body Shape Variation in Physics-based Characters. ACM Trans. Graph. (TOG) 2019, 38. [Google Scholar] [CrossRef]
- Merel, J.; Tassa, Y.; TB, D.; Srinivasan, S.; Lemmon, J.; Wang, Z.; Wayne, G.; Heess, N. Learning human behaviors from motion capture by adversarial imitation. arXiv 2017, arXiv:1707.02201. [Google Scholar]
- Merel, J.; Hasenclever, L.; Galashov, A.; Ahuja, A.; Pham, V.; Wayne, G.; Teh, Y.W.; Heess, N. Neural Probabilistic Motor Primitives for Humanoid Control. In Proceedings of the ICLR, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Xie, Z.; Berseth, G.; Clary, P.; Hurst, J.; van de Panne, M. Feedback Control for Cassie with Deep Reinforcement Learning. In Proceedings of the IROS, Madrid, Spain, 1–5 October 2018. [Google Scholar]
- Luo, Y.S.; Soeseno, J.H.; Chen, T.P.C.; Chen, W.C. CARL: Controllable Agent with Reinforcement Learning for Quadruped Locomotion. ACM Trans. Graph. (TOG) 2020, 39, 38. [Google Scholar] [CrossRef]
- Exarchos, I.; Jiang, Y.; Yu, W.; Liu, C.K. Policy Transfer via Kinematic Domain Randomization and Adaptation. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021. [Google Scholar]
- Schwind, W.J. Spring Loaded Inverted Pendulum Running: A Plant Model; University of Michigan: Ann Arbor, MI, USA, 1998. [Google Scholar]
- Green, K.; Godse, Y.; Dao, J.; Hatton, R.L.; Fern, A.; Hurst, J. Learning Spring Mass Locomotion: Guiding Policies with a Reduced-Order Model. IEEE RAL 2021, 6, 3926–3932. [Google Scholar] [CrossRef]
- Gong, Y.; Grizzle, J. Angular momentum about the contact point for control of bipedal locomotion: Validation in a lip-based controller. arXiv 2020, arXiv:2008.10763. [Google Scholar]
- Li, T.; Geyer, H.; Atkeson, C.G.; Rai, A. Using deep reinforcement learning to learn high-level policies on the atrias biped. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA 2019), Montreal, QC, Canada, 20–24 May 2019; pp. 263–269. [Google Scholar]
- Kim, D.; Di Carlo, J.; Katz, B.; Bledt, G.; Kim, S. Highly dynamic quadruped locomotion via whole-body impulse control and model predictive control. arXiv 2019, arXiv:1909.06586. [Google Scholar]
- Xie, Z.; Da, X.; Babich, B.; Garg, A.; van de Panne, M. GLiDE: Generalizable Quadrupedal Locomotion in Diverse Environments with a Centroidal Model. arXiv 2021, arXiv:2104.09771. [Google Scholar]
- Da, X.; Xie, Z.; Hoeller, D.; Boots, B.; Anandkumar, A.; Zhu, Y.; Babich, B.; Garg, A. Learning a contact-adaptive controller for robust, efficient legged locomotion. arXiv 2020, arXiv:2009.10019. [Google Scholar]
- Li, T.; Calandra, R.; Pathak, D.; Tian, Y.; Meier, F.; Rai, A. Planning in Learned Latent Action Spaces for Generalizable Legged Locomotion. IEEE Robot. Autom. Lett. 2021, 6, 2682–2689. [Google Scholar] [CrossRef]
- Kormushev, P.; Calinon, S.; Caldwell, D.G. Robot motor skill coordination with EM-based reinforcement learning. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 3232–3237. [Google Scholar]
- Mülling, K.; Kober, J.; Kroemer, O.; Peters, J. Learning to select and generalize striking movements in robot table tennis. Int. J. Robot. Res. 2013, 32, 263–279. [Google Scholar] [CrossRef]
- Ude, A.; Gams, A.; Asfour, T.; Morimoto, J. Task-specific generalization of discrete and periodic dynamic movement primitives. IEEE Trans. Robot. 2010, 26, 800–815. [Google Scholar] [CrossRef]
- Conkey, A.; Hermans, T. Active learning of probabilistic movement primitives. In Proceedings of the Humanoids, Toronto, ON, Canada, 15–17 October 2019; pp. 1–8. [Google Scholar]
- Kober, J.; Peters, J. Learning motor primitives for robotics. In Proceedings of the ICRA, Paris, France, 7–10 December 2009; pp. 2112–2118. [Google Scholar]
- Pastor, P.; Kalakrishnan, M.; Chitta, S.; Theodorou, E.; Schaal, S. Skill learning and task outcome prediction for manipulation. In Proceedings of the Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 3828–3834. [Google Scholar]
- Rai, A.; Sutanto, G.; Schaal, S.; Meier, F. Learning feedback terms for reactive planning and control. In Proceedings of the Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 2184–2191. [Google Scholar]
- Stulp, F.; Sigaud, O. Path integral policy improvement with covariance matrix adaptation. arXiv 2012, arXiv:1206.4621. [Google Scholar]
- Bahl, S.; Mukadam, M.; Gupta, A.; Pathak, D. Neural dynamic policies for end-to-end sensorimotor learning. arXiv 2020, arXiv:2012.02788. [Google Scholar]
- Jalics, L.; Hemami, H.; Zheng, Y.F. Pattern generation using coupled oscillators for robotic and biorobotic adaptive periodic movement. In Proceedings of the Robotics and Automation (ICRA), Albuquerque, NW, USA, 20–25 April 1997. [Google Scholar]
- Kajita, S.; Kanehiro, F.; Kaneko, K.; Fujiwara, K.; Yokoi, K.; Hirukawa, H. A realtime pattern generator for biped walking. In Proceedings of the Robotics and Automation (ICRA), Washington, DC, USA, 11–15 May 2002; Volume 1, pp. 31–37. [Google Scholar]
- Yang, J.F.; Lam, T.; Pang, M.Y.; Lamont, E.; Musselman, K.; Seinen, E. Infant stepping: A window to the behaviour of the human pattern generator for walking. Can. J. Physiol. Pharmacol. 2004, 82, 662–674. [Google Scholar] [CrossRef]
- Ijspeert, A.J. Central pattern generators for locomotion control in animals and robots: A review. Neural Netw. 2008, 21, 642–653. [Google Scholar] [CrossRef]
- Rosado, J.; Silva, F.; Santos, V. Adaptation of Robot Locomotion Patterns with Dynamic Movement Primitives. In Proceedings of the 2015 IEEE International Conference on Autonomous Robot Systems and Competitions, Vila Real, Portugal, 8–10 April 2015; pp. 23–28. [Google Scholar] [CrossRef]
- Schaller, N.U.; Herkner, B.; Villa, R.; Aerts, P. The intertarsal joint of the ostrich (Struthio camelus): Anatomical examination and function of passive structures in locomotion. J. Anat. 2009, 214, 830–847. [Google Scholar] [CrossRef] [PubMed]
- Wu, A.; Geyer, H. The 3-D spring–mass model reveals a time-based deadbeat control for highly robust running and steering in uncertain environments. IEEE TRO 2013, 29, 1114–1124. [Google Scholar] [CrossRef]
- Zhang, H.; Starke, S.; Komura, T.; Saito, J. Mode-adaptive neural networks for quadruped motion control. ACM Trans. Graph. (TOG) 2018, 37, 145. [Google Scholar] [CrossRef]
- Coumans, E.; Bai, Y. PyBullet. 2016–2019. Available online: http://pybullet.org (accessed on 3 March 2023).
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).