A Study of Energy-Efficient and Optimal Locomotion in a Pneumatic Artificial Muscle-Driven Snake Robot
Abstract
1. Introduction
2. Materials and Methods
2.1. Kinematic-Based Design Optimization
2.2. Muscle-Driven Snake Locomotion Control: Algorithms and Hardware
2.3. Energy Efficiency
- Efficiency of a single pneumatic artificial muscle;
- Efficiency of a single 2-link module;
- Cost of transportation of the entire system.
2.3.1. Energy Efficiency of Single Artificial Muscle
2.3.2. Energy Efficiency of a Single Muscle-Driven Module
2.3.3. Energy Efficiency of 6-Link Mechanism
2.4. Power Consumption
3. Results and Discussion
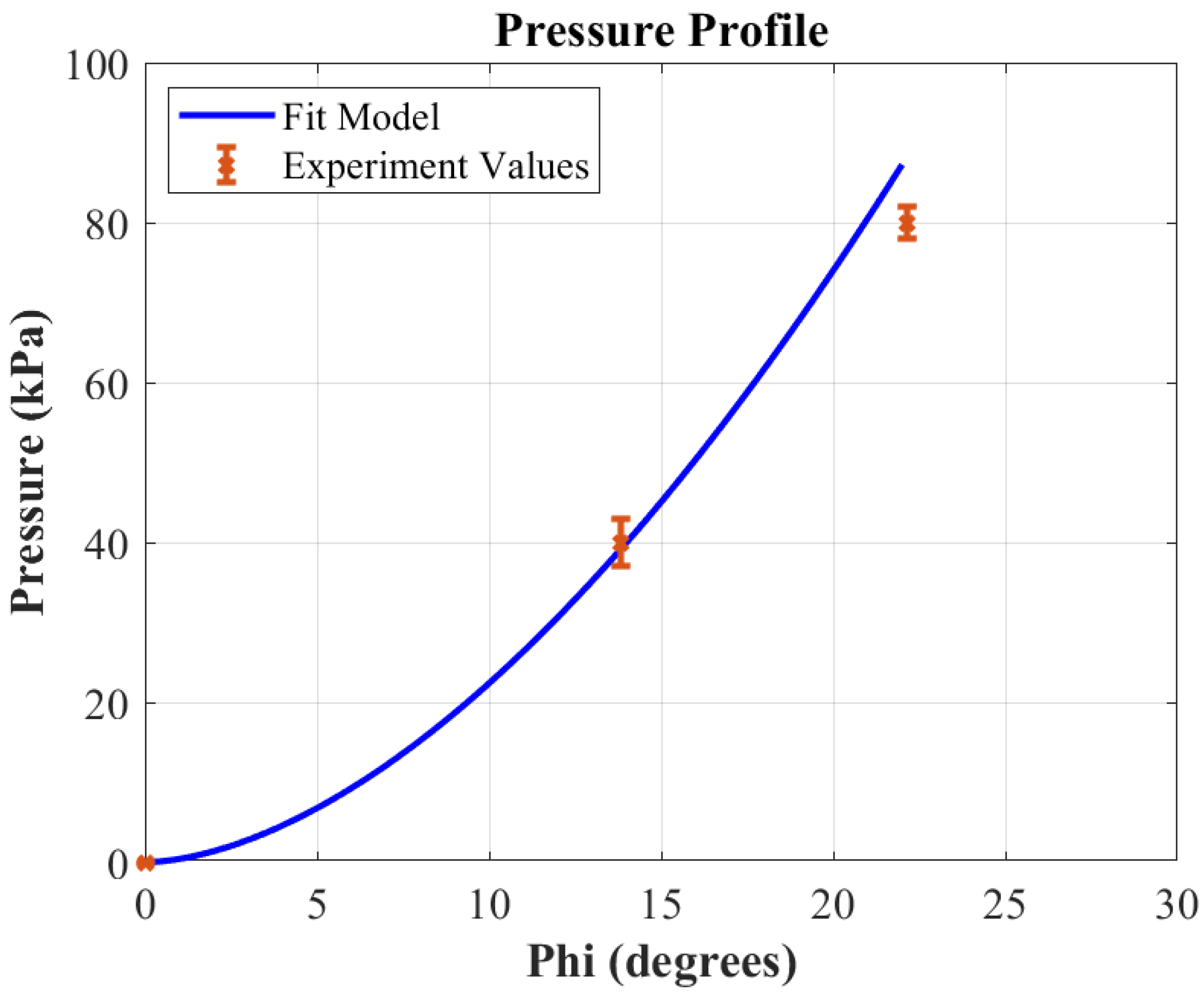
3.1. Design Optimization
3.2. Energy Efficiency
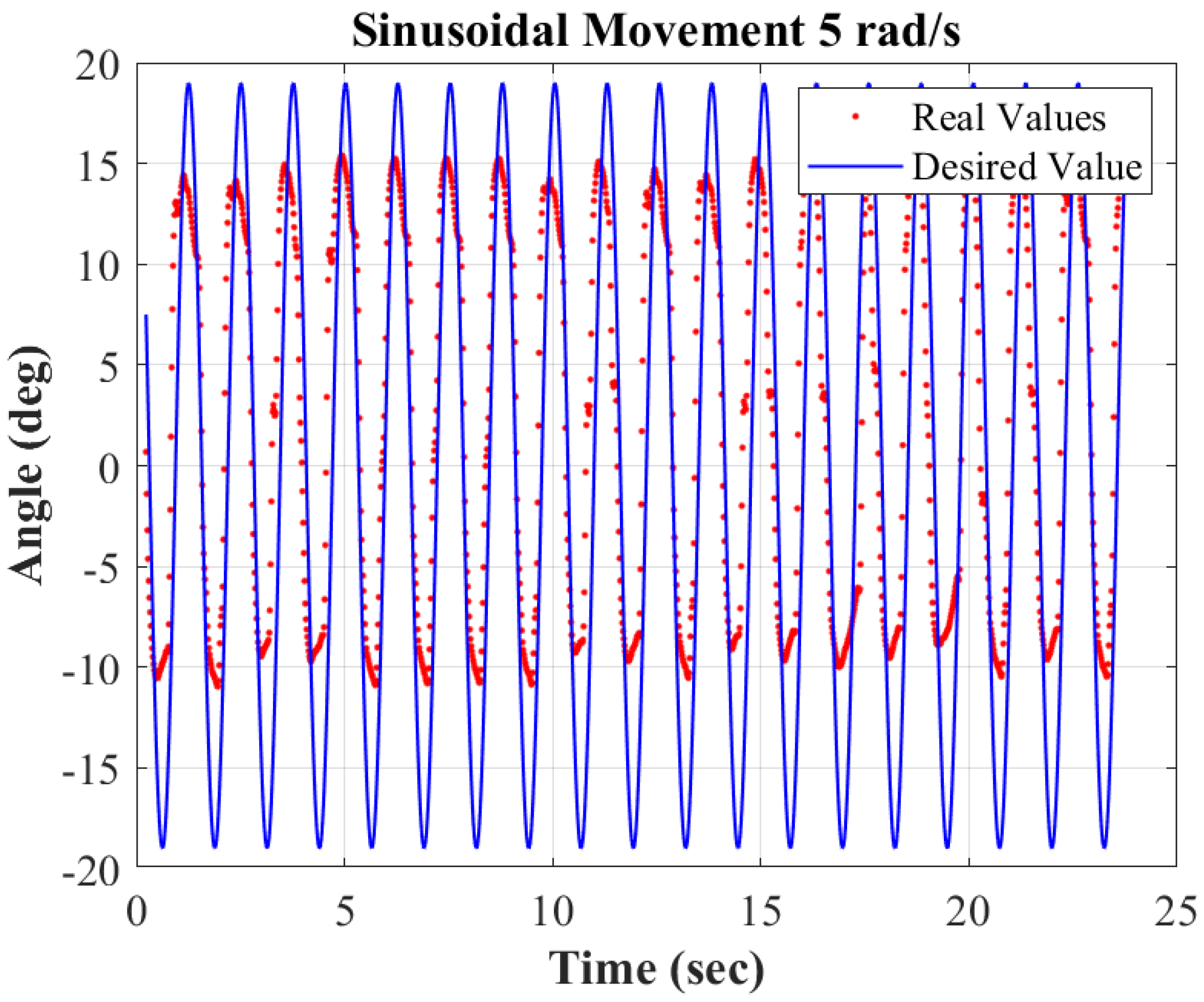
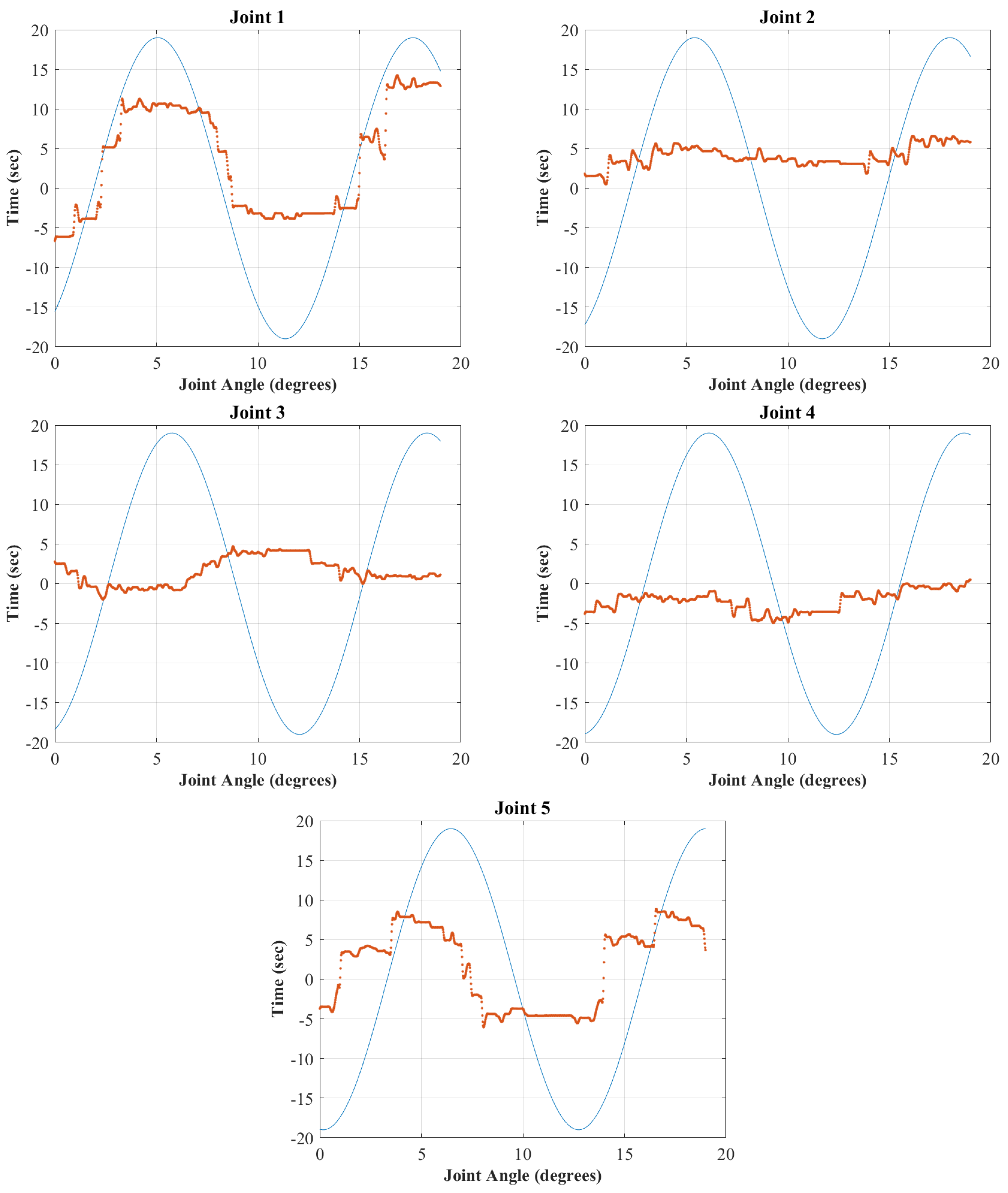
3.3. Control Test Results
3.4. The 6-Link Snake Robot Movement
3.5. Cost of Transportation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PAM | Pneumatic Artificial Muscle |
| COT | Cost of Transportation |
| 3D | 3-Dimensions |
| psi | pound per squared inch |
| PWM | Pulse Width Modulation |
Appendix A. The Length, Force, Torque, and Power Results of the Muscles
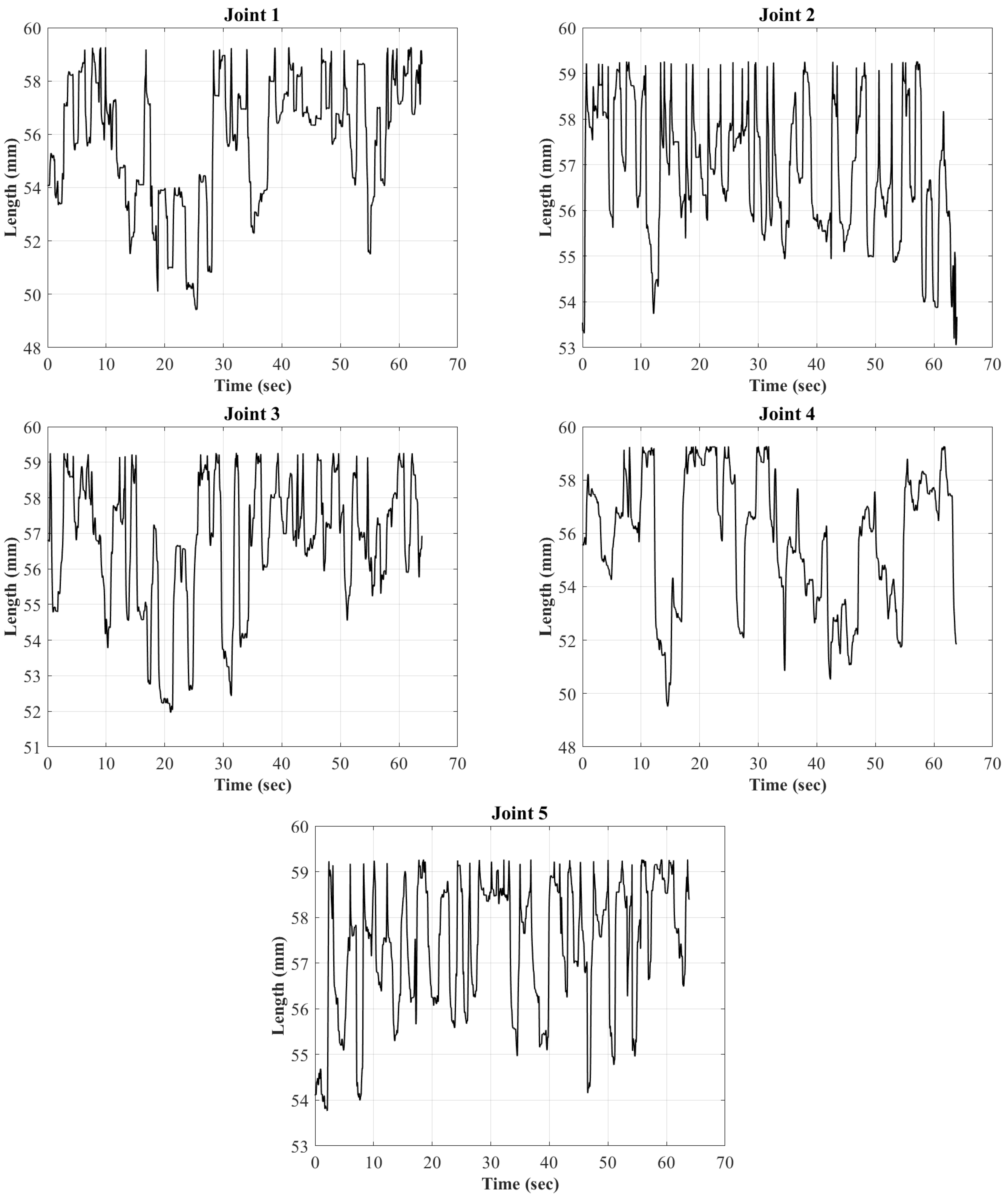
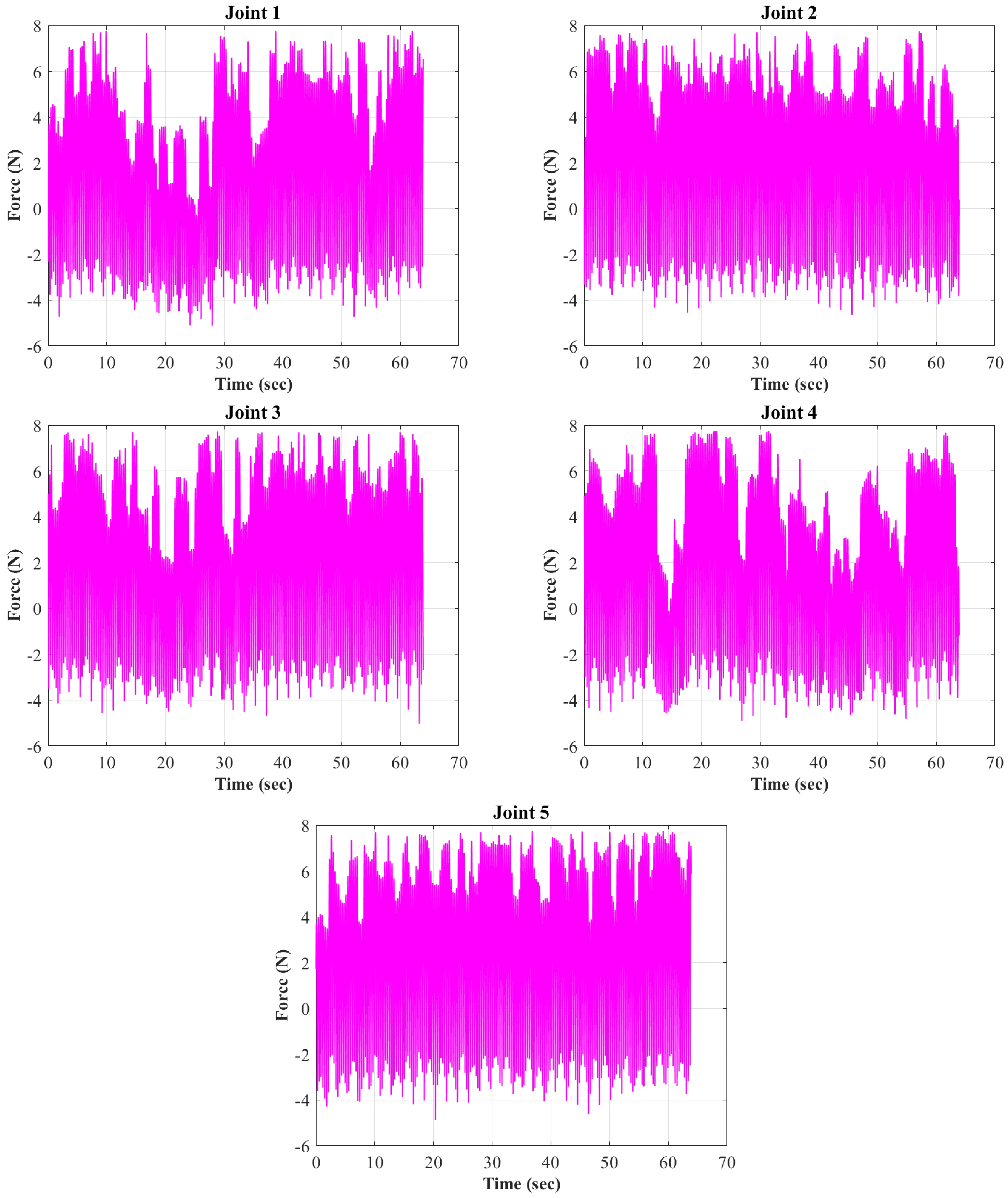


References
- Pettersen, K.Y. Snake robots. Annu. Rev. Control 2017, 44, 19–44. [Google Scholar] [CrossRef]
- Gray, J. The mechanism of locomotion in snakes. J. Exp. Biol. 1946, 23, 101–120. [Google Scholar] [CrossRef] [PubMed]
- Jayne, B.C. Muscular mechanisms of snake locomotion: An electromyographic study of the sidewinding and concertina modes of Crotalus cerastes, Nerodia fasciata and Elaphe obsoleta. J. Exp. Biol. 1988, 140, 1–33. [Google Scholar] [CrossRef] [PubMed]
- Jayne, B.C. Muscular mechanisms of snake locomotion: An electromyographic study of lateral undulation of the Florida banded water snake (Nerodia fasciata) and the yellow rat snake (Elaphe obsoleta). J. Morphol. 1988, 197, 159–181. [Google Scholar] [CrossRef]
- Hirose, S. Biologically Inspired Robots; Oxford Science Publications: Oxford, UK, 1993. [Google Scholar]
- Hirose, S.; Yamada, H. Snake-like robots [Tutorial]. IEEE Robot. Autom. Mag. 2009, 16, 88–98. [Google Scholar] [CrossRef]
- Dowling, K.J. Limbless Locomotion; Carnegie Mellon University: Pittsburgh, PA, USA, 1997. [Google Scholar]
- Rezapour, E.; Pettersen, K.Y.; Liljeback, P.; Gravdahl, J.T.; Kelasidi, E. Path following control of planar snake robots using virtual holonomic constraints: Theory and experiments. Robot. Biomim. 2014, 1, 3. [Google Scholar] [CrossRef]
- Liljebäck, P.; Pettersen, K.Y.; Stavdahl, O.; Gravdahl, J.T. Experimental Investigation of Obstacle-Aided Locomotion with a Snake Robot. IEEE Trans. Robot. 2011, 27, 792–800. [Google Scholar] [CrossRef]
- Rollinson, D.; Bilgen, Y.; Brown, B.; Enner, F.; Ford, S.; Layton, C.; Rembisz, J.; Schwerin, M.; Willig, A.; Velagapudi, P.; et al. Design and architecture of a series elastic snake robot. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 4630–4636. [Google Scholar] [CrossRef]
- Borenstein, J.; Hansen, M.; Borrell, A. The OmniTread OT4 serpentine robot—Design and performance. J. Field Robot. 2007, 24, 601–621. [Google Scholar] [CrossRef]
- Kota, S. Compliant systems using monolithic mechanisms. Smart Mater. Bull. 2001, 2001, 7–10. [Google Scholar] [CrossRef]
- Tolley, M.T.; Shepherd, R.F.; Galloway, K.C.; Wood, R.J.; Whitesides, G.M. A resilient, untethered soft robot. Soft Robot. 2014, 1, 213–223. [Google Scholar] [CrossRef]
- Marchese, A.D.; Onal, C.D.; Rus, D. Autonomous soft robotic fish capable of escape maneuvers using fluidic elastomer actuators. Soft Robot. 2014, 1, 75–87. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Zong, C.; Pancheri, F.; Chen, T.; Lueth, T.C. Design of topology optimized compliant legs for bio-inspired quadruped robots. Sci. Rep. 2023, 13, 4875. [Google Scholar] [CrossRef] [PubMed]
- Onal, C.D.; Rus, D. Autonomous undulatory serpentine locomotion utilizing body dynamics of a fluidic soft robot. Bioinspir. Biomim. 2013, 8, 026003. [Google Scholar] [CrossRef]
- Luo, M.; Agheli, M.; Onal, C.D. Theoretical modeling and experimental analysis of a pressure-operated soft robotic snake. Soft Robot. 2014, 1, 136–146. [Google Scholar] [CrossRef]
- Luo, M.; Pan, Y.; Skorina, E.H.; Tao, W.; Chen, F.; Ozel, S.; Onal, C.D. Slithering towards autonomy: A self-contained soft robotic snake platform with integrated curvature sensing. Bioinspir. Biomim. 2015, 10, 055001. [Google Scholar] [CrossRef] [PubMed]
- Branyan, C.; Fleming, C.; Remaley, J.; Kothari, A.; Tumer, K.; Hatton, R.L.; Mengüç, Y. Soft snake robots: Mechanical design and geometric gait implementation. In Proceedings of the 2017 IEEE International Conference on Robotics and Biomimetics (ROBIO), Macau, China, 5–8 December 2017; pp. 282–289. [Google Scholar] [CrossRef]
- Branyan, C.; Menğüç, Y. Soft Snake Robots: Investigating the Effects of Gait Parameters on Locomotion in Complex Terrains. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1–9. [Google Scholar]
- Luo, M.; Wan, Z.; Sun, Y.; Skorina, E.H.; Tao, W.; Chen, F.; Gopalka, L.; Yang, H.; Onal, C.D. Motion Planning and Iterative Learning Control of a Modular Soft Robotic Snake. Front. Robot. AI 2020, 7, 599242. [Google Scholar] [CrossRef] [PubMed]
- Arachchige, D.D.; Perera, D.M.; Mallikarachchi, S.; Kanj, I.; Chen, Y.; Gilbert, H.B.; Godage, I.S. Dynamic Modeling and Validation of Soft Robotic Snake Locomotion. arXiv 2023, arXiv:2303.02291. [Google Scholar]
- Arachchige, D.D.; Perera, D.M.; Mallikarachchi, S.; Kanj, I.; Chen, Y.; Godage, I.S. Wheelless Soft Robotic Snake Locomotion: Study on Sidewinding and Helical Rolling Gaits. arXiv 2023, arXiv:2303.02285. [Google Scholar]
- Godage, I.S. Swimming locomotion of Soft Robotic Snakes. arXiv 2019, arXiv:1908.05250. [Google Scholar]
- Ma, S. Analysis of snake movement forms for realization of snake-like robots. In Proceedings of the 1999 IEEE International Conference on Robotics and Automation (Cat. No. 99CH36288C), Detroit, MI, USA, 10–15 May 1999; Volume 4, pp. 3007–3013. [Google Scholar]
- Guo, Z.; Mahadevan, L. Limbless undulatory propulsion on land. Proc. Natl. Acad. Sci. USA 2008, 105, 3179–3184. [Google Scholar] [CrossRef]
- Zhang, X.; Chan, F.K.; Parthasarathy, T.; Gazzola, M. Modeling and simulation of complex dynamic musculoskeletal architectures. Nat. Commun. 2019, 10, 4825. [Google Scholar] [CrossRef]
- Zhang, X.; Naughton, N.; Parthasarathy, T.; Gazzola, M. Friction modulation in limbless, three-dimensional gaits and heterogeneous terrains. Nat. Commun. 2021, 12, 6076. [Google Scholar] [CrossRef] [PubMed]
- Geijtenbeek, T.; van de Panne, M.; van der Stappen, A.F. Flexible Muscle-Based Locomotion for Bipedal Creatures. ACM Trans. Graph. 2013, 32, 1–11. [Google Scholar] [CrossRef]
- Wang, J.M.; Hamner, S.R.; Delp, S.L.; Koltun, V. Optimizing Locomotion Controllers Using Biologically-Based Actuators and Objectives. ACM Trans. Graph. 2012, 31, 1–11. [Google Scholar] [CrossRef]
- Cruz Ruiz, A.; Pontonnier, C.; Pronost, N.; Dumont, G. Muscle-Based Control for Character Animation. Comput. Graph. Forum 2017, 36, 122–147. [Google Scholar] [CrossRef]
- Rezaei, S.M.; Barazandeh, F.; Haidarzadeh, M.S.; Sadat, S.M. The effect of snake muscular system on actuators’ torque. J. Intell. Robot. Syst. 2010, 59, 299–318. [Google Scholar] [CrossRef]
- Gupta, A. Lateral Undulation of a Snake-Like Robot; Massachusetts Institute of Technology: Cambridge, MA, USA, 2007. [Google Scholar]
- Bruce, J. What Defines Different Modes of Snake Locomotion? Integr. Comp. Biol. 2020, 60, 156–170. [Google Scholar] [CrossRef]
- Moon, B.R.; Gans, C. Kinematics, muscular activity and propulsion in gopher snakes. J. Exp. Biol. 1998, 201, 2669–2684. [Google Scholar] [CrossRef] [PubMed]
- Davis, S.; Tsagarakis, N.; Canderle, J.; Caldwell, D. Enhanced Modelling and Performance in Braided Pneumatic Muscle. Int. J. Robot. Res. 2003, 22, 213–217. [Google Scholar] [CrossRef]
- Jozsef, S.; Gabor, S.; Janos, G. Investigation and Application of Pneumatic Artificial Muscles. Biomech 2010, 3, 208–214. [Google Scholar] [CrossRef]
- Zhang, S.J. Robotic Artificial Muscles: Current Progress and Future Perspectives. IEEE Trans. Robot. 2019, 35, 761–781. [Google Scholar] [CrossRef]
- Schroder, J.; Erol, D.; Kawamura, K.; Dillman, R. Dynamic pneumatic actuator model for a model-based torque controller. In Proceedings of the 2003 IEEE International Symposium on Computational Intelligence in Robotics and Automation. Computational Intelligence in Robotics and Automation for the New Millennium (Cat. No. 03EX694), Kobe, Japan, 16–20 July 2003; Volume 1, pp. 342–347. [Google Scholar]
- Tondu, B.; Lopez, P. Modeling and control of McKibben artificial muscle robot actuators. IEEE Control Syst. Mag. 2000, 20, 15–38. [Google Scholar]
- Kothera, C.S.; Jangid, M.; Sirohi, J.; Wereley, N.M. Experimental characterization and static modeling of McKibben actuators. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Chicago, IL, USA, 5–10 November 2006; Volume 47659, pp. 357–367. [Google Scholar]
- Arcus, A.G. Modeling of a Dynamic McKibben Style Muscle System Using Material Properties. Master’s Thesis, Rochester Institute of Technology, Rochester, NY, USA, 2018. [Google Scholar]
- Balasubramanian, S.; Wei, R.; Perez, M.; Shepard, B.; Koeneman, E.; Koeneman, J.; He, J. RUPERT: An exoskeleton robot for assisting rehabilitation of arm functions. In Proceedings of the 2008 Virtual Rehabilitation, Reno, NV, USA, 8–12 March 2008; pp. 163–167. [Google Scholar]
- Kobayashi, H.; Hiramatsu, K. Development of muscle suit for upper limb. In Proceedings of the IEEE International Conference on Robotics and Automation, 2004. Proceedings. ICRA’04. 2004, New Orleans, LA, USA, 26 April–1 May 2004; Volume 3, pp. 2480–2485. [Google Scholar]
- Koeneman, E.; Schultz, R.; Wolf, S.; Herring, D.; Koeneman, J. A pneumatic muscle hand therapy device. In Proceedings of the The 26th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Francisco, CA, USA, 1–5 September 2004; Volume 1, pp. 2711–2713. [Google Scholar]
- Wongsiri, S.; Laksanacharoen, S. Design and construction of an artificial limb driven by artificial muscles for amputees. In Proceedings of the International Conference on Energy and the Environment, Berlin, Germany, 9–12 September 2003; pp. 11–12. [Google Scholar]
- Chou, C.P.; Hannaford, B. Measurement and modeling of McKibben pneumatic artificial muscles. IEEE Trans. Robot. Autom. 1996, 12, 90–102. [Google Scholar] [CrossRef]
- Inoue, H. Whither Robotics: Key Issues, Approaches and Applications. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems. IROS’96, Osaka, Japan, 4–8 November 1996. [Google Scholar]
- Granosik, G.; Borenstein, J. Integrated joint actuator for serpentine robots. IEEE/ASME Trans. Mechatron. 2005, 10, 473–481. [Google Scholar] [CrossRef]
- Wang, T.; Wang, Z.; Wu, G.; Lei, L.; Zhao, B.; Zhang, P.; Shang, P. Design and analysis of a snake-like surgical robot with continuum joints. In Proceedings of the 2020 5th International Conference on Advanced Robotics and Mechatronics (ICARM), Shenzhen, China, 18–21 December 2020; pp. 178–183. [Google Scholar]
- Kakogawa, A.; Jeon, S.; Ma, S. Stiffness design of a resonance-based planar snake robot with parallel elastic actuators. IEEE Robot. Autom. Lett. 2018, 3, 1284–1291. [Google Scholar] [CrossRef]
- Ute, J.; Ono, K. Fast and efficient locomotion of a snake robot based on self-excitation principle. In Proceedings of the 7th International Workshop on Advanced Motion Control. Proceedings (Cat. No. 02TH8623), Maribor, Slovenia, 3–5 July 2002; pp. 532–539. [Google Scholar]
- Meller, M. Improving actuation efficiency through variable recruitment hydraulic McKibben muscles: Modeling, orderly recruitment control, and experiments. Bioinspir. Biomim. 2020, 11, 065004. [Google Scholar] [CrossRef]
- Robinson, R.; Kothera, C.; Wereley, N. Variable Recruitment Testing of Pneumatic Artificial Muscles for Robotic Manipulators. IEEE/ASME Trans. Mechatron. 2015, 20, 1642–1652. [Google Scholar] [CrossRef]
- Lopez, M.; Haghshenas-Jaryani, M. A Muscle-Driven Mechanism for Locomotion of Snake-Robots. Automation 2022, 3, 1–26. [Google Scholar] [CrossRef]
- Lopez, M.; Haghshenas-Jaryani, M. A Muscle-driven Mechanism for Locomotion of Snake-Robots: Kinematics, Design, and Prototyping. In Proceedings of the 34th Florida Conference on Recent Advances in Robotics (FCRAR), Virtual, 13–14 May 2021. [Google Scholar]
- Haghshenas-Jaryani, M. Dynamics and Computed-Muscle-Force Control of a Planar Muscle-Driven Snake Robot. Actuators 2022, 11, 194. [Google Scholar] [CrossRef]
- Shi, W.; Stapersma, D.; Grimmelius, H.T. Comparison study on moving and transportation performance of transportation modes. Int. J. Energy Environ. 2008, 2, 179–190. [Google Scholar]
- Kelasidi, K.Y.P.E.; Gravdahl, J.T. Energy efficiency of underwater snake robot locomotion. In Proceedings of the 23rd Mediterranean Conference on Control and Automation (MED), Torremolinos, Spain, 16–19 June 2015. [Google Scholar]
- Charmant, J. Kinovea (0.9.5). 2021. Available online: https://www.kinovea.org/ (accessed on 18 June 2023).
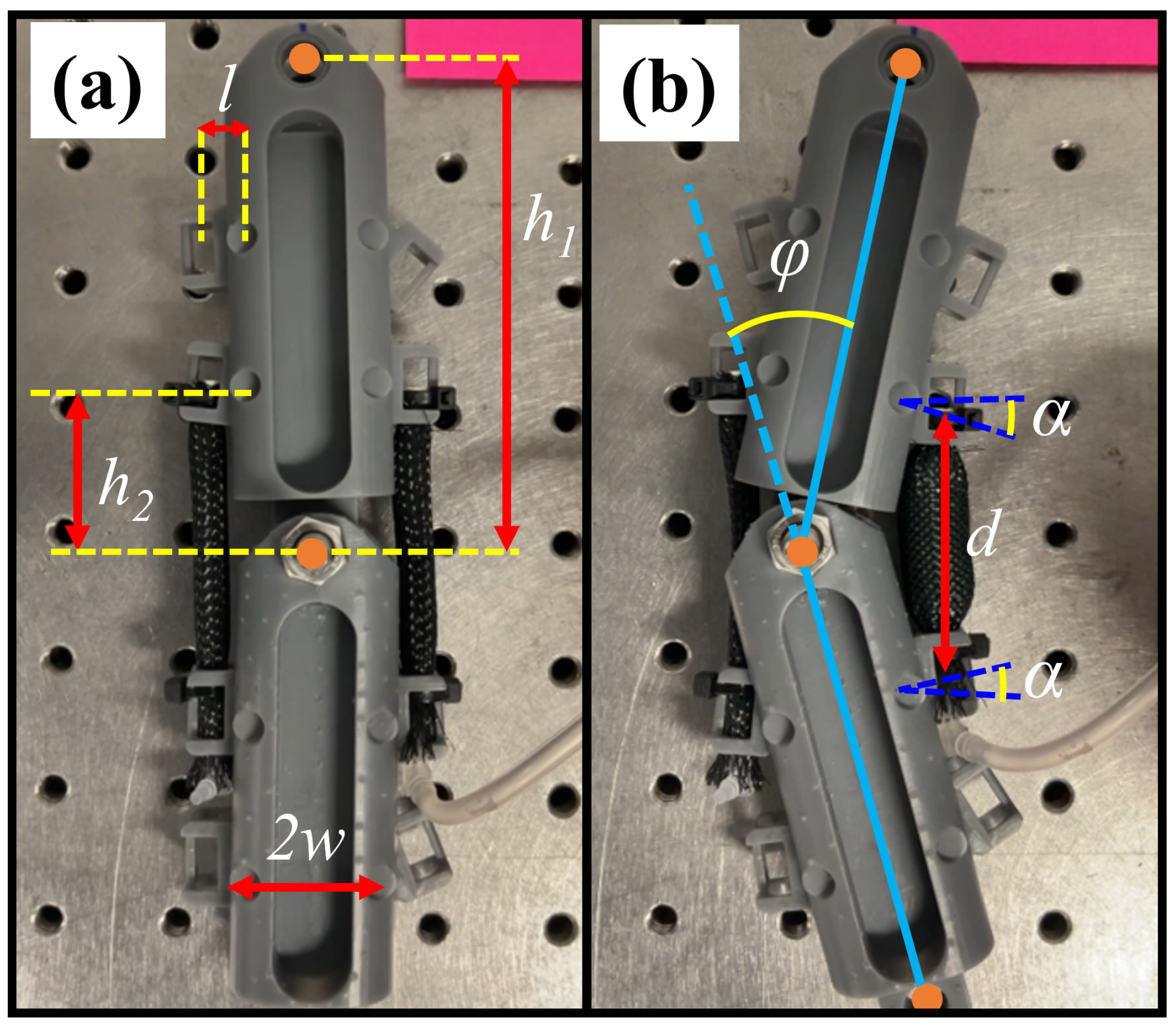
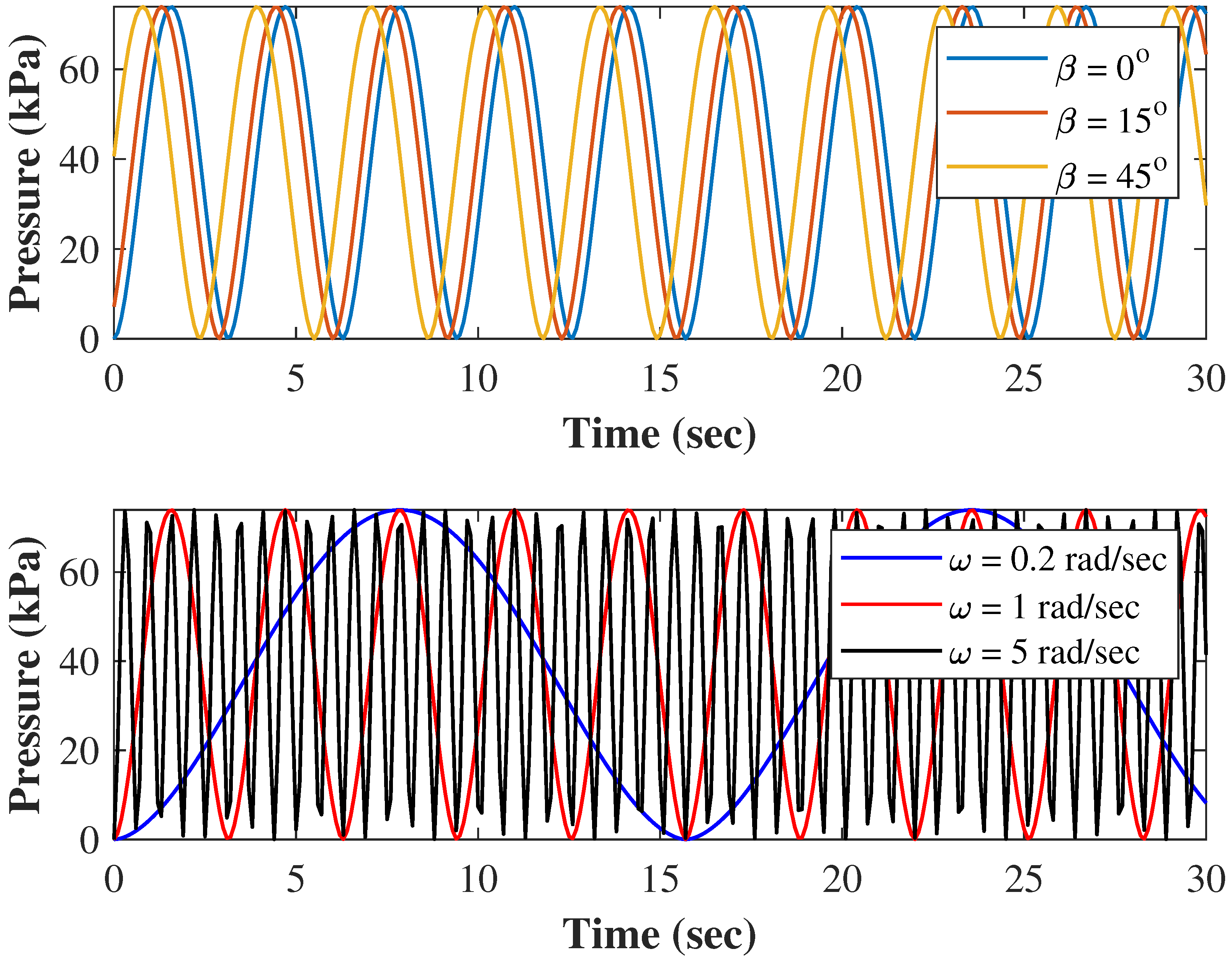


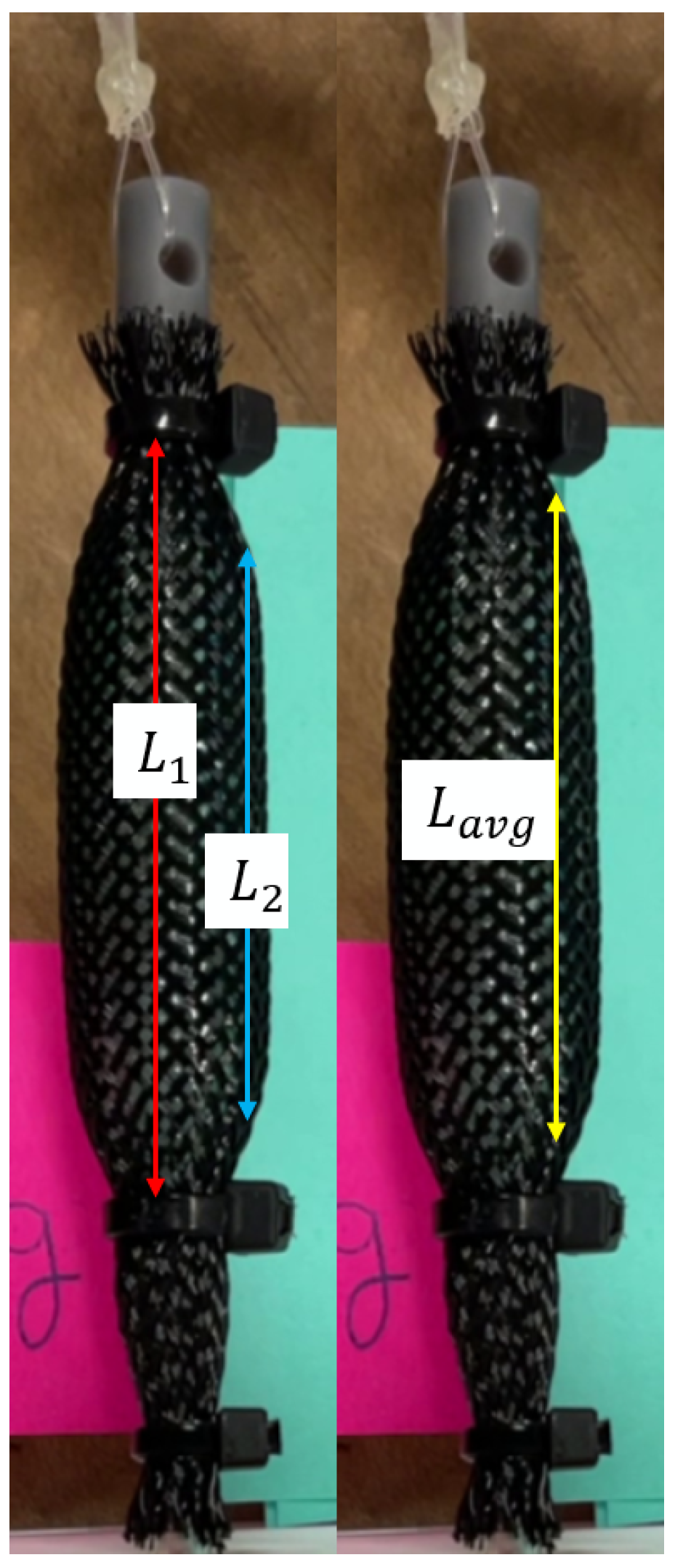

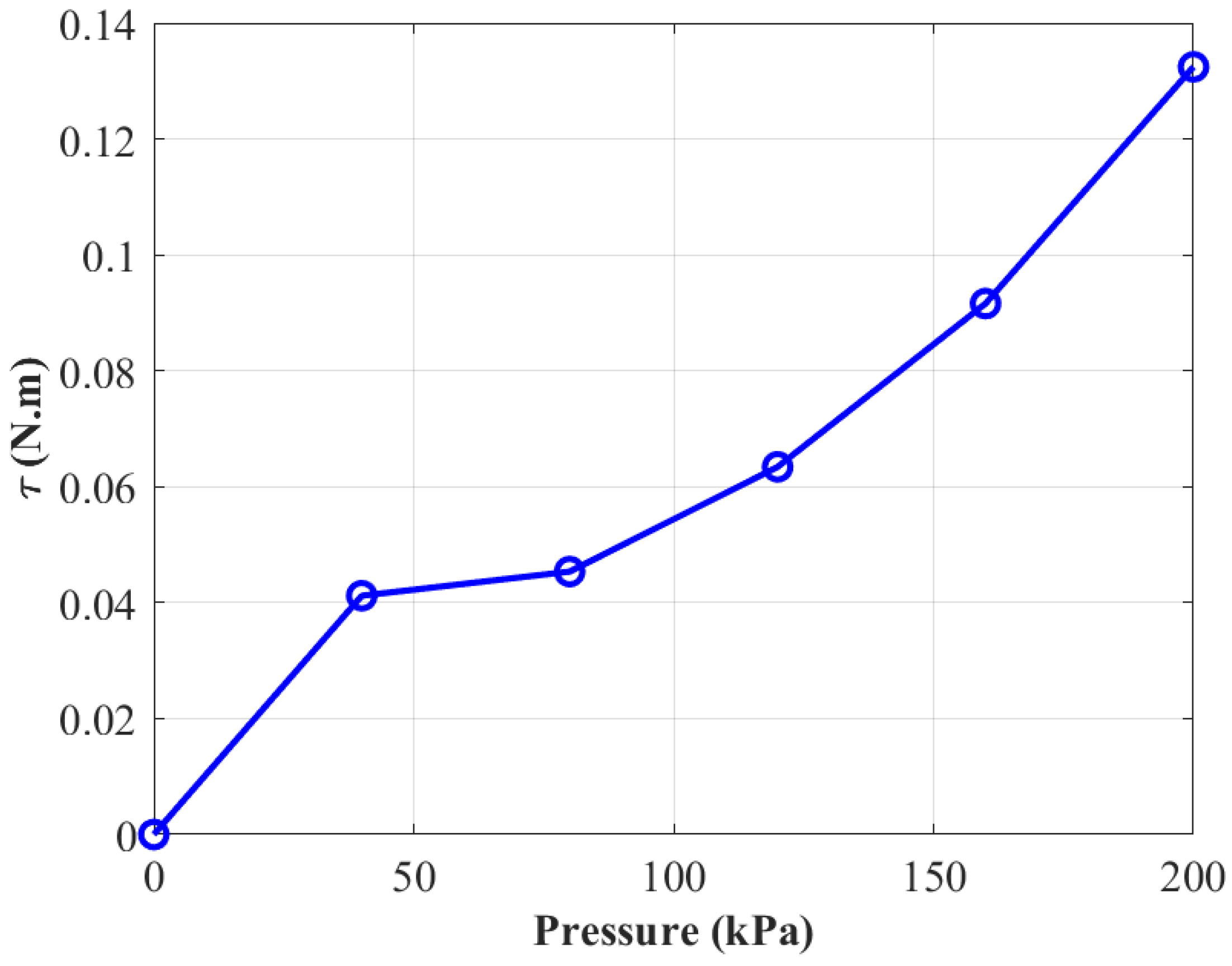




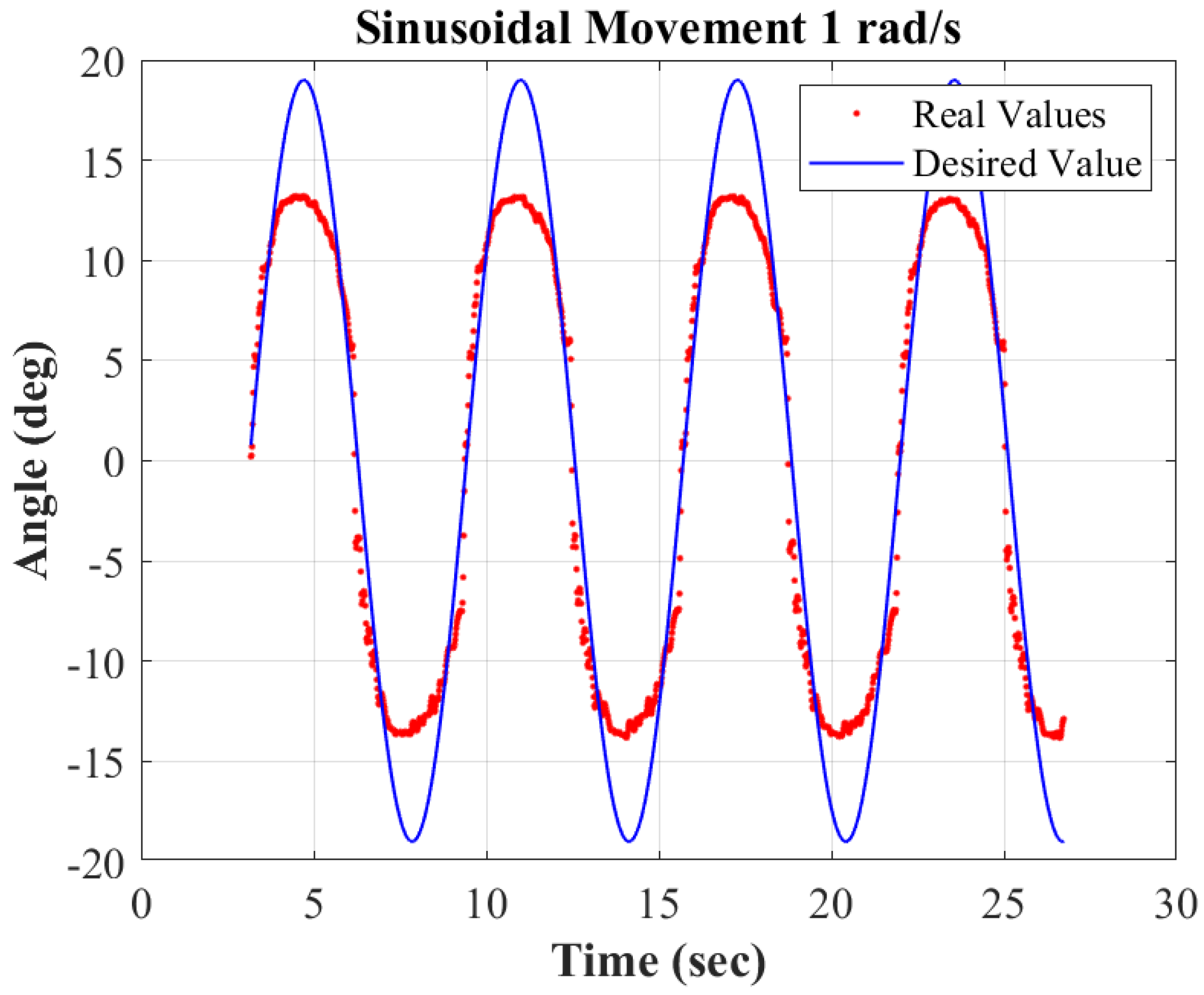




| Parameter | Definition | Optimized Value | Actual Value |
|---|---|---|---|
| (mm) | The distance from the joint to the attachment point | 30 | |
| (mm) | The resting length of muscle | 60 | |
| w (mm) | The half width of each link | 12 | |
| l (mm) | The distance from w to muscle attachment point | 7 | |
| The attachment point angle | No fixed value |
| Forward Velocity | |
|---|---|
| 20 rad/s | 1.2 mm/s |
| 10 rad/s | 1.6 mm/s |
| 2 rad/s | 0.83 mm/s |
| 1 rad/s | 0.78 mm/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lopez, M.; Haghshenas-Jaryani, M. A Study of Energy-Efficient and Optimal Locomotion in a Pneumatic Artificial Muscle-Driven Snake Robot. Robotics 2023, 12, 89. https://doi.org/10.3390/robotics12030089
Lopez M, Haghshenas-Jaryani M. A Study of Energy-Efficient and Optimal Locomotion in a Pneumatic Artificial Muscle-Driven Snake Robot. Robotics. 2023; 12(3):89. https://doi.org/10.3390/robotics12030089
Chicago/Turabian StyleLopez, Marcela, and Mahdi Haghshenas-Jaryani. 2023. "A Study of Energy-Efficient and Optimal Locomotion in a Pneumatic Artificial Muscle-Driven Snake Robot" Robotics 12, no. 3: 89. https://doi.org/10.3390/robotics12030089
APA StyleLopez, M., & Haghshenas-Jaryani, M. (2023). A Study of Energy-Efficient and Optimal Locomotion in a Pneumatic Artificial Muscle-Driven Snake Robot. Robotics, 12(3), 89. https://doi.org/10.3390/robotics12030089








