Abstract
Many spectroscopic diagnostics are routinely used as techniques to infer the plasma parameters from line emission spectra, but their accuracy depends on the numerical model or code used for the fitting process. However, the validation of a line shape code requires some steps: the comparison of the line shape code with other similar codes for some academic (simple) cases and then for more complex ones, the comparison of the fitting parameters obtained from the best fit of the experimental spectra with those obtained with other diagnostic techniques, and/or the comparison of the fitting parameters obtained by different codes to fit the same experimental data. Here we compare the profiles of the hydrogen Balmer β line in helium plasma computed by five codes for a selected set of plasma parameters and we report on the plasma parameters inferred by each of them from the fitting to a number of experimental spectra measured in a helium corona discharge where the pressure was in the range of 1–5 bars.
1. Introduction
The spectra of lines emitted in gases and plasmas are routinely used as a diagnostic technique to infer the plasma parameters such as the electron density and temperature, depending on the emitter environment and the different broadening mechanisms. Obviously, the accuracy of the deduced parameters depends on that of the line shape code used to fit the experimental data. It is therefore mandatory to check the validity of any line shape code before using it for diagnostic purposes. The series of international workshops on Spectral Line Shapes in Plasmas [1] is a unique opportunity allowing all line shape code developers to cross-check their codes (numerical models and/or simulations). Generally speaking, to validate a line shape code, one has to realize the following tasks or steps: compare the line shape code with other similar codes for some academic (simple) cases and then for more complex ones, fit an experimental emission spectrum and compare the deduced parameters corresponding to the best fit with those obtained with other independent diagnostic techniques if available, and/or compare the inferred parameters from the fitting attempts using different codes to fit the same experimental spectrum. During the last edition of this workshop series, that is, SLSP4 [2], many cases were proposed for the line shape code comparison and some of them are the subject of papers published in this issue. In the category of the challenging case consisting to confronting the codes to a real situation, it was proposed to analyze two lines emitted in a helium corona discharge where the pressure was increased from 1 to 5 bars. These are the He i 492 nm and the hydrogen Balmer-β (486 nm) lines measured simultaneously from the same plasma. The participants were asked to simultaneously fit both lines in order to get consistent plasma parameters but this has rarely been respected by contributors. Some of them have chosen to fit only the H-β line while others have considered both lines but independently from each other. However, even in this case, the two lines were not treated in a balanced way. Indeed, on the one hand, for the H-β line, five codes were used for comparisons with all the available experimental spectra while on the other hand for the He i 492 nm line, four codes and only the experimental data corresponding to the lowest pressures were considered. In view of these considerations, it has been decided to limit this paper to the H-β line only, the helium He i 492 nm line being the subject of another paper [3]. Therefore, here, we compare the profiles of the H-β line in a helium plasma computed by five codes for a selected set of plasma parameters and we report on the plasma parameters inferred by each of them from the fitting to a number of experimental spectra measured in a helium corona discharge where the pressure was in the range of 1–5 bars.
This paper is divided into two parts. The first part is devoted to the synthetic profiles of the H-β line emitted by hydrogen atoms perturbed by the electrons and the He+ ions of helium plasma. The second part is focused on comparisons with experimental spectra of the same line measured in a corona discharge in helium. The aim in the first part was to compare the pure Stark-broadened profiles of this line calculated by the contributing codes for a selected set of plasma parameters. The latter, assumed to correspond to conditions of a corona discharge in helium, are the following: two values for the electron density ne = 1015 and 1016 cm−3, three values for the electron and ion temperatures assumed to be equal: Te = Ti = 0.1, 0.2, and 0.4 eV. The choice to retain only the Stark broadening is aimed to highlight the differences between the participating codes and is justified by the fact that other broadening mechanisms are less important even though they are not completely negligible. Indeed, as we will see in the section devoted to the data fitting, Doppler and van der Waals broadenings have to be included as well as the instrumental function. The van der Waals broadening, which is due to the interactions of the hydrogen atoms with neutral helium atoms present in the partially ionized helium plasma, is roughly comparable to the Doppler broadening, unlike resonance broadening, which is due to the interactions of neutral emitters with neutrals of the same species.
2. Brief Description of the Codes
This section briefly describes the different codes contributing to this case study. Five codes were involved: two simulation methods and three models. The simulation codes are LSNS and SimU. LSNS involves a numerical integration of the time-dependent Schrödinger equation for the hydrogen wave function under the influence of a fluctuating electric field obtained from a particle simulation. More details can be found in Reference [4] and the references therein. SimU is well described in References [5,6]. The three models are PPP [7], QC_FFM (Reference [8] and the references therein) and ZEST. Since the ZEST (ZEeman-STark) line-shape code has been improved and upgraded to a new version [9], here, we describe the version that has been used for the calculations reported in this paper. ZEST relies on a quasi-static description of the ions and an impact approximation for the electrons. The Hamiltonian of the radiator includes the Stark effect in the dipole approximation for arbitrary multi-electron ions as well as the Zeeman Effect accounting for a static magnetic field. The impact of the magnetic field on the electron trajectories is not taken into account. The electrons are described by a collision operator calculated up to the second order of the electron-radiator interaction using the model reported in Reference [10]. The distribution of quasi-static ion fields is evaluated using analytical formulas adjusted on many Monte-Carlo simulations as a function of the plasma ion coupling parameter and the effective electron-ion screening parameter [11,12]. At the time of the calculations, ZEST neglected the collisional shift due to the electrons, the interference terms between upper and lower states, the non-diagonal terms of the collision operator, and the frequency dependence of the impact width. Using the unitary transformation that diagonalizes the radiator Hamiltonian, the resulting profile is then written as a sum of Lorentzian functions (or Voigt functions when accounting for the Doppler Effect) weighted by the strength of the Stark components and by the probability of the quasi-static ion fields. At the time of the calculations presented here, the ZEST code did not include the ion dynamics effects. Now, in the most recent version of ZEST [9], the ion dynamics effects are modeled within the framework of the fast Frequency-Fluctuation Model (fast FFM) [13]. In the next section, we compare the calculated profiles and the full widths at half-maximum for six subcases corresponding to the two densities ne = 1015 cm−3 and ne = 1016 cm−3.
3. Code Comparison through Profiles and Line Widths
3.1. H-β Line Profiles for the Lower Density
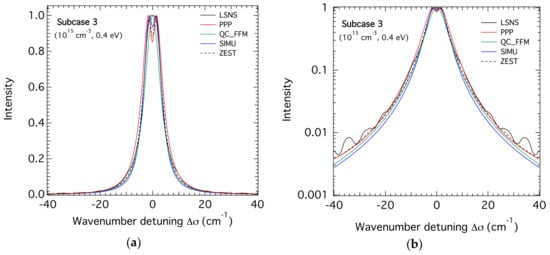
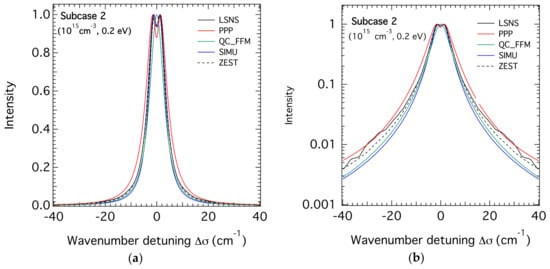
The results of the code calculations for the lower density case (ne = 1015 cm−3) are respectively illustrated for equal ion and electron temperatures of 0.1, 0.2, and 0.4 eV in Figure 1, Figure 2 and Figure 3 corresponding respectively to subcases 1, 2, and 3. It can be seen that all the codes except PPP are in an overall agreement in terms of widths and line shapes with some differences in the central line dip. The profiles calculated by PPP are broader than all the others, especially at the lowest temperature of 0.1 eV. This was excepted because this version of the PPP line shape code used for the treatment of the electron broadening the GBK (Griem-Blaha-Kepple) [14] collision operator does not depend on the frequency. This operator is known to overestimate the broadening in comparison to frequency-dependent collision operators in the framework of the impact approximation used for the treatment of the emitter-electron interactions. Note that in ZEST calculations, the electron broadening was treated using the impact limit of the model reported in Reference [10]. Such an operator is different from the GBK one used in PPP, but does not account for frequency-dependence either. Note that the small oscillations of the LSNS profiles highlighted by the use of a semi-logarithmic scale are a feature of the numerical Fourier Transform, which has no physical origin. They can be eliminated by computing the dipole autocorrelation function over longer times. This simulation tool has been applied to the spectrum corresponding to the lowest pressure in a separate study [15]. The calculations of the PPP code tend towards the other code calculations as the temperature increases from 0.1 to 0.4 eV. At 0.4 eV, all the profiles give close widths even though they differ in the filling of the line center dip. It is worth noting that PPP allows the use of a frequency-dependent collision operator for the electron broadening, but at the expense of computing time or through a post-processing treatment. This possibility was not used at the time of the SLSP 4 workshop, hence, we only report on the PPP calculations based on the GBK collision operator model.
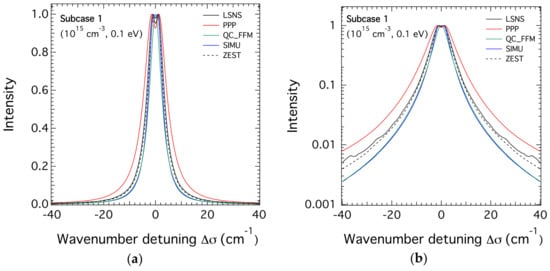
Figure 1.
The theoretical Stark profiles of the H-β line calculated for hydrogen atoms in a helium plasma with an electron density of 1015 cm−3 and a temperature of 0.1 eV for both plasma He+ ions and electrons. The profiles are centered at 486.1 nm and the wavenumber units are used; (a) linear scale. (b) semi-logarithmic scale.
3.2. H-β Line Profiles for the Highest Density
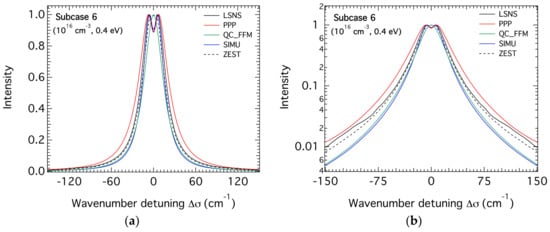
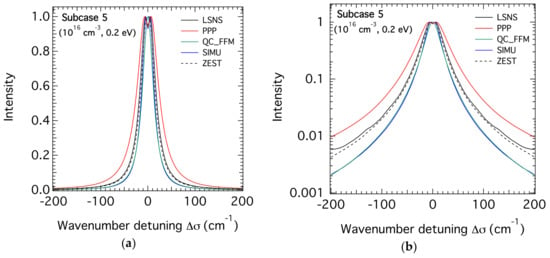
Similarly, the results of the code calculations for the higher density case (ne = 1016 cm−3) and the same temperatures as in the previous subsection are respectively illustrated in Figure 4, Figure 5 and Figure 6 which refer to subcases 4, 5, and 6, respectively. For this density, the expected discrepancy between the calculations carried out by the PPP code using the GBK collision operator and those of the other codes are more pronounced, confirming the non-validity of this form of this operator at high densities and low temperatures even though it tends to disappear with increasing temperatures. One can see that for the remaining calculations, SimU agrees well with QC_FFM on the one side and ZEST agrees well with LSNS on the other side. Note that the profiles calculated by LSNS and ZEST are a bit broader than those calculated by SimU and QC_FFM. These agreements concern the overall profiles, the line widths, and wings, but not the line center dip for which there are some discrepancies between the various code calculations.
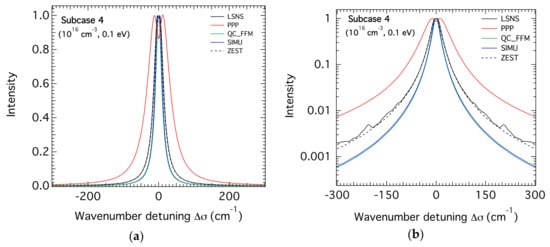
Figure 4.
The theoretical Stark profiles of the H-β line calculated for hydrogen atoms in a helium plasma with an electron density of 1016 cm−3 and a temperature of 0.1 eV for both plasma He+ ions and electrons. The profiles are centered at 486.1 nm and wavenumber units are used. (a) linear scale; (b) semi-logarithmic scale.
3.3. Comparison of the FWHM of the H-β Line
The FWHM (Full Widths at Half Maximum) of the H-β line versus the electron temperature (0.1, 0.2, and 0.4 eV) as calculated by the previously mentioned codes are illustrated in Figure 7 for both electron densities, that is, ne = 1015 and 1016 cm−3. This figure shows the relative dispersion of the FWHM as deduced from the codes when those of PPP are higher, especially at the highest density and lowest temperature. More details are shown in Table 1.
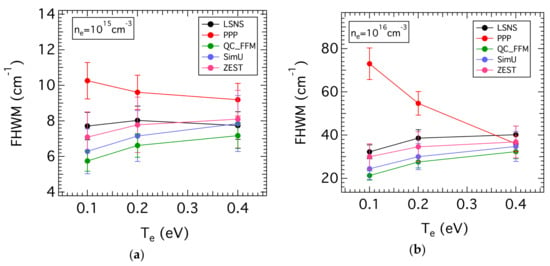
Figure 7.
The H-β line FWHM versus the electron temperature as deduced from the profiles calculated by the codes. (a) Lower electron density (ne = 1015 cm−3); (b) Higher electron density (ne = 1016 cm−3).

Table 1.
FWHM in units of cm−1 as deduced from the profiles calculated by each of the five codes LSNS, PPP, C_FFM, SimU, and ZEST. The FWHM ratio stands for the ratio of the highest value of the FWHM to each FWHM. The highest value corresponds to the PPP calculations except for ne = 1016 cm−3 and Te = 0.4 eV where it corresponds to the LSNS calculations.
In Table 1, the FWHM for each subcase corresponding to a couple of ne, Te, are presented as well as the ratio of the highest value of the FWHM to each FWHM value. In addition, the mean value of the FWHM calculated using all the values but the highest is also shown. The factor in the last column of the table represents the ratio of the FWHM obtained by the PPP to the mean value. For the lowest density, the mean value <FWHM> varies between 6.71 cm−1 for 0.1 eV to 7.71 cm−1 for 0.4 eV. The FWHM values of the profiles calculated by PPP are roughly about 1.2–1.5 higher than the average values. For the highest density, the mean value of the FWHM (excluding the highest value) is in the range 27–36 cm−1, with the lower value (27 cm−1) corresponding to the lowest temperature, that is, 0.1 eV. As explained previously, the FWHMs calculated by PPP are higher than those of the other codes. It is about 2.8 times the mean value for 0.1 eV and decreases down to be 1.7 times higher at 0.2 eV to eventually become equal to the mean value at temperatures of 0.4 eV or higher, leading to a very good agreement with the other codes. This means that the calculations done by PPP using the non-frequency depending collision operator can be safely used for comparisons with the experimental data provided that the temperatures are not too low and the density too high.
3.4. Reconsidering the PPP Calculations of the H-β Line
Following the previous discussion on the comparisons of profiles and trying to take advantage of the detailed comparisons of the H-β line widths presented in Table 1, we recalculated the profiles using the PPP code for each of the six subcases by dividing the electron density by the corresponding factor shown in the last column of Table 1. These calculations have been labeled PPPm. They are shown in Figure 8 and Figure 9 for the lowest density. It can be seen from both graphs that the reduction of the electron density by the correct factor allows for the PPP calculations labeled PPPm to approach the other calculations closely in terms of the line widths and wings, but introduces differences in the line center dip which becomes more pronounced with PPPm. Therefore, this artificial way to reduce the overestimated broadening due to the GBK collision operator roughly works and, therefore, one has to use a frequency-dependent collision operator, especially for low temperatures and high densities.
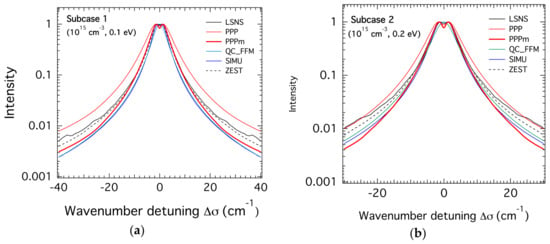
Figure 8.
The theoretical Stark profiles of the H-β line of Figure 1 and Figure 2 with the inclusion of the modified PPP calculations (PPPm: thick red solid line) where the electron density was scaled down by the mean corresponding factor explained at the end of Section 3.3. The same factor of 1.5 was used for both subcases (a) Te = Ti = 0.1 eV (b) Te = Ti = 0.2 eV.
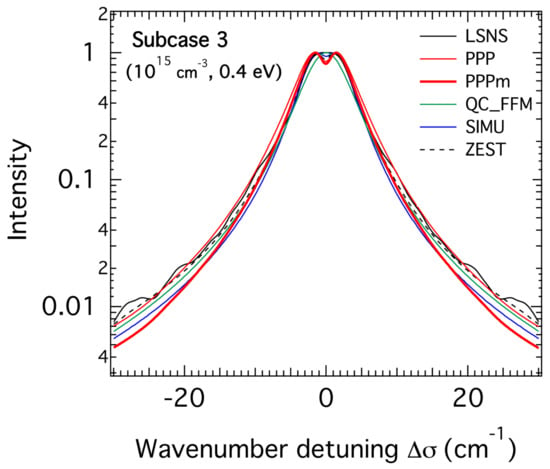
Figure 9.
The theoretical Stark profiles of the H-β line of Figure 3 (Te = Ti = 0.4 eV) with the inclusion of modified PPP calculations (PPPm: thick red solid line) where the electron density was scaled down by the mean corresponding factor explained at the end of Section 3.3. The factor used here is 1.2.
3.5. Electric Microfield Distributions
To be complete in the code comparisons and for a better understanding of the differences between the calculated profiles, we present the field distribution used by the codes except for QC_FFM on Figure 10 for the lowest density ne = 1015 cm−3. One can see no difference between the distributions calculated by LSNS, PPP, and ZEST but that which was calculated by SimU is different. This is not surprising since SimU, by simulating both electrons and ions, provides the total electric field corresponding to the doubled charge density. Its distribution is broader and shifted towards higher field values. For the other codes, the field distributions shown here are for ions only.
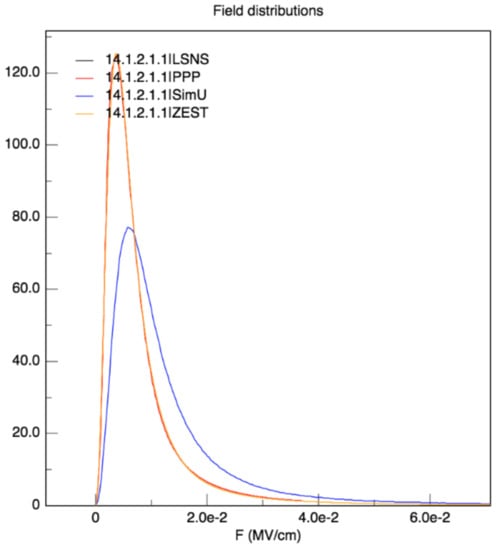
Figure 10.
The electric field distributions as calculated by the different line shape codes for the lowest electron density and temperature ne = 1015 cm−3 and Te = Ti = 0.1 eV. These concern ions only for LSNS, PPP, and ZEST codes. The SimU distribution represents that of the total electric field, that is, the ions and electrons.
4. Comparison with Experimental Spectra: Line Shape Fitting
4.1. Introducing the Experimental Spectra
The experimental spectra proposed as a best-fit challenge for the codes here were measured in a corona discharge in helium performed in an electrical engineering laboratory for the study of the dielectric properties of insulators [16,17]. The spectra of the H-β line were measured at room temperature for various values of pressure. The spectra corresponding to six values of the pressure in the range 1–5 bars are shown in Figure 11. Before presenting the fitting results of these spectra, it is necessary to give some insights into the broadening mechanisms affecting the H-β line emitted in helium plasma in which the hydrogen atoms represent a small fraction of the environment.
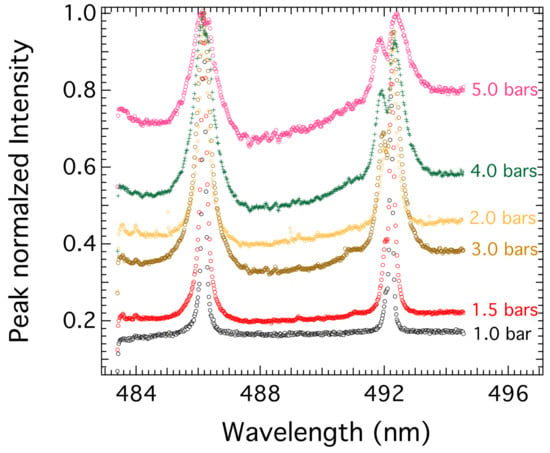
Figure 11.
The superposition of the available experimental spectra of the H-β 486.1 nm (left peak) and the He i 492 nm (right peak) lines measured at room temperature for pressures in the range of 1–5 bars.
4.2. Broadening Mechanisms of H-β Line in a Helium Plasma
The experimental spectral shapes of the H-β line emitted by a corona discharge in helium with hydrogen traces are subject to a competition between several broadening mechanisms. First of all, the natural broadening is intrinsic to each emitter but is very small in comparison to other mechanisms. There is also another unavoidable contribution from the instrumental function mainly due to the spectrometer entrance slit. For the present case, the instrumental function has been estimated from a helium lamp as a Gaussian with an FWHM of 0.09 nm [17]. Four other broadening mechanisms can potentially contribute to the line profile of the H-β line. Three of these mechanisms depend mainly on the temperature: Doppler broadening, resonance, and van der Waals broadenings. The fourth broadening mechanism that depends on the electron density is the Stark broadening. Resonance broadening is due to collisions of hydrogen atoms with other hydrogen atoms, it leads to a Lorentzian profile with an FWHM proportional to the ratio (P/T) of the pressure over the temperature of the hydrogen atoms that is, , with a linear dependence on the fraction of the hydrogen atoms in the helium plasma. Van der Waals broadening is attributed to the collisions of the hydrogen atoms with other neutrals which are connected to the emitter through a resonant transition. It is the case for the interactions of the hydrogen atoms with helium neutrals. Like resonance broadening, the van der Waals broadening mechanism results in a Lorentzian shape with FWHM proportional to the pressure P and inversely proportional to the power 0.7 of the temperature, that is, . Readers interested in these kinds of pressure broadening mechanisms between neutral atoms can refer, for instance, to the following papers: Papers [18,19,20,21,22,23]. In all the fittings presented here, the resonance broadening was estimated to be negligible in comparison to other broadening mechanisms and was therefore ignored. This can be easily justified, in particular, for low concentrations or fractions of neutral hydrogen atoms. We have estimated the van der Waals broadening FWHM for each of the six experimental spectra. These are tabulated in Table 2 and compared to the corresponding FWHM of the experimental spectra. It can be seen that the van der Waals broadening represents about one-third of the total broadening of the H-β line, the remaining broadening being due mainly to the Stark effect and to the Doppler effect to some extent.

Table 2.
The summary of the FWHM of the van der Waals broadening compared with the experimental FWHM of the six experimental spectra of the H-β line in a helium plasma considered in this paper.
4.3. Comparison with Experimental Data: Spectral Fitting
We have arbitrarily classified the six spectra into three categories: low pressure consisting of the two lower pressure values of 1 and 1.5 bars, intermediate pressure corresponding to pressures of 2 and 3 bars, and high pressure for the highest pressure values of 4 and 5 bars.
4.3.1. Cases of Low Pressure
The two spectra of these two low-pressure values of 1 and 1.5 bars were the most fitted with 6 attempts by 5 codes: LSNS, QC_FFM, ZEST, PPP, and PPP_GC. PPP_GC is a fitting procedure based on a Genetic Algorithm interfaced with the PPP code. It is described in Reference [24], where more recent fitting results of the H-β and He i 492 nm lines in the same conditions as those of this paper were considered. PPP was used with two contributions numbered n°1 and n°2, differing only by the used parameters for the comparison with the experimental spectra. The fitted spectra are presented in Figure 12.
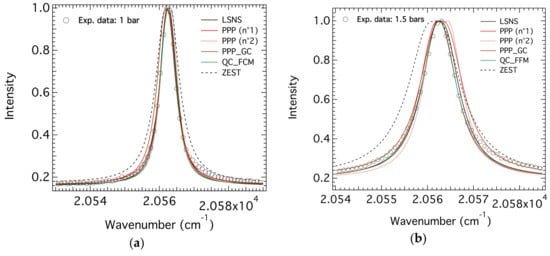
Figure 12.
The comparison/fitting of the low-pressure H-β spectra taking into account the Stark effect. Other broadening mechanisms like Doppler and van der Waals were not necessarily taken into account by all the codes. (a) P = 1 bar; (b) P = 1.5 bars.
In Figure 12, it can be seen that all the code attempts agree with the experimental data for both pressures except the calculations of ZEST. Deviations of the ZEST attempts increase with increasing pressure. It is worth noting that the ZEST calculations tried to interpret the hydrogen H-β (486.1 nm) and the He i 492 nm lines at the same time, using the same plasma conditions. The difficulty to find such conditions for both lines may explain the disagreement observed on this particular line. A better agreement would have been probably obtained if the two lines had been fitted independently. More details on the fitting and the deduced parameters will be summarized in Table 3 for the entire set of spectra.

Table 3.
The electron densities (in units of 1015 cm−3) as inferred from the fit of the experimental H-β spectra by the contributing codes. P is the pressure in units of bars.
4.3.2. Cases of Intermediate Pressures
The two spectra of these two intermediate pressure values of 2 and 3 bars were fitted by 4 attempts for the P = 2 bars case and only three attempts for the case P = 3 bars. For P = 2 bars, three codes were used (PPP (2 attempts), PPP_GC, and QC_FFM), while for P = 3 bars, only PPP (2 attempts) and QC_FFM were used. The fitted spectra are presented on Figure 13.
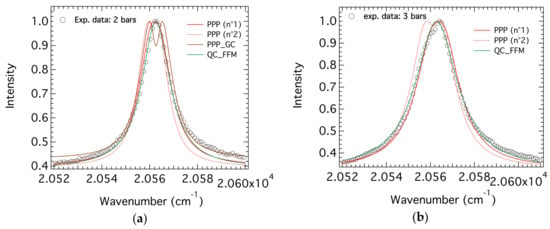
Figure 13.
The comparison/fitting of the intermediate pressure H-β spectra. (a) P = 2 bars; (b) P = 3 bars. The contributions are similar to those of Figure 12.
It can be seen from Figure 13a that the data are well fitted by the PPP calculations (n°1) and QC_FFM, the attempt of PPP_GC does not fit the spectrum. For case P = 3 bars illustrated in Figure 13b, one can see that both PPP (n°1) and QC_FFM are able to reproduce the experimental spectrum. As indicated previously, the best parameters will be summarized in Table 3.
4.3.3. Cases of High Pressures
The experimental spectra corresponding to the “high pressure” category were compared to theoretical profiles calculated by only PPP and QC_FFM, as shown in Figure 14. These spectra differ from the previous ones by their widths which are much larger and their asymmetry which can be clearly seen. These spectra are difficult to fit since they present some asymmetry in both around the line center and the line wings. If we ignore this and concentrate on the line widths, they are relatively well fitted by both codes QC_FFM and PPP. We will come back to the fitting parameters in the next section, in particular, in Table 3.
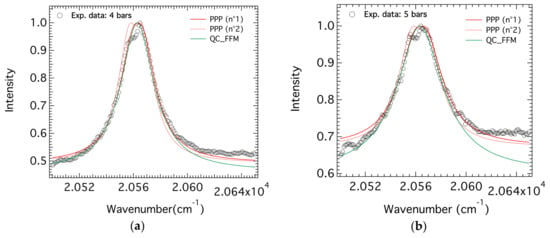
Figure 14.
The comparison/fitting of the high-pressure H-β spectra. (a) P = 4 bars; (b) P = 5 bars.
4.4. Interpretation of the Fitting Parameters
Before summarizing the plasma parameters inferred from the fitting of the experimental spectra of the H-β line as measured in a corona discharge in helium at room temperature but at a pressure in the range of 1–5 bars, it is necessary to clarify the hypotheses and assumptions considered by each participant in the fitting or comparison with the experimental data. Data fitting with the LSNS code are based on Stark broadening including the dynamics effect and the inclusion of the van der Waals broadening but with no instrumental function. The temperatures were fixed as follows: equal emitter (Ta) and ion (Ti) temperatures (Ta = Ti = 300 K), electron temperature (1 eV = 11,604 K). The only free parameter was the electron density. Profiles calculated with PPP to fit the spectra were based on the following: the Stark effect including ion dynamics, no instrumental function, the inclusion of van der Waals broadening without (PPP n°1), and with Doppler broadening (PPP n°2). In both cases, the temperatures were fixed and only the electron density was allowed to vary. The fixed temperatures were as follows: Ta = Ti = Te = 300 K for PPP n°1 calculations and Ta = Ti = 300 K and Te = 1 eV for PPP n°2 calculations. In the profiles computed with PPP_GC, the following effects were retained: the Stark broadening with the ion dynamics included as well as the Doppler and the van der Waals broadenings. The instrumental function was ignored. The ion and neutral temperatures were assumed to be equal and fixed to 300 K while allowing both the electron density and the temperature to vary in the prescribed domains. In QC_FFM calculations, in addition to the Stark broadening, the instrumental function and the Doppler broadening were added but not the van der Waals broadening. The temperatures were fixed at Ti = Ta = 0.1 eV; Te = 1 eV. ZEST calculations are based on the Stark broadening without the inclusion of ion dynamics nor van der Waals broadening. The temperatures were Ti = Te = 0.1 eV.
5. Discussion and Conclusions
Now we can present the results of the comparisons with the experimental data. For completeness, we have chosen to present them as a table in Table 3. The interpretation of these results is difficult as they were determined using other parameters which have been fixed differently from one code to another. However, this does not prevent drawing some conclusions. For the lowest pressure case where P = 1 bar, the deduced electron densities are in the range 1.5 × 1014–1.2 × 1015 cm−3. If one looks in more detail at the results, he/she can see that the PPP n°1 and PPP_GC values are very close even though the Doppler broadening in PPP n°1 was not included and the electron temperature was only 300 K while in PPP_GC, the Doppler effect was retained and the electron temperature was found to be ~1000 K. The PPP n°2 calculations retaining the Stark, Doppler, and van der Waals broadening for an electron temperature of 1 eV gave an electron density of the same order of magnitude, that is, 2.6 × 1014 cm−3. For the same temperatures as those of the PPP n°2 calculations and by retaining only the Stark and van der Waals broadenings, the LSNS calculations gave a density about 2 times higher, that is, 5 × 1014 cm−3. The electron densities obtained by QC_FFM and ZEST were respectively 8 × 1014 and 1.2 × 1015 cm−3 for an electron temperature of 1 eV and 0.1 eV, respectively. For the 1.5 bars case, similar results were obtained where the electron density values cover the range 3 × 1014–2.7 × 1015 cm−3. The lowest densities were obtained by the PPP and PPP_QC followed by LSNS. Again, the highest densities were obtained by QC_FFM and ZEST. For the P = 2 bars case, the PPP n°1 calculations gave the lowest density value, followed by the PPP n°2 and PPP_QC calculations with comparable values; QC_FFM gave an electron density about 5 times higher. For cases 4, 5, and 6 corresponding to pressures P = 3, 4, and 5 bars, PPP again gave electron densities about 5 times lower than those given by QC_FFM. It is clear that these comparisons do not allow for the determination of the electron density with accuracy as its determination depends on many factors such as the retained broadening mechanisms and the temperatures of the electrons in the addition of those of the ions and neutrals. It is clear that for low-temperature dense plasmas, accounting for neutral broadening is essential and any code which ignores it would inevitably overestimate the electron density to compensate for the missing van der Waals broadening in a way in which the higher the pressure, the larger the mistake. These are not the only reasons explaining the large dispersion of the deduced electron densities since, as we have seen, even the pure Stark calculations differ for some unfavorable conditions like high electron densities and low temperatures. Further, we concluded to the necessity of carrying out further analyses consisting in preferably fitting/analyzing both the H-β line and He i 492 nm lines simultaneously or at least fitting them separately but in a consistent manner. Some papers submitted to this issue have started in this way to improve this spectroscopic diagnostic.
Author Contributions
N.B. provided the experimental data. All authors contributed equally.
Acknowledgments
The work of E.S. was supported in part by the Israel Science Foundation.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Stambulchik, E. Review of the 1st spectral line shapes in plasmas code comparison workshop. High Energy Density Phys. 2013, 9, 528. [Google Scholar] [CrossRef]
- 4th SLSP Workshop. Available online: http://plasma-gate.weizmann.ac.il/projects/slsp/slsp4/ (accessed on 22 February 2018).
- Sheeba, R.R.; Koubiti, M.; Bonifaci, N.; Gilleron, F.; Pain, J.C.; Stambulchik, E. Broadening of the neutral helium 492 nm line in a corona discharge: Code comparison and data fitting. Atoms 2018, 6, 19. [Google Scholar] [CrossRef]
- Rosato, J.; Bufferand, H.; Koubiti, M.; Marandet, Y.; Stamm, R. A table of Balmer γ line shapes for the diagnostic of magnetic fusion plasmas. J. Quant. Spectrosc. Radiat. Transfer 2015, 165, 102–107. [Google Scholar] [CrossRef]
- Stambulchik, E.; Maron, Y. A study of ion-dynamics and correlation effects for spectral line broadening in plasma: K-shell lines. J. Quant. Spectrosc. Radiat. Transf. 2006, 99, 730–749. [Google Scholar] [CrossRef]
- Stambulchik, E.; Alexiou, S.; Griem, H.R.; Kepple, P.C. Stark broadening of high principal quantum number hydrogen Balmer lines in low-density laboratory plasmas. Phys. Rev. E 2007, 75, 016401. [Google Scholar] [CrossRef] [PubMed]
- Calisti, A.; Khelfaoui, F.; Stamm, R.; Talin, B.; Lee, R.W. Model for the line shapes of complex ions in hot and dense plasmas. Phys. Rev. A 1990, 42, 5433–5440. [Google Scholar] [CrossRef] [PubMed]
- Stambulchik, E.; Maron, Y. Quasicontiguous frequency-fluctuation model for calculation of hydrogen and hydrogenlike Stark-broadened line shapes in plasmas. Phys. Rev. E 2013, 87, 053108. [Google Scholar] [CrossRef] [PubMed]
- Gilleron, F.; Pain, J.C. ZEST: A fast code for simulating Zeeman-Stark line-shape functions. Atoms 2018, 6, 11. [Google Scholar] [CrossRef]
- Lee, R.W. Plasma line shapes for selected transitions in Hydrogen-, Helium- and Lithium-like ions. J. Quant. Spectrosc. Radiat. Transf. 1988, 40, 561–568. [Google Scholar] [CrossRef]
- Potekhin, A.; Chabrier, G.; Gilles, D. Electric microfield distributions in electron-ion plasmas. Phys. Rev. E 2002, 65, 036412. [Google Scholar] [CrossRef] [PubMed]
- Gilles, D.; Peyrusse, O. Fast and accurate line shape modeling of the H- and He-like Lyman series for radiative transfer calculations in plasmas. J. Quant. Spectrosc. Radiat. Transf. 1995, 53, 647–661. [Google Scholar] [CrossRef]
- Calisti, A.; Mossé, C.; Ferri, S.; Talin, B.; Rosmej, F.; Bureyeeva, L.A.; Lisitsa, V.S. Dynamic Stark broadening as the Dicke narrowing effect. Phys. Rev. E 2010, 81, 016406. [Google Scholar] [CrossRef] [PubMed]
- Griem, H.R.; Blaha, M.; Kepple, P.C. Stark-profile calculations for Lyman-series lines of one-electron ions in dense plasmas. Phys. Rev. A 1979, 19, 2421. [Google Scholar] [CrossRef]
- Rosato, J.; Bonifaci, N.; Li, Z.; Stamm, R. A spectroscopic diagnostic of the electron density in a corona discharge. J. Phys. Conf. Ser. 2017, 810, 012057. [Google Scholar] [CrossRef]
- Li, Z.-L.; Bonifaci, N.; Aitken, F.; Denat, A.; von Haeften, K.; Atrazhev, V.M.; Shakhatov, V.A. Spectroscopic investigation of liquid helium excited by a corona discharge: Evidence for bubbles and “red satellites”. Eur. Phys. J. Appl. Phys. 2009, 47, 2821. [Google Scholar] [CrossRef]
- Rosato, J.; Bonifaci, N.; Li, Z.; Stamm, R. Line shape modeling for the diagnostic of the electron density in a corona discharge. Atoms 2017, 5, 35. [Google Scholar] [CrossRef]
- Ali, A.W.; Griem, H.R. Theory of resonance broadening of spectral lines by atom-atom impacts. Phys. Rev. 1965, 4A, A1044. [Google Scholar] [CrossRef]
- Laux, C.O.; Spence, T.G.; Kruger, C.H.; Zare, R.N. Optical diagnostics of atmospheric pressure air plasmas. Plasma Sources Sci. Technol. 2003, 12, 125–138. [Google Scholar] [CrossRef]
- Nikiforov, A.Y.; Leys, C.; Gonzalez, M.A.; Walsh, J.L. Electron density measurement in atmospheric pressure plasma jets: Stark broadening of hydrogenated and non-hydrogenated lines. Plasma Sources Sci. Technol. 2015, 24, 034001. [Google Scholar] [CrossRef]
- Yubero, C.; Dimitrijevic, M.S.; García, M.C.; Calzada, M.D. Using the van der Waals broadening of the spectral atomic lines to measure the gas temperature of an argon microwave plasma at atmospheric pressure. Spectrochim. Acta B 2007, 62, 169–176. [Google Scholar] [CrossRef]
- Allard, N.; Kielkopf, J. The effect of neutral non resonant collisions on atomic spectral lines. Rev. Mod. Phys. 1982, 54, 1103. [Google Scholar] [CrossRef]
- Muñoz, J.; Dimitrijevic, M.S.; Yubero, C.; Calzada, M.D. Using the van der Waals broadening of spectral atomic lines to measure the gas temperature of an argon-helium microwave plasma at atmospheric pressure. Spectrochim. Acta B 2009, 64, 167–172. [Google Scholar] [CrossRef]
- Mossé, C.; Génésio, P.; Bonifaci, N.; Calisti, A. A new procedure to determine the plasma parameters from a genetic algorithm coupled with the spectral line shape PPP. Atoms 2018. submitted. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).