1. Introduction
Line-shape analysis is a very important tool for diagnostics of both laboratory and space plasmas. With the increasing sensitivity of measurements and spectral resolution, in all domains of wavelengths from far UV to infrared, reliable diagnostics need accurate calculations. Pressure broadening of spectral lines arises when an atom, ion, or molecule which emits or absorbs light in a gas or a plasma, is perturbed by its interactions with other particles of the medium. When projectiles are electron or ions, this is the so-called Stark broadening. It has been extensively developed for about 50 years and several different methods and numerical codes exist of varying complexity, and, necessarily, varying limits of applicability and accuracy.
The Spectral Line Shapes in Plasma (SLSP) recurrent workshop [
1] concerns Stark broadening of neutral or ionized atomic lines, and its aim is to compare different computational and analytical methods, in order to pinpoint sources of disagreements, infer limits of applicability, and assess accuracy. Numerous computational cases are considered in these workshops. They not only serve the purpose of code comparison, but also have applications in research of magnetic fusion, astrophysical, laser-produced plasmas, and so on. The workshop series was initiated in 2012 (SLSP1) [
2], the second one (SLSP2) was held in 2013 [
3] and since then the workshops are being held biannually (SLSP3 in 2015, and SLSP4 in 2017). The content of the workshop is prepared one year in advance by the participants through an on-line forum. The “Call for Submissions” [
4] document defines the case problems, the comparison quantities which are required, and the detailed format of the data files that are expected. The calculations are prepared before the workshop and the results are uploaded on a dedicated web interface. All the participants can download the results to discuss and work during and after the workshop.
A review of SLSP1 and SLSP2 for so called “isolated” lines has been made earlier [
5]. (We recall that the energy levels of isolated lines are not degenerate and neighbouring levels do not overlap.) In fact, the spread of the results of the cases studied in SLSP1 and SLSP2 (see, in particular, Section 4 of [
5]), demanded a deeper investigation. It was a focus at SLSP3, and the detailed analysis continued at SLSP4. There were also new topics for SLSP3 and SLSP4. A summary of the results is presented in the next sections.
2. Presentation of the Studied Cases
The
transitions in Li-like species present a puzzle by disagreement between experimental and different theoretical calculations [
6,
7,
8]. At SLSP3, the
resonance lines of the same sequence were studied with a deeper analysis of widths and shifts. The SLSP3 data also included the partial inelastic cross-sections. Only collisions with electrons in the dipole approximation were considered. The chosen lines were Li I
and B III
. The fine structure was ignored. At SLSP4, new topics were considered, such as the quadrupole interaction effects. The calculation of the elastic contribution in the form of pseudo “cross-section” was also added. Furthermore, the contributions of the so called “weak” and “strong” collisions were examined. As for SLSP3, only collisions with electrons were considered, the same lines were chosen, and the fine structure was still ignored.
For semiclassical models and simulations, the partial inelastic cross-sections are calculated in the following way: The
Lth partial wave contribution to the inelastic cross-section of transition from level
i to level
f (
) is, for a given energy
E:
where
is the impact parameter of the colliding electron and
is the statistical weight of the initial level
i.
is the so called transition matrix and
S is the scattering matrix. The adopted
and
are
and
where
,
m is the reduced atom–electron mass, nearly equal to the electron mass, and
L is the colliding electron orbital momentum. The elastic contribution has the form of a pseudo “cross-section”
, defined by
In order to separate contributions of so called “weak” and “strong” collisions, the relative “strongness” of a collision is defined based on breaking the perturbative unitarity:
which is averaged over the partial waves contributions:
The atomic data used are summarized in
Table 1. The level energies and oscillator strengths are taken from NIST [
9], and the quadrupole radial matrix elements are calculated by the R. D. Cowan’s code [
10]. Due to the restricted atomic model used (a basic two-level system), the calculations should not be considered realistic. This concerns Stark widths and, especially, Stark shifts of the lines–the true shift is a result of contributions from multiple levels with a strong cancellation [
11]. The widths and shifts were calculated on a grid of fixed energies and not for a Maxwellian distribution. The Debye shielding was ignored. However, considering the chosen density and energies, it was certainly negligible.
3. Short Description of the Methods and Codes
The methods and codes used by the participants are briefly described in the following: a quantum code GRASP/DARC, and three semi-classical codes: SCP, and STARCODE (two variants, with and without penetrating collisions), and SimU. In addition, an improvement of the SCP method has been made, only for the inelastic neutral–electron cross-section. It is denoted hereafter as SCPVB.
GRASP/DARC [
12] calculates electron-impact broadening and shifts. They are calculated in the frame of relativistic quantum mechanics.
GRASP [
13] obtains the energy levels and the electronic orbitals of the
N-electron target ion radiator, with the fine structure included. Then the Dirac Atomic
R-matrix Code (
DARC) is used to construct and solve the
-electron colliding system (the target ion + one free electron). Thus, there is no multipole expansion of the interaction potential, which cannot be limited e.g., to only the dipole one. Solving this system of coupled equations leads to the scattering
S-matrix. The widths and shifts are obtained through an adequate sum over the
l quantum numbers of the perturber electron, and through an average over the Maxwell distribution of the electrons.
SCP [
14], and earlier references therein, is a semi-classical perturbation method based on the standard impact approximation, both for electron and ion projectiles. It applies for isolated lines only. The atomic structure is an external input to the code. The classical perturber moves on a straight path for neutrals, and a hyperbola for ions. The long range Coulomb interaction potential is expanded up to second order. Then, the
S-matrix is obtained through a perturbation expansion in the frame of the evolution operator in interaction representation. Dipolar and quadrupole interactions are taken into account for the widths, and the dipole interaction is exclusively taken into account for the shifts. Thanks to adequate cut-offs, symmetrization and unitarity of the
S-matrix are fulfilled [
15]. Consequently, excitation cross-sections are zero under the threshold. Debye shielding is taken into account. Feshbach resonances for electron projectiles and ion lines are included in the code by use of the semi-classical limit of the Gailitis formula [
16], but has been removed for SLSP calculations.
SCPVB [
17] improves the calculation of the electron–neutral-atom
SCP inelastic cross-sections by accounting for the momentum and energy transfer during the collision. The momentum transfer is accounted for by considering the angular distribution of the velocity variation of the projectile electron in the course of the inelastic collision. This enables different weights associated to the
m quantum numbers of the kinetic momentum projection along the collision
axis, which is also the propagation direction of the incoming electron. The symmetrization procedure is also improved, by treating the first half of the collision under the initial conditions, whereas the second half is modeled under the final conditions.
STARCODE [
18] (with and without penetration) uses the impact approximation and the complete collision approximation. The classical perturber (electron or ion) moves along a classical path: a straight line for neutral atoms, and a hyperbola for ion radiators. The atomic structure of the quantum atom can be perturbed by interactions: thus, the possibility of penetration of the perturber, which modifies (softens) the interaction, can be taken into account. The calculations with and without the penetration effect taken into account will be designated below as
STARCODE-P and
STARCODE-NP, respectively. Long-range and short-range terms are taken into account in the expansion of the Coulomb interaction potential in the monopole, dipole and quadrupole terms. The
S matrix along with accurate estimates (based on the non-semiclassical and nonperturbative terms) is first obtained through the second-order perturbation expansion in the frame of the evolution operator in the interaction representation; since the error estimates are invariably unacceptably large, a full numerical solution of the Schrödinger equation follows, so that all results are based on this fully numerical solution. The only exception is ion broadening (not considered here), where rigorous bounds can usually show that the ion broadening is unimportant.
SimU [
19] is based on an
N-body numerical simulation of the motion of the interacting plasma particles (both ions and electrons, but for the present calculations, only electrons were modeled). The interaction potential includes dipole and quadrupole terms.
SimU treats isolated and overlapping lines, and dipole-allowed and dipole-forbidden radiative transitions as well. Trajectories are affected by the charge of the radiating ion and the perturbers. Since a Debye potential is assigned to the radiator, the trajectories of the perturbers are not hyperbolic for ionized elements. The evolution of the radiator is obtained from the resulting microfield histories by solving the (time-dependent) Schrödinger equation. Then, the line profile is obtained through the Fourier transform of the resulting radiator time-dependent dipole function.
4. Li I
In this section, the main results of Li I from SLSP3 and SLSP4 are summarized. The electron density assumed is . The grid of the electron projectile energies is , 2, 5, 10, 20, and 50 eV.
4.1. Width and Shift
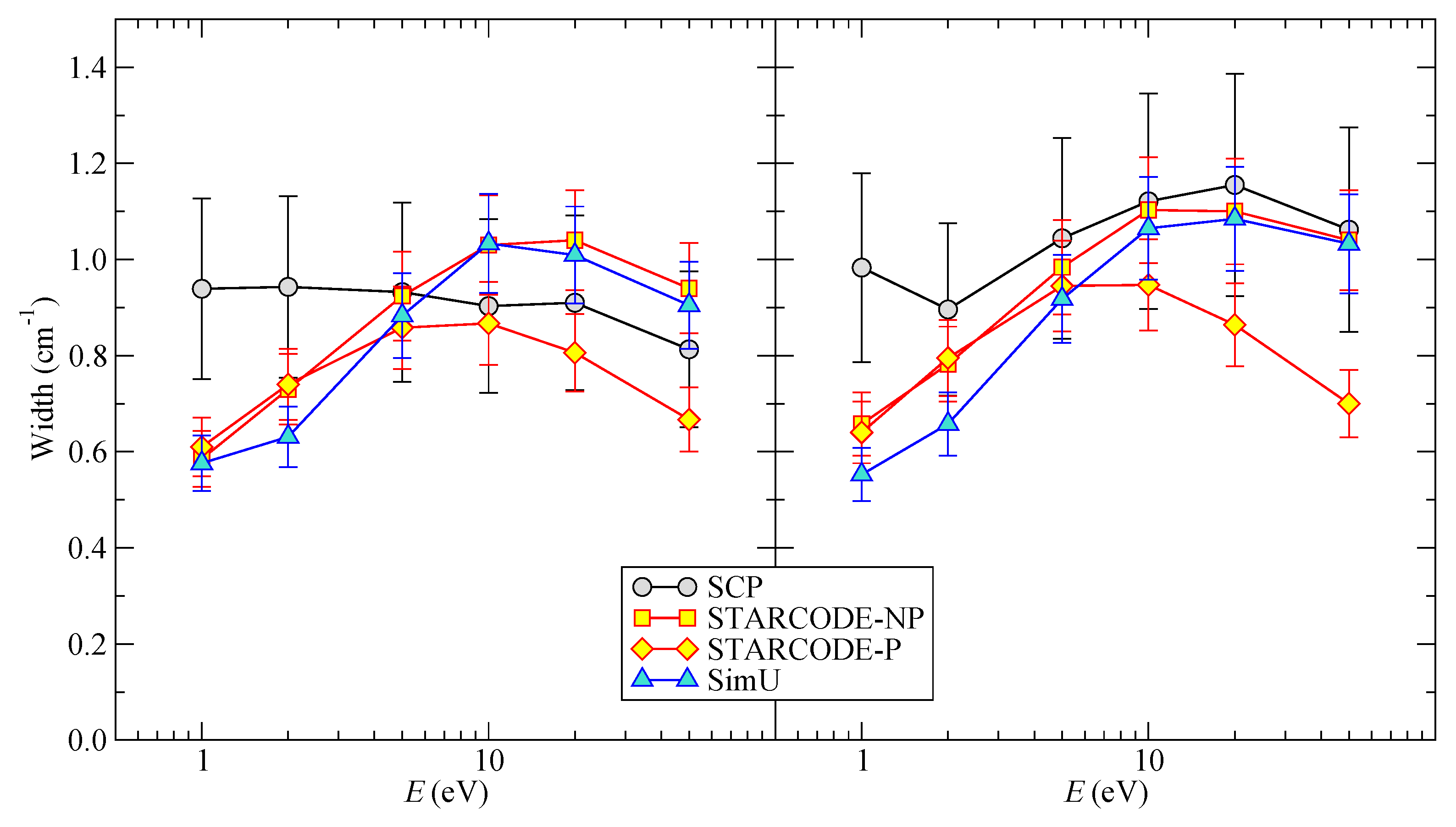
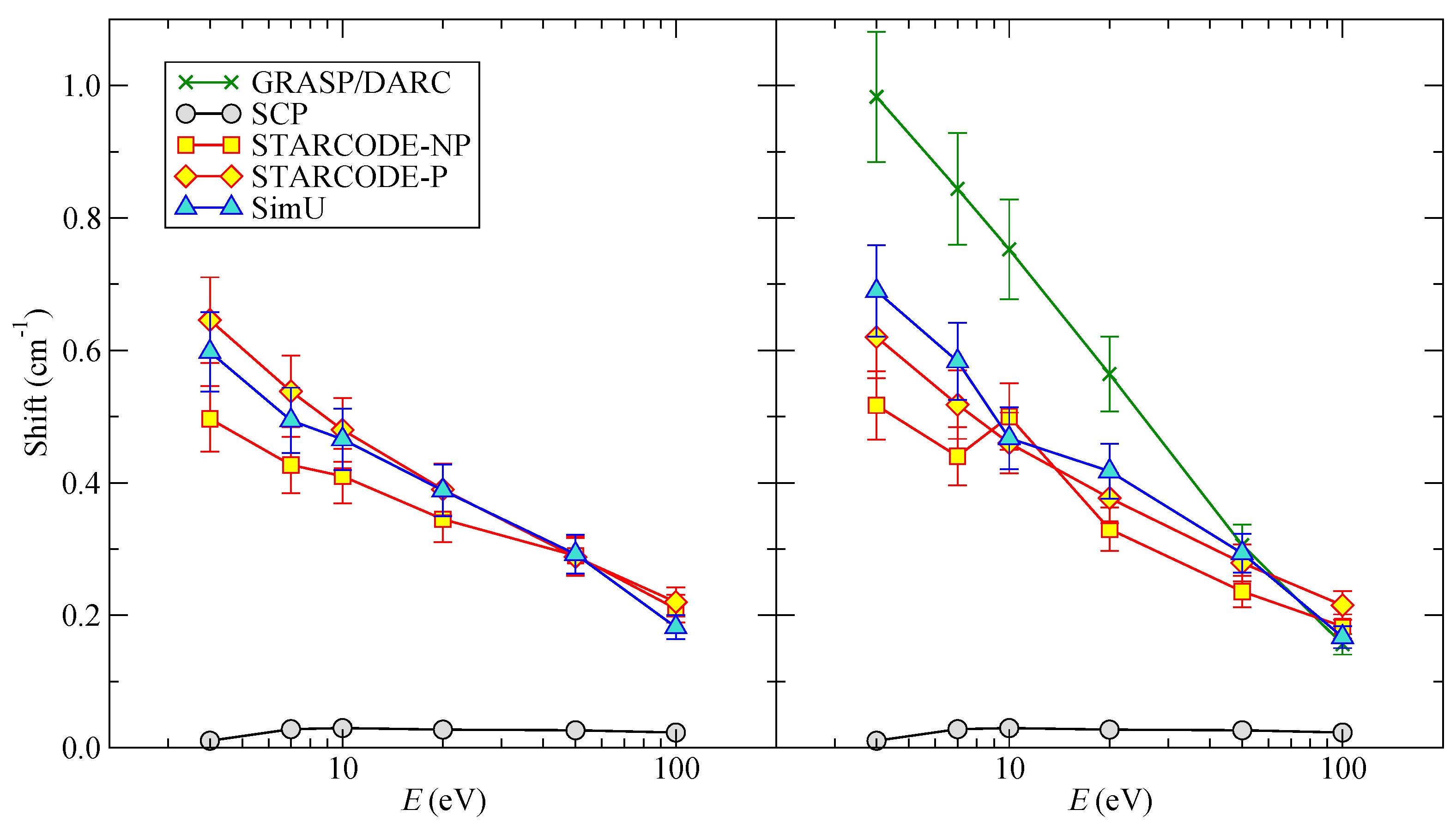
Figure 1 shows that results of the semi-classical (SC) codes are in a good agreement. The near-/under-threshold deviation between
SCP, on one hand, and
STARCODE and
SimU, is expected. Indeed, all SC codes consider electrons as classical projectiles ignoring the back-reaction due to changes in the internal quantum degrees of freedom of the radiator. As a result, the under-threshold excitation process remains allowed and, more generally, the direct and inverse processes are related through the detailed-balance relation corresponding to
. This is clearly nonphysical with respect to cross-sections, and in
SCP a symmetrization procedure [
15] is used as a workaround. Due to the symmetrization, a correct microreversibility of the cross-sections in excitation and de-excitation is obtained. Consequently, the excitation cross-sections are zero under the threshold. Penetrating collisions become more important at higher energies. Comparing the left and right part of
Figure 1, the effect of the quadrupole interaction is rather small for all codes (between 5% and 25%).
We note that in this and the following figures, the error bars designate estimated theoretical uncertainties of the calculations. The details on assessing the uncertainties for each code can be found in the respective publications given in
Section 3.
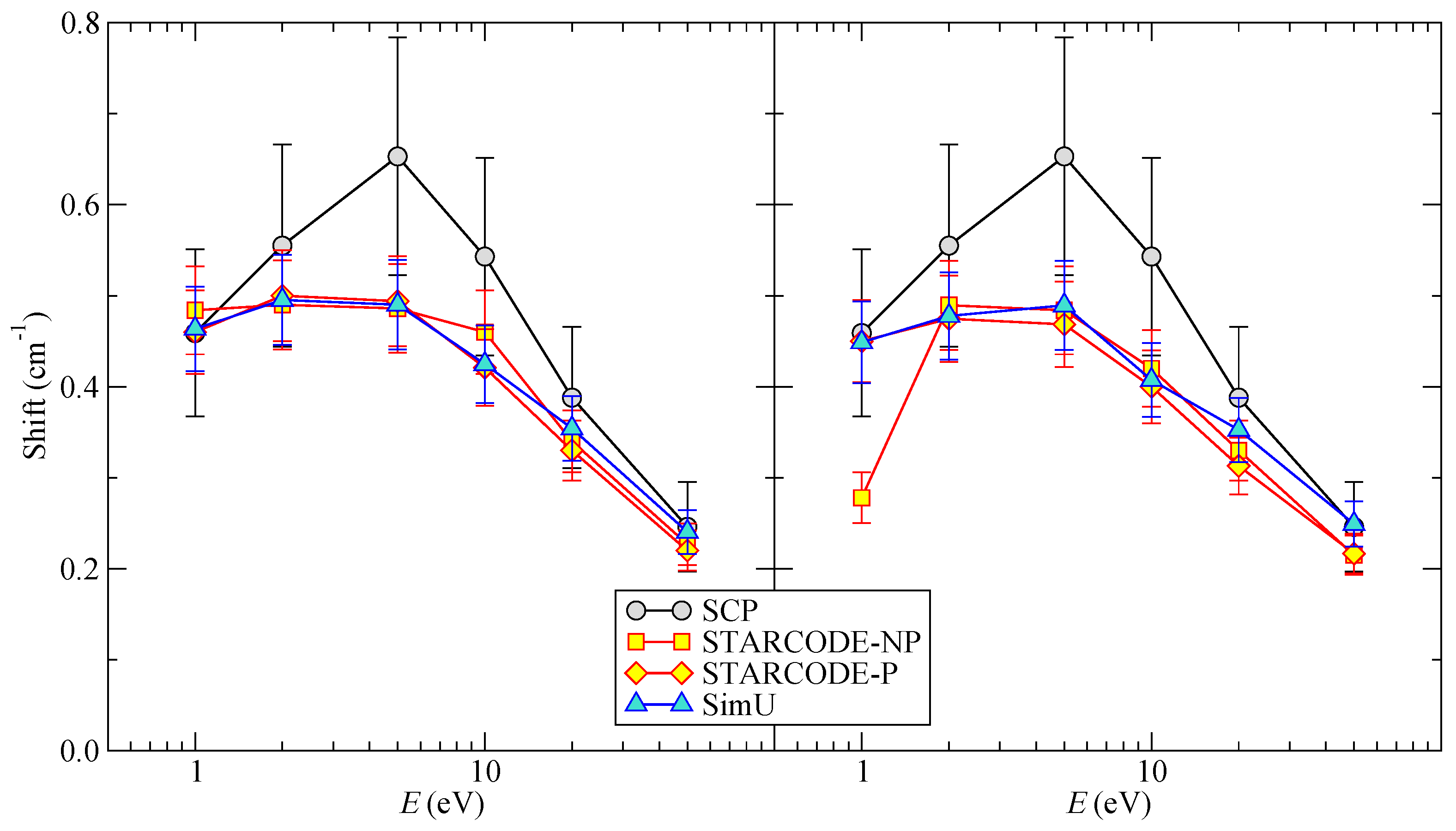
The shifts are shown in
Figure 2. Again, the SC codes mutually agree, except for an unexplained discrepancy at 5 eV. The effect of penetrating collisions is negligible. Similarly to the widths, the effect of quadrupoles is rather small. It should be noted that
SCP does not presently account for the quadrupole interaction when calculating the Stark shift; this will be enabled in a future version of the code. Therefore, the
SCP results in the left and right panels of
Figure 2 are identical.
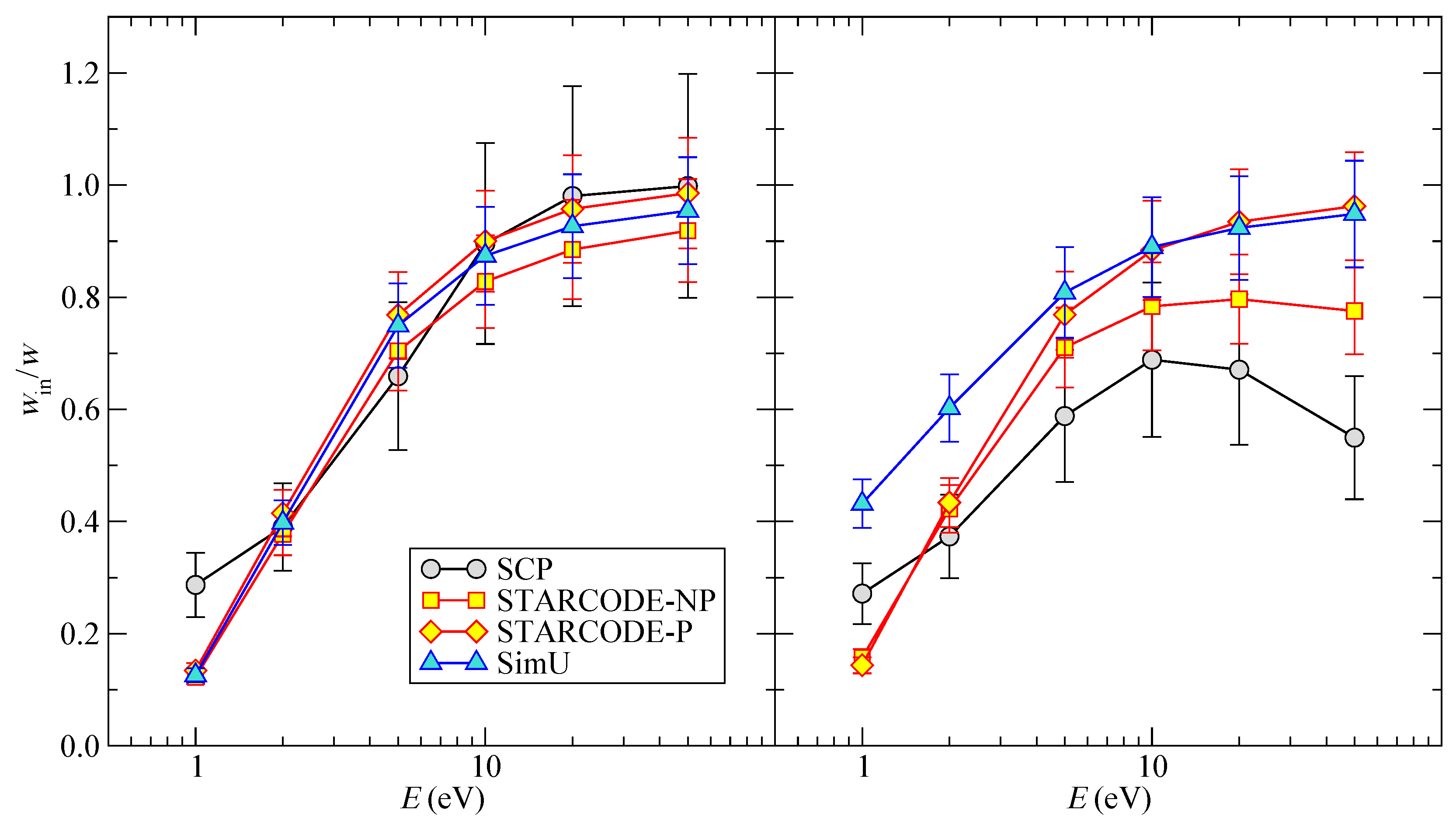
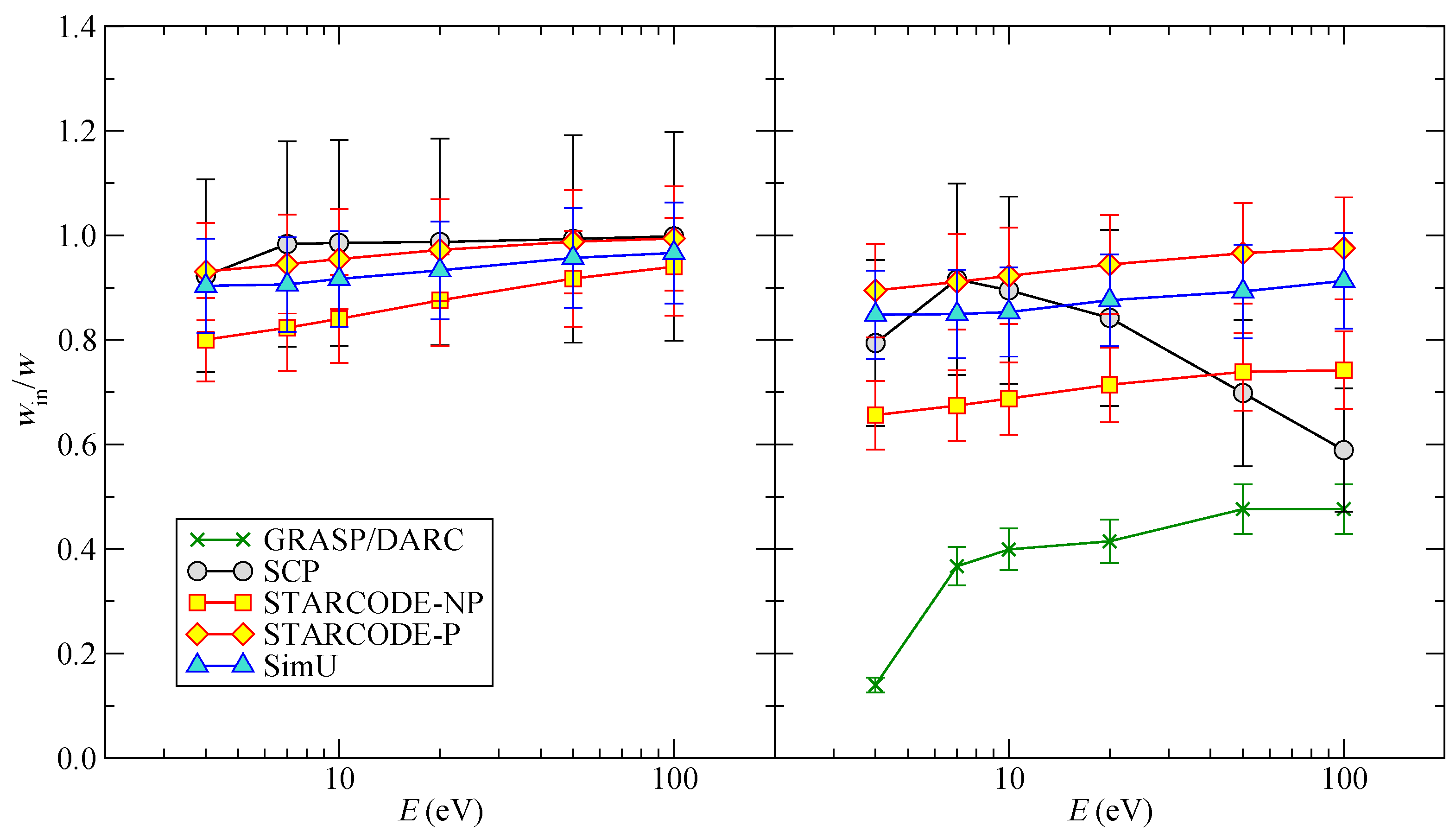
4.2. Fractional Inelastic Width
The fractional inelastic width is equal to the ratio between the total inelastic cross-section (excitation + de-excitation) and the total width cross-section (i.e., width before multiplying by velocity and density). The results are shown in
Figure 3. When only the dipole interaction is taken into account, all codes show a similar and expected behaviour–an increase of the contribution of the inelastic collisions when the energy increases. On the other hand, with the quadrupole interaction included, the behavior of
SCP and
STARCODE-NP (no penetration) show a minor decrease or saturation at higher energies.
4.3. Cross-Sections
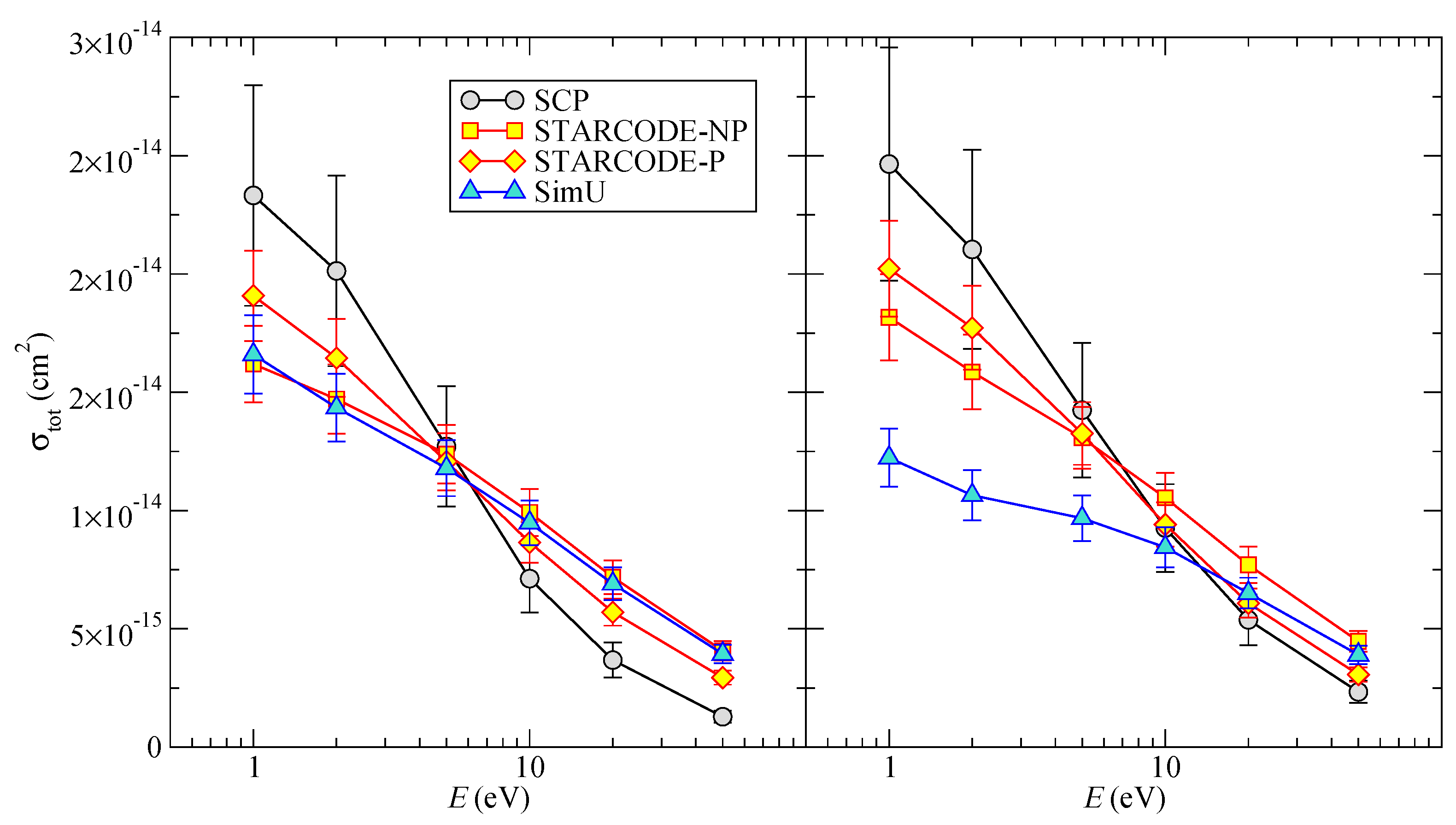
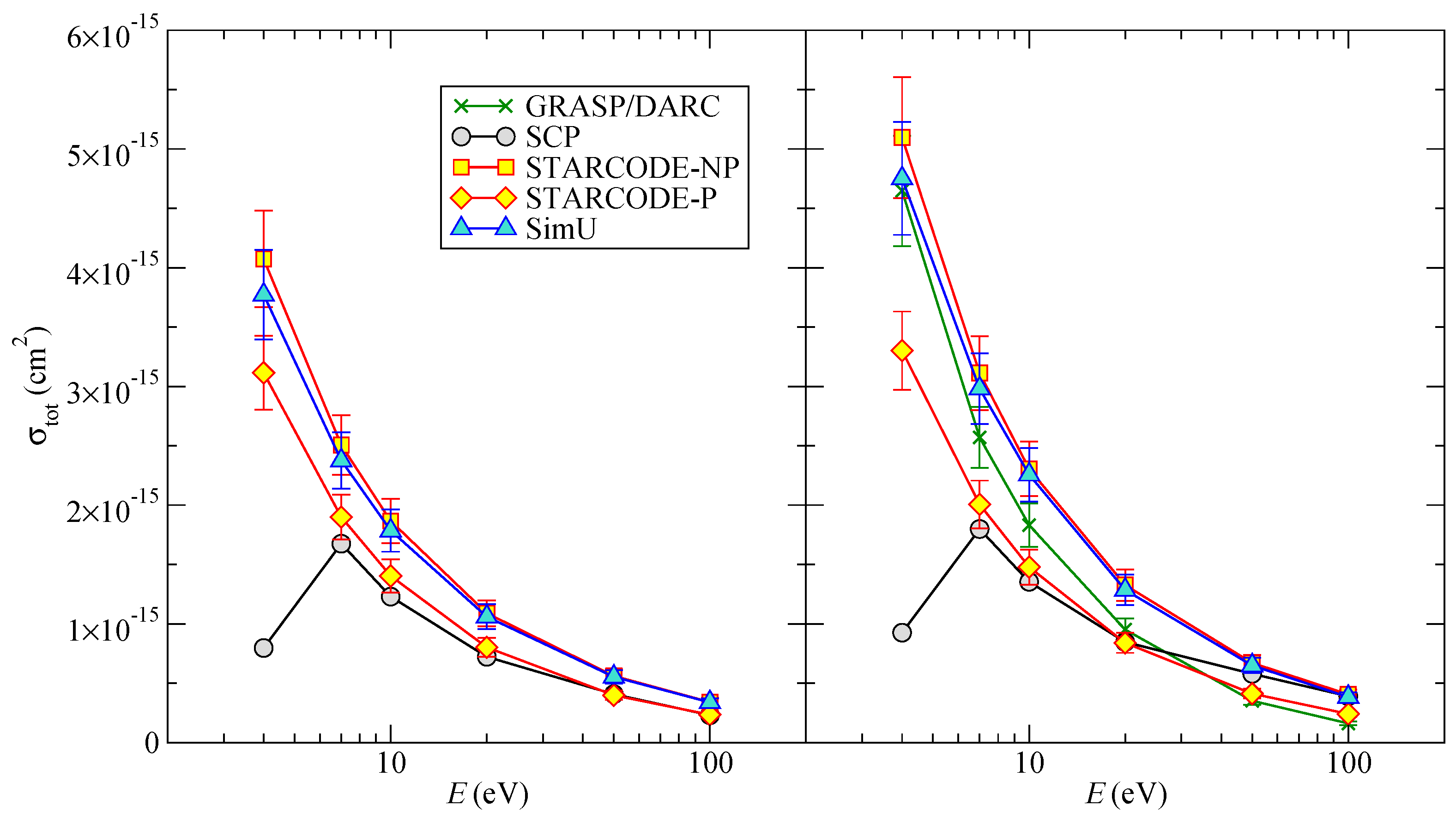
4.3.1. Total Cross-Section
The total cross-section is a sum over
L of the excitation, de-excitation, and the elastic pseudo cross-section:
As shown by
Figure 4, the difference between the codes is more pronounced than for the width and the shift.
4.3.2. Inelastic Excitation Cross-Section
The results of the calculations and of the experiment [
20] are shown in
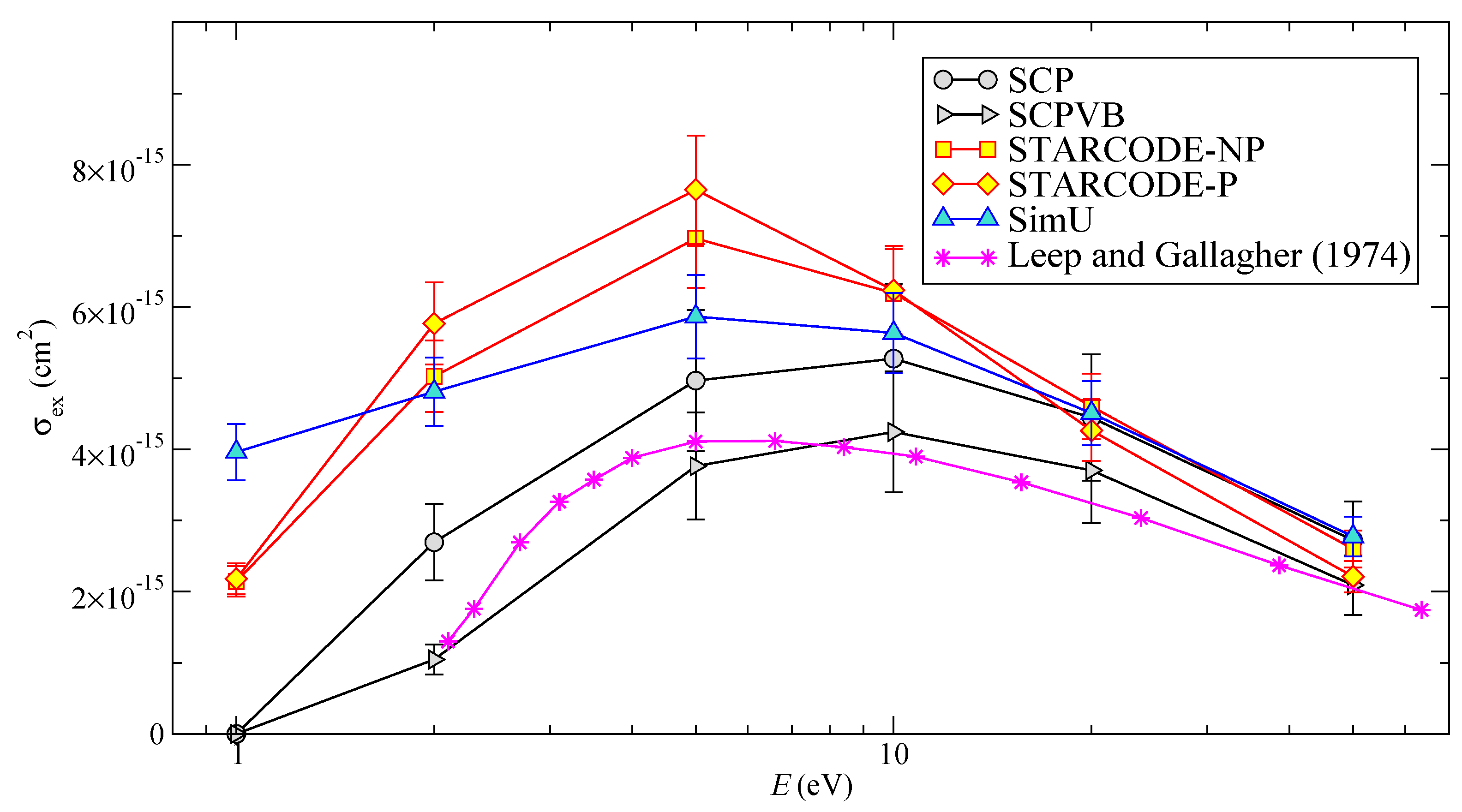
Figure 5. This comparison shows that the
SCPVB method improves the results of the ordinary
SCP inelastic cross-sections [
17], in particular due to the improvement of the symmetrization procedure, such that the
SCPVB results become rather close to the experimental values. Also, we note that
SCP and
SimU apparently have the same high-
E asymptote, which exceeds the experimental values by about one third.
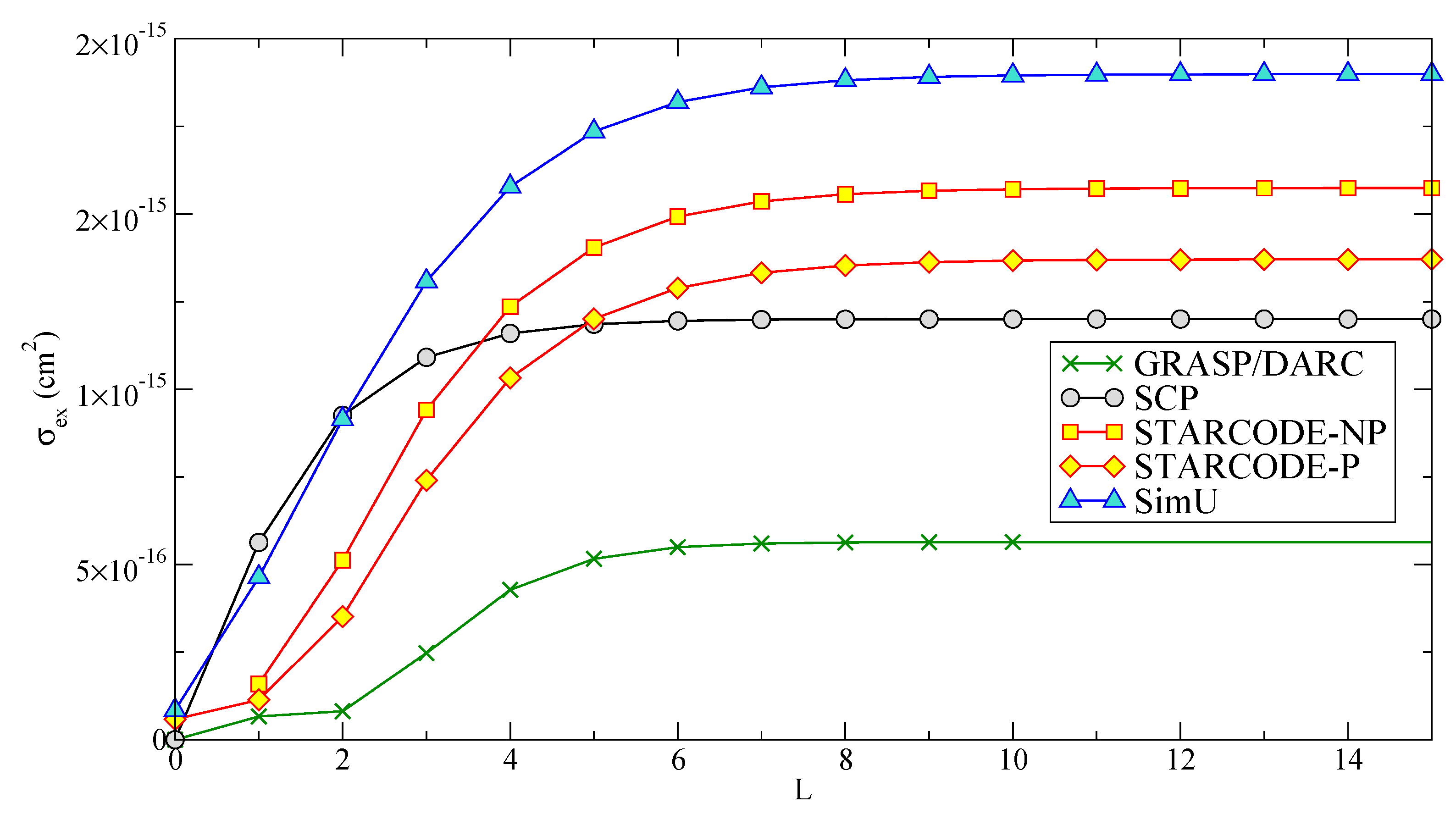
4.3.3. Partial Cumulative Excitation Cross-Section
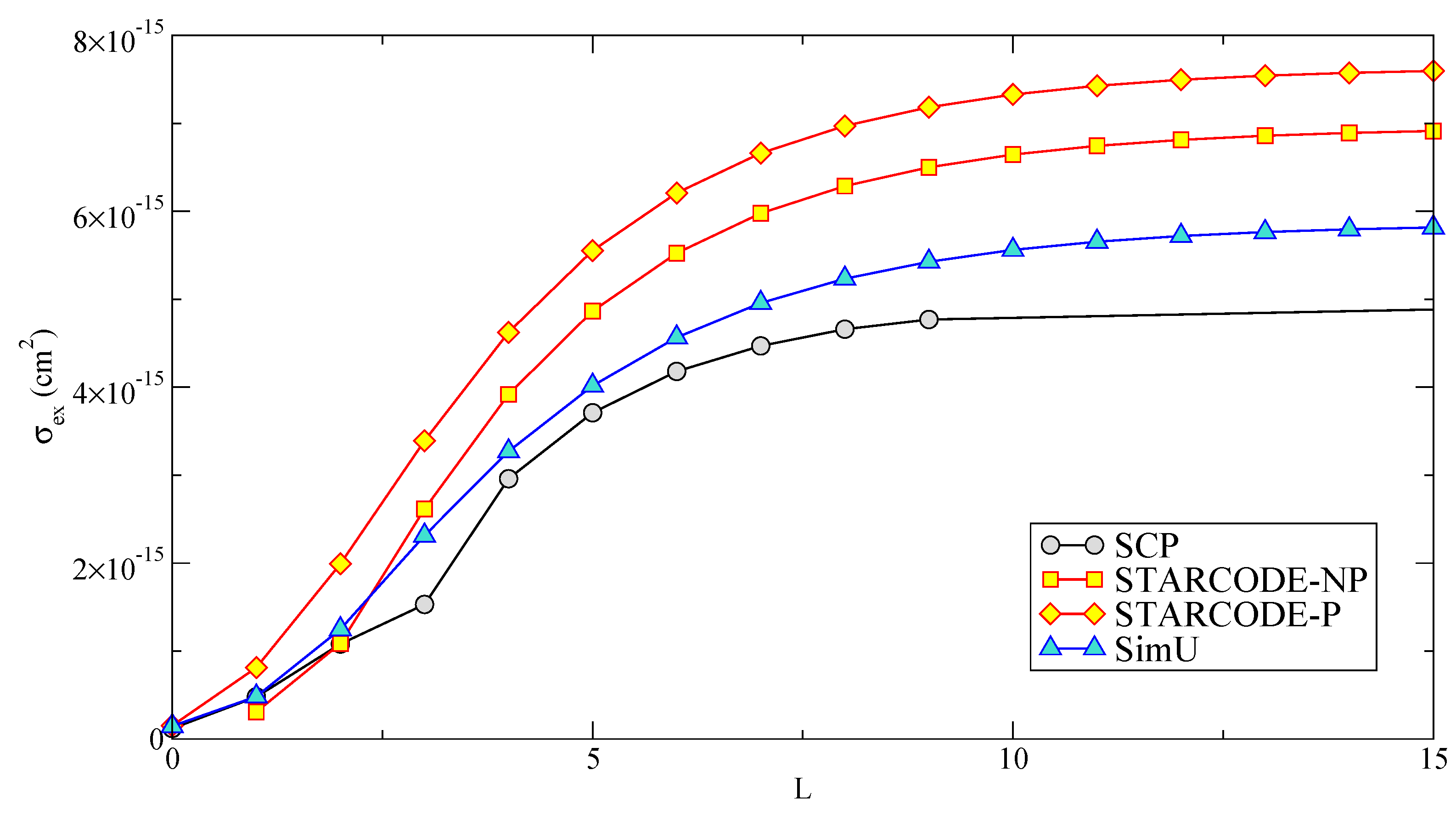
In the present paper, we show only a subset of the results, for
(
Figure 6). The figure shows that the contribution of the partial waves at first increases up to
and then decreases, with the sum converging at
L about 10. At the lower
, the sum over
L converges at
L about 5. At 10 eV, the sum converges for
L about 12–15, and at 20 eV, the sum converges at
. In general, the
S-wave (
) contribution is problematic for all SC codes based primarily on physical reasons. Indeed, for such an electron its “size”,
, is larger than the impact parameter, and hence, the picture of a classical particle breaks down. However, for the sake of the present code comparison, such calculations were performed where possible.
4.3.4. Elastic Pseudo Cross-Section
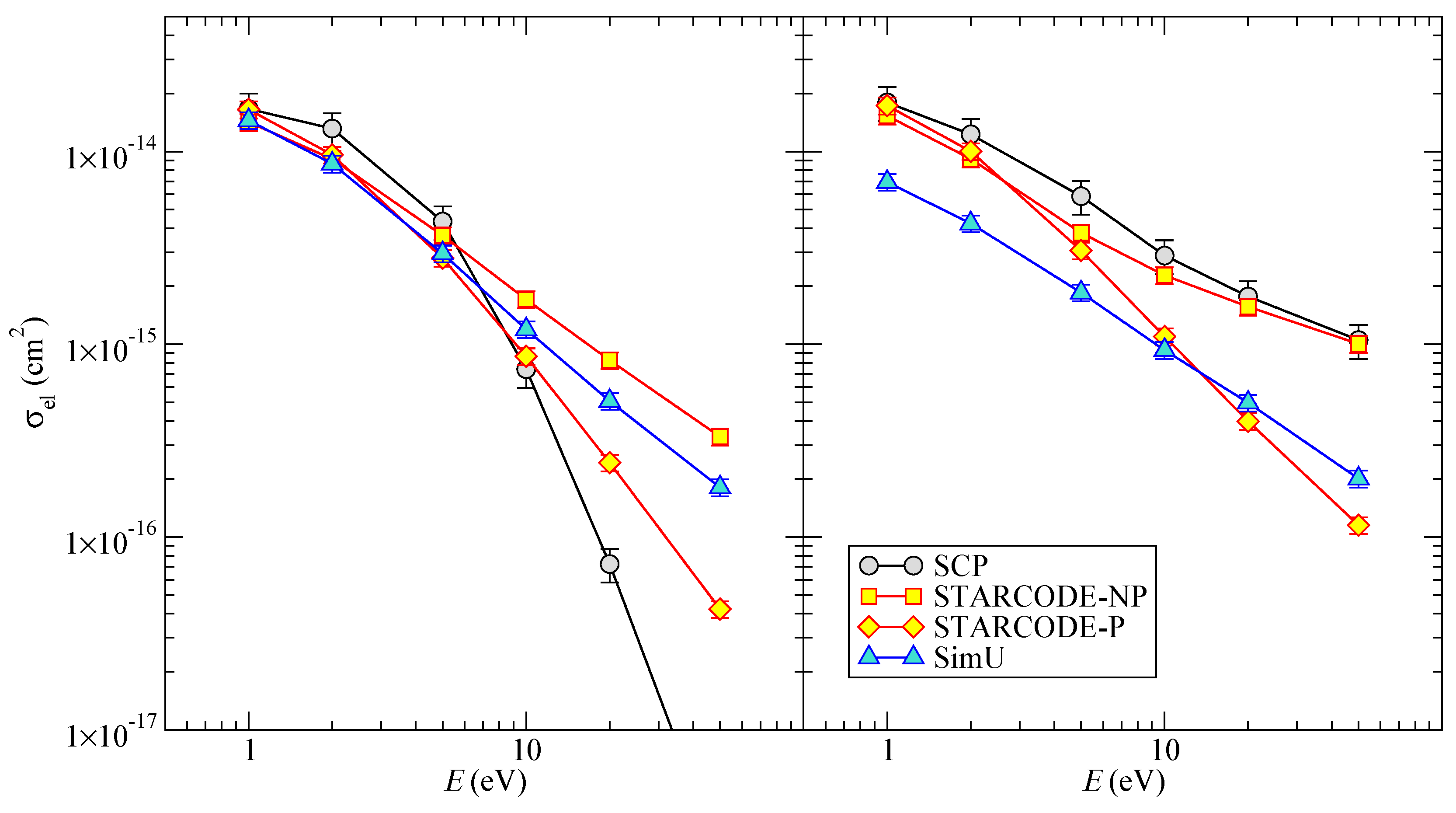
The elastic pseudo cross-sections are shown in
Figure 7. The differences between the results of the codes are more significant for elastic collisions than for inelastic ones. This is expected, because elastic (pseudo) cross-sections are very sensitive to close collisions. In addition the importance of the quadrupole interaction increases with energy, which was also expected, due to the range of the interaction:
for the dipole–dipole part, and
for the quadrupole part of the interaction. It is seen that at higher
E,
SCP and
STARCODE attribute higher relative importance to the quadrupole effect than
SimU. This explains the difference in the high-
E tails observed in
Figure 3.
5. B III
In this section, the main results of B III SLSP3 and SLSP4 are summarized. The electron density assumed is . The grid of the electron projectile energies is , 7, 10, 20, 30, 50, and 100 eV.
5.1. Width and Shift
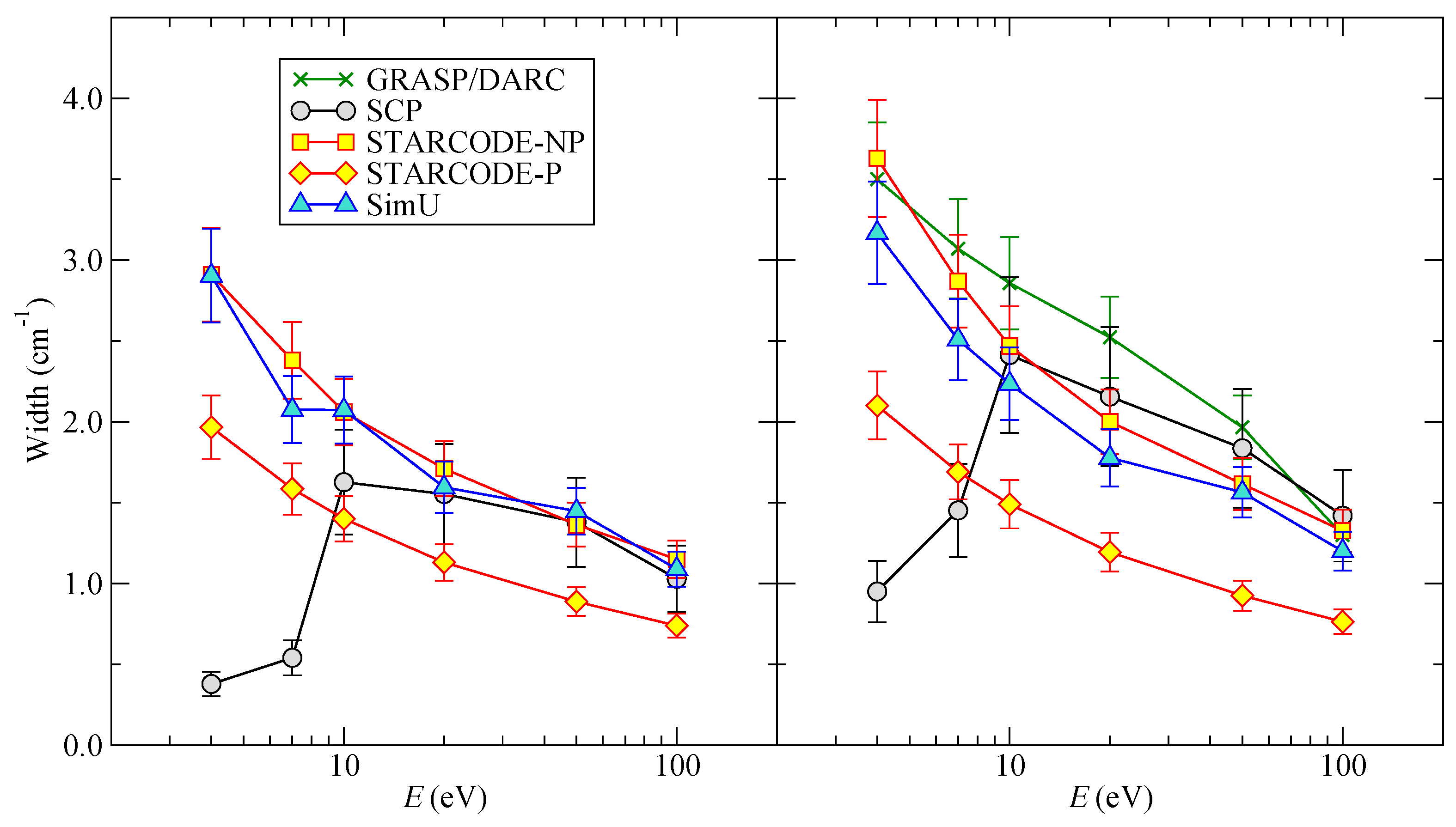
Figure 8 shows that semi-classical (SC) codes show a mutually good agreement. The low-
E deviation between
SCP and other SC can be explained by the symmetrization issue. The excitation part of the
SCP width is zero under the threshold. If Feshbach resonances were included as usual in the
SCP method for ions, the behavior of the
SCP width would be similar to the others and probably of the same order of magnitude.
GRASP/DARC cannot be calculated with dipole interaction only. Consequently, it appears only on the right part of
Figure 8. It agrees with the SC codes.
STARCODE-NP is of the same order of magnitude as SC ones, and, as expected,
STARCODE with penetration is smaller. The penetrating collisions are important for all energies. Similarly to the Li I results, the effect of the quadrupole interaction is not very important.
The B III
shifts are shown in
Figure 9. The
SCP shifts are significantly smaller than the shifts calculated by other SC codes. A source of this discrepancy remains unclear. Again,
GRASP/DARC is rather close to the other SC codes. Similar to the width, the effect of quadrupoles is minor for all codes.
5.2. Fractional Inelastic Width
Figure 10 shows results for the fractional inelastic width. If the dipole interaction is only taken into account, the results of all codes are very similar, corresponding to a major contribution of the inelastic collisions to the line broadening. However, with the quadrupole interaction taken into account, the spread between different calculations become much larger, with the
GRASP/DARC values significantly lower than the others, especially at lower energies. In addition,
SCP shows a behavior which qualitatively differs; the inclusion of Feshbach resonances, which were not taken into account in these calculations, might modify this comment, since it would increase the contribution of the dipole interaction under the excitation threshold. We should also recall that the inelastic quadrupole part is zero for
SCP, while
GRASP/DARC cannot separate the dipole part. We note that inclusion of the quadrupole interaction also worsens agreement between SC codes in the case of elastic pseudo cross-section of Li
(
Figure 7).
5.3. Cross-Sections
5.3.1. Total Cross-Section
The total cross-section is the sum of the total inelastic cross-section (excitation + de-excitation) and of the elastic pseudo cross-section. A comparison of the calculated results is shown in
Figure 11.
GRASP/DARC cannot separate dipole and quadrupole contributions. Therefore,
GRASP/DARC only appears on the right part of the figure. As for Li I,
SCP is zero under the threshold (6 eV for B III
), and the
SCP quadrupole part is zero. Its increasing behavior for low energies is explained by symmetrization and microreversibility.
5.3.2. Inelastic Excitation Cross-Section
Experimental B III
excitation cross-sections exist [
21]. However, we can only compare the SLSP4 calculations for the energy
, slightly above the threshold (6 eV). Looking at
Figure 2 of that paper, we see that the experimental cross-section is equal to
. The comparison between the experiment and the results of the calculations appears in
Table 2. It shows that all theoretical results, except
GRASP/DARC, are higher than the experimental ones by a factor varying between 1.5 to 2. The results of
GRASP/DARC reach the bottom of the error bar of the experimental result. This comparison shows that the origin of the puzzle between experimental and theoretical line widths is probably elsewhere.
5.3.3. Partial Cumulative Excitation Cross-Section
In the present paper, we will show only one example of the results: The chosen example is for
,
Figure 12. At 4 eV, under the threshold, the sum over
L converges at
L about 7. At 7 eV, the sum converges for
L about 10. At 20 eV, the sum converges at
L about 15. At 50 eV, the sum converges at
L about 30, and at 100 eV, the sum converges at
. This is expected, the higher the energy, the slower is the convergence.
5.3.4. Elastic Pseudo Cross-Section
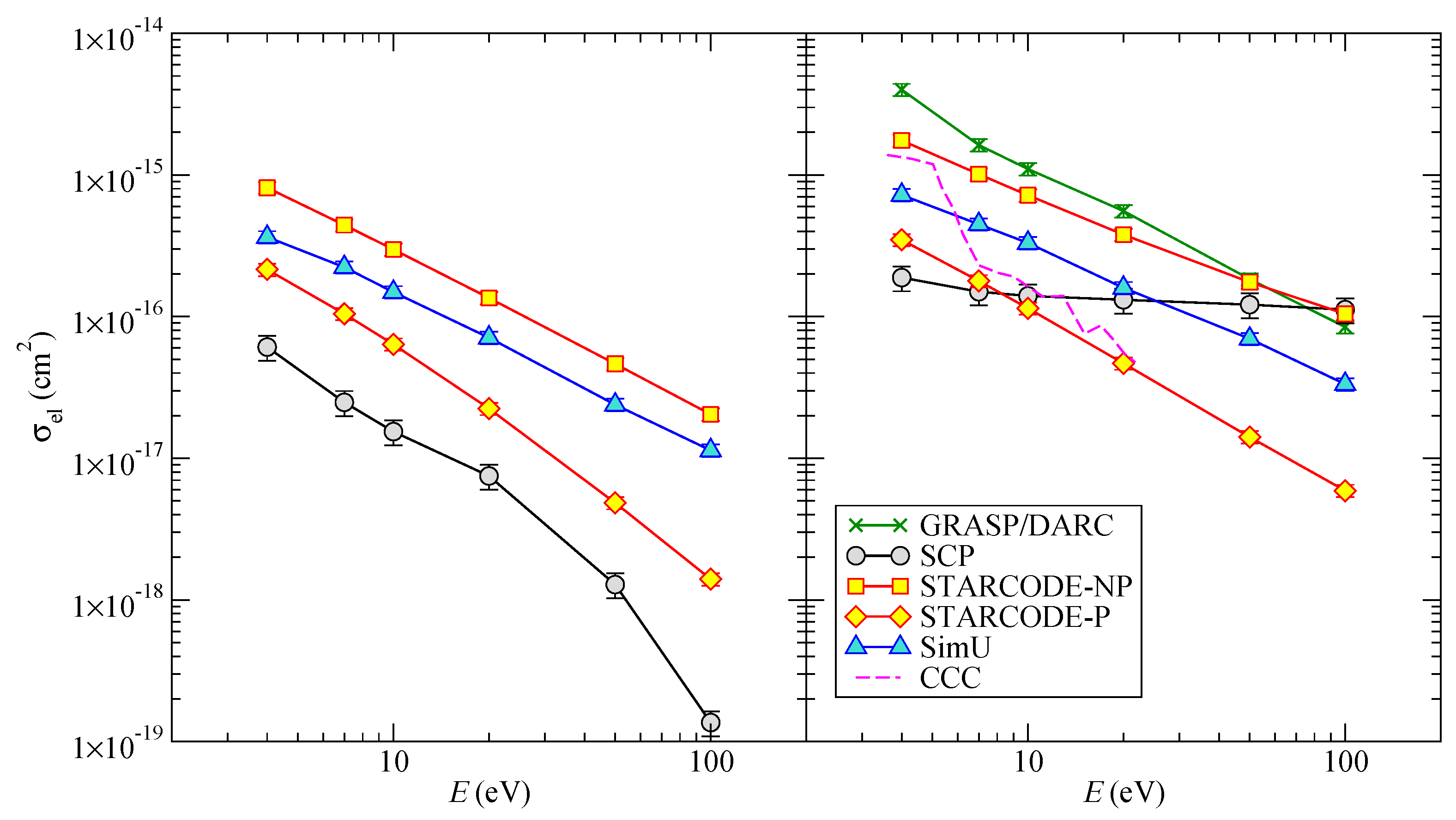
Figure 13 shows a large spread between the results of the different codes. In fact, close collisions are predominant for elastic collisions and this can explain this spread, because they are not well treated by approached methods. When the quadrupole part is taken into account, the
SCP behavior begins to increase with energy at relatively high energies, but remains small.
STARCODE-P results are the smallest, which is consistent with earlier results [
8].
GRASP/DARC results are the highest. This may explain why the
GRASP/DARC widths [
12] are not very different from those of approached methods. For comparison, fully quantum-mechanical results calculated by the convergent close coupling (
CCC) code [
22], as appeared in Ref. [
6], are shown. As noted in the previous SLSP workshops [
5], there are significant discrepancies between
CCC and
GRASP/DARC. In fact,
CCC seems to agree well with
STARCODE with penetration at high energies and
STARCODE without account of penetration for the lowest energy.
6. Conclusions
The present paper is only a brief summary of the results of SLSP3 and SLSP4 concerning isolated lines. In general, the agreement between the semiclassical codes is rather good as long as only the dipole interaction is accounted for. However, inclusion of the quadrupole term worsens the agreement, even though the relative importance of the quadrupole interaction is typically minor for the cases here considered. This implies a significant spread in the values of the quadrupole interaction alone as calculated by different approaches. It should be noted that the quadrupole interaction was introduced in the calculation cases defined for SLSP4 for the first time. Therefore, it is expected that progress in resolving the discrepancies will be made at the next, SLSP5, workshop. In addition, resolving disagreements between fully quantal calculations is an important task in establishing benchmark values.
Author Contributions
Each author performed calculations and provided results using their respective code: GRASP/DARC—B.D.; SCP—S.S.-B. and M.S.D.; SCPVB—V.B.; STARCODE—S.A.; SimU—E.S. All authors participated in the discussions and in the preparation of the manuscript.
Acknowledgments
All the participants of SLSP are warmly thanked for numerous discussions during the workshops. The organizational and financial support from the International Atomic Energy Agency for conducting the SLSP workshops is highly appreciated and gratefully acknowledged. This work has also been supported by the Paris Observatory, the PADC (Paris Data Center-OV), the CNRS and the “Programme National de Physique Stellaire” (PNPS) of CNRS/INSU, CEA and CNES, France. A part of this work has also been supported by the LABEX Plasma project and has received financial state aid managed by the Agence Nationale de la Recherche, as part of the programe “Investissements d’avenir” under reference ANR-11-IDEX-0004-02. This work has also been supported by the VAMDC (Virtual Atomic and Molecular Data Centre). VAMDC is funded under the Combination of Collaborative Projects and Coordination and Support Actions Funding Scheme of The Seventh Framework Program. Call topic: INFRA-2008-1.2.2 Scientific Data Infrastructure, Grant Agreement number: 239108. The support of the Ministry of Education, Science and Technological Development of the Republic of Serbia through project 176002 is gratefully acknowledged. The work of E.S. was supported in part by the Israel Science Foundation.
Conflicts of Interest
The authors declare no conflicts of interest
References
- Spectral Line Shapes in Plasmas Workshops. Available online: http://plasma-gate.weizmann.ac.il/slsp/ (accessed on 18 March 2018).
- Stambulchik, E. Review of the 1st Spectral Line Shapes in Plasmas code comparison workshop. High Energy Density Phys. 2013, 9, 528–534. [Google Scholar] [CrossRef]
- Stambulchik, E.; Calisti, A.; Chung, H.K.; González, M.Á. Special Issue on Spectral Line Shapes in Plasmas. Atoms 2014, 2, 378–381. [Google Scholar] [CrossRef]
- 4th Spectral Line Shapes in Plasmas Code Comparison Workshop, Call for Submissions. Available online: http://plasma-gate.weizmann.ac.il/uploads/slsp/4/cases.pdf (accessed on 18 March 2018).
- Alexiou, S.; Dimitrijević, M.S.; Sahal-Brechot, S.; Stambulchik, E.; Duan, B.; González-Herrero, D.; Gigosos, M.A. The Second Workshop on Lineshape Code Comparison: Isolated lines. Atoms 2014, 2, 157–177. [Google Scholar] [CrossRef]
- Griem, H.R.; Ralchenko, Y.V.; Bray, I. Stark broadening of the B III 2s − 2p lines. Phys. Rev. E 1997, 56, 7186–7192. [Google Scholar] [CrossRef]
- Griem, H.R.; Ralchenko, Y.V. Electron collisional broadening of isolated lines from multiply-ionized atoms. J. Quant. Spectrosc. Radiat. Transf. 2000, 65, 287–296. [Google Scholar] [CrossRef]
- Alexiou, S.; Lee, R.W.; Glenzer, S.H.; Castor, J.I. Analysis of discrepancies between quantal and semiclassical calculations of electron impact broadening in plasmas. J. Quant. Spectrosc. Radiat. Transf. 2000, 65, 15–22. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database (Version 5.4). Available online: http://physics.nist.gov/asd/ (accessed on 1 December 2016).
- Cowan, R.D. The Theory of Atomic Structure and Spectra; University of California Press: Berkeley, CA, USA; Los Angeles, CA, USA; London, UK, 1981. [Google Scholar]
- Stambulchik, E.; Maron, Y. Effect of high-n and continuum eigenstates on the Stark effect of resonance lines of atoms and ions. Phys. Rev. A 1997, 56, 2713–2719. [Google Scholar] [CrossRef]
- Duan, B.; Bari, M.A.; Wu, Z.; Yan, J. Electron-impact widths and shifts of B iii 2p–2s lines. Atoms 2014, 2, 207–214. [Google Scholar] [CrossRef]
- Dyall, K.G.; Grant, I.P.; Johnson, C.T.; Parpia, F.A.; Plummer, E.P. GRASP: A general-purpose relativistic atomic structure program. Comput. Phys. Commun. 1989, 55, 425–456. [Google Scholar] [CrossRef]
- Sahal-Bréchot, S.; Dimitrijević, M.S.; Ben Nessib, N. Widths and shifts of isolated lines of neutral and ionized atoms perturbed by collisions with electrons and ions: An outline of the semiclassical perturbation (SCP) method and of the approximations used for the calculations. Atoms 2014, 2, 225–252. [Google Scholar] [CrossRef]
- Seaton, M.J. The impact parameter method for electron excitation of optically allowed atomic transitions. Proc. Phys. Soc. 1962, 79, 1105–1117. [Google Scholar] [CrossRef]
- Fleurier, C.; Sahal-Brechot, S.; Chapelle, J. Stark profiles of some ion lines of alkaline earth elements. J. Quant. Spectrosc. Radiat. Transf. 1977, 17, 595–604. [Google Scholar] [CrossRef]
- Bommier, V. Semi-Classical Collision Formalism with Energy and Momentum Transfer; Solar Polarization 4; Casini, R., Lites, B.W., Eds.; ASP Conference Series; Astronomical Society of the Pacific: San Francisco, CA, USA, 2006; Volume 358, pp. 245–255. [Google Scholar]
- Alexiou, S.; Lee, R.W. Semiclassical calculations of line broadening in plasmas: Comparison with quantal results. J. Quant. Spectrosc. Radiat. Transf. 2006, 99, 10–20. [Google Scholar] [CrossRef]
- Stambulchik, E.; Maron, Y. A study of ion-dynamics and correlation effects for spectral line broadening in plasma: K-shell lines. J. Quant. Spectrosc. Radiat. Transf. 2006, 99, 730–749. [Google Scholar] [CrossRef]
- Leep, D.; Gallagher, A. Electron excitation of the lithium 6708-Å resonance line. Phys. Rev. A 1974, 10, 1082–1090. [Google Scholar] [CrossRef]
- Woitke, O.; Djurić, N.; Dunn, G.H.; Bannister, M.E.; Smith, A.C.H.; Wallbank, B.; Badnell, N.R.; Pindzola, M.S. Absolute cross sections for excitation of the 2s2S → 2p2P transition in B2+ and for electron-impact single ionization of B2+. Phys. Rev. A 1998, 58, 4512–4517. [Google Scholar] [CrossRef]
- Bray, I.; Fursa, D.V.; Kheifets, A.S.; Stelbovics, A.T. Electrons and photons colliding with atoms: Development and application of the convergent close-coupling method. J. Phys. B At. Mol. Opt. Phys. 2002, 35, R117. [Google Scholar] [CrossRef]
Figure 1.
Li I FWHM as a function of the energy E. (Left) the dipole interaction is only taken into account; (Right) the dipole and quadrupole interaction are both taken into account.
Figure 1.
Li I FWHM as a function of the energy E. (Left) the dipole interaction is only taken into account; (Right) the dipole and quadrupole interaction are both taken into account.
Figure 2.
Li I shift as a function of the energy E. (Left) the dipole interaction is only taken into account; (Right) the dipole and quadrupole interaction are both taken into account.
Figure 2.
Li I shift as a function of the energy E. (Left) the dipole interaction is only taken into account; (Right) the dipole and quadrupole interaction are both taken into account.
Figure 3.
Li I fractional inelastic width as a function of energy E. (Left) only the dipole interaction is taken into account; (Right) the dipole and quadrupole interactions are both taken into account.
Figure 3.
Li I fractional inelastic width as a function of energy E. (Left) only the dipole interaction is taken into account; (Right) the dipole and quadrupole interactions are both taken into account.
Figure 4.
Li I total cross-section as a function of the energy E. (Left) the dipole interaction is only taken into account; (Right) the dipole and quadrupole interaction are both taken into account.
Figure 4.
Li I total cross-section as a function of the energy E. (Left) the dipole interaction is only taken into account; (Right) the dipole and quadrupole interaction are both taken into account.
Figure 5.
Li I
excitation cross-section as a function of the energy
E: comparison with experiment [
20].
Figure 5.
Li I
excitation cross-section as a function of the energy
E: comparison with experiment [
20].
Figure 6.
Li I cumulative partial excitation cross-section as a function of L, for an energy equal to 5 eV.
Figure 6.
Li I cumulative partial excitation cross-section as a function of L, for an energy equal to 5 eV.
Figure 7.
Li I elastic pseudo cross-section as a function of energy E. (Left) only the dipole interaction is taken into account; (Right) the dipole and quadrupole interaction are both taken into account.
Figure 7.
Li I elastic pseudo cross-section as a function of energy E. (Left) only the dipole interaction is taken into account; (Right) the dipole and quadrupole interaction are both taken into account.
Figure 8.
B III FWHM as a function of the energy E. (Left) only the dipole interaction is taken into account; (Right) the dipole and quadrupole interaction are both taken into account.
Figure 8.
B III FWHM as a function of the energy E. (Left) only the dipole interaction is taken into account; (Right) the dipole and quadrupole interaction are both taken into account.
Figure 9.
B III shift as a function of the energy E. (Left) only the dipole interaction is taken into account; (Right) the dipole and quadrupole interaction are both taken into account.
Figure 9.
B III shift as a function of the energy E. (Left) only the dipole interaction is taken into account; (Right) the dipole and quadrupole interaction are both taken into account.
Figure 10.
B III fractional inelastic width as a function of energy E. (Left) only the dipole interaction is taken into account; (Right) the dipole and quadrupole interaction are both taken into account.
Figure 10.
B III fractional inelastic width as a function of energy E. (Left) only the dipole interaction is taken into account; (Right) the dipole and quadrupole interaction are both taken into account.
Figure 11.
B III total cross-section as a function of the energy E. (Left) only the dipole interaction is taken into account; (Right) the dipole and quadrupole interaction are both taken into account.
Figure 11.
B III total cross-section as a function of the energy E. (Left) only the dipole interaction is taken into account; (Right) the dipole and quadrupole interaction are both taken into account.
Figure 12.
B III cumulative excitation cross-section as a function of L, for an energy equal to 7 eV.
Figure 12.
B III cumulative excitation cross-section as a function of L, for an energy equal to 7 eV.
Figure 13.
B III elastic pseudo cross-section as a function of the energy E. (Left) only the dipole interaction is taken into account; (Right) the dipole and quadrupole interaction are both taken into account.
Figure 13.
B III elastic pseudo cross-section as a function of the energy E. (Left) only the dipole interaction is taken into account; (Right) the dipole and quadrupole interaction are both taken into account.
Table 1.
Atomic data used for the calculations: transition energies , absorption oscillator strengths f, and the reduced quadupole matrix elements .
Table 1.
Atomic data used for the calculations: transition energies , absorption oscillator strengths f, and the reduced quadupole matrix elements .
| Species | Transition | () | f | |
|---|
| Li I | | 14,903.89 | 0.7472 | |
| B III | | 48,381.07 | 0.3629 | |
Table 2.
B III excitation cross-sections for .
Table 2.
B III excitation cross-sections for .
| Code | () | Code/Experiment [21] Ratio |
|---|
| GRASP/DARC | 0.56 | 0.66 |
| SCP | 1.19 | 1.40 |
| STARCODE-NP | 1.57 | 1.84 |
| STARCODE-P | 1.37 | 1.57 |
| SimU | 1.90 | 2.20 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).