Dielectronic Recombination Strengths and Plasma Rate Coefficients of Lithium-like Argon Ions: Theory and Experiment

Abstract

Dielectronic recombination (DR) is widely recognized as a fundamental atomic process in many astrophysical and laboratory plasmas, where it plays a crucial role in determining ionization balance and level populations over a broad temperature range. Reliable DR resonance strengths and plasma rate coefficients for such plasma modeling can be computed using the Jena Atomic Calculator (JAC)—a relativistic code based on the multiconfiguration Dirac–Hartree–Fock (MCDHF) method. In this work, we investigate the DR of Li-like Ar¹⁵⁺ ions in their ground state (2s), focusing on resonances associated with the fine-structure core excitations $2s_{1/2}\to 2p_{1/2,3/2}$. The resulting fine-structure-resolved DR resonance strengths and plasma rate coefficients are in good agreement with recent high-resolution DR measurements of Ar¹⁵⁺ ions performed at the Main Cooler Storage Ring (CSRm) in Lanzhou, China. These results provide a stringent benchmark for JAC calculations and support their applicability in plasma modeling.

1. Introduction

Astrophysical plasmas are broadly categorized into two main categories [1]: (i) collisionally ionized plasmas and (ii) photoionized plasmas. Collisionally ionized plasmas [2] occur in diverse astrophysical environments, such as stellar atmospheres, supernova remnants, galaxies, and the intracluster medium (ICM) of galaxy clusters. Photoionized plasmas [3], by contrast, are typically observed in planetary nebulae, X-ray binary systems, and active galactic nuclei (AGN). Atomic physics underpins the interpretation of complex spectra from both plasma types, and the rapid advancement of observational capabilities enabled by next-generation telescopes has substantially heightened the demand for accurate, comprehensive, and versatile atomic data [4,5]. Dielectronic recombination (DR) is a fundamental atomic process that serves as a primary electron–ion recombination mechanism in plasmas and plays a critical role in the reliable modeling of plasma properties, including ionization balance and radiative characteristics [6].

Building on the seminal work of Burgess [7], who proposed a general empirical formulation for DR, parameterized expressions for DR rate coefficients were initially developed primarily for hydrogen-like and helium-like ions. Systematic dielectronic recombination (DR) studies became feasible in the early 1990s with the advent of merged-beam experiments at heavy-ion storage rings, which enabled high-resolution measurements that resolve fine-structure resonances in DR cross-sections [8]. These experimental advances have revealed the limitations of earlier theoretical data and, together with the steadily improving resolution of astronomical observations, have imposed stringent accuracy requirements on the DR rate coefficients employed in plasma modeling [9]. Consequently, the extensive DR data required today are largely generated by state-of-the-art, level-resolved theoretical calculations [10], whose reliability must be benchmarked against high-precision laboratory measurements [11]. Despite substantial experimental progress over the past three decades [12,13,14,15], the accurate theoretical characterization of low-lying DR resonances and their associated plasma rate coefficients remains a key challenge in modern atomic theory. To address these challenges, theoretical methodologies have evolved from nonrelativistic models to fully relativistic approaches, enabling level-resolved calculations of DR cross-sections. Accurate theoretical predictions and reliable assignments of well-resolved DR resonances not only enhance the fidelity of plasma modeling but also provide deeper insight into recombination mechanisms and fundamental effects, such as electron correlation [16]. To streamline calculations for multiply charged or highly charged ions along isoelectronic sequences, the Jena Atomic Calculator (JAC) [17]—a versatile atomic-structure code based on the multiconfiguration Dirac–Hartree–Fock (MCDHF) method—was developed to enable rapid and reliable evaluation of DR rate coefficients for plasma modeling [18,19]. Compared with other existing codes, JAC offers significantly simpler handling and control of different approximations, shell structures, and temperature regimes where doubly excited resonances must be considered.

Although lithium-like ions possess a relatively simple three-electron structure, their DR processes exhibit remarkably rich physics. The DR of lithium-like ions has therefore been investigated extensively, both experimentally and theoretically; here we briefly summarize the key findings. Early single-pass merged-beam experiments with limited energy resolution for Li-like B²⁺, C³⁺, N⁴⁺, and O⁵⁺ ions [20] showed overall agreement with configuration-averaged distorted-wave calculations, while clearly demonstrating the importance of intermediate coupling compared with pure LS coupling [21]. Subsequent high-resolution storage-ring measurements at TSR and CRYRING, employing the merged-beam technique, achieved energy resolutions sufficient to disentangle $\Delta n=0$ and $\Delta n=1$ resonances as well as their fine-structure components, covering ions from C³⁺ [22,23] up to Ar¹⁵⁺ [24] and even heavier systems such as Ni²⁵⁺ [25]. These studies further underscored the necessity of fully relativistic calculations for accurately reproducing individual resonance positions and widths. Moreover, DR experiments have provided a powerful tool for probing nuclear effects, including hyperfine splitting in Sc¹⁸⁺ ions [26] and isotopic shifts in Nd⁵⁷⁺ ions [27].

In this work, we present a benchmark study of DR resonance strengths for Li-like Ar¹⁵⁺ associated with the fine-structure $2s_{1/2}\to 2p_{1/2,3/2}$ core excitations, using the relativistic JAC code. The theoretical results are compared with high-resolution experimental data acquired at the main cooler storage ring (CSRm) of the Heavy Ion Research Facility in Lanzhou (HIRFL), China. The calculated resonance strengths for the $2p_{1/2}n\ell$ and $2p_{3/2}n\ell$ Rydberg series show very good agreement with the experimental measurements. In addition, we derive total DR plasma rate coefficients for the $\Delta n=0$ core excitation of Ar¹⁵⁺ ions initially in the $1s^{2}2s{}^{2}S_{1/2}$ ground state. The resulting plasma rate coefficients span temperatures of ${10}^3$ to ${10}^7$ K, relevant to both photoionized [3] and collisionally ionized plasmas [2], and show good agreement with experimentally derived values. This paper is structured as follows: Section 2 outlines the theoretical framework, experimental setup, and DR data analysis; Section 3 presents the results and discussion; and Section 4 provides a concise summary.

2. Theory and Experiment

2.1. Theory

DR is a resonant two-step electron–ion recombination process, which can be described as follows [1]:

$$A^{q+}\left(i\right)+e^{-}\to {\left[A^{(q-1)+}\right]}^{\ast \ast }\left(d\right)\to A^{(q-1)+(\ast )}\left(f\right)+\hslash \omega .$$

(1)

In the first step, a free electron is resonantly captured by the initial target ion $A^{q+}$ while a bound electron is simultaneously excited, forming a doubly excited intermediate state ${\left[A^{(q-1)+}\right]}^{\ast \ast }\left(d\right)$. In the second step, this intermediate state is stabilized via radiative decay, yielding a recombined ion in a bound final state $A^{(q-1)+(\ast )}\left(f\right)$ that lies below the first ionization limit.

Within the independent-resonance approximation (IRA) [28], the partial DR strength for the transition from an initial state i, via the doubly excited resonance state d, to a final bound state f is expressed as [18]

$$\begin{array}{c}\hfill S(i\to d\to f)={\displaystyle \frac{{\pi }^2{\hslash }^3}{2m_{\mathrm{e}}{E}_{\mathrm{d}}}}{\displaystyle \frac{g_d}{g_i}}{A}_a(d\to i){\displaystyle \frac{A_r(d\to f)}{{\mathrm{\Gamma }}_d}},\end{array}$$

(2)

where $E_{\mathrm{d}}$ is the resonance energy, i.e., the kinetic energy of the incident electron in the ion rest frame; $g_i$ and $g_d$ are the statistical weights of the initial and resonance states, respectively; $A_a(d\to i)$ and $A_r(d\to f)$ denote the autoionization and radiative decay rates. ${\mathrm{\Gamma }}_d=\hslash \left({\mathrm{\Gamma }}_d^{\mathrm{auto}}+{\mathrm{\Gamma }}_d^{\mathrm{rad}}\right)$ is the natural linewidth of the resonance state d, with ${\mathrm{\Gamma }}_d^{\mathrm{auto}}$ and ${\mathrm{\Gamma }}_d^{\mathrm{rad}}$ representing the total autoionization and radiative decay rates, respectively; ℏ is the reduced Planck constant; and $m_e$ is the electron rest mass. Within the JAC framework [17,18], calculations start with the construction of the ionic Hamiltonian, where electron–electron correlations are included via the Dirac–Coulomb interaction. In the present study, the Breit interaction is fully incorporated. Subsequently, Auger decay rates and radiative transition rates are computed using lowest-order perturbation theory, with the radiative contribution limited to electric dipole (E1) transitions between the relevant levels.

In storage-ring merged-beam DR experiments, the final states of recombined ions are typically unresolved. This approach naturally leads to the definition of the total resonance strength,

$$S(i\to d)=\sum _{f}S(i\to d\to f),$$

(3)

which sums over all final states f. This formulation is particularly suitable when the energy-dependent DR cross-section exhibits a Lorentzian line shape—or a similar distribution—centered at the resonance energy $E\approx E_d$.

$$\sigma (E\approx E_d)=S(i\to d){\displaystyle \frac{\mathrm{\Gamma }/2\pi }{{(E_d-E)}^2+{\mathrm{\Gamma }}_d^2/4}}.$$

(4)

This approximation is well-justified when the natural width ${\mathrm{\Gamma }}_d$ of the resonance state d is smaller than or comparable to the energy spread of the incident electron beam.

Theoretical DR and plasma recombination rate coefficients are calculated by folding the recombination cross-section $\sigma \left(v\right)$ with the relevant electron velocity distribution,

$$\alpha =\int v\sigma \left(v\right)f\left(v\right)d^{3}v,$$

(5)

where $f\left(v\right)$ represents the electron velocity distribution. In order to compare with merged-beam DR measurements, $f\left(v\right)$ is modeled by a flattened Maxwellian distribution that characterizes the electron beam and is specified by the longitudinal and transverse temperatures $k_B{T}_{\Vert }$ and $k_B{T}_{\perp }$, respectively [29]. For comparison with experimentally inferred plasma recombination rate coefficients, which depend on the plasma temperature, an isotropic Maxwellian velocity distribution is adopted for $f\left(v\right)$ [8]. In the present DR calculations for Li-like Ar¹⁵⁺ ions, the fine-structure core excitations $2s_{1/2}\to 2p_{1/2}$ and $2s_{1/2}\to 2p_{3/2}$ were treated as independent recombination channels. Resonances converging to these thresholds at high principal quantum numbers ($n>25$) were described using quantum defect theory (QDT), which enables efficient treatment of both Auger decay and radiative stabilization rates [30]. Prior to the evaluation of the final DR cross-sections, the theoretical excitation energies of the $2p_{1/2}$ and $2p_{3/2}$ fine-structure core levels were adjusted to their experimentally established spectroscopic values [18,31]. The applied energy shifts in this work were $-0.13$ eV for the $2p_{1/2}$ level and $-0.28$ eV for the $2p_{3/2}$ level.

2.2. Experiment

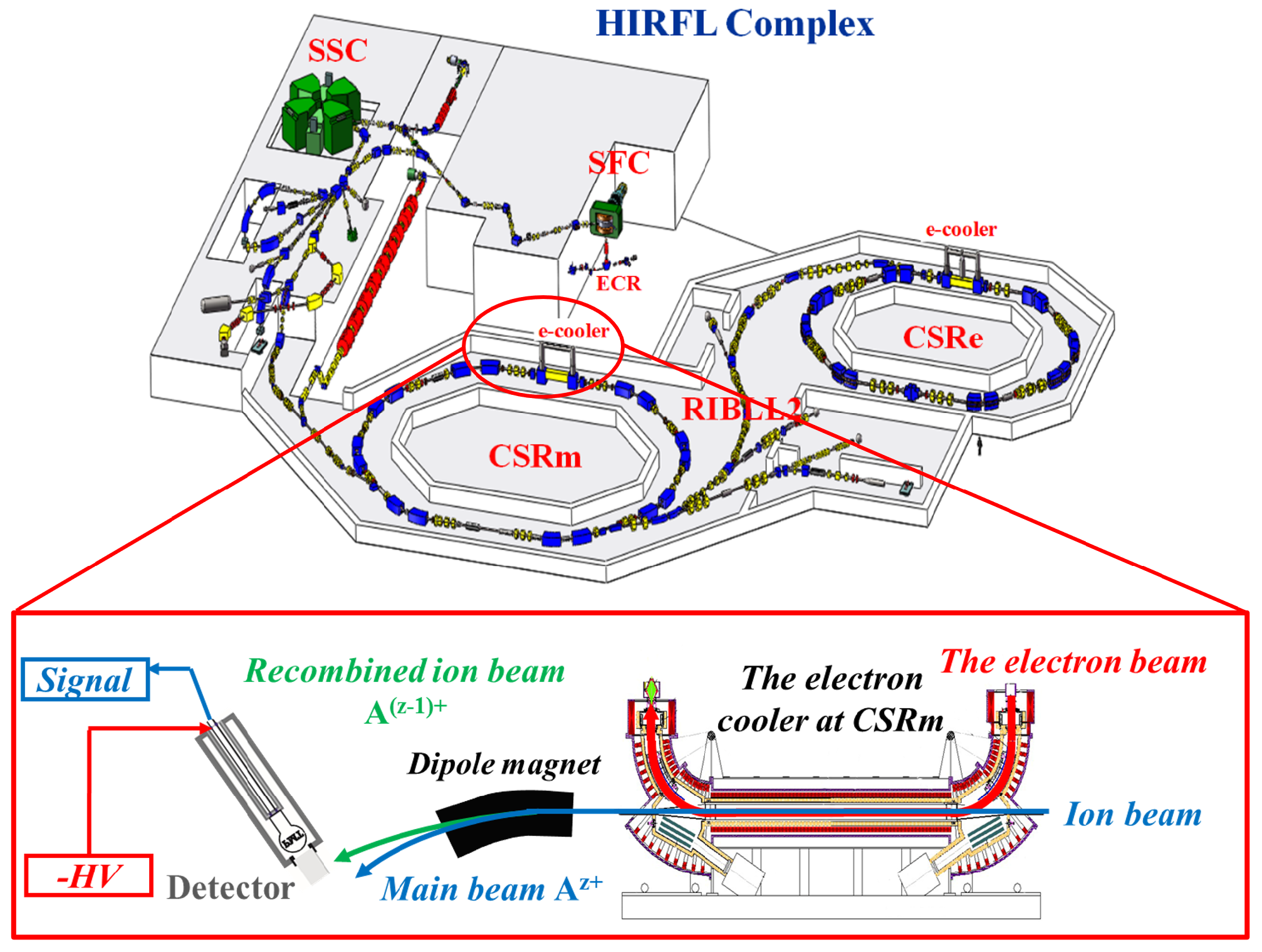
The experiment was performed at the HIRFL-CSRm of the Institute of Modern Physics (IMP), Chinese Academy of Sciences (CAS), Lanzhou, China. A schematic of the experimental setup is presented in Figure 1. Lithium-like Ar¹⁵⁺ ions were generated directly by a superconducting electron cyclotron resonance (ECR) ion source, accelerated via the sector-focused cyclotron (SFC), and subsequently injected into CSRm at a kinetic energy of 8.50 MeV/u. Typical stored beam currents ranged from 150 to 200 µA, corresponding to approximately (4.0–5.0) × 10⁸ ions.

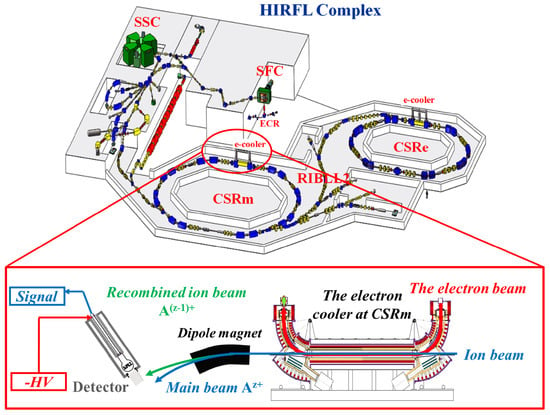
Figure 1. The DR experimental setup at HIRFL-CSRm. The lithium-like argon ions, produced from an ECR ion source, were accelerated by the SFC and then injected into the CSRm with a beam energy of 8.50 MeV/u. The electron cooler EC-35 was employed to cool the ion beam and was also used as a free-electron target in the DR measurements. The recombined ions, formed in the straight section of the electron cooler, were then separated from the primary ion beam in the first dipole magnet downstream of the electron cooler and detected by the particle detectors (YAP: Ce+ PMT).

The electron beam was generated by a hot-cathode electron gun and underwent adiabatic expansion as it propagated from a magnetic field of 125 mT in the gun region to 39 mT in the cooling section. This expansion yielded a low-temperature electron beam, facilitating high-resolution DR measurements. After injection, continuous interaction with the velocity-matched electron beam ($v_e=v_{\mathrm{ion}}$) established a dynamic balance between electron cooling and intrabeam scattering, reducing the relative ion-beam momentum spread to $\Delta p/p\sim 2\times {10}^{-4}$. To scan the relative collision energy, a detuning voltage $U_d$ was applied to the main high-voltage terminal of the electron cooler, shifting the electron energy away from the cooling condition and establishing a well-defined electron–ion relative energy.

Recombined ions generated in the interaction region propagated along the beamline and entered a downstream triplet dipole magnet. Due to their altered charge states, these recombined ions were spatially separated from the circulating primary beam and detected by a scintillation detector (YAP:Ce coupled to a photomultiplier tube, PMT), as illustrated in Figure 1. The overall detection efficiency was close to 100%. The absolute electron–ion recombination rate coefficient as a function of the electron–ion collision energy was extracted from the background-subtracted ${\mathrm{Ar}}^{14+}$ count rate R [32,33,34] according to

$${\alpha }_{\exp }\left(E\right)={\displaystyle \frac{RC}{N_i{n}_e(1-{\beta }_e{\beta }_i)L}},$$

(6)

where $N_i$ denotes the number of stored ions and $n_e$ is the electron beam density. The quantities ${\beta }_e=v_e/c$ and ${\beta }_i=v_{\mathrm{ion}}/c$ represent the laboratory-frame velocities of the electron and ion beams, respectively. The parameters $L=4.0$ m and $C=161.0$ m correspond to the effective interaction length and the circumference of the storage ring. The overall uncertainty of the experimentally determined recombination rate coefficient is estimated to be approximately 30% [15,35]. The dominant sources of uncertainty arise from the electron density profile, the electron and ion beam current determinations, the effective interaction length, and the ion-beam alignment, while the contribution from statistical counting uncertainties is comparatively small; see Ref. [15].

The DR contribution was isolated by subtracting the radiative recombination (RR) component from the measured total recombination rate coefficient:

$${\alpha }_{\mathrm{DR}}\left(E\right)={\alpha }_{\exp }\left(E\right)-{\alpha }_{\mathrm{RR}}\left(E\right).$$

(7)

It is important to note that, during the experiment, recombined ions pass through the CSRm dipole magnets after exiting the electron cooler and are exposed to dynamic electric fields. These fields can ionize recombined ions in high-n Rydberg states. Consequently, recombined ions with a principal quantum number n exceeding a critical cutoff value $n_{\mathrm{cut}}$ are field-ionized and thus undetected. The cutoff quantum number is estimated classically [23]:

$$n_{\mathrm{cut}}\approx {\left(6.2\times {10}^8\mathrm{V}/\mathrm{cm}{\displaystyle \frac{Q^3}{v_{i}B}}\right)}^{1/4},$$

(8)

where Q denotes the charge state of the ion, $v_i$ the ion velocity, and B the magnetic field strength, yielding $n_{\mathrm{cut}}\approx 115$ for the present experiment [36].

3. Results and Discussion

3.1. Merged-Beam DR Rate Coefficients

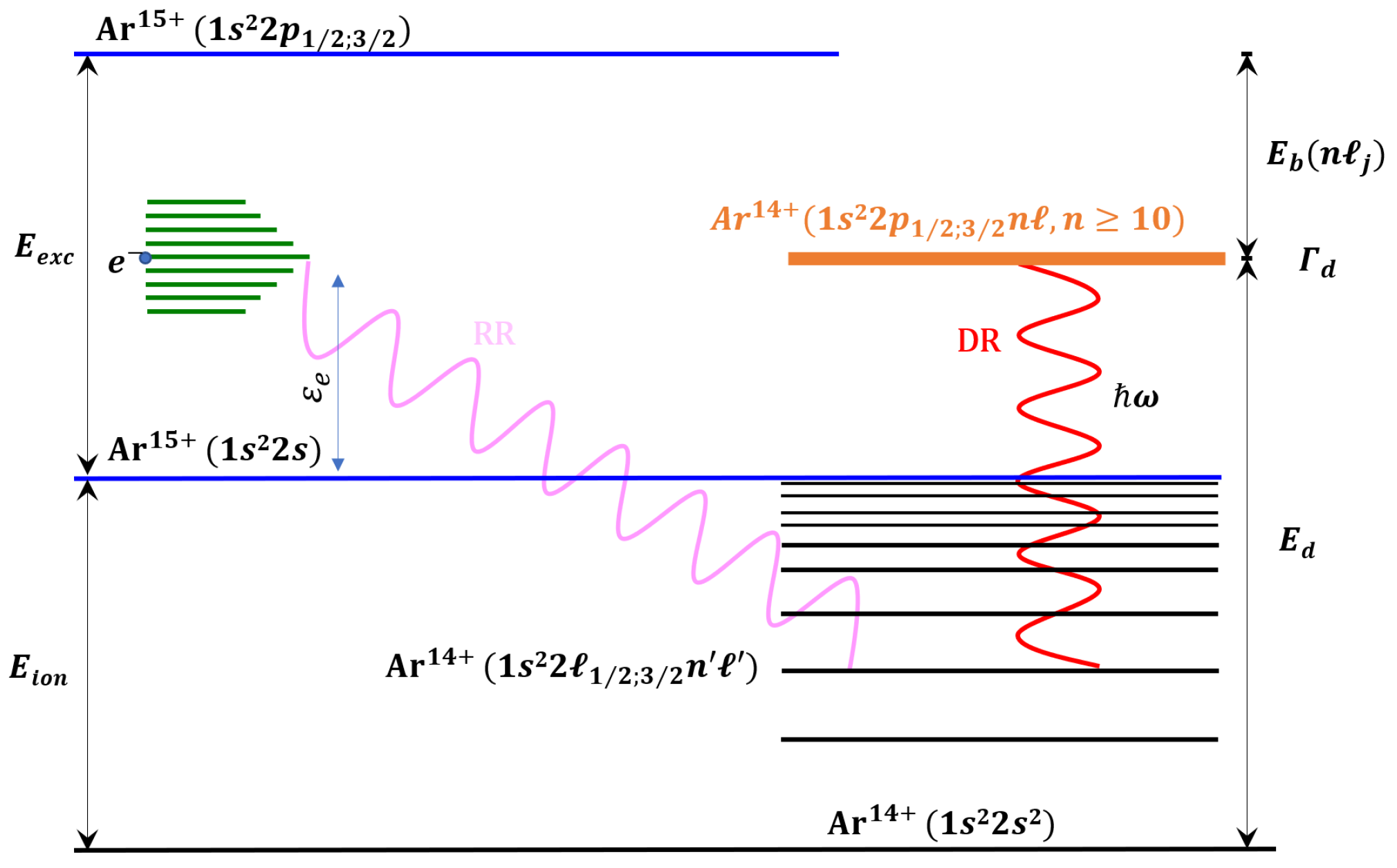
The DR channels associated with $\Delta n=0$ core excitations for Li-like Ar¹⁵⁺ ions are described as

$$\begin{array}{cc}\hfill {\mathrm{Ar}}^{15+}\left[2s{}^{2}S_{1/2}\right]+e^{-}& ⟹\left\{\begin{array}{c}{\mathrm{Ar}}^{14+}\left[2p{}^{2}P_{1/2}\left(31.8668\mathrm{eV}\right)\right](n\ell ),\hfill \\ {\mathrm{Ar}}^{14+}\left[2p{}^{2}P_{3/2}\left(35.0377\mathrm{eV}\right)\right](n\ell ),\hfill \end{array}\right.\hfill \\ \hfill & ⟹\dots ⟹{\mathrm{Ar}}^{14+}\left[2s^2{}^{1}S_0\right]+\gamma ,\hfill \end{array}$$

(9)

where $n=10,11,\dots$ denotes the principal quantum number of the captured electron. These processes are schematically depicted in Figure 2.

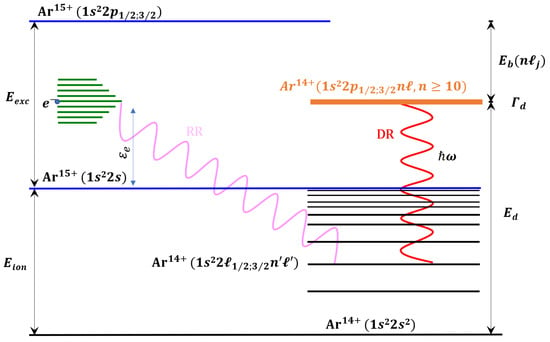
Figure 2. Dielectronic recombination of Li-like argon ions proceeds from the ground state $1s^{2}2s$, with a free electron captured into a doubly excited state, $1s^{2}2p_{1/2,3/2}n\ell$. The principal quantum number of the outer electron must satisfy $n\ge 10$ to ensure that the energy of the doubly excited state exceeds the first ionization threshold. The figure is schematic and not to scale.

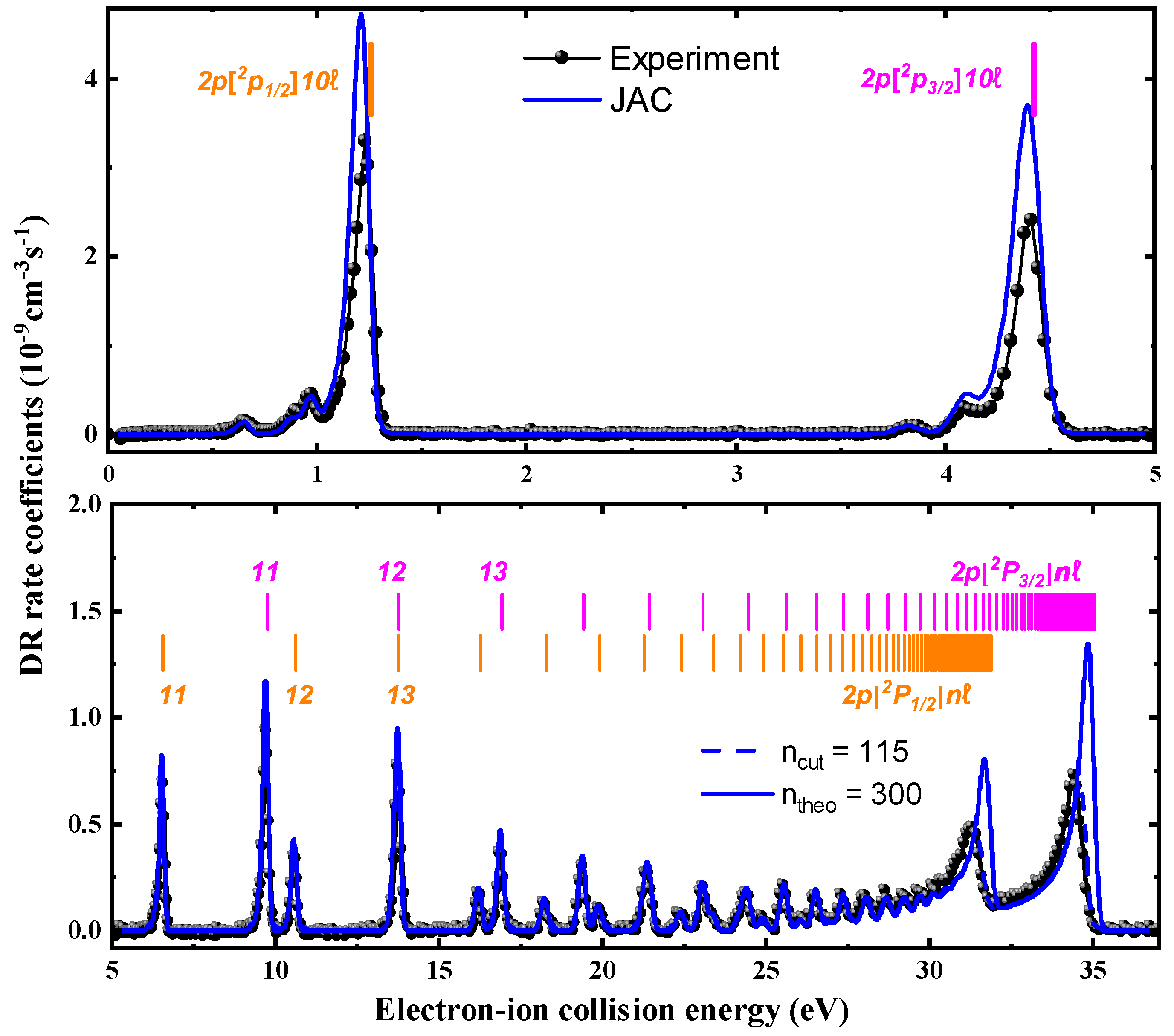
Figure 3 presents the experimentally measured DR rate coefficients for Li-like Ar¹⁵⁺ ions, alongside theoretical results computed using JAC. The theoretical rate coefficients were computed by convolving the DR resonance cross-sections with the electron-beam velocity distribution, as detailed in Section 2. In Figure 3, the positions of Rydberg resonances associated with the doubly excited intermediate states $2p_{1/2,3/2}n\ell$ are indicated by vertical bars. These resonance energies can be approximated via the Rydberg formula:

$$E_{\mathrm{d}}=E_{\mathrm{exc}}-I_{\mathrm{H}}{\left({\displaystyle \frac{Z}{n}}\right)}^2,$$

(10)

where $I_{\mathrm{H}}=13.605693$ eV is the Rydberg constant, $E_{\mathrm{exc}}$ is the energy of the core electronic transition, $Z=15$ is the ionic charge, and n denotes the principal quantum number of the captured electron.

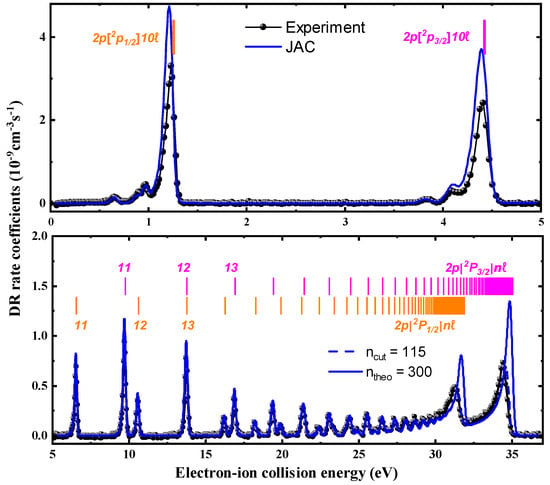
Figure 3. Experimental DR rate coefficients (black filled symbols) for Li-like ${\mathrm{Ar}}^{15+}$ are presented across the electron–ion collision energy range of 0–37 eV. DR series associated with $2s_{1/2}\to 2p_{1/2}$ and $2s_{1/2}\to 2p_{3/2}$ core excitations ($\Delta n=0$) are observed, with their resonance positions estimated by the Rydberg formula [Equation (10)] and indicated by short colored bars. Theoretical DR rate coefficients from the JAC codes are depicted by the blue solid and dashed lines. These theoretical curves account for recombination into Rydberg states, with principal quantum numbers extending up to $n_{theo}=300\gg n_{cut}\approx 115$—representing the field-ionization-free recombination rate coefficient.

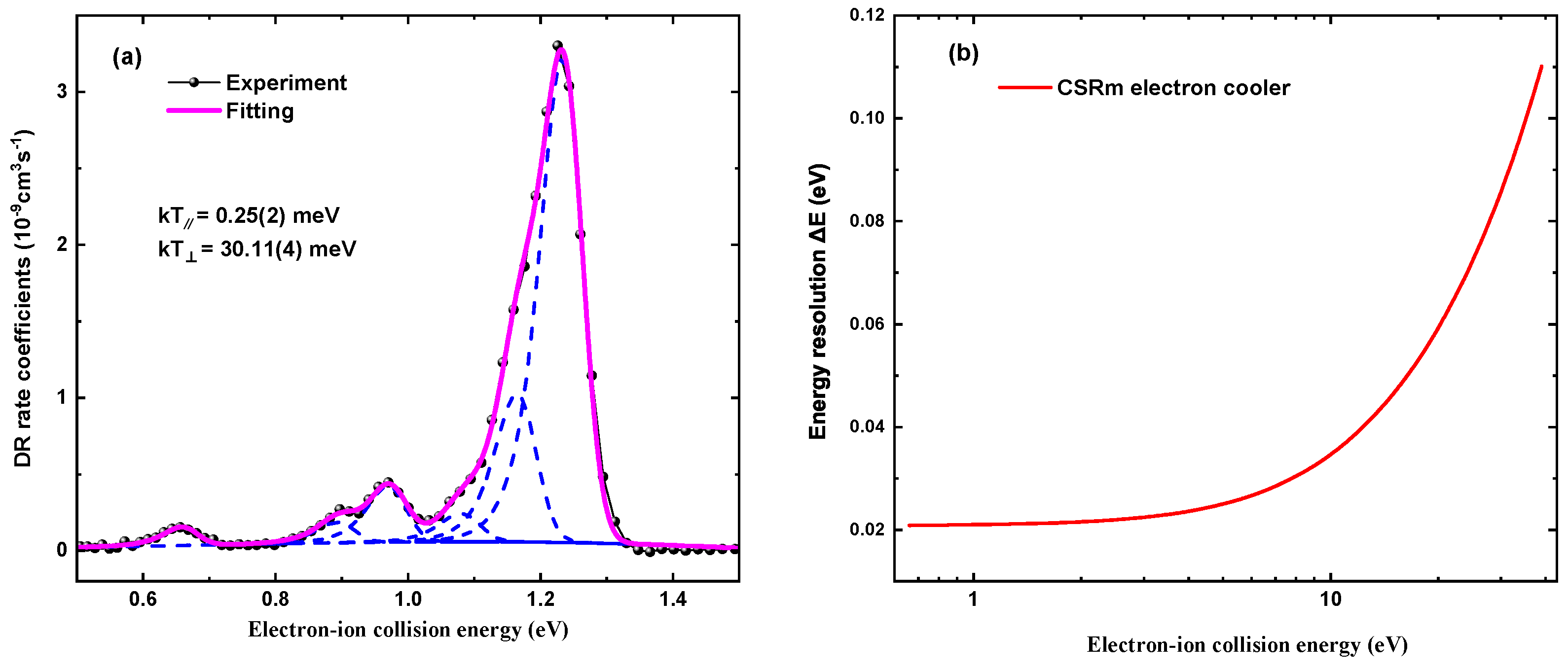
Figure 4a shows fits to the first four resonance peaks at relative collision energies <1.4 eV using a flattened Maxwellian distribution [29]. From these fits, longitudinal and transverse electron temperatures of $k_{\mathrm{B}}{T}_{\Vert }=0.25\left(2\right)$ meV and $k_{\mathrm{B}}{T}_{\perp }=30.11\left(4\right)$ meV were obtained, respectively.

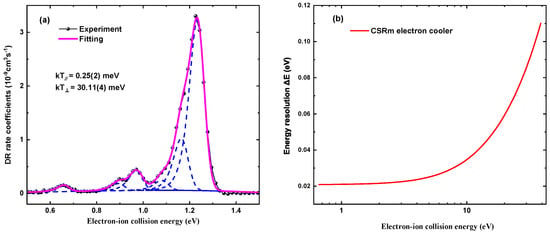
Figure 4. (a) Fit of the first 4 experimental resonance peaks at relative energies below 1.4 eV, as described in the reference by [36]. The experimental DR rate coefficient and peak fitting are shown by the black filled symbols and the solid magenta line. The individual fitted peaks are shown by dash blue lines. The fit resulted in $k_B{T}_{\Vert }=0.25\left(2\right)$ meV and $k_B{T}_{\perp }=30.11\left(4\right)$ meV. (b) Energy resolution of the DR experiments at storage ring CSRm as a function of electron–ion collision energies between 0.6 and 37 eV.

In heavy-ion storage-ring DR experiments, the experimental energy resolution is primarily determined by the electron-beam temperature and the longitudinal momentum spread of the ion beam. The energy resolution $\Delta E$ is given by [8,29]

$$\Delta E=\sqrt{{[ln\left(2\right)·k{T}_{\perp }]}^2+{[16ln\left(2\right)·E_{rel}·k{T}_{\Vert }]}^2}.$$

(11)

According to Equation (11), the energy resolution is governed by both the longitudinal and transverse electron temperatures. This behavior is reflected in Figure 4b, in which the dominance of the transverse term at low $E_{\mathrm{rel}}$ leads to an almost constant energy resolution, whereas with increasing collision energy the longitudinal contribution grows as a function of $E_{\mathrm{rel}}$ and thereby causes a pronounced broadening of the spread.

Within the present experimental energy resolution, some fine-structure components of the $2p_{1/2}10\ell$ DR resonances are partially resolvable, as shown in Figure 3 and Table 1. Compared with earlier measurements [37,38], the present experiment resolves an additional DR resonance at a relative energy of $E_{\mathrm{rel}}=0.902\mathrm{eV}$, which was not reported in previous studies. Based on the agreement between theoretical predictions and the experimental data, this resonance is assigned to the doubly excited state ${\left(2p_{1/2}10p_{1/2}\right)}_{J=0}$. This resonance is weak and narrow, and its visibility is therefore sensitive to the collision-energy resolution and the statistical quality of the experiment. The two resonances associated with the $2p_{1/2}10p_{3/2}$ configuration, having total angular momenta $J=1$ and $J=2$, are separated by an energy difference smaller than the experimental resolution and thus appear as a single feature centered at $E_{\mathrm{rel}}=0.988$ eV. A shoulder is observed at $E_{\mathrm{rel}}=1.183$ eV, which is interpreted as an unresolved superposition of four closely spaced resonances: ${\left(2p_{1/2}10d_{3/2}\right)}_{J=2}$, ${\left(2p_{1/2}10d_{5/2}\right)}_{J=2}$, ${\left(2p_{1/2}10d_{5/2}\right)}_{J=3}$, and ${\left(2p_{1/2}10d_{3/2}\right)}_{J=1}$. For states with higher orbital angular momentum ($\ell >2$), the calculated resonance energies lie above 1.200 eV, collectively contributing to the experimentally observed DR peak at $E_{\mathrm{rel}}=1.252$ eV. It is worth noting that the $2p_{3/2}10\ell$ DR resonances are also partially resolved. A detailed comparison of calculated resonance energies with fitted experimental values for both $2p_{1/2}10\ell$ and $2p_{3/2}10\ell$ DR resonances is provided in Table 1. Within the $\pm 30\%$ systematic uncertainty of the measurements, the JAC results show overall good agreement with the experiment. However, localized deviations of about 42% and 54% are observed near 1.2 eV and 4.4 eV, respectively, where a dense manifold of high-ℓ DR resonances strongly overlap, making an accurate theoretical description particularly challenging. These deviations are confined to a few isolated resonance features and do not reflect a systematic discrepancy over the entire energy range. For Li-like Ar¹⁵⁺ ions, the discrepancies between the JAC calculations and the high-resolution DR measurements therefore reach up to approximately 50% at certain resonances, which is comparable to the experimental uncertainty of about 30%. These localized deviations do not constitute order-of-magnitude differences and are thus not expected to have a significant impact on the resulting plasma rate coefficients. Similar resonance-specific discrepancies have been reported in recent benchmark studies of Na-like Fe¹⁵⁺ ions [35].

Table 1. Comparison of calculated and measured resonance energies ($E_d$) and strengths ($S_d$) for $2p_{1/2}10\ell$ and $2p_{3/2}10\ell$. The quoted uncertainties are fitting errors only.

Resonance a	${\mathit{E}}_{\mathit{d}}$ (eV)		${\mathit{S}}_{\mathit{d}}$ (${10}^{-19}\mathbf{eV}{\mathbf{cm}}^2$)
	Experiment b	JAC c	Experiment b	JAC
$2p_{1/2}10s_{1/2}$	$0.675\pm 0.005$	0.672	$17.8\pm 0.2$	22.5
${\left(2p_{1/2}10p_{1/2}\right)}_{J=1}$	$0.910\pm 0.001$	0.902	$18.5\pm 0.3$	23.2
$2p_{1/2}10p_{3/2}$	$0.988\pm 0.003$	0.976	$49.8\pm 0.3$	22.6
${\left(2p_{1/2}10p_{1/2}\right)}_{J=0}$	$1.098\pm 0.006$	1.040	$24.5\pm 0.4$	11.5
blend: $2p_{1/2}10d_{3/2},10d_{5/2}$	$1.183\pm 0.003$	1.168	$125.9\pm 0.5$	176.3
blend: $2p_{1/2}10\ell (\ell >d)$	$1.252\pm 0.002$	1.246	$408.6\pm 0.5$	696.1
$2p_{3/2}10s$	$3.874\pm 0.008$	3.841	$1.0\pm 0.1$	0.8
$2p_{3/2}10p$	$4.146\pm 0.003$	4.144	$3.0\pm 0.1$	5.3
blend: $2p_{3/2}10\ell (\ell >p)$	$4.477\pm 0.006$	4.400	$33.2\pm 0.3$	48.9

^a Dominant configurations with the largest mixing coefficients in intermediate coupling. ^b 1$\sigma$ statistical uncertainties from the fit only; systematic uncertainties from the absolute measurement (about 30%) are not included. ^c Weighted energy defined as $E=\sum E_d{S}_d/\sum S_d$.

For captured electrons with principal quantum numbers n = 10–15, the experiment clearly resolves the $2s_{1/2}\to 2p_{1/2}$ and $2s_{1/2}\to 2p_{3/2}$ transitions. With increasing free-electron energy, however, the high-n resonances can no longer be resolved. For $2p_{1/2}n\ell$ and $2p_{3/2}n\ell$ resonances with ($n>15$), the peaks are closely spaced and the energy broadening increases rapidly. Near the series limits of the $2p_{1/2}n\ell$ and $2p_{3/2}n\ell$ lines ($n\to \infty$), numerous DR resonances overlap, forming two distinct envelope structures. The discrepancies between experiment and theory observed near the $2p_{1/2,3/2}n\ell$ series limits at approximately 32 and 34 eV are attributed to field-ionization effects inherent to the storage-ring DR measurements. In the CSRm experiment, electrons captured into high-n Rydberg states with principal quantum numbers exceeding a critical value of $n_{\mathrm{cut}}\approx 115$ are field-ionized by the magnetic fields present in the storage ring, as discussed in Section 2. To derive the field-ionzation-free plasma rate coefficients that are not affected by field ionization, theoretical DR rate coefficients calculated with JAC ($n_{\mathrm{theo}}=300$) were used in the energy interval from 30 to 36 eV, where experimental data are influenced by field-ionization losses. The plasma rate coefficients were found to be insensitive to additional contributions from Rydberg states with $n>n_{\mathrm{theo}}$, indicating that such contributions can be safely neglected.

3.2. Plasma Rate Coefficients

For applications in plasma modeling, recombination data obtained from merged-beam experiments must be converted into rate coefficients appropriate for a thermal electron population. In such models, electrons are assumed to follow an isotropic Maxwell–Boltzmann distribution characterized by the plasma temperature $T_e$. The experimentally measured, energy-resolved recombination rate coefficients therefore require averaging over the electron kinetic energy distribution (isotropic Maxwell–Boltzmann distribution) in order to yield a plasma rate coefficient. For electron–ion energies $E\ll k_B{T}_e$, $\sigma \left(E\right)$ can be approximated as $\alpha \left(E\right)/v$, with $\alpha \left(E\right)$ denoting the measured merged-beam rate coefficient [39].

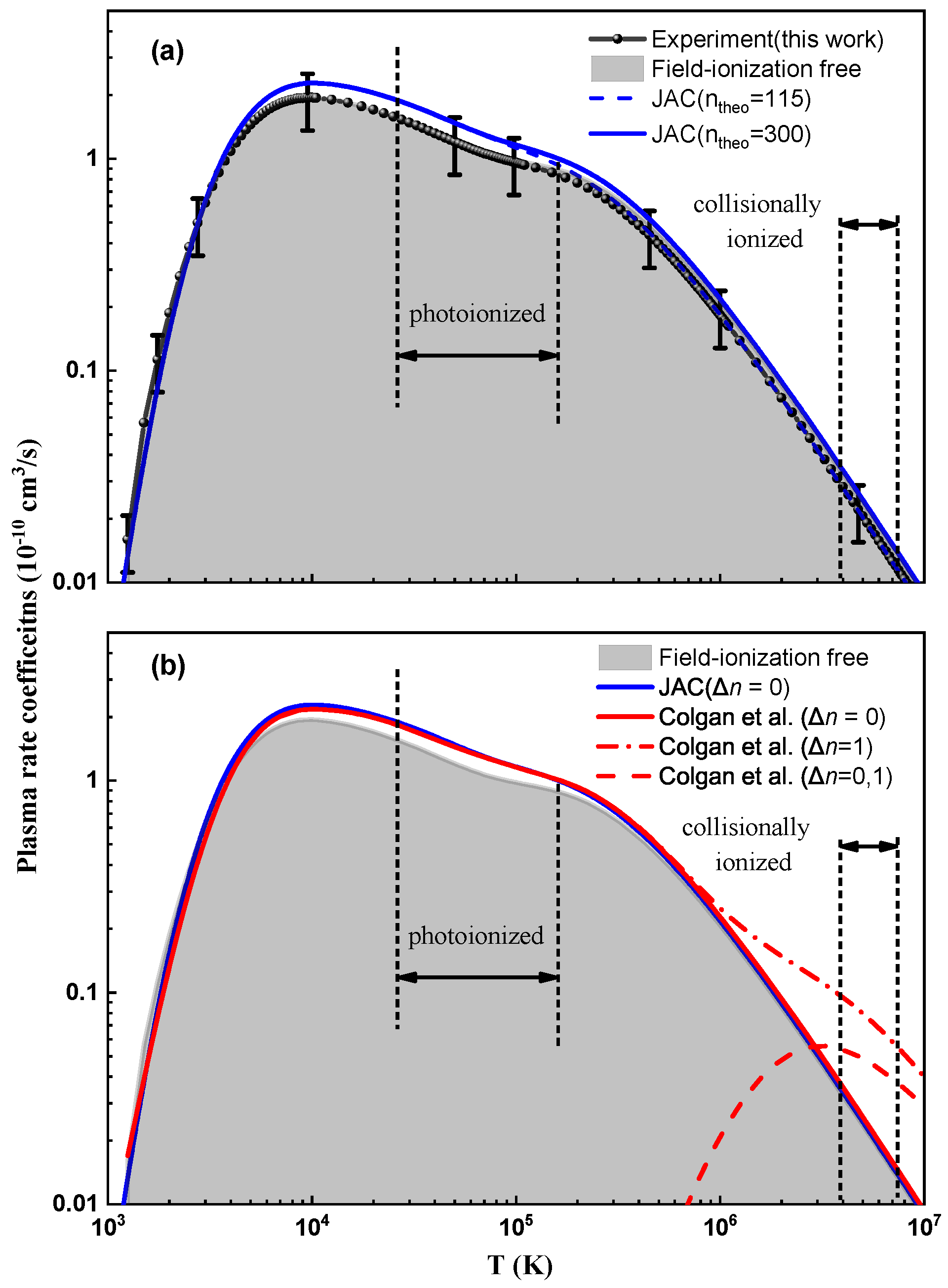
Figure 5a and Figure 5b compare the experimentally derived plasma rate coefficients with the present theoretical results obtained using the JAC code and with previously published theoretical data from the literature, respectively. As shown in Figure 5a, the plasma rate coefficients calculated with JAC are in good agreement with the experimental results within the experimental uncertainties over a wide temperature range, covering both the photoionized plasma regime ($4.9\times {10}^4$–$5.6\times {10}^5$ K) and the collisionally ionized plasma regime ($6.2\times {10}^6$–$6.9\times {10}^6$ K). Furthermore, the plasma rate coefficients are found to be insensitive to additional contributions from Rydberg states with principal quantum numbers $n>n_{\mathrm{cut}}$.

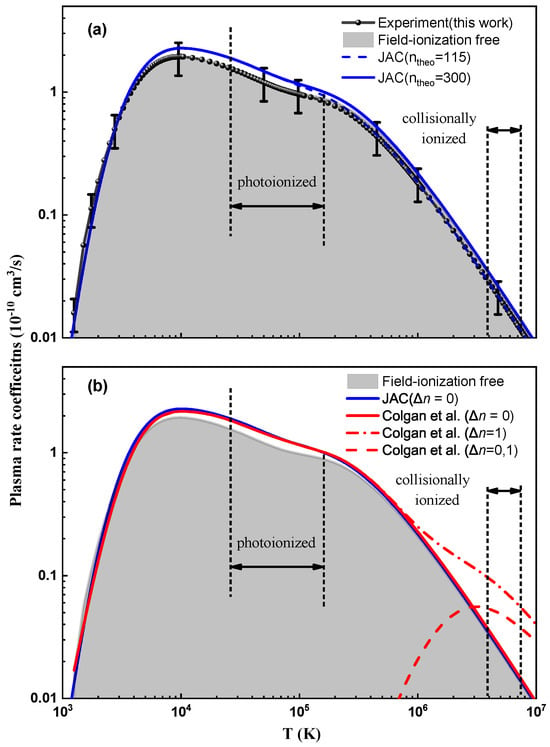
Figure 5. Plasma DR rate coefficients for initial Li-like Ar¹⁵⁺ ions as a function of plasma temperature T. (a) Comparison between the experimental results and present JAC calculations. The error bars denote the ±30% experimental uncertainty of the absolute rate coefficients. (b) Comparison of field-ionization-free plasma recombination rate coefficients (light gray area) with theoretical data available in the literature. The red solid, dash-dotted, and dashed curves denote the rate coefficients reported by Colgan et al. [40]. In both panels, the vertical dashed bars indicate the temperature ranges over which the fractional abundance of Li-like Ar ions exceeds 10% of its peak value in photoionized and collisionally ionized plasmas [2,3].

Figure 5b compares the experimentally derived plasma rate coefficients with the present theoretical results obtained using JAC, as well as with previously published data by Colgan et al. [40]. The data of Colgan et al. [40] include calculations considering only $\Delta n=0$ transitions, as well as those including both $\Delta n=0$ and $\Delta n=1$ transitions. Their plasma rate coefficients associated solely with $\Delta n=0$ transitions are in good agreement with both the current JAC results and the experimental data within the experimental uncertainties. Although the contribution from $\Delta n=1$ transitions is not fully covered by the present experiment, a comparison with the theoretical results allows us to draw an indirect conclusion that, at temperatures above $3.0\times {10}^6$ K, $\Delta n=1$ transitions play an important role in the modeling of high-temperature plasmas. Future storage-ring experiments with extended measurement ranges and improved sensitivity will be essential to directly probe the contribution of $\Delta n=1$ channels and to further constrain plasma recombination rate coefficients at high temperatures. Such measurements would provide valuable experimental benchmarks for theoretical models and database calculations used in high-temperature plasma applications.

To provide a compact representation of the experimentally derived and calculated $\Delta n=0$ plasma rate coefficients, the temperature-dependent results are expressed in terms of the fitting function

$$\alpha \left(T_e\right)=T_e^{-3/2}\sum _i{c}_i\exp \left(-{\displaystyle \frac{E_i}{k_B{T}_e}}\right),$$

(12)

where the fitting parameters $c_i$ and $E_i$ are listed in Table 2. Over the electron temperature range from ${10}^3$ K to ${10}^7$ K, this parameterization reproduces the rate coefficients with deviations below 2%.

Table 2. The fitted parameters for the DR plasma rate coefficients of Li-like ${\mathrm{Ar}}^{15+}$ forming ${\mathrm{Ar}}^{14+}$ are presented. The units of coefficients $c_i$ and $E_i$ are ${\mathrm{cm}}^3{\mathrm{s}}^{-1}{\mathrm{K}}^{3/2}$ and K, respectively. Values enclosed in square brackets denote powers of 10. The experimental results correspond to the field-ionized free DR plasma rate coefficients as elaborated in the text. The JAC results are obtained with a maximum principal quantum number $n_{max}=300$. The fourth column is derived from the recommended results reported by Colgan et al. [40].

No.	Experiment ($\mathbf{\Delta }\mathit{n}=0$)	JAC ($\mathbf{\Delta }\mathit{n}=0$)	Colgan ($\mathbf{\Delta }\mathit{n}=0,1$)
$c_1$	9.667 [−2]	4.441 [−3]	2.929 [−2]
$c_2$	7.835 [−3]	1.635 [−2]	1.507 [−1]
$c_3$	7.040 [−4]	2.180 [−3]	1.049 [−1]
$c_4$	3.035 [−5]	7.235 [−5]	1.086 [−1]
$c_5$	5.410 [−5]	7.709 [−4]	7.082 [−2]
$c_6$	7.186 [−6]	–	–
$E_1$	3.753 [5]	1.439 [5]	2.446 [5]
$E_2$	1.902 [4]	3.471 [5]	4.506 [6]
$E_3$	2.120 [3]	5.367 [4]	2.958 [7]
$E_4$	1.257 [8]	9.258 [4]	2.958 [7]
$E_5$	3.187 [8]	1.405 [4]	2.958 [7]
$E_6$	3.523 [6]	–	–

4. Summary

We have conducted a benchmark study of DR for Li-like Ar¹⁵⁺ ions for the fine-structure core excitations $2s_{1/2}\to 2p_{1/2,3/2}$ using the JAC code. The level-resolved resonance strengths for the $2p_{1/2}n\ell$ and $2p_{3/2}n\ell$ Rydberg series in the energy range of 0–37 eV show good agreement with high-resolution measurements at the CSRm. This agreement is particularly pronounced at low electron–ion collision energies of 0–5 eV, where fine-structure-resolved DR resonances of the $2p_{1/2}n{\ell }_j$ series have been partially resolved experimentally.

For plasma modeling, we have derived DR plasma rate coefficients for the $\Delta n=0$ core excitation of Ar¹⁵⁺ ions in the $1s^{2}2s{}^{2}S_{1/2}$ ground state. These coefficients cover a temperature range from ${10}^3$ to ${10}^7$ K, which is relevant to both photoionized and collisionally ionized plasmas. The resulting plasma rate coefficients are in good agreement with experimentally derived values, confirming the reliability of the present theoretical approach using the JAC code for plasma modeling applications. In future work, we plan to integrate electron–ion resonant processes with other key atomic processes (e.g., electron-impact excitation and ionization [41,42]) into a unified framework to more comprehensively simulate the radiative properties of plasmas.