Interfacing the B-Spline R-Matrix and R-Matrix with Time Dependence Computer Codes: An Update
Abstract
1. Introduction
2. Modifications to BSR
2.1. Phase Convention
2.2. Target States
3. Interface: New Utilities
3.1. bsr_Splinedata
3.2. bsr_Splinewaves
3.3. bsr_H
3.4. bsr_d
3.5. Usage
4. Example Illustrations: Multiphoton Ionization of Helium and High-Order Harmonic Generation in Carbon Atoms
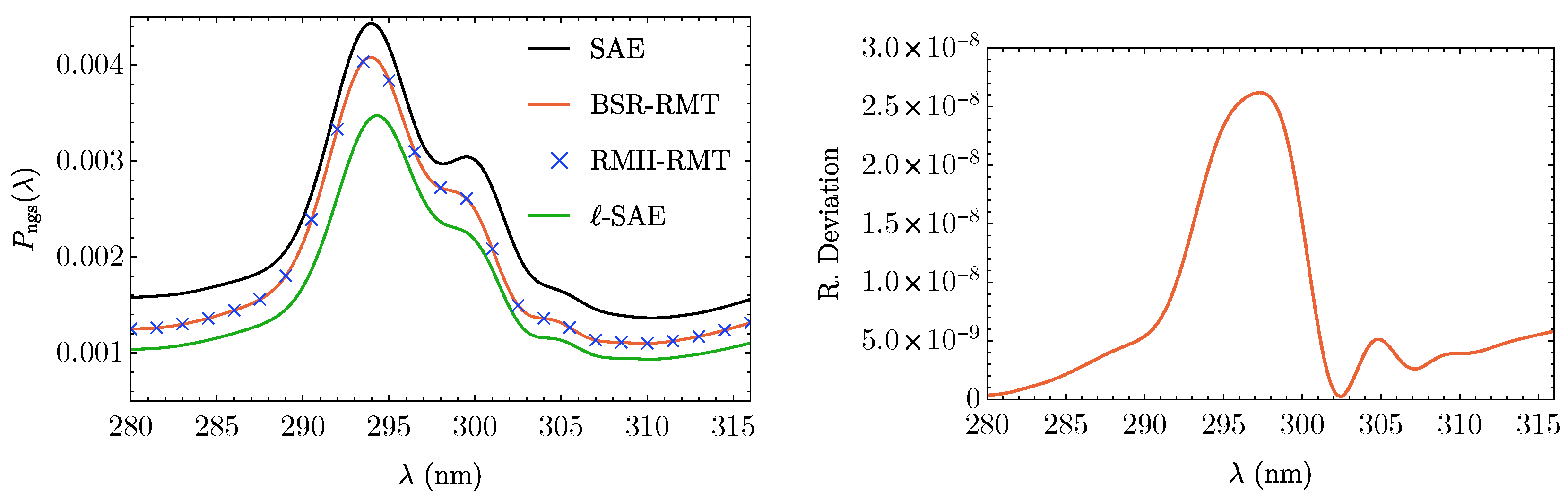
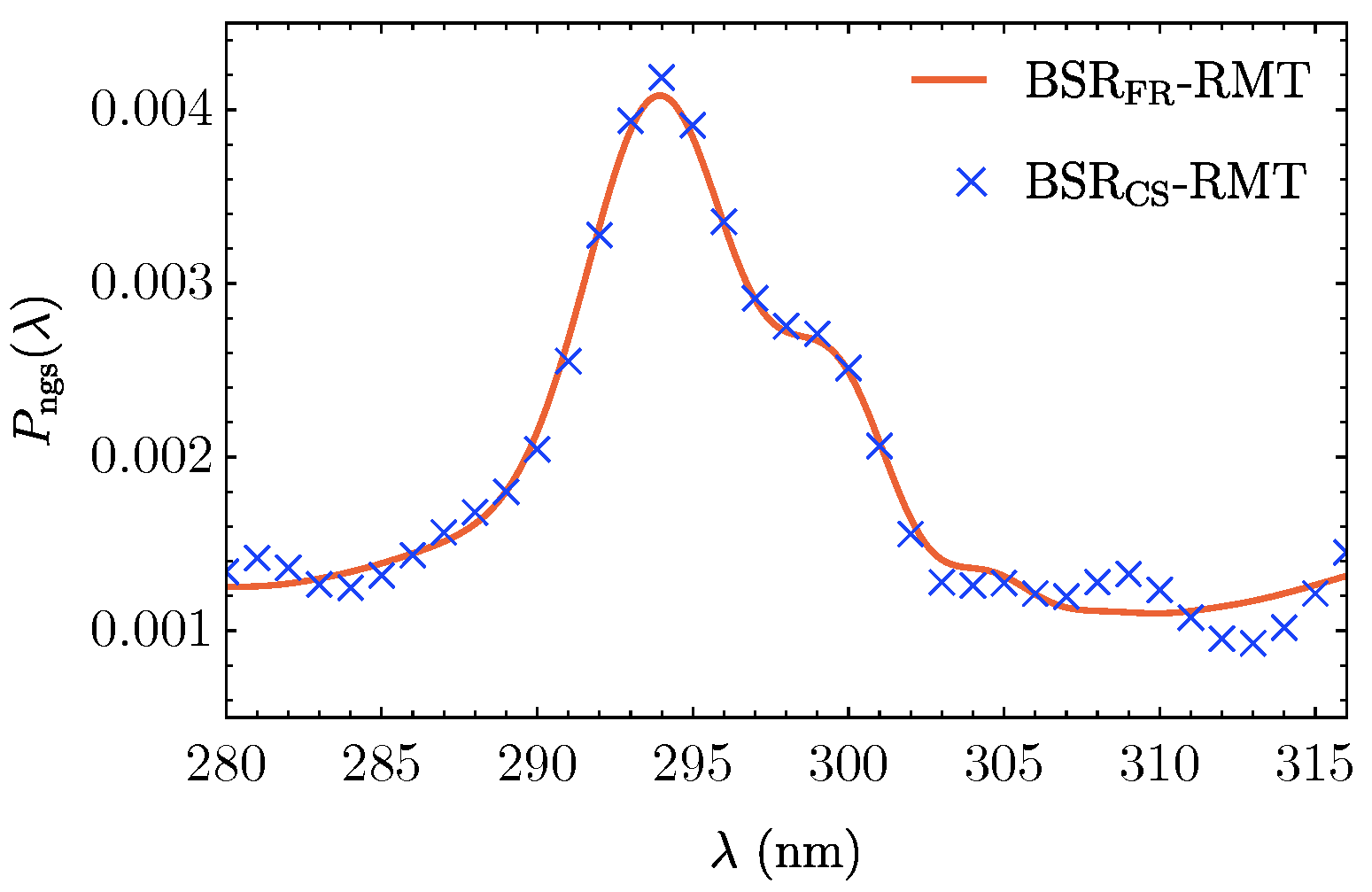
4.1. MPI in Helium
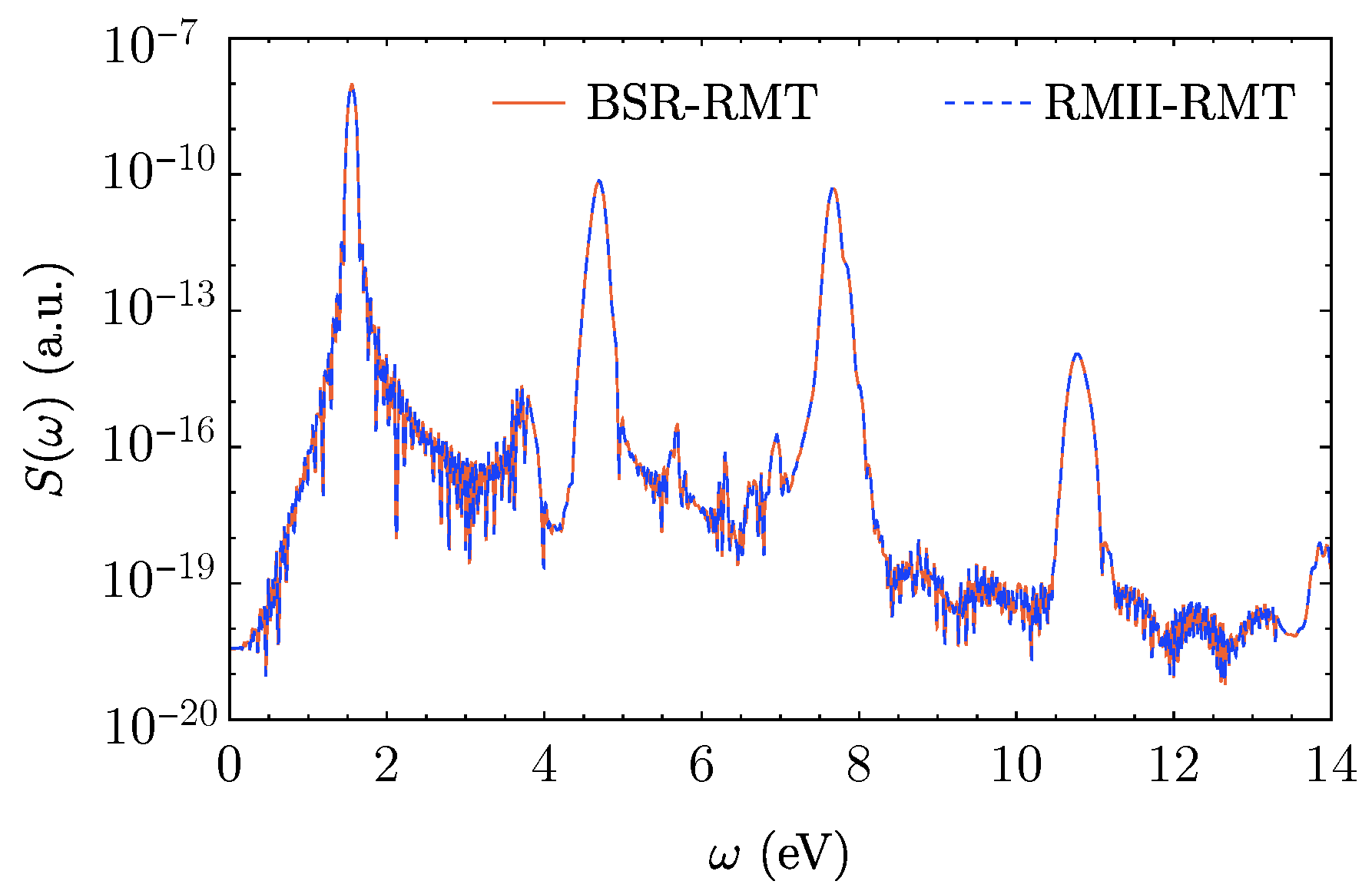
4.2. HHG in Carbon
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HHG | High-Harmonic Generation |
| TDSE | Time-Dependent Schrödinger Equation |
| BSR | B-Spline R-matrix |
| RMT | R-Matrix with Time dependence |
| MCHF | Multi-Configuration Hartree–Fock |
| RMII | RMATRX-II |
| MPI | Multiphoton Ionization |
| 1 | See [12] and references therein. |
| 2 | We use Version 3 of the libraries; see [20]. |
| 3 | Here, BSR–RMT indicates that the RMT code used input from BSR, and similarly for RMII-RMT. |
References
- Zatsarinny, O. BSR: B-spline atomic R-matrix codes. Comput. Phys. Commun. 2006, 174, 273–356. [Google Scholar] [CrossRef]
- Burke, P. R-Matrix Theory of Atomic Collisions: Application to Atomic, Molecular and Optical Processes; Springer Series on Atomic, Optical, and Plasma Physics; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Berrington, K.A.; Eissner, W.B.; Norrington, P.H. RMATRX1: Belfast atomic R-matrix codes. Comput. Phys. Commun. 1995, 92, 290–420. [Google Scholar] [CrossRef]
- Burke, P.G.; Burke, V.M.; Dunseath, K.M. Electron-impact excitation of complex atoms and ions. J. Phys. B 1994, 27, 5341. [Google Scholar] [CrossRef]
- Zatsarinny, O.; Bartschat, K. The B-spline R-matrix method for atomic processes: Application to atomic structure, electron collisions and photoionization. J. Phys. B 2013, 46, 112001. [Google Scholar] [CrossRef]
- Fernández-Menchero, L.; Conroy, A.; Ballance, C.; Badnell, N.; Mitnik, D.; Gorczyca, T.; Seaton, M. PSTGF: Time-independent R-matrix atomic electron-impact code. Comput. Phys. Commun. 2020, 256, 107489. [Google Scholar] [CrossRef]
- Berrington, K.A.; Burke, P.G.; Butler, K.; Seaton, M.J.; Storey, P.J.; Taylor, K.T.; Yan, Y. Atomic data for opacity calculations. II. Computational methods. J. Phys. B 1987, 20, 6379. [Google Scholar] [CrossRef]
- Burke, V.; Noble, C. FARM — A flexible asymptotic R-matrix package. Comput. Phys. Commun. 1995, 85, 471–500. [Google Scholar] [CrossRef]
- Burke, P.G.; Burke, V.M. Time-dependent R-matrix theory of multiphoton processes. J. Phys. B 1997, 30, L383. [Google Scholar] [CrossRef]
- Nikolopoulos, L.A.A.; Parker, J.S.; Taylor, K.T. Combined R-matrix eigenstate basis set and finite-difference propagation method for the time-dependent Schrödinger equation: The one-electron case. Phys. Rev. A 2008, 78, 063420. [Google Scholar] [CrossRef]
- Moore, L.; Lysaght, M.; Nikolopoulos, L.; Parker, J.; van der Hart, H.; Taylor, K.T. The RMT method for many-electron atomic systems in intense short-pulse laser light. J. Mod. Opt. 2011, 58, 1132–1140. [Google Scholar] [CrossRef]
- Schneider, B.I.; Hamilton, K.R.; Bartschat, K. Generalizations of the R-matrix method to the treatment of the interaction of short-pulse electromagnetic radiation with atoms. Atoms 2022, 10, 26. [Google Scholar] [CrossRef]
- Brown, A.C.; Armstrong, G.S.; Benda, J.; Clarke, D.D.; Wragg, J.; Hamilton, K.R.; Mašín, Z.; Gorfinkiel, J.D.; van der Hart, H.W. RMT: R-Matrix with time-dependence. Solving the semi-relativistic, time-dependent Schrödinger equation for general, multielectron atoms and molecules in intense, ultrashort, arbitrarily polarized laser pulses. Comput. Phys. Commun. 2020, 250, 107062. [Google Scholar] [CrossRef]
- Wragg, J.; Ballance, C.; van der Hart, H. Breit–Pauli R-Matrix approach for the time-dependent investigation of ultrafast processes. Comput. Phys. Commun. 2020, 254, 107274. [Google Scholar] [CrossRef]
- Mašín, Z.; Benda, J.; Gorfinkiel, J.D.; Harvey, A.G.; Tennyson, J. UKRmol+: A suite for modelling electronic processes in molecules interacting with electrons, positrons and photons using the R-matrix method. Comput. Phys. Commun. 2020, 249, 107092. [Google Scholar] [CrossRef]
- Wragg, J.; Clarke, D.D.; Armstrong, G.S.; Brown, A.C.; Ballance, C.P.; Van Der Hart, H.W. Resolving ultrafast spin-orbit dynamics in heavy many-electron atoms. Phys. Rev. Lett. 2019, 123, 163001. [Google Scholar] [CrossRef]
- Roantree, L.; Wragg, J.; Van Der Hart, H.; Brown, A. Energy-and angle-resolved spectral phases via semirelativistic ab initio RABBITT simulations. Phys. Rev. A 2023, 108, 023112. [Google Scholar] [CrossRef]
- Benda, J.; Gorfinkiel, J.; Mašin, Z.; Armstrong, G.; Brown, A.; Clarke, D.; van der Hart, H.; Wragg, J. Perturbative and nonperturbative photoionization of H2 and H2O using the molecular R-matrix-with-time method. Phys. Rev. A 2020, 102, 052826. [Google Scholar] [CrossRef]
- Zatsarinny, O.; Bartschat, K. Benchmark calculations for near-threshold electron-impact excitation of krypton and xenon atoms. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 074031. [Google Scholar] [CrossRef]
- Available online: https://github.com/zatsaroi (accessed on 27 August 2025).
- Edmonds, A.R. Angular Momentum in Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 1985. [Google Scholar]
- Zatsarinny, O. A general program for computing matrix elements in atomic structure with nonorthogonal orbitals. Comput. Phys. Commun. 1996, 98, 235–254. [Google Scholar] [CrossRef]
- Zatsarinny, O.; Fischer, C.F. A general program for computing angular integrals of the Breit–Pauli Hamiltonian with non-orthogonal orbitals. Comput. Phys. Commun. 2000, 124, 247–289. [Google Scholar] [CrossRef]
- Froese-Fischer, C.; Brage, T.; Jönsson, P. Computational Atomic Structure: An MCHF Approach; Routledge: Oxfordshire, UK, 1997. [Google Scholar] [CrossRef]
- Fischer, C.F. The MCHF atomic-structure package. Comput. Phys. Commun. 2000, 128, 635–636. [Google Scholar] [CrossRef]
- Hibbert, A. CIV3 — A general program to calculate configuration interaction wave functions and electric-dipole oscillator strengths. Comput. Phys. Commun. 1975, 9, 141–172. [Google Scholar] [CrossRef]
- Available online: https://github.com/JuanCarlosdelValle/Interface-BSR-RMT (accessed on 27 August 2025).
- Available online: https://gitlab.com/Uk-amor/RMT/rmatrixII (accessed on 27 August 2025).
- Bondy, A.T.; Saha, S.; del Valle, J.C.; Harth, A.; Douguet, N.; Hamilton, K.R.; Bartschat, K. High-order harmonic generation in helium: A comparison study. Phys. Rev. A 2024, 109, 043113. [Google Scholar] [CrossRef]
- del Valle, J.C.; Bartschat, K. The single-active-electron approximation with angular-momentum-dependent potentials: Application to the helium atom. Atoms 2025, 13, 43. [Google Scholar] [CrossRef]
- van der Hart, H.W. Ionization rates for He, Ne, and Ar subjected to laser light with wavelengths between 248.6 and 390 nm. Phys. Rev. A 2006, 73, 023417. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifschits, E.M. The Classical Theory of Fields; Pergamon Press: Oxford, UK, 1975; Volume 2. [Google Scholar] [CrossRef]
- Hamilton, K.R.; Bartschat, K.; Douguet, N.; Pamidighantam, S.V.; Schneider, B.I. Simulation for all: The atomic, molecular, and optical science gateway. Comput. Sci. Eng. 2023, 25, 68–72. [Google Scholar] [CrossRef]
- Wolcott, T.; Bartschat, K.; Pamidighantam, S.; Schneider, B.I.; Hamilton, K.R. Developing interoperable, accessible software via the atomic, molecular, and optical sciences gateway: A case study of the B-spline atomic R-matrix code graphical user interface. J. Chem. Phys. 2024, 161, 132501. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Del Valle, J.C.; Bondy, A.T.; Saha, S.; Hamilton, K.R.; Bartschat, K. Interfacing the B-Spline R-Matrix and R-Matrix with Time Dependence Computer Codes: An Update. Atoms 2025, 13, 75. https://doi.org/10.3390/atoms13090075
Del Valle JC, Bondy AT, Saha S, Hamilton KR, Bartschat K. Interfacing the B-Spline R-Matrix and R-Matrix with Time Dependence Computer Codes: An Update. Atoms. 2025; 13(9):75. https://doi.org/10.3390/atoms13090075
Chicago/Turabian StyleDel Valle, Juan C., Aaron T. Bondy, Soumyajit Saha, Kathryn R. Hamilton, and Klaus Bartschat. 2025. "Interfacing the B-Spline R-Matrix and R-Matrix with Time Dependence Computer Codes: An Update" Atoms 13, no. 9: 75. https://doi.org/10.3390/atoms13090075
APA StyleDel Valle, J. C., Bondy, A. T., Saha, S., Hamilton, K. R., & Bartschat, K. (2025). Interfacing the B-Spline R-Matrix and R-Matrix with Time Dependence Computer Codes: An Update. Atoms, 13(9), 75. https://doi.org/10.3390/atoms13090075






