External Radiation Assistance of Neutrinoless Double Electron Capture
Abstract
1. Introduction
2. Environmental Effect of the Neutrinoless Double Electron Capture (0ν2ec) Process
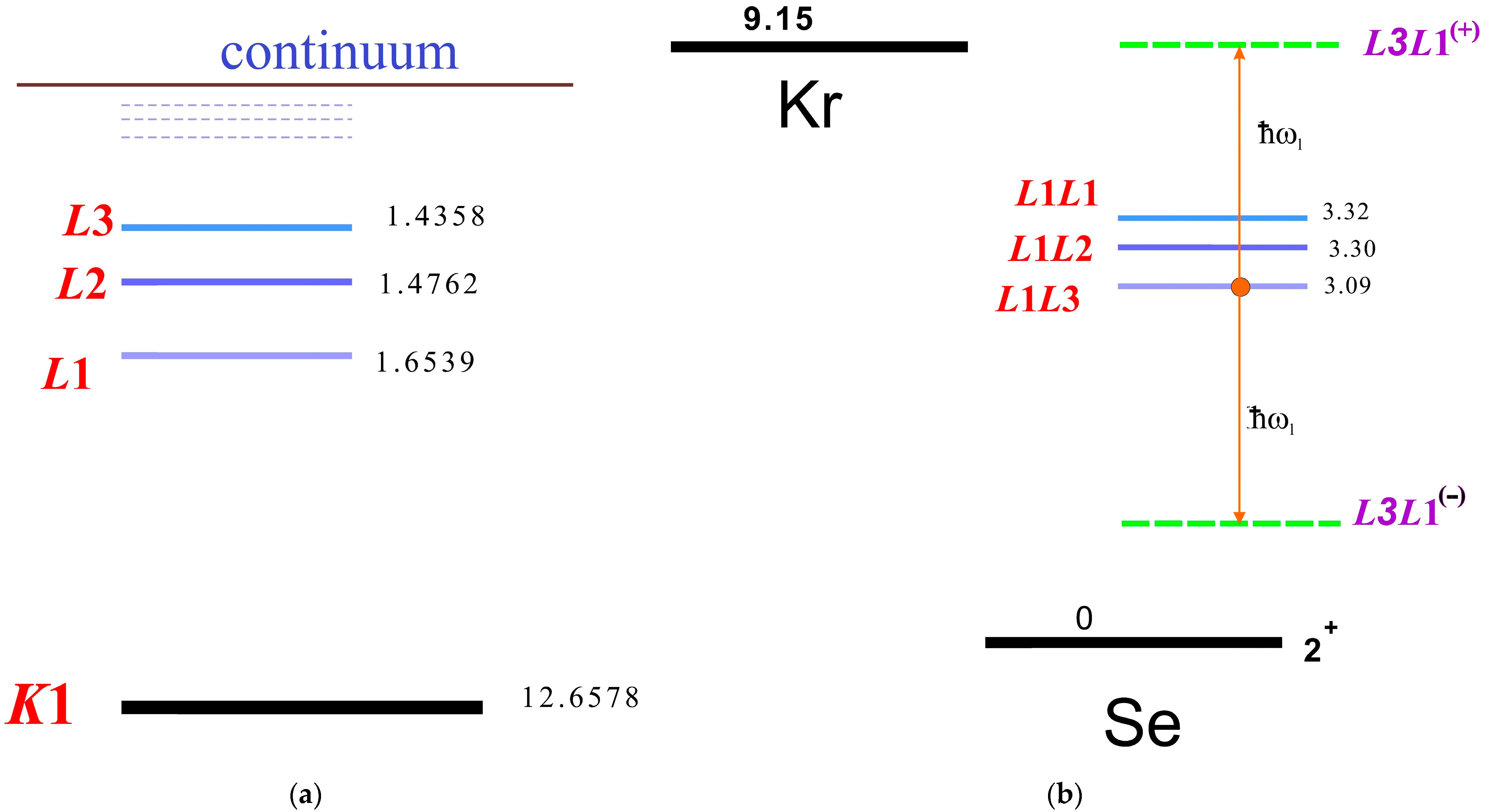
2.1. Resonant Character of the Neutrinoless Double Electron Capture (0ν2ec)
2.2. Resonance Tuning Using X-ray Radiation
3. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fukuda, Y.; Hayakawa, T.; Ichihara, E.; Inoue, K.; Ishihara, K.; Ishino, H.; Itow, Y.; Kajita, T.; Kameda, J.; Kasuga, S.; et al. Evidence for Oscillation of Atmospheric Neutrinos. Phys. Rev. Lett. 1998, 81, 1562. [Google Scholar] [CrossRef]
- Ahmad, Q.R.; Allen, R.C.; Andersen, T.C.; Anglin, J.D.; Barton, J.C.; Beier, E.W.; Bercovitch, M.; Bigu, J.; Biller, S.D.; Black, R.A.; et al. Direct Evidence for Neutrino Flavor Transformation from Neutral-Current Interactions in the Sudbury Neutrino Observatory. Phys. Rev. Lett. 2002, 89, 011301. [Google Scholar] [CrossRef]
- Eguchi, K.; Enomoto, S.; Furuno, K.; Goldman, J.; Hanada, H.; Ikeda, H.; Ikeda, K.; Inoue, K.; Ishihara, K.; Itoh, W.; et al. First Results from KamLAND: Evidence for Reactor Antineutrino Disappearance. Phys. Rev. Lett. 2003, 90, 021802. [Google Scholar] [CrossRef] [PubMed]
- Kajita, T. Nobel Lecture: Discovery of atmospheric neutrino oscillations. Rev. Mod. Phys. 2016, 88, 030501. [Google Scholar] [CrossRef]
- McDonald, A.B. Nobel Lecture: The Sudbury Neutrino Observatory: Observation of flavor change for solar neutrinos *. Rev. Mod. Phys. 2016, 88, 030502. [Google Scholar] [CrossRef]
- Majorana, E. Teoria simmetrica dell’elettrone e del positrone. Nuovo Cim. 1937, 14, 171–184. [Google Scholar] [CrossRef]
- Schechter, J.; Valle, J.W.F. Neutrinoless Double beta Decay in SU(2)×U(1) Theories. Phys. Rev. D 1982, 25, 2951. [Google Scholar] [CrossRef]
- Furry, W.H. On Transition Probabilities in Double Beta-Disintegration. Phys. Rev. 1939, 56, 1184–1193. [Google Scholar] [CrossRef]
- Dolinski, M.J.; Poon, A.W.; Rodejohann, W. Neutrinoless double-beta decay: Status and prospects. Annu. Rev. Nucl. Part. Sci. 2019, 69, 219–251. [Google Scholar] [CrossRef]
- Blaum, K.; Eliseev, S.; Danevich, F.A.; Tretyak, V.I.; Kovalenko, S.; Krivoruchenko, M.I.; Novikov, Y.N.; Suhonen, J. Neutrinoless double-electron capture. Rev. Mod. Phys. 2020, 92, 045007. [Google Scholar] [CrossRef]
- Winter, R.G.; Double, K. Capture and Single K Capture with Positron Emission. Phys. Rev. 1955, 100, 142–144. [Google Scholar] [CrossRef]
- Winter, R.G. Search for Double Beta Decay in Cadmium and Molybdenum. Phys. Rev. 1955, 99, 88. [Google Scholar] [CrossRef]
- Georgi, H.M.; Glashow, S.L.; Nussinov, S. Unconventional model of neutrino masses. Nucl. Phys. B 1981, 193, 297–316. [Google Scholar] [CrossRef]
- Voloshin, M.B.; Mitsel’makher, G.V.; Eramzhyan, R.A. Conversion of an atomic electron into a positron and double β + decay. JETP Lett. 1982, 35, 656–659. [Google Scholar]
- Bernabeu, J.; De Rujula, A.; Jarlskog, C. Neutrinoless double electron capture as a tool to measure the electron neutrino mass. Nucl. Phys. B 1983, 223, 15–28. [Google Scholar] [CrossRef]
- Sujkowski, Z.; Wycech, S. Neutrinoless double electron capture: A tool to search for Majorana neutrino. Phys. Rev. C 2004, 70, 052501. [Google Scholar] [CrossRef]
- Karpeshin, F.F. On neutrinoless double e capture problem. Phys. Part. Nucl. Lett. 2008, 5, 379–382. [Google Scholar] [CrossRef]
- Karpeshin, F.F.; Trzhaskovskaya, M.B. Shake-off in the 164Er neutrinoless double electronic capture and the dark matter puzzle. Phys. Rev. C 2023, 107, 045502. [Google Scholar] [CrossRef]
- Brümmer, T.; Bohlen, S.; Grüner, F.; Osterhoff, J.; Põder, K. Compact all-optical precision-tunable narrowband hard Compton X-ray source. Sci. Rep. 2022, 12, 16017. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X. Inverse Compton gamma-ray source driven by a plasma flying mirror. JOSA B 2023, 4, 3262–3268. [Google Scholar] [CrossRef]
- Geloni, G.; Saldin, E.; Samoylova, L.; Schneidmiller, E.; Sinn, H.; Tschentscher, T.; Yurkov, M. Coherence properties of the European XFEL. New J. Phys. 2010, 12, 035021. [Google Scholar] [CrossRef]
- Milne, C.J.; Schietinger, T.; Aiba, M.; Alarcon, A.; Alex, J.; Anghel, A.; Arsov, V.; Beard, C.; Beaud, P.; Bettoni, S.; et al. SwissFEL: The Swiss X-ray free electron laser. Appl. Sci. 2017, 7, 720. [Google Scholar] [CrossRef]
- Duris, J.; Li, S.; Driver, T.; Champenois, E.G.; MacArthur, J.P.; Lutman, A.A.; Zhang, Z.; Rosenberger, P.; Aldrich, J.W.; Coffee, R.; et al. Tunable isolated attosecond X-ray pulses with gigawatt peak power from a free-electron laser. Nat. Photonics 2020, 14, 30–36. [Google Scholar] [CrossRef]
- Budker, D.; Berengut, J.C.; Flambaum, V.V.; Gorchtein, M.; Jin, J.; Karbstein, F.; Krasny, M.W.; Litvinov, Y.A.; Pálffy, A.; Pascalutsa, V.; et al. Expanding Nuclear Physics Horizons with the Gamma Factory (Ann. Phys. 3/2022). Ann. Phys. 2022, 534, 2270005. [Google Scholar] [CrossRef]
- Agostini, M.; GERDA Collaboration; Allardt, M.; Bakalyarov, A.M.; Balata, M.; Barabanov, I.; Barros, N.; Baudis, L.; Bauer, C.; Bellotti, E.; et al. Limit on the radiative neutrinoless double electron capture of 36Ar from GERDA Phase I. Eur. Phys. J. C 2016, 76, 652. [Google Scholar] [CrossRef][Green Version]
- Angloher, G.; Bauer, M.; Bauer, P.; Bavykina, I.; Bento, A.; Bucci, C.; Canonica, L.; Ciemniak, C.; Defay, X.; Deuter, G.; et al. New limits on double electron capture of 40Ca and 180W. J. Phys. G 2016, 43, 095202. [Google Scholar] [CrossRef]
- Bikit, I.; Krmar, M.; Slivka, J.; Vesković, M.; Čonkić, L.; Aničin, I. New results on the double β decay of iron. Phys. Rev. C 1998, 58, 2566. [Google Scholar] [CrossRef]
- Gavrilyuk, Y.M.; Gangapshev, A.M.; Kazalov, V.V.; Kuzminov, V.V.; Panasenko, S.I.; Ratkevich, S.S. Indications of 2ν2K capture in 78Kr. Phys. Rev. C 2013, 87, 035501. [Google Scholar] [CrossRef]
- Ratkevich, S.S.; Gangapshev, A.M.; Gavrilyuk, Y.M.; Karpeshin, F.F.; Kazalov, V.V.; Kuzminov, V.V.; Yakimenko, S.P. Comparative study of the double-K-shell-vacancy production in single-and double-electron-capture decay. Phys. Rev. C 2017, 96, 065502. [Google Scholar] [CrossRef]
- Bukhner, E.; Vishnevskij, I.N.; Danevich, F.A. Rare decays of mercury nuclei. Sov. J. Nucl. Phys. 1990, 52, 193–197. [Google Scholar]
- Meshik, A.P.; Hohenberg, C.M.; Pravdivtseva, O.V.; Kapusta, Y.S. Weak decay of 130Ba and 132Ba: Geochemical measurements. Phys. Rev. C 2001, 64, 035205. [Google Scholar] [CrossRef]
- Zon, B.A.; Karpeshin, F.F. Acceleration of the decay of 235mU by laser-induced resonant internal conversion. Sov. Phys. JETP 1990, 70, 224. [Google Scholar]
- Karpeshin, F.F. Instantaneous Fission in Muonic Atoms and Resonance Conversion; Nauka: St. Petersburg, Russia, 2006. (In Russian) [Google Scholar]
- Karpeshin, F.F. Resonance Internal Conversion as the way of accelerating nuclear processes. Phys. Part. Nucl. 2006, 37, 522. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics: Non-Relativistic Theory. In Course of Theoretical Physics; Pergamon: New York, NY, USA, 1977; Volume 3. [Google Scholar]
- Kondratyev, V.N. Magnetorotational supernova neutrino emission spectra and prospects for observations by large-size underwater telescopes. Phys. At. Nucl. 2023, 86, 1083–1089. [Google Scholar] [CrossRef]

| Transition [Ref.] | Δ (keV) | Γ (eV) | Δ/Γ 103 |
|---|---|---|---|
| 36Ar→36S [25] | 427.65 | 1.04 | 411.2 |
| 40Ca→40Ar [26] | 187.10 | 1.32 | 141.74 |
| 50Cr→50Ti [27] | 1159.7 | 1.78 | 651.5 |
| 78Kr→78Se [28,29] | 5.83 | 7.6 | 0.773 |
| 196Hg→196Pt [30] | 661.8 ± 3.0 | 99 | 6.7 |
| 37.6 ± 3.0 | 58.3 | 0.645 | |
| 132Ba→132Xe [31] | 774.8 | 23.0 | 33.7 |
| 54Fe→54Cr [27] | 668.3 | 2.04 | 327.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kondratyev, V.N.; Karpeshin, F.F. External Radiation Assistance of Neutrinoless Double Electron Capture. Atoms 2024, 12, 27. https://doi.org/10.3390/atoms12050027
Kondratyev VN, Karpeshin FF. External Radiation Assistance of Neutrinoless Double Electron Capture. Atoms. 2024; 12(5):27. https://doi.org/10.3390/atoms12050027
Chicago/Turabian StyleKondratyev, Vladimir N., and Feodor F. Karpeshin. 2024. "External Radiation Assistance of Neutrinoless Double Electron Capture" Atoms 12, no. 5: 27. https://doi.org/10.3390/atoms12050027
APA StyleKondratyev, V. N., & Karpeshin, F. F. (2024). External Radiation Assistance of Neutrinoless Double Electron Capture. Atoms, 12(5), 27. https://doi.org/10.3390/atoms12050027







