Interaction of Protons with Noble-Gas Atoms: Total and Differential Cross Sections
Abstract
1. Introduction
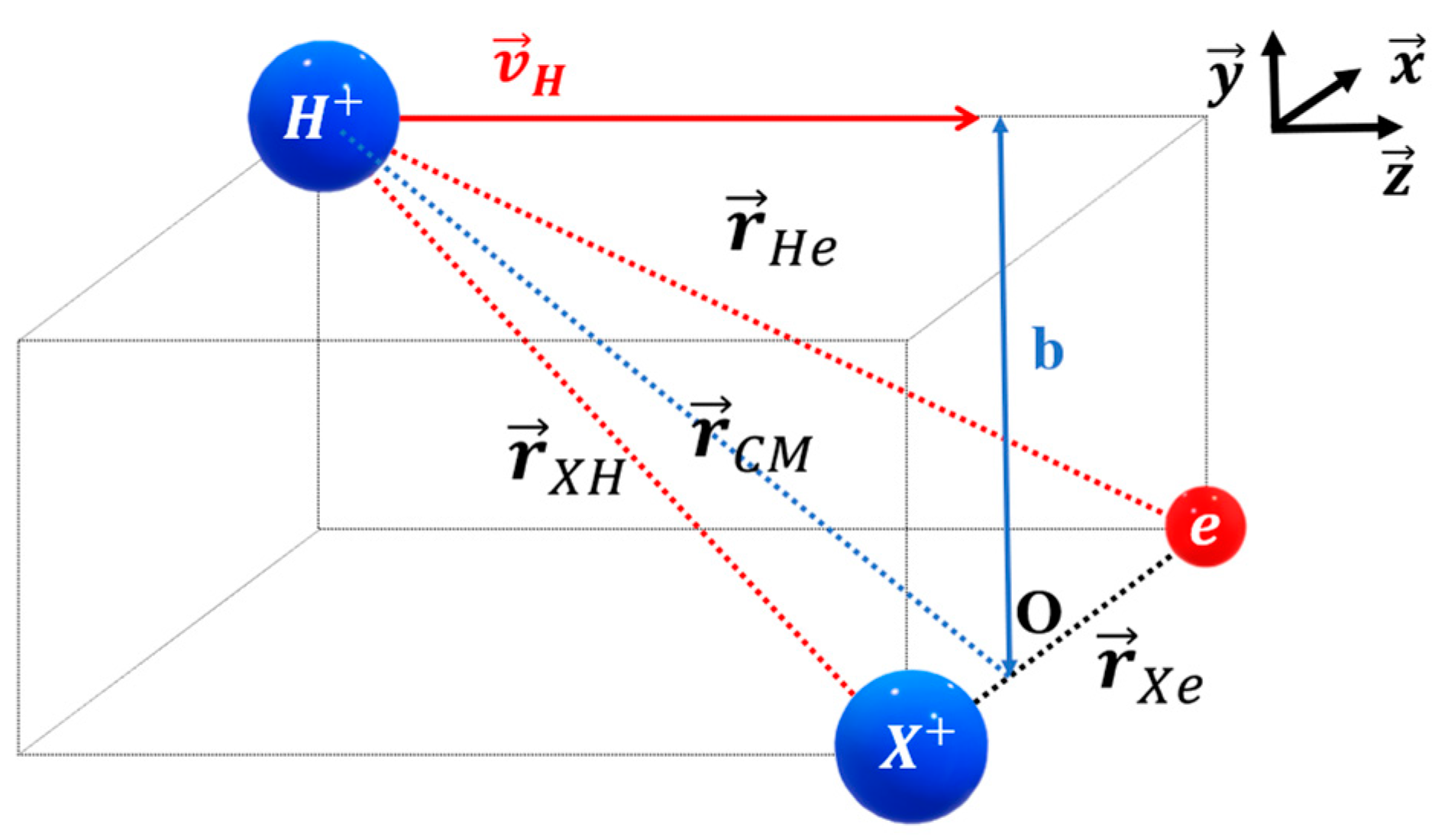
2. Theory
3. Results and Discussion
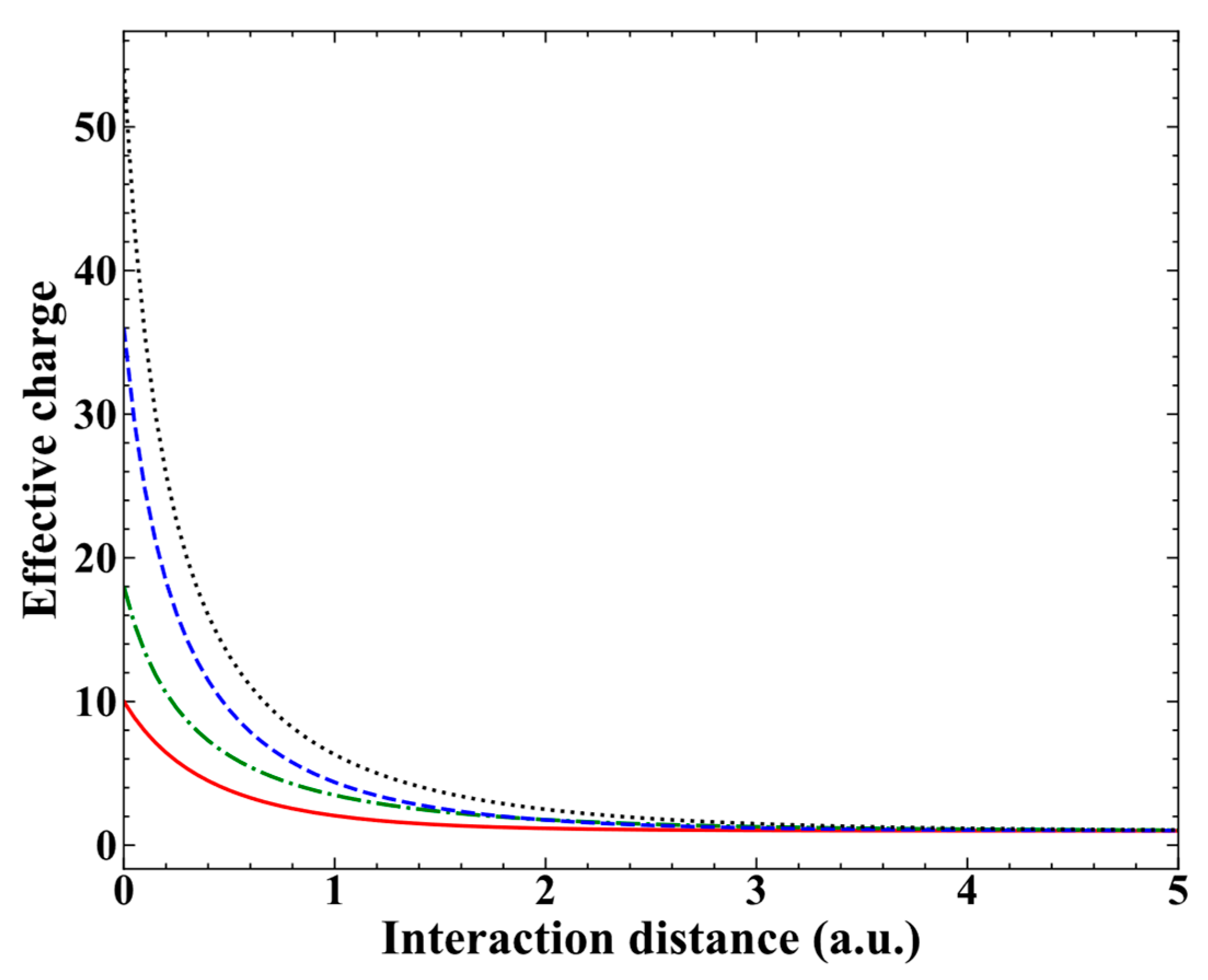
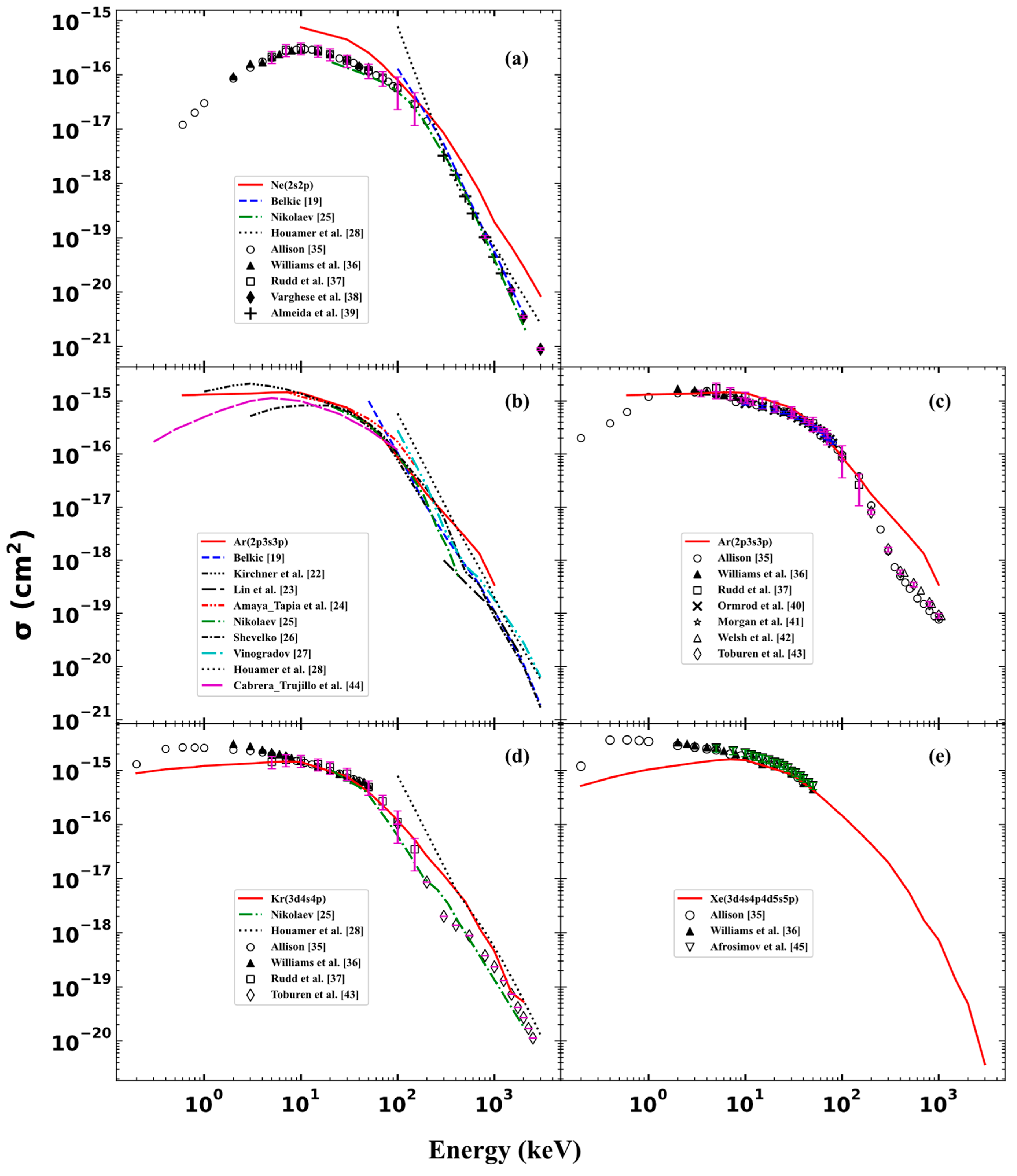
3.1. Total Cross Section for Single-Electron Capture
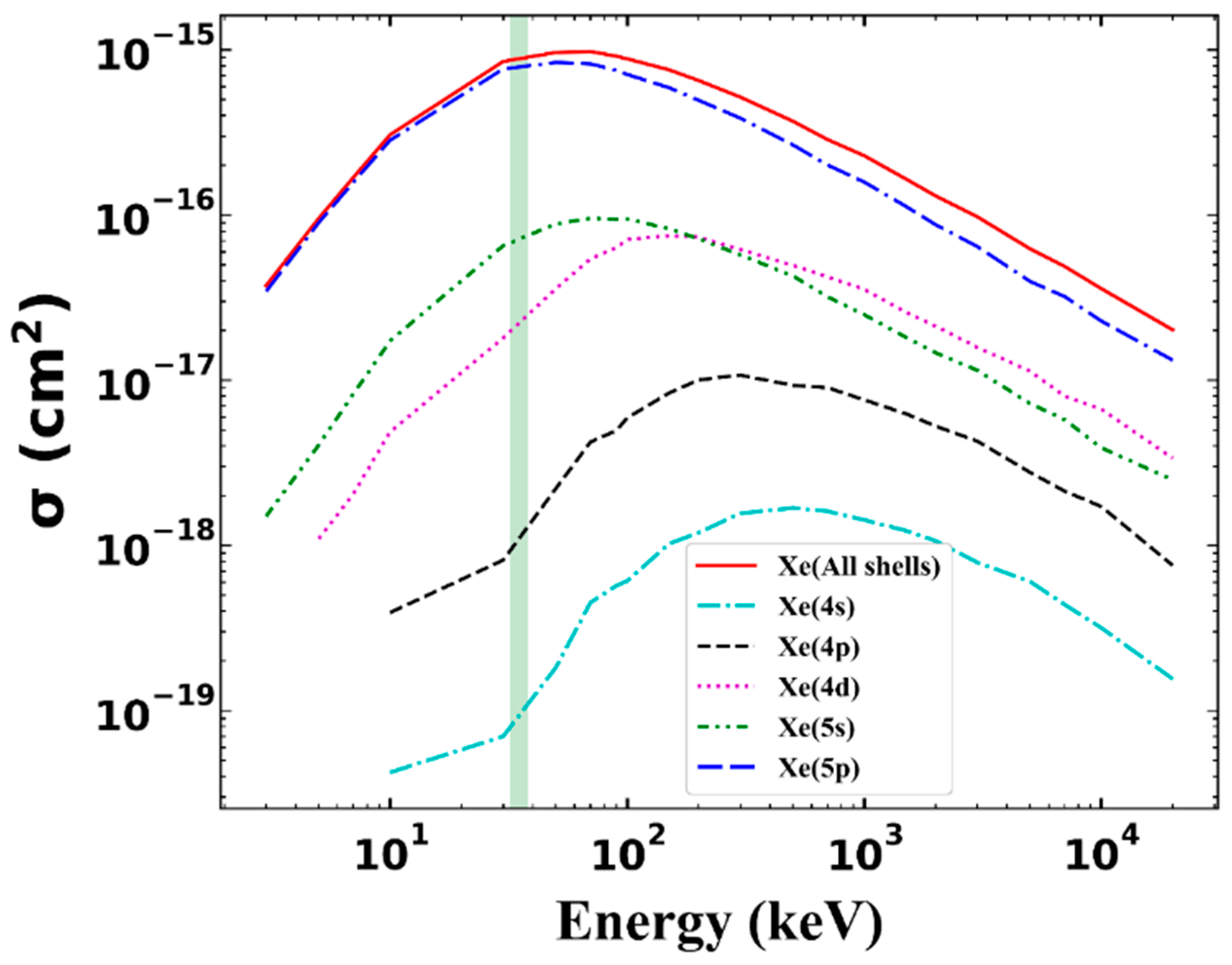
3.2. Total Cross Section for Single Ionization
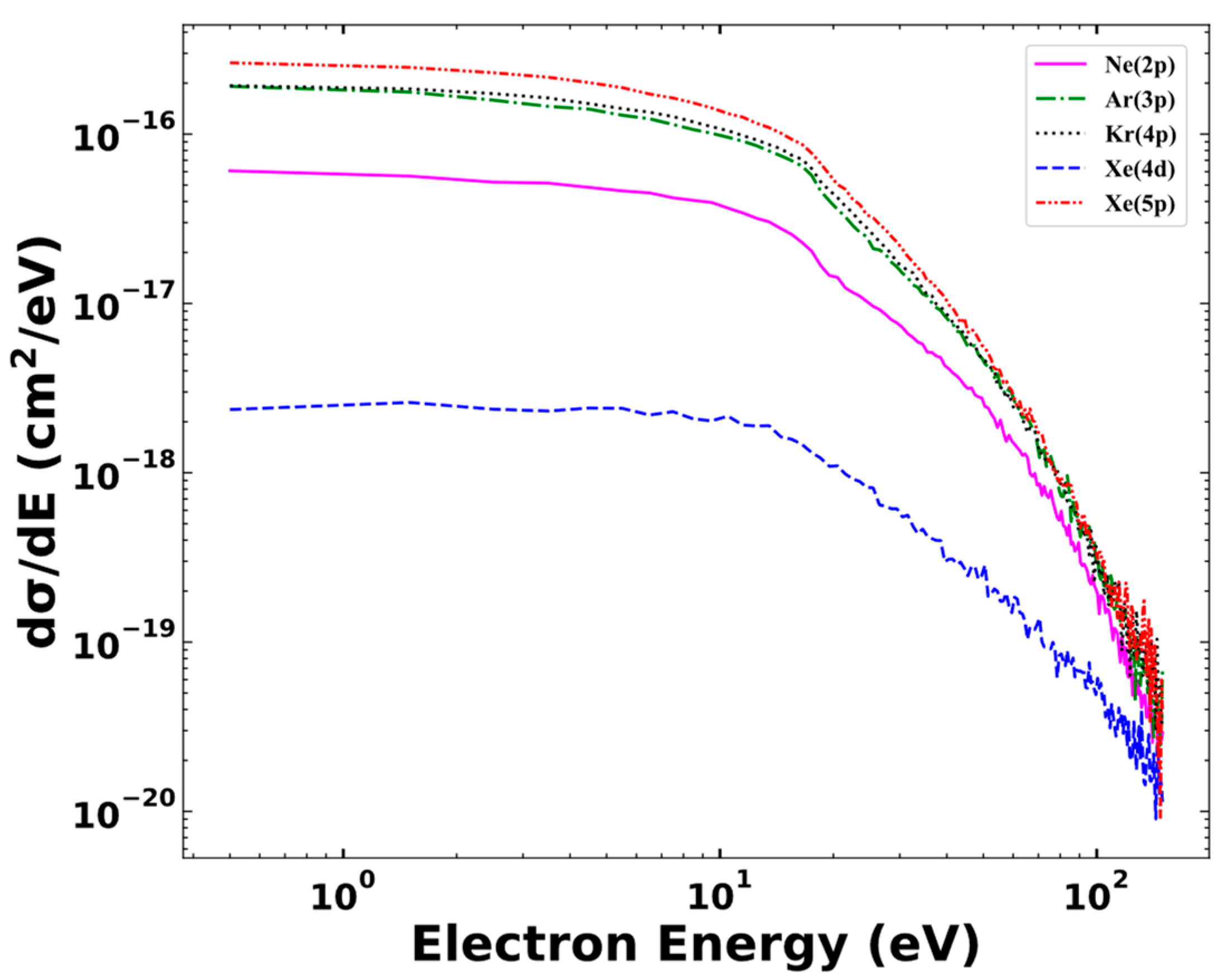
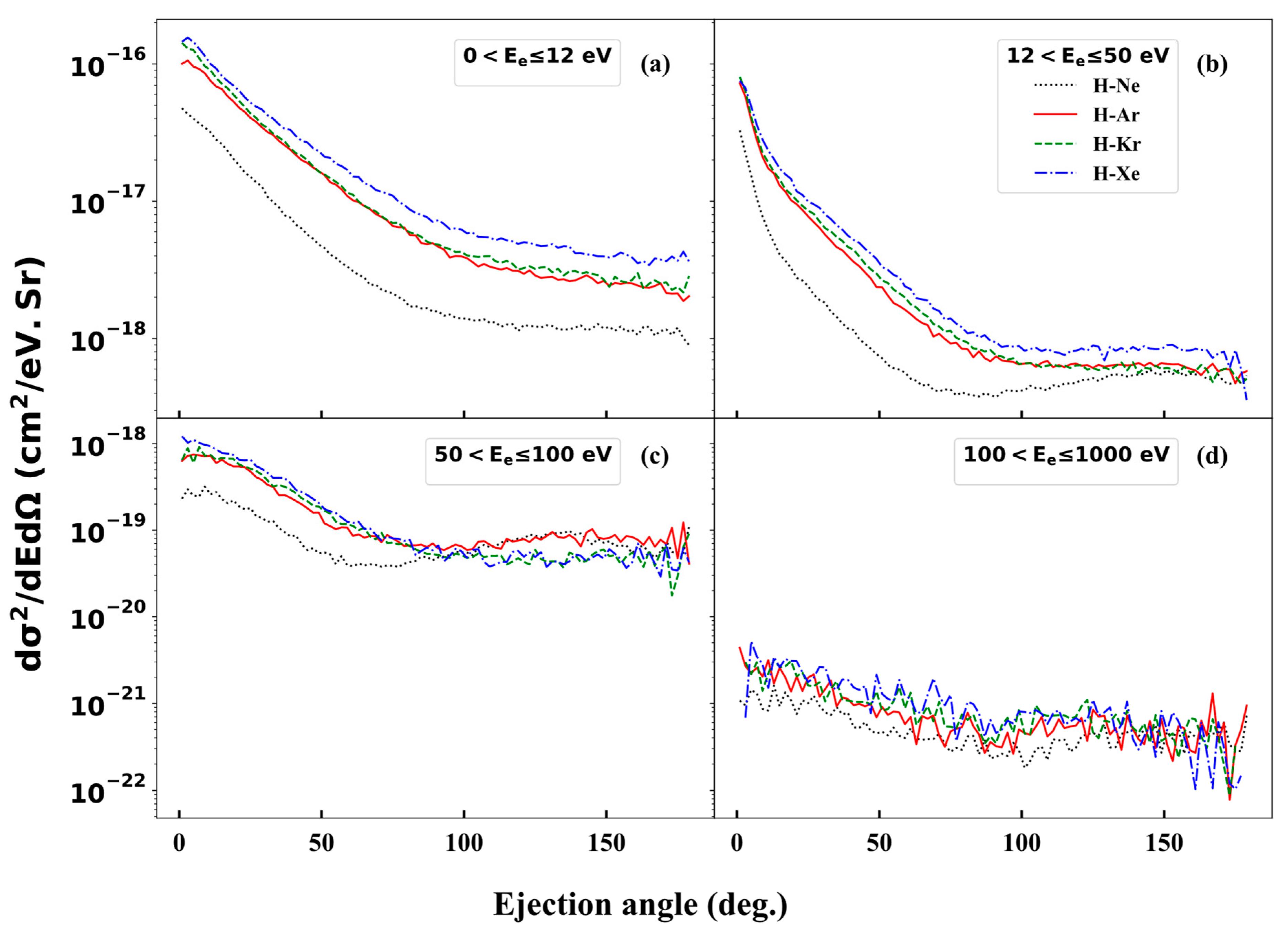
3.3. Single-Differential Cross Sections (SDCS) of Ionization
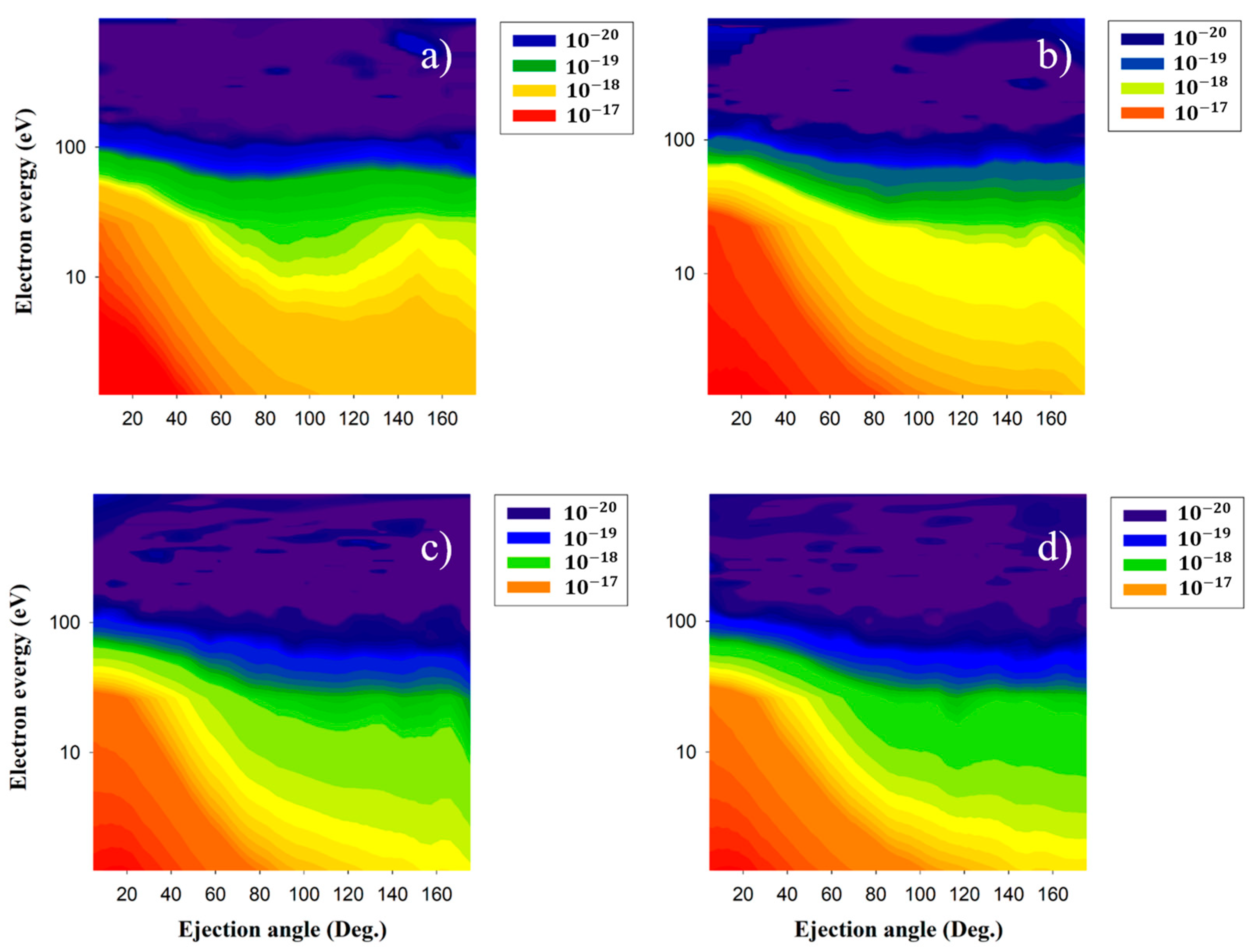
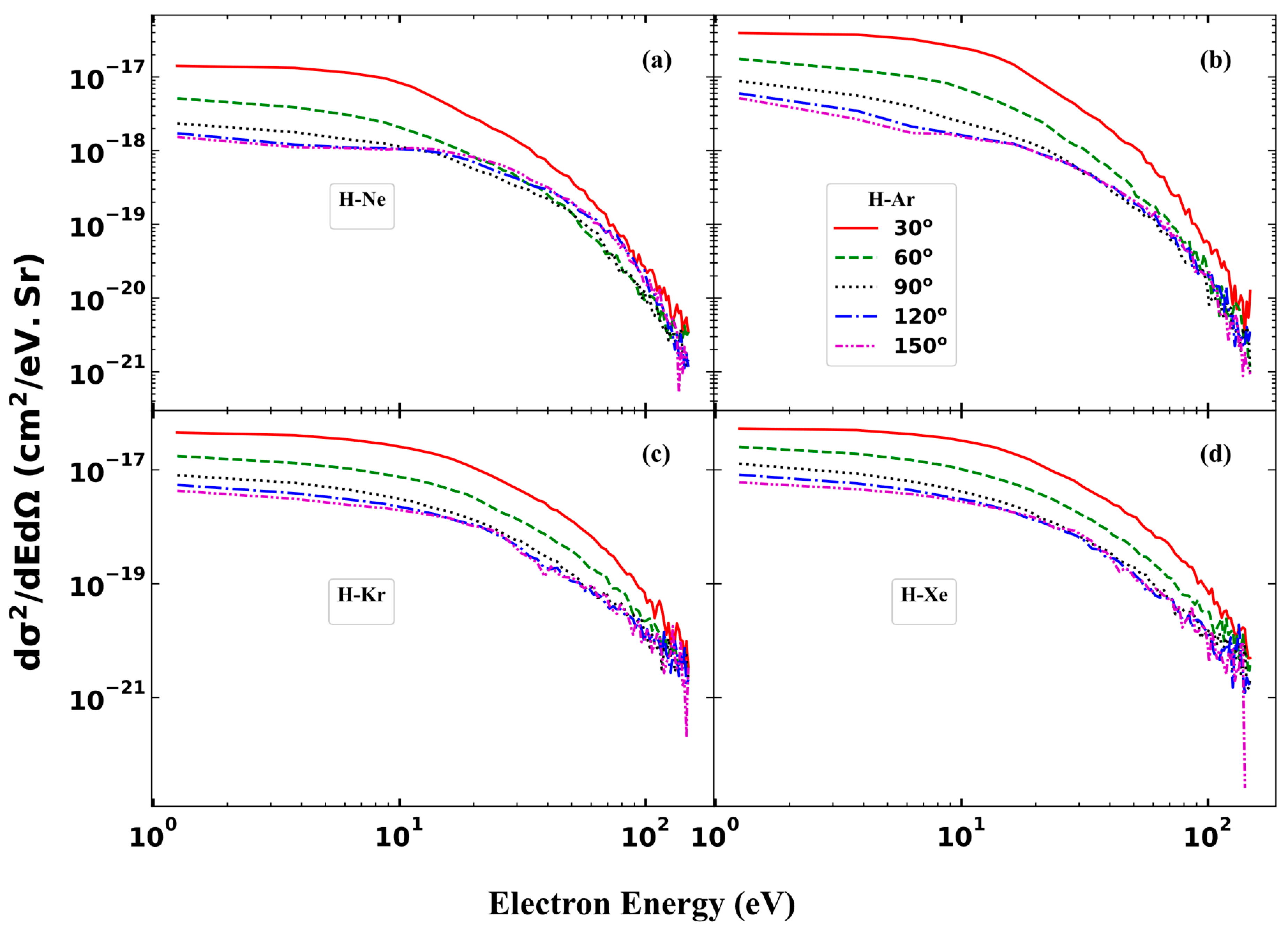
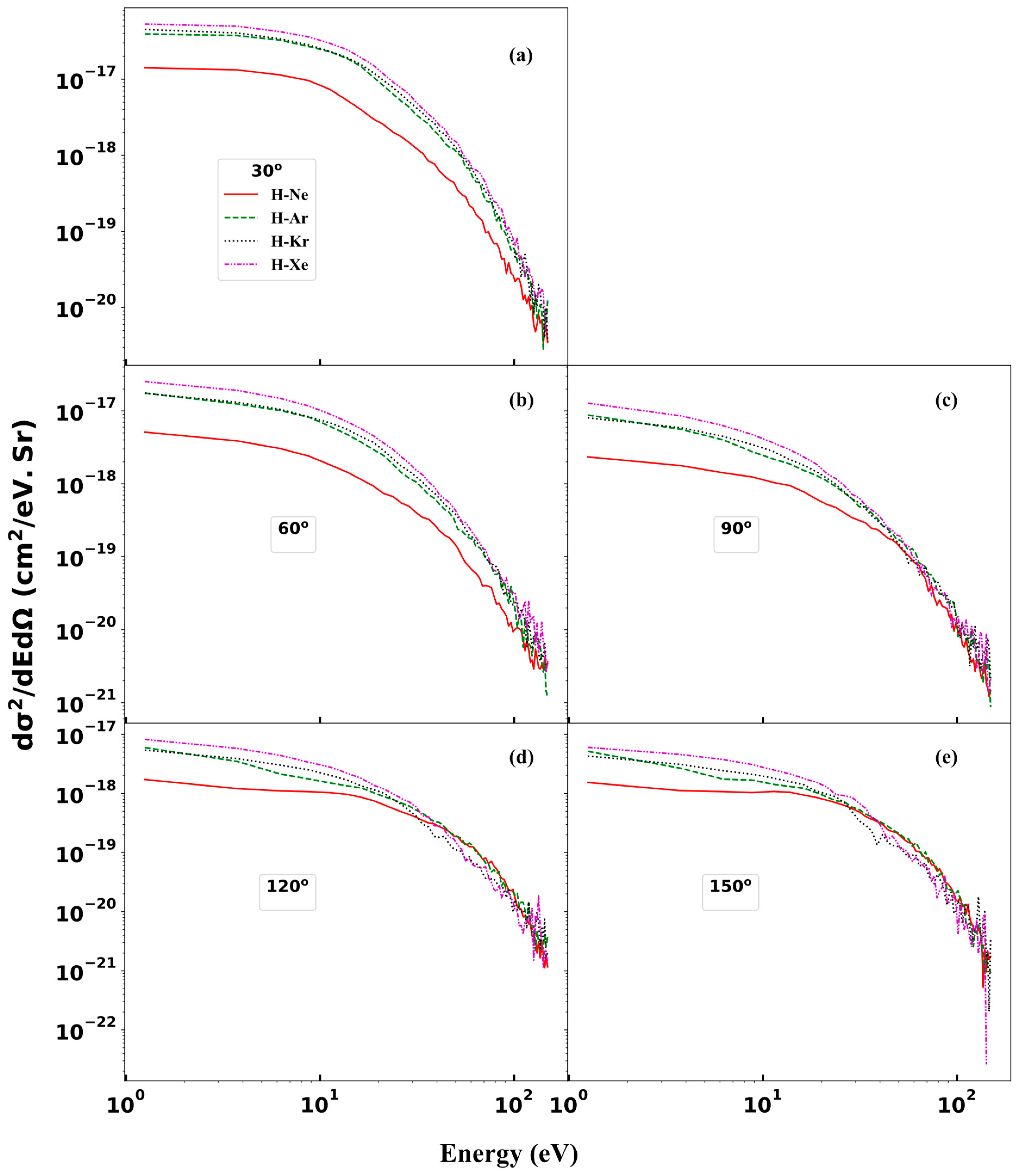
3.4. Double-Differential Cross Sections (DDCS)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bandyopadhyay, I.; Barbarino, M.; Bhattacharjee, A.; Eidietis, N.; Huber, A.; Isayama, A.; Kim, J.; Konovalov, S.; Lehnen, M.; Nardon, E.; et al. Summary of the IAEA Technical Meeting on Plasma Disruptions and Their Mitigation. Nucl. Fusion 2021, 61, 077001. [Google Scholar] [CrossRef]
- Hollmann, E.M.; Aleynikov, P.B.; Fülöp, T.; Humphreys, D.A.; Izzo, V.A.; Lehnen, M.; Lukash, V.E.; Papp, G.; Pautasso, G.; Saint-Laurent, F.; et al. Status of Research toward the ITER Disruption Mitigation System. Phys. Plasmas 2015, 22, 021802. [Google Scholar] [CrossRef]
- Bakhtiari, M.; Tamai, H.; Kawano, Y.; Kramer, G.J.; Isayama, A.; Nakano, T.; Kamiya, Y.; Yoshino, R.; Miura, Y.; Kusama, Y.; et al. Study of Plasma Termination Using High- Z Noble Gas Puffing in the JT-60U Tokamak. Nucl. Fusion 2005, 45, 318–325. [Google Scholar] [CrossRef]
- Lehnen, M.; Alonso, A.; Arnoux, G.; Baumgarten, N.; Bozhenkov, S.A.; Brezinsek, S.; Brix, M.; Eich, T.; Gerasimov, S.N.; Huber, A.; et al. Disruption Mitigation by Massive Gas Injection in JET. Nucl. Fusion 2011, 51, 123010. [Google Scholar] [CrossRef]
- Manas, P.; Kappatou, A.; Angioni, C.; McDermott, R.M. ASDEX Light Impurity Transport in Tokamaks: On the Impact of Neutral Beam Fast Ions. Nucl. Fusion 2020, 60, 056005. [Google Scholar] [CrossRef]
- Shiraki, D.; Commaux, N.; Baylor, L.R.; Eidietis, N.W.; Hollmann, E.M.; Lasnier, C.J.; Moyer, R.A. Thermal Quench Mitigation and Current Quench Control by Injection of Mixed Species Shattered Pellets in DIII-D. Phys. Plasmas 2016, 23, 062516. [Google Scholar] [CrossRef]
- Whyte, D.G.; Jernigan, T.C.; Humphreys, D.A.; Hyatt, A.W.; Lasnier, C.J.; Parks, P.B.; Evans, T.E.; Taylor, P.L.; Kellman, A.G.; Gray, D.S.; et al. Disruption Mitigation with High-Pressure Noble Gas Injection. J. Nucl. Mater. 2003, 313–316, 1239–1246. [Google Scholar] [CrossRef]
- Morozov, D.K.; Yurchenko, E.I.; Lukash, V.E.; Baronova, E.O.; Pozdnyakov, Y.I.; Rozhansky, V.A.; Senichenkov, I.Y.; Veselova, I.Y.; Schneider, R. Mechanisms of Disruptions Caused by Noble Gas Injection into Tokamak Plasmas. Nucl. Fusion 2005, 45, 882–887. [Google Scholar] [CrossRef]
- Brooks, J.N. Analysis of Noble Gas Recycling at a Fusion Plasma Divertor. Phys. Plasmas 1996, 3, 2286–2292. [Google Scholar] [CrossRef]
- Pusztai, I.; Pokol, G.; Dunai, D.; Réfy, D.; Pór, G.; Anda, G.; Zoletnik, S.; Schweinzer, J. Deconvolution-Based Correction of Alkali Beam Emission Spectroscopy Density Profile Measurements. Rev. Sci. Instrum. 2009, 80, 083502. [Google Scholar] [CrossRef]
- Brix, M.; Dodt, D.; Dunai, D.; Lupelli, I.; Marsen, S.; Melson, T.F.; Meszaros, B.; Morgan, P.; Petravich, G.; Refy, D.I.; et al. Recent Improvements of the JET Lithium Beam Diagnostic. Rev. Sci. Instrum. 2012, 83, 10D533. [Google Scholar] [CrossRef]
- Anda, G.; Dunai, D.; Lampert, M.; Krizsanóczi, T.; Németh, J.; Bató, S.; Nam, Y.U.; Hu, G.H.; Zoletnik, S. Development of a High Current 60 keV Neutral Lithium Beam Injector for Beam Emission Spectroscopy Measurements on Fusion Experiments. Rev. Sci. Instrum. 2018, 89, 013503. [Google Scholar] [CrossRef]
- Réfy, D.I.; Brix, M.; Gomes, R.; Tál, B.; Zoletnik, S.; Dunai, D.; Kocsis, G.; Kálvin, S.; Szabolics, T.; JET Contributors. Sub-Millisecond Electron Density Profile Measurement at the JET Tokamak with the Fast Lithium Beam Emission Spectroscopy System. Rev. Sci. Instrum. 2018, 89, 043509. [Google Scholar] [CrossRef]
- Zoletnik, S.; Anda, G.; Aradi, M.; Asztalos, O.; Bató, S.; Bencze, A.; Berta, M.; Demeter, G.; Dunai, D.; Hacek, P.; et al. Advanced Neutral Alkali Beam Diagnostics for Applications in Fusion Research (Invited). Rev. Sci. Instrum. 2018, 89, 10D107. [Google Scholar] [CrossRef]
- Zoletnik, S.; Hu, G.H.; Tál, B.; Dunai, D.; Anda, G.; Asztalos, O.; Pokol, G.I.; Kálvin, S.; Németh, J.; Krizsanóczi, T. Ultrafast Two-Dimensional Lithium Beam Emission Spectroscopy Diagnostic on the EAST Tokamak. Rev. Sci. Instrum. 2018, 89, 063503. [Google Scholar] [CrossRef]
- Al Atawneh, S.J.; Tőkési, K. Target Electron Removal in C5++H Collision. Nucl. Fusion 2022, 62, 026009. [Google Scholar] [CrossRef]
- Agueny, H.; Hansen, J.P.; Dubois, A.; Makhoute, A.; Taoutioui, A.; Sisourat, N. Electron Capture, Ionization and Excitation Cross Sections for keV Collisions between Fully Stripped Ions and Atomic Hydrogen in Ground and Excited States. At. Data Nucl. Data Tables 2019, 129–130, 101281. [Google Scholar] [CrossRef]
- Ziaeian, I.; Tőkési, K. State Selective Classical Electron Capture Cross Sections in Be4+ + H(1s) Collisions with Mimicking Quantum Effect. Sci. Rep. 2021, 11, 20164. [Google Scholar] [CrossRef]
- Belkić, D. Electron Capture in High-Energy Ion-Atom Collisions. Phys. Rep. 1979, 56, 279–369. [Google Scholar] [CrossRef]
- Olson, R.E. Electron Capture and Ionisation in H+, He2++Li Collisions. J. Phys. B At. Mol. Phys. 1982, 15, L163–L167. [Google Scholar] [CrossRef]
- Tőkési, K. State Selective Electron Capture in Low Energy Positron and Argon Collisions. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2012, 279, 62–65. [Google Scholar] [CrossRef]
- Kirchner, T.; Horbatsch, M.; Keim, M.; Lüdde, H.J. State-Selective Electron-Capture Calculations for p -Ar Collisions in an Independent Many-Electron Model. Phys. Rev. A 2004, 69, 012708. [Google Scholar] [CrossRef]
- Lin, C.D.; Tunnell, L.N. Subshell Electron Capture Cross Sections of Argon Atoms by Protons. J. Phys. B At. Mol. Phys. 1979, 12, L485–L490. [Google Scholar] [CrossRef][Green Version]
- Amaya-Tapia, A.; Martínez, H.; Hernández-Lamoneda, R.; Lin, C.D. Charge Transfer in H++Ar Collisions from 10 to 150 keV. Phys. Rev. A 2000, 62, 052718. [Google Scholar] [CrossRef]
- Nikolaev, V.S. Calculation of the Effective Cross Sections for Proton Charge Exchange in Collisions with Multi-Electron Atoms. Sov. Phys. JETP 1967, 24, 163. [Google Scholar]
- Shevelko, V.P. One-Electron Capture in Collisions of Fast Ions with Atoms. Z. Phys. A At. Nucl. 1978, 287, 19–26. [Google Scholar] [CrossRef]
- Vinogradov, A.V.; Shevel’Ko, V.P. Role of Inner Shells in Charge-Exchange between Protons and Multielectron Atoms. Sov. Phys. JETP 1971, 32, 593–601. [Google Scholar]
- Houamer, S.; Popov, Y.V.; Cappello, C.D. Total Cross Sections for Charge Transfer Reactions of Protons with Atomic and Molecular Targets at High Projectile Energies: The Role of Inner Orbitals. Phys. Lett. A 2009, 373, 4447–4452. [Google Scholar] [CrossRef]
- Ciappina, M.; Barrachina, R.O.; Navarrete, F.; Olson, R.E. Classical Trajectory and Monte Carlo Techniques. In Springer Handbook of Atomic, Molecular, and Optical Physics; Drake, G.W.F., Ed.; Springer Handbooks; Springer International Publishing: Cham, Switzerland, 2023; pp. 919–926. ISBN 978-3-030-73892-1. [Google Scholar]
- Garvey, R.H.; Jackman, C.H.; Green, A.E.S. Independent-Particle-Model Potentials for Atoms and Ions with 36 < Z ≤ 54 and a Modified Thomas-Fermi Atomic Energy Formula. Phys. Rev. A 1975, 12, 1144–1152. [Google Scholar] [CrossRef]
- Green, A.E.S. An Analytic Independent Particle Model for Atoms. In Advances in Quantum Chemistry; Elsevier: Amsterdam, The Netherlands, 1973; Volume 7, pp. 221–262. ISBN 978-0-12-034807-7. [Google Scholar]
- Reinhold, C.O.; Falcón, C.A. Classical Ionization and Charge-Transfer Cross Sections for H++He and H++Li+ Collisions with Consideration of Model Interactions. Phys. Rev. A 1986, 33, 3859–3866. [Google Scholar] [CrossRef]
- Al-Ajaleen, M.S.A.; Taoutioui, A.; Tokesi, K. Charge Transfer and Ionisation Cross-Sections in Collisions of Singly Charged Lithium Ions with Helium and Nitrogen Atoms. Plasma Phys. Control. Fusion 2023, 65, 065002. [Google Scholar] [CrossRef]
- Al-Ajaleen, M.; Tőkési, K. Total and Differential Ionization Cross Sections in Collision between Nitrogen Atom and Singly Charged Sodium Ion. Sci. Rep. 2023, 13, 14080. [Google Scholar] [CrossRef]
- Allison, S.K. Experimental Results on Charge-Changing Collisions of Hydrogen and Helium Atoms and Ions at Kinetic Energies above 0.2 Kev. Rev. Mod. Phys. 1958, 30, 1137–1168. [Google Scholar] [CrossRef]
- Williams, J.F.; Dunbar, D.N.F. Charge Exchange and Dissociation Cross Sections for H1+, H2+, and H3+ Ions of 2- to 50-keV Energy Incident Upon Hydrogen and the Inert Gases. Phys. Rev. 1966, 149, 62–69. [Google Scholar] [CrossRef]
- Rudd, M.E.; DuBois, R.D.; Toburen, L.H.; Ratcliffe, C.A.; Goffe, T.V. Cross Sections for Ionization of Gases by 5-4000-keV Protons and for Electron Capture by 5-150-keV Protons. Phys. Rev. A 1983, 28, 3244–3257. [Google Scholar] [CrossRef]
- Varghese, S.L.; Bissinger, G.; Joyce, J.M.; Laubert, R. Atomic Total Electron-Capture Cross Sections from C-, O-, F-, and S-Bearing Molecular Gases for MeV/u H+ and He+ Projectiles. Phys. Rev. A 1985, 31, 2202–2209. [Google Scholar] [CrossRef]
- Almeida, D.P.; De Castro Faria, N.V.; Freire, F.L.; Montenegro, E.C.; De Pinho, A.G. Collisional Formation and Destruction of Fast Negative Hydrogen Ions in He, Ne, and Ar Targets. Phys. Rev. A 1987, 36, 16–25. [Google Scholar] [CrossRef]
- Ormrod, J.H.; Michel, W.L. Charge Equilibrium Fractions and Charge-Exchange Cross Sections for Fast Ions in Nitrogen and Argon. Can. J. Phys. 1971, 49, 606–620. [Google Scholar] [CrossRef]
- Morgan, T.J.; Eriksen, F.J. Single- and Double-Electron Capture by 1-100-keV Protons in Collisions with Magnesium and Barium Atoms. Phys. Rev. A 1979, 19, 1448–1456. [Google Scholar] [CrossRef]
- Welsh, L.M.; Berkner, K.H.; Kaplan, S.N.; Pyle, R.V. Cross Sections for Electron Capture by Fast Protons in H2, He, N2, and Ar. Phys. Rev. 1967, 158, 85–92. [Google Scholar] [CrossRef]
- Toburen, L.H.; Nakai, M.Y.; Langley, R.A. Measurement of High-Energy Charge-Transfer Cross Sections for Incident Protons and Atomic Hydrogen in Various Gases. Phys. Rev. 1968, 171, 114–122. [Google Scholar] [CrossRef]
- Cabrera-Trujillo, R.; Amaya-Tapia, A.; Antillón, A. Differential, State-to-State, and Total-Charge-Transfer Cross Sections for H+ Colliding with Ar. Phys. Rev. A 2009, 79, 012712. [Google Scholar] [CrossRef]
- Afrosimov, V.; Mamaev, Y.A.; Panov, M.; Fedorenko, N. Investigation, by the Coincidence Method, of Charge State Changes Occurring in the Interaction Between H+, H0, and H- and the Xenon Atom. Sov. Phys. JETP 1969, 28, 97–110. [Google Scholar]
- Melo, W.S.; Santos, A.C.F.; Sant’Anna, M.M.; Sigaud, G.M.; Montenegro, E.C. Multiple Ionization of Noble Gases by 2.0 MeV Proton Impact: Comparison with Equi-Velocity Electron Impact Ionization. J. Phys. B At. Mol. Opt. Phys. 2002, 35, L187–L192. [Google Scholar] [CrossRef]
- Cavalcanti, E.G.; Sigaud, G.M.; Montenegro, E.C.; Schmidt-B Cking, H. Absolute Cross Sections for Multiple Ionization of Noble Gases by Swift Proton Impact. J. Phys. B At. Mol. Opt. Phys. 2003, 36, 3087–3096. [Google Scholar] [CrossRef]
- De Heer, F.J.; Schutten, J.; Moustafa, H. Ionization and Electron Capture Cross Sections for Protons Incident on Noble and Diatomic Gases between 10 and 140 keV. Physica 1966, 32, 1766–1792. [Google Scholar] [CrossRef]
- Clementi, E.; Roetti, C. Roothaan-Hartree-Fock Atomic Wavefunctions. At. Data Nucl. Data Tables 1974, 14, 177–478. [Google Scholar] [CrossRef]
- Bunge, C.F.; Barrientos, J.A.; Bunge, A.V. Roothaan-Hartree-Fock Ground-State Atomic Wave Functions: Slater-Type Orbital Expansions and Expectation Values for Z = 2–54. At. Data Nucl. Data Tables 1993, 53, 113–162. [Google Scholar] [CrossRef]
- Khandelwal, G.S.; Choi, B.H.; Merzbacher, E. Tables for Born Approximation Calculations of K- and L-Shell Ionization by Protons and Other Charged Particles. At. Data Nucl. Data Tables 1969, 1, 103–120. [Google Scholar] [CrossRef]
- Choi, B.-H.; Merzbacher, E.; Khandelwal, G.S. Tables for Born Approximation Calculations of L-Subshell Ionization by Simple Heavy Charged Particles. At. Data Nucl. Data Tables 1973, 5, 291–304. [Google Scholar] [CrossRef]
- Benka, O.; Kropf, A. Tables for Plane-Wave Born-Approximation Calculations of K- and L-Shell Ionization by Protons. At. Data Nucl. Data Tables 1978, 22, 219–233. [Google Scholar] [CrossRef]
- Johnson, D.E.; Basbas, G.; McDaniel, F.D. Nonrelativistic Plane-Wave Born-Approximation Calculations of Direct Coulomb M-Subshell Ionization by Charged Particles. At. Data Nucl. Data Tables 1979, 24, 1–11. [Google Scholar] [CrossRef]
- Sulik, B.; Koncz, C.; Tőkési, K.; Orbán, A.; Berényi, D. Evidence for Fermi-Shuttle Ionization in Intermediate Velocity C+ + Xe Collisions. Phys. Rev. Lett. 2002, 88, 073201. [Google Scholar] [CrossRef] [PubMed]


| Ne | 1.792 | 0.4515 | 2.710 | 0.3671 |
| Ar | 0.957 | 0.2165 | 3.500 | 0.2560 |
| Kr | 1.351 | 0.1872 | 4.418 | 0.1611 |
| Xe | 1.044 | 0.1107 | 5.101 | 0.1316 |
| Ne | Ar | Kr | Xe | |
|---|---|---|---|---|
| 2s | 48.5 | |||
| 2p | 21.6 | 248.4 | ||
| 3s | 29.3 | |||
| 3p | 15.7 | |||
| 3d | 93.8 | 676.4 | ||
| 4s | 27.5 | 213.2 | ||
| 4p | 14.1 | 145.5 | ||
| 4d | 67.5 | |||
| 5s | 23.3 | |||
| 5p | 12.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Ajaleen, M.; Tőkési, K. Interaction of Protons with Noble-Gas Atoms: Total and Differential Cross Sections. Atoms 2024, 12, 28. https://doi.org/10.3390/atoms12050028
Al-Ajaleen M, Tőkési K. Interaction of Protons with Noble-Gas Atoms: Total and Differential Cross Sections. Atoms. 2024; 12(5):28. https://doi.org/10.3390/atoms12050028
Chicago/Turabian StyleAl-Ajaleen, Musab, and Károly Tőkési. 2024. "Interaction of Protons with Noble-Gas Atoms: Total and Differential Cross Sections" Atoms 12, no. 5: 28. https://doi.org/10.3390/atoms12050028
APA StyleAl-Ajaleen, M., & Tőkési, K. (2024). Interaction of Protons with Noble-Gas Atoms: Total and Differential Cross Sections. Atoms, 12(5), 28. https://doi.org/10.3390/atoms12050028







