Atomic Models of Dense Plasmas, Applications, and Current Challenges
Abstract
1. Introduction
2. Atomic Modeling of Ideal Plasmas
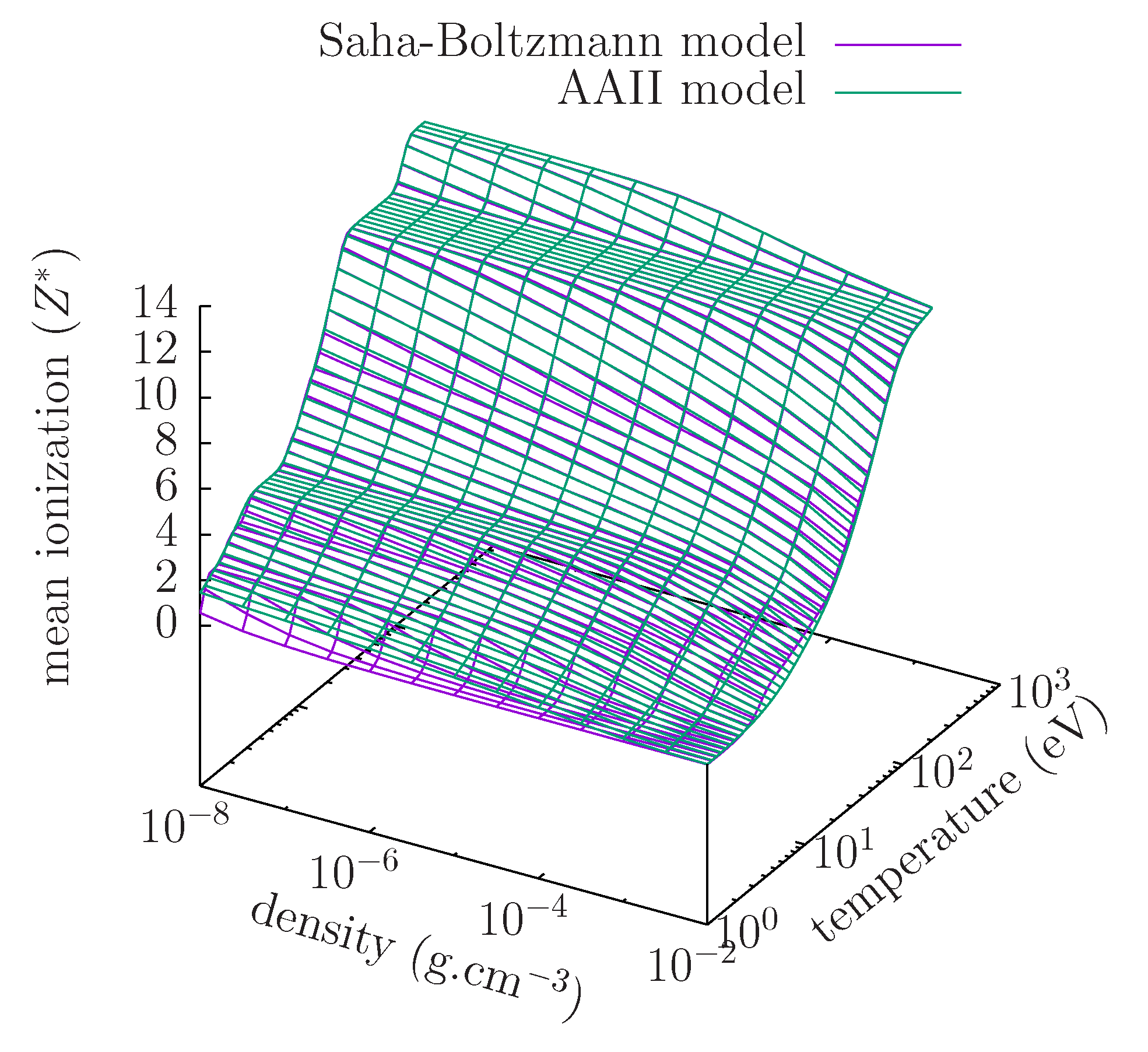
2.1. Saha–Boltzmann Model and Isolated Ion: A Variational Detailed Model of Ideal Plasma
2.2. Average-Atom Model of Isolated Ion from a Variational Perspective
3. Nonideality Corrections to Isolated Ions
3.1. General Considerations, Notion of Ionization-Potential Depression
3.2. Mean-Field Approach
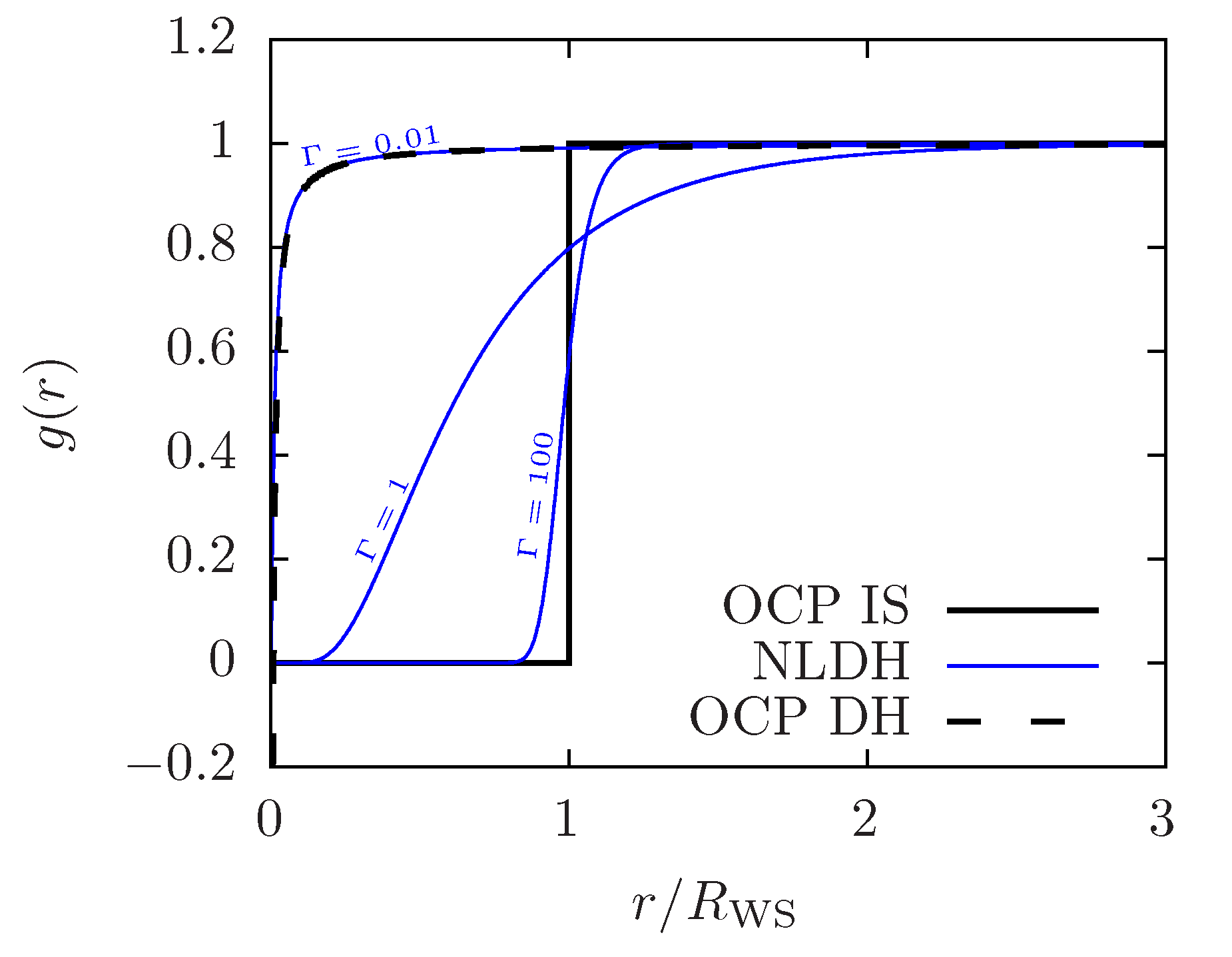
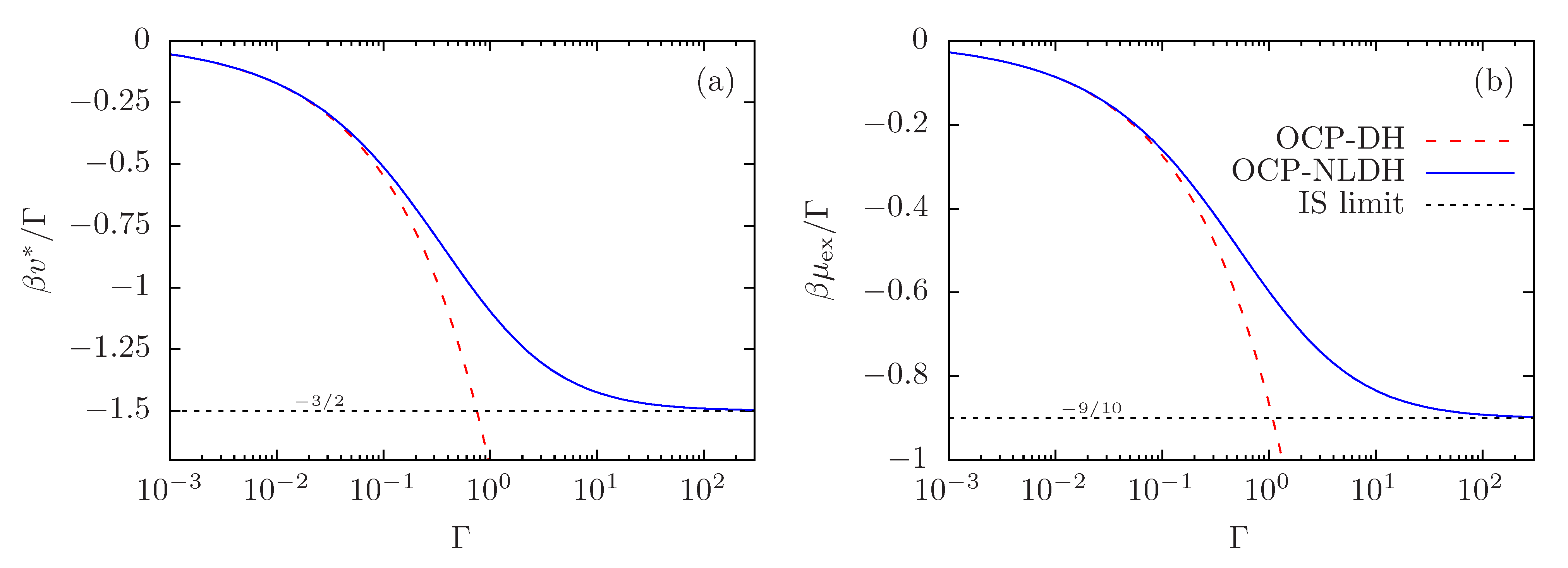
3.3. Debye–Hückel Model
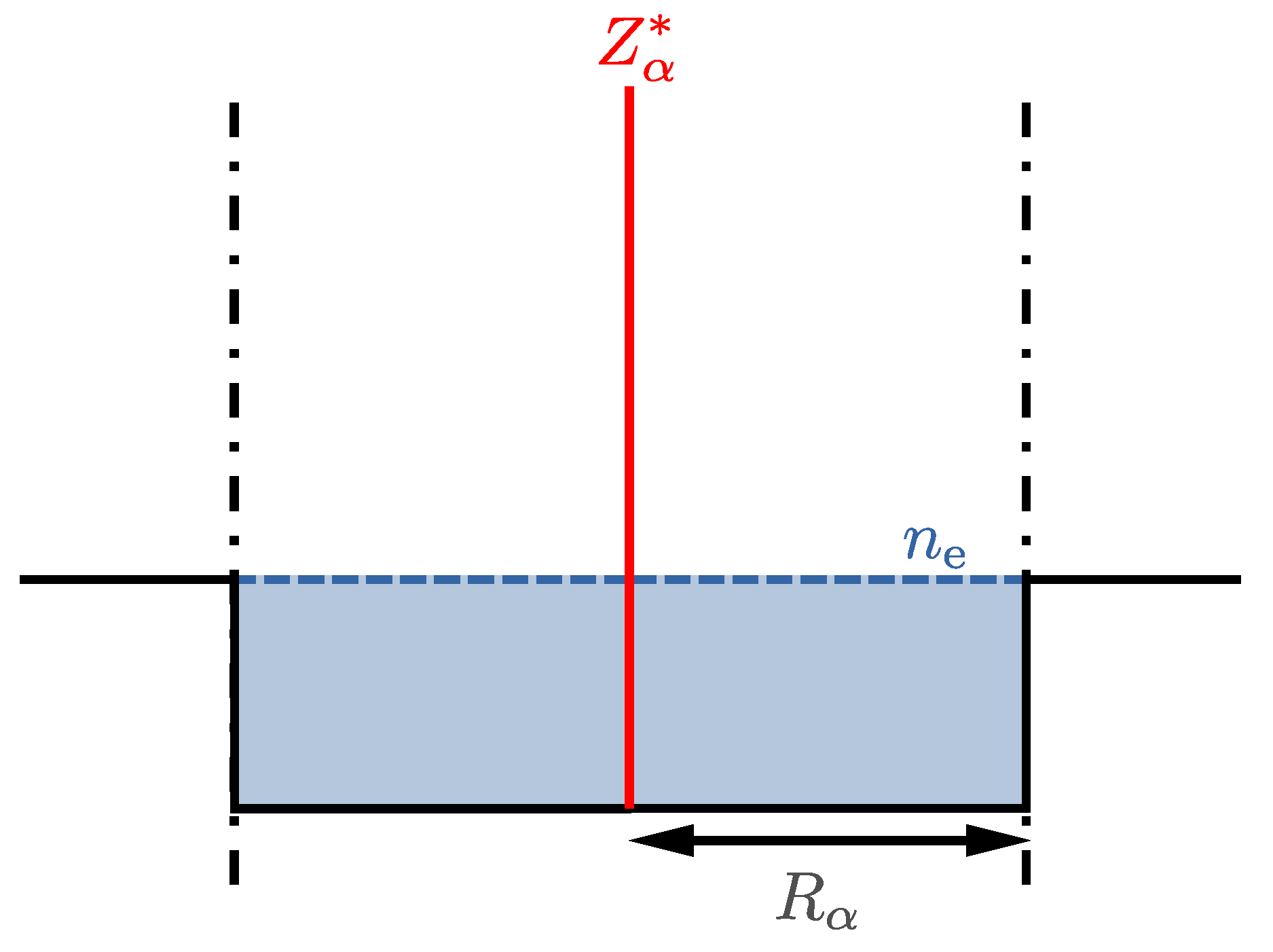
3.4. Ion-Sphere Model from a Classical-Plasma Perspective
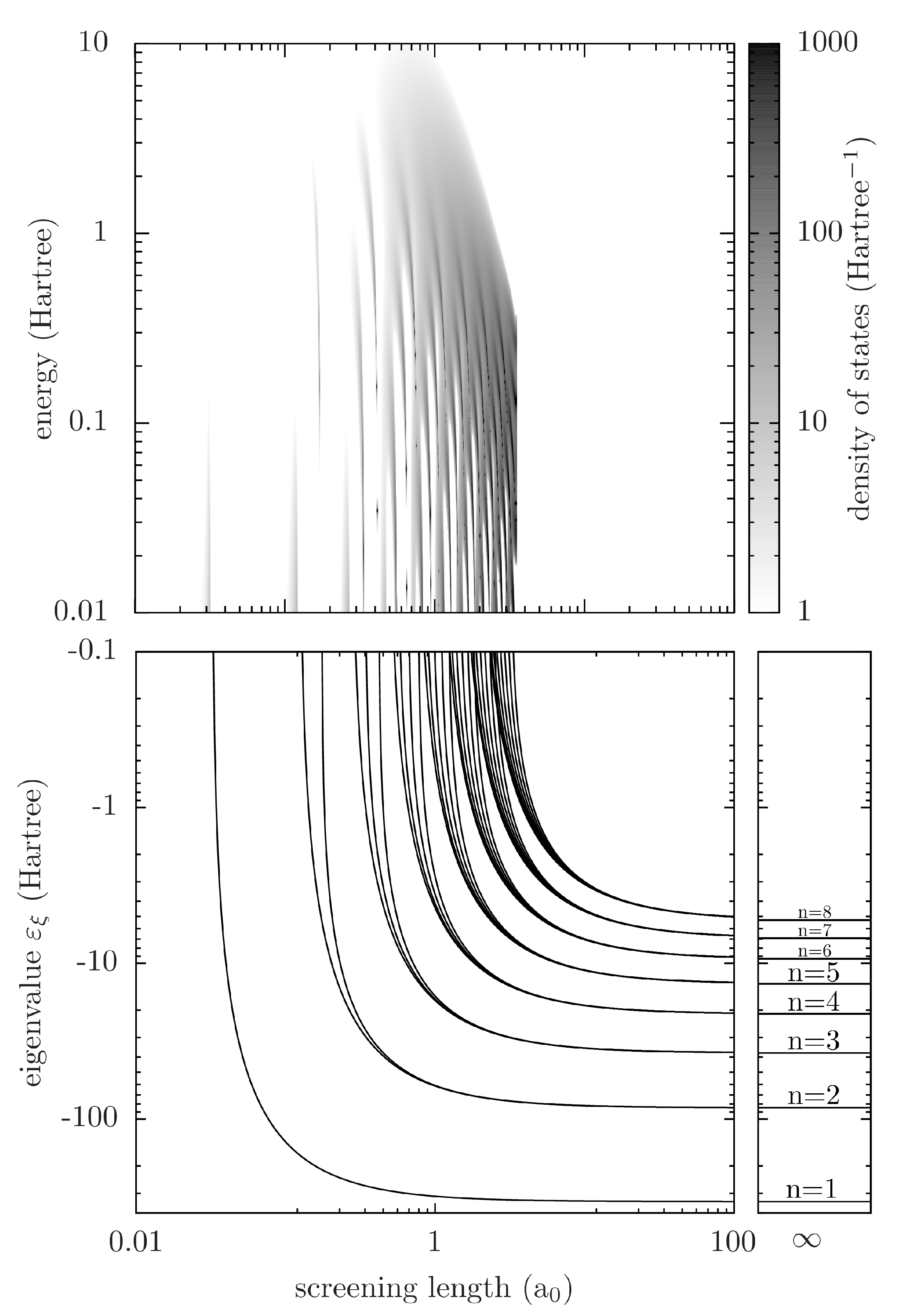
3.5. Divergence of Partition Functions, Suppression of Bound States, Screening and Limitations of the Nonideality Corrections
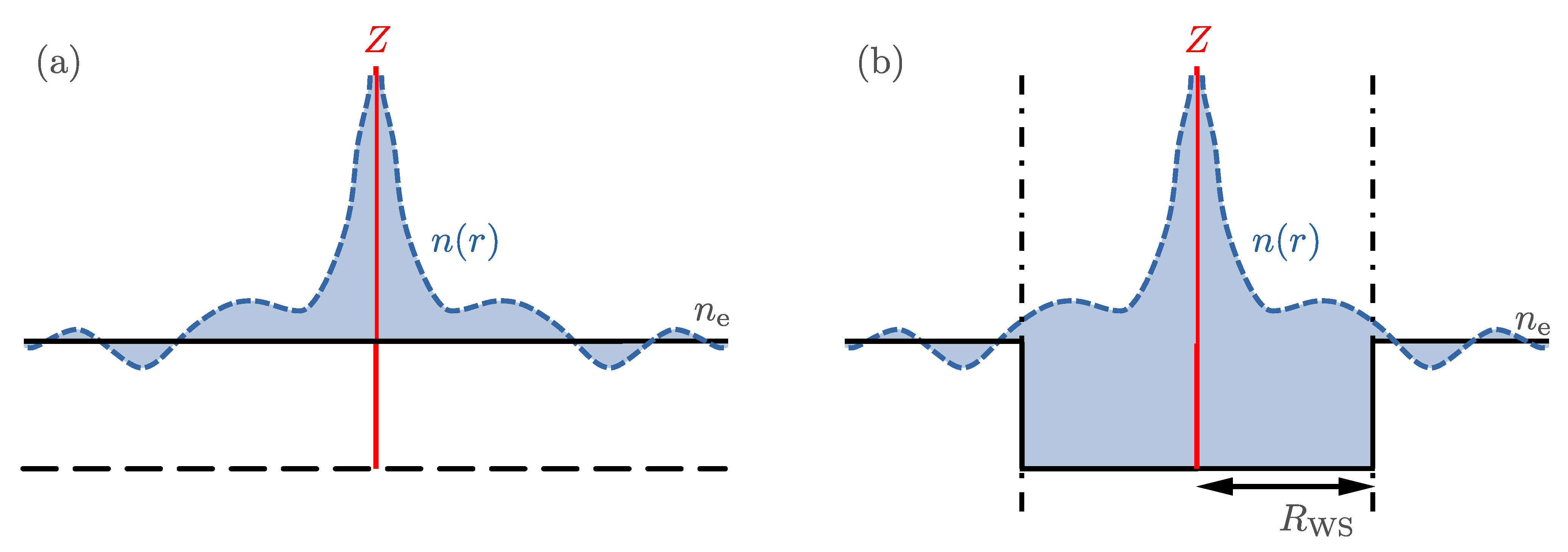
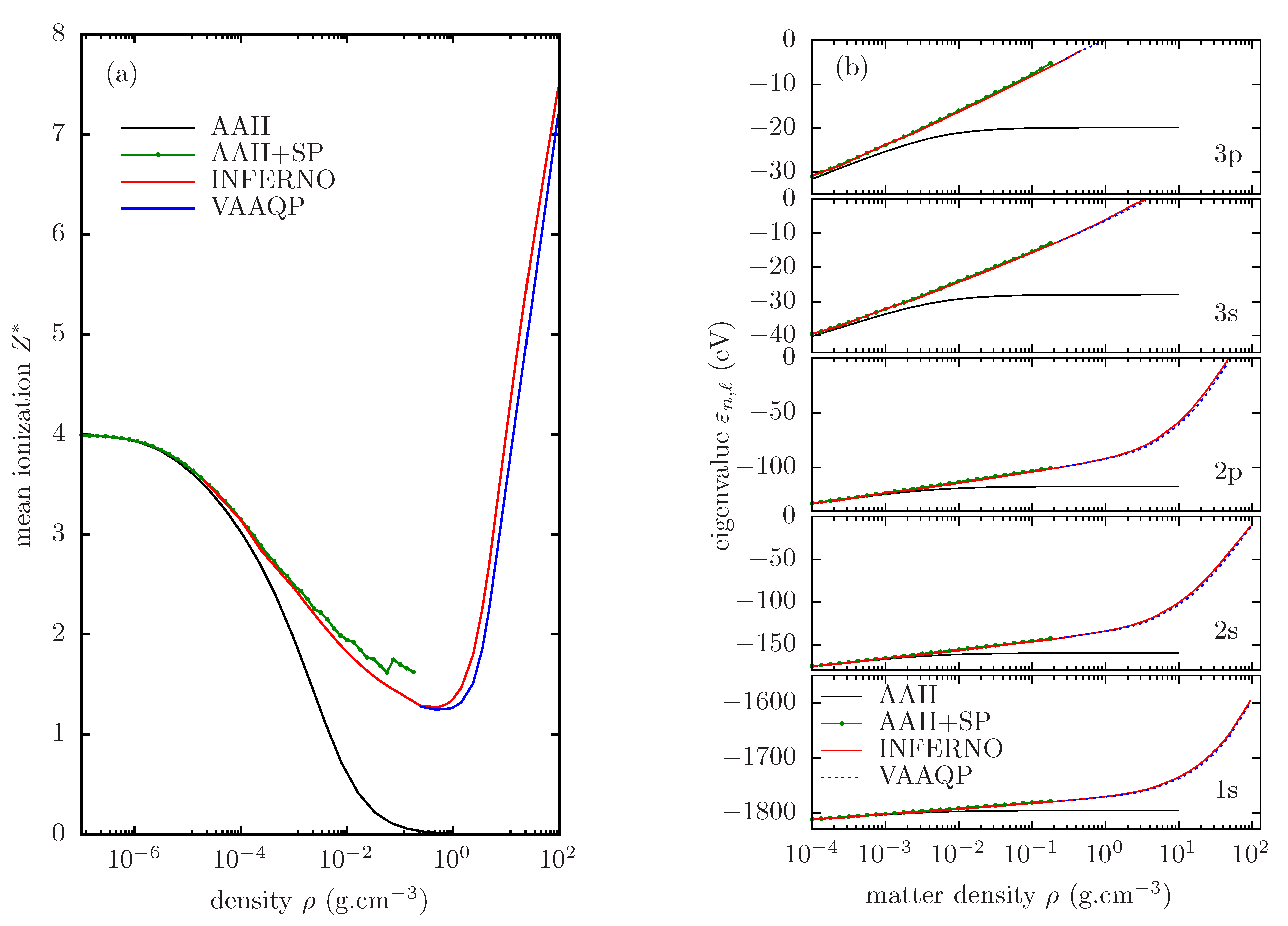
4. Atomic Models of Pressure-Ionized Plasmas
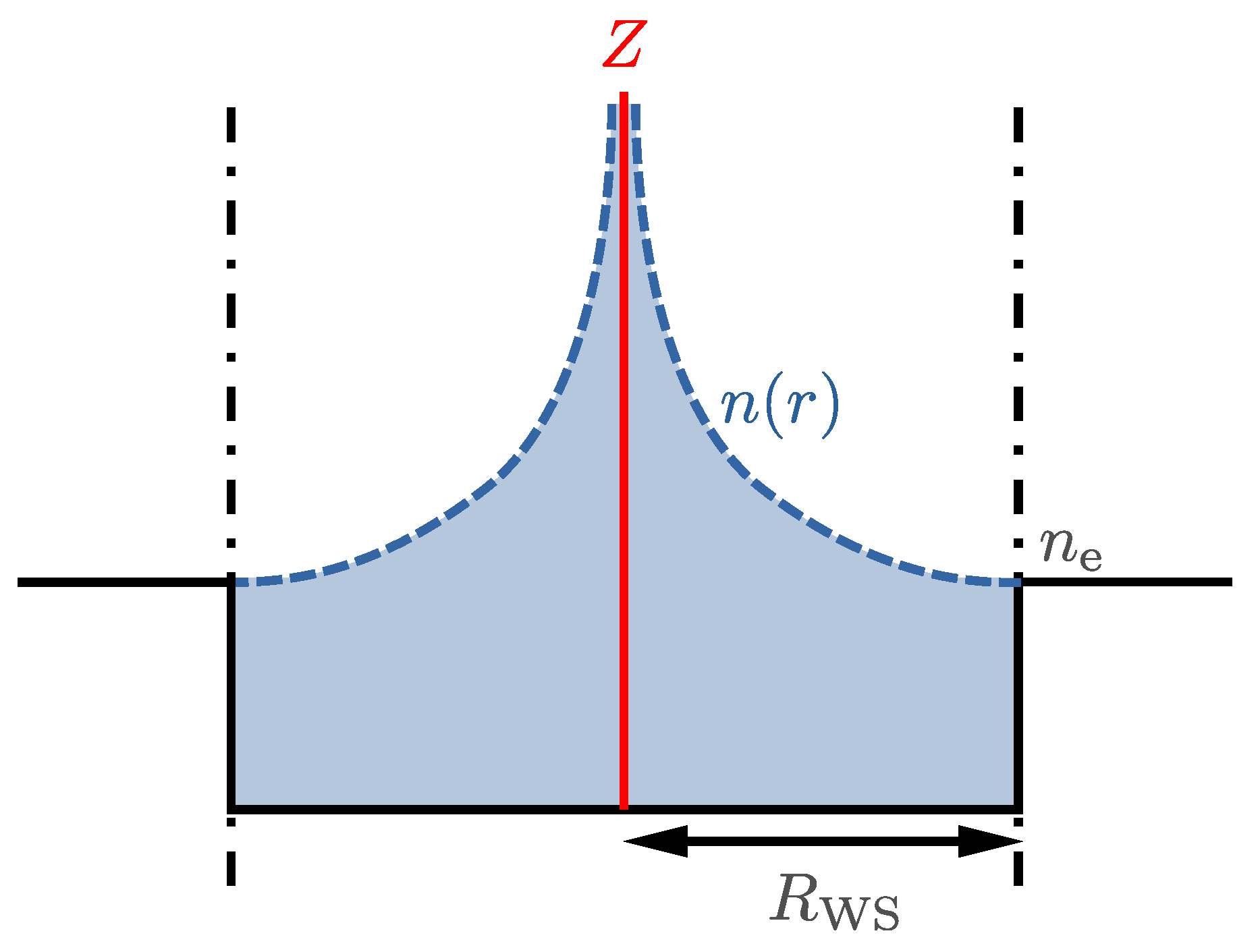
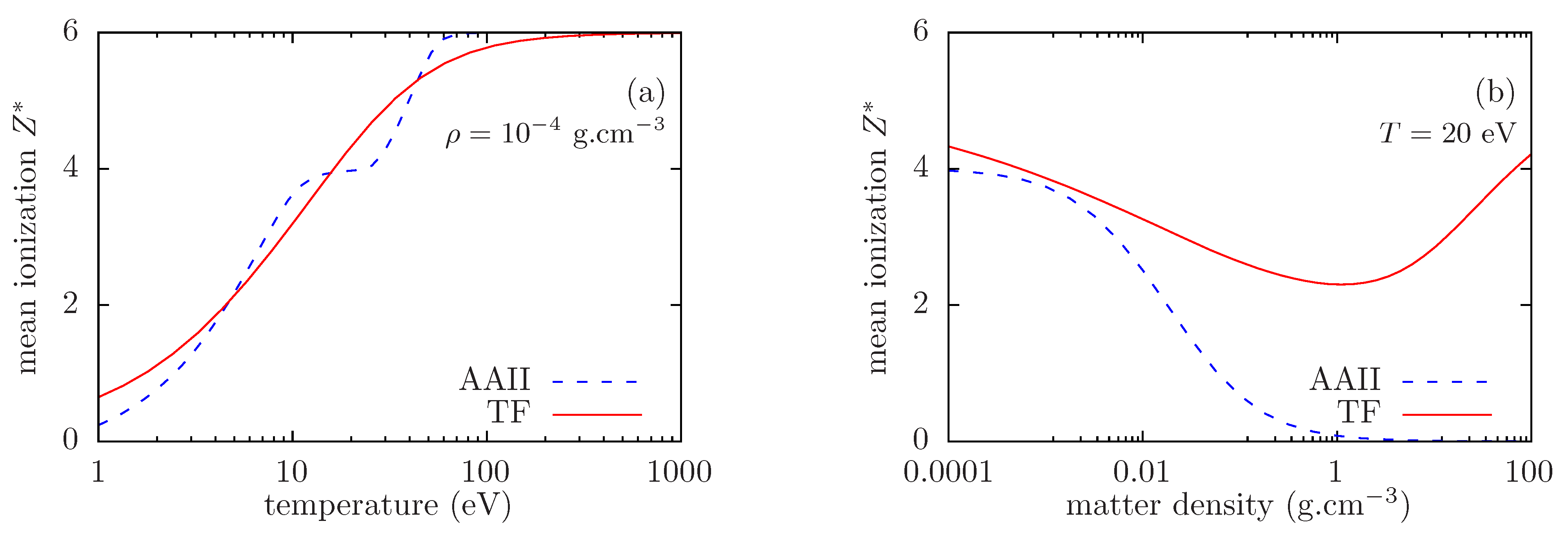
4.1. Thomas–Fermi Ion-in-Cell Model
4.2. Quantum Ion-in-Cell Models
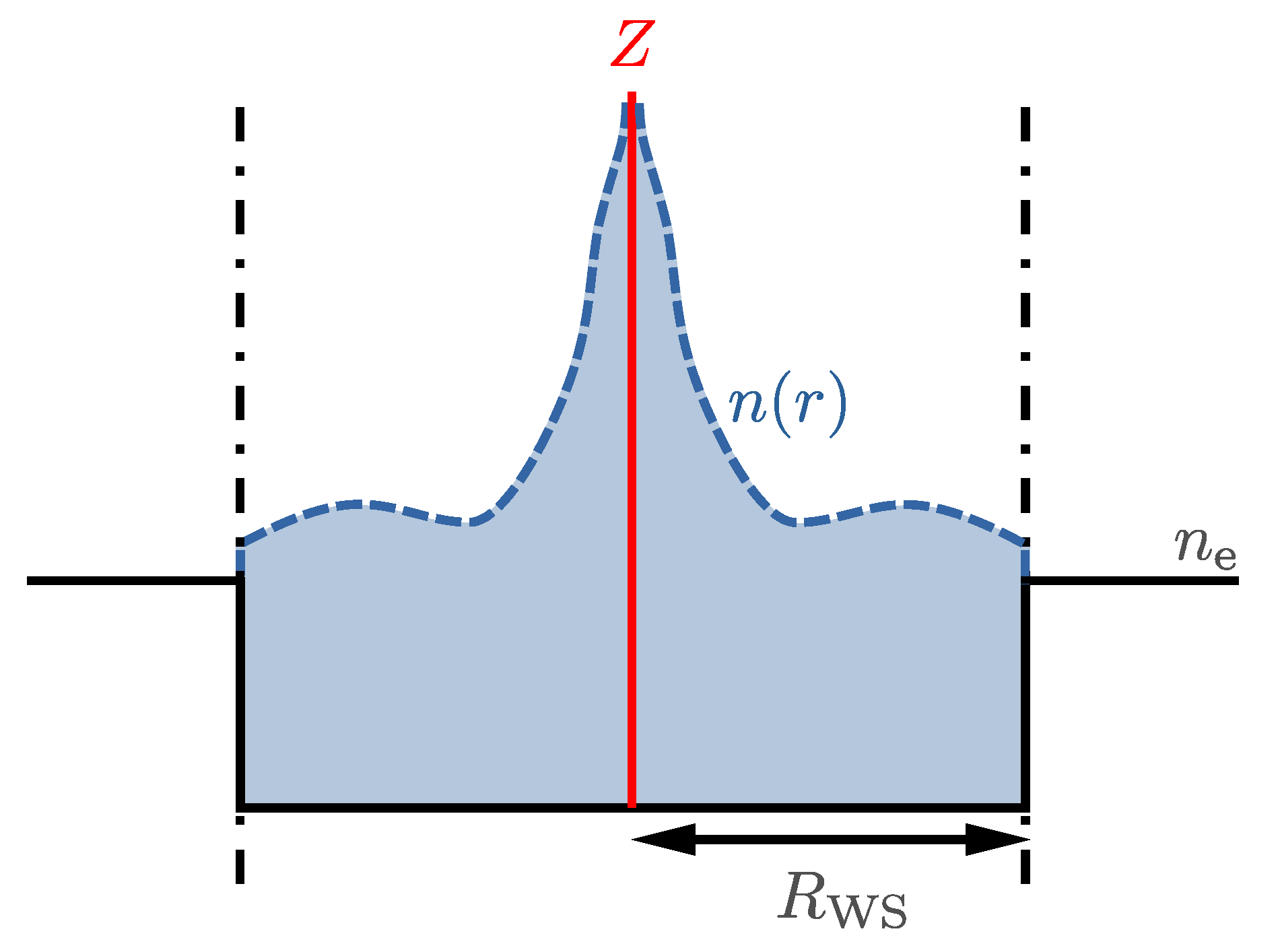
4.3. Ion-in-Jellium Models
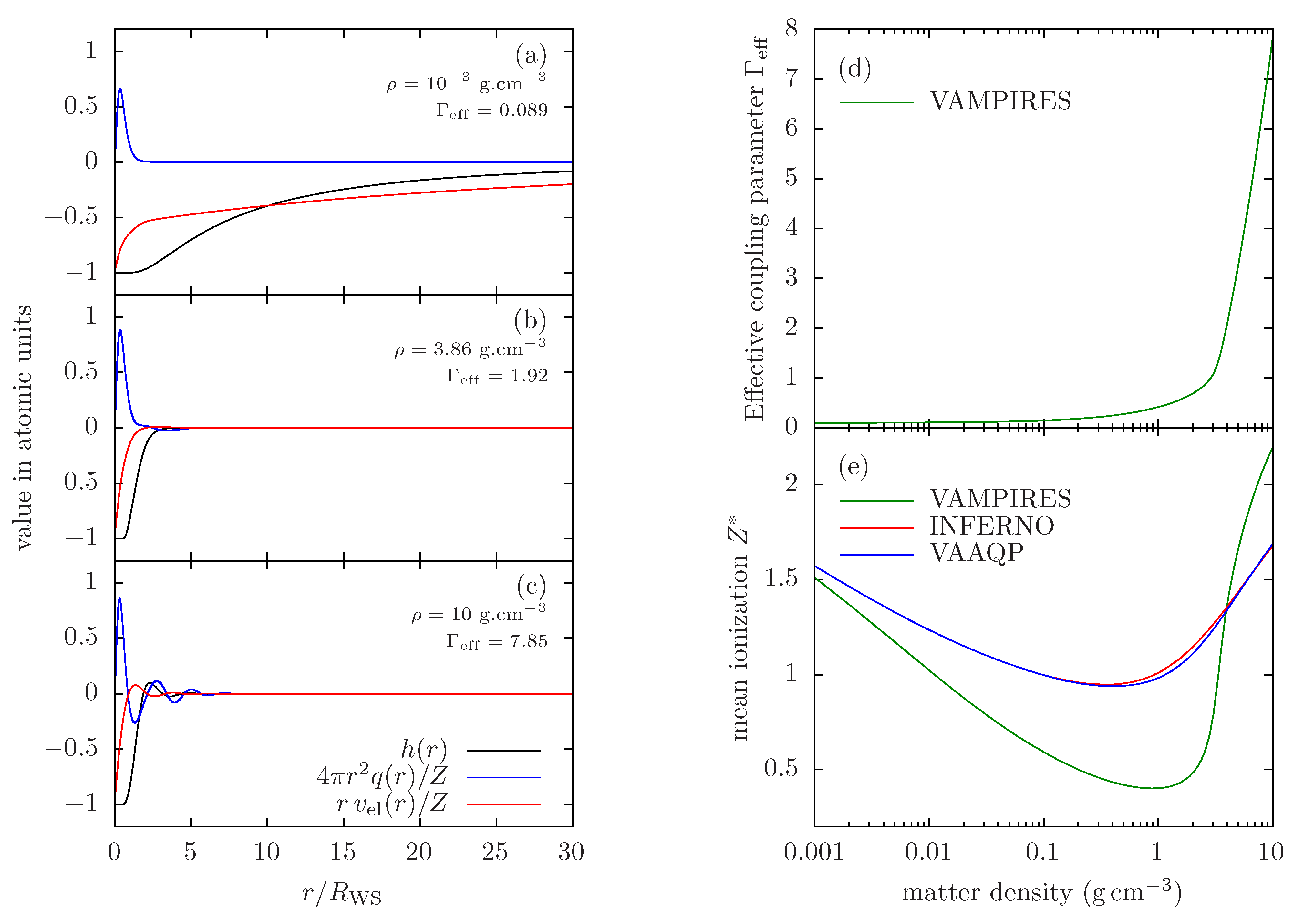
4.4. Going beyond the Cavity Hypothesis, the Difficulty of Dense-Plasma Atomic Modeling
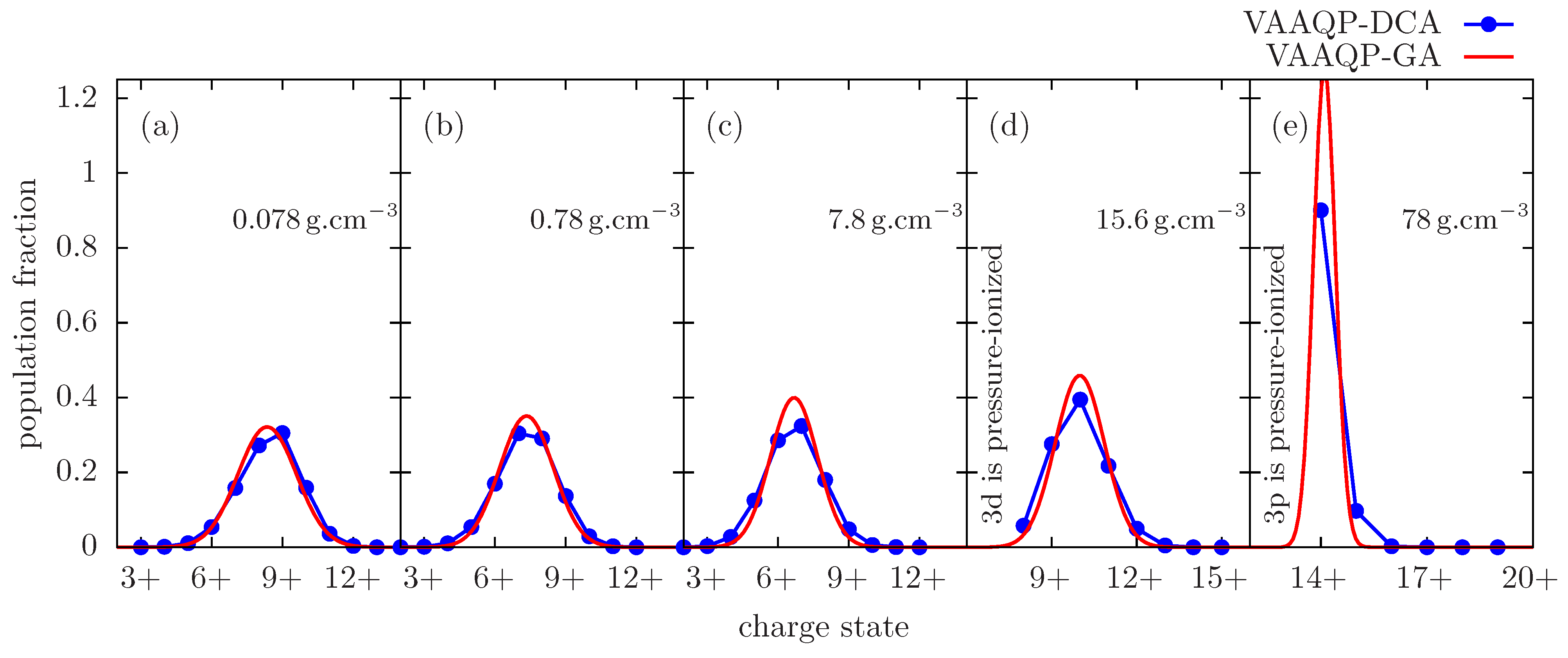
4.5. VAMPIRES Model
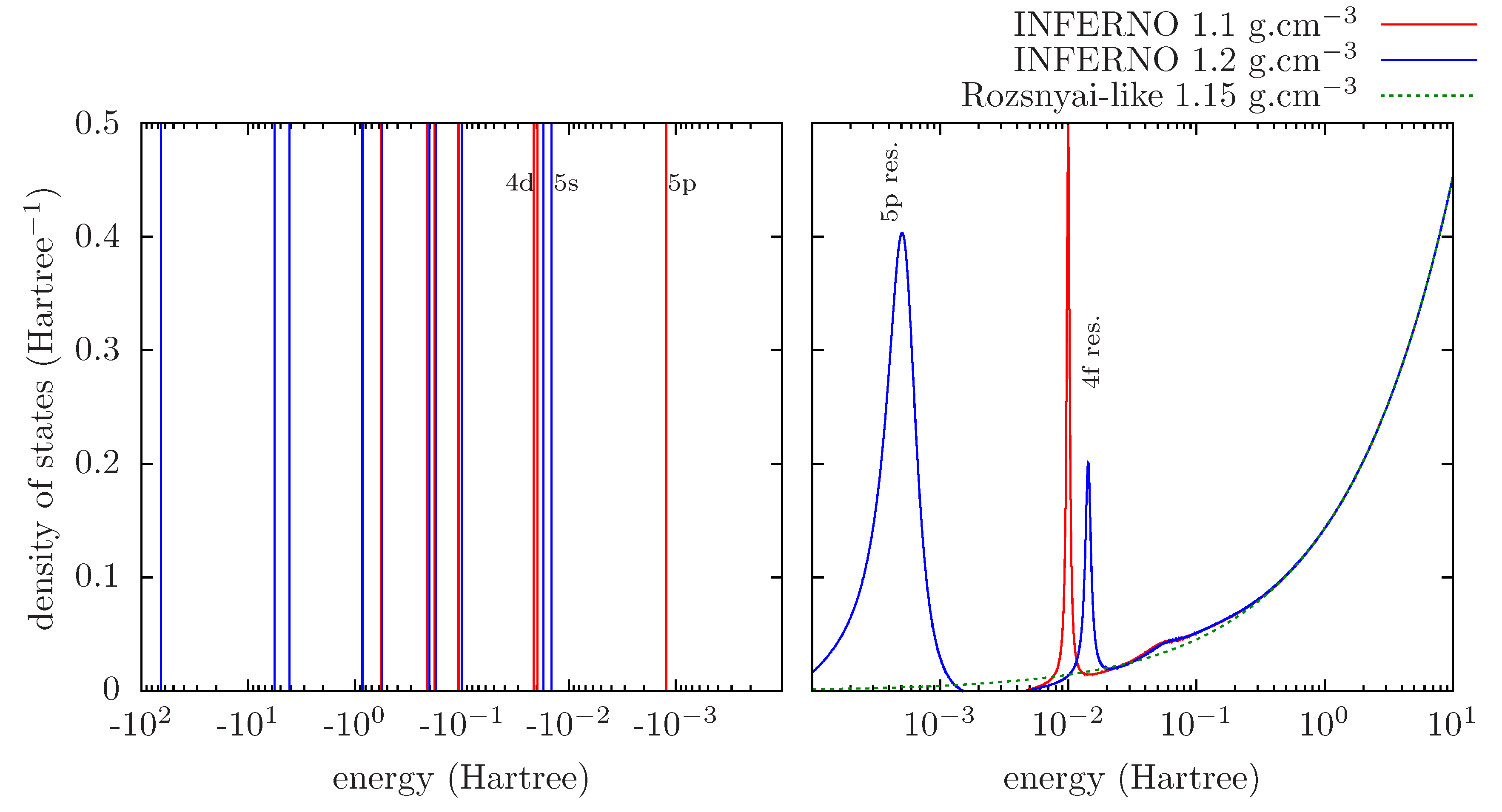
5. Radiative Processes and Photoabsorption in Dense Plasmas
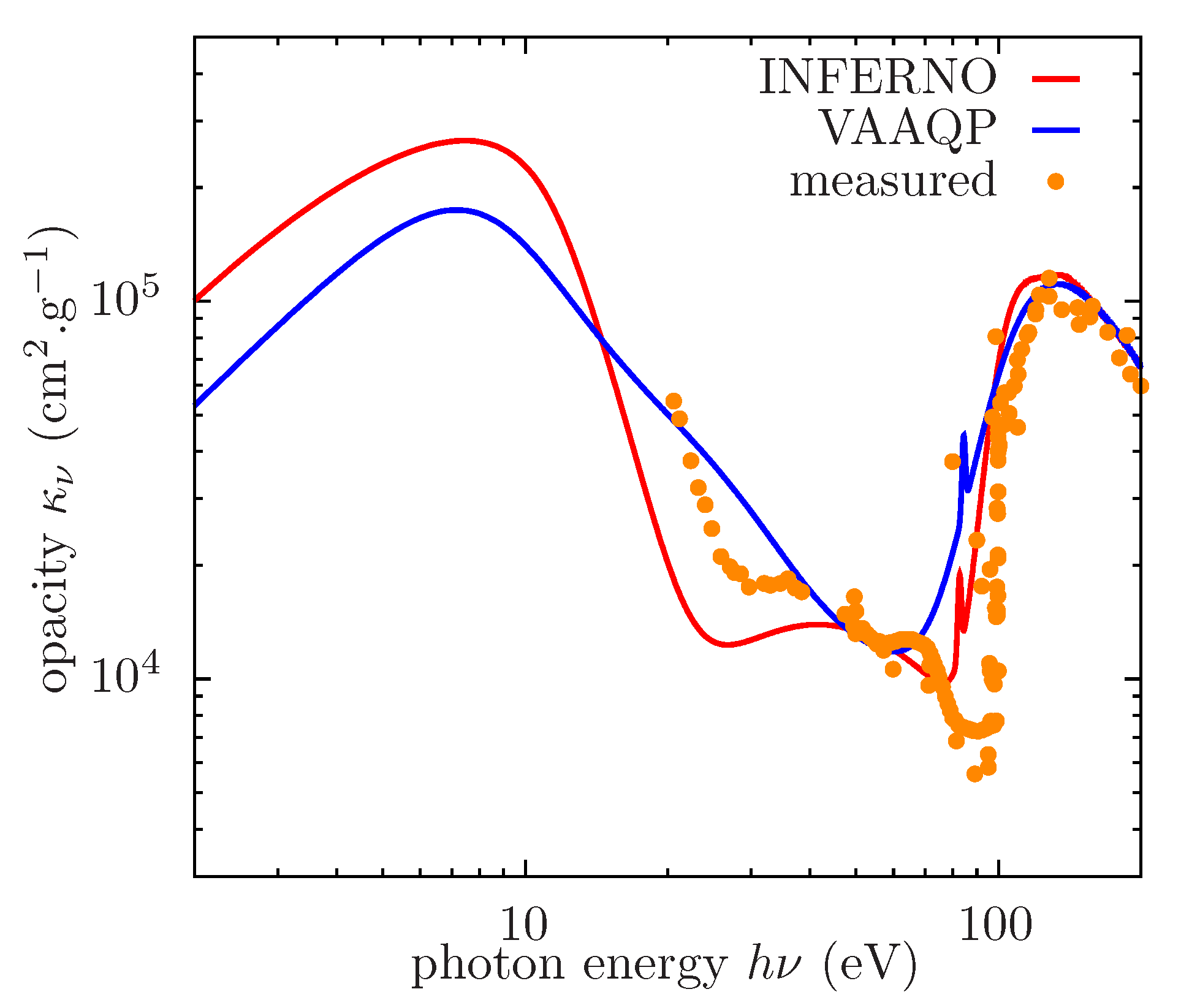
5.1. Independent Particle Approximation and the Effect of Screening
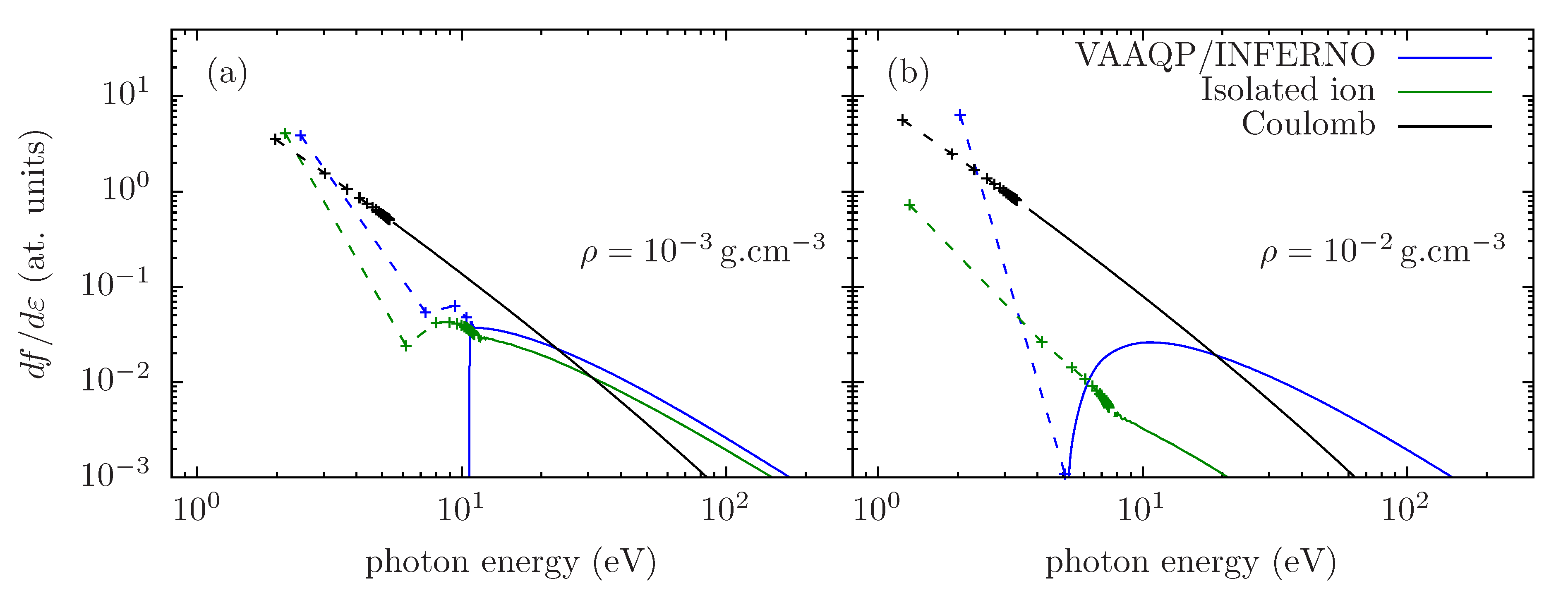
5.2. Fluctuations around the Average Atomic State and the Need for Detailed Modeling
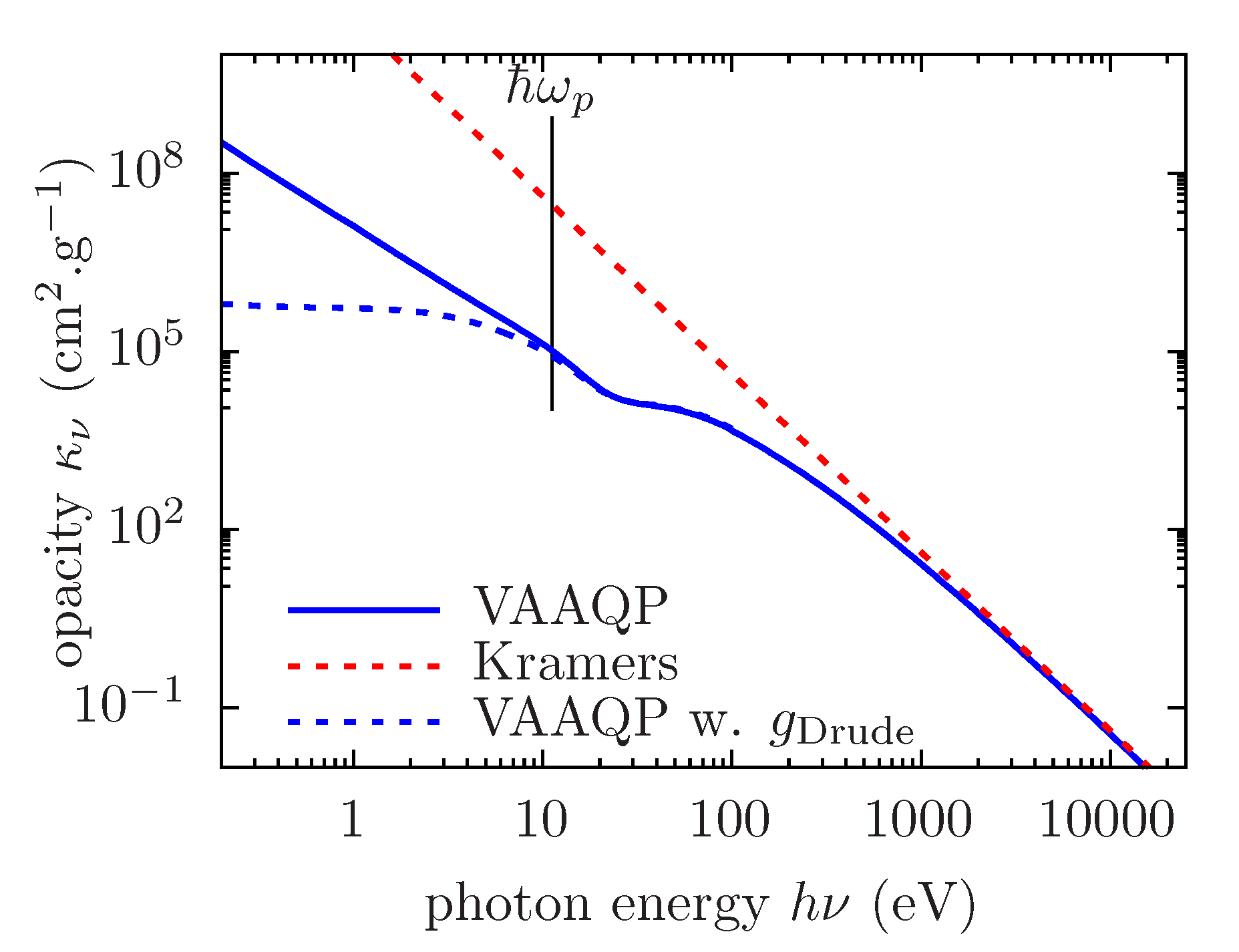
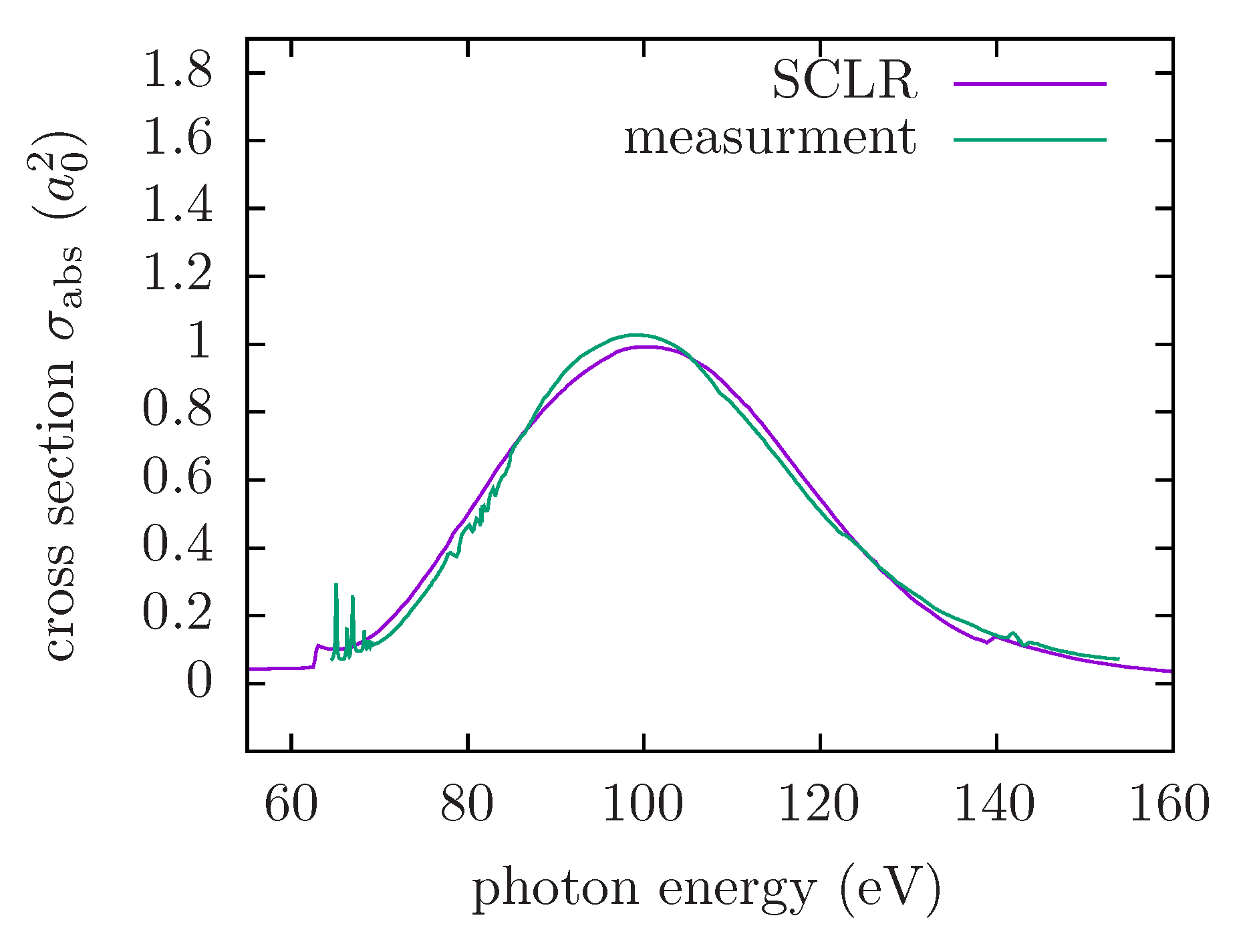
5.3. Collective Phenomena
5.4. Self-Consistent Linear Response
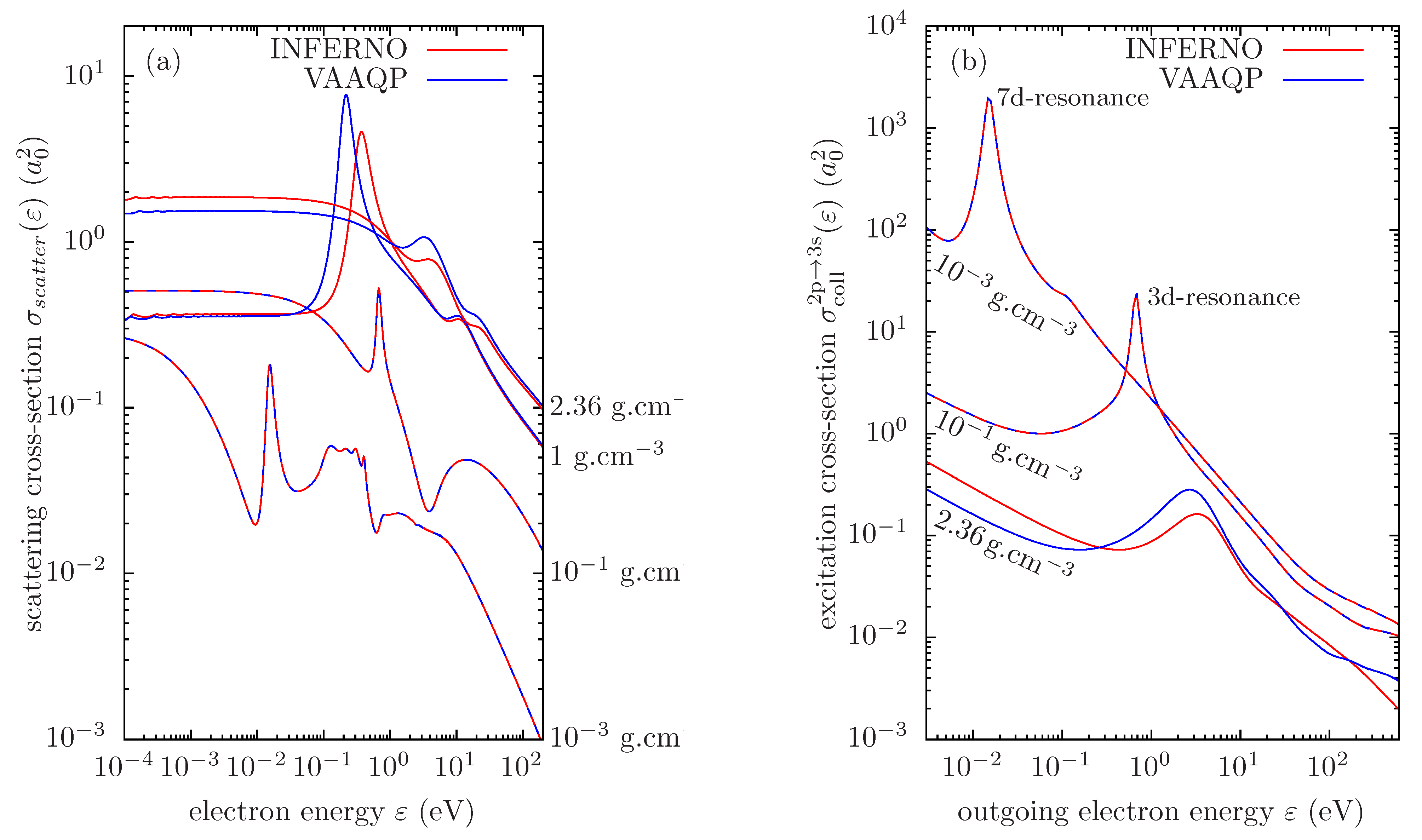
6. Some Words on Collisional Processes
7. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | In [94], this model is called “finite-temperature ion-sphere model”, whereas what we call in the present article “ion-sphere model” is called “uniform electron gas model”. |
References
- Dyson, F.J.; Lenard, A. Stability of Matter. I. J. Math. Phys. 1967, 8, 423–434. [Google Scholar] [CrossRef]
- Dyson, F.J.; Lenard, A. Stability of Matter. II. J. Math. Phys. 1968, 9, 698–711. [Google Scholar]
- Lebowitz, J.L.; Lieb, E.H. Existence of Thermodynamics for Real Matter with Coulomb Forces. Phys. Rev. Lett. 1969, 22, 631–634. [Google Scholar] [CrossRef]
- Lieb, E.H.; Lebowitz, J.L. The constitution of matter: Existence of thermodynamics for systems composed of electrons and nuclei. Adv. Math. 1972, 9, 316–398. [Google Scholar] [CrossRef]
- Lieb, E.H. The stability of matter. Rev. Mod. Phys. 1976, 48, 553–569. [Google Scholar] [CrossRef]
- Mihalas, D. Stellar Atmospheres; W H Freeman & Co.: New York, NY, USA, 1978. [Google Scholar]
- Ralchenko, Y. Modern Methods in Collisional-Radiative Modeling of Plasmas; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Baranger, M. Simplified Quantum-Mechanical Theory of Pressure Broadening. Phys. Rev. 1958, 111, 481–493. [Google Scholar] [CrossRef]
- Stambulchik, E.; Maron, Y. Stark effect of high-n hydrogen-like transitions: Quasi-contiguous approximation. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 095703. [Google Scholar] [CrossRef]
- Sobel’man, I.I.; Vainshtein, L.A.; Yukov, E.A. Excitation of Atoms and Broadening of Spectral Lines; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Boercker, D.B.; Iglesias, C.A.; Dufty, J.W. Radiative and transport properties of ions in strongly coupled plasmas. Phys. Rev. A 1987, 36, 2254–2264. [Google Scholar] [CrossRef] [PubMed]
- Talin, B.; Calisti, A.; Godbert, L.; Stamm, R.; Lee, R.W.; Klein, L. Frequency-fluctuation model for line-shape calculations in plasma spectroscopy. Phys. Rev. A 1995, 51, 1918–1928. [Google Scholar] [CrossRef] [PubMed]
- Gomez, T.A.; Nagayama, T.; Cho, P.B.; Kilcrease, D.P.; Fontes, C.J.; Zammit, M.C. Introduction to spectral line shape theory. J. Phys. B At. Mol. Opt. Phys. 2022, 55, 034002. [Google Scholar] [CrossRef]
- Racah, G. Theory of Complex Spectra. I. Phys. Rev. 1942, 61, 186–197. [Google Scholar] [CrossRef]
- Racah, G. Theory of Complex Spectra. II. Phys. Rev. 1942, 62, 438–462. [Google Scholar] [CrossRef]
- Racah, G. Theory of Complex Spectra. III. Phys. Rev. 1943, 63, 367–382. [Google Scholar] [CrossRef]
- Judd, B.R. Second Quantization and Atomic Spectroscopy; The Johns Hopkins University Press: Baltimore, MD, USA, 1967. [Google Scholar]
- Yutsis, A.P.; Levinson, I.B.; Vanagas, V.V. Mathematical Apparatus of the Theory of Angular Momentum; Israel Program for Scientific Translations Ltd.: Jerusalem, Israel, 1962. [Google Scholar]
- Bar-Shalom, A.; Klapisch, M. NJGRAF — An efficient program for calculation of general recoupling coefficients by graphical analysis, compatible with NJSYM. Comput. Phys. Commun. 1988, 50, 375–393. [Google Scholar] [CrossRef]
- Gaigalas, G.; Fritzsche, S.; Grant, I.P. Program to calculate pure angular momentum coefficients in jj-coupling. Comput. Phys. Commun. 2001, 139, 263–278. [Google Scholar] [CrossRef]
- Moszkowski, S.A. On the Energy Distribution of Terms and Line Arrays in Atomic Spectra. Prog. Theor. Phys. 1962, 28, 1–23. [Google Scholar] [CrossRef]
- Bauche-Arnoult, C.; Bauche, J.; Klapisch, M. Variance of the distributions of energy levels and of the transition arrays in atomic spectra. Phys. Rev. A 1979, 20, 2424–2439. [Google Scholar] [CrossRef]
- Bauche-Arnoult, C.; Bauche, J.; Klapisch, M. Variance of the distributions of energy levels and of the transition arrays in atomic spectra. II. Configurations with more than two open subshells. Phys. Rev. A 1982, 25, 2641–2646. [Google Scholar] [CrossRef]
- Bauche-Arnoult, C.; Bauche, J.; Klapisch, M. Variance of the distributions of energy levels and of the transition arrays in atomic spectra. III. Case of spin-orbit-split arrays. Phys. Rev. A 1985, 31, 2248–2259. [Google Scholar] [CrossRef] [PubMed]
- Perrot, F. Correlated fluctuations of electron populations in high temperature plasmas. Phys. A 1988, 150, 357–370. [Google Scholar] [CrossRef]
- Bar-Shalom, A.; Oreg, J.; Goldstein, W.H.; Shvarts, D.; Zigler, A. Super-transition-arrays: A model for the spectral analysis of hot, dense plasma. Phys. Rev. A 1989, 40, 3183–3193. [Google Scholar] [CrossRef] [PubMed]
- Blenski, T.; Grimaldi, A.; Perrot, F. A superconfiguration code based on the local density approximation. J. Quant. Spectrosc. Radiat. Transf. 2000, 65, 91–100. [Google Scholar] [CrossRef]
- Mazevet, S.; Abdallah, J. Mixed UTA and detailed line treatment for mid-Z opacity and spectral calculations. J. Phys. B At. Mol. Opt. Phys. 2006, 39, 3419. [Google Scholar] [CrossRef]
- Iglesias, C.A.; Sonnad, V. Partially resolved transition array model for atomic spectra. High Energy Density Phys. 2012, 8, 154–160. [Google Scholar] [CrossRef]
- Saha, M.N. Ionization in the solar chromosphere. Philos. Mag. 1920, 40, 472–488. [Google Scholar] [CrossRef]
- Saha, M.N. On a Physical Theory of Stellar Spectra. Proc. R. Soc. Lond. Ser. A 1921, 99, 135–153. [Google Scholar] [CrossRef]
- Slater, J.C. A Simplification of the Hartree–Fock Method. Phys. Rev. 1951, 81, 385–390. [Google Scholar] [CrossRef]
- Talman, J.D.; Shadwick, W.F. Optimized effective atomic central potential. Phys. Rev. A 1976, 14, 36–40. [Google Scholar] [CrossRef]
- Klapisch, M. A program for atomic wavefunction computations by the parametric potential method. Comput. Phys. Commun. 1971, 2, 239–260. [Google Scholar] [CrossRef]
- Slater, J.C. The Self Consistent Field and the Structure of Atoms. Phys. Rev. 1928, 32, 339–348. [Google Scholar] [CrossRef]
- Cowan, R.D. The Theory of Atomic Structure and Spectra; University of California Press: Berkeley, CA, USA, 1981. [Google Scholar]
- Froese-Fischer, C. The Hartree–Fock Method for Atoms: A Numerical Approach; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1977. [Google Scholar]
- Grant, I.P. Relativistic Quantum Theory of Atoms and Molecules: Theory and Computation; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Slater, J.C. The Theory of Complex Spectra. Phys. Rev. 1929, 34, 1293–1322. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Stochastic Problems in Physics and Astronomy. Rev. Mod. Phys. 1943, 15, 1–89. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Mermin, N.D. Thermal properties of the inhomogeneous electron gas. Phys. Rev. 1965, 137, A1441–A1443. [Google Scholar] [CrossRef]
- Slater, J.C. The virial and molecular structure. J. Chem. Phys. 1933, 1, 687. [Google Scholar] [CrossRef]
- Stewart, J.C.; Pyatt, K.D. Lowering of ionization potentials in plasmas. Astrophys. J. 1966, 144, 1203–1211. [Google Scholar] [CrossRef]
- Griem, H.R. High-Density Corrections in Plasma Spectroscopy. Phys. Rev. 1962, 128, 997–1003. [Google Scholar] [CrossRef]
- Percus, J.K. Chapter the pair distribution function in classical statistical mechanics. In The Equilibrium Theory of Classical Fluids; W. A. Benjamin, Inc.: New York, NY, USA, 1964; pp. II-33–II–170. [Google Scholar]
- Debye, P.; Hückel, E. Zur Theorie des Elektrolyte. I. Gefrierpunktserniedrigung und verwandte Erscheinungen. Phys. Z. 1923, 24, 185–206. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics; Pergamon Press: Oxford, UK, 1959. [Google Scholar]
- Kirkwood, J.G. Statistical Mechanics of Fluid Mixtures. J. Chem. Phys. 1935, 3, 300–313. [Google Scholar] [CrossRef]
- Piron, R.; Blenski, T. Simpler free-energy functional of the Debye–Hückel model of fluids and the non-uniqueness of free-energy functionals in the theory of fluids. Phys. Rev. E 2019, 99, 052134. [Google Scholar] [CrossRef] [PubMed]
- Brush, S.G.; Sahlin, H.L.; Teller, E. Monte Carlo Study of a One-Component Plasma. I. J. Chem. Phys. 1966, 45, 2102–2118. [Google Scholar] [CrossRef]
- Hansen, J. Statistical Mechanics of Dense Ionized Matter. I. Equilibrium Properties of the Classical One-Component Plasma. Phys. Rev. A 1973, 8, 3096–3109. [Google Scholar] [CrossRef]
- Springer, J.F.; Pokrant, M.A.; Stevens, F.A. Integral equation solutions for the classical electron gas. J. Chem. Phys. 1973, 58, 4863–4867. [Google Scholar] [CrossRef]
- Ng, K.C. Hypernetted chain solutions for the classical one-compoenent plasma up to Γ= 7000. J. Chem. Phys. 1974, 61, 2680–2689. [Google Scholar] [CrossRef]
- Carley, D.D. Computations of Radial Distribution Functions for a Classical Electron Gas. Phys. Rev. 1963, 131, 1406–1409. [Google Scholar] [CrossRef]
- Carley, D.D. Radial Distributions of Ions for a Primitive Model of an Electrolyte Solution. J. Chem. Phys. 1967, 46, 3783–3788. [Google Scholar] [CrossRef]
- Piron, R.; Blenski, T. Variational average-atom in quantum plasmas (VAAQP)—Application to radiative properties. High Energy Density Phys. 2013, 9, 702–713. [Google Scholar] [CrossRef]
- Morita, T. Theory of Classical Fluids: Hyper-Netted Chain Approximation, I. Prog. Theor. Phys. 1958, 20, 920–938. [Google Scholar] [CrossRef]
- Morita, T. Theory of Classical Fluids: Hyper-Netted Chain Approximation, II. Prog. Theor. Phys. 1959, 21, 361–382. [Google Scholar] [CrossRef][Green Version]
- Van Horn, H. Crystallization of a classical, one-component Coulomb plasma. Phys. Lett. A 1969, 28, 706–707. [Google Scholar] [CrossRef]
- Hansen, J. Crystallization of the classical one-component plasma. Phys. Lett. A 1972, 41, 213–214. [Google Scholar] [CrossRef]
- Slattery, W.L.; Doolen, G.D.; DeWitt, H.E. N dependence in the classical one-component plasma Monte Carlo calculations. Phys. Rev. A 1982, 26, 2255–2258. [Google Scholar] [CrossRef]
- Levinson, N. On the Uniqueness of the Potential in a Schrödinger Equation for a Given Asymptotic Phase. Danske Vidensk. Selsk. K. Mat.-Fys. Medd. 1949, 25, 9. [Google Scholar]
- Jauch, J.M. On the Relation Between Scatteriing Phase and Bound States. Helv. Phys. Acta 1957, 30, 143–156. [Google Scholar]
- Ma, Z.Q. The Levinson theorem. J. Phys. A Math. Gen. 2006, 39, R625–R659. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables.djvu; Dover Publication, Inc.: New York, NY, USA, 1965. [Google Scholar]
- Kittel, C. Quantum Theory of Solids; Wiley: Hoboken, NJ, USA, 1991. [Google Scholar]
- Bargmann, V. On the number of bound states in a central field of force. Proc. Nat. Acad. Sci. USA 1952, 38, 961–966. [Google Scholar] [CrossRef]
- Beth, E.; Uhlenbeck, G.E. The quantum theory of the non-ideal gas. II. Behaviour at low temperatures. Physica 1937, 4, 915–924. [Google Scholar] [CrossRef]
- Larkin, A.I. Thermodynamic functions of a low-temperature plasma. JETP 1960, 38, 1896–1898. [Google Scholar]
- Ebeling, W. Equation of State and Saha Equation of Partially Ionized Plasmas. Physica 1968, 38, 378–388. [Google Scholar] [CrossRef]
- Ebeling, W. Statistical Derivation of the Mass-Action Law for Interacting Gases ans Plasmas. Physica 1974, 73, 573–584. [Google Scholar] [CrossRef]
- Ebeling, W.; Kraeft, W.D.; Kremp, D.; Röpke, G. Energy Levels in Hydrogen Plasmas and the Planck–Larkin Partition Function—A Comment. Astrophys. J. 1985, 290, 24–27. [Google Scholar] [CrossRef]
- Rogers, F.J. On the Compensation of Bound and Scattering State Contributions to the Partition Functlon. Phys. Lett. 1977, 61A, 358–360. [Google Scholar] [CrossRef]
- Rogers, F.J. Occupation Numbers for Reacting Plasmas: The Role of the Planck–Larkin Partition Function. Astrophys. J. 1986, 310, 723. [Google Scholar] [CrossRef]
- Herzfeld, K.F. Über die Wahrscheinlichkeit der Quantenzustände. Ann. der Phys. 1916, 51, 261. [Google Scholar] [CrossRef]
- Urey, H.C. The Distribution of Electrons in the Various Orbits of the Hydrogen Atom. Astrophys. J. 1924, 59, 1. [Google Scholar] [CrossRef]
- Fermi, E. Über die Wahrscheinlichkeit der Quantenzustände. Z. Phys. 1924, 26, 54–56. [Google Scholar] [CrossRef]
- Feynman, R.P.; Metropolis, N.; Teller, E. Equation of State of Elements Based on the Generalized Fermi-Thomas Theory. Phys. Rev. 1949, 75, 1561–1573. [Google Scholar] [CrossRef]
- Latter, R. Temperature Behavior of the Thomas-Fermi Statistical Model for Atoms. Phys. Rev. 1955, 99, 1854–1870. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Note on exchange phenomena in the Thomas atom. Proc. Camb. Phil. Soc. 1930, 26, 376–385. [Google Scholar] [CrossRef]
- Kirzhnits, D.A. Quantum corrections to the Thomas–Fermi equation. JETP 1957, 5, 64. [Google Scholar]
- Latter, R. Atomic Energy Levels for the Thomas–Fermi and Thomas–Fermi–Dirac Potential. Phys. Rev. 1955, 99, 510–519. [Google Scholar] [CrossRef]
- Ball, J.A.; Wheeler, J.A.; Firemen, E.L. Photoabsorption and Charge Oscillation of the Thomas–Fermi Atom. Rev. Mod. Phys. 1973, 45, 333. [Google Scholar] [CrossRef]
- Ishikawa, K.; Felderhof, B.U. High-frequency photoabsorption by an ion immersed in a plasma as calculated from Bloch’s hydrodynamic model. Phys. A 1998, 253, 541–554. [Google Scholar] [CrossRef]
- Caizergues, C.; Blenski, T.; Piron, R. Linear response of a variational average atom in plasma: Semi-classical model. High Energy Density Phys. 2014, 12, 12–20. [Google Scholar] [CrossRef]
- Slater, J.C.; Krutter, H.M. The Thomas-Fermi Method for Metals. Phys. Rev. 1935, 47, 559–568. [Google Scholar] [CrossRef]
- Liberman, D.A. Self-consistent field model for condensed matter. Phys. Rev. B 1979, 20, 4981–4989. [Google Scholar] [CrossRef]
- Rozsnyai, B.F. Relativistic Hartree–Fock-Slater Calculations for Arbitrary Temperature and Matter Density. Phys. Rev. A 1972, 5, 1137–1149. [Google Scholar] [CrossRef]
- Wigner, E.; Seitz, F. On the Constitution of Metallic Sodium. Phys. Rev. 1933, 43, 804–810. [Google Scholar] [CrossRef]
- Wigner, E.; Seitz, F. On the Constitution of Metallic Sodium. II. Phys. Rev. 1934, 46, 509–524. [Google Scholar] [CrossRef]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; Harcourt College Publishers: San Diego, CA, USA, 1976. [Google Scholar]
- Rosmej, F.; Bennadji, K.; Lisitsa, V.S. Effect of dense plasmas on exchange-energy shifts in highly charged ions: An alternative approach for arbitrary pertubation potentials. Phys. Rev. A 2011, 84, 032512. [Google Scholar] [CrossRef]
- Massacrier, G.; Böhme, M.; Vorberger, J.; Soubiran, F.; Militzer, B. Reconciling ionization energies and band gaps of warm dense matter derived with ab initio simulations and average atom models. Phys. Rev. Res. 2021, 3, 023026. [Google Scholar] [CrossRef]
- Liberman, D.A. Inferno: A better model of atoms in dense plasmas. J. Quant. Spectrosc. Radiat. Transf. 1982, 27, 335. [Google Scholar] [CrossRef]
- Bennett, B.I.; Liberman, D.A. Inferno; Technical Report LA-10309-M; Los Alamos National Laboratory: Santa Fe, NM, USA, 1985.
- Piron, R. Variational Average-Atom in Quantum Plasmas (VAAQP). Ph.D. Thesis, École Polytechnique, Palaiseau, France, 2009. Available online: https://theses.hal.science/tel-00446558/ (accessed on 4 April 2024). (In French).
- Wilson, B.; Sonnad, V.; Sterne, P.; Isaacs, W. Purgatorio—A new implementation of the Inferno algorithm. J. Quant. Spectrosc. Radiat. Transf. 2006, 99, 658–679. [Google Scholar] [CrossRef]
- Pénicaud, M. An average atom code for warm matter: Application to aluminum and uranium. J. Phys. Condens. Matter 2009, 21, 095409. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Rosmej, F. Quantum-number-dependent energy level shifts of ionsin dense plasmas: A generalized analytical approach. Eur. Phys. Lett. 2012, 99, 33001. [Google Scholar] [CrossRef]
- Iglesias, C. On spectral line shifts from analytic fits to the ion-sphere model potential. High Energy Density Phys. 2019, 30, 41–44. [Google Scholar] [CrossRef]
- Beiersdorfer, P.; Brown, G.; McKelvey, A.; Shepherd, R.; Hoarty, D.J.; Brown, C.R.D.; Hill, M.P.; Hobbs, L.M.R.; James, S.F.; Morton, J.; et al. High-resolution measurments of Cl15+ line shifts in hot, solid-density plasmas. Phys. Rev. A 2019, 100, 012511. [Google Scholar] [CrossRef]
- Li, X.; Rosmej, F. Analytical approach to level delocalization and line shifts in finite temperature dense plasmas. Phys. Lett. A 2020, 384, 126478. [Google Scholar] [CrossRef]
- Zeng, J.; Ye, C.; Li, Y.; Yuan, J. Ionization potential depression in dense iron plasmas near solid density. Results Phys. 2022, 40, 105836. [Google Scholar] [CrossRef]
- Massacrier, G.; Dubau, J. A theoretical approach to N-electron ionic structure under dense plasma conditions: I. Blue and red shift. J. Phys. B At. Mol. Opt. Phys. 1990, 23, 2459S–2469S. [Google Scholar] [CrossRef]
- Arponen, J.; Hautojärvi, P.; Nieminen, R.; Pajanne, E. Charge density and positron annihilation at lattice defects in aluminium. J. Phys. F Met. Phys. 1973, 3, 2092–2108. [Google Scholar] [CrossRef]
- Manninen, M.; Nieminen, R.; Hautojärvi, P.; Arponen, J. Electrons and positrons in metal vacancies. Phys. Rev. B 1975, 12, 4012–4022. [Google Scholar] [CrossRef]
- Jena, P.; Singwi, K.S. Electronic structure of hydrogen in simple metals. Phys. Rev. B 1978, 17, 3518–3524. [Google Scholar] [CrossRef]
- Perrot, F. (CEA, DAM, DIF, F-91297 Arpajon, France) Private Communication. 1998. [Google Scholar]
- Blenski, T.; Cichocki, B. Variational approach to the average-atom-in-jellium and superconfigurations-in-jellium models with all electrons treated quantum-mechanically. High Energy Density Phys. 2007, 3, 34–47. [Google Scholar] [CrossRef]
- Blenski, T.; Cichocki, B. Variational theory of average-atom and superconfigurations in quantum plasmas. Phys. Rev. E 2007, 75, 056402. [Google Scholar] [CrossRef] [PubMed]
- Piron, R.; Blenski, T. Variational-average-atom-in-quantum-plasmas (VAAQP) code and virial theorem: Equation-of-state and shock-Hugoniot calculations for warm dense Al, Fe, Cu, and Pb. Phys. Rev. E 2011, 83, 026403. [Google Scholar] [CrossRef]
- Piron, R.; Blenski, T. Variational average-atom in quantum plasmas (VAAQP)—Recent progress, virial theorem and applications to the equation-of-state of warm dense Be. High Energy Density Phys. 2011, 7, 346–352. [Google Scholar] [CrossRef]
- Felderhof, B.U.; Ford, G.W.; Cohen, E.G.D. Cluster Expansion for the Dielectric Constant of a Polarizable Suspension. J. Stat. Phys. 1982, 28, 135–164. [Google Scholar] [CrossRef]
- Piron, R.; Blenski, T.; Cichocki, B. Variational Average-Atom in Quantum Plasmas (VAAQP)—A check of thermodynamic consistency. High Energy Density Phys. 2009, 5, 258–262. [Google Scholar] [CrossRef]
- Piron, R.; Blenski, T. Average-atom model calculations of dense-plasma opacities: Review and potential applications to white-dwarf stars. Contrib. Plasma Phys. 2018, 58, 30–41. [Google Scholar] [CrossRef]
- Percus, J.K. At the boundary between reduced density-matrix and density-functional theories. J. Chem. Phys. 2005, 122, 234103. [Google Scholar] [CrossRef]
- Lado, F. Effective Potential Description of the Quantum Ideal Gases. J. Chem. Phys. 1967, 47, 5369–5375. [Google Scholar] [CrossRef]
- Dharma-wardana, M.W.C.; Perrot, F. Simple Classical Mapping of the Spin-Polarized Quantum Electron Gas: Distribution Functions and Local-Field Corrections. Phys. Rev. Lett. 2000, 84, 959–962. [Google Scholar] [CrossRef] [PubMed]
- Perrot, F.; Blenski, T. Electronic structure and statistical mechanics of ionic configurations in hot plasmas. J. Phys. IV Fr. 2000, 10, Pr5-473–Pr5-479. [Google Scholar] [CrossRef]
- Dufty, J.; Dutta, S. Classical representation of a quantum system at equilibrium: Theory. Phys. Rev. E 2013, 87, 032101. [Google Scholar] [CrossRef]
- Dutta, S.; Dufty, J. Classical representation of a quantum system at equilibrium: Applications. Phys. Rev. E 2013, 87, 032102. [Google Scholar] [CrossRef]
- Chihara, J. Derivation of Quantal Hyper-Netted Chain Equation from the Kohn–Sham Theory. Prog. Theor. Phys. 1978, 59, 76–86. [Google Scholar] [CrossRef][Green Version]
- Hansen, J.P.; MacDonald, I.R. Theory of Simple Liquids; Academic Press: Cambridge, MA, USA, 1976. [Google Scholar]
- Chihara, J. Unified description of metallic and neutral liquids and plasmas. J. Phys. Condens. Matter 1991, 3, 8715. [Google Scholar] [CrossRef]
- Dewitt, H.E.; Rogers, F.J. Helmholtz free energy of electron screened plasmas in the hypernetted-chain (HNC) approximation. Phys. Lett. A 1988, 132, 273–275. [Google Scholar] [CrossRef]
- Anta, J.A.; Louis, A.A. Probing ion–ion and electron–ion correlations in liquid metals within the quantum hypernetted chain approximation. Phys. Rev. B 2000, 61, 11400–11410. [Google Scholar] [CrossRef]
- Starrett, C.E.; Saumon, D. Fully variational average atom model with ion–ion correlations. Phys. Rev. E 2012, 85, 026403. [Google Scholar] [CrossRef]
- Starrett, C.E.; Saumon, D. Electronic and ionic structures of warm and hot dense matter. Phys. Rev. E 2013, 87, 013104. [Google Scholar] [CrossRef]
- Starrett, C.; Saumon, D. A simple method for determining the ionic structure of warm dense matter. High Energy Density Phys. 2014, 10, 35–42. [Google Scholar] [CrossRef]
- Chihara, J. Average Atom Model based on Quantum Hyper-Netted Chain Method. High Energy Density Phys. 2016, 19, 38–47. [Google Scholar] [CrossRef]
- Morita, T.; Hiroike, K. A New Approach to the Theory of Classical Fluids. I. Prog. Theor. Phys. 1960, 23, 1003–1027. [Google Scholar] [CrossRef]
- Lado, F. Perturbation Correction for the Free Energy and Structure of Simple Fluids. Phys. Rev. A 1973, 8, 2548–2552. [Google Scholar] [CrossRef]
- Piron, R.; Blenski, T. Free-energy functional of the Debye–Hückel model of simple fluids. Phys. Rev. E 2016, 94, 062128. [Google Scholar] [CrossRef] [PubMed]
- Blenski, T.; Piron, R. Free-energy functional of the Debye–Hückel model of two-component plasmas. High Energy Density Phys. 2017, 24, 28–32. [Google Scholar] [CrossRef]
- Piron, R.; Blenski, T. Variational average-atom model of electron–ion plasma with correlations and quantum bound electrons. arXiv 2019, arXiv:1904.13289. [Google Scholar]
- Blenski, T.; Piron, R. Variational atomic model of plasma accounting for ion radial correlations and electronic structure of ions. Phys. Rev. E 2023, 107, 035209. [Google Scholar] [CrossRef] [PubMed]
- Kirkwood, J.G. Quantum Statistics of Almost Classical Assemblies. Phys. Rev. 1933, 44, 31–37. [Google Scholar] [CrossRef]
- Zwanzig, R.W. Transition from Quantum to “Classical” Partition Function. Phys. Rev. 1957, 106, 13–15. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Electrodynamics of Continuous Media; Pergamon Press: Oxford, UK, 1960. [Google Scholar]
- Błeński, T.; Cichocki, B. Linear response of partially ionized, dense plasmas. Laser Part. Beams 1992, 10, 299–309. [Google Scholar] [CrossRef][Green Version]
- Blenski, T.; Cichocki, B. Polarizability of partially ionized, dense plasmas (application to photo-absorption calculations). J. Quant. Spectrosc. Radiat. Transf. 1994, 51, 49–58. [Google Scholar] [CrossRef]
- Felderhof, B.U.; Blenski, T.; Cichocki, B. Dielectric function of an electron–ion plasma in the optical and X-ray regime. Phys. A 1995, 217, 161–174. [Google Scholar] [CrossRef]
- Fetter, A.L.; Walecka, J.D. Quantum Theory of Many-Particle Systems; Dover Publication, Inc.: Mineola, NY, USA, 2003. [Google Scholar]
- Stott, M.J.; Zaremba, E. Linear-response theory within the density-functional formalism: Application to atomic polarizabilities. Phys. Rev. A 1980, 21, 12–23. [Google Scholar] [CrossRef]
- Zangwill, A.; Soven, P. Density-functional approach to local-field effects in finite systems: Photoabsorption in the rare gases. Phys. Rev. A 1980, 21, 1561–1572. [Google Scholar] [CrossRef]
- Runge, E.; Gross, E.K.U. Density-Functional Theory for Time-Dependent Systems. Phys. Rev. Lett. 1984, 52, 997–1000. [Google Scholar] [CrossRef]
- Dhara, A.K.; Ghosh, S.K. Density-functional theory for time-dependent systems. Phys. Rev. A 1987, 35, 442–444. [Google Scholar] [CrossRef]
- Ghosh, S.K.; Dhara, A.K. Density-functional theory of many-electron systems subjected to time-dependent electric and magnetic fields. Phys. Rev. A 1988, 38, 1149–1158. [Google Scholar] [CrossRef] [PubMed]
- Bethe, H.A.; Salpeter, E.E. Quantum Mechanics of One- and Two-Electron Atoms; Springer: Berlin/Heidelberg, Germany, 1957. [Google Scholar]
- Perrot, F. A new approximation for calculating free-free absorption in hot dense plasmas. Laser Part. Beams 1996, 14, 731–748. [Google Scholar] [CrossRef]
- Kramers, H.A. On the theory of X-ray absorption and of the continuous X-ray spectrum. Philos. Mag. Ser. 6 1923, 46, 836–871. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B.; Raizer, Y.P. Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena; Academic Press: Cambridge, MA, USA, 1968. [Google Scholar]
- Shore, B.W. On the threshold behaviour of bound–bound and bound-free photoabsorption for the screened Coulomb potentials. J. Phys. B 2019, 8, 2023–2040. [Google Scholar] [CrossRef]
- Perrot, F. Model for atomic species in a dense plasma: Description and applications. Phys. Rev. A 1987, 35, 1235–1244. [Google Scholar] [CrossRef] [PubMed]
- Green, J.M. The statistical mechanics of the interdependent electrons in the screening constant model of the many-electron-atom. J. Quant. Spectrosc. Radiat. Transf. 1964, 4, 639–662. [Google Scholar] [CrossRef]
- Shalitin, D.; Stein, J.; Ron, A. Level and line broadening for Thomas–Fermi atoms at finite temperature. Phys. Rev. A 1984, 29, 2789–2795. [Google Scholar] [CrossRef]
- Stein, J.; Shalitin, D.; Ron, A. Average-atom models of line broadening in hot dense plasmas. Phys. Rev. A 1985, 31, 446–450. [Google Scholar] [CrossRef] [PubMed]
- Blenski, T.; Cichocki, B. Density-functional approach to the absorption bands in a dense, partially ionized plasma. Phys. Rev. A 1990, 41, 6973–6981. [Google Scholar] [CrossRef] [PubMed]
- Wei, H.G.; Shi, J.R.; Zhao, G.; Zhang, Y.; Dong, Q.L.; Li, Y.T.; Wang, S.J.; Zhang, J.; Liang, Z.; Zhang, J.Y.; et al. Opacity Studies of Silicon in Radiatively Heated Plasma. Astrophys. J. 2008, 683, 577–583. [Google Scholar] [CrossRef]
- Li, Y.; Gao, C.; Tian, Q.; Zeng, J.; Yuan, J. Ionization competition effects on population distribution and radiative opacity of mixture plasmas. Phys. Plasmas 2015, 22, 113302. [Google Scholar] [CrossRef]
- Liberman, D.A.; Albritton, J.R.; Wilson, B.G.; Alley, W.E. Self-consistent-field calculations of atoms and ions using a modified local-density approximation. Phys. Rev. A 1994, 50, 171–176. [Google Scholar] [CrossRef] [PubMed]
- Hansen, S.B. Self-consistent and detailed opacities from a non-equilibrium average-atom model. Phil. Trans. R. Soc. A 2023, 381, 20220212. [Google Scholar] [CrossRef]
- Johnson, W.R.; Guet, C.; Bertsch, G.F. Optical properties of plasmas based on an average-atom model. J. Quant. Spectrosc. Radiat. Transf. 2006, 99, 327–340. [Google Scholar] [CrossRef]
- Kuchiev, M.Y.; Johnson, W.R. Low-frequency plasma conductivity in the average-atom approximation. Phys. Rev. E 2008, 78, 026401. [Google Scholar] [CrossRef] [PubMed]
- Johnson, W. Low-frequency conductivity in the average-atom approximation. High Energy Density Phys. 2009, 5, 61–67. [Google Scholar] [CrossRef]
- Ziman, J.M. A theory of the electrical properties of liquid metals. I: The monovalent metals. Philos. Mag. J. Theor. Exp. Appl. Phys. 1961, 6, 1013–1034. [Google Scholar] [CrossRef]
- Somerville, W.B. The continuous absorption coefficient of the negative hydrogen molecular ion. Astrophys. J. 1964, 139, 192–197. [Google Scholar] [CrossRef]
- Ashkin, M. Radiative Absorption Cross Section of an Electron in the Field of an Argon Atom. Phys. Rev. 1966, 141, 41–44. [Google Scholar] [CrossRef]
- Henke, B.L.; Davis, J.C.; Gullikson, E.M.; Perera, R.C.C. A Preliminary Report on X-ray Photoabsorption Coefficients and Atomic Scattering Factors for 92 Elements in the 10–10,000 eV Region; Technical Report LBL–26259 UC–411; Lawrence Berkeley Laboratory: Berkeley, CA, USA, 1988.
- Haensel, R.; Keitel, G.; Schreiber, P.; Kunz, C. Optical Absorption of Solid Krypton and Xenon in the Far Ultraviolet. Phys. Rev. 1969, 188, 1375–1380. [Google Scholar] [CrossRef]
- Blenski, T. On the linear dynamic response of average atom in plasma. J. Quant. Spectrosc. Radiat. Transf. 2006, 99, 84–101. [Google Scholar] [CrossRef]
- Blenski, T.; Piron, R.; Caizergues, C.; Cichocki, B. Models of atoms in plasmas based on common formalism for bound and free electrons. High Energy Density Phys. 2013, 9, 687–695. [Google Scholar] [CrossRef]
- Caizergues, C.; Blenski, T.; Piron, R. Dynamic linear response of atoms in plasmas and photo-absorption cross-section in the dipole approximation. High Energy Density Phys. 2016, 18, 7–13. [Google Scholar] [CrossRef]
- Mahan, G.D.; Subbaswamy, K.R. Local Density Theory of Polarizability; Springer: New York, NY, USA, 1990. [Google Scholar]
- Sampson, D.H.; Zhang, H.L.; Fontes, C.J. A fully relativistic approach for calculating atomic data for highly charged ions. Phys. Rep. 2009, 477, 111–214. [Google Scholar] [CrossRef]
- Peyrusse, O. Atomic configuration averages and non-local thermodynamical equilibrium plasma spectroscopy calculations. J. Phys. B At. Mol. Opt. Phys. 1999, 32, 683–700. [Google Scholar] [CrossRef]
- Zeng, J.; Ye, C.; Liu, P.; Gao, C.; Li, Y.; Yuan, J. The Strong Enhancement of Electron-Impact Ionization Processes in Dense Plasma by Transient Spatial Localization. Int. J. Mol. Sci. 2022, 23, 6033. [Google Scholar] [CrossRef] [PubMed]
- van den Berg, Q.Y.; Fernandez-Tello, E.V.; Burian, T.; Chalupský, J.; Chung, H.K.; Ciricosta, O.; Dakovski, G.L.; Hájková, V.; Hollebon, P.; Juha, L.; et al. Clocking Femtosecond Collisional Dynamics via Resonant X-ray Spectroscopy. Phys. Rev. Lett. 2018, 120, 055002. [Google Scholar] [CrossRef] [PubMed]
- Zangwill, A.; Liberman, D. A nonrelativistic program for optical response in atoms using a time-dependent local density approximation. Comput. Phys. Commun. 1984, 32, 63–73. [Google Scholar] [CrossRef]
- Doolen, G.; Liberman, D.A. Calculations of photoabsorption by atoms using a linear response method. Phys. Scr. 1987, 36, 77. [Google Scholar] [CrossRef][Green Version]
- Davidson, S.J.; Foster, J.M.; Smith, C.C.; Warburton, K.A.; Rose, S.J. Investigation of the opacity of hot, dense aluminum in the region of its K edge. Appl. Phys. Lett. 1988, 52, 847–849. [Google Scholar] [CrossRef]
- Bruneau, J.; Chenais-Popovics, C.; Desenne, D.; Gauthier, J.C.; Geindre, J.P.; Klapisch, M.; Le Breton, J.P.; Louis-Jacquet, M.; Naccache, D.; Perrine, J.P. Time-resolved L-shell absorption spectroscopy: A direct measurement of density and temperature in a germanium laser-produced plasma. Phys. Rev. Lett. 1990, 65, 1435–1438. [Google Scholar] [CrossRef] [PubMed]
- Da Silva, L.B.; MacGowan, B.J.; Kania, D.R.; Hammel, B.A.; Back, C.A.; Hsieh, E.; Doyas, R.; Iglesias, C.A.; Rogers, F.J.; Lee, R.W. Absorption measurements demonstrating the importance of Δn=0 transitions in the opacity of iron. Phys. Rev. Lett. 1992, 69, 438–441. [Google Scholar] [CrossRef] [PubMed]
- Bailey, J.E.; Rochau, G.A.; Iglesias, C.A.; Abdallah, J.; MacFarlane, J.J.; Golovkin, I.; Wang, P.; Mancini, R.C.; Lake, P.W.; Moore, T.C.; et al. Iron-Plasma Transmission Measurements at Temperatures Above 150 eV. Phys. Rev. Lett. 2007, 99, 265002. [Google Scholar] [CrossRef] [PubMed]
- Bailey, J.E.; Nagayama, T.; Loisel, G.P.; Rochau, G.A.; Blancard, C.; Colgan, J.; Cosse, P.; Faussurier, G.; Fontes, C.J.; Gilleron, F.; et al. A higher-than-predicted measurement of iron opacity at solar interior temperatures. Nature 2015, 517, 56–59. [Google Scholar] [CrossRef] [PubMed]
- Renaudin, P.; Blancard, C.; Faussurier, G.; Noiret, P. Combined Pressure and Electrical-Resistivity Measurements of Warm Dense Aluminum and Titanium Plasmas. Phys. Rev. Lett. 2002, 88, 215001. [Google Scholar] [CrossRef] [PubMed]
- Korobenko, V.N.; Rakhel, A.D. Electrical resistivity and equation of state measurements on hot expanded aluminum in the metal-nonmetal transition range. Phys. Rev. B 2007, 75, 064208. [Google Scholar] [CrossRef]
- Gregori, G.; Glenzer, S.H.; Rogers, F.J.; Pollaine, S.M.; Landen, O.L.; Blancard, C.; Faussurier, G.; Renaudin, P.; Kuhlbrodt, S.; Redmer, R. Electronic structure measurements of dense plasmas. Phys. Plasmas 2004, 11, 2754–2762. [Google Scholar] [CrossRef]
- Sperling, P.; Rosmej, S.; Bredow, R.; Fletcher, L.B.; Galtier, E.; Gamboa, E.J.; Lee, H.J.; Reinholz, H.; Röpke, G.; Zastrau, U.; et al. Electrical conductivity calculations in isochorically heated warm dense aluminum. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 134002. [Google Scholar] [CrossRef]
- Kraus, D.; Chapman, D.A.; Kritcher, A.L.; Baggott, R.A.; Bachmann, B.; Collins, G.W.; Glenzer, S.H.; Hawreliak, J.A.; Kalantar, D.H.; Landen, O.L.; et al. X-ray scattering measurements on imploding CH spheres at the National Ignition Facility. Phys. Rev. E 2016, 94, 011202. [Google Scholar] [CrossRef] [PubMed]
- Swift, D.C.; Kritcher, A.L.; Hawreliak, J.A.; Lazicki, A.; MacPhee, A.; Bachmann, B.; Döppner, T.; Nilsen, J.; Collins, G.W.; Glenzer, S.; et al. Absolute Hugoniot measurements from a spherically convergent shock using X-ray radiography. Rev. Sci. Instrum. 2018, 89, 053505. [Google Scholar] [CrossRef]
- Hu, S.X.; Bishel, D.T.; Chin, D.A.; Nilson, P.M.; Karasiev, V.V.; Golovkin, I.E.; Gu, M.; Hansen, S.B.; Mihaylov, D.I.; Shaffer, N.R.; et al. Probing atomic physics at ultrahigh pressure using laser-driven implosions. Nat. Commun. 2022, 13, 6780. [Google Scholar] [CrossRef] [PubMed]
- Hoarty, D.J.; Allan, P.; James, S.F.; Brown, C.R.D.; Hobbs, L.M.R.; Hill, M.P.; Harris, J.W.O.; Morton, J.; Brookes, M.G.; Shepherd, R.; et al. Observations of the Effect of Ionization-Potential Depression in Hot Dense Plasma. Phys. Rev. Lett. 2013, 110, 265003. [Google Scholar] [CrossRef] [PubMed]
- Ciricosta, O.; Vinko, S.M.; Chung, H.K.; Cho, B.I.; Brown, C.R.D.; Burian, T.; Chalupský, J.; Engelhorn, K.; Falcone, R.W.; Graves, C.; et al. Direct Measurements of the Ionization Potential Depression in a Dense Plasma. Phys. Rev. Lett. 2012, 109, 065002. [Google Scholar] [CrossRef] [PubMed]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piron, R. Atomic Models of Dense Plasmas, Applications, and Current Challenges. Atoms 2024, 12, 26. https://doi.org/10.3390/atoms12040026
Piron R. Atomic Models of Dense Plasmas, Applications, and Current Challenges. Atoms. 2024; 12(4):26. https://doi.org/10.3390/atoms12040026
Chicago/Turabian StylePiron, Robin. 2024. "Atomic Models of Dense Plasmas, Applications, and Current Challenges" Atoms 12, no. 4: 26. https://doi.org/10.3390/atoms12040026
APA StylePiron, R. (2024). Atomic Models of Dense Plasmas, Applications, and Current Challenges. Atoms, 12(4), 26. https://doi.org/10.3390/atoms12040026




