Abstract
Polarons, quasiparticles resulting from the interaction between an impurity and the collective excitations of a medium, play a fundamental role in physics, mainly because they represent an essential building block for understanding more complex many-body phenomena. In this manuscript, we study the spectral properties of a single impurity mixed with identical bosons in a one-dimensional lattice with power-law hopping. In particular, based on the so-called T-matrix approximation, we show the existence of well-defined quasiparticle branches for several tunneling ranges and for both repulsive and attractive impurity-boson interactions. Furthermore, we demonstrate the persistence of the attractive polaron branch when the impurity-boson bound state is absorbed into the two-body continuum and that the attractive polaron becomes more robust as the range of the hopping increases. The results discussed here are relevant for the understanding of the equilibrium properties of quantum systems with power-law interactions.
1. Introduction
The study of a single impurity immersed in a many-body quantum system is one of the central topics in condensed matter physics that continuously reveals new intriguing phenomena. The polaron concept, originally proposed by Landau and Pekar [1,2] to describe the screening of electrons in a crystal, provides a useful approach to understanding nontrivial many-body properties. In recent years, the polaron idea has not only been used to describe electrons in solids but also impurities dressed by spin fluctuations [3,4], bound electron-hole pairs in semiconductors [5,6], hybrid impurities of light-matter nature [7,8], and to describe highly imbalanced mixtures in ultracold quantum gases [9,10,11,12], among others. Furthermore, the vast relevance of the polaron concept has recently encouraged the development of studies that explore the physics of impurities in more exotic scenarios. For instance, bipolarons (bound states between two polarons) [13,14,15,16,17], dipolar polarons [18,19,20,21], and charge polarons [22,23,24,25].
The introduction of optical lattices and optical tweezers on various experimental platforms has motivated the study of impurity physics beyond the homogeneous space scenario. Furthermore, the incorporation of quantum gas microscopy in lattice experiments has opened unique opportunities for the study of polarons since it allows the exploration of in situ properties, providing detailed and more accurate spatial information. Several studies have addressed the lattice polaron problem. In particular, the transport of impurities in one-dimensional lattices has been addressed within the weak and strong-coupling regime [26,27,28,29,30,31,32] and variational schemes have been employed to describe polarons and bipolarons in one-dimensional lattices [33]. More recently, the effects of the superfluid to Mott-insulator transition of two-dimensional bosons on the polaron physics have been analyzed for weak boson-impurity interactions [34], and a non-self-consistent T-matrix approximation has been employed to describe single impurities and the formation of bipolarons in square lattices [17].
Most of the current studies on lattice polarons consider short-range couplings, either contact interactions or nearest-neighbor hoppings, overlooking the effects of longer-range couplings. An interesting question is to study the physics of lattice polarons when the nearest-neighbor tunneling is replaced with a hopping whose amplitude follows a power law. This modification is of particular interest since power-law interactions arise in several quantum simulation platforms, such as trapped ions [35,36], polar molecules [37,38], Rydberg atoms [39], nuclear spins in solid-state systems [40], and atoms in photonic crystal waveguides [41]. Recently, the physics of quantum systems with long-range interactions has attracted plenty of attention [42]. In particular, it has been shown that power-law couplings lead to new Lieb-Robinson bounds for quantum information dynamics [43], exotic spin dynamics [44,45,46], multifractality and intriguing localization properties in the presence of a quasiperiodic potential [47,48,49,50], and modifications in both the superfluid to Mott-insulator transition and the Bose–Einstein condensation [51,52,53,54].
In this manuscript, we study the spectral properties of a single impurity mixed with identical bosons in a one-dimensional lattice with power-law hopping. To this end, we first examine the scattering problem of a single impurity and a single boson, based on the so-called T−matrix formalism, we show the effects of the range of the hopping on the two-body bound state. In particular, we illustrate the dependence of the energy of the dimer on the power of the hopping and the stability of the repulsively and attractively bound states. Afterward, we modify the two-body T−matrix to include the effects of a BEC and study the emergence of well-defined quasiparticle branches for different hopping ranges within the non-self-consistent approximation. It is important to mention that this approximation allows us to study the quasiparticle properties in a non-perturbative manner and treat strong and weak impurity-boson interactions within the same scheme. Within this approach, we analyze the spectral properties of the polarons and their dependence on the power of the hopping. In particular, we show the existence of polaron branches for repulsive and attractive interactions, we illustrate that the polaron branch for attractive interactions is well-defined even when the impurity-boson bound state disappears and that as the range of the hopping increases, the attractive polaron becomes more robust. The results here discussed go beyond previous findings, in the sense that they explore the consequences of the range of the hopping on the spectral properties of one-dimensional polarons. Furthermore, they are relevant for current experiments in quantum systems with power-law couplings.
This manuscript is organized as follows. In Section 2, we provide the model employed to describe single-impurity physics. Section 3 presents a brief summary of the main properties of a single particle moving in a lattice with power-law hopping. Then, Section 4 focuses on the two-body problem of an impurity atom and a Bose atom. In Section 5, we provide the main results of an impurity immersed in a Bose–Einstein condensate (BEC). Finally, in Section 6, we summarize and discuss our results.
2. Model
We consider a mobile impurity mixed with identical bosons in a one-dimensional lattice of length L and with inter-site couplings decaying as a power law with power . For simplicity, we consider the same power law for the bosons and the impurity. In the second quantization formalism, the Hamiltonian that describes the above system is given as follows
where () and () annihilates (creates) a boson and an impurity at site i, the tunneling amplitude between nearest neighbors is for the bosons and for the impurities, is the on-site boson-boson repulsion, is the chemical potential of the bosons, and is the on-site interaction between the bosons and the impurity. In contrast to the on-site boson-boson interaction, through the manuscript, we shall consider repulsive and attractive boson-impurity interactions. For simplicity, we set ℏ and the lattice constant a to unity, and consider the case of equal nearest-neighbor tunneling amplitudes, that is . It is important to mention here that case is also relevant as it considers the scenario where the bosons and the impurity have different masses. The inclusion of power-law hops increases the mobility of the particles in comparison with usual nearest-neighbor models. In particular, it has been shown [55] that for the single-particle propagation across the lattice is ballistic, that is, strongly bounded by the group velocity. For faster-than-ballistic propagation occurs. It is important to mention that from a thermodynamic point of view [42], hops in one-dimensional lattices are considered long-range when whereas short-range when . Through the manuscript, we consider , only. Finite-size approaches such as density matrix renormalization group calculations can address the impurity problem with long-range hoppings.
3. Single-Particle Physics
Before entering into the study of an impurity immersed in a BEC, it is convenient to briefly summarize the main characteristics of a single particle moving in a lattice with power-law hopping. The single-particle Hamiltonian is given as follows
The above Hamiltonian can be easily diagonalized using the Fourier transform operators
being the quasi-momentum within the first Brillouin zone. This procedure gives rise to the single-particle lattice dispersion
where is the polylogarithm function of order . Notice that is symmetric in k−space , and that is always real since is of the form with z a complex number and its complex conjugate. Furthermore, for , the lattice dispersion approaches to the well-known result of a lattice with nearest-neighbor hopping, that is . Using that with the Riemann zeta function, one can recognize that the energy of the zero-momentum mode is . Since converges when the real part of is greater than one, finite energies in the thermodynamic limit are obtained when . To be consistent with the latter, we shall focus our attention on only. It is worth mentioning that the case may also display interesting behavior since the particles can move along the whole lattice through energetically close processes. As previously mentioned, finite-size density matrix renormalization group calculations can address the impurity problem with long-range hoppings. Through the rest of the manuscript, we consider , that is, we choose the state of zero energy to be the state of zero momentum. In the upper panels of Figure 1, we illustrate the lattice dispersion as a function of the quasi-momentum k for several values of , the case corresponds to a lattice with nearest-neighbor hopping. As one can notice, for nearest-neighbor hops, the dispersion is a smooth function of k, while it becomes sharp-pointed at as decreases. The abrupt behavior of brings as a consequence that the derivative of the dispersion relation at , that is the group velocity of the mode, is undefined for , and thus resulting in a supersonic-like propagation [55]. Another fundamental property that is affected by the presence of power-law hopping is the density of states (DOS) , where denotes the imaginary part, and is a positive infinitesimal number that is included by hand to properly visualize the density of states (for the numerical calculations we take ). The lower panels of Figure 1 show the DOS as a function of the energy . To visualize all the panels in the same range of values, in the lower panels of Figure 1, we use the bandwidth for each . As decreases, the DOS loses its symmetry at the band edges, becoming smaller at the bottom of the band. That is, low-energy states become less dense compared to high-energy states. Consequently, the transition rate between single-particle eigenstates due to a perturbation of the Hamiltonian in Equation (2) decreases as the range of the hopping increases. As we will see later, the asymmetric behavior of the density of states has consequences on the physics of the polaron.
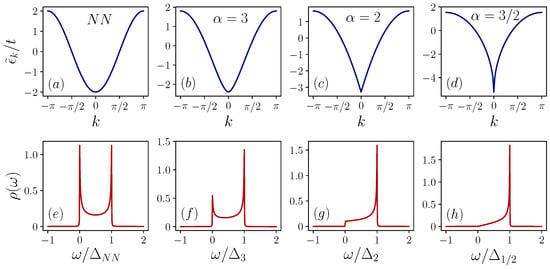
Figure 1.
Panels (a–d) show the lattice dispersion as a function of the quasi-momentum in the first Brillouin zone . Panels (e–h) illustrate the density of states as function of with the lattice bandwidth. Panels (a,e) are associated with a lattice with nearest-neighbor hopping.
4. Two-Body Scattering
In this section, we focus on the scattering of an impurity atom and a single boson in an empty lattice. To this end, we employ two different but equivalent approaches, the -matrix method and the wave function approach. The first scheme has the advantage of directly obtaining the spectral properties without the need to explicitly calculate the wave function of the system. On the other hand, as its name suggests, the wave function method focuses mainly on obtaining the two-body wave function, and therefore the two-body spatial properties are easier to obtain.
We begin by discussing the -matrix approach, the Hamiltonian of the two-body system can be rewritten as follows
is the non-interacting component of the system whereas couples the two particles by the on-site interaction. Using the above expressions, the equation of the scattering matrix takes the simple form
For general potentials , Equation (6) cannot be simplified any further, and one has to resort to numerical methods. However, for on-site interactions, one can straightforwardly obtain an explicit expression of the scattering matrix and thus simplify the numerical task. Using the momentum space representation, the scattering matrix is given as follows:
where is the pair propagator in an empty lattice which is given as follows:
It is important to mention, that for on-site interactions, the scattering matrix of the two-body problem depends on the total center-of-mass momentum P and on the energy of the pair only. The subscripts B and I in the above expressions indicate boson and impurity species, respectively. In Figure 2, we plot the spectral function as a function of and for several values of . In each panel, the dashed white lines enclose the two-body scattering continuum which due to the factor is within the region for all values of . As it is well-known, the poles of the scattering matrix are associated with bound states, in this context, a bound state between one boson and one impurity. Unlike the continuum scenario where the two-body scattering continuum is bounded from below, in lattice systems, the continuum is bounded above and below, and thus the matrix shows bound states for both negative and positive interactions. The former states are called attractively bound pairs and the latter repulsively bound pairs. In contrast to attractive dimers, a repulsively bound pair is not the ground state of the two-body system. However, due to energy constraints, the repulsively bound dimer is unable to decay by converting the interaction energy into kinetic energy, and therefore the repulsively bound state is dynamically stable. Repulsively bound pairs have been experimentally demonstrated in ultracold atomic gases confined in optical lattices with nearest-neighbor hoppings [56]. As one can see in Figure 2, the branch of repulsively bound states is pushed towards the continuum as decreases however, it is not absorbed. In contrast, the branch of attractively bound dimers is incorporated into the continuum as the range of the hopping increases. It is important to mention that in this scenario, no bound state solution exists for . As shown in Figure 2d, when there is no bound state branch for .
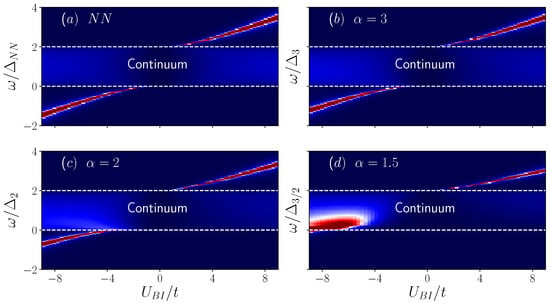
Figure 2.
Spectral function as a function of the interaction strength and the energy for vanishing quasi-momentum k. In each panel, the dashed white lines enclose the two-body scattering continuum. (a) Spectral function for nearest-neighbor hopping, (b) , (c) , and (d) .
To conclude this section, we investigate the spatial behavior of the two-body states. To this end, we explicitly calculate the wave function of the system. The pair wave function can be written as follows:
where and are the center-of-mass and relative coordinates, respectively, and is the relative coordinate wave function, which depends on the center-of-mass momentum k. After using the above ansatz in the Schrödinger equation , one can obtain the following equation for the coefficients of the relative wave function.
where is the Kronecker delta. Equation (10) can be numerically solved using standard linear algebra packages. In Figure 3, we illustrate the square modulus of as a function of the relative coordinate r for several power-law hops. Upper panels are associated with repulsively bound pairs, whereas lower panels correspond to attractively bound dimers. As can be seen, the spatial nature of the repulsively and attractively bound states is quite different as the range of the hopping increases. In particular, we show that the relative wave function for is delocalized and clearly nonvanishing at large distances. That is, the lowest energy eigenstate for ceases to be a bound state, as previously mentioned in the T-matrix analysis. The absence of bound states turns out to be a direct consequence of the unbounded dispersion as . The incorporation into the continuum and disappearance of bound state branches has been also observed in spin and disordered systems with power-law couplings [45,50].
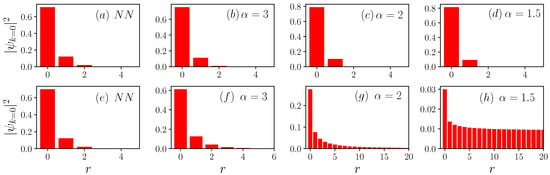
Figure 3.
Square modulus of the zero center-of-mass momentum wave function vs. the relative distance r. Upper panels are associated with repulsively bound pairs , whereas lower panels correspond to attractively bound dimers . (a,e) consider nearest-neighbor hopping, (b,f) , (c,g) , and (d,h) .
5. Impurity in a Bose–Einstein Condensate
We now analyze the physics of a single impurity immersed in the BEC and the formation of the polaron. The spectral properties of an impurity with quasi-momentum k can be described by the impurity Green’s function [57]
where is the self-energy of the impurity. The self-energy represents the contribution to the energy of the impurity due to the interactions between the impurity and its environment (the BEC). Due to the great complexity of many-body systems, an exact calculation of the self-energy is not feasible, for this reason, one has to make certain approximations. To calculate the self-energy, we employ the T-matrix approximation which has been successfully used to describe Bose polaron experiments [10,12,58,59,60]. As a first approximation, it is reasonable to expect that the T-matrix approach would be able to capture the effects of power-law tunneling on the elemental properties of the polaron. Other numerical schemes, such as self-consistent approaches [61,62,63] or density matrix renormalization group methods [64], could provide more accurate results. Within the T-matrix approximation, the self-energy of the impurity is simply the product of the matrix and the equilibrium density of the bosons , that is . In contrast to the two-body problem, the scattering matrix has to include the presence of the BEC. To do so, we assume that the BEC can be accurately described by the Bogoliubov theory. This procedure gives the chemical potential , the excitation spectrum , and the modified two-particle propagator
where is the usual Bogoliubov coherence factor
The substitution of into Equation (4) gives the scattering matrix . As expected, for , the scattering matrix is identical to the two-body scattering matrix . Before proceeding to show our results, let us briefly comment on the approximations we have made so far. The T-matrix approximation of the self-energy is a non-self-consistent approach since it takes into account the bare (non-interacting) impurity propagator in Equation (12). It is important to mention that this approximation allows us to study the quasiparticle properties in a non-perturbative manner and treat strong and weak interactions within the same scheme. Moreover, the non-self-consistent approximation is restricted to permit the binding of a single boson to the impurity, excluding the formation of bosonic clusters around the impurity [61]. This restriction can be removed using the self-consistent scheme, however, such an analysis lies beyond the scope of this manuscript. In this manuscript, we shall focus our attention on the non-self-consistent approximation only.
In Figure 4, we plot the spectral function of the polaron as a function of the impurity-boson interaction for vanishing quasi-momentum and several values of the power . In each panel, the yellow curve is associated with the energy of the dimer states, that is the poles of the matrix shown in Figure 2, the white dashed lines enclose the Bogoliubov continuum with energies , which is essentially indistinguishable from the two-particle continuum. For the numerical calculations, we take the value and . The reason for considering a small boson-boson interaction is to ensure that the bosonic system is far from the transition to the Mott phase. The Mott transition in one-dimensional lattices with nearest-neighbors hops takes place around the value [65,66]. Furthermore, in Ref. [51] the authors study the effects of power-law hops in the Bose-Hubbard model and show that the Mott phase is shrunk in the space as the range of the hopping increases. In other words, the critical interaction for the insulator transition increases. Taking into account the above results, it is reasonable to assume that is within the superfluid regime. In all numerical calculations, it was ensured that the spectral function was properly normalized
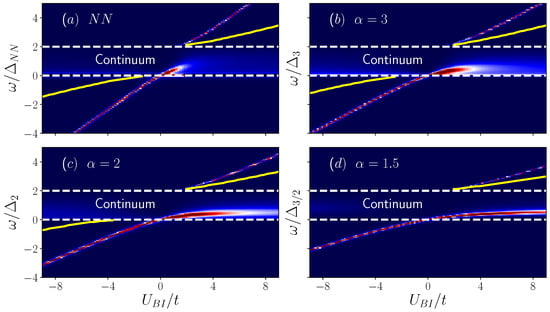
Figure 4.
Spectral function of the impurity as a function of the interaction strength and the energy . We consider and . The dashed white lines enclose the Bogoliubov continuum, the yellow curve is associated with the energy of the dimer states. (a) Spectral function for nearest-neighbor hopping, (b) , (c) , and (d) .
As one can notice from Figure 4, there are well-defined quasi-particle branches for both positive and negative interactions. The poles of are associated with the energies of the polaron . This energy can be found by solving the following self-consistent equation
where denotes the real part. For , the quasiparticle has a higher energy than the repulsive dimer and, like the latter, it is dynamically stable since there are no available states in which it can decay by converting the interaction energy into kinetic energy. As the range of the hopping increases, the energy of the impurity approaches the energy of the dimer for small , that is, the polaron becomes a dimer into a BEC. For , the quasiparticle branch has a smaller energy than the attractively bound pair. Remarkably, the attractive polaron is still well-defined even when the attractively bound pair is already absorbed into the continuum (see Figure 4d). This quasiparticle branch is the lattice analog of the attractive polaron in continuum gases that smoothly evolves into a damped repulsive polaron for positive impurity-boson interaction. Furthermore, as decreases, the broadening of the attractive polaron inside the Bogoliubov continuum is reduced. This can be physically understood from the asymmetry of the density of states (see Figure 1d). As the range of the hopping increases, the density of available states into which the polaron can decay decreases, and therefore the broadening of the impurity inside the Bogoliubov continuum is reduced.
Within the quasiparticle picture and in the vicinity of a pole, the impurity Green’s function in Equation (11) can be approximated as follows [57]
where is the quasiparticle residue, is the damping rate, and describes the incoherent scattering events that have no corresponding poles. The first term in is also called the coherent part since it corresponds to a coherently propagating particle, the polaron, at least for times . One can confirm this scenario by taking the time Fourier transform
As one can notice, the integration of the coherent part of is just a decaying plane wave with lifetime , with a particle weight given by the quasiparticle residue. The value of the residue indicates the spectral weight of the quasiparticle, when vanishes, the quasiparticle disappears. In terms of the self-energy, the residue, and the damping rate are given as follows
In Figure 5, we show the residue and damping rate of a zero-quasi-momentum polaron as a function of the impurity-boson interaction for several values of . As one can notice, the residue of the repulsive branch decreases as the range of the hopping increases, this behavior is in agreement with the previous observation that the polaron branch is pushed towards the bound state branch. Since , it is not possible to discern this branch in current experiments. In stark contrast, the residue of the attractive branch increases when the hopping range increases, making the polaron picture more robust and feasible to be observed. Physically, one can understand the strengthening of the polaron as a consequence of the increased mobility of the impurity as the tunneling range increases. In this scenario, collisions become less relevant. Furthermore, as previously pointed out, the density of available states into which the polaron can decay decreases as the range of the hopping increases. In Figure 5b, we illustrate the damping rate of the repulsive polaron branch as a function of the impurity-boson interaction for several values of . As one can notice, the damping does not change significantly with the tunneling range. It is important to mention that within the non-self-consistent approach, the attractive polaron acquires a finite damping. However, since the attractive polaron is the ground state of the system, this damping is strictly an artifact of the approximation. A self-consistent treatment would remove this issue.
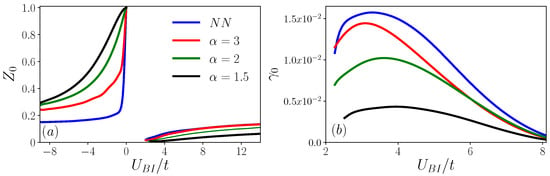
Figure 5.
(a) Quasiparticle residue as a function of the impurity-boson interaction for vanishing crystal momentum and several values of the power hopping . (b) Damping rate as a function of the impurity-boson interaction for vanishing crystal momentum and several values of the power hopping .
6. Conclusions
In recent years, great progress has been made in the implementation of power-law couplings in fully controllable quantum systems of trapped ions, Rydberg atoms, and photons in crystal waveguides. These developments have opened up exciting possibilities for the study of single and many-body physics beyond the short-range scenario. In particular, impurity physics is a subject that, despite being of great interest and that has been constantly evolving, remains mostly explored considering short-range couplings and thus omitting the effects of longer-range couplings.
In this manuscript, we have investigated the formation and spectral properties of a mobile impurity mixed with identical bosons in a one-dimensional lattice with power-law hopping. To this end, we first address the scattering problem of a single impurity and a single boson. By means of the T-matrix formalism, which for the two-body problem is an exact approach, we show that as the range of the hopping increases, the attractively bound pair branch approaches the two-body continuum and then disappears as it becomes incorporated by the scattering region. In contrast, the repulsively bound state branch stays out of the continuum. Afterward, we consider the problem of an impurity immersed in a BEC. Since this is a many-body problem that lacks an exact solution, we resort to several approximations. First, we assume that the bosons can be described by the Bogoliubov approximation and calculate the self-energy of the impurity within the non-self-consistent approximation of the T-matrix. In this approach, the two-body scattering matrix is modified to include the effects of the BEC on the impurity. It is important to mention that this approximation allows us to study the quasiparticle properties in a non-perturbative manner and treat strong and weak interactions within the same scheme. Using the non-self-consistent approximation of the T-matrix, we illustrate the effects of tunneling range on the impurity dressed by the BEC excitations. In particular, we show the existence of polaron branches for repulsive and attractive interactions. Furthermore, we illustrate that the polaron branch for attractive interactions is well-defined even when the impurity-boson bound state disappears. By calculating the quasiparticle residue, we demonstrate that as the hopping range increases, the residue of the attractive polaron increases, that is the polaron becomes more robust. One can understand the strengthening of the quasiparticle as a consequence of the increased mobility of the impurity as the tunneling range increases.
Many-body physics in quantum systems with power-law interactions is of current theoretical interest and is under development on several experimental platforms. Making the exploration of the physics of systems with power-law couplings feasible and interesting. In particular, the physics of impurities. We expect that our work will trigger further theoretical analysis as, for instance, the determination of the polaron properties using density matrix renormalization group techniques, the fate of the bipolaron formation beyond nearest-neighbor hops, and the role of the superfluid-Mott transition of the bosonic environment on the transport properties of the polaron, among others.
Funding
G.A.D.-C. acknowledges the support of the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy—EXC-2123 QuantumFrontiers—390837967.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data available upon request to the corresponding author.
Acknowledgments
I thank Rosario Paredes for the careful review of this manuscript and for the useful comments.
Conflicts of Interest
The author declares no conflict of interest.
References
- Landau, L.; Pekar, S. Effective mass of a polaron. J. Exp. Theor. Phys. 1948, 18, 419–423. [Google Scholar]
- Pekar, S. Theory of electromagnetic waves in a crystal with excitations. J. Phys. Chem. Solids 1958, 5, 11–22. [Google Scholar] [CrossRef]
- Dagotto, E.; Moreo, A.; Barnes, T. Hubbard model with one hole: Ground-state properties. Phys. Rev. B 1989, 40, 6721. [Google Scholar] [CrossRef] [PubMed]
- Kane, C.L.; Lee, P.A.; Read, N. Motion of a single hole in a quantum antiferromagnet. Phys. Rev. B 1989, 39, 6880. [Google Scholar] [CrossRef] [PubMed]
- Jakubczyk, T.; Nogajewski, K.; Molas, M.R.; Bartos, M.; Langbein, W.; Potemski, M.; Kasprzak, J. Impact of environment on dynamics of exciton complexes in a WS2 monolayer. 2D Mater. 2018, 5, 031007. [Google Scholar] [CrossRef]
- Singh, A.; Moody, G.; Tran, K.; Scott, M.E.; Overbeck, V.; Berghäuser, G.; Schaibley, J.; Seifert, E.J.; Pleskot, D.; Gabor, N.M.; et al. Trion formation dynamics in monolayer transition metal dichalcogenides. Phys. Rev. B 2016, 93, 041401. [Google Scholar] [CrossRef]
- Sidler, M.; Back, P.; Cotlet, O.; Srivastava, A.; Fink, T.; Kroner, M.; Demler, E.; Imamoglu, A. Fermi polaron-polaritons in charge-tunable atomically thin semiconductors. Nat. Phys. 2016, 13, 255–261. [Google Scholar] [CrossRef]
- Takemura, N.; Trebaol, S.; Wouters, M.; Portella-Oberli, M.T.; Deveaud, B. Polaritonic Feshbach resonance. Nat. Phys. 2014, 10, 500–504. [Google Scholar] [CrossRef]
- Schirotzek, A.; Wu, C.-H.; Sommer, A.; Zwierlein, M.W. Observation of Fermi Polarons in a Tunable Fermi Liquid of Ultracold Atoms. Phys. Rev. Lett. 2009, 102, 230402. [Google Scholar] [CrossRef]
- Jørgensen, N.B.; Wacker, L.; Skalmstang, K.T.; Parish, M.M.; Levinsen, J.; Christensen, R.S.; Bruun, G.M.; Arlt, J.J. Observation of Attractive and Repulsive Polarons in a Bose–Einstein Condensate. Phys. Rev. Lett. 2016, 117, 055302. [Google Scholar] [CrossRef]
- Scazza, F.; Valtolina, G.; Massignan, P.; Recati, A.; Amico, A.; Burchianti, A.; Fort, C.; Inguscio, M.; Zaccanti, M.; Roati, G. Repulsive Fermi Polarons in a Resonant Mixture of Ultracold 6Li Atoms. Phys. Rev. Lett. 2017, 118, 083602. [Google Scholar] [CrossRef] [PubMed]
- Hu, M.-G.; Van de Graaff, M.J.; Kedar, D.; Corson, J.P.; Cornell, E.A.; Jin, D.S. Bose Polarons in the Strongly Interacting Regime. Phys. Rev. Lett. 2016, 117, 055301. [Google Scholar] [CrossRef] [PubMed]
- Naidon, P. Two Impurities in a Bose–Einstein Condensate: From Yukawa to Efimov Attracted Polarons. J. Phys. Soc. Jpn. 2018, 87, 043002. [Google Scholar] [CrossRef]
- Camacho-Guardian, A.; Peña Ardila, L.A.; Pohl, T.; Bruun, G.M. Bipolarons in a Bose–Einstein Condensate. Phys. Rev. Lett. 2018, 121, 013401. [Google Scholar] [CrossRef]
- Huber, D.; Hammer, H.W.; Volosniev, A.G. In-medium bound states of two bosonic impurities in a one-dimensional Fermi gas. Phys. Rev. Res. 2019, 1, 033177. [Google Scholar] [CrossRef]
- Deng, F.L.; Shi, T.; Yi, S. Effective interactions between two impurities in quasi-two-dimensional dipolar Bose–Einstein condensates. Commun. Theor. Phys. 2020, 72, 075501. [Google Scholar] [CrossRef]
- Ding, S.; Domínguez-Castro, G.A.; Julku, A.; Camacho-Guardian, A.; Bruun, G.M. Polarons and bipolarons in a two-dimensional square lattice. SciPost Phys. 2023, 14, 143. [Google Scholar] [CrossRef]
- Ardila, L.A.; Pohl, T. Ground-state properties of dipolar Bose polarons. J. Phys. B At. Mol. Opt. Phys. 2018, 52, 015004. [Google Scholar] [CrossRef]
- Kain, B.; Ling, H.Y. Polarons in a dipolar condensate. Phys. Rev. A 2014, 89, 023612. [Google Scholar] [CrossRef]
- Nishimura, K.; Nakano, E.; Iida, K.; Tajima, H.; Miyakawa, T.; Yabu, H. Ground state of the polaron in an ultracold dipolar Fermi gas. Phys. Rev. A 2021, 103, 033324. [Google Scholar] [CrossRef]
- Guebli, N.; Boudjemâa, A. Effects of quantum fluctuations on the dynamics of dipolar Bose polarons. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 185303. [Google Scholar] [CrossRef]
- Astrakharchik, G.E.; Ardila, L.A.P.; Schmidt, R.; Jachymski, K.; Negretti, A. Ionic polaron in a Bose–Einstein condensate. Commun. Phys. 2021, 4, 94. [Google Scholar] [CrossRef]
- Christensen, E.R.; Camacho-Guardian, A.; Bruun, G.M. Charged Polarons and Molecules in a Bose–Einstein Condensate. Phys. Rev. Lett. 2021, 126, 243001. [Google Scholar] [CrossRef] [PubMed]
- Astrakharchik, G.E.; Peña Ardila, L.A.; Jachymski, K.; Negretti, A. Many-body bound states and induced interactions of charged impurities in a bosonic bath. Nat. Commun. 2023, 14, 1647. [Google Scholar] [CrossRef] [PubMed]
- Ding, S.; Drewsen, M.; Arlt, J.J.; Bruun, G.M. Mediated Interaction between Ions in Quantum Degenerate Gases. Phys. Rev. Lett. 2022, 129, 153401. [Google Scholar] [CrossRef]
- Bruderer, M.; Klein, A.; Clark, S.R.; Jaksch, D. Polaron physics in optical lattices. Phys. Rev. A 2007, 76, 011605(R). [Google Scholar] [CrossRef]
- Bruderer, M.; Klein, A.; Clark, S.R.; Jaksch, D. Transport of strong-coupling polarons in optical lattices. New J. Phys. 2008, 10, 033015. [Google Scholar] [CrossRef]
- Privitera, A.; Hofstetter, W. Polaronic slowing of fermionic impurities in lattice Bose–Fermi mixtures. Phys. Rev. A 2010, 82, 063614. [Google Scholar] [CrossRef]
- Massel, F.; Kantian, A.; Daley, A.J.; Giamarchi, T.; Törmä, P. Dynamics of an impurity in a one-dimensional lattice. New J. Phys. 2013, 15, 045018. [Google Scholar] [CrossRef][Green Version]
- Sarkar, S.; McEndoo, S.; Schneble, D.; Daley, A.J. Interspecies entanglement with impurity atoms in a lattice gas. New J. Phys. 2020, 22, 083017. [Google Scholar] [CrossRef]
- Keiler, K.; Mistakidis, S.I.; Schmelcher, P. Doping a lattice-trapped bosonic species with impurities: From ground state properties to correlated tunneling dynamics. New J. Phys. 2020, 22, 083003. [Google Scholar] [CrossRef]
- Hu, H.; Wang, A.-B.; Yi, S.; Liu, X.-J. Fermi polaron in a one-dimensional quasiperiodic optical lattice: The simplest many-body localization challenge. Phys. Rev. A 2016, 93, 053601. [Google Scholar] [CrossRef]
- Dutta, S.; Mueller, E.J. Variational study of polarons and bipolarons in a one-dimensional Bose lattice gas in both the superfluid and the Mott-insulator regimes. Phys. Rev. A 2013, 88, 053601. [Google Scholar] [CrossRef]
- Colussi, V.E.; Caleffi, F.; Menotti, C.; Recati, A. Lattice polarons across the superfluid to mott insulator transition. Phys. Rev. Lett. 2023, 130, 173002. [Google Scholar] [CrossRef] [PubMed]
- Zähringer, F.; Kirchmair, G.; Gerritsma, R.; Solano, E.; Blatt, R.; Roos, C.F. Realization of a Quantum Walk with One and Two Trapped Ions. Phys. Rev. Lett. 2010, 104, 100503. [Google Scholar] [CrossRef] [PubMed]
- Schmitz, H.; Matjeschk, R.; Schneider, C.; Glueckert, J.; Enderlein, M.; Huber, T.; Schaetz, T. Quantum Walk of a Trapped Ion in Phase Space. Phys. Rev. Lett. 2009, 103, 090504. [Google Scholar] [CrossRef]
- Yan, B.; Moses, S.A.; Gadway, B.; Covey, J.P.; Hazzard, K.R.A.; Rey, A.M.; Jin, D.S.; Ye, J. Observation of dipolar spin-exchange interactions with lattice-confined polar molecules. Nature 2013, 501, 521–525. [Google Scholar] [CrossRef]
- Yan, B.; Moses, S.A.; Gadway, B.; Covey, J.P.; Hazzard, K.R.A.; Rey, A.M.; Jin, D.S.; Ye, J. A degenerate Fermi gas of polar molecules. Science 2019, 363, 853–856. [Google Scholar]
- Browaeys, A.; Lahaye, T. Many-body physics with individually controlled Rydberg atoms. Nat. Phys. 2020, 16, 132–142. [Google Scholar] [CrossRef]
- Álvarez, G.A.; Suter, D.; Kaiser, R. Localization-delocalization transition in the dynamics of dipolar-coupled nuclear spins. Science 2015, 349, 846–848. [Google Scholar] [CrossRef]
- Hung, C.-L.; González-Tuleda, A.; Cirac, J.I.; Kimble, H.J. Quantum spin dynamics with pairwise-tunable, long-range interactions. Proc. Natl. Acad. Sci. USA 2016, 113, E4946–E4955. [Google Scholar] [CrossRef] [PubMed]
- Defenu, N.; Donner, T.; Macrì, T.; Pagano, G.; Ruffo, S.; Trombettoni, A. Long-range interacting quantum systems. arXiv 2021, arXiv:2109.01063. [Google Scholar]
- Tran, M.C.; Guo, A.Y.; Baldwin, C.L.; Ehrenberg, A.; Gorshkov, A.V.; Lucas, A. Lieb-Robinson Light Cone for Power-Law Interactions. Phys. Rev. Lett. 2021, 127, 160401. [Google Scholar] [CrossRef]
- Safavi-Naini, A.; Wall, M.L.; Acevedo, O.L.; Rey, A.M.; Nandkishore, R.M. Quantum dynamics of disordered spin chains with power-law interactions. Phys. Rev. A 2019, 99, 033610. [Google Scholar] [CrossRef]
- Macrì, T.; Lepori, L.; Pagano, G.; Lewenstein, M.; Barbiero, L. Bound state dynamics in the long-range spin-1/2 XXZ model. Phys. Rev. B 2021, 104, 214309. [Google Scholar] [CrossRef]
- Hermes, S.; Apollaro, T.J.G.; Paganelli, S.; Macrì, T. Dimensionality-enhanced quantum state transfer in long-range-interacting spin systems. Phys. Rev. A 2020, 101, 053607. [Google Scholar] [CrossRef]
- Roy, N.; Sharma, A. Fraction of delocalized eigenstates in the long-range Aubry-André-Harper model. Phys. Rev. B 2021, 103, 075124. [Google Scholar] [CrossRef]
- Domínguez-Castro, G.A.; Paredes, R. Enhanced transport of two interacting quantum walkers in a one-dimensional quasicrystal with power-law hopping. Phys. Rev. A 2021, 104, 033306. [Google Scholar] [CrossRef]
- Deng, X.; Kravtsov, V.E.; Shlyapnikov, G.V.; Santos, L. Duality in Power-Law Localization in Disordered One-Dimensional Systems. Phys. Rev. Lett. 2018, 120, 110602. [Google Scholar] [CrossRef]
- Domínguez-Castro, G.A.; Paredes, R. Localization of pairs in one-dimensional quasicrystals with power-law hopping. Phys. Rev. B 2022, 106, 134208. [Google Scholar] [CrossRef]
- Ferraretto, M.; Salasnich, L. Effects of long-range hopping in the Bose-Hubbard model. Phys. Rev. A 2019, 99, 013618. [Google Scholar] [CrossRef]
- Giachetti, G.; Defenu, N.; Ruffo, S.; Trombettoni, A. Berezinskii-Kosterlitz-Thouless Phase Transitions with Long-Range Couplings. Phys. Rev. Lett. 2021, 127, 156801. [Google Scholar] [CrossRef] [PubMed]
- Dias, W.S.; Bertrand, D.; Lyra, M.L. Bose–Einstein condensation in chains with power-law hoppings: Exact mapping on the critical behavior in d-dimensional regular lattices. Phys. Rev. E 2017, 95, 062105. [Google Scholar] [CrossRef]
- Jaouadi, A.; Telmini, M.; Charron, E. Bose–Einstein condensation with a finite number of particles in a power-law trap. Phys. Rev. A 2011, 83, 023616. [Google Scholar] [CrossRef]
- Storch, D.-M.; Worm, M.; Kastner, M. Interplay of soundcone and supersonic propagation in lattice models with power law interactions. New J. Phys. 2015, 17, 063021. [Google Scholar] [CrossRef]
- Winkler, K.; Thalhammer, G.; Lang, F.; Grimm, R.; Denschlag, J.H.; Daley, A.J.; Kantian, A.; Büchler, H.P.; Zoller, P. Repulsively bound atom pairs in an optical lattice. Nature 2006, 441, 853–856. [Google Scholar] [CrossRef]
- Bruus, H.; Flensberg, K. Many-Body Quantum Theory in Condensed Matter Physics: An Introduction; Oxford Graduate Texts; Oxford University Press: Oxford, UK, 2016. [Google Scholar]
- Ardila, L.A.; Jørgensen, N.B.; Pohl, T.; Giorgini, S.; Bruun, G.M.; Arlt, J.J. Analyzing a Bose polaron across resonant interactions. Phys. Rev. A 2019, 99, 063607. [Google Scholar] [CrossRef]
- Skou, M.G.; Skov, T.G.; Jørgensen, N.B.; Nielsen, K.K.; Camacho-Guardian, A.; Pohl, T.; Bruun, G.M.; Arlt, J.J. Non-equilibrium quantum dynamics and formation of the Bose polaron. Nat. Phys. 2021, 17, 731–735. [Google Scholar] [CrossRef]
- Yan, Z.Z.; Ni, Y.; Robens, C.; Zwierlein, M.W. Bose polarons near quantum criticality. Science 2020, 368, 190–194. [Google Scholar] [CrossRef] [PubMed]
- Rath, S.P.; Schmidt, R. Field-theoretical study of the Bose polaron. Phys. Rev. A 2013, 88, 053632. [Google Scholar] [CrossRef]
- Bruun, G.M.; Massignan, P. Decay of Polarons and Molecules in a Strongly Polarized Fermi Gas. Phys. Rev. Lett. 2010, 105, 020403. [Google Scholar] [CrossRef] [PubMed]
- Massignan, P.; Bruun, G.M. Repulsive polarons and itinerant ferromagnetism in strongly polarized Fermi gases. Eur. Phys. J. D 2011, 65, 83–89. [Google Scholar] [CrossRef]
- Schollwöck, U. The density-matrix renormalization group. Rev. Mod. Phys. 2005, 77, 259. [Google Scholar] [CrossRef]
- Danshita, I.; Polkovnikov, A. Superfluid-to-Mott-insulator transition in the one-dimensional Bose-Hubbard model for arbitrary integer filling factors. Phys. Rev. A 2011, 84, 063637. [Google Scholar] [CrossRef]
- Boéris, G.; Gori, L.; Hoogerland, M.D.; Kumar, A.; Lucioni, E.; Tanzi, L.; Inguscio, M.; Giamarchi, T.; D’Errico, C.; Carleo, G.; et al. Mott transition for strongly interacting one-dimensional bosons in a shallow periodic potential. Phys. Rev. A 2016, 93, 011601(R). [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).