Abstract
The detection of gravitational waves and electromagnetic signals from the neutron star merger GW170817 has provided evidence that these astrophysical events are sites where the r-process nucleosynthesis operates. The electromagnetic signal, commonly known as kilonova, is powered by the radioactive decay of freshly synthesized nuclei. However, its luminosity, colour and spectra depend on the atomic opacities of the produced elements. In particular, opacities of lanthanides and actinides elements, due to their large density of bound–bound transitions, are fundamental. The current work focuses on atomic structure calculations for lanthanide and actinide ions, which are important in kilonovae modelling of ejecta spectra. Calculations for Nd III and U III, two representative rare-earth ions, were achieved. Our aim is to provide valuable insights for future opacity calculations for all heavy elements. We noticed that the opacity of U III is about an order of magnitude greater than the opacity of Nd III due to a higher density of levels in the case of the actinide.
1. Introduction
The production mechanisms of elements heavier than iron have been studied for many decades. They involve a sequence of neutron captures and beta-decays. Depending on the neutron density reached in the astrophysical environment, one distinguishes between the s-process (s for slow) and r-process (r for rapid). While it has been known for a long time that the s-process operates on the asymptotic giant branch (AGB) stars, only recently have we been able to identify one of the astrophysical sites where the r-process operates [1]. This has been made possible by the observation of a kilonova associated with the collision of two neutron stars. This observation took place in August 2017 after the detection of gravitational waves from a neutron star merger by the LIGO-Virgo experiment, the well-known GW170817 event [2]. Its electromagnetic counterpart, designated by AT2017gfo [3], exhibits a number of unique characteristics that set it apart from other transients, including an unusually high optical brightness in the days following the explosion and a long-lived infrared emission that lasted nearly two weeks. These characteristics, which are associated with the ejecta’s rapid colour evolution, appear to be consistent with theoretical models of kilonovae, which consider them to be potential sites for the occurrence of heavy r-processes [4].
Numerous explanations have been put forward to account for the optical and near-infrared spectral features observed in this so-called kilonova. Due to a lack of information about the atomic properties of lanthanide and actinide ions, the majority of radiation transport simulations are based on grey opacity schemes in which the value of the opacity is adjusted to reproduce the colour of the emission. It is expected, however, that the opacities of the former ions are roughly 10 times higher than the ones associated with ironlike elements [5,6]. Regarding this lack of data, calculations for selected r-process elements [7,8,9,10,11] and for all lanthanide elements [12,13,14] have been published in recent years.
In this work, atomic structure and opacity calculations were carried out for two representative r-process ions, Nd III and U III. The expansion opacity is compared between these two ions in order to evaluate the possible impact of actinides. This is particularly significant given the scarcity of publications incorporating actinides into their opacity models. With this in mind, we discuss the effect of level density in the computation of expansion opacities and in particular how actinides can be prone to having a higher density of low-lying levels.
2. Methods
2.1. Expansion Opacities
Pinto & Eastman’s previous work on the light curves of type Ia supernovae [15] have shown bound–bound transitions to be the major source of opacity, accounting for two orders of magnitude more than contributions from electron scattering, bound–free, and free–free transitions.
In rapidly evolving environments, such as those of SN Ia and of kilonovae, the velocity gradient of the expansion of the ejecta is much greater than thermal and turbulent motions responsible for Doppler broadening. When that is the case, and by also assuming the impact of the overlap of strong lines is negligible (as demonstrated by Tanaka et al. 2020 for the case of lanthanides [14]), we can use the expansion opacity formalism to compute the bound–bound opacity for a certain wavelength grid [16,17]. Assuming homologously expanding ejecta with density , the expansion opacity at the time after the explosion is given as
where the sum is taken over all the lines within a wavelength interval of width . is the Sobolev’s optical depth
where n is the population of the lower level of the transition k with wavelength and is the oscillator strength of the line.
2.2. Atomic Calculations
Most of the calculations for this work were performed using the open source and freely available Flexible Atomic Code (FAC) [18]. In particular, the forked version of the original code, cFAC (version 1.6.3a), was used [19]. The atomic structure fully takes into account relativistic effect as it is based on the diagonalization of the Dirac-Coulomb Hamiltonian:
where and are the Dirac matrices and accounts for potential due to the nuclear charge. Higher order QED effects such as self-energy and vacuum polarization effects are included in the screened hydrogenic approximation, while the Breit interaction is only included in the zero energy limit for the exchanged photon. Relativistic configuration interaction (RCI) calculations are performed based on a set of atomic state functions (ASFs), , given by a superposition of configuration state functions (CSFs), , with the same symmetries,
The CSFs used in the calculation are constructed from a linear combination of Slater determinants of one-electron orbitals, which are determined by solving self-consistently a set of Dirac–Fock–Slater differential equations for a local central potential which includes both nuclear field and electron–electron interactions. In this approach, the central potential is derived using a self-consistent method that minimizes the energy of a chosen mean configuration. In all the calculations provided with FAC, and as it is typically considered, the central potential was optimized for the ground configuration, [Xe] in the case of Nd III and [Rn] for U III.
3. Results and Discussion
3.1. Nd III
Starting with Nd III, a summary of the configurations used in each of the calculations, including the total number of levels and lines computed, is given in Table 1. For all calculations, a [Xe] ground configuration was used for the core of the ion. We performed two different FAC calculations (labelled accordingly as Calculations A and B) which are distinguished only by the inclusion in the basis set of the additional configuration in Calculation A.

Table 1.
Summary of the different set of configurations used on different calculations for Nd III, including experimental results from NIST [20]. For the GRASP2K calculations [21], only the configurations from the multireference space are shown. The full active space of configurations used in that calculation is shown in Ref. [22].
We compare our results with structure calculations performed with the GRASP2K code by Gaigalas et al. [22] as well with the NIST [20] database. As expected, however, the number of levels and lines measured experimentally is still very reduced.
For the data supplied by Gaigalas et al., MCDHF calculations were initially performed for the states of the ground configuration. The wave functions derived from these calculations were adopted as the initial ones to calculate the states of the multireference configurations (given in Table 1). Subsequent RCI calculations account for a larger number of configurations not included in the initial MCDHF self-consistent field. The Breit interaction and leading order QED effects are also included at this stage. The full details of the calculation and the construction of the active space used are given in [22]. As a result of the increased degree of optimization, MCDHF-RCI calculations are expected to be more precise than RCI calculations based on a central-field potential. Nonetheless, the latter has been used in calculations for lanthanides, with a typical precision for the lowest energy states of each configuration of for neutral atoms and of less than for the first ionization stages (see, for example, [14]).
A visual comparison of our results with those of Gaigalas et al. and with the NIST data is shown in Figure 1. We can clearly see that the FAC results for Calculation B appear to match reasonably well to the ones obtained with the GRASP2K code, especially for the lowest lying configurations. A worse match is achieved for the and , as FAC seems to underestimate the energy values of those configurations. In order to compare our results, we have evaluated the difference in the lowest energy level of each configuration (normalized by the ionization potential) between our FAC calculations and the data from Gaigalas et al. and NIST. Agreement for Calculation A with the data from Gaigalas et al. and NIST is, on average, within 4.1% and 3.9%, respectively. Calculation B has an average agreement of 3.6% with Gaigalas et al. data and of 0.6% with NIST data. However, we also note that only data for the ground state and for are available in the NIST database. No other experimental data were found for Nd III configurations beyond .
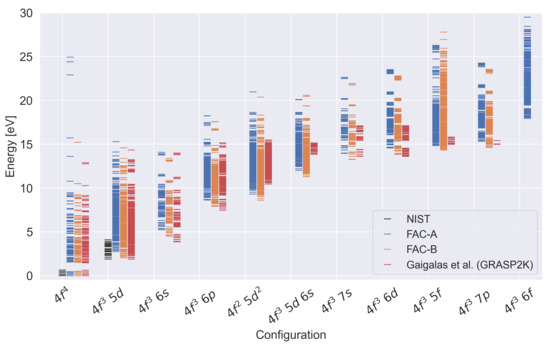
Figure 1.
Energy levels for configurations of Nd III calculated with FAC and compared with the results from Gaigalas et al. [22] and with NIST data [20].
In our particular case, the disparity of results between Calculations A and B of FAC points to the fact that the energy levels have not yet converged. Hence, although RCI codes can provide time-efficient calculations when only few configurations are included, which allow for systematic calculations of many ions (as achieved in [14]), one should note that the inclusion of a much higher number of configurations can have a considerable impact in the calculations.
3.2. U III
As for the U III, the basis set for the FAC RCI calculations was determined by increasing the principal quantum number of the configurations used in Nd III by one. The set of configurations from Calculation B of Nd III was chosen because it produced the best results when compared to the experimental NIST data. At the time of writing, the only experimental data available for actinide ions are from Blaise et al. [23]. Furthermore, two independent groups from the Los Alamos institute have developed calculations for the first ionized states of uranium with the CI-MBPT code [24] and the ATOMIC codes [25]. Only the data from Savukov et al. [26], which used a hybrid configuration interaction (CI) plus linearized coupled cluster (LCC) methods described in [27], are publicly available. Sultana N. Nahar of the Ohio State University’s Astronomy Department hosts and maintains the NORAD-Atomic-Data database [28], which contains calculations for a broad range of structure calculations for important astrophysical ions, including uranium, using the SUPERSTRUCTURE [29] algorithm. In that database, however, only highly ionized elements are available.
Table 2 provides an overview of the FAC calculation achieved in the work as well as the prior calculations for U III with the CI-MBPT code from Savukov et al. and of the experimental data from Blaise et al.

Table 2.
Summary of the different set of configurations used on the FAC calculation for U III. An overview of the experimental data from Blaise et al. [23]. The calculations produced by Savukov et al. [26] using a hybrid configuration interaction (CI) plus linearized coupled cluster (LCC) methods (described in [27]) are also shown. For the CI+LCC calculations, we only show the configurations for which levels and lines data were published.
We can observe from Figure 2 that, as with Nd III, we were able to reproduce the lowest lying levels fairly accurately when compared to both experimental and computational data. From spectroscopic studies, Blaise et al. determined to be the ground configuration for U III. On the other hand, the CI+LCC calculations suggest an electron in the shell in the ion’s lowest energy state. Our FAC calculations do provide better agreement with the experimental data in this regard, giving the even configuration as the ground state of U III. Comparisons for the lowest energies levels of each configuration were evaluated in the same way as for NdIII. We found relative differences of 3.4%, on average, when comparing our FAC calculation with the experimental data from Blaise et al. The agreement for the lowest energy levels with calculations from Savukov et al. was within 2.2%, on average.
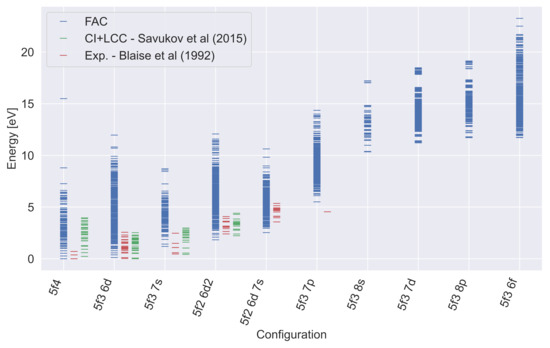
Figure 2.
Energy levels for configurations of U III calculated with FAC. The excitation energies are compared with the experimental results from Blaise et al. [23] and the CI+LCC calculations from Savukov et al. [26].
One important point to keep is the larger radius of the shell when compared to the shell [30]. As a result, electrons tend to be less deeply buried in the core and less shielded from the effect of outer valence electrons than electrons. This effect, associated with the higher Z of actinide elements can, in theory, contribute to a smaller gap between the ground state and the first few excited levels. In the particular case of U III, it is expected that the excitation energies of and are exceedingly close to each other.
The greater radius of shells also contributes to a significantly higher level density in U III when compared to the previously discussed calculations for Nd III, as can be seen in more detail in Figure 3, despite the fact that the same number of levels was calculated in both cases. The number of levels is particularly high in the case of the actinide at energies below 10 eV. This is especially important to consider in the opacity calculations as the population of low-lying levels is favoured in LTE conditions. The gap between the two peaks that we find at roughly 12 eV is likely due to the limited set of configurations used in the calculation, as it was based from the calculation on Nd III. Therefore, contributions from shells, for example, are not included, and can potentially contribute with energy levels at those energies.
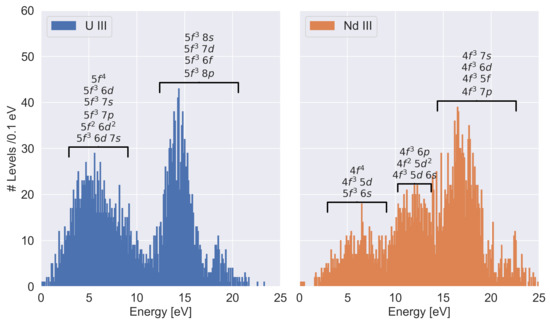
Figure 3.
Level density distribution of U III and Nd III as calculated from FAC. The configurations with greater contribution for each peak are also highlighted.
3.3. Expansion Opacities
Following previous works, the expansion opacity of Nd III and U III was calculated individually for each ion, assuming a gas composition given just by those ions and thermal population of excited states. This allows us to investigate the effect of only the computed bound–bound transitions on the opacity. They were evaluated over a time period of one day following the explosion, when the medium density was about g [12]. Additionally, a temperature of was specified based on prior estimates for doubly ionized ions [8,14]. The results are presented in Figure 4, including the expansion opacity calculated with the data provided by Gaigalas et al. [22] for Nd III (Strategy C). A good agreement was found between the opacity calculations using the data from Calculation B of Nd III and the data from Gaigalas et al., particularly at visible and infrared wavelengths (average deviations on the expansion opacity of 13% for Å). Differences at lower energies are due to our opacity calculations taking into account a greater number of high energy levels than Gaigalas et al. The spectrum obtained with Calculation A for Nd III is overall similar to the one presented here for Calculation B (both in shape and magnitude), with only minor differences at very high energies (∼1000 Å) due to the presence of more highly energetic levels.
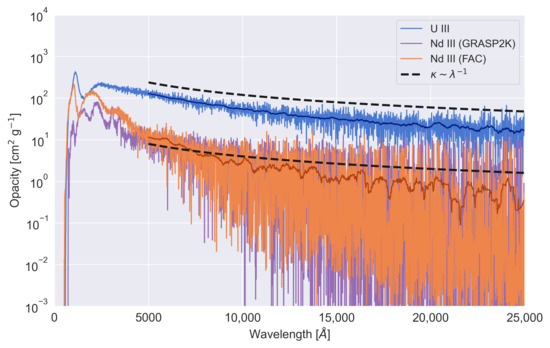
Figure 4.
Expansion opacity for U III and Nd III (Calculation B) from the calculations performed with FAC. The expansion opacity of Nd III calculated using the data from Gaigalas et al. [22] is also to provide a more visual comparison between the two results. The opacity was evaluated at day for the typical density and temperature values of g and assumed by other calculations. A wavelength bin of Å was used. An average over a set of 10 bins is also shown in darker blue and orange lines. The black dashed line highlights the wavelength dependence of the opacity following approximately a power law.
As it can be seen, the opacity of U III is nearly an order of magnitude greater than that of Nd III. This results can be explained by the higher density of low-lying levels in the case of U III, which have a greater contribution to the opacity in LTE than more excited ones. The difference is most noticeable in the visible range, and while it remains significant in the IR, it is less noticeable due to large fluctuations in the opacity of Nd III.
Another interesting observation is that the number of lines of both actinide and lanthanide elements seems to vary smoothly with the wavelength. In particular, we found that after the initial peak at , the number of transitions decreases smoothly with , especially at infrared wavelengths. This dependence is based on the low-energy tail seen empirically in the distribution of bound–bound transitions in Nd III and U III, that can be seen in Figure 5.
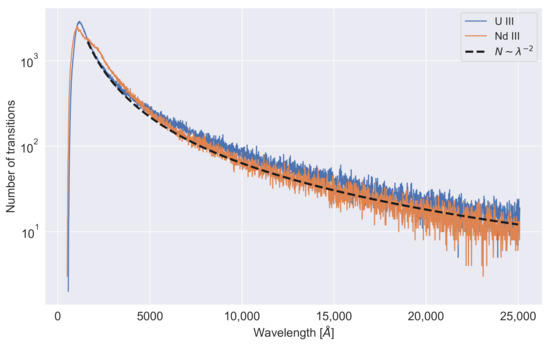
Figure 5.
Total number of lines for Nd III and U III as a function of the wavelength. The inverse power law dependence on the wavelength is highlighted. A wavelength bin of Å was used.
A parameterization of the opacities can, therefore, be obtained, when there is a high number of transitions with a high optical depth (). In that case
Equation 5 emphasizes the importance of the number of lines taken into account in these calculations. Given a high optical depth and LTE conditions, the primary source of opacity is the ion’s line count per unit wavelength, rather than individual strong transitions. As a result, the precision of individual lines will be negligible in environments where the density of levels is sufficiently high enough to sustain local thermodynamical equilibrium and a high optical depth. These insights are particularly pertinent in the case of lanthanides and actinides, owing to their extremely complicated shell structure, which makes accurate computation extremely difficult to achieve within a reasonable amount of time and computational resources.
4. Conclusions
In this work, the FAC code has been used to compute level energies, transition wavelengths and oscillator strengths for electric dipole (E1) transitions for Nd III and U III. We have noticed a reasonable agreement of the energies of low-lying levels with experimental data as well as with other theoretical calculations achieved for those ions. We predict the opacity of U III to be roughly an order of magnitude higher than of Nd III, in all wavelength ranges of interest. Moreover, the larger number of strong transitions of uranium makes the spectra extremely dependent on the number of transitions included, making the precision of individual lines negligible. Due to the higher density of levels expected for actinide elements when compared to lanthanides, we predict these differences to extend beyond Nd III and U III.
Author Contributions
Formal analysis, R.F.S., P.A. and A.F.; Project administration, G.M.-P. and J.P.M.; Supervision, J.M.S., G.M.-P. and J.P.M.; Validation, J.M.S., P.A., A.F. and G.M.-P.; Visualization, R.F.S.; Writing—original draft, R.F.S.; Writing—review & editing, R.F.S., J.M.S., P.A., A.F., G.M.-P. and J.P.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the Fundação para a Ciência e Tecnologia (FCT), Portugal through the contract UIDP/50 0 07/2020 (LIP). R.F.S. acknowledges the support from the ChETEC COST Action( CA16117) during his short-term scientific mission at GSI. A.F. and G.M.-P. acknowledge the support of the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (ERC Advanced Grant KILONOVA No. 885281).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cowan, J.J.; Sneden, C.; Lawler, J.E.; Aprahamian, A.; Wiescher, M.; Langanke, K.; Martínez-Pinedo, G.; Thielemann, F.K. Origin of the heaviest elements: The rapid neutron-capture process. Rev. Mod. Phys. 2021, 93, 015002. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Prospects for Observing and Localizing Gravitational-Wave Transients with Advanced LIGO and Advanced Virgo. LRR 2016, 19, 1. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. 2017, 848, L12. [Google Scholar] [CrossRef]
- Metzger, B.D.; Martínez-Pinedo, G.; Darbha, S.; Quataert, E.; Arcones, A.; Kasen, D.; Thomas, R.; Nugent, P.; Panov, I.V.; Zinner, N.T. Electromagnetic counterparts of compact object mergers powered by the radioactive decay of r-process nuclei. Mon. Not. R. Astron. Soc. 2010, 406, 2650–2662. [Google Scholar] [CrossRef]
- Barnes, J.; Kasen, D. Effect of a high opacity on the light curves of radioactively powered transients from compact object mergers. Astrophys. J. 2013, 775, 18. [Google Scholar] [CrossRef]
- Kasen, D.; Badnell, N.R.; Barnes, J. Opacities and spectra of the r-process ejecta from neutron star mergers. Astrophys. J. 2013, 774, 25. [Google Scholar] [CrossRef] [Green Version]
- Wollaeger, R.T.; Korobkin, O.; Fontes, C.J.; Rosswog, S.K.; Even, W.P.; Fryer, C.L.; Sollerman, J.; Hungerford, A.L.; Van Rossum, D.R.; Wollaber, A.B. Impact of ejecta morphology and composition on the electromagnetic signatures of neutron star mergers. Mon. Not. R. Astron. Soc. 2017, 478, 3298–3334. [Google Scholar] [CrossRef]
- Tanaka, M.; Kato, D.; Gaigalas, G.; Rynkun, P.; Radžiūtė, L.; Wanajo, S.; Sekiguchi, Y.; Nakamura, N.; Tanuma, H.; Murakami, I.; et al. Properties of Kilonovae from Dynamical and Post-merger Ejecta of Neutron Star Mergers. Astrophys. J. 2018, 852, 109. [Google Scholar] [CrossRef]
- Fontes, C.J.; Fryer, C.L.; Hungerford, A.L. A connection between atomic physics and gravitational wave spectroscopy. AIP Conf. Proc. 2017, 1811, 190. [Google Scholar] [CrossRef]
- Mccann, M.; Bromley, S.; Loch, S.D.; Ballance, C.P. Atomic data calculations for Au i–Au iii and exploration in the application of collisional-radiative theory to laboratory and neutron star merger plasmas. Mon. Not. R. Astron. Soc. 2021, 509, 4723–4735. [Google Scholar] [CrossRef]
- Pognan, Q.; Jerkstrand, A.; Grumer, J. On the validity of steady-state for nebular phase kilonovae. Mon. Not. R. Astron. Soc. 2022, 510, 3806–3837. [Google Scholar] [CrossRef]
- Kasen, D.; Metzger, B.; Barnes, J.; Quataert, E.; Ramirez-Ruiz, E. Origin of the heavy elements in binary neutron-star mergers from a gravitational-wave event. Nature 2017, 551, 80–84. [Google Scholar] [CrossRef] [PubMed]
- Fontes, C.J.; Fryer, C.L.; Hungerford, A.L.; Wollaeger, R.T.; Korobkin, O. A line-binned treatment of opacities for the spectra and light curves from neutron star mergers. Mon. Not. R. Astron. Soc. 2020, 493, 4143–4171. [Google Scholar] [CrossRef] [Green Version]
- Tanaka, M.; Kato, D.; Gaigalas, G.; Kawaguchi, K. Systematic opacity calculations for kilonovae. Mon. Not. R. Astron. Soc. 2020, 496, 1369–1392. [Google Scholar] [CrossRef]
- Eastman, R.G.; Pinto, P.A. Spectrum Formation in Supernovae: Numerical Techniques. Astrophys. J. 1993, 412, 731. [Google Scholar] [CrossRef]
- Pinto, P.A.; Eastman, R.G. The Physics of Type Ia Supernova Light Curves. I. Analytic Results and Time Dependence. Astrophys. J. 2000, 530, 744–756. [Google Scholar] [CrossRef]
- Pinto, P.A.; Eastman, R.G. The Physics of Type Ia Supernova Light Curves. II. Opacity and Diffusion. Astrophys. J. 2000, 530, 757–776. [Google Scholar] [CrossRef] [Green Version]
- Gu, M.F. The flexible atomic code. Can. J. Phys. 2008, 86, 675–689. [Google Scholar] [CrossRef]
- Stambulchik, E. cFAC—A Forked Version of FAC. 2020. Available online: https://github.com/fnevgeny/cfac (accessed on 20 December 2021).
- Kramida, A.; Ralchenko, Y.; Reader, J. No Title. NIST Atomic Spectra Database, Version 5.8; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2020. Available online: https://physics.nist.gov/asd (accessed on 9 April 2017).
- Jönsson, P.; Gaigalas, G.; Bieroń, J.; Fischer, C.F.; Grant, I.P. New version: Grasp2K relativistic atomic structure package. Comput. Phys. Commun. 2013, 184, 2197–2203. [Google Scholar] [CrossRef] [Green Version]
- Gaigalas, G.; Kato, D.; Rynkun, P.; Radžiūtė, L.; Tanaka, M.; Radžiūte, L.; Tanaka, M. Extended Calculations of Energy Levels and Transition Rates of Nd ii-iv Ions for Application to Neutron Star Mergers. Astrophys. J. Suppl. Ser. 2019, 240, 29. [Google Scholar] [CrossRef]
- Blaise, J.; Wyart, J.F. Energy Levels and Atomic Spectra of Actinides; Tables Internationales de Constantes: Paris, France, 1992; p. 479. [Google Scholar]
- Kozlov, M.G.; Porsev, S.G.; Safronova, M.S.; Tupitsyn, I.I. CI-MBPT: A package of programs for relativistic atomic calculations based on a method combining configuration interaction and many-body perturbation theory. Comput. Phys. Commun. 2015, 195, 199–213. [Google Scholar] [CrossRef] [Green Version]
- Hakel, P.; Sherrill, M.E.; Mazevet, S.; Abdallah, J.; Colgan, J.; Kilcrease, D.P.; Magee, N.H.; Fontes, C.J.; Zhang, H.L. The new Los Alamos opacity code ATOMIC. J. Quant. Spectrosc. Radiat. Transf. 2006, 99, 265–271. [Google Scholar] [CrossRef]
- Savukov, I.; Safronova, U.I.; Safronova, M.S. Relativistic configuration interaction plus linearized-coupled-cluster calculations of U2+ energies, g factors, transition rates, and lifetimes. Phys. Rev. A 2015, 92, 052516. [Google Scholar] [CrossRef] [Green Version]
- Safronova, M.S.; Kozlov, M.G.; Johnson, W.R.; Jiang, D. Development of a configuration-interaction plus all-order method for atomic calculations. Phys. Rev. A 2009, 80, 012516. [Google Scholar] [CrossRef] [Green Version]
- Nahar, S. Database NORAD-Atomic-Data for Atomic Processes in Plasma. Atoms 2020, 8, 68. [Google Scholar] [CrossRef]
- Eissner, W. SUPERSTRUCTURE—An atomic code. J. Phys. IV Proc. 1991, 1, C1-3–C1-13. [Google Scholar] [CrossRef] [Green Version]
- Cowan, R.D. The Theory of Atomic Structure and Spectra; University of California Press: Berkeley, CA, USA, 1981; p. 731. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).