Modified Equations of State for Dark Energy and Observational Limitations
Abstract
:1. Introduction
2. Observational Data
| CC Data | Data | ||||||
|---|---|---|---|---|---|---|---|
| Refs | Refs | ||||||
| 0.070 | 69 | 19.6 | Zhang 14 | 0.240 | 79.69 | 2.992 | Gaztañaga 09 |
| 0.090 | 69 | 12 | Simon 05 | 0.30 | 81.7 | 6.22 | Oka 14 |
| 0.120 | 68.6 | 26.2 | Zhang 14 | 0.31 | 78.18 | 4.74 | Wang 17 |
| 0.170 | 83 | 8 | Simon 05 | 0.34 | 83.8 | 3.66 | Gaztañaga 09 |
| 0.1791 | 75 | 4 | Moresco 12 | 0.350 | 82.7 | 9.13 | ChuangW 13 |
| 0.1993 | 75 | 5 | Moresco 12 | 0.36 | 79.94 | 3.38 | Wang 17 |
| 0.200 | 72.9 | 29.6 | Zhang 14 | 0.38 | 81.5 | 1.9 | Alam 17 |
| 0.270 | 77 | 14 | Simon 05 | 0.400 | 82.04 | 2.03 | Wang 17 |
| 0.280 | 88.8 | 36.6 | Zhang 14 | 0.430 | 86.45 | 3.974 | Gaztañaga 09 |
| 0.3519 | 83 | 14 | Moresco 12 | 0.44 | 82.6 | 7.8 | Blake 12 |
| 0.3802 | 83 | 13.5 | Moresco 16 | 0.44 | 84.81 | 1.83 | Wang 17 |
| 0.400 | 95 | 17 | Simon 05 | 0.48 | 87.79 | 2.03 | Wang 17 |
| 0.4004 | 77 | 10.2 | Moresco 16 | 0.51 | 90.4 | 1.9 | Alam 17 |
| 0.4247 | 87.1 | 11.2 | Moresco 16 | 0.52 | 94.35 | 2.64 | Wang 17 |
| 0.445 | 92.8 | 12.9 | Moresco 16 | 0.56 | 93.34 | 2.3 | Wang 17 |
| 0.470 | 89 | 34 | Ratsimbazafy | 0.57 | 87.6 | 7.83 | Chuang 13 |
| 0.4783 | 80.9 | 9 | Moresco 16 | 0.57 | 96.8 | 3.4 | Anderson 14 |
| 0.48 | 97 | 62 | Stern 10 | 0.59 | 98.48 | 3.18 | Wang 17 |
| 0.5929 | 104 | 13 | Moresco 12 | 0.600 | 87.9 | 6.1 | Blake 12 |
| 0.6797 | 92 | 8 | Moresco 12 | 0.61 | 97.3 | 2.1 | Alam 17 |
| 0.75 | 98.8 | 33.6 | Borghi 21 | 0.64 | 98.82 | 2.98 | Wang 17 |
| 0.7812 | 105 | 12 | Moresco 12 | 0.730 | 97.3 | 7.0 | Blake 12 |
| 0.8754 | 125 | 17 | Moresco 12 | 0.8 | 106.9 | 4.9 | Zhu 18 |
| 0.880 | 90 | 40 | Stern 10 | 0.978 | 113.72 | 14.63 | Zhao 19 |
| 0.900 | 117 | 23 | Simon 05 | 1.0 | 120.7 | 7.3 | Zhu 18 |
| 1.037 | 154 | 20.17 | Moresco 12 | 1.230 | 131.44 | 12.42 | Zhao 19 |
| 1.300 | 168 | 17 | Simon 05 | 1.5 | 161.4 | 30.9 | Zhu 18 |
| 1.363 | 160 | 33.6 | Moresco 15 | 1.526 | 148.11 | 12.75 | Zhao 19 |
| 1.430 | 177 | 18 | Simon 05 | 1.944 | 172.63 | 14.79 | Zhao 19 |
| 1.530 | 140 | 14 | Simon 05 | 2.0 | 189.9 | 32.9 | Zhu 18 |
| 1.750 | 202 | 40 | Simon 05 | 2.2 | 232.5 | 54.6; | Zhu 18 |
| 1.965 | 186.5 | 50.4 | Moresco 15 | 2.300 | 224 | 8.57 | Buska 13 |
| 2.330 | 224 | 8.0 | Bautista 17 | ||||
| 2.340 | 222 | 8.515 | Delubac 15 | ||||
| 2.360 | 226 | 9.33 | Font-Ribera 14 | ||||
| 2.40 | 227.6 | 9.10 | Bourboux 17 | ||||
3. Models
4. Results
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ade, P.A.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Riess, A.G.; Casertano, S.; Yuan, W.; Bowers, J.B.; Macri, L.; Zinn, J.C.; Scolnic, D. Cosmic Distances Calibrated to 1% Precision with Gaia EDR3 Parallaxes and Hubble Space Telescope Photometry of 75 Milky Way Cepheids Confirm Tension with ΛCDM. Astrophys. J. Lett. 2021, 908, L6. [Google Scholar] [CrossRef]
- Riess, A.G.; Yuan, W.; Macri, L.M.; Scolnic, D. A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km/s/Mpc Uncertainty from the Hubble Space Telescope and the SH0ES Team. Astrophys. J. Lett. 2021, 908, L6. [Google Scholar]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.M.; Scolnic, D. Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics Beyond LambdaCDM. Astrophys J. 2019, 876, 85. [Google Scholar] [CrossRef]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef] [Green Version]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rept. 2011, 505, 59–144. [Google Scholar] [CrossRef] [Green Version]
- Odintsov, S.D.; Oikonomou, V.K. Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution. Phys. Rept. 2017, 692, 1–104. [Google Scholar]
- Di Valentino, E.; Anchordoqui, L.A.; Ali-Haimoud, Y.; Amendola, L.; Arendse, N.; Asgari, M.; Ballardini, M.; Battistelli, E.; Benetti, M.; Birrer, S. Cosmology Intertwined II: The Hubble Constant Tension. Astropart. Phys. 2021, 131, 102605. [Google Scholar] [CrossRef]
- Di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the Realm of the Hubble tension—A Review of Solutions. Class. Quantum Grav. 2021, 38, 153001. [Google Scholar] [CrossRef]
- Kumar, S.; Nunes, R.C. Probing the interaction between dark matter and dark energy in the presence of massive neutrinos. Phys. Rev. D 2016, 94, 123511. [Google Scholar] [CrossRef] [Green Version]
- Kumar, S.; Nunes, R.C. Echo of interactions in the dark sector. Phys. Rev. D 2017, 96, 103511. [Google Scholar] [CrossRef] [Green Version]
- Pan, S.; Yang, W.; Di Valentino, E.; Saridakis, E.N.; Chakraborty, S. Interacting scenarios with dynamical dark energy: Observational constraints and alleviation of the H0 tension. Phys. Rev. D 2019, 100, 103520. [Google Scholar] [CrossRef] [Green Version]
- Di Valentino, E.; Melchiorri, A.; Mena, O.; Vagnozzi, S. Interacting dark energy in the early 2020s: A promising solution to the H0 and cosmic shear tensions. Phys. Dark Univ. 2020, 30, 100666. [Google Scholar] [CrossRef]
- Pan, S.; Sharov, G.S. A model with interaction of dark components and recent observational data. Mon. Not. R. Astron. Soc. 2017, 472, 4736. [Google Scholar] [CrossRef]
- Pan, S.; Sharov, G.S.; Yang, W. Field theoretic interpretations of interacting dark energy scenarios and recent observations. Phys. Rev. D 2020, 101, 103533. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Saez-Gomez, D.; Sharov, G.S. Testing the equation of state for viscous dark energy. Phys. Rev. D 2020, 101, 044010. [Google Scholar] [CrossRef] [Green Version]
- Odintsov, S.D.; Saez-Gomez, D.; Sharov, G.S. Is exponential gravity a viable description for the whole cosmological history? Eur. Phys. J. C 2017, 77, 862. [Google Scholar] [CrossRef] [Green Version]
- Odintsov, S.D.; Saez-Gomez, D.; Sharov, G.S. Testing logarithmic corrections to R2-exponential gravity by observational data. Phys. Rev. D 2019, 99, 024003. [Google Scholar] [CrossRef] [Green Version]
- Nojiri, S.; Odintsov, S.D.; Saez-Gomez, D.; Sharov, G.S. Modelling and testing the equation of state for (Early) dark energy. Phys. Dark Univ. 2021, 32, 100837. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Saez-Gomez, D.; Sharov, G.S. Analyzing the H0 tension in F(R) gravity models. Nucl. Phys. B 2021, 966, 115377. [Google Scholar] [CrossRef]
- Cooray, A.R.; Huterer, D. Gravitational Lensing as a Probe of Quintessence. Astrophys. J. 1999, 513, L95–L98. [Google Scholar] [CrossRef] [Green Version]
- Chevallier, M.; Polarski, D. Accelerating Universes with Scaling Dark Matter. Int. J. Mod. Phys. D 2001, 10, 213–224. [Google Scholar] [CrossRef] [Green Version]
- Linder, E.V. Exploring the expansion history of the universe. Phys. Rev. Lett. 2003, 90, 091301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barboza, E.M.; Alcaniz, J.S.; Zhu, Z.-H.; Silva, R. A generalized equation of state for dark energy. Phys. Rev. D 2009, 80, 043521. [Google Scholar] [CrossRef]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The Complete Light-curve Sample of Spectroscopically Confirmed Type Ia Supernovae from Pan-STARRS1 and Cosmological Constraints from The Combined Pantheon Sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Chen, L.; Huang, Q.-G.; Wang, K. Distance priors from Planck final release. J. Cosmol. Astropart. Phys. 2019, 1902, 028. [Google Scholar] [CrossRef] [Green Version]
- Nesseris, S.; Perivolaropoulos, L. Comparison of the legacy and gold SN Ia dataset constraints on dark energy models. Phys. Rev. D 2005, 72, 123519. [Google Scholar] [CrossRef] [Green Version]
- Efstathiou, G. To H0 or not to H0? Mon. Not. R. Astron. Soc. 2021, 505, 3866–3872. [Google Scholar] [CrossRef]
- Camarena, D.; Marra, V. On the use of the local prior on the absolute magnitude of Type Ia supernovae in cosmological inference. Mon. Not. R. Astron. Soc. 2021, 504, 5164–5171. [Google Scholar] [CrossRef]
- Nunes, R.C.; Di Valentino, E. Dark sector interaction and the supernova absolute magnitude tension. Phys. Rev. D 2021, 104, 063529. [Google Scholar] [CrossRef]
- Hu, W.; Sugiyama, N. Small Scale Cosmological Perturbations: An Analytic Approach. Astrophys. J. 1996, 471, 542–570. [Google Scholar] [CrossRef] [Green Version]
- Sharov, G.S.; Sinyakov, E.S. Cosmological models, observational data and tension in Hubble constant. Math. Model. Geom. 2020, 8, 1–20. [Google Scholar] [CrossRef]
- Simon, J.; Verde, L.; Jimenez, R. Constraints on the redshift dependence of the dark energy potential. Phys. Rev. D. 2005, 71, 123001. [Google Scholar] [CrossRef] [Green Version]
- Stern, D.; Jimenez, R.; Verde, L.; Kamionkowski, M.; Stanford, S.A. Cosmic Chronometers: Constraining the Equation of State of Dark Energy. I: H(z) Measurements. JCAP 2010, 1002, 008. [Google Scholar] [CrossRef] [Green Version]
- Moresco, M.; Cimatti, A.; Jimenez, R.; Pozzetti, L.; Zamorani, G.; Bolzonella, M.; Dunlop, J.; Lamareille, F.; Mignoli, M.; Pearce, H.; et al. Improved constraints on the expansion rate of the Universe up to z∼1.1 from the spectroscopic evolution of cosmic chronometers. JCAP 2012, 1208, 006. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Zhang, H.; Yuan, S.; Zhang, T.-J.; Sun, Y.-C. Four New Observational H(z) Data From Luminous Red Galaxies Sloan Digital Sky Survey Data Release Seven. Res. Astron. Astrophys. 2014, 14, 1221. [Google Scholar] [CrossRef] [Green Version]
- Moresco, M. Raising the bar: New constraints on the Hubble parameter with cosmic chronometers at z∼2. Mon. Not. R. Astron. Soc. 2015, 450, L16. [Google Scholar] [CrossRef] [Green Version]
- Moresco, M.; Pozzetti, L.; Cimatti, A.; Jimenez, R.; Maraston, C.; Verde, L.; Thomas, D.; Citro, A.; Tojeiro, R.; Wilkinson, D. A 6% measurement of the Hubble parameter at z∼0.45: Direct evidence of the epoch of cosmic re-acceleration. JCAP 2016, 1605, 014. [Google Scholar] [CrossRef] [Green Version]
- Ratsimbazafy, A.L.; Loubser, S.I.; Crawford, S.M.; Cress, C.M.; Bassett, B.A.; Nichol, R.C.; Väisänen, P. Age-dating Luminous Red Galaxies observed with the Southern African Large Telescope. Mon. Not. R. Astron. Soc. 2017, 467, 3239. [Google Scholar] [CrossRef] [Green Version]
- Borghi, N.; Moresco, M.; Cimatti, A. Towards a Better Understanding of Cosmic Chronometers: A new measurement of H(z) at z=0.7. arXiv 2021, arXiv:2110.04304. [Google Scholar] [CrossRef]
- Moresco, M.; Jimenez, R.; Verde, L.; Cimatti, A.; Lucia Pozzetti, L. Setting the Stage for Cosmic Chronometers. II. Impact of Stellar Population Synthesis Models Systematics and Full Covariance Matrix. Astrophys. J. 2020, 898, 82. [Google Scholar] [CrossRef]
- Moresco, M.; Amati, L.; Amendola, L.; Birrer, S.; Blakeslee, J.P.; Cantiello, M.; Cimatti, A.; Darling, J.; Valle, M.D.; Fishbach, M.; et al. Unveiling the Universe with Emerging Cosmological Probes. Astrophys. J. 2020, 898, 82. [Google Scholar] [CrossRef]
- Gaztañaga, E.; Cabre, A.; Hui, L. Clustering of Luminous Red Galaxies IV: Baryon Acoustic Peak in the Line-of-Sight Direction and a Direct Measurement H(z). Mon. Not. Roy. Astron. Soc. 2009, 399, 1663. [Google Scholar] [CrossRef] [Green Version]
- Blake, C.; Brough, S.; Colless, M.; Contreras, C.; Couch, W.; Croom, S.; Croton, D.; Davis, T.M.; Drinkwater, M.J.; Forster, K.; et al. The WiggleZ Dark Energy Survey: Joint measurements of the expansion and growth history at z<1. Mon. Not. R. Astron. Soc. 2012, 425, 405. [Google Scholar]
- Chuang, C.-H.; Wang, Y. Modeling the Anisotropic Two-Point Galaxy Correlation Function on Small Scales and Improved Measurements of H(z), DA(z), and f(z)σ8(z) from the Sloan Digital Sky Survey DR7 Luminous Red Galaxies. Mon. Not. R. Astron. Soc. 2013, 435, 255. [Google Scholar] [CrossRef] [Green Version]
- Chuang, C.-H.; Prada, F.; Cuesta, A.J.; Eisenstein, D.J.; Kazin, E.; Padmanabhan, N.; Sánchez, A.G.; Xu, X.; Beutler, F.; Manera, M.; et al. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Single-probe measurements and the strong power of f(z)σ8(z) on constraining dark energy. Mon. Not. R. Astron. Soc. 2013, 433, 3559. [Google Scholar] [CrossRef]
- Busca, N.G.; Delubac, T.; Rich, J.; Bailey, S.; Font-Ribera, A.; Kirkby, D.; Le Goff, J.-M.; Pieri, M.M.; Slosar, A.; Aubourg, E.; et al. Baryon Acoustic Oscillations in the Lyα forest of BOSS quasars. Astron. Astrophys. 2013, 552, A96. [Google Scholar] [CrossRef] [Green Version]
- Oka, A.; Saito, S.; Nishimichi, T.; Taruya, A.; Yamamoto, K. Simultaneous constraints on the growth of structure and cosmic expansion from the multipole power spectra of the SDSS DR7 LRG sample. Mon. Not. R. Astron. Soc. 2014, 439, 2515–2530. [Google Scholar] [CrossRef]
- Font-Ribera, A.; Kirkby, D.; Busca, N.; Miralda-Escudé, J.; Ross, N.P.; Slosar, A.; Rich, J.; Aubourg, E.; Bailey, S.; Bhardwaj, V.; et al. Quasar-Lyman α Forest Cross-Correlation from BOSS DR11: Baryon Acoustic Oscillations. J. Cosmol. Astropart. Phys. 2014, 2014, 027. [Google Scholar] [CrossRef]
- Delubac, T.; Bautista, J.E.; Busca, N.G.; Rich, J.; Kirkby, D.; Bailey, S.; Font-Ribera, A.; Slosar, A.; Lee, K.-G.; Pieri, M.M.; et al. Baryon Acoustic Oscillations in the Lyα forest of BOSS DR11 quasars. Astron. Astrophys. 2015, 574, A59. [Google Scholar] [CrossRef] [Green Version]
- Anderson, L.; Aubourg, E.; Bailey, S.; Beutler, F.; Bhardwaj, V.; Blanton, M.; Bolton, A.S.; Brinkmann, J.; Brownstein, J.R.; Burden, A.; et al. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Baryon Acoustic Oscillations in the Data Release 10 and 11 Galaxy Samples. Mon. Not. R. Astron. Soc. 2014, 441, 24. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Zhao, G.-B.; Chuang, C.-H.; Ross, A.J.; Percival, W.J.; Gil-Martín, H.; Cuesta, A.J.; Kitaura, F.-S.; Rodriguez-Torres, S.; Brownstein, J.R.; et al. The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Tomographic BAO analysis of DR12 combined sample in configuration space. Mon. Not. R. Astron. Soc. 2017, 469, 3762. [Google Scholar] [CrossRef]
- Alam, S.; Ata, M.; Bailey, S.; Beutler, F.; Bizyaev, D.; Blazek, J.A.; Bolton, A.S.; Brownstein, J.R.; Burden, A.; Chuang, C.-H.; et al. The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Cosmological analysis of the DR12 galaxy sample. Mon. Not. R. Astron. Soc. 2017, 470, 2617. [Google Scholar] [CrossRef] [Green Version]
- Bautista, J.E.; Busca, N.G.; Guy, J.; Rich, J.; Blomqvist, M.; Bourboux, H.M.; Pieri, M.M.; Font-Ribera, A.; Bailey, S.; Delubac, T.; et al. Measurement of baryon acoustic oscillation correlations at z=2.3 with SDSS DR12 Lyα-Forests. Astron. Astrophys. 2017, 603, A12. [Google Scholar] [CrossRef] [Green Version]
- Bourboux, H.; Le Goff, J.-M.; Blomqvist, M.; Busca, N.G.; Guy, J.; Rich, J.; Yèche, C.; Bautista, J.E.; Burtin, E.; Dawson, K.S.; et al. Baryon acoustic oscillations from the complete SDSS-III Lyα-quasar cross-correlation function at z=2.4. Astron. Astrophys. 2017, 608, A130. [Google Scholar] [CrossRef] [Green Version]
- Zhu, F.; Padmanabhan, N.; Ross, A.J.; White, M.; Percival, W.J.; Ruggeri, R.; Zhao, G.-B.; Wang, D.; Mueller, E.-M.; Burtin, E.; et al. The clustering of the SDSS-IV extended Baryon Oscillation Spectroscopic Survey DR14 quasar sample: Measuring the anisotropic Baryon Acoustic Oscillations with redshift weights. Mon. Not. R. Astron. Soc. 2018, 480, 1096. [Google Scholar] [CrossRef] [Green Version]
- Zhao, G.-B.; Wang, Y.; Saito, S.; Gil-Martín, H.; Percival, W.J.; Wang, D.; Chuang, C.-H.; Ruggeri, R.; Mueller, E.-M.; Zhu, F.; et al. The clustering of the SDSS-IV extended Baryon Oscillation Spectroscopic Survey DR14 quasar sample: Tomographic measurement of cosmic structure growth and expansion rate based on optimal redshift weights. Mon. Not. R. Astron. Soc. 2019, 482, 3497. [Google Scholar] [CrossRef] [Green Version]
- Ade, P.A.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2013 results. XVI. Cosmological parameters. Astron. Astrophys. 2014, 571, A16. [Google Scholar]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
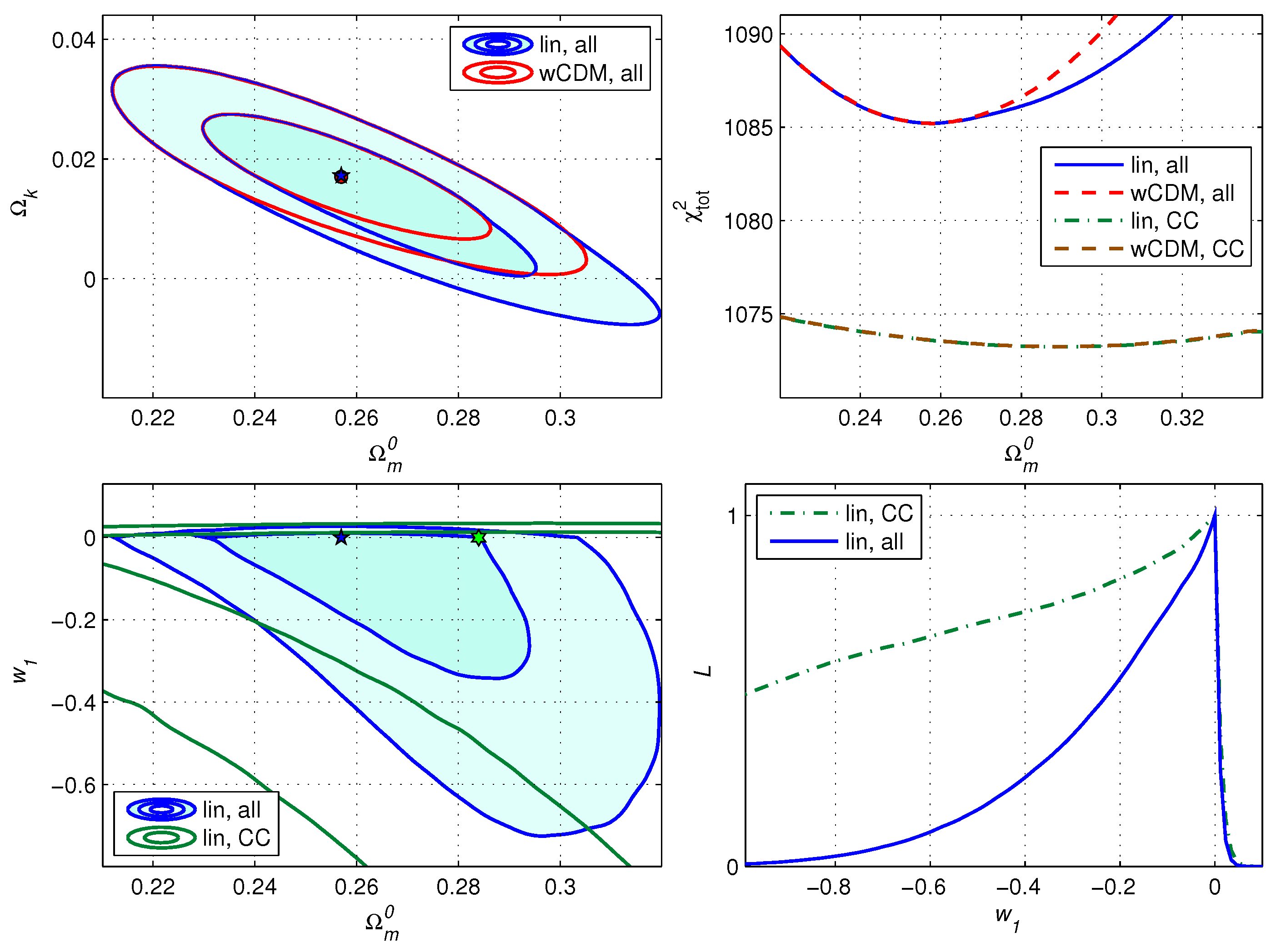
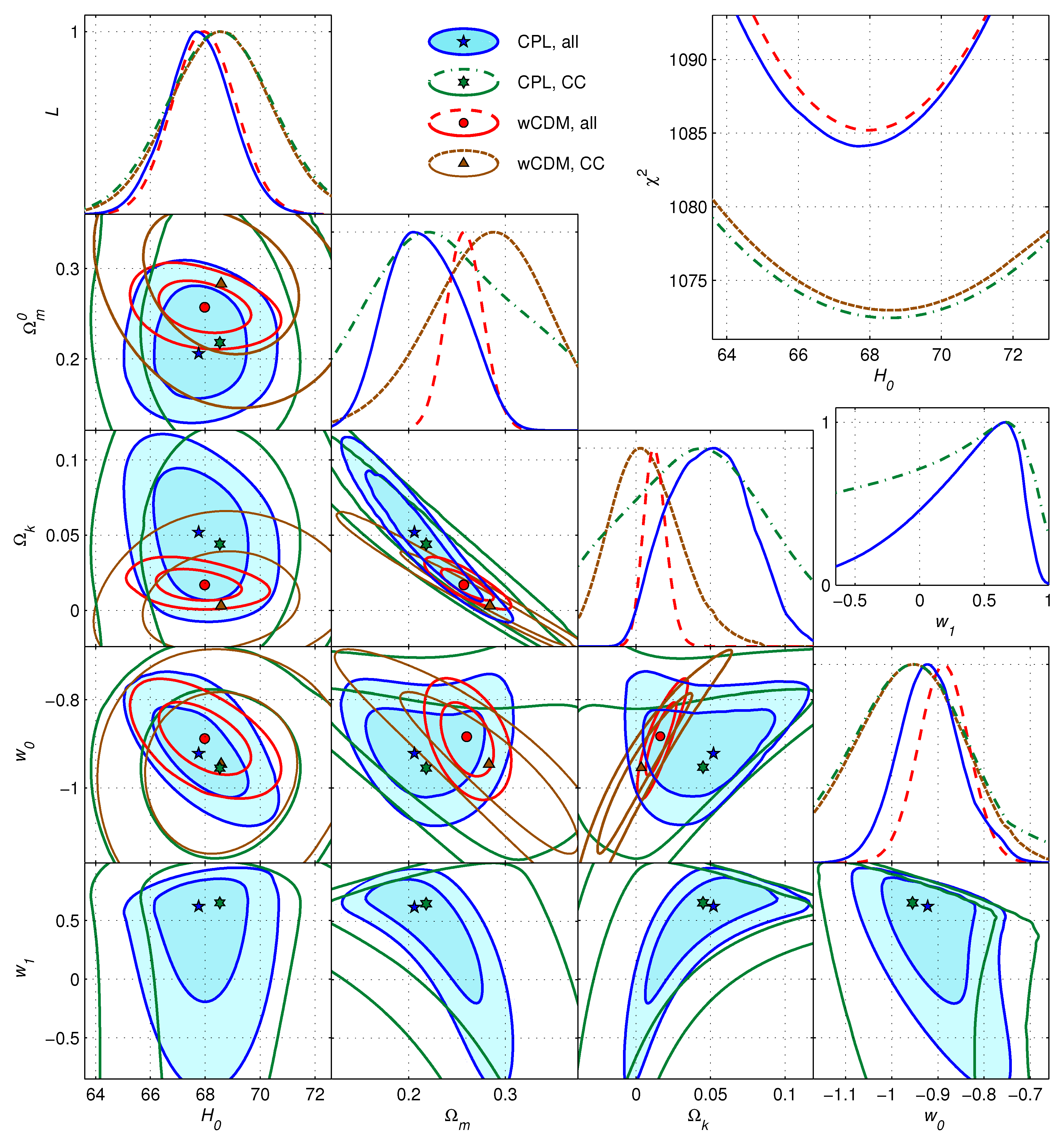
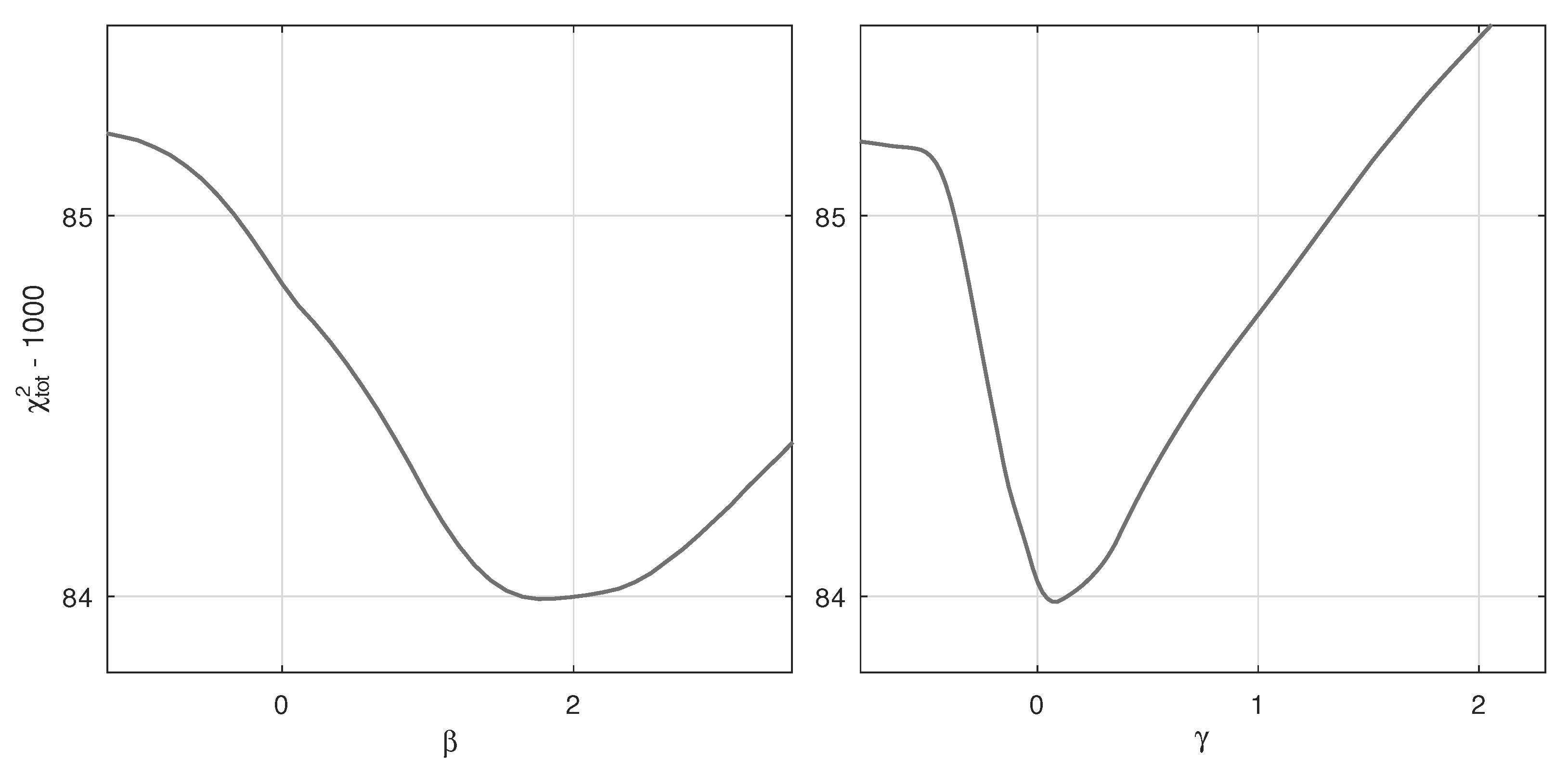
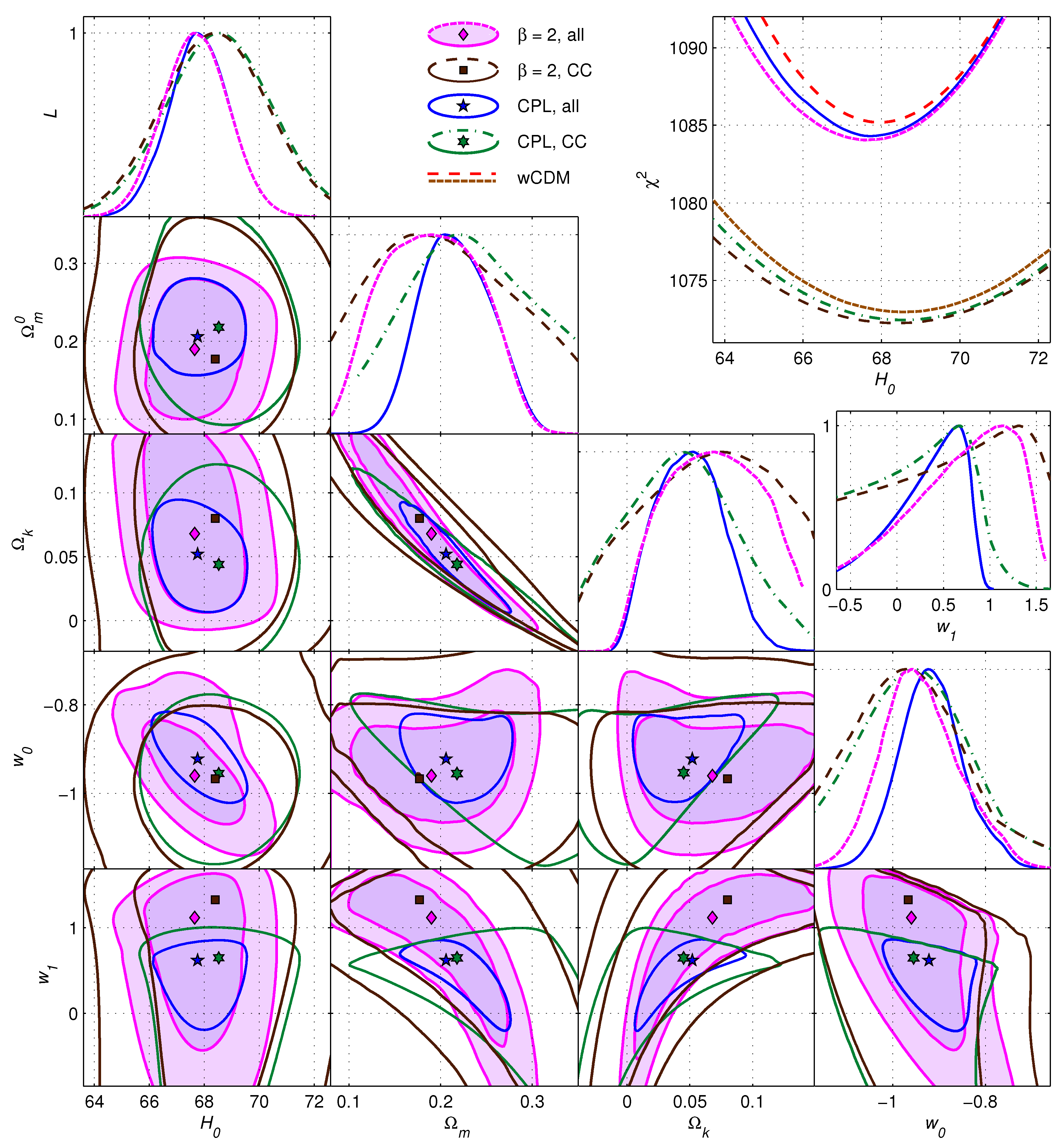

| Model | Data | ||||||
|---|---|---|---|---|---|---|---|
| CC | |||||||
| CPL | CC | ||||||
| CDM | CC | - | |||||
| CDM | CC | - | |||||
| all | |||||||
| CPL | all | ||||||
| CDM | all | - | |||||
| CDM | all | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharov, G.S.; Myachin, V.E. Modified Equations of State for Dark Energy and Observational Limitations. Universe 2022, 8, 201. https://doi.org/10.3390/universe8040201
Sharov GS, Myachin VE. Modified Equations of State for Dark Energy and Observational Limitations. Universe. 2022; 8(4):201. https://doi.org/10.3390/universe8040201
Chicago/Turabian StyleSharov, German S., and Vasily E. Myachin. 2022. "Modified Equations of State for Dark Energy and Observational Limitations" Universe 8, no. 4: 201. https://doi.org/10.3390/universe8040201
APA StyleSharov, G. S., & Myachin, V. E. (2022). Modified Equations of State for Dark Energy and Observational Limitations. Universe, 8(4), 201. https://doi.org/10.3390/universe8040201






