Abstract
We study neutrino propagation in a curved spacetime background described by the Schwarzschild solution with the addition of quantum corrections evaluated in the framework of perturbative quantum gravity at lowest order. In particular, we investigate neutrino oscillations and decoherence within the Gaussian wave packet description, finding that quantum gravity corrections significantly affect the intrinsic features of mixed particles and induce potentially measurable physical effects.
1. Introduction
Flavor mixing has become a frontier field of research in the physics of elementary particles ever since the experimental discovery of neutrinos more than sixty years ago [1,2]. Neutrinos’ non-vanishing mass, flavor mixing and oscillations provide some of the most important instances of phenomena that the Standard Model of elementary particle physics cannot account for [3]. Although some basic puzzles in the physics of neutrinos have been resolved, especially since the solar neutrino problem [4,5,6,7] has been understood and explained in terms of the neutrino oscillation mechanism [8,9] together with the MSW effect [10,11], some fundamental questions remain unanswered, such as whether neutrinos are Dirac or Majorana fermions.1 Another important open issue concerns the impossibility of relating the flavor and the mass bases by means of unitary transformations in the framework of quantum field theory [13,14,15,16,17,18].
Starting from the seminal investigations on matter interferometry in the presence of gravity [19] and the ensuing applications of such a formalism to the case of mixed particles (see the works [20,21,22,23] and references therein), a fundamental research branch relates to the fate of flavor mixing and neutrino oscillations when gravitational effects are taken into account. The possibility of providing a general prescription on neutrino oscillations that applies to any generic spacetime background was investigated in Refs. [24,25]. These studies have naturally inspired a significant number of developments, both in the context of general relativity [26,27,28,29,30] and in the framework of extended models of the gravitational interaction [31,32,33,34,35]. Moreover, studying the intertwining between flavor mixing and gravity may provide pivotal insights on the fundamental principles that lie at the heart of general relativity, such as general covariance [36,37,38,39,40,41] and the equivalence principle [28]. Indeed, concerning the former issue, it is known that the fulfillment of general covariance in the context of the inverse decay (i.e., the decay of an accelerated proton) is preserved even when the produced particles undergo flavor mixing, thus confirming that general covariance itself can still be deemed as a viable guiding principle in quantum field theory. At the same time, the above picture has a significant impact on the Unruh effect as well, since it provides for the first time both a theoretical check and an unambiguous explanation for such a phenomenon. On the other hand, regarding the latter case, it has been proved that, in the non-relativistic limit, flavor particles violate the weak formulation of the equivalence principle. The source of the violation amounts to a redefinition of the inertial mass which does not occur for the gravitational mass, thereby pointing towards a novel rephrasing of the equivalence principle in the quantum domain. From an astrophysical point of view, instead, neutrino fluxes expelled during star core collapses may represent a valuable information carrier [42,43,44,45], whereas heavy sterile neutrinos are plausible candidates for dark matter and dark energy [46,47]. In passing, it is also worth mentioning that some feasible scenarios for experimentally testing the quantum nature of the gravitational interaction involve schemes based on neutrino oscillations [48]. For a detailed overview of these and other related topics, the interested reader can consult Ref. [49].
In the present work, by exploiting the wave packet representation of flavor mixing, we will discuss gravitationally induced decoherence processes, another important trait of elementary particle physics in curved backgrounds. Specifically, by resorting to the non-covariant Gaussian wave packet description proposed in Refs. [50,51] and further developed in Refs. [52,53,54], we analyze the behavior of neutrino propagation and oscillations from the viewpoint of a locally inertial observer in a Schwarzschild spacetime which accounts for the leading perturbative quantum corrections to the classical gravitational potential. In such a picture, one considers general relativity as an effective field theory, which thus allows us to neglect all the unknown terms arising at high energies [55,56,57]. As our investigation is specific to neutrinos propagating in a weak gravitational field, the perturbative approach to quantum gravity outlined by Donoghue in Refs. [55,56,57] is particularly well-suited in order to emulate as much as possible an experimental setting in our Solar system.
The paper is organized as follows: in Section 2 we briefly review the Gaussian wave packet description of particle mixing. In Section 3 we introduce the metric of the quantum-corrected Schwarzschild spacetime in the weak-field limit and explore how it affects wave packet decoherence in the case of two-flavor mixing. Finally, in Section 4 we discuss our results and comment on future research directions.
Throughout the paper, we use Planck units and the mostly-positive signature convention for the metric .
2. Neutrino States in the Wave Packet Approximation
It is well known that flavor neutrinos can be regarded as a superposition of states with definite mass [3]. If we assume the mixed particle to be produced at a given point P, the ensuing state can be written as
with being the element of the complex conjugate Pontecorvo–Maki–Nakagawa–Sakata matrix [3] and , denoting the flavor and mass index, respectively. Mass states propagate freely in space; hence, it is straightforward to verify that their spatial and temporal variation after having introduced a “detection” point is given by the application of the usual evolution operator
where, in a curved background, we can recognize the covariant quantum phase [19]
Here, is the j-th four-momentum defined along the traveled path, that is
with indicating the j-th mass that enters the on-shell mass relation .
In order to take into account the presence of wave packets, we must modify Equation (1) so as to include a further term that ensures the localization of the system; specifically, at the starting point P, we see that
According to the non-covariant Gaussian prescription [52,53], we require a shape for our j-th wave packet that is peaked around a given value in momentum space. Therefore, we observe that
where
represents the j-th non-covariant Gaussian wave packet, normalized in such a way that
In the previous equation, defines the center of the peak, whereas is the width of the Gaussian function. Finally, the evolved flavor state that accounts for both Equations (2) and (5) can be written as2
Next, we introduce the corresponding density matrix as a projector [52]:
In order to proceed, we now need to define the metric that describes the curved background on which the neutrino propagation takes place.
3. Wave Packet Decoherence in a Quantum Schwarzschild Spacetime
In the following, we consider the quantum-corrected Schwarzschild metric written in isotropic spherical coordinates and in the weak-field limit. To better convey the relevance of quantum corrections, for the definition of the metric tensor we momentarily restore the standard units, thereby allowing for the appearance of ℏ, c and G. Under these circumstances, it is possible to show that the line element takes the form [55,56,57]
where and
is the quantum-corrected gravitational potential arising from treating general relativity as an effective field theory [55,56,57]. At this stage, post-Newtonian terms that go up to do not play a relevant role for the quantitative estimation of quantum gravitational effects, and therefore have been neglected in Equation (12).
Without loss of generality, we can restrict the attention to a neutrino propagating along the radial direction in the equatorial plane (i.e., and ). In this case, the non-vanishing components of the four-momentum defined in Equation (4) take the form3
where is the energy of the j-th mass eigenstate, which is a conserved quantity along the trajectory due to the fact that we are working with a static metric tensor. By resorting to the on-shell mass relation, we now observe that
which, together with Equation (13), allows us to deduce
Knowledge of such an expression is useful because it can be exploited to simplify the formula of the covariant phase (3). As a matter of fact, by recalling the choice of radial motion in the equatorial plane and Equation (13), we have
Assuming relativistic neutrinos, it is justified to require [52]. In this regime, the above equation becomes
By means of a straightforward integration, we obtain
where
In line with what has been showed in Refs. [52,53,54] and with the purpose of streamlining the upcoming calculations, we can expand the j-th energy component around the value , which is the center of the peak of the Gaussian distribution in momentum space. This procedure amounts to neglecting the intrinsic temporal spreading of the wave packet during neutrino propagation; in our case, such effect has no relevant consequences on neutrino coherence [52,53,54]. In light of the above, we can write at first order:
where and is the group velocity of the j-th mass eigenstate wave packet, whose magnitude in the relativistic regime is given by [53]:
with E being the average transition energy between the j-th and the k-th mass eigenstate.
In order to evaluate the flavor transition probability as well as the decoherence transition rates, we need to determine the analytic form of the quantity in Equation (10). To this aim, we first notice that, due to the magnitude of the velocities (21) and to the approximations made so far, we can fix the detection point for all the mass eigenstates at the same location , . This is related to the fact that the spreading of the wave packet is negligible for our current analysis, thereby preventing two distinct mass eigenstates from reaching a different location at the end of the propagation.
Similar considerations allow for a substantial simplification of the difference that enters directly in the definition of . In analogy with the procedure developed for the j-th mass eigenstate, by assuming
we obtain
with
We can now evaluate by means of an integration over momenta; by recalling Equations (6), (9) and (10), we have
where we have used the compact notation . Solving the integral yields
in which we recognize .
In typical oscillation experiments, neutrino decoherence turns out to be a function of the distance only [52,53]. Therefore, by integrating the previous expression over time we obtain
Finally, applying a Gaussian integration, we obtain as the product of three distinct contributions, i.e.,
In the above expression, the first factor
is a quantity that does not affect flavor oscillations, whilst the latter is associated to the factor
where we have defined . For our purposes, the relevant contribution is the third factor in Equation (28), i.e., , which contains the information on the damping process, and thus on the decoherence taking place during neutrino propagation. If we cast the result as a function of the leading-order term in , we obtain
In order to provide a meaningful interpretation of this result, we shall recast all the quantities in Equation (31) as functions of the physical quantities, including the physical distance between the initial and final points (which does not coincide with ) and the energy as measured by a local inertial observer who is at rest with respect to the neutrino propagation. We can carry out such reformulation by resorting to the tetrad fields associated with the line element (11). Tetrads allow to move from a general coordinate system to a locally inertial reference frame. Indeed, they are defined by the relation
where is the metric tensor belonging to the Riemannian manifold and is the Minkowski metric acting on the flat space tangent to the manifold at the given point x. To distinguish the indexes related to the flat space from the ones labeling the manifold, the former have been denoted with a hat. For a pedagogical introduction of tetrad fields, we refer the reader to Ref. [58].
Because of the form of the metric tensor in Equation (11), it is easy to verify that in our case
while all other combinations vanish. We can now observe that the energy E and the “local” energy are related by the following relation [24,25]:
whereas the physical distance L in a curved spacetime is defined as
By virtue of Equations (34) and (35), it is possible to cast Equation (31) in the weak-field limit as a function of physical parameters only, namely and L; explicitly, we have
The overall factor in the above expression is simply the zeroth-order approximation that describes the neutrino wave packet decoherence in flat spacetime [53]. The second term in the square brackets is the Schwarzschild-like gravitational contribution which is responsible for either an attenuation or a boosting of the damping process depending on the direction of the neutrino propagation [54]. The third term quantifies the damping effect produced by the quantum correction to the Schwarzschild potential. Both terms produce a suppression of the decoherence when the neutrino moves away from the gravitational source, i.e., ; vice versa, they both produce an enhancement of the decoherence when the neutrino approaches the source, i.e., . Finally, the last factor is irrelevant, as it simply shifts the zeroth-order term according to the chosen value of .
To provide a concrete idea of the difference in magnitude between the classical gravitational term and the quantum-corrected one appearing in the square brackets of Equation (36), we introduce the following quantities:
where we have restored standard units so as to let ℏ, c and G explicitly appear in the expression. We can then study the ratio as a function of the physical distance traveled by the neutrino. Because of the approximation we are currently considering, in generating the plot we fix and assume , since by taking the full expression (35) we would not gather an appreciable effect from the behavior of the curve. The results of the above analysis are summarized graphically in Figure 1.
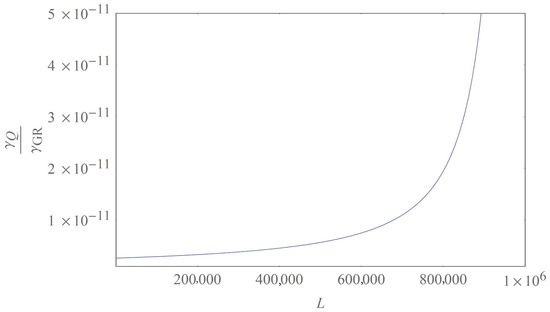
Figure 1.
Behavior of the ratio as a function of the physical distance L traveled by a propagating neutrino in the interval at the sample values , and . Should we restore the standard units, the above ratio would be further reduced by a factor equal to the squared Planck length .
As the figure shows, in the regime of weak gravitational fields the quantum corrections to the decoherence process occurring in a Schwarzschild spacetime are extremely small, but they still contribute to an overall enhancement or attenuation of the damping mechanism depending on the direction of the neutrino propagation. Clearly, an increase in the traveled distance L while keeping fixed translates in a narrowing of the gap between the starting position P and the gravitational source, thereby excluding the use of the weak-field approximation. On the other hand, this finding confirms that quantum gravity effects become more relevant as the regime of strong gravitational interaction is approached.
4. Discussion
We have investigated neutrino wave packet decoherence taking place in a spacetime described by a quantum-corrected Schwarzschild solution. By resorting to a non-covariant Gaussian wave packet description, we have seen how the density matrix associated with the propagating neutrino can be expressed as the product of two factors, one responsible for the flavor oscillation and one which governs the decoherence mechanism. In the analysis of the latter factor, we have cast the distances and the energies appearing in its expression as a function of the physical quantities, namely, the effective traveled length and the neutrino energy as measured by an inertial observer locally at rest. In so doing, we have obtained Equation (36), where we have been able to single out several contributions, each of which has a different origin. Apart from the distinctive damping term related to the Schwarzschild solution, we have isolated the relevant quantum gravitational contribution to leading order, addressing it as a parameter , which has a purely quantum nature and represents the implication of the one-loop correction stemming from treating general relativity as an effective field theory.
Since the gravitational decoherence of neutrino wave packets may potentially be tested, probing can grant access to the quantum nature of gravity via the corrections that we have identified in Equation (36). Of course, as Figure 1 conveys explicitly, the deviations from the standard Schwarzschild scenario appear to be extremely small, but one could spot a favorable window where to search for quantum gravitational effects by suitably tuning the traveled length of the mixed particle. Therefore, the results of the present work provide a further tool towards a comprehensive strategy to detect signatures of quantum gravity via the quantum wave packet analysis [59,60,61].
On a final note, we want to stress that, in order not to fine-tune the distance traveled by neutrinos while still attempting to magnify the quantum gravitational impact on wave packet decoherence, the most suitable environment where to search for such tiny signatures should in principle be characterized by extreme astrophysical conditions. As a matter of fact, in these scenarios it is expected that the implications of quantum gravity would be so significant that no low-energy approximation is required. To further corroborate the above statement, we point out that many examples along this direction can be encountered in literature. For instance, in the context of loop quantum gravity, the existence of primordial black holes which follow the laws of quantum gravity can be inferred by studying fast radio bursts [62] and other astrophysical signals [63]. Concerning standard black holes, in the framework of string theory it is argued that such celestial bodies are nothing but ultra-compact objects made up of strings (the so-called fuzzballs [64,65]). The peculiar nature of these physical entities is responsible for a huge number of features that renders them different from black holes, ranging from their multipolar structure [66] to ringdown, quasi-normal modes and echoes [67]. Finally, the thorough analysis of gamma ray bursts may shed light on the possibility of breaking Lorentz invariance while approaching the Planck scale, as envisaged by doubly special relativity [68,69].
Author Contributions
L.P. performed calculations and drafted the paper. F.I. and G.L. supervised the work. All authors discussed the results and edited the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Notes
| 1 | In this direction, a hypothetical observation of the neutrinoless double- decay would definitively settle the conundrum; for an updated review on this topic, see Ref. [12]. |
| 2 | For notational simplicity, we denote the dependence of a generic function as . |
| 3 | Note that the dependence of V on the radial coordinate will henceforth be taken for granted, and thus omitted. Furthermore, starting from here we also restore Planck units. |
References
- Reines, F.; Cowan, C.L. Detection of the free neutrino. Phys. Rev. 1953, 92, 830. [Google Scholar] [CrossRef] [Green Version]
- Cowan, C.L.; Reines, F.; Harrison, F.B.; Kruse, H.W.; McGuire, A.D. Detection of the free neutrino: A Confirmation. Science 1956, 124, 103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bilenky, S.M.; Pontecorvo, B. Lepton Mixing and Neutrino Oscillations. Phys. Rep. 1978, 41, 225–261. [Google Scholar] [CrossRef]
- Fukuda, Y.; Hayakawa, T.; Ichihara, E.; Inoue, K.; Ishihara, K.; Ishino, H.; Itow, Y.; Kajita, T.; Kameda, J.; Kasuga, S.; et al. Evidence for oscillation of atmospheric neutrinos. Phys. Rev. Lett. 1998, 81, 1562. [Google Scholar] [CrossRef] [Green Version]
- Fukuda, Y.; Hayakawa, T.; Ichihara, E.; Inoue, K.; Ishihara, K.; Ishino, H.; Itow, Y.; Kajita, T.; Kameda, J.; Kasuga, S.; et al. Measurements of the solar neutrino flux from Super-Kamiokande’s first 300 days. Phys. Rev. Lett. 1998, 81, 1158. [Google Scholar] [CrossRef] [Green Version]
- Ahn, M.H.; Aoki, S.; Bhang, H.; Boyd, S.; Casper, D.; Choi, J.H.; Fukuda, S.; Fukuda, Y.; Gajewski, W.; Hara, T.; et al. Indications of neutrino oscillation in a 250 km long baseline experiment. Phys. Rev. Lett. 2003, 90, 041801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ashie, Y.; Hosaka, J.; Ishihara, K.; Itow, Y.; Kameda, J.; Koshio, Y.; Minamino, A.; Mitsuda, C.; Miura, M.; Moriyama, S.; et al. Evidence for an oscillatory signature in atmospheric neutrino oscillation. Phys. Rev. Lett. 2004, 93, 101801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Giunti, C.; Kim, C.W. Fundamentals of Neutrino Physics and Astrophysics; Oxford Univ. Press: Oxford, UK, 2007. [Google Scholar]
- Kleinert, H. Particles and Quantum Fields; World Scientific: Singapore, 2016. [Google Scholar]
- Wolfenstein, L. Neutrino Oscillations in Matter. Phys. Rev. D 1978, 17, 2369. [Google Scholar] [CrossRef]
- Mikheyev, S.P.; Smirnov, A. Resonance Amplification of Oscillations in Matter and Spectroscopy of Solar Neutrinos. Sov. J. Nucl. Phys. 1985, 42, 913. [Google Scholar]
- Dolinski, M.J.; Poon, A.W.P.; Rodejohann, W. Neutrinoless Double-Beta Decay: Status and Prospects. Ann. Rev. Nucl. Part. Sci. 2019, 69, 219. [Google Scholar] [CrossRef] [Green Version]
- Blasone, M.; Vitiello, G. Quantum field theory of fermion mixing. Ann. Phys. 1995, 244, 283–311. [Google Scholar] [CrossRef] [Green Version]
- Fujii, K.; Habe, C.; Yabuki, T. Note on the field theory of neutrino mixing. Phys. Rev. D 1999, 59, 113003. [Google Scholar] [CrossRef] [Green Version]
- Hannabuss, K.C.; Latimer, D.C. The quantum field theory of fermion mixing. J. Phys. A 2000, 33, 1369. [Google Scholar] [CrossRef]
- Blasone, M.; Jizba, P.; Smaldone, L. Generalized generating functional for mixed-representation Green’s functions: A quantum mechanical approach. Phys. Rev. A 2017, 96, 052107. [Google Scholar] [CrossRef] [Green Version]
- Blasone, M.; Luciano, G.G.; Petruzziello, L.; Smaldone, L. Casimir effect for mixed fields. Phys. Lett. B 2018, 786, 278. [Google Scholar] [CrossRef]
- Blasone, M.; Illuminati, F.; Luciano, G.G.; Petruzziello, L. Flavor vacuum entanglement in boson mixing. Phys. Rev. A 2021, 103, 032434. [Google Scholar] [CrossRef]
- Stodolsky, L. Matter and Light Wave Interferometry in Gravitational Fields. Gen. Rel. Grav. 1979, 11, 391. [Google Scholar] [CrossRef]
- Ahluwalia, D.V.; Burgard, C. Gravitationally induced quantum mechanical phases and neutrino oscillations in astrophysical environments. Gen. Rel. Grav. 1996, 28, 1161. [Google Scholar] [CrossRef]
- Kojima, Y. Gravitational correction in neutrino oscillations. Mod. Phys. Lett. A 1996, 11, 2965. [Google Scholar] [CrossRef] [Green Version]
- Piriz, D.; Roy, M.; Wudka, J. Neutrino oscillations in strong gravitational fields. Phys. Rev. D 1996, 54, 1587. [Google Scholar] [CrossRef] [Green Version]
- Lambiase, G.; Papini, G.; Punzi, R.; Scarpetta, G. Neutrino optics and oscillations in gravitational fields. Phys. Rev. D 2005, 71, 073011. [Google Scholar] [CrossRef] [Green Version]
- Cardall, C.Y.; Fuller, G.M. Neutrino oscillations in curved spacetime: An Heuristic treatment. Phys. Rev. D 1997, 55, 7960. [Google Scholar] [CrossRef] [Green Version]
- Fornengo, N.; Giunti, C.; Kim, C.W.; Song, J. Gravitational effects on the neutrino oscillation. Phys. Rev. D 1997, 56, 1895. [Google Scholar] [CrossRef] [Green Version]
- Singh, P.; Mukhopadhyay, B. Gravitationally induced neutrino asymmetry. Mod. Phys. Lett. A 2003, 18, 779. [Google Scholar] [CrossRef] [Green Version]
- Mukhopadhyay, B. Neutrino asymmetry around black holes: Neutrinos interact with gravity. Mod. Phys. Lett. A 2005, 20, 2145. [Google Scholar] [CrossRef] [Green Version]
- Blasone, M.; Jizba, P.; Lambiase, G.; Petruzziello, L. Non-relativistic neutrinos and the weak equivalence principle apparent violation. Phys. Lett. B 2020, 811, 135883. [Google Scholar] [CrossRef]
- Capolupo, A.; Lambiase, G.; Quaranta, A. Neutrinos in curved spacetime: Particle mixing and flavor oscillations. Phys. Rev. D 2020, 101, 095022. [Google Scholar] [CrossRef]
- Blasone, M.; Luciano, G.G. Gravitational effects on neutrino decoherence in Lense-Thirring metric. arXiv 2021, arXiv:2110.00971. [Google Scholar]
- Capozziello, S.; Lambiase, G. Neutrino oscillations in Brans-Dicke theory of gravity. Mod. Phys. Lett. A 1999, 14, 2193. [Google Scholar] [CrossRef] [Green Version]
- Adak, M.; Dereli, T.; Ryder, L.H. Neutrino oscillations induced by space-time torsion. Class. Quant. Grav. 2001, 18, 1503. [Google Scholar] [CrossRef] [Green Version]
- Adak, M.; Dereli, T.; Ryder, L.H. Dirac equation in space-times with nonmetricity and torsion. Int. J. Mod. Phys. D 2003, 12, 145. [Google Scholar] [CrossRef] [Green Version]
- Capozziello, S.; De Laurentis, M. Extended Theories of Gravity. Phys. Rept. 2011, 509, 167. [Google Scholar] [CrossRef] [Green Version]
- Buoninfante, L.; Luciano, G.G.; Petruzziello, L.; Smaldone, L. Neutrino oscillations in extended theories of gravity. Phys. Rev. D 2020, 101, 024016. [Google Scholar] [CrossRef] [Green Version]
- Ahluwalia, D.V.; Labun, L.; Torrieri, G. Neutrino mixing in accelerated proton decays. Eur. Phys. J. A 2016, 52, 189. [Google Scholar] [CrossRef]
- Blasone, M.; Lambiase, G.; Luciano, G.G.; Petruzziello, L. Role of neutrino mixing in accelerated proton decay. Phys. Rev. D 2018, 97, 105008. [Google Scholar] [CrossRef] [Green Version]
- Cozzella, G.; Fulling, S.A.; Landulfo, A.G.S.; Matsas, G.E.A.; Vanzella, D.A.T. Unruh effect for mixing neutrinos. Phys. Rev. D 2018, 97, 105022. [Google Scholar] [CrossRef] [Green Version]
- Blasone, M.; Lambiase, G.; Luciano, G.G.; Petruzziello, L. Neutrino oscillations in the Unruh radiation. Phys. Lett. B 2020, 800, 135083. [Google Scholar] [CrossRef]
- Blasone, M.; Lambiase, G.; Luciano, G.G.; Petruzziello, L. On the β-decay of the accelerated proton and neutrino oscillations: A three-flavor description with CP violation. Eur. Phys. J. C 2020, 80, 130. [Google Scholar] [CrossRef]
- Salucci, P.; Esposito, G.; Lambiase, G.; Battista, E.; Benetti, M.; Bini, D.; Boco, L.; Sharma, G.; Bozza, V.; Buoninfante, L.; et al. Einstein, Planck and Vera Rubin: Relevant encounters between the Cosmological and the Quantum Worlds. Front. Phys. 2021, 8, 603190. [Google Scholar] [CrossRef]
- Wolfenstein, L. Neutrino oscillations and stellar collapse. Phys. Rev. D 1979, 20, 2634. [Google Scholar] [CrossRef]
- Hirata, K.; Kajita, T.; Koshiba, M.; Nakahata, M.; Oyama, Y.; Sato, N.; Suzuki, A.; Takita, M.; Totsuka, Y.; Kifune, T.; et al. Observation of a neutrino burst from the supernova SN1987A. Phys. Rev. Lett. 1987, 58, 1490. [Google Scholar] [CrossRef] [PubMed]
- Ahluwalia, D.V. Neutrino oscillations and supernovae. Gen. Rel. Grav. 2004, 36, 2183. [Google Scholar] [CrossRef]
- Mirizzi, A.; Tamborra, I.; Janka, H.T.; Saviano, N.; Scholberg, K.; Bollig, R.; Hudepohl, L.; Chakraborty, S. Supernova Neutrinos: Production, Oscillations and Detection. Riv. Nuovo Cim. 2016, 39, 1–112. [Google Scholar]
- Dvali, G. Neutrino probes of dark energy. Nature 2004, 432, 567. [Google Scholar] [CrossRef]
- Boyarsky, A.; Drewes, M.; Lasserre, T.; Mertens, S.; Ruchayskiy, O. Sterile neutrino Dark Matter. Prog. Part. Nucl. Phys. 2019, 104, 1–45. [Google Scholar] [CrossRef] [Green Version]
- Marletto, C.; Vedral, V.; Deutsch, D. Quantum-gravity effects could in principle be witnessed in neutrino-like oscillations. New J. Phys. 2018, 20, 083011. [Google Scholar] [CrossRef]
- Luciano, G.G.; Petruzziello, L. Testing gravity with neutrinos: From classical to quantum regime. Int. J. Mod. Phys. D 2020, 29, 2043002. [Google Scholar] [CrossRef]
- Giunti, C.; Kim, C.W. Coherence of neutrino oscillations in the wave packet approach. Phys. Rev. D 1998, 58, 017301. [Google Scholar] [CrossRef] [Green Version]
- Giunti, C. Coherence and wave packets in neutrino oscillations. Found. Phys. Lett. 2004, 17, 103. [Google Scholar] [CrossRef] [Green Version]
- Akhmedov, E.; Kopp, J.; Lindner, M. Collective neutrino oscillations and neutrino wave packets. JCAP 2017, 9, 017. [Google Scholar] [CrossRef] [Green Version]
- Chatelain, A.; Volpe, M.C. Neutrino decoherence in presence of strong gravitational fields. Phys. Lett. B 2020, 801, 135150. [Google Scholar] [CrossRef]
- Petruzziello, L. Comment on “Neutrino decoherence in presence of strong gravitational fields”. Phys. Lett. B 2020, 809, 135784. [Google Scholar] [CrossRef]
- Donoghue, J.F. Leading quantum correction to the Newtonian potential. Phys. Rev. Lett. 1994, 72, 2996. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Donoghue, J.F. General relativity as an effective field theory: The leading quantum corrections. Phys. Rev. D 1994, 50, 3874. [Google Scholar] [CrossRef] [Green Version]
- Bjerrum-Bohr, N.E.J.; Donoghue, J.F.; Holstein, B.R. Quantum corrections to the Schwarzschild and Kerr metrics. Phys. Rev. D 2003, 68, 084005. [Google Scholar] [CrossRef] [Green Version]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; W.H. Freeman and Company: San Francisco, CA, USA, 1973. [Google Scholar]
- Villalpando, C.; Modak, S.K. Minimal length effect on the broadening of free wave-packets and its physical implications. Phys. Rev. D 2019, 100, 024054. [Google Scholar] [CrossRef] [Green Version]
- Villalpando, C.; Modak, S.K. Indirect Probe of Quantum Gravity using Molecular Wave-packets. Class. Quant. Grav. 2019, 36, 215016. [Google Scholar] [CrossRef] [Green Version]
- Das, S.; Modak, S.K. A novel mechanism for probing the Planck scale. Class. Quant. Grav. 2022, 39, 015005. [Google Scholar] [CrossRef]
- Barrau, A.; Rovelli, C.; Vidotto, F. Fast Radio Bursts and White Hole Signals. Phys. Rev. D 2014, 90, 127503. [Google Scholar] [CrossRef] [Green Version]
- Barrau, A.; Bolliet, B.; Vidotto, F.; Weimer, C. Phenomenology of bouncing black holes in quantum gravity: A closer look. J. Cosmol. Astropart. Phys. 2016, 02, 022. [Google Scholar] [CrossRef] [Green Version]
- Lunin, O.; Mathur, S.D. Statistical interpretation of Bekenstein entropy for systems with a stretched horizon. Phys. Rev. Lett. 2002, 88, 211303. [Google Scholar] [CrossRef] [Green Version]
- Lunin, O.; Mathur, S.D. AdS/CFT duality and the black hole information paradox. Nucl. Phys. B 2002, 623, 342. [Google Scholar] [CrossRef] [Green Version]
- Bianchi, M.; Consoli, D.; Grillo, A.; Morales, J.F.; Pani, P.; Raposo, G. Distinguishing fuzzballs from black holes through their multipolar structure. Phys. Rev. Lett. 2020, 125, 221601. [Google Scholar] [CrossRef] [PubMed]
- Ikeda, T.; Bianchi, M.; Consoli, D.; Grillo, A.; Morales, J.F.; Pani, P.; Raposo, G. Black-hole microstate spectroscopy: Ringdown, quasinormal modes, and echoes. Phys. Rev. D 2021, 104, 066021. [Google Scholar] [CrossRef]
- Amelino-Camelia, G.; Smolin, L. Prospects for constraining quantum gravity dispersion with near term observations. Phys. Rev. D 2009, 80, 084017. [Google Scholar] [CrossRef] [Green Version]
- Abdo, A.A.; Ackermann, M.; Ajello, M.; Asano, K.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Baring, M.G.; et al. A limit on the variation of the speed of light arising from quantum gravity effects. Nature 2009, 462, 331. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).