Equations of State for Hadronic Matter and Mass-Radius Relations of Neutron Stars with Strong Magnetic Fields

Abstract

Neutron star is an important object for us to verify the equation of state of hadronic matter. For a specific choice of equations of state, mass and radius of a neutron star are determined, for which there are constraints from observations. According to some previous studies, since the strong magnetic field acts as a repulsive force, there is a possibility that neutron stars with strong magnetic fields may have relatively heavier masses than other non-magnetized neutron stars. In this paper, the structure of a neutron star with a strong internal magnetic field is investigated by changing its internal functional form to see how much the neutron star can be massive and also how radius of a neutron star can be within a certain range.

1. Introduction

To study a neutron star (NS) is an interesting and important subject in nuclear physics as it is a unique object of superdense hadronic matter, where its central density might be several times larger than the nuclear saturation density. Equation of state (EoS) for the nuclear matter that depends on the energy density functional is often utilized to discuss various properties of NSs, for instance, the mass–radius (MR) relation.

Historically, Oppenheimer and Volkoff (independently, Tolman) were the first who estimated its maximum mass of $M_{max}\sim 0.71$ solar mass ($M_{\odot }$) by employing a noninteracting strongly degenerate relativistic gas of neutrons in 1939 [1,2]. Discoveries of NSs with masses around twice the solar mass have made a strong impact on the nuclear physics community who had once believed that the maximum mass of an NS should not exceed 1.56 $M_{\odot }$ due to the occurrence of kaon condensation [3,4]. Indeed, several NSs with around 2 $M_{\odot }$ have been confirmed since 2010. The NS PSR J1614-2230 has the observed mass of 1.97 ± 0.04 $M_{\odot }$ [5] and the NS PSR J0348+0432 has mass of 2.01 ± 0.04 $M_{\odot }$ [6]. In 2021, the mass and equatorial radius of the millisecond-pulsar (MSP) J0740+6620 was constrained to be $M=2.{072}_{-0.066}^{+0.067}{M}_{\odot }$ and $R_{2.072M_{\odot }}=12.{39}_{-0.98}^{+1.30}$ km, respectively [7,8,9,10]. If NS matter consists of only nucleons with strong two- or three-body repulsive forces, massive NSs more than 2 $M_{\odot }$ can be easily described. However, hyperons are energetically favorable when the baryon chemical potential is large enough in the inner core of an NS. This leads to a reduction in the Fermi pressure to soften the EoS and to a reduction in the predicted maximum mass less than 2 $M_{\odot }$. This is called the hyperon puzzle. Since discoveries of massive NSs, many people have searched for the optimal EoSs that can achieve masses over 2 $M_{\odot }$. To obtain NS masses more than 2 $M_{\odot }$ is one of the goals to be achieved for the optimal EoSs.

There are some characteristic NSs: millisecond-pulsar, which has a short rotational period of less than 10 ms, and magnetar, which has a powerful magnetic field on its surface. As a part of external conditions to support over 2 $M_{\odot }$, the extremely rapid rotation and powerful magnetic field should be considered in the EoS study. In our recent studies [11,12], EoSs for a rapidly rotating NS with some deformation and a fixed magnetic field have been investigated. Although an unrealistically rapid rotation can modify the NS mass from 1.89 $M_{\odot }$ to 2 $M_{\odot }$, the rotational effects on the mass increase were found to be not so significant for the realistic frequency range of the observed millisecond-pulsars.

A magnetar is a type of the NS that has a strong magnetic field on the surface. Recently, up to 30 magnetars have been observed [13,14]. Maximumly, about ${10}^{15}$ G of the magnetic field on the surface has been found by the observation [13], but we do not yet know the generation mechanism of the strong magnetic fields, where and how they come from.

Another constraint on the EoS comes from the NS radius. From the observation of the GW170817 gravitational wave event, the upper limit radius is $13.6$ km [15] at the mass of M = 1.4 $M_{\odot }$. Moreover, another reports the upper limit radius $13.76$ km [16] at M = 1.4 $M_{\odot }$. The lower limit radius was reported as $10.{68}_{-0.04}^{+0.15}$ km [17] at M = 1.6 $M_{\odot }$. The upper limit of radius by NICER observations of PSR J0030+0451 is $13.{02}_{-1.06}^{+1.24}$ km [18] at $M=1.{44}_{-0.14}^{+0.15}$ $M_{\odot }$.

In this paper, the internal structure and MR relation of NS, including hyperon populations, are investigated by changing the functional form of a strong magnetic field. The strength of the magnetic field is fixed constant as ${10}^{12}$ G on the surface and over ${10}^{18}$ G near the center. The shape of the magnetic field is parametrized by two parameters $\alpha$ and $\gamma$. We first formulate the relativistic mean field (RMF) theory, including hyperons. Here, we introduce 12 different EoSs [19,20] depending on the different coupling constants between baryons and mesons. These EoSs have similar saturation properties at nuclear saturation density. This RMF includes a strong magnetic field, which has a functional form of baryon number density $\rho$. In this work, we solve the Tolman–Oppenheimer–Volkov (TOV) equations to obtain masses and radii for various EoSs by changing $\alpha$ and $\gamma$ parameters freely. Here, the MR relations are verified with respect to the constraints that maximum masses are within the range of observed masses and the radii at 1.4 solar mass are less than 13.76 km.

This paper is organized as follows. The formulation of the calculation is given in Section 2. The results are given in Section 3. Finally, a summary is given in Section 4.

2. Formulations

2.1. Equation of State

We adopt the relativistic mean field (RMF) theory based on the nonlinear Walecka model in this work. We assume that the NS matter is static and uniform in the high density region. The Lagrangian reads [19,20,21,22,23,24,25,26]

$$\begin{array}{c}\hfill \mathcal{L}=\sum _b{\mathcal{L}}_b+{\mathcal{L}}_m+\sum _l{\mathcal{L}}_l+{\mathcal{L}}_{em},\end{array}$$

(1)

where

$$\begin{array}{cc}\hfill {\mathcal{L}}_b& ={\overline{\psi }}_b\left(i{\gamma }_{\mu }{\partial }^{\mu }-m_b+g_{\sigma b}\sigma +g_{{\sigma }^{\ast }b}{\sigma }^{\ast }-g_{\omega b}{\gamma }_{\mu }{\omega }^{\mu }\right.\hfill \\ \hfill & -g_{\varphi b}{\gamma }_{\mu }{\varphi }^{\mu }-g_{\rho b}{\gamma }_{\mu }\mathbf{\tau }·{\mathbf{\rho }}^{\mu }\hfill \\ \hfill & \left.-q_b{\gamma }_{\mu }{A}^{\mu }-{\kappa }_b{\sigma }_{\mu \nu }{F}^{\mu \nu }\right){\psi }_b,\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill {\mathcal{L}}_m& =\frac{1}{2}\left({\partial }_{\mu }\sigma {\partial }^{\mu }\sigma -m_{\sigma }^2{\sigma }^2\right)+\frac{1}{2}\left({\partial }_{\mu }{\sigma }^{\ast }{\partial }^{\mu }{\sigma }^{\ast }-m_{{\sigma }^{\ast }}^2{\sigma }^{\ast 2}\right)\hfill \\ \hfill & +\frac{1}{2}{m}_{\omega }^2{\omega }_{\mu }{\omega }^{\mu }-\frac{1}{4}{\Omega }_{\mu \nu }{\Omega }^{\mu \nu }+\frac{1}{2}{m}_{\varphi }^2{\varphi }_{\mu }{\varphi }^{\mu }\hfill \\ \hfill & -\frac{1}{4}{\Phi }_{\mu \nu }{\Phi }^{\mu \nu }+\frac{1}{2}{m}_{\rho }^2{\mathbf{\rho }}_{\mu }·{\mathbf{\rho }}^{\mu }-\frac{1}{4}{\mathbf{P}}^{\mu \nu }·{\mathbf{P}}_{\mu \nu }\hfill \\ \hfill & -\frac{1}{3}b{m}_n{\left(g_{\sigma }\sigma \right)}^3-\frac{1}{4}c{\left(g_{\sigma }\sigma \right)}^4\hfill \\ \hfill & +\frac{1}{4!}\xi {\left(g_{\omega }^2{\omega }_{\mu }{\omega }^{\mu }\right)}^2+{\Lambda }_{\omega }\left(g_{\omega }^2{\omega }_{\mu }{\omega }^{\mu }\right)\left(g_{\rho }^2{\mathbf{\rho }}_{\mu }·{\mathbf{\rho }}^{\mu }\right),\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill {\mathcal{L}}_l& ={\overline{\psi }}_l\left(i{\gamma }_{\mu }{\partial }^{\mu }-q_l{\gamma }_{\mu }{A}^{\mu }-m_l\right){\psi }_l,\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill {\mathcal{L}}_{em}& =-\frac{1}{4}{F}^{\mu \nu }{F}_{\mu \nu }.\hfill \end{array}$$

(5)

Here, $b,m,l$, and $em$ indicate baryons, mesons, leptons, and photons, respectively. The field strengths are explicitly given as

$$\begin{array}{cc}\hfill F_{\mu \nu }& ={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu },\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill {\Omega }_{\mu \nu }& ={\partial }_{\mu }{\omega }_{\nu }-{\partial }_{\nu }{\omega }_{\mu },\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill {\Phi }_{\mu \nu }& ={\partial }_{\mu }{\varphi }_{\nu }-{\partial }_{\nu }{\varphi }_{\mu },\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill {\mathbf{P}}_{\mu \nu }& ={\partial }_{\mu }{\mathbf{\rho }}_{\nu }-{\partial }_{\nu }{\mathbf{\rho }}_{\mu }-g_{\rho }{\mathbf{\rho }}_{\mu }\times {\mathbf{\rho }}_{\nu }.\hfill \end{array}$$

(9)

Here, $\mathbf{\tau }/2$ represents the isospin operator and ${\sigma }_{\mu \nu }=\frac{i}{2}\left[{\gamma }_{\mu },{\gamma }_{\nu }\right]$, where ${\gamma }_{\mu }$ is Dirac $\gamma$ matrix. Characters in bold font represent isovector fields. The baryon octet p, n, $\Lambda$, ${\Sigma }^0$, ${\Sigma }^{\pm }$, ${\Xi }^0$, ${\Xi }^{-}$, the electron (0.511 MeV), the muon (105.7 MeV), and the tauon (1777 MeV) are considered for fermions [27]. The scalar-meson $\sigma$, the vector-meson $\omega$, and the vector-isovector-meson $\mathbf{\rho }$ with masses of $m_{\sigma }=511.198$ MeV, $m_{\omega }=783.0$ MeV, and $m_{\rho }=770.0$ MeV are considered for mesons, respectively. In addition, hidden-strangeness mesons, ${\sigma }^{\ast }$ and $\varphi$ with masses of $m_{{\sigma }^{\ast }}=975$ MeV, $m_{\varphi }=1020$ MeV are introduced. The coupling constants of nucleons with these mesons, $g_{\sigma N}$, $g_{\omega N}$, and $g_{\rho N}$, and some self-interactions among mesons are determined by fitting the physical quantities at the saturation density [19,21,22].

For seven kinds of EoSs employed in the present study, nuclear properties at saturation number density ${\rho }_0$ are given in Table 1. Here, TM1 and TM2 are different with respect to the slope parameter L, where L is closely related to the radius of an NS. The NL3 parametrization is fitted to the ground-state properties of both stable and unstable nuclei. This parametrization predicts very large, purely nucleonic NS maximum masses, but a symmetry energy slope parameter L is too large. Thus, we also consider the parametrization NL3$\omega \rho$ with a softer density dependence of the symmetry energy due to the inclusion of the nonlinear $\omega \rho$ term.

Table 1. Nuclear properties at saturation number density (${\rho }_0$ (fm${}^{-3}$)) predicted by seven kinds of EoSs used in this study [20,28]: energy per nucleon ($B/A$ (MeV)), incompressibility (K (MeV)), symmetry energy (J (MeV)), its slope parameter (L (MeV)), and curvature ($K_{sym}$ (MeV)) at the saturation point of uniform symmetric nuclear matter [29].

	GM1	GM3	TM1	TM2$\mathit{\omega }\mathit{\rho }$	NL3	NL3$\mathit{\omega }\mathit{\rho }$	DDME2
${\rho }_0$	0.153	0.153	0.146	0.146	0.148	0.148	0.152
$B/A$	$-16.3$	$-16.3$	$-16.3$	$-16.4$	$-16.30$	$-16.30$	$-16.14$
K	300	240	281.2	281.7	271.8	271.8	250.9
J	32.5	32.5	36.9	32.1	37.4	31.7	32.3
L	93.9	89.7	111.2	54.8	118.9	55.5	51.2
$K_{sym}$	17.9	$-6.5$	33.8	$-70.5$	$101.6$	$-7.6$	$-87.1$

The parameterizations of twelve EoSs (GM1, GM3, TM1-a, TM1-b, TM2$\omega \rho$-a, TM2$\omega \rho$-b, NL3-a, NL3-b, NL3$\omega \rho$-a, NL3$\omega \rho$-b, DDME2-a, and DDME2-b) are given as follows. The coupling constants of hyperons with mesons are determined by fitting the properties of hypernuclei in the quark model [20]. In the GM1 parameter set, coupling ratios, $R_{\sigma h}=g_{\sigma h}/g_{\sigma N}=0.6$, $R_{\omega h}=g_{\omega h}/g_{\omega N}=0.653$, and $R_{\rho h}=g_{\rho h}/g_{\rho N}=0.6$ are adopted. In the GM3 parameter set, coupling ratios, $R_{\sigma h}=g_{\sigma h}/g_{\sigma N}=0.6$, $R_{\omega h}=g_{\omega h}/g_{\omega N}=0.568$, and $R_{\rho h}=g_{\rho h}/g_{\rho N}=0.6$ are adopted. The GM3 EoS leads to neutron star with compactness smaller than GM1 EoS. As for other couplings of hyperons with the vector and the vector-isovector mesons, the following SU(6) values are adopted in the a-parameter sets (TM1-a, TM2$\omega \rho$-a, NL3-a, NL3$\omega \rho$-a, and DDME2-a):

$$\begin{array}{cc}\hfill & R_{\omega \Lambda }=\frac{2}{3},R_{\omega \Sigma }=\frac{2}{3},R_{\omega \Xi }=\frac{1}{3},\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill & R_{\rho \Sigma }=2,R_{\rho \Xi }=1,\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill & R_{\varphi \Lambda }=-\frac{\sqrt{2}}{3},R_{\varphi \Sigma }=-\frac{\sqrt{2}}{3},R_{\varphi \Xi }=-\frac{2\sqrt{2}}{3}.\hfill \end{array}$$

(12)

The difference of a- and b-parametrizations are as follows: (a) SU(6), i.e., $R_{\omega \Lambda }=2/3$, (b) $R_{\omega \Lambda }=1$, obtained for $R_{\varphi \Lambda }$ equal to its SU(6) value and $R_{\sigma \Lambda }$ and $R_{{\sigma }^{\ast }\Lambda }$ are calibrated to hypernuclear data with $\Delta B_{\Lambda \Lambda }=0.5$ MeV. The values of hyperon potentials in symmetric nuclear matter, $U_{\Lambda }^N=-30$ MeV, $U_{\Sigma }^N=0$ MeV, and $U_{\Xi }^N=-14$ MeV [20], are used to determine the value of $R_{\sigma h}$. Thus, ratios of the $\sigma$-$\Lambda$ coupling, the $\sigma$-$\Sigma$ coupling, and the $\sigma$-$\Xi$ coupling in EoS parameter sets except GM1 and GM3, are adopted as in Table 2.

Table 2. Adopted ratios of $\sigma$-$\Lambda$ coupling, $\sigma$-$\Sigma$ coupling, and $\sigma$-$\Xi$ coupling in EoS parameter sets.

EoS	${\mathit{R}}_{\mathit{\sigma }\mathit{\Lambda }}$	${\mathit{R}}_{\mathit{\sigma }\mathit{\Sigma }}$	${\mathit{R}}_{\mathit{\sigma }\mathit{\Xi }}$
TM1-a	0.64	0.56	0.32
TM1-b	0.91	0.56	0.32
TM2$\omega \rho$-a	0.64	0.55	0.32
TM2$\omega \rho$-b	0.93	0.55	0.32
NL3-a	0.67	0.59	0.33
NL3-b	0.97	0.59	0.33
NL3$\omega \rho$-a	0.67	0.59	0.33
NL3$\omega \rho$-b	0.97	0.59	0.33
DDME2-a	0.69	0.60	0.34
DDME2-b	0.98	0.60	0.34

Here, those EoSs with high incompressibility more than $K=240$ MeV are considered. All other details are given in [12].

2.2. Magnetic Fields

The neutron stars can be massive because of the pressure from magnetic fields. In this work, we investigate an NS with a strong magnetic field inside the NS. From observations, only the strength of the magnetic field on the surface is known and we need to assume the strength and the functional form of the magnetic field inside the NS.

In the following, a density-dependent magnetic field strength is adopted in this study [26,30],

$$\begin{array}{c}\hfill B\left(\rho \right)=B_s+B_0\left[1-exp\left\{-\alpha {\left(\frac{\rho }{{\rho }_0}\right)}^{\gamma }\right\}\right],\end{array}$$

(13)

where $B_0$ indicates the strength in a denser region than that of the saturation number density ${\rho }_0$ (0.153 fm${}^{-3}$) and $B_s$ indicates the strength of magnetic fields on the surface. Here, we adopt $B_s={10}^{12}$ G.

Since Equation (13) does not satisfy $\mathrm{div}\mathbf{B}=0$ in general, this form of the magnetic fields must be used with caution as a simple way to implement magnetic fields in an NS. With this problem in mind, however, it should be emphasized that for particles in a very small region of an NS, they feel almost a constant magnetic field, for which $\mathrm{div}\mathbf{B}=0$ is practically satisfied. For more realistic magnetic fields, different equations might be used [31].

Even if one assumes the form of Equation (13), one has free parameters $\alpha$, $\gamma$, and $B_0$. Up to now, there is no work of changing $\alpha$ and $\gamma$ parameters freely. In this work, we arbitrarily change $\alpha$ and $\gamma$ to investigate their effects on the radii and masses of NSs.

2.3. EoS of Hadronic Matter with Magnetic Fields

The energy density and the pressure of hadronic matter in the presence of the magnetic fields are given as

$$\begin{array}{c}\hfill \epsilon ={\epsilon }_m+B^2/2,\end{array}$$

(14)

$$\begin{array}{c}\hfill p=p_m+B^2/2,\end{array}$$

(15)

respectively, where ${\epsilon }_m$ and $p_m$ are the energy density and the pressure of hadrons where the contribution $B^2/2$ from the magnetic fields are neglected. However, it should be noted that, without $B^2/2$, the effects of the magnetic fields to ${\epsilon }_m$ and $p_m$ are included through the interaction between the magnetic field and each particle’s magnetic moment. All other details are given in Appendix A of Reference [12].

3. Results

3.1. Comparison of the Case without Magnetic Fields

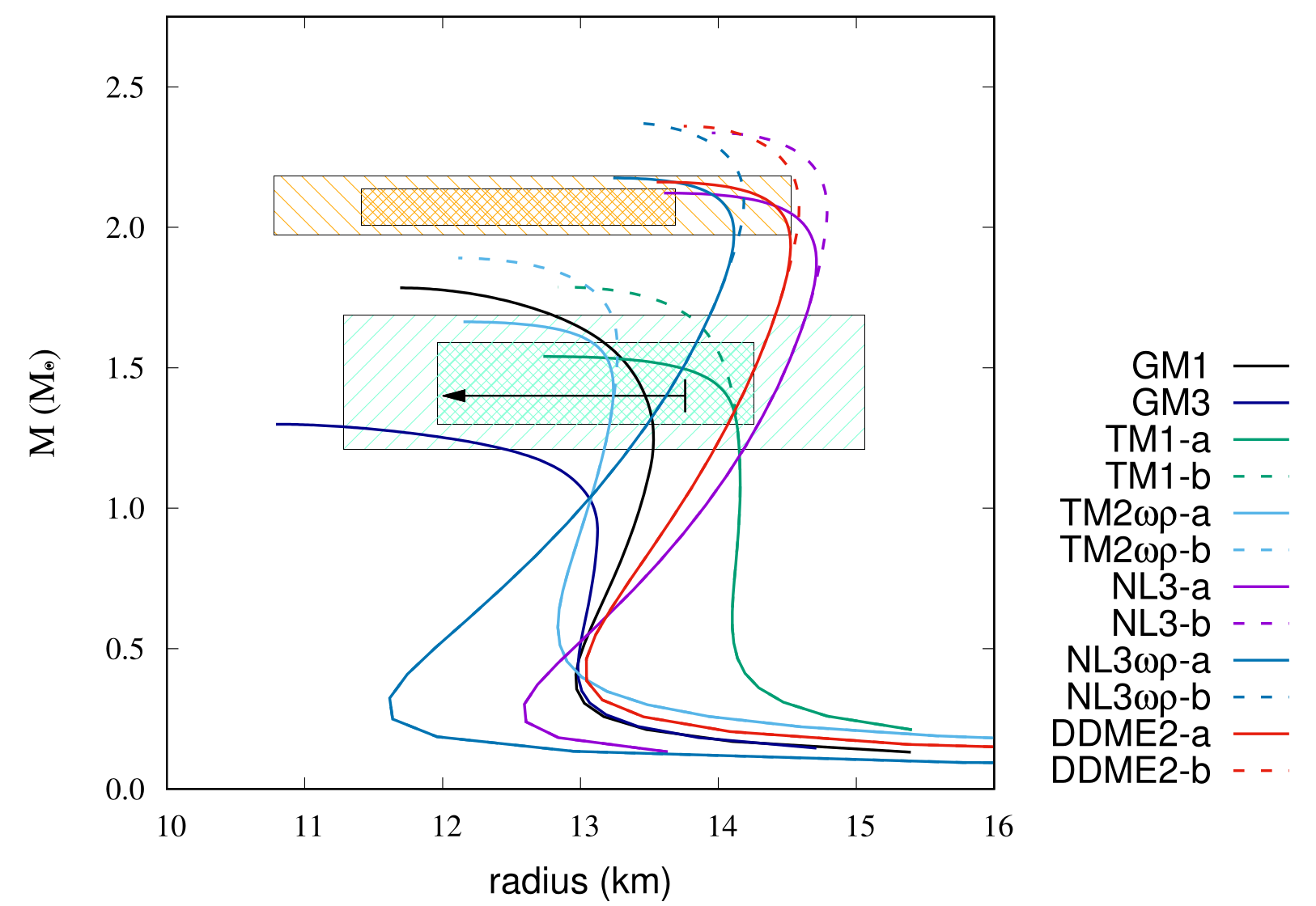
Figure 1 shows the MR relations of 12 EoSs without assuming any magnetic fields. The orange and light green dashed areas indicate pulsars PSR J0740+6620 and PSR J0030+ 0451, respectively. The thick area shows the one within 68% credibility and the thinner area shows the one within 90% credibility. Each EoS curve must go through these areas if they satisfy the observational constraints. The arrow indicates the upper limit of radius for 1.4 $M_{\odot }$ from the gravitational wave event GW170817.

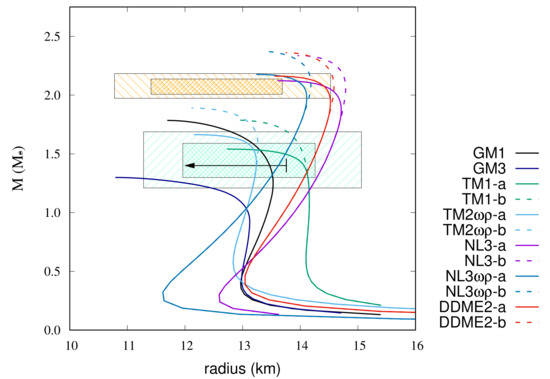
Figure 1. MR relations of 12 EoSs without magnetic fields. The unstable region in each EoS is not shown. The orange and light green dashed areas indicate pulsars PSR J0740+6620 and PSR J0030+0451 (68% (thick) and 90% (thin) credibility), respectively. The arrow indicates the upper limit of radius for 1.4 $M_{\odot }$ from the gravitational wave event GW170817. The colored lines represent the following: black (solid line), GM1 EoS; green (solid line), TM1-a EoS; green (dashed line), TM1-b EoS; light blue (solid line), TM2$\omega \rho$-a EoS; light blue (dashed line), TM2$\omega \rho$-b EoS; purple (solid line), NL3-a EoS; purple (dashed line), NL3-b EoS; dark blue (solid line), NL3$\omega \rho$-a EoS; dark blue (dashed line), NL3$\omega \rho$-b EoS; red (solid line), DDME2-a EoS; red (dashed line), DDME2-b EoS.

Only three EoSs (NL3a, NL3$\omega \rho$-a, and DDME2-a) barely satisfy the MR constraints (within 90% credibility for the maximum mass), but among them, only NL3$\omega \rho$-a (K = 271.8 MeV) satisfies the radius constraint at 1.4 $M_{\odot }$. It should be noted that DDME2 (K = 250.9 MeV) is a relatively soft EoS at nuclear saturation density, but it becomes harder in a higher density region.

Table 3 summarizes the maximum masses, radius at 1.4 $M_{\odot }$, and radius at 2.072 $M_{\odot }$ for 12 EoSs without magnetic fields. Only three kinds of EoSs (NL3, NL3$\omega \rho$, and DDME2) give masses of twice the solar mass.

Table 3. Maximum masses, radius at M = 1.4 $M_{\odot }$, and radius at M = 2.072 $M_{\odot }$ for 12 EoSs without magnetic fields.

EoS	Mmax (${\mathit{M}}_{\odot }$)	${\mathit{R}}_{1.4{\mathit{M}}_{\odot }}$ (km)	${\mathit{R}}_{2.072{\mathit{M}}_{\odot }}$ (km)
GM1	1.784	13.5	−
GM3	1.299	−	−
TM1-a	1.540	14.1	−
TM1-b	1.787	14.1	−
TM2$\omega \rho$-a	1.663	13.2	−
TM2$\omega \rho$-b	1.891	13.2	−
NL3-a	2.122	14.4	14.4
NL3-b	2.336	14.4	14.8
NL3$\omega \rho$-a	2.175	13.6	14.1
NL3$\omega \rho$-b	2.372	13.6	14.2
DDME-a	2.161	14.2	14.4
DDME-b	2.360	14.2	14.6

As general features, the maximum mass becomes smaller when hyperons are included, but the maximum mass increases when the magnetic field is implemented. The average radius increases when a strong magnetic field is implemented.

3.2. Changing $\alpha$ and $\gamma$ Parameters of the Magnetic Field Function

In this section, the magnetic field $B\left(\rho \right)$ in Equation (13) is also implemented, where $\alpha$ and $\gamma$ parameters are changed as free parameters.

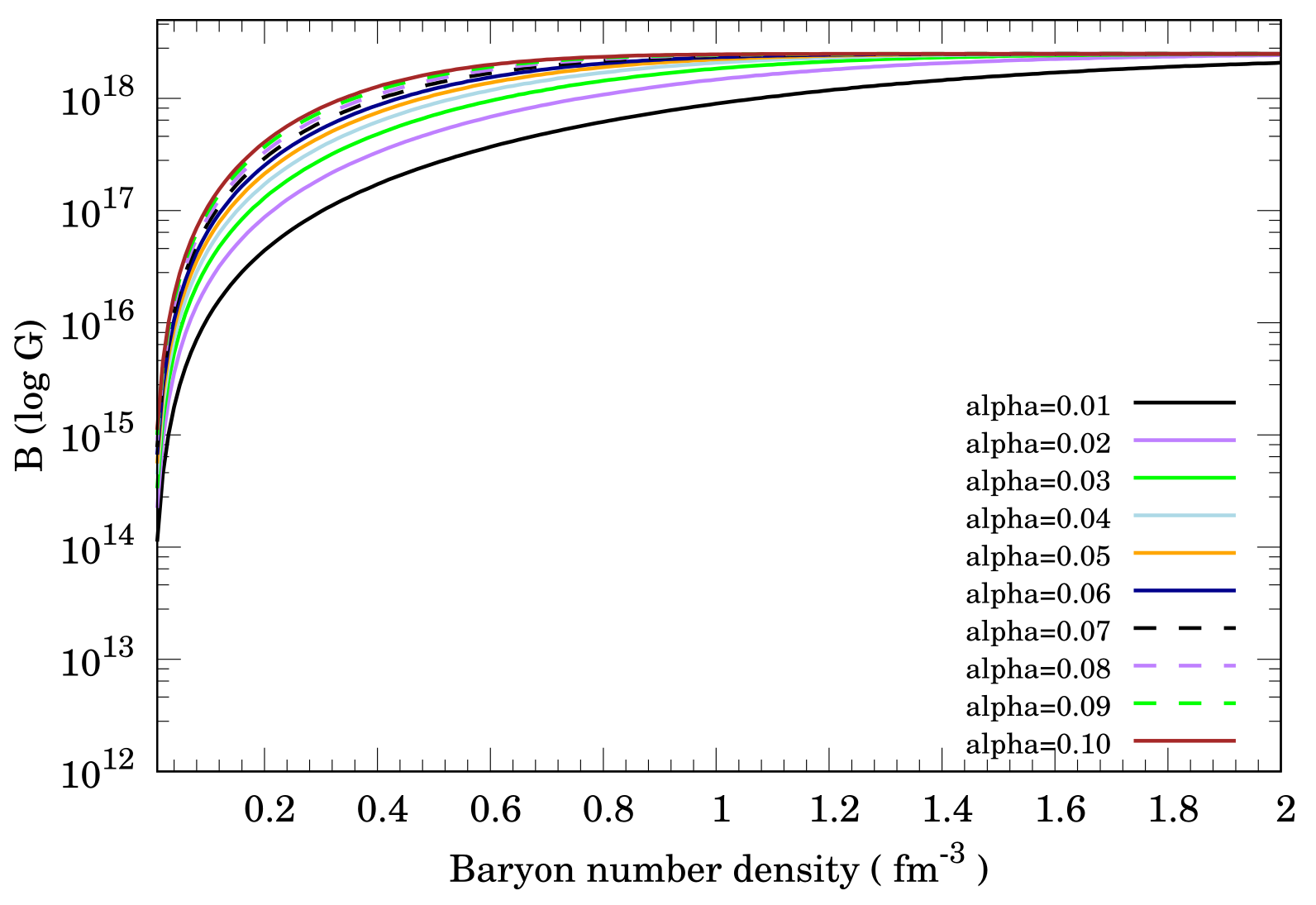
The $B\left(\rho \right)$ as a function of baryon number density $\rho$ for various $\alpha$ parameters is shown in Figure 2. Each line indicates a magnetic field with $B_0=2.5\times {10}^{18}$ G and $\gamma =2$. In Figure 2, as $\alpha$ becomes larger, the strength of the magnetic field B changes more abruptly. Even at baryon number density $\rho =0.01$ fm${}^{-3}$ and $\alpha =0.01$ (black solid line), the strength of magnetic field is $1\times {10}^{14}$ G. This indicates that parameter $\gamma$ strongly affects the strength of the magnetic field near the surface of an NS. Furthermore, the radius at 1.4 $M_{\odot }$ becomes larger when $\alpha$ becomes larger.

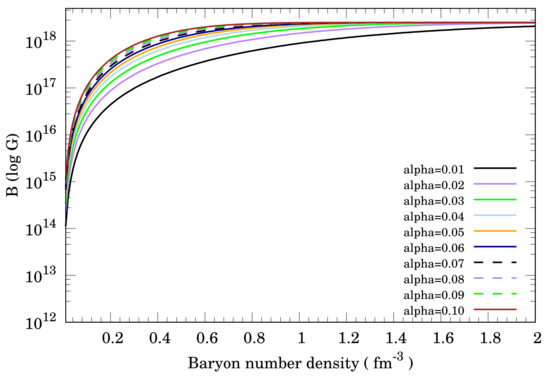
Figure 2. B($\rho$) as a function of baryon number density $\rho$ for various $\alpha$ parameters with $B_0=2.5\times {10}^{18}$ G and $\gamma =2$. The colored lines represent the following: black (solid line), magnetic fields $B\left(\rho \right)$ with $\alpha =0.01$; purple (solid line), magnetic fields $B\left(\rho \right)$ with $\alpha =0.02$; green (solid line), magnetic fields $B\left(\rho \right)$ with $\alpha =0.03$; light blue (solid line), magnetic fields $B\left(\rho \right)$ with $\alpha =0.04$; orange (solid line), magnetic fields $B\left(\rho \right)$ with $\alpha =0.05$; dark blue (solid line), magnetic fields $B\left(\rho \right)$ with $\alpha =0.06$; black (dashed line), magnetic fields $B\left(\rho \right)$ with $\alpha =0.07$; purple (dashed line), magnetic fields $B\left(\rho \right)$ with $\alpha =0.08$; green (dashed line), magnetic fields $B\left(\rho \right)$ with $\alpha =0.09$; brown (solid line), magnetic fields $B\left(\rho \right)$ with $\alpha =0.10$.

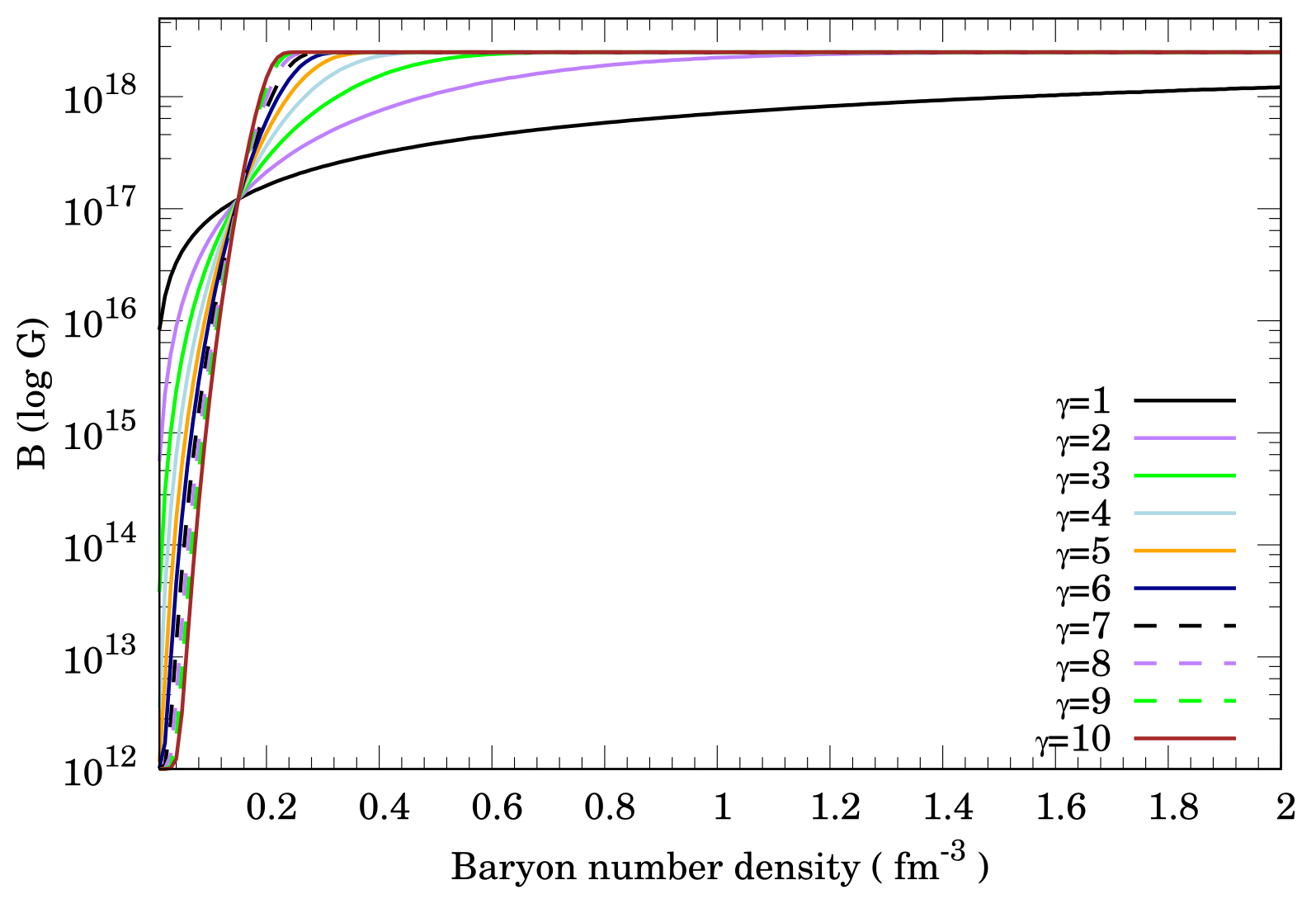
Next, the magnetic field $B\left(\rho \right)$ as a function of baryon number density $\rho$ for various $\gamma$ parameters is shown in Figure 3. Each line indicates a magnetic field with $B_0=2.5\times {10}^{18}$ G and $\alpha =0.05$. For $\rho >0.3$ fm${}^{-3}$, $B\left(\rho \right)$ is almost constant $B_0=2.5\times {10}^{18}$ G. Here, magnetic field strengths at saturation density ${\rho }_0$ are given as $B\left({\rho }_0\right)=1.23\times {10}^{17}$ G for any value of $\gamma$. Magnetic field strengths $B\left({\rho }_0\right)$ at saturation density ${\rho }_0$ for various $\alpha$ parameters are shown in Table 4.

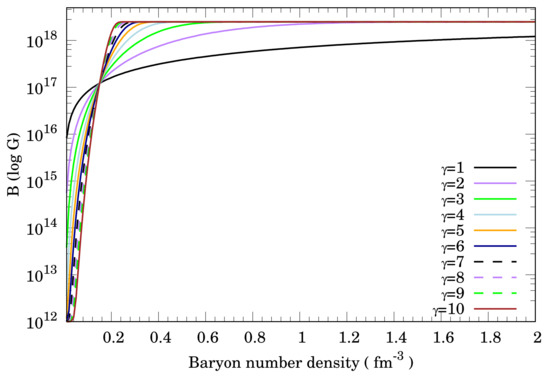
Figure 3. B($\rho$) as a function of baryon number density $\rho$ for various $\gamma$ parameters with $B_0=2.5\times {10}^{18}$ G and $\alpha =0.05$. The colored lines represent the following: black (solid line), magnetic fields $B\left(\rho \right)$ with $\gamma =1$; purple (solid line), magnetic fields $B\left(\rho \right)$ with $\gamma =2$; green (solid line), magnetic fields $B\left(\rho \right)$ with $\gamma =3$; light blue (solid line), magnetic fields $B\left(\rho \right)$ with $\gamma =4$; orange (solid line), magnetic fields $B\left(\rho \right)$ with $\gamma =5$; yellow (solid line), magnetic fields $B\left(\rho \right)$ with $\gamma =6$; dark blue (solid line), magnetic fields $B\left(\rho \right)$ with $\gamma =7$; red (solid line), magnetic fields $B\left(\rho \right)$ with $\gamma =8$; purple (dashed line), magnetic fields $B\left(\rho \right)$ with $\gamma =9$; brown (solid line), magnetic fields $B\left(\rho \right)$ with $\gamma =10$.

Table 4. Strengths of the magnetic field at saturation density ${\rho }_0=0.153$ fm${}^{-3}$ ( $B\left({\rho }_0\right)$ in unit of Gauss) for 12 EoSs with $B_0=2.5\times {10}^{18}$ G.

$\mathit{\alpha }$	$\mathit{B}\left({\mathit{\rho }}_0\right)$
0.01	$2.59\times {10}^{16}$
0.02	$5.05\times {10}^{16}$
0.03	$7.79\times {10}^{16}$
0.04	$9.90\times {10}^{16}$
0.05	$1.23\times {10}^{17}$
0.06	$1.47\times {10}^{17}$
0.07	$1.70\times {10}^{17}$
0.08	$1.93\times {10}^{17}$
0.09	$2.16\times {10}^{17}$

The maximum mass, radius at 1.4$M_{\odot }$, and radius at 2.072$M_{\odot }$ by changing $\alpha$ and $\gamma$ in Equation (13) are shown in Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11 and Table 12 for each EoSs. The MR relations by changing $\alpha$ and $\gamma$ are given in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 for those EoSs with various incompressibilities, which satisfy the observational constraints.

Figure 4 shows the MR relations of GM1 EoS with magnetic fields. The following EoSs go through 68% credibility with respect to the maximum mass and the radius at 1.4 $M_{\odot }$.

• For $\gamma =2$, $\alpha =$0.05, 0.06, and 0.07;
• For $\gamma =3$, $\alpha =$0.02, 0.03, and 0.04;
• For $\gamma =4$, $\alpha =$0.01.

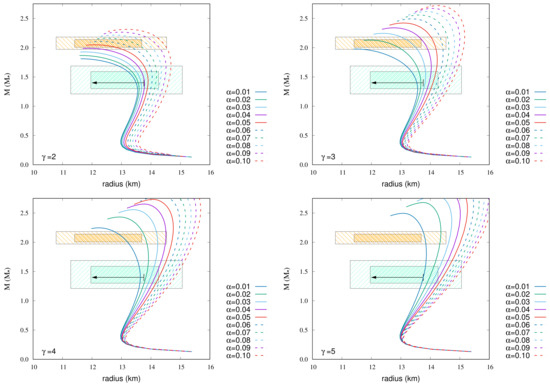
Figure 4. MR relations of GM1 EoS with magnetic fields. The strength of surface magnetic field strength $B_s$ is ${10}^{12}$ G, and the central magnetic field strength $B_0$ is $2.5\times {10}^{18}$ G. The arrow and colored hatched areas are the same as in Figure 1.

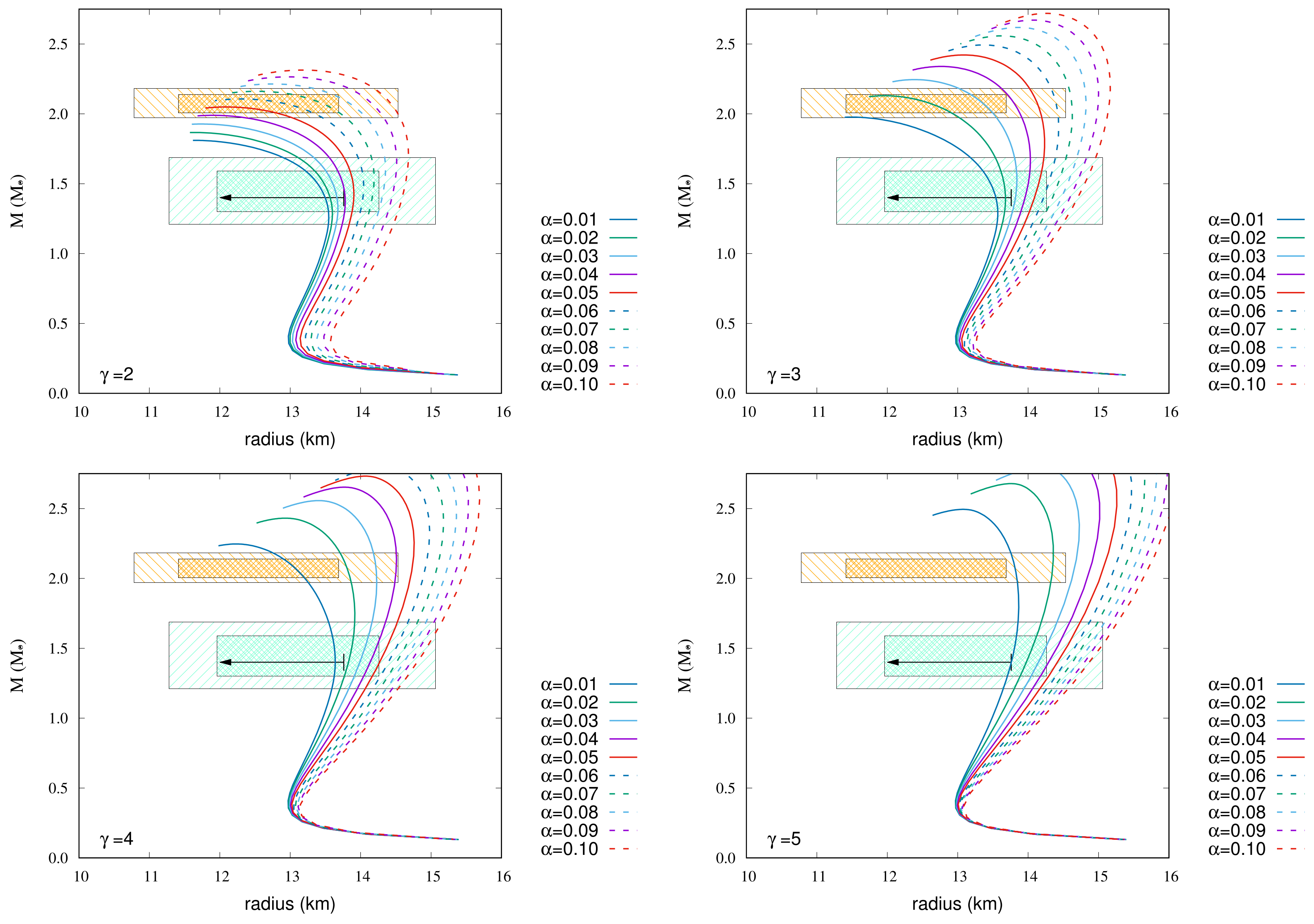
Figure 5 shows the MR relations of GM3 EoS with magnetic fields. The following EoSs go through 68% credibility with respect to the maximum mass and the radius at 1.4 $M_{\odot }$.

• For $\gamma =2$, $\alpha$ = 0.09;
• For $\gamma =3$, $\alpha$ = 0.03, 0.04, and 0.05;
• For $\gamma =4$, $\alpha$ = 0.01 and 0.02;
• For $\gamma =5$, $\alpha$ = 0.01.

Figure 6 shows the MR relations of NL3$\omega \rho$-a EoS with magnetic fields. The following EoSs go through 68% credibility with respect to the maximum mass and the radius at 1.4 $M_{\odot }$.

• For $\gamma =1$, $\alpha =$0.01;
• For $\gamma =2$, $\alpha =$0.01.

Figure 7 shows the MR relations of NL3$\omega \rho$-b EoS with magnetic fields. In this case, no EoSs go through 68% credibility with respect to the maximum mass and the radius at 1.4 $M_{\odot }$.

Table 5. Maximum mass ($M_{\max }$) in unit of $M_{\odot }$ and radius (km) at $M=1.4M_{\odot }$ ($R_{1.4M_{\odot }}$) and radius (km) at $M=2.072M_{\odot }$ ($R_{2.072M_{\odot }}$) for GM1 EoS with magnetic fields ($B_s={10}^{12}$ G, $B_0=2.5\times {10}^{18}$ G).

$\mathit{\gamma }=$ 2				$\mathit{\gamma }=$ 3
$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$	$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$
0.01	1.810	13.50	−	0.01	1.977	13.54	−
0.02	1.867	13.57	−	0.02	2.130	13.68	12.62
0.03	1.927	13.66	−	0.03	2.245	13.82	13.37
0.04	1.989	13.78	−	0.04	2.339	13.96	13.81
0.05	2.049	13.90	−	0.05	2.421	14.09	14.13
0.06	2.107	14.03	12.93	0.06	2.493	14.22	14.40
0.07	2.161	14.16	13.47	0.07	2.558	14.35	14.62
0.08	2.214	14.30	13.85	0.08	2.619	14.47	14.82
0.09	2.265	14.44	14.16	0.09	2.671	14.59	15.00
0.10	2.313	14.59	14.43	0.10	2.719	14.71	15.15
$\mathit{\gamma }=$ 4				$\mathit{\gamma }=$ 5
$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$	$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$
0.01	2.247	13.64	13.07	0.01	2.494	13.76	13.82
0.02	2.431	13.83	13.81	0.02	2.679	13.98	14.35
0.03	2.557	13.99	14.22	0.03	2.799	14.15	14.66
0.04	2.653	14.14	14.51	0.04	2.889	14.29	14.88
0.05	2.732	14.27	14.73	0.05	2.960	14.42	15.07
0.06	2.800	14.40	14.92	0.05	3.020	14.53	15.23
0.07	2.862	14.51	15.08	0.07	3.072	14.63	15.37
0.08	2.915	14.62	15.23	0.08	3.118	14.72	15.50
0.09	2.962	14.71	15.37	0.09	3.160	14.80	15.61
0.10	3.005	14.81	15.49	0.10	3.197	14.88	15.71

Table 5. Maximum mass ($M_{\max }$) in unit of $M_{\odot }$ and radius (km) at $M=1.4M_{\odot }$ ($R_{1.4M_{\odot }}$) and radius (km) at $M=2.072M_{\odot }$ ($R_{2.072M_{\odot }}$) for GM1 EoS with magnetic fields ($B_s={10}^{12}$ G, $B_0=2.5\times {10}^{18}$ G).

$\mathit{\gamma }=$ 2				$\mathit{\gamma }=$ 3
$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$	$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$
0.01	1.810	13.50	−	0.01	1.977	13.54	−
0.02	1.867	13.57	−	0.02	2.130	13.68	12.62
0.03	1.927	13.66	−	0.03	2.245	13.82	13.37
0.04	1.989	13.78	−	0.04	2.339	13.96	13.81
0.05	2.049	13.90	−	0.05	2.421	14.09	14.13
0.06	2.107	14.03	12.93	0.06	2.493	14.22	14.40
0.07	2.161	14.16	13.47	0.07	2.558	14.35	14.62
0.08	2.214	14.30	13.85	0.08	2.619	14.47	14.82
0.09	2.265	14.44	14.16	0.09	2.671	14.59	15.00
0.10	2.313	14.59	14.43	0.10	2.719	14.71	15.15
$\mathit{\gamma }=$ 4				$\mathit{\gamma }=$ 5
$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$	$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$
0.01	2.247	13.64	13.07	0.01	2.494	13.76	13.82
0.02	2.431	13.83	13.81	0.02	2.679	13.98	14.35
0.03	2.557	13.99	14.22	0.03	2.799	14.15	14.66
0.04	2.653	14.14	14.51	0.04	2.889	14.29	14.88
0.05	2.732	14.27	14.73	0.05	2.960	14.42	15.07
0.06	2.800	14.40	14.92	0.05	3.020	14.53	15.23
0.07	2.862	14.51	15.08	0.07	3.072	14.63	15.37
0.08	2.915	14.62	15.23	0.08	3.118	14.72	15.50
0.09	2.962	14.71	15.37	0.09	3.160	14.80	15.61
0.10	3.005	14.81	15.49	0.10	3.197	14.88	15.71

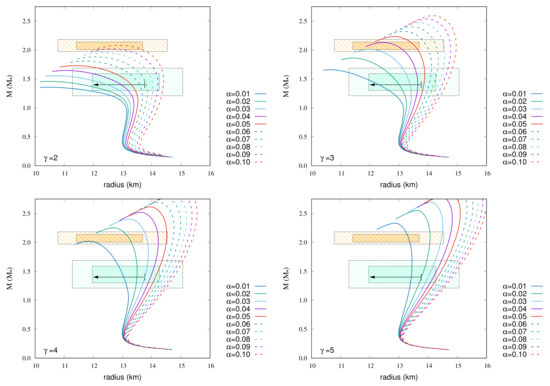
Figure 5. MR relations of GM3 EoS with magnetic fields. The strength of surface magnetic field strength $B_s$ is ${10}^{12}$ G, and the central magnetic field strength $B_0$ is $2.5\times {10}^{18}$ G. The arrow and colored hatched areas are the same as in Figure 1.

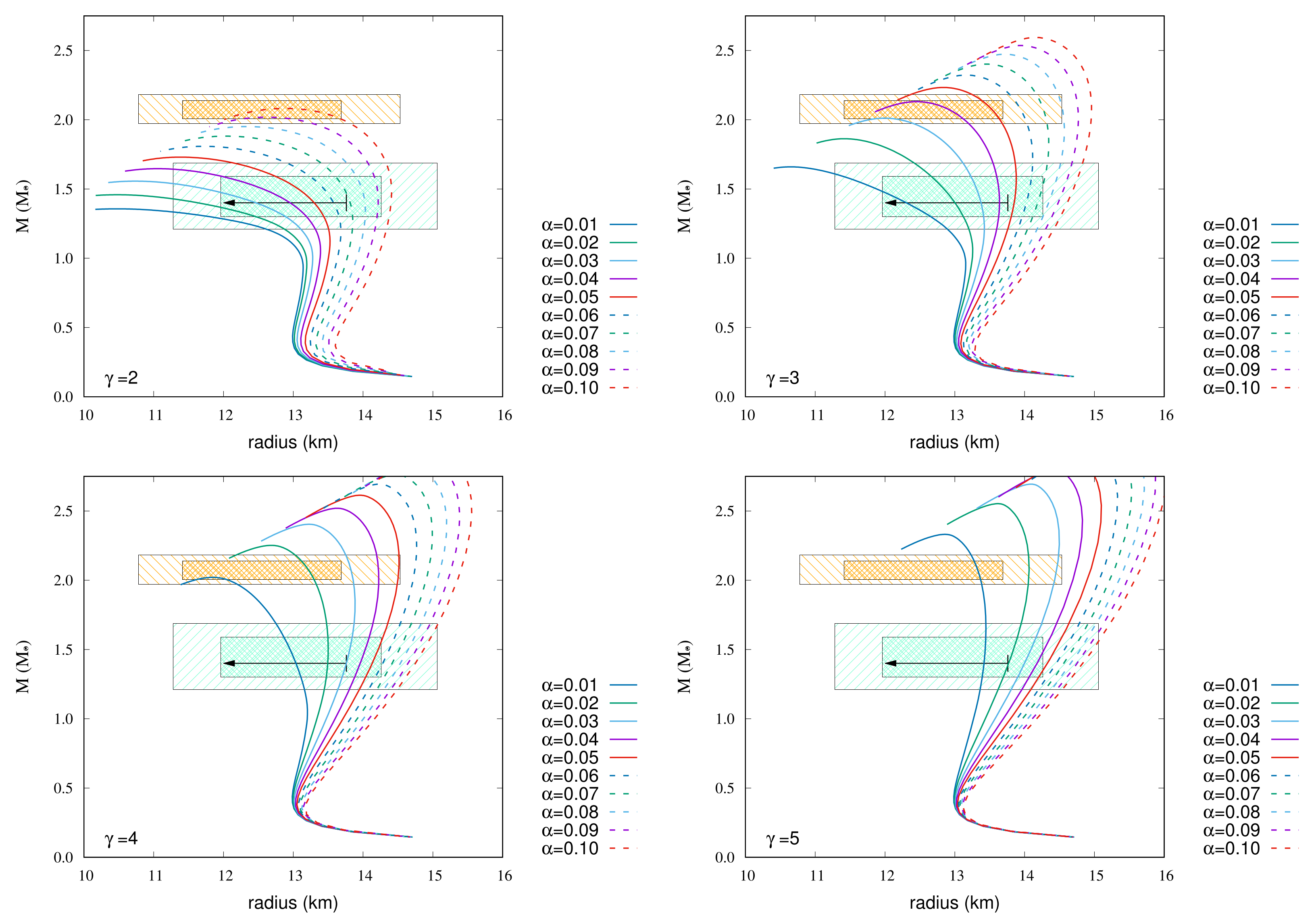
Table 6. Maximum mass ($M_{\max }$) in unit of $M_{\odot }$ and radius (km) at $M=1.4M_{\odot }$ ($R_{1.4M_{\odot }}$) and radius (km) at $M=2.072M_{\odot }$ ($R_{2.072M_{\odot }}$) for GM3 EoS with magnetic fields ($B_s={10}^{12}$ G, $B_0=2.5\times {10}^{18}$ G).

$\mathit{\gamma }=$ 2				$\mathit{\gamma }=$ 3
$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$	$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$
0.01	1.357	−	−	0.01	1.660	12.31	−
0.02	1.458	11.63	−	0.02	1.863	13.00	−
0.03	1.557	12.46	−	0.03	2.011	13.38	−
0.04	1.647	12.95	−	0.04	2.130	13.64	12.92
0.05	1.730	13.30	−	0.05	2.233	13.85	13.54
0.06	1.808	13.58	−	0.06	2.322	14.03	13.95
0.07	1.881	13.82	−	0.07	2.402	14.19	14.27
0.08	1.951	14.03	−	0.08	2.473	14.34	14.54
0.09	2.018	14.22	−	0.09	2.536	14.48	14.77
0.10	2.081	14.40	13.19	0.10	2.594	14.61	14.96
$\mathit{\gamma }=$ 4				$\mathit{\gamma }=$ 5
$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$	$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$
0.01	2.021	13.04		0.01	2.768	13.84	14.36
0.02	2.252	13.49	13.22	0.02	2.949	14.13	14.80
0.03	2.404	13.76	13.83	0.03	3.060	14.31	15.07
0.04	2.520	13.96	14.22	0.04	3.139	14.45	15.27
0.05	2.614	14.13	14.51	0.05	3.201	14.57	15.42
0.06	2.694	14.28	14.74	0.06	3.253	14.66	15.55
0.07	2.763	14.42	14.94	0.07	3.297	14.75	15.66
0.08	2.824	14.54	15.11	0.08	3.336	14.82	15.76
0.09	2.878	14.65	15.26	0.09	3.370	14.89	15.85
0.10	2.927	14.75	15.40	0.10	3.401	14.95	15.93

Table 6. Maximum mass ($M_{\max }$) in unit of $M_{\odot }$ and radius (km) at $M=1.4M_{\odot }$ ($R_{1.4M_{\odot }}$) and radius (km) at $M=2.072M_{\odot }$ ($R_{2.072M_{\odot }}$) for GM3 EoS with magnetic fields ($B_s={10}^{12}$ G, $B_0=2.5\times {10}^{18}$ G).

$\mathit{\gamma }=$ 2				$\mathit{\gamma }=$ 3
$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$	$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$
0.01	1.357	−	−	0.01	1.660	12.31	−
0.02	1.458	11.63	−	0.02	1.863	13.00	−
0.03	1.557	12.46	−	0.03	2.011	13.38	−
0.04	1.647	12.95	−	0.04	2.130	13.64	12.92
0.05	1.730	13.30	−	0.05	2.233	13.85	13.54
0.06	1.808	13.58	−	0.06	2.322	14.03	13.95
0.07	1.881	13.82	−	0.07	2.402	14.19	14.27
0.08	1.951	14.03	−	0.08	2.473	14.34	14.54
0.09	2.018	14.22	−	0.09	2.536	14.48	14.77
0.10	2.081	14.40	13.19	0.10	2.594	14.61	14.96
$\mathit{\gamma }=$ 4				$\mathit{\gamma }=$ 5
$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$	$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$
0.01	2.021	13.04		0.01	2.768	13.84	14.36
0.02	2.252	13.49	13.22	0.02	2.949	14.13	14.80
0.03	2.404	13.76	13.83	0.03	3.060	14.31	15.07
0.04	2.520	13.96	14.22	0.04	3.139	14.45	15.27
0.05	2.614	14.13	14.51	0.05	3.201	14.57	15.42
0.06	2.694	14.28	14.74	0.06	3.253	14.66	15.55
0.07	2.763	14.42	14.94	0.07	3.297	14.75	15.66
0.08	2.824	14.54	15.11	0.08	3.336	14.82	15.76
0.09	2.878	14.65	15.26	0.09	3.370	14.89	15.85
0.10	2.927	14.75	15.40	0.10	3.401	14.95	15.93

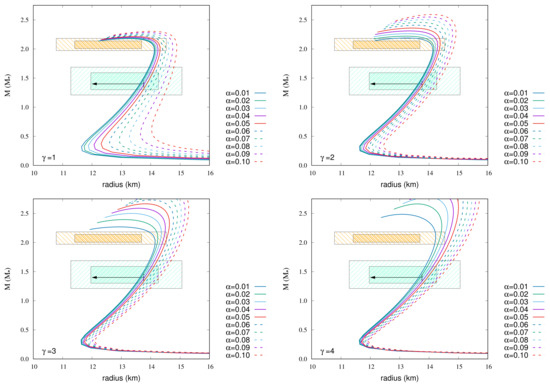
Figure 6. MR relations of NL3$\omega \rho$-a EoS with magnetic fields. The strength of surface magnetic field strength $B_s$ is ${10}^{12}$ G, and the central magnetic field strength $B_0$ is $2.5\times {10}^{18}$ G. The arrow and colored hatched areas are the same as in Figure 1.

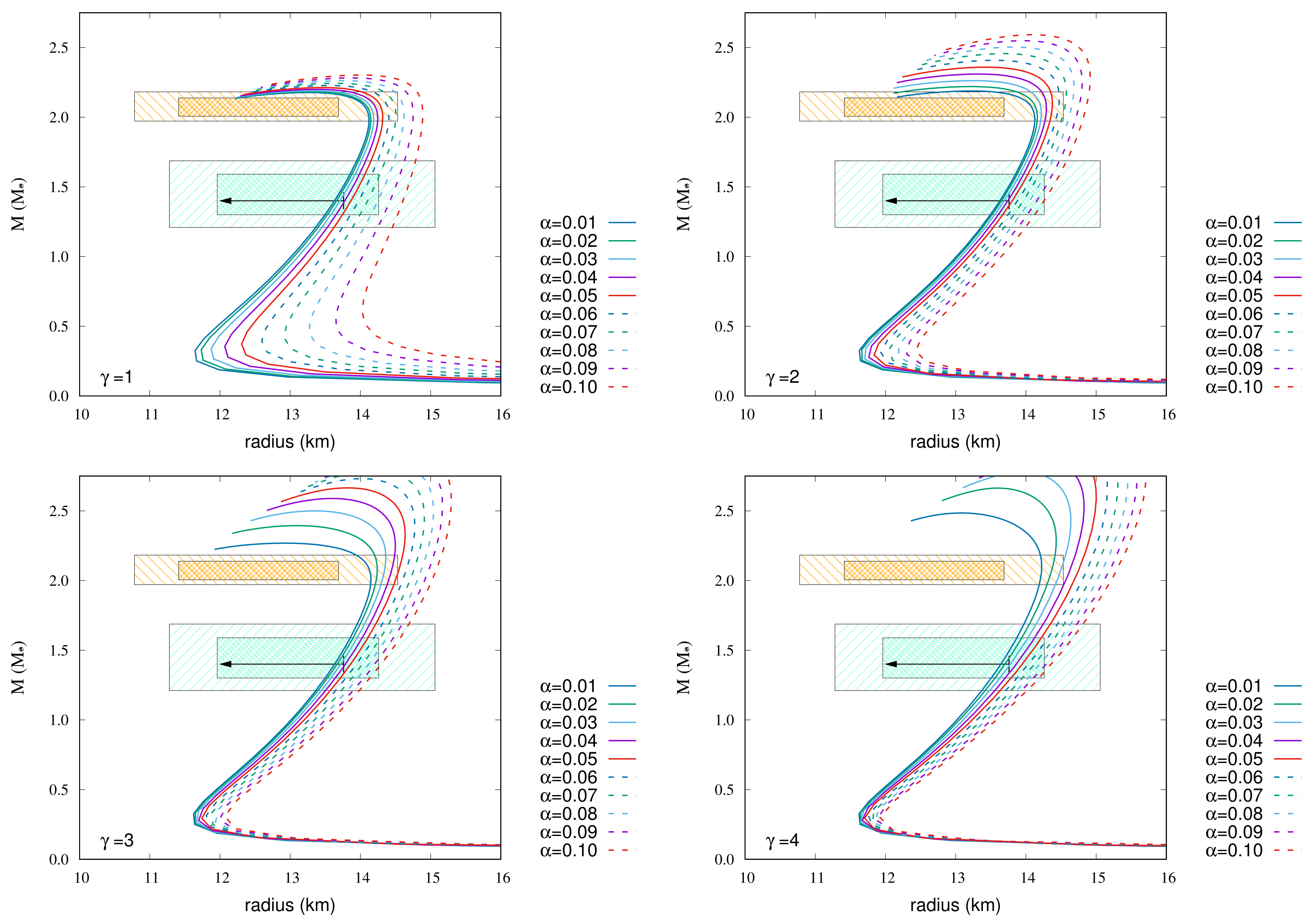
Table 7. Maximum mass ($M_{\max }$) in unit of $M_{\odot }$ and radius (km) at $M=1.4M_{\odot }$ ($R_{1.4M_{\odot }}$) and radius (km) at $M=2.072M_{\odot }$ ($R_{2.072M_{\odot }}$) for NL3$\omega \rho$-a EoS with magnetic fields ($B_s={10}^{12}$ G, $B_0=2.5\times {10}^{18}$ G).

$\mathit{\gamma }=$ 1				$\mathit{\gamma }=$ 2
$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$	$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$
0.01	2.177	13.63	14.07	0.01	2.188	13.63	14.08
0.02	2.182	13.66	14.10	0.02	2.220	13.65	14.14
0.03	2.190	13.71	14.15	0.03	2.262	13.69	14.21
0.04	2.200	13.78	14.21	0.04	2.310	13.74	14.29
0.05	2.212	13.87	14.29	0.05	2.359	13.81	14.38
0.06	2.227	13.98	14.39	0.06	2.409	13.88	14.47
0.07	2.244	14.10	14.49	0.07	2.457	13.96	14.55
0.08	2.262	14.25	14.61	0.08	2.503	14.05	14.65
0.09	2.282	14.42	14.75	0.09	2.549	14.16	14.75
0.10	2.303	14.61	14.88	0.10	2.592	14.26	14.86
$\mathit{\gamma }=$ 3				$\mathit{\gamma }=$ 4
$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$	$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$
0.01	2.268	13.63	14.13	0.01	2.485	13.64	14.22
0.02	2.394	13.67	14.24	0.02	2.664	13.70	14.37
0.03	2.500	13.72	14.34	0.03	2.782	13.78	14.50
0.04	2.589	13.79	14.44	0.04	2.869	13.86	14.63
0.05	2.665	13.86	14.55	0.05	2.939	13.95	14.75
0.06	2.731	13.94	14.65	0.06	2.997	14.04	14.87
0.07	2.789	14.03	14.76	0.07	3.047	14.12	14.98
0.08	2.841	14.12	14.87	0.08	3.089	14.21	15.09
0.09	2.887	14.21	14.97	0.09	3.127	14.29	15.19
0.10	2.930	14.30	15.08	0.10	3.161	14.37	15.29

Table 7. Maximum mass ($M_{\max }$) in unit of $M_{\odot }$ and radius (km) at $M=1.4M_{\odot }$ ($R_{1.4M_{\odot }}$) and radius (km) at $M=2.072M_{\odot }$ ($R_{2.072M_{\odot }}$) for NL3$\omega \rho$-a EoS with magnetic fields ($B_s={10}^{12}$ G, $B_0=2.5\times {10}^{18}$ G).

$\mathit{\gamma }=$ 1				$\mathit{\gamma }=$ 2
$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$	$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$
0.01	2.177	13.63	14.07	0.01	2.188	13.63	14.08
0.02	2.182	13.66	14.10	0.02	2.220	13.65	14.14
0.03	2.190	13.71	14.15	0.03	2.262	13.69	14.21
0.04	2.200	13.78	14.21	0.04	2.310	13.74	14.29
0.05	2.212	13.87	14.29	0.05	2.359	13.81	14.38
0.06	2.227	13.98	14.39	0.06	2.409	13.88	14.47
0.07	2.244	14.10	14.49	0.07	2.457	13.96	14.55
0.08	2.262	14.25	14.61	0.08	2.503	14.05	14.65
0.09	2.282	14.42	14.75	0.09	2.549	14.16	14.75
0.10	2.303	14.61	14.88	0.10	2.592	14.26	14.86
$\mathit{\gamma }=$ 3				$\mathit{\gamma }=$ 4
$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$	$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$
0.01	2.268	13.63	14.13	0.01	2.485	13.64	14.22
0.02	2.394	13.67	14.24	0.02	2.664	13.70	14.37
0.03	2.500	13.72	14.34	0.03	2.782	13.78	14.50
0.04	2.589	13.79	14.44	0.04	2.869	13.86	14.63
0.05	2.665	13.86	14.55	0.05	2.939	13.95	14.75
0.06	2.731	13.94	14.65	0.06	2.997	14.04	14.87
0.07	2.789	14.03	14.76	0.07	3.047	14.12	14.98
0.08	2.841	14.12	14.87	0.08	3.089	14.21	15.09
0.09	2.887	14.21	14.97	0.09	3.127	14.29	15.19
0.10	2.930	14.30	15.08	0.10	3.161	14.37	15.29

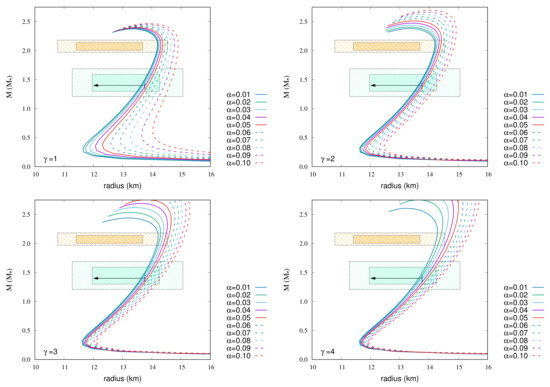
Figure 7. MR relations of NL3$\omega \rho$-b EoS with magnetic fields. The strength of surface magnetic field strength $B_s$ is ${10}^{12}$ G, and the central magnetic field strength $B_0$ is $2.5\times {10}^{18}$ G. The arrow and colored hatched areas are the same as in Figure 1.

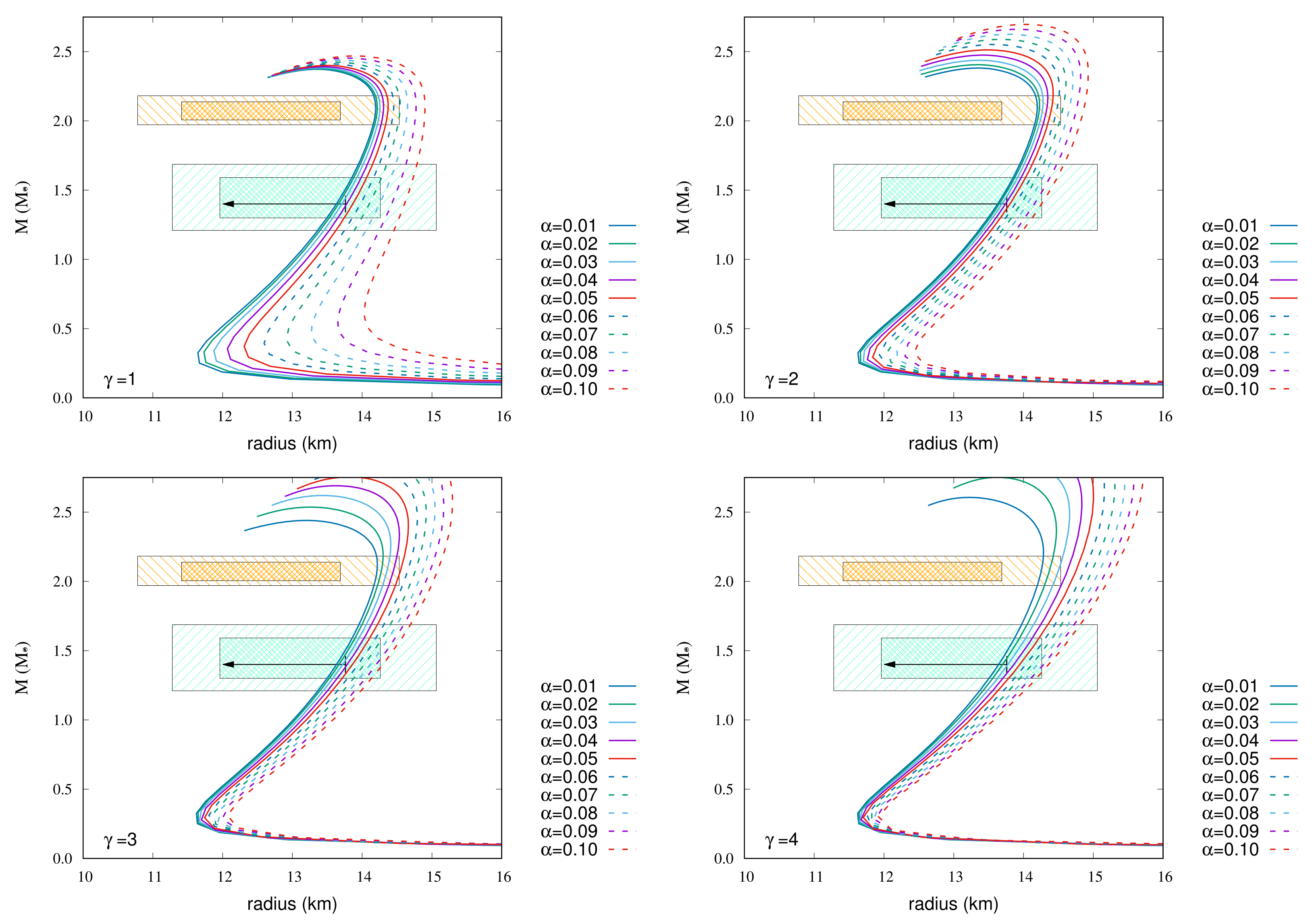
Table 8. Maximum mass ($M_{\max }$) in unit of $M_{\odot }$ and radius (km) at $M=1.4M_{\odot }$ ($R_{1.4M_{\odot }}$) and radius (km) at $M=2.072M_{\odot }$ ($R_{2.072M_{\odot }}$) for NL3$\omega \rho$-b EoS with magnetic fields ($B_s={10}^{12}$ G, $B_0=2.5\times {10}^{18}$ G).

$\mathit{\gamma }=$ 1				$\mathit{\gamma }=$ 2
$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$	$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$
0.01	2.373	13.63	14.19	0.01	2.381	13.63	14.19
0.02	2.377	13.66	14.21	0.02	2.405	13.65	14.23
0.03	2.383	13.71	14.25	0.03	2.438	13.69	14.27
0.04	2.390	13.78	14.30	0.04	2.475	13.74	14.33
0.05	2.400	13.87	14.37	0.05	2.512	13.81	14.39
0.06	2.411	13.98	14.45	0.06	2.551	13.88	14.47
0.07	2.424	14.10	14.54	0.07	2.588	13.96	14.56
0.08	2.438	14.25	14.65	0.08	2.625	14.05	14.65
0.09	2.453	14.42	14.77	0.09	2.661	14.16	14.75
0.10	2.469	14.61	14.90	0.10	2.696	14.26	14.86
$\mathit{\gamma }=$ 3				$\mathit{\gamma }=$ 4
$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$	$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$
0.01	2.440	13.63	14.21	0.01	2.606	13.64	14.25
0.02	2.536	13.67	14.27	0.02	2.751	13.70	14.37
0.03	2.620	13.72	14.35	0.03	2.848	13.78	14.50
0.04	2.691	13.79	14.45	0.04	2.924	13.86	14.63
0.05	2.754	13.86	14.55	0.05	2.984	13.95	14.75
0.06	2.808	13.94	14.65	0.06	3.033	14.04	14.87
0.07	2.855	14.03	14.76	0.07	3.076	14.12	14.98
0.08	2.900	14.12	14.87	0.08	3.114	14.21	15.09
0.09	2.940	14.21	14.97	0.09	3.149	14.29	15.19
0.10	2.977	14.30	15.08	0.10	3.180	14.37	15.29

Table 8. Maximum mass ($M_{\max }$) in unit of $M_{\odot }$ and radius (km) at $M=1.4M_{\odot }$ ($R_{1.4M_{\odot }}$) and radius (km) at $M=2.072M_{\odot }$ ($R_{2.072M_{\odot }}$) for NL3$\omega \rho$-b EoS with magnetic fields ($B_s={10}^{12}$ G, $B_0=2.5\times {10}^{18}$ G).

$\mathit{\gamma }=$ 1				$\mathit{\gamma }=$ 2
$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$	$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$
0.01	2.373	13.63	14.19	0.01	2.381	13.63	14.19
0.02	2.377	13.66	14.21	0.02	2.405	13.65	14.23
0.03	2.383	13.71	14.25	0.03	2.438	13.69	14.27
0.04	2.390	13.78	14.30	0.04	2.475	13.74	14.33
0.05	2.400	13.87	14.37	0.05	2.512	13.81	14.39
0.06	2.411	13.98	14.45	0.06	2.551	13.88	14.47
0.07	2.424	14.10	14.54	0.07	2.588	13.96	14.56
0.08	2.438	14.25	14.65	0.08	2.625	14.05	14.65
0.09	2.453	14.42	14.77	0.09	2.661	14.16	14.75
0.10	2.469	14.61	14.90	0.10	2.696	14.26	14.86
$\mathit{\gamma }=$ 3				$\mathit{\gamma }=$ 4
$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$	$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$
0.01	2.440	13.63	14.21	0.01	2.606	13.64	14.25
0.02	2.536	13.67	14.27	0.02	2.751	13.70	14.37
0.03	2.620	13.72	14.35	0.03	2.848	13.78	14.50
0.04	2.691	13.79	14.45	0.04	2.924	13.86	14.63
0.05	2.754	13.86	14.55	0.05	2.984	13.95	14.75
0.06	2.808	13.94	14.65	0.06	3.033	14.04	14.87
0.07	2.855	14.03	14.76	0.07	3.076	14.12	14.98
0.08	2.900	14.12	14.87	0.08	3.114	14.21	15.09
0.09	2.940	14.21	14.97	0.09	3.149	14.29	15.19
0.10	2.977	14.30	15.08	0.10	3.180	14.37	15.29

Figure 8 shows the MR relations of TM2$\omega \rho$-a EoS with magnetic fields. The following EoSs go through 68% credibility with respect to the maximum mass and the radius 1.4 $M_{\odot }$.

• For $\gamma =2$, $\alpha =$0.05 and 0.06;
• For $\gamma =3$, $\alpha =$0.02, 0.03, and 0.04;
• For $\gamma =4$, $\alpha =$0.01.

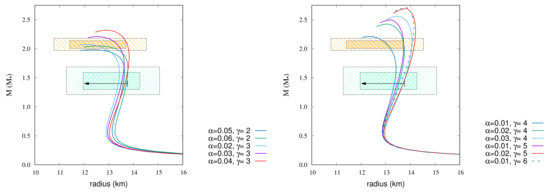
Figure 8. MR relations of TM2$\omega \rho$-a EoS with magnetic fields. The strength of surface magnetic field strength $B_s$ is ${10}^{12}$ G, and the central magnetic field strength $B_0$ is $2.5\times {10}^{18}$ G. The arrow and colored hatched areas are the same as in Figure 1.

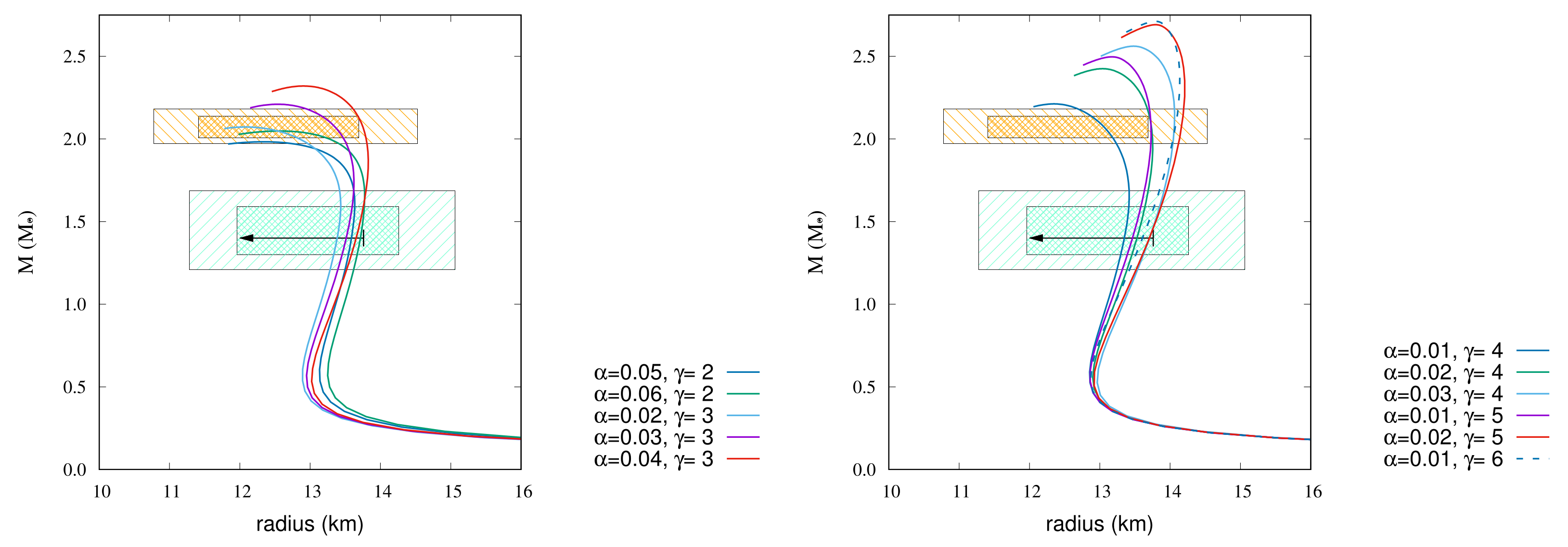
Figure 9 shows the MR relations of TM2$\omega \rho$-b EoS with magnetic fields. The following EoSs go through 68% credibility with respect to the maximum mass and the radius at 1.4 $M_{\odot }$.

1.

For $\gamma =2$, $\alpha =$0.03, 0.04, 0.05, and 0.06;

2.

For $\gamma =3$, $\alpha =$0.01, 0.02, 0.03, and 0.04;

Table 9. Maximum mass ($M_{\max }$) in unit of $M_{\odot }$ and radius (km) at $M=1.4M_{\odot }$ ($R_{1.4M_{\odot }}$) and radius (km) at $M=2.072M_{\odot }$ ($R_{2.072M_{\odot }}$) for TM2$\omega \rho$-a EoS with magnetic fields ($B_s={10}^{12}$ G, $B_0=2.5\times {10}^{18}$ G).

$\mathit{\gamma }$	$\mathit{\alpha }$	${\mathit{M}}_{\mathbf{max}}$	${\mathit{R}}_{1.4{\mathit{M}}_{\odot }}$	${\mathit{R}}_{2.072{\mathit{M}}_{\odot }}$
2	0.05	1.983	13.59	−
2	0.06	2.048	13.71	12.56
3	0.02	2.072	13.38	12.12
3	0.03	2.210	13.51	13.35
3	0.04	2.320	13.65	13.75
4	0.01	2.212	13.35	13.06
4	0.02	2.425	13.53	13.73
4	0.03	2.561	13.71	14.06
5	0.01	2.497	13.46	13.73
5	0.02	2.691	13.71	14.16
6	0.01	2.711	13.61	14.08

Table 9. Maximum mass ($M_{\max }$) in unit of $M_{\odot }$ and radius (km) at $M=1.4M_{\odot }$ ($R_{1.4M_{\odot }}$) and radius (km) at $M=2.072M_{\odot }$ ($R_{2.072M_{\odot }}$) for TM2$\omega \rho$-a EoS with magnetic fields ($B_s={10}^{12}$ G, $B_0=2.5\times {10}^{18}$ G).

$\mathit{\gamma }$	$\mathit{\alpha }$	${\mathit{M}}_{\mathbf{max}}$	${\mathit{R}}_{1.4{\mathit{M}}_{\odot }}$	${\mathit{R}}_{2.072{\mathit{M}}_{\odot }}$
2	0.05	1.983	13.59	−
2	0.06	2.048	13.71	12.56
3	0.02	2.072	13.38	12.12
3	0.03	2.210	13.51	13.35
3	0.04	2.320	13.65	13.75
4	0.01	2.212	13.35	13.06
4	0.02	2.425	13.53	13.73
4	0.03	2.561	13.71	14.06
5	0.01	2.497	13.46	13.73
5	0.02	2.691	13.71	14.16
6	0.01	2.711	13.61	14.08

3.

For $\gamma =4$, $\alpha =$0.01.

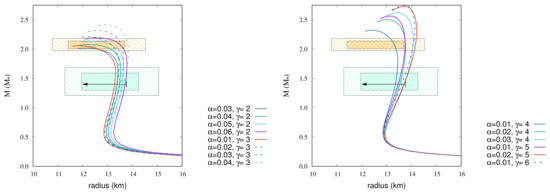
Figure 9. MR relations of TM2$\omega \rho$-b EoS with magnetic fields. The strength of surface magnetic field strength $B_s$ is ${10}^{12}$ G, and the central magnetic field strength $B_0$ is $2.5\times {10}^{18}$ G. The arrow and colored hatched areas are the same as in Figure 1.

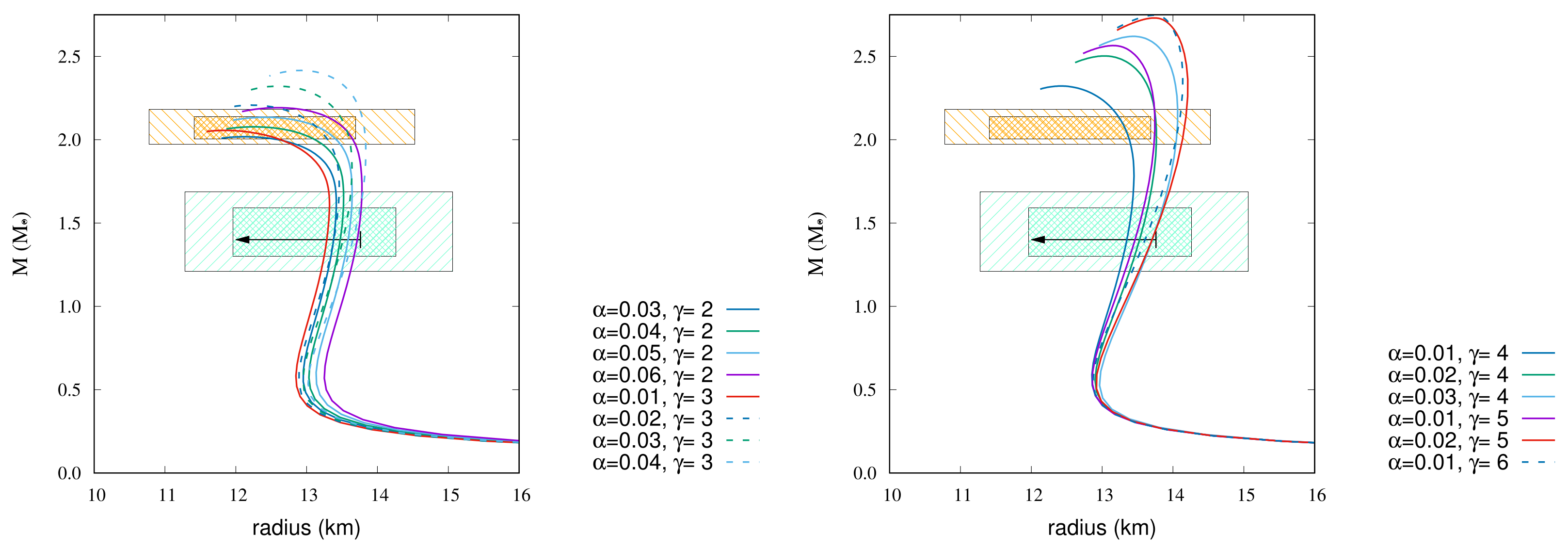
Table 10. Maximum mass ($M_{\max }$) in unit of $M_{\odot }$ and radius (km) at $M=1.4M_{\odot }$ ($R_{1.4M_{\odot }}$) and radius (km) at $M=2.072M_{\odot }$ ($R_{2.072M_{\odot }}$) for TM2$\omega \rho$-b EoS with magnetic fields ($B_s={10}^{12}$ G, $B_0=2.5\times {10}^{18}$ G).

$\mathit{\gamma }$	$\mathit{\alpha }$	${\mathit{M}}_{\mathbf{max}}$	${\mathit{R}}_{1.4{\mathit{M}}_{\odot }}$	${\mathit{R}}_{2.072{\mathit{M}}_{\odot }}$
2	0.03	2.018	13.38	−
2	0.04	2.077	13.47	12.51
2	0.05	2.135	13.59	13.18
2	0.06	2.192	13.71	13.52
3	0.01	2.056	13.28	−
3	0.02	2.207	13.38	13.15
3	0.03	2.321	13.51	13.55
3	0.04	2.416	13.65	13.81
4	0.01	2.322	13.35	13.32
4	0.02	2.503	13.53	13.76
4	0.03	2.620	13.71	14.06
5	0.01	2.565	13.46	13.74
5	0.02	2.731	13.71	14.16
6	0.01	2.748	13.61	14.08

Table 10. Maximum mass ($M_{\max }$) in unit of $M_{\odot }$ and radius (km) at $M=1.4M_{\odot }$ ($R_{1.4M_{\odot }}$) and radius (km) at $M=2.072M_{\odot }$ ($R_{2.072M_{\odot }}$) for TM2$\omega \rho$-b EoS with magnetic fields ($B_s={10}^{12}$ G, $B_0=2.5\times {10}^{18}$ G).

$\mathit{\gamma }$	$\mathit{\alpha }$	${\mathit{M}}_{\mathbf{max}}$	${\mathit{R}}_{1.4{\mathit{M}}_{\odot }}$	${\mathit{R}}_{2.072{\mathit{M}}_{\odot }}$
2	0.03	2.018	13.38	−
2	0.04	2.077	13.47	12.51
2	0.05	2.135	13.59	13.18
2	0.06	2.192	13.71	13.52
3	0.01	2.056	13.28	−
3	0.02	2.207	13.38	13.15
3	0.03	2.321	13.51	13.55
3	0.04	2.416	13.65	13.81
4	0.01	2.322	13.35	13.32
4	0.02	2.503	13.53	13.76
4	0.03	2.620	13.71	14.06
5	0.01	2.565	13.46	13.74
5	0.02	2.731	13.71	14.16
6	0.01	2.748	13.61	14.08

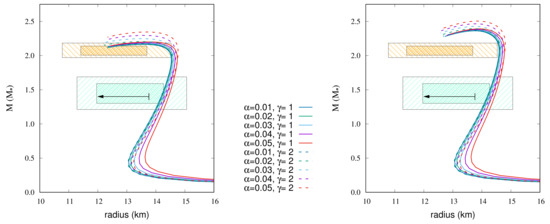
Figure 10. MR relations of DDME2-a (left) and DDME2-b (right) EoSs with magnetic fields. The strength of surface magnetic field strength $B_s$ is ${10}^{12}$ G, and the central magnetic field strength $B_0$ is $2.5\times {10}^{18}$ G. The arrow and colored hatched areas are the same as in Figure 1.

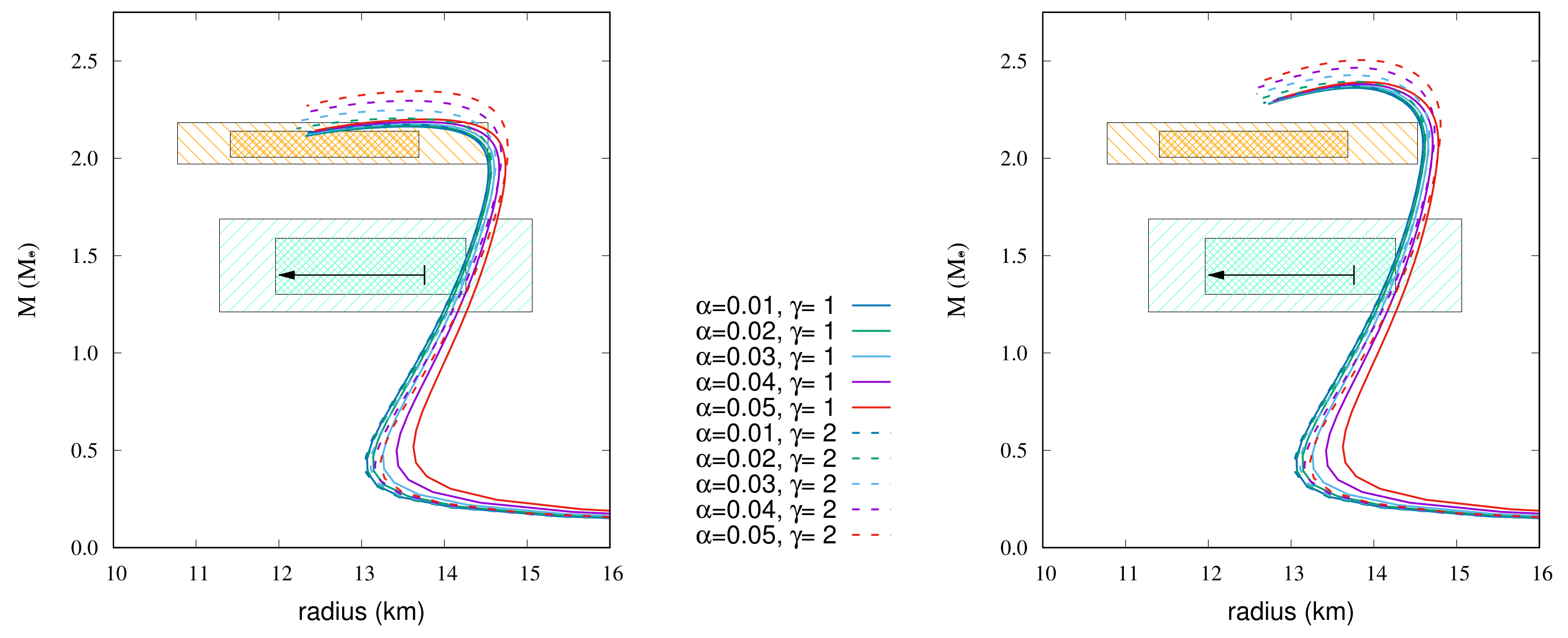
Table 11. Maximum mass ($M_{\max }$) in unit of $M_{\odot }$ and radius (km) at $M=1.4M_{\odot }$ ($R_{1.4M_{\odot }}$) and radius (km) at $M=2.072M_{\odot }$ ($R_{2.072M_{\odot }}$) for DDME2-a EoS with magnetic fields ($B_s={10}^{12}$ G, $B_0=2.5\times {10}^{18}$ G).

$\mathit{\gamma }=1$				$\mathit{\gamma }=2$
$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$	$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$
0.01	2.163	14.18	14.43	0.01	2.174	14.18	14.45
0.02	2.168	14.22	14.47	0.02	2.205	14.21	14.51
0.03	2.176	14.27	14.52	0.03	2.247	14.24	14.59
0.04	2.187	14.34	14.59	0.04	2.295	14.30	14.68
0.05	2.200	14.44	14.68	0.05	2.345	14.36	14.76

Table 11. Maximum mass ($M_{\max }$) in unit of $M_{\odot }$ and radius (km) at $M=1.4M_{\odot }$ ($R_{1.4M_{\odot }}$) and radius (km) at $M=2.072M_{\odot }$ ($R_{2.072M_{\odot }}$) for DDME2-a EoS with magnetic fields ($B_s={10}^{12}$ G, $B_0=2.5\times {10}^{18}$ G).

$\mathit{\gamma }=1$				$\mathit{\gamma }=2$
$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$	$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$
0.01	2.163	14.18	14.43	0.01	2.174	14.18	14.45
0.02	2.168	14.22	14.47	0.02	2.205	14.21	14.51
0.03	2.176	14.27	14.52	0.03	2.247	14.24	14.59
0.04	2.187	14.34	14.59	0.04	2.295	14.30	14.68
0.05	2.200	14.44	14.68	0.05	2.345	14.36	14.76

Table 12. Maximum mass ($M_{\max }$) in unit of $M_{\odot }$ and radius (km) at $M=1.4M_{\odot }$ ($R_{1.4M_{\odot }}$) and radius (km) at $M=2.072M_{\odot }$ ($R_{2.072M_{\odot }}$) for DDME2-b EoS with magnetic fields ($B_s={10}^{12}$ G, $B_0=2.5\times {10}^{18}$ G).

$\mathit{\gamma }=$ 1				$\mathit{\gamma }=$ 2
$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$	$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$
0.01	2.362	14.18	14.59	0.01	2.370	14.18	14.60
0.02	2.366	14.22	14.62	0.02	2.394	14.21	14.62
0.03	2.372	14.27	14.66	0.03	2.427	14.24	14.67
0.04	2.381	14.34	14.71	0.04	2.465	14.30	14.73
0.05	2.391	14.44	14.78	0.05	2.505	14.36	14.79

Table 12. Maximum mass ($M_{\max }$) in unit of $M_{\odot }$ and radius (km) at $M=1.4M_{\odot }$ ($R_{1.4M_{\odot }}$) and radius (km) at $M=2.072M_{\odot }$ ($R_{2.072M_{\odot }}$) for DDME2-b EoS with magnetic fields ($B_s={10}^{12}$ G, $B_0=2.5\times {10}^{18}$ G).

$\mathit{\gamma }=$ 1				$\mathit{\gamma }=$ 2
$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$	$\mathbf{\alpha }$	${\mathbf{M}}_{\max }$	${\mathbf{R}}_{\mathbf{1}.\mathbf{4}{\mathbf{M}}_{\odot }}$	${\mathbf{R}}_{\mathbf{2}.\mathbf{072}{\mathbf{M}}_{\odot }}$
0.01	2.362	14.18	14.59	0.01	2.370	14.18	14.60
0.02	2.366	14.22	14.62	0.02	2.394	14.21	14.62
0.03	2.372	14.27	14.66	0.03	2.427	14.24	14.67
0.04	2.381	14.34	14.71	0.04	2.465	14.30	14.73
0.05	2.391	14.44	14.78	0.05	2.505	14.36	14.79

Figure 10 shows the MR relations of DDME2-a (left) and DDME2-b (right) EoSs with magnetic fields. The following EoSs for DDME2-a go through 68% credibility with respect to the maximum mass and the radius at 1.4 $M_{\odot }$.

• For $\gamma =1$, $\alpha =$0.01, 0.02, and 0.03;
• For $\gamma =2$, $\alpha =$0.01.

4. Summary

In this work, the MR relations for magnetized neutron stars (NSs) have been investigated using twelve EoSs (seven kinds of EoSs). The NSs consist of nucleons and hyperons. They are implemented with magnetic fields, whose forms are changed by the shape parameters $\alpha$ and $\gamma$. The $\alpha$ and $\gamma$ are the damping factor and the exponent of the density dependence of a magnetic field, respectively.

First, we have found that, without any magnetic fields, only NL3$\omega \rho$-a EoS satisfies the constraint for mass and radius from observations. Second, we have found that many varieties of EoSs with the implement of strong magnetic fields give maximum masses over 2 $M_{\odot }$ and satisfy the constraints from the observations at the same time.

To summarize, using different shapes of the magnetic field, in this work, we have demonstrated that many kinds of EoSs with strong magnetic fields can satisfy the constraints on the maximum mass and the radius within the range by observations. Other EoSs with lower incompressibility ($K<240$ MeV) than those EoSs examined in this work will be studied in future work.