Abstract
In this review, we outline the expected tests of gravity that will be achieved at cosmological scales in the upcoming decades. We focus mainly on constraints on phenomenologically parameterized deviations from general relativity, which allow to test gravity in a model-independent way, but also review some of the expected constraints obtained with more physically motivated approaches. After reviewing the state-of-the-art for such constraints, we outline the expected improvement that future cosmological surveys will achieve, focusing mainly on future large-scale structures and cosmic microwave background surveys but also looking into novel probes on the nature of gravity. We will also highlight the necessity of overcoming accuracy issues in our theoretical predictions, issues that become relevant due to the expected sensitivity of future experiments.
1. Introduction
Since its first formulation in 1915, Einstein’s general relativity (GR) has demonstrated its ability to pass several observational tests. On the one hand, Einstein demonstrated that such a theory was able to explain the anomalous precession of Mercury’s perihelion, on the other hand, one of its theoretical predictions, the gravitational deflection of starlight by the Sun, was tested during the total solar eclipse of 29 May 1919 [1]. Following these early successes, several other predictions of GR passed observational tests in the following century, with the latest being the detection of gravitational waves [2] and the observation of a black hole shadow [3].
From the cosmological point of view, applying GR within the assumption of an expanding, isotropic and almost homogeneous Universe, has allowed to explain most of the observations done by cosmological surveys. However, in order to satisfy the observational constraints, one has to assume that the Universe is made not only of the particles included in the standard model of particle physics, but also by two unknown components: cold dark matter (CDM) and dark energy (DE). The presence of CDM, a matter component that only interacts gravitationally, is inferred both by cosmological and astrophysical observations (see, e.g., in [4,5,6]). These tell us that the amount of standard matter (from here on named baryons) predicted by big bang nucleosynthesis (BBN) cannot account for all the matter content required by observations, and this unknown CDM component needs to account for ≈25% of the current total energy budget of the Universe. With the contribution of relativistic particles being negligible at present time, and baryons accounting for only ≈5% of the total energy, the remaining of the content of the Universe is made up by DE. Such a component is needed to account for the late time acceleration of the Universe expansion, which was measured for the first time in the late 90s [7,8]. DE is generally identified with the cosmological constant , whose constant energy density and negative pressure allow to account for this accelerated phase. All these components make up the current standard cosmological model, the so called cosmological constant-cold dark matter model (CDM).
Notice that such a model assumes that GR is the correct description of gravity; while GR has been successfully tested, most of the bounds placed on deviations from it come from experiments done within the Solar System, and the assumption that this theory is a good description of gravity at cosmological scales might still be challenged. In particular, the long-known theoretical issues with the cosmological constant (the “fine tuning” and “coincidence” problems [9,10]), together with the recent tensions in the measurements of cosmological parameters (see, e.g., in [11]), have prompted the investigation of models alternative to CDM, including alternative theories of gravity (see, e.g., in [12]).
During the last two decades, the improvement of data from cosmological surveys has made possible to test the very foundation of the CDM model, i.e., the assumption that gravity is described by GR. Cosmic microwave background (CMB) and large-scale structures (LSS) surveys have the ability to probe the way that matter clusters and how it is distributed in the Universe, as well as giving insight on how matter distorts space-time through gravitational lensing. This allows to constrain possible departures from GR, thus providing observational tests of the theory of gravity at cosmological scales. The next two decades will see a further improvement of the quality of data, further improving our knowledge of the evolution of the Universe and, consequently, of the nature of gravity.
In this review, we want to highlight the progress on this investigation that will be achieved thanks to upcoming cosmological surveys. In Section 2, we will briefly review the landscape of alternative theories of gravity and we outline the parametric, model independent methods used to constrain departure from GR. We will then outline the currently available cosmological constraints in Section 3. In Section 4, we will review the expected improvement that future surveys will bring on tests of the gravitational theory, also highlighting the role of new cosmological probes. We will also outline in Section 5 the new challenges that the improved quality of data will pose, before summarizing the status and the perspective of this investigation in Section 6.
2. Testing Gravity at Cosmological Scales
In General Relativity it can be shown that the perturbed metric has only two scalar degrees of freedom [13] and for the spatially flat Friedmann–Lemaitre–Robertson–Walker (FLRW) spacetime, the perturbed line element takes the form
where t is the cosmic time, is the scale factor, and and are the gravitational scalar potentials. In this review, we will concentrate on sub-horizon scales, for which the wavemodes are , meaning that the scales we are interested in are much smaller than the Hubble horizon. This allows us to work in the quasi-static approximation, in which the time variation of the gravitational potentials is small compared to the Hubble time and one can neglect the time derivatives of these potentials in the perturbation equations. This also means that if we were to modify gravity with an extra scalar field, under this approximation we can also neglect the time derivatives of the scalar field fluctuations below the sound horizon of the scalar perturbation. While the quasi-static approximation is extremely useful to investigate alternative theories of gravity (see in [14,15,16] for further details), one has to be aware of its limitations; this approximation breaks down for scales larger than the sound horizon of the scalar field in which modifications are encoded, thus making this unsuitable to model observables at very large scales, or in cases where the speed of sound is much lower than the speed of light [17,18].
When including the full energy-momentum tensor, the first-order perturbed Einstein equations in Fourier space give two equations that describe the evolution of the two gravitational potentials and . These equations read [19,20,21,22]
where is the average dark matter density and is the co-moving density contrast with the fractional overdensity, and the peculiar velocity. The so-called Weyl potential can be defined as and it is also called the lensing potential, as it describes the propagation of relativistic particles. The ratio of the two gravitational potentials is denoted as , gravitational anisotropic stress or gravitational slip
The scale- and time-dependent functions , and stand for all possible deviations of Einstein gravity in these equations, being equal to unity when standard GR is recovered. This approach can encompass any modification by a scalar-tensor theory (see Section 2.2), but it allows also for more general and even agnostic parameter-free modifications of gravity that do not directly relate to any given model. Given that there are only two scalar degrees of freedom, it means that of course there is a relationship between , and , and they are related by
The function is usually probed best by experiments that probe the evolution of non-relativistic particles, as these directly trace the evolution of the potential. The parameter enters as an additional force affecting tracer particles and therefore it can be cast as an effective Newtonian constant with
in the linear regime and in Fourier space, with G being the standard Newton constant. On the other hand, relativistic particles, and therefore light, follow the equation for the Weyl potential, meaning that probes of gravitational lensing are mostly sensitive to the function .
For non-relativistic particles and under the assumption of zero anisotropic stress, one can find the growth equation for the density and the velocity perurbations ( and , respectively) by considering the conservation of the energy-momentum tensor and the linearly perturbed Einstein field equations [13]. For in which and in the Newtonian approximation, one can also derive this by looking at the Vlasov–Poisson system of equations [23]. When combining the perturbation equations for and , and again considering only sub-horizon scales, one obtains the following differential equation for the growth of matter perturbations :
where the dot represents a derivative with respect to t, the Hubble function is given by and we can see the effect of deviations from GR on the growth of perturbations in the function. Defining the so-called growth rate function via , one can obtain the following equation:
This growth rate function enters prominently in the determination of redshift space distortions for the galaxy power spectrum, as we will see below, and can be used to constrain redshift- and scale-dependent modifications of gravity that affect the growth of structures.
While the parameterization of departures from GR through the , and functions is widely used, there are other ways for these deviations to be described. An example is another common approach, which we will refer to as -parameterization. Such an approach focuses on possible deviations from the growth of structures expected in GR, encoding these in the growth rate as [24]
where is a free parameter that in the GR limit reduces to [24,25].
The two parameterizations can be related to each other, with the assumption of having modifications in the growth rate leading to , and the function that can be written, dropping for simplicity the z-dependence of , as [26]
Another relevant parameterization, often used to constrain deviations from GR, is the statistic [27,28,29]. This exploit the relation between the and potentials in GR and can be used to detect deviations from it using cosmological observables. In this review, we will not focus further on this particular approach, but we refer the reader to the the literature that investigates the possible constraints achievable with it (see, e.g., in [30,31,32]).
2.1. Examples of Modified Gravity Models: and Jordan–Brans–Dicke
While the functions of Equations (2)–(4) can trace generic deviations from GR, several models alternative to Einstein’s theory have been developed, and their phenomenology can be mapped into these functions. Here, we briefly review how this can be done for two examples of such alternative models: and Jordan–Brans–Dicke models.
The set of models known as theory [33], are obtained when modifying the Einstein–Hilbert action by assuming a function of the Ricci scalar, in the form such that
The field equations can be obtained after a variation of Equation (11) with respect to the metric and they read
where and □ is the d’Alambertian operator. These equations naturally reduce to Einstein’s field equations when .
We can recast the Einstein-frame action of Equation (11) as a scalar field action in the Jordan frame (for a modern review on these frames, see [34]), by replacing the term by , which is identical to the original Lagrangian, when varied with respect to the scalar field. An auxiliary field can be introduced, together with a potential . The scalar field action for is then obtained when replacing back into the original action, and it takes the form
This theory corresponds to the Generalized Jordan–Fierz–Brans–Dicke [35,36] theory with . When this parameter is not zero, there is a kinetic term added to the action in the form and when is just a constant, this reduces to the popular Jordan–Brans–Dicke theory [37].
In the case of gravity, the expressions for the gravitational potentials and its modifications defined above in Equations (2) and (3) become relatively simple and reflect the presence of an additional fifth force with a characteristic mass scale [38]
where is the second derivative of the function with respect to the Ricci scalar R. Assuming negligible matter anisotropic stress and again under the quasistatic approximation, one finds [16]
and
In the case of Jordan–Brans–Dicke, the modifications and become scale-independent and one can derive again the equations for , and in the quasi-static approximation [35,37,39,40]
2.2. General Scalar-Tensor Models
The two models described above fall in a more general class of theories, called scalar-tensor models. For scalar-tensor theories, the action in the Einstein frame, which defines its equations of motion, is expressed as
where is the scalar field, its potential and it couples to the matter fields through the Jordan frame metric , which is related to the metric as
The conformal parameter represents an universal coupling to matter and it implies that particles will feel a total gravitational potential which will be the sum of the standard Newtonian term and an additional contribution ,
whose consequence is the fact that matter particles of mass m are sensitive to a “fifth force” given by the gradient of the “conformal” contribution to the potential .
As can be expected, Equation (21) can be generalized to account for all possible theories of a scalar field coupled to matter and the metric tensor. Imposing that the equations of motion are only second order, this general action described the class of Horndeski theories [41,42]. This general action can be written as
where the four Lagrangian terms corresponds to different combinations of four functions of the scalar field and its kinetic energy , the Ricci scalar and the Einstein tensor and are given by [43,44]
After the gravitational wave event GW170817 [45,46], which constrained the propagation of gravitational waves to be practically equal to the speed of light [47], a large part of Horndeski theory, was ruled out, as in order to satisfy the observational bound the functions , and need to vanish [48]. As a consequence, the viable theories within this class remained to be Jordan–Brans–Dicke models and Cubic Galileons (Horndeski theories with Lagrangians up to ) [48,49,50,51,52,53]. See the work in [54] for a summary on the implications of the GW event on scalar-tensor theories and beyond.
For a generic Horndeski theory the two functions (expressing the effective gravitational constant) and (the gravitational slip) can be expressed as a combination of five free functions of time , which are related to the free functions in the Horndeski action [55,56]
The aim of this review is to focus as much as possible on model independent tests of gravity, but the Horndeski class of scalar-tensor theories is taken here as an example of a broad class that, while specifying to specif mechanisms of departure for GR, allows to remain reasonably agnostic. However, while the scalar-tensor theories that fall under the Horndeski class cover quite a large part of the alternatives theories of gravity of current interest for cosmology, the space of currently available theories is significantly wider. Several reviews focusing more in detail on the different classes of modified gravity models are available in the literature (see, e.g., in [36,54,55,57,58]), and we refer the reader to these should they be interested in this topic.
2.3. The -Parametrization in Modified Gravity
A physically meaningful parametrization of the linear Horndeski action, given bythe work in [15], is related to the Effective Field Theory of dark energy [59,60,61], where all possible deviations to the scalar-tensor action are parameterized linearly. This parametrization is of great help when discussing current cosmological constraints. It is defined using four functions of time—, , and —plus the effective Planck mass and a function of time for a given background specified by the time variation of the Hubble rate as a function of the scale factor a. The term measures the excess of speed of gravitational waves compared to light and after the event GW170817, this term is constrained to be effectively zero. The term quantifies the kineticity of the scalar field and therefore appears in models like K-mouflage, which require the K-mouflage screening [62] in order to pass solar system constraints. The coefficient quantifies the braiding or mixing of the kinetic terms of the scalar field and the metric and can cause dark energy clustering. It appears in modified gravity models where a fifth force is present [16]. Finally, quantifies the running rate of the effective Planck mass and it is generated by a non-minimal coupling. This parameter modifies the lensing terms, as it directly affects the lensing potential [54].
While this -parameterization is not easily mapped into the , and functions (see in [15] for specific mappings under certain limits), and it refers to the specific class of Horndeski theories rather than to generic deviations from GR, obtaining observational constraints on the functions is extremely useful to investigate the theory of gravity, as it allows to directly relate possible deviations from the expected GR behavior to physical effects.
2.4. Impact on Cosmological Observables
In Equations (2) and (3), we saw how the functions parameterizing departures from GR enter in the Poisson equations for relativistic and non-relativistic particles, while we have shown explicitly in Equation (8) how the function enters the expression for the growth rate of cosmological perturbations. These effects naturally enter the equations used to obtain theoretical predictions on observables, thus imprinting signatures of the gravity theory that can be detected by cosmological surveys.
Given their impact on the growth of structures and on gravitational lensing, natural candidates to test gravity are the LSS probes of galaxy clustering (GC) and weak lensing (WL). GC measures the two-point correlation function of galaxy positions either in three dimensions, i.e., angular positions and redshift, or using a two-dimensional tomographic approach (angular galaxy clustering) when the redshift information is not particularly good. The first approach is used for spectroscopic surveys, which provide a very small error on the redshift of the observed galaxies, while the second is more suited for photometric surveys.
For the former, one works in Fourier space, where the correlation function of galaxies, known as the observed galaxy power spectrum is directly related to the power spectrum of matter density perturbations in redshift space by [63,64,65,66]
where corresponds to the Alcock–Paczynski effect, is a damping term given by redshift errors and is the shot noise from estimating a continuous distribution out of a discrete set of points. is the cosine of the angle between the line of sight and the wave vector . Furthermore, the redshift space power spectrum, is given by [65,66]
where is the “Fingers of God” term that accounts for nonlinear peculiar velocity dispersions of the galaxies and K is the redshift space distortion term that depends—in linear theory, where it is known as the Kaiser term [67]—on the growth rate and the bias , but can be more complicated when taking into account nonlinear perturbation theory at mildly nonlinear scales [23,68,69]. For a detailed explanation of these terms, we refer the reader to the work in [70] and the many references therein.
As it can be seen in Equation (29), the growth rate enters the K term, thus imprinting in it possible signatures of departures from GR through Equation (8). In addition to this, also the contains information on the function, as it is obtained through Equation (2), thus making a spectroscopic survey of GC an ideal probe to test gravity.
While not able to provide a 3D information, a photometric GC survey would be able to provide constrain on deviations from the standard clustering of matter. In this case, one compares the angular power spectrum of galaxy correlations, obtained in tomographic redshift bins, with the theoretical predictions obtained as [70]
where the functions contain information on the galaxy distribution in the i-th bin and the galaxy bias needed to relate the correlation of galaxies to that of matter, is the co-moving distance and is the dimensionless Hubble parameter. Even though Equation (30) does not depend on the K term containing the growth rate, deviations from GR would still affect such an observable through its dependence on .
Photometric galaxy surveys also allow to measure the distortion of the shape of distant galaxies caused by the lensing effect produced by the matter distribution between them and the observers. The measurement of such a shear does not rely on the measurement of galaxy correlation functions and it is therefore a direct tracer of matter distribution, avoiding the dependence on the galaxy bias . Furthermore, for this observable, one can obtain the angular power spectrum [70]
where the window functions, or lensing kernels, contain information on the geometry of space-time, and is the Weyl power spectrum, coming from the Weyl potential defined Equation (3). This is related to the matter power spectrum by
In this equation, we can see clearly the observational signature of the lensing function defined above in Equation (3), thus making WL of distant galaxies an ideal probe to constrain deviations from the lensing effect expected in GR. Notice that in Equation (31) we neglected the contribution of intrinsic alignment, a systematic effect for such a measurement that is described in detail in [70].
The discussion above highlights the potential of LSS observations to test the theory of gravity, as the combination of GC and WL can bring information on two of the MG functions, and .
Alongside LSS observables, another mean to test the theory of gravity is through observations of the cosmic microwave background (CMB). This radiation is composed of photons coming from very high redshift, and the anisotropies in their temperature and polarization are related to the small perturbations in the matter–photon plasma in the early Universe. While departures from GR are expected to be relevant only at late times, signatures of these can still be detected or ruled out using CMB observations. The anisotropies in the CMB angular power spectra are indeed affected also by a number of secondary effects cause by the distribution of matter and its effect on photons during their travel to the observer from the last scattering surface. The main signatures of the theory of gravity on CMB spectra can indeed be found in the integrated Sachs–Wolfe (ISW) effect [71,72], caused by the time evolution of the potentials and , and in the lensing effect on CMB peaks [73,74], which is related to the Weyl potential. We show in Figure 1 an example of the effects of deviations from GR on CMB temperature and lensing potential power spectra, following the approach of the Planck Collaboration [75], highlighting the sensitivity of CMB measurements to signatures of the gravity theory. Such predictions were obtained using Equations (2) and (4), with the and functions parameterized as
where are free parameters and is the abundance of the dark energy component.
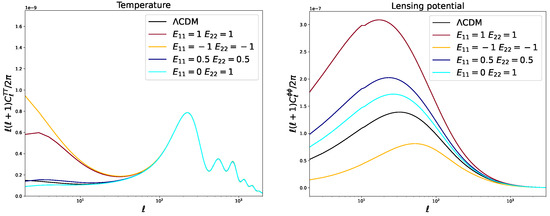
Figure 1.
Temperature (left) and lensing potential (right) CMB power spectra obtained for possible departures from GR. This figure is obtained using the same parameterization and parameter values in [75] using a private Boltzmann-solver.
Note that at this point, while we have focused in this section on perturbation observables, and we will do so throughout the paper, tests of gravity can be performed also using observations of the background expansion of the Universe. Indeed, models alternative to GR usually predict an expansion history that departs from the one expected in CDM, and observations of this can be used to constrain such models. Furthermore, such an investigation can be performed in a model independent way, e.g., by employing a cosmographic approach [76,77], which would allow to exploit to use observations of supernovae and baryon acoustic oscillations to constrain deviations from a cosmological constant driven Universe, and to connect the results to possible modifications of gravity (see, e.g., in [78]). Noteworthy, other observables could even allow to reconstruct the expansion history at even higher redshift, e.g., through Quasars or -ray bursts (see, e.g., in [79,80,81]).
2.5. Codes and Tools to Compute Cosmological Observables
Theoretical predictions for the evolution of cosmological perturbations and, consequently, for cosmological observables, can be obtained very efficiently when these perturbations are small, and linear perturbation theory can be applied. The so-called Einstein–Boltzmann solvers apply this formalism to evolve primordial perturbations to present time and to obtain prediction on the observables that we described ago. Two commonly used public codes of this kind are CAMB1 (Code for Anisotropies in the Microwave Background) [82,83], which is written mainly in fortran, and CLASS2 (Cosmic Linear Anisotropy Solving System) [84,85], which is mainly written in the C programming language. Both of these codes come with user-friendly python wrappers. These codes can be modified to account for alternative theories of gravity, or to account for parameterized departures from GR. While in the first case once implements specific modified gravity (MG) models or generic class of models solving their full scalar field equations, in the latter one modifies the evolution equations through Equations (2) and (4).
The most commonly used codes implementing the generic parametrization approach are ISitGR3 [86,87], MGCAMB4 [22,88] and, more recently, a branch of CLASS, called QSA_CLASS [89]. For the implementation of specific classes of alternatives to GR we will mention here the two most important ones, namely, hi_class5 [90] and EFTCAMB6 [91,92]. The first one, works directly on the Horndeski action of Equation (25) and its five free functions of time or, alternatively, by using the -parametrization defined in Section 2.3. On the other hand, EFTCAMB works within the formalism of the Effective Field Theory of Dark Energy [59,60,61], even though it allows a reparameterization of the EFT functions by means of the .
3. Current Constraints on Modified Gravity
The current state of the art for constraints on deviations from GR is given mainly by CMB and LSS observations.
Current CMB constraints come mainly from the observations of Planck [93], a satellite survey that obtained data from 2009 to 2013; the Planck Collaboration released in 2015 a paper dedicated to constraints on DE and modified gravity models, containing also bounds on possible deviations from GR [75], which were then updated in 2018 with the last data release of the collaboration [6].
In their latest results, the collaboration constrained deviations from GR parameterized as in Equations (33) and (34). We show in Figure 2 the results obtained fitting the Planck data using the parameterization of Equations (33) and (34) through MGCAMB, corresponding to those reported in [6]. One can notice how the and function are compatible with their GR limit within . As pointed out in [6,75], this agreement is worsened if CMB lensing reconstruction data are removed from the data combination; this is due to the fact that Planck data prefer a lensing amplitude higher than what one would expect in standard CDM, a preference that is reduced when lensing extraction data are included, and that can be explained by a departure from GR. The right panel of Figure 2 shows this effect highlighting how the function is degenerate with , the phenomenological parameter used to take into account deviations from a standard lensing effect [94].
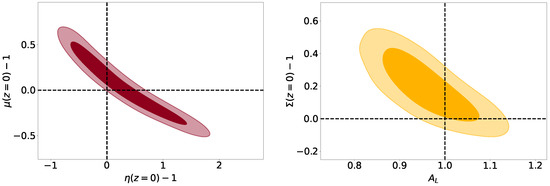
Figure 2.
and confidence level contours for and (left), and for and (right). The dashed lines show the expected values in a GR-CDM Universe.
Following the results of Planck, the observables useful to improve constraints on deviations from GR were those related to LSS observations. In particular, the Dark Energy Survey (DES) collaboration, after its latest data release, has employed a subset of its data, the DMASS galaxy catalog [95], in combination with baryon acoustic oscillations (BAO) and redshift space distortions (RSD) data from CMASS [96], and the CMB data from Planck to further improve the bounds on possible deviations from GR. The analysis performed uses a slightly different parameterization from the one of Equations (33) and (34), relying instead on [97]
where is the present time abundance of dark energy, and the GR limit is achieved for . The results obtained show a slight deviation from GR when DMASS and CMASS are combined, with and . However, when Planck data are included in the analysis, the GR limit is consistent with the results, with and [97].
Other results are available thanks to current data (see, e.g., in [98,99]), but qualitatively the same conclusions can be taken; the GR limit of the parameterized departures used is in agreement with the observational data or has a tension that is not statistically significant (≲2). However, the bounds obtained would still allow for some of the available alternative gravity models to be viable and to be candidates to explain the accelerated expansion of the Universe. In order to further put GR to test and possibly to rule out some of its alternatives, the next generation of observational surveys will be crucial.
4. Upcoming Constraints
In the previous section we summarized the current constraints on deviations from GR achievable with currently available data. Here, we focus instead on how Einstein’s theory could be tested in the upcoming decades.
We expect stronger constraints thanks to the improvement in sensitivity that future LSS and CMB surveys will have. This means that the same approach used until now can be applied using future surveys to constrain GR, and we discuss the expected improvement in Section 4.1 and Section 4.2.
However, new cosmological probes are now reaching a level of maturity that could allow us to use them to test gravity, and we will review the constraining power that these will bring to the investigation in Section 4.4.
4.1. LSS Forecast
Next-generation galaxy surveys will be one of the most powerful probes of cosmology in the upcoming decade. These were designed to measure cosmological parameters with precision, through the use of two-point statistics likeGC and WL. Among the most important upcoming missions there will be the Javalambre-Physics of the Accelerated Universe Astrophysical Survey (J-PAS) [100], the Dark Energy Spectroscopic Instrument (DESI) [101], Euclid [102,103], the Vera Rubin Observatory [104], WFIRST [105] and the SKA Observatory [106].
Euclid is a European space satellite mission that has an infrared spectrograph and a visible camera. The latter is capable of taking spectra of about 50 million galaxies in the sky from redshifts with a sub-percent accuracy in the redshift estimation, perfect for spectroscopic galaxy clustering studies. On the other hand, the visible camera will be able to take low-noise level pictures of ~1 billion galaxy shapes and positions up to a redshift of about , which makes it adequate to detect the tiny cosmic shear effect statistically, by looking at the change of ellipticities of the galaxies across space and time. It will cover an approximate area of 15,000 in the sky [70,103]. Euclid is expected to be launched by late 2022.
WFIRST, a NASA mission, will have similar capabilities in terms of area coverage, instruments and redshift range, but it will also serve other purposes, such as the search for exoplanets and detailed studies of stars [107]. On the spectroscopic side, but based on the ground, DESI will be at the forefront of the observation capabilities in the next years, with its mission starting in 2021 and with very good spectroscopic resolution, it will be able to capture up to 50 million galaxies on the night sky. It will be able to differentiate between several populations of galaxies, such as Luminous Red Galaxies (LRGs), Emission Line Galaxies (ELGs) and it also will be able to measure quasars and the Lyman- forest, which will allow the determination of independent clustering statistics along the history of the Universe [108]. On the side of photometric observables, the Vera Rubin Observatory will be the main ground-based experiment in the upcoming decade. Its Legacy Survey of Space and Time (LSST) will cover an area of about 20,000 and it will be capable of obtaining accurate shapes and angular positions of about a billion galaxies up to redshift . It will also serve other purposes such as the study of Supernovae and transients, making it a very versatile observatory [109]. Another photometric survey relevant for the purpose of gravity tests is J-PAS, a wide field survey carried out from the Javalambre Observatory in Spain, which started observations in 2015, and which will observe an area of 8500 .
The SKA Obesrvatory (SKAO) will instead provide a different window for cosmological investigation, as it will perform observations in the radio band. It will be the largest radio array ever built and it will provide observations of galaxy clustering and weak lensing from resolved galaxies and intensity mapping, through radio continuum and 21-cm line emission [106].
LSS surveys are extremely interesting for the purpose of testing gravity; these will be able to map the distribution of matter in the Universe by probing its evolution from primordial perturbations and the gravitational lensing effect that it has on photons (see Section 2). For this reason, the literature on this topic is extensive, and we report here a subset of the forecast results available as an example.
Most of the available forecast results, rely on the Fisher matrix approach [110,111,112], that allows to forecast the constraining power of future experiments. Despite its limitations, like assuming a Gaussian likelihood and a Gaussian posterior, the Fisher matrix allows us to obtain an optimistic bound [113] on the confidence contours of the model parameters, given a prior and a set of experimental settings. can be obtained by knowing the theoretical model (in the case of LSS, the observable power spectra) and its derivatives with respect to the parameters, together with a model for the experimental noise. The individual uncertainties on the cosmological parameters are then obtained by taking the inverse of , the so-called forecasted covariance matrix , with and looking at its diagonal elements, so that .
Such a method has been applied with several parameterizations for deviations from GR. Constraints on the parameter of Equation (9) have been obtained by the Euclid Consortium [70], whose results are shown in Figure 3. The authors found that combining photometric and spectroscopic observables (WL and spectroscopic GC), the parameter can be measured with a relative error ≲0.1, thus tightly constraining deviations from the growth of structure expected in GR, even in the case where the background expansion is given freedom to deviate from the standard cosmological constant, and the assumption of a flat Universe is dropped.
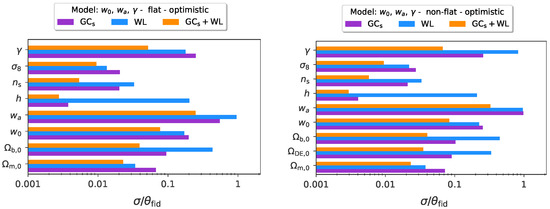
Figure 3.
Relative errors on cosmological parameters and on the controlling the deviation from the standard growth. The results shown here include spectroscopic galaxy clustering (purple), weak lensing (blue) and their combination (orange). This figure is obtained in [70].
Forecast constraints from Euclid have been also obtained for the functions and that parameterize deviations from both the standard growth and lensing effect. The authors of [114] constrained these functions exploring two different assumptions: a “late-time” parameterization where the two functions scale with the DE energy density and an “early-time” parameterization where the redshift trend of and is described with a Taylor expansion. Moreover, the authors explored a case in which the two functions are binned in redshift, an approach that allows to avoid any assumption on the evolution of these functions, at the expense of a higher number of parameters and, therefore, looser constraints. This analysis was performed assuming values of the free parameters that do not coincide with the GR limit, but are still not ruled out by Planck measurements (see Section 3).
In Figure 4, we show the constraints obtained in [114] when the ’late-time’ parameterization is assumed, i.e.,
where and are the free parameters ruling the amplitude of the deviation from GR, and the two functions can be combined to obtain following Equation (5). These results highlight how the GC and WL probes are complementary, with the former measuring the clustering of matter (and therefore constraining the function), while the latter is more sensitive to the function, as it probes the shear of galaxy shapes due to gravitational lensing. Combining these two probes, Euclid can reach constraints of and on the present day values of and respectively in the late-time parameterization, with the precision reaching and if instead the measurements for the two probes are assumed to come from the planned phase 2 of SKAO. In the binned case, the best constrained value of is measured with a precision of , while for the best precision in . Such a result highlights how upcoming surveys will allow to test gravity even without a priori assumptions on the redshift trend of the parameterized deviations from GR.
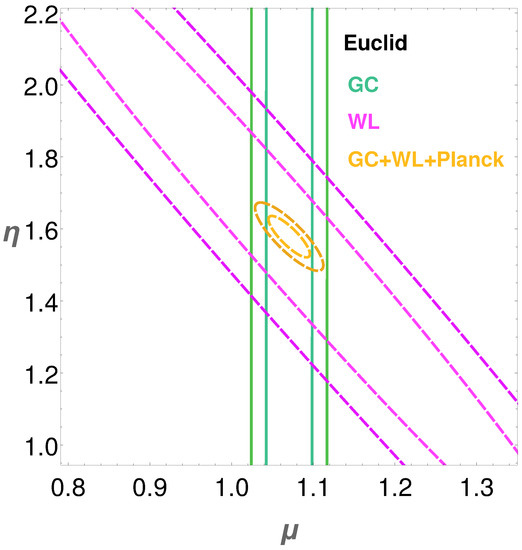
Figure 4.
and confidence level contours on the current values of and obtained using forecast observations for Euclid’s spectroscopic GC (green) and photometric WL (purple). The combination of the two is studied with CMB data from Planck also included (orange). Reprinted from the work in [114], with permission from Elsevier.
Notice that the constraints of [114] are obtained with a specific prescriptions for the nonlinear evolution of cosmological perturbations, which allows to include small scales in the analysis (see Section 5).
Constraints on a parameterization analogous to the one of Equations (37) and (38) were also obtained for the expected observations of J-PAS [115]. The authors of this paper show how the constraints achievable on the parameters ruling the amplitude of deviations from GR are competitive with those that can obtained from Euclid, thanks to the amount of data that J-PAS will obtain at low redshift, where such parameterization departs the most from the standard model. In this paper, the authors also explored the possibility for this functions to be scale-dependent, highlighting how future surveys such as J-PAS and Euclid can potentially detect a deviation from the scale independent behavior of GR.
The binned approach to constrain the MG functions and was also used in other forecast for upcoming missions (see, e.g., in [116,117]). Of particular interest is the approach of [117], where the binning of the functions, together with a principal component analysis (PCA) [118], was used to constrain these functions when the assumption that they are scale independent is dropped. The authors explored both the case in which the dependence on the scale k is arbitrary, thus binning the functions in both z and k, and the case in which the k-dependence is obtained by requiring that and come from physically motivated theories [119]. For this latter case, the authors write the MG functions as in Equations (26) and (27), and they bin in redshift the functions. The results in [117] show that the LSST survey, while unable to constrain individual functions due to their degeneracies, will be able to measure combinations of all of them with a precision of on the best constrained eigenmode, a measurement which will allow to constrain generic deviations from GR.
As discussed in Section 2, an alternative to the and function to test gravity is the use of the functions of Section 2.3. Constraints on these functions, that consider only departures from GR that fall under the Horndeski class, were also forecasted for upcoming LSS surveys.
In [39], the authors explore the possibility to constrain the functions parameterized as
They explore the bounds that can be obtained on the parameters from LSST and also using the intensity mapping survey of SKAO. We show in Figure 5 an example of the results of this analysis, showing the complementarity of the different probes. In particular one can notice how the combination of LSST clustering and weak lensing observations can significantly tighten the constraints on and , ruling the deviation from the standard Planck mass and braiding term respectively.
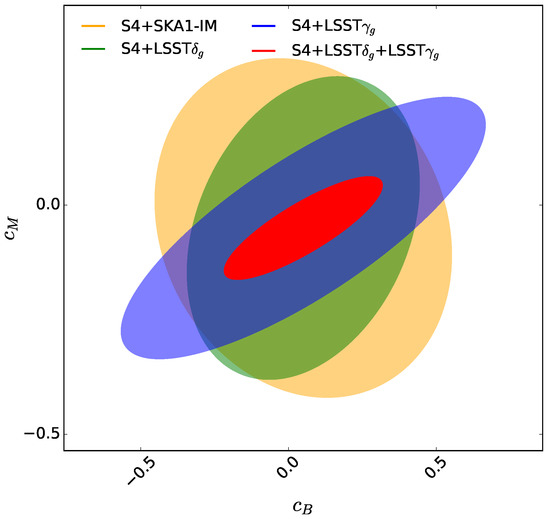
Figure 5.
Sixty-eight percent (68%) confidence level contours on and obtained combining a stage IV CMB survey with the expected measurements of intensity mapping from SKAO (yellow), weak lensing (blue) and galaxy clustering (green) from LSST, and the combination of the latter two (red). Reprinted figure with permission from the authors of [39] by the American Physical Society.
Another analysis, performed in [120], focuses on the impact of the choice of analysis method on the expected bounds on the , comparing the tomographic approach for weak lensing to an analysis that fully considers 3D information, finding that the latter can improve the constraints of ≈20%. Moreover, they investigate they impact of cutting the small scales out of the analysis; such a cut is necessary when one is not able to obtain theoretical predictions for scales at which the linear perturbation description is not valid anymore, which is a common issue for models that deviate from CDM. As shown in Figure 6 the impact of nonlinear scales can be critical to obtain stringent test of gravity, but the to fully exploit the data in such a regime can be extremely challenging, as we will discuss in Section 5.
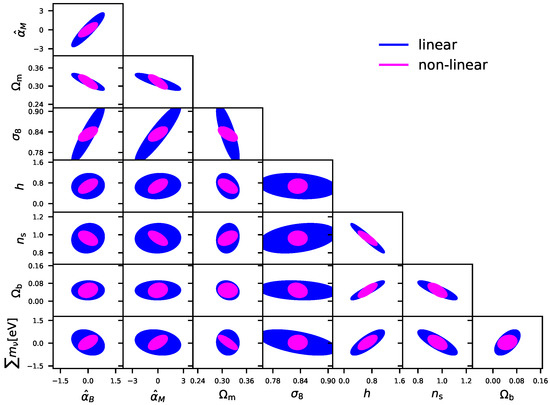
Figure 6.
confidence level contours on cosmological and MG parameters obtained by a Euclid-like survey cutting the nonlinear scales out of the analysis (blue) or including them (pink). This figure is taken from [120].
We conclude this section by stressing that in realistic settings, these constraints might suffer from degeneracies with nuisance parameters that account for observational effects such as intrinsic alignment of galaxies, galaxy bias and other systematic effects, which, if not accounted for, can severely limit the robustness of the constraints obtained on deviations from GR [121,122].
4.2. CMB
While the current CMB data provided by Planck have reached the cosmic variance limit for a wide range of multipoles in temperature, i.e., the correlation where most on the information on gravity can be extracted, we still expect an improvement in the constraints on deviations from GR from upcoming CMB surveys.
On the one hand, upcoming surveys and especially those performed by ground based telescopes, will be able to access smaller scales and therefore access higher multipoles with respect to Planck. On the other hand, upcoming surveys will significantly improve the sensitivity for polarization spectra, for which the cosmic variance limited data provided by Planck is much more limited in the range of multipoles. Both these improvement will allows to extract more information on the CMB lensing potential, by measuring temperature power spectra oscillation at high multipoles, and by improving the lensing reconstruction methods that also rely on a precise measure of polarization spectra [123].
As discussed in Section 3, most of the CMB constraining power on gravity comes from the impact of lensing on CMB observables; thus, thanks to the future improvements in its characterization, we can expect better constraints on deviations from GR.
For the purpose of testing gravity, the main CMB surveys expected in the upcoming decades are the Simons Observatory (SO) [124] and CMB-S4 [125]. The former is a new CMB experiment that is being built in Chile, while the second is an envisioned CMB survey that would consist of dedicated facilities at the South Pole, Chile and possibly a northern hemisphere site.
Most of the forecast obtained for future CMB surveys have been obtained in the context of scalar-tensor theories, rather than as generic deviations from GR, thus aiming to constrain either the functions included in the Horndeski Lagrangian, e.g., through the parameterization done with the functions described in Section 2.3.
Constraints on this kind of theories are indeed one of the science cases proposed in the CMB-S4 science book [125]; the authors considered simulated observations for this proposed experiment and use Planck measurements to complete the sky map in the areas not surveyed by CMB-S4 to obtain a full sky map. They find that the inclusion of CMB-S4 data can improve the constraints on the parameters ruling the deviations from GR in scalar-tensor theories, in particular with the bound on the speed of gravitational waves parameter that is improved by a factor ≈3, a constraint mainly due to the increased sensitivity of such a survey on primordial gravitational waves.
Despite the fact that future CMB surveys will improve our constraints on deviations from GR, such surveys will not be competitive by themselves with contemporary experiments mapping the LSS. The latter kind of surveys is indeed more suited to map the distribution of matter in the Universe and the evolution of perturbations at times when one expects deviations from GR to be relevant (if present). However, both SO and CMB-S4 surveys will contribute to this investigation when used in combination with LSS surveys, as they will break degeneracies between cosmological and MG parameters [124,125].
An investigation on the role played by CMB with respect to LSS surveys was carried out in [39]. Together with more general scalar tensor theories, the authors constrained the Jordan–Brans–Dicke theory obtaining bounds on the parameter . In Figure 7, we report the results found by the authors, which highlight how, even though CMB obtains constraints at redshifts where the modifications to gravity have no significant impact and it is therefore not competitive on its own, it can still be used to improve the constraints achieved with LSS.
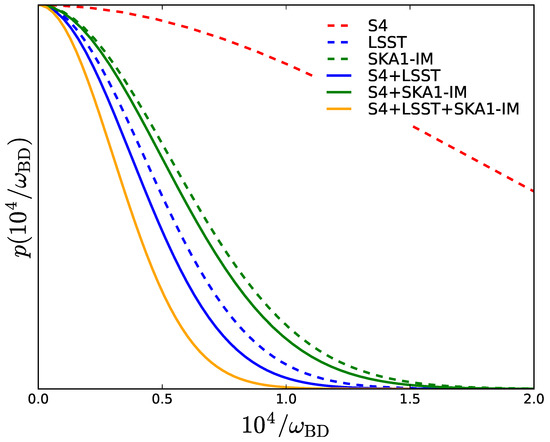
Figure 7.
Posterior distribution of obtained combining a CMB-S4 survey with contemporary stage IV LSS experiments. Reprinted figure with permission from the authors of [39] by the American Physical Society.
4.3. CMB-LSS Cross Correlation
While the improvement brought by the upcoming CMB and LSS surveys will be significant, a crucial boost in the sensitivity on departures from GR could be achieved considering the cross-correlation between CMB and LSS observables. The correlation between CMB temperature and galaxy positions allows to improve the sensitivity to the ISW effect, which would be instead severely limited by cosmic variance. This effect depends directly on the time derivatives of the Bardeen potentials and which can be changed significantly if one deviates from GR and, therefore, can potentially bring to strong constraints on such departures (see, e.g., in [126]).
Such a strong synergy was explored for the combination of Euclid with present and future CMB experiments, i.e., Planck, SO and CMB-S4 [127]. This analysis was done on the parameterization, thus in a particular framework where only the growth of structure is modified, while the lensing effect is unchanged with respect to GR.
The authors of [127] found that the inclusion of CMB data and its cross-correlation with Euclid observables will significantly improve the bound on the parameter that determines the deviation from GR. In Figure 8, we show the results reported in [127] for the bounds on ; the posterior distributions shown highlight that while including only CMB lensing to Euclid does not significantly improve the constraints, adding the full CMB observables and their correlation with Euclid leads to a significant improvement both when assuming a flat Universe and when dropping the flatness assumption.
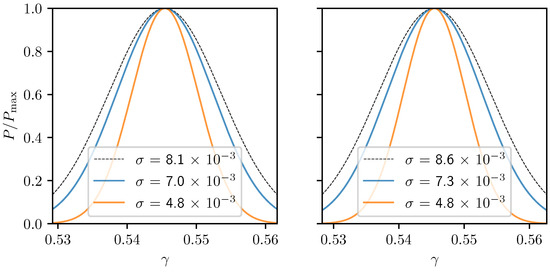
Figure 8.
1D posterior distribution for the parameter for Euclid alone (black), and adding CMB lensing (blue) and all CMB observables (orange). The CMB data here are taken to be SO-like. The left panel refers to a flat CDM cosmology, while the right one drops the flatness assumption. This figure is taken from in [127].
4.4. New Probes of Gravity
In the previous subsections, we focused on the expected cosmological tests of gravity that could be achieved thanks to upcoming CMB and LSS surveys. These constraints rely on improving the sensitivity with respect to current surveys, but still rely on the same observational probes to constrain deviations from GR.
However, recent observations have made available several new probes that could contribute in a significant way to the investigation of the theory of gravity.
After the first detection of a gravitational wave event [2], significant interest has been devoted to this new window on cosmological evolution. Concerning the investigation of the gravity theory, the observation of gravitational waves shows significant promise; as the existence of such a phenomenon is seen as one of the most striking validation of Einstein’s theory, deviations from the expected behavior of such events would constituted a smoking gun for violations of GR. Indeed, one expects that if the gravity theory is different from GR, several effects could potentially be observed when detecting gravitational waves, e.g., a difference between the propagation speed of light (c) and gravitational waves (), the emission of additional polarizations and a modified damping of the waves amplitude [128].
The difference between c and has been already tightly constrained thanks to a single GW event with an electromagnetic counterpart [45,46]. Such an event allowed to measure the speed of both propagations, constraining their relative difference to be smaller than ≈10 [47]. Such a strong constraint has significant consequences for the study of deviations from GR, with several possible alternative models being ruled out by this observation [50,51].
With the future increase in the number of observed events, as the amplitude of the observed waves is proportional to the inverse of the luminosity distance , we expect to be able to obtain distance–redshift relation catalogs through GW observations, if electromagnetic counterparts are available. Such catalogs have the potential to provide significant information on the theory of gravity. Indeed, in the presence of an additional factor in the friction term of gravitational waves, with corresponding to the GR limit, one expects to find a difference between the luminosity distances measured through GW () and electromagnetic probes () [129,130]
This possibility has been extensively explored in the literature, with forecast for the possible deviations from GR obtained for future GW observatories such as LISA [131] and the Einstein Telescope [132].
The LISA collaboration has indeed focused on this possible investigation with future observations, and produced forecast on possible deviations from GR using a simulated catalog of massive binary black holes merger events [133]. Here, the authors parameterized Equation (40) as
with and n free parameters. The results of their analysis are shown in Figure 9 which highlights how the constraining power of LISA can reach the level of on the parameter which dictates the amplitude of deviations from the GR expected damping of GW amplitudes. Forecast constraints for the same parameterization of Equation (41) were also obtained using a simulated Einstein Telescope catalog, finding a bound on of [130]. The expected constraining power on deviations from GR of both LISA and Einstein Telescope are therefore very similar even though the two experiments explore complementary ranges in redshift; this highlights how the use of GW catalogs has the potential to test gravity over an extended redshift range and possibly rule out several of the alternative theories of gravity that are currently available.
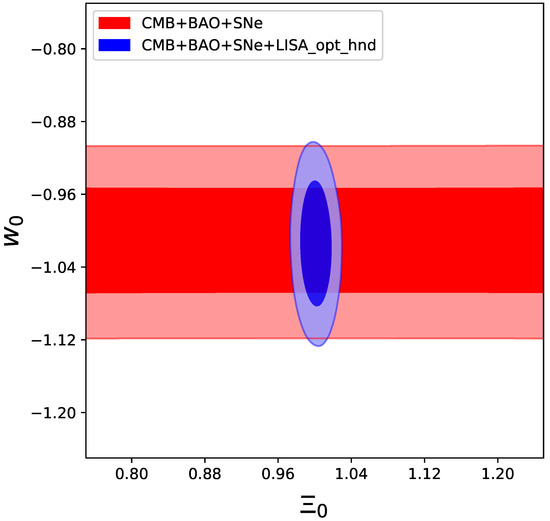
Figure 9.
Constraints on , parameterizing a constant DE equation of state, and obtained using CMB+BAO+SN (red) and when adding LISA forecast data to the previous combination (blue). This figure is taken from [133], where also different cases for the noise and for the seeds of the binaries have been investigated, and reproduced by permission of IOP Publishing. All rights reserved.
Despite the promise shown by these results, the forecast reported above do not consider the impact of screening mechanisms on the constraints that can be achieved. Alternative theories of gravity need to be screened in the local environment to satisfy Solar System constraints. It could be expected that such screening mechanisms will be also at play in the local environment where the merger happens. In such a case, both the observer and merger environments would be screened from MG effects. While most of the propagation area of a gravitational wave will not be screened, it has been shown that for screening mechanisms that fall into the chameleon class the deviation expected from the GR propagation only depends on the difference in the Planck mass at the observer and at the merger [134,135]. Such an effect would therefore completely remove any signature of departures from GR from the observations of GW luminosity distances.
In addition to the possibility to directly test gravity with GW, it has been shown how GWs can be included in the set of observations used to probe the distance duality relation (DDR) [136]. The DDR is a consequence of the assumptions at the foundation of our cosmological models, including the fact that it is based on a metric theory of gravity and that photons travel on null geodesic with their number conserved [137]. Such a relation connects the luminosity and angular distance as
While deviations from GR are not the only possible responsible for a deviation from the DDR, indeed a detection of this would prompt a serious investigation on the nature of gravity.
While the common observations to probe the DDR are supernovae (providing data on ) and BAO (measuring ), the independent luminosity distance measure that can be obtained with GWs could be crucial for such an investigation. As it does not rely on the observation of photons, a measurement of could be used to break degeneracies between cosmological parameters and those ruling the deviation from the standard DDR. This possibility was investigated in [136], where the authors used a simulated catalog with Einstein Telescope specifications, alongside simulated data for SNIa and BAO. The results found in their analysis are shown in Figure 10 where it can be seen how GW data can contribute in tightening the constraints on the parameter A, which determines the amplitude of the deviation from DDR, with the standard relation recovered for .
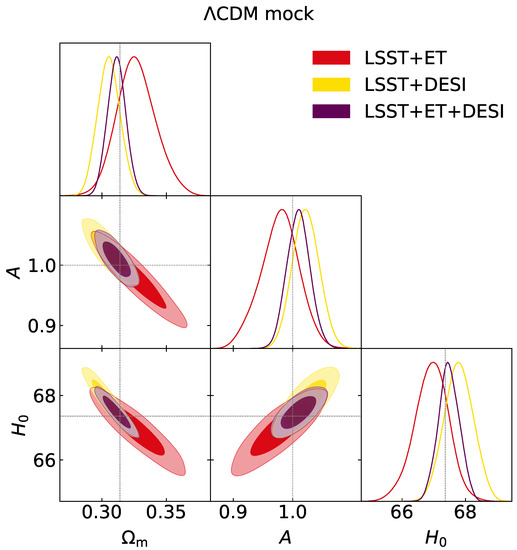
Figure 10.
Constraints on cosmological parameters and on the DDR breaking parameter A. The results are obtained for LSST+ET (red), LSST+DESI (yellow) and LSST+ET+DESI (purple). This figure is taken from in [136].
We conclude this overview by mentioning another probe that is becoming increasingly important for cosmology: strong lensing time delays (SLTD). The observation of SLTD has recently provided constraints on standard cosmological parameters, and it has been used to obtain an independent measurement for with respect to the one inferred from CMB or obtain from the distance ladder (see, e.g., in [138]). At the same time, such an observable can be used to constrain deviations from GR; bounds on the parameterized post-Newtonian parameter , which modifies the Weyl potential entering the lensing equations, have been obtained with current observations of strong lensing system [139,140], highlighting how future observations will be able to improve such bounds. Forecast on the constraining power of these observations have been done at the level of deviations from the standard CDM background expansion [141], while a multi-messenger approach, studying the possible detection of strongly lensed GW events, could be used to constrain deviations from the GR limit of the function Equation (3) at an level [142].
5. New Challenges
While the continuous improvements of observations will provide a great opportunity to test our gravity model, the increased sensitivity and the possibility to access previously unavailable scales will also put to test our ability to obtain accurate theoretical predictions without introducing biases due to approximations or assumptions.
One very known example of this possible issue is the modeling of nonlinear scales. LSS surveys will provide data at scales where the linear perturbation theory used to obtain theoretical predictions in any cosmological model cannot be used, as the amplitude of cosmological perturbations will be too high to use a linear approximation. If the analysis one performs is limited to the standard CDM model, this is not an issue; several N-body simulation performed for this model have allowed to obtain fitting functions that can complement our analytical theoretical predictions in the range of scales where these are not available. Codes like Halofit [143] or HMCode [144] have been integrated in the Boltzmann solvers CAMB and CLASS and allow to obtain predictions also at nonlinear scales.
However, one cannot rely on these codes if the goal of the analysis is to test gravity; the N-body simulations used to obtain the fitting functions assume GR and CDM, and their use in different contexts can lead to significant biases in the parameter estimation pipeline, already when they are applied to very minimal extensions of the standard concordance model [145,146].
One possible solution is to include in the analysis a theoretical error, modeled in such a way that it can account for the possible biases on the nonlinear theoretical predictions [147,148,149]. Such a method allows reducing the biases that incorrect modeling would propagate to the final estimate of the parameters, but at the expense of larger uncertainties. Moreover, while this approach works for simple extensions of the CDM, it might not be trivial to model the theoretical uncertainties when there is a more significant departure from the standard model, as is the case for deviations from GR.
Ideally, one would want to perform N-body simulation in all the models of interest, in order to obtain fitting functions similar to those obtained in CDM. This has been done for some specific models alternative to GR. Several interesting approaches have been taken in the literature such as COLA [150], Ramses [18], Ecosmog [151], -enics (an interesting finite-element method approach that can capture the nonlinear evolution of a scalar field) [152] and the simulation work on theories by several groups [153,154,155,156]. However, applying such an approach for all available models, or for model independent tests of gravity (performed through the and functions) is extremely difficult. In MG-evolution [157] the authors introduced the - parameterization into a relativistic N-body code and managed to obtain predictions for those generalized models at nonlinear scales.
N-body simulations are computationally expensive and therefore only few realizations in a reduced parameter space are available for modified gravity models. Therefore, several approaches have appeared recently in order to reduce the required computational time and to allow for a more versatile evaluation of the observables. These include fitting formulae based on simulations [158], emulators for and scalar-field theories [159,160,161] and hybrid approaches in which the halo model, perturbation theory and simulations are calibrated to create a model, such as REACT (see [162,163]). This code can compute predictions for and other modified gravity models which are approximately 5% accurate at scales 5 h/Mpc.
While the linear scales are exempt from this specific issue, very large-scale pose different challenges to our modeling capabilities. LSS observables at the extremely large scales that will be probed by experiments such as Euclid and SKAO can indeed be modeled using the linear approach; however, additional contributions from relativistic effects become relevant at such scales [164,165,166], and, in addition to this, the approximations usually done to facilitate analytical computations (e.g., the Limber approximation [167,168,169]) are not valid anymore. Computing the exact analytical spectra is extremely expensive from the computational point of view, but the use of approximated spectra can produce false detections of deviations from CDM already when simple extensions are considered [170]. Such an effect would be particularly important for tests of the theory of gravity, as deviations from GR are expected to produce significant signatures at these scales [171,172].
This issue has prompted several attempts to make the exact calculations less computationally expensive. For instance, fast Fourier transform (FFT) or logarithmic FFT (FFTLog) methods can be exploited to accelerate the computation of the theoretical predictions [173,174,175]. Alternatives are represented by the use of emulators also in this case, as these can allow to significantly speed up parameter estimation pipelines reducing the number of spectra for which the exact calculations need to be performed [161], or by the use of correction terms that allow to reduce the bias on parameter estimation [170].
In addition to this, exploiting the future data at extremely large-scale can raise the issue of validity of the quasi-static approximation, as we discussed in Section 2, further complicating the possibility of obtaining robust theoretical predictions when moving away from the GR paradigm.
We conclude by briefly mentioning that the theoretical modeling of observables is not the only issue that the improvement of surveys will bring to light. Parameter estimation pipelines commonly assume a Gaussian likelihood when comparing theoretical predictions to data, an assumption that might lead to inaccurate results given the extreme sensitivity that future data will have [176]. Overcoming such an issue will require to either improve the theoretical modeling of the likelihood function or to resort to methods that completely eliminate the necessity of computing such a function (see, e.g., in [177,178]). While such an issue is not specific to cosmological tests of gravity, the high sensitivity expected for future data requires the analysis to reach the best possible accuracy, in order to fully exploit the available data to obtain robust and unbiased constraints on the theory of gravity.
6. Summary
The aim of this review was to give an outlook of the future possibilities to test the theory of gravity at cosmological scales. We briefly reviewed a subset of the available alternatives to the theory of general relativity, which is at the base of the current standard cosmological model CDM. While it is indeed necessary to explore alternatives to GR from the theoretical point of view, here we focused mainly on how GR itself can be tested with cosmological observables, by means of parameterized descriptions of departures from the expected cosmological evolution in GR. We briefly reviewed the most common parameterizations available, introducing free functions that allow cosmological perturbations to evolve differently with respect to the standard model, thus allowing to search from signatures of non-standard behavior in cosmological observables.
We reviewed the state of the art of this investigation, highlighting how the most recent data, both from CMB and LSS, show a general agreement with GR, with deviations from the standard paradigm that are not statistically significant (≲2). Nevertheless, current data still leave open the possibility for a theory of gravity that does not coincide with GR.
Upcoming surveys will therefore be crucial to further improve the bounds on departures from the standard paradigm, thanks to the increase in sensitivity and the possibility to probe a larger range of scales. We reviewed forecast results for this investigation of both upcoming CMB and LSS surveys, highlighting how the latter can in principle provide much stronger constraints with respect to the former. In particular, we have shown how LSS surveys will be crucial to test gravity, thanks to their ability to probe the evolution of cosmological perturbations, through measurements of the matter distribution and growth rate, and the lensing effect that matter has on the path of photons, through measurements of the shear of distant galaxies. The two probes of GC and WL show a great complementarity and, if combined, they would allow to tightly constrain for deviations from GR, both when analyzing specific classes of alternative models and when purely phenomenological parameterizations are applied.
While future CMB surveys will have less constraining power on deviations from GR, their impact on tests of gravity will nevertheless be extremely important; we pointed out how the cross-correlation of CMB and LSS probes will allow to further improve the bounds on parameterized deviations from GR.
Throughout this review, we have considered future CMB and LSS surveys as the main tools to test the theory of gravity, given the great expertise that the cosmological community has built on them through an extended period of time. However, we also highlighted how relatively new observations, such as strong lensing time delays and gravitational waves could also be used for this purpose. In particular, we have shown how next-generation GW surveys will be able to tightly constrain deviations from the expected GR damping of the waves amplitude with distance, reaching an error of on the parameter ruling the amplitude of such deviations. Moreover, we have also highlighted how the detection of strongly lensed gravitational wave could lead to independent constraints of the deviation from the lensing effect expected in GR, while the combination of GW observations with BAO and SNIa could improve the bounds on departure from the distance duality relation, which would signal that the fundamental assumptions at the base of our cosmological model should be reviewed.
Finally, we focused our attention to the new challenges that we will face if we want to fully exploit this abundance of data that we will have available in the near future. We focused mainly on issues concerning the theoretical modeling of cosmological observables, pointing out that both very small and very large scale will put to test our ability to produce accurate theoretical predictions, showing how a failure from this point of view will make complicated to obtain robust tests of the theory of gravity.
Author Contributions
Conceptualization, M.M. and S.C.; writing—original draft preparation, M.M. and S.C.; writing—review and editing, M.M. and S.C.; visualization, M.M.; supervision, M.M.; project administration, M.M. All authors have read and agreed to the published version of the manuscript.
Funding
MM has received the support of a fellowship from “la Caixa” Foundation (ID 100010434), with fellowship code LCF/BQ/PI19/11690015, and the support of the Centro de Excelencia Severo Ochoa Program SEV-2016-059.
Acknowledgments
This paper is submitted to the Special Issue entitled “Large Scale Structure of the Universe”, led by N. Frusciante and F. Pace, and belongs to the section “Cosmology”. We thank the authors of [39,70,114,120,127,133] for granting us permission to use their figures in this review.
Conflicts of Interest
The authors declare no conflict of interest.
Notes
| 1 | https://camb.info, accessed on 15 December 2021 |
| 2 | https://lesgourg.github.io/class_public/class.html, accessed on 15 December 2021 |
| 3 | https://labs.utdallas.edu/mishak/isitgr/, accessed on 15 December 2021 |
| 4 | https://github.com/sfu-cosmo/MGCAMB, accessed on 15 December 2021 |
| 5 | http://miguelzuma.github.io/hi_class_public/, accessed on 15 December 2021 |
| 6 | http://eftcamb.org/, accessed on 15 December 2021 |
References
- Kennefick, D. Not only because of theory: Dyson, Eddington and the competing myths of the 1919 eclipse expedition. Einstein Stud. 2012, 12, 201–232. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Balokovic, M.; Barrett, J.; Bintley, D.; et al. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L1. [Google Scholar] [CrossRef]
- Corbelli, E.; Salucci, P. The Extended Rotation Curve and the Dark Matter Halo of M33. MNRAS 2000, 311, 441–447. [Google Scholar] [CrossRef]
- Markevitch, M.; Gonzalez, A.H.; Clowe, D.; Vikhlinin, A.; David, L.; Forman, W.; Jones, C.; Murray, S.; Tucker, W. Direct constraints on the dark matter self-interaction cross-section from the merging galaxy cluster 1E0657-56. Astrophys. J. 2004, 606, 819–824. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron Astrophys 2020, 641, A6, Erratum in Astron Astrophys 2021, 652, C4. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gillil, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Velten, H.E.S.; vom Marttens, R.F.; Zimdahl, W. Aspects of the cosmological “coincidence problem”. Eur. Phys. J. C 2014, 74, 3160. [Google Scholar] [CrossRef]
- Perivolaropoulos, L.; Skara, F. Challenges for ΛCDM: An update. arXiv 2021, arXiv:2105.05208. [Google Scholar]
- Di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the realm of the Hubble tension—a review of solutions. Class. Quant. Grav. 2021, 38, 153001. [Google Scholar] [CrossRef]
- Ma, C.P.; Bertschinger, E. Cosmological Perturbation Theory in the Synchronous and Conformal Newtonian Gauges. Astrophys. J. 1995, 455, 7. [Google Scholar] [CrossRef]
- Noller, J.; von Braun-Bates, F.; Ferreira, P.G. Relativistic scalar fields and the quasistatic approximation in theories of modified gravity. PRD 2014, 89, 023521. [Google Scholar] [CrossRef]
- Bellini, E.; Sawicki, I. Maximal freedom at minimum cost: Linear large-scale structure in general modifications of gravity. JCAP 2014, 7, 050. [Google Scholar] [CrossRef]
- Pogosian, L.; Silvestri, A. What can cosmology tell us about gravity? Constraining Horndeski gravity with Σ and μ. PRD 2016, 94, 104014. [Google Scholar] [CrossRef]
- Sawicki, I.; Bellini, E. Limits of quasistatic approximation in modified-gravity cosmologies. Phys. Rev. D 2015, 92, 084061. [Google Scholar] [CrossRef]
- Llinares, C.; Mota, D.F. Cosmological simulations of screened modified gravity out of the static approximation: Effects on matter distribution. Phys. Rev. D 2014, 89, 084023. [Google Scholar] [CrossRef]
- Caldwell, R.; Cooray, A.; Melchiorri, A. Constraints on a new post-general relativity cosmological parameter. PRD 2007, 76, 023507. [Google Scholar] [CrossRef]
- Zhao, G.B.; Pogosian, L.; Silvestri, A.; Zylberberg, J. Searching for modified growth patterns with tomographic surveys. PRD 2009, 79, 083513. [Google Scholar] [CrossRef]
- Amendola, L.; Kunz, M.; Sapone, D. Measuring the dark side (with weak lensing). JCAP 2008, 2008, 013. [Google Scholar] [CrossRef]
- Hojjati, A.; Zhao, G.B.; Pogosian, L.; Silvestri, A. MGCAMB: Modification of Growth with CAMB. Astrophys. Source Code Libr. 2011, 2011, ascl-1106. [Google Scholar]
- Bernardeau, F.; Colombi, S.; Gaztanaga, E.; Scoccimarro, R. Large-scale structure of the Universe and cosmological perturbation theory. Phys. Rep. 2002, 367, 1–248. [Google Scholar] [CrossRef]
- Linder, E.V. Cosmic growth history and expansion history. PRD 2005, 72, 043529. [Google Scholar] [CrossRef]
- Lahav, O.; Lilje, P.B.; Primack, J.R.; Rees, M.J. Dynamical effects of the cosmological constant. MNRAS 1991, 251, 128–136. [Google Scholar] [CrossRef]
- Mueller, E.M.; Percival, W.; Linder, E.; Alam, S.; Zhao, G.B.; Sánchez, A.G.; Beutler, F.; Brinkmann, J. The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Constraining modified gravity. MNRAS 2018, 475, 2122–2131. [Google Scholar] [CrossRef]
- Zhang, P.; Liguori, M.; Bean, R.; Dodelson, S. Probing Gravity at Cosmological Scales by Measurements which Test the Relationship between Gravitational Lensing and Matter Overdensity. Phys. Rev. Lett. 2007, 99, 141302. [Google Scholar] [CrossRef]
- Leonard, C.D.; Ferreira, P.G.; Heymans, C. Testing gravity with EG: Mapping theory onto observations. JCAP 2015, 12, 051. [Google Scholar] [CrossRef]
- Ghosh, B.; Durrer, R. The observable Eg statistics. JCAP 2019, 06, 010. [Google Scholar] [CrossRef]
- Ferreira, P.G. Cosmological Tests of Gravity. Ann. Rev. Astron. Astrophys. 2019, 57, 335–374. [Google Scholar] [CrossRef]
- Blake, C.; Amon, A.; Asgari, M.; Bilicki, M.; Dvornik, A.; Erben, T.; Giblin, B.; Glazebrook, K.; Heymans, C.; Hildebrandt, H.; et al. Testing gravity using galaxy-galaxy lensing and clustering amplitudes in KiDS-1000, BOSS and 2dFLenS. Astron. Astrophys. 2020, 642, A158. [Google Scholar] [CrossRef]
- Nunes, R.C.; Vagnozzi, S. Arbitrating the S8 discrepancy with growth rate measurements from redshift-space distortions. Mon. Not. Roy. Astron. Soc. 2021, 505, 5427. [Google Scholar] [CrossRef]
- Starobinsky, A.A. A new type of isotropic cosmological models without singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Catena, R.; Pietroni, M.; Scarabello, L. Einstein and Jordan frames reconciled: A frame-invariant approach to scalar-tensor cosmology. PRD 2007, 76, 084039. [Google Scholar] [CrossRef]
- Will, C.M. The confrontation between general relativity and experiment. Living Rev. Relativ. 2014, 17, 1–117. [Google Scholar] [CrossRef] [PubMed]
- Clifton, T.; Ferreira, P.G.; Padilla, A.; Skordis, C. Modified gravity and cosmology. Phys. Rep. 2012, 513, 1–189. [Google Scholar] [CrossRef]
- Brans, C.; Dicke, R.H. Mach’s principle and a relativistic theory of gravitation. Phys. Rev. 1961, 124, 925. [Google Scholar] [CrossRef]
- Sawicki, I.; Hu, W. Stability of cosmological solutions in f (R) models of gravity. PRD 2007, 75, 127502. [Google Scholar] [CrossRef]
- Alonso, D.; Bellini, E.; Ferreira, P.G.; Zumalacarregui, M. Observational future of cosmological scalar-tensor theories. PRD 2017, 95, 063502. [Google Scholar] [CrossRef]
- Joudaki, S.; Ferreira, P.G.; Lima, N.A.; Winther, H.A. Testing Gravity on Cosmic Scales: A Case Study of Jordan-Brans-Dicke Theory. arXiv 2020, arXiv:2010.15278. [Google Scholar]
- Horndeski, G.W. Second-order scalar-tensor field equations in a four-dimensional space. Int. J. Theor. Phys. 1974, 10, 363–384. [Google Scholar] [CrossRef]
- Deffayet, C.; Deser, S.; Esposito-Farese, G. Generalized Galileons: All scalar models whose curved background extensions maintain second-order field equations and stress tensors. PRD 2009, 80, 064015. [Google Scholar] [CrossRef]
- Deffayet, C.; Gao, X.; Steer, D.A.; Zahariade, G. From k-essence to generalized Galileons. PRD 2011, 84, 064039. [Google Scholar] [CrossRef]
- Kobayashi, T.; Yamaguchi, M.; Yokoyama, J. Generalized G-Inflation: —Inflation with the Most General Second-Order Field Equations—. Prog. Theor. Phys. 2011, 126, 511–529. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Goldstein, A.; Veres, P.; Burns, E.; Briggs, M.S.; Hamburg, R.; Kocevski, D.; Wilson-Hodge, C.A.; Preece, R.D.; Poolakkil, S.; Roberts, O.J.; et al. An Ordinary Short Gamma-Ray Burst with Extraordinary Implications: Fermi-GBM Detection of GRB 170817A. Astrophys. J. Lett. 2017, 848, L14. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Gravitational Waves and Gamma-rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. Lett. 2017, 848, L13. [Google Scholar] [CrossRef]
- Baker, T.; Bellini, E.; Ferreira, P.G.; Lagos, M.; Noller, J.; Sawicki, I. Strong constraints on cosmological gravity from GW170817 and GRB 170817A. PRL 2017, 119, 251301. [Google Scholar] [CrossRef]
- Langlois, D.; Saito, R.; Yamauchi, D.; Noui, K. Scalar-tensor theories and modified gravity in the wake of GW170817. PRD 2018, 97, 061501. [Google Scholar] [CrossRef]
- Ezquiaga, J.M.; Zumalacárregui, M. Dark Energy After GW170817: Dead Ends and the Road Ahead. Phys. Rev. Lett. 2017, 119, 251304. [Google Scholar] [CrossRef]
- Creminelli, P.; Vernizzi, F. Dark Energy after GW170817 and GRB170817A. PRL 2017, 119, 251302. [Google Scholar] [CrossRef] [PubMed]
- McManus, R.; Lombriser, L.; Peñarrubia, J. Finding Horndeski theories with Einstein gravity limits. JCAP 2016, 2016, 006. [Google Scholar] [CrossRef]
- Sakstein, J.; Jain, B. Implications of the neutron star merger GW170817 for cosmological scalar-tensor theories. PRL 2017, 119, 251303. [Google Scholar] [CrossRef] [PubMed]
- Ishak, M. Testing general relativity in cosmology. Living Rev. Relativ. 2019, 22, 1–204. [Google Scholar] [CrossRef] [PubMed]
- Koyama, K. Cosmological tests of modified gravity. Rep. Prog. Phys. 2016, 79, 046902. [Google Scholar] [CrossRef] [PubMed]
- Pogosian, L.; Silvestri, A.; Koyama, K.; Zhao, G.B. How to optimally parametrize deviations from general relativity in the evolution of cosmological perturbations. PRD 2010, 81, 104023. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution. Phys. Rept. 2017, 692, 1–104. [Google Scholar] [CrossRef]
- Saridakis, E.N.; Lazkoz, R.; Salzano, V.; Moniz, P.V.; Capozziello, S.; Jimenez, J.B.; De Laurentis, M.; Olmo, G.J.; Akrami, Y.; Bahamonde, S.; et al. Modified Gravity and Cosmology: An Update by the CANTATA Network. arXiv 2021, arXiv:2105.12582. [Google Scholar]
- Gubitosi, G.; Piazza, F.; Vernizzi, F. The Effective Field Theory of Dark Energy. JCAP 2013, 02, 032. [Google Scholar] [CrossRef]
- Bloomfield, J.K.; Flanagan, E.E.; Park, M.; Watson, S. Dark energy or modified gravity? An effective field theory approach. JCAP 2013, 08, 010. [Google Scholar] [CrossRef]
- Piazza, F.; Vernizzi, F. Effective Field Theory of Cosmological Perturbations. Class. Quant. Grav. 2013, 30, 214007. [Google Scholar] [CrossRef]
- Brax, P.; Valageas, P. The effective field theory of K-mouflage. JCAP 2016, 01, 020. [Google Scholar] [CrossRef]
- Ballinger, W.; Peacock, J.; Heavens, A. Measuring the cosmological constant with redshift surveys. MNRAS 1996, 282, 877–888. [Google Scholar] [CrossRef]
- Baldauf, T.; Mirbabayi, M.; Simonović, M.; Zaldarriaga, M. Equivalence principle and the baryon acoustic peak. PRD 2015, 92, 043514. [Google Scholar] [CrossRef]
- Wang, Y.; Percival, W.; Cimatti, A.; Mukherjee, P.; Guzzo, L.; Baugh, C.M.; Carbone, C.; Franzetti, P.; Garilli, B.; Geach, J.E.; et al. Designing a space-based galaxy redshift survey to probe dark energy. MNRAS 2010, 409, 737–749. [Google Scholar] [CrossRef]
- Taruya, A.; Nishimichi, T.; Saito, S. Baryon acoustic oscillations in 2D: Modeling redshift-space power spectrum from perturbation theory. PRD 2010, 82, 063522. [Google Scholar] [CrossRef]
- Kaiser, N. Clustering in real space and in redshift space. MNRAS 1987, 227, 1–21. [Google Scholar] [CrossRef]
- Scoccimarro, R.; Frieman, J. Loop corrections in non-linear cosmological perturbation theory. arXiv 1995, arXiv:astro-ph/9509047. [Google Scholar]
- Carrasco, J.J.M.; Hertzberg, M.P.; Senatore, L. The effective field theory of cosmological large scale structures. J. High Energy Phys. 2012, 2012, 1–40. [Google Scholar] [CrossRef]
- Blanchard, A.; Camera, S.; Carbone, C.; Cardone, V.F.; Casas, S.; Clesse, S.; Ilic, S.; Kilbinger, M.; Kitching, T.; Kunz, M.; et al. Euclid preparation: VII. Forecast validation for Euclid cosmological probes. A&A 2020, 642, A191. [Google Scholar] [CrossRef]
- Sachs, R.K.; Wolfe, A.M. Perturbations of a Cosmological Model and Angular Variations of the Microwave Background. ApJ 1967, 147, 73. [Google Scholar] [CrossRef]
- Kofman, L.A.; Starobinskii, A.A. Effect of the Cosmological Constant on Largescale Anisotropies in the Microwave Background. Sov. Astron. Lett. 1985, 11, 271–274. [Google Scholar]
- Acquaviva, V.; Baccigalupi, C. Dark energy records in lensed cosmic microwave background. PRD 2006, 74, 103510. [Google Scholar] [CrossRef]
- Carbone, C.; Baldi, M.; Pettorino, V.; Baccigalupi, C. Maps of CMB lensing deflection from N-body simulations in Coupled Dark Energy Cosmologies. JCAP 2013, 9, 004. [Google Scholar] [CrossRef]
- Ade, P.A.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Battaner, E.; et al. Planck 2015 results. XIV. Dark energy and modified gravity. A&A 2016, 594, A14. [Google Scholar] [CrossRef]
- Sahni, V.; Saini, T.D.; Starobinsky, A.A.; Alam, U. Statefinder: A New geometrical diagnostic of dark energy. JETP Lett. 2003, 77, 201–206. [Google Scholar] [CrossRef]
- Alam, U.; Sahni, V.; Saini, T.D.; Starobinsky, A.A. Exploring the expanding universe and dark energy using the Statefinder diagnostic. Mon. Not. Roy. Astron. Soc. 2003, 344, 1057. [Google Scholar] [CrossRef]
- Capozziello, S.; D’Agostino, R.; Luongo, O. Extended Gravity Cosmography. Int. J. Mod. Phys. D 2019, 28, 1930016. [Google Scholar] [CrossRef]
- Capozziello, S.; Izzo, L. Cosmography by GRBs. Astron. Astrophys. 2008, 490, 31. [Google Scholar] [CrossRef]
- Rezaei, M.; Pour-Ojaghi, S.; Malekjani, M. A Cosmography Approach to Dark Energy Cosmologies: New Constraints Using the Hubble Diagrams of Supernovae, Quasars, and Gamma-Ray Bursts. Astrophys. J. 2020, 900, 70. [Google Scholar] [CrossRef]
- Bargiacchi, G.; Benetti, M.; Capozziello, S.; Lusso, E.; Risaliti, G.; Signorini, M. Quasar cosmology: Dark energy evolution and spatial curvature. arXiv 2021, arXiv:astro-ph.CO/2111.02420. [Google Scholar]
- Lewis, A.; Challinor, A.; Lasenby, A. Efficient computation of CMB anisotropies in closed FRW models. Astrophys. J. 2000, 538, 473–476. [Google Scholar] [CrossRef]
- Howlett, C.; Lewis, A.; Hall, A.; Challinor, A. CMB power spectrum parameter degeneracies in the era of precision cosmology. JCAP 2012, 2012, 027. [Google Scholar] [CrossRef]
- Lesgourgues, J. The cosmic linear anisotropy solving system (CLASS) I: Overview. arXiv 2011, arXiv:1104.2932. [Google Scholar]
- Blas, D.; Lesgourgues, J.; Tram, T. The cosmic linear anisotropy solving system (CLASS). Part II: Approximation schemes. JCAP 2011, 2011, 034. [Google Scholar] [CrossRef]
- Dossett, J.N.; Ishak, M.; Moldenhauer, J. Testing general relativity at cosmological scales: Implementation and parameter correlations. PRD 2011, 84. [Google Scholar] [CrossRef]
- Dossett, J.N.; Ishak, M. Spatial curvature and cosmological tests of general relativity. PRD 2012, 86. [Google Scholar] [CrossRef]
- Zucca, A.; Pogosian, L.; Silvestri, A.; Zhao, G.B. MGCAMB with massive neutrinos and dynamical dark energy. JCAP 2019, 2019, 001. [Google Scholar] [CrossRef]
- Pace, F.; Battye, R.A.; Bellini, E.; Lombriser, L.; Vernizzi, F.; Bolliet, B. Comparison of different approaches to the quasi-static approximation in Horndeski models. JCAP 2021, 2021, 017. [Google Scholar] [CrossRef]
- Zumalacárregui, M.; Bellini, E.; Sawicki, I.; Lesgourgues, J.; Ferreira, P.G. Hi_class: Horndeski in the cosmic linear anisotropy solving system. JCAP 2017, 2017, 019. [Google Scholar] [CrossRef]
- Hu, B.; Raveri, M.; Silvestri, A.; Frusciante, N. EFTCAMB/EFTCosmoMC: Massive neutrinos in dark cosmologies. arXiv 2014, arXiv:1410.5807. [Google Scholar] [CrossRef]
- Hu, B.; Raveri, M.; Frusciante, N.; Silvestri, A. EFTCAMB/EFTCosmoMC: Numerical Notes v3.0. arXiv 2014, arXiv:1405.3590v4. [Google Scholar]
- Aghanim, N.; Akrami, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; et al. Planck 2018 results. I. Overview and the cosmological legacy of Planck. A&A 2020, 641, A1. [Google Scholar] [CrossRef]
- Calabrese, E.; Slosar, A.; Melchiorri, A.; Smoot, G.F.; Zahn, O. Cosmic Microwave Weak lensing data as a test for the dark universe. PRD 2008, 77, 123531. [Google Scholar] [CrossRef]
- Lee, S.; Huff, E.M.; Ross, A.J.; Choi, A.; Hirata, C.; Honscheid, K.; MacCrann, N.; Troxel, M.A.; Davis, C.; Eifler, T.F.; et al. Producing a BOSS-CMASS sample with DES imaging. MNRAS 2019, 489, 2887–2906. [Google Scholar] [CrossRef]
- Chuang, C.H.; Pellejero-Ibanez, M.; Rodriguez-Torres, S.; Ross, A.J.; Zhao, G.B.; Wang, Y.; Cuesta, A.J.; Rubino-Martin, J.A.; Prada, F.; Alam, S.; et al. The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Single-probe measurements from DR12 galaxy clustering – towards an accurate model. MNRAS 2017, 471, 2370–2390. [Google Scholar] [CrossRef]
- Lee, S.; Huff, E.M.; Choi, A.; Elvin-Poole, J.; Hirata, C.; Honscheid, K.; Maccrann, N.; Ross, A.J.; Troxel, M.A.; Eifler, T.F.; et al. Probing gravity with the DES-CMASS sample and BOSS spectroscopy. arXiv 2021, arXiv:astro-ph.CO/2104.14515. [Google Scholar] [CrossRef]
- Joudaki, S.; Mead, A.; Blake, C.; Choi, A.; de Jong, J.; Erben, T.; Conti, I.F.; Herbonnet, R.; Heymans, C.; Hildebrandt, H.; et al. KiDS-450: Testing extensions to the standard cosmological model. MNRAS 2017, 471, 1259–1279. [Google Scholar] [CrossRef]
- Abbott, T.M.C.; Abdalla, F.B.; Avila, S.; Banerji, M.; Baxter, E.; Bechtol, K.; Becker, M.R.; Bertin, E.; Blazek, J.; Bridle, S.L.; et al. Dark Energy Survey Year 1 Results: Constraints on Extended Cosmological Models from Galaxy Clustering and Weak Lensing. PRD 2019, 99, 123505. [Google Scholar] [CrossRef]
- Benitez, N.; Dupke, R.; Moles, M.; Sodre, L.; Cenarro, J.; Marin-Franch, A.; Taylor, K.; Cristobal, D.; Fernandez-Soto, A.; de Oliveira, C.M.; et al. J-PAS: The Javalambre-Physics of the Accelerated Universe Astrophysical Survey. arXiv 2014, arXiv:astro-ph.CO/1403.5237. [Google Scholar]
- Collaboration, D.; Aghamousa, A.; Aguilar, J.; Ahlen, S.; Alam, S.; Allen, L.E.; Prieto, C.A.; Annis, J.; Bailey, S.; Balland, C.; et al. The DESI Experiment Part I: Science, Targeting, and Survey Design; University of California: Berkeley, CA, USA, 2018. [Google Scholar]
- Amendola, L.; Appleby, S.; Avgoustidis, A.; Bacon, D.; Baker, T.; Baldi, M.; Bartolo, N.; Blanchard, A.; Bonvin, C.; Borgani, S.; et al. Cosmology and fundamental physics with the Euclid satellite. Living Rev. Relativ. 2018, 21, 1–345. [Google Scholar] [CrossRef] [PubMed]
- Laureijs, R.; Amiaux, J.; Arduini, S.; Augueres, J.L.; Brinchmann, J.; Cole, R.; Cropper, M.; Dabin, C.; Duvet, L.; Ealet, A.; et al. Euclid definition study report. arXiv 2011, arXiv:1110.3193. [Google Scholar]
- Ivezić, Ž.; Kahn, S.M.; Tyson, J.A.; Abel, B.; Acosta, E.; Allsman, R.; Alonso, D.; AlSayyad, Y.; Anderson, S.F.; Andrew, J.; et al. LSST: From Science Drivers to Reference Design and Anticipated Data Products. ApJ 2019, 873, 111. [Google Scholar] [CrossRef]
- Spergel, D.; Gehrels, N.; Baltay, C.; Bennett, D.; Breckinridge, J.; Donahue, M.; Dressler, A.; Gaudi, B.S.; Greene, T.; Guyon, O.; et al. Wide-Field InfrarRed Survey Telescope-Astrophysics Focused Telescope Assets WFIRST-AFTA 2015 Report. arXiv 2015, arXiv:1503.03757. [Google Scholar]
- Bacon, D.J.; Battye, R.A.; Bull, P.; Camera, S.; Ferreira, P.G.; Harrison, I.; Parkinson, D.; Pourtsidou, A.; Santos, M.G.; Wolz, L.; et al. Cosmology with Phase 1 of the Square Kilometre Array: Red Book 2018: Technical specifications and performance forecasts. Publ. Astron. Soc. Austral. 2020, 37, e007. [Google Scholar] [CrossRef]
- Spergel, D.; Gehrels, N.; Breckinridge, J.; Donahue, M.; Dressler, A.; Gaudi, B.; Greene, T.; Guyon, O.; Hirata, C.; Kalirai, J.; et al. WFIRST-2.4: What every astronomer should know. arXiv 2013, arXiv:1305.5425. [Google Scholar]
- Levi, M.; Bebek, C.; Beers, T.; Blum, R.; Cahn, R.; Eisenstein, D.; Flaugher, B.; Honscheid, K.; Kron, R.; Lahav, O.; et al. The DESI Experiment, a whitepaper for Snowmass 2013. arXiv 2013, arXiv:1308.0847. [Google Scholar]
- Abell, P.A.; Allison, J.; Anderson, S.F.; Andrew, J.R.; Angel, J.R.P.; Armus, L.; Arnett, D.; Asztalos, S.; Axelrod, T.S.; Bailey, S.; et al. Lsst science book, version 2.0. arXiv 2009, arXiv:0912.0201. [Google Scholar]
- Vogeley, M.S.; Szalay, A.S. Eigenmode analysis of galaxy redshift surveys I. theory and methods. arXiv 1996, arXiv:astro-ph/9601185. [Google Scholar] [CrossRef]
- Tegmark, M. Measuring cosmological parameters with galaxy surveys. PRL 1997, 79, 3806. [Google Scholar] [CrossRef]
- Tegmark, M.; Taylor, A.N.; Heavens, A.F. Karhunen-Loeve eigenvalue problems in cosmology: How should we tackle large data sets? ApJ 1997, 480, 22. [Google Scholar] [CrossRef]
- Carron, J. On the assumption of Gaussianity for cosmological two-point statistics and parameter dependent covariance matrices. Astron. Astrophys. 2013, 551, A88. [Google Scholar] [CrossRef]
- Casas, S.; Kunz, M.; Martinelli, M.; Pettorino, V. Linear and non-linear Modified Gravity forecasts with future surveys. Phys. Dark Univ. 2017, 18, 73–104. [Google Scholar] [CrossRef]
- Aparicio Resco, M.; Maroto, A.L.; Alcaniz, J.S.; Abramo, L.R.; Hernandez-Monteagudo, C.; Benitez, N.; Carneiro, S.; Cenarro, A.J.; Cristobal-Hornillos, D.; Dupke, R.A.; et al. J-PAS: Forecasts on dark energy and modified gravity theories. MNRAS 2020, 493, 3616–3631. [Google Scholar] [CrossRef]
- Asaba, S.; Hikage, C.; Koyama, K.; Zhao, G.B.; Hojjati, A.; Pogosian, L. Principal Component Analysis of Modified Gravity using Weak Lensing and Peculiar Velocity Measurements. JCAP 2013, 08, 029. [Google Scholar] [CrossRef]
- Hojjati, A.; Pogosian, L.; Silvestri, A.; Zhao, G.B. Observable physical modes of modified gravity. PRD 2014, 89, 083505. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Machine learning basics. Deep Learn. 2016, 1, 98–164. [Google Scholar]
- Silvestri, A.; Pogosian, L.; Buniy, R.V. Practical approach to cosmological perturbations in modified gravity. PRD 2013, 87, 104015. [Google Scholar] [CrossRef]
- Spurio Mancini, A.; Reischke, R.; Pettorino, V.; Schäfer, B.M.; Zumalacárregui, M. Testing (modified) gravity with 3D and tomographic cosmic shear. MNRAS 2018, 480, 3725–3738. [Google Scholar] [CrossRef]
- Laszlo, I.; Bean, R.; Kirk, D.; Bridle, S. Disentangling dark energy and cosmic tests of gravity from weak lensing systematics. MNRAS 2012, 423, 1750–1765. [Google Scholar] [CrossRef]
- Ferté, A.; Kirk, D.; Liddle, A.R.; Zuntz, J. Testing gravity on cosmological scales with cosmic shear, cosmic microwave background anisotropies, and redshift-space distortions. PRD 2019, 99, 083512. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VIII. Gravitational lensing. A&A 2020, 641, A8. [Google Scholar] [CrossRef]
- Ade, P.; Aguirre, J.; Ahmed, Z.; Aiola, S.; Ali, A.; Alonso, D.; Alvarez, M.A.; Arnold, K.; Ashton, P.; Austermann, J.; et al. The Simons Observatory: Science goals and forecasts. JCAP 2019, 2, 056. [Google Scholar] [CrossRef]
- Abazajian, K.N.; Adshead, P.; Ahmed, Z.; Allen, S.W.; Alonso, D.; Arnold, K.S.; Baccigalupi, C.; Bartlett, J.G.; Battaglia, N.; Benson, B.A.; et al. CMB-S4 Science Book, 1st ed.; Cornell University: Ithaca, NY, USA, 2016. [Google Scholar]
- Giannantonio, T.; Martinelli, M.; Silvestri, A.; Melchiorri, A. New constraints on parametrised modified gravity from correlations of the CMB with large scale structure. JCAP 2010, 4, 030. [Google Scholar] [CrossRef]
- Ilić, S.; Aghanim, N.; Baccigalupi, C.; Bermejo-Climent, J.R.; Fabbian, G.; Legr, L.; Paoletti, D.; Ballardini, M.; Archidiacono, M.; Douspis, M.; et al. Euclid preparation: XV. Forecasting cosmological constraints for the Euclid and CMB joint analysis. arXiv 2021, arXiv:2106.08346. [Google Scholar]
- Ezquiaga, J.M.; Zumalacárregui, M. Dark Energy in light of Multi-Messenger Gravitational-Wave astronomy. Front. Astron. Space Sci. 2018, 5, 44. [Google Scholar] [CrossRef]
- Belgacem, E.; Dirian, Y.; Foffa, S.; Maggiore, M. Gravitational-wave luminosity distance in modified gravity theories. PRD 2018, 97, 104066. [Google Scholar] [CrossRef]
- Belgacem, E.; Dirian, Y.; Foffa, S.; Maggiore, M. Modified gravitational-wave propagation and standard sirens. PRD 2018, 98, 023510. [Google Scholar] [CrossRef]
- Amaro-Seoane, P.; Audley, H.; Babak, S.; Baker, J.; Barausse, E.; Bender, P.; Berti, E.; Binetruy, P.; Born, M.; Bortoluzzi, D.; et al. Laser Interferometer Space Antenna. arXiv 2017, arXiv:1702.00786. [Google Scholar]
- Maggiore, M.; Van Den Broeck, C.; Bartolo, N.; Belgacem, E.; Bertacca, D.; Bizouard, M.A.; Branchesi, M.; Clesse, S.; Foffa, S.; Garcia-Bellido, J.; et al. Science Case for the Einstein Telescope. JCAP 2020, 3, 050. [Google Scholar] [CrossRef]
- Belgacem, E.; Calcagni, G.; Crisostomi, M.; Dalang, C.; Dirian, Y.; Ezquiaga, J.M.; Fasiello, M.; Foffa, S.; Ganz, A.; Garcia-Bellido, J.; et al. Testing modified gravity at cosmological distances with LISA standard sirens. JCAP 2019, 7, 024. [Google Scholar] [CrossRef]
- Dalang, C.; Lombriser, L. Limitations on Standard Sirens tests of gravity from screening. JCAP 2019, 10, 013. [Google Scholar] [CrossRef]
- Dalang, C.; Fleury, P.; Lombriser, L. Horndeski gravity and standard sirens. PRD 2020, 102, 044036. [Google Scholar] [CrossRef]
- Hogg, N.B.; Martinelli, M.; Nesseris, S. Constraints on the distance duality relation with standard sirens. JCAP 2020, 12, 019. [Google Scholar] [CrossRef]
- Martinelli, M.; Martins, C.J.A.P.; Nesseris, S.; Sapone, D.; Tutusaus, I.; Avgoustidis, A.; Camera, S.; Carbone, C.; Casas, S.; Ilic, S.; et al. Euclid: Forecast constraints on the cosmic distance duality relation with complementary external probes. A&A 2020, 644, A80. [Google Scholar] [CrossRef]
- Birrer, S.; Shajib, A.J.; Galan, A.; Millon, M.; Treu, T.; Agnello, A.; Auger, M.; Chen, G.F.; Christensen, L.; Collett, T.; et al. TDCOSMO-IV. Hierarchical time-delay cosmography – joint inference of the Hubble constant and galaxy density profiles. A&A 2020, 643, A165. [Google Scholar] [CrossRef]
- Jyoti, D.; Munoz, J.B.; Caldwell, R.R.; Kamionkowski, M. Cosmic Time Slip: Testing Gravity on Supergalactic Scales with Strong-Lensing Time Delays. PRD 2019, 100, 043031. [Google Scholar] [CrossRef]
- Yang, T.; Birrer, S.; Hu, B. The first simultaneous measurement of Hubble constant and post-Newtonian parameter from Time-Delay Strong Lensing. MNRAS 2020, 497, L56–L61. [Google Scholar] [CrossRef]
- Shiralilou, B.; Martinelli, M.; Papadomanolakis, G.; Peirone, S.; Renzi, F.; Silvestri, A. Strong Lensing Time Delay Constraints on Dark Energy: A Forecast. JCAP 2020, 04, 057. [Google Scholar] [CrossRef]
- Yang, T.; Hu, B.; Cai, R.G.; Wang, B. New probe of gravity: Strongly lensed gravitational wave multi-messenger approach. Astrophys. J. 2019, 880, 50. [Google Scholar] [CrossRef]
- Takahashi, R.; Sato, M.; Nishimichi, T.; Taruya, A.; Oguri, M. Revising the Halofit Model for the Nonlinear Matter Power Spectrum. Astrophys. J. 2012, 761, 152. [Google Scholar] [CrossRef]
- Mead, A.; Brieden, S.; Tröster, T.; Heymans, C. HMcode-2020: Improved modelling of non-linear cosmological power spectra with baryonic feedback. MNRAS 2021, 502, 1401–1422. [Google Scholar] [CrossRef]
- Martinelli, M.; Tutusaus, I.; Archidiacono, M.; Camera, S.; Cardone, V.F.; Clesse, S.; Casas, S.; Casarini, L.; Mota, D.F.; Hoekstra, H.; et al. Euclid: Impact of non-linear and baryonic feedback prescriptions on cosmological parameter estimation from weak lensing cosmic shear. A&A 2021, 649, A100. [Google Scholar] [CrossRef]
- Safi, S.; Farhang, M. Sensitivity of Cosmological Parameter Estimation to Nonlinear Prescription from Galaxy Clustering. Astrophys. J. 2021, 914, 65. [Google Scholar] [CrossRef]
- Audren, B.; Lesgourgues, J.; Bird, S.; Haehnelt, M.G.; Viel, M. Neutrino masses and cosmological parameters from a Euclid-like survey: Markov Chain Monte Carlo forecasts including theoretical errors. JCAP 2013, 2013, 026. [Google Scholar] [CrossRef]
- Sprenger, T.; Archidiacono, M.; Brinckmann, T.; Clesse, S.; Lesgourgues, J. Cosmology in the era of Euclid and the Square Kilometre Array. JCAP 2019, 02, 047. [Google Scholar] [CrossRef]
- Knabenhans, M.; Brinckmann, T.; Stadel, J.; Schneider, A.; Teyssier, R. Parameter inference with non-linear galaxy clustering: Accounting for theoretical uncertainties. arXiv 2021, arXiv:2110.01488. [Google Scholar]
- Winther, H.A.; Koyama, K.; Manera, M.; Wright, B.S.; Zhao, G.B. COLA with scale-dependent growth: Applications to screened modified gravity models. JCAP 2017, 2017, 006. [Google Scholar] [CrossRef]
- Li, B.; Zhao, G.B.; Teyssier, R.; Koyama, K. ECOSMOG: An efficient code for simulating modified gravity. JCAP 2012, 2012, 051. [Google Scholar] [CrossRef]
- Braden, J.; Burrage, C.; Elder, B.; Saadeh, D. φenics: Vainshtein screening with the finite element method. JCAP 2021, 2021, 010. [Google Scholar] [CrossRef]
- Puchwein, E.; Baldi, M.; Springel, V. Modified-Gravity-GADGET: A new code for cosmological hydrodynamical simulations of modified gravity models. MNRAS 2013, 436, 348–360. [Google Scholar] [CrossRef]
- Reverberi, L.; Daverio, D. fRevolution—relativistic cosmological simulations in f (R) gravity. Part I. Methodology. JCAP 2019, 2019, 35. [Google Scholar] [CrossRef]
- Baldi, M.; Villaescusa-Navarro, F.; Viel, M.; Puchwein, E.; Springel, V.; Moscardini, L. Cosmic degeneracies–I. Joint N-body simulations of modified gravity and massive neutrinos. MNRAS 2014, 440, 75–88. [Google Scholar] [CrossRef]
- Valogiannis, G.; Bean, R. Efficient simulations of large scale structure in modified gravity cosmologies with comoving Lagrangian acceleration. PRD 2017, 95, 103515. [Google Scholar] [CrossRef]
- Hassani, F.; Lombriser, L. N-body simulations for parametrized modified gravity. MNRAS 2020, 497, 1885–1894. [Google Scholar] [CrossRef]
- Winther, H.; Casas, S.; Baldi, M.; Koyama, K.; Li, B.; Lombriser, L.; Zhao, G.B. Emulators for the nonlinear matter power spectrum beyond ΛCDM. PRD 2019, 100, 123540. [Google Scholar] [CrossRef]
- Arnold, C.; Li, B.; Giblin, B.; Harnois-Déraps, J.; Cai, Y.C. FORGE–the f (R) gravity cosmic emulator project I: Introduction and matter power spectrum emulator. arXiv 2021, arXiv:2109.04984. [Google Scholar]
- Ramachandra, N.; Valogiannis, G.; Ishak, M.; Heitmann, K. Matter Power Spectrum Emulator for f(R) Modified Gravity Cosmologies. PRD 2021, 103, 123525. [Google Scholar] [CrossRef]
- Mancini, A.S.; Pourtsidou, A. KiDS-1000 Cosmology: Machine learning -accelerated constraints on Interacting Dark Energy with CosmoPower. arXiv 2021, arXiv:2110.07587. [Google Scholar]
- Bose, B.; Cataneo, M.; Tröster, T.; Xia, Q.; Heymans, C.; Lombriser, L. On the road to percent accuracy IV: ReACT - computing the non-linear power spectrum beyond ΛCDM. MNRAS 2020, 498, 4650–4662. [Google Scholar] [CrossRef]
- Cataneo, M.; Lombriser, L.; Heymans, C.; Mead, A.; Barreira, A.; Bose, S.; Li, B. On the road to percent accuracy: Non-linear reaction of the matter power spectrum to dark energy and modified gravity. MNRAS 2019, 488, 2121–2142. [Google Scholar] [CrossRef]
- Yoo, J. General Relativistic Description of the Observed Galaxy Power Spectrum: Do We Understand What We Measure? PRD 2010, 82, 083508. [Google Scholar] [CrossRef]
- Challinor, A.; Lewis, A. The linear power spectrum of observed source number counts. PRD 2011, 84, 043516. [Google Scholar] [CrossRef]
- Bonvin, C.; Durrer, R. What galaxy surveys really measure. PRD 2011, 84, 063505. [Google Scholar] [CrossRef]
- Limber, D.N. The Analysis of Counts of the Extragalactic Nebulae in Terms of a Fluctuating Density Field. ApJ 1953, 117, 134. [Google Scholar] [CrossRef]
- Limber, D.N. The Analysis of Counts of the Extragalactic Nebulae in Terms of a Fluctuating Density Field. II. ApJ 1954, 119, 655. [Google Scholar] [CrossRef]
- Kaiser, N. Weak Gravitational Lensing of Distant Galaxies. ApJ 1992, 388, 272. [Google Scholar] [CrossRef]
- Martinelli, M.; Dalal, R.; Majidi, F.; Akrami, Y.; Camera, S.; Sellentin, E. Ultra-large-scale approximations and galaxy clustering: Debiasing constraints on cosmological parameters. arXiv 2021, arXiv:2106.15604. [Google Scholar] [CrossRef]
- Baker, T.; Bull, P. Observational Signatures of Modified Gravity on Ultra-large Scales. ApJ 2015, 811, 116. [Google Scholar] [CrossRef]
- Villa, E.; Di Dio, E.; Lepori, F. Lensing convergence in galaxy clustering in ΛCDM and beyond. JCAP 2018, 04, 033. [Google Scholar] [CrossRef]
- Assassi, V.; Simonović, M.; Zaldarriaga, M. Efficient evaluation of angular power spectra and bispectra. JCAP 2017, 2017, 054. [Google Scholar] [CrossRef][Green Version]
- Campagne, J.E.; Neveu, J.; Plaszczynski, S. Angpow: A software for the fast computation of accurate tomographic power spectra. A&A 2017, 602, A72. [Google Scholar] [CrossRef]
- Grasshorn Gebhardt, H.S.; Jeong, D. Fast and accurate computation of projected two-point functions. PRD 2018, 97, 023504. [Google Scholar] [CrossRef]
- Sellentin, E.; Heymans, C.; Harnois-Déraps, J. The skewed weak lensing likelihood: Why biases arise, despite data and theory being sound. MNRAS 2018, 477, 4879–4895. [Google Scholar] [CrossRef]
- Alsing, J.; Charnock, T.; Feeney, S.; Wandelt, B. Fast likelihood-free cosmology with neural density estimators and active learning. MNRAS 2019, 488, 4440–4458. [Google Scholar] [CrossRef]
- Jeffrey, N.; Alsing, J.; Lanusse, F. Likelihood-free inference with neural compression of DES SV weak lensing map statistics. MNRAS 2021, 501, 954–969. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).