Abstract
The energy-momentum localization for a new four-dimensional and spherically symmetric, charged black hole solution that through a coupling of general relativity with non-linear electrodynamics is everywhere non-singular while it satisfies the weak energy condition, is investigated. The Einstein and Møller energy-momentum complexes have been employed in order to calculate the energy distribution and the momenta for the aforesaid solution. It is found that the energy distribution depends explicitly on the mass and the charge of the black hole, on two parameters arising from the space-time geometry considered, and on the radial coordinate. Further, in both prescriptions all the momenta vanish. In addition, a comparison of the results obtained by the two energy-momentum complexes is made, whereby some limiting and particular cases are pointed out.
1. Introduction
Even though the problem of energy-momentum localization has triggered a plethora of interesting research work, it still remains not fully answered for more than a century. The only step one can hope to make forward is to find a more powerful tool to handle this issue of general relativity.
The use of different tools for energy-momentum localization, like super-energy tensors [1,2,3], quasi-local definitions [4,5,6,7] and the energy-momentum complexes [8,9,10,11,12,13,14] has led to the development of several interesting works. As far as the energy-momentum complexes of Einstein [8], Landau-Lifshitz [10], Papapetrou [11], Bergmann-Thomson [12], and Weinberg [14] are concerned, they are pseudotensorial quantities and coordinate dependent. They can be used to perform calculations in Schwarzschild Cartesian coordinates and in Kerr-Schild Cartesian coordinates, and they have generated physically meaningful results [15,16,17,18,19,20,21]. The Møller energy-momentum complex [13] enables one to perform the calculation of energy and momenta in any coordinate system, including Schwarzschild Cartesian coordinates and Kerr-Schild Cartesian coordinates. In recent years, the Møller prescription has been the tool that provided physically meaningful results for many (), (), and () space-time geometries [22,23,24,25,26,27,28,29,30,31,32,33,34,35]. It is worth noting that different pseudotensors yield the same energy value for any metric of the Kerr-Schild class and also for solutions more general than those of the Kerr-Schild class (see [36,37,38]), for reviews and references). Moreover, the localization of energy-momentum has been studied in the context of teleparallel theory of gravitation whereby many similar results have been obtained [39,40,41,42,43,44,45,46,47].
The Einstein, Landau-Lifshitz, Papapetrou, Bergmann-Thomson, Weinberg, and Møller prescriptions are in agreement with the definition of the quasi-local mass given by Penrose [48] and developed by Tod [49] for some gravitating systems. Recently, the new concept in the localization of energy is that of quasi-local energy-momentum associated with a closed 2-surface. In fact, it has been demonstrated that “the quasi-local quantities could provide a more detailed characterization of the states of the gravitational field” [50]. The energy localization is also connected with the quasi-local energy given by Wang and Yau [51,52]. The rehabilitation of energy-momentum complexes concerns the searching for a common quasi-local energy value. Recently, an important discovery has been made, namely, by considering pseudotensors and quasi-local approaches in the context of the Hamiltonian formulation and with the choice of a four-dimensional isometric Minkowski reference geometry on the boundary, it is found that for any closed 2-surface there is a common value for the quasi-local energy for all expressions that are in agreement (to linear order) with the Freud superpotential or, put simply, all the quasi-local expressions in a large class yield the same energy-momentum [53,54].
This paper is organized as follows. In Section 2 we briefly present the non-singular black hole solution that satisfies the weak energy condition. In Section 3 the prescriptions of Einstein and Møller used for the calculation of the energy distribution and momenta are presented. In Section 4 we give the results obtained for the aforementioned non-singular black hole solution by applying the pseudotensorial definitions given in Section 3. Finally, in the Results and Discussion section we summarize the results and we focus on commenting about some limiting and particular cases. Throughout we have used geometrized units () and for the signature the choice has been (+,−,−,−). In the case of the Einstein prescription the calculations have been made in the Schwarzschild Cartesian coordinates , x, y, and for the Møller prescription the Schwarzschild coordinates were used. Further, Greek indices run from 0 to 3, while Latin indices take values from 1 to 3.
2. The Non-Singular Black Hole Solution Satisfying the Weak Energy Condition
In this section the new spherically symmetric and charged non-singular black hole solution that satisfies the weak energy condition developed by L. Balart and E. C. Vagenas [55] is introduced. This black hole solution has been found in the context of general relativity coupled to non linear electrodynamics via a term in the action, with the Lorentz-invariant scalar , while is the electromagnetic tensor that reduces to the Maxwellian field tensor in the weak field case. Here, is restricted only to the electric field. The black hole metric has been constructed by employing the Dagum distribution [56], a continuous probability distribution, given by
where , while the parameters a, b, p. For and , can be written as
Here, with the transformation the black hole metric function reads
with , while M and q are the mass and the charge of the black hole, respectively. For this black hole metric is non-singular everywhere, while for it satisfies the weak energy condition for every timelike vector , according to which the local energy density must be positive-definite. This general inequality is shown in [57] to be equivalent to two inequalities on the first and second derivative of the mass function w.r.t. r. In order to have a non-singular black hole solution that also satisfies the weak energy condition, one imposes the condition , so that the obtained new spherically symmetric, static and charged non-singular black hole metric has a line element of the form
with , , and the metric function now reads
The corresponding electric field is
For small values of the radial coordinate r, the family of metrics derived from (5) behaves as a de Sitter black hole
while asymptotically it behaves as the Schwarzschild black hole.
It is important to notice that a particular case is obtained for (hence ) and , so that the metric function (5) reads
and the black hole solution asymptotically behaves as the Reissner-Nordström solution. For all the other values of the parameters a and , the non-singular black hole space-time geometries with the metric function (5) do not asymptotically have the behaviour of the Reissner-Nordström solution. It must also be pointed out that only for the values and one gets a nonlinear electrodynamics model leading to Maxwell’s electrodynamics in the weak field approximation.
3. Einstein and Møller Prescriptions
The Einstein energy-momentum complex [8] defined for a () dimensional space-time is given by
The superpotentials are expressed as
and satisfy the necessary antisymmetric property
In the Einstein prescription the local conservation law holds:
Then, the energy and momentum can be calculated with
where and represent the energy and momentum density components, respectively.
Applying Gauss’ theorem, the energy-momentum becomes
with the outward unit normal vector over the surface element In Equation (14) represents the energy.
The expression for the Møller energy-momentum complex [13] is given by
with the Møller superpotentials
The Møller superpotentials are also antisymmetric:
In the Møller prescription the local conservation law is respected:
In Equation (15) is the energy density and represents the momentum density components.
In the Møller prescription, the energy and momentum distributions are given by
and the energy distribution can be evaluated with
Using Gauss’ theorem one obtains
4. Energy-Momentum Distribution of the Non-Singular Black Hole Solution Satisfying the Weak Energy Condition
In order to perform the calculations using the Einstein prescription, the metric given by the line element (4) is transformed into Schwarzschild Cartesian coordinates applying the coordinate transformation . Then, the line element takes the following form:
The calculations for and for the components of the superpotential (needed in Equation (14)) in quasi-Cartesian coordinates are
while the non-vanishing components of the superpotential are
With the aid of the line element (22), the expression for the energy-momentum distribution (14), and the expressions (24)–(26) for the superpotentials, the energy distribution in the Einstein prescription for the new charged non-singular black hole solution satisfying the weak energy condition is obtained as
while, due to Equation (23), we find that all the momentum components vanish:
In Figure 1, the energy distribution (27) obtained in the Einstein prescription is plotted as a function of r for four different values of the parameter a while , , and .
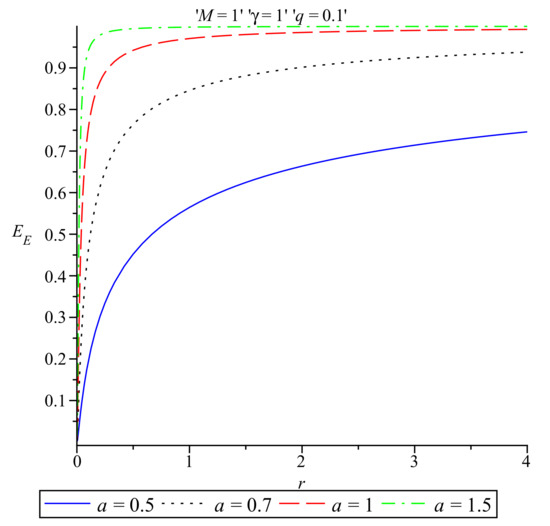
Figure 1.
Einstein energy vs. r for various values of the parameter a and .
Figure 2 exhibits the behaviour of the Einstein energy distribution as a function of r near the origin for four different values of the parameter a while , , and .
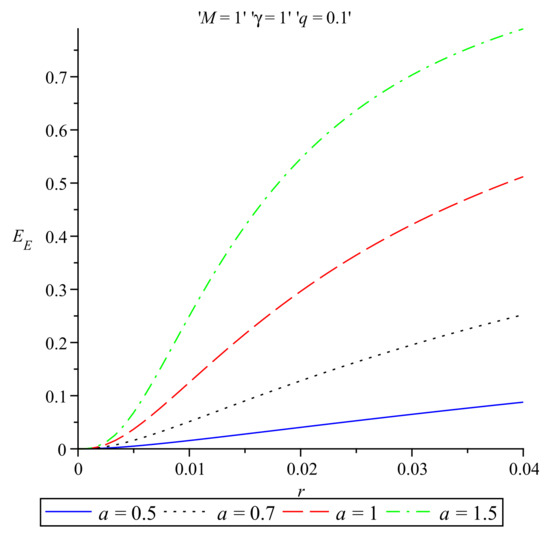
Figure 2.
Einstein energy vs. r near the origin for various values of the parameter a and .
Next, we apply the Møller prescription using Schwarzschild coordinates , for the line element (4) and the metric function (5). The only non-vanishing component of the Møller superpotential (16) is found to be
while all the other components vanish.
Inserting the above expression (29) of the Møller superpotential into Equation (21), we obtain the energy distribution in the Møller prescription:
from which we infer that the energy in the Møller prescription can be given in terms of the energy in the Einstein prescription.
Furthermore, as expected from the vanishing of the spatial components of the Møller superpotential, all the momentum components are found to be zero:
In Figure 3 the energy distribution in the Møller prescription for four different values of the parameter a and , , and is plotted, while in Figure 4 the behaviour of the Møller energy distribution near the origin is presented for four different values of the parameter a and , , and .
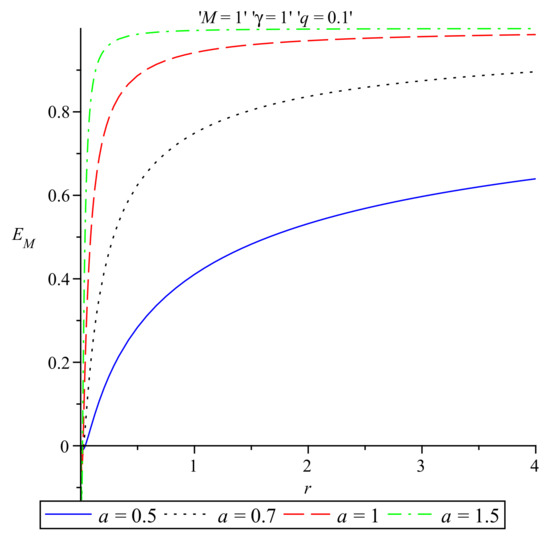
Figure 3.
Møller energy vs. r for various values of the parameter a and .
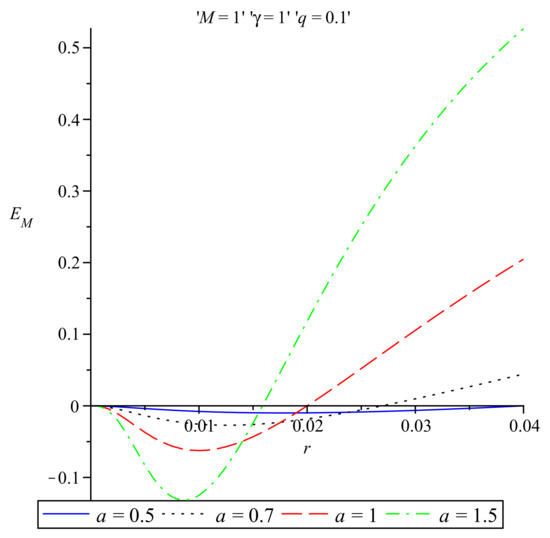
Figure 4.
Møller energy vs. r near the origin for various values of the parameter a and .
A comparison of the energy distributions in the Einstein and Møller prescriptions is given in Figure 5 for and , , and . Additionally, in Figure 6 an analogous comparison of the energy distributions in the Einstein and Møller prescriptions near the origin is presented for the same values of the parameters a, M, q, and , as in Figure 5.
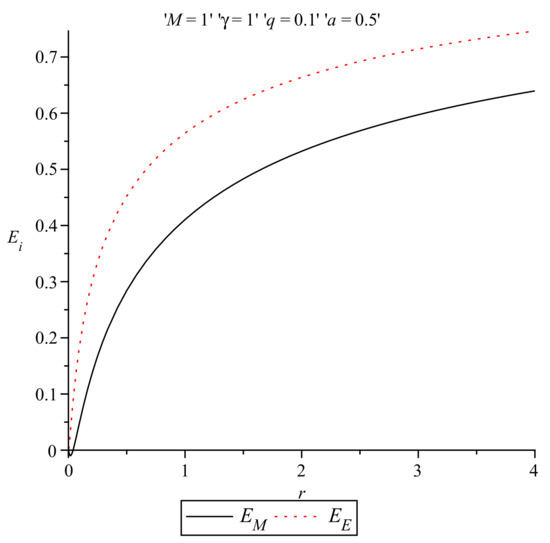
Figure 5.
Energy distributions in the Einstein and Møller prescriptions for and .
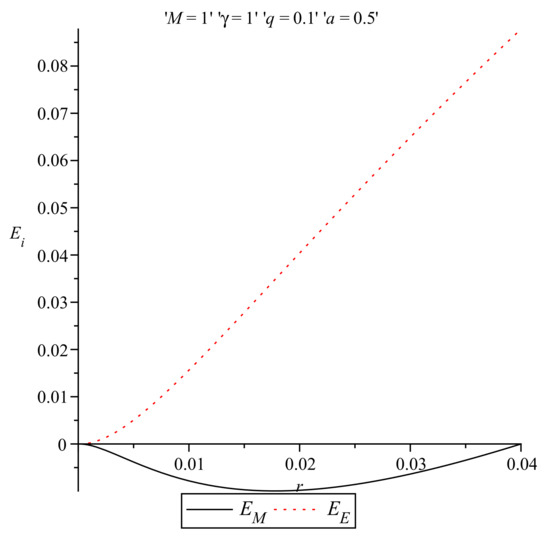
Figure 6.
Energy distributions in the Einstein and Møller prescriptions for and near origin.
5. Results and Discussion
The aim of this work is the study of the energy-momentum distribution for a new spherically symmetric and charged, non-singular black hole solution satisfying the weak energy condition.
To this purpose, the Einstein and Møller energy-momentum complexes have been applied and it has been found that all the momenta vanish in both pseudotensorial prescriptions. Additionally, the energy distributions obtained have well-defined expressions showing a dependence on the mass M, the charge the two parameters and a, introduced in Section 2, and on the radial coordinate r. Furthermore, the Møller energy is expressed in terms of the Einstein energy. Both energies acquire the same value M (ADM mass) for or for .
We have also studied the limiting behavior of the energy distribution for and , and for the particular cases and and , respectively. In Table 1 we summarize the physically meaningful results for these limiting and particular cases.

Table 1.
Limiting and particular values for the Einstein energy and the Møller energy .
At this point some remarks are needed to clarify the results. From Table 1 we conclude that the energy distribution in both prescriptions vanishes near the origin , while for either or both energies are equal to the ADM mass M, in agreement with the result obtained by Virbhadra for the energy distribution of the Schwarzschild black hole solution [38]. For the particular case and we get an expression for the energy distribution that depends on the mass M and the charge q of the black hole, as well as on the radial coordinate r for a model of general relativity coupled to nonlinear electrodynamics, the latter corresponding to Maxwell’s theory in the weak field approximation. Furthermore, the non-singular black hole solution with , and satisfies the weak energy condition and is described by the metric function , while asymptotically it behaves as the Reissner-Nordström solution. In fact, for this non-singular and charged black hole solution exhibits a de Sitter behaviour near zero.
In Figure 7 the energy distributions in the Einstein prescription and in the Møller prescription are presented, as a function of r, for the particular case and , while in Figure 8 the same functions for the same values of the parameters as in Figure 7 are presented near the origin.
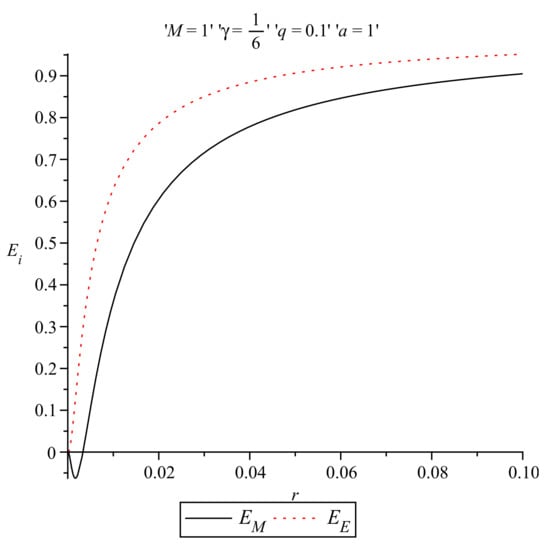
Figure 7.
Energy distributions in the Einstein and Møller prescriptions for and .
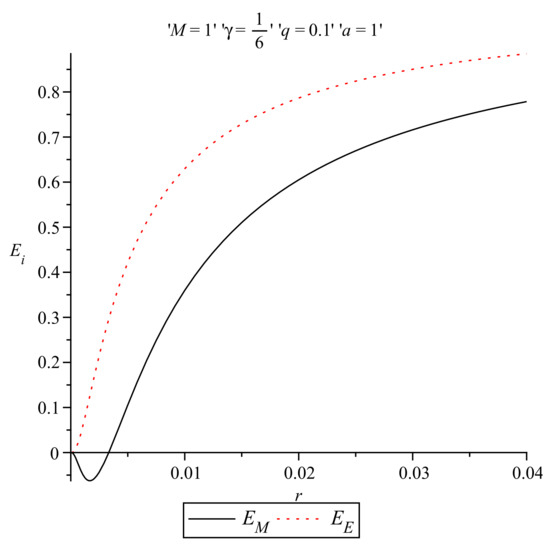
Figure 8.
Energy distributions in the Einstein and Møller prescriptions near the origin for and .
Looking closer at the behaviour of the energy distribution near zero, it is seen from Figure 2 that the Einstein energy tends to zero from positive values, as expected from expression (27), and it is an increasing function of r. The Møller energy, on the other hand, tends also to zero but, according to Figure 4, close enough to zero, when the radial coordinate r takes values , it acquires negative values before reaching zero, a result which is supported by Equation (30). For values of r greater than , the Møller energy is positive and increasing.
In Figure 5 and Figure 6, we consider the particular value as an example in order to compare the two energies obtained and we conclude that the Einstein energy is everywhere greater than the Møller energy. In fact, one can advocate that the positive energy region can be used for the effect of a convergent gravitational lens [58,59].
The negativity of the energy distribution in the case of the Møller prescription, for a range of values of r, a, , M and q pinpoints the difficulty of a physically meaningful interpretation of the energy in certain regions. The values of r where the energy distribution becomes negative depend on the roots of the equation (see Equation (30)). In fact, the energy becomes negative for . As an example, in Figure 9 we see that the energy distribution becomes negative for if we choose and . For larger values of r, the energy distribution becomes positive and then it increases monotonically.
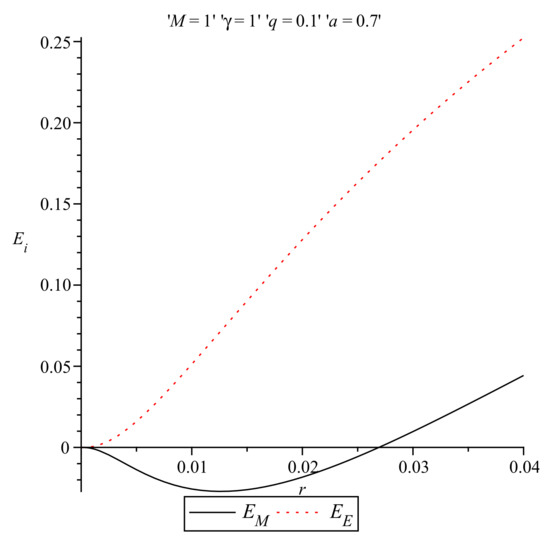
Figure 9.
Energy distributions in the Einstein and Møller prescriptions near the origin for and .
As pointed out in the Introduction, a modern viewpoint regarding the energy-momentum localization is suggested by a quasi-local energy-momentum associated with a closed 2-surface. The pseudotensors have this property, mostly since Penrose developed his definition of quasi-local mass [48]. Further, according to [50], since a generally accepted expression for the energy-momentum has not been found until today, some important criteria for the quasi-local energy-momentum expressions must be satisfied, basically (a) the expressions should yield the standard values at spatial infinity, and (b) they should not give negative values for the energy. In the case of the black hole solution that satisfies the weak energy condition and is under study in the present work, both the Einstein and Møller energy-momentum complexes do yield the standard values at infinity. In fact, in the Einstein prescription the energy takes only positive values, while in the case of the Møller prescription the energy takes negative values when r satisfies the inequality . We believe that this apparent weakness of the Møller prescription can be explained taking into account the properties of the particular metric considered. Indeed, a similar behaviour of the Møller energy-momentum complex was found in [60,61]. This strange behaviour is attributed to the particularities of these black hole solutions originating in the coupling of the gravitational field to non-linear electrodynamics.
Although the energy distribution in the Møller prescription does not exhibit the desired behaviour for every value of r, we can conclude that the two prescriptions used in the present work still represent useful tools for the energy-momentum localization. Given the problem that arises from the Møller prescription, it is important to use other energy-momentum complexes available, as well as the teleparallel equivalent theory of general relativity to perform new investigations of the energy-momentum localization for the four-dimensional spherically symmetric and charged, non-singular black hole solution satisfying the weak energy condition. We consider facing this challenge in a future work.
Author Contributions
Equal contribution from all the authors. Specifically, Conceptualization, I.R., T.G., F.R., M.-M.C., A.S., J.C.; Methodology, I.R.; Software, I.R., M.-M.C., A.S.; Validation, I.R., T.G., F.R., M.-M.C., A.S., J.C.; Formal Analysis, I.R., T.G., F.R., M.-M.C., A.S., J.C.; Investigation, I.R., T.G., F.R., M.-M.C., A.S., J.C.; Data Curation, I.R., T.G., F.R., M.-M.C., A.S., J.C.; Writing, I.R., T.G., F.R., M.-M.C., A.S., J.C.; Preparation, I.R., T.G., F.R., M.-M.C., A.S., J.C.; Writing—Review & Editing, I.R., T.G., F.R., M.-M.C., A.S., J.C.; Visualization, I.R., T.G., F.R., M.-M.C., A.S., J.C.; Supervision, I.R.; Project Administration, I.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bel, L. Définition d’une densité d’énergie et d’un état de radiation totale généralisée. Comptes Rendus Hebd. Séances Acad. Sci. 1958, 246, 3015–3018. [Google Scholar]
- Bonilla, M.A.G.; Senovilla, J.M.M. Some properties of the Bel and Bel-Robinson tensors. Gen. Relativ. Gravit. 1997, 29, 91–116. [Google Scholar] [CrossRef]
- Senovilla, J.M. Super-energy tensors. Class. Quantum Gravity 2000, 17, 2799–2841. [Google Scholar] [CrossRef]
- Brown, J.D.; York, J.W., Jr. Quasilocal energy and conserved charges derived from the gravitational action. Phys. Rev. D 1993, 47, 1407. [Google Scholar] [CrossRef] [PubMed]
- Hayward, S.A. Quasilocal gravitational energy. Phys. Rev. D 1994, 49, 831. [Google Scholar] [CrossRef]
- Chen, C.-M.; Liu, J.-L.; Nester, J.M. Quasi-local energy for cosmological models. Mod. Phys. Lett. A 2007, 22, 2039–2046. [Google Scholar] [CrossRef]
- Balart, L. Quasilocal energy, Komar charge and horizon for regular black holes. Phys. Lett. B 2010, 687, 280–285. [Google Scholar] [CrossRef]
- Einstein, A. Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin. Verlag der Königlichen Akademie der Wissenschaften, 1915; Volume 47, p. 778, Addendum: Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften. 1915; Volume 47, p. 799. Available online: https://einsteinpapers.press.princeton.edu/vol6-doc/ (accessed on 2 April 2020).
- Trautman, A. Conservation laws in general relativity. In Gravitation: An Introduction to Current Research; Witten, L., Ed.; John Wiley & Sons: New York, NY, USA, 1962; p. 169. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields; Pergamon Press: New York, NY, USA, 1987; p. 280. [Google Scholar]
- Papapetrou, A. Einstein’s theory of gravitation and flat space. Proc. Roy. Ir. Acad. A 1948, 52, 11–23. [Google Scholar]
- Bergmann, P.G.; Thomson, R. Spin and angular momentum in general relativity. Phys. Rev. 1953, 89, 400. [Google Scholar] [CrossRef]
- Møller, C. On the localization of the energy of a physical system in the general theory of relativity. Ann. Phys. 1958, 4, 347–371. [Google Scholar] [CrossRef]
- Weinberg, S. Gravitation and Cosmology: Principles and Applications of General Theory of Relativity; John Wiley & Sons: New York, NY, USA, 1972; p. 165. [Google Scholar]
- Vagenas, E.C. Effective mass of a radiating charged particle in Einstein’s universe. Mod. Phys. Lett. A 2004, 19, 213–222. [Google Scholar] [CrossRef]
- Multamaki, T.; Putaja, A.; Vilja, I.; Vagenas, E.C. Energy-momentum complexes in f(R) theories of gravity. Class. Quantum Gravity 2008, 25, 075017. [Google Scholar] [CrossRef]
- Rosen, N.; Virbhadra, K.S. Energy and momentum of cylindrical gravitational waves. Gen. Relativ. Gravit. 1993, 25, 429. [Google Scholar] [CrossRef]
- Virbhadra, K.S.; Parikh, J.C. A conformal scalar dyon black hole solution. Phys. Lett. B 1994, 331, 302–304. [Google Scholar] [CrossRef]
- Radinschi, I. Energy associated with the Bianchi type VI0 Universe. Chin. J. Phys. 2001, 39, 393. [Google Scholar]
- Sahoo, P.K.; Mahanta, K.L.; Goit, D.; Sinha, A.K.; Xulu, S.S.; Das, U.R.; Prasad, A.; Prasad, R. Einstein energy-momentum complex for a phantom black hole metric. Chin. Phys. Lett. 2015, 32, 020402. [Google Scholar] [CrossRef][Green Version]
- Tripathy, S.K.; Mishra, B.; Pandey, G.K.; Singh, A.K.; Kumar, T.; Xulu, S.S. Energy and Momentum of Bianchi Type Universes. Adv. High Energy Phys. 2015, 2015, 705262. [Google Scholar] [CrossRef]
- Yang, I.-C.; Radinschi, I. On the difference of energy between the Einstein and Møller prescription. Chin. J. Phys. 2004, 42, 40. [Google Scholar]
- Radinschi, I.; Grammenos, T. Møller’s energy-momentum complex for a spacetime geometry on a noncommutative curved D3-brane. Int. J. Theor. Phys. 2008, 47, 1363–1372. [Google Scholar] [CrossRef]
- Yang, I.-C.; Lin, C.-L.; Radinschi, I. The energy of a regular black hole in general relativity coupled to nonlinear electrodynamics. Int. J. Theor. Phys. 2009, 48, 248–255. [Google Scholar] [CrossRef]
- Radinschi, I.; Rahaman, F.; Ghosh, A. On the energy of charged black holes in generalized dilaton-axion gravity. Int. J. Theor. Phys. 2010, 49, 943–956. [Google Scholar] [CrossRef][Green Version]
- Radinschi, I.; Rahaman, F.; Banerjee, A. On the Energy of Hořava-Lifshitz black holes. Int. J. Theor. Phys. 2011, 50, 2906–2916. [Google Scholar] [CrossRef]
- Radinschi, I.; Rahaman, F.; Banerjee, A. The energy distribution of Hořava-Lifshitz black hole solutions. Int. J. Theor. Phys. 2012, 51, 1425–1434. [Google Scholar] [CrossRef]
- Abdel-Megied, M.; Gad, R.M. “Møller’s energy in the Kantowski-Sachs space-time. Adv. High Energy Phys. 2010, 2010, 379473. [Google Scholar] [CrossRef]
- Sharif, M.; Azam, M. Energy-momentum distribution: Some examples. Int. J. Mod. Phys. A 2007, 22, 1935. [Google Scholar] [CrossRef]
- Vagenas, E.C. Energy distribution in 2D stringy black hole backgrounds. Int. J. Mod. Phys. A 2003, 18, 5781. [Google Scholar] [CrossRef]
- Vagenas, E.C. Energy distribution in a BTZ black hole spacetime. Int. J. Mod. Phys. D 2005, 14, 573. [Google Scholar] [CrossRef]
- Vagenas, E.C. Energy distribution in the dyadosphere of a Reissner-Nordström black hole in Møller’s prescription. Mod. Phys. Lett. A 2006, 21, 1947. [Google Scholar] [CrossRef]
- Balart, L. Energy distribution of (2 + 1)-dimensional black holes with nonlinear electrodynamics. Mod. Phys. Lett. A 2009, 24, 2777. [Google Scholar] [CrossRef]
- Abbassi, A.M.; Mirshekari, S.; Abbassi, A.H. Energy-momentum distribution in static and nonstatic cosmic string space-times. Phys. Rev. D 2008, 78, 064053. [Google Scholar] [CrossRef]
- Matyjasek, J. Some remarks on the Einstein and Møller pseudotensors for static and spherically-symmetric configurations. Mod. Phys. Lett. A 2008, 23, 591–601. [Google Scholar] [CrossRef]
- Aguirregabiria, J.M.; Chamorro, A.; Virbhadra, K.S. Energy and angular momentum of charged rotating black holes. Gen. Relativ. Gravit. 1996, 28, 1393. [Google Scholar] [CrossRef]
- Xulu, S.S. Bergmann-Thomson Energy-Momentum Complex for Solutions More General than the Kerr-Schild Class. Int. J. Theor. Phys. 2007, 46, 2915–2922. [Google Scholar] [CrossRef]
- Virbhadra, K.S. Naked singularities and Seifert’s conjecture. Phys. Rev. D 1999, 60, 104041. [Google Scholar] [CrossRef]
- Møller, C. The four-momentum of an insular system in general relativity. Nucl. Phys. 1964, 57, 330–338. [Google Scholar] [CrossRef]
- Hayashi, K.; Shirafuji, T. New general relativity. Phys. Rev. D 1979, 19, 3524. [Google Scholar] [CrossRef]
- Nester, J.M.; So, L.L.; Vargas, T. Energy of homogeneous cosmologies. Phys. Rev. D 2008, 78, 044035. [Google Scholar] [CrossRef]
- Nashed, G.G.L. Energy of spherically symmetric space-times on regularizing teleparallelism. Int. J. Mod. Phys. A 2010, 25, 28–83. [Google Scholar] [CrossRef]
- Sharif, M.; Jawad, A. Energy contents of some well-known solutions in teleparallel gravity. Astrophys. Space Sci. 2011, 331, 257–263. [Google Scholar] [CrossRef]
- Maluf, J.W.; Veiga, M.V.O.; da Rocha-Neto, J.F. Regularized expression for the gravitational energy-momentum in teleparallel gravity and the principle of equivalence. Gen. Relativ. Gravit. 2007, 39, 227. [Google Scholar] [CrossRef]
- Sousa, A.; Pereira, R.B.; Silva, A.C. Energy and angular momentum densities in a Gödel-type universe in teleparallel geometry. Gravit. Cosmol. 2010, 16, 25–33. [Google Scholar] [CrossRef]
- Aygün, S.; Baysal, H.; Aktaş, C.; Yılmaz, I.; Sahoo, P.K.; Tarhan, I. Teleparallel energy-momentum distribution of various black hole and wormhole metrics. Int. J. Mod. Phys. A 2018, 33, 1850184. [Google Scholar] [CrossRef]
- Ganiou, M.G.; Houndjo, M.J.S.; Tossa, J. f(T) gravity and energy distribution in Landau-Lifshitz prescription. Int. J. Mod. Phys. D 2018, 27, 1850039. [Google Scholar] [CrossRef]
- Penrose, R. Quasi-local mass and angular momentum in general relativity. Proc. R. Soc. Lond. A Math. Phys. Sci. 1982, 381, 53–63. [Google Scholar]
- Tod, K.P. Some examples of Penrose’s quasi-local mass construction. Proc. R. Soc. Lond. A Math. Phys. Sci. 1983, 388, 457–477. [Google Scholar]
- Szabados, L.B. Quasi-local energy-momentum and angular momentum in general relativity. Living Rev. Relativ. 2009, 12, 4. [Google Scholar] [CrossRef]
- Wang, M.T.; Yau, S.T. Quasilocal mass in general relativity. Phys. Rev. Lett. 2009, 102, 021101. [Google Scholar] [CrossRef]
- Wang, M.T.; Yau, S.T. Isometric embeddings into the Minkowski space and new quasi-local mass. Commun. Math. Phys. 2019, 288, 919–942. [Google Scholar] [CrossRef]
- Chen, C.M.; Liu, J.L.; Nester, J.M. Gravitational energy is well defined. Int. J. Mod. Phys. D 2018, 27, 1847017. [Google Scholar] [CrossRef]
- Chen, C.M.; Liu, J.L.; Nester, J.M. Quasi-local energy from a Minkowski reference. Gen. Relativ. Gravit. 2018, 50, 158. [Google Scholar] [CrossRef]
- Balart, L.; Vagenas, E.C. Regular black holes with a nonlinear electrodynamics source. Phys. Rev. D 2014, 90, 124045. [Google Scholar] [CrossRef]
- Dagum, C. A new model of personal income distribution: Specification and estimation. Econ. Appl. 1977, 30, 413–437. [Google Scholar]
- Balart, L.; Vagenas, E.C. Regular black hole metrics and the weak energy condition. Phys. Lett. B 2014, 730, 14–17. [Google Scholar] [CrossRef]
- Virbhadra, K.S.; Ellis, G.F. Schwarzschild black hole lensing. Phys. Rev. D 2000, 62, 084003. [Google Scholar] [CrossRef]
- Virbhadra, K.S. Relativistic images of Schwarzschild black hole lensing. Phys. Rev. D 2009, 79, 083004. [Google Scholar] [CrossRef]
- Radinschi, I.; Grammenos, T.; Rahaman, F.; Spanou, A.; Islam, S.; Chattopadhyay, S.; Pasqua, A. Energy-momentum for a charged nonsingular black hole solution with a nonlinear mass function. Adv. High Energy Phys. 2017, 2017, 7656389. [Google Scholar] [CrossRef]
- Radinschi, I.; Rahaman, F.; Grammenos, T.; Islam, S. Einstein and Møller energy-momentum complexes for a new regular black hole solution with a nonlinear electrodynamics source. Adv. High Energy Phys. 2016, 2016, 9049308. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).