Quantum Gravity at the Corner
Abstract
1. Introduction
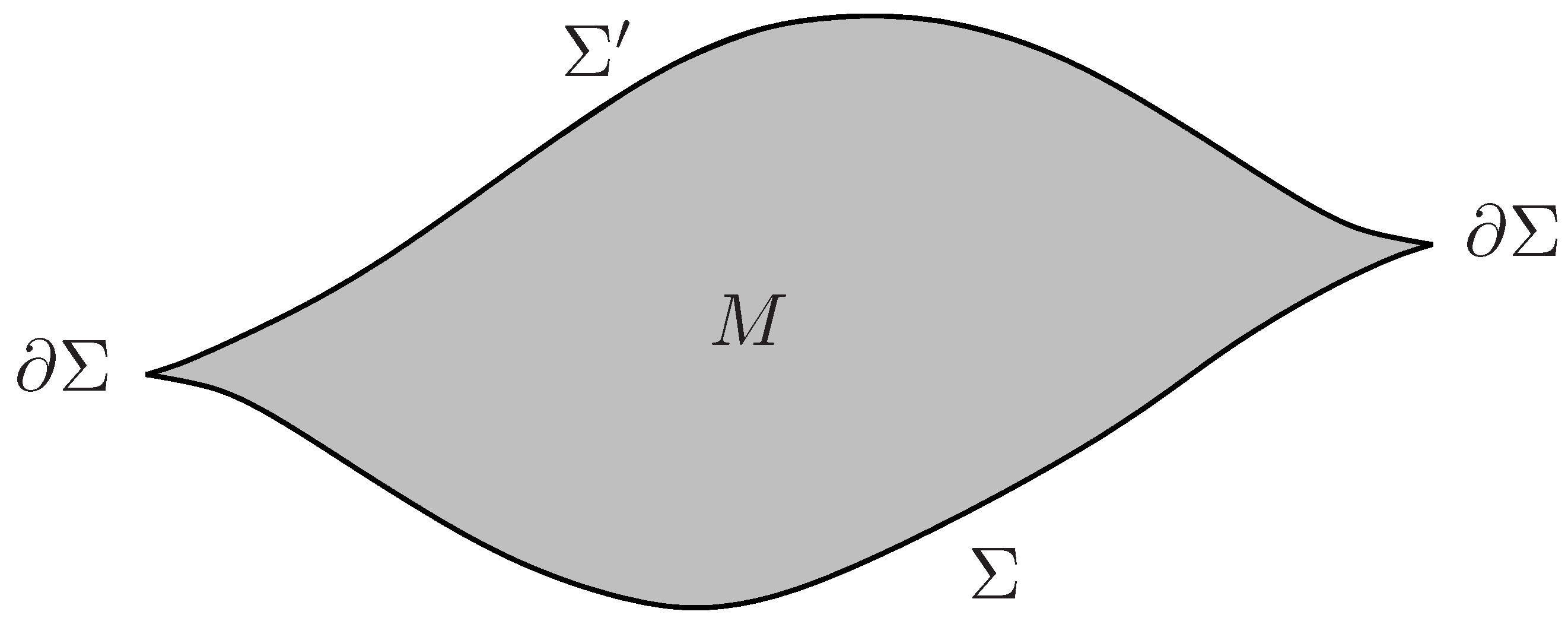
2. The Origin of the 2d Symplectic Structure
2.1. Symmetries
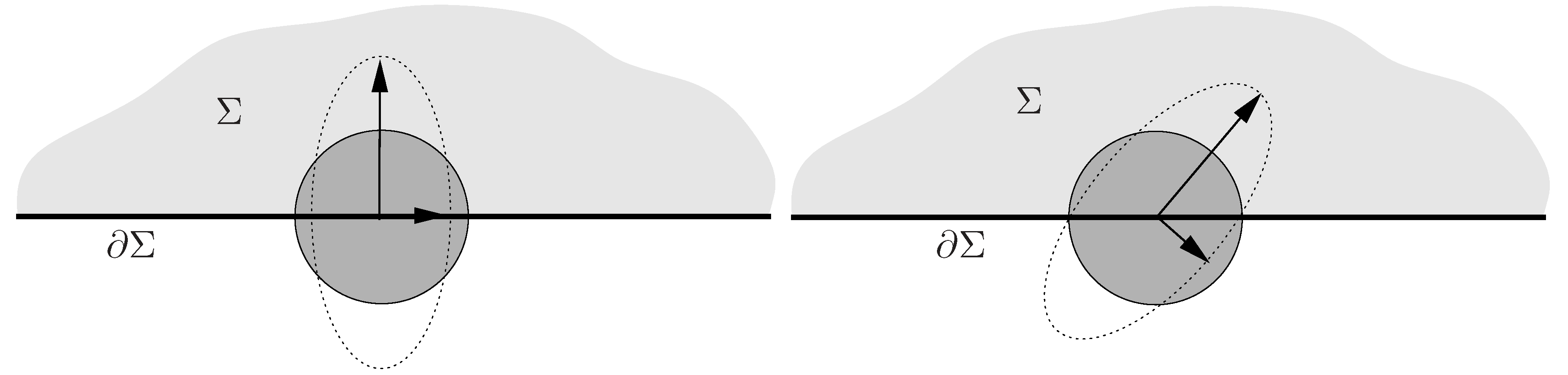
2.2. Hamiltonian Generators
3. Boundary Symplectic Structure
3.1. The Associated Boundary 2 + 1 Dynamical Theory
4. Quantisation: The Discrete Representation
4.1. Diffeomorphism Symmetry
4.2. Representation
4.3. The Geometry of the k Quantum Number
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Perez, A. Black Holes in Loop Quantum Gravity. Rep. Prog. Phys. 2017, 80, 126901. [Google Scholar] [CrossRef] [PubMed]
- Barbero, F.; Perez, A. Quantum Geometry and Black Holes. arXiv, 2015; arXiv:1501.02963. [Google Scholar]
- Barbero, F.; Lewandowski, J.; Villasenor, E.J. Quantum isolated horizons and black hole entropy. arXiv, 2011; arXiv:1203.0174. [Google Scholar]
- Ashtekar, A.; Krishnan, B. Isolated and dynamical horizons and their applications. Living Rev. Relat. 2004, 7, 10. [Google Scholar] [CrossRef] [PubMed]
- Ashtekar, A.; Baez, J.; Krasnov, K. Quantum Geometry of Isolated Horizons and Black Hole Entropy. Adv. Theor. Math. Phys. 2000, 4, 1–94. [Google Scholar] [CrossRef]
- Engle, J.; Perez, A.; Noui, K. Black hole entropy and SU(2) Chern-Simons theory. Phys. Rev. Lett. 2010, 105, 031302. [Google Scholar] [CrossRef] [PubMed]
- Engle, J.; Noui, K.; Perez, A. Black hole entropy from the SU(2)-invariant formulation of type I isolated horizons. Phys. Rev. D 2010, 82, 044050. [Google Scholar] [CrossRef]
- Perez, A.; Pranzetti, D. Static isolated horizons: SU(2) invariant phase space, quantization, and black hole entropy. Entropy 2011, 13, 744–777. [Google Scholar] [CrossRef]
- Freidel, L.; Yokokura, Y. Non-equilibrium thermodynamics of gravitational screens. Class. Quantum Gravity 2015, 32, 215002. [Google Scholar] [CrossRef]
- Bodendorfer, N. Black hole entropy from loop quantum gravity in higher dimensions. Phys. Lett. 2013, 726, 887–891. [Google Scholar] [CrossRef]
- Fernando, J.; Barbero, G. Real Ashtekar variables for Lorentzian signature space times. Phys. Rev. 1995, 51, 5507–5510. [Google Scholar]
- Immirzi, G. Quantum gravity and Regge calculus. Nucl. Phys. Proc. Suppl. 1997, 57, 65–72. [Google Scholar] [CrossRef]
- Lee, J.; Wald, R.M. Local symmetries and constraints. J. Math. Phys. 1990, 31, 725. [Google Scholar] [CrossRef]
- Ashtekar, A.; Engle, J.; Van Den Broeck, C. Quantum horizons and black hole entropy: Inclusion of distortion and rotation. Class. Quantum Gravity 2005, 22, L27–L34. [Google Scholar] [CrossRef]
- Beetle, C.; Engle, J. Generic isolated horizons in loop quantum gravity. Class. Quantum Gravity 2010, 27, 235024. [Google Scholar] [CrossRef]
- Frodden, E.; Perez, A.; Pranzetti, D.; Rken, C. Modelling black holes with angular momentum in loop quantum gravity. Gen. Relat. Gravity 2014, 46, 1828. [Google Scholar] [CrossRef]
- Freidel, L.; Geiller, M.; Ziprick, J. Continuous formulation of the Loop Quantum Gravity phase space. Class. Quantum Gravity 2013, 30, 085013. [Google Scholar] [CrossRef]
- Perez, A. No firewalls in quantum gravity: The role of discreteness of quantum geometry in resolving the information loss paradox. Class. Quantum Gravity 2015, 32, 084001. [Google Scholar] [CrossRef]
| 1. | |
| 2. | In the Chern–Simons description of the boundary degrees of freedom that is used in applications to isolated horizons, the fusion conditions between the boundary-induced connection and involves components of the Weyl curvature [14,15]. This requires the definition of a new boundary connection that is non-trivially related to the original one, making the final structure geometrically obscure. As we see here, the Bulk boundary connection is extremely natural. |
| 3. | When available, the Komar angular momentum is given by
|
| 4. | The relationship with the usual real coordinates metric components is
|
| 5. | Another way of getting a geometric intuition goes as follows: let us make a classical study by writing the triad in our fiducial coordinate system as
|
| 6. | In the normal gauge we can write and . The metric component generates the transformations
Therefore, it is conjugate to the coordinate and generates local rotations of the coordinates around the origin. Note that one can directly obtain such local differ from the action of as defined in (67). |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Freidel, L.; Perez, A. Quantum Gravity at the Corner. Universe 2018, 4, 107. https://doi.org/10.3390/universe4100107
Freidel L, Perez A. Quantum Gravity at the Corner. Universe. 2018; 4(10):107. https://doi.org/10.3390/universe4100107
Chicago/Turabian StyleFreidel, Laurent, and Alejandro Perez. 2018. "Quantum Gravity at the Corner" Universe 4, no. 10: 107. https://doi.org/10.3390/universe4100107
APA StyleFreidel, L., & Perez, A. (2018). Quantum Gravity at the Corner. Universe, 4(10), 107. https://doi.org/10.3390/universe4100107





