The Cosmological Perturbed Lightcone Gauge

Abstract

The lightcone gauge is a set of what are called the observational coordinates adapted to our past lightcone. We develop this gauge by producing a perturbed spacetime metric that describes the geometry of our past lightcone where observations are usually obtained. We connect the produced observational metric to the perturbed Friedmann-Lemaître-Robertson-Walker (FLRW) metric in the standard general gauge or what is the so-called 1+3 gauge. We derive the relations between these perturbations of spacetime in the observational coordinates and those perturbations in the standard metric approach, as well as the dynamical equations for the perturbations in observational coordinates. We also calculate the observables in the lightcone gauge and re-derive them in terms of Bardeen potentials to first order. A verification is made of the observables in the perturbed lightcone gauge with those in the standard gauge. The advantage of the method developed is that the observable relations are simpler than in the standard formalism, and they are expressed in terms of the metric components which in principle are measurable. We use the perturbed lightcone gauge in galaxy surveys and the calculations of galaxy number density contrast. The significance of the new gauge is that by considering the null-like light propagations the calculations are much simpler due to the non-consideration of the angular deviations.

1. Introduction

Cosmological observable quantities, henceforth simply referred to as observables, encode information about the state of the Universe at a particular cosmological redshift. In our past lightcone, we can obtain these observables that can give us our connection to the rest of the Universe. Hence, a precise measure of cosmological observables can directly determine the geometry of the observable part of the spacetime, in the so-called observational approach [1]. Furthermore, we can assume a dynamical theory for the spacetime curvature of the past lightcone, i.e., General Relativity (GR).

The observations are taken so that we can discover what these observations imply about the large-scale structure of the Universe. The idea was first discussed in [2], and Refs. [3,4,5,6] discussed the construction of the spacetime metric and ways to determine local matter density in the Universe directly from astronomical observations on our past lightcone as initial data for the field equations, and later to establish what is called now the lightcone gauge based on an observational coordinates set. The main aim was to a great extent that cosmology rather be a directly observational subject [3]. Therefore, they bring cosmologically interpretable astronomical observations into a confrontation with the cosmological theories, in order to reveal the structure of distant regions in the Universe.

The rest of this paper is organised as follows: in Section 2 and Section 3, we give a brief overview of the observational coordinates and the metric adapted to our past lightcone, where we needed to construct our perturbed lightcone gauge (PLG) in Section 4, by showing the relations between the perturbations of spacetime in observational coordinates and those perturbations in the standard metric approach. Section 5 is dedicated to the study of the observables of spacetime in the PLG and verified with those obtained in the standard perturbed gauge. In Section 6, we calculate the galaxy number density contrast using the PLG and we show verification with the standard gauge as well. Finally, in Section 7, we discuss the results and give our conclusions.

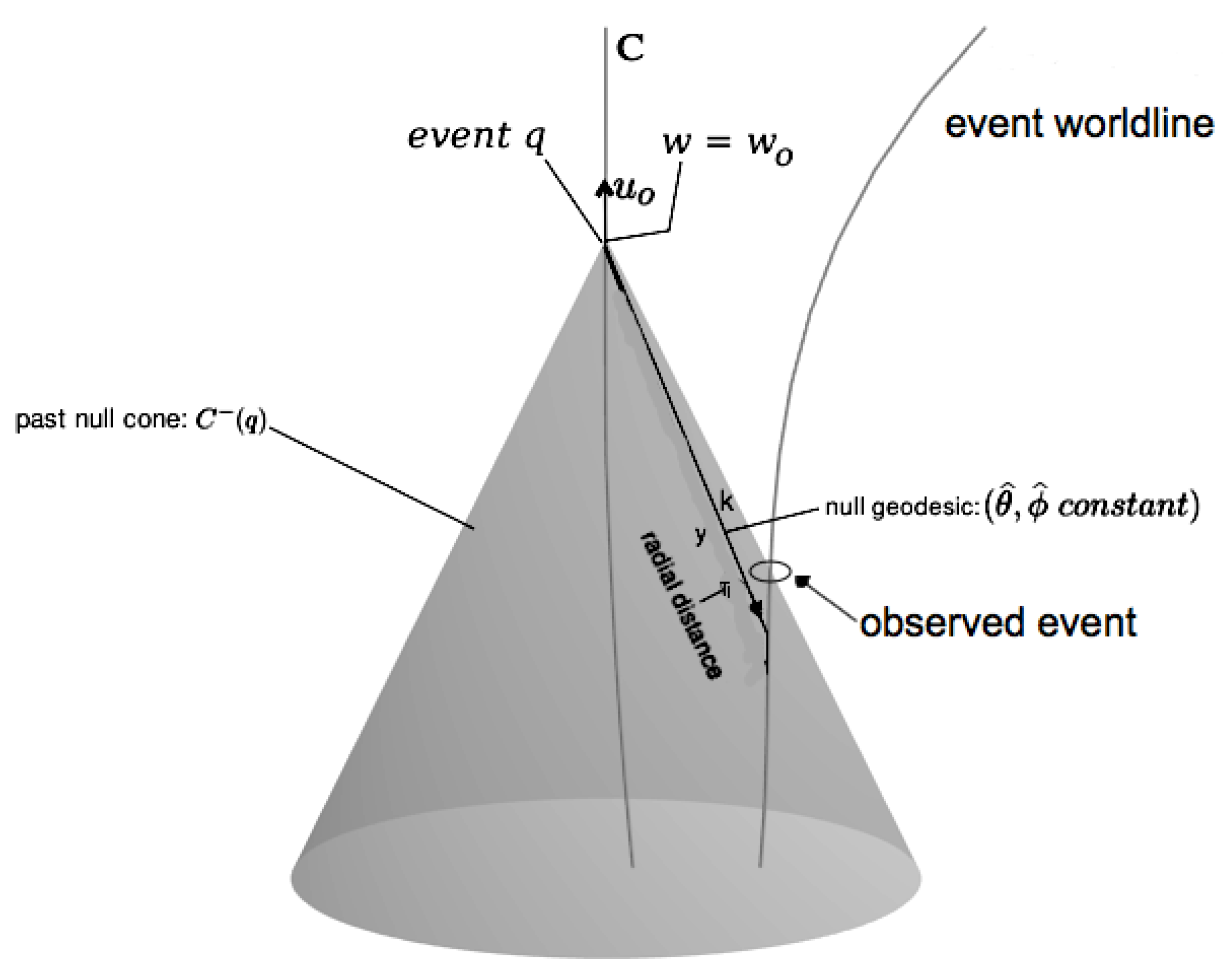
2. Observational Coordinates

A spacetime consists of a manifold $\mathcal{M}$ with a metric g. We shall assume the spacetime filled with a perfect fluid of the form

$$T_{\mu \nu }=\rho u_{\mu }{u}_{\nu }+p(g_{\mu \nu }+u_{\mu }{u}_{\nu }),u^{\mu }{u}_{\mu }=-1,$$

(1)

where $T_{\mu \nu }$ is the stress energy tensor and $u^{\mu }$ the average 4-velocity. The first step in constructing a set of observational coordinates is to identify fundamental observers. The integral curves of the velocity vector $u^{\mu }$ and their normalised 4-velocity, represent the worldlines of these fundamental observers, i.e., they are comoving with the galaxies. If $\tau$ is the proper time along these worldlines, then

$$u^{\mu }=\frac{d{x}^{\mu }}{d\tau }.$$

(2)

Let us now single out our worldline C, where C is a set of timelike geodesics generated by $u^{\mu }$ at the event attached to us, on Earth.

We will introduce the set of observational coordinates $x^{\mu }=:\{w,y,\widehat{\theta },\widehat{\varphi }\}$, constructed as follows, see Figure 1: the coordinate w is the past lightcones of the events on C, generated along our worldline. It can be normalized by measuring the proper time along the central worldline C (in other words, ${w|}_C{=\tau |}_C$). By choosing $w=w_0$ (arbitrary) to correspond to the event q here and now, the null cone generated then will represent the surfaces of events that happened on our past lightcone at constant $w_0$. Then, generically, q will be at the vertices of the lightcones where we receive information and signals from the Universe. Then, w is completely determined when $w_0$ has been chosen. The null geodesic vector field $k^{\mu }$ and $\nu$ the affine parameter along them, generating the ruling geodesics of these lightcones, will be written as

$$k=\partial /\partial \nu \Rightarrow k^{\mu }=d{x}^{\mu }/d\nu ,$$

(3)

where

$$k_{\mu }\equiv \partial w/\partial x^{\mu }=w_{,\mu }\Rightarrow k^{\mu }{k}_{\mu }=0.$$

(4)

This definition necessarily implies that k is hypersurface-orthogonal [7],

$$k_{\mu }{\nabla }_{\nu }=k_{\nu }{\nabla }_{\mu }.$$

(5)

Null geodesic vector fields are orthogonal to the null surfaces and generate the past-directed null geodesics along the past lightcone, on which w is constant:

$$k^{\mu }{\nabla }_{\nu }{k}^{\nu }=0\Rightarrow w_{,\mu }{k}^{\mu }=0.$$

(6)

Once the null geodesic vector condition is satisfied at the central worldline, one will find the same affine parameter in different directions, which is implying

$$k_{\mu }{u}^{\mu }=w_{,\mu }{u}^{\mu }\iff k_{\mu }{u}^{\mu }{|}_c=1,$$

(7)

and this shows that the affine parameter $\nu$ is uniquely defined geometrically on the null geodesics, and this defines the central condition. If we specify that $\nu =0$ on the worldline C, so the event “q” is given by

$$w=w_0,\nu =0.$$

(8)

The coordinate y measures distances down the null geodesics, and so represents both spatial distance from the worldline C, and time difference from “q”. There are various choices of y that might be suitable for different purposes, for example [3]:

• $y=\nu$, the unique affine parameter down the null geodesics through C determined by the central conditions on C (${\nu |}_c=0,u^{\mu }{k}_{\mu }{|}_C=1$). The spacetime metric will be simplified, but one loses the beautiful physical interpretation of observational coordinates;
• $y=r_A$, the angular distance, i.e., area distance down the null cones from C.
• $y=z$, galactic redshift observed from C, imposing $y=const$. along matter worldlines;
• y chosen as in one of the points 1–3 on the initial null cone $w=w_0$, and then specified thereafter to be comoving with the fluid; $y_{,\mu }{u}^{\mu }=0$.

When one of these specific choices has been made, y is uniquely defined on all the null cones. We will use such a choice of coordinate y as a coordinate comoving with the fluid, and determined by a unique specification on the initial null cone $w=w_0$. From Equations (3) and (4), we will have [3]

$$k_{\mu }={\delta }_{\mu }^0,k^{\mu }=d{x}^{\mu }/d\nu =(1/\beta ){\delta }_1^{\mu }\Rightarrow (1/\beta )=dy/d\nu \mathrm{for}\beta >0,$$

(9)

where $\beta$ is some function that determines the relation of the affine parameter $\nu$ to the coordinate y. Equation (9) shows the change of rate of the coordinate y down the null geodesics relative to the affine parameter $\nu$. As $y\to 0$, $\beta =const.$ when y is affine parameter; and $\beta \to 1$ when we choose $y=r_A$. Different values of y with constant values of $\nu$ represent an event at the same distance from q down the null cone in different directions. The coordinates $(\widehat{\theta },\widehat{\varphi })$ are angles on the “physical” sky. The observer sees the sky as the superposition of 2-spheres ($w_0$) embedded in the lightcone, then we can redefine $\widehat{\theta },\widehat{\varphi }$ as spherical coordinates on the celestial sphere with respect to the (physically non-rotating) reference frame ${\mathbf{e}}_{\mu }$1. They label the geodesics generating the past lightcone (they are constant along such geodesics) [3]. At a constant surface w,

$$k^{\mu }{\widehat{\theta }}_{,\mu }=k^{\mu }{\widehat{\varphi }}_{,\mu }=0.$$

(10)

They are based on a parallelly propagated orthonormal tetrad ${\mathbf{e}}_{\mu }$ [3] along C. Then, at a constant w and $\nu$, we have

$$\underset{\nu \to 0}{lim}\left\{\frac{d{s}^2}{{\nu }^2}{|}_{\begin{array}{c}w=const\\ \nu =const\end{array}}\right\}=d{\Omega }^2=d{\widehat{\theta }}^2+{sin}^2\widehat{\theta }d{\widehat{\varphi }}^2.$$

(11)

These coordinates do not necessarily cover all the spacetime, but they do cover that part which is observable from the worldline C.

3. Observational Metric

The metric components can be obtained from the previous discussions. From Equations (4) and (9), we see that

$$\begin{array}{}\mathrm{(12)}& k^{\mu }{k}_{\mu }=0\Rightarrow w_{,\mu }{g}^{\mu \nu }{w}_{,\nu }\Rightarrow g^{00}=0,\hfill \mathrm{(13)}& k^{\mu }=g^{\mu \nu }{k}_{\nu }\Rightarrow g^{\mu 0}=(1/\beta ){\delta }_1^{\mu },\hfill \end{array}$$

and thus

$$g^{\mu \nu }{g}_{\nu \gamma }={\delta }_{\gamma }^{\mu }\Rightarrow g^{0\nu }{g}_{\nu \gamma }={\delta }_{\gamma }^0\Rightarrow g_{1\gamma }=\beta {\delta }_{\gamma }^0.$$

(14)

We can get the general expression for $g^{\mu \nu }$ and compute its inverse by introducing new functions for the non-constrained components. We thus have [3],

$$g_{\mu \nu }=\left(\begin{array}{cccc}\alpha & \beta & v_2& v_3\\ \beta & 0& 0& 0\\ v_2& 0& h_{22}& h_{23}\\ v_3& 0& h_{23}& h_{33}\end{array}\right),g^{\nu \gamma }=\left(\begin{array}{cccc}0& 1/\beta & 0& 0\\ 1/\beta & \delta & {\sigma }_2& {\sigma }_3\\ 0& {\sigma }_2& h_{33}/h& -h_{23}/h\\ 0& {\sigma }_3& -h_{23}/h& h_{22}/h\end{array}\right),$$

(15)

where

$$\begin{array}{}\mathrm{(16)}& h=\det (h_{IJ})=h_{22}{h}_{33}-{(h_{23})}^2,\hfill \mathrm{(17)}& \delta =-(\alpha +\beta (v_2{\sigma }_2+v_3{\sigma }_3))/{\beta }^2.\hfill \end{array}$$

Here, we have defined

$$\begin{array}{ccc}\hfill {\sigma }_2& =& -(v_2{h}_{33}-v_3{h}_{23})/\beta h,\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill {\sigma }_3& =& -\left(v_3{h}_{22}-v_2{h}_{23}\right)/\beta h,\hfill \end{array}$$

(19)

where $(I,J)\in {\{2,3\}}^2$. The metric form above implies that the surfaces ${w|}_{const.}$ are null surfaces. However, it does not, as it stands, guarantee that these null surfaces are the past lightcones of the geodesic worldline C. To set this feature, one has to impose some limits on the behaviour of the metric tensor components near the worldline C [3]. When the coordinate y is taken to be the affine parameter or the area distance, these essential limits are [3]:

$$\underset{y\to 0}{lim}\alpha =-1,\underset{y\to 0}{lim}\beta =1,\underset{y\to 0}{lim}(v_I/y^2)=0,\underset{y\to 0}{lim}{h}_{IJ}d{x}^{I}d{x}^J/y^2=d{\Omega }^2.$$

(20)

When this coordinate y is taken to be point 4, from what we obtained above, and by making a coordinate transformation $y^{\prime }=y^{\prime }(w,y,\widehat{\theta },\widehat{\varphi }),w^{\prime }=w,{\widehat{\theta }}^{\prime }=\widehat{\theta },{\widehat{\varphi }}^{\prime }=\widehat{\varphi }$, as $y\to 0$, one finds the limits are found to be [3]

$$\underset{y\to 0}{lim}\alpha =-1,\underset{y\to 0}{lim}\beta ={\beta }_0(w,x^I),\underset{y\to 0}{lim}{v}_I=0,\underset{y\to 0}{lim}{h}_{IJ}d{x}^{I}d{x}^J/y^2={\beta }_0^{2}d{\Omega }^2.$$

(21)

These limits we just introduced guarantee the necessary conditions to make the null hypersurfaces to be the past lightcones of observer of the worldline C. Finally, we can say that we have observational coordinates if and only if the metric tensor components obey Equations (15) and (20) [3].

4. Perturbed Lightcone Gauge

The metric in the above mentioned coordinates reads:

$$d{s}^2=a^2(w-y)\left(-(1+\delta \alpha )d{w}^2+2(1+\delta \beta )dwdy+2v_{\widehat{I}}d{x}^{\widehat{I}}dw+h_{\widehat{I}\widehat{J}}d{x}^{\widehat{I}}d{x}^{\widehat{J}}\right),$$

(22)

where $\left(\widehat{I},\widehat{J}\right)\in {\left\{2,3\right\}}^2$ with $x^2=\widehat{\theta }$ and $x^3=\widehat{\varphi }$. In addition:

$$h_{\widehat{I}\widehat{J}}={\Omega }_{\widehat{I}\widehat{J}}+H_{\widehat{I}\widehat{J}},$$

(23)

with $H_{\widehat{I}\widehat{J}}$ representing the tensor perturbation. We consider a perturbed FLRW spacetime in an arbitrary gauge. The coordinate system is $x^{\mu }=(\eta ,\chi ,\theta ,\varphi )$. The metric in these coordinates reads:

$$d{s}^2=a^2{g}_{\mu \nu }d{x}^{\mu }d{x}^{\nu }=a^2(\eta )\left[-(1+2\varphi )d{\eta }^2+2B_{i}d{x}^{i}d\eta +\left({\gamma }_{ij}+2C_{ij}\right)d{x}^{i}d{x}^j\right],$$

(24)

where

$$C_{ij}=-\psi {\gamma }_{ij}+{\nabla }_i{\nabla }_{j}E+{\nabla }_i{F}_j+\frac{1}{2}{h}_{ij}.$$

(25)

At first order, the coordinate transformation reads:

$$\left\{\begin{array}{ccc}w& =& \eta +\chi +\delta w,\\ y& =& \chi +\delta y,\\ \widehat{\theta }& =& \theta +\delta \widehat{\theta },\\ \widehat{\varphi }& =& \varphi +\delta \widehat{\varphi }.\end{array}\right.$$

(26)

We also define the backward affine parameter along the past lightcone, $\lambda$. In the background, we have:

$$\frac{d}{d\lambda }=\frac{1}{a^2}\left[{\partial }_{\chi }+{\partial }_{\eta }\right].$$

(27)

Since we have $k^{\widehat{\mu }}=a^{-2}(1-\delta \beta ){\delta }_y^{\widehat{\mu }}$, we can write that

$$0=k^w=\frac{d\eta }{d\lambda }+\frac{d\chi }{d\lambda }+\frac{d\delta w}{d\lambda }=k^{\eta }+{\overline{k}}^{\chi }+\frac{d\delta w}{d\lambda }.$$

(28)

Therefore:

$$\delta w=-\int \left(k^{\eta }+{\overline{k}}^{\chi }\right)d\lambda .$$

(29)

Similarly, using $k^y=a^{-2}(1-\delta \beta )$, we get

$$\delta y=-\int \left(\frac{\delta \beta }{a^2}\right)d\lambda .$$

(30)

Using $k^{\widehat{I}}=0$:

$$\delta x^{\widehat{I}}=-\int k^{I}d\lambda {\delta }_I^{\widehat{I}}.$$

(31)

The Jacobian of the coordinate transformation is given by:

$$\frac{\partial x^{\widehat{\mu }}}{\partial x^{\nu }}=\left(\begin{array}{cccc}1+{\partial }_{\eta }\delta w& 1+{\partial }_{\chi }\delta w& {\partial }_{\theta }\delta w& {\partial }_{\varphi }\delta w\\ {\partial }_{\eta }\delta y& 1+{\partial }_{\chi }\delta y& {\partial }_{\theta }\delta y& {\partial }_{\varphi }\delta y\\ {\partial }_{\eta }\delta \widehat{\theta }& {\partial }_{\chi }\delta \widehat{\theta }& 1+{\partial }_{\theta }\delta \widehat{\theta }& {\partial }_{\varphi }\delta \widehat{\theta }\\ {\partial }_{\eta }\delta \widehat{\varphi }& {\partial }_{\chi }\delta \widehat{\varphi }& {\partial }_{\theta }\delta \widehat{\varphi }& 1+{\partial }_{\varphi }\delta \widehat{\varphi }\end{array}\right),$$

(32)

and we can write the inverse as

$$\begin{array}{ccc}\hfill \frac{\partial x^{\mu }}{\partial x^{\widehat{\nu }}}& =& {\delta }_{\nu }^{\mu }-{\delta }_0^{\mu }{\delta }_{\nu }^1-{\partial }_{\nu }{\delta }^{\widehat{\mu }}+{\delta }_{\nu }^1{\partial }_w{\delta }^{\widehat{\mu }}+{\delta }_0^{\mu }{\partial }_{\nu }\delta y-{\delta }_0^{\mu }{\delta }_{\nu }^1{\partial }_w\delta y.\hfill \end{array}$$

(33)

With all that, the metric quantities in the PLG system are given by:

$$\begin{array}{}\mathrm{(34)}& \hfill \delta \alpha & =& 2\left[-\varphi +{\partial }_{\eta }\int \left(\frac{1-\delta \beta }{a^2}+k^{\eta }\right)d\lambda \right],\hfill \mathrm{(35)}& \hfill v_{\widehat{I}}& =& \left[B_I-{\partial }_I\int \left(k^{\eta }+\frac{1-\delta \beta }{a^2}\right)d\lambda -{\gamma }_{IJ}{\partial }_{\eta }\int k^J{\delta }_J^{\widehat{J}}d\lambda \right]{\delta }_{\widehat{I}}^I,\hfill \mathrm{(36)}& \hfill H_{\widehat{I}\widehat{J}}& =& 2\left[C{\gamma }_{IJ}+{\gamma }_{K(I}{\partial }_{J)}\int k^{K}d\lambda \right]{\delta }_{\widehat{I}}^I{\delta }_{\widehat{J}}^J.\hfill \end{array}$$

Note that the equation for $\delta \beta$ is not constraining anything because $\frac{d}{d\lambda }\left(\delta y-\delta w\right)$ involves $\delta \beta$. Actually, after a bit of algebra, it leads to the identity:

$$2\varphi +k_{\chi }-2k_{\eta }+B_{\chi }=a^2{k}^{\chi }.$$

(37)

Using the fact that $k_{\eta }=g_{\eta \mu }{k}^{\mu }$, one finds that this identity is exactly satisfied.

The nullity of $g_{yy}$ also leads to a constraint:

$$k^{\eta }+k^{\chi }=\frac{1}{a^2}\left(n^{\chi }(\varphi +\psi )+B^{\chi }-n^{\chi }{\nabla }^{2}E-n^{\chi }{\nabla }_{\chi }{F}^{\chi }-\frac{1}{2}{n}^{\chi }{h}_{\chi }^{\chi }\right),$$

(38)

which is an identity resulting from the null geodesic equation. We have used the facts that

$$\begin{array}{}\mathrm{(39)}& \frac{\partial }{\partial y}{|}_{w=const.}=\frac{\partial }{\partial \eta }{{|}_{\chi =const.}+\frac{\partial }{\partial \chi }|}_{y=const.}=\frac{d}{d\eta },\hfill \mathrm{(40)}& \frac{\partial }{\partial w}{{|}_{y=const.}=-\frac{\partial }{\partial \eta }|}_{\chi =const.},\hfill \end{array}$$

which means that y mimics the behaviour of the affine parameter along the light ray. Finally, the nullity of $g_{y\widehat{I}}$ leads to:

$${\gamma }_{IJ}{k}^J=-{\partial }_I\int \left(k^{\eta }+k^{\chi }\right)d\lambda -B_I+{\nabla }^{(\chi }{\nabla }_{I)}E+{\nabla }^{(\chi }{F}_{I)}+\frac{1}{2}{h}_I^{\chi },$$

(41)

which also results from the null geodesic equation.

Therefore, we see that the very definition of the observational coordinates system via the relation $k^{\widehat{\mu }}={\beta }^{-1}{\delta }_y^{\widehat{\mu }}$ ensures that our PLG metric has the correct form.

5. Observables in the PLG

We are going to present here the observables that we can measure on our past lightcone. By using the PLG introduced above, we are going to get a set of observables defined by the PLG parameters. They are simpler but different in definitions from what we are used to in perturbed FLRW; a justification has been made between the two gauges.

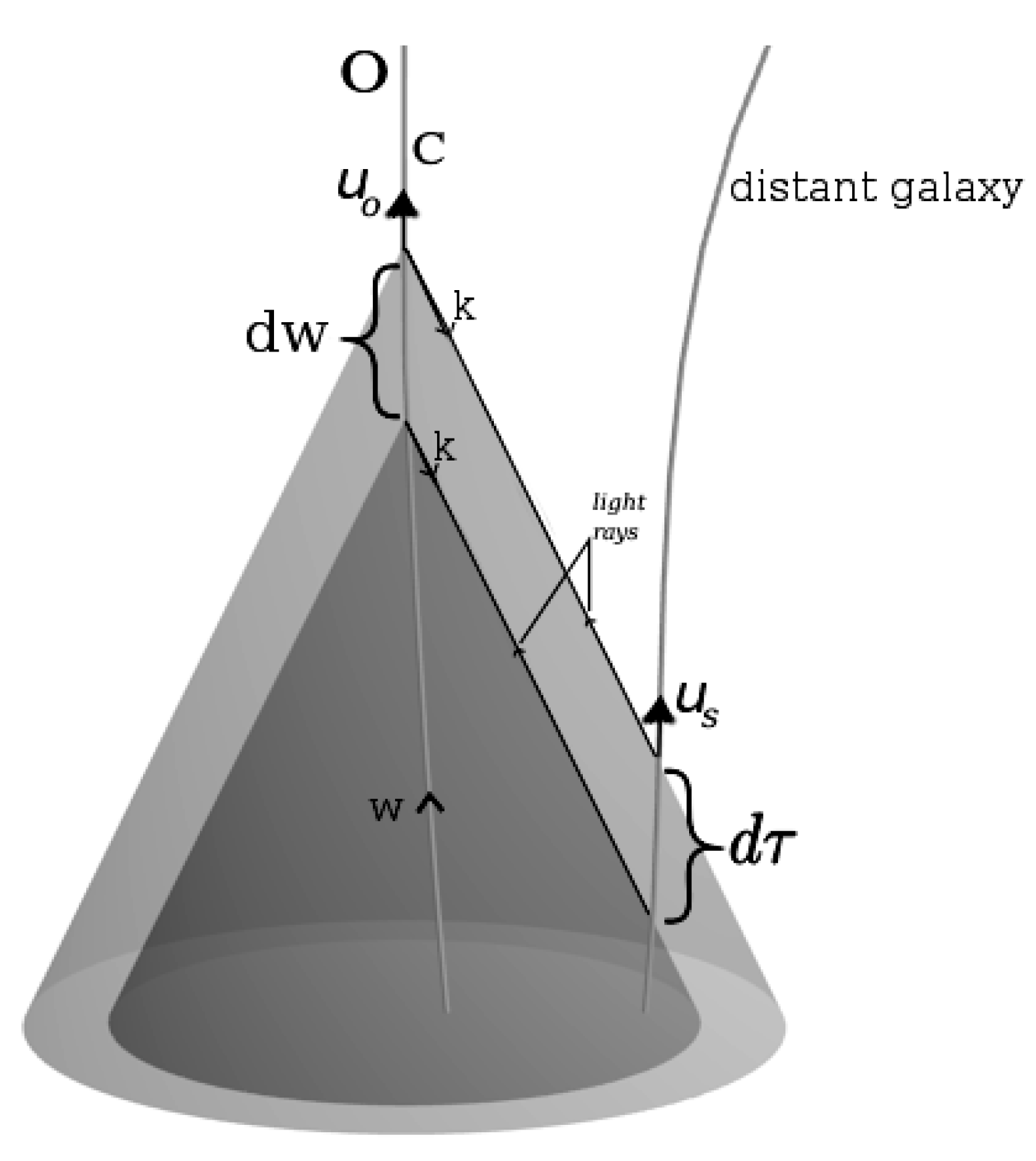
5.1. The Redshift of Distant Galaxies in the PLG

The redshift of a source crossing the lightcone is the time dilation observed from $C(w,y,\widehat{\theta },\widehat{\varphi })$ of a source of a proper time $\tau$ along its worldlines; crossing our past lightcone is determined by the ratio $dw/d\tau$ along our worldline, see Figure 2. The observed redshift z of its emitted light is determined by

$$1+z=\frac{{\lambda }_o}{{\lambda }_s}=\frac{a_c(w)}{a(w-y)}=\frac{dw}{d\tau }=u^w{|}_s=\frac{1}{a(w-y)}(1+\delta \alpha /2),$$

(42)

where $a_c(w)$ is the scale factor along the central worldline C at singular point $w_0{|}_C$ (it can be taken equal to 1 today), or we can use the expression

$$1+z=\frac{{(k^{\mu }{u}_{\mu })}_s}{{(k^{\mu }{u}_{\mu })}_o},$$

(43)

where we can normalise ${(k^{\mu }{u}_{\mu })}_o=1$, and we can re-write (43) as

$$1+z={(k_{\mu }{u}^{\mu })}_s,$$

(44)

and using (4) again, we will get

$$1+z={({\delta }_{\mu }^0{u}^{\mu })}_s={(u^w)}_s.$$

(45)

This shows that in the lightcone gauge the redshift of the source is its 4-velocity, where the 4-velocity of the source is directly observable because the redshift is directly measurable from the observed source spectrum.

We will use the Jacobian (32) to transform our above result into the standard model gauge, getting

$$u^w=\frac{\partial w}{\partial \eta }{u}^{\eta }+\frac{\partial w}{\partial x^i}{u}^i.$$

(46)

To first order, this can be expanded as

$$u^w=\frac{1}{a(w-y)}\left[1-\varphi +{\partial }_{\eta }\delta w+v^i{\delta }_i^1\right].$$

(47)

We could decompose $v^i$ into scalar and tensor parts as

$$\begin{array}{ccc}\hfill v^i& =& V^i+{\gamma }^{ij}[{\nabla }_j{E}^{\prime }+{\overline{B}}_j].\hfill \end{array}$$

(48)

To simplify the discussion, let us concentrate on scalar modes in the longitudinal gauge: $E=B=0$. Then, using the expression for $\delta w$, and the commutation rules Equation (A5), we obtain

$${\partial }_{\eta }\delta w=-\int \left[{\partial }_{\eta }\left(\frac{\varphi -\psi }{a^2}\right)+2\mathcal{H}\left(\frac{\varphi -\psi }{a^2}\right)\right]d\lambda .$$

(49)

Hence:

$${\partial }_{\eta }\delta w=-\int \frac{{\partial }_{\eta }(\varphi -\psi )}{a^2}d\lambda =-\int {\partial }_{\eta }(\varphi -\psi )d\eta .$$

(50)

Thus, remembering that, in Longitudinal gauge $\varphi =\Phi$, $\varphi -\psi =\Phi +\mathsf{\Psi }$, and $\overrightarrow{V}·\overrightarrow{n}=v^{\chi },$ we get:

$$u^w=\frac{1}{a(\eta )}{\left[1-\Phi +\int {\partial }_{\eta }\left(\Phi +\mathsf{\Psi }\right)d\eta +\overrightarrow{V}·\overrightarrow{n}\right]}_s^o,$$

(51)

evaluated from the source s to the observer on the central worldline o. This gives the expected expression for $1+z$ in terms of Bardeen’s potentials.

If we now look at scalars only in a general gauge, using the fact that ${\partial }_{\chi }$ and $\int d\lambda$ commute, we get, after a bit of algebra:

$$u^w=\frac{1}{a(\eta )}{\left[1+\mathcal{H}\left(B-E^{\prime }\right)-\Phi +\int {\left(\Phi +\mathsf{\Psi }\right)}^{\prime }d\eta +\overrightarrow{V}·\overrightarrow{n}\right]}_s^o.$$

(52)

Under a general gauge transformation, $\eta \to \eta -T$ and $x^i\to x^i-L^i$, we have

$$\begin{array}{c}\hfill B-E^{\prime }\to B-E^{\prime }-T,\mathrm{and}a(\eta )\to a(\eta )\left[1-\mathcal{H}T\right].\end{array}$$

(53)

Therefore, $u^w\to u^w$, and the redshift as a whole is indeed gauge invariant, although its background and first-order parts are manifestly not.

If one includes vectors and tensors, one finds:

$$u^w=\frac{1}{a(\eta )}{\left[1+\mathcal{H}\left(B-E^{\prime }\right)-\Phi +\int {\left(\Phi +\mathsf{\Psi }\right)}^{\prime }d\eta +\overrightarrow{V}·\overrightarrow{n}+\int {\left[\overrightarrow{\overline{\Phi }}·\overrightarrow{n}\right]}^{\prime }d\eta +\frac{1}{2}\int {\left[h(\overrightarrow{n},\overrightarrow{n})\right]}^{\prime }d\eta \right]}_s^o.$$

(54)

We can conclude that the 4-velocity of the observer in the PLG can cover the Sachs–Wolfe (SW) equation with the scalar contribution, and the so called integrated Sachs–Wolfe term, additional to vector and tensor contributions to the redshift.

5.2. The Area Distance in the PLG

The shape and size of the image of a source depends on the path taken by the light rays from the source to the observer through the spacetime by the null geodesics; i.e., it depends on the spacetime curvature. In fact they are both represented by the metric components $h_{\widehat{I}\widehat{J}}$, which are in principle, directly measurable. For an object of known size and shape observed at time $w_0$ and lying at distance y in the direction $\widehat{\theta },\widehat{\varphi }$, one has [3]

$$d{l}^2=h_{\widehat{I}\widehat{J}}(w_0,y,\widehat{\theta },\widehat{\varphi })d{x}^{\widehat{I}}d{x}^{\widehat{J}},$$

(55)

where $dl$ represents distance of the object perpendicular to the line of sight, which are known if the size, shape and orientation of the object are known. The term $d{x}^{\widehat{I}}$ represents the corresponding angular displacements at the image, which are directly measurable [3]. Comparing the angular measurements with the known dimensions, one can deduce $h_{\widehat{I}\widehat{J}}$. In addition, directly from (55) and (20), we get the area distance $r_A$ given by

$$r_A={\left[\frac{det\left[h_{IJ}\right]}{{sin}^2\widehat{\theta }}\right]}^{\frac{1}{4}},$$

(56)

where

$$\begin{array}{c}\hfill h_{\widehat{I}\widehat{J}}=\left(\begin{array}{cc}{a}^2{S}^2(y)(1+H_{\widehat{\theta }\widehat{\theta }})& a^2{S}^2(y)H_{\widehat{\theta }\widehat{\varphi }}\\ a^2{S}^2(y)H_{\widehat{\theta }\widehat{\varphi }}& a^2{S}^2(y)({sin}^2\widehat{\theta }+H_{\widehat{\varphi }\widehat{\varphi }})\end{array}\right).\end{array}$$

(57)

For simplicity, we express the embedded $S(y)$ in $H_{\widehat{I}\widehat{J}}$, thus defining the determinant as

$$det\left[h\right]=a^4{S}^4(y)({sin}^2\widehat{\theta }+H_{\widehat{\varphi }\widehat{\varphi }}+{sin}^2\widehat{\theta }{H}_{\widehat{\theta }\widehat{\theta }})-a^4{S}^4(y)H_{\widehat{\theta }\widehat{\varphi }}^2,$$

(58)

and therefore

$$r_A={\left(a^4{S}^4(y)[1+H_{\widehat{\theta }\widehat{\theta }}+\frac{1}{{sin}^2\widehat{\theta }}{H}_{\widehat{\varphi }\widehat{\varphi }}]\right)}^{\frac{1}{4}}.$$

(59)

This means the area distance in the PLG can be written in a very simple way as

$$r_A=a((w-y),\eta )S(y)\left[1+\frac{1}{4}{H}^T\right],$$

(60)

where $H^T$ is the trace, given by Equation (36), and according to Equation (A7), one can write

$$H^T=2C_I^I+2{\int }_{{\lambda }_s}^{\lambda }d{\lambda }^{\prime }{\nabla }_I{k}^I,$$

(61)

where $k^I$ is the null vector from the source position at $x_s$ and along the light trajectory to the observer position at $x_o$. Thus, the preceding equation becomes

$$\begin{array}{ccc}\hfill H^T& =& -4{\mathsf{\Psi }}_s-4\mathcal{H}(B-E^{\prime })+\frac{2}{({\eta }_o-{\eta }_s)}{\int }_{{\eta }_s}^{{\eta }_o}d\eta {\int }_{{\eta }_s}^{\eta }d{\eta }^{\prime }({\eta }^{\prime }-{\eta }_s)[({\nabla }^2-n^i{\nabla }_i^2-\frac{2}{\chi }{n}^i{\nabla }_i)(\Phi +\mathsf{\Psi })\hfill \\ & & -{\nabla }^2{\overline{B}}_i{n}^i-{\nabla }_{(i}{\overline{B}}_{j)}^{\prime }{n}^i{n}^j+\frac{2}{\chi }{\nabla }_{(i}{\overline{B}}_{j)}{n}^i{n}^j+{\nabla }^2{n}_j{F^j}^{\prime }+{\nabla }_{(i}{F}_{j)}^{″}{n}^j{n}^i-\frac{2}{\chi }{\nabla }_{(i}{F_{j)}}^{\prime }{n}^j{n}^i\hfill \\ & & +\frac{2}{\chi }{n}^i{n}^j\frac{1}{2}{h}_{ij}^{\prime }-{\nabla }^2{h}_{ij}{n}^i{n}^j.].\hfill \end{array}$$

(62)

Now, substituting back in Equation (60), the area distance is given by

$$\begin{array}{ccc}\hfill r_A(\mathbf{n},\eta )& =& a({\eta }_s)({\eta }_o-{\eta }_s)[1-{\mathsf{\Psi }}_s-\mathcal{H}(B-E^{\prime })+\frac{1}{2}\frac{1}{({\eta }_o-{\eta }_s)}{\int }_{{\eta }_s}^{{\eta }_o}d\eta (\eta -{\eta }_s)({\eta }_o-\eta )\hfill \\ & & \times (({\nabla }^2-n^i{n}^j{\nabla }_i{\nabla }_j-\frac{2}{({\eta }_o-\eta )}{n}^i{\nabla }_i)(\Phi +\mathsf{\Psi })-n^i{\nabla }^2{\overline{B}}_i+n^i{\nabla }^2{F}_i^{\prime }-{\nabla }_{(i}{\overline{B}}_{j)}^{\prime }{n}^i{n}^j\hfill \\ & & +{\nabla }_{(i}{F}_{j)}^{″}{n}^j{n}^i-{\nabla }^2{h}_{ij}{n}^i{n}^j-\frac{2}{({\eta }_o-\eta )}({\nabla }_{(i}{F}_{j)}^{\prime }{n}^j{n}^i+n^i{n}^j\frac{1}{2}{h}_{ij}^{\prime }+{\nabla }_{(i}{\overline{B}}_{j)}{n}^i{n}^j).)].\hfill \end{array}$$

(63)

This equation represents the area distance of an object in a general gauge including the vector and tensor modes contributions in the Friedmann universe, and it is equivalent to the expression of the area distance in our PLG, see Equation (60). The double integrals term in Equation (63) represents the integrated effects proportional to line-of-sight integrals of the scalar, vector and tensor modes and their time derivatives.

5.3. The Luminosity Distance in the PLG

The luminous rays received from a source of area distance $r_A$, observed at redshift z, is defined in the past-lightcone as

$$d_L={\left(1+z\right)}^2{r}_A=a(w-y)S(y){(u^w)}^2\left[1+\frac{1}{4}{H}^T\right],$$

(64)

from which we can write

$$\begin{array}{ccc}\hfill d_L(\mathbf{n},{\eta }_s)& =& \frac{S(\chi )}{a_s(\eta )}[1-2{\Phi }_o+2{\Phi }_s-{\mathsf{\Psi }}_s+\mathcal{H}(B-E^{{}^{\prime }})+2\mathbf{V}·\mathbf{n}\hfill \\ & & +2\int {(\Phi +\mathsf{\Psi })}^{\prime }d\eta -\int n^i{n}^j\left({\nabla }_{(i}{F}_{j)}^{\prime }\right.+\frac{1}{2}{h}_{ij}^{\prime }-{\nabla }_{(i}{\overline{B}}_{j)})d\eta \hfill \\ & & +\frac{1}{2}\frac{1}{({\eta }_o-{\eta }_s)}{\int }_{{\eta }_s}^{{\eta }_o}d\eta {\int }_{{\eta }_s}^{\eta }d{\eta }^{\prime }({\eta }^{\prime }-{\eta }_s)(({\nabla }^2-n^i{n}^j{\nabla }_i{\nabla }_j-\frac{2}{({\eta }_s-\eta )}{n}^i{\nabla }_i)(\Phi +\mathsf{\Psi })\hfill \\ & & -{\nabla }^2{\overline{B}}_i{n}^i-{\nabla }_{(i}{\overline{B}}_{j)}^{\prime }{n}^i{n}^j+\frac{2}{({\eta }_s-\eta )}{\nabla }_{(i}{\overline{B}}_{j)}{n}^i{n}^j+{\nabla }^2{n}_j{F^j}^{\prime }+n^j{n}^i{\nabla }_{(i}{F}_{j)}^{″}\hfill \\ & & -\frac{2}{({\eta }_s-\eta )}{\nabla }_{(i}{F}_{j)}^{\prime }{n}^j{n}^i+\frac{2}{({\eta }_s-\eta )}{n}^i{n}^j{h}_{ij}^{\prime }-{\nabla }^2{h}_{ij}{n}^i{n}^j)].\hfill \end{array}$$

(65)

Relating the above expression to the redshift of the source, therefore

$$z_s={\overline{z}}_s+\delta z_s,$$

(66)

where we can easily write

$$\begin{array}{ccc}\hfill \delta z_s& =& (1+{\overline{z}}_s)[{\mathsf{\Psi }}_o-{\mathsf{\Psi }}_s+\mathcal{H}(B-E^{{}^{\prime }})+\mathbf{V}·\mathbf{n}-{\int }_{{\eta }_s}^{{\eta }_o}{n}^i{\nabla }_i(\Phi +\mathsf{\Psi })d\eta \hfill \\ & & -{\int }_{{\eta }_s}^{{\eta }_o}{n}^i{n}^j\left({\nabla }_{(i}{F}_{j)}^{\prime }+\frac{1}{2}{h}_{ij}^{\prime }-{\nabla }_{(i}{\overline{B}}_{j)}\right)d\eta ],\hfill \end{array}$$

(67)

and we can assume that [8]

$$d_L(\mathbf{n},{\eta }_s)=d_L(\mathbf{n},\eta ({\overline{z}}_s))\equiv d_L(\mathbf{n},{\overline{z}}_s),$$

(68)

by taking the Taylor expansion

$$d_L(\mathbf{n},{\overline{z}}_s)=d_L(\mathbf{n},z_s)-\frac{d_L(\mathbf{n},z_s)}{d{z}_s}{|}_{z=\overline{z}}\delta z_s.$$

(69)

Then, the redshift luminosity distance is given by [9]

$$\begin{array}{ccc}\hfill \frac{d_L(\mathbf{n},z_s)}{d{z}_s}{|}_{z=\overline{z}}& =& {(1+z_s)}^{-1}{d}_L+{\mathcal{H}}_s^{-1}+O(1),\hfill \end{array}$$

(70)

with ${\overline{z}}_s+1=1/a({\eta }_s)$ at the background. This leads to

$$\begin{array}{ccc}\hfill \frac{d_L(\mathbf{n},z_s)}{d{z}_s}{|}_{z=\overline{z}}& =& (1+z_s)\left[-({\eta }_o-{\eta }_s+{\mathcal{H}}_s^{-1})\right][{\mathsf{\Psi }}_o-{\mathsf{\Psi }}_s+\mathcal{H}(B-E^{{}^{\prime }})+\mathbf{V}·\mathbf{n}\hfill \\ & & -{\int }_{{\eta }_s}^{{\eta }_o}{n}^i{\nabla }_i(\Phi +\mathsf{\Psi })d\eta -{\int }_{{\eta }_s}^{{\eta }_o}{n}^i{n}^j\left({\nabla }_{(i}{F}_{j)}^{\prime }+\frac{1}{2}{h}_{ij}^{\prime }-{\nabla }_{(i}{\overline{B}}_{j)}\right)d\eta ].\hfill \end{array}$$

(71)

Then, the redshift luminosity distance will be given as

$$\begin{array}{ccc}\hfill d_L(\mathbf{n},z_s)& =& (1+z_s)[({\eta }_o-{\eta }_s)+[({\eta }_o-{\eta }_s)-{\mathcal{H}}_s^{-1}]{\mathsf{\Psi }}_o-[2({\eta }_o-{\eta }_s)-{\mathcal{H}}_s^{-1}]{\mathsf{\Psi }}_s\hfill \\ & & +2({\eta }_o-{\eta }_s){\Phi }_s-{\mathcal{H}}_s^{-1}\mathcal{H}(B-E^{\prime })+[({\eta }_o-{\eta }_s)-{\mathcal{H}}_s^{-1}]\mathbf{V}·\mathbf{n}+2{\int }_{{\eta }_s}^{{\eta }_o}d\eta \Phi \hfill \\ & & +{\int }_{{\eta }_s}^{{\eta }_o}d\eta ({\eta }_s-\eta )n^i{\nabla }_i(-3\Phi +\mathsf{\Psi })+[({\eta }_o-{\eta }_s)-{\mathcal{H}}_s^{-1}]{\int }_{{\eta }_s}^{{\eta }_o}{n}^i{\nabla }_i(-\mathsf{\Psi }+\Phi )d\eta \hfill \\ & & +n^i{n}^j{\mathcal{H}}_s^{-1}{\int }_{{\eta }_s}^{{\eta }_o}\left({\nabla }_i{F}_j^{\prime }+\frac{1}{2}{h}_{ij}^{\prime }-{\nabla }_i{\overline{B}}_j\right)d\eta \hfill \\ & & +\frac{1}{2}{\int }_{{\eta }_s}^{{\eta }_o}d\eta (\eta -{\eta }_s)({\eta }_o-\eta )([{\nabla }^2-n^i{n}^j{\nabla }_i{\nabla }_j](\Phi +\mathsf{\Psi })-{\nabla }^2{n}^i({\overline{B}}_i-F_i^{\prime })\hfill \\ & & -n^i{n}^j[{\nabla }_{(i}{\overline{B}}_{j)}^{\prime }-{\nabla }_{(i}{F}_{j)}^{″}]-n^i{n}^j{\nabla }^2{h}_{ij}-\frac{2}{{\eta }_o-\eta }[{\nabla }_{(i}{F}_{j)}^{\prime }+\frac{1}{2}{h}_{ij}^{\prime }+{\nabla }_{(i}{\overline{B}}_{j)}]n^i{n}^j)].\hfill \end{array}$$

(72)

This is the famous expression of the redshift luminosity distance in a perturbed Friedmann universe in general gauge, as a function of the measured source redshift $z_s$ and its direction $\mathbf{n}$. It contains the angular and redshift fluctuations of the luminosity distance or what is called “gravitational redshift” in the first line apart from the background contribution. The second line can be the terms due to peculiar motion of the observer and emitter (Doppler terms). The third and fourth lines collect integrated effects proportional to line-of-sight integrals of $\mathsf{\Psi }$ and its time derivative, and the fifth and last line represents the lensing term with ${\nabla }^2\mathsf{\Psi }\propto \delta \rho$. This equation is obtained in [10,11], and is equivalent to our expression of luminosity distance in PLG, Equation (64), which we expressed in one single line in terms of the metric components, which in principle is measurable quantity.

6. Galaxy Surveys

The large-scale cosmic structure contains lots of information about the global properties of our Universe, and by analysing maps of galaxies we can probe the initial conditions of the Big Bang and its physical processes that have operated subsequently [12,13]. Statistical measurements of galaxy motions and clustering with the weak gravitational lensing provide some of the strongest evidence to date that Einstein’s GR is an accurate description of gravity on cosmological scales.

Galaxies are the building blocks which define the large-scale distribution of visible matter in the Universe and it can be used to trace the underlying dark matter distribution. Without dark matter, galaxy formation would occur substantially later in the Universe than it is observed. After this all dark matter ripples could grow freely, forming seeds into which the baryons could later fall. Such information requires a combination of the galaxies’ location in three dimensions and distance information from its redshift [14].

6.1. The Galaxy Number Count with the PLG

Suppose one counts the galaxies seen in a solid angle $d{\Omega }_0$ around the direction of observation $(\widehat{\theta },\widehat{\varphi })$, down to a distance y. An increment from $y⟶y+dy$ will result in including $dN$ new galaxies in the count, where $dN$ is the number of galaxies detected in a volume $dV$ of size as ($dy,d\widehat{\theta },d\widehat{\varphi }$) around a point on our past lightcone

$$dV=(r_A^{2}d{\Omega }_0)(u^{\mu }{k}_{\mu }d\nu ).$$

(73)

If the number density of galaxies at the position y is n, then (n$dV$) is the number of galaxies that will be contained in this volume. We will write $dN$ in the form

$$dN=f_{m}dV,$$

(74)

where $f_m$ is the selection function representing the fraction of galaxies in $dV$ that are actually detected and included in the number count; one can estimate $f_m$ from knowledge of the galactic brightness distribution and spectrum, the area distance $r_A$ and redshift z. In general, $f_m$ will depend on $w,y,\widehat{\theta }\mathrm{and}\widehat{\varphi }$. The number count of galaxies in a box of size ($dy,d\widehat{\theta },d\widehat{\Phi }$) around a point on our past lightcone can also be calculated as

$$dN=f_m{r}_A^2(1+z)d{\Omega }_0\beta dy,$$

(75)

where $d\nu =\beta dy$, and $\beta =a^2(1+\delta \beta )$. If y has been chosen to be an observable quantity, then $dN$ is directly measurable. As z and $r_A$ are known, one can estimate the selection function $f_m$, which depends on $r_A$, z, the galaxy properties and the observational limits and selection effects. Therefore, in principle, one could determine the quantity $\beta$ in terms of known quantities.

The geometric properties of spacetime play a role in the determination of the distribution of galaxies. Nevertheless, the observed redshift and position of galaxies are affected by the matter fluctuations and the gravity waves between the source galaxies and the observer. Therefore, the volume element constructed using the observed redshift and observed angle is different from the real physical volume occupied by the observed galaxies. The observed flux and redshift of the source galaxies are also different from their intrinsic properties. Therefore, the observed galaxy fluctuation field contains additional contributions arising from the distortion in observable quantities and these include tensor contributions as well as numerous scalar contributions [15]. Therefore, the observed galaxy number density is affected by perturbations given the total number of observed galaxies, and it contains additional contributions from the distortions in the observable quantities, compared to the standard description that galaxies simply trace the underlying matter distribution.

6.2. The Perturbation of Galaxy Number Counts $\Delta$

The number count of an overdensity galaxy number count is what we can measure when we divide the map of galaxy surveys with beams at fixed redshift and solid angle. By counting the galaxies in each pixel separately, we can study the fluctuation of the galaxy number and the distribution of dark matter. The number of overdensity galaxies in one pixel can be given by

$$\Delta =\frac{N-\overline{N}}{\overline{N}}=b·\frac{\delta \rho }{\rho }=b·\delta .$$

(76)

The number count $\Delta$ is an observable quantity; it relates the number of the galaxies in each pixel to the average numbers of the galaxies $\overline{N}$, and the distribution of dark matter $\delta$ and its bias b. Galaxy formation is a local process and its relation to the underlying matter density should be well defined and gauge invariant. The observable quantities such as observed galaxy counting should be independent of a choice of the gauge condition. The large-scale distribution of galaxies, the density fluctuation $\delta (\mathbf{x},t)$ which we calculate in a given Friedmann background, is not gauge invariant, and this is “the cosmological gauge problem” [16]. Since it depends on the background Friedmann universe, we compare the observed $\rho (\mathbf{x},t)$ with [17]:

$$\delta (\mathbf{x},t)\equiv \frac{\rho (\mathbf{x},t)-\overline{\rho }(t)}{\overline{\rho }(t)}.$$

(77)

In order to fix this problem, one has to consider individual observational effects like the redshift space distortions [18,19], the Alcock–Pacinski [20] or lensing [17,21].

For unbiased distribution, $\overline{\rho }$ is the mean galaxy density, i.e., $\overline{\rho }=\langle \rho \rangle$. Determining the spectrum in terms of directly observable quantities compares with determining gauge-invariant expression. The redshift density perturbation can be written as

$${\delta }_z(\mathbf{n},z)=\frac{\rho (\mathbf{n},z)-\langle \rho \rangle (z)}{\langle \rho \rangle (z)}.$$

(78)

Using the fact that $\rho =N/V$, and with a little of algebra, we can get [17]

$${\delta }_z(\mathbf{n},z)=\frac{N(\mathbf{n},z)-\langle N\rangle (z)}{\langle N\rangle (z)}-\frac{\delta V(\mathbf{n},z)}{V(z)},$$

(79)

where the physical survey volume density per redshift bin per solid angle can be written as a background part in a homogeneous world and a fluctuated quantity, since the solid angle and the redshift bin are distorted between the source and the observer:

$$V(\mathbf{n},z)=V(z)+\delta V(\mathbf{n},z).$$

(80)

The perturbation in the number density of galaxies is an observed quantity, and the volume perturbation also can be measured with other tracers than galaxies, and it is therefore measurable by itself and hence gauge invariant. Therefore, they are gauge-invariant quantities. Hence, ${\delta }_z(\mathbf{n},z)$ is gauge invariant. We can re-write Equation (79) as

$$\Delta (\mathbf{n},z)=\frac{N(\mathbf{n},z)-\langle N\rangle (z)}{\langle N\rangle (z)}={\delta }_z(\mathbf{n},z)+\frac{\delta V(\mathbf{n},z)}{V(z)},$$

(81)

which is a gauge-invariant expression.

6.2.1. The Computation of ${\delta }_z(\mathbf{n},z)$ in the PLG

The computation of ${\delta }_z(\mathbf{n},z)$ to first order will get

$$\begin{array}{ccc}\hfill {\delta }_z(\mathbf{n},z)& =& \frac{\rho (\mathbf{n},z)-\overline{\rho }(z)}{\overline{\rho }(z)},\hfill \end{array}$$

(82)

knowing that $\rho (\mathbf{n},z)=\overline{\rho }(\overline{z})+\delta \rho (\mathbf{n},z)$, and using the fact that $z=\overline{z}+\delta z$, then Equation (82) yields, to first order

$${\delta }_z(\mathbf{n},z)=\delta (\mathbf{n},z)-\frac{d\overline{\rho }}{d\overline{z}}\frac{\delta z(\mathbf{n},z(\eta ))}{\overline{\rho }(\overline{z})},$$

(83)

where $\frac{\delta \rho (\mathbf{n},z)}{\overline{\rho }(\overline{z})}=\delta (\mathbf{n},z)$, and by using $\frac{d\overline{\rho }}{d\overline{z}}=-3\frac{\overline{\rho }}{1+\overline{z}}$ the matter fluctuation (at the observed redshift) is given by

$${\delta }_z(\mathbf{n},z)=\delta (\mathbf{n},z)+3\frac{\delta z(\mathbf{n},z(\eta ))}{(1+\overline{z})}.$$

(84)

Since $1+z=(1+\overline{z})(1+\delta \alpha /2)$, and $\delta z=(1+\overline{z})\frac{1}{2}\delta \alpha$. Then, one can re-write Equation (84) as

$${\delta }_z(\mathbf{n},z)=\delta (\mathbf{n},z)+\frac{3}{2}\delta \alpha .$$

(85)

Here, we relate the perturbation variables in direction $\mathbf{n}$ at redshift z to their unperturbed position and time $\eta$. $\overline{z}=\overline{z}(\eta )$ is the redshift of the background universe that we measure on and $\delta z$ is the redshift perturbation to this universe, ${\delta }_z(\mathbf{n},z)=\delta (\mathbf{n},z)$ in a uniform-redshift frame $\delta z=0$. It is gauge invariant since is defined by observable quantities, where the time slicing is set by the observed redshift z, rather than by an arbitrary choice of coordinate systems or gauge conditions as for $\delta (\mathbf{n},z)$ and differs in its value contingent upon the gauge choice [22]. Moreover, by solving the background relation $\overline{z}=\overline{z}(\eta )$, we can write

$$\rho (\mathbf{n},\overline{z}(\eta ))=\overline{\rho }(\eta )+\delta \rho (\mathbf{n},\eta ).$$

(86)

Note that $\overline{\rho }(z)=\overline{\rho }(\overline{z}+\delta z)$ deviates to first order from $\overline{\rho }(\overline{z})$. Both $\delta z$ and $\delta \rho$ depend on the chosen background and are, hence, gauge dependent; however, their combination in Equation (83) must turn out to be gauge invariant as it is in principle observable.

6.2.2. The Volume Distortion in the PLG

The volume perturbation $\frac{\delta V}{V}$ should be gauge invariant because it is, in principle, a measurable quantity given unbiased volume tracers. The differential volume element (seen by a source with 4-velocity $u^{\mu }$) is given by

$$\begin{array}{}\mathrm{(87)}& \hfill dV& =& \sqrt{-g}{ϵ}_{\mu \nu \alpha \beta }{u}^{\mu }d{x}^{\nu }d{x}^{\alpha }d{x}^{\beta }\hfill \mathrm{(88)}& & =& v(\nu ,\alpha ,\beta )d{x}^{\nu }d{x}^{\alpha }d{x}^{\beta },\hfill \end{array}$$

where v is a volume density, which determines the volume perturbation

$$\frac{\delta V}{V}=\frac{v(z)-\overline{v}(z)}{\overline{v}(\overline{z})}=\frac{\delta v}{\overline{v}}.$$

(89)

Then, the volume perturbation in terms of redshift and sky position is determined by our observation coordinates $(w,y,\widehat{\theta },\widehat{\varphi })$, and therefore

$$\begin{array}{ccc}\hfill v& =& \sqrt{-g}{ϵ}_{0123}{u}^w\frac{\partial y}{\partial z}\frac{\partial \widehat{\theta }}{\partial {\widehat{\theta }}_s}\frac{\partial \widehat{\varphi }}{\partial {\widehat{\varphi }}_s}+\sqrt{-g}{ϵ}_{1230}{u}^y\frac{\partial w}{\partial z}\frac{\partial \widehat{\theta }}{\partial {\widehat{\theta }}_s}\frac{\partial \widehat{\varphi }}{\partial {\widehat{\varphi }}_s},\hfill \end{array}$$

(90)

where $ϵ$ has a permutation signature. The transformation matrix from the angles at the source to the angles at the observer is

$$\left|\frac{\partial ({\theta }_s,{\phi }_s)}{\partial ({\theta }_o,{\phi }_o)}\right|=1+\frac{\partial \delta \theta }{\partial \theta }+\frac{\partial \delta \phi }{\partial \phi }.$$

(91)

In homogeneous and isotropic backgrounds, the geodesics are straight lines, that is ${\theta }_s={\theta }_o$, ${\phi }_s={\phi }_o$, but in a perturbed universe, angles are perturbed with respect to each other:

$${\theta }_s={\theta }_0+\delta \theta ,{\phi }_s={\phi }_o+\delta \phi .$$

(92)

The angles between the source and the observer are fixed at the PLG. It can be shown that there is no angular displacement

$$\delta \widehat{\theta }=\delta \widehat{\varphi }=0.$$

(93)

This will lead to the volume perturbation being given as

$$\begin{array}{ccc}\hfill v& =& \sqrt{-g}{u}^w\frac{\partial y}{\partial z}-\sqrt{-g}{u}^y\frac{\partial w}{\partial z}.\hfill \end{array}$$

(94)

With instant light cone ${w|}_{const.}$, we get

$$v=\sqrt{-g}{u}^w\frac{\partial y}{\partial z}.$$

(95)

Furthermore, from Equation (22),

$$\sqrt{-g}=a^{4}S{(y)}^{2}sin(\theta )\left(1+\frac{H^T}{2}+\delta \beta \right),$$

(96)

and the 4-velocity of the source according to the PLG

$$u=\{(1+z),n_i{v}^i\}.$$

(97)

Since $\frac{dy}{dz}$ is the change in comoving distance y with redshift along the photon geodesic, we can re-write it as

$$\frac{dy}{dz}=\frac{d\overline{y}}{d\overline{z}}-\frac{d\overline{y}}{d\overline{z}}\frac{d\delta z}{d\overline{z}}+\frac{d\delta y}{d\overline{z}}.$$

(98)

Using the fact that $\overline{y}=\chi$, we can rewrite the above result as

$$\begin{array}{ccc}\hfill \frac{dy}{dz}& =& \frac{d\chi }{d\overline{z}}-\frac{d\chi }{d\overline{z}}\frac{d\delta z}{d\overline{z}}+\frac{d\delta y}{d\overline{z}}=\left(\frac{d\chi }{d\eta }-\frac{d\chi }{d\overline{z}}\frac{d\delta z}{d\eta }+\frac{d\delta y}{d\eta }\right)\frac{d\eta }{d\overline{z}}.\hfill \end{array}$$

(99)

Here, $dy/dz$ is to be understood as the change in co-moving distance y with respect to the redshift along the photon geodesic. The distinction between z and $\overline{z}$ is only relevant for background quantities. Therefore, Equation (95) will look like

$$v(z)=a^{4}S{(y)}^{2}sin(\theta )\left(1+\frac{H^T}{2}+\delta \beta \right)\left(1+z\right)\left(\frac{d\chi }{d\eta }-\frac{d\chi }{d\overline{z}}\frac{d\delta z}{d\eta }+\frac{d\delta y}{d\eta }\right)\frac{d\eta }{d\overline{z}}.$$

(100)

In Equation (99), the last term contains the redshift-space distortion, which will turn out to be the biggest correction to the power spectrum [17]. To lowest order along the photon geodesic, with $1+z=\frac{a_0}{a}=\frac{1}{a}$, we have

$$\frac{d\eta }{d\overline{z}}=-a{\mathcal{H}}^{-1}=-H^{-1},$$

(101)

where H is the physical Hubble parameter and $\mathcal{H}$ is the comoving Hubble parameter. With all the above taken into account, the volume element becomes

$$v(z)=-a^{4}S{(y)}^{2}sin(\theta )\left(1+\frac{H^T}{2}+\delta \beta \right)\left(1+\frac{1}{2}\delta \alpha \right)\left(\frac{d\chi }{d\eta }-\frac{1}{\mathcal{H}(1+\overline{z})}\frac{d\delta z}{d\eta }+\frac{d\delta y}{d\eta }\right){\mathcal{H}}^{-1},$$

(102)

or

$$v(z)=\frac{a^{4}S{(y)}^{2}sin(\theta )}{\mathcal{H}}\left(-1+\frac{1}{\mathcal{H}(1+\overline{z})}\frac{\partial \delta z}{\partial y}-\frac{\partial \delta y}{\partial y}-\frac{H^T}{2}-\delta \beta -\frac{1}{2}\delta \alpha \right),$$

(103)

where we have used the relations (39). Furthermore, we introduce the volume density as

$$\frac{\delta v}{\overline{v}}=\frac{v(z)-\overline{v}(z)}{\overline{v}(\overline{z})},$$

(104)

where

$$\overline{v}(z)=\overline{v}(\overline{z})+\frac{d\overline{v}(\overline{z})}{d\overline{z}}\delta z(\mathbf{n},z).$$

(105)

To obtain the fluctuation of v, just subtract the unperturbed part $\overline{v}(z)$ from v of Equation (103) (and additional 1/a factor coming from the background part of [1 + z] term)

$$\overline{v}(\overline{z})=\frac{S{(y)}^{2}sin(\theta )}{{(1+\overline{z})}^4\mathcal{H}},$$

(106)

and thus

$$\overline{v}(z)=\overline{v}(\overline{z})\left(1+\left[\frac{2}{S(y)\mathcal{H}}-4+\frac{{\mathcal{H}}^{\prime }}{{\mathcal{H}}^2}\right]\frac{\delta z}{1+\overline{z}}\right).$$

(107)

Putting all of these together, we obtain the volume density fluctuations given by

$$\begin{array}{c}\hfill \frac{\delta v}{\overline{v}}=\left(\frac{1}{\mathcal{H}(1+\overline{z})}\frac{\partial \delta z}{\partial y}-\frac{\partial \delta y}{\partial y}-\frac{H^T}{2}-\delta \beta +\left[\frac{2}{S(y)\mathcal{H}}+\frac{{\mathcal{H}}^{\prime }}{{\mathcal{H}}^2}-1\right]\frac{\delta \alpha }{2}\right).\end{array}$$

(108)

In addition, since from Equation (30), we can conclude

$$\frac{\partial \delta y}{\partial y}=\frac{d\delta y}{d\eta }=-\delta \beta .$$

(109)

Then,

$$\begin{array}{c}\hfill \frac{\delta v}{\overline{v}}=\left(\frac{1}{\mathcal{H}(1+\overline{z})}\frac{\partial \delta z}{\partial y}-\frac{H^T}{2}+\left[\frac{2}{S(y)\mathcal{H}}+\frac{{\mathcal{H}}^{\prime }}{{\mathcal{H}}^2}-1\right]\frac{\delta \alpha }{2}\right).\end{array}$$

(110)

With $S(y)=\overline{y}=({\eta }_o-{\eta }_s)$ in flat space, and $\delta z=\frac{1}{2}(1+\overline{z})\delta \alpha$, one can then write

$$\Delta (\mathbf{n},z)=\delta (\mathbf{n},z)+\frac{1}{2\mathcal{H}}\frac{\partial \delta \alpha }{\partial y}-\frac{H^T}{2}+\left[\frac{2}{\overline{y}\mathcal{H}}+\frac{{\mathcal{H}}^{\prime }}{{\mathcal{H}}^2}-1\right]\frac{\delta \alpha }{2}.$$

(111)

This is the expression for the density redshift perturbation in observational coordinates using the observational metric, and as indicated does not include unmeasurable monopole terms or a dipole term ${(n^i{V}_i)}_o$ that usually arises by the perturbation at the observer position. Moreover, it does not depend on the peculiar velocity of observer and emitter, and we do not need to compute the deviation vectors that relate the perturbed geodesic to the unperturbed one. It only depends on quantities in terms of the perturbed metric and in principle all can be measurable.

Equation (111) is a gauge-invariant expression, and we have discussed the first term earlier; the second term contains the Doppler term, the integrated Sachs–Wolfe, the gravitational redshift and the redshift-space distortion. The third term contains the lensing distortion and time delay, and the last term contains the redshift perturbation of the volume.

When we apply the gauge transformations into the density fluctuations to the equivalent expression in general gauge, the upcoming result is already obtained in [15,21,22]:

$$\begin{array}{ccc}\hfill \Delta (\mathbf{n},z)& =& D_g-\mathsf{\Psi }-\mathcal{H}(B-E^{\prime })+\frac{1}{\mathcal{H}}[{\mathsf{\Psi }}^{\prime }+{\partial }_{\chi }{V}_{\chi }-\left({\partial }_{\chi }{F}_{\chi }^{\prime }+\frac{1}{2}{h}_{\chi \chi }^{\prime }-{\partial }_{\chi }{\overline{B}}_{\chi })]\right.\hfill \\ & & +\left[\frac{2}{\overline{y}\mathcal{H}}+\frac{{\mathcal{H}}^{\prime }}{{\mathcal{H}}^2}\right]\left[-\Phi +\mathcal{H}(B-E^{\prime })+V_{\chi }+{\int }_{{\eta }_s}^{{\eta }_o}{(\Phi +\mathsf{\Psi })}^{\prime }d\eta -{\int }_{{\eta }_s}^{{\eta }_o}\left({\partial }_{\chi }{F}_{\chi }^{\prime }+\frac{1}{2}{h}_{\chi \chi }^{\prime }-{\partial }_{(\chi }{\overline{B}}_{\chi )}\right)d\eta \right]\hfill \\ & & -\frac{1}{{\eta }_o-{\eta }_s}{\int }_{{\eta }_s}^{{\eta }_o}({\eta }^{\prime }-{\eta }_s){\Delta }_{\Omega }\left((\Phi +\mathsf{\Psi })-{\overline{B}}_{\chi }+F_{\chi }^{\prime }-\frac{1}{2}{h}_{\chi \chi }\right)d{\eta }^{\prime }.\hfill \end{array}$$

(112)

$D_g$ is density fluctuation on the uniform curvature hypersurface

$$D_g\equiv \delta +3(1+w)(\psi )={\delta }^{long}-3(1+w)\mathsf{\Psi },$$

(113)

where ${\delta }^{long}$ is the density perturbations in the longitudinal gauge. Equation (112) represents the gauge-invariant redshift density fluctuation using an FLRW metric. The ${\mathcal{H}}^{-1}{\partial }_{\chi }\mathsf{\Psi }$ term is the gravitational redshift. The light emitted from a galaxy has to pass via that potential field and reach the observer. In so doing, the photon has to lose some of its own energy and hence become redshifted. This will result in changing the redshift of the beam. The term ${\mathcal{H}}^{-1}{\partial }_{\chi }(V_{\chi })$ is the redshift space distortion due to the galaxies’ peculiar velocity relative to the observer line of sight, and this is considered the largest signal correction on the intermediate scales [17]. The middle line comes from the redshift perturbation of the volume, and it contains a Doppler term; it also contains the ordinary and integrated Sachs–Wolfe terms. The third line (the integral) is the lensing distortion which corresponds to the change in the solid angle causing radial and angular volume distortions and time delay [23,24,25]; it is relevant especially on large scales. The rest of the terms have very small relativistic effects.

The standard Newtonian description of the galaxy power spectrum breaks down and the general relativistic description is therefore essential for understanding the observed galaxy power spectrum and deriving correct constraints from these measurements. The relativistic effects progressively become significant at low angular multipoles at high redshifts $z\ge 2$, where the relativistic effects are dominant and significant on the horizon scale, but they break the symmetry of the correlation function [26]. Due to these effects, $\Delta$ contains additional information $\delta ,V,\Phi ,\mathsf{\Psi }$; this can help with testing gravity by probing the relation between density, velocity and gravitational potentials.

7. Conclusions

In this paper, a lightcone gauge has been constructed and adapted to observations made on the null cone using observational coordinates. We developed this gauge by perturbing the lightcone, and reproducing a new linear perturbed gauge to satisfy us up to first-order calculations of the observables. We calculated the observables in the so-called lightcone gauge. The calculations of the observables in the new gauge introduced was much easier than the ones we usually obtain in the standard gauge. In addition, the most interesting feature in the results of the PLG is that they are a sum of the scalar, vector and tensor contributions to the standard gauge results.

We then used this perturbed gauge to compute the galaxy number density contrast, which is the truly measured quantity in large galaxy surveys. Our result contains the relativistic effects that have been produced due to the distortions of spacetime. With the use of the PLG, we could have them in terms of the metric components, which make it easy to be calculated since we considered null-like observations; we did not have to worry about deviations on the spatial positions of the galaxy. These effects do affect our observables and, by measuring them, we can use the result to test the relations between the density, velocity and gravitational potentials. Using the PLG gauge was an attempt to make the measuring of these relativistic effects achievable in the simplest way. Our results will be most significant for future galaxy survey catalogs like BOSS, DES, Euclid, and of significance to SLOAN-7 data analysis.