A Combination Strategy of Feature Selection Based on an Integrated Optimization Algorithm and Weighted K-Nearest Neighbor to Improve the Performance of Network Intrusion Detection

Abstract

With the widespread use of the Internet, network security issues have attracted more and more attention, and network intrusion detection has become one of the main security technologies. As for network intrusion detection, the original data source always has a high dimension and a large amount of data, which greatly influence the efficiency and the accuracy. Thus, both feature selection and the classifier then play a significant role in raising the performance of network intrusion detection. This paper takes the results of classification optimization of weighted K-nearest neighbor (KNN) with those of the feature selection algorithm into consideration, and proposes a combination strategy of feature selection based on an integrated optimization algorithm and weighted KNN, in order to improve the performance of network intrusion detection. Experimental results show that the weighted KNN can increase the efficiency at the expense of a small amount of the accuracy. Thus, the proposed combination strategy of feature selection based on an integrated optimization algorithm and weighted KNN can then improve both the efficiency and the accuracy of network intrusion detection.

1. Introduction

1.1. Background

With the popularization of the Internet, network security issues have attracted more and more attention. As one of the main security technologies, network intrusion detection technology emerges as the times require. There are two basic forms of intrusion detection system, namely the host intrusion detection system and network intrusion detection system. The host intrusion detection system generally takes the log of the operating system as the data source, and some hosts will interact with each other through the active system to obtain intrusion detection information. Using the network intrusion detection system, through monitoring the traffic on the network, the information can be obtained and extracted. Then, the known attack event is matched to determine whether it belongs to the attack event. As for network intrusion detection, both the system log and network data in the system can be analyzed to determine whether the system is attacked. However, not every data can help to filter attack data, so optimizing data might be one of the effective methods to improve the reliability and timeliness of the network intrusion detection system [1,2].

Since the network intrusion detection system mainly uses a large amount of data sourced with a high dimension, and the performance of a classifier depends on the quantity and quality of features used for attack detection and classification, feature selection based on the optimization algorithm promotes the identification of the most significant features for network intrusion detection, while the classifier can also be optimized [3,4,5]. In order to improve the performance of network intrusion detection, this paper tries to solve the problem from the viewpoints of both the feature selection based on the optimization algorithm and the classifier.

The feature selection of data is to retain the features with a greater contribution in the data and remove some redundant features or even noise features. At present, the feature selection is mainly divided into two methods, which are wrapper and filter. As for the wrapper method, Bouzgou et al. [6] proposed an approach combining mutual information and a limit learning machine, and the experiment proves that the proposed method of packaging mutual information is superior to the method of multi-layer perceptron in the calculation efficiency and error difference percentage. As for the filter method, binary transformation of the optimization algorithm has more advantages in solving problems. Particle swarm optimization (PSO) [7] algorithm is a commonly used optimization algorithm which imitates the characteristics of birds foraging in space, in which the points in space move towards the global optimal solution and the local optimal solution, and the moving speed of the points constantly changes according to the point moving speed in space. The use of the PSO algorithm and its variants has solved many problems in network intrusion detection [8], and it seems that nature inspired algorithms may possibly be utilized to help improve the performance of network intrusion detection.

Most of the classification algorithms use the known data to classify the unknown data, so as to get the category with classified data. The traditional method is K-nearest neighbor (KNN) [9]. KNN uses the Euclidean distance between the data as the judgment classification standard to classify the data to be tested, but the data is not always perfectly separated by the lines or faces of space. The support vector machine (SVM) [10] might possibly solve this kind of problem very well. When the categories of data cannot be separated perfectly, the SVM can map the data to a high-dimensional plane, so as to find a plane to separate them. Compared with other classification algorithms, naïve Bayes [11] classification is relatively simple, and its basic idea is that, for the known data to be classified, the probability of each category under this condition can be calculated, so as to determine the category of the data.

1.2. Related Work

Considering the optimization algorithm for feature detection of network intrusion detection, the moth-flame optimization (MFO) [12] algorithm is an intelligent optimization algorithm which originates from the behavior simulation of moth flying around the flame. Nowadays, the MFO algorithm is deeply studied to solve multi-objective problems, unconstrained optimization problems, global optimization problems, and so on [13,14,15,16,17,18]. The MFO algorithm has been proved to be effective in networks [19,20], manufacturing [21], power systems [22,23,24], control [25], energy [26,27,28], reliability analysis [29,30,31], autonomous robot navigation [32], testing [33], photovoltaic modules [34], biomedical science [35,36,37], and so on. The MFO algorithm can then be utilized to optimize and improve the accuracy of the classification algorithm for the purpose of network intrusion detection.

In the MFO algorithm, the moth only updates its position according to its own flame, so it has strong local search ability. However, its global convergence is relatively poor, and it is easy to fall into a local optimum. Xu et al. [38] presented an enhanced moth-flame optimization (EMFO) technique based on cultural learning (CL) and Gaussian mutation (GM), in which CL helps MFO to enhance its searching ability and the operator of GM is introduced to overcome the disadvantage of falling into local optimum. Pelusi et al. [39] proposed an improved MFO algorithm with a hybrid search phase to overcome the degeneration of the global search capability and convergence speed for the original MFO algorithm. Bhesdadiya et al. [40] proposed a hybrid method of the PSO algorithm with the MFO algorithm to extract the quality characteristics of both PSO and MFO.

Majhi et al. [41] introduced the MFO algorithm as a learning algorithm to optimize the feedforward of neural network and to classify the websites. Yu et al. [42] proposed a method to embed a quantum rotation gate and simulated annealing into the MFO algorithm, and validated the method in solving the problems of both feature selection and engineering design. Gupta et al. [43] proposed a modified MFO algorithm based on the navigation method of moths named transverse orientation for the selection of usability features to get an optimal solution. Elaziz et al. [44] introduced an alternative method to create an optimal subset from features that in turn represent the whole features through improving the efficiency of the MFO algorithm in searching for an optimal subset. Pankaja et al. [45] proposed a deep belief network (DBN) method based on the MFO algorithm for plant leaf recognition. Chaithanya et al. [46] applied the MFO algorithm to optimize the random forest (RF) parameters and obtain the optimal number of the regression tree to build an efficient methodology for network intrusion detection.

It seems that the MFO algorithm might possibly be optimized to improve its global convergence for the sake of feature selection, and the integration with the PSO algorithm offers a promising way to improve the performance of network intrusion detection.

1.3. Main Aim

The main aim of this paper is to take the results of classification optimization of weighted KNN with those of feature selection algorithm into consideration, and propose a combination strategy of feature selection based on an integrated optimization algorithm and weighted KNN, in order to improve the performance of network intrusion detection.

The remainder of this paper is organized as follows. Section 2 studies the feature selection based on the MFO algorithm integrating with the PSO algorithm, and presents a binary conversion method for feature selection. Section 3 demonstrates a combination strategy of feature selection based on the integrated optimization algorithm and weighted KNN for the sake of improving the performance of network intrusion detection. Section 4 validates the proposed combination strategy using experiments. Section 5 concludes this paper.

2. Feature Selection Based on an Integrated Optimization Algorithm

2.1. Moth-Flame Optimization (MFO) Algorithm

In the MFO algorithm, the set of moths is defined as $M$, in which $M_i$ is the i-th moth and $M_{ij}$ is the corresponding position of the i-th moth. Additionally, $OM$ is defined as its fitness value.

$$M=\left(\begin{array}{c}{M}_1\\ ⋮\\ M_i\end{array}\right)=\left(\begin{array}{ccc}{M}_1& \cdots & M_{1j}\\ ⋮& & ⋮\\ M_{i1}& \cdots & M_{ij}\end{array}\right).$$

The set of flames is defined as $F$, in which $F_i$ is the i-th flame and $F_{ij}$ is the corresponding position of the i-th flame. Additionally, $OF$ is defined as its fitness value.

$$F=\left(\begin{array}{c}{F}_1\\ ⋮\\ F_i\end{array}\right)=\left(\begin{array}{ccc}{F}_1& \cdots & F_{1j}\\ ⋮& & ⋮\\ F_{i1}& \cdots & F_{ij}\end{array}\right).$$

The MFO algorithm can be defined as the global optimal triple shown as follows:

$$\mathrm{MFO}=\left(I,P,T\right),$$

(1)

$$I:\phi \to \left\{M,OM\right\},$$

(2)

$$P:M\to M,$$

(3)

$$T:M\to \left\{true,false\right\}.$$

(4)

The description of the MFO algorithm can then be demonstrated as follow:

$$\begin{array}{c}M=I()\hfill \\ whileT\left(M\right)isequaltofalse\hfill \\ M=P\left(M\right);\hfill \\ End\hfill \end{array}$$

Since the MFO algorithm is inspired by the lateral flight of moths, the moths are updated by the flames as follows:

$$M_i=S\left(M_i,F_j\right),$$

(5)

$$S\left(M_i,F_j\right)=D_i{e}^{bt}cos(2\pi t)+F_j{}^{‘},$$

(6)

$$D_i=\left|F_j-M_i\right|.$$

(7)

The formula for flame updating is as follows:

$$\begin{array}{cc}flame& no\end{array}=round(N-L\frac{N-1}{T}),$$

(8)

where $N$ is the number of initial flames, $T$ is total number of the iterations, and $L$ is current number of the iterations.

The flow of the MFO algorithm is described as follows:

Step 1: $M$ is initialized by Formula (2), and $OM$ is calculated according to $M$;

Step 2: The position of $M$ and $OM$ is not changed, and $F$ and $OF$ can be obtained by matching and sequencing $M$ and $OM$;

Step 3: According to Formula (8), the number of moths is calculated, and the moths and flames at the end are removed;

Step 4: The distance between the moth and its corresponding $D_i$ is calculated by Formula (7);

Step 5: The updated value of each moth is calculated by substituting $D_i$ into Formula (6);

Step 6: According to $M$, calculate $OM$;

Step 7: Judge whether the end condition is met. Otherwise, go to Step 2.

2.2. Particle Swarm Optimization (PSO) Algorithm

The PSO algorithm is inspired by the collective flight of birds. The whole bird group seems to move under the control of a center. Assuming that there is only one place in the whole area, the easiest way to find things is to move towards the nearest bird. The PSO algorithm is then proposed, which takes birds in space. Supposing it is a particle, each particle has both social cognitive ability and self-cognitive ability, social cognitive ability and the optimal solution in the whole population, self-cognitive ability, and the optimal solution of the individual to the current position. Each dimension of each particle has its own speed $V_i=\left(v_{i1},v_{i2},\dots ,v_{ij}\right)T$ and moving distance $X_i=\left(x_{i1},x_{i2},...,x_{ij}\right)T$, the formulas of updating the speed and the moving distance are as follows.

$$v_{ij}^{}=v_{ij}^{}+c_{1}rand(pbes{t}_{ij}^{}-x_{ij}^{})+c_{2}rand(gbes{t}_j^{}-x_{ij}^{}),$$

(9)

$$x_{ij}^{}=x_{ij}^{}+v_{ij}^{},$$

(10)

where learning factors $c_1$ and $c_2$ are generally between [0, 2], $rand$ belongs to [0, 1], $pbest$ is the historical optimal solution and $gbest$ is the global optimal solution.

The flow of the PSO algorithm is as follows:

Step 1: Initialization of random position, population $N$ and its velocity $V$;

Step 2: Evaluate the fitness of each particle;

Step 3: For each particle, its current fitness value is compared with its historical optimal fitness value. If it is better, it is taken as $pbest$;

Step 4: For each particle, its current fitness value is compared with the global optimal fitness value. If it is better, it is taken as $gbest$;

Step 5: Put $pbest$ and $gbest$ into Formula (9) to get the velocity $V$;

Step 6: Substituting the velocity $V$ into Formula (10) to get a new position;

Step 7: Judge whether the end condition is met, otherwise go to Step 2.

2.3. An Integrated Optimization Algorithm

The principle of the MFO algorithm is to use each moth to make spiral flight around its corresponding flame to find the optimal solution. Considering the fact that the MFO algorithm is poor in the global search ability and easy to fall into the local optimum when it is applied to the feature selection of network intrusion detection, integration with the PSO algorithm may possibly get a better global search ability. Based on this, an optimization algorithm by integrating MFO with PSO (namely PMFO in short) is proposed.

The renewal of moths in the MFO algorithm is to find the optimal solution by spiraling each moth around the flame, and each moth in MFO only converges to its corresponding flame point. So let the moth first move to the direction of the global optimal solution (because each iteration of the flame is sorted according to the fitness value from large to small, so it is the global optimal solution) and the flame corresponding to each particle (since the flame is the historical optimal solution of the first moth), and then use the Formula (6) to do the local search, so that the search range of the moth can be increased and the effect is better. The proposed PMFO algorithm is demonstrated as follows.

Compared with MFO, the position updating mode of PMFO is different. Each moth corresponds to its own speed $V_i=\left(v_{i1},v_{i2},...,v_{ij}\right)T$. The speed updating formula is as follow:

$$v_{ij}^{}=v_{ij}^{}+c_{1}rand(F_{ij}^{}-x_{ij}^{})+c_{2}rand(F_{1j}^{}-x_{ij}^{}).$$

(11)

In which $F_{ij}$ is the historical optimal solution of each moth and $F_{1j}$ is the historical optimal solution of all moths up to this generation.

The moth moves first in the direction of $F_{ij}$ and $F_{0j}$, and the updating formula is as follows:

$$M_{ij}^{}=v_{ij}^{}+M_{ij}^{}.$$

(12)

At this time, the moth has flown forward for a certain distance, and then the updated position of the moth is used. If the result of the moth updating in PMFO is directly converted into binary system, the speed impact or the distance impact will be too large, so that the moth updating will be stopped. Thus, the distance renewal of PMFO moth is changed to the following formula.

$$D_i=\left|F_i-M_i\right|/numAttribute.$$

(13)

In which $numAttribute$ is the number of features.

In order to alleviate the influence of excessive speed $V$ in PMFO, both upper limit $V_{max}$ and lower limit $V_{min}$ are set.

$M$ is the moth that flies spirally to find the best solution, with the formula as follows:

$$M_{ij}^{}=D_i\times e^{bt}cos(2pt)+F_{ij}^{}.$$

(14)

Figure 1 provides the flow chart of proposed PMFO algorithm.

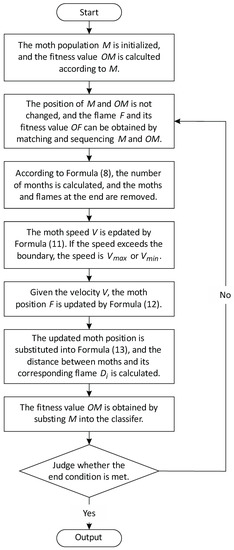
Figure 1. Flow chart of the proposed integrated optimization algorithm.

As is shown in Figure 1, the proposed integrated optimization algorithm is described as follows.

Step 1: The moth population $M$ is initialized, and OM is calculated according to $M$;

Step 2: The position of $M$ and $OM$ is not changed, and $F$ and its $OF$ can be obtained by matching and sequencing $M$ and OM;

Step 3: According to Formula (8), the number of moths is calculated, and the moths and flames at the end are removed;

Step 4: The moth speed $V$ is updated by Formula (11). If the speed exceeds the boundary, the speed is $V_{max}$ or $V_{min}$;

Step 5: Given the velocity $V$, the moth position $F$ is updated by Formula (12);

Step 6: The updated moth position is substituted into Formula (13), and the distance between moth and its corresponding $D_i$ is calculated;

Step 7: The fitness value $OM$ is obtained by substituting M into the classifier;

Step 8: Judge whether the end condition is met, otherwise go to Step 2.

2.4. Binary Conversion Method for Feature Selection

Since the proposed integrated optimization algorithm cannot be applied in the field of feature selection, a binary conversion method is proposed for feature selection. To do this, the following two principles are needed for the population initialization and the binary conversion.

• Population initialization
  In a binary algorithm, the value of particle feature can only be 0 or 1, in which 1 means the feature is selected, and 0 means not selected. Generally, 50% probability of feature selection is a common method of population initialization. The initialization function of selected particles is as follow.

  $$M_{ij}=\{\begin{array}{l}1rand()>0.5\\ 0otherwise\end{array}.$$

  (15)
• Binary conversion
  In order to solve the position updating problem of the algorithm above in binary space [47], this paper uses sigmoid function to map the updated real value of moth to [0, 1] to realize the 0 and 1 conversion of moth position. The binary conversion formula is as follows:

  $$sig(M_{ij})=\frac{1}{1+e^{-(M_{ij})}},$$

  (16)

  $$M_{ij}=\{\begin{array}{l}1rand()>=sig(M_{ij})\\ 0otherwise\end{array},$$

  (17)

  where $M_{ij}$ is the updated position of moth, and $rand()$ is the random number between [0, 1].

Figure 2 shows the flow chart of the binary PMFO (namely BPMFO in short) algorithm.

Figure 2. Flow chart of a binary algorithm for the proposed integrated optimization algorithm.

As shown in Figure 2, the BPMFO algorithm process is described as follows.

Step 1: The moth population M is initialized by Formula (14), and $OM$ is calculated according to M;

Step 2: The position of M and $OM$ is not changed, and $F$ and its $OF$ can be obtained by matching and sequencing M and OM;

Step 3: According to Formula (8), the number of moths is calculated, and the moths and flames at the end are removed;

Step 4: The moth speed V is updated by Formula (11). If the speed exceeds the boundary, the speed is $V_{max}$ or $V_{min}$;

Step 5: Given the velocity V, the moth position $F$ is updated by Formula (12);

Step 6: The updated moth position is substituted into Formula (13), and the distance between moth and its $D_i$ is calculated;

Step 7: The updated value of each moth is calculated by Formula (14);

Step 8: Formula (16) and Formula (17) are used to convert the updated value of moth into binary;

Step 9: The fitness value OM is obtained by substituting M into the classifier;

Step 10: Judge whether the end condition is met, otherwise go to Step 2.

3. A Combination Strategy to Improve the Performance of Network Intrusion Detection

3.1. Classification Algorithms for Network Intrusion Detection

A classification algorithm is an algorithm to classify the unknown data. At present, there are many kinds of classification algorithms, but they are basically based on the known data (training set) to classify the unknown data (test set). In general, the same kind of data has similar characteristics, and different kinds of data have obvious differences. However, in special cases, some of the same kind of data have very different characteristics, and different kinds of data may have similar characteristics. Thus, how to classify the data more accurately is the goal of each classification algorithm. Currently, the commonly used classification methods for network intrusion detection are KNN, SVM, naive Bayes, and so on.

3.1.1. K-Nearest Neighbor (KNN)

The KNN algorithm classifies by measuring the distance between data. The idea of KNN is that, in the feature space of the samples, select the most similar samples. As for the KNN algorithm, all the samples selected are classified correctly, and only a few sample data close to them are related to the determination of the category. Euclidean distance or Manhattan distance is generally used in KNN.

In short, the KNN algorithm classifies unknown data according to more data in objects, rather than a single sample.

3.1.2. Support Vector Machine (SVM)

The SVM is a two-classification model which is used to find a high-dimensional plane with the largest interval to solve the classification problem of a low-dimensional plane.

• When the samples are linearly separable, SVM can be learned by the method of maximum hard interval.
• When the samples are approximately linearly separable, SVM can be learned by the method of maximum soft interval.
• When the samples are not separable linearly, SVM can be learned by the method of maximum core technology and soft interval.

3.1.3. Naive Bayes

Compared with other classification algorithms, Naive Bayes classification algorithm is relatively simple. Its basic idea is to find out the probability of each category under this condition for the known data to be classified, so as to determine the category of the data.

The naive Bayes classification algorithm can be divided into following three stages.

• In the stage of preparing for classification, naive Bayes relies on attributes to distinguish categories, so this stage is a necessary stage for naive Bayes. Its main task is to determine the characteristics of attributes according to specific data sets, integrate the samples of the data sets to be classified by people, and integrate the data sets into training sets. This stage will have a crucial impact on the following classifier classification.
• In the training stage, the main purpose is to generate a classifier, calculate the frequency of data appearing in the training set and the probability evaluation of each tag by the classification of feature attributes, and then record the calculation. This stage is a mechanical stage, which can be completed by the program.
• In the application stage, classifiers are used to classify items. This stage is also a mechanical stage, which is completed by the program.

3.2. A Combination Strategy with Weighted KNN

Weighted KNN is used to calculate the Euclidean distance between the samples to be classified and the training samples, to add a weight to each dimension of the distance formula in KNN, to find the KNN samples closest to the samples to be classified, and then to judge the categories of the samples to be classified according to the categories of the KNN samples. In short, most of the samples belong to a certain category, then the samples also belong to a certain category.

Suppose the training set is $S=\left\{S_1,S_2,\dots ,S_m\right\}$, then $S_i=\{S_{i1},S_{i2},\dots ,S_{in}\}(S_i\in S)$. Assume that the number of samples to be classified is g, then $C=\left\{C_1,C_2,\dots ,C_g\right\}$ and $C_i=\{C_{g1},C_{g2},\dots ,C_{gn}\}(C_i\in C)$. Additionally, the set of distance weights is K, and $K_i=\{K_{11},K_{i2},\dots ,K_{qn}\}(K_i\in K)$. The distance weighting formula is calculated as follows:

$$distance\left(S_m,C_g,K_q\right)=\sqrt{{\displaystyle \sum _{i=0}^n{K}_{qi}(S_{mi}-C_{gi}{)}^2}}.$$

(18)

In the original data set $C=\left\{s_1,s_2,\dots ,s_g\right\}$, $s_1,s_2,\dots ,s_g$ are features of the original data set. $S_1=\left\{s_1,s_2,\dots ,s_g\right\}$ are selected by feature selection with $S_1\in S$. At the same time, the original data set $S=\left\{s_1,s_2,\dots ,s_n\right\}$ is substituted into the weighted KNN. The result of feature selection is $K=\left\{k_1,k_2,\dots ,k_n\right\}$, and the result of weight selection of weighted KNN is $S_1=\left\{s_1,s_2,\dots ,s_m\right\}$. Finally, the new feature subset $S_1$ selected from feature selection is substituted into the weighted KNN of weight $K_i$ to get the final classification result. The parameters of weighted KNN are combined with the results of feature selection based on the proposed integrated optimization algorithm, aiming at improving both the efficiency and the accuracy of network intrusion detection.

As for the combination strategy of feature selection based on the proposed integrated optimization algorithm and weighted KNN, the weight optimization of the weighted KNN and feature selection are independent of each other. When the result of feature selection or weighted KNN weight changes, the result of the other will not be affected. The procedure of the proposed combination strategy is then demonstrated in Figure 3.

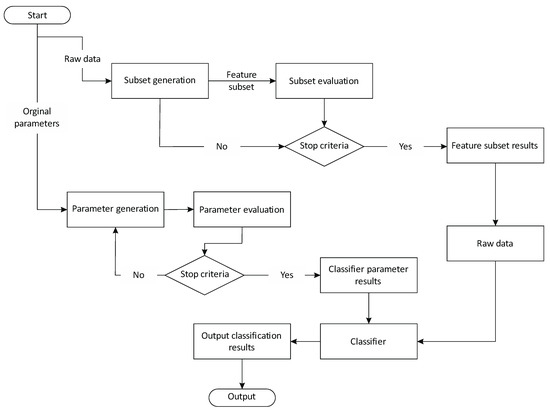
Figure 3. The procedure of proposed combination strategy.

4. Experimental Results

4.1. Method Validation of MFO-Optimized Weighted KNN

4.1.1. Data Sets for Network Intrusion Detection

Network intrusion detection system infers whether unknown access belongs to attack access through known data. The commonly used data set is KDD Cup 99 data set [48]. Each piece of data is defined as a data sequence from the beginning to the end of a connection. The whole data set can be roughly labeled as attack and normal. There are 39 kinds of abnormal attack access, 22 kinds of them in the training set, and 17 unknown attacks in the test set.

This paper uses about 10% of the data in the KDD Cup 99 data set. 4000 and 8000 data are extracted, half of which are classified as the training set and the other half of which are classified as the test set. The attack types are labeled as anomaly, and other data types are labeled as normal.

This paper first pre-processes the data set to 0–1 standardized as follow:

$$v^{\prime }=\frac{v-m_A}{M_A-m_A},$$

(19)

where V is the current value, $m_A$ is the minimum value, $M_A$ is the maximum value, and $v^{\prime }$ is the updated value.

4.1.2. Experimental Results and Analysis

Take the MFO algorithm, the PSO algorithm, and the grey wolf optimizer (GWO) algorithm for the experiments, and the maximum number of iterations is 50. The parameter settings for validation are described in Table 1.

Table 1. Parameter settings for validation.

Algorithm	Parameter Setting
MFO-KNN	b = 1; K = 10
PSO-KNN	$C_1,C_2$ = 2; Vmax = 1; Vmin = −1; K = 10
GWO-KNN	K = 10
KNN	K = 10
SVM	Gamma = 1.0
Naïve Bayes	None

Table 2 and Table 3 provide the results of 20 simulation experiments, in which MFO-KNN, PSO-KNN, and GWO-KNN include the average fitness value, running time and standard deviation. The basic classifiers include KNN, SVM, and naive Bayes, which have only the average fitness value and running time, since they do not improve weights.

Table 2. Experimental results of 4000 data sets.

	Average Fitness	Running Time (s)	Standard Deviation
MFO-KNN	0.940397	81.455	0.002536
PSO-KNN	0.923469	135.918	0.005140
GWO-KNN	0.939882	133.491	0.003167
KNN	0.925067	0.764	-
SVM	0.919361	0.594	-
Naïve Bayes	0.608596	0.109	-

Table 3. Experimental results of 8000 data sets.

	Average Fitness	Running Time (s)	Standard Deviation
MFO-KNN	0.968548	362.971	0.002122
PSO-KNN	0.958741	607.764	0.002986
GWO-KNN	0.955524	616.583	0.002622
KNN	0.937934	1.821	-
SVM	0.939921	1.439	-
Naïve Bayes	0.654419	0.204	-

It can be seen from Table 2 that, when both the test set and the training set are 2000, the average fitness value of MFO-KNN is higher than that of PSO-KNN and GWO-KNN, the running time is shorter than that of PSO-KNN and GWO-KNN, and the standard deviation is lower than that of PSO-KNN and GWO-KNN.

It can be seen from Table 3 that, when both the test set and the training set are 4000, the average fitness value of MFO-KNN is higher than that of PSO-KNN and GWO-KNN, the running time is shorter than that of PSO-KNN and GWO-KNN, and the standard deviation is lower than that of PSO-KNN and GWO-KNN.

Figure 4 and Figure 5 then show the fitness curves for MFO-KNN, PSO-KNN, and GWO-KNN of different data sets.

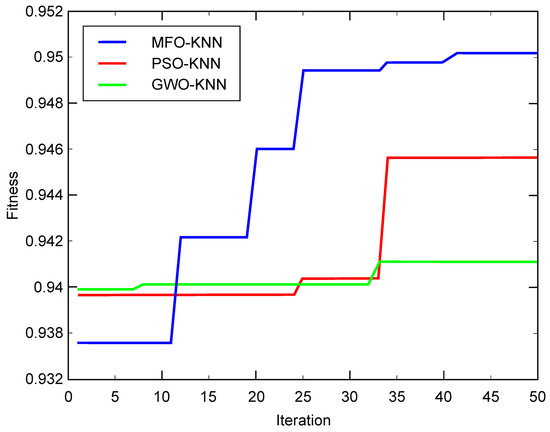
Figure 4. Fitness curve of 4000 data sets.

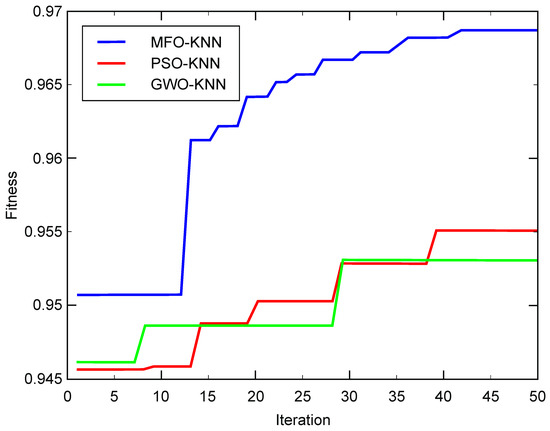
Figure 5. Fitness curve of 8000 data sets.

The convergence curves of the fitness values shown in Figure 4 and Figure 5 indicate that, the convergence effect of the MFO-KNN algorithm is better than that of the PSO-KNN algorithm and that of the GWO-KNN algorithm.

In summary, the MFO-optimized weighted KNN is superior to PSO-optimized weighted KNN and GWO-optimized weighted KNN in terms of solving ability, stability, and running time when applied to network intrusion detection.

4.2. Test Functions for the Integrated Optimization Algorithm

In order to validate the integrated optimization algorithm proposed in this paper, the PMFO algorithm and the MFO algorithm are considered to be applied in the test functions. Therefore, eight test functions are selected in this paper, four of which are unimodal test functions and another four are multimodal test functions [49]. Each function runs 20 times, and each iteration is 500 times. Then the performance of the algorithm is evaluated from two dimensions of average value and variance. Table 4 provides parameter setting of the validated algorithms.

Table 4. Parameter setting of the validated algorithms.

Algorithm	Parameter Setting
PMFO	C1, C2 = 2; b = 1; Vmax = 1; Vmin = −1
MFO	b = 1

Table 5 shows four unimodal functions as the test functions. Table 6 provides the results of unimodal test functions shown in Table 5.

Table 5. Unimodal test functions.

Test Function	Dimension	Definition Domain	Minimum Value
$f_1(x)={\displaystyle \sum _{i=1}^n{x}_i^2}$	20	(−100, 100)	0
$f_2(x)={\displaystyle \sum _{i=1}^n\left|x_i^{}\right|}+{\displaystyle \prod _{i=1}^n\left|x_i^{}\right|}$	20	(−10, 10)	0
$f_3(x)={\displaystyle \sum _{i=1}^n{([x_i^{}+0.5])}^2}$	20	(−100, 100)	0
$f_4(x)={\displaystyle \sum _{i=1}^{n}i{x}_i^4+random(0,1)}$	20	(−10, 10)	0

Table 6. Results of unimodal test functions.

Test Function	Algorithm	Average Value	Variance
$f_1(x)$	PMFO	2.3425 $\times {10}^{-14}$	1.2319 $\times {10}^{-13}$
	MFO	3.6716 $\times {10}^{-13}$	5.9147 $\times {10}^{-13}$
$f_2(x)$	PMFO	5.1893 $\times {10}^{-9}$	3.0818 $\times {10}^{-9}$
	MFO	7.8062 $\times {10}^{-9}$	9.2393 $\times {10}^{-9}$
$f_3(x)$	PMFO	0.082636	0.209585
	MFO	0.038062	0.043858
$f_4(x)$	PMFO	0.090248	0.050483
	MFO	0.108808	0.044769

As shown in Table 5, four functions are unimodal functions, in which the function dimension is fixed to 20, the definition domain of $f_1(x)$ and $f_3(x)$ is (−100, 100), and the definition domain of $f_2(x)$ and $f_4(x)$ is (−10, 10), and there is no local optimal value.

As is indicated in Table 6, the average value of MFO in the function $f_1(x)$ is 15.67 times of PMFO, the variance is 4.8 times; the average value of MFO in the function $f_2(x)$ is 1.5 times of PMFO, the variance is 3 times; the average value of PMFO in the function $f_3(x)$ is 2.17 times of MFO, the variance is 4.78 times; the average value of PMFO in the function $f_4(x)$ is 0.83 times of MFO, and the variance is 1.23 times.

Table 7 lists four multimodal test functions for validation, and Table 8 provides the results of multimodal test functions shown in Table 7.

Table 7. Multimodal test functions.

Test Function	Dimension	Definition Domain	Min. Value
$f_5(x)={\displaystyle \sum _{i=1}^n\left[x_i^2-10\cos (2\pi x_i)+10\right]}$	20	(−100, 100)	0
$f_6(x)=20-20\exp \left(-0.2\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n{x}^2}}\right)$	20	(−500, 500)	0
$f_7(x)=\frac{1}{4000}{\displaystyle \sum _{i=1}^n{x}_i^2-{\displaystyle \prod _{i=1}^n\cos (\frac{x_i}{\sqrt{i}})}}+1$	20	(−50, 50)	0
$\begin{array}{l}{f}_8(x)={\sin }^2(3\pi x_1)+{\displaystyle \sum _{i=1}^n{(x_i-1)}^2[1+{\sin }^2(3\pi x_1+1)]}+{(x_n-1)}^2\\ +{\displaystyle \sum _{i=1}^{n}u(x_i,5,100,4)}\\ u(x,a,k,m)=\{\begin{array}{ccc}k(x-a)& x>a& \\ 0& -a<x<a& \\ k(x+a)& x<-a& \end{array}\end{array}$	20	(−50, 50)	0

Table 8. Results of multimodal test functions.

Test Function	Algorithm	Average Value	Variance
$f_5(x)$	PMFO	0.1543	3.176
	MFO	7.7671	6.176
$f_6(x)$	PMFO	8.6771 $\times {10}^{-8}$	5.7615 $\times {10}^{-6}$
	MFO	2.0415 $\times {10}^{-7}$	1.7511 $\times {10}^{-7}$
$f_7(x)$	PMFO	0.009523	0.208581
	MFO	0.077749	0.171080
$f_8(x)$	PMFO	0.001649	0.005124
	MFO	0.004395	0.002523

As shown in Table 7, four functions are multimodal functions, in which the function dimension is fixed to 20, the definition domain of $f_5(x)$ is (−100, 100), the definition domain of $f_6(x)$ is (−500, 500) and the definition domain of $f_7(x)$ and $f_8(x)$ is (−50, 50), and there is no local optimal value.

As is indicated in Table 8, the average value of MFO in the function $f_5(x)$ is 50.33 times of PMFO, the variance is 1.94 times; the average value of MFO in the function $f_6(x)$ is 2.35 times of PMFO, the variance is 0.03 times; the average value of MFO in the function $f_7(x)$ is 8.16 times of PMFO, the variance is 0.82 times; the average value of MFO in the function $f_8(x)$ is 2.67 times of PMFO, and the variance is 0.49 times.

It can be concluded from the experimental results above that, in the unimodal functions $f_1(x)$, $f_2(x)$, $f_3(x)$ and $f_4(x)$, solving ability and stability of both the PMFO algorithm and the MFO algorithm are almost the same, and in the multimodal test functions $f_5(x)$, $f_6(x)$, $f_7(x)$, and $f_8(x)$, the PMFO algorithm is superior to the MFO algorithm in solving ability, but inferior to the MFO algorithm in the stability.

4.3. Binary Simulation Experiments for Feature Selection

In this paper, the UCI data set is considered to validate the BPMFO algorithm. Six data sets from UCI [50] are used, including Glass, Breast, Abalone, Wine, Iris, and Ecoli, which are shown in Table 9.

Table 9. UCI data sets for validation.

Data Set	Number of Data	Number of Categories	Number of Features
Glass	214	6	9
Breast	699	2	11
Abalone	4177	29	8
Wine	178	3	13
Iris	150	3	4
Ecoli	336	8	8

Because of the missing data in the Breast data set, this experiment considers deleting the missing data, and other data sets use the original data set. Two optimization algorithms, that are BPMFO and Binary MFO (namely BMFO in short) are used in the experiment. They are classified by SVM, and the kernel function of SVM is Gaussian function. The population of the algorithms is 10, and the number of iterations is 20. The cross-validation method chooses k-fold cross validation, with the value of k being 3, and the number of iterations is 20. Table 10 provides parameter setting of the validated algorithms.

Table 10. Parameter setting of the validated algorithms.

Algorithm	Parameter Setting
BPMFO	$C_1,C_2$ = 2; b = 1; Vmax = 1; Vmin = −1
BMFO	b = 1

The algorithms are evaluated from two aspects of average fitness value and filtering redundancy feature. Table 11 provides the comparison results of six data sets from UCI shown in Table 9.

Table 11. Comparison results of UCI data sets.

Data Set	Algorithm	Before Feature Selection	After Feature Selection	Fitness Value
Glass	BPMFO	9	2	0.797978
	BMFO	9	4	0.782778
Breast	BPMFO	11	4	0.966704
	BMFO	11	2	0.924271
Abalone	BPMFO	8	3	0.265281
	BMFO	8	3	0.262053
Wine	BPMFO	13	5	0.943396
	BMFO	13	6	0.934579
Iris	BPMFO	4	1	0.941945
	BMFO	4	1	0.941945
Ecoli	BPMFO	8	4	0.893901
	BMFO	8	6	0.893589

The BPMFO algorithm retains features 1 and 8 in the Glass data set, features 2, 3, 5, and 8 in the Breast data set, features 3, 6, and 8 in the Abalone data set, features 4, 7, 10, 12, and 13 in the Wine data set, feature 3 in the Iris data set, and features 1, 2, 4, and 6 in the Ecoli data set.

The reserved features of PMFO in Glass data set are 1, 3, 4, and 5, the reserved features in Breast data set are 3 and 4, the reserved features in Abalone data set are 3, 6, and 7, the features retained in the Wine data set are 1, 4, 6, 9, 12, and 13, the feature retained in the Iris data set is 3, and the features retained in the Ecoli data set are 1, 2, 4, 5, 6, and 7.

As is indicated in Table 11, in terms of fitness value, the fitness value of BPMFO in Glass data set is 0.0152 higher than that of BMFO, 0.042433 higher in Breast data set, 0.003228 higher in Abalone data set, 0.008817 higher in Wine data set, and 0.000312 higher in Ecoli data set. Note that the fitness value of BPMFO in the Iris data set is the same as that of BMFO.

It can be concluded from the experimental results above that, compared to the BMFO algorithm, the BPMFO algorithm has a certain improvement in solving ability, and has a significant improvement in eliminating redundant features and selecting features with a high contribution, which presents a practical value in feature selection.

4.4. Validation of The Combination Strategy

4.4.1. Selection of KNN Weights

In this section, the parameters of KNN are the same as PMFO optimizing KNN in Section 4.3 under the condition of 8000 data sets, and the experiment runs for 50 times. The average value of KNN weight for 50 times is then calculated and applied to the experiment. Table 12 is the weight table obtained from the experiment.

Table 12. Weight of each feature.

Feature	Weight	Feature	Weight
1	5.619589	21	3.658905
2	9.650791	22	4.694852
3	4.282662	23	7.443937
4	6.494251	24	2.886449
5	8.390892	25	2.702098
6	7.107178	26	6.152995
7	5.752698	27	2.928758
8	3.011028	28	7.309848
9	2.883600	29	5.841692
10	2.733738	30	9.088569
11	4.100507	31	5.612757
12	5.615577	32	4.074626
13	6.363829	33	2.119303
14	3.248322	34	4.254331
15	4.471637	35	5.930137
16	5.707215	36	2.171261
17	5.514407	37	5.624371
18	5.487701	38	6.962610
19	4.147335	39	7.559233
20	4.782790	40	4.223209

4.4.2. Selection of Feature Subsets

In this paper, the feature selection is applied to network intrusion detection. Both the occurrence times for feature numbers and the frequency of each feature are calculated.

Table 13 provides the occurrence times for feature numbers, and Table 14 gives the frequency of each feature.

Table 13. Occurrence times for feature numbers.

Feature Number	5	7	8	9	10	11	12	13	14
Occurrence Time	1	3	4	7	14	11	5	3	1

Table 14. Frequency of each feature.

Feature	Frequency	Feature	Frequency
1	9	21	6
2	37	22	28
3	17	23	29
4	8	24	11
5	10	25	10
6	8	26	8
7	10	27	12
8	5	28	14
9	17	29	8
10	11	30	14
11	9	31	19
12	9	32	12
13	13	33	15
14	9	34	17
15	9	35	42
16	6	36	5
17	6	37	14
18	10	38	9
19	5	39	13
20	5	40	7

As is indicated in Table 13, the number of features with the highest occurrence time is 10. As for Table 14, these 10 features with the highest frequency are selected, which are respectively the feature 2 with frequency 37, the feature 3 with frequency 17, the feature 9 with frequency 17, the feature 22 with frequency 28, the feature 23 with frequency 29, the feature 28 with frequency 14, the feature 31 with frequency 19, the feature 33 with frequency 15, the feature 34 with frequency 17, and the feature 35 with frequency 42. To sum up, the feature selection is 2, 3, 9, 22, 23, 28, 31, 33, 34, 35.

4.4.3. Simulation Experiments

For the purpose of simulation, four groups of comparative experiments are considered. In Group 1, both KNN weight selection and feature selection are used; in Group 2, only KNN weight selection is used; in Group 3, only feature selection is used; in Group 4, ordinary KNN is used and feature selection is not used.

The data set includes 20,000 data randomly selected from the original data set. Of those, 10,000 data are randomly selected for each experiment, half of which are training sets, and the other half of which are test sets. Each experiment is run 20 times. The experimental results are measured from two aspects including the average fitness value and the average running time.

The details of the simulation test results are demonstrated as follows:

In Group 1, the selected features are 2, 3, 9, 22, 23, 28, 31, 33, 34, 35, and the weights of KNN are 9.65, 4.28, 2.88, 4.69, 7.44, 7.31, 5.61, 2.11, 4.25, and 5.93.

In Group 2, all features are selected, and KNN weight is the result of weight optimization explained in this paper.

In Group 3, the selected features are 2, 3, 9, 22, 23, 28, 31, 33, 34, 35, and KNN weights are all 1.

In Group 4, all features are selected, and KNN weights are all 1.

Figure 6 provides the experimental results of running 20 times, and Table 15 shows the simulation experimental results for the average fitness values and the average running times.

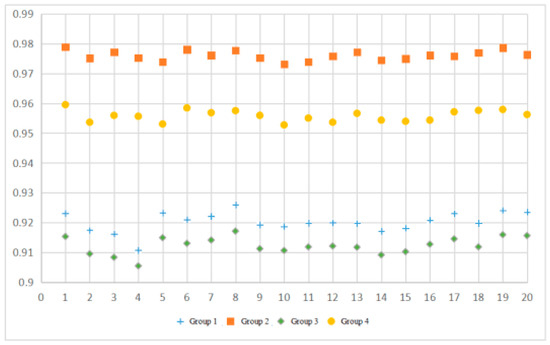
Figure 6. Experimental results of running 20 times.

Table 15. Simulation test results.

	Group 1	Group 2	Group 3	Group 4
Average fitness value	0.920181	0.976065	0.913096	0.955825
Average running time (ms)	8228	18,212	8154	18,150

As is shown in Figure 6 and Table 15, there are the results as follows:

• In terms of running time, Group 1 is 9884 ms faster than Group 2, 10,622 ms faster than Group 4, roughly the same as Group 3
• In terms of accuracy, Group 1 is 0.007085 higher than Group 3, Group 2 is 0.02024 higher than Group 4, Group 1 is 0.055884 lower than Group 2, and Group 1 is 0.035644 lower than Group 4.
• In terms of weighted KNN, Group 1 is 0.007085 higher than Group 3, and Group 2 is 0.02024 higher than Group 4.
• In terms of feature selection, Group 1 is 0.055884 lower than Group 2, Group 1 is 0.035644 lower than Group 4, but Group 1 is 9884 ms faster than Group 2, 10,622 ms faster than Group 4.

As for the same data set, Group 2 using weighted KNN and not using feature selection is higher than Group 4 using ordinary KNN but not using feature selection, higher than Group 1 using both feature selection and weighted KNN, higher than Group 3 using feature selection but not using weighted KNN.

It can be concluded from the experimental results above that the weighted KNN can greatly increase the efficiency at the expense of a small amount of the accuracy. In summary, the application of the proposed integrated optimization algorithm to promote both the feature selection and the weight of weighted KNN can significantly improve the accuracy of network intrusion detection, and almost equally in terms of efficiency.

5. Conclusions

In view of the problem that the MFO algorithm converges too fast and easily falls into local optimum, this paper first proposes an integrated optimization algorithm, namely the PMFO algorithm, which utilizes the MFO algorithm with a strong local search ability, and integrates the PSO algorithm with a speed updating method to make the individual population move along the direction of a global and historical optimum and increase the global convergence. Considering the characteristics of a large amount of data, high data dimension, and low recognition rate in current network intrusion detection, this paper then applies the proposed integrated optimization algorithm to classifier optimization and feature selection of network intrusion detection.

In order to improve both the efficiency and the accuracy of network intrusion detection, this paper aims to propose a combination strategy of feature selection based on the integrated optimization algorithm and weighted KNN, which combines the result of feature selection with the result of classifier optimization. This paper then combines the results of classification optimization of weighted KNN with those of feature selection, and apply them to network intrusion detection. The simulation results show that the combined strategy can effectively improve the performance of network intrusion detection.

In this paper, only KNN is considered to improve the performance of network intrusion detection. However, SVM and naive Bayes might also be selected for this purpose. In the future, SVM and naive Bayes will be utilized for parameter optimization.