Abstract
In this paper, a novel method to quantitatively analyze insulator degradation in a single layer solenoid is proposed. The suggested method employs renormalization of scattering parameters to efficiently detect changes of permittivity in a degraded solenoid. Firstly, a transmission line model, including a locally degraded part in the insulator, was developed, and it was determined that the phase information of the transmission parameter was very informative to check the permittivity change in the transmission line. To check the workability of this idea in a solenoid, a 30-turn single-layer solenoid was designed and fabricated, and 51 degraded states for mimicking insulation deterioration in each turn were introduced by installing additional insulator rings, which increased local relative permittivity. The phase data of the measured transmission parameter turned out to be useful for quantifying changes of the insulator in the solenoid. To maximize the detectability, the measured scattering parameters were renormalized with different reference impedances, which was very useful for detecting degradation in the transmission parameter. In this paper, detailed procedures for quantitatively analyzing degradation of an insulator are proposed and we verify that the suggested renormalization technique is very promising for effectively evaluating the degradation of a solenoid.
1. Introduction
Currently, there are 441 nuclear reactors in operation in 30 countries worldwide, which supplied approximately 10.2% of the global electricity in 2017 [1]. According to the International Atomic Energy Agency (IAEA) report, in 2019, 256.3 GW(e) of net capacity, representing more than 65% of power reactors, had been in operation for over 30 years. Long term operation and aging management programs are being implemented to increase nuclear power reactors globally to ensure continued safe and sustainable operations [2]. Each country operates by designating the overhaul period, equipment maintenance, and sensor calibration and replacement according to regulatory standards. However, unnecessary calibration and replacement occurs during the maintenance period due to the absence of a diagnostic model, requiring many human resources. Moreover, economic loss due to risk of malfunction, aging accumulation, and long maintenance periods is enormous [3]. Therefore, diagnostic models for various nuclear power plants (NPP) have been extensively studied [4,5,6,7,8].
The solenoid operated valve (SOV) is one of the elements widely used in nuclear power plants. Although the structure is a simple fundamental element, it is important when operating a nuclear power plant and, in particular, for controlling the flow rate [9]. The SOV can be divided into electrical parts, including windings and cores, and mechanical parts, including valves and plungers. The electrical parts are particularly essential because the solenoid generates primary power by receiving a signal from the control unit. A severe failure, such as a short circuit between windings, can occur due to a soft failure such as degradation of the winding in the dielectric due to aging. In other words, estimating the deterioration of the insulator in a solenoid is very important to the diagnostics and prognostics of the solenoid valve. To detect and classify the states of soft failure in the winding, both modeling and experimental studies about the aging effect of the solenoid have been conducted. Recently, an experimental analysis reported on the relationship between solenoid impedance and aging effects in insulation coating using an accelerated deterioration [10,11,12]. The circuit model-based approach can be powerful for estimating operation torque and the corresponding waveform of current; however, it has shortcomings for analyzing and detecting insulator degradation because it uses only equivalent lumped elements.
In this paper, a diagnostic study on the local degradation of an insulator in a single-layered solenoid winding based on measured two-port scattering S-parameters is conducted to overcome the shortcomings of a circuit-based approach. Assuming that a solenoid could be similar to a transmission line, a locally degraded insulator was modeled to derive the formulas so that the phase information of the renormalized transmission parameter could be effectively used to estimate the degradation of the insulator. These formulas were applied to the single-layered solenoid in which additional ring-shaped insulators were installed to mimic the degradation of the insulator. The appropriately renormalized transmission parameter successfully estimated the changes in the permittivity of the solenoid.
The remainder of this paper is organized as follows: In Section 2, the electrical model for a transmission line with local degradation is described, and the approximated formulas for the phase in on the transmission parameter are suggested; in Section 3, the single-layer solenoid is designed and fabricated, and the sheath rubber rings are installed on the bobbin of the solenoid for mimicking the local degradation of the insulator, the whole measurement schemes are presented, and the interface de-embedding process is also described; in Section 4, the results of the quantitative analysis for the local degradation are shown; and finally, the conclusion and summary of the suggested diagnostic method are given.
2. A Transmission Line Model Including a Locally Degraded Part Inside
Figure 1a shows a lumped circuit parameter model for a solenoid where Ls indicates the equivalent series inductance of the solenoid, Rs indicates the conductor’s resistance, and Cp and Ri are parallel capacitance and parallel resistance, respectively. This model has been used to estimate reactance [10,13,14], and induced torque with a plunger from measured voltage and current [15] in a low-frequency range. However, it is not suitable for estimating the distributed degradation of the insulator inside a solenoid due to the limit of lumped element modeling itself.
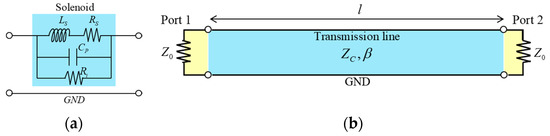
Figure 1.
(a) Lumped element model for a solenoid in low frequency range (under the second resonance frequency); (b) Finite length transmission line model emphasizing distribution elements.
A solenoid can indeed be quite different from a transmission line in that, most importantly, a transmission line repeats the same distributed elements as it travels from port 1 to port 2, as illustrated in Figure 1b, while a solenoid does not. It seems, however, that we could make a rough assumption that changes of permittivity in a solenoid could be estimated in the same way as the changes in a transmission line [16] are estimated using the S-parameters. Note that the signals in a solenoid travel anyway just as the signals in a transmission line travel, including the changes in permittivity inside the solenoid. Furthermore, it is promising to note that the distributed elements in a solenoid, due to the regular winding in the solenoid, are also similarly repeated as the signal travels, similar to the signal in a transmission line. Figure 1b illustrates a distributed model for a transmission line where ZC is the characteristic impedance of the transmission line, β is a propagation constant, and Z0 is the reference impedance of the measurement equipment. In the next section, assuming that the permittivity change in a solenoid could be similar to the permittivity change in a transmission line, the S-parameter formulas with a discontinuous parameter in the transmission line, to mimic the deterioration of the insulator inside, is developed.
2.1. Discontinuous Transmission Line Model Mimicking Deterioration of the Insulator
A local permittivity-degraded area in a winding can be modeled by a finite line with different electrical characteristics. Figure 2 shows a transmission line consisting of the following three sectionalized parts: area 1 (length l1, characteristic impedance ZC, and phase constant β) and area 3 (length l3, characteristic impedance ZC and phase constant β) are in a healthy state, and area 2 (length l2, characteristic impedance Z’C and phase constant β’) indicates the degraded part. That is, the pink area in the diagram indicates area 2, where the insulator locally deteriorates with the prime symbols. The total ABCD parameter with ‘t’ in the superscript can be calculated by multiplying three ABCD matrices in sequence as Equation (1) [17].
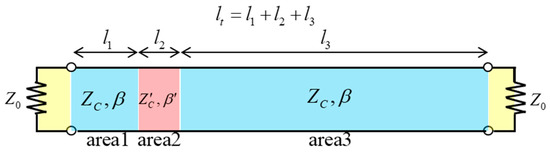
Figure 2.
Discontinuous transmission line model. The pink part is introduced for the degraded insulator, and the two sky blue parts are in healthy state.
Each element in the total ABCD matrix is expressed as Equation (2), and the total S-parameters, , can be represented as Equation (3) [17]. In the next two sections, the effect of area 2 on the total S-parameters is addressed in terms of the total change in permittivity.
2.2. Changes in Permittivity of the Transmission Parameter
Equation (4) shows , which was obtained from Equations (2) and (3) [17]. Assuming and to be real (negligible loss tangent), the phase of is also described as Equation (5).
Assuming , the phase of the transmission parameter could be reduced as Equation (6). Moreover, if , the phase of S21 is linearly decreased as frequency increases as in Equation (7a). For the healthy transmission line only, the phase of S21 can be as in Equation (7b). If the characteristic impedance ZC is not matched to a reference impedance Z0, the trace of the phase in S21 shows local fluctuations.
Equations (7a) and (7b) indicate that phase difference can be monitored with a locally degraded section in the transmission line, which could be used to diagnose the degradation of the solenoid. From the comparison of two phases, the discontinuous factor could be calculated as in Equation (8). Note that we assumed to calculate the phase difference of the two transmission parameters.
2.3. Renormalization Technique of an S-Parameter
From the previous section, we notice that the transmission S-parameter, which is measured with 50 Ω reference impedance, needs to be transformed to the S-parameter referenced for a suitable impedance depending on the device under test. This transformation can be implemented through the renormalization technique, which has been well established in the radio frequency (RF) field, especially for S-parameter reconstruction [18,19,20].
Figure 3 shows the concept of changing the termination impedance of an S-parameter. Figure 3a shows the S-parameter obtained from the measurement equipment, which is referenced to Z0, and Figure 3b shows the renormalized S-parameter when terminated with Znew. Basically, the S-parameter is one of the network parameters, which is dependent on the reference (termination) impedance, but the Z-parameter is not changed by the termination impedance. The relationship between those two parameters is expressed in Equations (9a) and (9b), where G and F are the termination impedance matrix and the real part of them, respectively, and I is the identity matrix. The star is for the conjugate of complex value. In Equation (9a), S is expressed in terms of Z, and Z is expressed in terms of S, in Equation (9b).

Figure 3.
(a) Two-port S-parameter terminated by Z0; (b) The renormalized two-port S-parameter terminated by Znew.
The new S-parameter can also be defined in terms of new G and F as in Equation (10), which comes from Equation (9a). Since the Z-parameter is unique in a given network, Equation (9b) can be plugged into Equation (10), and if we make use of reflection coefficient Γ, Equation (11) can be derived [21].
That is, the conversion process of measured S-parameter to the renormalized S-parameter can be obtained using Equation (11). Note that Γ is a diagonal reflection coefficient matrix from Z0 (G) and Znew (Gnew). Znew can be selected by the designer as needed. Through this technique, the reference impedance can be matched to the characteristic impedance of the device under test.
3. Fabrication and Measurement Setup for a Prototype of Single-Layered Solenoid
In this chapter, before applying the diagnosis method based on S-parameters for an actual solenoid, a 30-turn single layer solenoid was designed and fabricated. Then, the measurement setup for the prototype solenoid was set, and how to de-embed the interface region between the vector network analyzer (VNA) and the solenoid is described. For mimicking the degraded insulator region in the winding, other additional ring-shaped insulators were introduced between each turn to increase the effective dielectric constant in the solenoid.
3.1. Structure of a Prototype Single-Layered Solenoid
A prototype single-layered solenoid was designed and fabricated to simulate the electrical part of the solenoid valve (winding and metal housing). In order to improve the reproducibility in measurement, a spiral groove was introduced in the bobbin with regular/constant interval so that the shape of the winding could be fixed without moving. The AWG (American wire gauge) 19 magnetic wire (diameter 0.91 mm), which is coated with polyamide-imide (relative permittivity 3.9–5.4, loss tangent 0.05–0.042 at 1 MHz), was used in the winding [22]. The flange and bobbin of the solenoid are made of polyoxymethylene (POM, relative permittivity ~3.8, loss tangent 0.003). The outer structure for the electrical reference and shield was fabricated using aluminum (bulk conductivity 3.8 × 107 Siemens/m).
Detailed geometries of the solenoid with its size are described in Figure 4 and Table 1, respectively. The prototype solenoid has one layer to easily locate the additional ring-type insulators, and the whole solenoid is placed in a metal housing to mimic the real solenoid valve and to also keep the high-frequency signals clean. Figure 4c shows a picture of the manufactured solenoid prototype with RF cables connected at both sides. At both ends of the windings, wires are extended to touch N-type (F) to SMA (F) adaptor, connecting VNA. The yellow dashed lines in Figure 4c indicates the interface part between the solenoid and RF cable, which should be de-embedded for the extraction of solenoid’s characteristic from the measurement data.
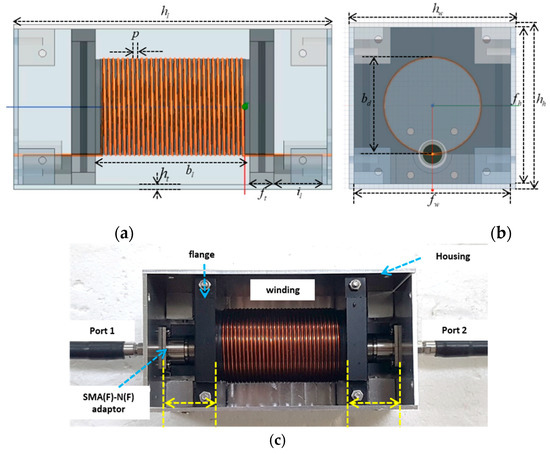
Figure 4.
Structure of prototype 30-turn single-layered solenoid. (a) Drawing in front view; (b) Drawing in port side view; (c) A picture from above with radio frequency (RF) cables connected and with upper housing removed.

Table 1.
Design parameters of the prototype single-layered solenoid.
3.2. Setup for Experimental Measurement and De-Embedding Interfaces
Figure 5a shows the experimental setup for the measurement of S-parameters of the prototype solenoid. The two red dashed lines indicate the electrical reference plane where the VNA is calibrated, and the two-port SOLT (short-open-load-thru) calibration was used for this measurement. The first interface from the solenoid was simplified to be modeled as a single wire above a conducting plane. The second interface to the VNA was modeled as a coaxial cable, as described in Figure 5b. The characteristic impedance of a single wire and coaxial cable can be effectively approximated as in Equations (12) and (13), respectively [23].
where SW represents a single wire on a plane, εeff is the effective permittivity in the background, and h is the height from the reference plane. Applying the physical data (rin = 0.57 mm, rout = 4.1 mm, h = 12.25 mm, εeff,coax = 1, and εeff,SW = 2.3), the characteristic impedance of each part can be calculated. Furthermore, the input impedance toward the VNA, as in Figure 5b [17], can be calculated as in Equation (14).
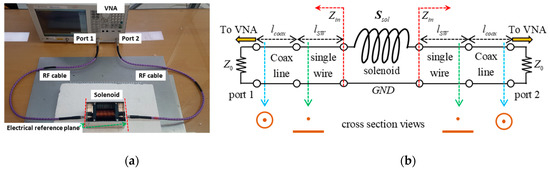
Figure 5.
Measurement for prototype solenoid. (a) A picture of the two-port measurement setup with the vector network analyzer (VNA); (b) Interfacing parts to the VNA and its cross-sectional views.
Since the Z0 in Equation (14) is the reference impedance in the VNA (50 Ω), the input impedance Zin can be calculated, of course, and reversely the Z0 can be calculated for a given input impedance value. If we need to convert Zin into the solenoid impedance, that is, if we need the input impedance Zin to be matched to the solenoid impedance, the new Z0 can be calculated using Equation (14). Since the measured S-parameter is based on the reference impedance of 50 Ω, it can be converted into new S-parameter based on the new Z0, which is calculated using Equation (14). In the equation, lcoax is 18 mm, and lSW is 14 mm, respectively, and if , then we have , as expected. Ssol in Figure 5b represents the de-embedded S-parameter of the solenoid using Equation (14). Keysight’s E5061B model of the vector network analyzer was used for the two-port measurement, and the measurement was performed with 1601 points from 1 kHz to 250 MHz on a linear scale. When measuring the solenoid’s S-parameter, the solenoid was enclosed by six sides of the aluminum harness plane for shielding, reducing interference from the outer electromagnetic environment.
3.3. Setup for Mimicking Degraded Insulator in the Prototype Solenoid
It is well known that most of the aging effect of a solenoid comes from dielectric degradation, which leads to an increase of permittivity, loss tangent, and leakage current [24,25,26,27]. The exact measurement of a loss tangent and a leakage current, however, usually requires the rated voltage and current at the nominal condition, and the rated voltage and current are large in amplitude, which could damage the electrical device. In this paper, we focus only on how to detect effective permittivity change to diagnose an aging effect in the insulator of a solenoid. One of the advantages of using S-parameter could be to use a few milliwatts in power, which would never damage the solenoid valve.
With a real physically degraded solenoid, one cannot know the exact location and the degree of degradation of the solenoid, which would be necessary to know to check the effectiveness of the proposed methodology. In this paper, ring-type insulators are installed to increase the effective perm ittivity of the insulator in which we know a priori the locations and the degree of permittivity change.
In the fabricated solenoid, sheath rubber rings with relative permittivity of 2–3 were employed between the turns in the prototype solenoid. Table 2 shows the number of rings and their locations on the solenoid. For one ring, all of the 31 locations were used one by one, and for two rings, location r3–4, r9–10, r15–16, r21–22, r27–28, r3,29 were used for installation, and so on. Note that the last one (r3,29) indicates the two rings are separately located at r3 and r29 (the red color in Table 2), while the others are consecutively installed. The number of rings and their locations in Table 2 imply both the level of effective permittivity and the scatteredness of the degradation in the insulator.

Table 2.
Number and location of sheath rubber rings installed on the solenoid. Rings are separated on the bobbin for the red-colored rings.
Figure 6a shows the cross-sectional views of a solenoid for a healthy condition (left side) and with installed ring-type insulators (right side). And Figure 6b,c shows the two pictures for the ring installation at r21, and r20–22, respectively.
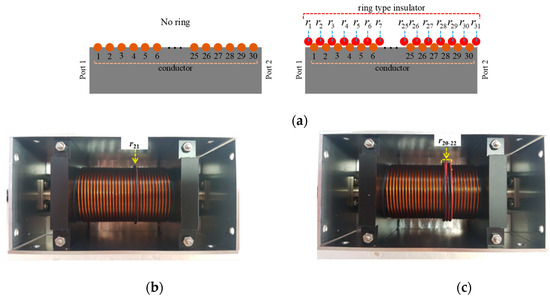
Figure 6.
Installation of ring-type insulators on the solenoid. (a) 30 conductor turns and 31-ring insulators are numbered from left and to right. (b) A picture of the solenoid when the 21st ring is installed, (c) A picture of the solenoid when three rings from the 20th to 22nd ring are installed, consecutively.
4. Detection of Insulator Degradation in Solenoid Using S-Parameters
In this chapter, we describe how to detect the degradation of the insulator in a solenoid based on the theory in Section 2. The formulas in Section 2 suggest that to transform the reference impedance of the measured S-parameters to the characteristic impedance of the solenoid (if any), and then the phase difference between the S-parameters of the degraded solenoid and the S-parameters of the healthy solenoid could be used to detect the insulator degradation in a solenoid, i.e., Equation (8) for S21/S12.
Since the solenoid is not a transmission line, its characteristic impedance could not be clearly defined but could be represented by a two-port impedance network, as described in Figure 5. To use Equation (8) for detecting the insulator degradation, one needs to find out an appropriate Zin, which most effectively transfers the signal. Figure 7 describes how to determine the appropriate Zin for the analysis.
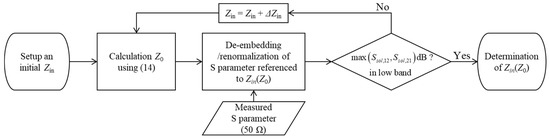
Figure 7.
Flow chart for determining Z0(Zin) to effectively renormalize scattering S-parameter for the diagnosis of insulator degradation.
Firstly, Zin is set, and then the measured S-parameters are converted with reference to the new Z0(Zin), and the solenoid S-parameters are checked if Ssol,12 is high enough in the low-frequency range. If Ssol,12 is high enough, then the final Z0(Zin) to be used is determined.
Quantitative Detection of Insulator Degradation Using Renormalized S-parameters
Figure 8 shows the magnitude and phase of the transmission S-parameter, Ssol,12, of the single-layered solenoid. One can find that the transmission characteristic has been significantly enhanced with 1500 Ω reference impedance as compared with 50 Ω reference impedance; for Ssol,12 with 1500 Ω reference impedance, the magnitude increases significantly in the low-frequency range up to ~100 MHz, and the phase decreases more linearly than Ssol,12 with 50 Ω reference impedance. This could suggest that the characteristic impedance of the single-layered solenoid would be close to 1500 Ω, not to 50 Ω in this specific frequency range up to 100 MHz. After ~100 MHz, the magnitude of Ssol,12 decreases more, but the phase keeps linearity up to ~250 MHz, as seen in Figure 8b. The Ssol,12 signals with degraded insulator (51 1–5 rings) are also shown in Figure 8 with 1500 Ω reference in various colors. Nevertheless, it is observed that the Ssol,12 signals are overlapped and become a thick trace, where it is not easy to identify each line. To identify the traces more clearly, the phase difference in Ssol,12, between the healthy and degraded solenoids, was calculated using Equation (8). Figure 9a shows the phase of Ssol,12 with 1500 Ω reference impedance, which has been wrapped between −π and π, and the nine points for the multiples of −π are indicated as sky blue colored squares. It can be seen that the curves get thicker as the frequency increases, which means that the differences are getting larger as the frequency increases.
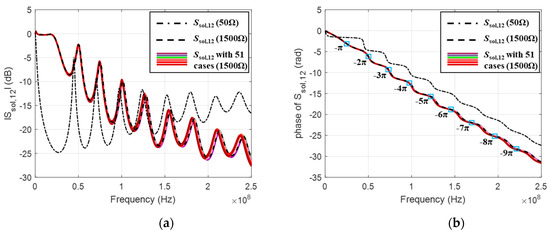
Figure 8.
Transmission parameter of one-layered solenoid, Ssol,12, referenced to 1500 Ω and 50 Ω. (a) Magnitude; (b) Phase characteristics. Colored traces are for 55 Ssol,12 data with 1–5 rings installed in the solenoid.
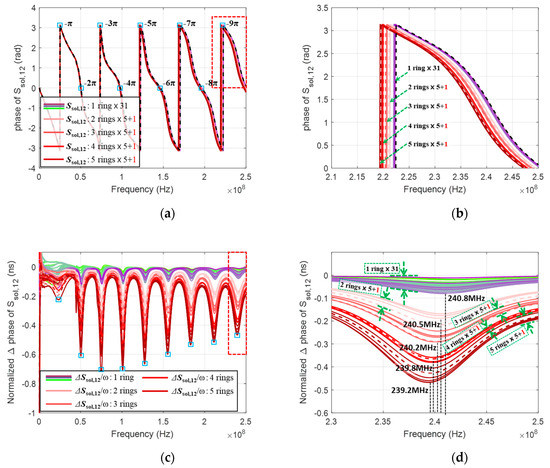
Figure 9.
(a) Phase of Ssol,12 with 1500 Ω reference impedance which has been wrapped between −π and π; (b) An enlargement of the red-dotted box in (a); (c) Normalized phase difference with respect to angular frequency using Equation (15); (d) An enlargement of the red-dotted box in (c).
Figure 9b shows an enlargement of the red-dotted box in Figure 9a, and it is clear that with more rings installed, the larger the phase difference becomes. Shown in Figure 9c is the simple difference between the two normalized phases for the healthy and degraded solenoids using Equation (15). Note that the phase has been normalized with respect to ω to minimize the frequency dependence.
where vp is phase velocity, and td is delay time due to the degraded section in the solenoid. One can see that the phase differences in Figure 9c are fluctuating even though they are normalized with respect to the frequency, especially at the local nine least peak frequencies. The local nine least peaks actually correspond to the nine sky-blue small boxes in Figure 9a and Figure 8b.
Figure 9d shows an enlargement of the red-colored box in Figure 9c. It is satisfactory to see that the thirty-one one-ring signals do not overlap with the six two-ring signals, which do not again overlap with the six 3-ring signals, which do not again overlap with six four-ring signals, which do not finally overlap with six five-ring signals. Note also that the dotted curves in Figure 9d are for the cases in which the rings are installed on the bobbin in separate turns, not consecutively, as described in Table 2. One can find that each dotted line can be grouped into the appropriate region where the total number of rings are the same. For example, the dotted curve for the two-rings (bright pink dotted curve) is grouped into the region where the five two-rings are located without overlapping with other regions. This means that the insulator degradation in a solenoid can be identified quantitatively by checking the phase difference of the solenoid transmission S-parameter with appropriate renormalization.
Note, however, that the least peak frequencies in Figure 9d are different from each other, due to the coefficient term in front of the tangent function in Equation (6). If ZC = Z0 in front of the tangent function in Equation (6), the least peak frequencies in Figure 9d could have the same values as Equation (6) predicts. Since we are using the measured S-parameters, which are converted into S-parameters with another reference impedance, the coefficient term in front of the tangent function in Equation (6) cannot be deleted in principle. However, we can try to use the phase information only without the coefficient term in front of the tangent function in Equation (6) if we pick up the phase data at multiples of π (−nπ: n = 1–9). That is, if we make use of the phase data at multiples of π only, the phase of Equation (6) will be zero anyway regardless of the coefficient term in front of the tangent function in Equation (6). It is known that the phase data can be used to calculate the effective permittivity of the insulator, and the effective permittivity in the solenoid can be calculated as Equation (16).
Figure 10a shows averaged effective permittivity data for each group of rings vs. frequency, and the variation seems to be too large to be physically meaningful. To pick up the meaningful data only, we need to use the data at the multiples of π only at the small sky-blue boxes in Figure 10a. The calculated results are summarized in Table 3, and Figure 10b illustrates the calculated effective permittivity at different frequencies, as in the small box inside. The permittivity data can be meaningful, noticing that the effective permittivity increases as the number of rings increases, but still, the data shows some dependence on frequency. The values of the effective permittivity are around 2.6–2.75 after 100 MHz.
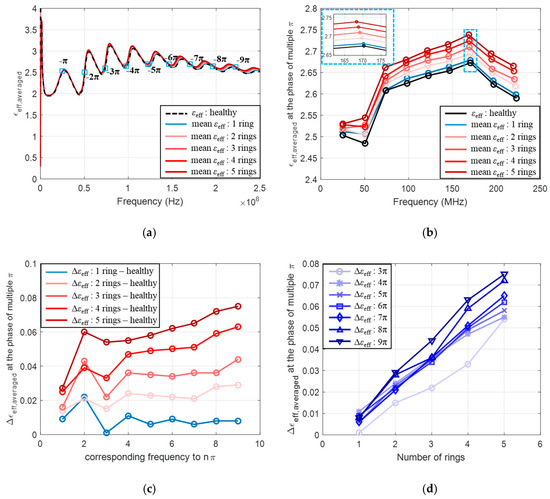
Figure 10.
(a) Calculated average effective permittivity for healthy and 1–5 rings installed using Equation (16); (b) Calculated average effective permittivity at the multiples of π; (c) Incremental (difference) average effective permittivity at the multiples of π; (d) Incremental (difference) average effective permittivity as the number of rings increases.

Table 3.
Estimated effective permittivity at the multiples of π as the number of rings increases.
The difference of the effective permittivity is shown in Figure 10c as n increases from 1 to 9, and the same data is shown in Figure 10d as the number rings increases. It is good to see that the increment of effective permittivity looks approximately proportional to the number of rings after the 3π. These graphs suggest that the insulator degradation of a solenoid could be quantitatively estimated using the proposed method in this paper. Note that in Figure 10d, n starts from 3, discarding n = 1 and 2 data, because of the obscure raw data in the low frequency region, as in Figure 9c.
5. Conclusions
In this paper, a novel method for quantitative diagnosis of insulator degradation in a solenoid is presented. First, a transmission line with a locally degraded insulator was introduced to estimate the local insulator degradation quantitatively, and it was found in the formulas that the transmission parameter (S21), especially the phase of S21, could be very useful to quantify the degradation in the insulator if the S-parameters are converted into other S-parameters with appropriate reference impedance using a renormalization technique.
For validation of a suggested idea, a single-layer solenoid with thirty turns was designed and fabricated. This prototype simulated the electrical part of a solenoid valve in the winding and housing as well. A two-port S-parameter measurement was set up, and additional sheath rubber rings were introduced to mimic the insulator degradation in the winding. The interface between measurement equipment and prototype solenoid was de-embedded, and the renormalization of S-parameters was conducted by choosing an appropriate reference impedance, which was about 1500 Ω in this specific case.
The phase difference of the renormalized S21 between healthy and degraded (with rings installed) solenoids showed clear classification into five groups (one–five rings), demonstrating the usefulness of the proposed method to quantify the degradation of the insulator. Furthermore, the increment of effective permittivity data (the difference from the healthy solenoid and the solenoid with rings installed) at multiple π clearly showed proportionality as the number of the rings increased.
This paper verified that the changes of an electrical characteristic caused by insulator degradation in a solenoid could be successfully quantified by the normalized phase difference and by the increment of effective permittivity of a solenoid using the renormalized transmission parameter (S21). We believe that the proposed method can be used for any solenoid valve to evaluate the degradation in the insulator part, including SOVs in NPP in an overhaul period. For the next step, the proposed method needs to be repeated for physically degraded solenoids. It is concluded that the suggested method would be very promising to quantitatively diagnose future degradation of a solenoid.
Author Contributions
Conceptualization, W.N.; Data curation, K.K. and J.H.; Formal analysis, W.N.; Methodology, W.N.; Project administration, J.C. and W.N.; Software, J.H.; Supervision, J.C. and W.N.; Validation, K.K.; Visualization, K.K.; Writing—original draft, K.K.; Writing—review and editing, W.N. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Nuclear Safety Research Program through the Korea Foundation of Nuclear Safety (KoFONS) using the financial resource granted by the Nuclear Safety and Security Commission (NSSC) of the Republic of Korea (no. 1805007).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| AWG | American Wire Gauge |
| GW(e) | Gigawatt electrical |
| IAEA | International Atomic Energy Agency |
| NPP | Nuclear power plant |
| RF | Radio frequency |
| S-parameters | Scattering parameters |
| S11 parameters | Input port voltage reflection coefficient in two-port network |
| S12 parameters | Reverse voltage gain in two-port network |
| S21 parameters | Forward voltage gain in two-port network |
| S22 parameters | Output port voltage reflection coefficient in two-port network |
| SOLT | Short-open-load-thru |
| SOV | Solenoid operated valve |
| VNA | Vector network analyzer |
| ZC | Characteristic impedance of the transmission line |
| Z0 | Reference impedance of the ports |
| Zin | Input impedance from the end of solenoid to port |
| β | Propagation constant of the transmission line |
| εeff | Effective permittivity |
| Γ | Matrix of the reflection coefficient from each port |
| td | Delay time |
| vp | Phase velocity |
References
- World Nuclear Association. World Nuclear Performance Report; World Nuclear Association: London, UK, 2020. [Google Scholar]
- International Atomic Energy Agency. Operating Experience with Nuclear Power Stations in Member States in 2019; International Atomic Energy Agency: Vienna, Austria, 2019. [Google Scholar]
- Varga, I.; Bartha, T.; Szabó, G.; Kiss, B. Status and Actual Risk Monitoring in a NPP Reactor Protection System. In Probabilistic Safety Assessment and Management; Springer: Berlin/Heidelberg, Germany, 2004; pp. 2654–2659. [Google Scholar]
- Upadhyaya, B.R.; Eryurek, E. Application of neural networks for sensor validation and plant monitoring. Nucl. Technol. 1992, 97, 170–176. [Google Scholar] [CrossRef]
- Ma, J.; Jiang, J. Applications of fault detection and diagnosis methods in nuclear power plants: A review. Prog. Nucl. Energy 2011, 53, 255–266. [Google Scholar] [CrossRef]
- Gong, Y.; Su, X.; Qian, H.; Yang, N. Research on fault diagnosis methods for the reactor coolant system of nuclear power plant based on D-S evidence theory. Ann. Nucl. Energy 2018, 112, 395–399. [Google Scholar] [CrossRef]
- Kwon, K.-C.; Kim, J.-H. A Stochastic Approach with Hidden Markov Model for Accident Diagnosis in Nuclear Power Plants. In Industrial and Engineering Applications of Artificial Intelligence and Expert Systems: Proceedings of the Tenth International Conference; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Wang, H.; Peng, M.-J.; Hines, J.W.; Zheng, G.-Y.; Liu, Y.-K.; Upadhyaya, B.R. A hybrid fault diagnosis methodology with support vector machine and improved particle swarm optimization for nuclear power plants. ISA Trans. 2019, 95, 358–371. [Google Scholar] [CrossRef] [PubMed]
- Ikonomopoulos, A.; Tsoukalas, L.H.; Uhrig, R.E.; Mullens, J.A. Monitoring nuclear reactor systems using neural networks and fuzzy logic. In Proceedings of the American Nuclear Society (ANS) Topical Meeting on Advances in Reactor Physics, Charleston, SC, USA, 8–11 March 1992. [Google Scholar]
- Jameson, N.J.; Azarian, M.H.; Pecht, M.; Wang, K.; Aidong, X. Electromagnetic coil equivalent circuit model sensitivity analysis for impedance-based insulation health monitoring. In Proceedings of the 2017 Prognostics and System Health Management Conference (PHM-Harbin), Harbin, China, 9–12 July 2017; pp. 1–6. [Google Scholar]
- Jameson, N.J.; Azarian, M.H.; Pecht, M. Improved electromagnetic coil insulation health monitoring using equivalent circuit model analysis. Int. J. Electr. Power Energy Syst. 2020, 119, 105829. [Google Scholar] [CrossRef]
- Jameson, N.J.; Azarian, M.H.; Pecht, M. Fault diagnostic opportunities for solenoid operated valves using physics-of-failure analysis. In Proceedings of the 2014 International Conference on Prognostics and Health Management, Cheney, WA, USA, 22–25 June 2014; pp. 1–6. [Google Scholar]
- Rahman, M.; Cheung, N.; Lim, K.W. A sensorless position estimator for a nonlinear solenoid actuator. In Proceedings of the IECON ’95—21st Annual Conference on IEEE Industrial Electronics, Orlando, FL, USA, 6–10 November 1995; p. 2. [Google Scholar]
- König, N.; Nienhaus, M. A Solution to Ambiguities in Position Estimation for Solenoid Actuators by Exploiting Eddy Current Variations. Sensors 2020, 20, 3441. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Zhao, X.; Li, C.; Jiao, Z.; Qu, F. Multiobjective Optimization of a Hollow Plunger Type Solenoid for High Speed On/Off Valve. IEEE Trans. Ind. Electron. 2017, 65, 3115–3124. [Google Scholar] [CrossRef]
- Zhijian, J.; Minglin, Z.; Zishu, Z. Fault location of transformer winding deformation using frequency response analysis. In Proceedings of the 2001 International Symposium on Electrical Insulating Materials (ISEIM 2001). 2001 Asian Conference on Electrical Insulating Diagnosis (ACEID 2001). 33rd Symposium on Electrical and Electronic Insulating Materials and Applications in System, Himeji, Japan, 22–22 November 2001; pp. 841–844. [Google Scholar]
- Pozar, D.M. Microwave Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Frei, J.; Cai, X.-D.; Muller, S. Multiport S-Parameter and T-Parameter Conversion with Symmetry Extension. IEEE Trans. Microw. Theory Tech. 2008, 56, 2493–2504. [Google Scholar] [CrossRef]
- Lu, H.-C.; Chu, T.-H. Multiport scattering matrix measurement using a reduced-port network analyzer. IEEE Trans. Microw. Theory Tech. 2003, 51, 1525–1533. [Google Scholar] [CrossRef]
- Chen, C.-J.; Chu, T.-H. Accuracy Criterion for S-Matrix Reconstruction Transforms on Multiport Networks. IEEE Trans. Microw. Theory Tech. 2011, 59, 2331–2339. [Google Scholar] [CrossRef]
- Kurokawa, K. Power Waves and the Scattering Matrix. IEEE Trans. Microw. Theory Tech. 1965, 13, 194–202. [Google Scholar] [CrossRef]
- Diaham, S.; Locatelli, M.-L. Dielectric properties of polyamide-imide. J. Phys. D Appl. Phys. 2013, 46, 185302. [Google Scholar] [CrossRef]
- Frankel, S. Characteristic Impedance of Parallel Wires in Rectangular Troughs. Proc. IRE 1942, 30, 182–190. [Google Scholar] [CrossRef]
- Arvia, E.M.; Sheldon, R.T.; Bowler, N. A capacitive test method for cable insulation degradation assessment. In Proceedings of the 2014 IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Des Moines, IA, USA, 19–22 October 2014; pp. 514–517. [Google Scholar]
- Tanaka, T. Aging of polymeric and composite insulating materials. Aspects of interfacial performance in aging. IEEE Trans. Dielectr. Electr. Insul. 2002, 9, 704–716. [Google Scholar] [CrossRef]
- Kim, K.; Shin, J.; Kim, B.-S.; Nah, W.; Lim, C.; Chai, J. Electrical and mechanical diagnosis of aging 600 V rated STP cables in a nuclear power plant. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 1574–1581. [Google Scholar] [CrossRef]
- Asipuela, A.; Mustafa, E.; Afia, R.S.A.; Adam, T.Z.; Khan, M.Y.A. Electrical Condition Monitoring of Low Voltage Nuclear Power Plant Cables: Tanδ and Capacitance. In Proceedings of the 2018 International Conference on Power Generation Systems and Renewable Energy Technologies (PGSRET), Islamabad, Pakistan, 10–12 September 2018; pp. 1–4. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).