Abstract
The objective of this research is to improve the hydrogen production and total profit of a real Steam Reforming plant. Given the impossibility of tuning the real factory to optimize its operation, we propose modelling the plant using Artificial Neural Networks (ANNs). Particularly, we combine a set of independent ANNs into a single model. Each ANN uses different sets of inputs depending on the physical processes simulated. The model is then optimized as a black-box system using metaheuristics (Genetic and Memetic Algorithms). We demonstrate that the proposed ANN model presents a high correlation between the real output and the predicted one. Additionally, the performance of the proposed optimization techniques has been validated by the engineers of the plant, who reported a significant increase in the benefit that was obtained after optimization. Furthermore, this approach has been favorably compared with the results that were provided by a general black-box solver. All methods were tested over real data that were provided by the factory.
1. Introduction
The chemical industry domain reveals the appearance of many research problems that can be handled with Artificial Intelligence (AI) techniques. The topic of this paper consists of improving the hydrogen production and total profit of a real Steam Reforming (SR) plant using AI techniques. Particularly, these techniques make possible modelling the behavior of a SR plant avoiding a lengthy and very expensive process of real parameters tuning (sometimes even impossible to perform in the real factory). Additionally, the optimization of the model can lead the factory to increase its benefit. A better performance of the factory implies a reduction in the products burned in the processes that occurs in the SR plant when producing hydrogen, which has a deep environmental interest.
In this research, we study a Steam Reforming plant owned by a well-known Spanish petrochemical company, whose industrial processes optimization are the subject of this research paper. SR is a method by which high-purity gaseous hydrogen (>99.9%) and some other substantially demanded gases are obtained from hydrocarbons, water, and other compounds. The real SR plant studied is located inside a refinery and it has many variables involved, such as the Natural Gas (NG) used in the process or the the temperature of the heaters. The gases produced, i.e., the outputs of the plant, such as gaseous hydrogen (H) or High-Pressure Steam (HPS), are part of the set of output elements, which can be exported, self-consumed in the SR process, or used to be part of other chemical processes.
The objective of this research is to increase the operational profit or the hydrogen production of the SR plant target of this project. The consideration of two alternative objectives is motivated by the real necessities of the SR plant. Particularly, the usual objective is to increase the benefit; however, sometimes there are situations with a high demand of hydrogen in order to supply other factories. In these cases, the objective of the SR plant changes from increasing the benefit to producing as much hydrogen as possible, without taking the associated costs into consideration.
In this paper, we propose to model the SR plant using Artificial Neural Networks (ANNs). The use of ANNs have been demonstrated a very efficient technique for the modelling of complex systems, when historical data regarding the inputs and outputs to the system are available. Therefore, the assemble of chemical reactions that occurs inside the studied SR plant has been modeled using a set of ANNs. The model proposed has been trained and validated with the data extracted from the real behavior of the SR plant in a one-year interval. Thus, it is possible to predict the SR plant behavior with a very high correlation between the modeled output and the original/real output, for a given a set of input values.
Once the proposed model has been validated, it can be fed with several input values in order to estimate the behavior of the plant in real situations. Hence, it is possible to optimize these inputs to meet certain objectives. In this paper, we study the performance of using two well-known metaheuristics, Genetic Algorithm (GA) and Memetic Algorithm (MA), in order to determine the best input configuration for the ANN model, when optimizing the two real and separated optimization problems that were previously introduced: the maximization of the H produced by the SR plant, and the maximization of the profit obtained by the sale of the production and the use of other gases in the plant. The use of metaheuristics for optimizing the inputs to the model, instead of other traditional techniques, is due to the capacity of these techniques to avoid being trapped in local optima, which is common in complex problems.
The main contributions of this research can be divided in two main groups: (i) the modelling of a whole SR real plant through a set of independent ANNs. Each ANN uses different sets of inputs, depending on the physical processes simulated. We demonstrate that the proposed ANN model, trained with real data, presents a high correlation between the real output and the predicted one. (ii) The model is then optimized as a black-box system using metaheuristics. The use of Memetic algorithms has been used for the first time in the SR context. The performance of the proposed optimization techniques has been validated by the engineers of the plant, who reported a significant increase in the benefit that was obtained after the optimization. Furthermore, this approach has been favorably compared with the results that were provided by a general black-box solver.
The rest of the paper is organized, as follows: in Section 2, we review the previous approaches in the literature related to the modelling and optimization of SR plants. In Section 3, we describe the optimization problems tackled in this research work. Subsequently, in Section 4 we present the ANN model designed. In order to optimize the inputs to the model, in Section 5 we describe the optimization techniques used to improve the behavior of the plant. In Section 6, we experimentally test our proposals and compare the obtained results with a general-purpose framework for black-box optimization problems. Finally, in Section 7 we expose our conclusions.
2. State of the Art
The modelling of real factories or other industrial facilities related to the hydrogen, and the later optimization of inputs to the model is not new, but it has been little explored in the Steam Reforming context.
Among the different modelling techniques existing in the literature, ANNs have been proved to be a robust method for modelling complex energy systems. In particular, in [1] the authors modeled an industrial hydrogen plant with a Multi-Layer Perceptron (MLP) network with one hidden layer. Similarly, in [2], the authors used another MLP network to model a combined heat and power plant. More recently, in [3], the authors modeled a component (the silica membrane reactor) of a SR plant also using a MLP.
On the other hand, the optimization of models (not necessarily based on ANNs) of SR plants, based on metaheuristic procedures, can also be found in the literature. In [4], the authors simulated a SR plant by mathematically modelling its different components using equations and the model was used to tackle a multi-objective optimization problem, with the well-known NSGA-II [5]. Particularly, they simultaneously maximized the produced hydrogen and exported steam flow rates. The model introduced in [4] was latter improved in [6], with the aim of considering transient conditions. In this case, the authors looked for the minimization of the cumulative deviation of the flow rate of hydrogen and the minimization of the cumulative deviation of the steam flow rate. The problem was also tackled using NSGA-II [5] as a multi-objective problem. In [7], a real SR plant was mathematically modelled based on the mass and energy balance equations. This time, the model was used in order to maximize the hydrogen production and the carbon dioxide ratio. The authors proposed a dynamic optimization procedure to find the optimal dynamic trajectory of the decision variables.
Finally, in the context of hydrogen production, we can also find the combination of the modelling based on ANNs and the optimization of the inputs based on metaheuristics [8]. However, the previous work only addresses the modelling and optimization of a cylindrical microreactor for hydrogen production.
In this research, we study a real SR plant that was previously introduced and partially modeled in [9]. In that paper, the authors compiled the inputs to the SR plant (with the help of the engineers working on it) and they performed a feature selection from the original inputs reducing the number of the considered variables from 191 to 22. In order to accomplish this reduction, several methods that are capable of detecting the most influential variables were experimentally compared: (i) empirical selection made by the engineers working in the plant; (ii) feature selection filtering techniques based on mutual information coefficient; and (iii) feature selection based on the Pearson correlation coefficient. Additionally, redundancy studies were performed in order to determine and eliminate the redundant variables. Among the tested methods, the best approach was the empirical selection that was made by the engineers in terms of the predictive performance. It is important to notice that this selection is based on the physical relationship of the inputs with each output modeled. We refer the reader to [9] for further details. The reduction of variables is relevant, because it helps to increase the capacity of generalization of any ANN system designed. Additionally, it avoids managing an extensive amount of data, and it facilitates the learning process of the weights within the networks. Once the input variable selection was performed, in [9] the authors used those variables in order to predict three outputs of the SR plant. To that aim, they designed three independent MLP networks: (1) to predict the hydrogen production, (2) to determine the natural gas burned, and (3) to predict the exported steam.
In this paper, we propose a new model based on the composition of ANNs for the SR plant introduced in [9]. Particularly, we consider new variables involved in the estimation of the benefit of the SR plant. Additionally, we applied a new stage with the optimization of the inputs to the network through the use of metaheuristic techniques (Genetic and Memetic algorithms). As far as we know, the modelling of a whole SR plant using ANNs and the later optimization of the benefit of the plant, based on metaheuristics, has never been tackled in the literature.
3. Problem Description
As it was previously introduced, we deal with two different optimization problems that are derived from a real scenario produced in a Steam Reforming industrial plant. Each optimization problem has a different objective function, but also a different number of variables that are involved in the optimization and different constraints. In fact, the objective function of one of the optimization problems (to maximize the hydrogen production) implies breaking a hard constraint in the other optimization problem (maintain the same hydrogen production). Therefore, they can not be considered at the same time as a multi-objective optimization problem. Generally speaking, the two problems tackled in this work are:
- Problem #1: maximize the H production in the SR plant, measured in kilograms per hour (kg/h).
- Problem #2: maximize the profit of the SR plant, obtained as the difference between the sale of the resulting gases minus the cost associated to the necessary products. It is measured in Euro per hour (€/h).
In the real context, a given solution to any of the previous optimization problems is evaluated by measuring the outputs of the SR plant. However, in the proposed simulation context, in order to evaluate a solution for any of the problems, we need to use a model of the whole SR plant, since the evaluation depends on the outputs of the model. The model proposed is based on a set of ANNs and it will be considered as a black-box model for optimization purposes. We describe the SR plant model in detail in Section 4. However, we will make reference to this model through this section using the acronym SRM (Steam Reforming Model).
Next, in Section 3.1 we describe the input variables, the input parameters, and the outputs of the SRM. Subsequently, in Section 3.2, we summarize the constraints of the model. Finally, in Section 3.3, we formally define the optimization problems that are tackled in this paper.
3.1. Inputs and Outputs of the Model
The SRM has 22 inputs and seven outputs. Among the inputs, 11 of them ( to ) are optimization variables (i.e., they can be modified and they are target of the optimization process), as we will see in Section 3.3. The meaning of each input variable is summarized in Table 1. The other 11 inputs ( to ) can be considered as parameters for the optimization process, since its values are constant during the time limit of 15 min. used for the optimization of the current state of the SR plant, but they might vary afterwards. Furthermore, the values of these parameters are provided by the company. Basically, the input variables are those that can be modified by the engineers using the control system of the SR plant. More precisely, among the 11 input variables, only 10 of them can be modified for the optimization problem #1, while all of them can be modified for the optimization problem #2.

Table 1.
Description of the input variables to the model, as measured in the Steam Reforming (SR) plant.
The meaning of the seven outputs produced by the SRM is summarized in Table 2. Among the outputs, represents the produced hydrogen, is the natural gas burned, and the high-pressure steam exported. Outputs , , and are related to different operational costs. Finally, contains values that will be used in order to verify restrictions that are related to the outputs of the SR plant. Notice that all the output values are measured in kg/h, except the output which is measured in Celsius degrees (C). The set of output values are necessary to both: verify some constraints (see Section 3.2) and calculate the value of the objective functions of each optimization problem (see Section 3.3).

Table 2.
Description of the output variables of the model.
3.2. Constraints
The solutions tested with the SRM must satisfy several constraints in order to be considered feasible solutions to the optimization problems. Specifically, in Table 3, we present the constraints that must be satisfied. In this table, for each constraint, we report an identifier (id), a description (constraint), and the problem affected by that constraint (#1 or #2). As we can observe, all of the compiled constraints must be satisfied when dealing with the optimization problem #2 while all except are considered for the optimization problem #1. In particular, to in Table 3 are constraints that establish the minimum and maximum values that each of the input variables to the SRM to can take. The constraint establishes the relationship between the input variables and . The constraint restricts the output value that can take. Finally, constraint indicates that the new quantity of produced hydrogen (represented by output ) must be approximately equal to the hydrogen currently being produced by the SR plant (). This is because the optimization problem #2 looks for the production of the same volume of hydrogen. However, in order to facilitate the finding of feasible solutions, the engineers from the SR plant have introduced a small constant, denoted by , which, in this case, is set to ±0.1% of the current hydrogen being produced.

Table 3.
Set of constraints.
It is important to clarify the existence of two different groups of constraints. The first group ( to ) are those that can be satisfied simply by providing values within a given range to the input variables (these constraints are known as apriori constraints). The second group of constraints ( and ) are called simulation constraints [10], because the simulation model needs to be launched in order to verify whether they are satisfied or not.
Notice, that in the optimization process, a set of values which satisfies the apriori constraints to is provided to the SRM. However, this can not assure that simulation constraints and are satisfied. Subsequently, after providing the input values to the SRM, it is necessary to run the model and observe the obtained and values. If the output values exceed the limits in and , then the solution provided is considered to be infeasible.
3.3. Optimization Problem
Once we have described the inputs (either variables or parameters), the outputs, and the constraints of the SRM, we formally define the optimization problems that are tackled in this paper.
As aforementioned, the objective of the optimization problem #1, represented by , is to maximize the kilograms per hour of H produced. The value of is directly reported by one of the outputs of SRM and, therefore, it is calculated with Equation (1).
Notice that we must provide to the SRM the input variables to , and the input parameters to . The SRM produces the outputs to , which will be used as inputs to compute the value of .
On the other hand, the objective of the optimization problem #2, represented by , is to maximize the profit of the SR plant. The value of is calculated with Equation (2).
Notice that, this time, has an additional input variable. Therefore, we provide the variable inputs to , and the input parameters to to the SRM in order to obtain outputs to , which will be used to compute the value of . In this equation, represents the produced H and represents the high-pressure steam, both measured in kilograms per hour (kg/h). Additionally, is an external function that determines the price per kg of either the hydrogen produced () or the high-pressure steam (HPS). Finally, the production cost (denoted as in Equation (2)) is calculated using the expression presented in Equation (3).
In this equation, () represents the natural gas (NG) consumed and () represents the low-pressure steam (LPS) consumed in the production process. Again, is a function that determines the price per kg of either the NG or the LPS consumed. It is important to notice that the price per kg of any of the gases referred in the previous equations is reported daily from the selling market. Therefore, for the optimization purposes, they can also be considered as additional input parameters.
With the previous definitions at hand, we mathematically formulate the two optimization problems tackled. In particular, the problem #1 is stated in Equation (4), together with its associated constraints.
Therefore, the addressed optimization problems themselves consist of tuning the input variables in each formulation, in order to independently maximize the objective functions that were previously presented.
4. Artificial Neural Network Model
An ANN is an interconnected assembly of simple processing elements, units, or nodes (known as neurons), whose functionality is inspired on the nervous system. The processing ability of the ANN is stored in the inter-unit connection strengths, or weights, obtained by a process of adaptation to/learning from, a set of training patterns. A MLP is a particular type of ANN, where neurons are arranged in layers, which are a collection of neurons in parallel. We refer the reader to [11] for a further description.
In this research, we propose a new model of the SR plant previously introduced, based on a set of MLPs, which receives the 22 variables selected in [9] as input parameters and which produces seven outputs (three derived from the previous work and four new ones introduced in this paper). Additionally, we propose the optimization of the input variables when considering the model as a black-box system, by using advanced Artificial Intelligence techniques that will be described in Section 5. In order to apply these techniques, to discover a combination of input parameters to the real SR plant that maximize certain output values, it is essential to design a model that predicts the plant performance with high precision.
The model designed is composed by seven MLPs. Each MLP models a different output of the SR plant. The decision about splitting the whole model into seven simpler models is due to the relationship existing in the physical processes simulated, determined by the engineers at the factory, and that have been previously studied in the literature [1,7]. Therefore, each ANN uses different sets of inputs depending on those physical processes simulated. Notice that the causal relationship between the inputs and the outputs determines the decisions made in the design of the network. Therefore, a modification in a subset of inputs is likely to produce a change in the result of the output at the real SR plant.
Each MLP is configured in such a way that it only receives part of the inputs to the model as input parameters, and it only produces one output, which corresponds with an output of the model. Notice, that the outputs of the seven MLPs are combined in the function which computes the benefit. Additionally, each MLP has only one hidden layer and the neurons use a sigmoid activation function. The model predicts the behavior of the plant for a given set of input values. The Universal Approximation Theorem states that a standard multilayer feed-forward network with a single hidden layer that contains a finite number of hidden neurons is an universal approximator in C(), in other words, it is capable of uniformly approximate any continuous function [12,13,14]. However, it is important to notice that, despite of the simplicity of the defined final structure of each MLP, more complex configurations were explored with the aim of looking for a better generalization capability for this case (including deep learning approaches) without finding relevant improvements with respect to the proposed one.
Figure 1 depicts the proposed model. The 22 inputs to the system are represented to the left, the model in the middle and the outputs to the right of the figure. Notice, that the inputs are classified into “variables” and “parameters” as it is described in Section 3.1. Additionally, in the ANN model, as depicted in Figure 1, it is possible to identify the seven MLPs designed. Each of them receives a different number of inputs, and some of the inputs are shared by more than one MLP. In Table 4 we compile the characteristics of each MLP by describing its architecture with the following format: inputs—neurons in the hidden layer—outputs. Notice, that the use of a different architecture for each MLP is based on a trial and error process, which determines the most suitable architecture attending to its generalization capacity. Particularly, we have tested the following architectures: no-hidden layer, one-hidden layer, two-hidden layers, and several deep learning models. The one-hidden layer model improved the results that were obtained by the no-hidden layer approach. However, we observed that architectures with more layers were not able to significantly improve the previous and simpler one. Therefore, we have selected the one-hidden layer model as reference. Furthermore, we explored different number of neurons (10, 20, and 30) in the hidden layer. As we can observe in Table 4, the best configuration of the MLPs was obtained with a maximum of 20 neurons in this layer. In Table 4, we also report the inputs involved in each MLP and the output produced. The meaning of each input and output variables was described in detail in Section 3.1. Notice that the proposed system behaves as a black-box model for optimization purposes. Therefore, the optimization process that will be applied and described later, does not need to know which input is linked to which MLP neither the real meaning of each input.
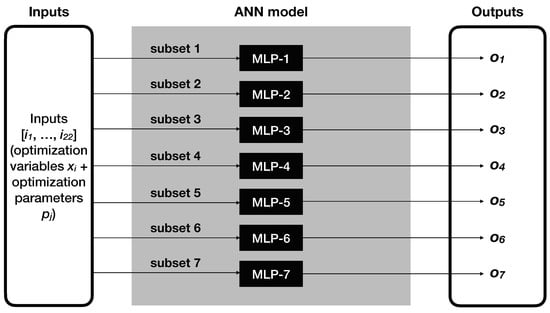
Figure 1.
Artificial Neural Networks model proposed.

Table 4.
Description of the inputs, outputs and architecture of each Multi-Layer Perceptron (MLP) within the ANN model proposed.
To end with the description of the ANN model, it is important to notice that each MLP was trained separately and the resultant trained network was assembled together with the other MLPs in a unique model.
5. Optimization Algorithms
An optimization problem is described by an objective function that is necessary to minimize/maximize, a set of decision variables that define the solution, and a set of constraints that must be satisfied. Once the SR plant target of this research has been modeled using the architecture that is presented in Section 4, we propose the optimization of the ANN model as a black-box system.
Black-box optimization is commonly referred to the resolution of optimization problems, where solutions are evaluated through the use of subroutines (or models), where the only control of what happens in them, from the optimization point of view, are the inputs that are provided to the model. Some of them might even be very expensive to execute, depending on the input arguments. Additionally, some constraints related to these problems might not be easy to control. For instance, they can be related with the outputs of the model, they can take different forms, such as yes/no values (instead of numerical ones), or even they can just be hidden constraints where the model does not provide a meaningful output [15]. Black-box optimization represents one of the most rapidly expanding fields of non-linear optimization research, due to its application in real contexts.
In this case, the input/output variables to the black-box model are those that are related to the ANN model. Usually, a particular value for each of the decision variables involved in an optimization problem defines what is known as a solution to the problem. However, in this case, a solution is formed by the values of the decision variables and the current values of the input parameters to the model. All of these 22 input values are used as inputs to the black-box model in order to obtain the outputs. Once the outputs of the model have been obtained, they are used to compute the objective functions and also to verify the simulation constraints. In this case, the existence of a different number of decision variables (10 or 11) depends on the problem tackled. However, in both problems, each variable can take a real value (i.e., we are facing a continuous optimization problem), which generates an uncountable number of possible solutions for each problem.
Next, we introduce the heuristic procedures that were proposed in order to optimize the input variables of the optimization problems, which have been combined into two different metaheuristics. Metaheuristics are stochastic techniques that are used to guide other heuristics to high-quality solutions for hard optimization problems, in a reasonable computing time. Although they cannot guarantee that the global optimum of the problem is reached, these techniques are very useful in real contexts, where the time that is needed to compute a solution is almost as important as the quality of the solution. Furthermore, they are not problem dependant since they only need to know the set of variables that are involved in the optimization process and a method to evaluate the quality of the solution obtained. We propose the use of two population-based metaheuristics in order to determine a good combination of input parameters for the black-box model introduced in Section 4: a Genetic Algorithm and a Memetic Algorithm. The selection of these two approaches instead of other metaheuristics is due the nature of the problem under study. Particularly, the population-based metaheuristics, which largely diversify the search, are suitable for contexts where the information that is provided by the evaluation of the objective function is scarse. This is the case of using a black-box model in order to evaluate the quality of the solutions found in the search process.
5.1. Genetic Algorithm
Genetic algorithms were originally introduced in [16], and they can be considered as an evolutionary bioinpired metaheuristic. They use abstractions that are based on the theory of biological evolution to describe optimization procedures and they have been widely used to tackle hard optimization problems in the past. GAs have been theoretically and empirically proved in order to provide robust search capabilities in complex spaces, offering a valid approach to problems that require efficient and effective search [17,18]. They are often used to optimize the input parameters of models related to the energy domain, as it can be seen in [19,20]. Although the original formulation of Genetic Algorithms was made for binary sequences, they have been subsequently extended to real numbers.
In this paper, we propose the use of a Genetic Algorithm with the classic design, in terms of the stages followed by the method. However, we use real numbers to codify the genes of the solution and adequate genetic operators derived of the representation used. The initial population is randomly generated, constructing one-by-one the individuals of the population. Specifically, the initialization procedure assigns a feasible real number to each of the optimization variables (genes), keeping the values of the parameters with the provided real values for each instance. Notice that this assignment of values only guarantees the satisfaction of the constraints related to the input variables (apriori constraints). Subsequently, in order to determine whether the input values provided do not violate the constraints where the outputs are involved (simulation constraints), it is necessary to run the black-box model. If any constraint is violated, then the solution is discarded and a new solution is generated until the necessary number of solutions are constructed.
Once the population is created, we start the evolutionary process. In this process, the selection operator used is the exponential ranking selection detailed in [21]. In particular, the exponential ranking sorts the individuals from the greatest to lowest fitness and calculates the probability of being selected using Equation (6). Notice that the exponential ranking selection is not a very common selection method in the literature of GAs, but it performs very well in problems of this domain.
where is the probability an individual i of being selected; n is the population size; and, c is a constant in the range [0,1) that balances the exploration/exploitation dilemma. When the value of c is high, the selection probability of the worse individuals increases. On the other hand, when the value of c is low, the probability of selection of the worse individuals decreases. In our case, we have tested the impact of two possible values of . Notice that we consider the use of elitism in our algorithmic design. This means that the best individual from the current population will be part of the population of the next generation.
The crossover operator used is based on a blending method with a probability of 0.7. This method combines the information that was coded in the genes of each parent by following the Equation (7) [22].
Let and be two chromosomes to be crossed, conformed by the genes , respectively. Subsequently, the new value for the ith gene of the new chromosomes obtained after the crossover (usually referred to as offspring) is given by the Equation (7).
The value, generated at random in the interval for each crossover operation, determines the influence of each parent in the new generated chromosomes (i.e., it can be closer to one of the parents or to the other one). It is important to notice that this method generates new chromosomes following the convex set definition, which states that any linear combination of points in a convex set will also belong the set [23]. This means that, if the two parent chromosomes are feasible, then the offsprings are also feasible solutions. In fact, we have selected this crossover method, because it holds this property. Notice that this is only true in relation with respect to the apriori constraints.
Finally, the mutation operator uses a uniform distribution in the valid range for each variable. This guarantees that the solution remains feasible with respect to the constraints that are related to the input variables.
It is important to notice that, in the case that any solution through the process becomes infeasible due to the simulation constraints, then the algorithm discards it. The technique of rejecting solutions that do not meet the constraints of the problem is known as death penalty, a popularly used method that works simply: no infeasible solution will be part of the population [24].
5.2. Memetic Algorithm
Memetic Algorithms were originally introduced in [25] and they are another evolutionary inspired metaheuristic. MAs can be considered to be an extension of the GA, since they use the same algorithmic schema with the introduction of an additional powerful strategy used for intensification purposes in this context, the local search. MAs have also been demonstrated to be a very successful optimization technique for hard optimization problems, as can be seen in [26,27,28].
In Algorithm 1, we present the pseudocode of the Memetic Algorithm proposed. Notice that we follow a classical implementation of the method. As we can see in the pseudocode, after an initial stage where the population is created, improved and evaluated (steps 1–3) the algorithm enters into a loop until the stopping criterion is matched (number of iterations, number of iterations without improvement, or just time). In each iteration of this loop (steps 4–13) the algorithm builds and evaluates new generations of individuals. Each generation is created in step 5, by first including the best element from the previous generation. Subsequently, the algorithm will conform the population, by iteratively applying the selection, crossover and mutation operations (steps 6–11). Notice that the pseudocode of the Genetic Algorithm (not provided here) is equal to this pseudocode, with the exception of steps 2 and 12, not present in GAs. The MA, in this case, tries to improve the quality of the individuals in the population by applying a local search procedure.
A local search is a heuristic procedure that starts from a feasible solution to an optimization problem and finds the best solution in the neighborhood (known as local optimum) by applying a chain of movements through the use of a particular move operator. A neighborhood of a solution is then defined as the set of all feasible solutions that can be reached by applying that particular operator.
| Algorithm 1 Memetic Algorithm |
|
The main novelty of the local search that is proposed for this problem is the move operator used, which is based on the insertion of a new real value in one of the variables of the solution. The real value inserted is based on a shift from the current value and it is obtained by adding/subtracting a constant value to the current one. Notice that we just consider feasible insertions (i.e., those which do not violate the apriori constraints of the problem that is described in Section 3.2).
Based on the previous move operator, we propose the use of two different local search procedures in order to improve the solutions. These procedures are based on the First-Improvement (FI) and Best-Improvement (BI) strategies, respectively. The FI strategy performs movements in the solution space one-by-one, accepting the first one, which improves the objective function of the current solution. On the other hand, the BI strategy tries all possible moves that are defined in a particular neighborhood and then it chooses the best option, among the ones that improve the objective function of the current solution. As a result of the two search strategies, we defined two different local search procedures that will conform two different Memetic Algorithms (named MA-FI and MA-BI, respectively).
As in the case of the GA previously presented, if any solution found through the search process becomes infeasible due to the uncontrollable constraints, then the algorithm discards it.
6. Experimental Results
To evaluate the proposals of this paper, in this section we carry on several experiments in order to confirm the contribution of the model proposed, as well as the metaheuristics used to optimize the inputs to the model.
The source code was programmed using Python. However, the code used to train and test the MLPs was automatically translated from Python to C by using Cython [29] to increase the performance. Notice that this was only done for the development of the ANN models. The rest of the code, which was related to the optimization process, was coded and run in Python. All the experiments were conducted in an Intel Core i7-3537U with two cores at 2.00 GHz.
There is a constraint on the execution time of the algorithm, since every 15 min. the optimization of a plant status must be completed to start a new optimization on another status.
In Section 6.1 we introduce the datasets used in our experimentation. Subsequently, in Section 6.2, we evaluate the prediction ability of the model proposed. In Section 6.3, we describe the general black-box optimization framework used to compare our proposals. Finally, in Section 6.4, we test the effectiveness of the metaheuristics that were proposed to optimize the inputs to the model.
6.1. Instances
We have used a wide dataset of information extracted from a real SR plant in order to evaluate the different proposals of this work. Particularly, the data used in our experiments were collected during a period of 1 year (from 14 February 2017 to 14 February 2018 ) every 15 min. The data was then filtered, after a preliminary analysis and, as a result, some periods were deleted, due to outliers, startup and shutdown periods, wrong tendencies, etc., obtaining a filtered set of data. Additionally, the data were filtered again in order to clean the noise, remove spurious registers, and delete data from transient periods, which do not represent an actual behavior of the plant in terms of prediction. Notice that the whole process of filtering the data was conducted in [9].
The resultant dataset was composed by 31,874 samples that are used in our experiments in the following sections. Each sample contains the status of the SR plant in a particular moment of the time. The status of the plant is represented by 22 different variables. Some of them are provided as input values in order to control the SR plant, while others are just measured and taken into consideration. These 22 input values also feed the inputs of the black-box model. Similarly, the seven associated output values, also provided in the instance for the particular instant in the time observed, are extracted from the measurements from the operation of the SR Plant.
6.2. Results Related to the Proposed Model
From the 31,874 samples that compose the considered dataset, the 70% of the samples (22,310) were randomly selected and used as training samples, while the remaining 30% (9562) were used as test samples. The training of the seven MLPs within the model were performed for 100 epoch for each MLP, using the Mean Square Error as the loss function, since we are handling a regression problem. We have used our own implementation of a stochastic gradient descent in on-line mode [30] with learning rate of 0.1.
In Table 5, we report several measures of the quality of the model in terms of prediction ability. Particularly, for each of the seven MLPs that compose the model, we report: the Root Mean Square Error (RMSE); the Mean Absolute Error (MAE); and, the Fraction of Variation Explained (FVE) by the model (also known as ). All of these values were obtained over the test samples following a cross-validation approach (i.e., test and training sets are disjoint, so the model is trained with the 70% of the samples and tested with the remaining 30%).

Table 5.
Estimated errors for each MLP of the model.
As it can be observed in Table 5, the high values of indicate a high similarity between the SR plant and the model. Therefore, it can be expected that the latter optimization of the model produces very similar results in the SR plant.
6.3. Comparison Framework
We have compared the results of the Genetic and Memetic algorithms with respect to the real outputs of the SR plant using real test data that were provided by the factory in order to test the effectiveness of our proposals. Additionally, we have included in our comparison a general framework to solve black-box optimization models, the Mesh Adaptive Direct Search (MADS) algorithm [31].
The MADS algorithm is based on the use of meshes, which represent a discretization of the space of variables [32]. This iterative algorithm performs an adaptive search in the meshes defined, and it also includes the control of the refinement of the meshes during the optimization process. In each iteration, MADS performs two main steps, named the search and the poll. The search step tries to identify a point in the current mesh that supposes an improvement of the solution. The poll step generates trial mesh points in the neighborhood of the best solution found until that moment. When an iteration fails to improve the current best solution, the next iteration is initiated on a finer mesh. We refer the reader to [15,31] for a detailed description of the method.
It is important to notice that we have used a public implementation of MADS provided by the software: Nonlinear Optimization by Mesh Adaptive Direct Search (NOMAD) [32,33,34]. Particularly, we used the latest version of the software (v3.9), which contains a C++ implementation of the algorithm, distributed under the GNU Lesser General Public License (LGPL).
6.4. Heuristic Results
Once the model has been designed and trained, the optimization phase is devoted to find a good combination of input values to optimize the objective functions reported in Section 3 (maximize the H production; and, maximize the profit of the plant).
From the total dataset of samples, we have selected 40 diverse instances (20 for each objective function) in order to evaluate the optimization algorithms. In general, the larger the test dataset, the better. However, 20 samples represent a reasonable rule-of-thumb in this context (as it is pointed out in [15]). For each objective we sorted all the samples in a descending order with respect to the quality of the solution. Let us remember that each sample corresponds to a real scenario of the SR plant, i.e., the set of input values to the plant and the produced outputs. Once the samples were sorted, then we selected a random instance in each of the following percentiles: 8, 10, 14, 20, 26, 30, 32, 38, 44, 49, 50, 56, 62, 68, 69, 74, 80, 86, 89, and 92, obtaining a total of 20 different instances per objective function. All of the algorithms were provided with the same initial point (the real values of the plant) for their optimization process.
In Table 6, we report the average improvement (in kg/h) obtained with the proposed algorithms with respect to the original production of H: the Genetic Algorithm (GA), the Memetic Algorithm based on First Improvement (MA-FI), and the Memetic Algorithm based on Best Improvement (MA-BI). We refer the reader to Section 5 for the description of each procedure. For each method we have tried different population sizes. Notice that the sizes of the population tried in the GA are much larger than the ones used for the MA, because the GA is faster than the MA and, therefore, it can handle more solutions within the same execution time. For each algorithm and population size, we have tested two different probability distributions of the ranking used in the selection operator. Each of them is parameterized by the value of the constant c in the table). Finally, we have also tested three different values for the probability that a particular gene suffers a mutation (denoted by in the table). In Table 6, we also report the production of H of the best solution that is produced by the general black-box optimization algorithm MADS [31]. In this case, there is not population size and the rest of the parameters provided for the GA, MA-FI, and MA-BI reported in the head of the columns of the table apply. However, we provide the result value in this table in order to ease the comparison among the methods.

Table 6.
Results of the metaheuristic procedures for the Objective Function 1 (H production, measured in kg/h).
The values that are reported in Table 6 are calculated as the result of the average of the improvement for each of the 20 instances considered for . Notice that each algorithm was running up to 15 min. (i.e., the time limit indicated by the engineers in the real SR plant), and all of them were provided with the same initial point (the actual status of the SR plant). As it is possible to observe, the maximum average improvement for the instances considered was 732.64 kg/h of H (highlighted in bold-type font in Table 6). This value was reached by the state-of-the-art algorithm MADS. However, the differences with the rest of the algorithms are neglectable, especially with those that were obtained by the GA with different parameter configurations.
Further than the average of the values of the objective function for each instance, it is common to use additional statistical measures in order to compare the results that were obtained by the tested algorithms, such as the traditional deviation to the best solution found. In the black-box optimization context, it is also common to report the performance of the algorithms, when compared for the same number of objective function evaluations, through the use of convergence plots, or performance profiles, among others (see Appendix A in [15] for a wider description). However, in this case, the use of metrics that are related to the number of evaluations of the objective function lacks of sense, since we are tackling a real optimization problem bounded by the time, but not by the number of evaluations. Furthermore, the evaluation is made by an ANN model that does not fall into any real-cost scenario.
In order to complete our comparisons, in Table 7, we report the average accuracy of the algorithms for the considered instances (the best results are highlighted in bold-type font), which compares the quality of the solutions provided by an algorithm with respect to the best solution found [15]. In particular, the accuracy is calculated, as follows:
where f represents the evaluation function, is the best solution found by the algorithm being evaluated a (in this case a={GA, MA-FI, MA-BI, MADS}), is the initial solution, and is the best-known solution for the instance. Notice that, in this case, we report the best value found by the algorithm within the time limit.

Table 7.
Accuracy of the methods for the Objective Function 1 (H production, measured in kg/h).
As we can observe in Table 7, and despite the fact of the small differences in the average of the objective function, it is not possible to find differences in terms of accuracy between MADS and most of the configurations of GA, even when reporting three decimal points. Additionally, the differences with respect to the MA configurations are very small.
The results that were found for the reported in Table 6 and Table 7 suggest that the optimization problem in this context does not suppose a hard task for any of the algorithms compared. In fact, a general framework for black-box optimization (MADS) is able to find the best solutions that were found in the experiment.
Similarly, in Table 8, we report the average improvement (in €/h) that was obtained with the proposed algorithms for the , with respect to the original profit of the SR plant. Again, we also report in this table the best solution produced by the general black-box optimization algorithm MADS [31]. Notice that, in this context, MADS was unable to find a feasible solution in four out of the 20 instances considered. Despite of the fact that we provided to all the algorithms the current status of the plant (which is considered a feasible starting solution), it might happen that the hydrogen production predicted by the model results in a deviation larger than with respect to the real one and, therefore, is violated. Subsequently, the solution is considered infeasible in our model. Therefore, we did not include those instances in the average reported for MADS. In this case, we could find larger differences among the methods. The best method was the MA-BI that was configured with a population of eight individuals, , which obtained an average improvement of 782.76 €/h (highlighted in bold-type font in Table 8). Notice that, in this case, all of the combinations of parameters within the MA outperformed either the MADS or the different GAs proposed.

Table 8.
Results of the metaheuristic procedures for the Objective Function 2 (increment in the profit of the SR plant measured in €/h).
Again, in Table 9, we report the accuracy for the evaluated methods. In this table, we can find significant differences between the best algorithm (highlighted in bold-type font) and the rest of the compared methods. Observing the results, we can conclude that the is considerably complicated for the evaluated methods than . In this case, all of the proposed MAs outperformed either the rest of the GA variants and also the results that were obtained by MADS.

Table 9.
Accuracy of the methods for the Objective Function 2 (increment in the profit of the SR plant measured in €/h).
Notice that the prices per ton necessary to calculate the profit of SR plant are very volatile. In our experiments, we have used the following values to calculate the objective function : natural gas = 16.05 €/ton; low-pressure steam = 13.00 €/ton; high-pressure steam = 19.01 €/ton; and, H = 1000.00 €/ton.
As a final experiment, in Figure 2, we graphically illustrate the behavior of the model (denoted as Modeled in the figure) and the optimized model (denoted as Optimized in the figure) with respect to the real behavior of the SR plant (denoted as Original in the figure) for a six months period. The ANN model predicts the behavior of the plant with high correlation, as it is possible to observe in the figure. On the other hand, the optimized model clearly increases the benefit per hour obtained.
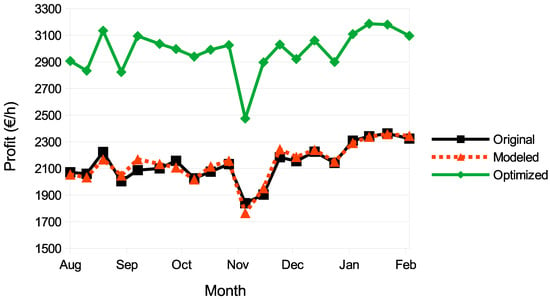
Figure 2.
Graphical interpretation of the results in a six-months period.
7. Conclusions
The objective of this research is to improve the performance of a real Steam Reforming plant by either increasing the H produced or increasing the profit of the factory. With that aim, we have modelled the SR plant as a whole model, composed by seven MLPs. The inputs to the model have been optimized using a Genetic Algorithm and a Memetic Algorithm, and the results obtained have been compared with a general black-box optimization algorithm in the literature.
The performance of the model proposed has been evaluated with different error measures with respect to the real outputs of the SR plant. The obtained results regarding the forecasts made by the model indicate that its behavior is very similar to the real SR plant. Additionally, the results that were obtained by the metaheuristics were compared with a general framework for black-box optimization (MADS) for the two objective functions considered. The proposed methods outperformed MADS in one of the objective functions; however, all of the tested methods reached almost the same results for the other objective function originally proposed.
The increase in the performance found with this new method has also been validated by the engineers in the real scenario. Notice that the potential benefits of the SR plant based on the solutions presented in the best scenario reported in Section 6 indicate that the annual profit could be raised up to several million €. Nevertheless, this situation is unrealistic, since there is an error margin in the model, and some of the solutions provided might be infeasible when applied in the real scenario. Furthermore, reaching these amounts would only be possible in a non-stopping 24/7 context that is able to tune the parameters of the SR plant instantly every 15 min. Unfortunately, the real SR plant is subject to many other operational restrictions not considered in this research, such as security policies and maintenance of the factory, which do not make possible the continuous update of the parameters of the SR plant. However, the tests that were made by the engineers in the real scenario after applying the techniques proposed in this paper (ANN model + optimization algorithms) have forecasted an estimated increase of 975.000 € in the annual profit of the plant. Notice, that this value was obtained by the engineers with the following procedure: (1) they operated the factory for two weeks with the configurations suggested by the optimizer; (2) they measured the real outputs of the factory and calculated the cost value per kg of produced hydrogen; (3) they calculated the regression line of the cost of the factory, depending on the amount of hydrogen produced; (4) they compared the predictions obtained from regression line with the cost before the optimization; and, (5) finally, based on the differences in the cost, they estimated the increment in the profit of the whole year.
Finally, we would like to highlight that the method proposed, which combines a model based on ANNs with heuristic algorithms to optimize the inputs to the model, open an enlightening perspective for many other optimization problems derived from the industry. This might improve the performance of many tasks in real scenarios with a very low adaptation effort and large benefits, avoiding the need of designing specific algorithms to handle them.
Author Contributions
Conceptualization, D.V. and F.S.; methodology, F.S. and E.G.P.; software, F.S. and J.B.-L.; validation, F.S., E.G.P. and D.V.; formal analysis, E.G.P.; investigation, E.G.P. and F.S.; resources, D.V.; data curation, D.V.; writing—original draft preparation, J.B.-L., F.S. and E.G.P.; writing—review and editing, F.S. and E.G.P.; supervision, F.S. and E.G.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been partially supported by the Ministerio de Ciencia, Innovación y Universidades (Spain) under grant ref. PGC2018-095322-B-C22; and by Comunidad de Madrid and European Regional Development Fund, grant ref. P2018/TCS-4566.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zamaniyan, A.; Joda, F.; Behroozsarand, A.; Ebrahimi, H. Application of artificial neural networks (ANN) for modeling of industrial hydrogen plant. Int. J. Hydrogen Energy 2013, 38, 6289–6297. [Google Scholar] [CrossRef]
- Rossi, F.; Velázquez, D.; Monedero, I.; Biscarri, F. Artificial neural networks and physical modeling for determination of baseline consumption of CHP plants. Expert Syst. Appl. 2014, 41, 4658–4669. [Google Scholar] [CrossRef]
- Ghasemzadeh, K.; Aghaeinejad-Meybodi, A.; Basile, A. Hydrogen production as a green fuel in silica membrane reactor: Experimental analysis and artificial neural network modeling. Fuel 2018, 222, 114–124. [Google Scholar] [CrossRef]
- Rajesh, J.; Gupta, S.; Rangaiah, G.; Ray, A. Multi-objective optimization of industrial hydrogen plants. Chem. Eng. Sci. 2001, 56, 999–1010. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Paris, France, 18–20 September 2000; Springer: Berlin/Heidelberg, Germany, 2000; pp. 849–858. [Google Scholar]
- Nandasana, A.D.; Ray, A.K.; Gupta, S.K. Dynamic model of an industrial steam reformer and its use for multiobjective optimization. Ind. Eng. Chem. Res. 2003, 42, 4028–4042. [Google Scholar] [CrossRef]
- Taji, M.; Farsi, M.; Keshavarz, P. Real time optimization of steam reforming of methane in an industrial hydrogen plant. Int. J. Hydrogen Energy 2018, 43, 13110–13121. [Google Scholar] [CrossRef]
- Zheng, T.; Zhou, W.; Yu, W.; Ke, Y.; Liu, Y.; Liu, R.; San Hui, K. Methanol steam reforming performance optimisation of cylindrical microreactor for hydrogen production utilising error backpropagation and genetic algorithm. Chem. Eng. J. 2019, 357, 641–654. [Google Scholar] [CrossRef]
- Velázquez, D.; Serradilla, F.; Monge, B.; Tristán, M.; Fernández, R. Modelling and optimizing syngas production. In Proceedings of the Nitrogen + Syngas International Conference, Berlin, Germany, 29 February–3 March 2016. [Google Scholar]
- Le Digabel, S.; Wild, S. A taxonomy of constraints in simulation-based optimization. arXiv 2015, arXiv:1505.07881. [Google Scholar]
- Gurney, K. An Introduction to Neural Networks; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Csáji, B.C. Approximation with artificial neural networks. Fac. Sci. Etvs Lornd Univ. Hung. 2001, 24, 48. [Google Scholar]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control. Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Hornik, K. Approximation capabilities of multilayer feedforward networks. Neural Netw. 1991, 4, 251–257. [Google Scholar] [CrossRef]
- Audet, C.; Hare, W. Derivative-Free and Blackbox Optimization; Springer Series in Operations Research and Financial Engineering; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; p. 302. [Google Scholar]
- Holland, J. Adaptation in natural and artificial systems: An introductory analysis with application to biology. In Control and Artificial Intelligence; University of Michigan Press: Michigan, MI, USA, 1975. [Google Scholar]
- Godefroid, P.; Khurshid, S. Exploring very large state spaces using genetic algorithms. In Proceedings of the International Conference on Tools and Algorithms for the Construction and Analysis of Systems, Grenoble, France, 8–12 April 2002; Springer: Berlin/Heidelberg, Germany, 2002; pp. 266–280. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning, 1st ed.; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1989. [Google Scholar]
- Ismail, M.; Moghavvemi, M.; Mahlia, T. Genetic algorithm based optimization on modeling and design of hybrid renewable energy systems. Energy Convers. Manag. 2014, 85, 120–130. [Google Scholar] [CrossRef]
- Ivanov, S.Y.; Ray, A.K. Multiobjective optimization of industrial petroleum processing units using Genetic algorithms. Procedia Chem. 2014, 10, 7–14. [Google Scholar] [CrossRef]
- Blickle, T.; Thiele, L. A comparison of selection schemes used in evolutionary algorithms. Evol. Comp. 1996, 4, 361–394. [Google Scholar] [CrossRef]
- Haupt, S. Practical Genetic Algorithms; John Wiley & Song, Inc.: State College, PA, USA, 2004; pp. 123–190. [Google Scholar]
- Nash, S.G.; Sofer, A. Linear and Nonlinear Programming; McGraw-Hill Inc.: New York, NY, USA, 1996. [Google Scholar]
- Michalewicz, Z.; Dasgupta, D.; Le Riche, R.G.; Schoenauer, M. Evolutionary algorithms for constrained engineering problems. Comput. Ind. Eng. 1996, 30, 851–870. [Google Scholar] [CrossRef]
- Moscato, P. On Evolution, Search, Optimization, Genetic Algorithms and Martial Arts: Towards Memetic Algorithms; Caltech Concurrent Computation Program, C3P Report; California Institute of Technology: Pasadena, CA, USA, 1989; Volume 826. [Google Scholar]
- Islam, M.M.; Singh, H.K.; Ray, T.; Sinha, A. An enhanced memetic algorithm for single-objective bilevel optimization problems. Evol. Comput. 2017, 25, 607–642. [Google Scholar] [CrossRef] [PubMed]
- Molina, D.; Lozano, M.; Sánchez, A.M.; Herrera, F. Memetic algorithms based on local search chains for large scale continuous optimisation problems: MA-SSW-Chains. Soft Comput. 2011, 15, 2201–2220. [Google Scholar] [CrossRef]
- Wei, K.; Dinneen, M.J. Runtime analysis to compare best-improvement and first-improvement in memetic algorithms. In Proceedings of the 2014 Annual Conference on Genetic and Evolutionary Computation, Vancouver, BC, Canada, 12–16 July 2014; ACM: New York, NY, USA, 2014; pp. 1439–1446. [Google Scholar]
- Behnel, S.; Bradshaw, R.; Dalcín, L.; Florisson, M.; Makarov, V.; Seljebotn, D. Cython: C-Extensions for Python. 2020. Available online: https://cython.org/ (accessed on 15 September 2020).
- Heskes, T.M.; Kappen, B. On-line learning processes in artificial neural networks. In North-Holland Mathematical Library; Elsevier: Amsterdam, The Netherlands, 1993; Volume 51, pp. 199–233. [Google Scholar]
- Audet, C.; Dennis, J., Jr. Mesh Adaptive Direct Search Algorithms for Constrained Optimization. SIAM J. Optim. 2006, 17, 188–217. [Google Scholar] [CrossRef]
- Abramson, M.; Audet, C.; Couture, G.; Dennis, J., Jr.; Le Digabel, S.; Tribes, C. The NOMAD Project. 2009. Available online: https://www.gerad.ca/nomad/ (accessed on 15 September 2020).
- Audet, C.; Le Digabel, S.; Tribes, C. NOMAD User Guide; Technical Report G-2009-37, Les cahiers du GERAD; Groupe D’Études et de Recherche en Analyse des Décisions: Montreal, QC, Canada, 2009. [Google Scholar]
- Le Digabel, S. Algorithm 909: NOMAD: Nonlinear Optimization with the MADS algorithm. ACM Trans. Math. Softw. 2011, 37, 1–15. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).