A Minimum Mean-Square-Error (MMSE) Decoder for Quasi-Orthogonal Space–Time Block Code

Abstract

The quasi-orthogonal space–time block code (QO-STBC) was introduced to achieve a full transmission rate for the four antennas system. In this paper, a decoding method for the QO-STBC is proposed to improve the bit-error-rate (BER) and to solve a rank-deficient problem. The proposed algorithm is based on the minimum mean-square-error (MMSE) technique. To overcome the implementation problem from the MMSE, an estimation method of the noise variance is developed in this paper. The proposed algorithm is implemented without matrix inversion, therefore, the proposed algorithm achieves a better BER than the conventional algorithms, as it has a low computational complexity. The simulation results show the low BER of the proposed algorithm in a Rayleigh fading channel.

1. Introduction

Transmit diversity has been applied for mitigating the effect of multi-path fading, as it can improve the performance without adding additional bandwidth and increasing transmit power. A space–time block code (STBC) is most widely used to provide transmit diversity [1,2,3,4,5,6,7,8,9]. The orthogonal STBC (O-STBC) was introduced to achieve full diversity and a full transmission rate for two transmit antennas [1]. The O-STBC has computational complexity for two transmit antennas, but that has degraded performance compared to space-time trellis codes. The STBC from orthogonal design (STBC-O) was developed from the theory of orthogonal designs [2]. The STBC-O is a generalization of the O-STBC for multiple antennas systems. However, the STBC-O is not capable of obtaining the full transmission rate for more than two transmit antennas systems. To overcome this drawback, several quasi orthogonal-STBC (QO-STBC) algorithms have been introduced [3,4,5] for the four antennas system. In [3], the columns of the transmission matrix were separated into groups according to a quasi-orthogonal design, in which the columns in each group are non-orthogonal and different groups are orthogonal. The algorithm was derived by minimizing the non-orthogonality that arises from increasing the transmission rate [4]. In [3,4], the QO-STBC algorithms have the full transmission rate for the four antennas system, but the detection matrix of these algorithms has interference terms, which are raised from neighboring channels. This phenomenon increases a computational complexity and decreases the bit-error-rate (BER). To solve these problems, the QO-STBC was developed using the transformation matrix in [5]. However, the BER result of this algorithm is higher than that of the conventional algorithms [10]. In addition, the QO-STBC faces a rank-deficient problem when the detection matrix is singular.

In this paper, a decoding method for the QO-STBC is proposed to improve the performance for systems that have four antennas, and to address the rank-deficient problem. The proposed algorithm is based on the minimum mean-square-error (MMSE) decoder. This decoder has a lower BER than that of the zero forcing (ZF) decoder. However, a limitation is that the MMSE decoder is not used in practical applications, as the noise variance is unknown in real-time applications [11]. To overcome this drawback, the proposed algorithm is derived by estimating the noise variance. Moreover, to reduce computational complexity, elementary matrices are used in the proposed algorithm without matrix inversion. In short, the proposed algorithm achieves a lower BER than other algorithms, while having low computational complexity without matrix inversion. Furthermore, the proposed algorithm is able to overcome a rank-deficient problem because a regularization term, which is an estimated noise variance, is added to the detection matrix. The simulation results illustrate that the BER of the proposed algorithm is smaller than that of the conventional algorithms in various environments.

In this paper, bold symbols are used for column vector (lower-case) and matrix (upper-case). The notations are used as follows;

$$\begin{array}{c}{(·)}^T\mathrm{transpose}\mathrm{of}\mathrm{a}\mathrm{avector}\mathrm{or}\mathrm{matrix};\hfill \\ {(·)}^{*}\mathrm{conjugate}\mathrm{of}\mathrm{a}\mathrm{complex}\mathrm{number};\hfill \\ {(·)}^H\mathrm{Hermitian}\mathrm{transpose}\mathrm{of}\mathrm{a}\mathrm{vector}\mathrm{or}\mathrm{matrix}.\hfill \end{array}$$

2. Review of the Conventional Algorithm

The received signal for the four antennas system is represented as

$$\begin{array}{c}\hfill \mathbf{r}\left(n\right)=\left[\begin{array}{c}{r}_1\left(n\right)\\ r_2^{*}\left(n\right)\\ r_3\left(n\right)\\ r_4^{*}\left(n\right)\end{array}\right]=\mathbf{H}\left(n\right)\mathbf{x}\left(n\right)+\mathbf{w}\left(n\right),\end{array}$$

(1)

where n is a time index; ${·}_j$ means an jth antenna; $\mathbf{x}\left(n\right)={\left[\begin{array}{cccc}{x}_1\left(n\right)& x_2\left(n\right)& x_3\left(n\right)& x_4\left(n\right)\end{array}\right]}^T$ is the input signal; $\mathbf{w}\left(n\right)={\left[\begin{array}{cccc}{w}_1\left(n\right)& w_2^{*}\left(n\right)& w_3\left(n\right)& w_4^{*}\left(n\right)\end{array}\right]}^T$ represents the measurement noise with zero-mean additive complex white Gaussian noise; $\mathbf{H}\left(n\right)$ represents the channel matrix. For convenience, the time index n is omitted in the following. The channel matrix of the system, which has four transmit antennas, is given by [3,4]

$$\begin{array}{cc}\hfill \mathbf{H}=& \left[\begin{array}{cccc}{h}_1& h_2& h_3& h_4\\ h_2^{*}& -h_1^{*}& h_4^{*}& -h_3^{*}\\ h_3& h_4& h_1& h_2\\ h_4^{*}& -h_3^{*}& h_2^{*}& -h_1^{*},\end{array}\right],\hfill \end{array}$$

(2)

where $h_j$ denotes the coefficient of the channel from the jth transmit antenna.

When the channel matrix is orthogonal, the detection matrix, which is defined as $\mathbf{D}\triangleq {\mathbf{H}}^H\mathbf{H}$, is a diagonal matrix. Thus, the signal is recovered using the linear decoding technique. However, this technique is not applied for the QO-STBC with the four transmission antennas, because the channel matrix is not orthogonal. In other words, the detection matrix has interference terms and it is presented as

$$\begin{array}{c}\hfill \mathbf{D}=\left[\begin{array}{cccc}\alpha & 0& \beta & 0\\ 0& \alpha & 0& \beta \\ \beta & 0& \alpha & 0\\ 0& \beta & 0& \alpha \end{array}\right],\end{array}$$

(3)

where $\alpha$ is the channel gain, which is defined as $\alpha ={\sum }_{i=1}^4{\left|h_i\right|}^2$, and $\beta$ denotes an interference term, which is defined as

$$\begin{array}{c}\hfill \beta =h_1{h}_3^{*}+h_2{h}_4^{*}+h_1^{*}{h}_3+h_2^{*}{h}_4.\end{array}$$

In short, off-diagonal terms decrease the performance and lead to the complex decoding method. In this case, the decoding algorithms such as the ZF and MMSE are used [11]. The ZF decoder is given as

$$\begin{array}{c}\hfill \widehat{\mathbf{x}}={\mathbf{D}}^{-1}{\mathbf{H}}^H\mathbf{r},\end{array}$$

(4)

and the MMSE decoder is obtained as

$$\begin{array}{c}\hfill \widehat{\mathbf{x}}={\mathbf{K}}^{-1}{\mathbf{H}}^H\mathbf{r}={(\mathbf{H}{\mathbf{H}}^H+{\gamma }^{-1}\mathbf{I})}^{-1}{\mathbf{H}}^H\mathbf{r},\end{array}$$

(5)

where $\gamma \triangleq {\sigma }_x^2/{\sigma }_w^2$; ${\sigma }_x^2$ is the input signal power; ${\sigma }_w^2$ means the noise variance; $\mathbf{I}$ denotes the identity matrix with appropriate dimension;

$$\begin{array}{c}\hfill \mathbf{K}=\left[\begin{array}{cccc}\kappa & 0& \beta & 0\\ 0& \kappa & 0& \beta \\ \beta & 0& \kappa & 0\\ 0& \beta & 0& \kappa \end{array}\right];\end{array}$$

(6)

$\kappa =\alpha +{\gamma }^{-1}$. The MMSE decoder, (5), looks similar to the ZF decoder, (4). A difference between the ZF and MMSE is the present of $\gamma$. Since $\gamma >0$, the MMSE has a low BER and $\mathbf{K}$ is always invertible. However, it is difficult to get $\gamma$ in practical applications. To overcome this drawback, estimation of the noise variance will be proposed in the next section.

3. Proposed Algorithm

3.1. Estimation of the Noise Variance

Taking the squared Euclidean norm and mathematical expectation of both sides of (1), the autocorrelation of the received signal is obtained as

$$\begin{array}{cc}\hfill \mathrm{E}\left\{{\mathbf{r}}^H\mathbf{r}\right\}=& \mathrm{E}\left\{{(\mathbf{H}\mathbf{x}+\mathbf{w})}^H(\mathbf{H}\mathbf{x}+\mathbf{w})\right\},\hfill \\ \hfill =& \mathrm{E}\{{\mathbf{x}}^H{\mathbf{H}}^H\mathbf{H}\mathbf{x}+2{\mathbf{x}}^H{\mathbf{H}}^H\mathbf{w}+{\mathbf{w}}^H\mathbf{w}\},\hfill \end{array}$$

(7)

where E means the expectation of random variables. If the noise $\mathbf{w}$ and the signal $\mathbf{x}$ are uncorrelated, the second term of the right hand side is neglected. (7) is rewritten as

$$\begin{array}{cc}\hfill \mathrm{E}\left\{{\mathbf{r}}^H\mathbf{r}\right\}=& \mathrm{E}\left\{{\mathbf{x}}^H{\mathbf{H}}^H\mathbf{H}\mathbf{x}\right\}+\mathrm{E}\left\{{\mathbf{w}}^H\mathbf{w}\right\}\hfill \\ \hfill =& \mathrm{E}\left\{\mathrm{Tr}\left\{\mathbf{D}\mathbf{x}{\mathbf{x}}^H\right\}\right\}+4{\sigma }_w^2,\hfill \end{array}$$

(8)

where $\mathrm{Tr}$ means the trace of the matrix. In terms of the noise variance, (8) is rearranged as

$$\begin{array}{c}\hfill 4{\sigma }_w^2=\mathrm{E}\{{\mathbf{r}}^H\mathbf{r}-\mathrm{Tr}\left\{\mathbf{D}\mathbf{x}{\mathbf{x}}^H\right\}\}.\end{array}$$

(9)

If the modulated input signal occurs with equal probability, then the expectation of cross-correlation between $x_i$ and $x_j$ for $i\ne j$ is zero, i.e., $\mathbf{x}{\mathbf{x}}^H\approx {\sigma }_x^2\mathbf{I}$. By using this circumstance, the estimation of the noise variance is calculated as

$$\begin{array}{c}\hfill {\sigma }_w^2\approxeq \frac{\mathrm{E}\{{\mathbf{r}}^H\mathbf{r}-4{\sigma }_x^2\alpha \}}{4}.\end{array}$$

(10)

The expected value of the signal is estimated using a moving-average method [12]. Therefore, the noise variance is obtained as

$$\begin{array}{cc}\hfill {\widehat{\sigma }}_w^2\left(n\right)=& \zeta {\widehat{\sigma }}_w^2(n-1)+(1-\zeta )\frac{{\mathbf{r}}^H\mathbf{r}-4{\sigma }_x^2\alpha }{4},\hfill \end{array}$$

(11)

and $\zeta (0\le \zeta <1)$ is a forgetting factor. However, several samples of ${\sigma }_w^2$ may be negative in early stages because of the fluctuation of an estimate. In this case, $\gamma$ cannot be calculated. To solve this drawback, (11) is modified as

$$\begin{array}{c}\hfill {\widehat{\sigma }}_w^2\left(n\right)=\left\{\begin{array}{cc}{\widehat{\sigma }}_w^2(n-1)\hfill & \mathrm{if}{\widehat{\sigma }}^2\left(n\right)<0\hfill \\ \zeta {\widehat{\sigma }}_w^2(n-1)+(1-\zeta )\frac{{\mathbf{r}}^H\mathbf{r}-4{\sigma }_x^2\alpha }{4}\hfill & \mathrm{others}\hfill \end{array}\right..\end{array}$$

(12)

3.2. Reducing the Computational Complexity

To obtain the diagonal matrix from the detection matrix, $\mathbf{K}$, the proposed algorithm is derived using four elementary matrices. By pre-multiplying $\mathbf{K}$ by ${\mathbf{E}}_1$ to eliminate $k_{31}$, where $k_{ik}$ means the $(i,k)$ entry of $\mathbf{K}$, a matrix is obtained as

$$\begin{array}{c}\hfill {\mathbf{E}}_1\mathbf{K}=\left[\begin{array}{cccc}\kappa & 0& \beta & 0\\ 0& \kappa & 0& \beta \\ 0& 0& \kappa -\beta \theta & 0\\ 0& \beta & 0& \kappa \end{array}\right],\end{array}$$

(13)

where

$$\begin{array}{c}\hfill {\mathbf{E}}_1=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ -\theta & 0& 1& 0\\ 0& 0& 0& 1\end{array}\right],\theta =\frac{\beta }{\kappa }.\end{array}$$

By using the above procedure, i.e., by pre-multiplying (13) by ${\mathbf{E}}_2,{\mathbf{E}}_3,$ and ${\mathbf{E}}_4$ to remove $k_{42},k_{13},$ and $k_{24}$, respectively, the diagonal matrix is finally given as

$$\begin{array}{c}\hfill \delta \mathbf{I}={\mathbf{E}}_4{\mathbf{E}}_3{\mathbf{E}}_2{\mathbf{E}}_1\mathbf{K}=\mathbf{E}\mathbf{K}\end{array}$$

(14)

where $\delta =\kappa -\frac{{\beta }^2}{\kappa }$,

$$\begin{array}{cc}\hfill {\mathbf{E}}_4=& \left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1-{\theta }^2& 0& -\theta \\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right],\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill {\mathbf{E}}_3=& \left[\begin{array}{cccc}1-{\theta }^2& 0& -\theta & 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right],\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill {\mathbf{E}}_2=& \left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& -\theta & 0& 1\end{array}\right],\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill \mathbf{E}=& {\mathbf{E}}_4{\mathbf{E}}_3{\mathbf{E}}_2{\mathbf{E}}_1=\left[\begin{array}{cccc}1& 0& -\theta & 0\\ 0& 1& 0& -\theta \\ -\theta & 0& 1& 0\\ 0& -\theta & 0& 1\end{array}\right].\hfill \end{array}$$

(18)

Note that $\mathbf{E}$ is similar to ${\mathbf{K}}^{-1}$, but it is easily obtained by using $\theta$, i.e., the proposed algorithm does not require any matrix inversion but can be calculated using $\theta$ and (18).

Since the proposed algorithm is derived not from a transformation of the channel matrix but from a change of the detection matrix, the encoding matrix is expressed as [4]

$$\begin{array}{c}\hfill \mathbf{X}=\left[\begin{array}{cccc}{x}_1& x_2& x_3& x_4\\ -x_2^{*}& x_1^{*}& -x_4^{*}& x_3\\ x_3& x_4& x_1& x_2\\ -x_4^{*}& x_3^{*}& -x_2^{*}& x_1^{*}\end{array}\right].\end{array}$$

(19)

From (14), the estimate of $\mathbf{x}$ is obtained as

$$\begin{array}{c}\hfill \widehat{\mathbf{x}}=\mathbf{E}{\mathbf{H}}^H\mathbf{r}=\mathbf{E}{\mathbf{H}}^H\mathbf{H}\mathbf{x}+\mathbf{E}{\mathbf{H}}^H\mathbf{w}.\end{array}$$

(20)

To sum up, the MMSE decoder is similar to the proposed algorithm. The main difference between the two algorithms is whether the noise variance is known or not. In other words, the MMSE decoder is not available in practical applications, because the noise variance is unknown [11]. On the other hand, the proposed algorithm can be used in real applications, because the noise variance is estimated in (12). In addition, the computational complexity of the conventional algorithm is higher than that of the proposed algorithm. The reason is that while the computation load of the conventional algorithm is 64 multiplications for the detection matrix and $O\left(n^3\right)$ for matrix inversion, that of the proposed algorithm is 16 multiplications each time.

4. Simulation Results

In this section, the BER performance of the proposed algorithm is illustrated through computer simulation for a Rayleigh fading channel. The modulation type was presumed to be the quadrature phase shift keying and the channel was assumed to be a zero-mean white Gaussian or correlated with the variance of $\frac{1}{2}$. The coefficient of the channel was perfectly known in the receiver [5]. The background noise $\mathbf{w}$ is added to $\mathbf{H}\mathbf{x}$.

Figure 1 compares the BER performance of the proposed algorithm at various forgetting factors in a Rayleigh fading channel. As can be seen, the BER performance can change slightly according to the forgetting factor in the proposed algorithm. Thus, from the next simulation, the parameter is selected as $\zeta =0.995$.

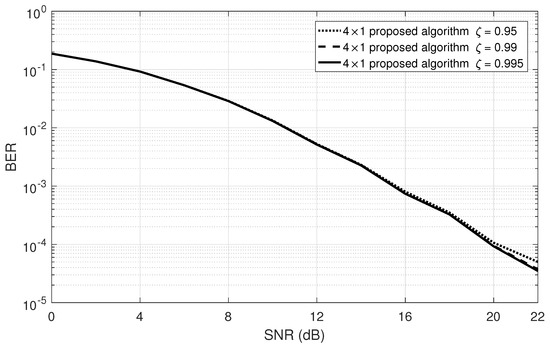
Figure 1. BER performance of the proposed algorithm at various forgetting factors for the four antennas system in a Rayleigh fading channel.

Figure 2 shows the BER performance of the proposed algorithm compared to that of the conventional QO-STBC algorithms under various signal-to-noise ratios (SNRs) from 6 dB to 22 dB for the four antennas system in a Rayleigh fading channel [5]. As shown in Figure 2, the proposed algorithm illustrates the lowest BER in all SNRs. In addition, the proposed algorithm is verified in the three antennas environment [5]. Figure 3 compares the BER of the proposed algorithm with that of the conventional algorithms in a Rayleigh fading channel. As a consequence, the proposed algorithm is more useful than the other algorithms.

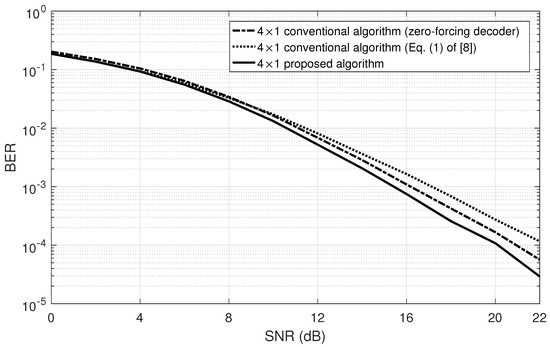
Figure 2. Bit-error-rate (BER) performance of the conventional quasi-orthogonal space–time block code (QO-STBC) and proposed algorithm as a function of the signal-to-noise ratio (SNR) for the four antennas system in a Rayleigh fading channel.

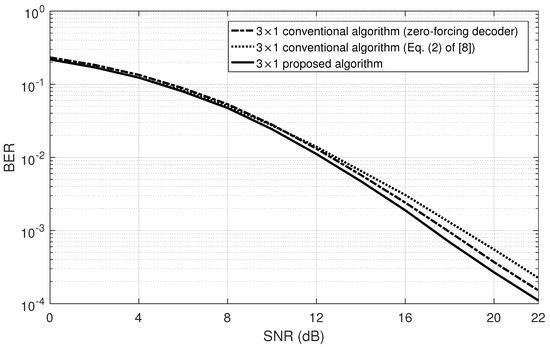
Figure 3. BER performance of the conventional QO-STBC and proposed algorithm as a function of the SNR for the three antennas system in a Rayleigh fading channel.

Figure 4 and Figure 5 compare again the conventional algorithms and proposed algorithm under a correlated Rayleigh fading channel (the correlation coefficient is 0.9) [13]. The proposed algorithm still achieves a better BER than the conventional algorithms.

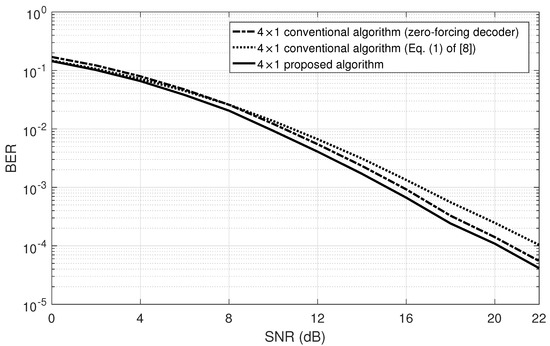
Figure 4. BER performance of the conventional QO-STBC and proposed algorithm as a function of the SNR for the four antennas system in a correlated Rayleigh fading channel (the correlation coefficient = 0.9).

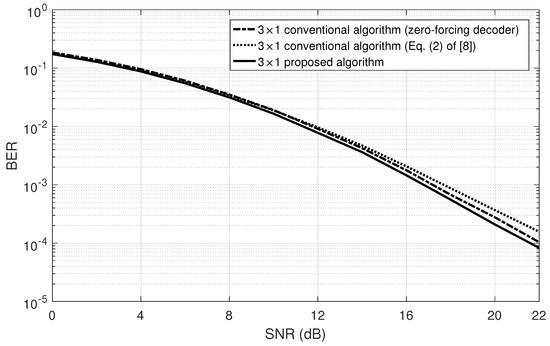
Figure 5. BER performance of the conventional QO-STBC and proposed algorithm as a function of the SNR for the three antennas system in a correlated Rayleigh fading channel (the correlation coefficient = 0.9).

5. Conclusions

In this paper, a decoding method for QO-STBC was proposed to achieve a lower BER result than the conventional algorithms, and to overcome the rank-deficient problem. The proposed algorithm contains the estimation algorithm of the noise variance to overcome the implementation problem from the MMSE. Moreover, it has low computational complexity without matrix inversion. Therefore, the proposed algorithm achieves a low BER and small computational complexity. Simulation results verified that the proposed algorithm had a small BER compared to the conventional algorithms in a Rayleigh fading channel.