An Enhanced Multi-Objective Gray Wolf Optimization for Virtual Machine Placement in Cloud Data Centers

Abstract

Cloud computing offers various services. Numerous cloud data centers are used to provide these services to the users in the whole world. A cloud data center is a house of physical machines (PMs). Millions of virtual machines (VMs) are used to minimize the utilization rate of PMs. There is a chance of unbalanced network due to the rapid growth of Internet services. An intelligent mechanism is required to efficiently balance the network. Multiple techniques are used to solve the aforementioned issues optimally. VM placement is a great challenge for cloud service providers to fulfill the user requirements. In this paper, an enhanced levy based multi-objective gray wolf optimization (LMOGWO) algorithm is proposed to solve the VM placement problem efficiently. An archive is used to store and retrieve true Pareto front. A grid mechanism is used to improve the non-dominated VMs in the archive. A mechanism is also used for the maintenance of an archive. The proposed algorithm mimics the leadership and hunting behavior of gray wolves (GWs) in multi-objective search space. The proposed algorithm was tested on nine well-known bi-objective and tri-objective benchmark functions to verify the compatibility of the work done. LMOGWO was then compared with simple multi-objective gray wolf optimization (MOGWO) and multi-objective particle swarm optimization (MOPSO). Two scenarios were considered for simulations to check the adaptivity of the proposed algorithm. The proposed LMOGWO outperformed MOGWO and MOPSO for University of Florida 1 (UF1), UF5, UF7 and UF8 for Scenario 1. However, MOGWO and MOPSO performed better than LMOGWO for UF2. For Scenario 2, LMOGWO outperformed the other two algorithms for UF5, UF8 and UF9. However, MOGWO performed well for UF2 and UF4. The results of MOPSO were also better than the proposed algorithm for UF4. Moreover, the PM utilization rate (%) was minimized by 30% with LMOGWO, 11% with MOGWO and 10% with MOPSO.

1. Introduction

Cloud computing is a newly emerging field in information technology. Cloud computing offers various services. Generally, there are three categories of cloud computing services: software as a service, platform as a service and infrastructure as a service. The services provided by the cloud are shown in Figure 1.

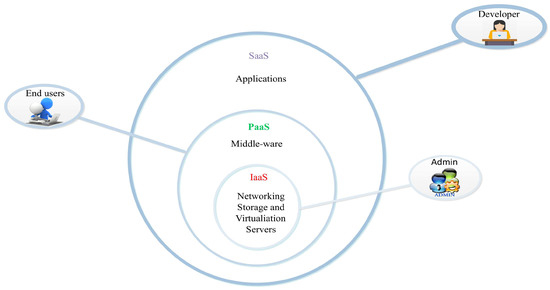
Figure 1. Cloud services.

Furthermore, there are three types of cloud networks: public, private and hybrid. Public clouds provide numerous services for all users. Anyone ub the world can access these services using the Internet. However, a specific organization can deploy a private cloud for their use only. The services provided by a private cloud can only be accessed using a private network. The combination of the public and private cloud is known as a hybrid cloud, in which some services provided by the cloud can be accessed through a private network, while others can be accessed using the Internet [1], as shown in Figure 2.

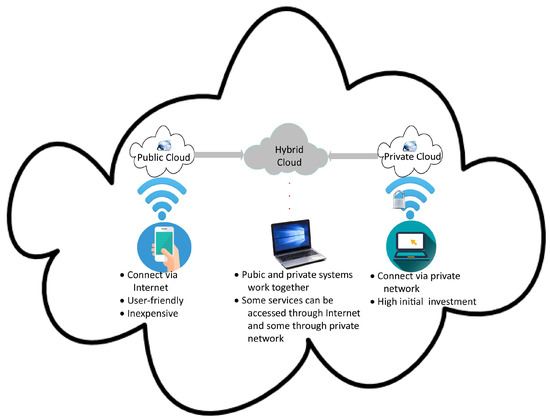
Figure 2. Types of clouds.

Cloud data centers have multiple physical machines (PMs). Thus, an efficient management is required to handle complex cloud data centers for the deployment of clouds. Cloud data centers consist of many PMs. Cloud operators want to reduce cost by minimizing the number of PMs [1]. Virtualization technology provides the facility of virtual machines (VMs) to run multiple applications. VMs are allocated to fulfill the requirements of the users [2]. The number of VMs is increasing dramatically. The dramatic growth of VMs and applications cause unbalanced network resources [3]. A mechanism is required to balance the load of a network.

The main approaches used to balance the load of a network are VM integration and intelligent task assignment. Further, VM integration involves two approaches: VM placement and VM migration. An intelligent placement of the VMs according to the capacity of each PM is the sole purpose of VM placement approach. VM migration is the process of moving tasks from overloaded or underloaded servers to the normal servers. An upper and lower threshold is already defined; migration is done when the capacity of PMs reach a critical value. An intelligent task assignment involves artificial intelligence to balance the load efficiently. However, the cost is increased using intelligent task assignment [3].

VM placement is an NP-hard problem [3]. An efficient mechanism is required to place the VMs intelligently. The sole purpose of the VM placement is to minimize the wastage of cloud resources. In this paper, an enhanced levy based multi-objective gray wolf optimization algorithm (LMOGWO) is proposed for VM placement. Multi-objectivity is the most important challenge in solving real engineering problems. In multi-objective problems, more than one objective function needs to be optimized. Normally, two approaches are used to handle multi-objective problems: a priori and a posteriori. A priori combines all objectives of the multi-objective problem and treats them as a single objective problem. Furthermore, a set of weights are assigned to all problems. This approach finds a single optimum solution. In a posteriori method, the formulation of the multi-objective problems is maintained. The decision makers choose the solution from all obtained values based on their needs. However, a theorem called no free launch (NFL) proves that it is not necessary for any optimization technique to solve all optimization problem [4].

In this paper, an archive is attached to save the non-dominant solutions. Furthermore, it mimics the leadership hierarchy of gray wolves (GWs). The leadership mechanism is based on positions of alpha, beta and delta wolves. However, the positions of alpha, beta and delta are calculated using a step size of levy flight.

1.1. Limitations of Research and Contributions

Cloud computing provides an access to the computing resources: network, applications, storage, and servers. These resources are provided on demand to users [1]. With the increasing size of cloud data centers, the number of PMs also increases. The concept of virtualization is given to minimize the number of PMs. Virtual machines (VMs) allow users to run their applications [2]. VMs are increasing dramatically with the development of the cloud data center [3].

VM allocation is an NP-hard problem. VM allocation is a process of deploying a number of VMs to provide quality of services (QoS). The main questions arising in VM allocation are: How many VMs should be deployed? Which type of VMs is the best? Which physical server should allocate the VM? [3]. An optimal VM placement is needed to utilize the resources efficiently. However, the solution cannot be calculated as it is an NP-hard problem. Moreover, VM placement problem is computationally expensive.

In this paper, LMOGWO is proposed for multi-objective optimization to solve VM placement problem. The adaptivity of the proposed algorithm is tested on nine well-known multi-objective benchmark functions, i.e., congress on evolutionary computation (CEC) 2009 [4]. LMOGWO is proposed to place the VMs intelligently in archive according to their positions in cloud data centers. An efficient VM placement is done in this paper. The proposed algorithm is the hybrid of levy flight and MOGWO algorithm. The length of a step size is calculated using levy flight. The contributions of this work are listed below:

• An enhanced levy based MOGWO is proposed to solve the VM placement problem.
• An archive is attached to save the history of VMs.
• Leader selection mechanism is used to select the best three leaders(VMs), i.e., alpha, beta and delta to fulfill the requirements of users.
• Levy flight is used to generate a long jump towards the optimal solution. The position of GWs is then updated using step size of levy flight.
• Bin packing is used to pack the VMs in minimum number of physical servers.
• Best fit strategy is used to optimally pack the number of VMs in physical servers without wasting resources.
• The proposed algorithm efficiently minimized the utilization rate of PMs.

1.2. Implementation Practice Guidelines

Levy based MOGWO algorithm is proposed to solve VM placement problem efficiently. The steps involved in implementation are as follows:

• Initialize a population of GWs.
• Calculate the objective value of each particle.
• Find the non-dominated solutions.
• Select three leaders (alpha, beta and delta) from an archive.
• Calculate step length using levy flight.
• Update the positions of the leaders using gray wolf optimization plus step size.
• Update an archive.
• Select the leaders from an archive.

An archive is attached to save and retrieve the history of GWs. A leadership mechanism is used to find the first three best solutions. The three leaders from an archive guide other wolves to attack a prey. Omega wolves follow their leaders. Levy flight is used to calculate the length of a step size. Then, step size is added with the position updating formula to take long steps towards an optimal solution. The  the remainder of the paper is organized as follows. Related work is discussed in Section 2. Section 3 presents detailed description of the proposed work. Problem formulation is given in Section 4. The discussion of results is discussed in Section 5. Conclusion and future studies are given in Section 6.

2. Related Work

Riahi et al. proposed a multi-objective genetic algorithm (GA) in [1] to solve VM placement problem. Bernoulli simulations are also done to verify the adaptivity of the proposed work. The basic purpose of the work is to reduce the utilization rate of physical servers inside the cloud. A framework is also proposed to reduce the wastage of resources inside the cloud. In the real-time experiment, the VM placement problem in the targeted company is successfully optimized. It also reduces the operational cost. However, there is no mechanism to handle big data efficiently. The growing rate of data is high, thus there should be some solution to solve the aforementioned problem.

Guo, Y. et al. proposed a shadow routing approach in [2]. An intelligent VM-to-PM packing is done to avoid the wastage of cloud resources. The main focus of the proposed work is to save energy and cost. Furthermore, VM placement problem is also considered via VM auto-scaling. A strategy is proposed to deal with the dynamic applications and the user requests. The proposed algorithm is adaptive; there is no need to solve the optimization problem from scratch. The experimental results prove the compatibility of the proposed algorithm. However, VM placement is an NP-hard problem. Cloud data centers are complex, thus further enhancement is needed to solve the VM placement problem.

Fu, X. et al. proposed layered VM migration algorithms in [3]. The regions are first divided on the basis of the bandwidth utilization rate in the cloud data centers. Two algorithms are proposed to reduce the cloud resources efficiently. Inter-region migration is done between two regions. The basic concept of the inter-region migration algorithm is to migrate the tasks from overloaded or underloaded regions to normal regions. The other algorithm provides migration within the same region and is known as intra-region migration. The authors performed this work to balance the bandwidth utilization rate to avoid congestion. Congestion can cause delay, thus a mechanism is proposed to overcome the aforementioned issues. However, migration of one task increases the overall cost.

Mirjalili, S. et al. proposed a multi-objective gray wolf optimization algorithm [4]. Two new components are introduced with simple GWO algorithm. A fixed sized archive is attached to save the non-dominated solutions. It also mimics the leadership hierarchy of GWs. Four type of wolves are considered: $\alpha$, $\beta$, $\delta$ and $\omega$ wolves. $\alpha$ wolf is a leader and it has the best value. The second best value is the $\beta$ wolf and third best value is $\delta$. The remaining wolves are $\omega$. $\alpha$ guides other wolves in hunting. The proposed algorithm is further tested on 10 well-known benchmark functions to verify the adaptiveness of the given algorithm. Both bi-objective and tri-objective functions are used. However, the proposed algorithm cannot perform well for more than four-objective problems.

Jensi, R. et al. proposed an enhanced particle swarm optimization algorithm in [5]. It is a hybrid of levy flight and simple particle swarm optimization algorithm. The proposed work is done to solve global optimization problems. There are some issues in simple particle swarm optimization algorithm, e.g., trapping in local optima and premature convergence rate. The authors proposed a framework to solve the aforementioned issues. Twenty-one benchmark functions are also used to compare the proposed work with two existing algorithms. However, the proposed algorithm can only solve single-objective problems.

Rayati et al. proposed a framework for modified transactive control system in smart grid [6]. Furthermore, edge theorem is used to tune the control parameters efficiently. A flexible and reliable communication platform is developed. A cloud-based framework is considered. A work is done to mitigate the challenges of irregular wind power. However, a further robust mechanism is required to handle the challenges of wind power.

Lopez et al. proposed a novel architecture for cloud computing. The cloud resources are leveraged in [7]. Time series forecasting is done for load prediction. The main purpose of prediction is to deal with the demand response. Load balancing algorithms are also proposed to balance the load of a cloud data centers. The cloud applications and users are increasing dramatically, thus load balancing is necessary for the cloud computing environment. Experimental tests are performed to verify the adaptiveness of the proposed work. However, there is a variation in demands of users. Thus, an efficient mechanism is needed to tackle the varying demands.

Liu, J. et al. proposed a cloud energy storage in [8]. Basically, it is a pool of energy storage devices. The sole purpose of the work done is to minimize the storage cost. The proposed mechanism is implemented in the residential area of Ireland to check the compatibility of the given framework. The main considerations in the experiment are load and electricity price. The authors proposed two decision-making models for consumer and cloud energy storage operator. In the first model, it is assumed that the user and operator both have perfect information. In another case, the operator does not have a correct prediction about the user. However, an enhanced model is required to provide an accurate information of a user to the operator.

Yang, T. et al. considered energy efficiency for both servers and data centers in the cloud computing environment [9]. The authors proposed a genetic algorithm based VM placement approach and configuration of communication traffic. Furthermore, VPTCA is proposed for energy efficient data centers planning. The proposed work reduces energy consumption and transmission load. Load balancing is also done. However, VM placement is an NP-hard problem. Further enhancement is required.

Munshi, A.A. et al. proposed an eco-system to handle big data of smart grid in [10]. The proposed system depends on lambda architecture. The sole purpose of the proposed work is to perform parallel batching and real-time operations. Distributed data are considered for this purpose. The proposed work uses Hadoop big data lake to store data of all smart devices. Some data mining techniques are also used on big data. The eco-system handles the massive amount of data. However, there is a limit of big data lake and the smart users are increasing dramatically. Thus, there should be some mechanism to handle the dynamic behavior of smart devices.

Wu, L. et al. proposed an efficient scheme for cloud deployment in [11]. The authors proposed an efficient identity-based-encryption scheme with the bilinear pairing. A cloud is considered along with smart grid to store the data of smart devices efficiently. The performance of the cloud is increased in terms of computational cost and storage overhead. The cost is reduced by 39.24%. However, there is a chance of delay because there is no mechanism to balance the load of a cloud.

Multi-objective non-dominated sorting GA was proposed by Guerrero, C. et al. [12]. The authors proposed a mechanism to solve VM allocation and VM template selection problems. The basic objectives of the work done are the minimization of power consumption and reduction of PM resource wastage. To solve the aforementioned issues, the authors presented an approach focusing on virtualized Hadoop. Power consumption is reduced by 1.9 %. However, VM allocation is not an optimal solution to deal with the rapidly increasing cloud users.

Cao, Z. et al. investigated bi-objective optimization problem in [13]. Dynamic VM consolidation approach is proposed to minimize the migration cost and save energy. A heterogeneous cloud data centers are considered. An improved grouping genetic algorithm is proposed to solve the aforementioned issues. The authors reduced energy consumption. Migration cost is also minimized. However, VM consolidation problem still needs to be optimized.

Javaid, N. et al. proposed two pricing schemes in [14]. Information and communication technology is used with the traditional grid to make it smart. Scalability is needed to handle the rapidly increasing smart devices and users in demand-side. Cao et al. proposed a cost-oriented optimization mechanism for demand-side management. The flexible and cost-efficient optimization is done in cloud data centers. On-demand pricing strategy is proposed for short-term users. It works similar to pay as you go. The other pricing scheme is for long-term users and known as the reserved instance. The cost per unit for reserved instance is less than the other one. However, a user has to give upfront payment for reserved instance.

Javaid, S. et al. proposed a hybrid-genetic-wind-driven algorithm in [15]. The authors performed this work to schedule the electricity load between on-peak and off-peak hours. A residential area is considered. Furthermore, user comfort is maximized, electricity cost and peak to average ratio are minimized. Scheduling is done for both single and multiple homes to verify the adaptiveness of the proposed algorithm. However, further enhancement is required to solve the aforementioned objectives.

A cloud fog based smart grid model is proposed in [16]. The basic purpose of the proposed work is to manage the cloud resources efficiently. A hybrid artificial bee ant colony optimization algorithm is proposed to solve the aforementioned problem. The proposed algorithm efficiently balanced the load of cloud data centers. Response time and processing time is also optimized. However, load balancing algorithms are not enough to handle complex cloud data centers.

Bakhsh, R. et al. proposed a demand-side management technique to control the load of smart homes in [17]. Priorities are defined for time-varying home appliances. An evolutionary-accretive-comfort algorithm is proposed. The proposed algorithm is based on a genetic algorithm. The main objective of the proposed work is to minimize energy consumption. However, user comfort is compromised in the scheduling process.

Chekired, D.A. et al. proposed scheduling algorithms to assign priorities to electric vehicles in [18]. The problem of electric vehicles charging and discharging is considered. The main focus of proposed work is to provide power at public supply stations during on-peak and off-peak hours. Two types of users are considered in this paper, i.e., calendar users and random users. Four priority levels are assigned to solve the aforementioned issue. If the demand of user is less than or equal to the generation of power, then Priority 1 is given to calendar users and Priority 3 to random users for charging. Priorities 2 and 4 are given for discharging of calendar and random users. In another case, i.e., demand is greater than the generation, the Priorities 1 and 3 are given for discharging of vehicles. Priorities 2 and 4 are assigned for charging of electric vehicles. However, the disposal of batteries pollutes the environment badly.

Heidari, A.A. et al. proposed cloud-fog based system in [19]. An efficient scheduling mechanism is developed to efficiently schedule the requests coming from smart homes. A chance of delay for smart devices is considered. Furthermore, response time and processing time is optimized. Total cost is also minimized. A 5G home energy management controller is attached to each home to provide a communication mechanism between fog and smart homes. Micro-grids are also deployed near the residential area to fulfill the energy demand of users. However, complex cloud data centers and rapidly increasing users cannot be tackled by only using load balancing algorithms.

Wu, Q. et al. proposed an enhanced modified GWO algorithm in [20]. The proposed algorithm is a hybrid of simple GWO algorithm and levy flight. Simple GWO algorithm stuck in local minima. Thus, the proposed work is done for efficient global and real-time optimization problems. Furthermore, 29 complex test functions are used to verify the compatibility of the proposed work. However, the global optimization problems have more than one objective function to be optimized. The proposed algorithm provides an optimal solution for a single objective.

Kong, Y. et al. [21] proposed a decentralized belief propagation based method. The sole purpose of the proposed work is multi-agent task allocation. Both the open and dynamic grid and cloud environment are considered. The performance of task allocation is improved. The authors proposed a mechanism to provide an online response to the users in order to improve the performance of the cloud environment. User satisfaction is also an important factor. Thus, an efficient communication mechanism is presented. However, an agent can perform one task at a time. This can increase delay.

Levy-based whale optimization algorithm is proposed in [22]. The authors proposed an efficient VM placement mechanism to minimize the cost, save energy and reduce wastage of resources. The sole purpose of the work done is to minimize the utilization rate of PMs in the cloud data centers. A variable sized bin packing problem is used to pack the maximum number of VMs into a minimum number of PMs. Moreover, the best fit strategy is used to provide optimal results. However, VM placement is an NP-hard problem. A mechanism is required to balance the load of complex data centers.

Khosravi, A. et al. aimed to minimize energy consumption [23]. Different parameters are investigated that affect energy. The basic purpose of the work done is to keep the environment green. The total cost is equal to the energy consumed plus overhead energy. Multiple VM placement algorithms are proposed to minimize the energy consumption optimally. Moreover, the cost of energy consumption is also reduced. However, there is no mechanism to provide energy continuously as renewable energy resources are considered.

Wang, H. et al. proposed energy-aware dynamic VM consolidation in [24]. The sole purpose of this work is to minimize energy consumption. Service level agreement is also considered. VM placement and VM migration both are done in this paper. Space aware best fit strategy is used for VM placement. High CPU utilization based migration is also done to balance the cloud environment efficiently. Energy consumption is minimized optimally. The load of the cloud environment is also balanced. However, an efficient mechanism is still required to handle complex cloud data centers as VM placement is an NP-hard problem and VM migration may increase migration cost.

Zhou, A. et al. proposed a model to assure the quality of VMs [25]. A reliable technique is required to enhance the reliability of the cloud environment. A redundant VM placement optimization approach is proposed to increase the reliability of the whole network. Three algorithms are proposed. The first algorithm helps to select an appropriate VM. The second algorithm ensures an efficient backup of VMs. The heuristic algorithm is also proposed to assign tasks of users to the VMs according to the capacity of each VM. However, the complexity of algorithms is increased.

Vakilinia, S. considered optimization problem in the cloud data centers in [26]. A workload is increased when a number of jobs arrive at the same time. Thus, an efficient mechanism is needed to solve the aforementioned issues. The authors gave us a solution to divide the problems into two parts. First, the optimization of the servers is performed. Then, migration is done to balance the load of cloud data centers. However, migration of task increases the cost.

Naz, M. et al. proposed an efficient mechanism for demand-side electricity management in [27]. It maintains the balance between the generation of energy and demand of the load. A two-way communication architecture between user and generation unit is proposed. Renewable energy resources are used for the generation of power. To balance the load between on-peak and off-peak hours, a hybrid gray wolf evolution algorithm is proposed. Real-time and critical-time pricing is used. The proposed technique efficiently shifted the load from on-peak hours to off-peak hours and maintained the balance between energy generation and demand. However, shifting load to off-peak hours can also create a peak in those hours.

Duong-Ba, T.H. et al. proposed a joint strategy to solve both VM placement and VM migration problems in [28]. It aims to reduce power consumption and minimize wastage of resources. Multi-objective optimization is considered in this work. The proposed algorithm efficiently reduced the energy consumption. The sole purpose of VM placement and VM migration is to balance the load of the cloud data centers. However, VM placement is an NP-hard problem and VM migration may increase cost. Thus, an efficient mechanism is required to solve the aforementioned problems.

A home energy management system was proposed by Khalid, A. et al. [29]. The basic purpose of work done is to balance the load through coordination. Energy consumption is optimized efficiently. It also reduced the electricity cost and peak to average ratio. However, an important factor is ignored i.e., user comfort.

Liu, X. et al. considered VM allocation problem in [30]. The basic purpose of the proposed work is to maximize the availability and reliability of resources provided by the cloud. Two selection methods are proposed to solve the aforementioned issues. Ziafat et al. proposed simplex linear programming and GrEA-based method to solve VM allocation problem efficiently. A geographically distributed cloud is considered for experiments. The proposed mechanism achieved an optimal trade-off between user requirements and utilization rate of resources. However, VM allocation is an NP-hard problem. Thus, an efficient mechanism is required to deal with complex cloud data centers.

Liu, X.-F. et al. proposed an efficient mechanism to solve VM placement [31]. The authors were inspired by the performance of an ant colony optimization algorithm. Thus, they used an ant colony optimization algorithm to place the VMs intelligently. The main purpose of the proposed work is to minimize the utilization rate of PMs to save energies and minimize cost efficiently. It efficiently minimized the usage of PMs and reduced the cost. However, the cloud data centers are complex and VM placement in an initial phase is not an efficient way to manage the resources. The related work is summarized in Table 1.

Table 1. Related work.

Techniques	Objectives	Achievements	Limitations
Multi-objective based genetic algorithm [1]	Efficient VM placement	Reduce the usage of running servers	VM placement problem is an NP-hard problem
Shadow routing-based approach [2]	Auto scaling of VMs and intelligent packing of VMs in minimum number of PMs	Reduced energy consumption and cost	Provides approach for only private clouds
Layered VM migration [3]	Congestion and delay of network	Balanced network resources and minimized delay	Migration cost is increased
MOGWO [4]	For mechanism to solve multi-objective problems	Achieved an optimal solution to solve multi-objective problems	Can not handle more than four objectives
Levy based particle swarm optimization algorithm [5]	Provide an efficient mechanism to solve premature convergence problem	Enhanced global optimization, avoided trapping and optimized premature convergence	Performs well for single objective problems
Modified transactive control system [6]	Mitigate challenges of irregular wind power	Provided robust, optimal and flexible solutions	The cost of energy is increased
A novel framework to deploy cloud computing platform [7]	Load balancing	Used time-series forecasting to balance the load efficiently	Discontinuous network
Cloud based energy storage pool [8]	High cost for energy storage devices	Developed cost-efficient energy storage pool for users	Great power loss for implementation purpose
VM placement based on genetic algorithm [9]	Network congestion in network, wastage of energy resources	Balanced transmission load and reduced energy consumption	VM placement problem is an NP-hard problem
Eco-system [10]	Management of real time smart grid data	Handle big data of smart grid	There may be a chance of congestion
Identity based encryption with bilinear pairing [11]	Minimize wastage of time	Efficient performance of cloud in terms of cost	There is an extra energy consumption
Multi-objective non-dominated sorting genetic algorithm [12]	VM allocation and VM template selection	Reduced power consumption and minimized wastage of resources	VM allocation is not efficient for rapidly growing users
Improved grouping genetic algorithm [13]	Dynamic VM consolidation problem	Minimized migration cost and reduced energy consumption	Further enhancement is required to solve VM consolidation problem
Cost-oriented optimization mechanism for smart grid user [14]	User comfort in terms of minimum cost	Efficient pricing schemes for users	Upfront payment for long-term users
Hybrid genetic-wind driven [15]	Efficient mechanism to balance the load of smart grid	The cost is minimized	During scheduling, user comfort is compromised
Hybrid artificial bee ant colony optimization [16]	Cloud resource management	Optimized response time and processing time	Load balancing algorithms can not handle complex cloud data centers
An evolutionary accretive-comfort algorithm [17]	Control load of smart homes	Minimized energy consumption	During scheduling, user comfort is compromised
Scheduling algorithm for electric vehicles charging and discharging [18]	Power supply station at public places	Balanced the load of electric vehicles during on-peak and off-peak hours	Disposal of batteries pollute the environment
5G home energy management controller [19]	Balanced load of smart grid	Optimally balanced the load and provided communication architecture between smart homes and fog	Load balancing algorithms can not balance load of dramatically increasing smart users

Cloud data centers and number of users are increasing dramatically. With the increase in number of tasks, an efficient mechanism is required to balance the load of cloud data centers. Resource management is an important objective of cloud data centers to efficiently handle the tasks. Numerous researchers are focused on solving the aforementioned objective. The authors of [1,2,3,4,5] considered several objectives to be optimized for efficient load balancing of the cloud. VM placement, VM autoscalling, task management and global optimization are considered, respectively. Further, the authors of [7,8,9,11,12,13] proposed different mechanisms for efficient resource management. The authors of [16,18,19,20] focused on efficient task scheduling. Efficient VM placement, VM consolidation, VM migration and optimization problem are solved in [22,24,25,26]. The authors of [30,31] proposed GreA and ACO to solve VM allocation and VM placement problem. However, VM placement problem is an NP-hard problem.

Several swarm intelligence optimization algorithms are used to solve the VM placement problem. An enhanced levy based MOGWO is proposed to solve the VM placement problem efficiently. The proposed algorithm is inspired from leadership mechanism of grey wolves. In other swarm intelligence optimization algorithms, only one best known point is taken. However, in GWO, three best positions are considered and these leaders then guide the remaining wolves to attack a prey.

3. Proposed Scheme

LMOGWO is proposed to solve the problem of VM placement. An archive is attached to the LMOGWO to save the list of non-dominated VMs. A selection mechanism of leaders ($\alpha ,\beta$ and $\delta$) is proposed to attack a prey efficiently. Three best VMs are selected to entertain the requests coming from users. Levy flight is used with MOGWO to take long steps towards an optimal solution.

3.1. Multi Objective Gray Wolf Optimization Algorithm (MOGWO)

GWs belong to the Canidae family. GWO is a swarm intelligent technique. This algorithm mimics the hunting behavior of GWs. GWs are famous for hunting in groups. They usually live in packs. The main inspiration of MOGWO is the leadership hierarchy of GWs. Mathematically, it is formulated as: the top best solution is taken as the alpha ($\alpha$) wolf, the other two best solutions are considered as beta ($\beta$) and delta ($\delta$) wolves and the remaining solutions are assumed to be omega ($\omega$) wolves, as shown in Figure 3. Omega wolves are guided by three leader wolves, i.e., alpha, beta and delta. Omega wolves have to follow the leaders in hunting (optimization) mechanism. Further, most of the swarm intelligence algorithms do not have leaders that handle a whole swarm. Three strategies are used to imitate the hunting behavior of wolves:

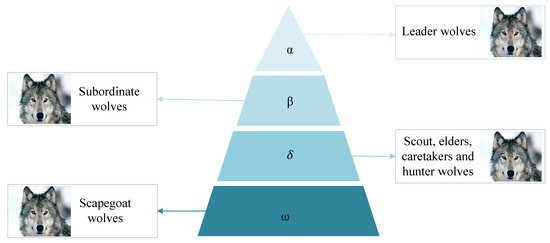
Figure 3. Leadership hierarchy of wolves.

• Searching
• Encircling
• Attacking

3.1.1. Searching (Exploration)

GWs normally search the prey according to the positions of leaders, i.e., alpha, beta and delta. Usually, random value is assigned to A in an initialization phase. When the value of |A| > 1, the wolves diverge from each other to search for prey. After finding a prey, the wolves converge towards prey and the value of |A| < 1.

3.1.2. Encircling (Exploration)

Encircling is the most important step in the hunting process. Encircling is a process of surrounding a prey in some type of harassment, so wolves can attack that prey. Encircling should be good enough to make attacking and hunting easy. Mathematically, the encircling behavior of GWs is formulated as [4]:

$$\overrightarrow{D}=|\overrightarrow{(C)}·\overrightarrow{X_p}(t)-\overrightarrow{X}(t)|$$

(1)

$$\overrightarrow{X}(t+1)=\overrightarrow{X_p}(t)-\overrightarrow{A}·\overrightarrow{D}$$

(2)

where t is the current iteration, $\overrightarrow{A}$ and $\overrightarrow{C}$ are coefficient vectors, $\overrightarrow{X_p}$ indicates the position of a prey and $\overrightarrow{X}$ shows the position of a wolf. The $\overrightarrow{A}$ and $\overrightarrow{C}$ vectors are calculated as [4]:

$$\overrightarrow{A}=2\overrightarrow{a}·\overrightarrow{r_1}-\overrightarrow{a}$$

(3)

$$\overrightarrow{C}=2·\overrightarrow{r_2}$$

(4)

After multiple iterations, the value of $\overrightarrow{a}$ decreases linearly from 2 to 0. The random vectors are $r_1$ and $r_2$ and their value is within [0, 1], as shown in Figure 4.

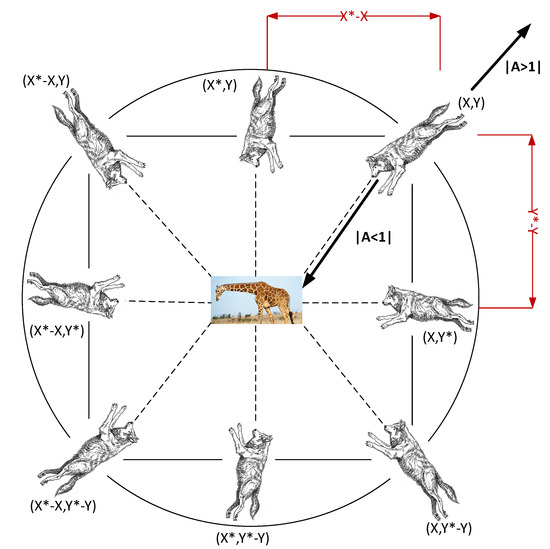
Figure 4. Position Updating Mechanism of Wolves and Effect of A.

3.1.3. Attacking (Exploitation)

Hunting a prey is normally guided by alpha. Other wolves participate in hunting according to their leadership hierarchy. Good encircling is very important for hunting. When prey is not able to move, the wolves just attack. In an abstract search space, the optimal position of a prey is not known. It is supposed that the alpha, beta and delta have better knowledge so other wolves follow them. Omega wolves update their position according to the optimal position of the leaders. During optimization, the following formulas run to find the promising regions of the search space [4]:

$${\overrightarrow{D}}_{\alpha }=|\overrightarrow{C_1}·{\overrightarrow{X}}_{\alpha }-\overrightarrow{X}|$$

(5)

$${\overrightarrow{D}}_{\beta }=|\overrightarrow{C_2}·{\overrightarrow{X}}_{\beta }-\overrightarrow{X}|$$

(6)

$${\overrightarrow{D}}_{\delta }=|\overrightarrow{C_3}·{\overrightarrow{X}}_{\delta }-\overrightarrow{X}|$$

(7)

$${\overrightarrow{X}}_1={\overrightarrow{X}}_{\alpha }-{\overrightarrow{A}}_1·({\overrightarrow{D}}_{\alpha })$$

(8)

$${\overrightarrow{X}}_2={\overrightarrow{X}}_{\beta }-{\overrightarrow{A}}_2·({\overrightarrow{D}}_{\beta })$$

(9)

$${\overrightarrow{X}}_3={\overrightarrow{X}}_{\delta }-{\overrightarrow{A}}_3·({\overrightarrow{D}}_{\delta })$$

(10)

$$\overrightarrow{X}(t+1)=\frac{{\overrightarrow{X}}_1+{\overrightarrow{X}}_2+{\overrightarrow{X}}_3}{3}$$

(11)

Two new components are integrated with GWO for multi-objective optimization. One is an archive, which is responsible for storing the Pareto front of non-dominated wolves (VMs). An archive is mostly used to store and retrieve Pareto optimal solutions [4]. Leader selection strategy of wolves (VMs) is the second component of multi-objective optimization. Three best VMs are used to entertain the user requirement. First, alpha VM is used to fulfill the requirement of user. Then, beta and delta VMs are used. There is an archive controller to control the archive whenever a new wolf position (solution) wants to enter in the archive or the archive is full. The following cases are considered here for an archive [4]:

• The new value should have a better solution than the existing ones in the archive. Otherwise, it is not allowed for a new value to be inserted in the archive.
• If the new wolf has better value, then the solutions in the archive have to leave the archive and allow a new solution to come inside it.
• If the value of both solutions is same, the new solution is allowed to be moved into the archive.
• If the archive is full, the grid mechanism finds the most crowded segment to omit its solutions. Then, the new solutions should enter the least crowded segment.

The leader selection mechanism is the second component of MOGWO. The first three best solutions found are alpha, beta and delta. Other wolves follow the leaders. There might be some special cases. The first three leaders should be selected from the least crowded segment. If there are only two solutions in the least crowded hypercube, the third one should be selected from second least crowded one. There is also a chance to select a delta wolf from the third least crowded segment. Through this hierarchy, there is no chance to select the same wolf as alpha and beta. The Pseudocode of MOGWO is given in Algorithm 1 [4]:

Algorithm 1 Pseudocode of the MOGWO algorithm.

3.2. Levy Flight Distribution

Levy distribution is used to calculate the step length of the random walk. It usually starts from one best-known location. Levy flight generates a new generation at a distance according to the levy distribution. It selects the most encouraging new generation. The basic steps involved in levy flight are as follows:

• Select the random direction.
• Generate a new step.

Power-law is used to balance the step size of levy distribution. The formula of power-law is [5]:

$$L(s)\sim {|s|}^{-1-\beta }$$

(12)

where 0 $<\beta <$ 2 is an index.

3.3. Simple Levy Distribution

The mathematical representation of levy distribution is [5]:

$$\begin{array}{c}\hfill D_{it}=\left\{\begin{array}{c}L(s,\gamma ,\mu )=\sqrt{\frac{\gamma }{2\pi }}exp\left[\begin{array}{c}\frac{\gamma }{2(s-\mu )}\end{array}\right]\frac{1}{{(s-\mu )}^{3{/}_2}},\hfill \\ \mathrm{if}0\le \mu \le s\le inf\hfill \\ 0,\mathrm{if}s\le 0\hfill \end{array}\right\}\end{array}$$

(13)

where $\mu$ is a shift parameter, and a scale parameter $\gamma >0$ is used to control the distribution scaling.

Fourier Transform

Generally, Fourier transform is used to define levy distribution [5].

$$F(k)=exp[\alpha |k{|}^{\beta }],0<\beta \le 2$$

(14)

where $\alpha$ is a scale factor. The value of $\alpha$ is 0.5 and $\beta \in (0,2)$. $\beta$ is the levy index.

For random walk, Mantegna’s algorithm is used to calculate the step length [5]:

$$S=\frac{u}{{|v|}^{1{/}_{\beta }}}$$

(15)

where u and v are drawn from normal distribution [5].

$$u\sim N(O,{\sigma }_u^2),v\sim N(O,{\sigma }_v^2)$$

(16)

where

$${\sigma }_u=\frac{\Gamma (1+\beta )sin(\pi \beta {/}_2)}{\Gamma (1+\beta {/}_2)\beta 2^{\beta -1}{/}_2}$$

(17)

The following formula is used to calculate the step size:

$$\mathrm{step}\mathrm{size}=0.01\times S$$

(18)

3.4. Levy Based Multi-Objective Gray Wolf Optimization Algorithm (LMOGWO)

The basic steps of the proposed algorithm are the same as MOGWO. Levy distribution is used for the generation of a long step towards the optimal solution (position of prey). The following equation is used to update the position of alpha, beta and delta.

$$\overrightarrow{X}(t+1)=\frac{{\overrightarrow{X}}_1+{\overrightarrow{X}}_2+{\overrightarrow{X}}_3}{3}+\mathrm{step}\mathrm{size}$$

(19)

The position of the three leaders will be continuously updated until they are not ready to attack a prey. N represents number of wolves and M is the number of objectives. The Pseudo code and flowchart of LMOGWO is given in Algorithm 2 and Figure 5.

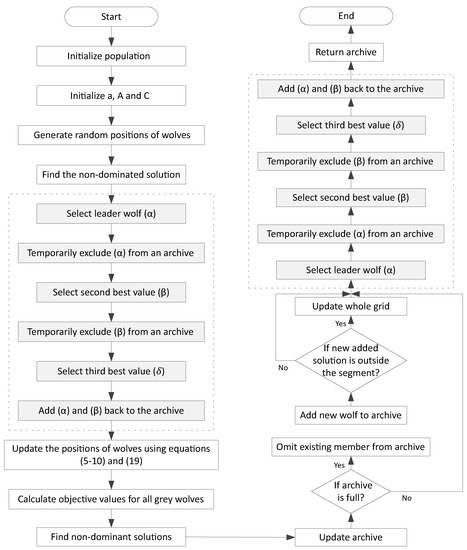
Figure 5. Flowchart of LMOGWO.

Algorithm 2 Pseudocode of the LMOGWO algorithm.

An optimization algorithm is proposed to solve VM placement problem. Bin packing is used to pack the number of VMs into minimum number of PMs. Minimization of PMs utilization rate minimizes the energy consumption and cost. An archive is the memory used to store and retrieve the history. Archive controller is used to manage the archive. The proposed mechanism is inspired from leadership hierarchy of GWs.

4. Problem Formulation

Bin packing is used to solve the VM placement problem efficiently [32]. Multiple physical hosts having different capacities are used to pack number of VMs. Packing s number of items (VMs) into a single physical host is performed to optimize the resources of cloud data centers. Multi-objective VM optimization problem is used. Two objectives are considered in this work: minimization of utilization rate of physical servers and wastage of resources. The first objective is formulated as follows [32]:

$$min\sum _{j=1}^n\sum _{k=1}^m{c}_k·y_{jk}$$

subject to

$$\sum _{j=1}^n{x}_{ij}=1$$

(20)

$$\sum _{k=1}^m{y}_{jk}\le 1$$

(21)

$$\sum _{i=1}^n{w}_i·x_{ij}\le \sum _{k=1}^m{W}_k·y_{jk}$$

(22)

$$c_k=\sum _{k=1}^m{W}_k·y_{jk}-\sum _{i=1}^n{w}_i·x_{ij}$$

(23)

$$x_{ij}\in \{0,1\}$$

$$y_{jk}\in \{0,1\}$$

for $i=1,\dots ,n,j=1,\dots ,n$ and $k=1,\dots ,m$; n is the items and bins; types of items used are represented as m; $c_k$ represents the wasted space of k type of bin of type k; $y_{jk}$ is a binary variable used to show that the physical server i of type k contains VMs; $x_{ij}$ is also a binary variable and it shows that the VM i is assigned to the physical server j; $w_j$ is weight of VMs (items); and $W_k$ is the capacity of physical server of type k. It is the worst case if number of VMs is set to be equal to the physical servers. Further, best-fit strategy is used to optimally pack the number of VMs without wasting resources. Best-fit strategy arranges the number of VMs in descending order and then packs them in physical servers to minimize the wastage of resources. However, the workload of physical hosts increases with an increase of number of VMs inside them.

5. Results and Discussion

This section includes parameters setting, results and discussion of results.

5.1. Parameters Setting (Scenario 1)

LMOGWO was compared with the simple MOGWO and multi-objective particle swarm optimization (MOPSO). The initial parameters for MOGWO are given below:

• $\alpha$ = 0.1: grid inflation parameter;
• $\beta$ = 4: leader selection parameter; and
• nGrid = 10: number of grids per dimension.

For MOPSO, the initial parameters chosen are given below:

• $\alpha$ = 0.1: grid inflation parameter;
• $\beta$ = 4: leader selection parameter;
• nGrid = 10: number of grids per dimension;
• c1 = 1: personal learning co-efficient;
• c2 = 2: global learning co-efficient; and
• $\omega$ = 0.5.

For all experiments, 100 search agents were considered and the number of iteration was 50. To check the adaptivity of the proposed algorithm, nine benchmark functions were implemented that are given in [4]. These benchmark functions are given in Table 2 and Table 3. In the literature, these benchmark problems are proven to be the most challenging problems [4].

Table 2. Bi-objective benchmark functions.

Name	Mathematical Formulation
UF1	$f_1=x_1+\frac{2}{J_1}{\sum }_{jϵJ_1}{[x_j-sin(6\pi x_1+\frac{j\pi }{n})]}^2,f_2=1-\sqrt{x}+\frac{2}{|J_2|}{\sum }_{jϵJ_2}{[x_j-sin(6\pi x_1+\frac{j\pi }{n})]}^2$ $J_1$ = {j|j is odd and $2\le j\le n\}$, $J_2$ = {j|j is an even and $2\le j\le n\}$
UF2	$f_1=x_1+\frac{2}{|J_1|}{\sum }_{jϵJ_1}{y}_j^2,f_2=1-\sqrt{x}+\frac{2}{|J_2|}{\sum }_{jϵJ_2}{y}_j^2$ $J_1$ = {j|j is odd and $2\le j\le n\}$, $J_2$ = {j|j is an even and $2\le j\le n\}$ $$\begin{gathered} y_j=\{x_j-[0.3x_1^{2}cos(24\pi x_1+\frac{4j\pi }{n})+0.6x_i]cos(6\pi x_1+\frac{j\pi }{n}) if jϵJ_1 \\ {x}_j-[0.3x_1^{2}cos(24\pi x_1+\frac{4j\pi }{n})+0.6x_i]sin(6\pi x_1+\frac{j\pi }{n}) if jϵJ_2\} \end{gathered}$$
UF3	$f_1=x_1+\frac{2}{|J_1|}{\sum }_{jϵJ_1}h(y_j),f_2=1-x^2+\frac{2}{|J_2|}{\sum }_{jϵJ2}h(y_j)$ $J_1$ and $J_2$ are the same as those of UF1, $y_j=x_j-sin(6\pi x_1+\frac{j\pi }{n}),j=2,3,\dots ,n,h(t)=\frac{|t|}{1+e^{2|t|}}$
UF4	$$\begin{gathered} f_1=x_1+(\frac{1}{2N}+ϵ)|sin(2N\pi x_1)|+\frac{2}{|J_1|}{\sum }_{jϵJ1}h(y_i), \\ {f}_2=1-x_1+(\frac{1}{2N}+ϵ)|sin(2N\pi x_1)|+\frac{2}{|J_2|}{\sum }_{jϵJ2}h(y_i) \end{gathered}$$ $J_1$ and $J_2$ are the identical to those of UF1, $ϵ>0,y_j=x_j-sin(6\pi x_1+\frac{j\pi }{n}),j=2,3,\dots ,n$ $h(t)=2t^2-cos(4\pi t)+1$
UF5	$$\begin{gathered} f_1=x_1+max\{0,2(\frac{1}{2N}+ϵ)sin(2N\pi x_1)\}\frac{2}{|J_1|}(4{\sum }_{jϵJ_1}{y_j}^2-2{\prod }_{jϵJ_1}cos(\frac{{20}_{j\pi }}{\sqrt{j}}+1)) \\ {f}_2=1-x_1+max\{0,2(\frac{1}{2N}+ϵ)sin(2N\pi x_1)\}\frac{2}{|J_2|}(4{\sum }_{jϵJ_2}{y_j}^2-2{\prod }_{jϵJ_2}cos(\frac{{20}_{j\pi }}{\sqrt{j}}+1)) \end{gathered}$$ $J_1$ and $J_2$ are the identical to those of UF1, $ϵ>0,y_j=x_j-sin(6\pi x_1+\frac{j\pi }{n}),j=2,3,\dots ,n$
UF6	$f_1=5\sqrt{x_1}+\frac{2}{|J_1|}{\sum }_{jϵJ_1}{y_j}^2,f_2=1-5\sqrt{x_1}+\frac{2}{|J_2|}{\sum }_{jϵJ_2}{y_j}^2$ $J_1$ and $J_2$ are the identical to those of UF1, $ϵ>0, y_j=x_j-sin(6\pi x_1+\frac{j\pi }{n}),j=2,3,\dots ,n$

Table 3. Tri-objective benchmark functions.

Name	Mathematical Formulation
UF7	$f_1=cos(0.5x_1\pi )cos(0.5x_2\pi )+\frac{2}{|J_1|}{\sum }_{jϵJ_1}(x_j-2x_{2}sin{(2\pi x_1+\frac{j\pi }{n})}^2)$ $f_2=cos(0.5x_1\pi )sin(0.5x_2\pi )+\frac{2}{|J_2|}{\sum }_{jϵJ_2}(x_j-2x_{2}sin{(2\pi x_1+\frac{j\pi }{n})}^2)$ $f_3=sin(0.5x_2\pi )+\frac{2}{|J_2|}{\sum }_{jϵJ_3}(x_j-2x_{2}sin{(2\pi x_1+\frac{j\pi }{n})}^2)$ $J_1=\{j|3\le j\le n,$ and j-1 is a multiplication of 3}, $J_2=\{j|3\le j\le n,$ and j-2 is a multiplication of 3}, $J_3=\{j|3\le j\le n,$ and j is a multiplication of 3}
UF8	$f_1=0.5[max\{0,(1+ϵ)(1-4{(2x_1-1)}^2)\}+2x_1]x_2+\frac{2}{|J_1|}{\sum }_{jϵJ_1}(x_j-2x_{2}sin{(2\pi x_1+\frac{j\pi }{n})}^2)$ $f_2=0.5[max\{0,(1+ϵ)(1-4{(2x_1-1)}^2)\}+2x_1]x_2+\frac{2}{|J_2|}{\sum }_{jϵJ_2}(x_j-2x_{2}sin{(2\pi x_1+\frac{j\pi }{n})}^2)$ $f_3=1-x_2+\frac{2}{|J_3|}{\sum }_{jϵJ_3}(x_j-2x_{2}sin{(2\pi x_1+\frac{j\pi }{n})}^2)$ $J_1=\{j|3\le j\le n,$ and j-1 is a multiplication of 3}, $J_2=\{j|3\le j\le n,$ and j-2 is a multiplication of 3}, $J_3=\{j|3\le j\le n,$ and j is a multiplication of 3}, $ϵ=0.1$
UF9	$f_1=cos(0.5x_1\pi )cos(0.5x_2\pi )+\frac{2}{|J_1|}{\sum }_{jϵJ_1}[4y_j^2-cos(8\pi y_j)+1]$ $f_2=cos(0.5x_1\pi )sin(0.5x_2\pi )+\frac{2}{|J_2|}{\sum }_{jϵJ_2}[4y_j^2-cos(8\pi y_j)+1]$ $f_3=sin(0.5x_2\pi )+\frac{2}{|J_3|}{\sum }_{jϵJ_3}[4y_j^2-cos(8\pi y_j)+1]$ $J_1=\{j|3\le j\le n,$ and j-1 is a multiplication of 3}, $J_2=\{j|3\le j\le n,$ and j-2 is a multiplication of 3}, $J_3=\{j|3\le j\le n,$ and j is a multiplication of 3},

Inverted generational distance (IGD) was used for measuring convergence. The mathematical formulation of generational distance and IGD is the same. IGD is formulated as follows [4]:

$$IGD=\frac{\sqrt{{\sum }_{i=1}^n{d}_i^2}}{n}$$

(24)

where n shows the number of true Pareto optimal solution. $d_i$ describes the Euclidean distance between the value that is closest to the obtained Pareto front and the ith value of true Pareto front. In IGD, the Euclidean distance for every solution is calculated with respect to its closest Pareto optimal solution found in the search space.

5.2. Comparison of Algorithms

True Pareto front obtained by LMOGWO was compared with MOGWO and MOPSO using six bi-objective and three tri-objective benchmark functions. LMOGWO outperformed MOGWO and MOPSO. The obtained solutions of LMOGWO are closer to the Pareto optimal solutions. However, the obtained solution with UF2 is far away from the Pareto front. LMOGWO only performed poorly for UF2. LMOGWO performed better than other algorithms because of its leadership hierarchy and step size towards an optimal solution. LMOGWO performed well for UF1, UF5 and UF8. The obtained value of LMOGWO for these functions is much better than other algorithms.

5.3. Discussion of Results

For problem UF1, LMOGWO gave very good results as compared to the other two algorithms. The obtained results of LMOGWO are closer to the Pareto optimal values. The results of the algorithm for UF2 show that the obtained solution of LMOGWO is not closer to the Pareto obtained solution. LMOGWO, MOGWO, and MOPSO performed equally for test functions UF3, UF4, UF6, UF7 and UF9. Some of the obtained solutions are closer to the Pareto front and others are far away from the Pareto optimal solutions. LMOGWO outperformed MOGWO and MOPSO for benchmark functions UF5 and UF8. The obtained values are closer to the true Pareto front. The results of MOGWO and MOPSO for UF1, UF5 and UF8 are not as bad; a few of the obtained solutions are closer to the Pareto front. However, most of the solutions are not good. The proposed algorithm performed well for both bi-objective and tri-objective functions. LMOGWO updates the position of three leaders (alpha, beta and delta) and takes long steps towards optimal value. The convergence of LMOGWO can be observed in Figure 6.

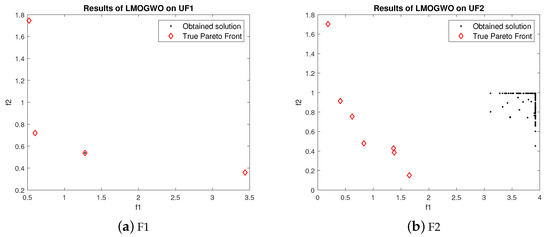
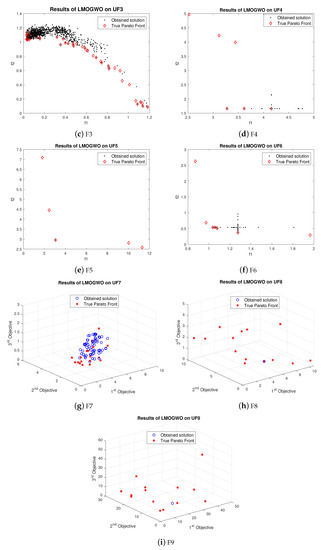
Figure 6. Results of LMOGWO.

For UF1, the few obtained results with MOGWO are nearer to the Pareto front. However, most obtained values are far away from Pareto optimal values. The obtained results of MOGWO are better than the proposed algorithm. Most of the obtained values are closer to the true Pareto front. However, some results are not nearer to the Pareto front. The performance of MOGWO and MOPSO for UF2 is somewhat similar. The performances of MOGWO and MOPSO are stabler than the proposed algorithm. LMOGWO, MOGWO, and MOPSO performed equally for test functions UF3, UF4, UF6, UF7 and UF9. Some of the obtained solutions are closer to the Pareto front and others are far away from the Pareto optimal solutions. The results of MOGWO is not as bad, few of the obtained solutions are closer to the Pareto front. However, most of the solutions are not good. MOGWO update the position according to the position of leader. MOGWO handles three leaders (alpha, beta and delta). Leader wolves guide other wolves to hunt a prey. The convergence of MOGWO can be observed in Figure 7.

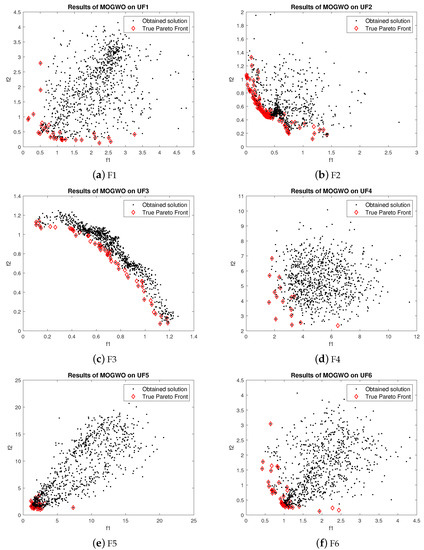
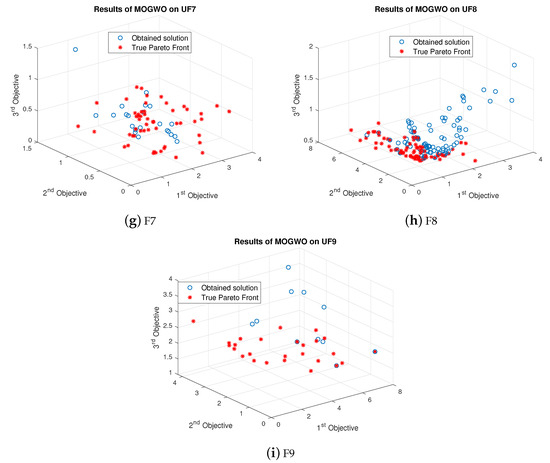
Figure 7. Results of MOGWO.

For UF1, the few obtained results with MOPSO are nearer to the Pareto front. However, most of the obtained values are far away from Pareto optimal solutions. The obtained results of MOGWO and MOPSO for UF2 are somewhat similar. However, MOGWO and MOPSO outperformed LMOGWO for test function UF2. The performances of MOGWO and MOPSO are stabler than the proposed algorithm. LMOGWO, MOGWO, and MOPSO performed equally for test functions UF3, UF4, UF6, UF7 and UF9. Some of the obtained solutions are closer to the Pareto front and others are far away from the Pareto optimal solutions. LMOGWO outperformed MOPSO for benchmark functions UF5 and UF8. The results of MOPSO are not as bad; few of the obtained solutions are closer to the Pareto front. However, most of the solutions are not good. MOPSO only updates the position of a particle. MOPSO optimizes the problem globally. MOPSO finds and updates the personal best and global best values. The convergence of MOPSO can be observed in Figure 8.

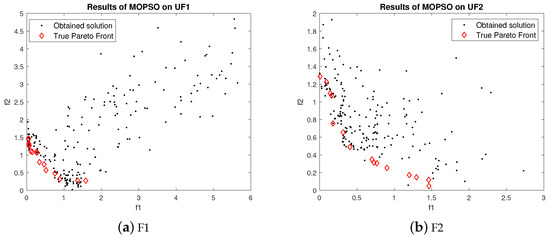
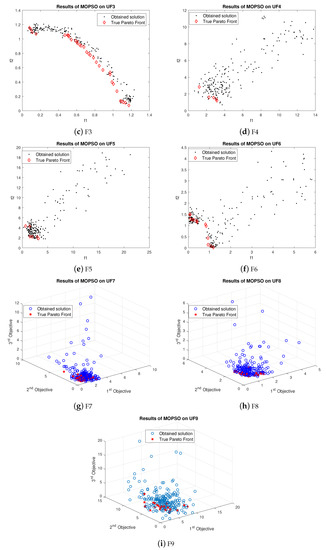
Figure 8. Results of MOPSO.

LMOGWO algorithm gives very reasonable results on both bi-objective and tri-objective benchmark tests. High convergence of LMOGWO shows the attacking behavior of GWs and updating the positions of omega wolves according to the positions of other wolves when |A|<1. The step size is taken using levy flight through Mantegna’s algorithm. After half of the iterations, alpha, beta, and delta provide the most promising region found in search space. A and C are very important parameters. A is controlling parameter and C is a stochastic parameter.

The results of MOPSO show that it only updates the position of a particle, while LMOGWO updates three non-dominated solutions. MOGWO updates only positions of alpha, beta, and delta. However, LMOGWO also takes long jumps towards the optimal solution. The high convergence and coverage of LMOGWO are due to the leading mechanism of the GWs. Selection of three leaders and the large step towards prey assist LMOGWO to outperform. High convergence is due to the leader selecting mechanism. High coverage is because of maintenance of archive.

5.4. Parameters Setting, Comparison of Algorithms and Discussion of Results (Scenario 2)

To verify the adaptivity of the proposed algorithm, we changed the parameters as follows. The initial parameters for LMOGWO and MOGWO are given below:

• $\alpha$ = 1.0: grid inflation parameter;
• $\beta$ = 1.5: leader selection parameter; and
• nGrid = 20: number of grids per dimension.

For MOPSO, the initial parameters chosen are given below:

• $\alpha$ = 1.5: grid inflation parameter;
• $\beta$ = 3: leader selection parameter;
• nGrid = 10: number of grids per dimension;
• c1 = 1: personal learning co-efficient;
• c2 = 2: global learning co-efficient; and
• $\omega$ = 0.5.

For all experiments, 200 search agents were considered and the number of iteration was 10. LMOGWO performed better than the other two algorithms (MOGWO and MOPSO). The proposed algorithm outperformed for UF5, UF8 and UF9. However, the results of MOGWO are better than LMOGWO for UF2 and UF4. MOPSO also performed well for UF4.

For UF1, few obtained results of LMOGWO are closer to the true Pareto front. Most of the obtained results are far away from optimal values. However, the results of LMOGWO are not significant on UF2. Almost all obtained results are not close to the true Pareto front. The obtained results of LMOGWO for UF3 are average. Only a few obtained values are closer to the Pareto optimal values. For UF4, LMOGWO again performed poorly. All of the obtained values are far away from the optimal solutions. However, LMOGWO outperformed the other two algorithms (MOGWO and MOPSO) for UF5 and UF9. It performed well for one bi-objective and one tri-objective function. For UF6, UF7 and UF8, the obtained results of the proposed algorithms are neither good nor bad. Some of the obtained values are closer to the true Pareto front and others are far away.

We can conclude that the value of leader selection parameter, i.e., beta, is very important. After decreasing the value of $\beta$, the obtained results are not as good as before. However, LMOGWO outperformed MOGWO and MOPSO for UF5, UF8 and UF9. The results are given in Figure 9.

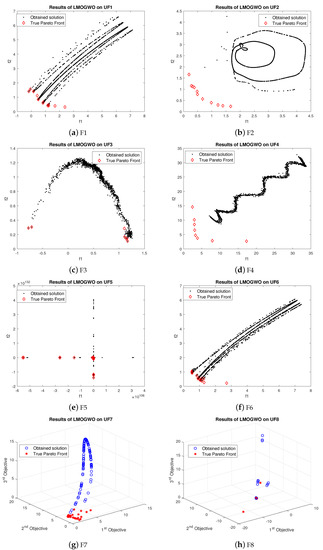
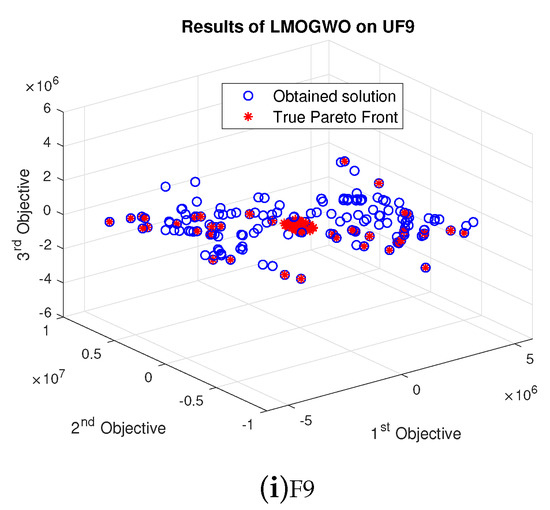
Figure 9. Results of LMOGWO for Scenario 2.

The results of MOGWO after changing parameters are shown in Figure 10. MOGWO performance is neither good nor bad. It performed poorly for only one tri-objective test function. However, the obtained results of MOGWO for all functions are not optimal. It outperformed the proposed algorithm for UF2 and UF4.

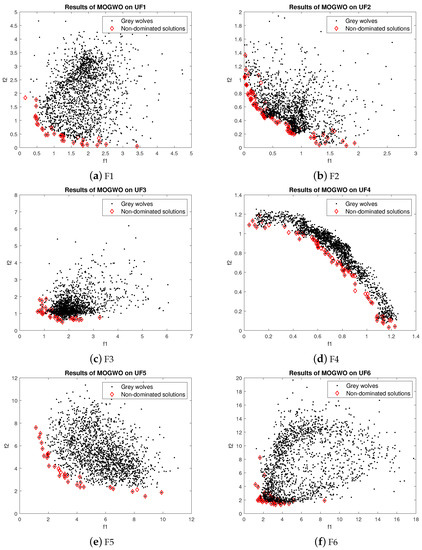
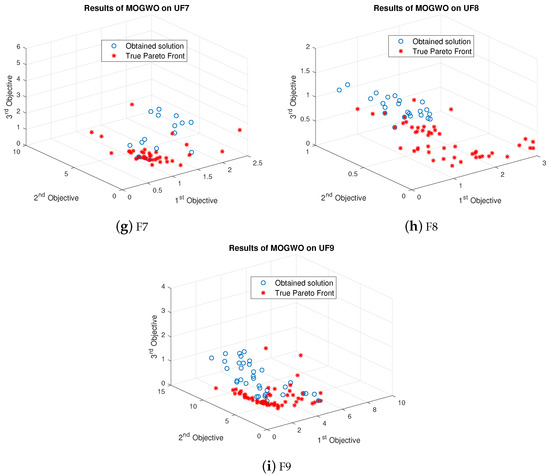
Figure 10. Results of MOGWO for Scenario 2.

For UF1, UF2, UF3, UF4, UF5, UF6, UF7 and UF9, the results of MOGWO are very similar. Few obtained values are near the Pareto optimal values, while most. values are far away from the true Pareto front. MOGWO outperformed the proposed algorithm for UF2 and UF4. However, most of its obtained values are also not close to the true Pareto front. The results of MOGWO are not good for UF8. The obtained values are scattered in the multi-objective search space. The leadership hierarchy plays an important role in MOGWO. After decreasing the value of beta and increasing value of alpha, the results are no longer the same.

The results after changing the parameters of MOPSO are discussed below and graphically shown in Figure 11. It outperformed the proposed algorithm for one bi-objective function. It also performed better than MOGWO for one tri-objective benchmark function. However, the obtained results of MOPSO are not close to the optimal value for UF2.

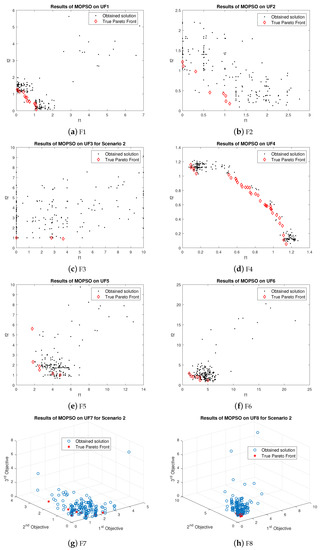
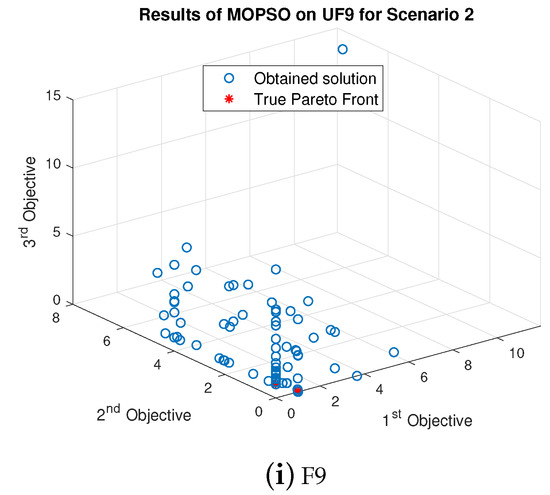
Figure 11. Results of MOPSO for Scenario 2.

For UF1, UF3, UF4, UF5, UF6, UF7, UF8 and UF9, only a few obtained results are closer to the optimal solutions. However, most of the obtained results are far away from the true Pareto front. For UF4, MOGWO outperformed the proposed algorithm as the results of LMOGWO are bad for this function. Moreover, the obtained results of MOPSO for UF8 are better than the results of MOGWO.

From extensive simulations, we can conclude that beta (leader selection parameter) is an important factor for all three algorithms. However, c1 and c2 are also important for MOPSO to perform well. The proposed algorithm outperformed MOGWO and MOPSO for UF5, UF8 and UF9, The proposed algorithm still performed better than the other two algorithms even after changing the parameters. LMOGWO outperformed for both bi-objective and tri-objective functions. However, LMOGWO can only work for the problem having four objective functions maximum because the archive becomes full quickly when there are more than four objectives. This algorithm performs well for the problem having continuous variables.

It is worth discussing here that A is the main controlling parameter. LMOGWO searches locally and exploits the search space according to the value of A. Further, the constant value of A affects the performance of proposed LMOGWO. Moreover, C is also an important parameter because it defines the distance between wolves and prey. C favors exploration and avoids local optima. C provides random values not only during initial iterations but also during final iterations.

High convergence of the proposed LMOGWO is because of the attacking and position updating strategy of GWs. After half of the iterations, the GWs start exploiting the search space according to the positions of $\alpha ,\beta ,\delta$ and $\omega$. Further, the mature convergence of the LMOGWO depends on the position updating mechanism based on the leadership hierarchy of GWs.

5.5. Bin Packing

Bin packing is used to place the VMs efficiently. Best fit strategy of bin packing is then used to optimally pack the number of VMs in PMs. The sole purpose of work done is to minimize the utilization rate of PMs. It also reduces the cost and saves the energy. However, it increases the workload of PM. It can be envisioned from the results in Figure 12 that the proposed algorithm efficiently packed the VMs into PMs. LMOGWO outperformed other two algorithms. The PM utilization rate (%) was minimized by 30% with LMOGWO, 11% with MOGWO and 10% with MOPSO. The proposed algorithm jumps towards the optimal solution. However, MOGWO moves towards the optimality slowly and there is a problem of premature convergence in MOPSO.

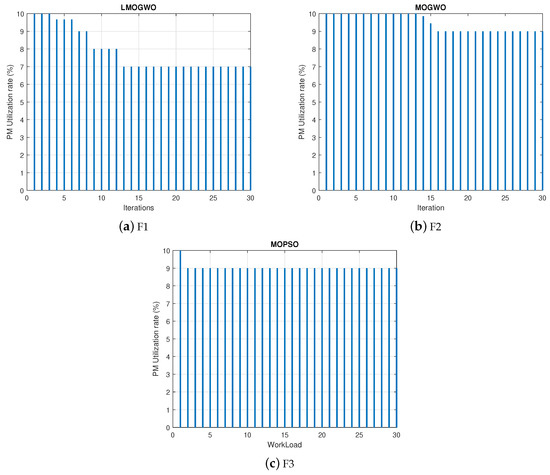
Figure 12. Results of LMOGWO, MOGWO and MOPSO using bin packing.

6. Conclusions

This paper proposes LMOGWO to solve the VM placement problem efficiently. For multi-objective optimization, two components are integrated with simple GWO. An archive is attached to save the list of non-dominant VMs. An archive is used to store and retrieve the best non-dominated VMs during the optimization process. A grid mechanism is also integrated to improve the non-dominated VMs in the archive. It mimics the leadership hierarchy of GWs. MOGWO selects the leaders ($\alpha$, $\beta$ and $\delta$) from an archive. Moreover, the step size of levy flight is attached with MOGWO to update the positions of leader wolves. $\omega$ wolves update their positions according to the leaders. All other wolves follow the guidance of the leader wolves. A mechanism is also used to maintain the archive. Research was performed to maintain the archive and provide optimal leadership mechanism. LMOGWO was then compared with simple MOGWO and MOPSO. The proposed algorithm was tested on nine standard benchmark functions. Six bi-objective test functions were used while the other three were tri-objective functions. The results show that the proposed algorithm outperformed MOGWO for UF1, UF5, UF7 and UF8. It performed better than MOPSO for UF1, UF4, UF5, UF7 and UF8 for Scenario 1. However, MOGWO and MOPSO outperformed LMOGWO for UF2. For Scenario 2, LMOGWO outperformed MOGWO and MOPSO for UF5, UF8 and UF9. However, MOGWO performed better than the proposed algorithm for UF2 and UF4. MOPSO also performed better than the proposed algorithm for UF4. Further, the PM utilization rate (%) was minimized by 30% with LMOGWO, 11% with MOGWO and 10% with MOPSO.

Future Studies

In the future, we will propose a mechanism to handle the complex objective problems (i.e., more than four objective problems). As most real-world engineering problems have multiple objective problems to be optimized. Further, we will propose more algorithms to solve VM placement problem as it is an NP-hard problem. Thus, more enhancement is required for efficient VM placement as the number of VMs is increasing rapidly.